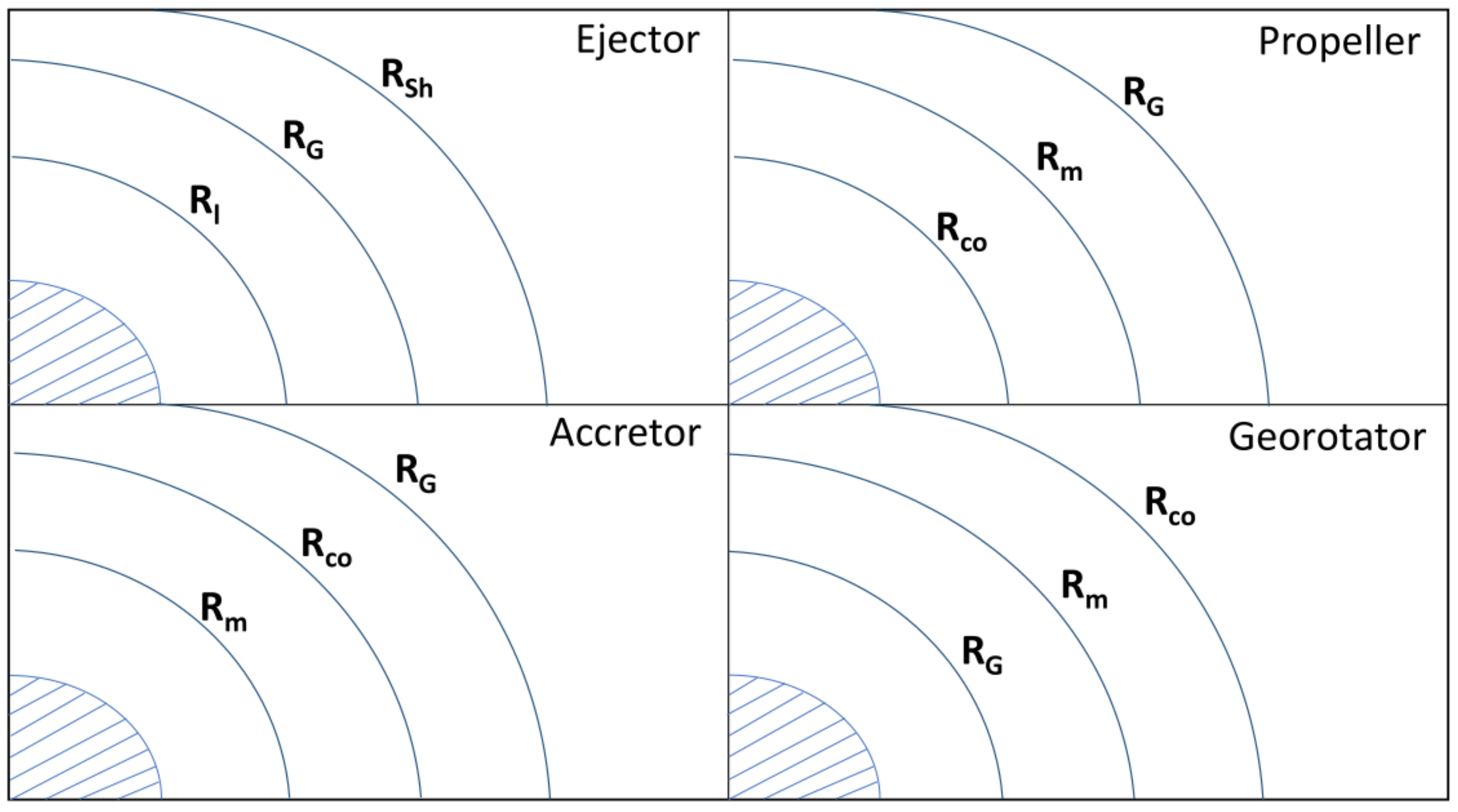
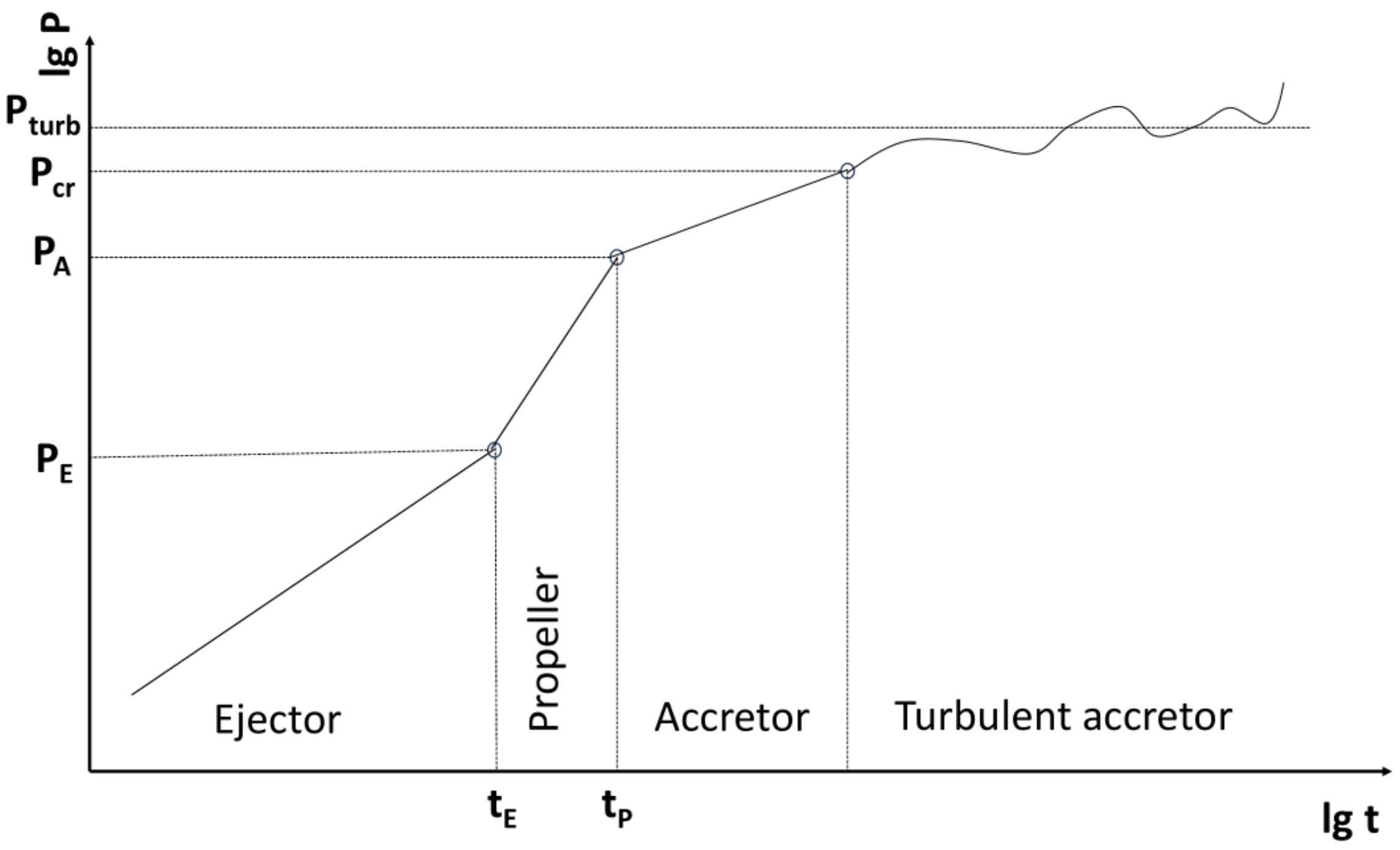
Spin Evolution of Neutron Stars
Abstract
1. Introduction
2. Fallback
3. Ejector Stage and Radio Pulsar Activity
3.1. Pulsar ‘Death Line’
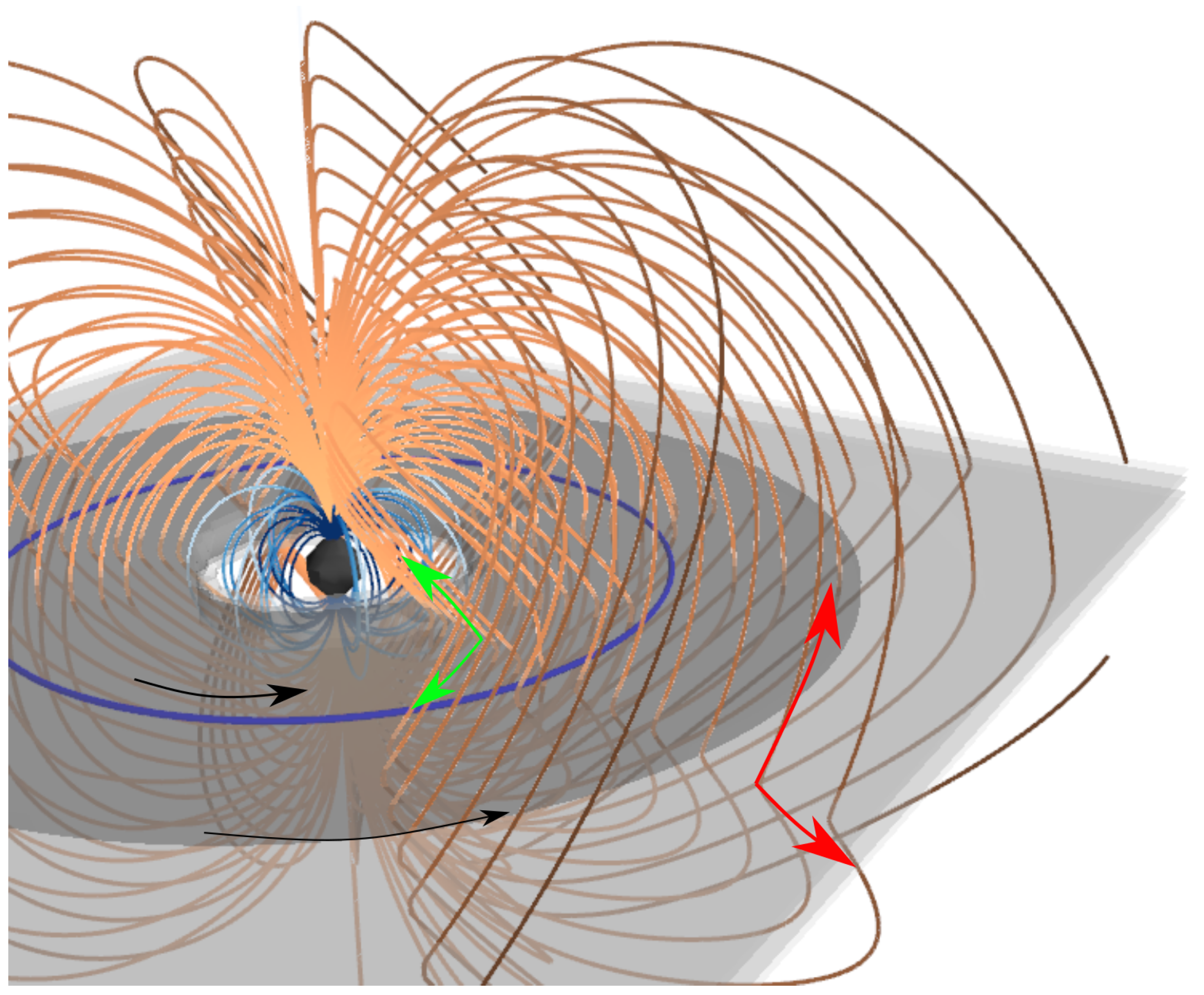
3.2. Spin-Down of a Star with Vacuum Magnetosphere
3.3. Spin-Down of a Star with Plasma-Filled Magnetosphere
3.4. Observational Verification
3.4.1. Magnetic Angle Evolution
3.4.2. Pulsar Timing Irregularities and Braking Indices
3.4.3. Isolated Neutron Stars Birthrate
4. Propeller Stage
4.1. Theory
4.2. Observations
5. Accretion
5.1. General Properties of Accretion Flows onto Magnetized NSs
5.2. Isolated Neutron Stars
5.3. Accretion in Binaries
5.3.1. Variety of NSs in Binary Systems
5.3.2. Spin-Up by an Aligned Disc
5.3.3. Spin-Up of an Inclined Dipole
5.3.4. Spin-Down Torques and Equilibrium
5.3.5. Misaligned Spin-Up Torques
5.3.6. Quasi-Spherical Accretion Regime
5.3.7. Recycled and Transitional Pulsars
5.3.8. Magnetic Field Burial by Accretion
6. Exotic and Hypothetical Stages
6.1. Georotator
6.2. Pulsating Magnetospheres and Other Exotic Regimes
7. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AINS | Accreting isolated neutron star |
| AMXP | Accreting millisecond X-ray pulsar |
| CCO | Central compact object |
| EOS | Equation of state |
| HMXB | High mass X-ray binary |
| INS | Isolated neutron star |
| ISM | Interstellar medium |
| LXMB | Low mass X-ray binary |
| MHD | Magnetohydrodynamic |
| MSP | Millisecond pulsar |
| MTD | Magnetically threaded disc |
| NS | Neutron star |
| PIC | Particle-in-cell |
| RPP | Rotation powered pulsar |
| SDI | Spin–disc interaction |
| SN | Supernova |
| SNR | Supernova remnant |
| TMSP | Transitional millisecond pulsar |
| UV | Ultra-violet |
| XRP | X-ray pulsar |
References
- Lipunov, V.M. Astrophysics of Neutron Stars; Astronomy and Astrophysics Library; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Lyutikov, M. Centrifugal barriers in magnetospheric accretion. Mon. Not. R. Astron. Soc. 2023, 520, 4315–4323. [Google Scholar] [CrossRef]
- Abolmasov, P.; Biryukov, A. Inertial oscillation modes of an inclined dipolar magnetosphere as a source of band-limited noise in X-ray pulsars. Mon. Not. R. Astron. Soc. 2020, 496, 13–18. [Google Scholar] [CrossRef]
- Igoshev, A.P.; Popov, S.B.; Hollerbach, R. Evolution of Neutron Star Magnetic Fields. Universe 2021, 7, 351. [Google Scholar] [CrossRef]
- Colgate, S.A. Neutron-Star Formation, Thermonuclear Supernovae, and Heavy-Element Reimplosion. Astrophys. J. 1971, 163, 221. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Ivanova, L.N.; Nadezhin, D.K. Nonstationary Hydrodynamical Accretion onto a Neutron Star. Sov. Astron. 1972, 16, 209. [Google Scholar]
- Chevalier, R.A. Neutron Star Accretion in a Supernova. Astrophys. J. 1989, 346, 847. [Google Scholar] [CrossRef]
- Metzger, B.D.; Beniamini, P.; Giannios, D. Effects of Fallback Accretion on Protomagnetar Outflows in Gamma-Ray Bursts and Superluminous Supernovae. Astrophys. J. 2018, 857, 95. [Google Scholar] [CrossRef]
- Muslimov, A.; Page, D. Delayed Switch-on of Pulsars. Astrophys. J. Lett. 1995, 440, L77. [Google Scholar] [CrossRef]
- Geppert, U.; Page, D.; Zannias, T. Submergence and re-diffusion of the neutron star magnetic field after the supernova. Astron. Astrophys. 1999, 345, 847–854. [Google Scholar]
- Ho, W.C.G. Evolution of a buried magnetic field in the central compact object neutron stars. Mon. Not. R. Astron. Soc. 2011, 414, 2567–2575. [Google Scholar] [CrossRef]
- Viganò, D.; Pons, J.A. Central compact objects and the hidden magnetic field scenario. Mon. Not. R. Astron. Soc. 2012, 425, 2487–2492. [Google Scholar] [CrossRef]
- Pons, J.A.; Viganò, D.; Geppert, U. Pulsar timing irregularities and the imprint of magnetic field evolution. Astron. Astrophys. 2012, 547, A9. [Google Scholar] [CrossRef][Green Version]
- Igoshev, A.P.; Elfritz, J.G.; Popov, S.B. Post-fall-back evolution of multipolar magnetic fields and radio pulsar activation. Mon. Not. R. Astron. Soc. 2016, 462, 3689–3702. [Google Scholar] [CrossRef]
- Bernal, C.G.; Lee, W.H.; Page, D. Hypercritical accretion onto a magnetized neutron star surface: A numerical approach. Rev. Mex. De Astron. Y Astrofis. 2010, 46, 309–322. [Google Scholar]
- Bernal, C.G.; Page, D.; Lee, W.H. Hypercritical Accretion onto a Newborn Neutron Star and Magnetic Field Submergence. Astrophys. J. 2013, 770, 106. [Google Scholar] [CrossRef]
- Fraija, N.; Bernal, C.G.; Morales, G.; Negreiros, R. Hypercritical accretion scenario in central compact objects accompanied with an expected neutrino burst. Phys. Rev. D 2018, 98, 083012. [Google Scholar] [CrossRef]
- Shigeyama, T.; Kashiyama, K. Repulsion of fallback matter due to central energy source in supernova. Publ. Astron. Soc. Jpn. 2018, 70, 107. [Google Scholar] [CrossRef]
- Zhong, Y.; Kashiyama, K.; Shigeyama, T.; Takasao, S. A Necessary Condition for Supernova Fallback Invading Newborn Neutron-star Magnetosphere. Astrophys. J. 2021, 917, 71. [Google Scholar] [CrossRef]
- Parfrey, K.; Spitkovsky, A.; Beloborodov, A.M. Torque Enhancement, Spin Equilibrium, and Jet Power from Disk-Induced Opening of Pulsar Magnetic Fields. Astrophys. J. 2016, 822, 33. [Google Scholar] [CrossRef]
- Wang, Z.; Chakrabarty, D.; Kaplan, D.L. A debris disk around an isolated young neutron star. Nature 2006, 440, 772–775. [Google Scholar] [CrossRef]
- Chatterjee, P.; Hernquist, L.; Narayan, R. An Accretion Model for Anomalous X-Ray Pulsars. Astrophys. J. 2000, 534, 373–379. [Google Scholar] [CrossRef]
- Jones, P.B. Interaction and ablation of fall-back discs in isolated neutron stars. Mon. Not. R. Astron. Soc. 2007, 382, 871–878. [Google Scholar] [CrossRef][Green Version]
- Benli, O.; Ertan, Ü. Long-term evolution of anomalous X-ray pulsars and soft gamma repeaters. Mon. Not. R. Astron. Soc. 2016, 457, 4114–4122. [Google Scholar] [CrossRef]
- Janka, H.T.; Wongwathanarat, A.; Kramer, M. Supernova Fallback as Origin of Neutron Star Spins and Spin-kick Alignment. Astrophys. J. 2022, 926, 9. [Google Scholar] [CrossRef]
- Popov, S.B.; Turolla, R. Initial spin periods of neutron stars in supernova remnants. Astroph. Sp. Sci. 2012, 341, 457–464. [Google Scholar] [CrossRef][Green Version]
- Fu, L.; Li, X.D. Population Synthesis of Young Isolated Neutron Stars: The Effect of Fallback Disk Accretion and Magnetic Field Evolution. Astrophys. J. 2013, 775, 124. [Google Scholar] [CrossRef]
- Caleb, M.; Heywood, I.; Rajwade, K.; Malenta, M.; Stappers, B.W.; Barr, E.; Chen, W.; Morello, V.; Sanidas, S.; van den Eijnden, J.; et al. Discovery of a radio-emitting neutron star with an ultra-long spin period of 76 s. Nat. Astron. 2022, 6, 828–836. [Google Scholar] [CrossRef]
- Hurley-Walker, N.; Zhang, X.; Bahramian, A.; McSweeney, S.J.; O’Doherty, T.N.; Hancock, P.J.; Morgan, J.S.; Anderson, G.E.; Heald, G.H.; Galvin, T.J. A radio transient with unusually slow periodic emission. Nature 2022, 601, 526–530. [Google Scholar] [CrossRef]
- Hurley-Walker, N.; Rea, N.; McSweeney, S.J.; Meyers, B.W.; Lenc, E.; Heywood, I.; Hyman, S.D.; Men, Y.P.; Clarke, T.E.; Coti Zelati, F.; et al. A long-period radio transient active for three decades. Nature 2023, 619, 487–490. [Google Scholar] [CrossRef]
- Ronchi, M.; Rea, N.; Graber, V.; Hurley-Walker, N. Long-period Pulsars as Possible Outcomes of Supernova Fallback Accretion. Astrophys. J. 2022, 934, 184. [Google Scholar] [CrossRef]
- Aguilera, D.N.; Pons, J.A.; Miralles, J.A. 2D Cooling of magnetized neutron stars. Astron. Astrophys. 2008, 486, 255–271. [Google Scholar] [CrossRef]
- Manchester, R.N.; Hobbs, G.B.; Teoh, A.; Hobbs, M. The Australia Telescope National Facility Pulsar Catalogue. Astron. J. 2005, 129, 1993–2006. [Google Scholar] [CrossRef]
- Beskin, V.S.; Chernov, S.V.; Gwinn, C.R.; Tchekhovskoy, A.A. Radio Pulsars. Space Sci. Rev. 2015, 191, 207–237. [Google Scholar] [CrossRef]
- Beskin, V.S. Radio pulsars: Already fifty years! Phys. Uspekhi 2018, 61, 353–380. [Google Scholar] [CrossRef]
- Lorimer, D.R.; Kramer, M. Handbook of Pulsar Astronomy; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Shklovskii, I.S. Possible Causes of the Secular Increase in Pulsar Periods. Sov. Astron. 1970, 13, 562. [Google Scholar]
- Beskin, V.S.; Istomin, A.Y. Pulsar death line revisited—II. ‘The death valley’. Mon. Not. R. Astron. Soc. 2022, 516, 5084–5091. [Google Scholar] [CrossRef]
- Krolik, J.H. Multipolar Magnetic Fields in Neutron Stars. Astrophys. J. Lett. 1991, 373, L69. [Google Scholar] [CrossRef]
- Kantor, E.M.; Tsygan, A.I. The Death Lines of Radio Pulsars for Dipolar and Asymmetric Magnetic Fields. Astron. Rep. 2004, 48, 1029–1036. [Google Scholar] [CrossRef][Green Version]
- Pétri, J. Multipolar electromagnetic fields around neutron stars: Exact vacuum solutions and related properties. Mon. Not. R. Astron. Soc. 2015, 450, 714–742. [Google Scholar] [CrossRef]
- Pétri, J. Multipolar electromagnetic fields around neutron stars: General-relativistic vacuum solutions. Mon. Not. R. Astron. Soc. 2017, 472, 3304–3336. [Google Scholar] [CrossRef]
- Sturrock, P.A. A Model of Pulsars. Astrophys. J. 1971, 164, 529. [Google Scholar] [CrossRef]
- Ruderman, M.A.; Sutherland, P.G. Theory of pulsars: Polar gaps, sparks, and coherent microwave radiation. Astrophys. J. 1975, 196, 51–72. [Google Scholar] [CrossRef]
- Spitkovsky, A. Electrodynamics of Pulsar Magnetospheres. In Proceedings of the Young Neutron Stars and Their Environments; Camilo, F., Gaensler, B.M., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2004; Volume 218, p. 357. [Google Scholar] [CrossRef]
- Goldreich, P.; Julian, W.H. Pulsar Electrodynamics. Astrophys. J. 1969, 157, 869. [Google Scholar] [CrossRef]
- Kou, F.F.; Tong, H. Rotational evolution of the Crab pulsar in the wind braking model. Mon. Not. R. Astron. Soc. 2015, 450, 1990–1998. [Google Scholar] [CrossRef]
- Harding, A.K.; Contopoulos, I.; Kazanas, D. Magnetar Spin-Down. Astrophys. J. Lett. 1999, 525, L125–L128. [Google Scholar] [CrossRef]
- Xu, R.X.; Qiao, G.J. Pulsar Braking Index: A Test of Emission Models? Astrophys. J. Lett. 2001, 561, L85–L88. [Google Scholar] [CrossRef]
- Contopoulos, I.; Spitkovsky, A. Revised Pulsar Spin-down. Astrophys. J. 2006, 643, 1139–1145. [Google Scholar] [CrossRef]
- Chen, K.; Ruderman, M. Pulsar Death Lines and Death Valley. Astrophys. J. 1993, 402, 264. [Google Scholar] [CrossRef]
- Muslimov, A.G.; Tsygan, A.I. General relativistic electric potential drops above pulsar polar caps. Mon. Not. R. Astron. Soc. 1992, 255, 61–70. [Google Scholar] [CrossRef]
- Zhang, B.; Harding, A.K.; Muslimov, A.G. Radio Pulsar Death Line Revisited: Is PSR J2144-3933 Anomalous? Astrophys. J. Lett. 2000, 531, L135–L138. [Google Scholar] [CrossRef]
- Faucher-Giguère, C.A.; Kaspi, V.M. Birth and Evolution of Isolated Radio Pulsars. Astrophys. J. 2006, 643, 332–355. [Google Scholar] [CrossRef]
- Rawley, L.A.; Taylor, J.H.; Davis, M.M. Period derivative and orbital eccentricity of binary pulsar 1953 + 29. Nature 1986, 319, 383. [Google Scholar] [CrossRef]
- Gullón, M.; Miralles, J.A.; Viganò, D.; Pons, J.A. Population synthesis of isolated neutron stars with magneto-rotational evolution. Mon. Not. R. Astron. Soc. 2014, 443, 1891–1899. [Google Scholar] [CrossRef]
- Graber, V.; Ronchi, M.; Pardo-Araujo, C.; Rea, N. Isolated pulsar population synthesis with simulation-based inference. arXiv 2023, arXiv:2312.14848. [Google Scholar] [CrossRef]
- Beskin, V.S.; Litvinov, P.E. Pulsar death line revisited—I. Almost vacuum gap. Mon. Not. R. Astron. Soc. 2022, 510, 2572–2582. [Google Scholar] [CrossRef]
- Spitkovsky, A. Time-dependent Force-free Pulsar Magnetospheres: Axisymmetric and Oblique Rotators. Astrophys. J. Lett. 2006, 648, L51–L54. [Google Scholar] [CrossRef]
- Beskin, V.S.; Gurevich, A.V.; Istomin, Y.N. Physics of the Pulsar Magnetosphere; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Novoselov, E.M.; Beskin, V.S.; Galishnikova, A.K.; Rashkovetskyi, M.M.; Biryukov, A.V. Orthogonal pulsars as a key test for pulsar evolution. Mon. Not. R. Astron. Soc. 2020, 494, 3899–3911. [Google Scholar] [CrossRef]
- Hewish, A.; Bell, S.J.; Pilkington, J.D.H.; Scott, P.F.; Collins, R.A. Observation of a Rapidly Pulsating Radio Source. Nature 1968, 217, 709–713. [Google Scholar] [CrossRef]
- Pacini, F. Energy Emission from a Neutron Star. Nature 1967, 216, 567–568. [Google Scholar] [CrossRef]
- Deutsch, A.J. The electromagnetic field of an idealized star in rigid rotation in vacuo. Ann. D’Astrophysique 1955, 18, 1. [Google Scholar]
- Satherley, J.C.; Gordon, C. A pedagogical review of the vacuum retarded dipole model of pulsar spin down. Publ. Astron. Soc. Aust. 2022, 39, e038. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Gunn, J.E. On the Nature of Pulsars. I. Theory. Astrophys. J. 1969, 157, 1395. [Google Scholar] [CrossRef]
- Davis, L.; Goldstein, M. Magnetic-Dipole Alignment in Pulsars. Astrophys. J. Lett. 1970, 159, L81–L86. [Google Scholar] [CrossRef]
- Good, M.L.; Ng, K.K. Electromagnetic torques, secular alignment, and spin-down of neutron stars. Astrophys. J. 1985, 299, 706–722. [Google Scholar] [CrossRef]
- Melatos, A. Radiative precession of an isolated neutron star. Mon. Not. R. Astron. Soc. 2000, 313, 217–228. [Google Scholar] [CrossRef]
- Biryukov, A.; Beskin, G.; Karpov, S. Monotonic and cyclic components of radio pulsar spin-down. Mon. Not. R. Astron. Soc. 2012, 420, 103–117. [Google Scholar] [CrossRef]
- Goldreich, P. Neutron Star Crusts and Alignment of Magnetic Axes in Pulsars. Astrophys. J. Lett. 1970, 160, L11. [Google Scholar] [CrossRef]
- Beskin, V.S.; Zheltoukhov, A.A. Anomalous torque applied to a rotating magnetized sphere in a vacuum. Phys. Uspekhi 2014, 57, 799–806. [Google Scholar] [CrossRef]
- Contopoulos, I.; Kazanas, D.; Fendt, C. The Axisymmetric Pulsar Magnetosphere. Astrophys. J. 1999, 511, 351–358. [Google Scholar] [CrossRef]
- Gruzinov, A. Power of an Axisymmetric Pulsar. Phys. Rev. Lett. 2005, 94, 021101. [Google Scholar] [CrossRef]
- McKinney, J.C. Relativistic force-free electrodynamic simulations of neutron star magnetospheres. Mon. Not. R. Astron. Soc. 2006, 368, L30–L34. [Google Scholar] [CrossRef]
- Timokhin, A.N. On the force-free magnetosphere of an aligned rotator. Mon. Not. R. Astron. Soc. 2006, 368, 1055–1072. [Google Scholar] [CrossRef]
- Parfrey, K.; Beloborodov, A.M.; Hui, L. Introducing PHAEDRA: A new spectral code for simulations of relativistic magnetospheres. Mon. Not. R. Astron. Soc. 2012, 423, 1416–1436. [Google Scholar] [CrossRef]
- Kalapotharakos, C.; Contopoulos, I. Three-dimensional numerical simulations of the pulsar magnetosphere: Preliminary results. Astron. Astrophys. 2009, 496, 495–502. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Spitkovsky, A.; Li, J.G. Time-dependent 3D magnetohydrodynamic pulsar magnetospheres: Oblique rotators. Mon. Not. R. Astron. Soc. 2013, 435, L1–L5. [Google Scholar] [CrossRef]
- Pétri, J. The pulsar force-free magnetosphere linked to its striped wind: Time-dependent pseudo-spectral simulations. Mon. Not. R. Astron. Soc. 2012, 424, 605–619. [Google Scholar] [CrossRef]
- Philippov, A.; Tchekhovskoy, A.; Li, J.G. Time evolution of pulsar obliquity angle from 3D simulations of magnetospheres. Mon. Not. R. Astron. Soc. 2014, 441, 1879–1887. [Google Scholar] [CrossRef]
- Philippov, A.A.; Spitkovsky, A.; Cerutti, B. Ab Initio Pulsar Magnetosphere: Three-dimensional Particle-in-cell Simulations of Oblique Pulsars. Astrophys. J. Lett. 2015, 801, L19. [Google Scholar] [CrossRef]
- Pétri, J. Electrodynamics and Radiation from Rotating Neutron Star Magnetospheres. Universe 2020, 6, 15. [Google Scholar] [CrossRef]
- Beskin, V.S.; Gurevich, A.V.; Istomin, I.N. Spin-Down of Pulsars by the Current—Comparison of Theory with Observations. Astroph. Sp. Sci. 1984, 102, 301–326. [Google Scholar] [CrossRef]
- Beskin, V.S.; Nokhrina, E.E. On the role of the current loss in radio pulsar evolution. Astroph. Sp. Sci. 2007, 308, 569–573. [Google Scholar] [CrossRef][Green Version]
- Beskin, V.S.; Istomin, Y.N.; Philippov, A.A. Radio pulsars: The search for truth. Phys. Uspekhi 2013, 56, 164–179. [Google Scholar] [CrossRef]
- Rankin, J.M. Toward an Empirical Theory of Pulsar Emission. IV. Geometry of the Core Emission Region. Astrophys. J. 1990, 352, 247. [Google Scholar] [CrossRef]
- Tauris, T.M.; Manchester, R.N. On the Evolution of Pulsar Beams. Mon. Not. R. Astron. Soc. 1998, 298, 625–636. [Google Scholar] [CrossRef]
- Weltevrede, P.; Johnston, S. The population of pulsars with interpulses and the implications for beam evolution. Mon. Not. R. Astron. Soc. 2008, 387, 1755–1760. [Google Scholar] [CrossRef]
- Young, M.D.T.; Chan, L.S.; Burman, R.R.; Blair, D.G. Pulsar magnetic alignment and the pulsewidth-age relation. Mon. Not. R. Astron. Soc. 2010, 402, 1317–1329. [Google Scholar] [CrossRef]
- Lyne, A.; Graham-Smith, F.; Weltevrede, P.; Jordan, C.; Stappers, B.; Bassa, C.; Kramer, M. Evolution of the Magnetic Field Structure of the Crab Pulsar. Science 2013, 342, 598–601. [Google Scholar] [CrossRef] [PubMed]
- Arzamasskiy, L.; Philippov, A.; Tchekhovskoy, A. Evolution of non-spherical pulsars with plasma-filled magnetospheres. Mon. Not. R. Astron. Soc. 2015, 453, 3540–3553. [Google Scholar] [CrossRef][Green Version]
- Espinoza, C.M.; Lyne, A.G.; Stappers, B.W.; Kramer, M. A study of 315 glitches in the rotation of 102 pulsars. Mon. Not. R. Astron. Soc. 2011, 414, 1679–1704. [Google Scholar] [CrossRef]
- Haskell, B.; Melatos, A. Models of pulsar glitches. Int. J. Mod. Phys. D 2015, 24, 1530008. [Google Scholar] [CrossRef]
- Zhou, S.; Gügercinoğlu, E.; Yuan, J.; Ge, M.; Yu, C. Pulsar Glitches: A Review. Universe 2022, 8, 641. [Google Scholar] [CrossRef]
- Boynton, P.E.; Groth, E.J.; Hutchinson, D.P.; Nanos, G.P., Jr.; Partridge, R.B.; Wilkinson, D.T. Optical Timing of the Crab Pulsar, NP 0532. Astrophys. J. 1972, 175, 217. [Google Scholar] [CrossRef]
- Cordes, J.M.; Helfand, D.J. Pulsar timing. III—Timing noise of 50 pulsars. Astrophys. J. 1980, 239, 640–650. [Google Scholar] [CrossRef]
- D’Alessandro, F.; McCulloch, P.M.; Hamilton, P.A.; Deshpande, A.A. The timing noise of 45 southern pulsars. Mon. Not. R. Astron. Soc. 1995, 277, 1033–1046. [Google Scholar] [CrossRef]
- Urama, J.O.; Link, B.; Weisberg, J.M. A strong correlation in radio pulsars with implications for torque variations. Mon. Not. R. Astron. Soc. 2006, 370, L76–L79. [Google Scholar] [CrossRef]
- Hobbs, G.; Lyne, A.G.; Kramer, M. An analysis of the timing irregularities for 366 pulsars. Mon. Not. R. Astron. Soc. 2010, 402, 1027–1048. [Google Scholar] [CrossRef]
- Nice, D.J.; Altiere, E.; Bogdanov, S.; Cordes, J.M.; Farrington, D.; Hessels, J.W.T.; Kaspi, V.M.; Lyne, A.G.; Popa, L.; Ransom, S.M.; et al. Timing and Interstellar Scattering of 35 Distant Pulsars Discovered in the PALFA Survey. Astrophys. J. 2013, 772, 50. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Nice, D.J.; Taylor, J.H.; Thorsett, S.E. Timing Behavior of 96 Radio Pulsars. Astrophys. J. 1994, 422, 671. [Google Scholar] [CrossRef]
- Ekşi, K.Y.; Andaç, I.C.; Çıkıntoğlu, S.; Gügercinoğlu, E.; Vahdat Motlagh, A.; Kızıltan, B. The Inclination Angle and Evolution of the Braking Index of Pulsars with Plasma-filled Magnetosphere: Application to the High Braking Index of PSR J1640-4631. Astrophys. J. 2016, 823, 34. [Google Scholar] [CrossRef]
- Hobbs, G.; Lyne, A.G.; Kramer, M.; Martin, C.E.; Jordan, C. Long-term timing observations of 374 pulsars. Mon. Not. R. Astron. Soc. 2004, 353, 1311–1344. [Google Scholar] [CrossRef]
- Zhang, S.N.; Xie, Y. Why Do the Braking Indices of Pulsars Span a Range of More Than 100 Millions? Astrophys. J. 2012, 761, 102. [Google Scholar] [CrossRef]
- Biryukov, A.; Beskin, G.; Karpov, S.; Chmyreva, L. Evidence of long-term cyclic evolution of radio pulsar periods. Adv. Space Res. 2007, 40, 1498–1504. [Google Scholar] [CrossRef]
- Archibald, R.F.; Gotthelf, E.V.; Ferdman, R.D.; Kaspi, V.M.; Guillot, S.; Harrison, F.A.; Keane, E.F.; Pivovaroff, M.J.; Stern, D.; Tendulkar, S.P.; et al. A High Braking Index for a Pulsar. Astrophys. J. Lett. 2016, 819, L16. [Google Scholar] [CrossRef]
- Marshall, F.E.; Guillemot, L.; Harding, A.K.; Martin, P.; Smith, D.A. A New, Low Braking Index for the LMC Pulsar B0540-69. Astrophys. J. Lett. 2016, 827, L39. [Google Scholar] [CrossRef]
- Ou, Z.W.; Tong, H.; Kou, F.F.; Ding, G.Q. Fluctuating neutron star magnetosphere: Braking indices of eight pulsars, frequency second derivatives of 222 pulsars and 15 magnetars. Mon. Not. R. Astron. Soc. 2016, 457, 3922–3933. [Google Scholar] [CrossRef]
- Igoshev, A.P.; Popov, S.B. Braking indices of young radio pulsars: Theoretical perspective. Mon. Not. R. Astron. Soc. 2020, 499, 2826–2835. [Google Scholar] [CrossRef]
- Janssen, G.H.; Stappers, B.W. 30 glitches in slow pulsars. Astron. Astrophys. 2006, 457, 611–618. [Google Scholar] [CrossRef]
- Tsang, D.; Gourgouliatos, K.N. Timing Noise in Pulsars and Magnetars and the Magnetospheric Moment of Inertia. Astrophys. J. Lett. 2013, 773, L17. [Google Scholar] [CrossRef][Green Version]
- Melatos, A.; Link, B. Pulsar timing noise from superfluid turbulence. Mon. Not. R. Astron. Soc. 2014, 437, 21–31. [Google Scholar] [CrossRef]
- Hamil, O.; Stone, J.R.; Urbanec, M.; Urbancová, G. Braking index of isolated pulsars. Phys. Rev. D 2015, 91, 063007. [Google Scholar] [CrossRef]
- Hamil, O.; Stone, N.J.; Stone, J.R. Braking index of isolated pulsars. II. A novel two-dipole model of pulsar magnetism. Phys. Rev. D 2016, 94, 063012. [Google Scholar] [CrossRef]
- Cheng, K.S. Outer magnetospheric fluctuations and pulsar timing noise. Astrophys. J. 1987, 321, 799–804. [Google Scholar] [CrossRef]
- Kramer, M.; Lyne, A.G.; O’Brien, J.T.; Jordan, C.A.; Lorimer, D.R. A Periodically Active Pulsar Giving Insight into Magnetospheric Physics. Science 2006, 312, 549–551. [Google Scholar] [CrossRef] [PubMed]
- Contopoulos, I. A note on the cyclic evolution of the pulsar magnetosphere. Astron. Astrophys. 2007, 475, 639–642. [Google Scholar] [CrossRef][Green Version]
- Lyne, A.; Hobbs, G.; Kramer, M.; Stairs, I.; Stappers, B. Switched Magnetospheric Regulation of Pulsar Spin-Down. Science 2010, 329, 408. [Google Scholar] [CrossRef] [PubMed]
- Barsukov, D.P.; Tsygan, A.I. The influence of nondipolar magnetic field and neutron star precession on braking indices of radiopulsars. Mon. Not. R. Astron. Soc. 2010, 409, 1077–1087. [Google Scholar] [CrossRef][Green Version]
- Ridley, J.P.; Lorimer, D.R. Isolated pulsar spin evolution on the diagram. Mon. Not. R. Astron. Soc. 2010, 404, 1081–1088. [Google Scholar] [CrossRef]
- Keane, E.F.; Kramer, M. On the birthrates of Galactic neutron stars. Mon. Not. R. Astron. Soc. 2008, 391, 2009–2016. [Google Scholar] [CrossRef]
- Vranešević, N.; Melrose, D.B. Pulsar current revisited. Mon. Not. R. Astron. Soc. 2011, 410, 2363–2369. [Google Scholar] [CrossRef][Green Version]
- Pires, A.M.; Motch, C.; Turolla, R.; Treves, A.; Popov, S.B. The isolated neutron star candidate 2XMM J104608.7-594306. Astron. Astrophys. 2009, 498, 233–240. [Google Scholar] [CrossRef]
- Rigoselli, M.; Mereghetti, S.; Suleimanov, V.; Potekhin, A.Y.; Turolla, R.; Taverna, R.; Pintore, F. XMM-Newton observations of PSR J0726-2612, a radio-loud XDINS. Astron. Astrophys. 2019, 627, A69. [Google Scholar] [CrossRef]
- Turolla, R. Isolated Neutron Stars: The Challenge of Simplicity. In Neutron Stars and Pulsars; Astrophysics and Space Science Library; Becker, W., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 357, p. 141. [Google Scholar] [CrossRef]
- Gotthelf, E.V.; Vasisht, G. A New View on Young Pulsars in Supernova Remnants: Slow Radio-quiet & X-ray Bright. In Proceedings of the IAU Colloquium 177: Pulsar Astronomy—2000 and Beyond; Astronomical Society of the Pacific Conference Series; Kramer, M., Wex, N., Wielebinski, R., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2000; Volume 202, p. 699. [Google Scholar] [CrossRef]
- Beniamini, P.; Hotokezaka, K.; van der Horst, A.; Kouveliotou, C. Formation rates and evolution histories of magnetars. Mon. Not. R. Astron. Soc. 2019, 487, 1426–1438. [Google Scholar] [CrossRef]
- Tammann, G.A.; Loeffler, W.; Schroeder, A. The Galactic supernova rate. Astrophys. J. Suppl. Ser. 1994, 92, 487–493. [Google Scholar] [CrossRef]
- Diehl, R.; Halloin, H.; Kretschmer, K.; Lichti, G.G.; Schönfelder, V.; Strong, A.W.; von Kienlin, A.; Wang, W.; Jean, P.; Knödlseder, J.; et al. Radioactive 26Al from massive stars in the Galaxy. Nature 2006, 439, 45–47. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, J.G.; Hohle, M.M.; Neuhäuser, R. Determination of a temporally and spatially resolved supernova rate from OB stars within 5 kpc. Astron. Nachrichten 2014, 335, 935–948. [Google Scholar] [CrossRef]
- Vranesevic, N.; Manchester, R.N.; Lorimer, D.R.; Hobbs, G.B.; Lyne, A.G.; Kramer, M.; Camilo, F.; Stairs, I.H.; Kaspi, V.M.; D’Amico, N.; et al. Pulsar Birthrates from the Parkes Multibeam Survey. Astrophys. J. Lett. 2004, 617, L139–L142. [Google Scholar] [CrossRef]
- Lorimer, D.R.; Faulkner, A.J.; Lyne, A.G.; Manchester, R.N.; Kramer, M.; McLaughlin, M.A.; Hobbs, G.; Possenti, A.; Stairs, I.H.; Camilo, F.; et al. The Parkes Multibeam Pulsar Survey—VI. Discovery and timing of 142 pulsars and a Galactic population analysis. Mon. Not. R. Astron. Soc. 2006, 372, 777–800. [Google Scholar] [CrossRef]
- Popov, S.B.; Pons, J.A.; Miralles, J.A.; Boldin, P.A.; Posselt, B. Population synthesis studies of isolated neutron stars with magnetic field decay. MNRAS 2010, 401, 2675–2686. [Google Scholar] [CrossRef]
- Kaspi, V.M. Grand unification of neutron stars. Proc. Natl. Acad. Sci. USA 2010, 107, 7147–7152. [Google Scholar] [CrossRef]
- Igoshev, A.P.; Popov, S.B. Modified pulsar current analysis: Probing magnetic field evolution. Mon. Not. R. Astron. Soc. 2014, 444, 1066–1076. [Google Scholar] [CrossRef][Green Version]
- Gullón, M.; Pons, J.A.; Miralles, J.A.; Viganò, D.; Rea, N.; Perna, R. Population synthesis of isolated neutron stars with magneto-rotational evolution—II. From radio-pulsars to magnetars. Mon. Not. R. Astron. Soc. 2015, 454, 615–625. [Google Scholar] [CrossRef]
- Shvartsman, V.F. Two generations of pulsars. Radiophys. Quantum Electron. 1970, 13, 1428–1440. [Google Scholar] [CrossRef]
- Illarionov, A.F.; Sunyaev, R.A. Why the Number of Galactic X-ray Stars Is so Small? Astron. Astrophys. 1975, 39, 185. [Google Scholar]
- Pringle, J.E.; Rees, M.J. Accretion Disc Models for Compact X-Ray Sources. Astron. Astrophys. 1972, 21, 1. [Google Scholar]
- Davidson, K.; Ostriker, J.P. Neutron-Star Accretion in a Stellar Wind: Model for a Pulsed X-Ray Source. Astrophys. J. 1973, 179, 585–598. [Google Scholar] [CrossRef]
- Davies, R.E.; Fabian, A.C.; Pringle, J.E. Spindown of neutron stars in close binary systems. Mon. Not. R. Astron. Soc. 1979, 186, 779–782. [Google Scholar] [CrossRef]
- Davies, R.E.; Pringle, J.E. Spindown of neutron stars in close binary systems—II. Mon. Not. R. Astron. Soc. 1981, 196, 209–224. [Google Scholar] [CrossRef]
- Shakura, N.I. The long-period X-ray pulsar 3U 0900-40 as a neutron star with an abnormally strong magnetic field. Sov. Astron. Lett. 1975, 1, 223–225. [Google Scholar]
- Fabian, A.C. Slowly rotating neutron stars and transient X-ray sources. Mon. Not. R. Astron. Soc. 1975, 173, 161–165. [Google Scholar] [CrossRef]
- Ikhsanov, N.R. On the duration of the subsonic propeller state of neutron stars in wind-fed mass-exchange close binary systems. Astron. Astrophys. 2001, 368, L5–L7. [Google Scholar] [CrossRef]
- Shakura, N.; Postnov, K.; Kochetkova, A.; Hjalmarsdotter, L. Theory of quasi-spherical accretion in X-ray pulsars. Mon. Not. R. Astron. Soc. 2012, 420, 216–236. [Google Scholar] [CrossRef]
- Wang, Y.M.; Robertson, J.A. ‘Propeller’ action by rotating neutron stars. Astron. Astrophys. 1985, 151, 361–371. [Google Scholar]
- Romanova, M.M.; Toropina, O.D.; Toropin, Y.M.; Lovelace, R.V.E. Magnetohydrodynamic Simulations of Accretion onto a Star in the “Propeller” Regime. Astrophys. J. 2003, 588, 400–407. [Google Scholar] [CrossRef]
- Toropin, Y.M.; Toropina, O.D.; Savelyev, V.V.; Romanova, M.M.; Chechetkin, V.M.; Lovelace, R.V.E. Spherical Bondi Accretion onto a Magnetic Dipole. Astrophys. J. 1999, 517, 906–918. [Google Scholar] [CrossRef][Green Version]
- Francischelli, G.J.; Wijers, R.A.M.J. On Fossil Disk Models of Anomalous X-Ray Pulsars. arXiv 2002, arXiv:astro-ph/0205212. [Google Scholar] [CrossRef]
- Stella, L.; White, N.E.; Rosner, R. Intermittent Stellar Wind Acceleration and the Long-Term Activity of Population I Binary Systems Containing an X-Ray Pulsar. Astrophys. J. 1986, 308, 669. [Google Scholar] [CrossRef]
- Campana, S.; Gastaldello, F.; Stella, L.; Israel, G.L.; Colpi, M.; Pizzolato, F.; Orlandini, M.; Dal Fiume, D. The Transient X-Ray Pulsar 4U 0115+63 from Quiescence to Outburst through the Centrifugal Transition. Astrophys. J. 2001, 561, 924–929. [Google Scholar] [CrossRef]
- Campana, S.; Stella, L.; Mereghetti, S.; Colpi, M.; Tavani, M.; Ricci, D.; Dal Fiume, D.; Belloni, T. Aquila X-1 from Outburst to Quiescence: The Onset of the Propeller Effect and Signs of a Turned-on Rotation-powered Pulsar. Astrophys. J. Lett. 1998, 499, L65–L68. [Google Scholar] [CrossRef]
- Campana, S.; Stella, L.; Kennea, J.A. Swift Observations of SAX J1808.4-3658: Monitoring the Return to Quiescence. Astrophys. J. Lett. 2008, 684, L99. [Google Scholar] [CrossRef][Green Version]
- Tsygankov, S.S.; Mushtukov, A.A.; Suleimanov, V.F.; Poutanen, J. Propeller effect in action in the ultraluminous accreting magnetar M82 X-2. Mon. Not. R. Astron. Soc. 2016, 457, 1101–1106. [Google Scholar] [CrossRef]
- Cui, W. Evidence for “Propeller” Effects in X-Ray Pulsars GX 1+4 and GRO J1744-28. Astrophys. J. Lett. 1997, 482, L163–L166. [Google Scholar] [CrossRef][Green Version]
- Tsygankov, S.S.; Mushtukov, A.A.; Suleimanov, V.F.; Doroshenko, V.; Abolmasov, P.K.; Lutovinov, A.A.; Poutanen, J. Stable accretion from a cold disc in highly magnetized neutron stars. Astron. Astrophys. 2017, 608, A17. [Google Scholar] [CrossRef]
- Campana, S.; Stella, L.; Mereghetti, S.; de Martino, D. A universal relation for the propeller mechanisms in magnetic rotating stars at different scales. Astron. Astrophys. 2018, 610, A46. [Google Scholar] [CrossRef]
- Lutovinov, A.A.; Tsygankov, S.S.; Karasev, D.I.; Molkov, S.V.; Doroshenko, V. GRO J1750-27: A neutron star far behind the Galactic Center switching into the propeller regime. Mon. Not. R. Astron. Soc. 2019, 485, 770–776. [Google Scholar] [CrossRef]
- De, K.; Daly, F.A.; Soria, R. Infrared spectroscopy of SWIFT J0850.8-4219: Identification of the second red supergiant X-ray binary in the Milky Way. arXiv 2023, arXiv:2309.07833. [Google Scholar] [CrossRef]
- Barcons, X.; Barret, D.; Decourchelle, A.; den Herder, J.W.; Dotani, T.; Fabian, A.C.; Fraga-Encinas, R.; Kunieda, H.; Lumb, D.; Matt, G.; et al. Athena (Advanced Telescope for High ENergy Astrophysics) Assessment Study Report for ESA Cosmic Vision 2015–2025. arXiv 2012, arXiv:1207.2745. [Google Scholar] [CrossRef]
- Bondi, H. On spherically symmetrical accretion. Mon. Not. R. Astron. Soc. 1952, 112, 195. [Google Scholar] [CrossRef]
- Edgar, R. A review of Bondi-Hoyle-Lyttleton accretion. New Astron. 2004, 48, 843–859. [Google Scholar] [CrossRef]
- Shvartsman, V.G. Ionization Zones around Neutron Stars: Hα Emission, Heating of the Interstellar Medium, and the Influence on Accretion. Sov. Astron. 1971, 14, 662. [Google Scholar]
- Shvartsman, V.F. Gamma and radio emission of neutrons stars in the state of accretion. Astrophysics 1970, 6, 56–62. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Rees, M.J.; Silk, J. Some Observable Consequences of Accretion by Defunct Pulsars. Astrophys. Lett. 1970, 6, 179. [Google Scholar]
- Blaes, O.; Rajagopal, M. The Statistics of Slow Interstellar Accretion onto Neutron Stars. Astrophys. J. 1991, 381, 210. [Google Scholar] [CrossRef]
- Blaes, O.; Madau, P. Can We Observe Accreting, Isolated Neutron Stars? Astrophys. J. 1993, 403, 690. [Google Scholar] [CrossRef]
- Madau, P.; Blaes, O. Constraints on Accreting, Isolated Neutron Stars from the ROSAT and EUVE Surveys. Astrophys. J. 1994, 423, 748. [Google Scholar] [CrossRef]
- Blaes, O.; Warren, O.; Madau, P. Accreting, Isolated Neutron Stars. III. Preheating of Infalling Gas and Cometary H II Regions. Astrophys. J. 1995, 454, 370. [Google Scholar] [CrossRef]
- Popov, S.B.; Colpi, M.; Treves, A.; Turolla, R.; Lipunov, V.M.; Prokhorov, M.E. The Neutron Star Census. Astrophys. J. 2000, 530, 896–903. [Google Scholar] [CrossRef][Green Version]
- Boldin, P.A.; Popov, S.B. The evolution of isolated neutron stars until accretion: The role of the initial magnetic field. Mon. Not. R. Astron. Soc. 2010, 407, 1090–1097. [Google Scholar] [CrossRef]
- Blondin, J.M.; Raymer, E. Hoyle-Lyttleton Accretion in Three Dimensions. Astrophys. J. 2012, 752, 30. [Google Scholar] [CrossRef]
- Toropina, O.D.; Romanova, M.M.; Toropin, Y.M.; Lovelace, R.V.E. Propagation of Magnetized Neutron Stars through the Interstellar Medium. Astrophys. J. 2001, 561, 964–979. [Google Scholar] [CrossRef]
- Toropina, O.D.; Romanova, M.M.; Lovelace, R.V.E. Bondi-Hoyle accretion on to a magnetized neutron star. Mon. Not. R. Astron. Soc. 2012, 420, 810–816. [Google Scholar] [CrossRef]
- Lipunov, V.M.; Popov, S.B. Evolution of the periods of isolated neutron stars: A spindown theorem. Astron. Rep. 1995, 39, 632–637. [Google Scholar]
- Popov, S.B.; Prokhorov, M.E.; Khoperskov, A.V.; Lipunov, V.M. Stochastic spin evolution of neutron stars. arXiv 2001, arXiv:astro-ph/0110022. [Google Scholar] [CrossRef]
- Prokhorov, M.E.; Popov, S.B.; Khoperskov, A.V. The period distribution of old accreting isolated neutron stars. Astron. Astrophys. 2002, 381, 1000–1006. [Google Scholar] [CrossRef]
- Popov, S.B.; Postnov, K.A.; Shakura, N.I. Settling accretion on to isolated neutron stars from interstellar medium. Mon. Not. R. Astron. Soc. 2015, 447, 2817–2820. [Google Scholar] [CrossRef]
- Treves, A.; Colpi, M. The observability of old isolated neutron stars. Astron. Astrophys. 1991, 241, 107. [Google Scholar]
- Manning, R.A.; Jeffries, R.D.; Willmore, A.P. Are there any isolated old neutron stars in the ROSAT Wide Field Camera survey? Mon. Not. R. Astron. Soc. 1996, 278, 577–585. [Google Scholar] [CrossRef]
- Treves, A.; Turolla, R.; Zane, S.; Colpi, M. Isolated Neutron Stars: Accretors and Coolers. Publ. Astron. Soc. Pac. 2000, 112, 297–314. [Google Scholar] [CrossRef]
- Popov, S.B.; Colpi, M.; Prokhorov, M.E.; Treves, A.; Turolla, R. The LOG N-LOG S Distributions of Accreting and Cooling Isolated Neutron Stars. Astrophys. J. Lett. 2000, 544, L53–L56. [Google Scholar] [CrossRef][Green Version]
- Turner, M.L.; Rutledge, R.E.; Letcavage, R.; Shevchuk, A.S.H.; Fox, D.B. A Limit on the Number of Isolated Neutron Stars Detected in the ROSAT All-Sky-Survey Bright Source Catalog. Astrophys. J. 2010, 714, 1424–1440. [Google Scholar] [CrossRef][Green Version]
- Sana, H.; de Mink, S.E.; de Koter, A.; Langer, N.; Evans, C.J.; Gieles, M.; Gosset, E.; Izzard, R.G.; Le Bouquin, J.B.; Schneider, F.R.N. Binary Interaction Dominates the Evolution of Massive Stars. Science 2012, 337, 444. [Google Scholar] [CrossRef] [PubMed]
- Manchester, R.N. Millisecond Pulsars, their Evolution and Applications. J. Astrophys. Astron. 2017, 38, 42. [Google Scholar] [CrossRef]
- Archibald, A.M.; Stairs, I.H.; Ransom, S.M.; Kaspi, V.M.; Kondratiev, V.I.; Lorimer, D.R.; McLaughlin, M.A.; Boyles, J.; Hessels, J.W.T.; Lynch, R.; et al. A Radio Pulsar/X-ray Binary Link. Science 2009, 324, 1411. [Google Scholar] [CrossRef]
- Bahramian, A.; Degenaar, N. Low-Mass X-ray Binaries. In Handbook of X-ray and Gamma-ray Astrophysics; Bambi, C., Santangelo, A., Eds.; Springer: Singapore, 2023; p. 120. [Google Scholar] [CrossRef]
- Strohmayer, T.E.; Zhang, W.; Swank, J.H.; Smale, A.; Titarchuk, L.; Day, C.; Lee, U. Millisecond X-Ray Variability from an Accreting Neutron Star System. Astrophys. J. Lett. 1996, 469, L9. [Google Scholar] [CrossRef]
- Hasinger, G.; van der Klis, M. Two patterns of correlated X-ray timing and spectral behaviour in low-mass X-ray binaries. Astron. Astrophys. 1989, 225, 79–96. [Google Scholar]
- Méndez, M.; Belloni, T. Is there a link between the neutron-star spin and the frequency of the kilohertz quasi-periodic oscillations? Mon. Not. R. Astron. Soc. 2007, 381, 790–796. [Google Scholar] [CrossRef]
- Malacaria, C.; Jenke, P.; Roberts, O.J.; Wilson-Hodge, C.A.; Cleveland, W.H.; Mailyan, B.; on behalf of the GBM Accreting Pulsars Program Team. The Ups and Downs of Accreting X-Ray Pulsars: Decade-long Observations with the Fermi Gamma-Ray Burst Monitor. Astrophys. J. 2020, 896, 90. [Google Scholar] [CrossRef]
- Raguzova, N.V.; Popov, S.B. Be X-ray binaries and candidates. Astron. Astrophys. Trans. 2005, 24, 151–185. [Google Scholar] [CrossRef]
- Reig, P. Be/X-ray binaries. Astroph. Sp. Sci. 2011, 332, 1–29. [Google Scholar] [CrossRef]
- Corbet, R.H.D. Be/neutron star binaries: A relationship between orbital period and neutron star spin period. Astron. Astrophys. 1984, 141, 91–93. [Google Scholar]
- Kretschmar, P.; El Mellah, I.; Martínez-Núñez, S.; Fürst, F.; Grinberg, V.; Sander, A.A.C.; van den Eijnden, J.; Degenaar, N.; Maíz Apellániz, J.; Jiménez Esteban, F.; et al. Revisiting the archetypical wind accretor Vela X-1 in depth. Case study of a well-known X-ray binary and the limits of our knowledge. Astron. Astrophys. 2021, 652, A95. [Google Scholar] [CrossRef]
- Lai, D. Theory of Disk Accretion onto Magnetic Stars. Eur. Phys. J. Web Conf. 2014, 64, 01001. [Google Scholar] [CrossRef]
- Ghosh, P.; Lamb, F.K. Accretion by rotating magnetic neutron stars. III. Accretion torques and period changes in pulsating X-ray sources. Astrophys. J. 1979, 234, 296–316. [Google Scholar] [CrossRef]
- Wang, Y.M. On the Torque Exerted by a Magnetically Threaded Accretion Disk. Astrophys. J. Lett. 1995, 449, L153. [Google Scholar] [CrossRef]
- Shakura, N.I.; Sunyaev, R.A. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 24, 337–355. [Google Scholar]
- Shi, C.S.; Zhang, S.N.; Li, X.D. Super Strong Magnetic Fields of Neutron Stars in Be X-Ray Binaries Estimated with New Torque and Magnetosphere Models. Astrophys. J. 2015, 813, 91. [Google Scholar] [CrossRef]
- Doroshenko, V.; Poutanen, J.; Tsygankov, S.S.; Suleimanov, V.F.; Bachetti, M.; Caiazzo, I.; Costa, E.; Di Marco, A.; Heyl, J.; La Monaca, F.; et al. Determination of X-ray pulsar geometry with IXPE polarimetry. Nat. Astron. 2022, 6, 1433–1443. [Google Scholar] [CrossRef]
- Johnson, T.J.; Venter, C.; Harding, A.K.; Guillemot, L.; Smith, D.A.; Kramer, M.; Çelik, Ö.; den Hartog, P.R.; Ferrara, E.C.; Hou, X.; et al. Constraints on the Emission Geometries and Spin Evolution of Gamma-Ray Millisecond Pulsars. Astrophys. J. Suppl. Ser. 2014, 213, 6. [Google Scholar] [CrossRef][Green Version]
- Bozzo, E.; Ascenzi, S.; Ducci, L.; Papitto, A.; Burderi, L.; Stella, L. Magnetospheric radius of an inclined rotator in the magnetically threaded disk model. Astron. Astrophys. 2018, 617, A126. [Google Scholar] [CrossRef]
- Wang, Y.M. Torque Exerted on an Oblique Rotator by a Magnetically Threaded Accretion Disk. Astrophys. J. Lett. 1997, 475, L135–L137. [Google Scholar] [CrossRef][Green Version]
- Aly, J.J.; Kuijpers, J. Flaring interactions between accretion disk and neutron star magnetosphere. Astron. Astrophys. 1990, 227, 473–482. [Google Scholar]
- Matt, S.; Pudritz, R.E. Accretion-powered Stellar Winds as a Solution to the Stellar Angular Momentum Problem. Astrophys. J. Lett. 2005, 632, L135–L138. [Google Scholar] [CrossRef]
- Romanova, M.M.; Ustyugova, G.V.; Koldoba, A.V.; Lovelace, R.V.E. Warps, bending and density waves excited by rotating magnetized stars: Results of global 3D MHD simulations. Mon. Not. R. Astron. Soc. 2013, 430, 699–724. [Google Scholar] [CrossRef]
- Zanni, C.; Ferreira, J. MHD simulations of accretion onto a dipolar magnetosphere. II. Magnetospheric ejections and stellar spin-down. Astron. Astrophys. 2013, 550, A99. [Google Scholar] [CrossRef]
- Ireland, L.G.; Matt, S.P.; Zanni, C. Magnetic Braking of Accreting T Tauri Stars II: Torque Formulation Spanning Spin-up and Spin-down Regimes. Astrophys. J. 2022, 929, 65. [Google Scholar] [CrossRef]
- Parfrey, K.; Tchekhovskoy, A. Accreting Neutron Stars in 3D GRMHD Simulations: Jets, Magnetic Polarity, and the Interchange Slingshot. arXiv 2023, arXiv:2311.04291. [Google Scholar] [CrossRef]
- Das, P.; Porth, O. Three-dimensional GRMHD simulations of neutron star jets. arXiv 2023, arXiv:2311.05301. [Google Scholar] [CrossRef]
- Chashkina, A.; Popov, S.B. Magnetic field estimates for accreting neutron stars in massive binary systems and models of magnetic field decay. New Astron. 2012, 17, 594–602. [Google Scholar] [CrossRef]
- Vasilopoulos, G.; Petropoulou, M.; Koliopanos, F.; Ray, P.S.; Bailyn, C.B.; Haberl, F.; Gendreau, K. NGC 300 ULX1: Spin evolution, super-Eddington accretion, and outflows. Mon. Not. R. Astron. Soc. 2019, 488, 5225–5231. [Google Scholar] [CrossRef]
- Bildsten, L.; Chakrabarty, D.; Chiu, J.; Finger, M.H.; Koh, D.T.; Nelson, R.W.; Prince, T.A.; Rubin, B.C.; Scott, D.M.; Stollberg, M.; et al. Observations of Accreting Pulsars. Astrophys. J. Suppl. Ser. 1997, 113, 367–408. [Google Scholar] [CrossRef]
- Parmar, A.N.; White, N.E.; Stella, L.; Izzo, C.; Ferri, P. The Transient 42 Second X-Ray Pulsar EXO 2030+375. I. The Discovery and the Luminosity Dependence of the Pulse Period Variations. Astrophys. J. 1989, 338, 359. [Google Scholar] [CrossRef]
- Kluźniak, W.; Rappaport, S. Magnetically Torqued Thin Accretion Disks. Astrophys. J. 2007, 671, 1990–2005. [Google Scholar] [CrossRef]
- Wang, C.; Lai, D.; Han, J.L. Neutron Star Kicks in Isolated and Binary Pulsars: Observational Constraints and Implications for Kick Mechanisms. Astrophys. J. 2006, 639, 1007–1017. [Google Scholar] [CrossRef]
- Wang, Y.M. Spin-reversed accretion as the cause of intermittent spindown in slowX-ray pulsars. Astron. Astrophys. 1981, 102, 36–44. [Google Scholar]
- El Mellah, I.; Sundqvist, J.O.; Keppens, R. Accretion from a clumpy massive-star wind in supergiant X-ray binaries. Mon. Not. R. Astron. Soc. 2018, 475, 3240–3252. [Google Scholar] [CrossRef]
- Biryukov, A.; Abolmasov, P. Magnetic angle evolution in accreting neutron stars. Mon. Not. R. Astron. Soc. 2021, 505, 1775–1786. [Google Scholar] [CrossRef]
- Kato, S.; Yoshizawa, A. A Steady Hydrodynamical Turbulence in Differentially Rotating Disks. Publ. Astron. Soc. Jpn. 1997, 49, 213–220. [Google Scholar] [CrossRef]
- González-Galán, A.; Kuulkers, E.; Kretschmar, P.; Larsson, S.; Postnov, K.; Kochetkova, A.; Finger, M.H. Spin period evolution of GX 1+4. Astron. Astrophys. 2012, 537, A66. [Google Scholar] [CrossRef]
- Hessels, J.W.T.; Ransom, S.M.; Stairs, I.H.; Freire, P.C.C.; Kaspi, V.M.; Camilo, F. A Radio Pulsar Spinning at 716 Hz. Science 2006, 311, 1901–1904. [Google Scholar] [CrossRef]
- Patruno, A.; Haskell, B.; Andersson, N. The Spin Distribution of Fast-spinning Neutron Stars in Low-mass X-Ray Binaries: Evidence for Two Subpopulations. Astrophys. J. 2017, 850, 106. [Google Scholar] [CrossRef]
- Bildsten, L. Gravitational Radiation and Rotation of Accreting Neutron Stars. Astrophys. J. Lett. 1998, 501, L89–L93. [Google Scholar] [CrossRef]
- Owen, B.J.; Lindblom, L.; Cutler, C.; Schutz, B.F.; Vecchio, A.; Andersson, N. Gravitational waves from hot young rapidly rotating neutron stars. Phys. Rev. D 1998, 58, 084020. [Google Scholar] [CrossRef]
- Patruno, A.; Haskell, B.; D’Angelo, C. Gravitational Waves and the Maximum Spin Frequency of Neutron Stars. Astrophys. J. 2012, 746, 9. [Google Scholar] [CrossRef]
- Tauris, T.M. Spin-Down of Radio Millisecond Pulsars at Genesis. Science 2012, 335, 561. [Google Scholar] [CrossRef]
- Patruno, A.; Watts, A.L. Accreting Millisecond X-ray Pulsars. In Timing Neutron Stars: Pulsations, Oscillations and Explosions; Astrophysics and Space Science Library; Belloni, T.M., Méndez, M., Zhang, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; Volume 461, pp. 143–208. [Google Scholar] [CrossRef]
- Papitto, A.; de Martino, D. Transitional Millisecond Pulsars. In Millisecond Pulsars; Astrophysics and Space Science Library; Bhattacharyya, S., Papitto, A., Bhattacharya, D., Eds.; Springer: Cham, Switzerland, 2022; Volume 465, pp. 157–200. [Google Scholar] [CrossRef]
- Archibald, A.M.; Bogdanov, S.; Patruno, A.; Hessels, J.W.T.; Deller, A.T.; Bassa, C.; Janssen, G.H.; Kaspi, V.M.; Lyne, A.G.; Stappers, B.W.; et al. Accretion-powered Pulsations in an Apparently Quiescent Neutron Star Binary. Astrophys. J. 2015, 807, 62. [Google Scholar] [CrossRef]
- Veledina, A.; Nättilä, J.; Beloborodov, A.M. Pulsar Wind-heated Accretion Disk and the Origin of Modes in Transitional Millisecond Pulsar PSR J1023+0038. Astrophys. J. 2019, 884, 144. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Komberg, B.V. Pulsars and close binary systems. Sov. Astron. 1974, 18, 217. [Google Scholar]
- Melatos, A.; Phinney, E.S. Hydromagnetic Structure of a Neutron Star Accreting at Its Polar Caps. Publ. Astron. Soc. Aust. 2001, 18, 421–430. [Google Scholar] [CrossRef]
- Payne, D.J.B.; Melatos, A. Burial of the polar magnetic field of an accreting neutron star—I. Self-consistent analytic and numerical equilibria. Mon. Not. R. Astron. Soc. 2004, 351, 569–584. [Google Scholar] [CrossRef]
- Konar, S.; Bhattacharya, D. Magnetic field evolution of accreting neutron stars—II. Mon. Not. R. Astron. Soc. 1999, 303, 588–594. [Google Scholar] [CrossRef][Green Version]
- Litwin, C.; Brown, E.F.; Rosner, R. Ballooning Instability in Polar Caps of Accreting Neutron Stars. Astrophys. J. 2001, 553, 788–795. [Google Scholar] [CrossRef]
- Kulsrud, R.M.; Sunyaev, R. Anomalous diffusion across a tera-Gauss magnetic field in accreting neutron stars. J. Plasma Phys. 2020, 86, 905860602. [Google Scholar] [CrossRef]
- Payne, D.J.B.; Melatos, A. Burial of the polar magnetic field of an accreting neutron star—II. Hydromagnetic stability of axisymmetric equilibria. Mon. Not. R. Astron. Soc. 2007, 376, 609–624. [Google Scholar] [CrossRef]
- Lipunov, V.M.; Prokhorov, M.E. Ejection from Pulsars in Binary Systems. Astroph. Sp. Sci. 1984, 98, 221–236. [Google Scholar] [CrossRef]
- Popov, S.B. Scenarios for GCRT J1745-3009. arXiv 2008, arXiv:0812.4587. [Google Scholar] [CrossRef]
- Sumiyoshi, K.; Kojo, T.; Furusawa, S. Equation of state in neutron stars and supernovae. arXiv 2022, arXiv:2207.00033. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; De Grandis, D.; Igoshev, A. Magnetic Field Evolution in Neutron Star Crusts: Beyond the Hall Effect. Symmetry 2022, 14, 130. [Google Scholar] [CrossRef]
- Wang, J. Physical Environment of Accreting Neutron Stars. Adv. Astron. 2016, 2016, 3434565. [Google Scholar] [CrossRef][Green Version]
- Armitage, P.J. Lecture notes on accretion disk physics. arXiv 2022, arXiv:2201.07262. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abolmasov, P.; Biryukov, A.; Popov, S.B. Spin Evolution of Neutron Stars. Galaxies 2024, 12, 7. https://doi.org/10.3390/galaxies12010007
Abolmasov P, Biryukov A, Popov SB. Spin Evolution of Neutron Stars. Galaxies. 2024; 12(1):7. https://doi.org/10.3390/galaxies12010007
Chicago/Turabian StyleAbolmasov, Pavel, Anton Biryukov, and Sergei B. Popov. 2024. "Spin Evolution of Neutron Stars" Galaxies 12, no. 1: 7. https://doi.org/10.3390/galaxies12010007
APA StyleAbolmasov, P., Biryukov, A., & Popov, S. B. (2024). Spin Evolution of Neutron Stars. Galaxies, 12(1), 7. https://doi.org/10.3390/galaxies12010007





