Abstract
This review has two parts. The first one is devoted to the Barbier–Chalonge–Divan (BCD) spectrophotometric system, also known as the Paris spectral classification system. Although the BCD system has been applied and is still used for all stellar objects from O to F spectral types, the present account mainly concerns normal and ‘active’ B-type stars. The second part treats topics related to stellar rotation, considered one of the key phenomena determining the structure and evolution of stars. The first part is eminently observational. In contrast, the second part deals with observational aspects related to stellar rotation but also recalls some supporting or basic theoretical concepts that may help better understand the gains and shortcomings of today’s existent interpretation of stellar data.
1. Introduction
This review is dedicated to the BCD spectrophotometric system (Barbier–Chalonge–Divan; spectral classification system of Paris) applied to normal and active B-type stars and their rotation. This paper presents observational and theoretical aspects related to the topics covered.
Although the BCD spectrophotometry and rotation may seem to be disjoint themes, the main reason for their joint presentation resides in the fact that BCD spectroscopy has allowed to obtain the apparent astrophysical parameters of rapidly rotating B-type stars with and without emission lines (Be, B[e]), whose correction for the effects induced by the rapid rotation on their emitted energy distribution gave access, for the first time, to the knowledge of their true mass and evolutionary state. Be stars have been long considered to be in the phase of the secondary contraction, which favors the increase in the surface rapid rotation, an outstanding characteristic of these objects.
Among the main advantages of the BCD spectrophotometry over spectroscopy are: the deduced parameters refer to stellar layers that are on average deeper than those producing the spectral lines, and thus, they can provide a more faithful description of the central body of the object; these parameters are not affected by the interstellar extinction nor by the disturbing emissions and absorptions produced in the circumstellar media that characterize active B-type stars, such as Be and B[e] stars.
With the exception of , the first corrections that were made for effects due to rapid rotation on the stellar observational parameters were made on the astrophysical parameters () obtained with the BCD system. With them, it has been possible to demonstrate with certainty that the Be phenomenon can appear at any moment in the evolution of B-type stars in the main sequence, between the Zero-Age-Main-Sequence (ZAMS) and the Terminal-Age-Main-Sequence (TAMS). The ages of isolated individual stars obtained in this way take into account the evolutionary changes carried by the rotation. On the other hand, they are complementary to those deduced by the method of isochrones applied to normal and active stars in galactic clusters.
The BCD system is easy to use, and only requires spectra with low spectral resolution which are obtained for a short spectral domain, between the near ultraviolet and the visible. Moreover, their reduction is easily automatable. With the help of large telescopes and modern detectors, its use can be easily generalized to characterize stellar populations in other galaxies and possibly in environments of cosmological interest.
Rotation is a complex phenomenon that induces changes in the stellar geometry, determines non-uniform distributions of the surface temperature and gravity, and induces an important series of internal stellar instabilities. These instabilities produce a redistribution of the angular momentum stored by the star during its formation phases. This redistribution leads to internal and surface differential rotation, destabilizes stellar internal regions to convection and favors the creation of magnetic fields. Due to the rotation, a star evolves as having a smaller effective mass and the characteristics of the emitted spectrum depend on the angle of observation.
The amount of angular momentum, its internal distribution and the initial chemical composition, determine the observed spectral characteristics of rotating stars. It is then important to have some information on the circumstances related to stellar formation, and on the theoretical bases that help understand the internal structure of rotating stars that lead to the spectrum finally emitted by the star, particularly the Spectral-Energy-Distribution (SED) studied with the BCD system.
It is worth noting that, when speaking of active B-type stars, we consider objects where observational characteristics indicating some specific physical properties are enhanced. These properties may concern line emission, flux excess, abundance peculiarities and outbursts. The division between active and nonactive objects may be artificial. Stars that are in the pre-main sequence (pre-MS) evolution phases are currently considered in the category of active objects. They are, however, progenitors of what will probably be inactive stars, which they will remain during all of their life in the MS, or a large fraction of it. Likewise, objects apparently inactive during a considerable period of their life in the MS phase may at some point acquire the conditions to manifest particularities, as it happens with Be and B[e] stars. This means that, in the account of stellar activities, it is equally important to consider normal states that can, if certain conditions are met, evolve into properties labeled as active. Evolution in binary systems can trigger such conditions, particularly to display the Be and B[e] phenomena. Then, in this review, we deal with both types of objects, normal and active.
Section 2 is dedicated to the presentation of the BCD spectrophotometric system, and encompasses the basic definitions, its use for field and cluster B-type stars, normal, Bn, Be, helium-weak and helium-strong B-types star and B[e] stars. A short account is given on its development to date. Although the application of this system to objects with complex spectra can lead to some uncertainties, it is nevertheless a method that in many circumstances can provide valuable complements to the spectroscopic results. In this section, emphasis is placed on the need for the detailed modeling of BCD parameters, particularly the second Balmer discontinuity in Be stars, because it can carry important information about the structure of the circumstellar disc (CD) zones close to the central object, where the transfer of the angular momentum is organized to the rest of the CD.
The effects induced by the rotation on the spectra emitted by stars are discussed in Section 3. Some theoretical generalities are exposed about the possible content and distribution of the angular momentum in a dynamically stable self-gravitating object. They allow us to visualize the limits of current rotating star models and think about the improvements that could be made. Herein, some elements of the astrophysical parameter correction technique are given the for rotational effects that ultimately allow us to determine the true mass and evolutionary state of a rapidly rotating star. The mixing of the chemical composition and the redistribution in stellar interiors is shortly discussed in Section 4. In Section 5, a detailed presentation of the uncertainties that affect the parameter is given, including the effect of differential rotation on the stellar surface. The important contribution of interferometry to the study of rotating normal active and B-type stars is exposed in Section 6. Section 7 is devoted to the origin of the stellar angular momentum and its internal evolution. Debates are exposed which consider fast rotators as isolated objects, but also as possible results of the phenomenon of merging in binary systems. Observational results are shown that confirm the fast rotation of the Be stars, but not the generality of their quasi-critical rotation. The evolution of rotational velocities in single tars is presented in Section 8. In Section 9, it is shown that the evolution of B-type stars may imply phenomenological kinship between Bn and Be stars. The rotation of magnetic B-type stars is presented in Section 10 and that of B[e] stars in Section 11. A discussion and the concluding remarks are presented in Section 12.
2. B-Type Stars Observed with the BCD Spectrophotometric System
2.1. Brief Historical Account
Daniel Chalonge (1895–1977), one of the most talented students of the renowned physicist Charles Fabry (1867–1945), started studying the continuum energy distribution of stars in wavelength regions around the Balmer discontinuity during two observation missions in 1934 at the Swiss stations of Arosa and Jungfraujoch. The first results were published by Chalonge [1], Arnulf et al. [2], wherein the main interest was to measure the Balmer discontinuity (BD), the color gradients of the energy distribution on both sides of the BD and to standardize the correction for atmospheric absorption, particularly that due to the ozone at Å. Furthermore, in 1938, D. Chalonge introduced the micro-photometer, especially designed to record the spectra he was to use for their research. The calibration lamp that enabled converting the spectral micro photograms into spectrophotometric intensities was then described by Guérin [3].
The Chalonge spectrograph gave definite characteristics to the Paris stellar spectrophotometric classification system which was presented by Baillet et al. [4]. The spectra obtained with this instrument are 15 mm long from 3100 to 6100 Å, their dispersion varies from 580 Å/mm at 6000 Å, to 220 Å/mm at H and 78 Å/mm at 3100 Å. On each cm photographic plate, 20 stellar spectra were recorded with intensity of 13 and wavelength calibration spectra interspersed in the middle of the plate. All these spectra have a triangular shape due to an oscillating chassis that enables to collect a more significant number of ultraviolet photons, which are strongly absorbed by the atmosphere, and disperse over a wider surface of the plate, the blue–red photons avoiding thus over-exposures.
2.2. Basics of the BCD system
The BCD stellar classification scheme is based on three parameters: the logarithmic flux drop, D dex, of the BD; the wavelength of the midpoint of the intensity decrease, commonly presented in the reduced form Å, where is the actual wavelength of the midpoint of the discontinuity; the blue spectral gradient between 4000 and 4600 Å, m. Usually, two other gradients are also given, defined over the 4000 and a 6100 Å wavelength interval and generally determined only for stars hotter than the A0 spectral type, and defined between 3150 and 3700 Å (see the definition of these gradients in Equations (3) and (5)).
The value of D is calculated at Å, as , where is the Paschen side of the flux and is the flux in the Balmer continuum. The value of is obtained by the extrapolation of the rectified Paschen continuum to Å, for which a relation such as is used because this relation as a function of is nearly a straight line. can be the flux of a comparison star or simply the Planck function, calculated for a higher effective temperature than that expected for the studied star.
In the original application of the BCD method, the normalization of intensities is obtained with standard stars. Some of these standard stars were published in Divan [5]. The zero-scale value of the BD determinations in the BCD system was determined using the discontinuity of the B0-type supergiant Ori [6], whose D was determined in an absolute way with a laboratory black body. The values of D are determined within a typical error dex.
At first glance, Equation (1) seems to define a value perfectly independent of the interstellar extinction. However, while can be identified without proceeding to any energy distribution extrapolation, is necessarily extrapolated and thus depends on the Paschen energy distribution over a larger wavelength region, which can be affected (reddened) by the interstellar extinction. At the same time, the error on D carried by this extinction is relatively small
where is the stellar intrinsic gradient and is the gradient excess due to the interstellar extinction which, translated into the UBV Johnson–Cousins’ photometric system is [7,8]. This means that, for mag, the discontinuity D can be considered unperturbed by the interstellar extinction. Otherwise, a short iteration using Equation (2) may rapidly converge to the correct estimate of D.
Because the coalescence of the higher lines of the Balmer series shifts the apparent BD to longer wavelengths, to avoid uncertainties on the identification of the last recorded merged member, which depends on the spectral resolution power and the plate photographic optical sensitivity, Barbier and Chalonge [9] introduced the parameter . It is determined by the intersection of the pseudo-continuum that joins the overlapping wings of the coalescent Balmer lines, with the line (see Figure 1 and Figure 2). This parameter is currently given as Å. It can be determined within an error not larger than to 3 Å.
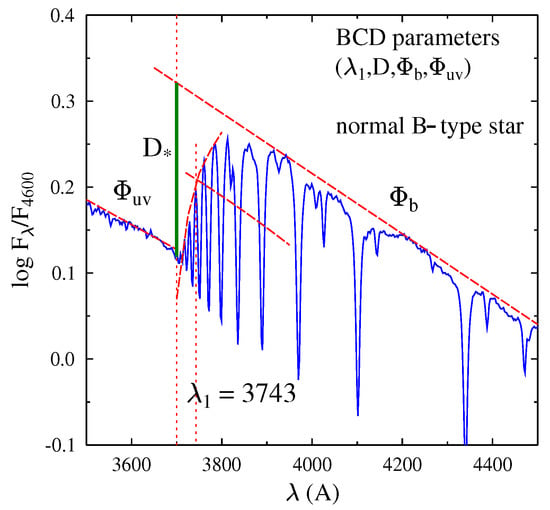
Figure 1.
Graphical explanation of the BCD spectrophotometric parameters ( determination for a B-type normal star. The photospheric (heavy full line) and the parameters are indicated. The slopes that define the gradients and are also indicated. The spectrum was obtained in the Complejo Astronómico El Leoncito (CASLEO), San Juan, Argentina. Adapted from Aidelman et al. [10].
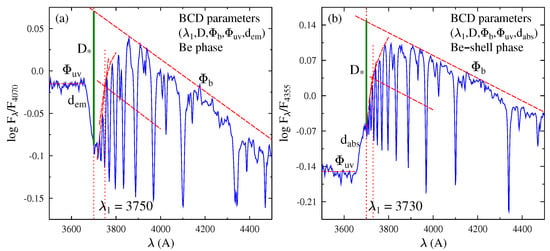
Figure 2.
Same as in Figure 1, but in (a) is shown the energy distribution of a Be star, whose second component of the BD is in emission (flux excess). In (b), the spectrum is for a Be star in shell phase, where the second component of the BD appears in absorption (flux deficiency). As for Figure 1, spectra were obtained in the Complejo Astronómico El Leoncito (CASLEO), San Juan, Argentina, with the Boller and Chivens spectrograph mounted on the J. Sahade 2.15 m telescope. Adapted from Aidelman et al. [10].
The value of D roughly ranges from 0.035 dex for O4-5 type stars to nearly 0.500 dex for A2-type stars, and then back for cooler spectral types to 0.035 dex in F9-type stars. The goes roughly from 70 Å for dwarfs to Å for supergiants, which indicates that is a well-resolved quantity useful for the stellar luminosity class classification. The unreddened gradient varies in a continuous way from m in O-type stars passing by m in early A-type stars, and attains m at spectral type F9. This gradient can, in some cases, help determine whether a given value of D corresponds to the hot or cold section of the BCD spectral classification system. In general, is affected by the interstellar reddening, and an iterated value of the color excess can eventually disentangle the right spectral classification side. Figure 1 shows the various BCD parameters determined from the spectrum of a B-type star around the BD. In Figure 2, the determination of the BCD parameters in the Be stars is shown. Specific details on the BCD parameters of Be stars are given in Section 2.5.1.
When carrying out the spectrophotometric study of the energy distribution near the Balmer discontinuity, two other parameters were obtained: the color gradient , given in m and defined for the 3200–3700 Å spectral region, and the Paschen gradient defined in two versions: the already mentioned valid for the spectral regions 4000–4800 Å, and defined over the 400–6700 Å spectral region; both are given in m. The determination of requires determining the amount of ozone absorption in the near UV spectral region. Using wavelength units in m, a color gradient is defined as [11]:
which for a black body at temperature T becomes :
where cm·deg is the radiation constant. Assuming that, for a given stellar energy distribution , can be considered being constant between two wavelengths and of the chosen continuum energy distribution, and the expression for becomes:
As the local temperature of the formation region of the Paschen continuum is close to the stellar effective temperature, from Equations (4) and (5), we note that stars with the same effective temperature but different surface gravity define a common region in the plane (). This fact was used by Barbier and Chalonge [12] and by Chalonge and Divan [13] to determine the curvilinear quadrilaterals that characterize the BCD classification system.
The spectral classification system developed in 1943 at Yerkes Observatory by W. W. Morgan, Philip Childs Keenan, and Edith Marie Kellman, widely known as the MK (or MKK) classification or the Yerkes system, retained the sequence of stellar spectral types named O, B, A, F, G, K, M. They also introduced a range of luminosity classes which indicate whether the star is a supergiant, giant, dwarf or some intermediate class. Barbier and Chalonge [12], Barbier [14] and Chalonge [15] linked the MK classification to the BCD classification based on the parameters, but only using the MK classification of stars made by Keenan and Morgan [16] themselves. To this end, the authors of the BCD classification system simply delimited the common region occupied by stars having the same MK spectral type with curves of intrinsic constant parameters. In the same way, they have drawn the ‘horizontal’ lines that separate the MK luminosity classes. The BCD authors attempted to keep inside a common strip of stars, which are all spectral types having the same MK luminosity class label assigned by Morgan and Keenan. Each spectral type obtained in the BCD system and labeled with a given MK designation thus represents a rather wide range of parameters, characterizing a curvilinear quadrilateral. The ‘vertical’ curves of constant gradients or separate the spectral types and the ‘horizontal’ curves separate the luminosity classes. Chalonge and Divan [13] is considered today as the founding publication of the BCD stellar classification system.
The largest collection of () parameters of early-type stars can be found in Chalonge and Divan [13], Underhill et al. [17], Zorec and Briot [18], Underhill et al. [17] and Zorec et al. [19].
A graphical presentation of BD calculated with the LTE model atmospheres is presented in Underhill et al. [17], and a comparison between BD determinations with the LTE and non-LTE model of non-extended atmospheres was made in Zorec [20], where it is shown that differences are of the order of some dex, which is much smaller than the measurement uncertainties. Rough estimates of using the LTE models of extended atmospheres with 12,000 K [21] show that the differences are of the same order of magnitude as given above.
2.3. Relation between the BCD Quantities and the Physical Parameters of Stars
A very useful relation implying that the parameters are the calibration of the visual absolute magnitude obtained with stars in the solar neighborhood [8]. This calibration enabled the estimation of the distance modulus ( is the apparent visual magnitude corrected for interstellar extinction) of several Galactic clusters using only a small number of cluster members. As it is known, regions with different metallicities are characterized by different absolute magnitude scales. Relations must then be determined with stars that belong to regions characterized by the specific metallicity. The above calibration of determined for the solar metallicity when used for stars in the Magellanic Clouds produces deviations of to the expected values [22,23].
In the diagram, the parameter s defined as the value of D taken at Åis considered the spectral type classification parameter in the BCD system. Chalonge and Divan [24] showed the high sensitivity of the BD to the stellar effective temperature.
As noted above, the color gradient was introduced in 1955 in the BCD system to distinguish F-type stars from B-type stars having the same () pairs. Later, for stars with spectral types later than A3, Chalonge and Divan [25] have shown the deviation , where is the curve joining the lowest points in a relation, which is strongly correlated with the [Fe/H] abundance ratio.
An observed value of or also provides an estimation of the ISM extinction as follows [7,8]
where and are the intrinsic gradients of stars corresponding to their parameters. Relations similar to those in Equation (6) must be redefined each time the gradients characterize spectral regions that are not the same as those that define the original BCD and gradients [10,26].
The great advantage of the BCD system is that it can be used for a wide range of spectral types going from mid-O-type to late F-type stars, and it relies on low-resolution spectra obtained over a relatively short wavelength range (3500–4500 Å), which automated reduction codes can treat. It might then be a valuable tool to characterize faint stars in clusters, or belonging to stellar populations in distant regions of our Galaxy, or those of other more or less neighboring galaxies, using the multi-object spectrographs and/or spectro-imaging devices of large modern telescopes.
The and calibrations for normal B-type stars were then revisited by Zorec and Briot [18] and Zorec et al. [19], respectively. The and calibrations were presented in Zorec [20] and partially in Divan and Zorec [27]. These calibrations are reproduced in Figure 3.
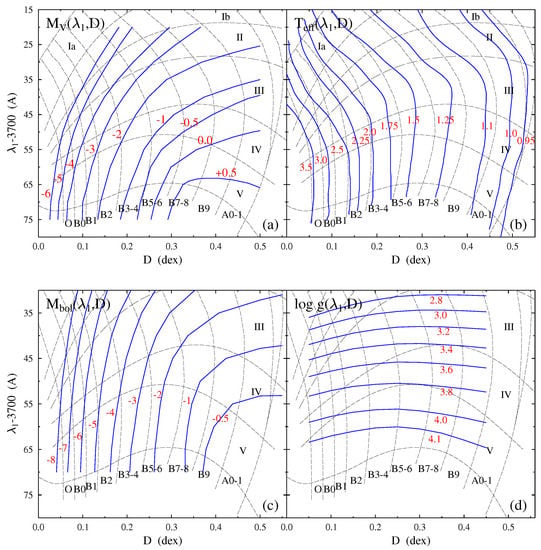
Figure 3.
Empirical calibrations of absolute magnitudes and and parameters and as a function of the BCD parameters . The horizontal black dashed lines separate the MK luminosity classes indicated on the left side of each panel. The vertical black dashed lines separate the groups of the MK spectral types specified at the bottom of each panel. The blue lines represent the calibrations of the indicated astrophysical parameters, respectively, labeled in red (in units of magnitude for and ), for effective temperatures and dex for . Figures adapted: (a) from Zorec and Briot [18], (b) from Zorec et al. [19], (c,d) from Zorec [20].
2.4. The BCD System Today
The original Challonge spectrograph has not been in service since December 1988. Other instruments have then been employed to perpetuate the BCD system today. Recently, the most frequent use of the BCD system was made in Argentina, where low-resolution spectra are obtained at the Complejo Astronómico El Leoncito (CASLEO), San Juan, with the Boller and Chivens spectrograph mounted on the J. Sahade 2.15 m telescope. The instrumental configuration consists of a 600 l/mm grating (# 80), a slit width of 250 m and a CCD detector of pixels. The spectra cover the 3500–4700 Å wavelength range with a 2-pixel of 4.53 Å, or R = 900. A standard reduction procedure is applied to the spectroscopic images using over-scan, bias- and flat-field corrections. When needed for faint stars, dark-frame subtractions are carried out. The He-Ne-Ar comparison and spectrophotometric flux standard star spectra are regularly obtained, respectively, for wavelength and flux calibrations. The low-resolution spectra for the BCD spectrophotometry are obtained with the widest possible opening of the slit, which thus minimizes light losses and enables to obtain spectra to carry out correct spectrophotometric measurements. Observations are made at the lowest possible zenith angle to minimize refraction effects due to the Earth’s atmosphere and thus to avoid other light losses as a function of wavelength. Generally, observations are reduced with the IRAF software package, and all spectra are fully corrected for atmospheric extinction and calibrated with flux standard stars regularly observed during the same run, e.g., [10,28].
Mennickent et al. [29] conducted spectroscopic observations at Cerro Tololo Inter-American Observatory, Chile (CTIO), Las Cumbres Observatory, USA (LCO), and La Silla European Southern Observatory (ESO) Chile Observatory in 2003 to produce BCD classifications of double-periodic blue variables in the Magellanic Clouds observed in the OGLE survey [30]. At CTIO, the 1.5 m telescope was used with the Cassegrain spectrograph and the Loral 1-K detector. Grating 26 tilted at 15.95o and a slit width of 2 arcsecs yielded a spectral range of 3500–5300 Å, with a resolution of 2 Å. Wavelength calibration functions with a typical standard deviation of 0.1 Å were obtained with around 30 He-Ar lines for the comparison spectra. Observations of the standard stars were used for flux calibrations. They used the NTT (ESO New Technology Telescope) with the EMMI blue arm at La Silla in medium dispersion grating mode, with grating No 4. This instrumental setup and a 1 arcsec slit yielded a spectral range of 3500–5050 Å and a resolution of 5 Å. The wavelength calibration functions have a standard deviation of 0.2–0.3 Å. The standard stars were observed with a 5-arcsec slit for flux calibrations. At LCO, the Irénée du Pont 2.5 m telescope was used with the modular spectrograph and the SiTe2 detector. The combination of grating 600 blazed at 5000 Å, with a slit width of 1.5 arcsec, yielded a spectral range of 4000–6050 Å with a resolution of 2.5 Å. About 60 He-Ar-Fe lines in the comparison spectra enabled wavelength calibration functions with a standard deviation of 0.2–0.3 Å.
Gkouvelis et al. [26] studied a large population of Be stars photometrically detected by the IPHAS survey [31] and used them as galactic structure tracers. The study was based on the analysis of the follow-up spectroscopy of stars performed during the period 2005–2012 at the 1.5 m Fred Laurence Whipple Observatory (FLWO) Tillinghast telescope on Mount Hopkins in Arizona, using the Fast Spectrograph for the Tillinghast Telescope (FAST) spectrograph [32]. The data were taken with the 300 l/mm grating and a projected slit width of 3". The data were in a wavelength range from 3500 to 7500 Å at a spectral resolution of Å. Since the BCD requires flux-calibrated spectra each night, they selected calibration spectra from the FAST archive to ensure that all spectra were calibrated with flux standards observed the same night. The calibration has been performed using standard image reduction and IRAF analysis facility routines. The authors selected sources with spectra having SNR around the Balmer discontinuity. Gkouvelis et al. [26] developed a semi-automatic procedure to obtain the fundamental parameters and distances of stars based on the BCD system.
Additional mid-resolution (2–4 Å) and high SNR (30–100 at 3700 Å) spectra of a number of stars were obtained at the Roque de Los Muchachos Observatory in La Palma, Canary Islands, Spain, to transform the resolution of spectra into that currently used in the BCD system since the astrophysical parameters of the studied stars were obtained using the calibrations established with the original BCD quantities, the details of which can be found in [26]. For this task, the telescopes and instruments used were the Isaac Newton Telescope (INT) equipped with the Intermediate Dispersion Spectrograph (IDS), and the Nordic Optical Telescope (NOT), using the Andalucía Faint Object Spectrograph and Camera (ALFOSC).
A series of B emission-line stars for BCD classification were acquired with the VLT/X- shooter instruments [33]. X-shooter is a multiwavelength medium-resolution spectrograph mounted at the Cassegrain focus of UT2 of the VLT at ESO Paranal with a mirror diameter of 8.2 m. The X-shooters’ three arms are UVB, covering 300,550 nm; VIS, covering 550–1010 nm; and NIR, covering 1000–2500 nm. The resolution depends on the chosen slit width. It ranges from R = 1890 to 9760 in the UVB, from 3180 to 18,110 in the VIS, and from 3900 to 11,490 in the NIR arm, respectively, [34]. The spectra were reduced with the ESO Recipe Flexible Execution Workbench (REFLEX) for X-shooter [35], a workflow environment to run ESO VLT pipelines. This workflow provides an interactive way to reduce VLT science data. The steps executed by the ESO X-shooter pipeline include bias subtraction, flat fielding, wavelength and flux calibration, and order merging. The authors did not give details on the spectrophotometric reliability of their spectra.
Another series of spectroscopic observations to carry out BCD classification was selected by Shokry et al. [36] from the NOAO Indo-U.S Archive of Coudé Feed Stellar Spectra [37]. The spectra of 1273 stars were carried out using the 0.9 m Coudé Feed telescope at Kitt Peak National Observatory in the spectral range of 3460–9464 Åat a low-resolution of 1.2 Å FWHM [37]. Nearly 140 B-type star spectra exist in this archive, but only 83 spectra were suitable to apply the BCD method because their spectra were either badly calibrated or were not obtained in the wavelength domain required for BCD.
2.5. Be Stars Observed with the BCD System
2.5.1. Main Characteristics of the Balmer Discontinuity in Be stars
Be phenomenon is defined in B-type stars, which are not supergiants and have shown some emission in their hydrogen Balmer line spectrum at least once [38,39]. The numerous known properties and reviewed definitions of classical Be stars are nicely summarized in Rivinius et al. [40]. They have two outstanding characteristics: they are rapid rotators and, on average, are the fastest among the non-degenerate stellar population; and they show spectral and photometric variability in all spectral domains.
It is known that supergiants can have emission components in their Balmer line spectrum due to their extended atmosphere. Moreover, they may have some emission in the hydrogen Paschen lines due to non-LTE effects. The Be phenomenon is thus conceptually associated with the capability of a star to create by its own a circumstellar disc (CD) or envelope where line emissions are formed. The Be phenomenon can be present in stars of mid-to-late O spectral type, B-type objects and early A-type stars.
Barbier and Chalonge [41] noticed that the continuum spectrum of Tau (HD 37202) presented a peculiar BD. From the confluence point of the last seen members of the Balmer line series, towards shorter wavelengths, there is a stall of the level of the energy distribution, called the ‘second BD component in absorption’ (scBD in absorption), which attains its maximum absorption at the theoretical limit of the Balmer line series ( Å). Barbier and Chalonge [41] attributed this phenomenon to a circumstellar medium having low gas pressure. During the first observation missions in the BCD system, roughly from 1941 to 1948 at the Swiss Jungfraujoch station and the Institut d’Astrophysique in Paris, where the main objective was to obtain a large enough number of stars of all classes to develop their spectrophotometric stellar classification system, Barbier, Chalonge and their colleagues incidentally observed also a series of B-type stars that displayed the above-noted behavior of the BD, but also other B-type stars where the stall corresponds to a flux excess that steadily increases from roughly 3650 Å to a maximum at 3648 Å. This flux excess was called the ‘second BD component in emission’ (scBD in emission).
Be stars with strong emission lines generally display a second BD component in emission, while those with a shell-line spectrum have a second BD component in absorption. They can lose their line and continuum emission or absorption characteristics to acquire a transitory B-normal aspect. Since the IAU Coll. No 98 [42], it is customary to call each of these spectroscopic aspects a ‘phase’ of the Be phenomenon. In Figure 2, examples of Be stars are shown with the second BD component in emission and in absorption. The total BD of Be stars is written as
where is the stellar proper or photospheric BD component, and d ( absorption; emission) is the second BD component due to the circumstellar gaseous environment. Many Be stars have undergone either B⇄Be (59 Cyg [43,44]), or B⇄Be-shell (88 Her [45]; CrB [46]) phase transitions. Some of them had shown both types of transitions as 59 Cyg [44], Cas [47]; however, Pleione (28 Tau) is the most typical example [48,49]. These transitions are detected in the behavior of the Balmer line profiles as well as by the changes of the continuum spectrum around the BD Zorec [20], de Loore et al. [50], Divan et al. [51].
One of the first interpretations of the continuum energy distributions such as those displayed in Figure 2 in terms of a circumstellar gaseous envelope was made by Barbier [52]. He used the BCD spectra of Cas (HD 5394) obtained from 1934.6 until 1943.5 [12,53,54,55,56]. The spectra obtained from 1934.6 to 1935.5, before the huge stellar outburst in 1937.5, characterized by a brightening of nearly two magnitudes, were considered to represent the star during a normal or emission-less phase. Considering a spherical circumstellar envelope, the observed BCD parameters were interpreted using the following expression for the observed radiation flux
where is the underlying photospheric stellar flux, S is the effective emitting surface of the circumstellar envelope, E is the source function of this envelope, is the non-LTE bound-free opacity of the envelope made up of hydrogen atoms, and s is a parameter defined as with being the exponential integral of the third order. With Equation (8), rarely cited, but many times re-invented in the specialized literature of Be stars, D. Barbier described the normal, Be and Be-shell phases of Cas. He concluded that these phase changes occur with opacities and . The estimated geometrical dilution factor characterizing the extent of the circumstellar envelope producing emission and absorption in the analyzed wavelength region is , which implies relatively short distances from the stellar surface.
There is a list of approximately 50 Be stars in the original BCD archives which were observed several times with the original Chalonge spectrograph, although quite irregularly until 1983. The individual observations were almost never published, except for Cas, X Per (HD 24534) [50], 59 Cyg (HD 200120) [43], HD 60848 [51] and 88 Her (HD 162732) [45,57]. The photospheric BCD () parameters for nearly 50 Be stars were published in Zorec and Briot [18], Zorec [20].
2.5.2. The Apparent HR Diagram of Be Stars
Only when there is a powerful emission in the scBD does the scBD overlap the photospheric component of the BD and makes its determination somewhat uncertain. Additionally, the Paschen continuum is perturbed by the radiation from the circumstellar medium, which introduces a change in its distribution and makes the determination of more difficult. Nevertheless, the reddening or bluing of the gradient due to the circumstellar environment can be interpreted as an increased ISM reddening because, in the short wavelength range concerned by these gradients, the circumstellar and ISM reddening laws are barely distinguished. The perturbed value of the BD can then be corrected as indicated in Equation (2) to obtain the genuine . In the remaining cases, the value of is constant within the limits of the uncertainty of its determination, even though the intensity of the line and continuum circumstellar emission may change. It is remarkable that during the ‘shell’ phases, very frequently remains almost unperturbed, and the determination of does not offer any additional difficulty. When the presence of the circumstellar medium rather strongly perturbs the determination of , the value of can be slightly uncertain as well.
Excluding the very extreme cases of the presence of strong emission, corrections on and are small or negligible. We can then consider the pair () as parameters characterizing the photosphere of the observed stellar hemisphere of the Be star. Following these considerations, Divan [58] proposed a spectral classification of Be stars in terms of ().
An in-depth study based on a new data set of BCD parameters added to the existing collection allowed Zorec [20] to present a diagram where, for the first time, it is shown with unperturbed parameters by the circumstellar medium that the Be phenomenon can appear at any moment of the stellar evolution in the main sequence (MS), as well as a little later. This diagram is shown in Figure 4, where l in Å is the value of Å, determined at dex and can be considered as the BCD continuous luminosity class parameter. Let us note that, until the 1980s, the HR diagrams of Be stars were constructed with photometric data not corrected for the effects due to the circumstellar emission or absorption. The Be phenomenon was then believed to likely appear in the late evolutionary phases of OBA stars on the MS [59]. It was thus suggested that the occurrence of the Be phenomenon could be related to the short secondary contraction period that follows the hydrogen exhaustion in the core [60], where the increase in the stellar rotational rate favors the reaching of its critical limit.
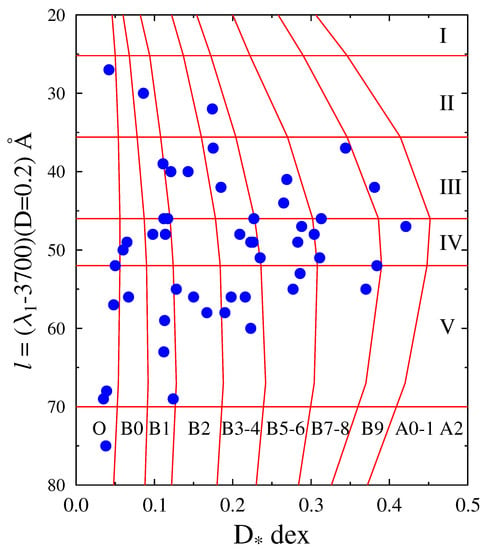
Figure 4.
BCD spectral classification diagram for Be stars in terms of luminosity class parameter l against the photospheric BD, . This is one of the first HR-type diagrams showing that the Be phenomenon can appear at whatever evolutionary phase because (l characterizes the stellar photosphere of the central star [20].
In the diagram of Figure 4, we note that Be stars earlier than the spectral type B3-4 appear over an extensive range of luminosity classes. The tendency for the remaining stars is that the phenomenon tends to be present at more evolved evolutionary stages on the MS with a later B spectral type. Later studies on the evolutionary stages of Be stars in the solar neighborhood have confirmed this result [61].
Finally, it is worth noting that the () or () parameters reflect the photospheric characteristics of the stellar hemisphere distorted by rotation and projected towards the observer. They are then considered as apparent parameters that need to be corrected for the effects induced by the rapid rotation to obtain a more realistic view of the real physical properties and evolutionary status of Be stars.
2.5.3. Correlations of the BCD Parameters with the Emission Characteristics of Be Stars
It has been known for a long time that one of the main characteristics of Be stars is their line and continuum variations [62,63,64]. As much as it concerns, the variations in the continuum spectrum have very different time scales. Among them, long-term variations deserved attention in the BCD system because they have a clear impact on the values of the gradient (or ) and on the scBD (see Figure 5).
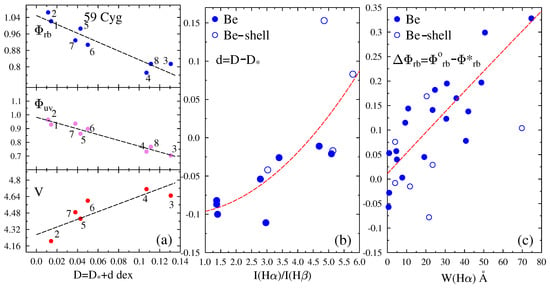
Figure 5.
(a) Variation of gradients , and magnitude V against the total BD of 59 Cyg from 1948 to 1981 (1: Spt.48, 2: Oct.65, 3: Jul.77, 4: Nov.77, 5: Jun. 79, 6: Nov.79, 7: Jul.80, 8: Spt.81). (b) Second component d of the BD against the Balmer line decrement . (c) Reddening and bluing of the gradient corrected from ISM extinction against the equivalent width of the emission component of . In (b,c), filled circles are for Be phases and open circles for Be-shell phases of Be stars.
Moujtahid et al. [65] interpreted the long-term spectrophotometric variations of Be stars in terms of sporadic mass ejections from which their CD is formed and dissipated. According to the dissipating disc model, these authors predicted ‘loop-shaped’ relations between the flux excess in the V magnitude () and the emission excess in the second component of BD (). Similar loop-shaped behavior in a color-magnitude diagram of Be stars of the Small Magellanic Cloud (SMC) (EROS microlensing experiment, e.g., [66]) was sometime later discussed by de Wit et al. [67] who also based their interpretation on a simple-time-dependent model, where the bound–free and free–free emissions is produced by an outflowing CD. These authors also discussed the correlation between the optical and the near-IR flux excess, from which they concluded that their outflowing CD model could provide reasonable explanations for the observations.
The short- and long-lived outbursts discovered by Hubert and Floquet [68] were also reported for some Be stars by Mennickent et al. [69] (MACHO microlensing experiment, e.g., [70]) and Keller et al. [71] (OGLE, e.g., [72]). These authors definitively provided the required observational proof to realize that the long-term photometric behaviors of Be stars are related to the formation of CDs by sudden huge mass ejections, their subsequent dissipation and partial re-accretion onto the star.
2.5.4. Disc-Shaped Envelopes in Be Stars, Just a Few Reminders
In the approaches mentioned above by Moujtahid et al. [65] and de Wit et al. [67], the authors used simplified heuristic representations of the radiation produced by a CD as a function of its optical depth changes during its expansion and dissipation phases. New models have since been proposed, which are worth recalling because they suggest a deeper physical perception of the CD structure in Be stars, its formation and evolution. However, this reminder aims to focus on the observational aspects put forward by the BCD system on the spectrophotometric behavior of Be stars that today’s most accepted theories of the formation and evolution of a CD should take into account. In fact, BCD data refer to the structure of the CD in regions close to the star, where interactions between an already existent environment, discrete ejecta and a variable stellar wind take place. In these regions, angular momentum transport is organized over the entire extent of the disc. This finally enables the disc to acquire a Keplerian rotation and a subsonic expansion over a large part of its structure.
The envelopes of Be stars deserved attentive discussions since Limber and Marlborough [73] concluded that their support in the equatorial plane must be centrifugal and that viscosity (turbulent or magnetic) should be the agent to provide the required transfer of angular momentum from the star to the envelope. They did not elaborate their suggestion. A steady-state solution for a CD formed through mass ejections forced by rotation was obtained by Limber [74], provided the functional dependence of the azimuth velocity, , with R in the disc was specified. In this solution, the radial velocity, is subsonic near the star and supersonic far from the star. Based on a formulation by Limber and Marlborough [73], Marlborough [75] proposed a model for the Be star’s CD density in hydrostatic equilibrium in the zdirection. This model was then used by [76,77,78,79] to produce extensive predictions of the emission profiles in the Balmer lines, continuum flux excesses and line and continuum polarization.
It could also be mentioned that in the 1970s, a series of ad hoc models were proposed for the Be star circumstellar envelopes (or discs) that aimed at inferring from observations the likely dynamical conditions controlling their structure, as can be seen in the reviews by [49,80,81,82]. Traces of the extensive discussions and considerable efforts provided to disentangle the physical nature of envelopes around Be stars can be found in Slettebak and Snow [83], Waters and Marlborough [84], where step by step, the idea of disc-shaped envelopes has been progressively adopted against spheroidal envelopes [85,86]. There is also the problem of the structure of the stellar atmospheres underlying these circumstellar environments. In the future, much attention must be paid to the suggestions made by Thomas [87] and the references therein concerning the properties of atmospheres of active stars having, in addition to the atmospheric structures modified by the rapid rotation, a more or less permanent supply of non-thermal energy by the sources of hydrodynamic and magnetic nature, to better understand the internal structure of these objects. Up to now, instead, few authors have studied the consequences produced by the deviations from the classical thermal structure of stellar atmospheres on the emitted spectra, e.g., [88,89,90,91,92,93,94,95,96].
The two main observational constraints finally establish the limits for a strict modeling frame of CDs in Be stars. According to the correlation between the FWHM (full width at half maximum) of emission lines with the parameter of Be stars [97,98], discs have rotational support, which implies that there is a mechanism that transports angular momentum to the disc and makes it in Keplerian rotation. On the other hand, there is no evidence of supersonic radial velocities in the discs.
Apart from the mechanisms that produce the discrete mass ejection, which remain widely unknown, the disc formation and its further dissipation are now nicely explained by the viscous decretion disc model (VDD). The disc-shaped envelopes start to take hold with Lee et al. [99], who, following the analysis of the dynamics of viscous discs by Shakura and Sunyaev [100], Pringle [101], suggested that angular momentum is transferred from the stellar interior to the equatorial surface. The matter, thus supplied to the inner edge of the disc, drifts outward thanks to the angular momentum transfer through the viscous stress. Following further developments in the frame of viscous accretion discs [102], accretion and excretion discs [103], Okazaki [104], Okazaki [105] proposed the model of ‘viscous decretion discs’ that respects the observation constraints mentioned above. Among the first explorations of the dynamical properties of VDD were those carried out by Haubois et al. [106], while in the frame of these models, the line emission, polarimetric and photometric behaviors of Be stars were carried out by, e.g., Ghoreyshi et al. [107] and references therein.
According to VDD models, the particle density structure in a disc that is in hydrostatic equilibrium in the vertical direction is described by the following relation [108]
where R is the radial cylindrical distance in the disc, z is the vertical coordinate, is the base disc density, the exponent n is a free parameter or determined by the VDD model, is the sound speed, is the Keplerian velocity, and is the vertical disc height scale, G is the gravitational constant, and is the stellar mass. Haubois et al. [106] noted that the exponent n in the radial density function is a function of R, as it was also noted empirically by Zorec et al. [96]. The relation changes during the disc evolution from formation to dissipation. Generally, the variable average value of n is used in the literature, which changes as the CD structure evolves, i.e., from at the disc formation phases, near its steady state, to when it dissipates. However, at the disc formation phases, it can locally be near the star and away from the star. When a steady state of the disc is temporarily attained, it has the average value [109].
Detailed studies on the temperature distribution in the CD of Be stars show that the temperature distribution is highly non-uniform. Its global behavior depends on the physical inputs and on the assumptions made in the models [109,110,111,112,113,114]. The CD temperature decreases in the equatorial region near the star and increases somewhat at larger distances and higher zcoordinates. On the contrary, by including viscous heating, Kurfürst et al. [108] found that the temperature grows in the equatorial regions and decreases towards larger distances in both R and z coordinates.
It has long been known that the source function of Balmer lines, in its representation according to an equivalent two-level atom with continuum, is strongly dominated by photoionization processes [115,116,117,118,119]. The stellar radiation field thus dominates the production and destruction of line photons, and the source function is dissociated from local temperature and density in the line formation region. Therefore, Balmer lines are blind to the temperature structure of the CD. This phenomenon does not concern FeII lines where the temperature dependence of the source function is high [96,120], as well as for the bound-free and free-free continuum radiation.
2.5.5. What Can BCD-like Data Contribute to the Study of Be Star CDs?
Moujtahid et al. [65] have shown that the photometric behavior of a Be star in the visible spectral range is a function of the structure of the CD near the central object as well as of the aspect angle under which the star+CD system is seen. This dependency is also valid for the scBD. Balmer lines, such as H and H, and FeII emission lines also form in the CD regions which are very close to the central object. The aforementioned VVD models should also be applied to the study of changes in these spectral and spectrophotometric characteristics to disentangle the properties of the CD regions, which make the transition between the star and the CD layers that organize the angular momentum transport and are responsible for the Keplerian rotation of the Be star CD.
The mentioned transition region may have particular dynamic characteristics. Stellar winds, mostly when they are massive as predicted by Curé [121], can contribute to the global dynamics of the mass around the star, not only with an added huge amount of mass but also with momentum and energy. The massive discrete ejecta and the fraction of the already existent environment, ablated by winds, produce a mass-loaded flux that can take the aspect of an expanding windblown bubble. These types of phenomena were studied by Hartquist et al. [122], Dyson and Hartquist [123] and Arthur et al. [124]. According to these authors, the most simplified structure of the circumstellar environment in the stationary snowplow phase encompasses three dynamically distinct regions: a wind expansion region; a decelerated, subsonic wind momentum-dominated core; a pressure-dominated supersonic expanding halo. Such a phenomenological picture may then characterize the transition region to other regions where the viscous transport of angular momentum and mass can occur.
The reasons that underlie the triggering of sporadic massive mass ejections are still unknown. Without specifically mentioning them, Kroll and Hanuschik [125] have modeled some characteristics of the ejection proper and its consequences that can lead to the formation of CDs. Kee et al. [126] have proposed that the combination of prograde g-modes of stellar non-radial pulsation could lead to sporadic mass ejections, provided that stars are at nearly critical rotation, which seems far from being a generalized phenomenon [127]. Krtička et al. [128] examined the nature of the mass loss via an equatorial decretion disc in massive stars with near-critical rotation induced by the evolution of the stellar interior. This mechanism stems from the angular momentum loss needed to keep the star near but below the critical rotation. This suggestion suffers from two shortcomings: there is no evidence for the near critical rotation to exist in all Be stars, and the predicted mass-loss rates do not conform with the estimates obtained by modeling the photometric behavior of Be stars with the VVD models [129].
Although the MiMeS experiment yielded no detection of an organized magnetic field with dipole field components weaker than 100 G in Be stars [130,131], random bipolar spot distributions may exist [132] with magnetic fields compatible with the MiMeS non-detections. Hope for its possible existence should not be lost because the average solar magnetic field on the surface does not exceed 2–3 G. This experiment would probably consider the Sun a star without a magnetic field.
Magnetic fields in Be stars can, however, be entertained by sub-photospheric convection as predicted by Cantiello et al. [133], Cantiello and Braithwaite [134], Cantiello and Braithwaite [135], as well as by deeper convective regions induced by the rapid rotation as suggested by Maeder et al. [136] and Clement [137]. Hard X-ray emission in Cas and in Cas class of stars [138] is supposed to be a phenomenon connected with surface magnetic field excluding the effects related with an accreting companion [139]. The X-ray emissions observed in Cas could hardly be explained with the possible soft X-ray emissions predicted by the radiation-hydrodynamics simulations of the nonlinear evolution of instabilities in radiatively driven stellar winds [140].
The subphotospheric differential rotation [141] associated with the deep envelope convection [136,137] can also favor the creation of magnetic fields and subsequent magneto-hydrodynamical instabilities that end up with sporadic mass ejections, e.g., [142].
The low probability that Be stars are critical rotators (see discussion on this issue in Section 7.4), the simultaneous presence of rapid and slow stellar winds, discrete mass ejections, and the existence of surface ‘hidden’ magnetic fields in Be stars justifies the above short recall of the CD models, which aims to focus attention on the scBD. Their correct physical modeling might provide clues to understanding the complex physics that organizes the formation of CDs in Be stars.
2.6. BCD Parameters of B and Be Stars in Clusters
Spectroscopic investigations of open galactic clusters are generally scarce and limited to a reduced sample of cluster members. To study the physical parameters of galactic clusters and their individual members, observations of B and Be stars were made in the BCD spectrophotometric system at the CASLEO observatory in Argentina. These studies were published in Aidelman et al. [10], Aidelman et al. [143] and Aidelman et al. [144]. Data for the following open clusters were obtained: Collinder 223, Hogg 16, NGC 2645, NGC 3114, NGC 3766, NGC 4755, NGC 6025, NGC 6087, NGC 6250, NGC 6383 and NGC 6530. The BCD parameters were derived using the interactive code MIDE3700 [10]. For all the studied stars, the astrophysical parameters , , and were determined. They enabled determining the ISM extinction in the direction of each studied cluster and to provide distances and cluster age estimates, stellar masses () and ages of individual stars. They were obtained by interpolation in models of stellar evolution. The relation between the red-blue gradient of energy distribution and the classical color excess was redetermined according to the spectral wavelength interval Å used to define the BCD-like color gradients.
From a sample of 230 B stars in the direction of the 11 open clusters studied, six new Be stars were found, including four blue straggler candidates, and 15 B-type stars, called Bdd, which have a double Balmer discontinuity. Neither of these show line emission features or previously been reported as Be stars. The spectra of these Bdd may perhaps indicate the presence of circumstellar envelopes. These data enabled to discuss the distribution of the fraction of B, Be, and Bdd star cluster members per spectral subtype. The authors concluded that the majority of the Be stars are dwarfs and their distribution against the spectral type presents a maximum at the spectral type B2-B4 in young and intermediate-age open clusters (<40 Myr). There is another maximum of Be stars at spectral type B6–B8 in open clusters older than 40 Myr, where the population of Bdd stars also becomes relevant. In conclusion, these results support previous statements that the Be phenomenon is present along the whole MS phase, from Zero Age Main Sequence (ZAMS) to Terminal Age of Main Sequence (TAMS). There is clear evidence for the augmentation of stars with circumstellar envelopes as the cluster age increases. The Be phenomenon reaches its maximum in clusters of intermediate age (10–40 Myr), and the number of B stars with circumstellar envelopes (Be plus Bdd stars) is also high for the older clusters (40–100 Myr).
Figure 6, Figure 7 and Figure 8 show spectra observed in the CASLEO of cluster Be stars having the scBD in absorption, cluster Be stars displaying an scBD in emission, and the spectra of cluster B stars here named Bdd. Figure 9 illustrates the HR diagram obtained using the BCD parameters of the B and Be stars observed in the cluster NGC 3114.
Figure 6.
Low -resolution flux-calibrated spectra taken in CASLEO for Be stars in clusters with the scBD in absorption. Adapted from Aidelman et al. [144].
Figure 7.
Low-resolution flux-calibrated spectra taken in CASLEO for Be stars in clusters with the scBD in emission. Adapted from Aidelman et al. [144].
Figure 8.
Low-resolution flux-calibrated spectra taken in CASLEO for Bdd stars in clusters. Adapted from Aidelman et al. [144].
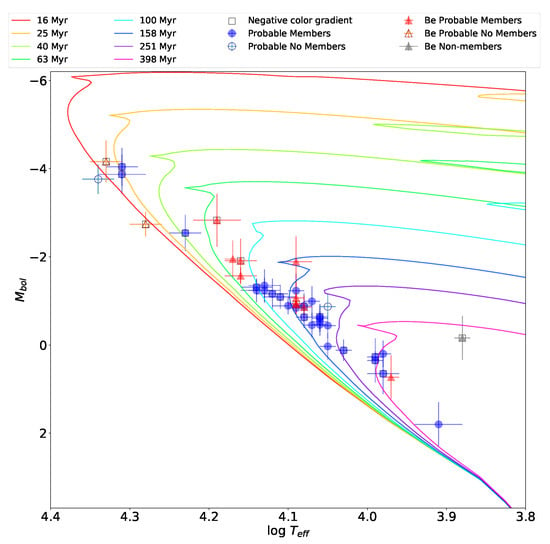
Figure 9.
HR diagram of B and Be stars (members or probably not members) in NGC 3114 whose parameters were determined using the BCD system. The isochrones are from Ekström et al. [145]. Adapted from Aidelman et al. [143].
In the left panel of Figure 10, the parameter values obtained with the BCD calibrations and those derived using models of stellar evolution are compared. There is an unexplained difference between both estimates in the interval that implies overestimated values by 0.5 dex. However, except for only two objects, the agreement between the magnitudes is excellent (right panel of Figure 10).
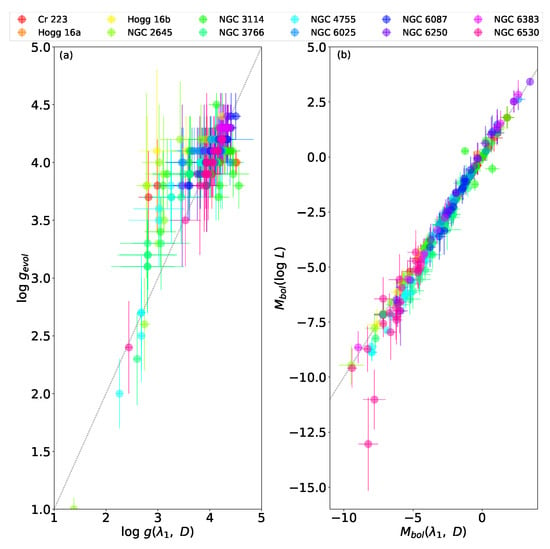
Figure 10.
(a) Comparison of parameters of cluster stars obtained using evolutionary tracks without rotation with those derived from the BCD calibration. (b) Comparison of parameters obtained using the evolutionary tracks of stars without rotation with those derived from the BCD calibration. Adapted from Aidelman et al. [144].
2.7. Bn Stars Observed with the BCD System
As noted by, e.g., Cochetti et al. [146], a significant fraction of stars have a spectral type sub-tagged by the letter ‘n’ or ‘nn’ for showing the presence of ‘nebulous’ or ‘very nebulous’ metal lines in their spectrum. Given the temperature range covered by most of these, the rotational origin of their line-broadening is a logical explanation. In particular, Bn stars are mostly B spectral type MS stars that display broad absorption spectral lines and broad hydrogen lines in absorption. Because a high rotation rate is an essential factor in the development of the Be phenomenon, the possible link between Bn and Be stars deserves a thorough exploration. Mechanisms related to the distribution of the internal angular momentum can be present with different degrees of intensity in Bn stars, which at some point of the stellar evolution may enable the star to display the Be phenomenon.
Taking the magnitude-limited sample of well-known bright O-, B-, and A-type stars in the Bright stars catalog [147], Supplement to the bright stars catalog [148] and errata to both of them published since then, Zorec [149] attempted to determine the possible difference existing between the Initial Mass Functions (IMF) of B stars with and without emission lines. To this end, the assumption was made that: the distribution in the space of Be stars mirrors that of other B-type stars; the relation between the visible absolute magnitude and mass is the same for both groups of objects; their main sequence lifetime is, on average, not strongly different; the star formation rate is constant for each class of objects. These simplifications imply that the ratio between the IMF of the B and Be stars is determined by the ratio of the respective present-day mass functions, which are proportional to the respective counts of main sequence stars [150,151], i.e., , where M is the stellar mass in the interval , is the IMF, and are the counts of main sequence Be and B stars, respectively. The function against is shown in Figure 11. The extrapolation of the regression line obtained for stars from spectral types B0–B7 and the stellar counts of stars cooler than B7 readily shows that there may be approximately 150 missing, still undiscovered, or ‘latent’ Be stars. This estimate approaches the number of counted Bn stars in the same magnitude-limited counting volume.
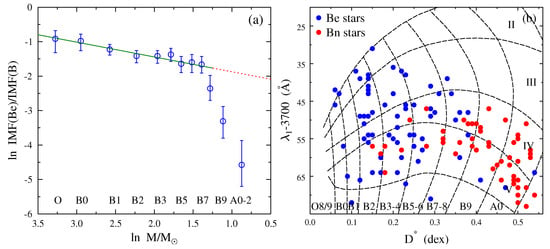
Figure 11.
(a) Fraction of Be stars compared to the entire number of B-type stars; adapted from Zorec and Briot [18]; and (b) BCD parameters of Be and Bn stars; adapted from Cochetti et al. [146].
To the above IMF determination, corrections for the over luminosity of Be stars [18] and the blurring of absolute magnitude vs. mass relations for fast rotation should be taken into account [152]. Nevertheless, once these corrections are made, the final estimate of “missing” Be stars does not changes sensitively [153]. Figure 11a compares B and Bn star countings. In Figure 11b is shown the diagram of Be and Bn stars studied in the aforementioned magnitude-limited volume by Cochetti et al. [146], where it appears that Bn stars are more frequently found among the late B spectral types.
Among the reasons that may explain the lack of Be stars with spectral types cooler than B7 is that, for effective temperatures, 12,500 K, the average CD temperature in the effective emitting volume, drops to K [109], so that hydrogen atoms are almost neutral and the recombination rates very low. Thus, there may be potential Be stars among stars having a late B spectral types which, at the moment, are considered Bn. On the other hand, B-type stars, having seen pole-on, show apparently thin absorption lines, but they can be rapid rotators indeed. The actual number of late B-type stars with high rotation should then be higher than actually found. Finally, it has been shown that the time scales of internal angular momentum transfer to the external layers responsible for a more effective reach of the surface near-critical rotation rates are longer for late B-type stars [154] than for the earlier ones.
Some Bn stars are classified as such in the Bright stars catalog and its Supplement and have been found to have emission lines, and have since been considered to be Be stars, e.g., [146,155,156].
Of particular interest is the observation made by De Marco et al. [157] which was also extensively reported by Aidelman et al. [144] and Cochetti et al. [146], where late B-type stars have a larger BD than expected for their () parameters. As much as it concerns this kind of star in the Cochetti et al. sample, no Balmer line emission has been seen. In all these cases, the authors suggest the possible existence of a CD. Using the models of rapidly rotating photospheres, Porter and Townsend [158] leans towards an explanation involving the gravitational darkening effect induced by a rapid stellar rotation. Nevertheless, their calculations produce a tiny scBD in absorption, whose magnitude is far from the observed stall in absorption. As shown in Figure 8, there is also a case with an apparent scBD in emission (HD 152853). Perhaps the spectra of a higher resolution than those shown in this work may indicate whether there is a genuine scBD in emission or a conjunction of strong spectral lines that give the spectrum such an appearance.
2.8. He-Weak and He-Strong Stars Observed with the BCD System
As compared to the so-called ‘normal’ upper main sequence stars of approximately the same effective temperature and surface gravity, those having abnormal abundances of some chemical species are called Ap/Bp stars or chemically peculiar (CP) stars [159]. Moreover, among CP stars, class subdivisions are made: CP1 or Am stars (metallic-line A-type) which have weak CaII and strong heavy metal lines. These stars do not have large-scale organized magnetic fields. Many of them may not be magnetic at all. They are called CP2 when it comes to Si, Cr and SrCrEu Ap stars, CP3 or HgMn stars (CP3), there are also CP4 or B-type objects with excessively weak or abnormally strong lines of He I. According to the strength of the HeI lines, they are called He-weak and He-strong stars, which represent the high-temperature tail of Ap/Bp stars [160]. The interaction of variable multipolar magnetic fields with the gravitational and radiative diffusion processes induces non-homogeneous distributions of different chemical elements. On the contrary, CP1 and CP3 do not have such strong magnetic fields.
Knowing that the determination of astrophysical parameters (effective temperature, surface gravity, visual and bolometric absolute magnitudes) for these stars is often much more complex than for normal stars due to their abundance anomalies. Several methods were employed by Cidale et al. [161] to study the evolutionary status of stars and the physical processes that take place in their atmospheres and interiors. Among these is the BCD spectrophotometric method carried out on low-resolution spectra obtained at the CASLEO Observatory in Argentina. The parameters thus obtained were compared to those estimated through integrated fluxes, which enable simultaneously obtaining effective temperatures and angular diameters and to parameters drawn from the fitting of the observed energy distributions with non-LTE models atmosphere calculations for different He/H abundance ratios. The non-LTE synthetic spectra were obtained with the TLUSTY and SYNSPEC codes and references therein [162], assuming the following He/H ratios: 0.1, 0.2, 0.5 and 1.0. From the TLUSTY website, the atomic models were taken, i.e., 9 levels for HI, 20 individual levels for HeI and 20 levels for HeII. The stark broadening of HeI lines are from Dimitrijevic and Sahal-Brechot [163], Dimitrijevic and Sahal-Brechot [164] or computed with approximate relations [165]. A microturbulence velocity of 2 km s was used. All spectra were reduced to the resolution of the spectra observed in CASLEO.
Cidale et al. [161] concluded that the effective temperatures, surface gravities, and the bolometric absolute magnitudes of He-weak stars estimated with the BCD system agree well with those issued from the integrated flux method and with other estimates previously derived based on several different methods found in the literature. There are, however, discrepancies between the absolute visual magnitudes derived using the HIPPARCOS parallaxes and the BCD values by approximately mag for He-weak stars and mag when it comes to He-strong stars. For He-strong stars, we note that the BCD calibration, based on stars in the solar environment, leads to overestimated values of . Using model atmosphere calculations with enhanced He/H abundance ratios, it was noted that the larger the He/H ratios, the smaller the BD, which explains the overestimation. Nevertheless, these calculations enabled introducing a method to estimate the He/H abundance ratio in He-strong stars based on the BD discrepancy
It is worth noting that the behavior of HD 37479 was observed at different epochs and showed near-UV flux, Balmer jump and line intensity variations, while the Paschen continuum does not seem to undergo detectable changes [161]. The intensity of H lines increased when that of He I lines decreased, and the near-UV flux was lower. A noticeable difference was detected in the equivalent widths of spectral lines () and on the He/H line ratio as measured in short periods. There was also some flux excess in the Balmer continuum near the BD, reminiscent of the scBD seen in Be stars, although such a flux excess in He-strong stars needs to be studied to see whether it is a matter of emission. On the contrary, it was proven that the stellar remains relatively unchanged when there are substantial variations of He and H lines. Figure 12 shows the difficulties of obtaining the best fit with the model atmosphere calculations of energy distributions of He-strong and He-weak stars.
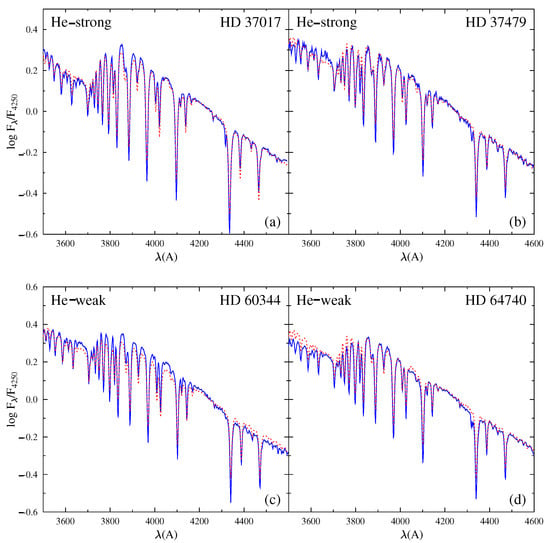
Figure 12.
Examples of energy distributions of He-strong (a,b) and He-weak stars (c,d). Fluxes are normalized to the flux at Å. Observed fluxes are marked with solid blue lines, while models are shown with red dotted lines. The figure is adapted from Cidale et al. [161].
As much as it concerns the evolutionary status of He-weak and He-strong stars, both types of He-peculiar stars seem to be in the MS evolutionary phase. The He-strong stars are situated roughly within the 19,000 K region of the HR diagram, and the He-weak are in the 19,000 K zone. However, the determinations for a much larger number of He-strong and He-weak stars are desirable to obtain more significant insights into their evolutionary status.
2.9. B[e] Stars Observed with the BCD System
The B[e] stars are identified according to criteria used in previous studies, such as Allen and Swings [166], Allen and Swings [167] and Zickgraf [168]. They encompass the four main characteristics that can be expressed in terms of physical conditions that characterize the circumstellar medium (CM) around the stars [169]. They are: (1) strong Balmer emission lines; (2) low excitation permitted emission lines of predominantly low ionization metals in the optical spectrum, e.g., Fe II; (3) forbidden emission lines of [Fe II] and [O I] in the optical spectrum; and (4) a strong near- or mid-infrared excess due to hot circumstellar dust.
Lamers et al. [169] reviewed the classification criteria of the B[e]-type stars in terms of physical characteristics of the stars and of the circumstellar matter (CM). According to their physical characteristics, Lamers et al. [169] suggested that instead of the name ‘B[e] stars’, that the term ‘B[e] phenomenon’ be used. These authors identified five different classes of stars which show the B[e] phenomenon: (a) B[e] supergiants, named in short ‘sgB[e] stars’; (b) pre-main sequence B[e]-type stars, or ‘HAeB[e] stars’; (c) compact planetary nebulae B[e]-type stars, or ‘cPNB[e] stars’; (d) symbiotic B[e]-type stars, or ‘SymB[e] stars’; and (e) unclassified B[e]-type stars, or ‘unclB[e]’ stars. Several classification criteria for each group have been specified to more clearly describe their characteristics. In some cases, stars can satisfy more than one of these criteria; their evolutionary phase is not obvious. If so, the stars are said of unclear type, or ‘unclB[e]’ class.
The sgB[e] stars form the most homogeneous group of B[e] stars. It is formed by B-type supergiants, and most of them were discovered in the Large Magellanic Cloud (LMC) and Small Magellanic Cloud (SMC) [170,171,172,173,174,175,176]. Objects with similar characteristics were also identified in the Galaxy, e.g., [177,178,179]. The properties of sgB[e] stars were reviewed by Zickgraf [168] and Kraus [180]. The main criteria defining them are: (a) that the stars show the B[e] phenomenon; (b) they should be supergiants with ; (c) there must be indications of mass loss in the optical spectrum, e.g., P Cygni profiles of the Balmer lines, or double-peaked Balmer emission lines with violet shifted central absorption; (d) hybrid spectra, i.e., simultaneous presence of narrow low excitation emission lines and of broad absorption features of higher-excitation lines; (e) enhanced N-abundance with abundance ratio of N/C or an enhanced He/H ratio, which indicates that the star, indeed, is in an evolved evolution stage where the products of the CN-cycle have reached the stellar surface; (f) in the Galaxy, they have a high extinction with mag confirmed by the presence of strong interstellar bands, because they are probably massive stars located at large distances in the galactic plane; and (g) generally, the photometric variations of B[e] supergiants are minor, roughly from 0.1 to 0.2 mag.
In the case of HAeB[e] stars, apart from showing the B[e] phenomenon, these are: (a) associated with star-forming regions, although in some cases they seem to be isolated; (b) they show spectroscopic evidence of accretion or infall of matter on the star, evidenced by the presence of inverse P Cygni line profiles; (c) these objects have , suggesting that they are probably progenitors of stars in the mass range from 2 to about 15 [181]; (d) these stars show large irregular photometric variations on time scales from some days to 103 days, usually characterized by a variable extinction [182]; and (e) the energy distribution shows the presence of warm and cool dust.
Ciatti et al. [183] suggested that some objects designated as BQ[ ] stars are of low mass, probably evolving into a planetary nebula. Apart from showing the B[e] phenomenon, objects designated as cPNB[e] stars have: (a) spectra which indicate they are possibly nebulae; (b) their luminosity is ; (c) in addition to the forbidden low ionization lines, there are forbidden emission lines of high excitation, such as [O III], [S III], [Ne III], [Ar III] and [Ar V]; (d) the spectrum can show evidence for N enhancement due to an evolved evolutionary phase; and (e) their energy distribution can show the presence of cold dust ( K) as a possible remnant due to the AGB wind.
Symbiotic stars are interacting binaries with a cool giant and a compact hot object [184]. They can present the B[e] phenomenon and are named SymB[e] stars if: (a) the visual spectrum shows evidence for a cool star, in particular the TiO band, unless the cool star is heavily obscured; (b) the presence of a late-type stellar spectrum in the near-infrared is noted.
There are objects showing the B[e] phenomenon, such as HD 45677, HD 50138, HD 87643, and MWC 349A, which cannot be classified into one of these groups because they do not fit the criteria for a given class or they can share more than one class. The cited objects and roughly half of those in the original list of B[e] stars were considered unclassified B[e] stars or unclB[e].
Miroshnichenko [185], Miroshnichenko et al. [186] suggested a new classification for stars with the B[e] phenomenon based on the time of dust formation in their CM. The properties of the unclassified Galactic B[e] stars were then analyzed again, which enabled to conclude that these objects are binary systems that are currently undergoing or have recently undergone a phase of rapid mass exchange associated with a strong mass loss and dust formation. Since then, the name FS CMa stars (HD 45677) was suggested, and classification criteria were proposed for the unclassified B[e] stars. However, this does not mean that the newly presented class contains all the unclB[e] stars. In this context, the star MWC 137 can be mentioned, whose evolutionary state has long been badly defined. The object was sometimes considered HAeB[e] because of a massive star with an optical nebula embedded in a dusty and cold molecular gas component. The finding of CO, a sign of processed matter around the central object, excludes the pre-main-sequence nature of MWC 137, and suggests that the star must be classified sgB[e] [187]. In Kraus et al. [188], a long account of classifying difficulties of MWC 137 can be found. In this work, a period of 1.93 days was also found, probably due to stellar pulsation but not to a binary. Let us also mention that CI Cam, a star with an orbital period of 19.41 days [189], which was first considered unclB[e], and then the FS CMa candidate, which is now classified as a Galactic sgB[e], which underwent a dramatic X-ray outburst in 1998 [190]. The classification into the FS CMa may sometimes be controversial because the binary nature is not straightforward to determine and the presence of warm dust cannot only be explained by its creation during a mass transfer episode but also by wind–wind and wind–atmosphere interactions. Moreover, some FS CMa stars are now considered post-merger objects, as IRAS 17449+2320 [191], where the H line of IRAS 17449+2320 shows night-to-night variability. This is an atypical phenomenon for FS CMa stars, but notwithstanding present in some of them.
As it comes from the above description of objects with the B[e] phenomenon, one of the most subtle challenges concerning the knowledge of their nature is to determine their right evolutionary state. Unfortunately, because the spectra of these objects are strongly marred by line emissions, flux excesses and high ISM extinctions, it is difficult to determine the fundamental parameters that can unambiguously reveal their evolutionary state. Because the BCD system provides parameters that are free from or can be easily corrected for the ISM extinction and perturbation due to their circumstellar environment, a series of low-resolution spectra were obtained at the CASLEO Observatory in Argentina of several stars presenting the B[e] phenomenon. The purpose was to obtain effective temperatures, surface gravities, and photospheric visual and bolometric absolute magnitudes and determine their position in the evolutionary diagram. Up to now, some recent papers were published presenting the BCD parameter determinations of stars with the B[e] phenomenon by Cidale et al. [28], Aidelman et al. [192] and Arias et al. [193]. However, the first observations in the BCD system of a star presenting the B[e] phenomenon were carried on HD 45677 from Dec. 1963 to Jan. 1967, during which the star underwent huge flux variations in the blue and visible spectral region. Burnichon et al. [194] determined the photospheric () parameters of this object and classified it as B2IV, in agreement with older classifications dating back to Merrill [195] and Swings and Struve [196], Swings and Struve [197], who assigned the B2 spectral type according to the line spectrum. Using observations in the original BCD system from 1959 to 1980, Zorec et al. [198] updated the spectral classification, putting the star in a wider range of luminosity classes, from B2V to B2III-IV. On the other hand, the spectroscopic distance derived thanks to the BCD parameters () and the conservative estimation of the amount of energy absorbed by the circumstellar dust in the far-UV and re-emitted in the far-IR imposed the choice of a B2V type, which agreed with the HIPPARCOS parallax [199]. In this work, the BCD classification of HD 50138 was given, for which these authors assigned the B6III-IV spectral type. Thanks to the characterization of the photosphere of HD 45677, Moujtahid et al. [200] studied the far-UV ISM extinction towards this object. They disentangled the interstellar and the circumstellar absorption components from each other.
Both objects, HD 45677 and HD 50138, are considered today of FS CMa class [185]. A discussion is nevertheless presented in Lamers et al. [169] on whether these stars could be regarded as of the HAeB[e] class because they are projected towards the southern filament of the Orion and Monoceros system of molecular clouds. While according to their distance estimates, they can, in principle, be considered as an isolated HAeB[e] class [201,202] located in the Gould belt plane between the Orion and Vela complexes, they have large spatial velocities so that it should not be excluded, they escaped from the Monoceros molecular clouds. Jeřábková et al. [203] preferred the merger solution for HD 50138, although its binary nature is not sure [204].
Low-resolution spectra in the Å wavelength interval of 23 stars presenting the B[e] phenomenon were obtained at CASLEO, Argentina, to determine their BCD parameters and subsequent physical parameters [28]. It was possible to clearly see the BD in only 15 stars of the observed set. For the remaining stars, other methods were used to estimate their effective temperatures. In some cases, significant differences between the effective temperatures derived using the BCD classification system and those obtained elsewhere, either based on photometric or spectroscopic analysis, imply spectral-type classification disagreements that range from 2 to 3 up to 6 B sub-spectral types. It clearly shows the difficulty of determining the photospheric characteristics of these types of objects and assigning them an evolutionary status. For HD 53179, a double star system, and for HD 45677 and HD 50138, which are also suspected of being binaries, Cidale et al. [28] predicted the characteristics of the components that are consistent with the observed parameters.
In the study carried out on B[e] stars, the observed stars in the BCD system were reported by Arias et al. [193]. In this work, authors attempted to improve the spectral classification and infer the properties of the circumstellar environments in a selected group of five bright IRAS sources (IRAS 02155+6410, MWC 728, AS 119, MWC 819, and IRAS 07080+0605). One of them, IRAS IRAS 07080+0605, displays a large infrared excess; four are unclB[e] stars or FS CMa stars. It was only possible to determine the BCD parameters for the star AS 119, its spectral type, and the quantities that enabled to estimate its spectroscopic distance, which agrees with the HIPPARCOS parallax. Their medium-resolution spectra in the region of 2.17–2.39 m and in the L band were shown for the first time. Infrared features, such as the absorption molecular CO bands and metallic lines, reveal the presence of a late-type companion in MWC 728 and suggest the possible binary nature in AS 119. The binary nature of MWC 728 was previously suggested by Miroshnichenko et al. [205], and that of AS 119 by Miroshnichenko et al. [206]. The star IRAS 07080+0605 shows evidence of a surrounding cool CO molecular cloud. According to the L-band spectra, CS molecular emission may be present in MWC 819, which suggests that the object is a protoplanetary nebula. However, Polster et al. [207] considers that the molecular lines and the late-type spectrum can be produced by a disc. This assumption seems to be confirmed by the polarimetric observations by Zickgraf and Schulte-Ladbeck [208].
In Figure 13 and Figure 14, there are examples of energy distributions of B[e] stars observed in CASLEO, Argentina, to determine their astrophysical parameters according to the BCD system. In these figures, some spectral line identifications are shown. Let us comment on the spectrum of AS 202 in Figure 13. Miroshnichenko [185] has classified this object as an FS CMa star and considered it as a binary with an A0-2-type and K-type components. Other references on this object can be found in Condori et al. [209]. According to this stellar classification, the features at 4200 and 4686 Å that could belong to HeII are dubious and require further investigation to decide whether they are lines or spectral glitches. However, in other spectra of AS 202 and obtained in other recent epochs, not shown here, Balmer lines have nascent emissions, and some metallic lines have P-Cyg profiles. They can be taken as signatures of some kind of activity or interaction between components.
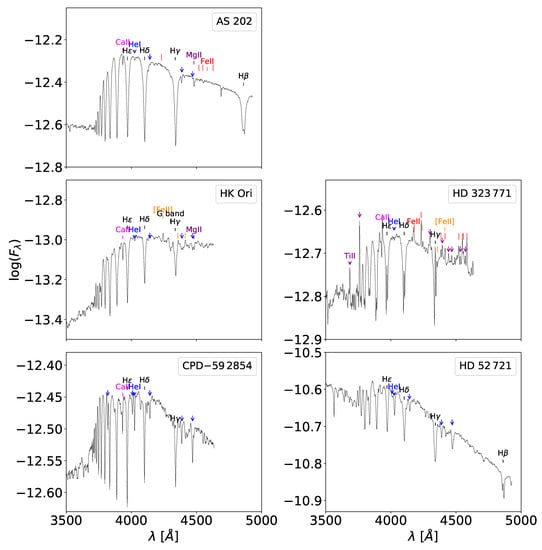
Figure 13.
Examples of the energy distributions of B[e] stars without a second component of the BD in which some spectral line identifications are shown. The spectra were observed at CASLEO, Argentina. Figure adapted from Aidelman et al. [192].
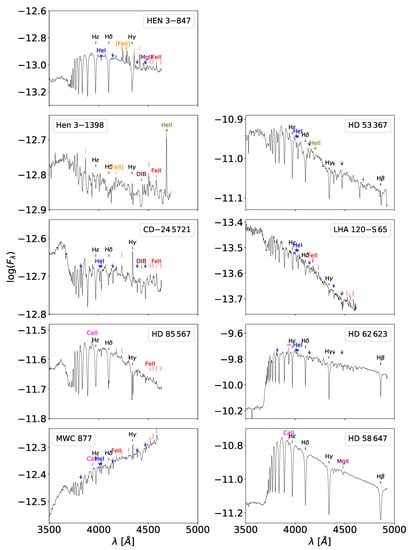
Figure 14.
Examples of energy distributions of B[e] stars with a second component of the BD in which some spectral line identifications are shown. The spectra were observed at CASLEO, Argentina. Figure adapted from Aidelman et al. [192].
Stars in transition phases means that they sometimes show the B[e] phenomenon, and sometimes the characteristics of luminous blue variables (LBVs) undergo strong and irregular mass ejection events. At the moment, these changes seem impossible to predict with stellar evolution models. Moreover, since these stars are deeply embedded in their circumstellar environments, only a few of them were studied in some detail. To bring new elements to describe the central objects of these kinds of stars, low-resolution spectra were obtained for a sample of 14 stars with the B[e] phenomenon and characteristics of LBVs to measure their BCD parameters [192]. Aidelman et al. [192] were thus able to determine a complete set of physical parameters and related quantities such as luminosity, distance modulus and distance for each studied star. In this group, there are two pre-main sequence HAeB[e] stars, seven main-sequence B[e]-type stars, two B[e] supergiants and three LBV candidates. With the help of the size–luminosity relation, estimates of the inner radius of the dusty disc around the pre-MS and MS B[e] stars were obtained. The use of the BCD system showed its utility in deriving stellar parameters and physical properties of B-type stars in transition phases. Once this method is combined with near-IR color–color diagrams, additional elements can help specify the evolutionary stage and character of B[e] stars. Figure 15 summarizes the results concerning the evolutionary status of stars studied by Aidelman et al. [192] in two HR diagrams. Figure 15a displays classical evolutionary tracks for rotating and not rotating stars. Figure 15b shows a spectroscopic HR diagram (sHR) defined according to Langer and Kudritzki [210].
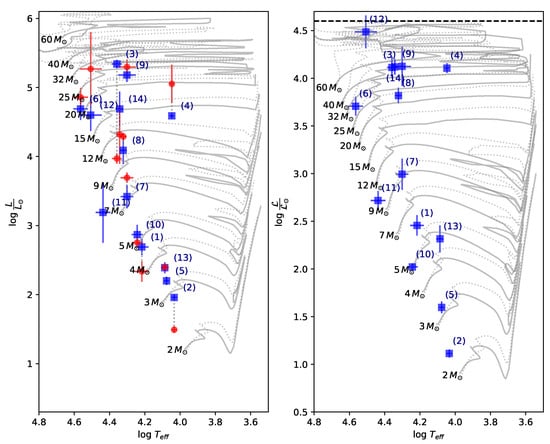
Figure 15.
Left: The HR diagram of the stars studied in Aidelman et al. [192] where the distances have been calculated using the absolute magnitudes (blue squares). The red circles indicate the positions of stars as if they were located at distances given by Gaia EDR3 (Bailer-Jones et al., 2021). Evolutionary tracks with and without rotation ( and are from Ekström et al. [145]). Right: The spectroscopic HR (sHR) diagram as defined by Langer and Kudritzki [210]. The dashed black line at corresponds to the Eddington luminosity limit for a hydrogen-rich composition. The numbers identify the studied stars and the B[e] class classification is indicated in braces: 1 = Hen 3-847 (msB[e]), 2 = FX Vel (msB[e]), 3 = Hen 3-1398 (sgB[e]), 4 = HD 62,623 (sgB[e]), 5 = HK Ori (HAeB[e]), 6 = CPD-24 2653 (msB[e]), 7 = HD 85,567 (evolved msB[e]), 8 = CPD-59 2854 (LBV), 9 = MWC 877 (LBV), 10 = HD 323,771 (HAeB[e]), 11 = HD 52,721 (msB[e]), 12 = HD 53,367 (msB[e]), 13 = HD 58,647 (evolved msB[e]), 14 = LHA 120-S 65 (LBV). Adapted from Aidelman et al. [192].
The determination of the astrophysical parameters of B[e] stars is highly challenged by the physics of these stars and their complicated spectra. The structure of the outermost atmospheric layers of these objects can be perturbed not only by their possible (interacting) binary nature but also by the presence of circumstellar gaseous and dusty envelopes or discs, whose structure is still relatively unknown. In B-type stars with high effective temperatures, the BD is small and subjected to relatively high uncertainties, which also affect the estimate of the parameter. However, the BCD parameters depend on the continuum energy distribution and are thus related to the physical properties of atmospheric layers that on average are deeper than those in which spectral lines are formed.
The main problem in determining the astrophysical parameters of B[e] stars using high-resolution spectra is the identification of genuine photospheric lines. Moreover, the circumstellar environments affect the depth of these lines. These changes can translate in different ways, into increased absorptions, partial filling up by some emission, and by the veiling effect. It may then not be surprising that the astrophysical parameters of some B[e] stars had fundamental parameters that differed according to the methods used to determine them. It is interesting to note the case of HD 62,623, where the BD and the are unambiguously determined. According to them, Aidelman et al. [192] obtain K, while Chentsov et al. [211] and Miroshnichenko et al. [212] using spectroscopy determine K.
Although establishing the correct evolutionary phase of a star shows that the B[e] phenomenon cannot avoid the use of well-determined stellar physical parameters, as those determined by Aidelman et al. [192] with the BCD system, still other criteria must be called upon for help. On the one hand, to decide whether the phenomenon concerns the evolution of a single star or the consequence of merger phenomena implies stellar evolution in a binary system [213,214,215,216]. On the other hand, well-determined rotational parameters and surface abundances of chemical elements are required, as is the case of sgB[e] stars. These determinations are needed to decide whether they are in a post-MS evolutionary phase or share this same place in the HR diagram because they are in the blue loop after the red supergiant phase [213,217,218,219]. Similar questions may be raised regarding the B[e]⇄LBV transitions.
3. Rotation of B-Type Stars: Theory and Observations
3.1. Introduction
It is not the purpose of the present review to make an exhaustive report on the structure of rotating stars, but it is worth recalling some concepts that underlay models currently used to interpret observations, to grasp possible difficulties and needed theoretical improvements more easily.
In the classical modeling frame of stellar structure, the Vogt–Russell theorem stipulates that ‘the structure of a star in hydrostatic and thermal equilibrium is uniquely determined by the total mass and the run of the chemical composition throughout the stars, provided that the total pressure P and the specific internal energy, the constituent equations are functions only of the local density ρ, temperature T and chemical composition’ [220]. In a more simplified way and for a common user mode, a non-rotating star is mainly characterized by the following reduced sets of parameters, the mass , the radius and the chemical composition (), with the possibility of using whatever possible combination of two independent quantities from the set () instead of (), knowing that the luminosity and the surface gravity (S is the area of the stellar surface; is the Štefan-Boltzmann constant; G is the gravitational constant).
Rotation upsets this modeling scheme in the sense that its action on the stellar structure depends on the amount of the global angular momentum stored in the star, (J total angular momentum) and its internal distribution, i.e., distribution of the specific angular momentum ( is the angular velocity; and z are the cylindrical coordinates).
Rotation generates important effects on the structure and evolution of stars. There are first hydrostatic structural changes because of the centrifugal force, which causes a thermal imbalance that leads to meridional circulation currents [221], which in turn induce several hydrodynamical instabilities [222,223] and magnetic instabilities [224,225,226,227,228,229]. These instabilities produce turbulent motions which trigger the mixing of chemical composition and the redistribution of the internal angular momentum.
It is well known that, given a total angular momentum, the motion implying the least energy is that of uniform rotation [230]. Although the physical circumstances in the stellar interiors created by the evolution of stars might then be thought to favor a tendency to recover uniform rotation, other internal rotation laws can prevail over a long interval of time, provided they satisfy some general dynamic stability criteria as the Solberg–Høiland stability criteria against axisymmetric perturbations [229,231].
3.2. Rigid against Differential Rotation; Some Theoretical Principles
Since, in a gaseous rotating body, the specific angular momentum ranges from pole to equator as (where is the polar radius; is the equatorial radius), this body can no longer be spherical, but does acquire either an axisymmetric or triaxial equilibrium configuration, which depends on its internal structure, amount and distribution of the angular momentum [231,232].
3.2.1. Rigid Rotation of Homogeneous Bodies
In a homogeneous body, the internal density distribution corresponds to a polytrope with the index . The solution of hydrostatic equations describing its equilibrium conditions at rigid rotation produces two kinds of rotational sequences. From the virial theorem, the results show that the value of the ratio of rotational kinetic energy K to the gravitational potential W in this case is limited to the range of values . The first sequence of equilibrium configurations is called Maclaurin’s solution and represents a sequence of axisymmetric spheroids. branches off Jacobi’s sequence of triaxial ellipsoids, whose mechanical energy is lower than for Maclaurin’s spheroids and which are thus more stable. However, the analysis of sectorial modes of oscillation shows that homogeneous Maclaurin’s spheroids and Jacobi’s ellipsoids become dynamically unstable for .
3.2.2. Rigid Rotation of Polytropes with Index
For centrally condensed bodies, i.e., self-gravitating systems with s polytropic index , there is a maximum value of that depends on the polytropic index n at which the rotating configurations terminate, because the surface effective gravity becomes zero: , , [231]. Thus, stars in rigid rotation in the Zero Age Main Sequence (ZAMS) and beyond can only be characterized with very low rotational energies, i.e., , so that they can never acquire a global triaxial ellipsoidal configuration. If the mechanisms of angular momentum redistribution led to a huge concentration of angular momentum in the stellar core during the stellar evolution, the core could in principle attain the condition , until dissipation takes over and prevents the formation of a triaxial core [233].
3.2.3. Differential Rotation of Polytropes with Index
If for some reason, a self-gravitating object stores more rotational energy than allowed by at rigid rotation, i.e., the object is necessarily in differential rotation with , the angular momentum must be redistributed in the stellar interior in such a way that the Solberg–Høiland stability criterion is satisfied [231], which in a very simplified way, implies that the Rayleigh dynamic stability condition (where r is the radial coordinate) is obeyed over the entire internal structure of the object.
The dynamical instability of rotating homogeneous spheroids and ellipsoids against sectorial modes of oscillation noted in Section 3.2.1 also appears in differentially rotating polytropes (), but for values of , where the value of depends on the index n and on the law of internal differential rotation [231].
It is worth noting that the amount of total specific angular momentum a star can store depends on the energy ratio and it is roughly cms.
3.2.4. Barotropes and Baroclines
An object rotating with a conservative rotation law, i.e., the angular velocity depends only on the distance to the rotation axis (, i.e., angular velocity constant over cylinders) is said barotrope. According to Poincaré–Wavre’s theorem, as can be seen in [231] (p. 78), in barotropes, the shape of the star and the effective gravity can be derived from a potential, the effective gravity is perpendicular to surfaces of constant density (isopycnic surfaces) and the surfaces of equal pressure (isobars) and the isopycnic surfaces coincide. Otherwise, when the internal angular velocity is a function of both cylindrical coordinates, , the rotation law is said non-conservative and the stellar structure is considered barocline. In that case, the above listed properties derived from Poincaré–Wavre’s theorem are not obeyed anymore.
Rigid rotation is very frequently used to construct models of rotating stars, and it is a particular case of barotropes characterized by the special conservative law constant that holds over the entire stellar structure.
3.3. Geometry of Rotating Stars
Assuming that stars have genuine axial rotation, their geometry is shaped by the equilibrium established between the gravitational and the inertial centrifugal force. Since the centrifugal acceleration is larger, the larger the distance of regions from the rotational axis is, the more stellar layers are enlarged steadily from the pole towards the equator. Moreover, because rotating stars behave as having lower effective masses (see Section 3.5), the lower the effective mass becomes, the larger the core density is [234,235]. As polar regions undergo lesser centrifugal accelerations, the increased gravitational force in these directions and the increased central density produce a polar flattening or dimple, whose depth depends on the rotational law and the amount of angular momentum stored in the star [236].
The calculation technique of the geometry of a rotating star depends on whether the rotation law is conservative, or not conservative . When conservative rotation laws are assumed, the effective gravity at any point in the star is given by [231]
where is the total potential function
where the rotational potential is added to the gravitational potential . The rotational potential exists only if the rotation law is conservative. The gravitational potential is related to the density through the Poisson equation
with G as the constant of gravitation. Equations (12) and (13) can be solved simultaneously using the iterative self-consistent field (SCM) method introduced by Ostriker and Mark [237], largely used in the literature to study stellar structure and evolution with rotation in the original form, or with some modifications, e.g., [234,235,238,239,240,241,242,243,244]. A somewhat different method to calculate rotating stellar structures was introduced by Endal and Sofia [245], where the equipotential surfaces have the role of an independent parameter. Iterative methods based on the integrated form of the Poisson equation were introduced by Eriguchi and Mueller [246], Hachisu [247] and Eriguchi and Mueller [248] (see also references in those papers). An elegant two-dimensional finite-difference iterative technique applied to the problem of finding the gravitational potential associated with an axisymmetric density distribution was introduced by Clement [137], Clement [249].
Methods to calculate baroclinic stellar structures (i.e., stellar structures with non-conservative rotation laws) were developed by Uryu and Eriguchi [250], Uryu and Eriguchi [251] and Fujisawa [252]. To date, the most extensively used baroclinic models are those calculated by Meynet and Maeder [253] and Meynet and Maeder [254], and with some modifications by Heger et al. [255].
The turbulence in the stellar interior related to the differential rotation produced by the evolution and transport of the angular momentum is anisotropic and characterized by a strong horizontal transport that favors the establishment of a constant angular velocity on isobars, called a ‘shellular’ angular velocity distribution. On account of this specific differential rotational law, in Meynet and Maeder [253], the following auxiliary function was defined
which has the property of determining surfaces constant that are parallel to isobaric surfaces, which is also useful to obtain relations that enable prediction the observational parameters affected by rotation.
The calculation of parameters that can be tested with observations also needs specific expressions describing the geometry of the stellar surface. In general, it is accepted that the gravitational potential of rotating centrally condensed objects can be given by a multipole expansion [256]
where is the radius of the undistorted star by rotation, are the zonal harmonic coefficients and are the Legendre polynomials. To calculate the geometry of a rotating stellar surface, Equation (15) is considered with all coefficients , which is then known as the Roche approximation. When the stellar surface is assumed to rotate as a rigid body, constant, Equation (12) is considerably simplified. Considering constant, from Equation (12), the equation giving the radius vector for any azimuthal angle of the rotating stellar surface is given by
where and are the polar and the equatorial radii, respectively, and is the force ratio of the centrifugal acceleration to the gravitational acceleration
where V is the equatorial linear velocity and is the equatorial critical velocity. Equation (16) admits the widely known analytical solution for the radius vector , e.g., [257], which describes the shape of the stellar surface at rigid rotation
with the additional definition
Using the algorithm by Clement [249] and barotropic representations adapted for the stars of masses and at evolutionary stages near the ZAMS and the TAMS, rotating either as rigid or differential rotators with conservative rotation laws of the form (see details in [141])
where is a free parameter, and the obtained iso-density surfaces are shown in Figure 16 and Figure 17. Let us note that horizontal shear instabilities will probably destroy the cylindrical differential rotation enforcing a ’shellular’ rotation law [222,223,229]. According to these assumptions, the polar dimples have a low probability of existing in ’normal’ stars. However, it has been shown in this review that new approaches on the rotating stellar structures suggest that the internal rotational profile should neither be rigid, cylindrical or shellular. In their discussion of stellar shapes with polar dimples, Smith and Collins [236] concluded that the predicted photometric effects are not present in the observational literature, which suggests that strong differential rotation is not common among stars. In a previous work by Collins and Smith [258] also dedicated to the photometric effect of cylindrical differential rotation in the A stars, concluded that “photometry alone can only put rather weak constraints on the degree of differential rotation within stars”.
Figure 16.
Rigid rotators. (a): Iso-density surfaces in model stars of in the ZAMS rotating at (a) ; (a) ; (a) s; (b): Iso-density surfaces in stars of in the TAMS rotating at (b) ; (b) ; (b) s. The iso-density surfaces are labeled with the corresponding density ratios , which are the same in all panels of the figure. Adapted from Zorec [20], Zorec et al. [141].
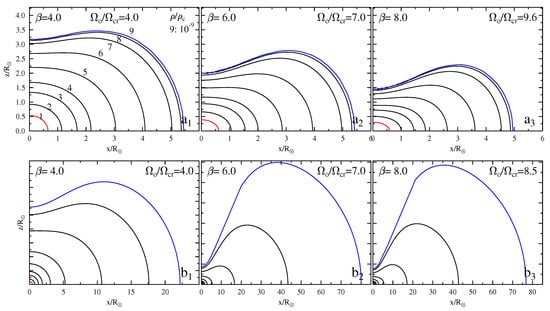
Figure 17.
Differential rotators. (a): Iso-density surfaces in model stars of in the ZAMS having the internal rotation law (20) whose parameters and are indicated: (a1) , ; (a2) , ; (a3) , . is for the critical rigid rotation. The iso-density surfaces are labeled with the corresponding density ratios , which are the same as in Figure 16 and for all panels of this figure. (b): Iso-density surfaces in the model stars of in the TAMS having the internal rotation law (20), whose parameters and are indicated: (b1) , ; (b2) , ; (b3) , . is for the critical rigid rotation. In each panel, the ordinates are in the same scale as the abscissas, but they differ from one to the other panel. Adapted from Zorec et al. [141].
When it comes to non-conservative rotation laws, it is no longer possible to define a rotational potential. In such cases, Maeder [229] suggested that the surface of a star can be identified as the region where an arbitrary displacement ds does not imply any work performed by the effective gravity, i.e., . It can then be shown that the effective gravity can be expressed in the form
where the function is defined in Equation (14) so that that the condition can be given the form
whose integration over a meridian curve leads to the relation
which is the equation required to calculate the shape of a star having non-conservative rotational laws. However, with the following change in coordinates describing the stellar surface and , whilst the integration by parts of Equation (23) produces
that with the definition can be put in the following more workable form
In relation (25), the function that describes the geometry of the stellar surface also appears in the integrand in terms of , is obtained by iteration. Using the Maunder representation of the surface angular velocity as a function of the azimuthal angle given by
geometrical shapes of stellar surfaces such as those shown in Figure 18 can be easily obtained. Since in Equation (25), it is I(0) = 1/2, for rigid rotation, this relation acquires the known form
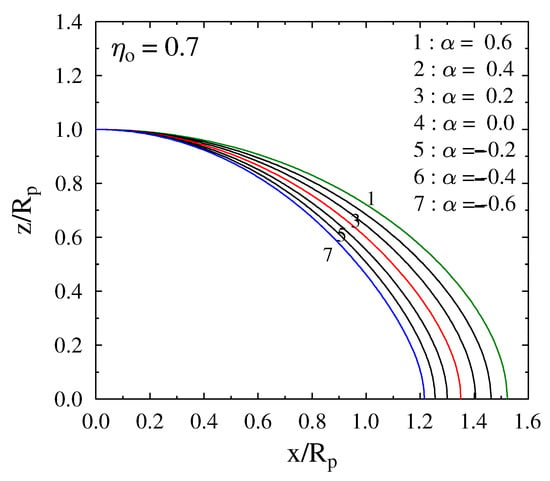
Figure 18.
Geometrical shape of stars having the average surface rotational parameter , and latitudinal differential rotations given by Equation (26) for several values of the parameter . The rigid rotation () is indicated by the red line.
The value of for rigid rotation can be estimated using the interpolation expression obtained in Frémat et al. [259] by interpolation in models of rotating stars calculated by Bodenheimer [235], Clement [137], and Zorec [20]
3.4. On the Critical Rotation Rates
From the relations in Equations (27) and (28), the radii of the stars at critical rigid rotation can be calculated as is the stellar radius without rotation. Thus, the equatorial critical linear velocity is [127]
When characterizing stars rotating at critical rotation rates, it may be worth recalling the following relations between the ratio of angular velocities , the ratio of linear velocities at the equator and the equatorial acceleration ratio
where and are the angular velocities and equatorial radii, with the subindex ‘c’ indicating the respective parameters at critical rotation. The parameter and the velocity ratios compare to each other as
which is worth recalling because we frequently refer to a near-critical rotation when actually corresponds to and to , which cannot be considered as a critical equilibrium condition in terms of forces. In Figure 19, these quantities are compared, where the error bars indicate the differences due to stellar masses and ages on the MS of early-type stars.
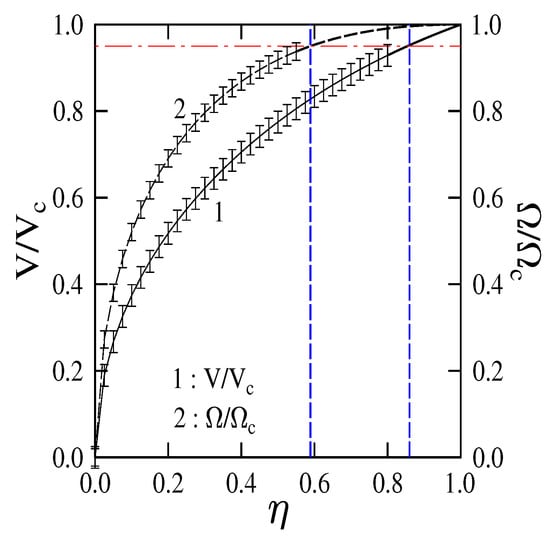
Figure 19.
Angular velocity ratio as a function of . The uncertainty bars indicate differences for masses and ages in the main-sequence phase. It is shown that the (red line) identifies the force ratio . The ratio (red line) corresponds to . Adapted from Zorec et al. [260].
3.5. Notes on the Stellar Effective Mass, Total Energy Production and Age
An important effect related to the reduction in the local gravitational force due to the centrifugal force is that it makes a star behave as an object with a lower effective mass
where represents the pressure-averaged ratio of the centrifugal to gravitational acceleration [261,262]. A larger ratio means a lower stellar mass, but the global lowering of the stellar effective mass, proportional to the stellar mass, is larger the higher the total angular momentum content is. This effect also controls the radiative energy production, e.g., [137,235,244,263,264]. The lowering of the emitted bolometric luminosity calculated by Clement [137], Bodenheimer [235], Sackmann [262] can be represented with the following interpolation relation [259]
where is the bolometric luminosity emitted by the parent non-rotating star, and is defined in Equations (17).
Due to a lower effective mass, rotating stars begin evolving in the ZAMS at a somewhat lower effective temperature and bolometric luminosity than corresponding to a non-rotating star having the same mass. As evolution goes on, chemical mixing provides new opacity conditions to the stellar envelope and the bolometric luminosity augments so that the evolutionary paths in the MS run over those of stars of the same mass and without rotation [229]. Since rotating stars evolve as having a lower effective mass, they evolve with longer evolutionary time scales, which, additionally, are sensitively prolonged due to the hydrogen dredged into the extended convective core by overshooting, as provided by the meridional circulation [265]. In massive stars, the mass-loss phenomenon through stellar winds also has a significant impact on the stellar evolution in the MS, e.g., [145,229]. To the mass-loss phenomena, the sporadic huge mass ejections should also be added, whose triggering mechanisms and total amount of ejected mass are still not well explained. These take place in Be stars, which are rapid rotators (see Section 2.5.3).
3.6. Effects of the Rotation on the Emitted Radiation Field
Rotating stars of high and intermediate mass can be described assuming that they have a photosphere in radiative and hydrostatic equilibrium. According to the radiative equilibrium, the temperature gradient is proportional to the emitted radiation flux and the pressure gradient is proportional to the effective gravity
The detailed analytical treatment of these equations led to a relation that describes the emergent radiative flux as a function of the latitudinal coordinate and is commonly known as the gravity darkening relation
called the von Zeipel theorem [266], which describes the non-uniform distribution of the emitted radiation flux or the surface effective temperature as a function of the stellar latitude. In Equation (35), is the Štefan–Boltzmann constant, L is the stellar bolometric luminosity, G is the constant of gravitation, M is the stellar mass, is the gravitational darkening function and is the surface effective gravity. Physically, von Zeipel’s theorem can be understood in terms of a radiation field flowing out of the star isotropically. As a consequence of the geometrical deformation of the star, the stellar surface covering a given solid angle gains less energy per unit of surface in the equator than for the same solid angle does in the polar region.
The theorem raised the known von Zeipel’s paradox, which stipulates the impossibility of having stable barotropic stellar models in radiative equilibrium, e.g., [267]. This produces the setting up of a permanent meridional circulation due to the latitudinal thermal imbalance between the pole and the equator.
In the original von Zeipel’s formulation for stars in rigid rotation, the gravity darkening term is written as , where and are independent of , and constant = 1 for radiative envelopes, while constant for convective envelopes [268,269]. The original von Zeipel gravity-darkening law holds only for stars with a conservative rotation law and radiative atmospheres in which the transfer of energy is approximated by a diffusion equation. Using radiation transfer equations, Smith and Worley [270] showed that, if meridional circulation is neglected, the gravity darkening (GD) relation is approximately and it recovers its original form if meridional circulation is taken into account. However, according to these authors, for non-conservative rotation laws, there is no a simple relation between and .
The GD relation in Equation (35), in spite of the noted dependencies, is still frequently written as
where is considered independent of the stellar colatitude (for the definition of see Equations (17) and (30)). In such a case, we have [127]
This relation shows that for and when . The current interferometric imaging and modeling of rapidly rotating atmospheres produce inferences of the gravity-darkening exponent in intermediate-mass stars , e.g., [271,272,273,274,275,276].
Kippenhahn [277] studied the GD relation for non-conservative rotation laws and showed that , whose value depends on the specific rotation law. Maeder [278] considered the case of a rotating star with the non-conservative “shellular” profile of the form , where r is the radial coordinate of an associated spherical star. In this case, the star is baroclinic and the properties valid for barotropic structures cannot be applied. He considered that all intervening quantities can be developed linearly around their average on an isobar. For chemically homogeneous stellar surfaces in radiative equilibrium where horizontal flux contributions are ignored, he obtained the expression for the emerging bolometric radiation flux
where the additional term favors a flux increase in the polar regions and a decrease in the equatorial zone. In more recent formulations of von Zeipel’s theorem, also useful for stellar surfaces in differential rotation, the gravity-darkening function in Equation (35) is no longer a constant but a complex function of the surface angular velocity that, following Maunder and Maunder [279], can be written as [260,280]
where and are fitting parameters. The sign of indicates whether the angular velocity is accelerated towards the pole or towards the equator. Espinosa Lara and Rieutord [280] and Zorec et al. [260] showed that, if the original form of the gravitational darkening relation is conserved, due to the dependence of the function f with (), the exponent averaged over the stellar surface becomes a strong function of ).
The most outstanding consequence of the von Zeipel theorem and the geometrical deformation of the star induced by the rotation is that the spectrum emitted by a rotating stars is dependent on the aspect angle under which the object is observed, e.g., [281,282]. This happens in particular for the observed absolute bolometric luminosity, and consequently, also for the visual absolute magnitude.
Due to the lowering of the production of the stellar radiative energy, its geometrical changes and the gravitational darkening effect, the position of a rotating star in the HR diagram depicted just with fundamental parameters averaged over the surface, i.e., ; with respect to another object without rotation, will tend to be at a lower bolometric luminosity and at a lower effective temperature [235,283,284]. However, the detailed position of a star in the HR diagram still depends on the precise values of the apparent quantities (), which in turn rely on the internal rotation law on the amount of stored angular momentum, and on the inclination angle i of the rotation axis with respect to the observer [285,286,287].
3.7. ‘Apparent’ and ‘Parent Non-Rotating Counterpart’ Parameters
The spectrum of a rotating star can be represented as the integrated flux of radiation emitted per unit of wavelength interval per steradian in the direction towards the observer defined by the aspect angle i (inclination angle between the stellar rotation axis and the line of sight). It is given by [281,282,288]
where is the co-latitude dependent radius vector to the surface of the star distorted by rotation; ( is the unit vector normal to the stellar surface and is the unit vector representing the direction of the line of sight); ( is the unit vector in the direction of ); is the dependent monochromatic specific radiation intensity calculated for the local effective temperatures and surface effective gravity .
To study the effects of fast rotation on the fundamental stellar parameters it is useful to use two types of fundamental parameters. The reference model parameters of stellar atmospheres in radiative and hydrostatic equilibrium at each point of the observed hemisphere to calculate Equation (40), are called ‘parent non-rotating counterpart’ (pnrc) fundamental parameters and are noted as , and (bolometric luminosity). The fundamental parameters obtained by fitting the spectral energy distribution in a given spectral domain using classic plane-parallel model atmospheres in radiative and hydrostatic equilibrium take the name of ‘apparent fundamental parameters’, , and . The apparent, hemisphere-dependent bolometric luminosity, effective temperature, effective gravity and rotation parameter ( or , which are synonymous for models that are considered rigid rotators in the ZAMS) are then functions of at least seven unknowns: mass , age ( is the time a star can spend in the MS evolutionary phase), initial metallicity Z, equatorial rotation parameter , surface differential rotation (Maunder) parameter and power in the von Zeipel relation and the inclination angle i
where and stand for the actual and critical stellar equatorial radii, generally determined using the 2D models of rigidly rotating stars as in Zorec et al. [141] and Zorec and Royer [289]. The functions , and carry all the information relative to the geometrical deformation of the rotating star and of its GD over the observed hemisphere. The last equation of the system Equations (41), which determines the equatorial linear rotational velocity, contains the correction term that takes the Stoeckley effect into account (see Section 5.4). The dependence on the exponent of the gravitational darkening is also included in and , because their prediction is based on spectral lines affected by the GD. The above five-fold parametric dependency is also valid for the equivalent widths of spectral lines, the line FWHM, the zeroes of the Fourier transform of spectral lines, as well as the energy distributions and spectrophotometric parameters such as of the BCD system, which are highly sensitive to (). For completeness, it must be noted that the functions , and also depend on the differential rotation law and on the specific relation representing the von Zeipel gravitational darkening. However, the system of Equation (41) must be completed with relations giving the surface-averaged fundamental parameters, because they are required as entry quantities to the models of stellar evolution with rotation to infer the mass M and the age t [145,254,290]
In Figure 20, the functions , and calculated with the code FASTROT [61,127,259] are shown. In these references, the details concerning the solution by iteration of Equations (41) and (42) can also be seen. From Figure 20, it is apparent that functions , and can in some cases be weakly dependent on over the interval , which introduces a source of indeterminacy of the physical and fundamental parameters. This can be particularly sensitive when it comes to the estimate of the inclination angle i. As i is determined once has been determined as a solution of Equation (41), the error on the estimate of i runs as , which could be a significant source of the lack of estimated angles approaching 90o [291]. The distributions of inclination angle estimates are strongly asymmetrical. An in-depth statistical processing of these estimates makes it possible to correct the under-estimates that may occur when [292]. Apart from the interferometric inferences of i, the system Equation (41) thus remains a useful method to determine this quantity in B stars with and without emission, in contrast to that in Sigut and Ghafourian [291], which can only be applied to Be stars.
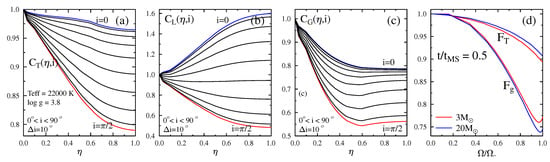
Figure 20.
(a) Function ; (b) function ; and (c) function . The pnrc parameters used here are 20,000, and inclination angles in the interval at steps . (d) Functions and are for and two stellar masses. Adapted from Zorec et al. [61], Zorec et al. [127].
Since a significant part of the present review is devoted to the BCD parameters, it can perhaps be timely to also show the effects due to the rapid rotation directly on the apparent BCD parameters , which is given in Figure 21.
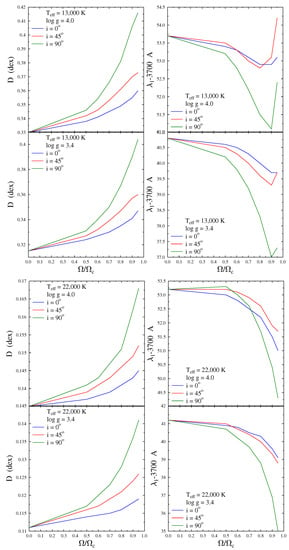
Figure 21.
Apparent parameters modified by the stellar rapid rotation in stars having the indicated pnrc fundamental parameters and for several inclination angles. Adapted from Zorec et al. [61].
Finally, it is worth noting that FASTROT is a calculation code adapted for stellar atmospheres where the plan-parallel approximation is valid. For stellar sufficiently extended atmospheres, where the mean free path of photons is of the same order as the size of the atmosphere, curvature effects must be taken into account, because they can modify the source functions of lines and continua by orders of magnitude, as may be the case for some B[e] stars. The case of extended spherical atmospheres has already deserved some attention, as can be seen in, e.g., [293,294,295,296,297]. However, the effect of the atmospheric curvature also needs to be studied in the frame of rotationally deformed atmospheres, where the gravitational darkening effect can produce changes in the internal atmospheric temperature, as briefly mentioned in Section 5.5.1.
4. CNO Abundances and Stellar Rotation
As already noted in the introduction, the geometrical structural distortions induced by the rotation cause a thermal imbalance and lead to meridional circulation currents [221] that in turn induce a number of hydrodynamic [222,223] and magnetic instabilities [226,228]. These instabilities produce turbulent motions which trigger the mixing of chemical composition and the redistribution of the internal angular momentum. The predictions of quantities such as luminosity, stellar lifetimes, surface chemical abundances and mass-loss rates depend not only on the masses, initial rotation laws in the ZAMS and metallicity, but also on the prescriptions used to calculate the multiple diffusion coefficients that characterize the chemical and angular momentum diffusion. Extensive tests of surface chemical abundances of He and CNO abundances synthesized in the rotating stellar core were carried out in B and Be stars in the Milky Way (MW), SMC and LMC to validate the models of rotating stars, e.g., [298,299,300,301,302,303,304,305,306,307] and the references therein. In these contributions, contrasting results can be found, mainly on the surface N abundance, which according to models is meant to be enriched in rapid rotators. Thus, an unexpected significant enrichment was detected for MS stars in LMC with km s, and with and without overabundance for LMC B-type stars with km s. This enrichment was attributed to merger phenomena in binary systems. No significant N enrichment seems to exist among rapidly rotating MW B-type stars. It was also noted that the N enrichment of B and Be stars was quite similar and that observed abundances in Be stars in the LMC agree with those predicted with population synthesis models calculated by Brott et al. [308] assuming that Be stars do not rotate faster than .
Since the spectral signatures of the CN elements are rather small, their atmospheric abundances can be more easily detected in stars with higher metallicity, and are in general better determined in stars with km s, which implies pole-on seen fast rotators. Among somewhat evolved MS fast rotators, the enrichment of N is expected to be larger in pole-on stars than in those with km s. This phenomenon is due to two concomitant effects that the radiation pressure tends to produce, namely CN elements being synthesized in the stellar core and raised to the surface being drifted towards gravity darkened and thus cooler equatorial regions [309], where their lines cannot be excited enough to produce observable spectral signatures. Except for Dunstall et al. [306], other cited contributions did not correct spectra for veiling effects in Be stars. The correction for the veiling effect sensitively increases the estimate of their chemical abundances. According to Potter et al. [307], the models of rotating stars need refined tuning of several diffusion constants, because abundance predictions strongly depend on their values. Uncertainties affecting the values of these constants make it so that, at the moment, the comparison of theory with observations is rather uncertain. Finally, the explanation of abnormal abundances stemming from single rapidly rotating stars is challenged by the possibility that the observed objects could be members of evolved close binary systems, where the spin-up towards the near critical rotation of one of the components and the N enrichment are both due to the accreted mass during a mass-transfer phenomenon [215,310].
5. Measurement of the Rotational Velocity in Early-Type Stars
The most straightforward though apparent information regarding a star as a rotator is obtained through the parameter , where V is the true equatorial linear velocity and i is the inclination angle of the stellar rotation axis with respect to the observer. For a given star, V and cannot be disentangled straightforwardly, unless a complementary analysis is performed on the stellar spectra emitted by the hemisphere deformed by rotation and projected towards the observer (see Section 3.6).
Shajn and Struve [311] discussed the broadening effect that rotation can produce in spectral lines, and two years later Struve [312] pledged that the rotation should be considered as an independent stellar fundamental parameter. Among the first determinations of for early-type stars can be cited those of Elvey [313], who used a graphical method where the observed MgII 4481 line profiles were compared to spun-up thin line profiles. Carroll [314] introduced a method based on the Fourier transform (FT) of line profiles that is today still currently used to determine the . The method introduced by Elvey [313] and previously suggested by Shajn and Struve [311] was systematized by Slettebak [315], who determined the parameter for 123 early-type stars with and without emission lines.
Since these pioneering works on the stellar rotation, a large series of studies based on different methods have been dedicated to the determination of the of early-type stars, whatever their normal or active character. Following Howarth [316], we classify these methods into the following broad groups: (1) Methods based on the FWHM of observed line profiles that are compared with model FWHM calculated as in Slettebak et al. [317], where the limb-darkening (LD) in the line profiles and the GD effect are taken into account. In the old days, the comparison of observed FWHM was performed with observed or synthetic line profiles enlarged by a rotational broadening function; (2) Methods based on the FT, where neither the wavelength-dependent limb-darkening within the line profiles nor the gravitational darkening effect can be considered; (3) Methods that determine the parameter by fitting the observed line profiles with synthetic line profiles calculated for a given spectral domain with static model atmospheres, which are broadened with a rotational broadening function that does not consider the change in line profiles due to wavelength-dependent limb-darkening, nor the effects of the GD, e.g., [318,319]. The determination by the cross-correlation of observed high-resolution spectra against an observed or synthetic spectral template where lines are not considered broadened by rotation, e.g., [320] can also be associated to this category. Measurements based on the calibration of the FWHM lines as in Daflon et al. [321] are considered in this category; (4) Methods where observed line profiles are fitted with spectra calculated with model atmospheres that take into account the limb-darkening varying with wavelength in the interval of line profiles, but using not deformed stars by rotation neither affected by the GD effect [322]; and (5) Methods that use synthetic spectra calculated for stars deformed by rotation and gravity darkened, where the limb-darkening in the local line profiles is consistently taken into account, e.g., [259,323]. In Table 1, which is not intended to be exhaustive, the determinations of normal and active B-type stars are listed.

Table 1.
Non-exhaustive table of determinations for early-type stars.
5.1. Rotational Broadening in Gaia DR3
The third release of the Gaia catalog Gaia DR3, ref. [363], provides what is, to date, the largest survey of rotational line-broadening measurements (i.e., for ). It is based on the analysis of the data obtained by the Radial Velocity Spectrometer (RVS), ref. [364]. Two measurements of rotational line-broadening are available. The first value was obtained by taking the median of the measurements performed on epoch/transit RVS spectra, prior to the radial velocity (RV) determination. It is named vbroad in the gaia_source table. The second estimate was directly measured on the co-added RVS data by the ESP-HS module of the Apsispipeline [365]. Its determination was inserted in the process that led to the computation of the astrophysical parameters (APs: and ) and the interstellar reddening of/towards O-, B-, and A-type stars from the simultaneous fitting of the Gaia BP/RP and RVS spectra with synthetic ones. The value is saved in the field vsini_esphs of the Gaia DR3 astrophysical_parameters table. Both estimates were made by ignoring any broadening mechanisms other than rotation (e.g., they assumed the absence of macroturbulent motions, as can be seen in Section 5.6) and were based on the maximization/optimization of the cross-correlation between the observed and theoretical spectra (which we assimilated to method 3 in Table 1).
It is worth reminding that the RVS wavelength domain ( 846–876 nm) is centered on the NIR Ca II triplet lines, which reach their maximum strength in F-, G- and K-type stars. In B-type stars (Figure 22), the higher members of the Paschen series dominate the whole spectrum and carry most of the spectroscopic information available to measure the line-broadening. This partly explains the behavior of the vbroad measurements, as reported by Frémat et al. [366]. In particular, at the B-type stars’ temperature range, the values are usually expected to be underestimated and strongly affected by the noise at . Furthermore, because of issues related to the RV determination of O-, B-, and A-type stars [366,367], all the vbroad measurements obtained for targets hotter than were filtered out during the post-processing [368]. Finally, no vbroad measurement is available in the catalog when, in more than 40% of the epoch RVS spectra, the emission in the Paschen lines is rising above the local (pseudo-)continuum [368].
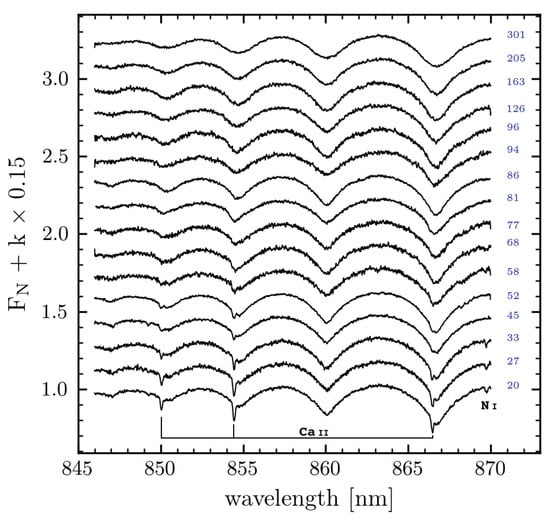
Figure 22.
Variation with vsini_esphs (noted in blue, in ) of published Gaia DR3 RVS spectra with , 11,500 12,500 , . The spectra were normalized to the pseudo-continuum by the Gaia pipeline () and vertically shifted relatively to each other.
While the vsini_esphs estimate is expected to suffer from the same limitations, its value for the hot stars was kept as being part of the AP determination carried out by the ESP-HS algorithm. We compare in Figure 23 the values found in Gaia DR3 to those published in some of the most recent studies listed in Table 1 a similar comparison is presented for vbroad in Figure 11 of [366]. Although the studies we consider in this plot have analyzed stars brighter than , (with the exception of [362], whose study includes mainly fainter stars), there is little overlap with Gaia DR3 vsini_esphs measurements. This is due: (1) to the filters applied during the post-processing and based on the analysis of the goodness-of-fit distributions in both BP/RP and RVS domains; and (2) to the degeneracy between the APs at increasing interstellar reddening, as can be seen in, e.g., Figure 2 of [369] during the selection of the target based on the spectral type tagging (spectraltype_esphs). As can be seen in Figure 23, a significant scatter is observed relative to ground-based measurements (which are usually obtained at higher resolving power and in better suited wavelength domains). However, the measurement remains fairly representative of the rotational broadening, as can be measured in the RVS spectra.
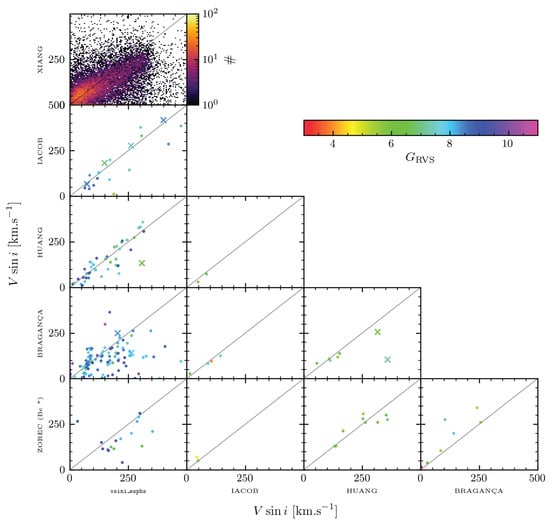
Figure 23.
Comparison of the Gaia DR3vsini_esphsestimates obtained for B- and O-type stars with measurements found in various catalogs as noted by the axis labels: XIANG [362], IACOB [358,360], HUANG [353], BRAGANÇA [355], and ZOREC [127]. The color code usually follows the (see corresponding color bar), except for the XIANG vs. vsini_esphs panel where the data were sampled into 5 bins. In the IACOB, HUANG, and BRAGANÇA plots, the crosses highlight those targets known, according to Simbad (CDS), for showing emission-lines. In these comparisons, we only took into account those targets with .
Similarly to what was performed for the determination of vbroad, the ESP-HS avoided using the RVS data that could be affected by line emission. In these cases, the APs were derived by analyzing the BP/RP data only, and no line-broadening was derived. The decision to flag the spectrum for possibly having emission lines was based on the pseudo-equivalent width of the H line directly measured on the RP spectrum [370]. Because of the low-resolving power of the data, of the steep decrease in the instrument response in the blue wing of H, and of the method adopted, a fraction of weak H emittors were not flagged [371,372] and still have their vsini_esphsvalue published (see lower left panel of Figure 23, where we plot the estimates obtained by [127] for a sample of Be stars). In these cases, a representative broadening value may still be expected, as long as the spectrum of the star does not show any characteristics of stars with shell-like absorption.
5.2. Caveats on the FT and ‘Spun-Up’-Based Methods
When Carroll [314] introduced their method to determine the parameter based on the Fourier transform (FT) of spectral lines, he clearly warned that an easy solution would be to represent the effect of the limb-darkening on the intensity of a spectral line non-affected by rotation by splitting the line profile into a product of line profile proper and a limb-darkening function, whose objective was to have a function to carry out the Fourier transform analytically
where is a polynomial, or whatever other function of (, is the cosine of the angle between the normal to the stellar surface and the line of sight), and is the line profile seen at . Thus, this form does not take into account the effect of the limb-darkening in the line profile itself, which at Carroll’s time, was already known to have the following approximate analytical aspect [373]
where , and depend on the line absorption coefficient. This form is far from that described in Equation (43), where the function depends only on the constants related to the continuum spectrum, but not concerning the studied spectral line proper. This inconsistency is inherent to all applications of this FT methods [374,375], even though complicated forms of are proposed, thinking that the parameters will then be more precise. This same comment is also valid for all methods where spectra are first calculated for non-rotating stellar atmospheres and then spectral lines are broadened according to different projected velocities using rotational broadening functions based on limb-darkening expressions like in Equation (43). Finally, Collins and Truax [376] notes that these methods do not take into account the effects carried on the spectral lines by the gravity darkening induced by rotation, although these authors based their criticisms online profile representations resembling that of Carroll.
5.3. Uncertainties on the Related to the Non-Consideration of Velocity Fields in the Calculations of Radiation Transfer in Spectral Lines
The line profiles used for the further broadening by rotation are obtained by radiative transfer calculations that consider static stellar atmospheres. Already known are the asymmetries of spectral lines produced by velocity fields in non-rotating stellar atmospheres, as can be seen in e.g., [119] and references therein. However, line asymmetries can be particularly significant when they are calculated using radiative transfer codes that take into account velocity fields in rotating stellar atmospheres, as shown in Korčáková and Kubát [297], Korčáková and Kubát [377], Korčáková and Kubát [378]. Nevertheless, further progress on the calculation of broadened line profiles by rotation can be expected if the aforementioned codes will also consider the non-spherical geometries of stellar atmospheres whose temperature structure in depth is calculated consistently with the deviations introduced by the gravity darkening, discussed in Section 5.5.1. Another discussion of asymmetrical rotational broadened line profiles is given in Section 5.10.
Many B-type stars have spectra marred by the presence of circumstellar envelopes or discs. To this end, CMFGEN is a code that was developed to model the spectra of a variety of objects with moving extended atmospheres: O stars, Wolf–Rayet stars, luminous blue variables, A and B stars, central stars of planetary nebula and supernovae, as seen in [379,380,381] and the references therein. Spectral lines predicted by this code, submitted to rotational broadening, can be of particular interest for studying B[e] stars, mainly in helping to identify genuine photospheric signatures in their observed spectra, otherwise strongly perturbed by the signatures of complicated gaseous and dusty circumstellar environments.
5.4. Uncertainty on the Related with the Gravity Darkening
As noted in Section 3.6, in rapid rotators, the emitted bolometric flux weakens from the pole to the equator as a function of the surface effective gravity [260,266,278,280]. The contribution of the radiation to the total -dependent flux in a spectral line broadened by the rotation is thus less effective from the equatorial regions, which consequently translates into an underestimated parameter. As this effect was first studied by Stoeckley [382], in what follows, we refer to it as Stoeckley’s effect. As already quoted in Equation (41), the expected value of corrected from the Stoeckley’s effect can be written as
where is the apparent or observed projected rotational, and is the correction for the underestimation induced by the effects associated with the rapid rotation that hereafter, and depending on the circumstances, we call Stoeckley’s correction or Stoeckley’s underestimation. After Stoeckley [383], a number of authors have calculated , in particular Townsend et al. [384], Cranmer [385] and Frémat et al. [259], who calculated this correction in the frame of a strict surface rigid rotation with the classical formulation of the GD effect by von Zeipel [266]. A schematic representation of the relation between the true and the observed one is shown in Figure 24.
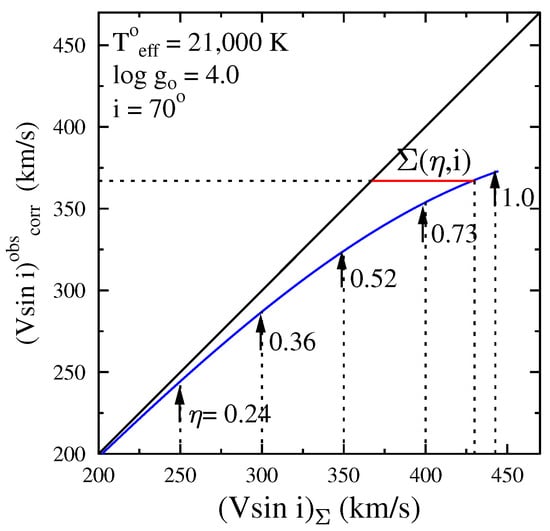
Figure 24.
The blue line represents the relation between the observed corrected from observational uncertainties (ordinates) against the corrected from Stoeckley’s underestimation (abscissas). This relation was calculated with He I 4 471 line profiles for models with parameters 21,000 K and , inclination angle , and ratios ranging from 0 to 1.0. The red bars indicate Stoeckley’s correction for an arbitrary near critical parameter. The values indicated in the figure are for the actual parameters in abscissas. Adapted from Zorec et al. [127].
A particular underestimation of the parameter can be produced if no attention is paid to the spectral lines that are formed in the polar regions of rapidly rotating stars. Heap [386], Heap [387] discovered that the parameter of Tau determined using the classical spun-up measurement methods of photospheric lines in the spatial ultraviolet (far-UV) observed with the satellite Copernicus were twice as low than in the visible, and that the effective temperature required to model the far-UV lines was higher than for those in the visible spectral range. She concluded that this discrepancy is due to the gravity darkening, according to which the hot polar regions contribute with smaller line broadening linear velocities than the somewhat cooler equatorial regions, which contribute with the largest line broadening radial velocities. This hypothesis was confirmed with model calculations by Hutchings [388], Hutchings and Stoeckley [389] and Sonneborn and Collins [390]. The rotation of a larger set of rapid rotators using far-UV lines of SiIII and of FeII observed by the satellite IUE was studied by Carpenter et al. [391], who made models of gravity-darkened stellar atmospheres and concluded that the obtained parameters agree with those obtained from spectral lines in the visible, which is another way to confirm the gravity-darkening effect in rapid rotators and warns of the necessity of using other than simple FT analysis or spun-up profiles to determine the parameter from lines whose formation is sensitive to the local formation conditions of temperature and gravity, particularly when it comes to rapid rotators.
5.5. Effects on the Related with the Structure of Rotating Stellar Atmospheres
Stress is put here on the formation of spectral lines in gravity-darkened stellar atmospheres. The phenomena concern: (1) the thermal structure in the depth of stellar atmospheres as a function of the colatitude and its incidence on the line source function; and (2) the sensitivity of line source functions to local physical conditions.
5.5.1. The Thermal Structure in Depth of Rotating Stellar Atmospheres
Very early, it was recognized that the rotation and simultaneous hydrostatic and radiative equilibrium contradict each other, and that the latitudinal variation of the temperature in the stellar atmosphere produces a non-vanishing dependent divergence of radiation flux [392], which unleashes the horizontal diffusion of light that has to be treated properly to obtain a stable atmospheric thermal structure. Two-dimensional radiation transfer calculations in stars deformed by rotation, similar to those started by Pustyl’Nik [393] and Hadrava [394], might perhaps be able to tackle these questions and predict the reliable dependencies of the line source functions with as well as GD relations that can be considered consistent with the right thermal structures of rotating atmospheres. Unfortunately, to date, there are no such detailed models. The current approximation used to model the spectra emitted by rotating objects is to assume that at each latitude , the structure of the atmosphere as a function of the optical depth corresponds to that of a classical plane-parallel model atmosphere characterized by the local parameters [], where is inferred with the adopted GD law. The thermal structures of rotating atmospheres used to date have never been demonstrated to be consistent, because the horizontal radiation flux was never taken into account. It is worth mentioning that the improbable physical structure of the atmosphere in the equatorial regions of a fast rotator, that the relationship in Equation (35) leads to, implies that, for , the radiative flux is canceled so that . The low temperature condition is not a sufficient condition to make the atmosphere convective, a state that actually requires the specific entropy to decrease towards the surface of the star, which imposes conditions not only on the temperature gradient but also on the density gradient [229]. By simulating the effects produced by some extreme physical circumstances masking the above outlined situation, predictions show that there can be significant changes in the line intensities and their widths, which may lead to estimates of that sensitively depend on the chosen spectral lines [260].
5.5.2. The Line Source Functions in a Gravity Darkened Atmosphere
It has long been known that due to the non-LTE effects and atomic structures proper, the source function of spectral lines have selective sensitivities to collisional and radiative processes that dominate the population of atomic levels [87,116,119]. Because the gravity-darkened atmospheres in rapidly rotating stars induce a wide range of electron temperatures and densities over the hemisphere projected toward the observer, spectral lines with different sensitivities to local formation conditions do not reflect the same physical properties prevailing in the observed hemisphere. Owing to these differences, the spectra of rotating stars interpreted with models calculated for non-rotating atmospheres can produce not only different values of apparent ()-parameters, but they also produce different estimates of the (the details of which can be found in [260]).
5.6. Effects of the Microturbulence and the Macroturbulence on the Determination the Vsin i
Microturbulence and macroturbulence hide a series of motions that are not yet well identified. It was recognized very early on that spectral lines undergo broadening due to the random motions of eddies in stellar atmospheres [395,396]. Underhill [397], Underhill [398], and Rosendhal [399] reported that these effects should be present mainly in early-type stars with low surface gravity. Random motions of eddies of the order or lower than the mean free-path of photons were called microturbulence and can affect the line absorption coefficient producing the so-called ‘second-class’ line broadening [396]. Movements of the eddies implying distance scales larger than the photon mean that free-paths were called macroturbulence, but they do not change the effective mean atomic-line absorption coefficient. In this case, the line broadening is simply produced by the Doppler effect associated with the macroscopic motion of eddies and was called ‘first class’. More recently, Cantiello et al. [133] and Grassitelli et al. [400] evoked the subphotospheric convection to account for the microturbulent motions, while Aerts et al. [401], Aerts et al. [402] suggested that, in B-type stars, macroturbulence could be ascribed to the low-amplitude gravity modes of non-radial pulsations. The errors affecting the and macroturbulence velocity () determinations over the time series of line variations are star-dependent. Aerts et al. [402] find that the maximum error on the is 60 km s and the averaged error is 8 km s. Regarding the maximum error on the estimate is also 60 km s, while its averaged error is 17 km s. Similar conclusions were also put forward by Simón-Díaz [403]. Howarth et al. [320] claimed that macroturbulence can be an important line-broadening mechanism in O- and early B-type supergiants, which adds to rotation. Nevertheless, its determination is not unique, because the same broadening can be produced by combining large ranges of macroturbulent velocities and values [404].
To describe the line broadening carried by macroturbulent motions, two models are used: isotropic Gaussian and anisotropic with radial and tangential components, where each has a Gaussian-dependent velocity distribution [405,406]. The anisotropic model depends on at least three free parameters, but they are reduced to only one so that both models are characterized by a unique dispersion of macroturbulent velocities . The anisotropic model generally produces the more effective fits of spectral line profiles, leading to slightly larger values of than the isotropic model does [358,407,408]. However, they both mask still unidentified line-broadening phenomena.
Macroturbulence was mostly explored in early-type stars, mainly supergiants, which all have low values of cf. [320,352,404,407,408,409].
However, macroturbulence was also suggested for later B-type supergiants [408]. As found in Simón-Díaz and Herrero [358] and Sundqvist et al. [409], macroturbulence should not be entirely negligible in early-type dwarfs and giants. Using the rotational period of two magnetic O-type stars (HD 108 and HD 191612), [409] found that the apparent rotational velocity of the star is km s. This same parameter redetermined with the Fourier transform method becomes km s. It can then be expected that macroturbulent-like movements also exist in the atmospheres from B-type dwarfs to the giants of lower effective temperatures than those explored in the above cited works. This can be the case of all those stars that undergo non-radial pulsations and a wide funnel of instabilities induced by the rotation. The photospheric spectral lines currently used to determine the parameters of Be stars can then legitimately also be expected to be affected by macroturbulence. The macroturbulent motions are detected when apparent rotational velocities are km , while lines broadened by km seem to remain fairly insensitive to the broadening induced by macroturbulence. However, this does not mean that, in these cases, it does not exist, as in Be stars, where atmospheres can undergo significant upheavals maintained by non-radial pulsations, a large spectrum of instabilities induced by the rapid rotation and possible disordered magnetic fields generated by under-photospheric convection [133,134,136,137].
5.7. Effects Carried by the Differential Rotation on the Value of Vsin i
The existence of a surface differential rotation in B and Be and other massive stars was speculated or predicted with models by a number of authors cf. [20,260,289,410,411,412,413,414,415,416], who derived parameters indicating its possible existence. To support this hypothesis, two different theoretical approaches to the stellar structure can be mentioned, wherein the results indicate that there are mechanisms capable of inducing differential rotation at the surface of early-type stars. Using conservative rotation laws [137] or non-conservative ‘shellular’ rotation laws [136] for models of stellar structures, it was shown that the two convection zones in the envelope associated with increased opacity due to He and Fe ionization can be considerably enlarged in depth by the rapid rotation. These regions together establish an entire convective zone beneath the surface that spreads out over a non-negligible region: from 1/8 of the stellar radius at the pole to nearly 1/4 at the equator [136]. However, differential rotation in convective zones can be induced in the same way it is induced in the Sun [417]. Following the solar rotational picture, where the convective layers have differential rotation, we may expect that some coupling can exist between convection and rotation beneath the surface in rapidly rotating massive and intermediate mass stars, whose imprint on the outermost stellar layers will translate into an angular velocity dependent on the latitude.
Solving the baroclinic balance relation obtained with the curl of the time-independent momentum equation of an inviscid, axisymmetric rotating star without magnetic fields, Zorec et al. [141] obtained solutions for the angular velocity distribution in the envelope under several conditions: (1) the surfaces of specific entropy S are parallel to the surfaces of specific angular momentum j, ; (2) the surfaces of specific entropy and angular velocity coincide, i.e., ; and (3) the surfaces of specific entropy S are parallel to the surfaces of constant specific rotational kinetic energy, . In Figure 25, some examples of curves that obey these assumptions are shown. Rieutord [415], Espinosa Lara and Rieutord [418], Rieutord et al. [419] and Gagnier et al. [420] presented a new consistent way to compute a two-dimensional model of a fast rotating star including the large-scale flows, where among many other improvements, the calculated internal and surface differential rotation have some similarities to those shown in Figure 25.
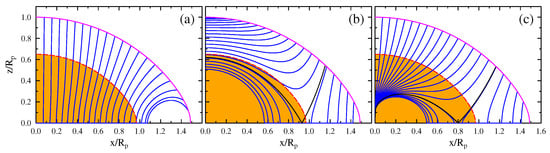
Figure 25.
Curves of internal constant angular velocity in the stellar envelope (blue lines). (a) Curves corresponding to the condition ; (b) curves obtained with ; and (c) curves calculated for . The solutions are valid in the convective envelope, i.e., above the shaded central region [S = specific entropy; j = specific angular momentum; and = distance to the rotation axis]. Ordinates coincide with the rotation axis; abscissas are in the equatorial plane. Adapted from Zorec et al. [141].
The curves can have surface imprints as an atmospheric latitudinal differential rotation that can be sketched using the following relation
where is the distance to the rotation axis; is the normalized radius vector that describes the stellar surface, is the polar angular velocity, , and are constants. It follows that from Equation (46) that the equatorial angular velocity is . The Doppler displacement due to radial velocity at a point in the stellar surface is
where the reference system is centered on the star, with the z axis is positively directed toward the observer and the x and y axes are in the plane of the sky. To more clearly characterize the Doppler displacements described by Equation (47), this relation is normalized by the displacement produced in the limb at the equator
where is the angular velocity at the equator and is a constant independent of that represents an isoradial velocity curve. Figure 26a,b show constant for angular velocities accelerating from the pole toward the equator, while Figure 26c shows a case where is accelerated from the equator towards the pole. In cases ‘a’ and ‘b’, the maximum Doppler displacement is produced at the stellar limb in the equator, while in case ‘c’, this maximum is produced in the middle of the closed circles (‘owl’ eyes) on the visible part of the meridian contained in the plane. In this case, the curve is also closed and contains the equatorial limb point, while all the remaining curves for are closed. In Figure 26b, two curves are shown (red dotted and dashed curves) that produce the same Doppler displacement, i.e., , where denotes the radial velocity for rigid rotation (red dotted line) and is for differential rotation (red-dashed curve). Both isoradial velocity curves coincide at the equator, nevertheless, the curve is longer than for . This is the main source for the difference detected in the residual intensities of absorption lines broadened by rigid and differential rotation laws.
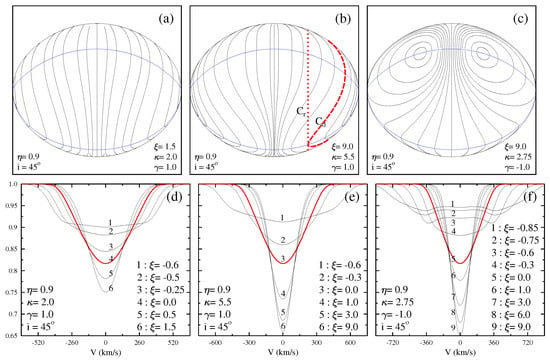
Figure 26.
Upper series: Curves of constant radial velocity contributing to the rotational Doppler broadening of spectral lines. (a) curves for a Maunder-like surface angular velocity law with ; (b) curves for a law given by Equation (46) with , so that ; (c) curves for a law given by Equation (46) with , so that . In cases (a,b), the largest Doppler displacement is produced in the limb at the equator, while in case (c), the largest Doppler displacement is produced in the center of the upper closed curves. Case (b) identifies the lines producing the same Doppler displacement, , where (red dotted line) indicates a rigid surface rotation, and (red-dashed line) a differential surface rotation. In all cases, the parent Doppler displacement from rigid rotation is determined by the straight line touching the corresponding curve at the equator. Lower series: Gaussian line profiles broadened by rotation, whose intensity and equivalent width depends on the effective temperature and gravity such as a HeI 4471 transition: (d) line profiles for the curves of constant radial velocities of the type shown in (a) for several parameters in Equation (46); (e) line profiles are for the constant radial velocities shown in (b) for several parameters ; (f) line profiles are for the constant radial velocities shown in (c) for several parameters . Calculations include gravitational darkening. The parent non-rotating object has 22,000 K and . The angular velocity law is given by Equation (46) with the same parameters () as in the corresponding upper blocks, except that takes a wider range of values. In all cases, represents the rigid rotation and the corresponding line profile is red-highlighted. In all blocks, the ordinates are the same. Adapted from Zorec et al. [127].
Putting and in Equation (46), the known Maunder relation is recovered and used here below to produce examples of effects due to the surface differential rotation on the value of
In Figure 27, the parameters in km s obtained are shown with the FT technique of the HeI 4471 and MgII 4481 lines broadened by differential rotation. In the ordinates, the measured apparent parameter is given, while in the abscissas is given the nominal rotational quantity that would correspond to the true equatorial velocity . Thus, if the stars had their atmosphere in differential rotation, the parameters obtained with the currently used measurement methods would depend on the degree of differential rotation and sensitively differ from the expected values if they were rigid rotators. The difference is due, on the one hand, to the geometry of the constant radial-velocity curves contributing to the individual monochromatic Doppler displacements that contribute to the broadening of a spectral line, and on the other hand, to the inadequacy of the measurement methods, which are not adapted to the physical circumstances imposed by the differential rotation. In stars rotating with an angular velocity accelerated from the pole toward the equator (), the measured implies that , where is the actual linear rotational velocity of the equator. Conversely, a differential rotation accelerated from the equator toward the pole () leads to a where . It also follows from these results that, for a given absolute value , the differences are larger for than for .
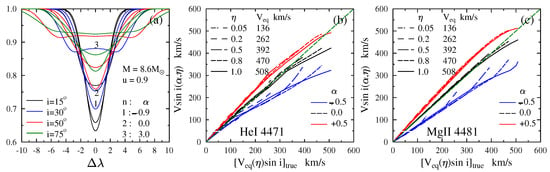
Figure 27.
(a) Gaussian absorption lines broadened by rotation, whose intensity and equivalent width depend on the effective temperature and gravity, as does the HeI 4471 transition. The gravitational darkening is calculated for an object of mass and fractional age rotating at the equator with . The angular velocity law used in the calculations is given by Equation (46). The colors indicate inclination angles, but in this figure, only the (blue) corresponding to different values of are explicitly identified. (b) Measured parameters in km s by means of the FT technique of the HeI 4471 line broadened by differential rotation characterized by the different values of the parameter in an object having 23,000 and rotating at different rates . In abscissas, there are the true equatorial for the same rates . (c) Idem for the MgII 4481 line. Adapted from Zorec et al. [127].
5.8. Line Profiles Produced by Near-Critical Rigid Rotators
Jeffery [421] pointed out that the line profiles emitted by rapidly rotating B-type stars may have flattened cores or even present emission-like reversals. This phenomenon is partially due to the GD effect that makes the local absorption contributions from the equatorial regions to the broadened profile reduced. On the other hand, due to the stellar rotational flattening, the iso-radial velocity curves constant can be shorter than some of them for slightly larger radial velocities, thus favoring a less efficient absorption that translates into an apparent reversal or emission in the broadened line core. This phenomenon was widely studied by Takeda et al. [422], Takeda et al. [423] in the metal lines of Vega ( Lyr, HD 172167). The formation of emission-like reversals due to similar physical circumstances, but in objects with surface differential rotation was evoked by Zorec [424].
5.9. Double Valued Vsini
Objects with angular velocity laws accelerated toward the pole may present polar dimples [235,236,258,260]. In such configurations, the largest contribution to the Doppler broadening of spectral lines comes from a point situated on an intermediate latitude on the stellar meridian facing the observer. For large inclination angles, the contribution to the line broadening produced by the closed curves corresponding to (see Figure 26c) can be partially hidden in the troughs, which, in addition, can be more or less dimmed by the limb-darkening. The relation between the FWHM of spectral lines and the then becomes double valued, as shown in Zorec [20], Zorec [153], Zorec [424]. Photometric, spectroscopic and interferometric measurements have not yet been able to signal the existence of ’normal’ stars with polar dimples, as mentioned in Section 3.3.
5.10. Asymmetrical Rotational Broadening Functions: Expanding Layers and tidal Interactions
When a common rotational broadening function (RBF) is determined by the deconvolution of all spectral lines present in a given spectral range, there is only a small chance that its shape is entirely symmetric [425,426]. This is because lines due to a variety of elements and their different ionization states are formed in atmospheric layers having different physical conditions and perhaps characterized by different velocity fields entertained by non-radial pulsations, convection movements, more or less expanding layers of nascent stellar winds, etc. It can be shown that, independently of the sign of the skewness of the RBF, the derived parameters are somewhat underestimated [260].
During the 1970s and 1980s, a large amount of literature dealt with the spectral line formation problem in moving stellar atmospheres (as can be seen in [86,87,119,427,428,429,430,431,432,433,434,435,436,437]). The typical outbursts and fadings in Be stars, which are thought to be the consequences of huge discrete ejections of mass [68,69,71,438], also imply that there are periods with outward accelerated layers in the stellar atmospheres. The combination of expanding velocities with rotation produces broadened and blue-shifted spectral lines that can be schematically described with rotation-expansion broadening functions (REBF). These functions are asymmetric, and depending on the ratio of characteristic velocities , they can become truncated. This phenomenon was analytically studied in the frame of uniform expansions by Duval and Karp [439] and numerically in Zorec et al. [260]. Their results suggest that: (1) the underestimation of cannot be negligible if the studied B and Be stars were observed at phases when their atmospheres were driven by expanding velocity fields; and (2) the blue-shifts of lines can be more or less chaotic; they could partially explain irregular radial velocity drifts, which are sometimes suspected due to undisclosed binaries.
6. Interferometry of Rotating Stars
Because optical and IR long baseline interferometry is sensitive to the stellar geometry and to its brightness distribution projected onto the sky, this technique has become an important tool to study the effects of stellar rotation all over the HR diagram. The mathematical implement to study stars by interferometry is the CittertZernike theorem, which establishes a relation between the complex visibility and the Fourier transform of the brightness distribution on the object. Moreover, the spectro-interferometry (differential interferometry) is a new technique combining high spectral and angular resolution, which enables the study of phenomena that induce chromatic signatures produced by spots, large-scale mass motions such as differential rotation, zonal currents triggered by the hydrodynamic instabilities and non-radial pulsations. In this technique, the phase of the interference fringes is proportional to the barycenter of the stellar brightness distribution [440,441,442,443]. Among the most important contributions with these modern techniques were those made with interferometers including: (1) the Center for High Angular Resolution Astronomy (CHARA) array, e.g., [444], formed by six telescopes of 1 m distributed in a y-shaped configuration having 15 baselines ranging from 34 to 331 m, and joined by several beam combiner instruments operating from the visible to near-IR in the San Gabriel Mountains of southern California; (2) the Navy Prototype Optical Interferometer (NPOI), e.g., [445] in Arizona, which is a long-baseline optical interferometer with subarrays for imaging and for astrometry. The imaging subarray consists of six movable siderostats of 50 cm with baseline lengths from 2 to 437 m; (3) the Palomar Testbed Interferometer (PTI), e.g., [446], a long-baseline infrared interferometer (operating in the H and K bands) installed at Palomar Observatory having baselines up to 110 m; and (4) the Very-Large Telescope Interferometer (VLTI), e.g., [447,448]) on Cerro Paranal (Chile). This European Southern Observations (ESO) interferometer includes four unit telescopes (UTs) of 8.2 m and four auxiliary telescopes (ATs) of 1.8 m that can form six baselines, all with different lengths and orientations. The baselines (AT and UT) range from 16 to 140 m. The light beams collected by the individual telescopes are brought together in the VLTI using a complex system of mirrors in underground tunnels. At the beginning, the beam combiner instruments active at near and mid-infrared wavelengths were AMBER, MIDI, PRIMA and VINCI. Today, the operating instruments are GRAVITY, MATISSE, and PIONIER (https://www.eso.org/sci/facilities/paranal/telescopes/vlti.html). Details on the properties of the visibility curves calculated for rapid rotators that can be detected with these instruments may be found in Domiciano de Souza [449], Domiciano de Souza [450].
The first although unsuccessful attempt to measure the geometrical deformation of a rapidly rotating star was carried on Altair (HD 187642, an A7-type star), which dates back to Brown [451]. Domiciano de Souza et al. [452] were the first who determined the apparent rotational flattening of Achernar (HD 10144, a B5IIIe star) using the VINCI instrument at the VLTI. They obtained a flattening ratio much higher than the limit imposed by the Roche approximation (). Vinicius et al. [453] discussed the fundamental parameters of this star and suggested that a circumstellar disc may contribute with additional IR radiation to produce an apparently excessively large flattening. This possibility was lately studied by Kanaan et al. [454] who concluded that the disc should be smaller than that foreseen by Vinicius et al. [453]. Kervella and Domiciano de Souza [455] found that the Be star Achernar also presents a polar wind. Later interferometric observations of this star during an emissionless phase by Domiciano de Souza et al. [275] lead the authors to determine the actual flattening of the star , which corresponds to a critical velocity ratio and a measured GD exponent in units of used in this review (i.e., in the present review, we used the exponent related with the bolometric flux: , while other authors may consider this exponent related with the effective temperature: ). Technical aspects and interferometric results on B-type stars as rotators are summarized in van Belle [456].
The study of the photocenter displacement using interferometric data obtained for Regulus ( Leo, a bright B7V star) with AMBER at high spectral resolution across the spectral line enabled Hadjara et al. [457] to determine the stellar flattening , the critical rotational velocity ratio , the inclination angle and the GD exponent in units used herein. Vega ( Lyr), the second brightest star in the northern hemisphere after Arcturus, has been long suspected of being a rapidly rotating star seen nearly pole-on, e.g., [458], deserving attentive interferometric studies [459,460,461,462]. Concerning Vega, the authors concluded that the star rotates at () and that the inclination angle of its rotation axis is . The B-type star Per was observed with the VEGA/CHARA interferometer by Challouf et al. [463], and the data were analyzed using a code of stellar rotation, CHARRON [464,465], in order to derive the stellar physical parameters. The estimated stellar flatness is , the inclination angle and the velocity ratio .
As noted in Section 5.7, the iso-radial velocity curves in the observed hemisphere of a star having surface differential rotation are not straight lines but curves. These curved lines induce distortion effects on the spectral lines and thus on the position of the wavelength dependent position of the brightness distribution barycenters that could in principle be exploited by the spectro-interferometric techniques [466] to derive the inclination angle of stars and the Maunder differential rotation parameter (as can be seen in Section 5.7). Differential rotation also induces changes on the stellar geometry that can be distinguished from those induced by the rigid rotation which could also be studied by interferometry [141]. In order to constrain the parameters empirically characterizing the surface differential rotation, instruments operating in the visible range are needed to combine high spatial resolution (∼0.2 mass) and spectral resolution as high as 100,000 in order to reach 0.1 Å in spectral lines which are sensitive to this effect, in particular the HeI lines. It is estimated that with spectral resolutions of 20,000, it would perhaps be possible to have access to parameters of the differential rotation if the measurements of radial velocities are made with precision km s and phase shifts with [467,468].
Apart from the above cited works, a significant number of Be stars were observed by interferometry with VLTI/AMBER, VLTI/MIDI (mid-IR) and CHARA/VEGA (visible) that enable carrying out statistical studies on the geometrical and kinematic properties of their CD [467,469,470,471,472,473,474,475,476,477,478]. However, as the inclination angles of the rotation axis can be estimated by the interferometric methods, in some of the above cited works, the critical velocity ratio has also been estimated for many of the studied Be stars. Meilland et al. [469] concluded that CMa has a rotation ratio no larger than . In Meilland et al. [472], it is shown that Sco must have . From a study of eight Be stars [473], it comes that they have on average , with extreme values for Cen and for Col. Stee et al. [476] concluded that Cas is a critical rotator. An interesting discussion was presented by Delaa et al. [467] on the Be star Cephei, whose previous estimates of range from [479] to [273] and the exponents of the von Zeipel relation ranging from to , respectively. Delaa et al. [467] obtained that, in this star, (as an exponent of the von Zeipel relation), and demonstrated that a differential rotation at the surface of a fast rotating star may affect the brightness distribution over the stellar disc and significantly modify the value of the exponent. Accordingly, other parameters, particularly inclination angle, can also be affected. Recently, Cochetti et al. [478] observed 26 Be stars and determined the critical velocity ratio for seventeen of them, the average value of which is .
7. The Origin of the Stellar Angular Momentum
7.1. First Findings and Discussions
The rotation velocities of young stars are related to the mechanisms of star formation by means of angular momentum dissipation processes in protostellar clouds. Apart from the highly puzzling questions associated with the problem of how stars dispose of angular momentum and how the angular momentum transfer proceeds between discs and protostellar clouds [480,481,482], observational studies have inquired into the nature of the relation between stars and protostellar clouds.
Leaning on the idea by Larson [483], where it is suggested that the processes of star formation through the dynamics characterizing the collapse of protostellar clouds are controlled by the rate of dissipation of angular momentum, it was postulated that the rotation of stars may also depend on their location in the Galaxy. Accordingly, Burki and Maeder [484] showed that the size of young open clusters (age Myr) in the solar neighborhood increases with the galactocentric distance. They also noted that, within 1 kpc from the Sun, the averages of B and Be stars of spectral type B0–B4 increase towards the galactic center, while the fraction of binaries does not seem to depend on the galactocentric distance in the studied environment. Their conclusion was that the noted gradient of rotational velocities can be due to the collapsing time of protostellar clouds, where a higher content of heavy elements can accelerate the collapsing process with a consequent lesser dissipation of angular momentum, thus forming stars with higher rotational velocities.
Using a representative sample of rather early-type stars (spectral types B0–B5), Wolff et al. [327] noted quite a large number of slow rotators that they could not account for neither by magnetic braking, loss of angular momentum through tidal interaction in close binaries, nor by evolution from the ZAMS in the frame of angular momentum conservation. They suggested that the stars were formed with initial low angular momentum and that their observed rotational velocity, as well as the random orientation of inclinations, are the consequence of gravitational interactions in the proto-cluster clouds.
Guthrie [485] tried to clarify the picture foreseen by Wolff et al. [327], where the sample of stars with luminosity class V seemed to be underrepresented and that there is a bias against Be stars. To this end, Guthrie [485] studied the distribution of parameters of B-type stars in young and older subgroups of OB associations and field stars. For B0–B5 type stars, in both subgroups, the distributions of are quite similar for km s, but in the older subgroups, there is an excess of objects with km s. A noticeable difference exists between the distributions of of B0–B5 compared with those of B6–A0 stars in young subgroups. The latter have clear bi-modal distributions. When it comes to B0–B5 field stars, those of luminosity class V do not reveal a striking difference in the distributions between fields and older subgroups of associations. B0–B5 field stars of luminosity classes III–V have a similar distribution to those above, but they have a high fraction of rotators with km s. These results suggest that there may be a difference between the rotational properties of stars in tightly bound clusters as compared to those of field stars which probably originated in loose stellar systems.
Knowing that the ratio between the specific angular momentum in an interstellar cloud and that of an average star is approximately (, there must exist an efficient mechanism of angular momentum dissipation. When this dissipation proceeds through successive collapses, theoretical predictions say that the rotation axes should tend to be perpendicularly aligned to the galactic plane [481,486]. According to Guthrie [485] and the references therein, the -distribution of late B-type stars in tightly bound clusters has a bimodal distribution of true rotational velocities V, where it is then speculated that the group of larger values of V could be broad and the axes of rotation being rather aligned, i.e., while there is a paucity of from roughly 80 to 160 km s, the larger values of V correspond to a distribution of from 160 to 400 km s with a maximum at km s. The distribution of V for all B-type field stars is consistent with a Maxwellian law, in accordance with which was predicted by Deutsch [487] using methods of statistical mechanics and assuming random orientations of the axes of rotation. Guthrie [485] concluded that the older subgroups originally had a similar distribution of rotational velocities to those of young subgroups, but the excess of slow rotators was probably formed at a later epoch, out of materials with low or exhausted angular momentum.
Maeder et al. [488] used the fraction of Be stars in different galactic regions and Magellanic Clouds as a surrogate indicator for the influence of the metallicity on the rapid rotation of stars. The results show that the lower the metallicity the faster is, the stellar rotation, a phenomenon that can be easily explained assuming that, under similar distributions of initial angular momentum, stars having lower metallicity rotate faster because their radii at the ZAMS are smaller than those of stars with higher metallicity. Keller [337] also studied the effect of metallicity on the rotation of B-type stars in the LMC. He concluded that stars in clusters rotate more rapidly than in the surrounding field regions, and that both field stars and stars in clusters rotate more rapidly in the LMC than in the Galaxy.
7.2. Stellar Axial Rotation of Field and Cluster B and Be Stars
Strom et al. [340] formulated the hypothesis that large differences can exist among the rotational velocities of stars born in forming regions having large densities compared to those formed in regions with low densities. The hypothesis is that differences in accretion rates should leave imprints characterizing the axial rotation of stars, because higher accretion rates in denser regions produce a higher rotation favored by the initial radii along the birth line, which are larger among stars having masses in the range 4.5–9. These objects should then show the largest differences in the rotation speeds, which is a direct result of a greater spin-up during the contraction period towards the ZAMS. However, at even higher masses, the difference in rotation speeds between the cluster and field stars can be smaller, because the initial radii along the birth line are similar, or they can even be identical if the birth line joins the ZAMS.
Strom et al. [340] have compared the rotational velocities of B0–B9 stars in the dense double cluster h and Persei with those in the nearby field having roughly same ages ranging from 12 to 15 Myr. The age group represented by masses in the range – have twice as large average rotational velocities than nearby field stars do. This ratio is about one and a half that of the field for objects with masses from 5 to , and velocities are just slightly different between the younger groups with 9–, as foreseen in the above formulated hypothesis. This hypothesis was studied in two other contributions by Wolff et al. [347] and Wolff et al. [348]. In the first one, using a large sample of B0–B3 stars in nine clusters and respective neighborhood fields, the authors confirmed that the rotation velocities of stars in clusters are larger than for field stars, and that there is a lack of slow rotators among stars in the clusters. Moreover, the velocities of stars with masses from 6 to do not seem to change significantly over an initial evolutionary period from the ZAMS up to 12 Myr. In the second contribution, it is shown that rotation velocities in the compact R136 LMC cluster are larger than those in the nearby field stars, and also that the LMC stellar rotation velocities both in the R136 LMC cluster and field are larger than those in the MW stars in similar clusters and fields. In these last comparisons, the difference between LCM metallicity and the average one in the MW plays a significant role in the establishment of the noted axial rotation velocity difference.
In a study of rotational velocities of B stars in the Galactic clusters NGC 3293, NGC 4755 and NGC 6611, Dufton et al. [318] note that, in the two older clusters NGC 3293 and NGC 4755, the true rotational velocities of all B-type stars have a Gaussian distribution, and that the are larger than those of field stars, which agrees with the conclusions by Strom et al. [340]. They also find a spin-down effect for stars with masses , which is probably due to angular momentum loss by strong stellar winds.
Huang and Gies [323] studied the rotation of B-type stars in 19 MW open clusters with ages spanning from 6 to 73 Myr. As compared to nearby field stars, clusters have fewer slow rotators, which in a way agrees with the findings in the above cited works by Strom et al. [340] and Wolff et al. [347]. At ages Myr, the number of rapid rotators increases. However, contrarily to Strom et al. [340] and Wolff et al. [347], Huang and Gies [323] speculated that the field stars rotate more slowly than their counterpart in clusters because they are slightly more evolved. In Huang and Gies [489], the authors addressed the study of the evolution of the axial rotation of OB stars in clusters with masses in the range from 8.5 to and find that the rotation of these objects slows down during the MS phase. The small number of rapid rotators found in their sample are supposed to be spun up in the short secondary contraction phase, or by mass-transfer in close binaries. Their sample has many He-weak and He-strong objects having 23,000 K. For stars with 18,000 K, the He abundance is characterized by a broadly scattered distribution, which impedes to differentiate between the He-weak, He-normal, and He-strong stars. This makes it impossible to study the He abundance changes due to evolution. However, the He abundance augments at advanced evolutionary stages in more massive and highly rotating stars, which supports the theoretical prediction of mixing induced by rotation. By comparing the rotational velocities of the field and the cluster samples, Huang and Gies [349] concluded that the main reason for the overall slower rotation of the field sample is that it contains a larger fraction of older stars than found in clusters. Since in the approach by Huang and Gies [349], the estimated parameters are better surrogates of stellar ages than the spectral-type groups defined in Strom and Wolff et al., where they considered the spectral classes as indicators of groups having distinct evolutionary stages, their conclusions cast some doubts on the incidence of higher densities in the formation environments to produce faster rotators.
The interesting subject of the stellar rotation census of B-type stars from ZAMS to TAMS was addressed by Huang et al. [353], where the results indicate that the rotational distribution functions of for the least evolved B stars show that those with lower masses are born with a larger proportion of rapid rotators than higher mass B stars. Nevertheless, the upper limit of separating highly rotating B stars from B stars without emission lines is smaller among the higher mass B stars. The spin-down rates observed in stars with masses agree rather well with theoretical predictions, but the rates are larger for the low-mass group (mass ). The faster spin-down in the low-mass B stars agrees well with the predictions based on differential rotation if the angular momentum is conserved by individual shells. The results also suggest that, among the fastest rotators, which are probably Be stars, the most massive ones have probably been spun up by evolution. It is not excluded that the merger phenomenon in binaries may explain the rapid rotation in many cases over the full range of B star masses.
Using the data published in all the above cited works, the quoted results are summarized in a graphical way in terms of the true rotational velocities V and ratios , and ( is the critical equatorial velocity) as a function of the stellar mass and fractional age ( is the time spent by a star in the MS) in Figure 28 and Figure 29. The distributions of velocities and velocity ratios are histograms smoothed using the methods specified in Zorec et al. [127]. From Figure 28, it can be concluded that field stars are slightly more evolved than those in clusters, as claimed in Huang and Gies’ papers. It is also obvious that in clusters, there is a good probability of finding a larger fraction of more rapid stars, as suggested by Strom et al. [340] and Wolff et al. [347]. Figure 29 resumes the evolution of field and cluster stars, which shows that within the margins of uncertainties, there is a small difference among the field stars with mass , as found in the first quarter of the MS lifespan. The diagram suggests a slight acceleration of the rotation for the low-mass stellar group that passes from the fractional age intervals to . They show no particular evolution until the last age interval , except that, in this last case, the distribution of against the mass is more scattered. Concerning the cluster stars, it is apparent that the less massive stars have on average larger values of than the more massive ones, but for all masses and fractional age intervals, they have on average larger ratios than field stars. In the age interval , there seem to be a lowering of ratios among the less massive cluster objects. The acceleration noted for stars with should not be taken at face value, since there are very few objects entering the calculation of . The behavior of the rotational velocities of field stars with masses is described in some detail in Section 8.4.
Figure 28.
Two left blocks: smoothed and normalized distributions of the true V and ratios of the B-type star rotational velocities with masses (upper row) and with masses (lower row). Right blocks: histograms of fractional age distributions of stars in the respective left blocks.
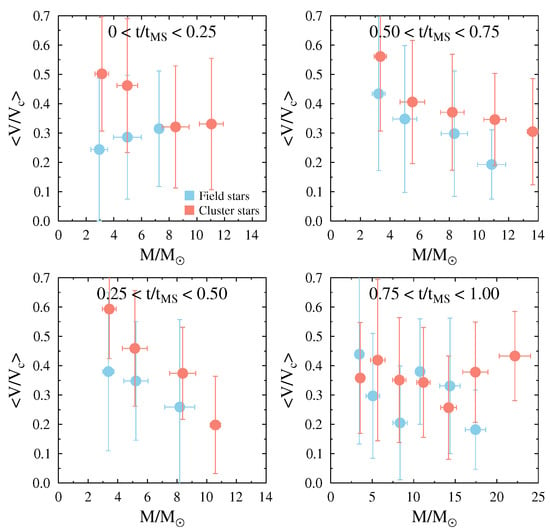
Figure 29.
Average ratios of true velocities of field and cluster B-type stars against the stellar mass per fractional age intervals.
7.3. What about Be Stars?
In the preceding studies, no particular attention was paid to Be stars for reasons that can lead them to become rapid rotators. There are at least three reasons that were observationally put to test in order to try to understand why they are extreme rotators: (1) the Be star may have been born as a rapid rotator; (2) the mass transfer can produce efficient spin up; and (3) evolutionary factors can produce spin up during the MS evolution of B stars.
Fabregat and Torrejón [490] concluded that the highest fractions of Be stars in clusters having spectral types B0–B2 appear more often at ages from 13 to 25 Myr, which could be interpreted that they have undergone evolutionary spun up by the end of a B star’s MS lifetime. Keller et al. [491] also finds that the fraction of Be stars attains a maximum at the end of the MS. Similar behavior can be seen in the Be population of young clusters in the Magellanic Clouds. These results may suggest that there is an evolutionary enhancement of the frequency of the Be phenomenon toward the end of the MS lifetime as a consequence of a spin-up produced by angular momentum redistribution phenomena related to the stellar evolution.
From a photometric study of Be stars in more than 50 MW open clusters, McSwain and Gies [492] noted that the frequency of Be stars correlates neither with the gradient of the metallicity in the Galaxy, as could be expected from the discussion by Maeder et al. [488], nor with the cluster density proposed by Strom et al. [340] and Wolff et al. [347]. On the contrary, McSwain and Gies [492] found that the fraction of Be stars increased with age until 100 Myr, and Be stars are most common among the most massive B-type stars above the ZAMS. They showed that a spin-up phase at the TAMS cannot produce the observed distribution of Be stars, but up to 73% of the detected Be stars must have been spun up by mass transfer in binary systems. The remaining Be stars could be rapid rotators at birth.
In the above-cited photometric studies, no correction of magnitudes and photometric color indices were carried for overluminosty and reddening induced by the circumstellar discs of Be stars [18,152], nor were they corrected for rapid rotation effects [259], which can introduce significant age overestimates [493]. Using BCD parameters, which avoid the perturbation effects due to circumstellar emissions, Zorec [20] showed that Be stars appear throughout the MS evolution lifespan. Correcting fundamental parameters for rotational effects, Zorec et al. [61] brought additional proof that the Be phenomenon can appear at any evolutionary stage from ZAMS to TAMS.
As noted in the introductory paragraph of this section, stars can gain angular momentum thanks to mass transfer phenomena in binary systems [494,495]. Klement et al. [496] confirmed the existence of far-infrared SED turndowns in a series of 26 Be stars, which can be due to the presence of companion stars that influence the structure of the Be star CD. The confirmation of the mass transfer phenomenon as responsible for the rapid rotation of these Be stars is now suspended to the confirmation of the subdwarf nature of their companions. A further discussion on the merger phenomenon is performed in Section 8.1.
7.4. Distribution of the Rotational Velocities of B and Be Stars
Among the first statistical studies carried out on the distribution of parameters can be noted the discussion by Huang [497]. He speculated on the possibility that the spin vector of the star follows a Maxwellian distribution, as previously suggested by van Dien [498] for B-type stars. Assuming that the rotational velocity decreases as the space velocity increases when stars become older, Huang [497] also expected to find some correlation between the rotational velocity and the space velocity, but the results were not conclusive.
Since the projection factor obliterates the actual information carried by the true stellar axial rotational velocity V, Slettebak [499] and Slettebak and Howard [500] used a homogeneous sample of parameters to study the distribution of the true velocity V of B-type stars gathered in two sub-spectral type groups: B2–B5 and B8–A2. To this end, he employed the analytical representation of the true rotational velocities suggested by van Dien [498]
where J and are free parameters which can be determined using the Abel-like integral equation studied by Kuiper [501] and Chandrasekhar and Münch [502], which transforms into the distribution of apparent rotational distribution assuming that the inclination angles are distributed at random. Slettebak concluded that the mean true rotational velocity of the main-sequence stars with types B2–B5 is approximately 200 , which is a little larger than the corresponding one for the B8–A2 stars. In both groups, no distinction was made between B-types stars with and without emission. Moreover, the subdivision of main-sequence stars into B1–B3 and B5–B7 groups shows that the B5–B7 stars have the greatest axial rotation, and the stars of intermediate luminosity have a smaller axial rotation than the main-sequence stars. A detailed study of true rotational velocities of stars in groups of spectral types O9–B1.5 and B2–B5 was carried out by Balona [324]. The parameters were transformed into the system established by Slettebak et al. [317] and the distributions of were corrected for measurement uncertainties using the method of Eddington [503]. The stellar sample was carefully divided into dwarfs, giants, supergiants, but also dwarf and giant emission-line stars, and binaries. Balona [324] used polynomials to represent the distribution functions and and concluded that B stars probably do not rotate as solid bodies. Because of difficulties to decide whether the studied Be stars were dwarfs or giants, no conclusion was drawn on their critical rotation. Nevertheless, the distributions of the Be star true rotational velocities show that almost all are far from being rotating near their break-up velocity.
From a compilation of rotational parameters, in Figure 30, the distributions of true rotational velocities of B stars are shown with and without emission lines listed in the Bright Stars Catalog [147,148]. These distributions were calculated using the Lucy–Richardson method [504,505]. Corrections for observational uncertainties as detailed in Zorec et al. [127] were taken into account to transform the distributions of into distributions of true rotational velocities. These enable having a first overview of the effect of the evolution of rotational velocities, as well as differences between their values for B and Be stars. The population of B stars without emission lines encompasses objects of different classes, Bn, B magnetic, etc., which can be readily realized due to the irregular aspect of their distributions. The distributions of true rotational velocities are shown in Figure 30, where it can be seen, mostly for Be stars, that the lower the maxima of distributions are, the more evolved the stars are. The evolution of rotational velocities in Be stars has also been studied by Yudin [506], who shows that the average of ratios per spectral type classes increases as stars evolve in the MS.
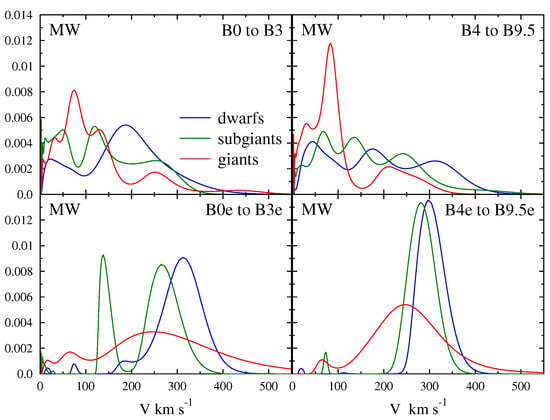
Figure 30.
Normalized distributions of true rotational velocities of Milky Way (MW) B and Be stars separated by spectral type groups and luminosity classes. Velocities are not corrected for the gravitational darkening effect. Adapted from Zorec [153].
In the above discussions, the overestimation of the parameters due to the GD effect in stars with rapid rotation was not taken into account. For the first time, this was performed by Stoeckley [382] in a study of Be stars. As already noted in Section 5.4, the GD effect induced an underestimation of the parameters in rapid rotators, which encouraged Stoeckley [382] and Townsend et al. [384] to conclude that Be stars rotate close to the equatorial breakup velocity. Cranmer [385] and Zorec et al. [127] produced distributions of ratios with parameters corrected for GD effects which enable the calculation of the fraction of Be stars which are critical rotators in the studied sample. This correction uses the theorem of von Zeipel with , which overestimates the GD effect [260,280]. Cranmer [385] and Zorec et al. [127] conclude that just a tiny fraction of Be stars are perhaps critical rotators. The distribution of their is near symmetrical, it covers the range of velocity fraction , and the maximum of their frequency is at (as can be seen in Figure 31). The small fraction of stars in the interval could have these characteristics only temporarily. This could be due to the prograd velocities of non-radial pulsations that add to the stellar rapid rotation, and put the object in conditions of critical rotation that help trigger discrete mass ejections [126]. This could also correspond to evolutionary phenomena, as discussed by Krtička et al. [128]. Nevertheless, the large majority of Be stars do not rotate at their critical limit. Marsh Boyer et al. [354] also concluded that Be stars in the h and Per clusters are not critical rotators, but no clear correction of the measured parameters for the GD effect is apparent in this work.
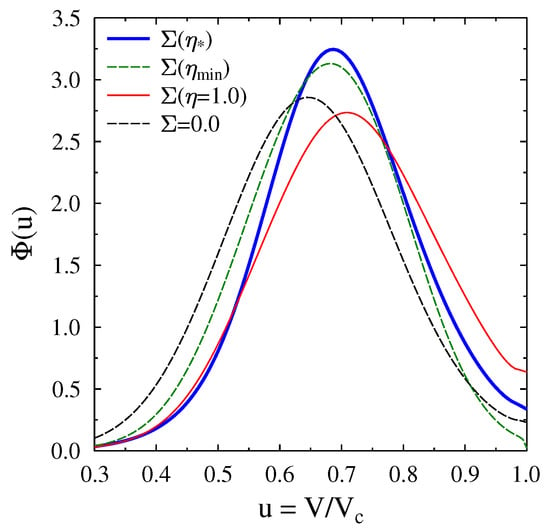
Figure 31.
Distributions obtained with Stoeckley’s corrections calculated for different values of : ; ; and . Adapted from Zorec et al. [127].
Because the distribution of ratios depends on Stoeckley’s correction given in Equation (45), it is worth showing its dependence on the adopted value of the acceleration ratio . In Figure 31, four extreme cases are shown: (a) all stars have the lower possible rotational parameter , i.e., the value derived when we consider that (dashed green line); (b) Stoeckley’s corrections estimated for the critical rotation, i.e., (red line); (c) neglecting Stoeckley’s correction, i.e., in all stars (black dashed line); (d) Stoeckley’s corrections estimated for derived for each star individually (blue full line). As expected, approximation (a) produces a slight excess of slow rotators (dashed green line); solution (b) is characterized by an excess of rapid rotators; (c) the distribution is shifted to smaller values of .
In this section, we mentioned several methods that were used by different authors to obtain the distribution of the true rotational velocities of stars, particularly those of Be stars used to test their critical or non-critical character as rotators. There exist, however, other methods to deconvolve the known Fredholm integral that relates the distribution of apparent rotational velocities with the probability distribution of true rotational velocities, although so far, they have not been applied to discuss the specific cases of stellar rotational velocities. Curé et al. [507] developed a method to deconvolve this inverse problem through the cumulative distribution function for true stellar rotational velocities, which completes thus the work of Chandrasekhar and Münch [502]. Christen et al. [508] discretized the Fredholm integral using the Tikhonov regularization method to directly obtain the probability distribution function for stellar rotational velocities. Orellana et al. [509] proposed a method based on the maximum likelihood (ML) estimate to determine the true rotational velocity probability density function expressed as the sum of known distribution families.
7.5. Rotational Velocities of B and Be Stars as a Function of the Metallicity
Stars with low metallicities undergo less violent nuclear reactions and are consequently more compact. Given a similar distribution of total angular momenta in media of different metallicities, stars will on average have faster rotational velocities the lower the metallicity is. Motivated by this fact, much effort has then been devoted to comparing the rotation rates of OB stars to the center of our Galaxy and as a function of the metallicity in our neighboring SMC and LMC dwarf galaxies. These comparisons have been made using Be stars as testimonials and as rotators, knowing that they are indeed very fast rotators. Thus, Maeder et al. [488] found that the fraction of number of Be stars increases if the metallicity decreases. On the other hand, Martayan et al. [345], Martayan et al. [346] studied the distribution of true velocity ratios as a function of the Be star mass and as a function of the metallicity, using MW, SMC and LMC stars. Their results, summarized in Rivinius et al. [40], show that the Be stars of all masses have on average relations closer to 1 the lower the metallicity of the medium is where they were formed. The angular velocities of SMC Oe/Be stars are on average in the ZAMS, which are in the theoretically predicted zone for the Long-Gamma-Ray-bursts (LGRBs) progenitors [510]. Martayan et al. [511] discussed this occurrence and considered that low-metallicity early Be and Oe stars can be potential LGRB progenitors. They estimated the yearly rate per galaxy of LGRBs and the number of LGRBs produced in the local universe up to , which agreed with the observed rate.
Recently, Ramachandran et al. [512] compared the distributions of parameters of OB stars in the MW [318,355,358], SMC [346,356,357] and LMC [350,513]. These distributions concern all OB stellar masses together, without particular distinction regarding the object peculiarities. From these comparisons, rough relations were obtained showing the variations of peaks of distributions and fractions of stars having km s as a function of metallicity. The relations obtained are
which clearly show that the lower the metallicity is, the larger the rotational velocities are. These relations depend on the characteristics of the evolution of the stellar rotational velocities in environments having different metallicities. In fact, apart from of the stellar size dependent on the metallicity of the medium where they are formed, which may characterize the initial stellar rotational velocity, the further evolution of the stellar surface rotational velocity is also determined by the mass-loss rate. These rates are significant in massive stars and they depend on the metallicity. They are stronger the higher metallicity is [514].
7.6. Two Different Visions on the Origin of the Stellar Angular Momentum
Krumholz [515] summarized and discussed the two main different classes of models proposed for the formation of massive stars. The first postulates that massive stars are assembled in a similar way to their lower mass counterparts, i.e., from in-falling material located in a rotating protostellar core, channeled by a magnetic field and rooted in the star through a circumstellar accretion disc, called the ’magnetospherically mediated accretion’ (MMA). According to Bonnell et al. [516], massive stars should form preferentially in cluster-forming environments. The second class of models stipulates that massive stars start their formation as low-mass protostellar cores in clusters and then grow up via mergers of cores located in regions where the density of cores is high (as can be seen in [517] and references therein). They can be referred to as ’core merger’ models (CM). Wolff et al. [341] tackled the problem of determining through observational tests which of these contrasting models—MMA or CM—dominates in nature. Data for O-type stars combined with data in the literature show that over a mass range from 0.2 to the specific angular momentum of stars varies slowly and continuously as . Moreover, nearly all stars in this mass range rotate along the birth line at rates that are not larger than . These findings lead the authors to conclude that a single mechanism must be at work to keep the rotation rates low and at similar values for stars of all masses at birth, and that their results seem to rule out CM models, or at best, they must be the exception. The continuity of angular momentum properties across the whole mass range from M stars to O stars argues for a common formation mechanism through a disc.
Because a high fraction of massive stars, perhaps the majority, are born as members of close binary systems, the populations of early-type MS stars may contain stellar mergers and several products of mass transfer in binaries. de Mink et al. [215], de Mink et al. [216] have undertaken the simulation of a massive binary-star population typical for our Galaxy, assuming continuum star formation. de Mink et al. [215], de Mink et al. [216] have found that 4–17% of early-type stars can be the products of mergers in binary systems and that 15–40% of MS massive stars are the products of binary interactions. Due to these binary interactions, 10–25% of all massive MS stars have rotational velocities in excess of 200 km s. In spite of several uncertainties related to the mass transfer efficiency and the detailed treatment of magnetic braking, the fraction of rapid rotators these authors derive is quite similar to the observed one. This casts some doubts on whether single stars can be formed as rapid rotators. Predictions allow for the possibility that all early-type Be stars result from binary interactions. Finally, the interpretation of anomalies of chemical abundances induced by rotational mixing is also strongly challenged by this working frame.
8. Understanding the Evolution of Rotational Velocities in Single Early-Type Stars
8.1. Models of Stellar Evolution with Rotation
In spite of the numerous efforts made to understand the evolution of rotating stars e.g., [154,255,290,518,519], the results obtained until now cannot be entirely validated, because they depend on several strong assumptions which are difficult to confirm, and because the model predictions have not been confronted with observations in all its aspects.
One of the greatest unknowns concerns the internal angular momentum transport. On the one hand, models by Maeder and Meynet [154] are based on diffusive and advective transport of angular momentum, while those by Heger et al. [255] consider only diffusive transports of angular momentum. More recently, Potter et al. [307], Potter et al. [519], Potter et al. [520] considered ‘shellular’ rotational velocity distribution as in the aforementioned models, but have taken into account both diffusive and advective transports of angular momentum, and tested several prescriptions for the many intervening diffusion coefficients. Moreover, they did not impose rigid rotation in the stellar convective core. On the other hand, all these models make, however, evolve stars assuming rigid rotation at the Zero-Age-Main-Sequence (ZAMS). This implies that, in all cases, stars are assumed to have the minimum possible content of total angular momentum, which is limited to a ratio of kinetic rotation energy, K, to gravitational potential, W, not exceeding the ratio for a rigid critical rotation . This rotation law switches in quite short time scales to a differential rotation law, in some y [254,521]. Internal differential rotation in stars has then every chance to be present before the stellar ZAMS phase. Nevertheless, before the ZAMS each star had a long pre-main sequence (PMS) evolutionary history, where, in any of its stages, it does not necessarily acquire a strict rigid rotation. Rigid rotation in the ZAMS is mainly supposed to be justified because: (a) dynamic stability against axisymmetric perturbations could be warranted for rigid stellar rotators [230]; and (b) the redistribution of angular momentum can be promoted by the turbulent viscosity [136]. It is then generally assumed that in the PMS full convection phase, stars become rigid rotators. However, Wolff et al. [522] concluded from the comparison of rotational rates on both sides of the convective–radiative boundary that stars do not rotate as solid bodies during the transition from the convective to radiative evolutionary tracks.
On theoretical grounds, it can be argued that, in the regions unstable to convection, the redistribution of the specific angular momentum can be controlled by the convective plumes [523], which favor the existence of rotation laws characterized by constant. Moreover, 2D hydrodynamic calculations show that convection does not maintain rigid rotation, but it produces an internal angular velocity distribution profile ( = distance to the rotation axis), with a value of p that corresponds to an intermediate configuration between the complete redistribution of specific angular momentum and rigid rotation, ( is for rigid rotation) [263,524,525]. It was rather recently shown that, in the stellar convective cores of rotating stars, thanks to the Reynolds stresses, there is a continuous redistribution of angular momentum that leads to a kind of cylindrical differential rotation because of a readjustment that tries to establish a constant specific angular momentum distribution, far from a rigid rotation condition [526,527,528,529]. According to these comments, initial (or ZAMS) internal rotation laws can be differential, which may enable, in principle, to concentrate larger amounts of angular momentum towards the stellar core than that enabled by the rigid rotation at critical regimes, i.e., global energy ratios that could attain . Finally, it can be noted that the solar convective regions, which are not only characterized by significant turbulence, but rotate differentially, do not conform to any intermediate rotation law between the above and extreme frames [417]. This rotation law may finally look like one of those that are inferred if it is assumed that the baroclinic balance relation is obeyed [141].
Undoubtedly, knowledge of the way that the internal angular momentum distribution is built up during the stellar formation processes may carry important consequences for the further evolution of stars on the MS. The magnetic coupling between the accretion disc and the star is believed to spin down PMS objects below the critical surface rotation. However, Rosen et al. [530] showed that such magnetic torques are insufficient to spin down massive PMS stars due to their short formation times and high accretion rates. The mechanism can only be effective if the disc lifetime of massive stars is longer than believed, or the magnetic fields are stronger than suggested by observations. Haemmerlé et al. [531] have tackled this problem assuming that the accreted matter has an angular velocity equal to that of the accreting stellar surface. These authors considered stellar masses ranging from 2 to 22 and found that the stars more massive than approximately 8 cannot reach the ZAMS with velocity rates higher than , and that for a given ratio , the internal differential rotation is of approximately 80% for objects with 2 , but decreases for more massive stars, reaching the 20% in stars with 14 . Moreover, the studied mechanism does not enable one to obtain rapidly rotating massive stars in the ZAMS. In another contribution, Haemmerlé et al. [532] studied several accretion scenarios and noted that smooth angular momentum accretion ends up with an angular momentum barrier that impedes the formation of massive stars. They observed that because shear instabilities and meridional circulation are quite ineffective to transport angular momentum during the accretion phase, the internal rotational profile reflects the angular momentum accretion history. This transport is more efficient by convection. However, as during the accretion phase, large radiative zones are formed and the angular momentum is conserved locally, which can lead to significant internal differential rotation. Whatever the angular momentum accretion scenario during the PMS period, the internal rotation acquires its initial MS structure in a short fraction of the MS life span and depends on the stellar mass, its chemical composition and the total angular momentum stored by the star. This leaves the open question of what the right accretion scenario is?
8.2. Rigid or Differential Rotation: First Observational Guesses
The effects carried by the rapid rotation on the stellar fundamental parameters scale according to the ratio of centrifugal to gravitational accelerations, . From , it is also apparent that, for a given total angular momentum , which implies that the lower the stellar mass, the larger the effects induced by the rotation can be. This can be one of the reasons why, in the past, more attention was paid to studying the internal rotational properties in late-type stars. Knowing that, for inclination angles distributed at random, it is , the displacement in absolute magnitude from the zero rotation main sequence (ZRMS), that can be studied using the parameters by adopting the following expression [257,267,533,534]
with k being a constant over large MS spectral type domains. In this expression, the value of k can testify to the nature of the internal stellar rotation: rigid or differential. In a first attempt, Maeder [535] considered that the expression in Equation (52) should be written as , since, from observations, both quantities vary as a function of the spectral type. However, in Maeder and Peytremann [281] and Maeder and Peytremann [285], the relation in Equation (52) was adopted to conclude that stars in the interval B6–A7 are nearly rigid rotators, while the stars of later spectral types do not rotate as rigid bodies. In contrast with these results and also basing their research on the use of Equation (52), Smith [536] came to the conclusion that, in spite of the uncertainties marring the estimate of k, particularly the empirical definition of the ZRMS, late-type stars in the Praesepe and Hyades clusters with absolute magnitudes in the range likely have internal differential rotation, although the rotation profile could not be determined. Some time after, Cotton and Smith [537] inquired into the values that k may have according to the models of stars rotating with different internal rotation laws.
Following Oke and Greenstein [538] and Sandage [539], who investigated how rotation varied in groups of stars across the HR diagram, Danziger and Faber [540] addressed the question of the distribution of angular momentum in evolving A and F stars by considering two limiting points of view: (a) all stellar shells in a star are completely coupled, so that they rotate as rigid bodies; and (b) all stellar shells in a star are completely uncoupled from each other, so that they are differential rotators.
Danziger and Faber [540] concluded that stars with radii expanded by the evolution of a factor of no more than 2 seem to rotate as solid bodies, but at more evolved stages, observations suggest differential rotation. Using similar arguments, Balona [324] concluded that B-type stars are likely differential rotators. In the same line of thought, and respecting the progenetic relations of spectral types according to the average luminosity classes of stars classified in the BCD system, Zorec [20], Zorec [153] noted that the B and Be stars of luminosity classes IV and III should behave as having internal rotation laws intermediate between rigid and completely differential, as shown in Figure 32. According to this figure, Be stars seem to have a more rigid rotation than B stars without emission, but the separations of points in the figure are within the uncertainty bars.
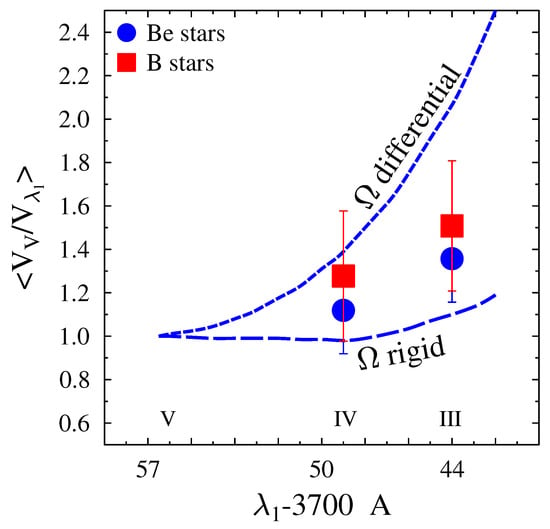
Figure 32.
Average true rotational velocity ratios ( = true rotational velocity of stars of luminosity class V (dwarfs); = true rotational velocity of stars of other luminosity classes identified by an average parameter marked in the abscissas) compared to the sequences of evolution of model ratios of true rotational velocities assuming rigid rotation over the MS evolutionary life span and complete differential rotation. Adapted from Zorec [20], Zorec [153].
8.3. Rigid or Differential Rotation: Extreme Behaviors
More detailed studies of the evolution of late B- and early A-type stars were made by Zorec and Royer [289], where the observed distributions of rotational velocities from a statistically reliable sample were compared with the models of stellar evolution with rotation calculated by Ekström et al. [541]. To facilitate the understanding of the observed evolution of rotation velocities, let us again consider the already mentioned extreme cases of their evolution. If it is assumed that late B- and early A-type stars evolve to conserve their angular momentum, and that, in the ZAMS, they are rigid rotators, as assumed by the existent models of stellar evolution, then stars on the ZAMS should not have amounts of total angular momentum larger than they can bear at critical rigid rotation in the terminal age main sequence (TAMS), i.e., . Within this restrictive condition, the evolution of the surface rotational velocities may respond to either an entire redistribution of the angular momentum at any instant, or to a total lack of exchange of angular momentum among the stellar shells, i.e., conserving the specific angular momentum. For the rigid rotation case, the equatorial velocity at a time t elapsed from the ZAMS is roughly given by
where , and are the stellar equatorial linear rotational velocity, the radius and the moment of inertia at time t and at the ZAMS, respectively. The moment of inertia is calculated using 2D models of stellar structures with rotation [141].
In the second case, the specific angular momentum will become increasingly centrally condensed as evolution goes on, so that the amount left on the surface will decrease strongly as the star evolves from ZAMS to TAMS. For simplicity, we neglect the geometrical deformation of the stellar surface due to the rotation. The angular momentum of a spherical shell of width is then given by
where and are the density and the angular velocity at radius r and time t. can be assumed to be uniform over each shell, i.e., a ‘shellular’ distribution of the angular velocity. If r and are the radii at times t and of the same shell, whose mass and angular momentum are conserved, we have
which, for the equatorial velocity at t and in the stellar surface, implies that
where and are the equatorial radii of the star at times t and , respectively. The details of calculations of the surface stellar rotational velocities in these two extreme cases can be seen in Zorec and Royer [289].
For the sake of comparing the evolution of rotational velocities with model predictions, the observed parameters in Zorec and Royer [289] were grouped by mass and age intervals so as to obtain averages that were converted into assuming a random distribution of the inclination angles. In this section, we compared the observed true velocity ratios against the fractional time ( which is the life span of a star from the ZAMS to the TAMS) for stars with masses ranging from and 3.0, with the calculated evolution of velocity ratios according to Equations (53) and (55). This comparison is shown in Figure 33. Figure 33a shows the ratios against the fractional time , and in Figure 33b, the ratios are compared. The width of the shaded curves corresponds to the mass range used for the calculation. The outstanding characteristic of curves is that they increase fast in the first third of the MS phase, and they decrease more or less monotonically in the second half of the MS phase. Owing to the shown uncertainties, it is not possible to say that the slopes reveal a slightly faster decrease than predicted for differential rotators. If it were actually the case, this decrease could imply some redistribution of angular momentum toward the center of the stars. In Figure 33b, the evolution of ratios is shown against the fractional time , where the calculated evolution of velocity ratios according to Equation (55) was omitted. Even if the evolution of differential rotators is not shown in the figure, we notice that the shape of the curve differs strongly from what is predicted from the two mentioned extreme possibilities of angular momentum redistribution. For both mass-groups, in the first third of the MS, the ratio increases faster than suggested by the theoretical predictions. The reaches a maximum at . Then, there is a decrease that lasts roughly , which is followed by a rather uniform value of until the TAMS. In Figure 33, the error bars represent the uncertainties associated with the averages of velocity ratios and fractional ages.
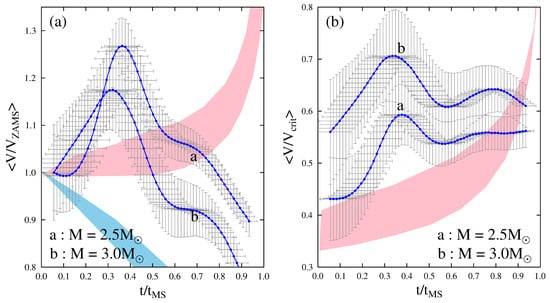
Figure 33.
(a) Evolution of the averaged equatorial velocity ratio in the MS lifetime span, where is the true equatorial velocity of stars on the ZAMS having masses 2.5 and 3. The shaded region corresponds to the theoretical evolution of the ratios for strict rigid rotators (pink) and differential rotators (blue). (b) Evolution of the equatorial velocity ratio in the MS life time span. The ratios of true equatorial velocities are calculated for two masses: 2.5 and . The shaded regions correspond to the theoretical evolution of the ratio of strict rigid rotators whose total angular momentum is (pink). Let us note that, in this figure, the ratio was used, while in Figure 32, we have , where replaces and indicates the mean velocities per luminosity class. Adapted from Zorec and Royer [289].
8.4. Rigid or Differential Rotation: Comparison of Models with Observations
The aim of this section is to shortly review some aspects of the evolution of the observed surface rotational velocities already used in the preceding section of late B- and early A-type stars that we take as witnesses of what can be expected as possible trends or behaviors in more massive stars, i.e., ‘normal’ or ‘active’. Here, the comparison is made with detailed theoretical predictions, but only for stellar masses because, at the time of Zorec and Royer [289], it was the only one at disposal.
Figure 34 shows the comparison of the evolution of observed velocity ratios and presented in Zorec and Royer [289] with those obtained by Ekström et al. [541] for model stars with mass and different initial . The respective model values correspond to the initial velocities V in the ordinates in Figure 34b, where velocities are presented as ratios . The differences between observations and theoretical predictions shown in Figure 34a are eloquent enough to see that, in the first half of the MS evolutionary phase, the angular momentum in actual stars may undergo different redistribution processes than those considered in the theoretical predictions. In Figure 34b, the theoretical ratios reveal an initial short period where a star redistributes its internal angular momentum passing from a rigidly rotating object to a differential rotator at a low-energy regime [154], but the remaining predicted evolution does not resemble the one inferred from the observed rotation velocities.
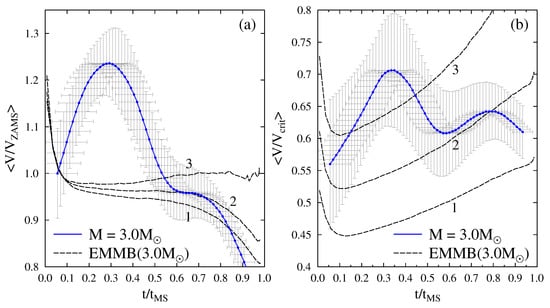
Figure 34.
Comparison of the observed evolution of equatorial velocity ratios in the MS lifetime span for stars with inferred from observations with theoretical ones calculated by Ekström et al. [541] (EMMB) for different on the ZAMS. (a) The evolution of ratios; (b) evolution of ratios. Curves 1, 2 and 3 refer to the different values of , which correspond to the values of V in the initial ratios of panel b. Adapted from Zorec and Royer [289].
A different insight into the evolution of rotational velocities can be obtained by comparing the minimum value of the total angular momentum in rigid rotators required to account for the equatorial velocities, as shown in Figure 33. Because the mass loss rate in stars with masses is very low, they can be considered to evolve as conserving their total angular momentum all along the MS phase. According to Figure 33, four evolutionary epochs can be distinguished: there is the first time interval , which represents the ZAMS or the near ZAMS stage, then corresponds to the epoch when V is maximum, followed by the epoch characterized by the inflection of V, and finally, , which corresponds to the evolution approaching the TAMS. For each evolutionary stage the angular momentum required by the rigid rotation associated with the observed velocity V can be estimated, as well as the angular momentum that corresponds to the respective critical rigid rotation . These values of are given in Table 2, together with the observed rotational velocity V at the indicated evolutionary stages. Thus, we note: (i) in all cases, it is ; (ii) for evolutionary stages from to 0.6, it is , which implies that, to explain the observed rotational velocities, more rotational kinetic energy would be required than the inferred for rigid rotators on the ZAMS; (iii) the condition for all evolutionary stages means that the evolution of rotational velocities in the MS can be consistent with the low regimes of rotational energies, i.e., ; (iv) knowing that, for all evolutionary stages, including the ZAMS, the estimated total specific angular momentum is for rigid rotators, and the values at any imply that there must be some transfer of angular momentum towards the stellar surface. However, because rigid rotation in the initial ZAMS epoch demands , later evolutionary phases where would imply , which is nonsensical. An increase in could then be possible if stars actually evolve as differential rotators having . However, the condition suggests that they could be differential rotators with a low energy regime () on the ZAMS; and (v) because the total angular momentum is conserved during the MS for the studied masses, in stages where , stars have to redistribute their total angular momentum and end up behaving as neat differential rotators in their MS phase ().

Table 2.
Synopsis of the average evolution of equatorial velocities of and stars.
Yang et al. [542] discussed the results by Zorec and Royer [289] and showed that they can be reproduced by making evolved models with differential rotation since the ZAMS, where the angular momentum transport is caused by hydrodynamic instabilities during the MS phase. In their picture, the observed initial acceleration should result in an effect of outward transport of angular momentum stored in the stellar interior, while in the last evolutionary stages in the MS, the core and the radiative envelope become uncoupled with the envelope being uniformly rotated. However, the rapid decrease in the equatorial velocity during the middle MS phase remains unexplained.
The bi-modality of rotational velocities of stars with masses put forward by Zorec and Royer [289] was revisited by Sun et al. [543] with a huge stellar sample from the LAMOST medium-resolution survey [544]. Minor differences in the distributions of rotation velocity ratios seem to be looming, but in a sample having approximately 14,000 stars, a finer selection of binary candidates and chemically peculiar stars might be required to definitely assess the new results. These authors have, however, found that a bimodal rotation distribution, composed of two branches of slowly and rapidly rotating stars, emerges for more stars with masses , whereas for those with , the gap between the bifurcated branches becomes prominent. They also find that metal-poor ( dex) objects only exhibit a single branch of slow rotators, while metal-rich ( dex) stars clearly show two branches. The difference could perhaps be due to some unknown high spin-down mechanism, while in the metal-poor sub-sample, this can partly be produced by magnetic fields.
8.5. Rigid or Differential Rotation: New Observational Inferences
The knowledge of the internal angular momentum distribution in a star may give significant clues to the understanding of its origin and evolution. After the method developed by Rhodes et al. [545] and applied by Deubner et al. [546] to study the subphotospheric rotation of the Sun, to our knowledge, Ando [547] was one of the first to propose a method to estimate the inner rotational angular velocity in stars, which is based on the rotational frequency splitting of non-radial pulsations. The method was meant to produce reliable results provided that the identification of pulsation modes is correct and that the mass and evolutionary stage of stars are correctly estimated. The method uses the one-zone approximation to calculate the frequency splitting. This zone is identified with an effective radius that eventually enables determining its angular velocity. Unfortunately, the application of the method to three B-type stars (53 Per, Cep, 12 Lac) was not conclusive on their differential rotation character due to the uncertainties marring the observational quantities.
Improved methods to infer the internal rotation of stars based on asteroseismic measurements were developed since then [548]. Their application revealed internal differential rotation and put constraints on the internal rotation of some main-sequence B stars, e.g., [549,550,551,552]. Detailed developments in this field are summarized and discussed in Aerts et al. [553], where from a stellar sample of more than 1200 stars with masses , the authors concluded that: ’single stars rotate nearly uniformly during the core-hydrogen and core-helium burning phases; stellar cores spin up to a factor of 10 faster than the envelope during the red giant phase; the angular momentum of the helium-burning core of stars is in agreement with the angular momentum of white dwarfs; observations reveal a strong decrease of core angular momentum when stars have a convective core that current theories of angular momentum transport fail to explain’. More recently, from a compilation of 52 slowly pulsating B stars for which the internal rotation has been measured asteroseismically, Pedersen [554] also concluded that the core rotation frequencies decrease as a function of age and put forward indications of angular momentum transport taking place on the main sequence.
Incompletely and sparsely concerning different B- and near B-type objects, as well as methods and models used to interpret asteroseismic data, let us quote some recent works. Based on a simple three-zone modeling of the internal rotation Hatta et al. [555] inferred via the interpretation of asteroseismic data of KIC 11145123, a MS star, that its radiative region rotates almost uniformly, while the convective core may be rotating about 6 times faster than the radiative region above. They also found some evidence for a latitudinal differential rotation in the outer envelope. The study of gravity modes probed the stellar interior near the convective core and enabled the calibration of internal mixing processes in 26 rotating stars with masses between 3 and 10 solar masses covering the entire slowly pulsating B stars (SPB) instability strip and having rotation rates . The study revealed a wide range of internal mixing profiles, which could provide further guidance for three-dimensional hydrodynamic simulations of transport processes in the deep interiors of stars. In particular, Burssens et al. [556] found that the rotational frequencies in HD 192575 (B0.5 V) are different at radii and , namely , implying differential rotation. HD 129929 is a massive () slowly rotating Cephei pulsator (surface rotation V∼2 km s), where the interpretation by Salmon et al. [557] of its rich spectrum of detected oscillations revealed the presence of radial differential rotation with the stellar core rotating ∼3.6 times faster than the surface. From a test of hydrodynamic and magnetic instability transport processes of angular momentum, it was realized that the impact of the Tayler magnetic instability on the angular momentum transport is insufficient to account for the asteroseismic inferences, but they can be accounted for with hydrodynamic processes. Long ground-based photometric surveys, e.g., [558] and the recent 4-year data provided by the Kepler mission [559] and the references therein have enabled the identification of rapid rotators among classical B-star pulsators (considered SPB), where the properties of their internal structure and pulsations might perhaps become an approximation for Be stars. This is the case of KIC 7760680 [560], which is found to be a nearly rigid rotator with .
The surface differential rotation could be considered as an imprint of the internal rotation profile [141]. Departures of line profiles broadened by rotation from theoretical predictions due to a surface rigid rotation were studied by Stoeckley [410], Stoeckley and Morris [561], Buscombe and Stoeckley [562], Stoeckley et al. [563] and Stoeckley and Buscombe [412]. In these studies on the surface differential rotation, the interpretation of line profiles based on the specific models of the surface rotation lead the authors to suggest that most of the studied O-, B- and A-type stars with and without emission lines on the MS may have surface differential rotation with the angular velocity accelerated towards the pole. The shapes of spectral lines varying with the stellar latitude of Lyr were studied by Elste [564] using the classical methods of line broadening. The raised uncertainties on their interpretation stem on several more or less competing effects, i.e., limb-darkening on gravitational darkened atmospheres due to rapid rotation, macro-turbulent motions, and differential rotation.
The existence of zonal currents in the atmospheres of rapidly rotating stars analogous to those found in planetary atmospheres was suggested by Cranmer and Collins [414]. The induced Doppler displacement resulting from such zonal wind belts can distort the line profiles broadened by rotation leading to significant departures from the line profiles predicted by the classical model of rotating stars, which may be interpreted as components of differential rotation, but they do not necessarily act as imprints of the stellar subphotospheric rotation. These zonal wind belts also lead to changes in the photospheric polarization from those characteristic models with uniform rotation. In any case, Collins and Truax [376] concluded that the effects due to limb-darkening, differential rotation in rapidly rotating stars cannot be disentangled using classical methods to measure line rotational line broadening. Interferometric methods to study the surface differential rotation were proposed by Domiciano de Souza et al. [466] and Zorec et al. [141].
9. Be and Bn Stars, Rapid Rotation Siblings?
9.1. Evolutionary Status of Be Stars
Zorec et al. [61] studied a sample of approximately 100 galactic field Be stars by taking into account the effects induced by the fast rotation on their astrophysical parameters. The program stars were observed in the BCD spectrophotometric system, which enabled to minimize the perturbations produced by the circumstellar environment on the spectral photospheric signatures. This approach is one of the first attempts at determining stellar masses and ages by using simultaneously model atmospheres and evolutionary tracks, both calculated for rotating objects. The stellar fractional ages ( is the amount of time a rotating star spends in the main sequence evolutionary phase), as revealed by the mass-dependent trend as shown in Figure 35. This trend shows that there are Be stars spread over the whole interval of the main sequence evolutionary phase, and that the distribution of points in the () diagram indicates that among massive stars () the Be phenomenon is present at smaller age ratios than for less massive stars (). Such a distribution can be due, on the one hand, to higher mass-loss rates in massive objects, which can reduce the surface fast rotation and prevents the phenomenon occurring at later stages of the MS phase. On the other hand, the meridional circulation time scales to transport angular momentum from the core to the surface are longer the lower the stellar mass is, which then demands the Be phenomenon to appear at later epochs of the MS evolutionary phase.
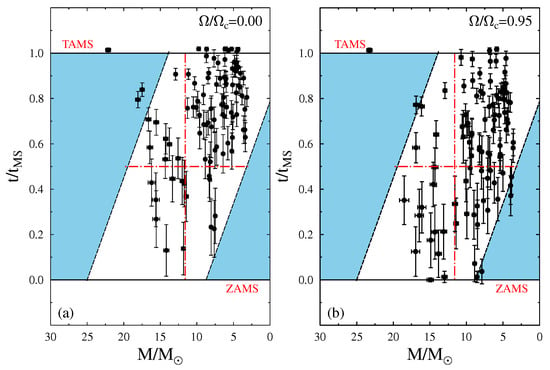
Figure 35.
Age ratios against the mass of Be stars studied in Zorec et al. [61]. (a) Parameters derived using evolutionary tracks without rotation; and (b) parameters derived using evolutionary tracks with rotation. Adapted from Zorec et al. [61].
9.2. Distribution of Rotational Velocities of Bn Stars
Herein, the results obtained in Cochetti et al. [146] are reported, where the stellar samples are marred by some selection effects. Bn stars are currently identified as such when they are seen rather equator-on, otherwise, the lack of emissions in their spectra does not enable us to identify those which rotate rapidly but are seen pole-on. Figure 36a,b show the distributions of the observed of their program Be and Bn stars corrected for the GD effect. In these figures, histograms correspond to the velocity ratios . The superimposed green curves describe the smoothed distributions of the ratios corrected for observational uncertainties. The cited authors preferred to use the ratios instead of the parameters because the critical equatorial velocity was consistently estimated with the mass and evolutionary state of each star, which then minimizes somewhat mass- and evolution-related effects on the distributions [127].
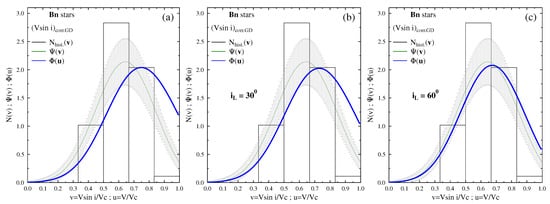
Figure 36.
Distributions of ratios of rotational velocities of Bn stars correction for GD effects. (a) Histograms of velocity ratios v; functions (v) are the smoothed histograms after correction for observational uncertainties (green curves); functions are distributions of true velocity ratios (blue curves). (b,c): histograms, functions from (a) and distributions of true velocity ratios corrected for GD effect and for the density probabilities of inclination angles bridled at inclinations and , respectively. Adapted from Cochetti et al. [146].
Because pole-on Bn stars are unavoidably missing in this discussion, the distributions of their rotational velocities do not respect the randomness of inclination angles. Nonetheless, the distributions of the ratios of true velocities for both Be and Bn stars were calculated as the inclination angles were distributed at random. These are the distributions shown in Figure 36a,b (blue curves). The lack of randomness of the inclination angles in the distributions of Be star rotational velocities in this work is impossible to correct. However, they attempted to account for this lack in the distributions of Bn rotational velocities. To this end, the transformation of the distribution of ratios into ratios of true velocity ratios was carried out with a probability density distribution of inclination angles that was obliterated from up to some limiting inclination using a ’guillotine’ function , details of which can be found in [146]. The most outstanding result that can be drawn from Figure 36b,c is that changing the value of affects neither the skewness of the distribution nor its mode. The only characteristic that seems to vary a little more concerns the number of the fastest rotating stars: the higher the limiting inclination angle is, the lower the number of fast rotators is, and accordingly, the larger the number of objects just behind the mode.
9.3. Evolutionary Status of Bn Stars
Since Bn and Be stars are both rapid rotators, we can ask whether they have similar structures or other common properties that would enable us to consider them both as members of a single population and, in particular, to think of Bn stars as potential Be stars. A first insight into the apparent differences between Bn and Be stars was shown in Figure 11b using the HR diagram in terms of the BCD () parameters. When () are transformed into fundamental quantities (), an HR diagram can be obtained as shown in Figure 37, which concerns the samples of Bn and Be stars studied in Cochetti et al. [146]. In Figure 37a, parameters are not corrected for the effects of rapid rotation, while in Figure 37b they are corrected for rotational effects assuming for all plotted stars. The main difference seen in Figure 37 is that Bn stars have masses , while Be stars are present in the whole mass interval .
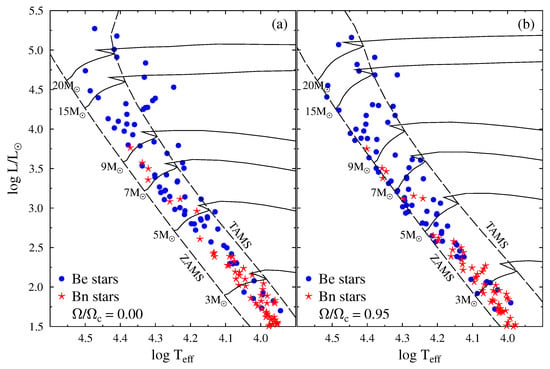
Figure 37.
Panela: Hertzsprung–Russell diagram of Be (blue points) and Bn stars (red stars) studied by Cochetti et al. [146] where () are not treated for rotational effects. Panelb: same as in Panel a, but parameters are corrected for rotational effects, assuming that for all stars, it is . The evolutionary tracks are from Ekström et al. [145] without rotation (Panel a), and with rotation (Panel b) where Vo = 300 km s in the ZAMS. Adapted from Cochetti et al. [146].
Another way of presenting the evolutionary stage of Bn and Be stars is using masses and fractional ages (), as shown in diagrams of Figure 38. In Figure 38a,b parameters () are plotted without and with correction for rotation effects, respectively. Figure 38 c and d are zooms of Figure 38a and b for masses , respectively, in order to better see the behavior of Bn stars (red stars) from that of Be stars (blue points). These () diagrams suggest that Bn stars seem to fill up an apparent gap of Be stars nested in the mass range , which encompasses a more or less large evolutionary span. When rotational effects are not accounted for, Be and Bn stars are likely located in the second half of the MS. Otherwise, corrections carried on the estimates of () for rotational effects considering , Be stars are redistributed from the ZAMS to the TAMS, while Bn are scattered over a rather large evolutionary time interval downwards to the ZAMS.
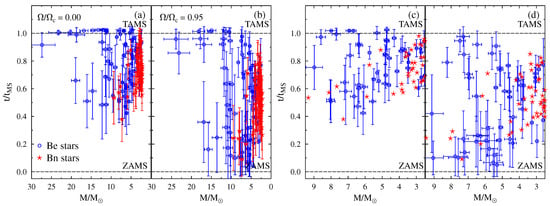
Figure 38.
Fractional age vs. stellar mass not treated for rotation (panels a,c), and using the parameters corrected for rotational effects (panels b,d). Panels c and d are the zooms of a and b for masses , respectively. Error bars indicate uncertainties affecting the and determinations. Adapted from Cochetti et al. [146].
9.4. Rotational Velocities of Be and Bn Stars in the ZAMS
Having a rather small number of B and Be stars in their discussion, Cochetti et al. [146] could not determine the true rotational velocities V for a statistically significant sample having fractional ages in a reduced interval near the ZAMS, i.e., , in order for them to be considered witnesses of the respective distribution of rotational velocities in the initial phases of their MS evolution. Such distributions could provide information to answer the question as to why some B-type rapid rotators in ZAMS can or cannot display the Be phenomenon. To infer vague insights into these distributions, they used the model predictions of changes of the surface rotational velocity [145], which somewhat depends on the prescribed mass-loss rates. Mass loss is indeed a key phenomenon that controls the evolution of stars and their surface rotational velocity, so that high uncertainties may also affect predictions accordingly. In Ekström et al. [145], two series of models were considered for stars with metallicity . The first series of models depends on the mass-loss rates given by de Jager et al. [565] and Kudritzki and Puls [566], here called EMMB; these rates are specified as Ṁ(EMMB) mass-loss rates. The second series of models relies on mass-loss rates suggested by Vink et al. [567], referred here to as Ṁ(VdKL). These two mass-loss prescriptions differ somewhat for and carry differences in the evolution of the velocity ratios by the end of the MS phase, mostly for stars with masses . By interpolating in the curves of the theoretically predicted evolution of ratios , the velocities for , the epoch at which objects acquire a stabilized rotational law [254], Cochetti et al. [146] obtained the distributions of true equatorial velocities V of Be and Bn stars in the ZAMS shown in Figure 39.
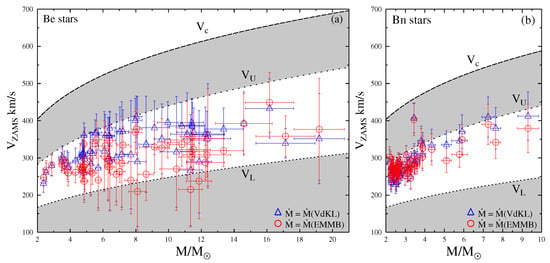
Figure 39.
Equatorial rotational velocities of Be (panel a) and Bn (panel b) stars deduced using the models of stellar evolution by Ekström et al. [541] with mass-loss rates Ṁ(EMMB) (red circles) and Ṁ(VdKL) (blue triangles). In the figure, the curve of in the ZAMS is shown as a function of the stellar mass and the limiting curves and that surround the deduced values. Panel (b) is reduced to the mass interval concerning the program Bn stars. Adapted from Cochetti et al. [146].
Apart from a slight shift in the points dependent on Ṁ(EMMB) toward slightly lower VZAMS values than those calculated using models with Ṁ(VdKL) mass-loss rates for stellar masses , the effect that seems to be more marked among Be stars, probably because, for Bn stars, the mass-loss rates are lower or zero, no other significant difference is apparent in this figure. Then, since both types of objects begin their MS evolutionary phase with similar rotational velocities and only a fraction of these objects at some moment display the Be phenomenon, it is worth inquiring a little further into the distributions of to uncover whether they can reveal other properties that may distinguish Bn and Be stars in the ZAMS. In Figure 40, it is seen that, independently of the mass-loss rate prescription, the distributions of have different skewness signs when it comes to Bn or to Be stars, and that the of Be stars can attain lower values than in the Bn ones. At the moment, it is not possible to say anything more that would enable to conclude that these characteristics are responsible for only some B stars becoming Be.
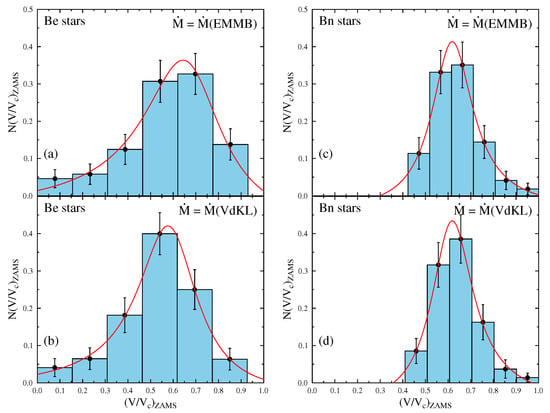
Figure 40.
Normalized histograms showing the distribution of ratios in the ZAMS derived for Be (panels a,b) and Bn (panels c,d) stars. The results shown in panels a and c were obtained with EMMB mass-loss rates, while in panels b,d, the results are for VdKL mass-loss rates. Error bars indicate sampling uncertainties according to the errors associated with the measured parameters. Fitted Pearson distributions are superimposed (red curves) to better perceive the differences in the asymmetries (skewness) of distributions for each type of stars. Adapted from Cochetti et al. [146].
As already noted, the models on which these conclusions are based use specific receipts for the diffusion coefficients. They are not all the same in the models by Maeder and Meynet [154] and Heger et al. [255], and are still different in those by Potter et al. [519]. From the results obtained by Potter et al. [519] concerning the TAMS rotational velocities, it comes that they are different according to the used prescription for the diffusion coefficients. The conclusions reported here on the velocities of Be and Bn stars must then be considered as a mere first approach.
10. Rotation of Magnetic B-Type Stars
Magnetic fields can be detected in almost all types of objects over the entire HR- diagram, cool and hot stars assumed to be single or in binary systems. The presence of magnetic fields may carry significant consequences on the internal stellar rotation, its structure and evolution [568], as well as shaping their circumstellar discs or envelopes. Most often, magnetic fields are measured using spectropolarimetric techniques, but their presence can also be suggested from photometric and spectroscopic studies. Directly, magnetic fields are detected through the Zeeman effect that splits spectral lines into several distinctly polarized components. The easiest detection of the magnetic field signatures is from the Stokes V polarized vector, whose measurement is frequently performed with the Least-Squares-Deconvolution method (LSD) [569,570].
Stellar photospheric magnetic fields are basically of two types, fossil magnetic fields that concern mainly early-type stars which have radiative envelopes, and dynamo-driven fields in stars with convective envelopes. In hot stars, magnetic fields are thought to be frozen in the radiative envelope during the early stages of the stellar evolution in the MS. They frequently have few kG, are rather stable [571], and detected in quite few cases, no more than approximately 10% of mid- to early-type stars [572].
Among the youngest and most rapidly rotating magnetic OB-type stars, the H line can be seen in emission, whose origin is assigned to a ‘magnetosphere’ [573,574,575]. According to Petit et al. [575], there are two types of magnetospheres: the dynamic magnetosphere and centrifugal magnetosphere. In a dynamic magnetosphere, the stellar rotation is not fast enough for the radiation-accelerated wind plasma to be slowed down by gravity, and eventually pulled back to the star. The presence of dynamic magnetospheres is generally more detected through far-UV lines and by H emission, but apparently, this only happens in O-type stars. The centrifugal magnetosphere exists when, in the magnetosphere, the gravitational infall is prevented by the centrifugal force [576,577]. Plasma densities in centrifugal magnetospheres can be significantly higher than in dynamic magnetospheres, which enable the H emission to become strong enough to be detected. Using the Kepler corotation radius , where centrifugal and gravitational forces are equivalent, and the Alfvén radius , which indicates the extent of close magnetic loops, H emission is detected when ( stellar radius) and [578,579]. Moreover, there is a correlation between the H emission strength and radio luminosity [580]. Magnetic stars with H emission are generally in the first quarter of their MS evolutionary phase [578,581].
Hot magnetic stars can be distinguished from the non-magnetic ones because: (a) they have peculiar abundances, mainly of He, Fe and Si, either over- or under-abundant that currently appear in He-strong or He-weak stars, which are thought to arise due to radiative diffusion in strongly magnetized atmospheres. As these abundance irregularities cover some fraction of the stellar surface, spectroscopic and photometric variability modulated by the rotation can be detected. It is then possible to determine the reliable rotational periods ; (b) Magnetic stars are on average less rapid rotators than the non-magnetic ones, which is attributed to a loss in angular momentum through a magnetically confined magnetic field [582,583]. This last property also explains that, among them, the more rapidly rotating stars appear at evolutionary stages with [578]. Extensive compilations and the newly determined astrophysical parameters of hot magnetic stars, in particular and , can be found in Shultz et al. [580], Shultz et al. [584], Shultz et al. [585]. Data suggest that the magnetic star HD 142990 might undergo an irregular rotational evolution [586].
Several surveys aiming to measure magnetic fields in early-type stars have taken mainly advantage of instruments such as ESPaDOnS, FORS2, Narval, and HARPSpol spectropolarimeters (3.6 m CFHT telescope, French 2 m TBL, 3.6 m ESO telescope): MiMeS collaboration [130,587,588], BinaMIcs for magnetism in hot and cool binary stars [589], BOB (B fields in OB stars) collaboration as an ESO large survey [588,590,591,592,593,594,595], and LIFE collaboration dedicated to the magnetic field and evolution of hot stars [596,597]. Thanks to the TESS and BRITE space missions, it was also possible to find many magnetic hot stars, including pulsating ones. Using TESS data, the MOBSTER collaboration has shown that the rotational ratio decreases with stellar age, consistently with the magnetic braking observed in a population of magnetic chemically peculiar stars [598]. A number of known magnetic B-type stars were also observed by BRITE and BRITEpol, and the results were commented by Shultz et al. [599].
Since magnetic B-type stars are also considered chemically peculiar, most often classified as He-strong and He-weak because their abundances do not agree with those in normal stars having the same () parameters, it could also be interesting to see in what way they can be distinguished according to the physical parameters, particularly as rotators. In Figure 41, the He-weak (red points), He-strong (blue points), and those that have not yet been classified are clearly separated as a function of certain parameters, particularly as rotators, and the intensity of their surface magnetic field (here, we consider the maximum value measured of the longitudinal magnetic field taken in absolute value ). Data are from Shultz et al. [580], Shultz et al. [584], Shultz et al. [585]. According to the existing data, He-weak stars have , 21,000 K, , and true rotational velocities km,s. No distinction between He-strong and He-weak stars can be established in the () diagram. He-weak stars follow tight () and () relations, but there is no clear distinction between He-strong and He-weak objects in the () diagram. Probably more detailed relations could be established using the quantitative indices of their chemical peculiarity, namely the index (He/H) or the discrepancy of the Balmer discontinuity given in Equation (10).
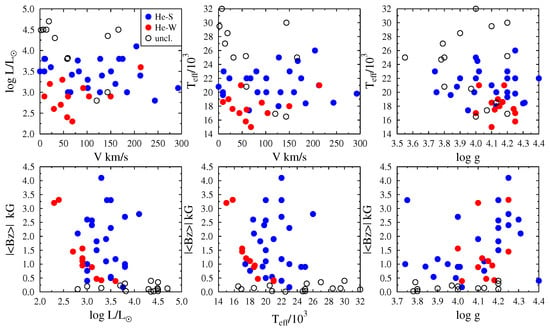
Figure 41.
Magnetic B-type stars differentiated into He-weak (red points), He-strong (blue points) and He-unclassified (open black circles).
11. Rotation of B[e] Stars
Excluding cPNB[e] and SymB[e] stars that identify very specific evolutionary stages or environmental conditions in binary systems, the stellar classes HAeB[e], sgB[e] and FS CMa stars are of particular interest for studies of stellar formation and acquisition of angular momentum, as well as of advanced evolutionary properties associated with rotation. However, these phenomena can be understood either as concerning single stars, or objects whose rotational properties respond to evolution in close binary systems [213,215]. The characterization of these objects is not only dependent on their aspects as rotators, but also on the formation mechanisms of their circumstellar discs or envelopes. Both characterizations can be formation- and stellar evolution-related. Unfortunately, the spectra of B[e] stars rarely display features that could be attributed to the photosphere of the central object, which explains the lack of determinations for this class of stars. Moreover, the fraction of confirmed binaries among them is still not sufficiently high to decide whether their characteristics are related to phenomena taking place in single stars, or if they obey evolution phenomena in a close binary system.
Whatever the possibility, near-critical rotation is frequently evoked to create their circumstellar environment. This is particularly the case for sgB[e] objects considered single-evolved stars. If stars are very massive, the Eddington factor can approach , which enables the ratio by the end of the MS evolutionary phase [213]. Since, in post-MS phases, the surface velocity of stars evolves as , the critical velocity ratio can then be attained only in the blue loop passing from the red-supergiant to the blue-supergiant phase [213]. Because such an evolutionary phase is rather short, it may explain the scarcity of sgB[e] stars. The critical rotation is accompanied by a strong gravity darkening, which can favor the existence of fast polar winds, as well as slow and dense equatorial winds [121]. They may account for the characteristics of the two-component wind in sgB[e] proposed by Zickgraf et al. [170] and Zickgraf [168] for the hypergiant R126 star in the LMC, where rough estimates suggest an Eddington factor .
The rotational velocity was estimated for HD 45677 (prototype of FS CMA class stars) and HD 50138, and according to their astrophysical parameters, they have rotational velocities that are far from being critical today. However, their nature as critical rotators lasts a rather short time. Assuming that these stars today have the observed characteristics because they underwent a merger phenomenon, theoretical predictions by Schneider et al. [600] suggest that their initial possible critical rotator nature should only last for a while, because the magnetic field created in the ’merging’ process slows down the stellar surface rapid rotation. During this process, a dense envelope prevents the direct observation of such objects.
The B[e] stars HD 45677 and HD 50138 were considered by some authors as unclB[e], because they may be escaped from the background molecular clouds on which they appear to overlap [169].
12. Concluding Remarks
The main conclusions drawn from the first part of this report is that the BCD spectrophotometric system is a powerful observational method to study normal and ‘active’ (or abnormal) stars over a large spectral type interval. Its qualities are:
(1) The BCD system produces parameters that depend on the continuum energy distribution and are thus related to the physical properties of atmospheric layers that are on average deeper than those where the spectral lines are formed;
(2) The reduction in low-resolution spectra required in the BCD system can be easily automated which can provide the rapid physical characterization of stellar objects not only in deep regions of our Galaxy, but also in other galactic and more or less distant extra-galactic systems;
(3) The rather short wavelength interval that is required to be observed () does not impose long exposure times;
(4) Excepting for some stellar examples where the extreme spectral peculiarities cannot be apprehended straightforwardly (mainly stars of B[e] class), the spectral signatures from the photospheric regions and those emitted by their close circumstellar regions can be clearly separated;
(5) The BCD () spectrophotometric quantities are independent, or can easily be rendered independent of the interstellar and circumstellar perturbing extinctions, which helps obtain astrophysical parameters [] free from the marring effects of these media;
(6) The second component of the Balmer discontinuity, not yet studied in detail in a theoretical approach of Be stars, keeps precious information on the transition region between the star and the circumstellar disc, where the transfer of angular momentum to the disc is organized;
(7) Discrepancies of the Balmer discontinuity reveal abnormal surface chemical abundances, mainly of He, which can be controlled either by phenomena related with rotation or with stellar magnetic fields.
Although the BCD system was devised to classify the stars of spectral types between O and F, it provides important apparent quantities for both normal and active stars, which can be easily corrected by eliminating effects induced by the rapid rotation. These then enable to estimate the true stellar masses and determine the corresponding evolutionary states. This characteristic of the BCD system inspired us to jointly present two topics, BCD and rotation, which at first glance, appear to be disjoint.
In the second part of the text, a short review was presented on the study of normal and active B-type stars as rotators. Reminders of some supporting theoretical concepts were added. The line of thought of this review was related to the angular momentum of stars, its origin and internal redistribution, although without discussing the hydrodynamic and magneto-hydrodynamic instabilities that control its evolution. We addressed the problem of uncertainties marring the parameter determination and treated the calculation of the geometrical deformation of stars with surface differential rotation. The interpretation of astrophysical parameters and the determination of fundamental parameters in rotating stars was discussed. Observational and theoretical approaches concerning the origin of the stellar angular momentum in field and cluster stars were shortly described. There are still dark areas concerning the mass and angular momentum accretion during the stellar formation phases, so that it is today impossible to assert how much angular momentum stars can or cannot store. The modeling and measurement of quantities related to the stellar structure considered as physical laboratories to probe rotation and the related phenomenology show that there are still open questions concerning the actual content of angular momentum and its internal redistribution. It is thus worth mentioning that the existent models of stellar evolution systematically impose rigid rotation in the ZAMS, while many theoretical approaches of rotating stellar structures suggest that stars are differential rotators already at their initial MS evolutionary phase. Differential rotation enables the star to have larger amounts of angular momentum than supported by the rigid rotation. Even though stars may try to attain a state of minimal rotational energy (i.e., rigid rotation) during their evolution in the MS, it should not be excluded that some of their activities are related to phenomena where they try to get rid of a certain amount or ‘excess’ of angular momentum. In the most currently calculated models, the ‘shellular’ distribution of angular velocity is assumed to prevail and control the evolution of rotating stars. However, new approaches regarding the stellar structure suggest that the internal rotational profile is neither rigid, cylindrical nor ‘shellular’. Moreover, it was shown in Clement [137] and Maeder et al. [136] that rapid rotation can destabilize radiative zones against convection. This convection should happen in deeper and extended zones than just in a small subphotospheric region. It can produce differential rotation in depth and generate magnetic fields. Activities related to magnetic instabilities could then trigger mass ejection phenomena to build up the circumstellar discs in Be stars. To this purpose, non-radial pulsation was evoked many times. Unfortunately, to be effective, this mechanism requires stars to rotate near critical rates, a phenomenon which, among Be stars, is more exception than the rule. Differences between the predicted evolution of surface rotational velocities with the observed one of intermediate-mass stars were pointed out, which testify the existence of unsolved problems concerning the mechanisms that control the internal angular momentum redistribution. The rapid rotation of Be stars and of Bn stars was studied and their evolution compared during the MS evolutionary phase. A short account is given of magnetic B-type stars, where rotation is nothing but a phenomenon that helps the magnetosphere in some of these objects have enough circumstellar matter to produce a detectable line emission. A kind of distinction is also noted between He-weak (apparently slow rotators) and He-strong stars (apparently rapid rotators) in diagrams () and (). Regarding the stars presenting the B[e] phenomenon, a lot of work is still required to identify the genuine photospheric spectral lines that will enable determining their actual rotation rate and identifying what phenomena underlie the origin of a sgB[e] star.
Radiation transfer codes adapted for extended moving media, some of which have been cited in this review, can certainly provide valuable tools for studying the complex spectra of B[e] stars. However, the extended atmospheres of these objects probably have non-spherical geometry, whose shape depends on their rotation law. In addition, the extended atmosphere could be affected by gravitational darkening, which induces a thermal structure controlled not only by the radial radiative flux but also by a horizontal one. The horizontal radiative flux has not yet even been considered in the plane-parallel atmospheres of rapidly rotating stars. As B[e] stars can also undergo mass loss phenomena through winds and discrete ejections, their extended atmospheres can be in non-radiative equilibrium, which increases the non-LTE effects. The classical methods used to calculate the radiative transfer in extended atmospheres to date may be insufficient to tackle the described phenomenological pattern. In these cases, Monte Carlo simulations might perhaps be appropriate to carry out the modeling of the radiation transfer in the mentioned complex atmospheres.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data in Figure 41: Reduced ESPaDOnS spectra are available at the CFHT archive maintained by the CADC5, where they can be found via standard stellar designations. ESPaDOnS and Narval data can also be obtained at the PolarBase archive6. Kepler-2 and TESS data are available at the MAST archive7. Hipparcos data are available through SIMBAD and VizieR. DAO and uGMRT observations are available from the authors upon request. Data in all the remaining figures are available through SIMBAD and VizieR.
Acknowledgments
With these few words, I would like to pay tribute to the memory of Lucienne Divan who introduced me to the secrets of the BCD system. Due to the many contributions cited in this paper that we have written together, Yves Frémat should be listed as a co-author of the present review. I am particularly grateful to him for his contribution to Section 5.1. I cannot find the right words to thank him for his great friendship, wise advice, productive discussions and his precious scientific complicity. The long and permanent support from Anne-Marie Hubert has marked my scientific career, which I wish to note and thank warmly. I am deeply grateful to the Argentinian scientists, colleagues of my Alma Mater, with whom the collaboration has continued to grow over the years as evidenced by the documents we signed with Lydia Cidale and her team, notably Maria-Laura Arias, Yael Aidelman, Janina Cochetti and René Rohrmann. My foray into the world of interferometry was only possible thanks to the friendship and complicity of Aramando Domiciano de Souza, Philippe Stee and Omar Delaa. I would like to thank the guest editors Lydia Sonia Cidale, Michaela Kraus, and María Laura Arias for their kind invitation to write this review. I am deeply grateful to the anonymous referees for their numerous and valuable suggestions, grammatical corrections and corrections to the content that helped to substantially improve this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chalonge, D. Étude du spectre continu de quelques étoiles entre 3100 et 4600 Å. J. Obs. 1936, 19, 149. [Google Scholar]
- Arnulf, A.; Barbier, D.; Chalonge, D.; Safir, H. Étude du rayonnement continu de quelques étoiles entre 3100 et 4600 Å (I). Annales d’Astrophysique 1938, 1, 293. [Google Scholar]
- Guérin, P. Réalisation et étude d’une lampe luminiscente étalon secondarie de répartition spectrale. In Contributions de l’Institut d’Astrophysique de Paris; CNRS; 1954; Volume 162, p. 1. [Google Scholar]
- Baillet, A.; Chalonge, D.; Divan, L. Quartz spectograph with oscillating plateholder for stellar spectrophotometry. Review of some applications. Nouvelle Revue d’Optique 1973, 4, 151–158. [Google Scholar] [CrossRef]
- Divan, L. List of Spectrophotometric Standards in Use at the Institut d’ASTROPHYSIQUE of Paris. In Spectral Classification and Multicolour Photometry: Proceedings of the IAU Symposium No. 24, Saltsjöbaden, Sweden, 17–21 August 1964; Loden, K., Loden, L.O., Sinnerstad, U., Eds.; Academic Press: London, UK, 1966; Volume 24, p. 311. [Google Scholar]
- Divan, L. Discussion: Notes on the definition of the Balmer discontinuity in the BCD system. In Proceedings of the Problems of Calibration of Absolute Magnitudes and Temperature of Stars, Geneva, Switzerland, 12–15 September 1972; Reidel: Dordrecht, The Netherlands; Boston, MA, USA, 1973; Volume 54, p. 267. [Google Scholar]
- Divan, L. Recherches sur la loi d’absorption de la poussière interstellaire et sur le spectre continu des étoiles O et B. Annales d’Astrophysique 1954, 17, 456. [Google Scholar]
- Chalonge, D.; Divan, L. La classification stellaire BCD: Paramètre caractéristique du type spectral calibration en magnitudes absolues. Astron. Astrophys. 1973, 23, 69. [Google Scholar]
- Barbier, D.; Chalonge, D. On the Continuous Spectrum of Stars with Extended Atmospheres. Astrophys. J. 1939, 90, 627–629. [Google Scholar] [CrossRef]
- Aidelman, Y.; Cidale, L.S.; Zorec, J.; Arias, M.L. Open clusters. I. Fundamental parameters of B stars in NGC 3766 and NGC 4755. Astron. Astrophys. 2012, 544, A64. [Google Scholar] [CrossRef]
- Allen, C.W. Astrophysical Quantities, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Barbier, D.; Chalonge, D. Étude du rayonnement continu de quelques étoiles entre 3 100 et 4 600 Å (4e Partie-discussion générale). Annales d’Astrophysique 1941, 4, 30. [Google Scholar]
- Chalonge, D.; Divan, L. Recherches sur les spectres continus stellaires. V. Etude du spectre continu de 150 etoiles entre 3150 et 4600 A. Annales d’Astrophysique 1952, 15, 201. [Google Scholar]
- Barbier, D. Introduction to the stellar classification based on the Balmer discontinuity. In Proceedings of the Frinciples of Stellar Classification, Paris, France, 29 June–4 July 1953; CNRS. 1955; p. 47. [Google Scholar]
- Chalonge, D. Classification using two or three parameters of early type stars. In Proceedings of the Frinciples of Stellar Classification, Paris, France, 29 June–4 July 1953; CNRS. 1955; p. 55. [Google Scholar]
- Keenan, P.C.; Morgan, W.W. Classification of Stellar Spectra. In Proceedings of the 50th Anniversary of the Yerkes Observatory and Half a Century of Progress in Astrophysics; Hynek, J.A., Ed.; McGraw-Hill: New York, NY, USA, 1951; p. 12. [Google Scholar]
- Underhill, A.B.; Divan, L.; Prevot-Burnichon, M.L.; Doazan, V. Effective temperatures, angular diameters, distances and linear radii for 160 O and B stars. Mon. Not. R. Astron. Soc. 1979, 189, 601–605. [Google Scholar] [CrossRef]
- Zorec, J.; Briot, D. Absolute magnitudes of B emission line stars: Correlation between the luminosity excess and the effective temperature. Astron. Astrophys. 1991, 245, 150. [Google Scholar]
- Zorec, J.; Cidale, L.; Arias, M.L.; Frémat, Y.; Muratore, M.F.; Torres, A.F.; Martayan, C. Fundamental parameters of B supergiants from the BCD system. I. Calibration of the (λ1, D) parameters into Teff. Astron. Astrophys. 2009, 501, 297–320. [Google Scholar] [CrossRef]
- Zorec, J. Thèse d’État, Structure et Rotation difféRentielle dans les Étoiles B avec et sans Émission; Université Paris VII: Paris, France, 1986. [Google Scholar]
- Husser, T.O.; Wende-von Berg, S.; Dreizler, S.; Homeier, D.; Reiners, A.; Barman, T.; Hauschildt, P.H. A new extensive library of PHOENIX stellar atmospheres and synthetic spectra. Astron. Astrophys. 2013, 553, A6. [Google Scholar] [CrossRef]
- Divan, L. Quantitative Spectral Classsification in the BCD System for LMC Supergiants. In Proceedings of the Spectral Classification and Multicolour Photometry, Villa Carlos Paz, Argentina, 18–24 October 1971; Reidel: Dordrecht, The Netherlands; Boston, MA, USA, 1973; Volume 50, p. 27. [Google Scholar]
- Divan, L. Calibration en Magnitudes Absolute de la Classification BCD. Application à la DéTERMINATION du Module de Distance du Grand Nuage de Magellan. In Proceedings of the Problems of Calibration of Absolute Magnitudes and Temperature of Stars, Geneva, Switzerland, 12–15 September 1972; Reidel: Dordrecht, The Netherlands; Boston, MA, USA, 1973; Volume 54, p. 78. [Google Scholar]
- Chalonge, D.; Divan, L. BCD classification: Relation between the spectral type and the effective temperature. Astron. Astrophys. 1977, 55, 121–124. [Google Scholar]
- Chalonge, D.; Divan, L. BCD system of stellar classification and chemical composition. Astron. Astrophys. 1977, 55, 117–120. [Google Scholar]
- Gkouvelis, L.; Fabregat, J.; Zorec, J.; Steeghs, D.; Drew, J.E.; Raddi, R.; Wright, N.J.; Drake, J.J. Physical parameters of IPHAS-selected classical Be stars. I. Determination procedure and evaluation of the results. Astron. Astrophys. 2016, 591, A140. [Google Scholar] [CrossRef]
- Divan, L.; Zorec, J. Absolute magnitudes and other basic parameters of O and B stars. In Proceedings of the The Scientific Aspects of the Hipparcos Space Astrometry Mission; Perryman, M.A.C., Guyenne, T.D., Høg, E., Jaschek, C., Lacroute, P., Eds.; ESA: Paris, France, 1982; Volume 177, pp. 101–104. [Google Scholar]
- Cidale, L.; Zorec, J.; Tringaniello, L. BCD spectrophotometry of stars with the B[e] phenomenon. I. Fundamental parameters. Astron. Astrophys. 2001, 368, 160–174. [Google Scholar] [CrossRef]
- Mennickent, R.E.; Cidale, L.; Díaz, M.; Pietrzyński, G.; Gieren, W.; Sabogal, B. Revealing the nature of double-periodic blue variables in the Magellanic Clouds. Mon. Not. R. Astron. Soc. 2005, 357, 1219–1230. [Google Scholar] [CrossRef]
- Zebrun, K.; Soszynski, I.; Wozniak, P.R.; Udalski, A.; Kubiak, M.; Szymanski, M.; Pietrzynski, G.; Szewczyk, O.; Wyrzykowski, L. The Optical Gravitational Lensing Experiment. Difference Image Analysis of LMC and SMC Data. The Catalog. Acta Astron. 2001, 51, 317–329. [Google Scholar]
- Witham, A.R.; Knigge, C.; Drew, J.E.; Greimel, R.; Steeghs, D.; Gänsicke, B.T.; Groot, P.J.; Mampaso, A. The IPHAS catalogue of Hα emission-line sources in the northern Galactic plane. Mon. Not. R. Astron. Soc. 2008, 384, 1277–1288. [Google Scholar] [CrossRef]
- Fabricant, D.; Cheimets, P.; Caldwell, N.; Geary, J. The FAST Spectrograph for the Tillinghast Telescope. Publ. Astron. Soc. Pac. 1998, 110, 79–85. [Google Scholar] [CrossRef]
- Shokry, A.; Rivinius, T.; Mehner, A.; Martayan, C.; Hummel, W.; Townsend, R.H.D.; Mérand, A.; Mota, B.; Faes, D.M.; Hamdy, M.A.; et al. Stellar parameters of Be stars observed with X-shooter. Astron. Astrophys. 2018, 609, A108. [Google Scholar] [CrossRef]
- Vernet, J.; Dekker, H.; D’Odorico, S.; Kaper, L.; Kjaergaard, P.; Hammer, F.; Randich, S.; Zerbi, F.; Groot, P.J.; Hjorth, J.; et al. X-shooter, the new wide band intermediate resolution spectrograph at the ESO Very Large Telescope. Astron. Astrophys. 2011, 536, A105. [Google Scholar] [CrossRef]
- Freudling, W.; Romaniello, M.; Bramich, D.M.; Ballester, P.; Forchi, V.; García-Dabló, C.E.; Moehler, S.; Neeser, M.J. Automated data reduction workflows for astronomy. The ESO Reflex environment. Astron. Astrophys. 2013, 559, A96. [Google Scholar] [CrossRef]
- Shokry, A.; Nouh, M.I.; Saad, S.M.; Helmy, I. Fundamental parameters of some B-type stars using NOAO Indo-U.S. Library. New Astron. 2022, 93, 101780. [Google Scholar] [CrossRef]
- Valdes, F.; Gupta, R.; Rose, J.A.; Singh, H.P.; Bell, D.J. The Indo-US Library of Coudé Feed Stellar Spectra. Astrophys. J. Suppl. Ser. 2004, 152, 251–259. [Google Scholar] [CrossRef]
- Jaschek, M.; Slettebak, A.; Jaschek, C. Be star terminology. Be Star Newsl. 1981, 4, 9–11. [Google Scholar]
- Collins, G.W., I. The Use of Terms and Definitions in the Study of be Stars (review Paper). In Proceedings of the 92nd Colloquium of the International Astronomical Union, Boulder, CO, USA, 18–22 August 1986; Cambridge University Press: Cambridge, UK, 1987; p. 3. [Google Scholar]
- Rivinius, T.; Carciofi, A.C.; Martayan, C. Classical Be stars. Rapidly rotating B stars with viscous Keplerian decretion disks. Astron. Astrophys. Rev. 2013, 21, 69. [Google Scholar] [CrossRef]
- Barbier, D.; Chalonge, D. Remarques préliminaires sur quelques propriétés de la discontinuité de Balmer dans les spectres stellaires. Annales d’Astrophysique 1939, 2, 254. [Google Scholar]
- Jaschek, M.; Groth, H.G. (Eds.) IAU Symp. 89: Be Stars; 1982; Volume 89. [Google Scholar]
- Divan, L.; Zorec, J. Behavior of the energy distribution of 59 CYG in the far-ultraviolet and in the visible. In Proceedings of the Third European IUE Conference, Madrid, Spain, 10–13 May 1982; European Space Agency: Paris, France, 1982; Volume 176, pp. 291–293. [Google Scholar]
- Hubert-Delplace, A.M.; Hubert, H. The recent peculiar Behaviour of the be star, HD 200120, 59 Cyg. Astron. Astrophys. 1981, 44, 109–113. [Google Scholar]
- Divan, L.; Zorec, J. BCD spectrophotometry of the Be-shell star 88 Her. In Proceedings of the Be Stars; Jaschek, M., Groth, H.G., Eds.; Cambridge University Press: Cambridge, UK, 1982; Volume 98, pp. 61–63. [Google Scholar]
- Doazan, V.; Marlborough, J.M.; Morossi, C.; Peters, G.J.; Rusconi, L.; Sedmak, G.; Stalio, R.; Thomas, R.N.; Willis, A. Ultraviolet and visual variability of theta CrB during a normal B-phase following a shell phase (1980-1985). Astron. Astrophys. 1986, 158, 1–13. [Google Scholar]
- Doazan, V.; Franco, M.; Rusconi, L.; Sedmak, G.; Stalio, R. The long-term variations of γ Cas in the visual. Astron. Astrophys. 1983, 128, 171–180. [Google Scholar]
- Hirata, R.; Kogure, T. The spectral variation of Pleione in 1969–1975. Publ. Astron. Soc. Jpn. 1976, 28, 509–515. [Google Scholar]
- Kogure, T.; Hirata, R. The Be star phenomena. I. General properties. Bull. Astron. Soc. India 1982, 10, 281–309. [Google Scholar]
- de Loore, C.; Altamore, A.; Baratta, G.B.; Bunner, A.N.; Divan, L.; Doazan, V.; Hensberge, H.; Sterken, C.; Viotti, R. First coordinated campaign of X-ray and ground-based observations of X-Persei = 3U 0352+30. Astron. Astrophys. 1979, 78, 287–291. [Google Scholar]
- Divan, L.; Zorec, J.; Andrillat, Y. A Be type variation in an O star. Astron. Astrophys. 1983, 126, L8–L10. [Google Scholar]
- Barbier, D. Le spectre continu de Gamma Cassiopeiae. Annales d’Astrophysique 1948, 11, 13. [Google Scholar]
- Barbier, D.; Chalonge, D.; Vassy, E. In Proceedings of the Journal de Physique. Société Française de Physique; 1935; Volume 6, p. 137. [Google Scholar]
- Chalonge, D.; Safir, H. Proceedings of the C.R. Acad. Sci. Paris; Elsevier of behalf of the French Academy of Sciences: Issy-les-Moulineaux, France, 1936; Volume 203, p. 1329.
- Barbier, D.; Chalonge, D. Sur le spectre continu de Nova Herculis 1934 dans la région de courtes longueurs d’onde. Annales d’Astrophysique 1940, 3, 26. [Google Scholar]
- Barbier, D.; Chalonge, D.; Canavaggia, R. Étude du rayonnement continu de quelques étoiles entre 3 100 et 4 600 Å-V: Nouvelles mesures de D et λ1. Annales d’Astrophysique 1947, 10, 195. [Google Scholar]
- Zorec, J.; Divan, L.; Hoeflich, P. Phase variations of 88 Herculis: Do the UV observations confirm a connection between these variations and the changes of the phospheric parameters of the underlying star? Astron. Astrophys. 1989, 210, 279–283. [Google Scholar]
- Divan, L. Quantitative Spectral Classification of STARS Stars on Low Dispersion Spectra. In Proceedings of the IAU Colloq. 47: Spectral Classification of the Future, Vatican City, 11–15 July 1978; Vatican Observatory: Albano laziale, Italy, 1979; Volume 9, p. 247. [Google Scholar]
- Mermilliod, J.C. Stellar content of young open clusters. II. Be stars. Astron. Astrophys. 1982, 109, 48–65. [Google Scholar]
- Schmidt-Kaler, T. Die galaktischen Emissions-B-Sterne: (Spectralklassifikation, Photometrie, Entwicklung und Verteilung in der Milchstraszenebene). Veroeffentlichungen Des Astron. Inst. Der Univ. Bonn 1964, 70, 1. [Google Scholar]
- Zorec, J.; Frémat, Y.; Cidale, L. On the evolutionary status of Be stars. I. Field Be stars near the Sun. Astron. Astrophys. 2005, 441, 235–248. [Google Scholar] [CrossRef]
- Hubert, A.M. Variability in the Circumstellar Envelope of Be Stars. In Proceedings of the Pulsation; Rotation; and Mass Loss in Early-Type Stars; Balona, L.A., Henrichs, H.F., Le Contel, J.M., Eds.; Kluwer Academic Publishers: New York, NY, USA, 1994; Volume 162, p. 341. [Google Scholar]
- Hubert, A.M.; Floquet, M.; Gomez, A.E.; Aletti, V. Photometric Variability of B and Be Stars. In Proceedings of the ESA Symposium ‘Hipparcos-Venice 97’, Venice, Italy, 13–16 May 1997; Volume 402, pp. 315–318. [Google Scholar]
- Moujtahid, A.; Hubert, A.M.; Zorec, J.; Ballereau, D.; Chauville, J.; Floquet, M.; Mon, M. Correlated Spectroscopic and Spectrophotometric Behaviours of Be Stars. In Proceedings of the IAU Colloq. 175: The Be Phenomenon in Early-Type Stars, Alicantem, Spain, 28 June–2 July 1999; The University of Chicago Press: Chicago, NY, USA, 2000; Volume 214, p. 514. [Google Scholar]
- Moujtahid, A.; Zorec, J.; Hubert, A.M. Long-term visual spectrophotometric behaviour of Be stars. II. Correlations with fundamental stellar parameters and interpretation. Astron. Astrophys. 1999, 349, 151–168. [Google Scholar]
- Aubourg, E.; Bareyre, P.; Brehin, S.; Gros, M.; de Kat, J.; Lachieze-Rey, M.; Laurent, B.; Lesquoy, E.; Magneville, C.; Milsztajn, A.; et al. Search for very low-mass objects in the Galactic Halo. Astron. Astrophys. 1995, 301, 1. [Google Scholar]
- de Wit, W.J.; Lamers, H.J.G.L.M.; Marquette, J.B.; Beaulieu, J.P. The remarkable light and colour variability of Small Magellanic Cloud Be stars. Astron. Astrophys. 2006, 456, 1027–1035. [Google Scholar] [CrossRef]
- Hubert, A.M.; Floquet, M. Investigation of the variability of bright Be stars using HIPPARCOS photometry. Astron. Astrophys. 1998, 335, 565–572. [Google Scholar]
- Mennickent, R.E.; Pietrzyński, G.; Gieren, W.; Szewczyk, O. On Be star candidates and possible blue pre-main sequence objects in the Small Magellanic Cloud. Astron. Astrophys. 2002, 393, 887–896. [Google Scholar] [CrossRef]
- Alcock, C.; Akerlof, C.W.; Allsman, R.A.; Axelrod, T.S.; Bennett, D.P.; Chan, S.; Cook, K.H.; Freeman, K.C.; Griest, K.; Marshall, S.L.; et al. Possible gravitational microlensing of a star in the Large Magellanic Cloud. Nature 1993, 365, 621–623. [Google Scholar] [CrossRef]
- Keller, S.C.; Bessell, M.S.; Cook, K.H.; Geha, M.; Syphers, D. Blue Variable Stars from the MACHO Database. I. Photometry and Spectroscopy of the Large Magellanic Cloud Sample. Astron. J. 2002, 124, 2039–2044. [Google Scholar] [CrossRef]
- Udalski, A.; Kubiak, M.; Szymanski, M. Optical Gravitational Lensing Experiment. OGLE-2—The Second Phase of the OGLE Project. Acta Astron. 1997, 47, 319–344. [Google Scholar]
- Limber, D.N.; Marlborough, J.M. The Support of the Envelopes of be Stars. Astrophys. J. 1968, 152, 181. [Google Scholar] [CrossRef]
- Limber, D.N. Circumstellar Envelopes Formed Through Rotationally Forced Ejection. II. Astrophys. J. 1967, 148, 141. [Google Scholar] [CrossRef]
- Marlborough, J.M. Models for the Envelopes of be Stars. Astrophys. J. 1969, 156, 135. [Google Scholar] [CrossRef]
- Poeckert, R.; Marlborough, J.M. Intrinsic linear polarization of Be stars as a function of V sini. Astrophys. J. 1976, 206, 182–195. [Google Scholar] [CrossRef]
- Poeckert, R.; Marlborough, J.M. Linear polarization of Halpha in the Be star Gamma Cassiopeiae. Astrophys. J. 1977, 218, 220–226. [Google Scholar] [CrossRef]
- Poeckert, R.; Marlborough, J.M. A model for gamma Cassiopeiae. Astrophys. J. 1978, 220, 940–961. [Google Scholar] [CrossRef]
- Poeckert, R.; Marlborough, J.M. Be star models: Observable effects of model parameters. Astrophys. J. Suppl. Ser. 1978, 38, 229–252. [Google Scholar] [CrossRef]
- Marlborough, J.M. Models for the Circumstellar Envelopes of be Stars (review Paper). In Proceedings of the Be and Shell Stars; Slettebak, A., Ed.; Reidel Pub. Co.: Dordrecht, The Netherlands; Boston, MA, USA, 1976; Volume 70, p. 335. [Google Scholar]
- Poeckert, R. Model atmospheres of Be stars. In Proceedings of the Be Stars; Jaschek, M., Groth, H.G., Eds.; Dordrecht, D. Reidel Publishing Co.: Dordrecht, The Netherlands; Boston, MA, USA, 1982; Volume 98, pp. 453–477. [Google Scholar]
- Hirata, R.; Kogure, T. The Be star phenomena. II—Spectral formation and structure of envelopes. Bull. Astron. Soc. India 1984, 12, 109–151. [Google Scholar]
- Slettebak, A.; Snow, T.P. Physics of Be stars. In Proceedings of the 92nd Colloquium of the International Astronomical Union, Boulder, CO, USA, 18–22 August 1986; University Press: Cambridge, UK, 1987. [Google Scholar]
- Waters, L.B.F.M.; Marlborough, J.M. The Structure of the Circumstellar Material in Be Stars. In Proceedings of the Pulsation; Rotation; and Mass Loss in Early-Type Stars; Balona, L.A., Henrichs, H.F., Le Contel, J.M., Eds.; Kluwer Academic Publishers: New York, NY, USA, 1994; Volume 162, p. 399. [Google Scholar]
- Doazan, V.; Stalio, R.; Thomas, R.N. Empirical atmospheric velocity patterns from combined IUE and visual observations: The Be-similar stars. In Proceedings of the Four Years of IUE Research, Conference Held in NASA, Goddard Space Flight Center, Greenbelt, MD, USA, 30 March–1 April 1982; NASA: Washington, DC, USA, 1982; Volume 2238, pp. 584–588. [Google Scholar]
- Underhill, A.B.; Doazan, V.; Lesh, J.R.; Aizenman, M.L.; Thomas, R.N. B Stars with and without Emission Lines. Monograph Series on Nonthermal Phenomena in Stellar Atmospheres; NASA: Washington, DC, USA, 1982; Volume 456. [Google Scholar]
- Thomas, R.N. Stellar Atmospheric Structural Patterns; NASA: Washington, DC, USA, 1983; Volume 471. [Google Scholar]
- Catala, C.; Kunasz, P.B.; Praderie, F. Line formation in the wind of AB Aur. Astron. Astrophys. 1984, 134, 402–413. [Google Scholar]
- Catala, C. Line formation in the winds of Herbig Ae/Be stars. The C IV resonancelines. Astron. Astrophys. 1988, 193, 222–228. [Google Scholar]
- Cidale, L.S.; Ringuelet, A.E. Rigorous Treatment of the Radiative Transfer Problem in Stellar Winds: Significance of the Velocity Law and the Chromosphere in the H alpha Profile. Astrophys. J. 1993, 411, 874. [Google Scholar] [CrossRef]
- Vazquez, A.C.; Cidale, L.S.; Ringuelet, A.E. Expanding Atmospheric Model Including a Chromosphere. I. Study of the Infrared Excess in Be Stars. Astrophys. J. 1993, 419, 286. [Google Scholar] [CrossRef]
- Cidale, L.S.; Vazquez, A.C. Expanding Atmospheric Model Including a Chromosphere. II. Be Stars: Center-to-Limb Variation of the Emergent Intensity. Astrophys. J. 1995, 453, 393. [Google Scholar] [CrossRef]
- Boehm, T.; Catala, C.; Donati, J.F.; Welty, A.; Baudrand, J.; Butler, C.J.; Carter, B.; Collier-Cameron, A.; Czarny, J.; Foing, B.; et al. Azimuthal structures in the wind and chromosphere of the Herbig AE star AB Aurigae. Results from the MUSICOS 1992 campaign. Astron. Astrophys. 1996, 120, 431–450. [Google Scholar] [CrossRef]
- Cidale, L.S. Diagnosis of Stellar Winds and Temperature Structures in Be Stars through the Analysis of Mg II Lines. Astrophys. J. 1998, 502, 824–832. [Google Scholar] [CrossRef]
- Bouret, J.C.; Catala, C. NLTE calculations of neutral helium lines in the wind of the Herbig Ae star AB Aurigae. Astron. Astrophys. 2000, 359, 1011–1024. [Google Scholar]
- Zorec, J.; Arias, M.L.; Cidale, L.; Ringuelet, A.E. Be star disc characteristics near the central object. Astron. Astrophys. 2007, 470, 239–247. [Google Scholar] [CrossRef]
- Hanuschik, R.W. Stellar V/sin/i and Optical Emission Linewidths in Be-Stars. Astrophys. Space Sci. 1989, 161, 61–73. [Google Scholar] [CrossRef]
- Ballereau, D.; Chauville, J.; Zorec, J. Some Fe II emission-line profiles of nine southern Be stars. Astron. Astrophys. 1995, 111, 457. [Google Scholar]
- Lee, U.; Osaki, Y.; Saio, H. Viscous excretion discs around Be stars. Mon. Not. R. Astron. Soc. 1991, 250, 432–437. [Google Scholar] [CrossRef]
- Shakura, N.I.; Sunyaev, R.A. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 24, 337–355. [Google Scholar]
- Pringle, J.E. Accretion discs in astrophysics. Annu. Rev. Astron. Astrophys. 1981, 19, 137–162. [Google Scholar] [CrossRef]
- Pringle, J.E. The properties of external accretion discs. Mon. Not. R. Astron. Soc. 1991, 248, 754. [Google Scholar] [CrossRef]
- Narita, S.; Kiguchi, M.; Hayashi, C. The Structure and Evolution of Thin Viscous Disks. I. Non-steady Accretion and Excretion. Publ. Astron. Soc. Jpn. 1994, 46, 575–587. [Google Scholar]
- Okazaki, A.T. Viscous Transonic Outflow in Equatorial Discs of Be Stars. Commun. Konkoly Obs. Hung. 1997, 100, 407–412. [Google Scholar]
- Okazaki, A.T. Viscous Transonic Decretion in Disks of Be Stars. Publ. Astron. Soc. Jpn. 2001, 53, 119–125. [Google Scholar] [CrossRef]
- Haubois, X.; Carciofi, A.C.; Rivinius, T.; Okazaki, A.T.; Bjorkman, J.E. Dynamical Evolution of Viscous Disks around Be Stars. I. Photometry. Astrophys. J. 2012, 756, 156. [Google Scholar] [CrossRef]
- Ghoreyshi, M.R.; Carciofi, A.C.; Jones, C.E.; Faes, D.M.; Baade, D.; Rivinius, T. A Multi-Observing Technique Study of the Dynamical Evolution of the Viscous Disk around the Be Star ω CMa. Astrophys. J. 2021, 909, 149. [Google Scholar] [CrossRef]
- Kurfürst, P.; Feldmeier, A.; Krtička, J. Two-dimensional modeling of density and thermal structure of dense circumstellar outflowing disks. Astron. Astrophys. 2018, 613, A75. [Google Scholar] [CrossRef]
- Carciofi, A.C.; Bjorkman, J.E. Non-LTE Monte Carlo Radiative Transfer. II. Nonisothermal Solutions for Viscous Keplerian Disks. Astrophys. J. 2008, 684, 1374–1383. [Google Scholar] [CrossRef]
- Millar, C.E.; Marlborough, J.M. Rates of Energy Gain and Loss in the Circumstellar Envelopes of Be Stars: The Poeckert-Marlborough Model. Astrophys. J. 1998, 494, 715–723. [Google Scholar] [CrossRef]
- Millar, C.E.; Marlborough, J.M. Rates of Energy Gain and Loss in the Circumstellar Envelopes of BE Stars: Diffuse Radiation. Astrophys. J. 1999, 516, 276–279. [Google Scholar] [CrossRef]
- Carciofi, A.C.; Bjorkman, J.E. Non-LTE Monte Carlo Radiative Transfer. I. The Thermal Properties of Keplerian Disks around Classical Be Stars. Astrophys. J. 2006, 639, 1081–1094. [Google Scholar] [CrossRef]
- Sigut, T.A.A.; Jones, C.E. The Thermal Structure of the Circumstellar Disk Surrounding the Classical Be Star γ Cassiopeiae. Astrophys. J. 2007, 668, 481–491. [Google Scholar] [CrossRef]
- McGill, M.A.; Sigut, T.A.A.; Jones, C.E. The Effect of Density on the Thermal Structure of Gravitationally Darkened Be Star Disks. Astrophys. J. Suppl. Ser. 2013, 204, 2. [Google Scholar] [CrossRef]
- Thomas, R.N. The Source Function in a Non-Equilibrium Atmosphere. I. The Resonance Lines. Astrophys. J. 1957, 125, 260. [Google Scholar] [CrossRef]
- Thomas, R.N. Some Aspects of Non-Equilibrium Thermodynamics in the Presence of a Radiation Field; University of Colorado Press: Boulder, CO, USA, 1965. [Google Scholar]
- Jefferies, J.T. Spectral Line Formation; Blaisdell: Waltham, MA, USA, 1968. [Google Scholar]
- Mihalas, D. Stellar Atmospheres; W.H. Freeman: San Francisco, CA, USA, 1978. [Google Scholar]
- Hubeny, I.; Mihalas, D. Theory of Stellar Atmospheres; Princeton University Press: Princeton, NJ, USA, 2014. [Google Scholar]
- Viotti, R. Forbidden and permitted emission lines of singly ionized iron as a diagnostic in the investigation of stellar emission-line spectra. Astrophys. J. 1976, 204, 293–300. [Google Scholar] [CrossRef]
- Curé, M. The Influence of Rotation in Radiation-driven Wind from Hot Stars: New Solutions and Disk Formation in Be Stars. Astrophys. J. 2004, 614, 929–941. [Google Scholar] [CrossRef]
- Hartquist, T.W.; Dyson, J.E.; Pettini, M.; Smith, L.J. Mass-loaded astronomical flows—I. General principles and their application to RCW 58. Mon. Not. R. Astron. Soc. 1986, 221, 715–726. [Google Scholar] [CrossRef]
- Dyson, J.E.; Hartquist, T.W. Astronomical Bubbles with Clumpy Cores and Accelerating Haloes. Astrophys. Lett. Commun. 1992, 28, 301. [Google Scholar]
- Arthur, S.J.; Dyson, J.E.; Hartquist, T.W. Mass-loaded flows—VII. Transonic flows from the cores of planetary nebulae. Mon. Not. R. Astron. Soc. 1994, 269, 1117–1122. [Google Scholar] [CrossRef][Green Version]
- Kroll, P.; Hanuschik, R.W. Dynamics of Self-Accreting Disks in Be Stars. In Proceedings of the IAU Colloq. 163: Accretion Phenomena and Related Outflows, Port Douglas, Queensland, Australia, 15–19 July 1996; Astronomical Society of the Pacific: San Francisco, CA, USA, 1997; Volume 121, p. 494. [Google Scholar]
- Kee, N.D.; Owocki, S.; Townsend, R.; Müller, H.R. Pulsational Mass Ejection in Be Star Disks. In Proceedings of the Bright Emissaries: Be Stars as Messengers of Star-Disk Physics; Sigut, T.A.A., Jones, C.E., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2016; Volume 506, p. 47. [Google Scholar]
- Zorec, J.; Frémat, Y.; Domiciano de Souza, A.; Royer, F.; Cidale, L.; Hubert, A.M.; Semaan, T.; Martayan, C.; Cochetti, Y.R.; Arias, M.L.; et al. Critical study of the distribution of rotational velocities of Be stars. I. Deconvolution methods, effects due to gravity darkening, macroturbulence, and binarity. Astron. Astrophys. 2016, 595, A132. [Google Scholar] [CrossRef]
- Krtička, J.; Owocki, S.P.; Meynet, G. Mass and angular momentum loss via decretion disks. Astron. Astrophys. 2011, 527, A84. [Google Scholar] [CrossRef]
- Granada, A.; Ekström, S.; Georgy, C.; Krtička, J.; Owocki, S.; Meynet, G.; Maeder, A. Populations of rotating stars. II. Rapid rotators and their link to Be-type stars. Astron. Astrophys. 2013, 553, A25. [Google Scholar] [CrossRef]
- Wade, G.A.; Neiner, C.; Alecian, E.; Grunhut, J.H.; Petit, V.; Batz, B.d.; Bohlender, D.A.; Cohen, D.H.; Henrichs, H.F.; Kochukhov, O.; et al. The MiMeS survey of magnetism in massive stars: Introduction and overview. Mon. Not. R. Astron. Soc. 2016, 456, 2–22. [Google Scholar] [CrossRef]
- Wade, G.A.; Petit, V.; Grunhut, J.H.; Neiner, C.; MiMeS Collaboration. Magnetic Fields of Be Stars: Preliminary Results from a Hybrid Analysis of the MiMeS Sample. In Proceedings of the Bright Emissaries: Be Stars as Messengers of Star-Disk Physics, Astronomical Society of the Pacific: Proceedings of a Meeting held at The University of Western Ontario, London, ON, Canada, 11–13 August 2014; Astronomical Society of the Pacific Conference Series; Sigut, T.A.A., Jones, C.E., Eds.; 2016; Volume 506, p. 207. [Google Scholar]
- Kochukhov, O.; Sudnik, N. Detectability of small-scale magnetic fields in early-type stars. Astron. Astrophys. 2013, 554, A93. [Google Scholar] [CrossRef]
- Cantiello, M.; Langer, N.; Brott, I.; de Koter, A.; Shore, S.N.; Vink, J.S.; Voegler, A.; Lennon, D.J.; Yoon, S.C. Sub-surface convection zones in hot massive stars and their observable consequences. Astron. Astrophys. 2009, 499, 279–290. [Google Scholar] [CrossRef]
- Cantiello, M.; Braithwaite, J. Magnetic spots on hot massive stars. Astron. Astrophys. 2011, 534, A140. [Google Scholar] [CrossRef]
- Cantiello, M.; Braithwaite, J. Envelope Convection, Surface Magnetism, and Spots in A and Late B-type Stars. Astrophys. J. 2019, 883, 106. [Google Scholar] [CrossRef]
- Maeder, A.; Georgy, C.; Meynet, G. Convective envelopes in rotating OB stars. Astron. Astrophys. 2008, 479, L37–L40. [Google Scholar] [CrossRef]
- Clement, M.J. On the equilibrium and secular instability of rapidly rotating stars. Astrophys. J. 1979, 230, 230–242. [Google Scholar] [CrossRef]
- Smith, M.A.; Lopes de Oliveira, R.; Motch, C. A Census of the Class of X-ray Active γ Cas Stars. In Proceedings of the Bright Emissaries: Be Stars as Messengers of Star-Disk Physics, Astronomical Society of the Pacific: Proceedings of a Meeting held at The University of Western Ontario, London, ON, Canada, 11–13 August 2014; Astronomical Society of the Pacific Conference Series; Sigut, T.A.A., Jones, C.E., Eds.; 2016; Volume 506, p. 299. [Google Scholar]
- Smith, M.A.; Lopes de Oliveira, R.; Motch, C. The X-ray emission of the γ Cassiopeiae stars. Adv. Space Res. 2016, 58, 782–808. [Google Scholar] [CrossRef]
- Owocki, S.P.; Castor, J.I.; Rybicki, G.B. Time-dependent Models of Radiatively Driven Stellar Winds. I. Nonlinear Evolution of Instabilities for a Pure Absorption Model. Astrophys. J. 1988, 335, 914. [Google Scholar] [CrossRef]
- Zorec, J.; Frémat, Y.; Domiciano de Souza, A.; Delaa, O.; Stee, P.; Mourard, D.; Cidale, L.; Martayan, C.; Georgy, C.; Ekström, S. Differential rotation in rapidly rotating early-type stars. I. Motivations for combined spectroscopic and interferometric studies. Astron. Astrophys. 2011, 526, A87. [Google Scholar] [CrossRef]
- Apparao, K.M.V.; Antia, H.M.; Chitre, S.M. Rapidly rotating stars and the Be star phenomenon. Astron. Astrophys. 1987, 177, 198–200. [Google Scholar]
- Aidelman, Y.; Cidale, L.S.; Zorec, J.; Panei, J.A. Open clusters. II. Fundamental parameters of B stars in Collinder 223, Hogg 16, NGC 2645, NGC 3114, and NGC 6025. Astron. Astrophys. 2015, 577, A45. [Google Scholar] [CrossRef]
- Aidelman, Y.; Cidale, L.S.; Zorec, J.; Panei, J.A. Open clusters. III. Fundamental parameters of B stars in NGC 6087, NGC 6250, NGC 6383, and NGC 6530 B-type stars with circumstellar envelopes. Astron. Astrophys. 2018, 610, A30. [Google Scholar] [CrossRef]
- Ekström, S.; Georgy, C.; Eggenberger, P.; Meynet, G.; Mowlavi, N.; Wyttenbach, A.; Granada, A.; Decressin, T.; Hirschi, R.; Frischknecht, U.; et al. Grids of stellar models with rotation. I. Models from 0.8 to 120 M⊙ at solar metallicity (Z = 0.014). Astron. Astrophys. 2012, 537, A146. [Google Scholar] [CrossRef]
- Cochetti, Y.R.; Zorec, J.; Cidale, L.S.; Arias, M.L.; Aidelman, Y.; Torres, A.F.; Frémat, Y.; Granada, A. Be and Bn stars: Balmer discontinuity and stellar-class relationship. Astron. Astrophys. 2020, 634, A18. [Google Scholar] [CrossRef]
- Hoffleit, D.; Jaschek, C. The Bright Star Catalogue. Fourth Revised Edition. (Containing Data Compiled through 1979); Yale University Observatory: New Haven, CT, USA, 1982. [Google Scholar]
- Hoffleit, D.; Saladyga, M.; Wlasuk, P. A Supplement to the Bright Star Catalogue. Containing Data Compiled through 1981 for Stars 7.10 V and Brighter That Are Not in the Bright Star Catalogue; Yale University Observatory: New Haven, CT, USA, 1983. [Google Scholar]
- Zorec, J. On the Initial Mass Function of Be Stars and the Missing Be Stars of Late Spectral Types. In Proceedings of the IAU Colloq. 175: The Be Phenomenon in Early-Type Stars, Alicante, Spain, 28 June–2 July 1999; The University of Chicago Press: Chicago, NY, USA, 2000; Volume 214, p. 51. [Google Scholar]
- Scalo, J.M. The Stellar Initial Mass Function. Fund. Cosmic Phys. 1986, 11, 1–278. [Google Scholar]
- Rana, N.C. Mass function of stars in the solar neighbourhood. Astron. Astrophys. 1987, 184, 104–118. [Google Scholar]
- Zorec, J.; Briot, D. Critical study of the frequency of Be stars taking into account their outstanding characteristics. Astron. Astrophys. 1997, 318, 443–460. [Google Scholar]
- Zorec, J. Rotation and Properties of Be Stars (Invited Review). In Proceedings of the Stellar Rotation; Maeder, A., Eenens, P., Eds.; Cambridge University Press: Cambridge, UK, 2004; Volume 215, p. 73. [Google Scholar]
- Maeder, A.; Meynet, G. The Evolution of Rotating Stars. Annu. Rev. Astron. Astrophys. 2000, 38, 143–190. [Google Scholar] [CrossRef]
- Cote, J.; van Kerkwijk, M.H. New bright Be stars and the Be star frequency. Astron. Astrophys. 1993, 274, 870–876. [Google Scholar]
- Ghosh, K.K.; Apparao, K.M.V.; Pukalenthi, S. Observations of BN and AN stars: New Be stars. Astron. Astrophys. 1999, 134, 359–364. [Google Scholar] [CrossRef][Green Version]
- De Marco, O.; Lanz, T.; Ouellette, J.A.; Zurek, D.; Shara, M.M. First Evidence of Circumstellar Disks around Blue Straggler Stars. Astrophys. J. Lett. 2004, 606, L151–L154. [Google Scholar] [CrossRef][Green Version]
- Porter, J.M.; Townsend, R.H.D. On the Evidence of Disks around Blue Straggler Stars. Astrophys. J. Lett. 2005, 623, L129–L132. [Google Scholar] [CrossRef][Green Version]
- Jaschek, C.; Jaschek, M. The Classification of Stars; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Osmer, P.S.; Peterson, D.M. The composition and evolutionary status of the helium-rich stars. Astrophys. J. 1974, 187, 117–129. [Google Scholar] [CrossRef]
- Cidale, L.S.; Arias, M.L.; Torres, A.F.; Zorec, J.; Frémat, Y.; Cruzado, A. Fundamental parameters of He-weak and He-strong stars. Astron. Astrophys. 2007, 468, 263–272. [Google Scholar] [CrossRef]
- Hubeny, I.; Lanz, T. Non-LTE Line-blanketed Model Atmospheres of Hot Stars. I. Hybrid Complete Linearization/Accelerated Lambda Iteration Method. Astrophys. J. 1995, 439, 875. [Google Scholar] [CrossRef]
- Dimitrijevic, M.S.; Sahal-Brechot, S. Stark broadening of neutral helium lines. J. Quant. Spectrosc. Radiat. Transf. 1984, 31, 301–313. [Google Scholar] [CrossRef]
- Dimitrijevic, M.S.; Sahal-Brechot, S. Stark broadening of He I lines. Astron. Astrophys. 1990, 82, 519–529. [Google Scholar]
- Freudenstein, S.A.; Cooper, J. A simple formula for estimating Stark widths of neutral lines. Astrophys. J. 1978, 224, 1079–1084. [Google Scholar] [CrossRef]
- Allen, D.A.; Swings, J.P. Infrared Excesses and Forbidden Emission Lines in Early-Type Stars. Astrophys. Lett. 1972, 10, 83. [Google Scholar]
- Allen, D.A.; Swings, J.P. The spectra of peculiar Be star with infrared excesses. Astron. Astrophys. 1976, 47, 293–302. [Google Scholar]
- Zickgraf, F.J. Current Definition of B[e] Stars. In Proceedings of the B[e] Stars; Hubert, A.M., Jaschek, C., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA, 1998; Volume 233, p. 1. [Google Scholar] [CrossRef]
- Lamers, H.J.G.L.M.; Zickgraf, F.J.; de Winter, D.; Houziaux, L.; Zorec, J. An improved classification of B[e]-type stars. Astron. Astrophys. 1998, 340, 117–128. [Google Scholar]
- Zickgraf, F.J.; Wolf, B.; Stahl, O.; Leitherer, C.; Klare, G. The hybrid spectrum of the LMC hypergiant R 126. Astron. Astrophys. 1985, 143, 421–430. [Google Scholar]
- Zickgraf, F.J.; Wolf, B.; Stahl, O.; Leitherer, C.; Appenzeller, I. B(e)-supergiants of the Magellanic Clouds. Astron. Astrophys. 1986, 163, 119–134. [Google Scholar]
- Zickgraf, F.J.; Wolf, B.; Stahl, O.; Humphreys, R.M. S 18: A new B(e) supergiant in the Small Magellanic Cloud with evidence for an excretion disk. Astron. Astrophys. 1989, 220, 206–214. [Google Scholar]
- Zickgraf, F.J.; Stahl, O.; Wolf, B. IR survey of OB emission-line stars in the SMC: Detection of a new B E supergiant, AV 172. Astron. Astrophys. 1992, 260, 205–212. [Google Scholar]
- Zickgraf, F.J.; Kovacs, J.; Wolf, B.; Stahl, O.; Kaufer, A.; Appenzeller, I. R4 in the Small Magellanic Cloud: A spectroscopic binary with a B[e]/LBV-type component. Astron. Astrophys. 1996, 309, 505–514. [Google Scholar]
- Zickgraf, F.J.; Humphreys, R.M.; Lamers, H.J.G.L.M.; Smolinski, J.; Wolf, B.; Stahl, O. Spectroscopic study of the outflowing disk winds of B[e] supergiants in the Magellanic Clouds. Astron. Astrophys. 1996, 315, 510–520. [Google Scholar]
- Gummersbach, C.A.; Zickgraf, F.J.; Wolf, B. B[e] phenomenon extending to lower luminosities in the Magellanic Clouds. Astron. Astrophys. 1995, 302, 409. [Google Scholar]
- Wolf, B.; Stahl, O. The absorption spectrum of the Be star MWC 300. Astron. Astrophys. 1985, 148, 412–416. [Google Scholar]
- McGregor, P.J.; Hyland, A.R.; Hillier, D.J. Atomic and Molecular Line Emission from Early-Type High-Luminosity Stars. Astrophys. J. 1988, 324, 1071. [Google Scholar] [CrossRef]
- Winkler, H.; Wolf, B. An analysis of high resolution spectra of the Be -stars CPD -52 9243and MWC 300. Astron. Astrophys. 1989, 219, 151–157. [Google Scholar]
- Kraus, M. A Census of B[e] Supergiants. Galaxies 2019, 7, 83. [Google Scholar] [CrossRef]
- Palla, F.; Stahler, S.W. The Pre-Main-Sequence Evolution of Intermediate-Mass Stars. Astrophys. J. 1993, 418, 414. [Google Scholar] [CrossRef]
- Bibo, E.A.; The, P.S. The type of variability of Herbig Ae/Be stars. Astron. Astrophys. 1991, 89, 319. [Google Scholar]
- Ciatti, F.; D’Odorico, S.; Mammano, A. Properties and evolution of BQ[] stars. Astron. Astrophys. 1974, 34, 181–186. [Google Scholar]
- Kenyon, S.J. The Symbiotic Stars; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Miroshnichenko, A.S. Toward Understanding the B[e] Phenomenon. I. Definition of the Galactic FS CMa Stars. Astrophys. J. 2007, 667, 497–504. [Google Scholar] [CrossRef][Green Version]
- Miroshnichenko, A.S.; Manset, N.; Kusakin, A.V.; Chentsov, E.L.; Klochkova, V.G.; Zharikov, S.V.; Gray, R.O.; Grankin, K.N.; Gandet, T.L.; Bjorkman, K.S.; et al. Toward Understanding the B[e] Phenomenon. II. New Galactic FS CMa Stars. Astrophys. J. 2007, 671, 828–841. [Google Scholar] [CrossRef]
- Kraus, M. The pre- versus post-main sequence evolutionary phase of B[e] stars. Constraints from 13CO band emission. Astron. Astrophys. 2009, 494, 253–262. [Google Scholar] [CrossRef]
- Kraus, M.; Liimets, T.; Moiseev, A.; Sánchez Arias, J.P.; Nickeler, D.H.; Cidale, L.S.; Jones, D. Resolving the Circumstellar Environment of the Galactic B[e] Supergiant Star MWC 137.II. Nebular Kinematics and Stellar Variability. Astron. J. 2021, 162, 150. [Google Scholar] [CrossRef]
- Barsukova, E.A.; Burenkov, A.N.; Goranskij, V.P. Sudden strengthening of He II emission line in the spectrum of B[e] star CI Cam. Astron. Telegr. 2021, 14362, 1. [Google Scholar]
- Smith, D.; Remillard, R.; Swank, J.; Takeshima, T.; Smith, E. XTE J0421+560. IAU Circ. 1998, 6855, 1. [Google Scholar]
- Korčáková, D.; Sestito, F.; Manset, N.; Kroupa, P.; Votruba, V.; Šlechta, M.; Danford, S.; Dvořáková, N.; Raj, A.; Chojnowski, S.D.; et al. First detection of a magnetic field in low-luminosity B[e] stars. New scenarios for the nature and evolutionary stages of FS CMa stars. Astron. Astrophys. 2022, 659, A35. [Google Scholar] [CrossRef]
- Aidelman, Y.; Cidale, L.S.; Kraus, M. Aias, M.L.; Zorec, J. Fundamental parameters of B[e] stars. Astron. Astrophys. 2022. submitted. [Google Scholar]
- Arias, M.L.; Cidale, L.S.; Kraus, M.; Torres, A.F.; Aidelman, Y.; Zorec, J.; Granada, A. Near-infrared Spectra of a Sample of Galactic Unclassified B[e] Stars. Publ. Astron. Soc. Pac. 2018, 130, 114201. [Google Scholar] [CrossRef]
- Burnichon, M.L.; Chalonge, D.; Divan, L.; Swings, L. Etude de l’etoile Be HD 45677. J. Obs. 1967, 50, 391. [Google Scholar]
- Merrill, P.W. Bright iron lines in the spectrum of HD 45677. Astrophys. J. 1928, 67, 405–408. [Google Scholar] [CrossRef]
- Swings, P.; Struve, O. Spectrographic Observations of Peculiar Stars. Astrophys. J. 1940, 91, 546. [Google Scholar] [CrossRef]
- Swings, P.; Struve, O. Spectrographic Observations of Peculiar Stars.VI. Astrophys. J. 1943, 98, 91. [Google Scholar] [CrossRef]
- Zorec, J.; Moujtahid, A.; Ballereau, D.; Chauville, J. Fundamental Parameters of Two B[e] Stars: HD 45677 and HD 50138. In Proceedings of the B[e] Stars; Hubert, A.M., Jaschek, C., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA, 1998; Volume 233, p. 55. [Google Scholar] [CrossRef]
- Zorec, J. Distances, Kinematics and Distribution of B[e] Stars in Our Galaxy. In Proceedings of the B[e] Stars; Hubert, A.M., Jaschek, C., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA, 1998; Volume 233, p. 27. [Google Scholar] [CrossRef]
- Moujtahid, A.; Zorec, J.; Hubert, A.M. Ultraviolet Extinction of Circumstellar Dust in the B[e] Star HD 45677. In Proceedings of the Ultraviolet Astrophysics Beyond the IUE Final Archive; Wamsteker, W., Gonzalez Riestra, R., Harris, B., Eds.; ESA Publications Division: Noordwijk, The Netherlands, 1998; Volume 413, p. 261. [Google Scholar]
- Grinin, V.P.; Kiselev, N.N.; Minikulov, N.K. Observations of “zodiacal light” of the isolated Herbig Ae-star BF Ori. Pisma v Astronomicheskii Zhurnal 1989, 15, 1028–1038. [Google Scholar]
- Grinin, V.P.; Kiselev, N.N.; Minikulov, N.K.; Chernova, G.P.; Voshchinnikov, N.V. The investigations of ‘zodiacal light’ of isolated AE-Herbig stars with non-periodic Algol-type minima. Astrophys. Space Sci. 1991, 186, 283–298. [Google Scholar] [CrossRef]
- Jeřábková, T.; Korčáková, D.; Miroshnichenko, A.; Danford, S.; Zharikov, S.V.; Kříček, R.; Zasche, P.; Votruba, V.; Šlechta, M.; Škoda, P.; et al. Time-dependent spectral-feature variations of stars displaying the B[e] phenomenon. III. HD 50138. Astron. Astrophys. 2016, 586, A116. [Google Scholar] [CrossRef][Green Version]
- Kluska, J.; Benisty, M.; Soulez, F.; Berger, J.P.; Le Bouquin, J.B.; Malbet, F.; Lazareff, B.; Thiébaut, E. A disk asymmetry in motion around the B[e] star MWC158. Astron. Astrophys. 2016, 591, A82. [Google Scholar] [CrossRef]
- Miroshnichenko, A.S.; Zharikov, S.V.; Danford, S.; Manset, N.; Korčáková, D.; Kříček, R.; Šlechta, M.; Omarov, C.T.; Kusakin, A.V.; Kuratov, K.S.; et al. Toward Understanding the B[e] Phenomenon. V. Nature and Spectral Variations of the MWC 728 Binary System. Astrophys. J. 2015, 809, 129. [Google Scholar] [CrossRef]
- Miroshnichenko, A.S.; Bernabei, S.; Polcaro, V.F.; Viotti, R.F.; Norci, L.; Manset, N.; Klochkova, V.G.; Rudy, R.J.; Lynch, D.K.; Venturini, C.C.; et al. Optical and Near-IR Observations of the B[e] Star AS 119. In Proceedings of the Stars with the B[e] Phenomenon; Kraus, M., Miroshnichenko, A.S., Eds.; University of Chicago Press: Vlieland, The Netherlands, 2006; Volume 355, p. 347. [Google Scholar]
- Polster, J.; Korčáková, D.; Manset, N. Time-dependent spectral-feature variations of stars displaying the B[e] phenomenon. IV. V2028 Cygni: Modelling of Hα bisector variability. Astron. Astrophys. 2018, 617, A79. [Google Scholar] [CrossRef]
- Zickgraf, F.J.; Schulte-Ladbeck, R.E. Polarization characteristics of galactic Be stars. Astron. Astrophys. 1989, 214, 274–284. [Google Scholar]
- Condori, C.A.H.; Borges Fernandes, M.; Kraus, M.; Panoglou, D.; Guerrero, C.A. The study of unclassified B[e] stars and candidates in the Galaxy and Magellanic Clouds†. Mon. Not. R. Astron. Soc. 2019, 488, 1090–1110. [Google Scholar] [CrossRef]
- Langer, N.; Kudritzki, R.P. The spectroscopic Hertzsprung-Russell diagram. Astron. Astrophys. 2014, 564, A52. [Google Scholar] [CrossRef]
- Chentsov, E.L.; Klochkova, V.G.; Miroshnichenko, A.S. Spectral variability of the peculiar A-type supergiant 3Pup. Astrophys. Bull. 2010, 65, 150–163. [Google Scholar] [CrossRef]
- Miroshnichenko, A.S.; Danford, S.; Zharikov, S.V.; Klochkova, V.G.; Chentsov, E.L.; Vanbeveren, D.; Zakhozhay, O.V.; Manset, N.; Pogodin, M.A.; Omarov, C.T.; et al. Properties of Galactic B[e] Supergiants. V. 3 Pup-Constraining the Orbital Parameters and Modeling the Circumstellar Environments. Astrophys. J. 2020, 897, 48. [Google Scholar] [CrossRef]
- Langer, N.; Heger, A. B[e] Supergiants: What is Their Evolutionary Status? In Proceedings of the B[e] Stars; Hubert, A.M., Jaschek, C., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA, 1998; Volume 233, p. 235. [Google Scholar]
- Podsiadlowski, P.; Morris, T.S.; Ivanova, N. Massive Binary Mergers: A Unique Scenario for the sgB[e] Phenomenon? In Proceedings of the Stars with the B[e] Phenomenon; Kraus, M., Miroshnichenko, A.S., Eds.; University of Chicago Press: Vlieland, The Netherlands, 2006; Volume 355, p. 259. [Google Scholar]
- de Mink, S.E.; Langer, N.; Izzard, R.G.; Sana, H.; de Koter, A. The Rotation Rates of Massive Stars: The Role of Binary Interaction through Tides, Mass Transfer, and Mergers. Astrophys. J. 2013, 764, 166. [Google Scholar] [CrossRef]
- de Mink, S.E.; Sana, H.; Langer, N.; Izzard, R.G.; Schneider, F.R.N. The Incidence of Stellar Mergers and Mass Gainers among Massive Stars. Astrophys. J. 2014, 782, 7. [Google Scholar] [CrossRef]
- Zickgraf, F.J. Discussion Session: Is there an Evolutionary Link between B[e] Supergiants and LBVs? In Proceedings of the Stars with the B[e] Phenomenon; Kraus, M., Miroshnichenko, A.S., Eds.; University of Chicago Press: Vlieland, The Netherlands, 2006; Volume 355, p. 211. [Google Scholar]
- Meynet, G.; Maeder, A. Single Massive Stars at the Critical Rotational Velocity: Possible Links with Be and B[e] Stars. In Proceedings of the Stars with the B[e] Phenomenon; Kraus, M., Miroshnichenko, A.S., Eds.; University of Chicago Press: Vlieland, The Netherlands, 2006; Volume 355, p. 27. [Google Scholar]
- Georgy, C.; Saio, H.; Ekström, S.; Meynet, G. The Advanced Stages of Stellar Evolution: Impact of Mass Loss, Rotation, and Link With B[e] Stars. In Proceedings of the The B[e] Phenomenon: Forty Years of Studies; Miroshnichenko, A., Zharikov, S., Korčáková, D., Wolf, M., Eds.; Insititut of Physics Publishing: Prague, Czech Republic, 2017; Volume 508, p. 99. [Google Scholar]
- Cox, J.P.; Giuli, R.T. Principles of Stellar Structure; Gordon and Breach: New York, NY, USA, 1968. [Google Scholar]
- Sweet, P.A. The importance of rotation in stellar evolution. Mon. Not. R. Astron. Soc. 1950, 110, 548. [Google Scholar] [CrossRef]
- Zahn, J.P. Instability and Mixing Processes in Upper Main Sequence Stars. In Proceedings of the Saas-Fee Advanced Course 13: Astrophysical Processes in Upper Main Sequence Stars; Cox, A.N., Vauclair, S., Zahn, J.P., Eds.; Geneva Observatory: Sauverny, France, 1983; p. 253. [Google Scholar]
- Zahn, J.P. Circulation and turbulence in rotating stars. Astron. Astrophys. 1992, 265, 115–132. [Google Scholar]
- Ferraro, V.C.A. The non-uniform rotation of the Sun and its magnetic field. Mon. Not. R. Astron. Soc. 1937, 97, 458. [Google Scholar] [CrossRef]
- Ferraro, V.C.A.; Plumpton, C. An Introduction to Magneto-Fluid Mechanics. J. Plasma Phys. 1967, 1, 499. [Google Scholar] [CrossRef]
- Spruit, H.C. Differential rotation and magnetic fields in stellar interiors. Astron. Astrophys. 1999, 349, 189–202. [Google Scholar]
- Spruit, H.C. Dynamo action by differential rotation in a stably stratified stellar interior. Astron. Astrophys. 2002, 381, 923–932. [Google Scholar] [CrossRef]
- Spruit, H.C. Angular Momentum Transport and Mixing by Magnetic Fields (Invited Review). In Proceedings of the Stellar Rotation; Maeder, A., Eenens, P., Eds.; 2004; Volume 215, p. 356. [Google Scholar]
- Maeder, A. Physics, Formation and Evolution of Rotating Stars; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Fujimoto, M.Y. Dynamical stability of differentially rotating bodies to non-axisymmetric perturbations. Astron. Astrophys. 1987, 176, 53–58. [Google Scholar]
- Tassoul, J.L. Theory of Rotating Stars; University Press: Princeton, NJ, USA, 1978. [Google Scholar]
- Chandrasekhar, S. Ellipsoidal Figures of Equilibrium; New Haven Yale University Press: New Haven, CT, USA, 1969. [Google Scholar]
- Kippenhahn, R.; Meyer-Hofmeister, E.; Thomas, H.C. Rotation in Evolving Stars. Astron. Astrophys. 1970, 5, 155. [Google Scholar]
- Mark, J.W.K. Rapidly Rotating Stars. III. Massive Main-Sequence Stars. Astrophys. J. 1968, 154, 627. [Google Scholar] [CrossRef]
- Bodenheimer, P. Rapidly Rotating Stars. VII. Effects of Angular Momentum on Upper-Main Models. Astrophys. J. 1971, 167, 153. [Google Scholar] [CrossRef]
- Smith, R.C.; Collins, G.W., I. Differential rotation and polar hollows. Mon. Not. R. Astron. Soc. 1992, 257, 340–352. [Google Scholar] [CrossRef][Green Version]
- Ostriker, J.P.; Mark, J.W.K. Rapidly rotating stars. I. The self-consistent-field method. Astrophys. J. 1968, 151, 1075–1088. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Bodenheimer, P. Rapidly Rotating Stars. II. Massive White Dwarfs. Astrophys. J. 1968, 151, 1089. [Google Scholar] [CrossRef]
- Bodenheimer, P.; Ostriker, J.P. Rapidly Rotating Stars.VI. Pre-Main—Evolution of Massive Stars. Astrophys. J. 1970, 161, 1101. [Google Scholar] [CrossRef]
- Jackson, S. Rapidly Rotating Stars. V. The Coupling of the Henyey and the Self-Consistent Methods. Astrophys. J. 1970, 161, 579. [Google Scholar] [CrossRef]
- Bodenheimer, P.; Ostriker, J.P. Rapidly Rotating Stars. VIII. Zero-Viscosity Polytropic Sequences. Astrophys. J. 1973, 180, 159–170. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Blinnikov, S.I. Static Criteria for Stability of Arbitrarily Rotating Stars. Astron. Astrophys. 1974, 31, 391. [Google Scholar]
- Blinnikov, S.I. Self-consistent field method in the theory of rotating stars. Soviet Ast. 1975, 19, 151–156. [Google Scholar]
- Jackson, S.; MacGregor, K.B.; Skumanich, A. On the Use of the Self-consistent-Field Method in the Construction of Models for Rapidly Rotating Main-Sequence Stars. Astrophys. J. Suppl. Ser. 2005, 156, 245–264. [Google Scholar] [CrossRef][Green Version]
- Endal, A.S.; Sofia, S. The evolution of rotating stars. I. Method and exploratory calculations for a 7 M sun star. Astrophys. J. 1976, 210, 184–198. [Google Scholar] [CrossRef]
- Eriguchi, Y.; Mueller, E. A general computational method for obtaining equilibria of self-gravitating and rotating gases. Astron. Astrophys. 1985, 146, 260–268. [Google Scholar]
- Hachisu, I. A Versatile Method for Obtaining Structures of Rapidly Rotating Stars. Astrophys. J. Suppl. Ser. 1986, 61, 479. [Google Scholar] [CrossRef]
- Eriguchi, Y.; Mueller, E. Structure of rapidly rotating axisymmetric stars. I—A numerical method for stellar structure and meridional circulation. Astron. Astrophys. 1991, 248, 435–447. [Google Scholar]
- Clement, M.J. On the solution of Poisson’s equation for rapidly rotating stars. Astrophys. J. 1974, 194, 709–714. [Google Scholar] [CrossRef]
- Uryu, K.; Eriguchi, Y. Structures of Rapidly Rotating Baroclinic Stars-Part One—A Numerical Method for the Angular Velocity Distribution. Mon. Not. R. Astron. Soc. 1994, 269, 24. [Google Scholar] [CrossRef][Green Version]
- Uryu, K.; Eriguchi, Y. Structures of rapidly rotating baroclinic stars—II. an extended numerical method for realistic stellar models. Mon. Not. R. Astron. Soc. 1995, 277, 1411–1429. [Google Scholar] [CrossRef]
- Fujisawa, K. A versatile numerical method for obtaining structures of rapidly rotating baroclinic stars: Self-consistent and systematic solutions with shellular-type rotation. Mon. Not. R. Astron. Soc. 2015, 454, 3060–3072. [Google Scholar] [CrossRef]
- Meynet, G.; Maeder, A. Stellar evolution with rotation. I. The computational method and the inhibiting effect of the μ-gradient. Astron. Astrophys. 1997, 321, 465–476. [Google Scholar]
- Meynet, G.; Maeder, A. Stellar evolution with rotation. V. Changes in all the outputs of massive star models. Astron. Astrophys. 2000, 361, 101–120. [Google Scholar]
- Heger, A.; Langer, N.; Woosley, S.E. Presupernova Evolution of Rotating Massive Stars. I. Numerical Method and Evolution of the Internal Stellar Structure. Astrophys. J. 2000, 528, 368–396. [Google Scholar] [CrossRef]
- Hubbard, W.B.; Slattery, W.L.; Devito, C.L. High zonal harmonics of rapidly rotating planets. Astrophys. J. 1975, 199, 504–516. [Google Scholar] [CrossRef]
- Collins, G.W., I. Continuum Emission from Rotating Non-Gray Stellar Atmospheres. II. Astrophys. J. 1966, 146, 914. [Google Scholar] [CrossRef]
- Collins, G.W., II; Smith, R.C. The photometric effect of rotation in the A stars. Mon. Not. R. Astron. Soc. 1985, 213, 519–552. [Google Scholar] [CrossRef][Green Version]
- Frémat, Y.; Zorec, J.; Hubert, A.M.; Floquet, M. Effects of gravitational darkening on the determination of fundamental parameters in fast-rotating B-type stars. Astron. Astrophys. 2005, 440, 305–320. [Google Scholar] [CrossRef]
- Zorec, J.; Rieutord, M.; Espinosa Lara, F.; Frémat, Y.; Domiciano de Souza, A.; Royer, F. Gravity darkening in stars with surface differential rotation. Astron. Astrophys. 2017, 606, A32. [Google Scholar] [CrossRef]
- Milne, E.A. The equilibrium of a rotating star. Mon. Not. R. Astron. Soc. 1923, 83, 118–147. [Google Scholar] [CrossRef][Green Version]
- Sackmann, I.J. Rapid Uniform Rotation Along the Main Sequence II. Astron. Astrophys. 1970, 8, 76. [Google Scholar]
- Deupree, R.G. Stellar Evolution with Arbitrary Rotation Laws. IV. Survey of Zero-Age Main-Sequence Models. Astrophys. J. 2001, 552, 268–277. [Google Scholar] [CrossRef]
- Gillich, A.; Deupree, R.G.; Lovekin, C.C.; Short, C.I.; Toqué, N. Determination of Effective Temperatures and Luminosities for Rotating Stars. Astrophys. J. 2008, 683, 441–448. [Google Scholar] [CrossRef][Green Version]
- Higgins, E.R.; Vink, J.S. Massive star evolution: Rotation, winds, and overshooting vectors in the mass-luminosity plane. I. A calibrated grid of rotating single star models. Astron. Astrophys. 2019, 622, A50. [Google Scholar] [CrossRef]
- von Zeipel, H. The radiative equilibrium of a rotating system of gaseous masses. Mon. Not. R. Astron. Soc. 1924, 84, 665–683. [Google Scholar] [CrossRef]
- Roxburgh, I.W. On stellar rotation, III. Thermally generated magnetic fields. Mon. Not. R. Astron. Soc. 1966, 132, 201. [Google Scholar] [CrossRef][Green Version]
- Lucy, L.B. Gravity-Darkening for Stars with Convective Envelopes. Zeitschrift für Astrophysik 1967, 65, 89. [Google Scholar]
- Rieutord, M. Physical Processes Leading to Surface Inhomogeneities: The Case of Rotation. In Lecture Notes in Physics: Cartograpy of the Sun and the Stars; Rozelot, J.P., Neiner, C., Eds.; Springer International Publishing Switzerland: Cham, Switzerland, 2016; Volume 914, p. 101. [Google Scholar] [CrossRef]
- Smith, R.C.; Worley, R. Gravity-darkening in stars for general rotation laws. Mon. Not. R. Astron. Soc. 1974, 167, 199–214. [Google Scholar] [CrossRef][Green Version]
- Monnier, J.D.; Zhao, M.; Pedretti, E.; Thureau, N.; Ireland, M.; Muirhead, P.; Berger, J.P.; Millan-Gabet, R.; Van Belle, G.; ten Brummelaar, T.; et al. Imaging the Surface of Altair. Science 2007, 317, 342. [Google Scholar] [CrossRef] [PubMed]
- Monnier, J.D.; Che, X.; Zhao, M.; Ekström, S.; Maestro, V.; Aufdenberg, J.; Baron, F.; Georgy, C.; Kraus, S.; McAlister, H.; et al. Resolving Vega and the Inclination Controversy with CHARA/MIRC. Astrophys. J. Lett. 2012, 761, L3. [Google Scholar] [CrossRef]
- Zhao, M.; Monnier, J.D.; Pedretti, E.; Thureau, N.; Mérand, A.; ten Brummelaar, T.; McAlister, H.; Ridgway, S.T.; Turner, N.; Sturmann, J.; et al. Imaging and Modeling Rapidly Rotating Stars: α Cephei and α Ophiuchi. Astrophys. J. 2009, 701, 209–224. [Google Scholar] [CrossRef]
- Che, X.; Monnier, J.D.; Zhao, M.; Pedretti, E.; Thureau, N.; Mérand, A.; ten Brummelaar, T.; McAlister, H.; Ridgway, S.T.; Turner, N.; et al. Colder and Hotter: Interferometric Imaging of β Cassiopeiae and α Leonis. Astrophys. J. 2011, 732, 68. [Google Scholar] [CrossRef]
- Domiciano de Souza, A.; Kervella, P.; Moser Faes, D.; Dalla Vedova, G.; Mérand, A.; Le Bouquin, J.B.; Espinosa Lara, F.; Rieutord, M.; Bendjoya, P.; Carciofi, A.C.; et al. The environment of the fast rotating star Achernar. III. Photospheric parameters revealed by the VLTI. Astron. Astrophys. 2014, 569, A10. [Google Scholar] [CrossRef]
- Domiciano de Souza, A.; Bouchaud, K.; Rieutord, M.; Espinosa Lara, F.; Putigny, B. The evolved fast rotator Sargas. Stellar parameters and evolutionary status from VLTI/PIONIER and VLT/UVES. Astron. Astrophys. 2018, 619, A167. [Google Scholar] [CrossRef]
- Kippenhahn, R. Rotational darkening—Rotational brightening. Astron. Astrophys. 1977, 58, 267–271. [Google Scholar]
- Maeder, A. Stellar evolution with rotation IV: Von Zeipel’s theorem and anisotropic losses of mass and angular momentum. Astron. Astrophys. 1999, 347, 185–193. [Google Scholar]
- Maunder, E.W.; Maunder, A.S.D. Sun, rotation period of the, from Greenwich sun-spot measures, 1879–1901. Mon. Not. R. Astron. Soc. 1905, 65, 813–825. [Google Scholar] [CrossRef]
- Espinosa Lara, F.; Rieutord, M. Gravity darkening in rotating stars. Astron. Astrophys. 2011, 533, A43. [Google Scholar] [CrossRef]
- Maeder, A.; Peytremann, E. Stellar Rotation. Astron. Astrophys. 1970, 7, 120. [Google Scholar]
- Collins, G.W., I. Further Note on Terminology—Specific Luminosity. Astron. Astrophys. 1973, 26, 315. [Google Scholar]
- Moss, D.; Smith, R.C. REVIEW ARTICLE: Stellar rotation and magnetic stars. Reports on Progress in Physics 1981, 44, 831–891. [Google Scholar] [CrossRef]
- Zorec, J. L’effet de la rotation sur la magnitude absolue des étoiles. In Proceedings of the Ecole de Printemps d’Astrophysique de Goutelas: HIPPARCOS; 1993; pp. 407–425. [Google Scholar]
- Maeder, A.; Peytremann, E. Uniformly Rotating Stars with Hydrogen- and Metallic-Line Blanketed Model Atmospheres. Astron. Astrophys. 1972, 21, 279. [Google Scholar]
- Collins, G.W., I; Sonneborn, G.H. Some effects of rotation on the spectra of upper-main-sequence stars. Astrophys. J. Suppl. Ser. 1977, 34, 41–94. [Google Scholar] [CrossRef]
- Slettebak, A.; Kuzma, T.J.; Collins, G.W., I. Effects of stellar rotation on spectral classification. Astrophys. J. 1980, 242, 171–187. [Google Scholar] [CrossRef]
- Collins, G.W., I. Continuum Emission from a Rotating Non-Gray Stellar Atmosphere. Astrophys. J. 1965, 142, 265. [Google Scholar] [CrossRef]
- Zorec, J.; Royer, F. Rotational velocities of A-type stars. IV. Evolution of rotational velocities. Astron. Astrophys. 2012, 537, A120. [Google Scholar] [CrossRef]
- Georgy, C.; Ekström, S.; Eggenberger, P.; Meynet, G.; Haemmerlé, L.; Maeder, A.; Granada, A.; Groh, J.H.; Hirschi, R.; Mowlavi, N.; et al. Grids of stellar models with rotation. III. Models from 0.8 to 120 M⊙ at a metallicity Z = 0.002. Astron. Astrophys. 2013, 558, A103. [Google Scholar] [CrossRef]
- Sigut, T.A.A.; Ghafourian, N.R. Comparing Be Star Inclination Angles Determined from Hα Fitting and Gravitational Darkening. arXiv 2022, arXiv:2209.06885. [Google Scholar]
- Morel, T.; Blazère, A.; Semaan, T.; Gosset, E.; Zorec, J.; Frémat, Y.; Blomme, R.; Daflon, S.; Lobel, A.; Nieva, M.F.; et al. The Gaia-ESO survey: A spectroscopic study of the young open cluster NGC 3293. Astron. Astrophys. 2022, 665, A108. [Google Scholar] [CrossRef]
- Grant, L.P.; Peraiah, A. Spectral line formation in extended stellar atmo-spheres. Mon. Not. R. Astron. Soc. 1972, 160, 239. [Google Scholar] [CrossRef]
- Simonneau, E. Radiative transfer in atmospheres with spherical symmetry. J. Quant. Spectrosc. Radiat. Transf. 1976, 16, 741–753. [Google Scholar] [CrossRef]
- Simonneau, E. Radiative transfer in atmospheres with spherical symmetry—IV. The non-conservative problem. J. Quant. Spectrosc. Radiat. Transf. 1980, 23, 73–81. [Google Scholar] [CrossRef]
- Lopez, R.; Simonneau, E.; Isern, J. Model atmospheres for type I supernovae—Curvature effects. Astron. Astrophys. 1987, 184, 249–255. [Google Scholar]
- Korčáková, D.; Kubát, J. Emergent line profiles from rapidly rotating stars. Memorie della Societa Astronomica Italiana Supplementi 2005, 7, 130. [Google Scholar]
- Frémat, Y.; Zorec, J.; Levenhagen, R.; Leister, N.; Hubert, A.M.; Floquet, M.; Neiner, C. Chemical Composition of Early Type Be Stars. In Proceedings of the CNO in the Universe; Charbonnel, C., Schaerer, D., Meynet, G., Eds.; University of Chicago Press: Chicago, NY, USA, 2003; Volume 304, p. 57. [Google Scholar]
- Frémat, Y.; Zorec, J.; Hubert, A.M. Chemical Composition of the Pole-On Be Star HD 120991. In Proceedings of the Stellar Rotation; Maeder, A., Eenens, P., Eds.; Cambridge University Press: Cambridge, UK, 2004; Volume 215, p. 224. [Google Scholar]
- Frémat, Y.; Zorec, J.; Levenhagen, R.; Leister, N.; Hubert, A.M.; Floquet, M.; Neiner, C. CNO abundances in Early Type Be Stars. In Proceedings of the Stellar Rotation; Maeder, A., Eenens, P., Eds.; Cambridge University Press: Cambridge, UK, 2004; Volume 215, p. 222. [Google Scholar]
- Lennon, D.J.; Lee, J.K.; Dufton, P.L.; Ryans, R.S.I. A Be star with a low nitrogen abundance in the SMC cluster NGC 330. Astron. Astrophys. 2005, 438, 265–271. [Google Scholar] [CrossRef]
- Hunter, I.; Dufton, P.L.; Smartt, S.J.; Ryans, R.S.I.; Evans, C.J.; Lennon, D.J.; Trundle, C.; Hubeny, I.; Lanz, T. The VLT-FLAMES survey of massive stars: Surface chemical compositions of B-type stars in the Magellanic Clouds. Astron. Astrophys. 2007, 466, 277–300. [Google Scholar] [CrossRef]
- Hunter, I.; Brott, I.; Lennon, D.J.; Langer, N.; Dufton, P.L.; Trundle, C.; Smartt, S.J.; de Koter, A.; Evans, C.J.; Ryans, R.S.I. The VLT FLAMES Survey of Massive Stars: Rotation and Nitrogen Enrichment as the Key to Understanding Massive Star Evolution. Astrophys. J. Lett. 2008, 676, L29. [Google Scholar] [CrossRef]
- Hunter, I.; Brott, I.; Langer, N.; Lennon, D.J.; Dufton, P.L.; Howarth, I.D.; Ryans, R.S.I.; Trundle, C.; Evans, C.J.; de Koter, A.; et al. The VLT-FLAMES survey of massive stars: Constraints on stellar evolution from the chemical compositions of rapidly rotating Galactic and Magellanic Cloud B-type stars. Astron. Astrophys. 2009, 496, 841–853. [Google Scholar] [CrossRef]
- Trundle, C.; Dufton, P.L.; Hunter, I.; Evans, C.J.; Lennon, D.J.; Smartt, S.J.; Ryans, R.S.I. The VLT-FLAMES survey of massive stars: Evolution of surface N abundances and effective temperature scales in the Galaxy and Magellanic Clouds. Astron. Astrophys. 2007, 471, 625–643. [Google Scholar] [CrossRef]
- Dunstall, P.R.; Brott, I.; Dufton, P.L.; Lennon, D.J.; Evans, C.J.; Smartt, S.J.; Hunter, I. The VLT-FLAMES survey of massive stars: Nitrogen abundances for Be-type stars in the Magellanic Clouds. Astron. Astrophys. 2011, 536, A65. [Google Scholar] [CrossRef]
- Potter, A.T.; Tout, C.A.; Brott, I. Towards a unified model of stellar rotation—II. Model-dependent characteristics of stellar populations. Mon. Not. R. Astron. Soc. 2012, 423, 1221–1233. [Google Scholar] [CrossRef][Green Version]
- Brott, I.; Evans, C.J.; Hunter, I.; de Koter, A.; Langer, N.; Dufton, P.L.; Cantiello, M.; Trundle, C.; Lennon, D.J.; de Mink, S.E.; et al. Rotating massive main-sequence stars. II. Simulating a population of LMC early B-type stars as a test of rotational mixing. Astron. Astrophys. 2011, 530, A116. [Google Scholar] [CrossRef]
- Porter, J.M. On the possibility that rotation causes latitudinal abundance variations in stars. Astron. Astrophys. 1999, 341, 560–566. [Google Scholar]
- Langer, N.; Cantiello, M.; Yoon, S.C.; Hunter, I.; Brott, I.; Lennon, D.; de Mink, S.; Verheijdt, M. Rotation and Massive Close Binary Evolution. In Proceedings of the Massive Stars as Cosmic Engines; Bresolin, F., Crowther, P.A., Puls, J., Eds.; 2008; Volume 250, pp. 167–178. [Google Scholar] [CrossRef][Green Version]
- Shajn, G.; Struve, O. On the rotation of the stars. Mon. Not. R. Astron. Soc. 1929, 89, 222–239. [Google Scholar] [CrossRef]
- Struve, O. Axial rotation as a major factor in stellar spectroscopy. Observatory 1931, 54, 80–84. [Google Scholar]
- Elvey, C.T. The rotation of stars and the contours of Mg+ 4481. Astrophys. J. 1930, 71, 221–230. [Google Scholar] [CrossRef]
- Carroll, J.A. The spectroscopic determination of stellar rotation and its effect on line profiles. Mon. Not. R. Astron. Soc. 1933, 93, 478–507. [Google Scholar] [CrossRef]
- Slettebak, A. On the Axial Rotation of the Brighter O and B Stars. Astrophys. J. 1949, 110, 498. [Google Scholar] [CrossRef]
- Howarth, I.D. Rotation and Line Broadening in OBA Stars (Invited Review). In Proceedings of the Stellar Rotation; Maeder, A., Eenens, P., Eds.; Cambridge University Press: Cambridge, UK, 2004; Volume 215, p. 33. [Google Scholar]
- Slettebak, A.; Collins, G.W., I; Boyce, P.B.; White, N.M.; Parkinson, T.D. A system of standard stars for rotational velocity determinations. Astrophys. J. Suppl. Ser. 1975, 29, 137–159. [Google Scholar] [CrossRef]
- Dufton, P.L.; Smartt, S.J.; Lee, J.K.; Ryans, R.S.I.; Hunter, I.; Evans, C.J.; Herrero, A.; Trundle, C.; Lennon, D.J.; Irwin, M.J.; et al. The VLT-FLAMES survey of massive stars: Stellar parameters and rotational velocities in NGC 3293, NGC 4755 and NGC 6611. Astron. Astrophys. 2006, 457, 265–280. [Google Scholar] [CrossRef]
- Díaz, C.G.; González, J.F.; Levato, H.; Grosso, M. Accurate stellar rotational velocities using the Fourier transform of the cross correlation maximum. Astron. Astrophys. 2011, 531, A143. [Google Scholar] [CrossRef]
- Howarth, I.D.; Siebert, K.W.; Hussain, G.A.J.; Prinja, R.K. Cross-correlation characteristics of OB stars from IUE spectroscopy. Mon. Not. R. Astron. Soc. 1997, 284, 265–285. [Google Scholar] [CrossRef]
- Daflon, S.; Cunha, K.; de Araújo, F.X.; Wolff, S.; Przybilla, N. The Projected Rotational Velocity Distribution of a Sample of OB stars from a Calibration Based on Synthetic He I Lines. Astron. J. 2007, 134, 1570–1578. [Google Scholar] [CrossRef][Green Version]
- Stoeckley, T.; Mihalas, D. Limb Darkening and Rotation Broadening of Neutral Helium and Ionized Magnesium Line Profiles in Early-Type Stars; NCAR: Boulder, CO, USA, 1973; Volume NCAR. [Google Scholar]
- Huang, W.; Gies, D.R. Stellar Rotation in Young Clusters. I. Evolution of Projected Rotational Velocity Distributions. Astrophys. J. 2006, 648, 580–590. [Google Scholar] [CrossRef][Green Version]
- Balona, L.A. Equivalent widths and rotational velocities of southern early-type stars. Mem. R. Astron. Soc. 1975, 78, 51. [Google Scholar]
- Conti, P.S.; Ebbets, D. Spectroscopic studies of O-type stars. VII. Rotational velocities V sin i and evidence for macroturbulent motions. Astrophys. J. 1977, 213, 438–447. [Google Scholar] [CrossRef]
- Slettebak, A. Spectral types and rotational velocities of the brighter Be stars and A-F type shell stars. Astrophys. J. Suppl. Ser. 1982, 50, 55–83. [Google Scholar] [CrossRef]
- Wolff, S.C.; Edwards, S.; Preston, G.W. The origin of stellar angular momentum. Astrophys. J. 1982, 252, 322–336. [Google Scholar] [CrossRef]
- Abt, H.A.; Morrell, N.I. The Relation between Rotational Velocities and Spectral Peculiarities among A-Type Stars. Astrophys. J. Suppl. Ser. 1995, 99, 135. [Google Scholar] [CrossRef]
- Halbedel, E.M. Rotational Velocity Determinations for 164 Be and B Stars. Publ. Astron. Soc. Pac. 1996, 108, 833. [Google Scholar] [CrossRef]
- Penny, L.R. Projected Rotational Velocities of O-Type Stars. Astrophys. J. 1996, 463, 737. [Google Scholar] [CrossRef]
- Brown, A.G.A.; Verschueren, W. High S/N Echelle spectroscopy in young stellar groups. II. Rotational velocities of early-type stars in SCO OB2. Astron. Astrophys. 1997, 319, 811–838. [Google Scholar]
- Steele, I.A.; Negueruela, I.; Clark, J.S. A representative sample of Be stars . I. Sample selection, spectral classification and rotational velocities. Astron. Astrophys. 1999, 137, 147–156. [Google Scholar] [CrossRef]
- Chauville, J.; Zorec, J.; Ballereau, D.; Morrell, N.; Cidale, L.; Garcia, A. High and intermediate-resolution spectroscopy of Be stars 4481 lines. Astron. Astrophys. 2001, 378, 861–882. [Google Scholar] [CrossRef]
- Abt, H.A.; Levato, H.; Grosso, M. Rotational Velocities of B Stars. Astrophys. J. 2002, 573, 359–365. [Google Scholar] [CrossRef]
- Royer, F.; Gerbaldi, M.; Faraggiana, R.; Gómez, A.E. Rotational velocities of A-type stars. I. Measurement of v sin i in the southern hemisphere. Astron. Astrophys. 2002, 381, 105–121. [Google Scholar] [CrossRef]
- Royer, F.; Grenier, S.; Baylac, M.O.; Gómez, A.E.; Zorec, J. Rotational velocities of A-type stars in the northern hemisphere. II. Measurement of v sin i. Astron. Astrophys. 2002, 393, 897–911. [Google Scholar] [CrossRef]
- Keller, S.C. Rotation of Early B-type Stars in the Large Magellanic Cloud: The Role of Evolution and Metallicity. Publ. Astron. Soc. Aust. 2004, 21, 310–317. [Google Scholar] [CrossRef][Green Version]
- Penny, L.R.; Sprague, A.J.; Seago, G.; Gies, D.R. Effects of Metallicity on the Rotational Velocities of Massive Stars. Astrophys. J. 2004, 617, 1316–1322. [Google Scholar] [CrossRef]
- Glebocki, R.; Gnacinski, P. VizieR Online Data Catalog: Catalog of Stellar Rotational Velocities (Glebocki+ 2005); VizieR Online Data Catalog; 2005; p. III/244. [Google Scholar]
- Strom, S.E.; Wolff, S.C.; Dror, D.H.A. B Star Rotational Velocities in h and χ Persei: A Probe of Initial Conditions during the Star Formation Epoch? Astron. J. 2005, 129, 809–828. [Google Scholar] [CrossRef]
- Wolff, S.C.; Strom, S.E.; Dror, D.; Lanz, L.; Venn, K. Stellar Rotation: A Clue to the Origin of High-Mass Stars? Astron. J. 2006, 132, 749–755. [Google Scholar] [CrossRef]
- Frémat, Y.; Neiner, C.; Hubert, A.M.; Floquet, M.; Zorec, J.; Janot-Pacheco, E.; Renan de Medeiros, J. Fundamental parameters of Be stars located in the seismology fields of COROT. Astron. Astrophys. 2006, 451, 1053–1063. [Google Scholar] [CrossRef]
- Mokiem, M.R.; de Koter, A.; Evans, C.J.; Puls, J.; Smartt, S.J.; Crowther, P.A.; Herrero, A.; Langer, N.; Lennon, D.J.; Najarro, F.; et al. The VLT-FLAMES survey of massive stars: Mass loss and rotation of early-type stars in the SMC. Astron. Astrophys. 2006, 456, 1131–1151. [Google Scholar] [CrossRef]
- Levenhagen, R.S.; Leister, N.V. Spectroscopic analysis of southern B and Be stars. Mon. Not. R. Astron. Soc. 2006, 371, 252–262. [Google Scholar] [CrossRef][Green Version]
- Martayan, C.; Frémat, Y.; Hubert, A.M.; Floquet, M.; Zorec, J.; Neiner, C. Effects of metallicity, star-formation conditions, and evolution in B and Be stars. I. Large Magellanic Cloud, field of NGC 2004. Astron. Astrophys. 2006, 452, 273–284. [Google Scholar] [CrossRef]
- Martayan, C.; Frémat, Y.; Hubert, A.M.; Floquet, M.; Zorec, J.; Neiner, C. Effects of metallicity, star-formation conditions, and evolution in B and Be stars. II. Small Magellanic Cloud, field of NGC 330. Astron. Astrophys. 2007, 462, 683–694. [Google Scholar] [CrossRef]
- Wolff, S.C.; Strom, S.E.; Dror, D.; Venn, K. Rotational Velocities for B0-B3 Stars in Seven Young Clusters: Further Study of the Relationship between Rotation Speed and Density in Star-Forming Regions. Astron. J. 2007, 133, 1092–1103. [Google Scholar] [CrossRef]
- Wolff, S.C.; Strom, S.E.; Cunha, K.; Daflon, S.; Olsen, K.; Dror, D. Rotational Velocities for Early-Type Stars in the Young Large Magellanic Cloud Cluster R136: Further Study of the Relationship Between Rotation Speed and Density in Star-Forming Regions. Astron. J. 2008, 136, 1049–1060. [Google Scholar] [CrossRef][Green Version]
- Huang, W.; Gies, D.R. Stellar Rotation in Field and Cluster B Stars. Astrophys. J. 2008, 683, 1045–1051. [Google Scholar] [CrossRef][Green Version]
- Hunter, I.; Lennon, D.J.; Dufton, P.L.; Trundle, C.; Simón-Díaz, S.; Smartt, S.J.; Ryans, R.S.I.; Evans, C.J. The VLT-FLAMES survey of massive stars: Atmospheric parameters and rotational velocity distributions for B-type stars in the Magellanic Clouds. Astron. Astrophys. 2008, 479, 541–555. [Google Scholar] [CrossRef]
- Penny, L.R.; Gies, D.R. A FUSE Survey of the Rotation Rates of Very Massive Stars in the Small and Large Magellanic Clouds. Astrophys. J. 2009, 700, 844–858. [Google Scholar] [CrossRef]
- Fraser, M.; Dufton, P.L.; Hunter, I.; Ryans, R.S.I. Atmospheric parameters and rotational velocities for a sample of Galactic B-type supergiants. Mon. Not. R. Astron. Soc. 2010, 404, 1306–1320. [Google Scholar] [CrossRef]
- Huang, W.; Gies, D.R.; McSwain, M.V. A Stellar Rotation Census of B Stars: From ZAMS to TAMS. Astrophys. J. 2010, 722, 605–619. [Google Scholar] [CrossRef]
- Marsh Boyer, A.N.; McSwain, M.V.; Aragona, C.; Ou-Yang, B. Physical Properties of the B and Be Star Populations of h and χ Persei. Astron. J. 2012, 144, 158. [Google Scholar] [CrossRef][Green Version]
- Bragança, G.A.; Daflon, S.; Cunha, K.; Bensby, T.; Oey, M.S.; Walth, G. Projected Rotational Velocities and Stellar Characterization of 350 B Stars in the Nearby Galactic Disk. Astron. J. 2012, 144, 130. [Google Scholar] [CrossRef]
- Dufton, P.L.; Langer, N.; Dunstall, P.R.; Evans, C.J.; Brott, I.; de Mink, S.E.; Howarth, I.D.; Kennedy, M.; McEvoy, C.; Potter, A.T.; et al. The VLT-FLAMES Tarantula Survey. X. Evidence for a bimodal distribution of rotational velocities for the single early B-type stars. Astron. Astrophys. 2013, 550, A109. [Google Scholar] [CrossRef]
- Ramírez-Agudelo, O.H.; Simón-Díaz, S.; Sana, H.; de Koter, A.; Sabín-Sanjulían, C.; de Mink, S.E.; Dufton, P.L.; Gräfener, G.; Evans, C.J.; Herrero, A.; et al. The VLT-FLAMES Tarantula Survey. XII. Rotational velocities of the single O-type stars. Astron. Astrophys. 2013, 560, A29. [Google Scholar] [CrossRef]
- Simón-Díaz, S.; Herrero, A. The IACOB project. I. Rotational velocities in northern Galactic O- and early B-type stars revisited. The impact of other sources of line-broadening. Astron. Astrophys. 2014, 562, A135. [Google Scholar] [CrossRef]
- Garmany, C.D.; Glaspey, J.W.; Bragança, G.A.; Daflon, S.; Borges Fernandes, M.; Oey, M.S.; Bensby, T.; Cunha, K. Projected Rotational Velocities of 136 Early B-type Stars in the Outer Galactic Disk. Astron. J. 2015, 150, 41. [Google Scholar] [CrossRef]
- Holgado, G.; Simón-Díaz, S.; Herrero, A.; Barbá, R.H. The IACOB project. VII. The rotational properties of Galactic massive O-type stars revisited. Astron. Astrophys. 2022, 665, A150. [Google Scholar] [CrossRef]
- Solar, M.; Arcos, C.; Curé, M.; Levenhagen, R.S.; Araya, I. Automatic algorithm to obtain v sin i values via Fourier transform in the BeSOS database. Mon. Not. R. Astron. Soc. 2022, 511, 4404–4416. [Google Scholar] [CrossRef]
- Xiang, M.; Rix, H.W.; Ting, Y.S.; Kudritzki, R.P.; Conroy, C.; Zari, E.; Shi, J.R.; Przybilla, N.; Ramirez-Tannus, M.; Tkachenko, A.; et al. Stellar labels for hot stars from low-resolution spectra. I. The HotPayne method and results for 330 000 stars from LAMOST DR6. Astron. Astrophys. 2022, 662, A66. [Google Scholar] [CrossRef]
- Vallenari, A.; Brown, A.G.A.; Prusti, T.; de Bruijne, J.H.J.; Arenou, F.; Babusiaux, C.; Biermann, M.; Creevey, O.L.; Ducourant, C.; et al.; Gaia Collaboration Gaia Data Release 3: Summary of the content and survey properties. arXiv 2022, arXiv:arXiv:2208.00211. [Google Scholar]
- Sartoretti, P.; Blomme, R.; David, M.; Seabroke, G. Gaia DR3 documentation Chapter 6: Spectroscopy. Gaia DR3 documentation, European Space Agency; Gaia Data Processing and Analysis Consortium. 2022. Available online: https://gea.esac.esa.int/archive/documentation/GDR3/index.html (accessed on 1 February 2022).
- Creevey, O.L.; Sordo, R.; Pailler, F.; Frémat, Y.; Heiter, U.; Thévenin, F.; Andrae, R.; Fouesneau, M.; Lobel, A.; Bailer-Jones, C.A.L.; et al. Gaia Data Release 3: Astrophysical parameters inference system (Apsis) I—Methods and content overview. arXiv 2022, arXiv:2206.05864. [Google Scholar] [CrossRef]
- Frémat, Y.; Royer, F.; Marchal, O.; Blomme, R.; Sartoretti, P.; Guerrier, A.; Panuzzo, P.; Katz, D.; Seabroke, G.M.; Thévenin, F.; et al. Gaia Data Release 3: Properties of the line broadening parameter derived with the Radial Velocity Spectrometer (RVS). arXiv 2022, arXiv:2206.10986. [Google Scholar] [CrossRef]
- Blomme, R.; Frémat, Y.; Sartoretti, P.; Guerrier, A.; Panuzzo, P.; Katz, D.; Seabroke, G.M.; Thevenin, F.; Cropper, M.; Benson, K.; et al. Gaia Data Release 3: Hot-star radial velocities. arXiv 2022, arXiv:2206.05486. [Google Scholar] [CrossRef]
- Katz, D.; Sartoretti, P.; Guerrier, A.; Panuzzo, P.; Seabroke, G.M.; Thévenin, F.; Cropper, M.; Benson, K.; Blomme, R.; Haigron, R.; et al. Gaia Data Release 3 Properties and validation of the radial velocities. arXiv 2022, arXiv:2206.05902. [Google Scholar] [CrossRef]
- Gaia Collaboration; Creevey, O.L.; Sarro, L.M.; Lobel, A.; Pancino, E.; Andrae, R.; Smart, R.L.; Clementini, G.; Heiter, U.; Korn, A.J.; et al. Gaia Data Release 3: A Golden Sample of Astrophysical Parameters. arXiv 2022, arXiv:arXiv:2206.05870. [Google Scholar] [CrossRef]
- Ulla, A.; Creevey, O.L.; Álvarez, M.A.; Andrae, R.; Bailer-Jones, C.A.L.; Bellas-Velidis, I.; Brugaletta, E.; Carballo, R.; Dafonte, C.; Delchambre, L.; et al. Gaia DR3 Documentation Chapter 11: Astrophysical Parameters. Gaia DR3 Documentation, European Space Agency; Gaia Data Processing and Analysis Consortium. 2022. Available online: https://gea.esac.esa.int/archive/documentation/GDR3/index.html (accessed on 1 February 2022).
- Fouesneau, M.; Frémat, Y.; Andrae, R.; Korn, A.J.; Soubiran, C.; Kordopatis, G.; Vallenari, A.; Heiter, U.; Creevey, O.L.; Sarro, L.M.; et al. Gaia Data Release 3: Apsis II – Stellar Parameters. arXiv 2022, arXiv:2206.05992. [Google Scholar] [CrossRef]
- Shridharan, B.; Mathew, B.; Bhattacharyya, S.; Robin, T.; Arun, R.; Kartha, S.S.; Manoj, P.; Nidhi, S.; Maheshwar, G.; Paul, K.T.; et al. Emission line star catalogues post-Gaia DR3: A validation of Gaia DR3 data using LAMOST OBA emission catalogue. arXiv 2022, arXiv:2209.13221. [Google Scholar] [CrossRef]
- Plaskett, H.H. The formation of the magnesium b lines in the solar atmosphere. Mon. Not. R. Astron. Soc. 1931, 91, 870. [Google Scholar] [CrossRef][Green Version]
- Gray, D.F. The Observation and Analysis of Stellar Photospheres; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Levenhagen, R.S. A Fourier Transform Method for Vsin i Estimations under Nonlinear Limb-darkening Laws. Astrophys. J. 2014, 797, 29. [Google Scholar] [CrossRef]
- Collins, G.W., I; Truax, R.J. Classical Rotational Broadening of Spectral Lines. Astrophys. J. 1995, 439, 860. [Google Scholar] [CrossRef]
- Korčáková, D.; Kubát, J. Radiative transfer in moving media. I. Discontinuous finite element method for one-dimensional atmospheres. Astron. Astrophys. 2003, 401, 419–428. [Google Scholar] [CrossRef][Green Version]
- Korčáková, D.; Kubát, J. Radiative transfer in moving media. II. Solution of the radiative transfer equation in axial symmetry. Astron. Astrophys. 2005, 440, 715–725. [Google Scholar] [CrossRef][Green Version]
- Hillier, D.J.; Lanz, T. CMFGEN: A non-LTE Line-Blanketed Radiative Transfer Code for Modeling Hot Stars with Stellar Winds. In Proceedings of the Spectroscopic Challenges of Photoionized Plasmas; Ferland, G., Savin, D.W., Eds.; University of Chicago Press: Chicago, NY, USA, 2001; Volume 247, p. 343. [Google Scholar]
- Hillier, D.J. The atomic physics underlying the spectroscopic analysis of massive stars and supernovae. Astrophys. Space Sci. 2011, 336, 87–93. [Google Scholar] [CrossRef]
- Hillier, D.J. Hot Stars with Winds: The CMFGEN Code. In Proceedings of the From Interacting Binaries to Exoplanets: Essential Modeling Tools; Richards, M.T., Hubeny, I., Eds.; Cambridge Unversity Press: Cambridge, UK, 2012; Volume 282, pp. 229–234. [Google Scholar] [CrossRef][Green Version]
- Stoeckley, T.R. Distribution of rotational velocities in Be stars. Mon. Not. R. Astron. Soc. 1968, 140, 141. [Google Scholar] [CrossRef]
- Stoeckley, T.R. Absorption line strengths in rotating stars. Mon. Not. R. Astron. Soc. 1968, 140, 149. [Google Scholar] [CrossRef]
- Townsend, R.H.D.; Owocki, S.P.; Howarth, I.D. Be-star rotation: How close to critical? Mon. Not. R. Astron. Soc. 2004, 350, 189–195. [Google Scholar] [CrossRef]
- Cranmer, S.R. A Statistical Study of Threshold Rotation Rates for the Formation of Disks around Be Stars. Astrophys. J. 2005, 634, 585–601. [Google Scholar] [CrossRef]
- Heap, S.R. Ultraviolet Observations of be Stars (review Paper). In Proceedings of the Be and Shell Stars; Slettebak, A., Ed.; 1976; Volume 70, p. 165. [Google Scholar]
- Heap, S.R. Apparent wavelength dependence of ν sin i for Zeta Tauri. Astrophys. J. Lett. 1977, 218, L17–L19. [Google Scholar] [CrossRef]
- Hutchings, J.B. V sin i Values in the Far Ultraviolet. Publ. Astron. Soc. Pac. 1976, 88, 5. [Google Scholar] [CrossRef]
- Hutchings, J.B.; Stoeckley, T.R. V and i in rotating stars from Copernicus UV data. Publ. Astron. Soc. Pac. 1977, 89, 19–22. [Google Scholar] [CrossRef]
- Sonneborn, G.H.; Collins, G.W., I. On the wavelength dependence of rotational line broadening. Astrophys. J. 1977, 213, 787–790. [Google Scholar] [CrossRef]
- Carpenter, K.G.; Slettebak, A.; Sonneborn, G. Rotational velocities of later B type and A type stars as determined from ultraviolet versus visual line profiles. Astrophys. J. 1984, 286, 741–746. [Google Scholar] [CrossRef]
- Osaki, Y. On the Atmosphere of a Rotating Star. Publ. Astron. Soc. Jpn. 1966, 18, 7. [Google Scholar]
- Pustyl’Nik, I. Radiative transfer in the atmospheres of rotating stars. Izv. Akad. Nauk Ehstonskoj SSR 1970, 19, 428–435. [Google Scholar] [CrossRef]
- Hadrava, P. Radiative transfer in rotating stars. Astron. Astrophys. 1992, 256, 519–524. [Google Scholar]
- Unsöld, A.; Struve, O. Curves of Growth and Line Contours. Astrophys. J. 1949, 110, 455. [Google Scholar] [CrossRef]
- Huang, S.S.; Struve, O. A Study of Line Profiles: The Spectrum of Rho Leonis. Astrophys. J. 1953, 118, 463. [Google Scholar] [CrossRef]
- Underhill, A.B. On the Effect of Radiation Pressure in the Atmospheres of Early-Type Stars. Mon. Not. R. Astron. Soc. 1949, 109, 562. [Google Scholar] [CrossRef][Green Version]
- Underhill, A.B. Numerical experiments concerning the rotational broadening of spectral lines. Bull. Astron. Institutes Neth. 1968, 19, 526. [Google Scholar]
- Rosendhal, J.D. Evolutionary Effects in the Rotation of Supergiants. Astrophys. J. 1970, 159, 107. [Google Scholar] [CrossRef]
- Grassitelli, L.; Fossati, L.; Simón-Diáz, S.; Langer, N.; Castro, N.; Sanyal, D. Observational Consequences of Turbulent Pressure in the Envelopes of Massive Stars. Astrophys. J. Lett. 2015, 808, L31. [Google Scholar] [CrossRef]
- Aerts, C.; Puls, J.; Godart, M.; Dupret, M.A. Collective pulsational velocity broadening due to gravity modes as a physical explanation for macroturbulence in hot massive stars. Astron. Astrophys. 2009, 508, 409–419. [Google Scholar] [CrossRef]
- Aerts, C.; Simón-Díaz, S.; Groot, P.J.; Degroote, P. On the use of the Fourier transform to determine the projected rotational velocity of line-profile variable B stars. Astron. Astrophys. 2014, 569, A118. [Google Scholar] [CrossRef]
- Simón-Díaz, S. Asteroseismology of OB stars with hundreds of single snapshot spectra (and a few time-series of selected targets). In Proceedings of the IAU Symposium; Meynet, G., Georgy, C., Groh, J., Stee, P., Eds.; 2015; Volume 307, pp. 194–199. [Google Scholar] [CrossRef]
- Ryans, R.S.I.; Dufton, P.L.; Rolleston, W.R.J.; Lennon, D.J.; Keenan, F.P.; Smoker, J.V.; Lambert, D.L. Macroturbulent and rotational broadening in the spectra of B-type supergiants. Mon. Not. R. Astron. Soc. 2002, 336, 577–586. [Google Scholar] [CrossRef]
- Gray, D.F. Atmospheric turbulence measured in stars above the main sequence. Astrophys. J. 1975, 202, 148–164. [Google Scholar] [CrossRef]
- Gray, D.F. The Observation and Analysis of Stellar Photospheres; Cambridge Astrophysics, Series; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Simón-Díaz, S.; Herrero, A. Fourier method of determining the rotational velocities in OB stars. Astron. Astrophys. 2007, 468, 1063–1073. [Google Scholar] [CrossRef]
- Dufton, P.L.; Ryans, R.S.I.; Simón-Díaz, S.; Trundle, C.; Lennon, D.J. B-type supergiants in the Small Magellanic Cloud: Rotational velocities and implications for evolutionary models. Astron. Astrophys. 2006, 451, 603–611. [Google Scholar] [CrossRef][Green Version]
- Sundqvist, J.O.; Simón-Díaz, S.; Puls, J.; Markova, N. The rotation rates of massive stars. How slow are the slow ones? Astron. Astrophys. 2013, 559, L10. [Google Scholar] [CrossRef]
- Stoeckley, T.R. Determination of aspect and degree of differential rotation, from line profiles in rapidly rotating stars. Mon. Not. R. Astron. Soc. 1968, 140, 121. [Google Scholar] [CrossRef]
- Zorec, J.; Divan, L.; Mochkovitch, R.; Garcia, A. Differential rotation in B and Be stars. In Proceedings of the IAU Colloq. 92: Physics of Be Stars; Slettebak, A., Snow, T.P., Eds.; Cambridge University Press: Cambridge, UK, 1987; pp. 68–70. [Google Scholar]
- Stoeckley, T.R.; Buscombe, W. Axial inclination and differential rotation for 19 rapidly rotating stars. Mon. Not. R. Astron. Soc. 1987, 227, 801–813. [Google Scholar] [CrossRef]
- Zorec, J.; Mochkovitch, R.A.; Garcia, A. The Angular Momentum Loss and the Differential Rotation in B-Stars and Be-Stars. In Proceedings of the NATO ASIC Proc. 316: Angular Momentum and Mass Loss for Hot Stars; Willson, L.A., Stalio, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1990; p. 239. [Google Scholar]
- Cranmer, S.R.; Collins, G.W., II. The effects of zonal atmospheric currents on the spectra of rotating early-type stars. Astrophys. J. 1993, 412, 720–730. [Google Scholar] [CrossRef]
- Rieutord, M. The dynamics of the radiative envelope of rapidly rotating stars. I. A spherical Boussinesq model. Astron. Astrophys. 2006, 451, 1025–1036. [Google Scholar] [CrossRef]
- Espinosa Lara, F.; Rieutord, M. The dynamics of a fully radiative rapidly rotating star enclosed within a spherical box. Astron. Astrophys. 2007, 470, 1013–1022. [Google Scholar] [CrossRef]
- Schou, J.; Antia, H.M.; Basu, S.; Bogart, R.S.; Bush, R.I.; Chitre, S.M.; Christensen-Dalsgaard, J.; Di Mauro, M.P.; Dziembowski, W.A.; Eff-Darwich, A.; et al. Helioseismic Studies of Differential Rotation in the Solar Envelope by the Solar Oscillations Investigation Using the Michelson Doppler Imager. Astrophys. J. 1998, 505, 390–417. [Google Scholar] [CrossRef]
- Espinosa Lara, F.; Rieutord, M. Self-consistent 2D models of fast-rotating early-type stars. Astron. Astrophys. 2013, 552, A35. [Google Scholar] [CrossRef]
- Rieutord, M.; Espinosa Lara, F.; Putigny, B. An algorithm for computing the 2D structure of fast rotating stars. J. Comput. Phys. 2016, 318, 277–304. [Google Scholar] [CrossRef]
- Gagnier, D.; Rieutord, M.; Charbonnel, C.; Putigny, B.; Espinosa Lara, F. Evolution of rotation in rapidly rotating early-type stars during the main sequence with 2D models. Astron. Astrophys. 2019, 625, A89. [Google Scholar] [CrossRef]
- Jeffery, C.S. Quasi-emission lines in rotating B stars. Mon. Not. R. Astron. Soc. 1991, 249, 327. [Google Scholar] [CrossRef][Green Version]
- Takeda, Y.; Kawanomoto, S.; Ohishi, N. High-Resolution and High-S/N Spectrum Atlas of Vega. Publ. Astron. Soc. Jpn. 2007, 59, 245–261. [Google Scholar] [CrossRef]
- Takeda, Y.; Kawanomoto, S.; Ohishi, N. Rotational Feature of Vega Revealed from Spectral Line Profiles. Astrophys. J. 2008, 678, 446–462. [Google Scholar] [CrossRef][Green Version]
- Zorec, J. Emission-like feature due to a latitudinal differential rotation. In Proceedings of the Pulsation; Rotation; and Mass Loss in Early-Type Stars; Balona, L.A., Henrichs, H.F., Le Contel, J.M., Eds.; Kluwer Academic Publishers: New York, NY, USA, 1994; Volume 162, pp. 257–258. [Google Scholar]
- Reiners, A.; Schmitt, J.H.M.M. Rotation and differential rotation in field F- and G-type stars. Astron. Astrophys. 2003, 398, 647–661. [Google Scholar] [CrossRef]
- Reiners, A.; Schmitt, J.H.M.M. Differential rotation in rapidly rotating F-stars. Astron. Astrophys. 2003, 412, 813–819. [Google Scholar] [CrossRef]
- Sobolev, V.V. Moving Envelopes of Stars; Harvard University Press: Cambridge, UK, 1960. [Google Scholar] [CrossRef]
- Kalkofen, W. Methods in Radiative Transfer; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- Mihalas, D.; Mihalas, B.W. Foundations of radiation hydrodynamics; New York: Oxford University Press, 1984. [Google Scholar]
- Kunasz, P.B. The theory of line transfer in expanding atmospheres. In Progress in Stellar Spectral Line Formation Theory; Beckman, J.E., Crivellari, L., Eds.; Springer Science & Business Media: Berlin, Germany, 1985; Volume 152, pp. 319–333. [Google Scholar]
- Kalkofen, W. Numerical Radiative Transfer; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Conti, P.S.; Underhill, A.B.; Jordan, S.; Thomas, R.N.; Goldberg, L.; Pecker, J.C.; Baade, D.; Divan, L.; Garmany, C.D.; Henrichs, H.F.; et al. O Stars and Wolf-Rayet Stars; NASA: Washington, DC, USA, 1988; Volume 497. [Google Scholar]
- Sen, K.K.; Wilson, S.J. Radiative Transfer in Moving Media: Basic Mathematical Methods for Radiative Transfer In Spherically Symmetrical Moving Media; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Stee, P. (Ed.) Radiative Transfer and Hydrodynamics in Astrophysics; EAS Publications Series; EDP Sciences: Les Ulis, France, 2002; Volume 5. [Google Scholar]
- Ivan Hubeny, D.M.; Werner, K. (Eds.) Stellar Atmosphere Modeling; Astronomical Society of the Pacific Conference Series; University Chicago Press: Chicago, NY, USA, 2003; Volume 288. [Google Scholar]
- Cannon, C.J. The Transfer of Spectral Line Radiation; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Furenlid, I.; Young, A. Mass loss and rotation in early-main-sequence B stars. Astrophys. J. Lett. 1980, 240, L59–L61. [Google Scholar] [CrossRef]
- Cook, K.H.; Alcock, C.; Allsman, H.A.; Axelrod, T.S.; Freeman, K.C.; Peterson, B.A.; Quinn, P.J.; Rodgers, A.W.; Bennett, D.P.; Reimann, J.; et al. Variable Stars in the MACHO Collaboration Database. In Proceedings of the IAU Colloq. 155: Astrophysical Applications of Stellar Pulsation; Stobie, R.S., Whitelock, P.A., Eds.; Cambridge University Press: Cambridge, UK, 1995; Volume 83, p. 221. [Google Scholar]
- Duval, P.; Karp, A.H. The combined effects of expansion and rotation on spectral line shapes. Astrophys. J. 1978, 222, 220–225. [Google Scholar] [CrossRef]
- Chelli, A.; Petrov, R.G. Model fitting and error analysis for differential interferometry. I. General formalism. Astron. Astrophys. 1995, 109, 389–399. [Google Scholar]
- Chelli, A.; Petrov, R.G. Model fitting and error analysis for differential interferometry. II. Application to rotating stars and binary systems. Astron. Astrophys. 1995, 109, 401–415. [Google Scholar]
- Vakili, F.; Mourard, D.; Bonneau, D.; Morand, F.; Stee, P. Subtle structures in the wind of P Cygni. Astron. Astrophys. 1997, 323, 183–188. [Google Scholar]
- Jankov, S.; Vakili, F.; Domiciano de Souza, A., Jr.; Janot-Pacheco, E. Interferometric-Doppler imaging of stellar surface structure. Astron. Astrophys. 2001, 377, 721–734. [Google Scholar] [CrossRef]
- ten Brummelaar, T.A.; McAlister, H.A.; Ridgway, S.T.; Bagnuolo, W.G., Jr.; Turner, N.H.; Sturmann, L.; Sturmann, J.; Berger, D.H.; Ogden, C.E.; Cadman, R.; et al. First Results from the CHARA Array. II. A Description of the Instrument. Astrophys. J. 2005, 628, 453–465. [Google Scholar] [CrossRef]
- Armstrong, J.T.; Mozurkewich, D.; Rickard, L.J.; Hutter, D.J.; Benson, J.A.; Bowers, P.F.; Elias, N.M., I; Hummel, C.A.; Johnston, K.J.; Buscher, D.F.; et al. The Navy Prototype Optical Interferometer. Astrophys. J. 1998, 496, 550–571. [Google Scholar] [CrossRef]
- Colavita, M.M.; Wallace, J.K.; Hines, B.E.; Gursel, Y.; Malbet, F.; Palmer, D.L.; Pan, X.P.; Shao, M.; Yu, J.W.; Boden, A.F.; et al. The Palomar Testbed Interferometer. Astrophys. J. 1999, 510, 505–521. [Google Scholar] [CrossRef]
- Glindemann, A.; Albertsen, M.; Andolfato, L.; Avila, G.; Ballester, P.; Bauvir, B.; Delplancke, F.; Derie, F.; Dimmler, M.; Duhoux, P.; et al. VLTI technical advances: Present and future. In Proceedings of the New Frontiers in Stellar Interferometry; Traub, W.A., Ed.; SPIE: Washington, DC, USA, 2004; Volume 5491, p. 447. [Google Scholar] [CrossRef]
- Petrov, R.G.; Malbet, F.; Weigelt, G.; Antonelli, P.; Beckmann, U.; Bresson, Y.; Chelli, A.; Dugué, M.; Duvert, G.; Gennari, S.; et al. AMBER, the near-infrared spectro-interferometric three-telescope VLTI instrument. Astron. Astrophys. 2007, 464, 1–12. [Google Scholar] [CrossRef]
- Domiciano de Souza, A. Long Baseline Interferometry of Rotating Stars across the HR Diagram: Flattening, Gravity Darkening, Differential Rotation. In Lecture Notes on Physics: The Rotation of Sun and Stars; Rozelot, J.P., Neiner, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 765, pp. 171–194. [Google Scholar] [CrossRef]
- Domiciano de Souza, A. Interferometric Surface Mapping of Rapidly Rotating Stars: Application to the Be star Achernar. In Lecture Notes in Physics; Rozelot, J.P., Neiner, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 914, p. 159. [Google Scholar] [CrossRef]
- Brown, R.H. The Intensity Interferometer; Its Application to Astronomy; Taylor and Francis LTD London and Halsted Press: London, UK, 1974. [Google Scholar]
- Domiciano de Souza, A.; Kervella, P.; Jankov, S.; Abe, L.; Vakili, F.; di Folco, E.; Paresce, F. The spinning-top Be star Achernar from VLTI-VINCI. Astron. Astrophys. 2003, 407, L47–L50. [Google Scholar] [CrossRef]
- Vinicius, M.M.F.; Zorec, J.; Leister, N.V.; Levenhagen, R.S. α Eridani: Rotational distortion, stellar and circumstellar activity. Astron. Astrophys. 2006, 446, 643–660. [Google Scholar] [CrossRef]
- Kanaan, S.; Meilland, A.; Stee, P.; Zorec, J.; Domiciano de Souza, A.; Frémat, Y.; Briot, D. Disk and wind evolution of Achernar: The breaking of the fellowship. Astron. Astrophys. 2008, 486, 785–798. [Google Scholar] [CrossRef]
- Kervella, P.; Domiciano de Souza, A. The polar wind of the fast rotating Be star Achernar. VINCI/VLTI interferometric observations of an elongated polar envelope. Astron. Astrophys. 2006, 453, 1059–1066. [Google Scholar] [CrossRef]
- van Belle, G.T. Interferometric observations of rapidly rotating stars. Astron. Astrophys. Rev. 2012, 20, 51. [Google Scholar] [CrossRef]
- Hadjara, M.; Petrov, R.G.; Jankov, S.; Cruzalèbes, P.; Spang, A.; Lagarde, S. Differential interferometry of the rapid rotator Regulus. Mon. Not. R. Astron. Soc. 2018, 480, 1263–1277. [Google Scholar] [CrossRef]
- Gray, R.O. The spectroscopic and photometric effects of rotation in the A-type stars. J. R. Astron. Soc. Can. 1988, 82, 336–348. [Google Scholar]
- McAlister, H.A.; ten Brummelaar, T.A.; Gies, D.R.; Huang, W.; Bagnuolo, W.G., Jr.; Shure, M.A.; Sturmann, J.; Sturmann, L.; Turner, N.H.; Taylor, S.F.; et al. First Results from the CHARA Array. I. An Interferometric and Spectroscopic Study of the Fast Rotator α Leonis (Regulus). Astrophys. J. 2005, 628, 439–452. [Google Scholar] [CrossRef]
- Aufdenberg, J.P.; Mérand, A.; Coudé du Foresto, V.; Absil, O.; Di Folco, E.; Kervella, P.; Ridgway, S.T.; Berger, D.H.; ten Brummelaar, T.A.; McAlister, H.A.; et al. First Results from the CHARA Array. VII. Long-Baseline Interferometric Measurements of Vega Consistent with a Pole-On, Rapidly Rotating Star. Astrophys. J. 2006, 645, 664–675. [Google Scholar] [CrossRef]
- Peterson, D.M.; Hummel, C.A.; Pauls, T.A.; Armstrong, J.T.; Benson, J.A.; Gilbreath, G.C.; Hindsley, R.B.; Hutter, D.J.; Johnston, K.J.; Mozurkewich, D.; et al. Vega is a rapidly rotating star. Nature 2006, 440, 896–899. [Google Scholar] [CrossRef]
- Peterson, D.M.; Hummel, C.A.; Pauls, T.A.; Armstrong, J.T.; Benson, J.A.; Gilbreath, G.C.; Hindsley, R.B.; Hutter, D.J.; Johnston, K.J.; Mozurkewich, D.; et al. Resolving the Effects of Rotation in Altair with Long-Baseline Interferometry. Astrophys. J. 2006, 636, 1087–1097. [Google Scholar] [CrossRef][Green Version]
- Challouf, M.; Nardetto, N.; Domiciano de Souza, A.; Mourard, D.; Tallon-Bosc, I.; Aroui, H.; Farrington, C.; Ligi, R.; Meilland, A.; Mouelhi, M. Flattening and surface-brightness of the fast-rotating star δ Persei with the visible VEGA/CHARA interferometer. Astron. Astrophys. 2017, 604, A51. [Google Scholar] [CrossRef][Green Version]
- Domiciano de Souza, A.; Vakili, F.; Jankov, S.; Janot-Pacheco, E.; Abe, L. Modelling rapid rotators for stellar interferometry. Astron. Astrophys. 2002, 393, 345–357. [Google Scholar] [CrossRef]
- Domiciano de Souza, A.; Zorec, J.; Vakili, F. CHARRON: Code for High Angular Resolution of Rotating Objects in Nature. In Proceedings of the SF2A-2012: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics; Boissier, S., de Laverny, P., Nardetto, N., Samadi, R., Valls-Gabaud, D., Wozniak, H., Eds.; EDP Sciences: Les Ulis, France, 2012; pp. 321–324. [Google Scholar]
- Domiciano de Souza, A.; Zorec, J.; Jankov, S.; Vakili, F.; Abe, L.; Janot-Pacheco, E. Stellar differential rotation and inclination angle from spectro-interferometry. Astron. Astrophys. 2004, 418, 781–794. [Google Scholar] [CrossRef]
- Delaa, O.; Zorec, J.; Domiciano de Souza, A.; Mourard, D.; Perraut, K.; Stee, P.; Frémat, Y.; Monnier, J.; Kraus, S.; Che, X.; et al. Spectrally resolved interferometric observations of α Cephei and physical modeling of fast rotating stars. Astron. Astrophys. 2013, 555, A100. [Google Scholar] [CrossRef]
- Stee, P.; Allard, F.; Benisty, M.; Bigot, L.; Blind, N.; Boffin, H.; Borges Fernandes, M.; Carciofi, A.; Chiavassa, A.; Creevey, O.; et al. Science cases for a visible interferometer. arXiv 2017, arXiv:1703.02395. [Google Scholar]
- Meilland, A.; Millour, F.; Stee, P.; Domiciano de Souza, A.; Petrov, R.G.; Mourard, D.; Jankov, S.; Robbe-Dubois, S.; Spang, A.; Aristidi, E.; et al. An asymmetry detected in the disk of κ Canis Majoris with AMBER/VLTI. Astron. Astrophys. 2007, 464, 73–79. [Google Scholar] [CrossRef]
- Meilland, A.; Millour, F.; Stee, P.; Spang, A.; Petrov, R.; Bonneau, D.; Perraut, K.; Massi, F. δ Centauri: A new binary Be star detected by VLTI/AMBER spectro-interferometry. Astron. Astrophys. 2008, 488, L67–L70. [Google Scholar] [CrossRef]
- Meilland, A.; Stee, P.; Chesneau, O.; Jones, C. VLTI/MIDI observations of 7 classical Be stars. Astron. Astrophys. 2009, 505, 687–693. [Google Scholar] [CrossRef]
- Meilland, A.; Delaa, O.; Stee, P.; Kanaan, S.; Millour, F.; Mourard, D.; Bonneau, D.; Petrov, R.; Nardetto, N.; Marcotto, A.; et al. The binary Be star δ Scorpii at high spectral and spatial resolution. I. Disk geometry and kinematics before the 2011 periastron. Astron. Astrophys. 2011, 532, A80. [Google Scholar] [CrossRef]
- Meilland, A.; Millour, F.; Kanaan, S.; Stee, P.; Petrov, R.; Hofmann, K.H.; Natta, A.; Perraut, K. First spectro-interferometric survey of Be stars. I. Observations and constraints on the disk geometry and kinematics. Astron. Astrophys. 2012, 538, A110. [Google Scholar] [CrossRef]
- Meilland, A.; Stee, P.; Spang, A.; Malbet, F.; Massi, F.; Schertl, D. The binary Be star δ Scorpii at high spectral and spatial resolution. II. The circumstellar disk evolution after the periastron. Astron. Astrophys. 2013, 550, L5. [Google Scholar] [CrossRef]
- Delaa, O.; Stee, P.; Meilland, A.; Zorec, J.; Mourard, D.; Bério, P.; Bonneau, D.; Chesneau, O.; Clausse, J.M.; Cruzalebes, P.; et al. Kinematics and geometrical study of the Be stars 48 Persei and ψ Persei with the VEGA/CHARA interferometer. Astron. Astrophys. 2011, 529, A87. [Google Scholar] [CrossRef]
- Stee, P.; Delaa, O.; Monnier, J.D.; Meilland, A.; Perraut, K.; Mourard, D.; Che, X.; Schaefer, G.H.; Pedretti, E.; Smith, M.A.; et al. The relationship between γ Cassiopeiae’s X-ray emission and its circumstellar environment. II. Geometry and kinematics of the disk from MIRC and VEGA instruments on the CHARA Array. Astron. Astrophys. 2012, 545, A59. [Google Scholar] [CrossRef]
- Stee, P.; Meilland, A.; Stee, P.; Meilland, A. VLTI, CHARA and NPOI Observations of Be Stars. In Proceedings of the Circumstellar Dynamics at High Resolution, Proceedings on the ESO/IAG/USPWorkshop, Foz do Iguaçu, Brazil, 27 February–2 March 2012; Astronomical Society of the Pacific Conference Series; Carciofi, A.C., Rivinius, T., Eds.; ASP; 2012; Volume 464, p. 167. [Google Scholar]
- Cochetti, Y.R.; Arcos, C.; Kanaan, S.; Meilland, A.; Cidale, L.S.; Curé, M. Spectro-interferometric observations of a sample of Be stars. Setting limits to the geometry and kinematics of stable Be disks. Astron. Astrophys. 2019, 621, A123. [Google Scholar] [CrossRef]
- van Belle, G.T.; Ciardi, D.R.; ten Brummelaar, T.; McAlister, H.A.; Ridgway, S.T.; Berger, D.H.; Goldfinger, P.J.; Sturmann, J.; Sturmann, L.; Turner, N.; et al. First Results from the CHARA Array. III. Oblateness, Rotational Velocity, and Gravity Darkening of Alderamin. Astrophys. J. 2006, 637, 494–505. [Google Scholar] [CrossRef][Green Version]
- Pelletier, G.; Pudritz, R.E. Hydromagnetic Disk Winds in Young Stellar Objects and Active Galactic Nuclei. Astrophys. J. 1992, 394, 117. [Google Scholar] [CrossRef]
- Bodenheimer, P. Angular Momentum Evolution of Young Stars and Disks. Annu. Rev. Astron. Astrophys. 1995, 33, 199–238. [Google Scholar] [CrossRef]
- Ray, T. Losing spin: The angular momentum problem. Astron. Geophys. 2012, 53, 5–19. [Google Scholar] [CrossRef][Green Version]
- Larson, R.B. Processes in Collapsing Interstellar Clouds. Annu. Rev. Astron. Astrophys. 1973, 11, 219. [Google Scholar] [CrossRef]
- Burki, G.; Maeder, A. Observational tests on star formation I: Size variation of very young clusters through the Galaxy. Astron. Astrophys. 1976, 51, 247–254. [Google Scholar]
- Guthrie, B.N.G. The rotation of early-type stars and the problem of star formation. Mon. Not. R. Astron. Soc. 1984, 210, 159–171. [Google Scholar] [CrossRef][Green Version]
- Bodenheimer, P. Evolution of rotating interstellar clouds. III. On the formation of multiple star systems. Astrophys. J. 1978, 224, 488–496. [Google Scholar] [CrossRef]
- Deutsch, A.J. Maxwellian Distributions for Stellar Rotations. In Proceedings of the IAU Colloq. 4: Stellar Rotation; Slettebak, A., Ed.; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 1970; p. 207. [Google Scholar]
- Maeder, A.; Grebel, E.K.; Mermilliod, J.C. Differences in the fractions of Be stars in galaxies. Astron. Astrophys. 1999, 346, 459–464. [Google Scholar]
- Huang, W.; Gies, D.R. Stellar Rotation in Young Clusters. II. Evolution of Stellar Rotation and Surface Helium Abundance. Astrophys. J. 2006, 648, 591–606. [Google Scholar] [CrossRef]
- Fabregat, J.; Torrejón, J.M. On the evolutionary status of Be stars. Astron. Astrophys. 2000, 357, 451–459. [Google Scholar]
- Keller, S.C.; Grebel, E.K.; Miller, G.J.; Yoss, K.M. UBVI and Hα Photometry of the h and χ Persei Cluster. Astron. J. 2001, 122, 248–256. [Google Scholar] [CrossRef]
- McSwain, M.V.; Gies, D.R. The Evolutionary Status of Be Stars: Results from a Photometric Study of Southern Open Clusters. Astrophys. J. Suppl. Ser. 2005, 161, 118–146. [Google Scholar] [CrossRef]
- Maeder, A. Influence of axial stellar rotation of age estimates of open star clusters. Astron. Astrophys. 1971, 10, 354–361. [Google Scholar]
- Packet, W. On the spin-up of the mass accreting component in a close binary system. Astron. Astrophys. 1981, 102, 17–19. [Google Scholar]
- Pols, O.R.; Cote, J.; Waters, L.B.F.M.; Heise, J. The formation of Be stars through close binary evolution. Astron. Astrophys. 1991, 241, 419. [Google Scholar]
- Klement, R.; Carciofi, A.C.; Rivinius, T.; Ignace, R.; Matthews, L.D.; Torstensson, K.; Gies, D.; Vieira, R.G.; Richardson, N.D.; Domiciano de Souza, A.; et al. Prevalence of SED Turndown among Classical Be Stars: Are All Be Stars Close Binaries? Astrophys. J. 2019, 885, 147. [Google Scholar] [CrossRef]
- Huang, S.S. A Statistical Study of the Rotation of the Stars. Astrophys. J. 1953, 118, 285. [Google Scholar] [CrossRef]
- van Dien, E. Axial Rotation of the Brighter Stars in the Pleiades Cluster. J. R. Astron. Soc. Can. 1948, 42, 249. [Google Scholar]
- Slettebak, A. The Spectra and Rotational Velocities of the Bright Stars of Draper Types B8-A2. Astrophys. J. 1954, 119, 146. [Google Scholar] [CrossRef]
- Slettebak, A.; Howard, R.F. Axial Rotation in the Brighter Stars of Draper Types B2-B5. Astrophys. J. 1955, 121, 102. [Google Scholar] [CrossRef]
- Kuiper, G.P. Problems of Double-Star Astronomy. I. Publ. Astron. Soc. Pac. 1935, 47, 15. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Münch, G. On the Integral Equation Governing the Distribution of the True and the Apparent Rotational Velocities of Stars. Astrophys. J. 1950, 111, 142. [Google Scholar] [CrossRef]
- Eddington, A.S. On a formula for correcting statistics for the effects of a known error of observation. Mon. Not. R. Astron. Soc. 1913, 73, 359–360. [Google Scholar] [CrossRef]
- Lucy, L.B. An iterative technique for the rectification of observed distributions. Astron. J. 1974, 79, 745. [Google Scholar] [CrossRef]
- Richardson, W.H. Bayesian-Based Iterative Method of Image Restoration. J. Opt. Soc. Am. 1972, 62, 55. [Google Scholar] [CrossRef]
- Yudin, R.V. Statistical analysis of intrinsic polarization, IR excess and projected rotational velocity distributions of classical Be stars. Astron. Astrophys. 2001, 368, 912–931. [Google Scholar] [CrossRef]
- Curé, M.; Rial, D.F.; Christen, A.; Cassetti, J. A method to deconvolve stellar rotational velocities. Astron. Astrophys. 2014, 565, A85. [Google Scholar] [CrossRef]
- Christen, A.; Escarate, P.; Curé, M.; Rial, D.F.; Cassetti, J. A method to deconvolve stellar rotational velocities II. The probability distribution function via Tikhonov regularization. Astron. Astrophys. 2016, 595, A50. [Google Scholar] [CrossRef]
- Orellana, R.; Escárate, P.; Curé, M.; Christen, A.; Carvajal, R.; Agüero, J.C. A method to deconvolve stellar rotational velocities. III. The probability distribution function via maximum likelihood utilizing finite distribution mixtures. Astron. Astrophys. 2019, 623, A138. [Google Scholar] [CrossRef]
- Yoon, S.C.; Langer, N.; Norman, C. Single star progenitors of long gamma-ray bursts. I. Model grids and redshift dependent GRB rate. Astron. Astrophys. 2006, 460, 199–208. [Google Scholar] [CrossRef]
- Martayan, C.; Zorec, J.; Frémat, Y.; Ekström, S. Can massive Be/Oe stars be progenitors of long gamma ray bursts? Astron. Astrophys. 2010, 516, A103. [Google Scholar] [CrossRef]
- Ramachandran, V.; Hamann, W.R.; Oskinova, L.M.; Gallagher, J.S.; Hainich, R.; Shenar, T.; Sander, A.A.C.; Todt, H.; Fulmer, L. Testing massive star evolution, star formation history, and feedback at low metallicity. Spectroscopic analysis of OB stars in the SMC Wing. Astron. Astrophys. 2019, 625, A104. [Google Scholar] [CrossRef]
- Ramachandran, V.; Hamann, W.R.; Hainich, R.; Oskinova, L.M.; Shenar, T.; Sander, A.A.C.; Todt, H.; Gallagher, J.S. Stellar population of the superbubble N 206 in the LMC. II. Parameters of the OB and WR stars, and the total massive star feedback. Astron. Astrophys. 2018, 615, A40. [Google Scholar] [CrossRef]
- Puls, J.; Vink, J.S.; Najarro, F. Mass loss from hot massive stars. Astron. Astrophys. Rev. 2008, 16, 209–325. [Google Scholar] [CrossRef]
- Krumholz, M.R. Massive Star Formation: A Tale of Two Theories. In Proceedings of the New Horizons in Astronomy: Frank N. Bash Symposium, Proceedings, Frank N Bash Symp. No 2005: New Horizons in Astronomy, Austin, TX, USA, 16–18 October 2005; Kannappan, S.J., Redfield, S., Kessler-Silacci, J.E., Landriau, M., Drory, N., Eds.; University of Chicago Press: Chicago, NY, USA, 2006; Volume 352, p. 31. [Google Scholar]
- Bonnell, I.A.; Vine, S.G.; Bate, M.R. Massive star formation: Nurture, not nature. Mon. Not. R. Astron. Soc. 2004, 349, 735–741. [Google Scholar] [CrossRef]
- Bally, J.; Zinnecker, H. The Birth of High-Mass Stars: Accretion and/or Mergers? Astron. J. 2005, 129, 2281–2293. [Google Scholar] [CrossRef][Green Version]
- Endal, A.S.; Sofia, S. Rotation in solar-type stars. I—Evolutionary models for the spin-down of the sun. Astrophys. J. 1981, 243, 625–640. [Google Scholar] [CrossRef]
- Potter, A.T.; Tout, C.A.; Eldridge, J.J. Towards a unified model of stellar rotation. Mon. Not. R. Astron. Soc. 2012, 419, 748–759. [Google Scholar] [CrossRef]
- Potter, A.T.; Chitre, S.M.; Tout, C.A. Stellar evolution of massive stars with a radiative α-Ω dynamo. Mon. Not. R. Astron. Soc. 2012, 424, 2358–2370. [Google Scholar] [CrossRef]
- Denissenkov, P.A.; Ivanova, N.S.; Weiss, A. Main-sequence stars of 10 and 30 M_sun: Approaching the steady-state rotation. Astron. Astrophys. 1999, 341, 181–189. [Google Scholar]
- Wolff, S.C.; Strom, S.E.; Hillenbrand, L.A. The Angular Momentum Evolution of 0.1-10 Msolar Stars from the Birth Line to the Main Sequence. Astrophys. J. 2004, 601, 979–999. [Google Scholar] [CrossRef]
- Tayler, R.J. Convection in rotating stars. Mon. Not. R. Astron. Soc. 1973, 165, 39. [Google Scholar] [CrossRef][Green Version]
- Deupree, R.G. Stellar Evolution with Arbitrary Rotation Laws. III. Convective Core Overshoot and Angular Momentum Distribution. Astrophys. J. 1998, 499, 340–347. [Google Scholar] [CrossRef]
- Deupree, R.G. Two-dimensional Hydrodynamic Simulations of Zero-Age Main-Sequence Convective Cores. Astrophys. J. 2000, 543, 395–405. [Google Scholar] [CrossRef]
- Kichatinov, L.L.; Rüdiger, G. Differential rotation in stellar convective envelopes. Astron. Lett. 1997, 23, 731–734. [Google Scholar]
- Browning, M.K.; Brun, A.S.; Toomre, J. Simulations of Core Convection in Rotating A-Type Stars: Differential Rotation and Overshooting. Astrophys. J. 2004, 601, 512–529. [Google Scholar] [CrossRef]
- Arnett, W.D.; Meakin, C. Turbulent Mixing in Stars: Theoretical Hurdles. In Proceedings of the Chemical Abundances in the Universe: Connecting First Stars to Planets; Cunha, K., Spite, M., Barbuy, B., Eds.; 2010; Volume 265, pp. 106–110. [Google Scholar] [CrossRef]
- Augustson, K.C.; Brun, A.S.; Toomre, J. The Magnetic Furnace: Intense Core Dynamos in B Stars. Astrophys. J. 2016, 829, 92. [Google Scholar] [CrossRef]
- Rosen, A.L.; Krumholz, M.R.; Ramirez-Ruiz, E. What Sets the Initial Rotation Rates of Massive Stars? Astrophys. J. 2012, 748, 97. [Google Scholar] [CrossRef]
- Haemmerlé, L.; Eggenberger, P.; Meynet, G.; Maeder, A.; Charbonnel, C. Star formation with disc accretion and rotation. I. Stars between 2 and 22 M⊙ at solar metallicity. Astron. Astrophys. 2013, 557, A112. [Google Scholar] [CrossRef][Green Version]
- Haemmerlé, L.; Eggenberger, P.; Meynet, G.; Maeder, A.; Charbonnel, C.; Klessen, R.S. Massive star formation by accretion. II. Rotation: How to circumvent the angular momentum barrier? Astron. Astrophys. 2017, 602, A17. [Google Scholar] [CrossRef][Green Version]
- Strittmatter, P.A. Stellar Rotation and Stellar Luminosity in Praesepe. Astrophys. J. 1966, 144, 430. [Google Scholar] [CrossRef]
- Strittmatter, P.A.; Sargent, W.L.W. Stellar Rotation and the Position of the Metallic-Line Stars in the Color-Magnitude Diagram. Astrophys. J. 1966, 145, 130. [Google Scholar] [CrossRef]
- Maeder, A. Stellar Rotation. Publ. Obs. Geneva 1968, 75, 125. [Google Scholar]
- Smith, R.C. Effects of rotation in the colour-magnitude diagrams of Praesepe and the Hyades. Mon. Not. R. Astron. Soc. 1971, 151, 463. [Google Scholar] [CrossRef][Green Version]
- Cotton, A.; Smith, R.C. The theoretical spread of the main sequence due to stellar rotation. Observatory 1983, 103, 8–12. [Google Scholar]
- Oke, J.B.; Greenstein, J.L. The Rotational Velocities of - - and G-Type Giant Stars. Astrophys. J. 1954, 120, 384. [Google Scholar] [CrossRef]
- Sandage, A.R. Axial Rotation and Stellar Evolution. Astrophys. J. 1955, 122, 263. [Google Scholar] [CrossRef]
- Danziger, I.J.; Faber, S.M. Rotation of evolving A and F stars. Astron. Astrophys. 1972, 18, 428. [Google Scholar]
- Ekström, S.; Meynet, G.; Maeder, A.; Barblan, F. Evolution towards the critical limit and the origin of Be stars. Astron. Astrophys. 2008, 478, 467–485. [Google Scholar] [CrossRef]
- Yang, W.; Bi, S.; Meng, X.; Tian, Z. Evolution of Rotational Velocities of A-type Stars. Astrophys. J. Lett. 2013, 765, L36. [Google Scholar] [CrossRef][Green Version]
- Sun, W.; Duan, X.W.; Deng, L.; de Grijs, R. Exploring the Stellar Rotation of Early-type Stars in the LAMOST Medium-resolution Survey. II. Statistics. Astrophys. J. 2021, 921, 145. [Google Scholar] [CrossRef]
- Sun, W.; Duan, X.W.; Deng, L.; de Grijs, R.; Zhang, B.; Liu, C. Exploring the Stellar Rotation of Early-type Stars in the LAMOST Medium-resolution Survey. I. Catalog. Astrophys. J. Suppl. Ser. 2021, 257, 22. [Google Scholar] [CrossRef]
- Rhodes, E.J., Jr.; Deubner, F.L.; Ulrich, R.K. A new technique for measuring solar rotation. Astrophys. J. 1979, 227, 629–637. [Google Scholar] [CrossRef]
- Deubner, F.L.; Ulrich, R.K.; Rhodes, E.J., Jr. Solar p-mode oscillations as a tracer of radial differential rotation. Astron. Astrophys. 1979, 72, 177–185. [Google Scholar]
- Ando, H. A New Method for Determining the Internal Rotational Angular Velocity of the Stars. Astrophys. Space Sci. 1980, 73, 159–174. [Google Scholar] [CrossRef]
- Reese, D.R. Internal rapid rotation and its implications for stellar structure and pulsations. Eur. Phys. J. Conf. 2015, 101, 05007. [Google Scholar] [CrossRef]
- Aerts, C.; Thoul, A.; Daszyńska, J.; Scuflaire, R.; Waelkens, C.; Dupret, M.A.; Niemczura, E.; Noels, A. Asteroseismology of HD 129929: Core Overshooting and Nonrigid Rotation. Science 2003, 300, 1926–1928. [Google Scholar] [CrossRef]
- Pamyatnykh, A.A.; Handler, G.; Dziembowski, W.A. Asteroseismology of the β Cephei star ν Eridani: Interpretation and applications of the oscillation spectrum. Mon. Not. R. Astron. Soc. 2004, 350, 1022–1028. [Google Scholar] [CrossRef]
- Briquet, M.; Morel, T.; Thoul, A.; Scuflaire, R.; Miglio, A.; Montalbán, J.; Dupret, M.A.; Aerts, C. An asteroseismic study of the β Cephei star θ Ophiuchi: Constraints on global stellar parameters and core overshooting. Mon. Not. R. Astron. Soc. 2007, 381, 1482–1488. [Google Scholar] [CrossRef]
- Dziembowski, W.A.; Pamyatnykh, A.A. The two hybrid B-type pulsators: ν Eridani and 12 Lacertae. Mon. Not. R. Astron. Soc. 2008, 385, 2061–2068. [Google Scholar] [CrossRef]
- Aerts, C.; Mathis, S.; Rogers, T.M. Angular Momentum Transport in Stellar Interiors. Annu. Rev. Astron. Astrophys. 2019, 57, 35–78. [Google Scholar] [CrossRef]
- Pedersen, M.G. Internal rotation and inclinations of slowly pulsating B stars: Evidence of interior angular momentum transport. arXiv 2022, arXiv:2208.14497. [Google Scholar] [CrossRef]
- Hatta, Y.; Sekii, T.; Takata, M.; Kurtz, D.W. The Two-dimensional Internal Rotation of KIC 11145123. Astrophys. J. 2019, 871, 135. [Google Scholar] [CrossRef]
- Burssens, S.; Bowman, D.M.; Michielsen, M.; Simón-Díaz, S.; Aerts, C. Internal rotation and mixing in the massive star HD192575. In Proceedings of the Posters from the TESS Science Conference II (TSC2), Virtually, 2–6 August 2021; p. 75. [Google Scholar] [CrossRef]
- Salmon, S.J.A.J.; Moyano, F.D.; Eggenberger, P.; Haemmerlé, L.; Buldgen, G. Backtracing the internal rotation history of the β Cep star HD 129929. Astron. Astrophys. 2022, 664, L1. [Google Scholar] [CrossRef]
- Salmon, S.J.A.J.; Montalbán, J.; Reese, D.R.; Dupret, M.A.; Eggenberger, P. The puzzling new class of variable stars in NGC 3766: Old friend pulsators? Astron. Astrophys. 2014, 569, A18. [Google Scholar] [CrossRef]
- Pedersen, M.G.; Aerts, C.; Pápics, P.I.; Michielsen, M.; Gebruers, S.; Rogers, T.M.; Molenberghs, G.; Burssens, S.; Garcia, S.; Bowman, D.M. Internal mixing of rotating stars inferred from dipole gravity modes. Nat. Astron. 2021, 5, 715–722. [Google Scholar] [CrossRef]
- Moravveji, E.; Townsend, R.H.D.; Aerts, C.; Mathis, S. Sub-inertial Gravity Modes in the B8V Star KIC 7760680 Reveal Moderate Core Overshooting and Low Vertical Diffusive Mixing. Astrophys. J. 2016, 823, 130. [Google Scholar] [CrossRef]
- Stoeckley, T.R.; Morris, C.S. Rotational distortion of stellar absorption lines. I. Parameters from photographic spectra. Astrophys. J. 1974, 188, 579–594. [Google Scholar] [CrossRef]
- Buscombe, W.; Stoeckley, T.R. Absorption Line Profiles and Rotational Velocities for 59 Stars. Astrophys. Space Sci. 1975, 37, 197–220. [Google Scholar] [CrossRef]
- Stoeckley, T.R.; Carroll, R.W.; Miller, R.D. Absorption line profiles for 39 rapidly rotating stars. Mon. Not. R. Astron. Soc. 1984, 208, 459. [Google Scholar] [CrossRef]
- Elste, G.H. Line Shapes of Rotating Stars with Application to Alpha Lyrae. Astrophys. J. 1992, 384, 284. [Google Scholar] [CrossRef]
- de Jager, C.; Nieuwenhuijzen, H.; van der Hucht, K.A. Mass loss rates in the Hertzsprung-Russell diagram. Astron. Astrophys. 1988, 72, 259–289. [Google Scholar]
- Kudritzki, R.P.; Puls, J. Winds from Hot Stars. Annu. Rev. Astron. Astrophys. 2000, 38, 613–666. [Google Scholar] [CrossRef]
- Vink, J.S.; de Koter, A.; Lamers, H.J.G.L.M. New theoretical mass-loss rates of O and B stars. Astron. Astrophys. 2000, 362, 295–309. [Google Scholar]
- Keszthelyi, Z.; de Koter, A.; Götberg, Y.; Meynet, G.; Brands, S.A.; Petit, V.; Carrington, M.; David-Uraz, A.; Geen, S.T.; Georgy, C.; et al. The effects of surface fossil magnetic fields on massive star evolution: IV. Grids of models at Solar, LMC, and SMC metallicities. Mon. Not. R. Astron. Soc. 2022, 517, 2028–2055. [Google Scholar] [CrossRef]
- Donati, J.F.; Semel, M.; Carter, B.D.; Rees, D.E.; Collier Cameron, A. Spectropolarimetric observations of active stars. Mon. Not. R. Astron. Soc. 1997, 291, 658–682. [Google Scholar] [CrossRef]
- Kochukhov, O.; Makaganiuk, V.; Piskunov, N. Least-squares deconvolution of the stellar intensity and polarization spectra. Astron. Astrophys. 2010, 524, A5. [Google Scholar] [CrossRef]
- Oksala, M.E.; Wade, G.A.; Townsend, R.H.D.; Owocki, S.P.; Kochukhov, O.; Neiner, C.; Alecian, E.; Grunhut, J. Revisiting the Rigidly Rotating Magnetosphere model for σ Ori E—I. Observations and data analysis. Mon. Not. R. Astron. Soc. 2012, 419, 959–970. [Google Scholar] [CrossRef]
- Grunhut, J.H.; Wade, G.A.; MiMeS Collaboration. The Incidence of Magnetic Fields in Massive Stars: An Overview of the MiMeS Survey Component. AIP Conf. Proc. 2012, 1429, 67. [Google Scholar]
- Babel, J.; Montmerle, T. On the Periodic X-Ray Emission from the O7 V Star theta 1 Orionis C. Astrophys. J. Lett. 1997, 485, L29–L32. [Google Scholar] [CrossRef]
- ud-Doula, A.; Owocki, S.P. Dynamical Simulations of Magnetically Channeled Line-driven Stellar Winds. I. Isothermal, Nonrotating, Radially Driven Flow. Astrophys. J. 2002, 576, 413–428. [Google Scholar] [CrossRef]
- Petit, V.; Owocki, S.P.; Wade, G.A.; Cohen, D.H.; Sundqvist, J.O.; Gagné, M.; Maíz Apellániz, J.; Oksala, M.E.; Bohlender, D.A.; Rivinius, T.; et al. A magnetic confinement versus rotation classification of massive-star magnetospheres. Mon. Not. R. Astron. Soc. 2013, 429, 398–422. [Google Scholar] [CrossRef]
- Townsend, R.H.D.; Owocki, S.P. A rigidly rotating magnetosphere model for circumstellar emission from magnetic OB stars. Mon. Not. R. Astron. Soc. 2005, 357, 251–264. [Google Scholar] [CrossRef]
- Ud-Doula, A.; Owocki, S.P.; Townsend, R.H.D. Dynamical simulations of magnetically channelled line-driven stellar winds—II. The effects of field-aligned rotation. Mon. Not. R. Astron. Soc. 2008, 385, 97–108. [Google Scholar] [CrossRef]
- Shultz, M.; Wade, G.; Rivinius, T.; Neiner, C.; Alecian, E.; Petit, V.; Grunhut, J.; MiMeS Collaboration; BinaMIcS Collaboration. What can magnetic early B-type stars tell us about early B-type stars in general? In Proceedings of the Lives and Death-Throes of Massive Stars; Eldridge, J.J., Bray, J.C., McClelland, L.A.S., Xiao, L., Eds.; Cambridge University Press: Cambridge, UK, 2017; Volume 329, pp. 126–130. [Google Scholar] [CrossRef]
- Shultz, M.E.; Owocki, S.; Rivinius, T.; Wade, G.A.; Neiner, C.; Alecian, E.; Kochukhov, O.; Bohlender, D.; ud-Doula, A.; Landstreet, J.D.; et al. The magnetic early B-type stars—IV. Breakout or leakage? H α emission as a diagnostic of plasma transport in centrifugal magnetospheres. Mon. Not. R. Astron. Soc. 2020, 499, 5379–5395. [Google Scholar] [CrossRef]
- Shultz, M.E.; Owocki, S.P.; ud-Doula, A.; Biswas, A.; Bohlender, D.; Chandra, P.; Das, B.; David-Uraz, A.; Khalack, V.; Kochukhov, O.; et al. MOBSTER—VI. The crucial influence of rotation on the radio magnetospheres of hot stars. Mon. Not. R. Astron. Soc. 2022, 513, 1429–1448. [Google Scholar] [CrossRef]
- Shultz, M.E.; Wade, G.A.; Rivinius, T.; Alecian, E.; Neiner, C.; Petit, V.; Owocki, S.; ud-Doula, A.; Kochukhov, O.; Bohlender, D.; et al. The magnetic early B-type stars—III. A main-sequence magnetic, rotational, and magnetospheric biography. Mon. Not. R. Astron. Soc. 2019, 490, 274–295. [Google Scholar] [CrossRef]
- Weber, E.J.; Davis, L.J. The Angular Momentum of the Solar Wind. Astrophys. J. 1967, 148, 217–227. [Google Scholar] [CrossRef]
- Ud-Doula, A.; Owocki, S.P.; Townsend, R.H.D. Dynamical simulations of magnetically channelled line-driven stellar winds—III. Angular momentum loss and rotational spin-down. Mon. Not. R. Astron. Soc. 2009, 392, 1022–1033. [Google Scholar] [CrossRef]
- Shultz, M.E.; Wade, G.A.; Rivinius, T.; Neiner, C.; Alecian, E.; Bohlender, D.; Monin, D.; Sikora, J.; MiMeS Collaboration; BinaMIcS Collaboration. The magnetic early B-type stars I: Magnetometry and rotation. Mon. Not. R. Astron. Soc. 2018, 475, 5144–5178. [Google Scholar] [CrossRef]
- Shultz, M.E.; Wade, G.A.; Rivinius, T.; Alecian, E.; Neiner, C.; Petit, V.; Wisniewski, J.P.; MiMeS Collaboration; BinaMIcS Collaboration. The magnetic early B-type Stars II: Stellar atmospheric parameters in the era of Gaia. Mon. Not. R. Astron. Soc. 2019, 485, 1508–1527. [Google Scholar] [CrossRef]
- Shultz, M.; Rivinius, T.; Das, B.; Wade, G.A.; Chandra, P. The accelerating rotation of the magnetic He-weak star HD 142990. Mon. Not. R. Astron. Soc. 2019, 486, 5558–5566. [Google Scholar] [CrossRef]
- Grunhut, J.H.; Wade, G.A.; Neiner, C.; Oksala, M.E.; Petit, V.; Alecian, E.; Bohlender, D.A.; Bouret, J.C.; Henrichs, H.F.; Hussain, G.A.J.; et al. The MiMeS survey of Magnetism in Massive Stars: Magnetic analysis of the O-type stars. Mon. Not. R. Astron. Soc. 2017, 465, 2432–2470. [Google Scholar] [CrossRef]
- Fossati, L.; Castro, N.; Schöller, M.; Hubrig, S.; Langer, N.; Morel, T.; Briquet, M.; Herrero, A.; Przybilla, N.; Sana, H.; et al. B fields in OB stars (BOB): Low-resolution FORS2 spectropolarimetry of the first sample of 50 massive stars. Astron. Astrophys. 2015, 582, A45. [Google Scholar] [CrossRef]
- Alecian, E.; Neiner, C.; Wade, G.A.; Mathis, S.; Bohlender, D.; Cébron, D.; Folsom, C.; Grunhut, J.; Le Bouquin, J.B.; Petit, V.; et al. The BinaMIcS project: Understanding the origin of magnetic fields in massive stars through close binary systems. In Proceedings of the New Windows on Massive Stars; Meynet, G., Georgy, C., Groh, J., Stee, P., Eds.; Cambridge University Press: Cambridge, UK, 2015; Volume 307, pp. 330–335. [Google Scholar] [CrossRef]
- Castro, N.; Fossati, L.; Hubrig, S.; Simón-Díaz, S.; Schöller, M.; Ilyin, I.; Carrol, T.A.; Langer, N.; Morel, T.; Schneider, F.R.N.; et al. B fields in OB stars (BOB). Detection of a strong magnetic field in the O9.7 V star HD 54879. Astron. Astrophys. 2015, 581, A81. [Google Scholar] [CrossRef][Green Version]
- Fossati, L.; Castro, N.; Morel, T.; Langer, N.; Briquet, M.; Carroll, T.A.; Hubrig, S.; Nieva, M.F.; Oskinova, L.M.; Przybilla, N.; et al. B fields in OB stars (BOB): On the detection of weak magnetic fields in the two early B-type stars beta CMa and epsilon CMa. Possible lack of a “magnetic desert” in massive stars. Astron. Astrophys. 2015, 574, A20. [Google Scholar] [CrossRef]
- Hubrig, S.; Schöller, M.; Fossati, L.; Morel, T.; Castro, N.; Oskinova, L.M.; Przybilla, N.; Eikenberry, S.S.; Nieva, M.F.; Langer, N. B fields in OB stars (BOB): FORS 2 spectropolarimetric follow-up of the two rare rigidly rotating magnetosphere stars HD 23478 and HD 345439. Astron. Astrophys. 2015, 578, L3. [Google Scholar] [CrossRef]
- Morel, T.; Castro, N.; Fossati, L.; Hubrig, S.; Langer, N.; Przybilla, N.; Schöller, M.; Carroll, T.; Ilyin, I.; Irrgang, A.; et al. The B Fields in OB Stars (BOB) Survey. In Proceedings of the New Windows on Massive Stars; Meynet, G., Georgy, C., Groh, J., Stee, P., Eds.; Cambridge University Press: Cambridge, UK, 2015; Volume 307, pp. 342–347. [Google Scholar] [CrossRef]
- Przybilla, N.; Fossati, L.; Hubrig, S.; Nieva, M.F.; Järvinen, S.P.; Castro, N.; Schöller, M.; Ilyin, I.; Butler, K.; Schneider, F.R.N.; et al. B fields in OB stars (BOB): Detection of a magnetic field in the He-strong star CPD-57° 3509. Astron. Astrophys. 2016, 587, A7. [Google Scholar] [CrossRef]
- Schöller, M.; Hubrig, S.; Fossati, L.; Carroll, T.A.; Briquet, M.; Oskinova, L.M.; Järvinen, S.; Ilyin, I.; Castro, N.; Morel, T.; et al. B fields in OB stars (BOB): Concluding the FORS 2 observing campaign. Astron. Astrophys. 2017, 599, A66. [Google Scholar] [CrossRef]
- Oksala, M.E.; Neiner, C.; Georgy, C.; Przybilla, N.; Keszthelyi, Z.; Wade, G.; Mathis, S.; Blazère, A.; Buysschaert, B. The evolution of magnetic fields in hot stars. In Proceedings of the The Lives and Death-Throes of Massive Stars; Eldridge, J.J., Bray, J.C., McClelland, L.A.S., Xiao, L., Eds.; 2017; Volume 329, pp. 141–145. [Google Scholar] [CrossRef]
- Neiner, C.; Oksala, M.E.; Georgy, C.; Przybilla, N.; Mathis, S.; Wade, G.; Kondrak, M.; Fossati, L.; Blazère, A.; Buysschaert, B.; et al. Discovery of magnetic A supergiants: The descendants of magnetic main-sequence B stars. Mon. Not. R. Astron. Soc. 2017, 471, 1926–1935. [Google Scholar] [CrossRef]
- Kobzar, O.; Khalack, V.; Bohlender, D.; Mathys, G.; Shultz, M.E.; Bowman, D.M.; Paunzen, E.; Lovekin, C.; David-Uraz, A.; Sikora, J.; et al. Analysis of eight magnetic chemically peculiar stars with rotational modulation. Mon. Not. R. Astron. Soc. 2022. [Google Scholar] [CrossRef]
- Shultz, M.; Wade, G.A.; Neiner, C.; Kochukhov, O. Magnetic Stars Observed by BRITE. In Proceedings of the 3rd BRITE Science Conference; Wade, G.A., Baade, D., Guzik, J.A., Smolec, R., Eds.; Polish Astronomical Society: Warsawm, Poland, 2018; Volume 8, pp. 146–153. [Google Scholar]
- Schneider, F.R.N.; Ohlmann, S.T.; Podsiadlowski, P.; Röpke, F.K.; Balbus, S.A.; Pakmor, R.; Springel, V. Stellar mergers as the origin of magnetic massive stars. Nature 2019, 574, 211–214. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).