Gravitational Instability of Gas–Dust Circumnuclear Disks in Galaxies
Abstract
1. Introduction
2. Observational Data
2.1. Gas and Dust in the Circumnuclear Disk of NGC 4736
2.2. Mini-Disk Rotation Curve and the Central Black Hole
3. The Model
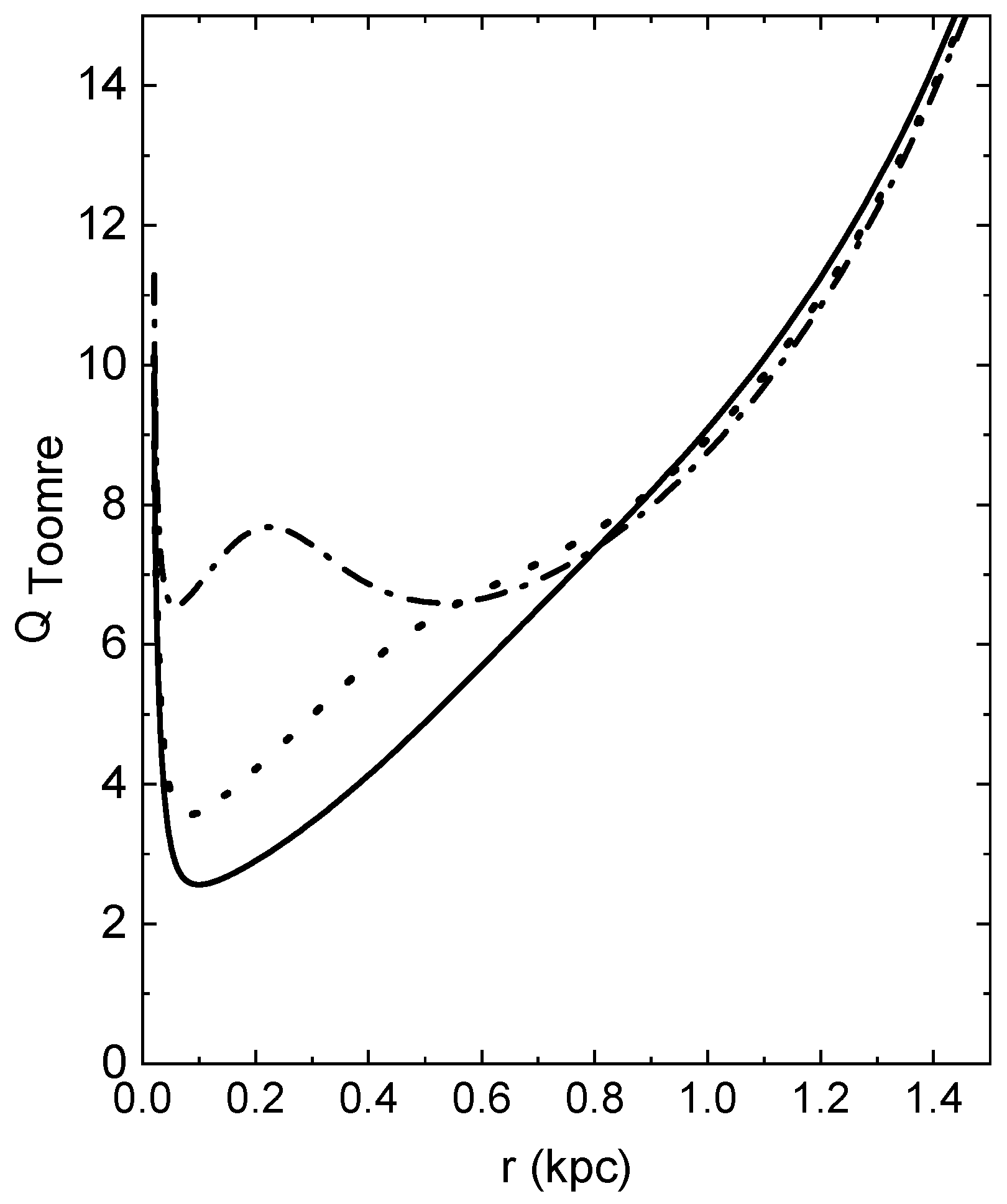
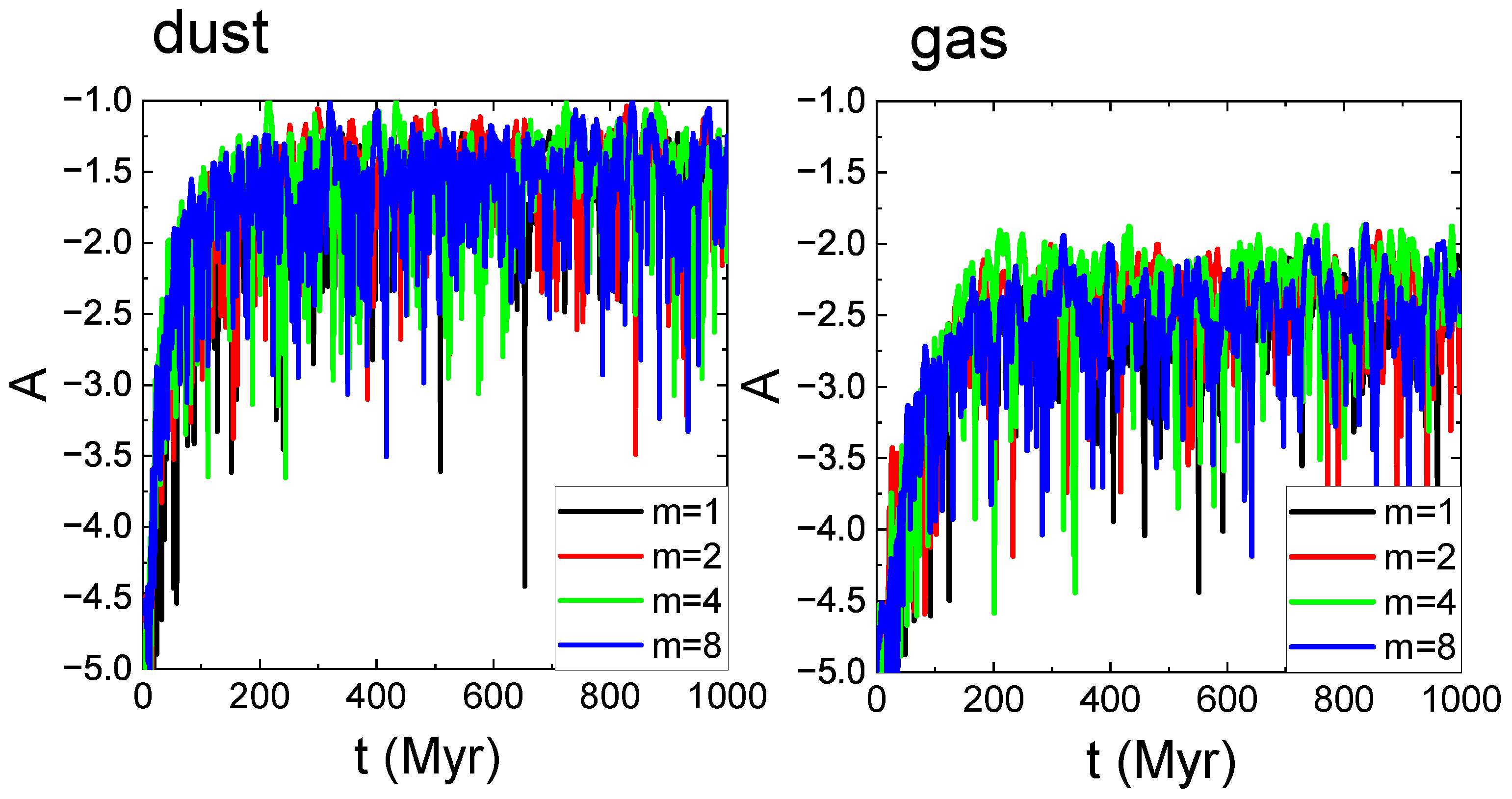
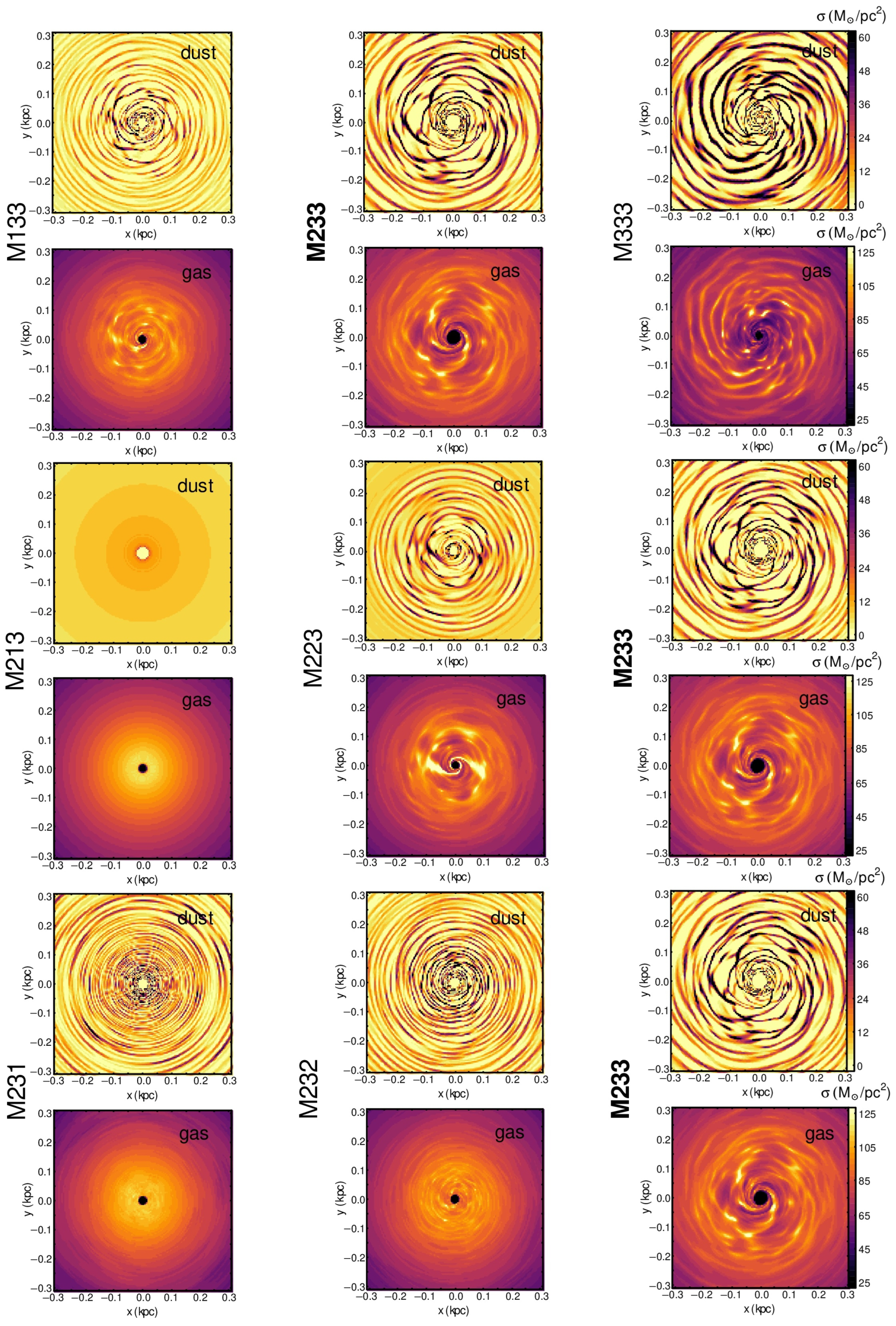
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carollo, C.M.; Stiavelli, M.; de Zeeuw, P.T.; Mack, J. Spiral Galaxies with WFPC2.I.Nuclear Morphology, Bulges, Star Clusters, and Surface Brightness Profiles. Astron. J. 1997, 114, 2366. [Google Scholar] [CrossRef]
- Carollo, C.M.; Stiavelli, M. Spiral Galaxies with WFPC2. III. Nuclear Cusp Slopes. Astron. J. 1998, 115, 2306–2319. [Google Scholar] [CrossRef]
- Carollo, C.M.; Stiavelli, M.; Mack, J. Spiral Galaxies with WFPC2. II. The Nuclear Properties of 40 Objects. Astron. J. 1998, 116, 68–84. [Google Scholar] [CrossRef]
- Martini, P.; Regan, M.W.; Mulchaey, J.S.; Pogge, R.W. Circumnuclear Dust in Nearby Active and Inactive Galaxies. II. Bars, Nuclear Spirals, and the Fueling of Active Galactic Nuclei. Astrophys. J. 2003, 589, 774–782. [Google Scholar] [CrossRef]
- Gan, Z.; Hensley, B.S.; Ostriker, J.P.; Ciotti, L.; Schiminovich, D.; Pellegrini, S. Infrared Emission from Cold Gas Dusty Disks in Massive Ellipticals. Astrophys. J. 2020, 901, 7. [Google Scholar] [CrossRef]
- Englmaier, P.; Shlosman, I. Density Waves inside the Inner Lindblad Resonance: Nuclear Spirals in Disk Galaxies. Astrophys. J. 2000, 528, 677–686. [Google Scholar] [CrossRef]
- Wada, K.; Koda, J. Multi-Phase Gas Dynamics in a Weak Barred Potential. Publ. Astron. Soc. Jpn. 2001, 53, 1163–1170. [Google Scholar] [CrossRef]
- Wong, T.; Blitz, L. Noncircular Gas Kinematics and Star Formation in the Ringed Galaxy NGC 4736. Astrophys. J. 2000, 540, 771–796. [Google Scholar] [CrossRef]
- Kim, W.T.; Elmegreen, B.G. Nuclear Spiral Shocks and Induced Gas Inflows in Weak Oval Potentials. Astrophys. J. Lett. 2017, 841, L4. [Google Scholar] [CrossRef]
- Trani, A.A.; Mapelli, M.; Ballone, A. Forming Circumnuclear Disks and Rings in Galactic Nuclei: A Competition Between Supermassive Black Hole and Nuclear Star Cluster. Astrophys. J. 2018, 864, 17. [Google Scholar] [CrossRef]
- Elmegreen, B.G.; Elmegreen, D.M.; Brinks, E.; Yuan, C.; Kaufman, M.; Klarić, M.; Montenegro, L.; Struck, C.; Thomasson, M. Dust Spirals and Acoustic Noise in the Nucleus of the Galaxy NGC 2207. Astrophys. J. Lett. 1998, 503, L119–L122. [Google Scholar] [CrossRef]
- Orlova, N.; Korchagin, V.; Theis, C. The Influence of a Cold Dust Component on the Nuclear Disk Structure. Astron. Nachr. Suppl. 2003, 324, 37. [Google Scholar]
- Noh, H.; Vishniac, E.T.; Cochran, W.D. An examination of the M = 1 instability in a low-mass protoplanetary disk. Astrophys. J. 1992, 397, 347–352. [Google Scholar] [CrossRef]
- Theis, C.; Orlova, N. Are galactic disks dynamically influenced by dust? Astron. Astrophys. 2004, 418, 959–978. [Google Scholar] [CrossRef]
- Toomre, A. On the gravitational stability of a disk of stars. Astrophys. J. 1964, 139, 1217–1238. [Google Scholar] [CrossRef]
- Terrazas, B.A.; Bell, E.F.; Woo, J.; Henriques, B.M. Supermassive black holes as the regulators of star formation in central galaxies. Astrophys. J. 2017, 844, 170. [Google Scholar] [CrossRef]
- Shioya, Y.; Tosaki, T.; Ohyama, Y.; Murayama, T.; Yamada, T.; Ishizuki, S.; Taniguchi, Y. Molecular Gas in the Poststarburst Galactic Nucleus of NGC 4736. Publ. Astron. Soc. Jpn. 1998, 50, 317–323. [Google Scholar] [CrossRef]
- Gerin, M.; Casoli, F.; Combes, F. Molecular gas in the RSAB galaxy NGC 4736. Astron. Astrophys. 1991, 251, 32. [Google Scholar]
- Tominaga, R.T.; Takahashi, S.Z.; Inutsuka, S.i. Revised Description of Dust Diffusion and a New Instability Creating Multiple Rings in Protoplanetary Disks. Astrophys. J. 2019, 881, 53. [Google Scholar] [CrossRef]
- Tominaga, R.T.; Takahashi, S.Z.; Inutsuka, S.i. Secular Gravitational Instability of Drifting Dust in Protoplanetary Disks: Formation of Dusty Rings without Significant Gas Substructures. Astrophys. J. 2020, 900, 182. [Google Scholar] [CrossRef]
- Chan, R.; Herrera, L.; Santos, N.O. Dynamical Instability for Shearing Viscous Collapse. Mon. Not. R. Astron. Soc. 1994, 267, 637. [Google Scholar] [CrossRef]
- Herrera, L.; Le Denmat, G.; Santos, N.O. Dynamical instability for non-adiabatic spherical collapse. Mon. Not. R. Astron. Soc. 1989, 237, 257–268. [Google Scholar] [CrossRef]
- Kormendy, J.; Kennicutt, R.C., Jr. Secular Evolution and the Formation of Pseudobulges in Disk Galaxies. Annu. Rev. Astron. Astrophys. 2004, 42, 603–683. [Google Scholar] [CrossRef]
- Elmegreen, D.M.; Elmegreen, B.G.; Eberwein, K.S. Dusty Acoustic Turbulence in the Nuclear Disks of Two LINER Galaxies NGC 4450 and NGC 4736. Astrophys. J. 2002, 564, 234–243. [Google Scholar] [CrossRef]
- Van der Laan, T.P.R.; Armus, L.; Beirao, P.; Sandstrom, K.; Groves, B.; Schinnerer, E.; Draine, B.T.; Smith, J.D.; Galametz, M.; Wolfire, M.; et al. Heating and cooling of the neutral ISM in the NGC 4736 circumnuclear ring. Astron. Astrophys. 2015, 575, A83. [Google Scholar] [CrossRef]
- Muñoz-Tuñón, C.; Caon, N.; Aguerri, J.A.L. The Inner Ring of NGC 4736: Star Formation on a Resonant Pattern. Astron. J. 2004, 127, 58–74. [Google Scholar] [CrossRef]
- Caldú-Primo, A.; Schruba, A.; Walter, F.; Leroy, A.; Bolatto, A.D.; Vogel, S. Spatially Extended and High-Velocity Dispersion Molecular Component in Spiral Galaxies: Single-Dish Versus Interferometric Observations. Astron. J. 2015, 149, 76. [Google Scholar] [CrossRef]
- Patra, N.N. Theoretical modelling of two-component molecular discs in spiral galaxies. Astron. Astrophys. 2020, 638, A66. [Google Scholar] [CrossRef]
- Muñoz-Mateos, J.C.; Gil de Paz, A.; Boissier, S.; Zamorano, J.; Dale, D.A.; Pérez-González, P.G.; Gallego, J.; Madore, B.F.; Bendo, G.; Thornley, M.D.; et al. Radial Distribution of Stars, Gas, and Dust in Sings Galaxies. II. Derived Dust Properties. Astrophys. J. 2009, 701, 1965–1991. [Google Scholar] [CrossRef]
- Muñoz-Mateos, J.C.; Boissier, S.; Gil de Paz, A.; Zamorano, J.; Kennicutt, R.C., Jr.; Moustakas, J.; Prantzos, N.; Gallego, J. Radial Distribution of Stars, Gas, and Dust in SINGS Galaxies. III. Modeling the Evolution of the Stellar Component in Galaxy Disks. Astrophys. J. 2011, 731, 10. [Google Scholar] [CrossRef]
- Asplund, M.; Grevesse, N.; Sauval, A.J.; Scott, P. The Chemical Composition of the Sun. Annu. Rev. Astron. Astrophys. 2009, 47, 481–522. [Google Scholar] [CrossRef]
- Kroupa, P. On the variation of the initial mass function. Mon. Not. R. Astron. Soc. 2001, 322, 231–246. [Google Scholar] [CrossRef]
- Kokusho, T.; Kaneda, H.; Bureau, M.; Suzuki, T.; Murata, K.; Kondo, A.; Yamagishi, M.; Tsuchikawa, T.; Furuta, T. Dust properties in the cold and hot gas phases of the ATLAS3D early-type galaxies as revealed by AKARI. Astron. Astrophys. 2019, 622, A87. [Google Scholar] [CrossRef]
- Draine, B.T. Physics of the Interstellar and Intergalactic Medium; Princeton University Press: Princeton, NJ, USA, 2011; ISBN 978-0-691-12214-4. [Google Scholar] [CrossRef]
- Maiolino, R.; Marconi, A.; Oliva, E. Dust in active nuclei. II. Powder or gravel? Astron. Astrophys. 2001, 365, 37–48. [Google Scholar] [CrossRef]
- Maiolino, R.; Marconi, A.; Salvati, M.; Risaliti, G.; Severgnini, P.; Oliva, E.; La Franca, F.; Vanzi, L. Dust in active nuclei. I. Evidence for “anomalous” properties. Astron. Astrophys. 2001, 365, 28–36. [Google Scholar] [CrossRef]
- Jałocha, J.; Bratek, Ł.; Kutschera, M. Is Dark Matter Present in NGC 4736? An Iterative Spectral Method for Finding Mass Distribution in Spiral Galaxies. Astrophys. J. 2008, 679, 373–378. [Google Scholar] [CrossRef]
- Stone, J.M.; Norman, M.L. ZEUS-2D: A Radiation Magnetohydrodynamics Code for Astrophysical Flows in Two Space Dimensions. I. The Hydrodynamic Algorithms and Tests. Astrophys. J. Suppl. Ser. 1992, 80, 753. [Google Scholar] [CrossRef]
- Cha, S.H.; Nayakshin, S. A numerical simulation of a ‘Super-Earth’ core delivery from ∼100 to ∼8 au. Mon. Not. R. Astron. Soc. 2011, 415, 3319–3334. [Google Scholar] [CrossRef]
- Zhu, Z.; Nelson, R.P.; Dong, R.; Espaillat, C.; Hartmann, L. Dust Filtration by Planet-induced Gap Edges: Implications for Transitional Disks. Astrophys. J. 2012, 755, 6. [Google Scholar] [CrossRef]
- Vorobyov, E.I.; Akimkin, V.; Stoyanovskaya, O.; Pavlyuchenkov, Y.; Liu, H.B. Early evolution of viscous and self-gravitating circumstellar disks with a dust component. Astron. Astrophys. 2018, 614, A98. [Google Scholar] [CrossRef]
- Stoyanovskaya, O.P.; Snytnikov, V.N.; Vorobyov, E.I. Analysis of Methods for Computing the Trajectories of Dust Particles in a Gas-Dust Circumstellar Disk. Astron. Rep. 2017, 61, 1044–1060. [Google Scholar] [CrossRef]
- Stoyanovskaya, O.P.; Vorobyov, E.I.; Snytnikov, V.N. Analysis of Numerical Algorithms for Computing Rapid Momentum Transfers between the Gas and Dust in Simulations of Circumstellar Disks. Astron. Rep. 2018, 62, 455–468. [Google Scholar] [CrossRef]
- Epstein, P.S. On the Resistance Experienced by Spheres in their Motion through Gases. Phys. Rev. 1924, 23, 710–733. [Google Scholar] [CrossRef]
- Goodman, J.; Pindor, B. Secular Instability and Planetesimal Formation in the Dust Layer. Icarus 2000, 148, 537–549. [Google Scholar] [CrossRef]
- van Leer, B. Towards the Ultimate Conservative Difference Scheme. IV. A New Approach to Numerical Convection. J. Comput. Phys. 1977, 23, 276. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in Fortran 90: Numerical Recipes in Fortran 77V. 2. Numerical Recipes in Fortran 90; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Kennicutt, R.C., Jr. The Star Formation Law in Galactic Disks. Astrophys. J. 1989, 344, 685. [Google Scholar] [CrossRef]
- Laibe, G.; Price, D.J. Dusty gas with one fluid. Mon. Not. R. Astron. Soc. 2014, 440, 2136–2146. [Google Scholar] [CrossRef]
- Nakanishi, H.; Sofue, Y. Three-Dimensional Distribution of the ISM in the Milky Way Galaxy: II. The Molecular Gas Disk. Publ. Astron. Soc. Jpn. 2006, 58, 847–860. [Google Scholar] [CrossRef]


| Model | a | Model | a | ||||
|---|---|---|---|---|---|---|---|
| M111 | 0.05 | 0.1 m | 0.3 kpc | M223 | 0.1 | 1.0 m | 0.9 kpc |
| M112 | 0.05 | 0.1 m | 0.6 kpc | M231 | 0.1 | 5.0 m | 0.3 kpc |
| M113 | 0.05 | 0.1 m | 0.9 kpc | M232 | 0.1 | 5.0 m | 0.6 kpc |
| M121 | 0.05 | 1.0 m | 0.3 kpc | M233 | 0.1 | 5.0 m | 0.9 kpc |
| M122 | 0.05 | 1.0 m | 0.6 kpc | M311 | 0.2 | 0.1 m | 0.3 kpc |
| M123 | 0.05 | 1.0 m | 0.9 kpc | M312 | 0.2 | 0.1 m | 0.6 kpc |
| M131 | 0.05 | 5.0 m | 0.3 kpc | M313 | 0.2 | 0.1 m | 0.9 kpc |
| M132 | 0.05 | 5.0 m | 0.6 kpc | M321 | 0.2 | 1.0 m | 0.3 kpc |
| M133 | 0.05 | 5.0 m | 0.9 kpc | M322 | 0.2 | 1.0 m | 0.6 kpc |
| M211 | 0.1 | 0.1 m | 0.3 kpc | M323 | 0.2 | 1.0 m | 0.9 kpc |
| M212 | 0.1 | 0.1 m | 0.6 kpc | M331 | 0.2 | 5.0 m | 0.3 kpc |
| M213 | 0.1 | 0.1 m | 0.9 kpc | M332 | 0.2 | 5.0 m | 0.6 kpc |
| M221 | 0.1 | 1.0 m | 0.3 kpc | M333 | 0.2 | 5.0 m | 0.9 kpc |
| M222 | 0.1 | 1.0 m | 0.6 kpc |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tkachenko, R.; Korchagin, V.; Jmailov, B. Gravitational Instability of Gas–Dust Circumnuclear Disks in Galaxies. Galaxies 2023, 11, 41. https://doi.org/10.3390/galaxies11020041
Tkachenko R, Korchagin V, Jmailov B. Gravitational Instability of Gas–Dust Circumnuclear Disks in Galaxies. Galaxies. 2023; 11(2):41. https://doi.org/10.3390/galaxies11020041
Chicago/Turabian StyleTkachenko, Roman, Vladimir Korchagin, and Boris Jmailov. 2023. "Gravitational Instability of Gas–Dust Circumnuclear Disks in Galaxies" Galaxies 11, no. 2: 41. https://doi.org/10.3390/galaxies11020041
APA StyleTkachenko, R., Korchagin, V., & Jmailov, B. (2023). Gravitational Instability of Gas–Dust Circumnuclear Disks in Galaxies. Galaxies, 11(2), 41. https://doi.org/10.3390/galaxies11020041






