Two Classes of Gamma-ray Bursts Distinguished within the First Second of Their Prompt Emission
Abstract
1. Introduction
2. GRB Light Curves
2.1. BATSE
2.2. Swift/BAT
2.3. Fermi/GBM
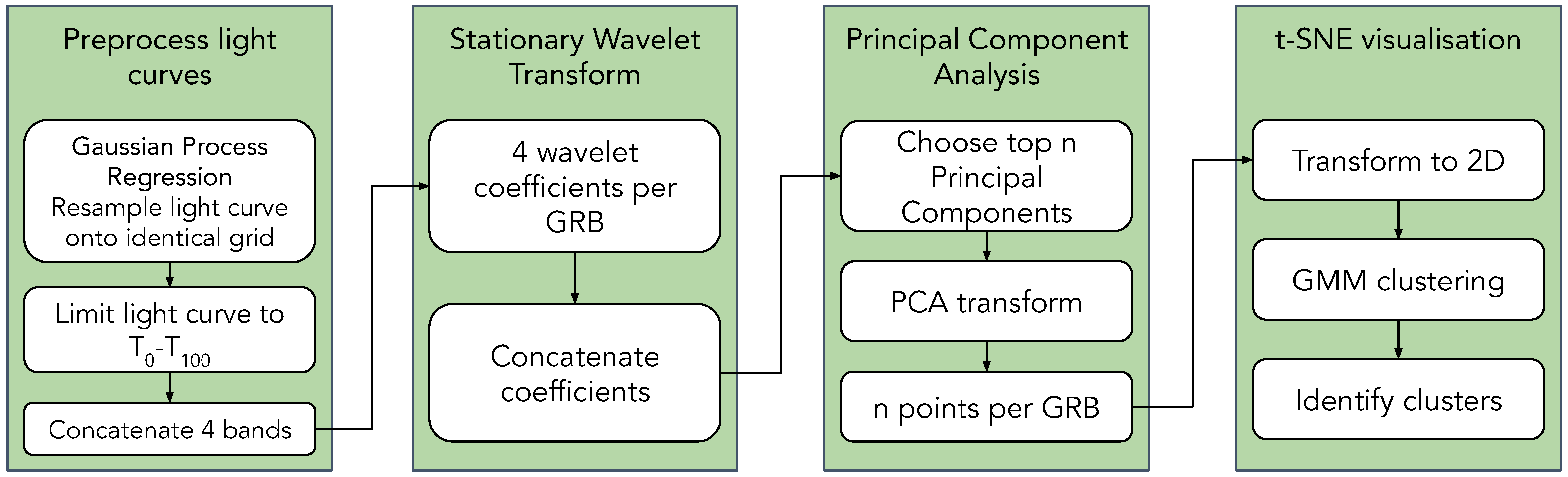
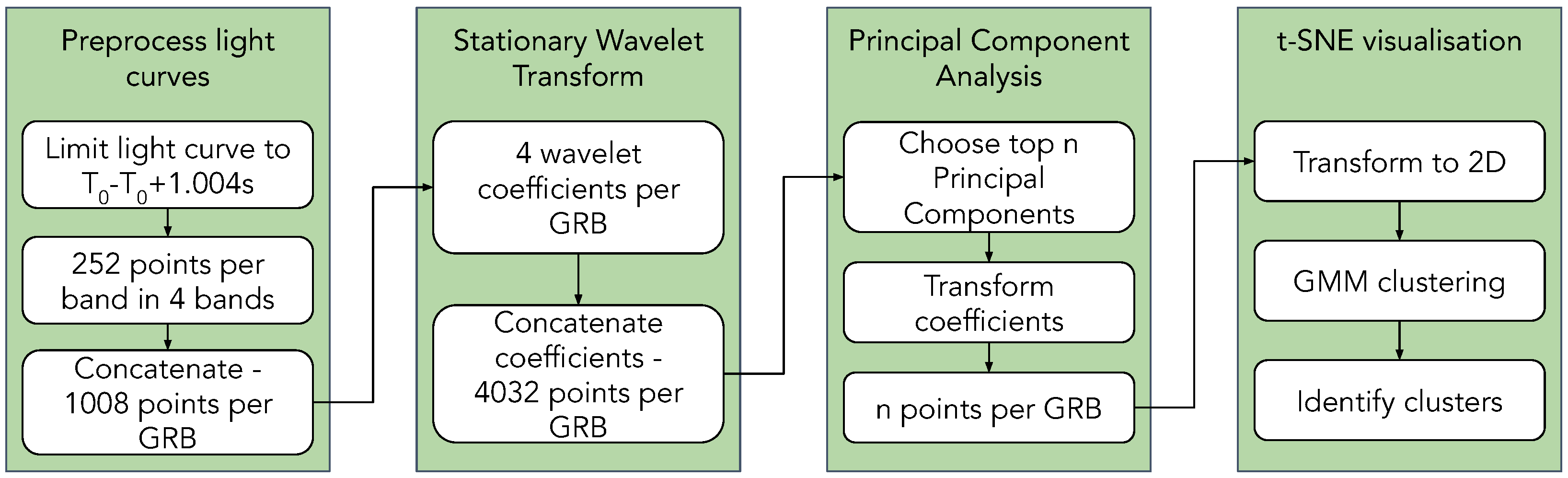
3. Feature Extraction
3.1. Light Curve Pre-Processing
3.1.1. 64 ms Light Curves
3.1.2. 4 ms Light Curves
3.2. Wavelet Decomposition
3.3. Principal Component Analysis
3.4. t-SNE
3.5. GMM Clustering
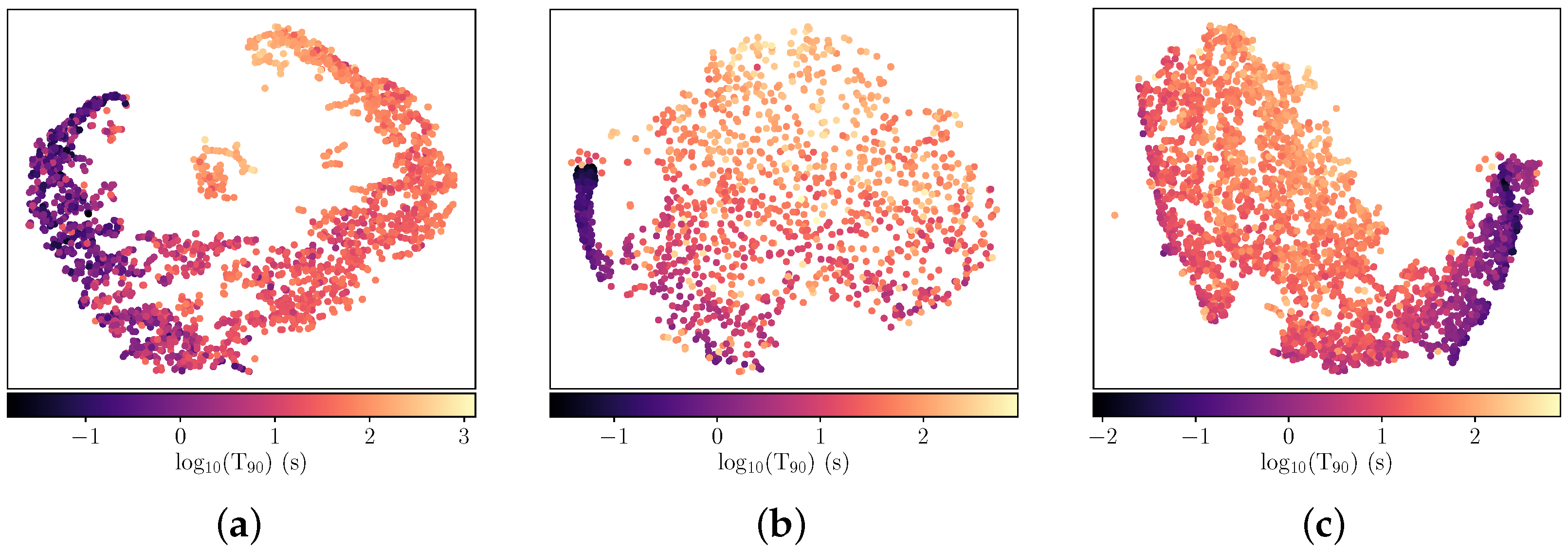
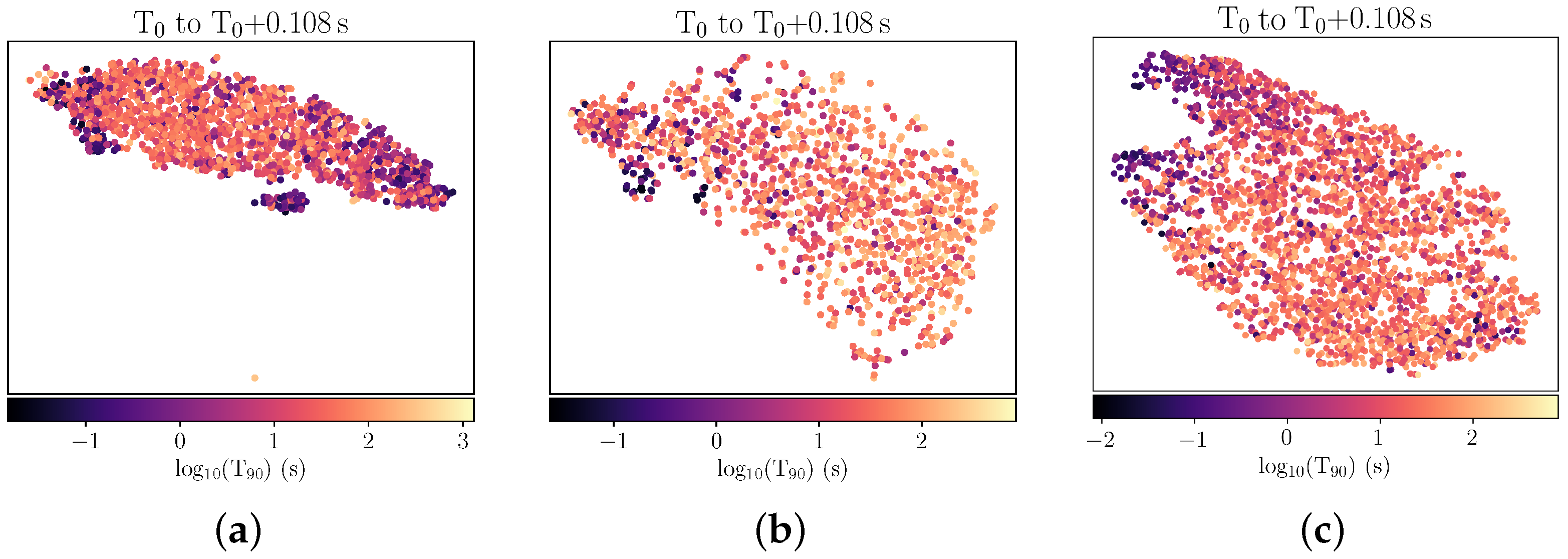
4. Results
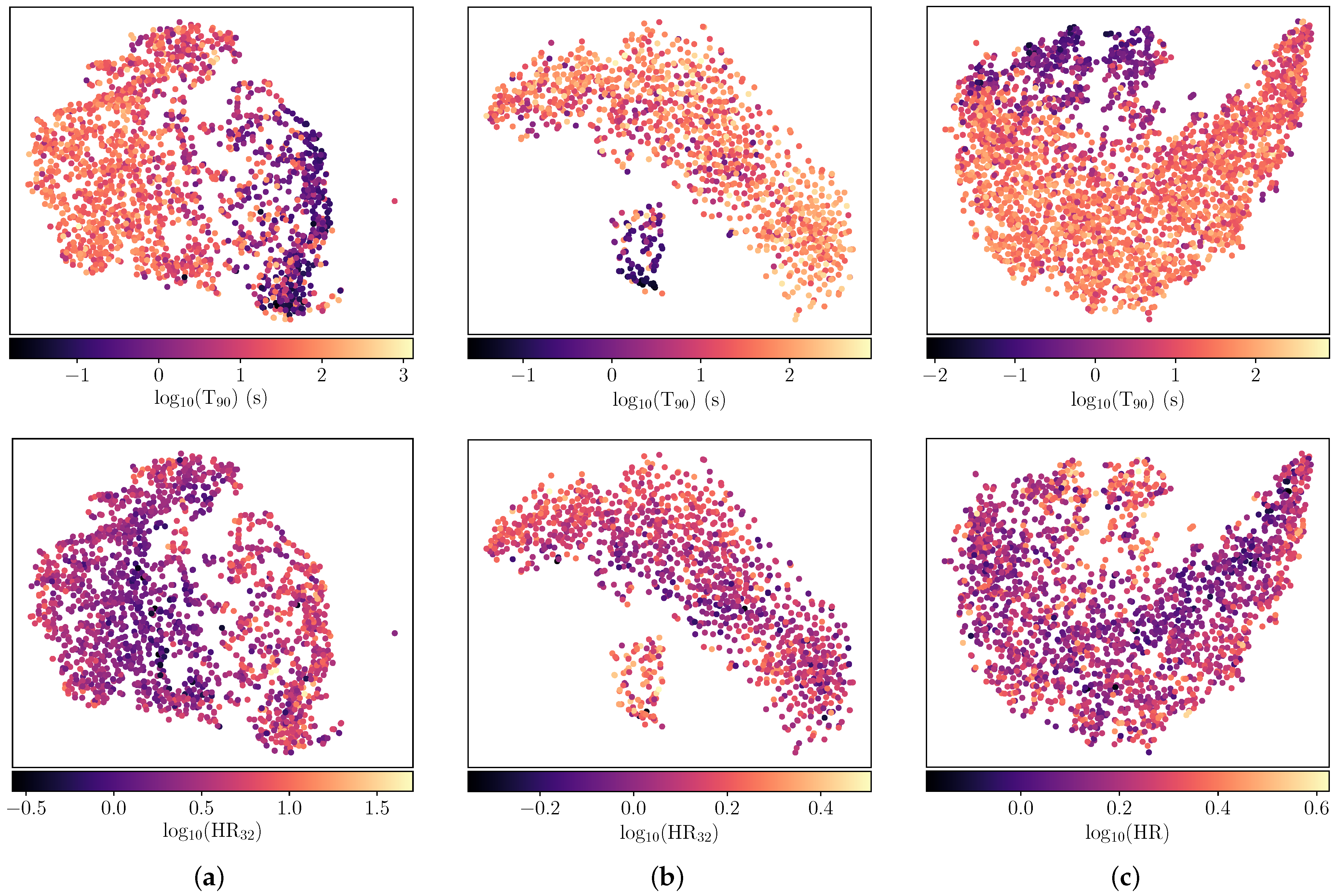
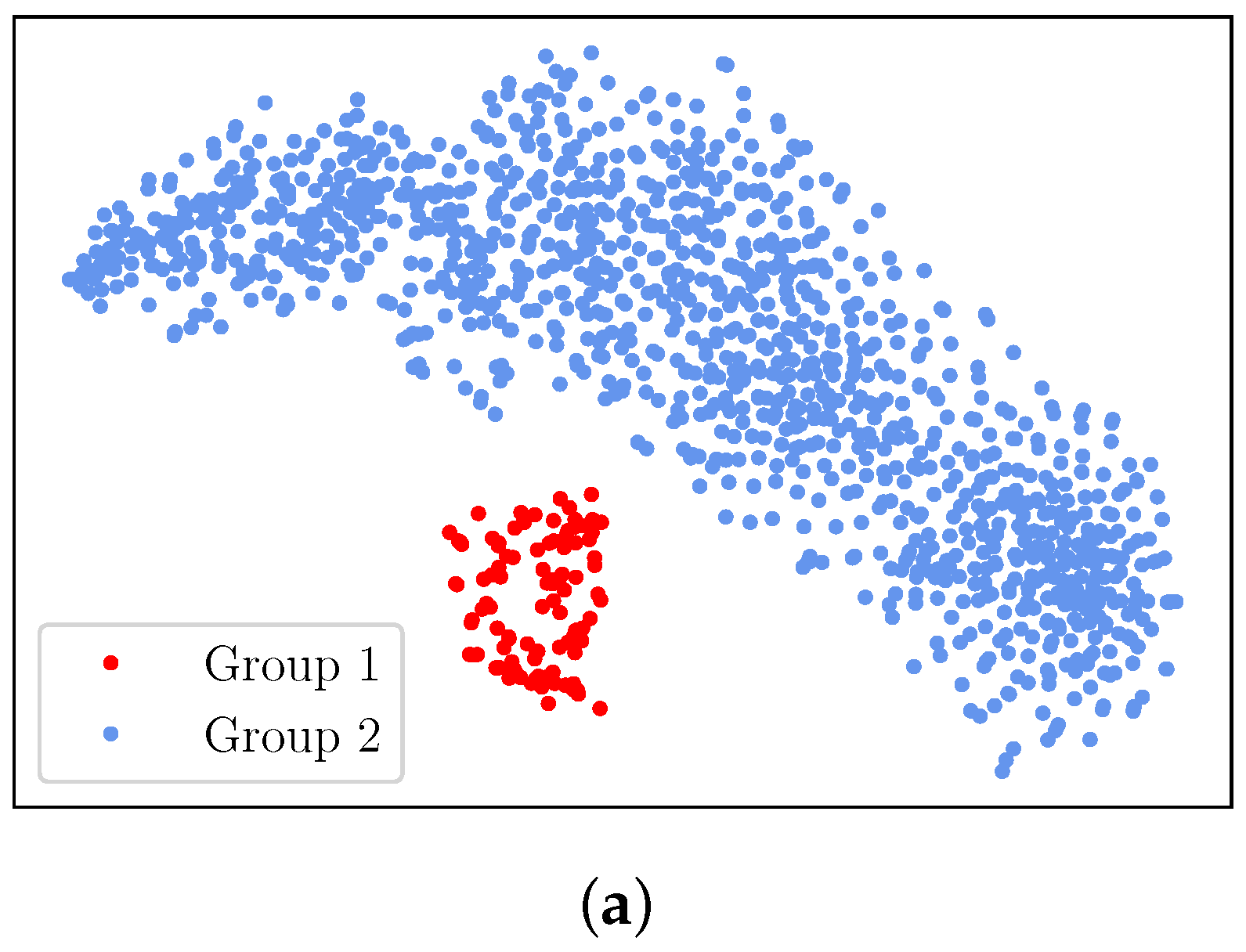
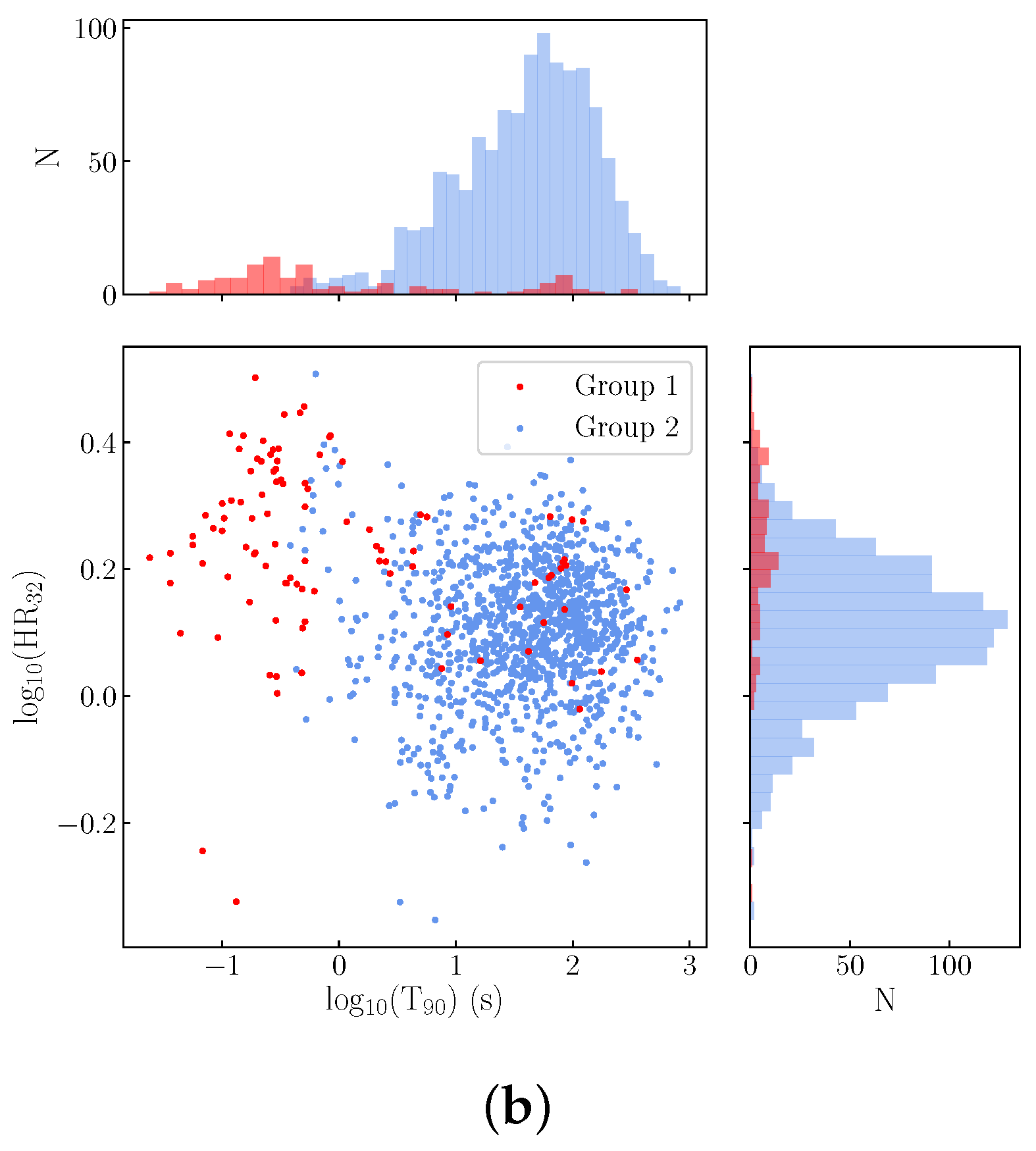
4.1. 64 ms Results
4.2. 4 ms Results
4.3. Properties of GRB Clusters Identified in the First Second Post-Trigger
5. Consistency Checks
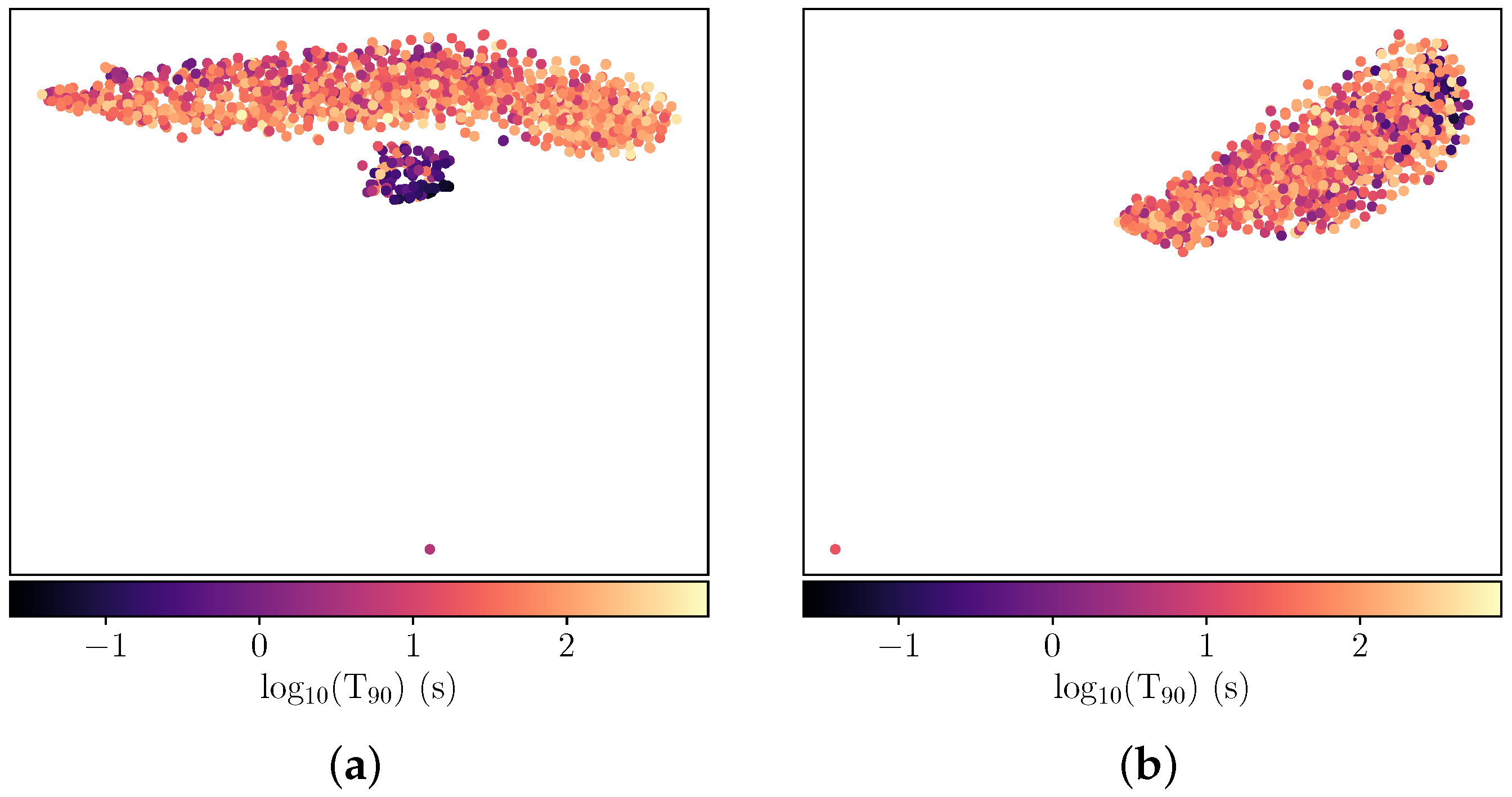
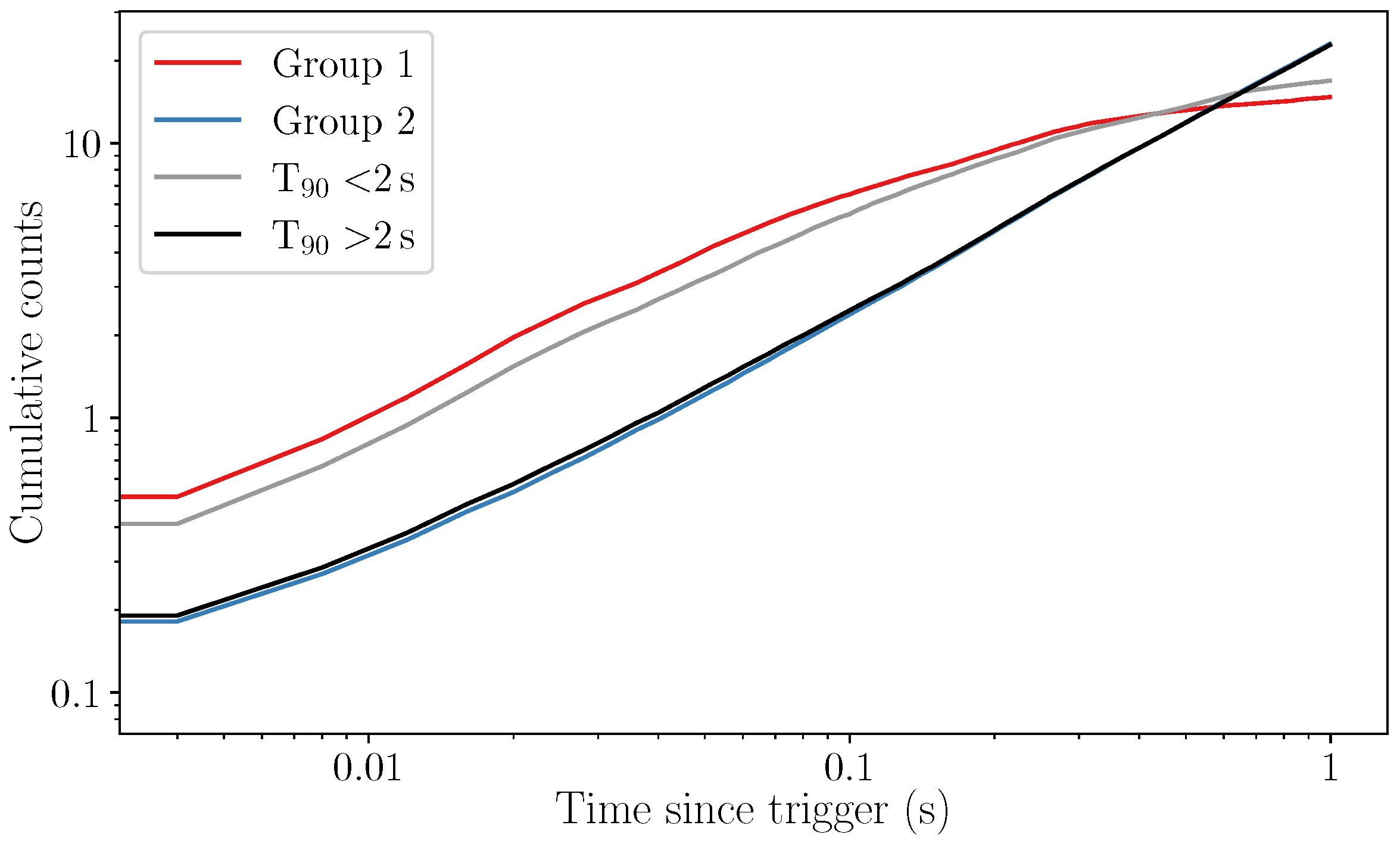
5.1. T100 vs. T1 Analysis
5.2. Inter-Comparison of Swift/BAT and Fermi/GBM Results
5.3. Time Intervals
5.4. Light Curve Classifications
5.5. Collapsar ‘Contamination’
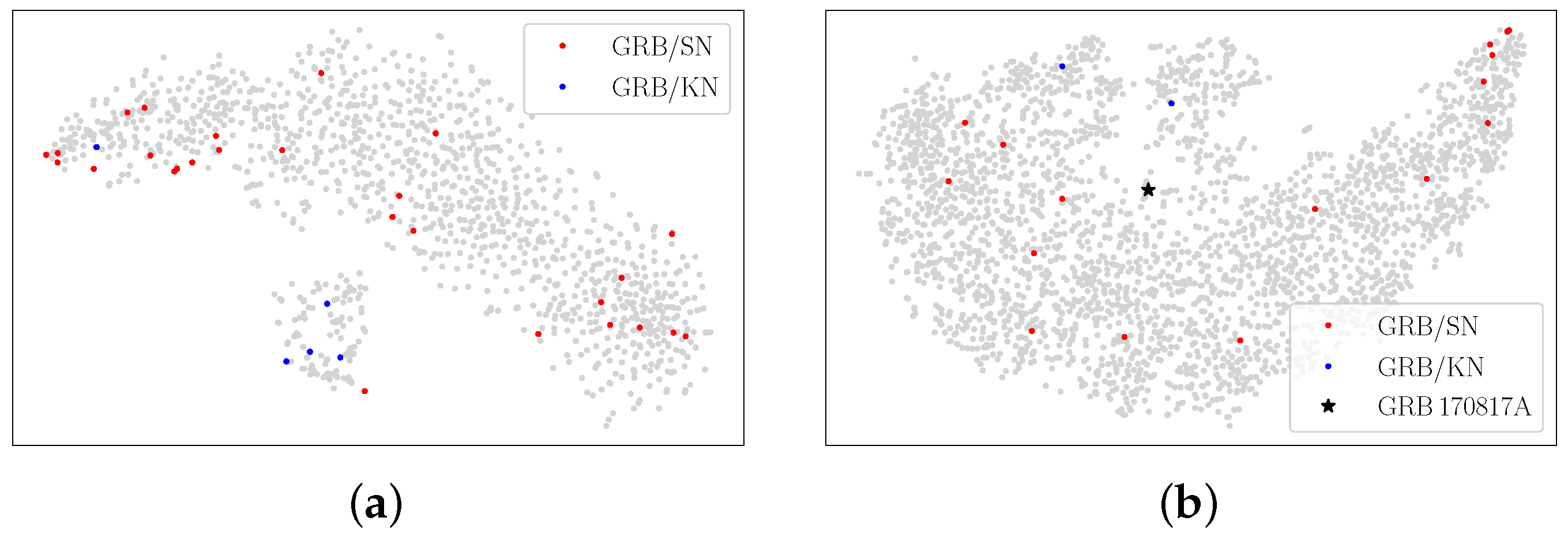
6. Notable GRBs
6.1. GRBs with Associated Supernovae
6.2. GRBs with Possible Kilonovae
7. Discussion
Cumulative Counts
8. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kouveliotou, C.; Meegan, C.A.; Fishman, G.J.; Bhat, N.P.; Briggs, M.S.; Koshut, T.M.; Paciesas, W.S.; Pendleton, G.N. Identification of Two Classes of Gamma-Ray Bursts. Astrophys. J. 1993, 413, L101. [Google Scholar] [CrossRef]
- Perley, D.A.; Niino, Y.; Tanvir, N.R.; Vergani, S.D.; Fynbo, J.P.U. Long-Duration Gamma-Ray Burst Host Galaxies in Emission and Absorption. Space Sci. Rev. 2016, 202, 111–142. [Google Scholar] [CrossRef]
- Galama, T.J.; Vreeswijk, P.M.; van Paradijs, J.; Kouveliotou, C.; Augusteijn, T.; Böhnhardt, H.; Brewer, J.P.; Doublier, V.; Gonzalez, J.F.; Leibundgut, B.; et al. An unusual supernova in the error box of the γ-ray burst of 25 April 1998. Nature 1998, 395, 670–672. [Google Scholar] [CrossRef]
- Hjorth, J.; Sollerman, J.; Møller, P.; Fynbo, J.P.U.; Woosley, S.E.; Kouveliotou, C.; Tanvir, N.R.; Greiner, J.; Andersen, M.I.; Castro-Tirado, A.J.; et al. A very energetic supernova associated with the γ-ray burst of 29 March 2003. Nature 2003, 423, 847–850. [Google Scholar] [CrossRef]
- Stanek, K.Z.; Matheson, T.; Garnavich, P.M.; Martini, P.; Berlind, P.; Caldwell, N.; Challis, P.; Brown, W.R.; Schild, R.; Krisciunas, K.; et al. Spectroscopic Discovery of the Supernova 2003dh Associated with GRB 030329. Astrophys. J. 2003, 591, L17–L20. [Google Scholar] [CrossRef]
- Woosley, S.E.; Bloom, J.S. The Supernova Gamma-Ray Burst Connection. Annu. Rev. Astron. Astrophys. 2006, 44, 507–556. [Google Scholar] [CrossRef]
- MacFadyen, A.I.; Woosley, S.E. Collapsars: Gamma-Ray Bursts and Explosions in “Failed Supernovae”. Astrophys. J. 1999, 524, 262–289. [Google Scholar] [CrossRef]
- Eichler, D.; Livio, M.; Piran, T.; Schramm, D.N. Nucleosynthesis, neutrino bursts and γ-rays from coalescing neutron stars. Nature 1989, 340, 126–128. [Google Scholar] [CrossRef]
- Narayan, R.; Paczynski, B.; Piran, T. Gamma-Ray Bursts as the Death Throes of Massive Binary Stars. Astrophys. J. 1992, 395, L83. [Google Scholar] [CrossRef]
- Berger, E. Short-Duration Gamma-Ray Bursts. Annu. Rev. Astron. Astrophys. 2014, 52, 43–105. [Google Scholar] [CrossRef]
- Berger, E. A Short Gamma-ray Burst “No-host” Problem? Investigating Large Progenitor Offsets for Short GRBs with Optical Afterglows. Astrophys. J. 2010, 722, 1946–1961. [Google Scholar] [CrossRef]
- Tunnicliffe, R.L.; Levan, A.J.; Tanvir, N.R.; Rowlinson, A.; Perley, D.A.; Bloom, J.S.; Cenko, S.B.; O’Brien, P.T.; Cobb, B.E.; Wiersema, K.; et al. On the nature of the ‘hostless’ short GRBs. Mon. Not. R. Astron. Soc. 2014, 437, 1495–1510. [Google Scholar] [CrossRef]
- Goldstein, A.; Veres, P.; Burns, E.; Briggs, M.S.; Hamburg, R.; Kocevski, D.; Wilson-Hodge, C.A.; Preece, R.D.; Poolakkil, S.; Roberts, O.J.; et al. An Ordinary Short Gamma-Ray Burst with Extraordinary Implications: Fermi-GBM Detection of GRB 170817A. Astrophys. J. 2017, 848, L14. [Google Scholar] [CrossRef]
- Savchenko, V.; Ferrigno, C.; Kuulkers, E.; Bazzano, A.; Bozzo, E.; Brandt, S.; Chenevez, J.; Courvoisier, T.L.; Diehl, R.; Domingo, A.; et al. INTEGRAL detection of the first prompt gamma-ray signal coincident with the gravitational-wave event GW170817. Astrophys. J. 2017, 848, L15. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. 2017, 848, L12. [Google Scholar] [CrossRef]
- Horváth, I. A Third Class of Gamma-Ray Bursts? Astrophys. J. 1998, 508, 757–759. [Google Scholar] [CrossRef]
- Salmon, L.; Martin-Carrillo, A.; Hanlon, L. Two Dimensional Clustering of Swift/BAT and Fermi/GBM Gamma-Ray Bursts. Galaxies 2022. submitted. [Google Scholar] [CrossRef]
- Norris, J.P.; Bonnell, J.T. Short Gamma-Ray Bursts with Extended Emission. Astrophys. J. 2006, 643, 266–275. [Google Scholar] [CrossRef]
- Barkov, M.V.; Pozanenko, A.S. Model of the extended emission of short gamma-ray bursts. Mon. Not. R. Astron. Soc. 2011, 417, 2161–2165. [Google Scholar] [CrossRef]
- Norris, J.P.; Gehrels, N.; Scargle, J.D. Threshold for Extended Emission in Short Gamma-Ray Bursts. Astrophys. J. 2011, 217, 411. [Google Scholar] [CrossRef]
- D’Avanzo, P. Short gamma-ray bursts: A review. J. High Energy Astrophys. 2015, 7, 73–80. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, B.B.; Liang, E.W.; Gehrels, N.; Burrows, D.N.; Mészáros, P. Making a Short Gamma-Ray Burst from a Long One: Implications for the Nature of GRB 060614. Astrophys. J. 2007, 655, L25–L28. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, B.B.; Virgili, F.J.; Liang, E.W.; Kann, D.A.; Wu, X.F.; Proga, D.; Lv, H.J.; Toma, K.; Mészáros, P.; et al. Discerning the Physical Origins of Cosmological Gamma-ray Bursts Based on Multiple Observational Criteria: The Cases of z = 6.7 GRB 080913, z = 8.2 GRB 090423, and Some Short/Hard GRBs. Astrophys. J. 2009, 703, 1696–1724. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, B.; Yuan, Q. A Comparative Study of Long and Short GRBs. II. A Multiwavelength Method to Distinguish Type II (Massive Star) and Type I (Compact Star) GRBs. Astrophys. J. 2020, 897, 154. [Google Scholar] [CrossRef]
- Tarnopolski, M. Distinguishing short and long Fermi gamma-ray bursts. Mon. Not. R. Astron. Soc. 2015, 454, 1132–1139. [Google Scholar] [CrossRef]
- Goldstein, A.; Preece, R.D.; Briggs, M.S. A New Discriminator for Gamma-ray Burst Classification: The Epeak-fluence Energy Ratio. Astrophys. J. 2010, 721, 1329–1332. [Google Scholar] [CrossRef]
- Qin, Y.P.; Chen, Z.F. Statistical classification of gamma-ray bursts based on the Amati relation. Mon. Not. R. Astron. Soc. 2013, 430, 163–173. [Google Scholar] [CrossRef]
- Lü, H.J.; Liang, E.W.; Zhang, B.B.; Zhang, B. A New Classification Method for Gamma-ray Bursts. Astrophys. J. 2010, 725, 1965–1970. [Google Scholar] [CrossRef]
- Lü, H.J.; Zhang, B.; Liang, E.W.; Zhang, B.B.; Sakamoto, T. The ‘amplitude’ parameter of gamma-ray bursts and its implications for GRB classification. Mon. Not. R. Astron. Soc. 2014, 442, 1922–1929. [Google Scholar] [CrossRef]
- Zhang, S.; Shao, L.; Zhang, B.B.; Zou, J.H.; Sun, H.Y.; Yao, Y.J.; Li, L.L. A Tight Three-parameter Correlation and Related Classification on Gamma-Ray Bursts. arXiv 2022, arXiv:2201.10861. [Google Scholar] [CrossRef]
- Hakkila, J.; Giblin, T.W.; Roiger, R.J.; Haglin, D.J.; Paciesas, W.S.; Meegan, C.A. How Sample Completeness Affects Gamma-Ray Burst Classification. Astrophys. J. 2003, 582, 320–329. [Google Scholar] [CrossRef]
- Bromberg, O.; Nakar, E.; Piran, T.; Sari, R. Short versus Long and Collapsars versus Non-collapsars: A Quantitative Classification of Gamma-Ray Bursts. Astrophys. J. 2013, 764, 179. [Google Scholar] [CrossRef]
- Jespersen, C.K.; Severin, J.B.; Steinhardt, C.L.; Vinther, J.; Fynbo, J.P.U.; Selsing, J.; Watson, D. An Unambiguous Separation of Gamma-Ray Bursts into Two Classes from Prompt Emission Alone. Astrophys. J. 2020, 896, L20. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition—The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Meredith, D.C.; Ryan, J.M.; Young, C.A.; Lestrade, J.P. Wavelet Analysis of Gamma Ray Bursts. AIP Conf. Proc. 1994, 307, 701. [Google Scholar] [CrossRef]
- Young, C.A.; Meredith, D.C.; Ryan, J.M. A Compact Representation of Gamma-Ray Burst Time Series. Astrophys. Space Sci. 1995, 231, 119–122. [Google Scholar] [CrossRef]
- Bagoly, Z.; Balázs, L.G.; Horváth, I.; Mészáros, A. Wavelet Analysis of the BATSE 64ms GRB Lightcurves. ASP Conf. Ser. 2004, 312, 51. [Google Scholar]
- Hurley, K.J.; McBreen, B.; Quilligan, F.; Delaney, M.; Hanlon, L. Wavelet analysis and lognormal distributions in GRBs. AIP Conf. Ser. 1998, 428, 191–195. [Google Scholar] [CrossRef]
- Quilligan, F.; Hurley, K.J.; McBreen, B.; Hanlon, L.; Duggan, P. Characteristic properties of peaks in GRBs. Astron. Astrophys. Suppl. Ser. 1999, 138, 419–420. [Google Scholar] [CrossRef][Green Version]
- Quilligan, F.; McBreen, B.; Hanlon, L.; McBreen, S.; Hurley, K.J.; Watson, D. Temporal properties of gamma ray bursts as signatures of jets from the central engine. Astron. Astrophys. 2002, 385, 377–398. [Google Scholar] [CrossRef]
- Qin, Y.P.; Liang, E.W.; Xie, G.Z.; Su, C.Y. Statistical Properties of the Highest Pulses in Gamma-Ray Bursts. Chin. J. Astron. Astrophys. 2003, 3, 38–48. [Google Scholar] [CrossRef][Green Version]
- Walker, K.C.; Schaefer, B.E.; Fenimore, E.E. Gamma-Ray Bursts Have Millisecond Variability. Astrophys. J. 2000, 537, 264–269. [Google Scholar] [CrossRef]
- MacLachlan, G.A.; Shenoy, A.; Sonbas, E.; Dhuga, K.S.; Eskandarian, A.; Maximon, L.C.; Parke, W.C. The minimum variability time-scale and its relation to pulse profiles of Fermi GRBs. Mon. Not. R. Astron. Soc. 2012, 425, L32–L35. [Google Scholar] [CrossRef]
- MacLachlan, G.A.; Shenoy, A.; Sonbas, E.; Dhuga, K.S.; Cobb, B.E.; Ukwatta, T.N.; Morris, D.C.; Eskandarian, A.; Maximon, L.C.; Parke, W.C. Minimum variability time-scales of long and short GRBs. Mon. Not. R. Astron. Soc. 2013, 432, 857–865. [Google Scholar] [CrossRef]
- Golkhou, V.Z.; Butler, N.R. Uncovering the Intrinsic Variability of Gamma-Ray Bursts. Astrophys. J. 2014, 787, 90. [Google Scholar] [CrossRef]
- Golkhou, V.Z.; Butler, N.R.; Littlejohns, O.M. The Energy Dependence of GRB Minimum Variability Timescales. Astrophys. J. 2015, 811, 93. [Google Scholar] [CrossRef]
- Varughese, M.M.; von Sachs, R.; Stephanou, M.; Bassett, B.A. Non-parametric transient classification using adaptive wavelets. Mon. Not. R. Astron. Soc. 2015, 453, 2848–2861. [Google Scholar] [CrossRef]
- Lochner, M.; McEwen, J.D.; Peiris, H.V.; Lahav, O.; Winter, M.K. Photometric Supernova Classification with Machine Learning. Astrophys. J. 2016, 225, 31. [Google Scholar] [CrossRef]
- Vargas dos Santos, M.; Quartin, M.; Reis, R.R.R. On the cosmological performance of photometrically classified supernovae with machine learning. Mon. Not. R. Astron. Soc. 2020, 497, 2974–2991. [Google Scholar] [CrossRef]
- Norris, J.P.; Share, G.H.; Messina, D.C.; Dennis, B.R.; Desai, U.D.; Cline, T.L.; Matz, S.M.; Chupp, E.L. Spectral Evolution of Pulse Structures in Gamma-Ray Bursts. Astrophys. J. 1986, 301, 213. [Google Scholar] [CrossRef]
- Golenetskii, S.V.; Mazets, E.P.; Aptekar, R.L.; Ilinskii, V.N. Correlation between luminosity and temperature in γ-ray burst sources. Nature 1983, 306, 451–453. [Google Scholar] [CrossRef]
- Fenimore, E.E.; in ’t Zand, J.J.M.; Norris, J.P.; Bonnell, J.T.; Nemiroff, R.J. Gamma-Ray Burst Peak Duration as a Function of Energy. Astrophys. J. 1995, 448, L101. [Google Scholar] [CrossRef]
- Nemiroff, R.J.; Norris, J.P.; Kouveliotou, C.; Fishman, G.J.; Meegan, C.A.; Paciesas, W.S. Gamma-Ray Bursts Are Time-asymmetric. Astrophys. J. 1994, 423, 432. [Google Scholar] [CrossRef]
- Norris, J.P.; Nemiroff, R.J.; Bonnell, J.T.; Scargle, J.D.; Kouveliotou, C.; Paciesas, W.S.; Meegan, C.A.; Fishman, G.J. Attributes of Pulses in Long Bright Gamma-Ray Bursts. Astrophys. J. 1996, 459, 393. [Google Scholar] [CrossRef]
- Hakkila, J.; Preece, R.D. Unification of Pulses in Long and Short Gamma-Ray Bursts: Evidence from Pulse Properties and Their Correlations. Astrophys. J. 2011, 740, 104. [Google Scholar] [CrossRef]
- Hakkila, J.; Horváth, I.; Hofesmann, E.; Lesage, S. Properties of Short Gamma-ray Burst Pulses from a BATSE TTE GRB Pulse Catalog. Astrophys. J. 2018, 855, 101. [Google Scholar] [CrossRef]
- Cheng, L.X.; Ma, Y.Q.; Cheng, K.S.; Lu, T.; Zhou, Y.Y. The time delay of gamma-ray bursts in the soft energy band. Astron. Astrophys. 1995, 300, 746. [Google Scholar]
- Norris, J.P.; Marani, G.F.; Bonnell, J.T. Connection between Energy-dependent Lags and Peak Luminosity in Gamma-Ray Bursts. Astrophys. J. 2000, 534, 248–257. [Google Scholar] [CrossRef]
- Wu, B.; Fenimore, E. Spectral Lags of Gamma-Ray Bursts From Ginga and BATSE. Astrophys. J. 2000, 535, L29–L32. [Google Scholar] [CrossRef][Green Version]
- Ukwatta, T.N.; Dhuga, K.S.; Stamatikos, M.; Dermer, C.D.; Sakamoto, T.; Sonbas, E.; Parke, W.C.; Maximon, L.C.; Linnemann, J.T.; Bhat, P.N.; et al. The lag-luminosity relation in the GRB source frame: An investigation with Swift BAT bursts. Mon. Not. R. Astron. Soc. 2012, 419, 614–623. [Google Scholar] [CrossRef]
- Ukwatta, T.N.; Stamatikos, M.; Dhuga, K.S.; Sakamoto, T.; Barthelmy, S.D.; Eskandarian, A.; Gehrels, N.; Maximon, L.C.; Norris, J.P.; Parke, W.C. Spectral Lags and the Lag-Luminosity Relation: An Investigation with Swift BAT Gamma-ray Bursts. Astrophys. J. 2010, 711, 1073–1086. [Google Scholar] [CrossRef]
- Hakkila, J.; Giblin, T.W.; Norris, J.P.; Fragile, P.C.; Bonnell, J.T. Correlations between Lag, Luminosity, and Duration in Gamma-Ray Burst Pulses. Astrophys. J. 2008, 677, L81. [Google Scholar] [CrossRef]
- Bernardini, M.G.; Ghirlanda, G.; Campana, S.; Covino, S.; Salvaterra, R.; Atteia, J.L.; Burlon, D.; Calderone, G.; D’Avanzo, P.; D’Elia, V.; et al. Comparing the spectral lag of short and long gamma-ray bursts and its relation with the luminosity. Mon. Not. R. Astron. Soc. 2015, 446, 1129–1138. [Google Scholar] [CrossRef]
- Hakkila, J.; Preece, R.D. Gamma-Ray Burst Pulse Shapes: Evidence for Embedded Shock Signatures? Astrophys. J. 2014, 783, 88. [Google Scholar] [CrossRef]
- Bhat, P.N.; Fishman, G.J.; Meegan, C.A.; Wilson, R.B.; Kouveliotou, C.; Paciesas, W.S.; Pendleton, G.N.; Schaefer, B.E. Spectral Evolution of a Subclass of Gamma-Ray Bursts Observed by BATSE. Astrophys. J. 1994, 426, 604. [Google Scholar] [CrossRef]
- Band, D.L. Gamma-Ray Burst Spectral Evolution through Cross-Correlations of Discriminator Light Curves. Astrophys. J. 1997, 486, 928–937. [Google Scholar] [CrossRef]
- Ford, L.A.; Band, D.L.; Matteson, J.L.; Briggs, M.S.; Pendleton, G.N.; Preece, R.D.; Paciesas, W.S.; Teegarden, B.J.; Palmer, D.M.; Schaefer, B.E.; et al. BATSE Observations of Gamma-Ray Burst Spectra. II. Peak Energy Evolution in Bright, Long Bursts. Astrophys. J. 1995, 439, 307. [Google Scholar] [CrossRef]
- Borgonovo, L.; Ryde, F. On the Hardness-Intensity Correlation in Gamma-Ray Burst Pulses. Astrophys. J. 2001, 548, 770–786. [Google Scholar] [CrossRef]
- Peng, Z.Y.; Ma, L.; Lu, R.J.; Fang, L.M.; Bao, Y.Y.; Yin, Y. Spectral hardness evolution characteristics of tracking gamma-ray burst pulses. New Astron. 2009, 14, 311–320. [Google Scholar] [CrossRef][Green Version]
- Lu, R.J.; Hou, S.J.; Liang, E.W. The Ep-flux Correlation in the Rising and Decaying Phases of gamma-ray Burst Pulses: Evidence for Viewing Angle Effect? Astrophys. J. 2010, 720, 1146–1154. [Google Scholar] [CrossRef]
- Hakkila, J.; Lien, A.; Sakamoto, T.; Morris, D.; Neff, J.E.; Giblin, T.W. Swift Observations of Gamma-Ray Burst Pulse Shapes: GRB Pulse Spectral Evolution Clarified. Astrophys. J. 2015, 815, 134. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Nava, L.; Ghisellini, G. Spectral-luminosity relation within individual Fermi gamma rays bursts. Astron. Astrophys. 2010, 511, A43. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Ghisellini, G.; Nava, L.; Burlon, D. Spectral evolution of Fermi/GBM short gamma-ray bursts. Mon. Not. R. Astron. Soc. 2011, 410, L47–L51. [Google Scholar] [CrossRef]
- Lu, R.J.; Wei, J.J.; Liang, E.W.; Zhang, B.B.; Lü, H.J.; Lü, L.Z.; Lei, W.H.; Zhang, B. A Comprehensive Analysis of Fermi Gamma-Ray Burst Data. II. Ep Evolution Patterns and Implications for the Observed Spectrum-Luminosity Relations. Astrophys. J. 2012, 756, 112. [Google Scholar] [CrossRef]
- Kocevski, D.; Petrosian, V. On the Lack of Time Dilation Signatures in Gamma-Ray Burst Light Curves. Astrophys. J. 2013, 765, 116. [Google Scholar] [CrossRef]
- Littlejohns, O.M.; Tanvir, N.R.; Willingale, R.; Evans, P.A.; O’Brien, P.T.; Levan, A.J. Are gamma-ray bursts the same at high redshift and low redshift? Mon. Not. R. Astron. Soc. 2013, 436, 3640–3655. [Google Scholar] [CrossRef]
- Fishman, G.; Johnson, W.N. Proceedings of the Gamma Ray Observatory Science Workshop; Johnson, W.N., Ed.; NASA/GSFC Greenbelt: Greenbelt, MD, USA, 1989; pp. 2–39. [Google Scholar]
- Gehrels, N.; Chincarini, G.; Giommi, P.; Mason, K.O.; Nousek, J.A.; Wells, A.A.; White, N.E.; Barthelmy, S.D.; Burrows, D.N.; Cominsky, L.R.; et al. The Swift Gamma-Ray Burst Mission. Astrophys. J. 2004, 611, 1005–1020. [Google Scholar] [CrossRef]
- Meegan, C.; Lichti, G.; Bhat, P.N.; Bissaldi, E.; Briggs, M.S.; Connaughton, V.; Diehl, R.; Fishman, G.; Greiner, J.; Hoover, A.S.; et al. The Fermi Gamma-ray Burst Monitor. Astrophys. J. 2009, 702, 791–804. [Google Scholar] [CrossRef]
- Lien, A.; Sakamoto, T.; Barthelmy, S.D.; Baumgartner, W.H.; Cannizzo, J.K.; Chen, K.; Collins, N.R.; Cummings, J.R.; Gehrels, N.; Krimm, H.A.; et al. The Third Swift Burst Alert Telescope Gamma-Ray Burst Catalog. Astrophys. J. 2016, 829, 7. [Google Scholar] [CrossRef]
- Goldstein, A.; Cleveland, W.H.; Kocevski, D. Fermi GBM Data Tools: V1.04. 2020. Available online: https://fermi.gsfc.nasa.gov/ssc/data/analysis/gbm (accessed on 26 April 2022).
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and analysis of computer experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
- De, G.; Matthews, A.G.; Van Der Wilk, M.; Nickson, T.; Fujii, K.; Boukouvalas, A.; León-Villagrá, P.; Ghahramani, Z.; Hensman, J. GPflow: A Gaussian process library using TensorFlow. J. Mach. Learn. Res. 2017, 18, 1299–1304. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: tensorflow.org (accessed on 15 March 2021).
- Daubechies, I. Ten Lectures on Wavelets; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Holschneider, M.; Kronland-Martinet, R.; Morlet, J.; Tchamitchian, P. A Real-Time Algorithm for Signal Analysis with the Help of the Wavelet Transform. In Wavelets. Time-Frequency Methods and Phase Space; Combes, J.M., Grossmann, A., Tchamitchian, P., Eds.; Spinger: Berlin/Heidelberg, Germany, 1989; p. 286. [Google Scholar]
- Addison, P.S. The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Rhif, M.; Ben Abbes, A.; Farah, I.R.; Martínez, B.; Sang, Y. Wavelet transform application for/in non-stationary time-series analysis: A review. Appl. Sci. 2019, 9, 1345. [Google Scholar] [CrossRef]
- Lee, G.; Gommers, R.; Waselewski, F.; Wohlfahrt, K.; O’Leary, A. PyWavelets: A Python package for wavelet analysis. J. Open Source Softw. 2019, 4, 1237. [Google Scholar] [CrossRef]
- Daubechies, I. Orthonormal bases of compactly supported wavelets. Commun. Pure Appl. Math. 1988, 41, 909–996. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417. [Google Scholar] [CrossRef]
- Hinton, G.E.; Roweis, S.T. Stochastic neighbor embedding. Adv. Neural Inf. Process. Syst. 2003, 15, 857–864. [Google Scholar]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Maaten, L.v.d.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Fraley, C.; Raftery, A.E. MCLUST: Software for model-based cluster analysis. J. Classif. 1999, 16, 297–306. [Google Scholar] [CrossRef]
- Scrucca, L.; Fop, M.; Murphy, T.B.; Raftery, A.E. mclust 5: Clustering, classification and density estimation using Gaussian finite mixture models. R J. 2016, 8, 289–317. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Baudry, J.P.; Raftery, A.E.; Celeux, G.; Lo, K.; Gottardo, R. Combining Mixture Components for Clustering. J. Comput. Graph. Stat. 2010, 19, 332–353. [Google Scholar] [CrossRef]
- Gibson, S.L.; Wynn, G.A.; Gompertz, B.P.; O’Brien, P.T. Fallback accretion on to a newborn magnetar: Short GRBs with extended emission. Mon. Not. R. Astron. Soc. 2017, 470, 4925–4940. [Google Scholar] [CrossRef]
- Racusin, J.L.; Oates, S.R.; Schady, P.; Burrows, D.N.; de Pasquale, M.; Donato, D.; Gehrels, N.; Koch, S.; McEnery, J.; Piran, T.; et al. Fermi and Swift Gamma-ray Burst Afterglow Population Studies. Astrophys. J. 2011, 738, 138. [Google Scholar] [CrossRef]
- Burgess, J.M.; Greiner, J.; Bégué, D.; Giannios, D.; Berlato, F.; Lipunov, V.M. Viewing Short Gamma-Ray Bursts From a Different Angle. Front. Astron. Space Sci. 2020, 7, 40. [Google Scholar] [CrossRef]
- Koen, C.; Bere, A. On multiple classes of gamma-ray bursts, as deduced from autocorrelation functions or bivariate duration/hardness ratio distributions. Mon. Not. R. Astron. Soc. 2012, 420, 405–415. [Google Scholar] [CrossRef]
- Tarnopolski, M. Analysis of gamma-ray burst duration distribution using mixtures of skewed distributions. Mon. Not. R. Astron. Soc. 2016. [Google Scholar] [CrossRef]
- Tarnopolski, M. Analysis of the Duration-Hardness Ratio Plane of Gamma-Ray Bursts Using Skewed Distributions. Astrophys. J. 2019, 870, 105. [Google Scholar] [CrossRef]
- Bromberg, O.; Nakar, E.; Piran, T.; Sari, R. An Observational Imprint of the Collapsar Model of Long Gamma-Ray Bursts. Astrophys. J. 2012, 749, 110. [Google Scholar] [CrossRef]
- Cano, Z.; Wang, S.Q.; Dai, Z.G.; Wu, X.F. The Observer’s Guide to the Gamma-Ray Burst Supernova Connection. Adv. Astron. 2017, 2017, 8929054. [Google Scholar] [CrossRef]
- Ashall, C.; Mazzali, P.A.; Pian, E.; Woosley, S.E.; Palazzi, E.; Prentice, S.J.; Kobayashi, S.; Holmbo, S.; Levan, A.; Perley, D.; et al. GRB 161219B/SN 2016jca: A powerful stellar collapse. Mon. Not. R. Astron. Soc. 2019, 487, 5824–5839. [Google Scholar] [CrossRef]
- Melandri, A.; Malesani, D.B.; Izzo, L.; Japelj, J.; Vergani, S.D.; Schady, P.; Sagués Carracedo, A.; de Ugarte Postigo, A.; Anderson, J.P.; Barbarino, C.; et al. GRB 171010A/SN 2017htp: A GRB-SN at z = 0.33. Mon. Not. R. Astron. Soc. 2019, 490, 5366–5374. [Google Scholar] [CrossRef]
- Izzo, L.; Rossi, A.; Malesani, D.; Heintz, K.; Selsing, J.; Schady, P.; Starling, R.; Sollerman, J.; Leloudas, G.; Cano, Z.; et al. GRB 180728A: Discovery of the associated supernova. GRB Coord. Netw. 2018, 23142, 1. [Google Scholar]
- Selsing, J.; Izzo, L.; Rossi, A.; Malesani, D.; Heintz, K.; Schady, P.; Starling, R.; Sollerman, J.; Leloudas, G.; Cano, Z.; et al. GRB 180728A: Classification of the associated SN 2018fip. GRB Coord. Netw. 2018, 23181, 1. [Google Scholar]
- Hu, Y.D.; Castro-Tirado, A.J.; Kumar, A.; Gupta, R.; Valeev, A.F.; Pandey, S.B.; Kann, D.A.; Castellón, A.; Agudo, I.; Aryan, A.; et al. 10.4 m GTC observations of the nearby VHE-detected GRB 190829A/SN 2019oyw. Astron. Astrophys. 2021, 646, A50. [Google Scholar] [CrossRef]
- Ahumada, T.; Singer, L.P.; Anand, S.; Coughlin, M.W.; Kasliwal, M.M.; Ryan, G.; Andreoni, I.; Cenko, S.B.; Fremling, C.; Kumar, H.; et al. Discovery and confirmation of the shortest gamma ray burst from a collapsar. arXiv 2021, arXiv:2105.05067. [Google Scholar] [CrossRef]
- Rossi, A.; Rothberg, B.; Palazzi, E.; Kann, D.A.; D’Avanzo, P.; Klose, S.; Perego, A.; Pian, E.; Savaglio, S.; Stratta, G.; et al. The peculiar short-duration GRB 200826A and its supernova. arXiv 2021, arXiv:2105.03829. [Google Scholar] [CrossRef]
- Zhang, B.B.; Liu, Z.K.; Peng, Z.K.; Li, Y.; Lü, H.J.; Yang, J.; Yang, Y.S.; Yang, Y.H.; Meng, Y.Z.; Zou, J.H.; et al. A Peculiarly Short-duration Gamma-Ray Burst from Massive Star Core Collapse. arXiv 2021, arXiv:2105.05021. [Google Scholar] [CrossRef]
- Berger, E.; Fong, W.; Chornock, R. An r-process Kilonova Associated with the Short-hard GRB 130603B. Astrophys. J. 2013, 774, L23. [Google Scholar] [CrossRef]
- Tanvir, N.R.; Levan, A.J.; Fruchter, A.S.; Hjorth, J.; Hounsell, R.A.; Wiersema, K.; Tunnicliffe, R.L. A ‘kilonova’ associated with the short-duration γ-ray burst GRB 130603B. Nature 2013, 500, 547–549. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.P.; Fan, Y.Z.; Wei, D.M. An r-process macronova/kilonova in GRB 060614: Evidence for the merger of a neutron star-black hole binary. In Proceedings of the 13th International Symposium on Origin of Matter and Evolution of Galaxies (OMEG2015), Beijing, China, 24–27 June 2015; EDP Sciences: Les Ulis, France, 2016; Volume 109, p. 08002. [Google Scholar]
- Yang, B.; Jin, Z.P.; Li, X.; Covino, S.; Zheng, X.Z.; Hotokezaka, K.; Fan, Y.Z.; Piran, T.; Wei, D.M. A possible macronova in the late afterglow of the long-short burst GRB 060614. Nat. Commun. 2015, 6, 7323. [Google Scholar] [CrossRef] [PubMed]
- Perley, D.A.; Metzger, B.D.; Granot, J.; Butler, N.R.; Sakamoto, T.; Ramirez-Ruiz, E.; Levan, A.J.; Bloom, J.S.; Miller, A.A.; Bunker, A.; et al. GRB 080503: Implications of a Naked Short Gamma-Ray Burst Dominated by Extended Emission. Astrophys. J. 2009, 696, 1871–1885. [Google Scholar] [CrossRef]
- Jin, Z.P.; Hotokezaka, K.; Li, X.; Tanaka, M.; D’Avanzo, P.; Fan, Y.Z.; Covino, S.; Wei, D.M.; Piran, T. The Macronova in GRB 050709 and the GRB-macronova connection. Nat. Commun. 2016, 7, 12898. [Google Scholar] [CrossRef]
- Troja, E.; Ryan, G.; Piro, L.; van Eerten, H.; Cenko, S.B.; Yoon, Y.; Lee, S.K.; Im, M.; Sakamoto, T.; Gatkine, P.; et al. A luminous blue kilonova and an off-axis jet from a compact binary merger at z = 0.1341. Nat. Commun. 2018, 9, 4089. [Google Scholar] [CrossRef]
- Kasliwal, M.M.; Korobkin, O.; Lau, R.M.; Wollaeger, R.; Fryer, C.L. Infrared Emission from Kilonovae: The Case of the Nearby Short Hard Burst GRB 160821B. Astrophys. J. 2017, 843, L34. [Google Scholar] [CrossRef]
- Jin, Z.P.; Li, X.; Wang, H.; Wang, Y.Z.; He, H.N.; Yuan, Q.; Zhang, F.W.; Zou, Y.C.; Fan, Y.Z.; Wei, D.M. Short GRBs: Opening Angles, Local Neutron Star Merger Rate, and Off-axis Events for GRB/GW Association. Astrophys. J. 2018, 857, 128. [Google Scholar] [CrossRef]
- Lamb, G.P.; Tanvir, N.R.; Levan, A.J.; de Ugarte Postigo, A.; Kawaguchi, K.; Corsi, A.; Evans, P.A.; Gompertz, B.; Malesani, D.B.; Page, K.L.; et al. Short GRB 160821B: A Reverse Shock, a Refreshed Shock, and a Well-sampled Kilonova. Astrophys. J. 2019, 883, 48. [Google Scholar] [CrossRef]
- Troja, E.; Castro-Tirado, A.J.; Becerra González, J.; Hu, Y.; Ryan, G.S.; Cenko, S.B.; Ricci, R.; Novara, G.; Sánchez-Rámirez, R.; Acosta-Pulido, J.A.; et al. The afterglow and kilonova of the short GRB 160821B. Mon. Not. R. Astron. Soc. 2019, 489, 2104–2116. [Google Scholar] [CrossRef]
- Fong, W.; Laskar, T.; Rastinejad, J.; Escorial, A.R.; Schroeder, G.; Barnes, J.; Kilpatrick, C.D.; Paterson, K.; Berger, E.; Metzger, B.D.; et al. The Broadband Counterpart of the Short GRB 200522A at z = 0.5536: A Luminous Kilonova or a Collimated Outflow with a Reverse Shock? Astrophys. J. 2021, 906, 127. [Google Scholar] [CrossRef]
- Xu, D.; Starling, R.L.C.; Fynbo, J.P.U.; Sollerman, J.; Yost, S.; Watson, D.; Foley, S.; O’Brien, P.T.; Hjorth, J. In Search of Progenitors for Supernovaless Gamma-Ray Bursts 060505 and 060614: Re-examination of Their Afterglows. Astrophys. J. 2009, 696, 971–979. [Google Scholar] [CrossRef]
- Price, P.A.; Berger, E.; Fox, D.B. GRB 060614: Redshift. GRB Coord. Netw. 2006, 5275, 1. [Google Scholar]
- Fugazza, D.; Malesani, D.; Romano, P.; Tagliaferri, G.; Covino, S.; Chincarini, G.; Della Valle, M.; Fiore, F.; Stella, L. GRB 060614: Redshift confirmation. GRB Coord. Netw. 2006, 5276, 1. [Google Scholar]
- Della Valle, M.; Chincarini, G.; Panagia, N.; Tagliaferri, G.; Malesani, D.; Testa, V.; Fugazza, D.; Campana, S.; Covino, S.; Mangano, V.; et al. An enigmatic long-lasting γ-ray burst not accompanied by a bright supernova. Nature 2006, 444, 1050–1052. [Google Scholar] [CrossRef] [PubMed]
- Fynbo, J.P.U.; Watson, D.; Thöne, C.C.; Sollerman, J.; Bloom, J.S.; Davis, T.M.; Hjorth, J.; Jakobsson, P.; Jørgensen, U.G.; Graham, J.F.; et al. No supernovae associated with two long-duration γ-ray bursts. Nature 2006, 444, 1047–1049. [Google Scholar] [CrossRef]
- Gal-Yam, A.; Fox, D.B.; Price, P.A.; Ofek, E.O.; Davis, M.R.; Leonard, D.C.; Soderberg, A.M.; Schmidt, B.P.; Lewis, K.M.; Peterson, B.A.; et al. A novel explosive process is required for the γ-ray burst GRB 060614. Nature 2006, 444, 1053–1055. [Google Scholar] [CrossRef]
- Gehrels, N.; Norris, J.P.; Barthelmy, S.D.; Granot, J.; Kaneko, Y.; Kouveliotou, C.; Markwardt, C.B.; Mészáros, P.; Nakar, E.; Nousek, J.A.; et al. A new γ-ray burst classification scheme from GRB060614. Nature 2006, 444, 1044–1046. [Google Scholar] [CrossRef]
- Lu, Y.; Huang, Y.F.; Zhang, S.N. A Tidal Disruption Model for the Gamma-Ray Burst of GRB 060614. Astrophys. J. 2008, 684, 1330–1335. [Google Scholar] [CrossRef][Green Version]
- Meng, Y.Z.; Geng, J.J.; Zhang, B.B.; Wei, J.J.; Xiao, D.; Liu, L.D.; Gao, H.; Wu, X.F.; Liang, E.W.; Huang, Y.F.; et al. The Origin of the Prompt Emission for Short GRB 170817A: Photosphere Emission or Synchrotron Emission? Astrophys. J. 2018, 860, 72. [Google Scholar] [CrossRef]
- Li, L.; Ryde, F.; Pe’er, A.; Yu, H.F.; Acuner, Z. Bayesian Time-Resolved Spectroscopy of Multi-Pulsed GRBs: Variations of Emission Properties amongst Pulses. arXiv 2020, arXiv:2012.03038. [Google Scholar]
- Dereli-Bégué, H.; Pe’er, A.; Ryde, F. Classification of Photospheric Emission in Short GRBs. Astrophys. J. 2020, 897, 145. [Google Scholar] [CrossRef]
- Li, L. Multipulse Fermi Gamma-Ray Bursts. I. Evidence of the Transition from Fireball to Poynting-flux-dominated Outflow. Astrophys. J. 2019, 242, 16. [Google Scholar] [CrossRef]
- Acuner, Z.; Ryde, F.; Pe’er, A.; Mortlock, D.; Ahlgren, B. The Fraction of Gamma-Ray Bursts with an Observed Photospheric Emission Episode. Astrophys. J. 2020, 893, 128. [Google Scholar] [CrossRef]
- Acuner, Z.; Ryde, F. Clustering of gamma-ray burst types in the Fermi GBM catalogue: Indications of photosphere and synchrotron emissions during the prompt phase. Mon. Not. R. Astron. Soc. 2018, 475, 1708–1724. [Google Scholar] [CrossRef]
- Ryde, F. The Cooling Behavior of Thermal Pulses in Gamma-Ray Bursts. Astrophys. J. 2004, 614, 827–846. [Google Scholar] [CrossRef]
- McBreen, S.; McBreen, B.; Hanlon, L.; Quilligan, F. Cumulative light curves of gamma-ray bursts and relaxation systems. Astron. Astrophys. 2002, 393, L29–L32. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. Prospects for observing and localizing gravitational-wave transients with Advanced LIGO, Advanced Virgo and KAGRA. Living Rev. Relativ. 2020, 23, 3. [Google Scholar] [CrossRef]
- Ivezić, Ž.; Kahn, S.M.; Tyson, J.A.; Abel, B.; Acosta, E.; Allsman, R.; Alonso, D.; AlSayyad, Y.; Anderson, S.F.; Andrew, J.; et al. LSST: From Science Drivers to Reference Design and Anticipated Data Products. Astrophys. J. 2019, 873, 111. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Pandas Development Team. Pandas-dev/Pandas: Pandas. 2020. Available online: https://doi.org/10.5281/zenodo.3509134 (accessed on 23 June 2021).
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 56–61. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]


| Parameter | p-Value |
|---|---|
| T90 | 4.3 × 10−42 |
| HR32 | 1.7 × 10−19 |
| 1.9 × 10−3 | |
| Fluence (15–350 keV) | 2.9 × 10−22 |
| GRB | T1 Group | T100 Group | T90 (s) | HR32 |
|---|---|---|---|---|
| GRB041220 | 2 | 2 | 5.6 | 1.3 |
| GRB041223 | 2 | 2 | 109.1 | 1.8 |
| GRB041224 | 2 | 2 | 177.6 | 1.2 |
| ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| GRB200809B | ⋯ 1 | 2 | 4.2 | 1.8 |
| GRB200819A | 2 | 2 | 26.9 | 1.0 |
| GRB200829A | ⋯ 1 | 2 | 13.1 | 1.9 |
| Sample | Number of Bursts | |||
|---|---|---|---|---|
| T90 < 2 s | T90 > 2 s | |||
| T1 | T100 | T1 | T100 | |
| Swift/BAT sample | 107 | 107 | 1144 | 1147 |
| Group 1 | 73 | 91 | 32 | 14 |
| Group 2 | 34 | 16 | 1112 | 1133 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salmon, L.; Hanlon, L.; Martin-Carrillo, A. Two Classes of Gamma-ray Bursts Distinguished within the First Second of Their Prompt Emission. Galaxies 2022, 10, 78. https://doi.org/10.3390/galaxies10040078
Salmon L, Hanlon L, Martin-Carrillo A. Two Classes of Gamma-ray Bursts Distinguished within the First Second of Their Prompt Emission. Galaxies. 2022; 10(4):78. https://doi.org/10.3390/galaxies10040078
Chicago/Turabian StyleSalmon, Lána, Lorraine Hanlon, and Antonio Martin-Carrillo. 2022. "Two Classes of Gamma-ray Bursts Distinguished within the First Second of Their Prompt Emission" Galaxies 10, no. 4: 78. https://doi.org/10.3390/galaxies10040078
APA StyleSalmon, L., Hanlon, L., & Martin-Carrillo, A. (2022). Two Classes of Gamma-ray Bursts Distinguished within the First Second of Their Prompt Emission. Galaxies, 10(4), 78. https://doi.org/10.3390/galaxies10040078






