Abstract
Studies of Gamma-ray Burst (GRB) properties, such as duration and spectral hardness, have found evidence for additional classes beyond the short-hard (merger) and long-soft (collapsar) prototypes. Several clustering analyses of the duration-hardness plane identified a third, intermediate duration, class. In this work, Gaussian Mixture Model-based (GMM) clustering is applied to the Swift/BAT and Fermi/GBM samples of GRBs. The results obtained by the hierarchical combination of Gaussian components (or clusters) based on an entropy criterion are presented. This method counteracts possible overfitting arising from the application of Gaussian models to non-Gaussian underlying data. While the initial GMM clustering of the hardness-duration plane identifies three components (short/intermediate/long) for the Swift/BAT and Fermi/GBM samples, only two components (short/long) remain once the entropy criterion is applied. The analysis presented here suggests that the intermediate duration class may be the result of overfitting, rather than evidence of a distinct underlying population.
1. Introduction
The bimodal duration distribution of Gamma-ray Bursts (GRBs) suggests the separation of GRBs at T90 ≈ 2 s into short/hard and long/soft classes [1]. The association of long GRBs with star forming galaxies [2] and Type Ic supernovae (Galama et al. [3], Woosley and Bloom [4]; for a review, see Cano et al. [5]) provides an observational link between long GRBs and the deaths of massive stars, supporting the collapsar scenario [6]. There is substantial evidence to support compact object mergers (neutron star–neutron star or neutron star–black hole) as the progenitors of short GRBs [7,8]. The location offsets of short GRBs from their host galaxies [9,10], their proximity to elliptical galaxies [11], and the association of GRB 170817A, an unusual short GRB, with the neutron star merger event GW170817 detected by aLIGO [12,13,14], all support the merger hypothesis for the origin of short GRBs.
Other formation scenarios for short GRBs include the accretion-induced collapse of a white dwarf, double white dwarf mergers, or neutron star–white dwarf mergers [15,16,17], possibly leading to an unstable magnetar remnant. There are notable exceptions to the short-merger/long-collapsar paradigm, such as the short-collapsar event GRB 200826A [18,19,20], and GRB 060614, a long GRB without a supernova [21]. It has been suggested that many of the short duration GRBs of high redshift arise from collapsars [22]. Consideration of additional GRB characteristics, such as late X-ray flares in some short GRBs, and the non-detection of a supernova associated with some long GRBs [23], led to the suggestion of a new classification scheme [21], with Type I (massive star origin) and Type II (compact object merger origin) GRBs defined by many multiple observational criteria beyond the traditional duration and hardness [22,24]. Lü et al. [25] suggested a new parameter , based on the isotropic equivalent energy and peak energy, to classify bursts. Additionally, Donaghy et al. [26] considered 10 observational criteria for HETE-2 bursts, concluding that the best criteria to classify GRBs as ‘short population’ or ‘long population’ bursts are host galaxy properties, spectral lag, and the presence of a long-soft bump or gravitational waves.
In view of the diversity in GRB phenomenology, a definitive classification of GRBs based on duration alone is challenging. Several studies have found evidence for an additional ‘intermediate’ duration class of GRBs, first identified through Gaussian fits to the duration distribution of GRBs in the Third BATSE catalogue [27] and, subsequently, in fits to the GRB duration distributions of BeppoSAX [28], RHESSI [29], and Swift [30,31,32,33,34,35]. This class appears as an additional Gaussian ‘component’ required for the best-fit solution. However, the observed duration distribution can be recovered by modelling it as two skewed distributions [31,36,37], without requiring a third component.
GRB catalogues provide a set of standard parameters measured for each GRB, including duration (T90), hardness ratio (HR), fluence (S), peak flux (PF), peak energy (Epeak), and spectral fit parameters, including the low and high energy spectral indices of the Band function [38], which fits the keV-MeV GRB spectrum, typically denoted in the literature as α and β, respectively. In the case of Fermi/GBM, the catalogue contains over 300 parameters for each GRB [39,40]. The availability of such large GRB catalogues allows the application of bivariate and multidimensional analyses to the data.
Table 1 summarises the previous studies, along with the resulting number of components identified for different GRB datasets. Between two and five classes of GRBs are found, depending on the sample, parameters, and methods used. Clustering of the duration-hardness plane of the final BATSE GRB catalogue identified three [41,42,43] or five [44,45,46] classes of GRBs separated by their duration, fluence, and hardness. Unsupervised neural network analysis also revealed an intermediate class [47] or two classes [48,49]. However, only two classes were found in the BATSE sample using self-organising maps [50] and fits to the duration-hardness plane with skewed bivariate distributions [51,52].
The clustering of the duration and hardness of Swift/BAT GRBs [53,54] and the clustering of light curve shape indicators [55] identified three classes of bursts. Gaussian Mixture Model-based (GMM) clustering applied to the Fermi/GBM sample revealed that GRB 170817A fit within the intermediate class in the duration-hardness plane [56], and that five classes could be identified by clustering spectral fit parameters, fluences, and durations [57]. Principal Component Analysis (PCA) also identified three classes in Fermi/GBM [58] and BATSE [59] samples.

Table 1.
Methods and resulting components identified in clustering, fitting, and dimensionality reduction techniques applied to GRB populations. HR denotes Hardness Ratio, PF denotes Peak Flux, and S represents fluence. Studies which consider intrinsic properties such as redshift-corrected duration and hardness are marked with a *.
Table 1.
Methods and resulting components identified in clustering, fitting, and dimensionality reduction techniques applied to GRB populations. HR denotes Hardness Ratio, PF denotes Peak Flux, and S represents fluence. Studies which consider intrinsic properties such as redshift-corrected duration and hardness are marked with a *.
| Study | Method | Parameters | Components |
|---|---|---|---|
| BATSE | |||
| Horváth [27] | Fit (Gaussian) | T | 3 |
| Mukherjee et al. [41] | Clustering (Hierarchical) | T, HR, PF, S | 3 |
| Hakkila et al. [48] | Supervised pattern recognition | T, HR, PF, S, E, , | 2 |
| Balastegui et al. [47] | Clustering (Hierarchical), PCA, Neural Network | T, PF, S | 3 |
| Horváth [60] | Fit (log-normal) | T | 3 |
| Rajaniemi and Mähönen [50] | Self-Organising Maps | T, HR, S | 2 |
| Hakkila et al. [49] | Clustering (k-means), Neural Network | T, HR, S | 2 |
| Chattopadhyay et al. [42] | Clustering (k-means, Dirichlet mixture) | T, HR, PF, S | 3 |
| Zitouni et al. [32] | Fit (Gaussian) | T | 2 |
| Zhang et al. [61] | Fit (Gaussian) | T | 2 |
| Bhave et al. [54] | Clustering (Gaussian Mixture-Model) | T, HR | 2 |
| Chattopadhyay and Maitra [44] | Clustering (k-means, Gaussian Mixture-Model) | T, HR, PF, S | 5 |
| Swift | |||
| Kulkarni and Desai [35] | Fit (log-normal) | T | 2 |
| Chattopadhyay and Maitra [45] | Clustering (Ellipsoidal Gaussian, t-mixture) | T, PF, S | 5 |
| Tarnopolski [51] | Fit (Skewed bi-variate) | T, HR | 2 |
| Tarnopolski [52] | Fit (Skewed bi-variate) | T, HR | 2 |
| Tóth et al. [46] | Clustering (Gaussian Mixture-Model) | T, HR, PF, S | 5 |
| Modak [43] | Clustering (Fuzzy) | T, HR, PF, S | 3 |
| Horváth et al. [62] | Fit (log-normal) | T | 3 |
| Zhang and Choi [63] | Fit (log-normal) | T | 2 |
| Zhang and Choi [63] * | Fit (log-normal) | T | 2 |
| Huja et al. [30] | Fit (Gaussian) | T | 3 |
| Huja et al. [30] * | Fit (Gaussian) | T | 1 |
| Horváth et al. [64] | Fit (Gaussian) | T, HR | 3 |
| Veres et al. [53] | Clustering (Hierarchical, k-means) | T, HR | 3 |
| Koen and Bere [31] | Clustering (Gaussian) | T, HR | 3 |
| Tsutsui and Shigeyama [55] | Clustering (Gaussian) | Light curve shape indicators | 3 |
| Zitouni et al. [32] | Fit (Gaussian) | T | 3 |
| Zitouni et al. [32] * | Fit (Gaussian) | T | 3 |
| Horváth and Tóth [33] | Fit (log-normal) | T | 3 |
| Tarnopolski [34] | Fit (Skew-normal) | T | 3 |
| Tarnopolski [34] * | Fit (Skew-normal) | T | 1 |
| Yang et al. [65] * | Clustering (Gaussian Mixture-Model) | T, HR | 2 |
| Zhang et al. [61] | Fit (Gaussian) | T | 3 |
| Zhang et al. [61] * | Fit (Gaussian) | T | 2 |
| Bhave et al. [54] | Clustering (Gaussian Mixture-Model) | T, HR | 3 |
| Bhave et al. [54] * | Clustering (Gaussian Mixture-Model) | T, HR | 3 |
| Kulkarni and Desai [35] | Fit (log-normal) | T | 3 |
| Kulkarni and Desai [35] * | Fit (log-normal) | T | 2 |
| Fermi | |||
| Zhang et al. [61] | Fit (Gaussian) | T | 2 |
| Bhave et al. [54] | Clustering (Gaussian Mixture-Model) | T, HR | 2 |
| Kulkarni and Desai [35] | Fit (log-normal) | T | 2 |
| Acuner and Ryde [57] | Clustering (Gaussian Mixture-Model) | T, S, E, , | 5 |
| Horváth et al. [56] | Clustering (Gaussian Mixture-Model) | T, HR | 3 |
| Zitouni et al. [66] | Fit (Gaussian) | T | 2 |
| Zitouni et al. [66] * | Fit (Gaussian) | T | 2 |
| Horváth et al. [58] | Principal Component Analysis | T, PF, S, E, , | 3 |
| Tarnopolski [51] | Fit (skewed bivariate) | T, HR | 2 |
| BeppoSAX | |||
| Horváth [28] | Fit (log-normal) | T | 3 |
| Kulkarni and Desai [35] | Fit (log-normal) | T | 2 |
| RHESSI | |||
| Řípa et al. [29] | Fit (log-normal) | T | 2 |
| Řípa et al. [29] | Fit (log-normal) | T, HR | 3 |
| Řípa et al. [67] | Clustering (Gaussian Mixture-Model, k-means) | T, HR | 3 |
| INTEGRAL | |||
| Minaev et al. [68] | Fit (log-normal) | T | 2 |
| Konus-Wind | |||
| Svinkin et al. [69] | Fit (log-normal) | T | 2 |
| Svinkin et al. [69] | Clustering (Gaussian Mixture Model) | T, HR | 3 |
| Multiple samples | |||
| Minaev and Pozanenko [70] * | Fit (Skew-normal) | T, E, E | 2 |
Observational bias has been suggested as a possible origin of the putative intermediate class. Bias caused by short temporal trigger windows favours short low-fluence bursts (fluence-duration bias; Hakkila et al. [49]), while the low signal-to-noise ratios of long faint bursts can cause them to be mistaken for short bursts (‘tip-of-the-iceberg’ effect; Lü et al. [71]). However, neither of these effects have been able to reproduce the third class in simulations. It has been shown that the third class can arise as a consequence of fitting symmetrical models to the GRB duration distribution, which may be skewed rather than symmetrical [31,36,37,51], possibly as a result of the GRB pulse shapes [72].
The significant number of GRBs with measured redshift in the Swift and Fermi samples has allowed studies of intrinsic properties, which have pointed to the existence of two classes in the Fermi/GBM sample [32]. For the Swift/BAT sample of bursts, one [30,34], two [35,61,63,65], or three [32,54] classes have been identified. However, cosmological time dilation applied to GRB durations has not been found to transform a rest-frame two-component Gaussian duration distribution to the observed skewed one [73]. While there are now more than 400 Swift GRBs with measured redshift, there are only 25 short duration bursts with T2 s. The rest-frame studies outlined in Table 1 note that the short duration sample is not statistically significant, and a larger sample is required [54,65].
This paper reports on an updated two-dimensional clustering analysis in the duration-hardness plane of the large Fermi/GBM and Swift/BAT GRB samples. Advancing previous studies, the analysis presented here makes use of an entropy criterion to identify ‘excess’ components that may be identified in the standard GMM clustering of data but which arise from the application of Gaussian models to non-Gaussian underlying data [74]. This method has been applied in other astrophysical contexts, for example in the clustering of stars [75]. As the number of short GRBs with redshift has not grown significantly since previous studies, this paper focuses on GMM clustering using observed, rather than intrinsic, properties.
2. Datasets and Data Preparation
2.1. Swift/BAT
The Third Swift/BAT Catalogue [76] contains 1388 bursts detected between 17 December 2004 and 28 August 2020 and provides the durations, spectral fit parameters, fluxes, and fluences calculated in the simple Power-Law (PL) and Cut-off Power-Law (CPL) models. The hardness ratio HR for each GRB was calculated as the ratio of the fluence in energy range 3 (50–100 keV) to energy range 2 (25–50 keV), given by
where is the photon flux at energy E. For the PL model, this is given by
where is the PL index, and is the normalisation factor at 50 keV, with units of photons . The CPL model is described as
where is the CPL index, is the normalisation factor at 50 keV, with units of photons , and is the peak energy in keV of the or spectrum. This is the flux density integrated over the energy range, also known as the spectral flux density.
The sample of 1388 bursts was filtered to remove 52 GRBs for which no duration or best-fit model was documented. A further 20 GRBs with duration or hardness errors in excess of 50% of their magnitude were removed, resulting in a final sample of 1316 GRBs for clustering.
2.2. Fermi/GBM
The Fermi/GBM catalogue was accessed using the Fermi/GBM Data Tools [40] and limited to the period between 10 August 2008 and 17 March 2021, which yielded a sample of 3001 bursts. The hardness ratio was calculated by comparing the counts detected in the 8–50 keV band to the 50–300 keV band. Counts within the T interval were summed from the 64 ms light curves, generated using Time-Tagged Event (TTE) data in the Fermi/GBM Data Tools. Only triggered detectors were used, and the background subtraction was performed using the background intervals defined in the Fermi/GBM catalogue. Bursts with no documented duration or incorrect background subtraction were removed, resulting in a sample of 2669 bursts. Prior to clustering, 36 outliers were identified by the R package HDOutliers [77] and removed from the sample, leaving a final sample of 2633 bursts for clustering.
3. Clustering Methods
3.1. GMM Clustering
GMM clustering was carried out in R using the mclust [78]. GMM clustering assumes that the observed data are generated from a mixture of K components, where the density of each component is described by a multivariate Gaussian distribution. mclust fit 14 different models to the data, parameterised by the shape (spherical or ellipsoidal) and volume. In the case of ellipsoidal models, the alignment of the axes and the difference in shape of the fitted ellipsoidals was specified. This is known as Volume-Shape-Orientation (VSO) decomposition. For a given model, the volume, shape, and orientation can be constrained to equal variance, denoted by ‘E’. If the variance is free to change, the model is denoted ‘V’. Additionally, the orientation of the clusters relative to each other can be constrained to Equal or Varying, or a model can have alignment limited to the coordinate axis, and is labelled ‘I’. For example, ‘EVI’ denotes equal volume components, with variable shapes (i.e., not spherical) and orientation aligned with the axes.
mclust makes use of the Bayesian Information Criterion (BIC; Schwarz et al. [79]) to compare mixture models fitted on the data. The best-fit model and number of components are chosen based on the largest BIC value. A difference in BIC value between models of 6–10 is considered significant, while a difference of greater than 2 provides positive evidence for a better fit [80]. This standard GMM fit method is the same as that employed in some previous studies, for example Horváth et al. [56] and Bhave et al. [54].
3.2. Combination of Gaussian Components
In the case where Gaussian components were overlapping or components were suspected to be non-Gaussian, as has been shown for the BATSE and Fermi/GBM GRB duration distributions [51,52], the mclust function clustCombi was used to hierarchically combine components using an entropy criterion [74]. Entropy is a measure of the uncertainty of the observations belonging to a certain cluster or component. Thus, a large decrease in entropy signifies a better fit with smaller uncertainty. For mclust, the final number of components was chosen based on the observed ‘elbow’ in the entropy plot. The number of components at which the elbow occurred pointed to a large decrease in entropy and, therefore, a model with smaller uncertainty.
There are several methods for joining Gaussian Mixture components. In comparison to the entropy criterion, these methods have limitations, for example, requiring spherical components [81] or one-dimensional data [82]. Other suggested methods assume the number of clusters [83] or make use of hard clustering methods, which assigns points to one cluster rather than applying a probabilistic method (e.g., Tantrum et al. [84]). The method employed in this study was a soft-clustering probabilistic method, which is computationally efficient and applicable to multiple dimensions. Hence, it was the chosen method to achieve a robust clustering result for the complex GRB datasets.
4. Results
The results of the initial mclust fit and subsequent clustCombi method applied to the Swift/BAT and Fermi/GBM samples are summarised in Table 2.

Table 2.
Number of components (K), Bayesian Information Criterion (BIC) values, models, and number of bursts (#) identified in the mclust and subsequent clustCombi fits to the Swift/BAT and Fermi/GBM samples.
4.1. Swift/BAT
The BIC values for the top three models versus the number of components, resulting from the application of mclust to the full Swift/BAT sample, are shown in Figure 1a. The ‘VEI’ model with three components had the largest BIC value. The three components were labelled ‘long’, ‘intermediate’, and ‘short’ according to their durations and are projected onto the hardness-duration plane in Figure 1b. The clear round edge between the intermediate and long components suggests that a Gaussian was being fit to a non-Gaussian component.
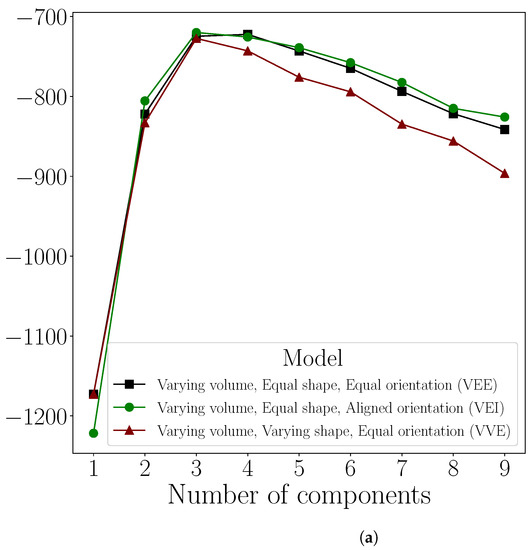
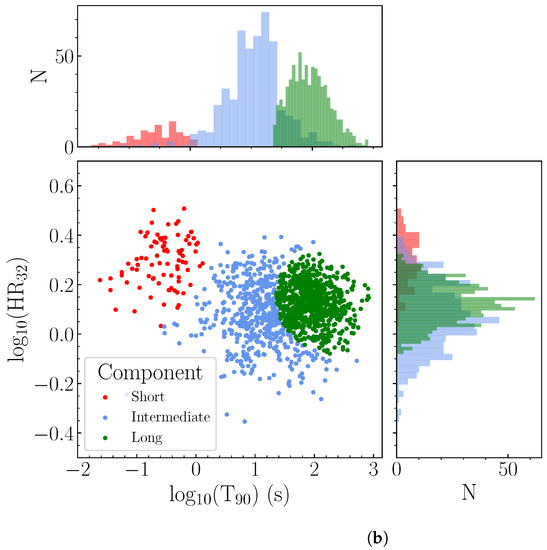
Figure 1.
(a) BIC values of the top three mclust models fit to the Swift/BAT sample and (b) the resulting duration-hardness plane for the best-fit three-component model (VEI).
After clustCombi was applied, the ‘intermediate’ and ‘long’ components were combined, producing a large decrease in entropy as shown in Figure 2. The two remaining components or classes were labelled ‘long’ and ‘short’, as shown in Figure 3. Table 2 presents the sample size of the classes.
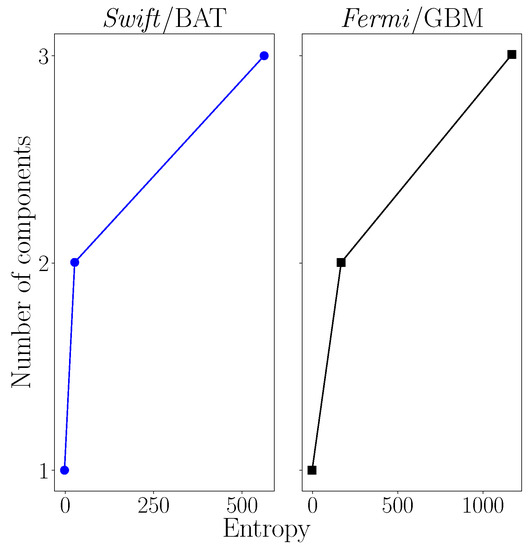
Figure 2.
Entropy plots returned by clustCombi depicting the entropy of the initial mclust fits (three components) and the entropy after combination of the initial mclust components for Swift/BAT (left) and Fermi/GBM (right). An inflection, or elbow, in the entropy plot signifies a model with the optimal number of components.
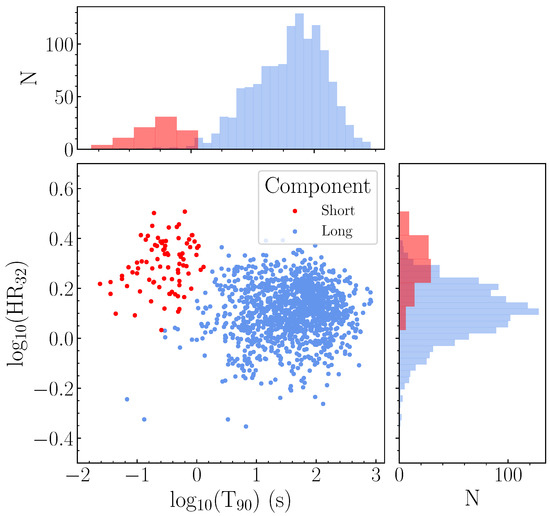
Figure 3.
The results of clustCombi applied to the components identified by mclust in the duration-hardness plane for Swift/BAT.
The distributions of the duration (T) and hardness ratio (HR) are depicted in the violin plot in Figure 4. The mean, standard deviation, and median values of these parameters for the long and the short classes are presented in Table 3.
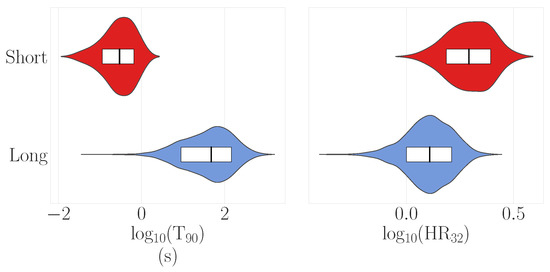
Figure 4.
Violin plots showing the distribution of the duration (T) and hardness ratio (HR) for the Swift/BAT ‘short’ (red) and ‘long’ (blue) classes identified by clustCombi. The median of each parameter is marked as a black line within the box, which represents the 1 interval (i.e., the 16th to 84th percentile).

Table 3.
Mean (), standard deviation (), and median of the properties of the Swift/BAT ‘long’ and ‘short’ classes identified by clustCombi.
4.2. Fermi/GBM
For Fermi/GBM, the initial mclust fit indicated that a three-component fit to the data was preferred. The BIC values of the top three models are shown in Figure 5a. The three best-fit components are depicted in Figure 5b. The three-component ‘VEI’ model exhibited a BIC value difference of ∼6 compared to the next best model; thus, it was considered a significant result. The classification components were labelled ‘short’, ‘intermediate’, and ‘long’, according to their duration. The boundary between the ‘intermediate’ and ‘long’ components exhibited a similar round-edge feature as identified in the results for Swift/BAT.
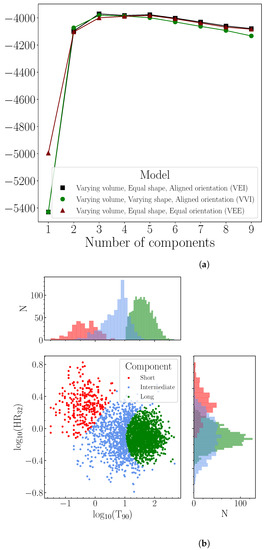
Figure 5.
(a) BIC values of the top three mclust models fit to the Fermi/GBM sample and (b) the resulting duration-hardness plane for the best-fit three-component model (VEI).
The results obtained from applying clustCombi to this sample are shown in Figure 6, indicating that a model consisting of two components or classes, rather than three, provided a better fit to the data, based on a decrease in entropy depicted in the entropy plot in Figure 2. The number of bursts in the ‘long’ and ‘short’ classes identified by clustCombi is presented in Table 2.
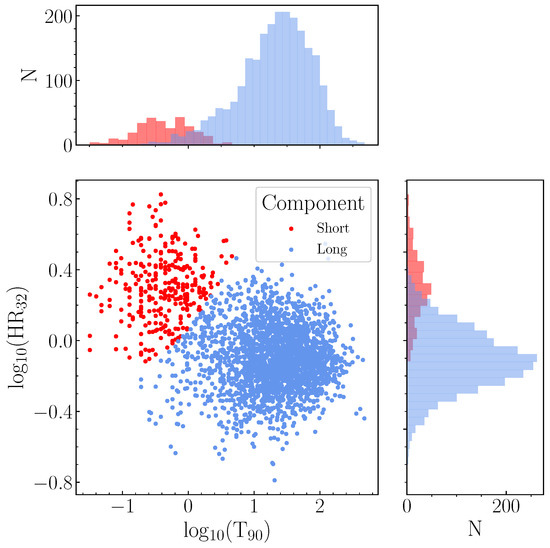
Figure 6.
The results of clustCombi applied to the components identified by mclust in the duration-hardness plane for Fermi/GBM.
The violin plot in Figure 7 for the Fermi/GBM sample demonstrates the distributions of the duration and hardness ratio, while the summary statistics of these populations are presented in Table 4.
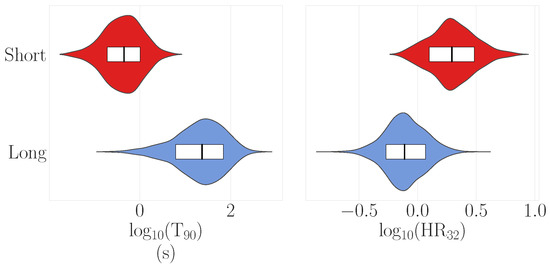
Figure 7.
Violin plots showing the distribution of the duration (T) and hardness ratio (HR) for the Fermi/GBM ‘short’ (red) and ‘long’ (blue) classes identified by clustCombi. The median of each parameter is marked as a black line within the box, which represents the 1 interval (i.e., the 16th to 84th percentile).

Table 4.
Mean (), standard deviation (), and median of the properties of the Fermi/GBM ‘long’ and ‘short’ classes identified by clustCombi.
5. Discussion
5.1. Swift/BAT
For Swift/BAT, the three components identified in Figure 1b had a similar size and structure to those identified in the GMM clustering by Bhave et al. [54]. In this analysis, the hardness ratio was computed using the best-fit model for Swift, consistent with the method undertaken by Bhave et al. [54], enabling comparison of results. The clear-cut round boundary between the intermediate and long components in Figure 1b was also found by Bhave et al. [54] and is a signature of the application of a Gaussian model to a non-Gaussian underlying distribution.
The result of applying clustCombi after the GMM clustering indicated that the intermediate duration component, combined with the long duration component, provided a better fit to the sample of Swift/BAT bursts (Figure 3). Thus, the intermediate class was likely identified by the overfitting resulting from GMM clustering applied to the complex distribution of Swift/BAT bursts in duration-hardness space.
Figure 4 and Table 3 show that the mean duration of the short class identified by clustCombi was T 0.3 s (1 standard deviation of 0.29 s), while the long class had a mean T 70 s (1 standard deviation of 101 s). This is consistent with the peaks of the Swift short (T 2 s) and long (T 2 s) duration distributions [85]. The shorter duration class had a larger hardness ratio than the longer duration class, as expected from the traditional short/long paradigm. The separation between the short and long classes occurred at T 0.5–2 s. This is in agreement with the findings of Bromberg et al. [86], whose modelling of the duration distribution of Swift/BAT bursts using the Collapsar model suggested a separation at T 0.8 s.
5.2. Fermi/GBM
Prior to the removal of the 36 outlier bursts, mclust initially suggested a fit with four components in the Fermi/GBM sample. The fit included one group of bursts with very high or very low hardness ratios situated in a halo around the three groups in Figure 5b. These outlier bursts were effectively removed using HDOutliers (Section 2), following previous studies including Tóth et al. [46], Horváth et al. [56,58] and were likely the result of unsuitable background subtraction. Upon removal of the outliers, mclust identified three components, which were similar to the components obtained for Swift/BAT (Figure 5b). The intermediate duration component contained more bursts than the class identified by Horváth et al. [56], whose intermediate class only contained bursts with low spectral hardness. This difference can be attributed to their smaller sample size of 1298 bursts.
A signature of a Gaussian component is visible at the sharp boundary between the intermediate and long duration components in Figure 5b, indicating an arbitrary Gaussian component was identified. Consistent with the results obtained for Swift/BAT, the intermediate component was disregarded when clustCombi was applied, indicating that it was likely an overfitting component identified by the GMM clustering procedure. Thus, a short and long duration class remained.
In this analysis, the hardness ratio was computed using the background-subtracted counts to be consistent with previous Fermi/GBM studies and to enable direct comparison with those results. The short and long duration classes in Figure 6 were comparable to the classes found in previous GMM clustering analyses by Bhave et al. [54], Bhat et al. [87], and in skewed bi-variate fits carried out by Tarnopolski [51]. Table 4 and Figure 7 show that the short duration class was spectrally harder than the long duration class, as expected. The mean duration of the classes were 0.64 s (1 standard deviation of 0.65 s) and 38.6 s (1 standard deviation of 23.4 s) for the short and long classes, respectively. This result is consistent with the mean durations of the short (0.82 s) and long (28.3 s) classes identified in the GMM clustering of the third Fermi/GBM catalogue [87].
5.3. Comparison to GRB Subclasses
Groups 1 and 2 of the Swift/BAT and Fermi/GBM samples resemble the traditional short/hard and long/soft prototypes. The groups can be compared to several subclasses of GRBs, including those with associated supernovae, extended emission episodes, and plateaus. The longer duration Group 2 contained all 49 bursts with an X-ray plateau from the platinum sample identified by Dainotti et al. [88]. Similarly, all bursts in the sample with an optical plateau [89] and those with an associated supernova and a plateau [90] lay in Group 2. The Swift sample analysed also contained four ultra-long GRBs from the Gold sample and five possible ultra-long GRBs from the Silver sample of Gendre et al. [91]. All of these bursts resided in Group 2 as expected, given their duration.
Short GRBs with extended emission episodes have challenged the typical duration-based classification scheme of GRBs. The population of Swift GRBs with extended emission identified by Gibson et al. [92] contains bursts chosen from the sample in Kaneko et al. [93] and Gompertz et al. [94,95]. The Gibson et al. [92] sample was found to only contain bursts from Group 2 of our Swift/BAT results. This is understandable, given that the rebrightening exhibited in their light curves can lead to an increase in the measured T [70], thus placing them in Group 2. The extended emission episodes are typically softer than the initial spike, dominating the overall detected fluence, thus resulting in a longer duration GRB.
Group 2 resembled the standard long-duration group for both the Swift and Fermi samples. Thus, bursts with associated supernovae were expected to belong to this group. The sample of supernova-associated GRBs from Cano et al. [5] was updated to include more recent events GRB 161219B/SN 2016jca [96], GRB 171205A/SN 2017htp [97], GRB 180728A/SN 2018fip [98,99], GRB 190114C/SN 2019jrj and GRB 190829A/AT2019oyw [100], and GRB 200826A [18,19,20]. There were 25 Swift and 15 Fermi GRB-SN cases within the sample analysed, all of which resided in Group 2 as expected. The only confirmed GRB with a kilonova, GRB 170817, was also in Group 1 of the Fermi sample.
5.4. Selection Effects
Svinkin et al. [69] suggested that T, the time during which 50% of the counts above background are recorded, is a more robust duration measure than T, since it may be less affected by detector energy ranges. To eliminate possible selection effects and to verify the two-component solutions, the clustering analysis was repeated using T as the duration parameter. For Swift/BAT, the initial mclust fit returned a three-component solution similar to Figure 1b—the short duration group remained the same, while the two long duration groups also exhibited the clear-cut spherical feature identified in the T analysis. When clustCombi was applied, a two group-solution was the best fit. Group 1 and Group 2 were identical to the groups found in the T analysis. Thus, for Swift/BAT, this method did not favour T over T as a duration measure, and the results further supported the two-group solution.
For Fermi/GBM, the initial mclust fit identified an extra long duration group in a four-component solution. The long duration group in Figure 5b was split in two, with the remaining structure matching the results of the T analysis. clustCombi resulted in a two-component fit closely resembling the structure and makeup of Group 1 and Group 2 of the T fit. However, Group 1 contained ≈ 100 more GRBs than the T fit. For Fermi/GBM, the two-component fit was supported, and while the T parameter returned slightly different proportions in each group, it did not demonstrate any clear advantage over T as a duration parameter.
6. Conclusions
GMM clustering with mclust identified three Gaussian components of Swift/BAT and Fermi/GBM bursts in the duration-hardness plane. The third component resembled the intermediate duration group identified in previous studies. However, combining components, based on an entropy criterion, identified a short and long duration class only for both samples.
This study highlights the drawbacks of fitting GRB populations with model-based methods. Similar model-based fitting methods, including the log-normal fit procedures applied to GRB duration distributions, have exhibited components thought to be identified incorrectly due to the inherently skewed distribution of long GRB durations [31,36]. Table 1 highlights the diversity of results from model-based studies.
The lack of consensus regarding a definitive number of GRB classes, both in the analysis presented here and in previous studies of GRB catalogues, is a motivator for a model-independent analysis of GRB light curves. The light curves may also contain more information than the summary data provided by the GRB catalogues. Fourier analysis of the Swift/BAT GRB light curves by Jespersen et al. [101] identified two classes of bursts. Following on from the analysis presented in this paper is a wavelet-based feature extraction analysis of GRB light curves from Swift/BAT, BATSE and Fermi/GBM (Salmon et al. [102], in preparation).
Author Contributions
Conceptualization, L.S., L.H. and A.M.-C.; methodology, L.S., L.H. and A.M.-C.; software, L.S.; validation, L.S., L.H. and A.M.-C.; formal analysis, L.S.; investigation, L.S.; resources, L.S., L.H. and A.M.-C.; data curation, L.S.; writing—original draft preparation, L.S.; writing—review and editing, L.H. and A.M.-C.; visualization, L.S.; supervision, L.H. and A.M.-C.; project administration, L.H. and A.M.-C.; funding acquisition, L.H. and A.M.-C. All authors have read and agreed to the published version of the manuscript.
Funding
L.S. acknowledges the Irish Research Council Postgraduate Scholarship No GOIPG/2017/1525. L.H. acknowledges support from Science Foundation Ireland (Grant number 19/FFP/6777) and the EU H2020 (Grant agreement 871158).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This paper makes use of the Swift/BAT catalogue [76], which can be accessed through the online Swift/BAT Gamma-ray Burst Catalogue 1. The Fermi/GBM catalogue is accessed through the Fermi/GBM data tools [40].
Acknowledgments
This research made use of the following Python packages: NumPy [103], Matplotlib [104] and pandas [105,106]. The authors are grateful to Brendan Murphy and Michael Fop for their assistance with mclust.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Note
| 1 | https://swift.gsfc.nasa.gov/results/batgrbcat/, (accessed on 16 June 2022). |
References
- Kouveliotou, C.; Meegan, C.A.; Fishman, G.J.; Bhat, N.P.; Briggs, M.S.; Koshut, T.M.; Paciesas, W.S.; Pendleton, G.N. Identification of Two Classes of Gamma-ray Bursts. Astrophys. J. 1993, 413, L101. [Google Scholar] [CrossRef]
- Perley, D.A.; Niino, Y.; Tanvir, N.R.; Vergani, S.D.; Fynbo, J.P.U. Long-Duration Gamma-ray Burst Host Galaxies in Emission and Absorption. Space Sci. Rev. 2016, 202, 111–142. [Google Scholar] [CrossRef]
- Galama, T.J.; Vreeswijk, P.M.; van Paradijs, J.; Kouveliotou, C.; Augusteijn, T.; Böhnhardt, H.; Brewer, J.P.; Doublier, V.; Gonzalez, J.F.; Leibundgut, B.; et al. An unusual supernova in the error box of the γ-ray burst of 25 April 1998. Nature 1998, 395, 670–672. [Google Scholar] [CrossRef]
- Woosley, S.E.; Bloom, J.S. The Supernova Gamma-ray Burst Connection. Annu. Rev. Astron. Astrophys. 2006, 44, 507–556. [Google Scholar] [CrossRef]
- Cano, Z.; Wang, S.Q.; Dai, Z.G.; Wu, X.F. The Observer’s Guide to the Gamma-ray Burst Supernova Connection. Adv. Astron. 2017, 2017, 8929054. [Google Scholar] [CrossRef]
- MacFadyen, A.I.; Woosley, S.E. Collapsars: Gamma-ray Bursts and Explosions in “Failed Supernovae”. Astrophys. J. 1999, 524, 262–289. [Google Scholar] [CrossRef]
- Eichler, D.; Livio, M.; Piran, T.; Schramm, D.N. Nucleosynthesis, neutrino bursts and γ-rays from coalescing neutron stars. Nature 1989, 340, 126–128. [Google Scholar] [CrossRef]
- Narayan, R.; Paczynski, B.; Piran, T. Gamma-ray Bursts as the Death Throes of Massive Binary Stars. Astrophys. J. 1992, 395, L83. [Google Scholar] [CrossRef]
- Berger, E. A Short Gamma-ray Burst “No-host” Problem? Investigating Large Progenitor Offsets for Short GRBs with Optical Afterglows. Astrophys. J. 2010, 722, 1946–1961. [Google Scholar] [CrossRef]
- Tunnicliffe, R.L.; Levan, A.J.; Tanvir, N.R.; Rowlinson, A.; Perley, D.A.; Bloom, J.S.; Cenko, S.B.; O’Brien, P.T.; Cobb, B.E.; Wiersema, K.; et al. On the nature of the ‘hostless’ short GRBs. Mon. Not. R. Astron. Soc. 2014, 437, 1495–1510. [Google Scholar] [CrossRef]
- Berger, E. Short-Duration Gamma-ray Bursts. Annu. Rev. Astron. Astrophys. 2014, 52, 43–105. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. 2017, 848, L12. [Google Scholar] [CrossRef]
- Goldstein, A.; Veres, P.; Burns, E.; Briggs, M.S.; Hamburg, R.; Kocevski, D.; Wilson-Hodge, C.A.; Preece, R.D.; Poolakkil, S.; Roberts, O.J.; et al. An Ordinary Short Gamma-ray Burst with Extraordinary Implications: Fermi-GBM Detection of GRB 170817A. Astrophys. J. 2017, 848, L14. [Google Scholar] [CrossRef]
- Savchenko, V.; Ferrigno, C.; Kuulkers, E.; Bazzano, A.; Bozzo, E.; Brandt, S.; Chenevez, J.; Courvoisier, T.L.; Diehl, R.; Domingo, A.; et al. INTEGRAL detection of the first prompt gamma-ray signal coincident with the gravitational-wave event GW170817. Astrophys. J. 2017, 848, L15. [Google Scholar] [CrossRef]
- Qin, B.; Wu, X.P.; Chu, M.C.; Fang, L.Z.; Hu, J.Y. The Collapse of Neutron Stars in High-Mass Binaries as the Energy Source for the Gamma-ray Bursts. Astrophys. J. 1998, 494, L57–L59. [Google Scholar] [CrossRef]
- Levan, A.J.; Wynn, G.A.; Chapman, R.; Davies, M.B.; King, A.R.; Priddey, R.S.; Tanvir, N.R. Short gamma-ray bursts in old populations: Magnetars from white dwarf-white dwarf mergers. Mon. Not. R. Astron. Soc. Lett. 2006, 368, L1–L5. [Google Scholar] [CrossRef]
- Metzger, B.D.; Quataert, E.; Thompson, T.A. Short-duration gamma-ray bursts with extended emission from protomagnetar spin-down. Mon. Not. R. Astron. Soc. Lett. 2008, 385, 1455–1460. [Google Scholar] [CrossRef]
- Ahumada, T.; Singer, L.P.; Anand, S.; Coughlin, M.W.; Kasliwal, M.M.; Ryan, G.; Andreoni, I.; Cenko, S.B.; Fremling, C.; Kumar, H.; et al. Discovery and confirmation of the shortest gamma ray burst from a collapsar. arXiv 2021, arXiv:2105.05067. [Google Scholar] [CrossRef]
- Rossi, A.; Rothberg, B.; Palazzi, E.; Kann, D.A.; D’Avanzo, P.; Klose, S.; Perego, A.; Pian, E.; Savaglio, S.; Stratta, G.; et al. The peculiar short-duration GRB 200826A and its supernova. arXiv 2021, arXiv:2105.03829. [Google Scholar] [CrossRef]
- Zhang, B.B.; Liu, Z.K.; Peng, Z.K.; Li, Y.; Lü, H.J.; Yang, J.; Yang, Y.S.; Yang, Y.H.; Meng, Y.Z.; Zou, J.H.; et al. A Peculiarly Short-duration Gamma-ray Burst from Massive Star Core Collapse. arXiv 2021, arXiv:2105.05021. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, B.B.; Liang, E.W.; Gehrels, N.; Burrows, D.N.; Mészáros, P. Making a Short Gamma-ray Burst from a Long One: Implications for the Nature of GRB 060614. Astrophys. J. 2007, 655, L25–L28. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, B.B.; Virgili, F.J.; Liang, E.W.; Kann, D.A.; Wu, X.F.; Proga, D.; Lv, H.J.; Toma, K.; Mészáros, P.; et al. Discerning the Physical Origins of Cosmological Gamma-ray Bursts Based on Multiple Observational Criteria: The Cases of z = 6.7 GRB 080913, z = 8.2 GRB 090423, and Some Short/Hard GRBs. Astrophys. J. 2009, 703, 1696–1724. [Google Scholar] [CrossRef]
- Hjorth, J.; Bloom, J.S. The Gamma-ray Burst—Supernova Connection. In Gamma-Ray Bursts; Cambridge University Press: Cambridge, MA, USA, 2012; Chapter 9; pp. 169–190. [Google Scholar]
- Li, Y.; Zhang, B.; Yuan, Q. A Comparative Study of Long and Short GRBs. II. A Multiwavelength Method to Distinguish Type II (Massive Star) and Type I (Compact Star) GRBs. Astrophys. J. 2020, 897, 154. [Google Scholar] [CrossRef]
- Lü, H.J.; Liang, E.W.; Zhang, B.B.; Zhang, B. A New Classification Method for Gamma-ray Bursts. Astrophys. J. 2010, 725, 1965–1970. [Google Scholar] [CrossRef]
- Donaghy, T.Q.; Lamb, D.Q.; Sakamoto, T.; Norris, J.P.; Nakagawa, Y.; Villasenor, J.; Atteia, J.L.; Vanderspek, R.; Graziani, C.; Kawai, N.; et al. HETE-2 Localizations and Observations of Four Short Gamma-ray Bursts: GRBs 010326B, 040802, 051211 and 060121. arXiv 2006, arXiv:astro-ph/0605570. [Google Scholar]
- Horváth, I. A Third Class of Gamma-ray Bursts? Astrophys. J. 1998, 508, 757–759. [Google Scholar] [CrossRef]
- Horváth, I. Classification of BeppoSAX’s gamma-ray bursts. Astrophys. Space Sci. 2009, 323, 83–86. [Google Scholar] [CrossRef]
- Řípa, J.; Wigger, C.; Huja, D.; Hudec, R. Gamma-ray Burst Classes Found in the Rhessi Data Sample. Baltic Astron. 2009, 18, 305–310. [Google Scholar]
- Huja, D.; Mészáros, A.; Řípa, J. A comparison of the gamma-ray bursts detected by BATSE and Swift. Astron. Astrophys. 2009, 504, 67–71. [Google Scholar] [CrossRef]
- Koen, C.; Bere, A. On multiple classes of gamma-ray bursts, as deduced from autocorrelation functions or bivariate duration/hardness ratio distributions. Mon. Not. R. Astron. Soc. Lett. 2012, 420, 405–415. [Google Scholar] [CrossRef]
- Zitouni, H.; Guessoum, N.; Azzam, W.J.; Mochkovitch, R. Statistical study of observed and intrinsic durations among BATSE and Swift/BAT GRBs. Astrophys. Space Sci. 2015, 357, 7. [Google Scholar] [CrossRef]
- Horváth, I.; Tóth, B.G. The duration distribution of Swift Gamma-ray Bursts. Astrophys. Space Sci. 2016, 361, 155. [Google Scholar] [CrossRef]
- Tarnopolski, M. Analysis of the observed and intrinsic durations of gamma-ray bursts with known redshift. Astrophys. Space Sci. 2016, 361, 125. [Google Scholar] [CrossRef]
- Kulkarni, S.; Desai, S. Classification of gamma-ray burst durations using robust model-comparison techniques. Astrophys. Space Sci. 2017, 362, 70. [Google Scholar] [CrossRef]
- Tarnopolski, M. Distinguishing short and long Fermi gamma-ray bursts. Mon. Not. R. Astron. Soc. Lett. 2015, 454, 1132–1139. [Google Scholar] [CrossRef]
- Tarnopolski, M. Analysis of gamma-ray burst duration distribution using mixtures of skewed distributions. Mon. Not. R. Astron. Soc. 2016, 458, 2024–2031. [Google Scholar] [CrossRef]
- Band, D.L. Gamma-ray Burst Spectral Evolution through Cross-Correlations of Discriminator Light Curves. Astrophys. J. 1997, 486, 928–937. [Google Scholar] [CrossRef]
- Von Kienlin, A.; Meegan, C.A.; Paciesas, W.S.; Bhat, P.N.; Bissaldi, E.; Briggs, M.S.; Burns, E.; Cleveland, W.H.; Gibby, M.H.; Giles, M.M.; et al. The Fourth Fermi-GBM Gamma-ray Burst Catalog: A Decade of Data. Astrophys. J. 2020, 893, 46. [Google Scholar] [CrossRef]
- Goldstein, A.; Cleveland, W.H.; Kocevski, D. Fermi GBM Data Tools: v1.1.1. 2020. Available online: https://fermi.gsfc.nasa.gov/ssc/data/analysis/gbm (accessed on 17 June 2022).
- Mukherjee, S.; Feigelson, E.D.; Jogesh Babu, G.; Murtagh, F.; Fraley, C.; Raftery, A. Three Types of Gamma-ray Bursts. Astrophys. J. 1998, 508, 314–327. [Google Scholar] [CrossRef]
- Chattopadhyay, T.; Misra, R.; Chattopadhyay, A.K.; Naskar, M. Statistical Evidence for Three Classes of Gamma-ray Bursts. Astrophys. J. 2007, 667, 1017–1023. [Google Scholar] [CrossRef]
- Modak, S. Distinction of groups of gamma-ray bursts in the BATSE catalog through fuzzy clustering. Astron. Comput. 2021, 34, 100441. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Maitra, R. Gaussian-mixture-model-based cluster analysis finds five kinds of gamma-ray bursts in the BATSE catalogue. Mon. Not. R. Astron. Soc. Lett. 2017, 469, 3374–3389. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Maitra, R. Multivariate t-mixture-model-based cluster analysis of BATSE catalogue establishes importance of all observed parameters, confirms five distinct ellipsoidal sub-populations of gamma-ray bursts. Mon. Not. R. Astron. Soc. Lett. 2018, 481, 3196–3209. [Google Scholar] [CrossRef]
- Tóth, B.G.; Rácz, I.I.; Horváth, I. Gaussian-mixture-model-based cluster analysis of gamma-ray bursts in the BATSE catalog. Mon. Not. R. Astron. Soc. Lett. 2019, 486, 4823–4828. [Google Scholar] [CrossRef]
- Balastegui, A.; Ruiz-Lapuente, P.; Canal, R. Reclassification of gamma-ray bursts. Mon. Not. R. Astron. Soc. Lett. 2001, 328, 283–290. [Google Scholar] [CrossRef]
- Hakkila, J.; Haglin, D.J.; Pendleton, G.N.; Mallozzi, R.S.; Meegan, C.A.; Roiger, R.J. Gamma-ray Burst Class Properties. Astrophys. J. 2000, 538, 165–180. [Google Scholar] [CrossRef]
- Hakkila, J.; Giblin, T.W.; Roiger, R.J.; Haglin, D.J.; Paciesas, W.S.; Meegan, C.A. How Sample Completeness Affects Gamma-ray Burst Classification. Astrophys. J. 2003, 582, 320–329. [Google Scholar] [CrossRef]
- Rajaniemi, H.; Mähönen, P. Classifying gamma-ray bursts using self-organizing maps. Astrophys. J. 2002, 566, 202. [Google Scholar] [CrossRef]
- Tarnopolski, M. Analysis of the Duration-Hardness Ratio Plane of Gamma-ray Bursts Using Skewed Distributions. Astrophys. J. 2019, 870, 105. [Google Scholar] [CrossRef]
- Tarnopolski, M. Multivariate Analysis of BATSE Gamma-ray Burst Properties Using Skewed Distributions. Astrophys. J. 2019, 887, 97. [Google Scholar] [CrossRef]
- Veres, P.; Bagoly, Z.; Horváth, I.; Mészáros, A.; Balázs, L.G. A Distinct Peak-flux Distribution of the Third Class of Gamma-ray Bursts: A Possible Signature of X-ray Flashes? Astrophys. J. 2010, 725, 1955–1964. [Google Scholar] [CrossRef]
- Bhave, A.; Kulkarni, S.; Desai, S.; Srijith, P.K. Two Dimensional Clustering of Gamma-ray Bursts using durations and hardness. arXiv 2017, arXiv:1708.05668. [Google Scholar] [CrossRef]
- Tsutsui, R.; Shigeyama, T. On the subclasses in Swift long gamma-ray bursts: A clue to different central engines. Publ. Astron. Soc. Jpn. 2014, 66, 42. [Google Scholar] [CrossRef]
- Horváth, I.; Tóth, B.G.; Hakkila, J.; Tóth, L.V.; Balázs, L.G.; Rácz, I.I.; Pintér, S.; Bagoly, Z. Classifying GRB 170817A/GW170817 in a Fermi duration-hardness plane. Astrophys. Space Sci. 2018, 363, 53. [Google Scholar] [CrossRef]
- Acuner, Z.; Ryde, F. Clustering of gamma-ray burst types in the Fermi GBM catalogue: Indications of photosphere and synchrotron emissions during the prompt phase. Mon. Not. R. Astron. Soc. Lett. 2018, 475, 1708–1724. [Google Scholar] [CrossRef]
- Horváth, I.; Hakkila, J.; Bagoly, Z.; Tóth, L.V.; Rácz, I.I.; Pintér, S.; Tóth, B.G. Multidimensional analysis of Fermi GBM gamma-ray bursts. Astrophys. Space Sci. 2019, 364, 105. [Google Scholar] [CrossRef]
- Modak, S.; Chattopadhyay, A.K.; Chattopadhyay, T. Clustering of Gamma-ray bursts through kernel principal component analysis. arXiv 2017, arXiv:1703.05532. [Google Scholar] [CrossRef]
- Horváth, I. A further study of the BATSE Gamma-ray Burst duration distribution. Astron. Astrophys. 2002, 392, 791–793. [Google Scholar] [CrossRef]
- Zhang, Z.B.; Yang, E.B.; Choi, C.S.; Chang, H.Y. Classifying gamma-ray bursts with Gaussian Mixture Model. Mon. Not. R. Astron. Soc. Lett. 2016, 462, 3243–3254. [Google Scholar] [CrossRef]
- Horváth, I.; Balázs, L.G.; Bagoly, Z.; Veres, P. Classification of Swift’s gamma-ray bursts. Astron. Astrophys. 2008, 489, L1–L4. [Google Scholar] [CrossRef]
- Zhang, Z.B.; Choi, C.S. An analysis of the durations of Swift gamma-ray bursts. Astron. Astrophys. 2008, 484, 293–297. [Google Scholar] [CrossRef]
- Horváth, I.; Bagoly, Z.; Balázs, L.G.; de Ugarte Postigo, A.; Veres, P.; Mészáros, A. Detailed Classification of Swift’s Gamma-ray Bursts. Astrophys. J. 2010, 713, 552–557. [Google Scholar] [CrossRef][Green Version]
- Yang, E.B.; Zhang, Z.B.; Jiang, X.X. Two dimensional classification of the Swift/BAT GRBs. Astrophys. Space Sci. 2016, 361, 257. [Google Scholar] [CrossRef]
- Zitouni, H.; Guessoum, N.; AlQassimi, K.M.; Alaryani, O. Distributions of pseudo-redshifts and durations (observed and intrinsic) of Fermi GRBs. Astrophys. Space Sci. 2018, 363, 223. [Google Scholar] [CrossRef]
- Řípa, J.; Mészáros, A.; Veres, P.; Park, I.H. On the Spectral Lags and Peak Counts of the Gamma-ray Bursts Detected by the RHESSI Satellite. Astrophys. J. 2012, 756, 44. [Google Scholar] [CrossRef]
- Minaev, P.Y.; Pozanenko, A.S.; Loznikov, V.M. Short gamma-ray bursts in the SPI-ACS INTEGRAL experiment. Astrophys. Bull. 2010, 65, 326–333. [Google Scholar] [CrossRef]
- Svinkin, D.S.; Aptekar, R.L.; Golenetskii, S.V.; Frederiks, D.D.; Ulanov, M.V.; Tsvetkova, A.E. Classification of gamma-ray bursts observed with Konus-Wind. J. Phys. Conf. Ser. 2019, 1400, 022010. [Google Scholar] [CrossRef]
- Minaev, P.Y.; Pozanenko, A.S. The Ep,I-Eiso correlation: Type I gamma-ray bursts and the new classification method. Mon. Not. R. Astron. Soc. Lett. 2020, 492, 1919–1936. [Google Scholar] [CrossRef]
- Lü, H.J.; Zhang, B.; Liang, E.W.; Zhang, B.B.; Sakamoto, T. The ‘amplitude’ parameter of gamma-ray bursts and its implications for GRB classification. Mon. Not. R. Astron. Soc. Lett. 2014, 442, 1922–1929. [Google Scholar] [CrossRef]
- Tarnopolski, M. How does the shape of gamma-ray bursts’ pulses affect the duration distribution? Mon. Not. R. Astron. Soc. 2021, 507, 1450–1457. [Google Scholar] [CrossRef]
- Tarnopolski, M. Can the Cosmological Dilation Explain the Skewness in the Gamma-ray Burst Duration Distribution? Astrophys. J. 2020, 897, 77. [Google Scholar] [CrossRef]
- Baudry, J.P.; Raftery, A.E.; Celeux, G.; Lo, K.; Gottardo, R. Combining Mixture Components for Clustering. J. Comput. Graph. Stat. 2010, 19, 332–353. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, M.A.; Hillenbrand, L.A.; Carpenter, J.M.; Avelar Menendez, A.R. The Formation of a Stellar Association in the NGC 7000/IC 5070 Complex: Results from Kinematic Analysis of Stars and Gas. Astrophys. J. 2020, 899, 128. [Google Scholar] [CrossRef]
- Lien, A.; Sakamoto, T.; Barthelmy, S.D.; Baumgartner, W.H.; Cannizzo, J.K.; Chen, K.; Collins, N.R.; Cummings, J.R.; Gehrels, N.; Krimm, H.A.; et al. The Third Swift Burst Alert Telescope Gamma-ray Burst Catalog. Astrophys. J. 2016, 829, 7. [Google Scholar] [CrossRef]
- Fraley, C. HDoutliers: Leland Wilkinson’s Algorithm for Detecting Multidimensional Outliers, R Package Version 1.0.2. 2020. Available online: https://CRAN.R-project.org/package=HDoutliers (accessed on 17 June 2022).
- Scrucca, L.; Fop, M.; Murphy, T.B.; Raftery, A.E. mclust 5: Clustering, classification and density estimation using Gaussian finite mixture models. R J. 2016, 8, 289–317. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Kass, R.E.; Raftery, A.E. Bayes Factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Wang, N.; Raftery, A.E. Nearest-neighbor variance estimation (NNVE) robust covariance estimation via nearest-neighbor cleaning. J. Am. Stat. Assoc. 2002, 97, 994–1019. [Google Scholar] [CrossRef]
- Walther, G. Detecting the presence of mixing with multiscale maximum likelihood. J. Am. Stat. Assoc. 2002, 97, 508–513. [Google Scholar] [CrossRef]
- Li, J. Clustering based on a multilayer mixture model. J. Comput. Graph. Stat. 2005, 14, 547–568. [Google Scholar] [CrossRef]
- Tantrum, J.; Murua, A.; Stuetzle, W. Assessment and pruning of hierarchical model based clustering. In Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; pp. 197–205. [Google Scholar]
- Sakamoto, T.; Barthelmy, S.D.; Baumgartner, W.H.; Cummings, J.R.; Fenimore, E.E.; Gehrels, N.; Krimm, H.A.; Markwardt, C.B.; Palmer, D.M.; Parsons, A.M.; et al. The Second Swift Burst Alert Telescope Gamma-ray Burst Catalog. Astrophys. J. Suppl. Ser. 2011, 195, 2. [Google Scholar] [CrossRef]
- Bromberg, O.; Nakar, E.; Piran, T.; Sari, R. Short versus Long and Collapsars versus Non-collapsars: A Quantitative Classification of Gamma-ray Bursts. Astrophys. J. 2013, 764, 179. [Google Scholar] [CrossRef]
- Bhat, P.N.; Meegan, C.A.; von Kienlin, A.; Paciesas, W.S.; Briggs, M.S.; Burgess, J.M.; Burns, E.; Chaplin, V.; Cleveland, W.H.; Collazzi, A.C.; et al. The Third Fermi GBM Gamma-ray Burst Catalog: The First Six Years. Astrophys. J. Suppl. Ser. 2016, 223, 28. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Lenart, A.Ł.; Sarracino, G.; Nagataki, S.; Capozziello, S.; Fraija, N. The X-Ray Fundamental Plane of the Platinum Sample, the Kilonovae, and the SNe Ib/c Associated with GRBs. Astrophys. J. 2020, 904, 97. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Livermore, S.; Kann, D.A.; Li, L.; Oates, S.; Yi, S.; Zhang, B.; Gendre, B.; Cenko, B.; Fraija, N. The Optical Luminosity-Time Correlation for More than 100 Gamma-ray Burst Afterglows. Astrophys. J. 2020, 905, L26. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Nagataki, S.; Maeda, K.; Postnikov, S.; Pian, E. A study of gamma ray bursts with afterglow plateau phases associated with supernovae. Astron. Astrophys. 2017, 600, A98. [Google Scholar] [CrossRef]
- Gendre, B.; Joyce, Q.T.; Orange, N.B.; Stratta, G.; Atteia, J.L.; Boër, M. Can we quickly flag ultra-long gamma-ray bursts? Mon. Not. R. Astron. Soc. Lett. 2019, 486, 2471–2476. [Google Scholar] [CrossRef]
- Gibson, S.L.; Wynn, G.A.; Gompertz, B.P.; O’Brien, P.T. Fallback accretion on to a newborn magnetar: Short GRBs with extended emission. Mon. Not. R. Astron. Soc. Lett. 2017, 470, 4925–4940. [Google Scholar] [CrossRef]
- Kaneko, Y.; Bostancı, Z.F.; Göğüs, E.; Lin, L. Short gamma-ray bursts with extended emission observed with Swift/BAT and Fermi/GBM. Mon. Not. R. Astron. Soc. Lett. 2015, 452, 824–837. [Google Scholar] [CrossRef]
- Gompertz, B.P.; O’Brien, P.T.; Wynn, G.A.; Rowlinson, A. Can magnetar spin-down power extended emission in some short GRBs? Mon. Not. R. Astron. Soc. Lett. 2013, 431, 1745–1751. [Google Scholar] [CrossRef]
- Gompertz, B.P.; O’Brien, P.T.; Wynn, G.A. Magnetar powered GRBs: Explaining the extended emission and X-ray plateau of short GRB light curves. Mon. Not. R. Astron. Soc. Lett. 2014, 438, 240–250. [Google Scholar] [CrossRef]
- Ashall, C.; Mazzali, P.A.; Pian, E.; Woosley, S.E.; Palazzi, E.; Prentice, S.J.; Kobayashi, S.; Holmbo, S.; Levan, A.; Perley, D.; et al. GRB 161219B/SN 2016jca: A powerful stellar collapse. Mon. Not. R. Astron. Soc. Lett. 2019, 487, 5824–5839. [Google Scholar] [CrossRef]
- Melandri, A.; Malesani, D.B.; Izzo, L.; Japelj, J.; Vergani, S.D.; Schady, P.; Sagués Carracedo, A.; de Ugarte Postigo, A.; Anderson, J.P.; Barbarino, C.; et al. GRB 171010A/SN 2017htp: A GRB-SN at z = 0.33. Mon. Not. R. Astron. Soc. Lett. 2019, 490, 5366–5374. [Google Scholar] [CrossRef]
- Izzo, L.; Rossi, A.; Malesani, D.; Heintz, K.; Selsing, J.; Schady, P.; Starling, R.; Sollerman, J.; Leloudas, G.; Cano, Z.; et al. GRB 180728A: Discovery of the associated supernova. GRB Coord. Netw. 2018, 23142, 1. [Google Scholar]
- Selsing, J.; Izzo, L.; Rossi, A.; Malesani, D.; Heintz, K.; Schady, P.; Starling, R.; Sollerman, J.; Leloudas, G.; Cano, Z.; et al. GRB 180728A: Classification of the associated SN 2018fip. GRB Coord. Netw. 2018, 23181, 1. [Google Scholar]
- Hu, Y.D.; Castro-Tirado, A.J.; Kumar, A.; Gupta, R.; Valeev, A.F.; Pandey, S.B.; Kann, D.A.; Castellón, A.; Agudo, I.; Aryan, A.; et al. 10.4 m GTC observations of the nearby VHE-detected GRB 190829A/SN 2019oyw. Astron. Astrophys. 2021, 646, A50. [Google Scholar] [CrossRef]
- Jespersen, C.K.; Severin, J.B.; Steinhardt, C.L.; Vinther, J.; Fynbo, J.P.U.; Selsing, J.; Watson, D. An Unambiguous Separation of Gamma-ray Bursts into Two Classes from Prompt Emission Alone. Astrophys. J. 2020, 896, L20. [Google Scholar] [CrossRef]
- Salmon, L.; Martin-Carrillo, A.; Hanlon, L. Two Classes of Gamma-ray Bursts Distinguished within the First Second of Their Prompt Emission. Galaxies 2022. submitted. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Pandas Development Team. Pandas-Dev/pandas, Pandas-v1.4.2. 2020. Available online: https://doi.org/10.5281/zenodo.3509134 (accessed on 17 June 2022).
- Wes McKinney. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; van der Walt, S., Millman, J., Eds.; SciPy: Austin, TX, USA, 2010; pp. 56–61. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).