Abstract
On 11 February 2016, the LIGO and Virgo scientific collaborations announced the first direct detection of gravitational waves, a signal caught by the LIGO interferometers on 14 September 2015, and produced by the coalescence of two stellar-mass black holes. The discovery represented the beginning of an entirely new way to investigate the Universe. The latest gravitational-wave catalog by LIGO, Virgo and KAGRA brings the total number of gravitational-wave events to 90, and the count is expected to significantly increase in the next years, when additional ground-based and space-born interferometers will be operational. From the theoretical point of view, we have only fuzzy ideas about where the detected events came from, and the answers to most of the five Ws and How for the astrophysics of compact binary coalescences are still unknown. In this work, we review our current knowledge and uncertainties on the astrophysical processes behind merging compact-object binaries. Furthermore, we discuss the astrophysical lessons learned through the latest gravitational-wave detections, paying specific attention to the theoretical challenges coming from exceptional events (e.g., GW190521 and GW190814).
1. Introduction
Merging compact-object binaries are binary systems composed of two compact objects that are so close to each other to merge via gravitational wave (GW) emission within the age of the Universe. The members of such binaries can be white dwarfs (WDs), neutron stars (NSs), black holes (BHs), and their combinations, e.g., neutron star-black hole binary (NSBH) systems. These systems have been investigated for decades by many authors, who predicted their existence through theoretical studies that go from the formation and evolution of the stellar progenitors to accurate numerical relativity simulations of the final merger phase [1,2,3,4,5,6,7,8,9].
From the observational point of view, proving the existence of merging compact-object binaries has always been challenging. While such systems are potentially loud GW sources, catching their GW signal is not straightforward. The passage of a GW produces a relative change in the distance between two points which is
where r is the distance from the GW source, is the orbital separation of the binary, L is the reference distance, and are the masses of the GW source, G is the gravitational constant, and c is the speed of light [10]. The factor is minuscule (∼), thus, when a GW reaches the Earth, it causes an extremely small perturbation, which is very hard to detect.
Even without direct evidences of GWs, the loss of orbital energy of a compact binary via GWs was verified through radio observations of the binary pulsar PSR B1913 + 16 [11]. The observed orbital decay of the Hulse–Taylor binary is remarkably consistent with a GW-induced shrinking. This system, which is expected to merge in Myr, provided not only an additional confirmation of the Einstein’s theory of general relativity, but it also suggested to us that there might be not just one, but a population of binary neutron stars (BNSs) that can merge in relatively short times via GW emission.
For the first direct evidence of merging compact-object binaries and their GW’s fingerprint, we had to wait until 14 September 2015, when the two ground-based interferometers of the Laser Interferometer Gravitational-wave Observatory (LIGO) were able to measure the effect of a passing GW. The signal, named GW150914, was attributed to the coalescence of two stellar-mass BHs with masses and [12,13]1. The event carried many scientific implications with itself and it laid the foundations of a new way to investigate the Universe by allowing us to access data never collected before.
The initial identification of GW150914 was made through an unmodelled, low-latency search for GW bursts, which is a search procedure that does not assume any particular morphology of the GW signal, i.e., it is agnostic with respect to the source’s properties [12,14,15]. Later, the event was recovered also by other matched-filter pipelines [16]. GW150914 established the existence of binary black holes (BBHs) and that stellar-mass BHs can merge in a Hubble time, becoming detectable sources of GWs. However, the biggest surprise came from the masses of the BHs: we did not expect to detect stellar BHs with masses ≳ .
Prior to GW150914, our knowledge of stellar-mass BHs was limited to electromagnetic observations of Galactic BH X-ray binaries. At the time of GW150914 discovery, there were only a handful of known BHs with confirmed dynamical mass measurements, most of them with mass ≲ [17,18,19]. Theoretical models did not predict the existence of BHs with masses ≳ , with a few remarkable exceptions [20,21,22,23,24,25,26,27]; thus, we could have only approximate ideas about where the BHs of GW150914 came from. One of the very few clues we were able to obtain was that the heavy compact objects likely formed in a low-metallicity environment, where stellar winds are quenched and stars can retain enough mass to turn into heavy BHs [13].
The only solid conclusion was that GW150914 marked a new starting point for the astrophysical community. It gave an unprecedented boost to the development of new theoretical models to study the formation and evolution of compact-object binaries and their progenitor stars, with a new goal: providing an astrophysical interpretation to GW sources.
From the theoretical point of view, two main formation channels have been proposed so far for the formation of merging compact objects. In the isolated binary channel, two progenitor stars are bound since their formation; they evolve, and then turn into (merging) compact objects at the end of their life, without experiencing any kind of external perturbation [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. This scenario is driven by single and binary stellar evolution processes, and it is sometimes referred to as the “field” scenario, because it assumes that binaries are born in low-density environments, i.e., that they evolve in isolation. In contrast, in the dynamical channel, two compact objects get very close to each other after one (or more) gravitational interactions with other stars or compact objects. This evolutionary scenario is quite common in dense stellar environments (e.g., star clusters), and it is driven mainly by stellar dynamics [27,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61]. In reality, the two formation pathways might have a strong interplay. In star clusters, the orbital parameters of binaries might be perturbed by many passing-by objects. Dynamical interactions might be strong enough to eject the stellar binary from the cluster and to trigger the merger event in the field. Such an apparently isolated merger would not have occurred if the progenitor stars had evolved in isolation. Such hybrid scenarios blur the line between the dynamical and the isolated binary channel, and they have already been investigated by various authors [62,63,64,65].
Our theoretical knowledge of the formation scenarios is hampered by the uncertainties and degeneracies of the astrophysical models. Single-star evolutionary tracks, the strength of stellar winds (especially for massive stars at low metallicity), core-collapse and pair-instability supernova (PISN), the orbital parameters of binary stars at birth, binary mass transfer, compact-object birth kicks, stellar mergers, tidal interactions, common envelope (CE), and GW recoil, are only part of the uncertain ingredients of the unknown recipe of merging binaries. In contrast, stellar dynamics is simple and elegant, but developing accurate and fast algorithms for the long-term evolution of tight binaries is challenging. Furthermore, studying the evolution of small-scale systems (2 bodies within ∼ pc) in large star clusters (≳ objects within a few pc) is computationally intensive [66,67,68,69,70,71,72,73,74,75].
Therefore, disentangling different shades of flavors by tasting the final result and going back to the responsible ingredients is very challenging. The consequence is that the GW catalog is growing faster than our theoretical understanding of merging compact-object binaries. At the time of writing, we have already achieved an historic breakthrough: we have just started talking about a population of BHs. Indeed, the latest Gravitational Wave Transient Catalog (GWTC) reports ∼90 events2, mostly BBH mergers, and the count is expected to significantly increase in the next years, at even faster rates than ever because new ground-based interferometers will be operational and the existing ones will increase their sensitivity [79,80].
The catalog already contains many flavors of BBHs that challenge even up-to-date theoretical models. For instance, GW190814 (see Section 5.1) is an event with very asymmetric masses, a merger that most theoretical models find very difficult to explain [81]. Furthermore, the lightest member is a mystery compact object with an uncertain nature: it can be the heaviest NS or the lightest BH ever observed and its mass falls right into the lower mass gap (see Section 2.7). GW190521 (see Section 5.2) is the event with the heaviest BHs, with at least one of the two falling in the upper mass gap (see Section 2.9) [82,83]. Its merger product, a BH with mass , is the first confirmation of the existence of intermediate-mass BHs. GW200105_162426 and GW200115_042309 (see Section 5.4) are the first NSBHs ever observed [84]. GW170817 is associated with a merger of two NSs and it is the only event observed not only through GWs but also throughout the whole electromagnetic spectrum, a crucial milestone for multi-messenger astronomy [85]. There are also 5 events with preference for negatively aligned spins with respect to the orbital angular momentum of the binary, including the mentioned GW200115_042309. Spins and their in-plane components might provide important insights on the formation channels (see Section 2.11). The BH mass distribution and the inferred BBH merger rate make the current scenario even more complex. The former seems to have statistically significant substructures, that is, it shows up as clumpy, with BHs that tend to accumulate at chirp masses3 , whereas the latter increases with redshift [80,86,87,88].
Rather than presenting new results, in this work we review our knowledge of the main astrophysical processes that lead to merging compact-object binaries, focusing mainly on BHs. Furthermore, we discuss the clues we can currently collect on the astrophysical origin of some exceptional GW events, and we discuss the main astrophysical lessons learned so far. This is surely a rapidly evolving field (see also the reviews by [89,90]), and most of the topics reported in this work would deserve a review on their own right. Here, we just give an overview of the main aspects that are relevant for the formation of compact objects.
In Section 2 we discuss the evolution of single stars and their relation to compact remnants, Section 3 deals with binary stellar evolution processes, in Section 4 we examine the effects of stellar dynamics, Section 5 presents the astrophysical lessons learned through GW events, and Section 6 contains a summary and a brief outline of future prospects.
2. Single Stars
Throughout this work, we will often refer to population-synthesis simulations. To conduct statistical studies on stellar populations and their compact objects, we should follow self-consistently the evolution of any possible type of single and/or binary star from its formation to its death, and possibly beyond. This is prohibitive if we consider that simulating the evolution of just one star from the main sequence until core collapse might take days (if the complex underlying algorithms converge). Thus, for fast population-synthesis studies, the evolution of single stars is approximated through either (i) fitting formulas to detailed stellar evolution calculations (e.g., [35]) or (ii) the interpolation of look-up tables containing pre-evolved stellar evolution tracks for different stars at various metallicity (e.g., [22]). Binary stellar evolution (see Section 3) and other additional processes (e.g., supernova explosions) are generally added through analytical prescriptions on top of the single-star approximations. Fast population-synthesis codes are currently the main resource available to study compact objects from single and binary stars.
2.1. Overview
The life of a star can be thought as a series of gravitational contractions of the whole structure, and expansions under the influence of thermonuclear fusions of increasingly heavy elements in the core, until the formation of the nuclides of the iron group. Each gravitational contraction increases the central temperature until the heaviest element is ignited. After the exhaustion of input elements in the core, the burning process continues in an outer shell while the core contains the heavier products of the previous thermonuclear reactions.
The fusion of elements lighter than iron is an exothermic reaction, which means that it releases energy, balancing the thermal energy that stars lose via radiation. However, the average binding energy per nucleon starts to decrease for elements heavier than iron-56, thus forming these elements is an endothermic process, i.e., it requires energy. In reality, (i) the chain of nuclear reactions could continue until the formation of nickel-62, which is the nuclide with the highest binding energy per nucleon, but photodisintegration suppresses its formation, and (ii) iron-56 forms as nickel-56 decays ( and ), therefore, nickel-56 is the heaviest element that stars can produce efficiently through nuclear fusion ().
Stars spend most of their life on the main sequence, that is transforming hydrogen into helium in their innermost regions. The moment when a star ignites hydrogen in its core defines the zero age main sequence (ZAMS). The ZAMS line appears as a quasi-diagonal line in the Hertzsprung-Russell diagram (Figure 1), which is a standard tool for representing the evolutionary stage of stellar populations. While the bulk of the properties of a star is determined only by its mass at the ZAMS (), the mass of the final compact remnant crucially depends also on parameters like the chemical composition and stellar rotation. These parameters control the efficiency of the processes that affect the final mass of the remnant, i.e., they determine how much mass is lost through stellar winds, how much the stellar core can grow, and how much mass is lost in the supernova (SN) explosion.
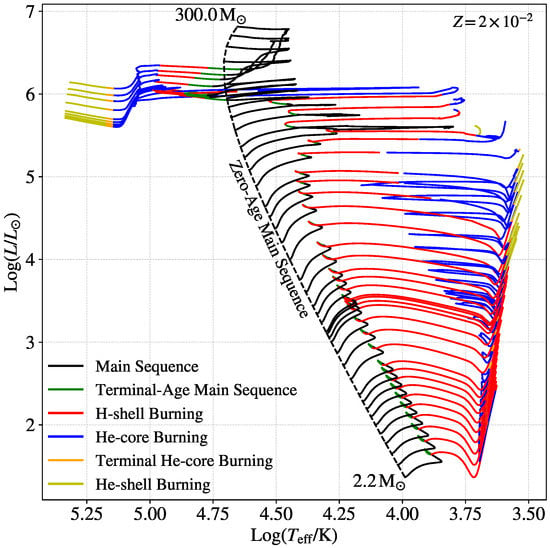
Figure 1.
Hertzsprung-Russell diagram (luminosity versus effective temperature) that shows the ZAMS (dashed black line) of stars with masses in the range –, at metallicity . The plot also shows the stars’ main evolutionary stages (solid lines) until carbon ignition, and it has been obtained through the SEVN population-synthesis code [97] coupled with the look-up tables for single-star evolution from the PARSEC code [98,99].
However, as a first approximation, is indicative of which remnant the star will leave at the end of its life. Very low-mass stars () do not reach the threshold temperature for helium ignition, and after their long (≳70 Gyr) main sequence phase, they become helium WDs (e.g., [91]). Stars with ignite helium and form a carbon-oxygen (CO) core but do not reach temperatures high enough to ignite CO. After the formation of a CO-core, nuclear reactions in the core stop. At this point, the star is supported only by electron degeneracy pressure. At the end of its life, the star will eject most of its outer shells creating a planetary nebula. What is left at the center is a CO WD (e.g., [91]). Stars with ZAMS masses above can reach iron elements, and their life will end with a SN, possibly leaving behind a NS () or a BH ().
The limits of these mass ranges are quite uncertain. We might say that these limits are the zero-level uncertainty to our understanding of the mass spectrum of compact objects. On the one hand, the uncertainty stems from theoretical modeling of detailed stellar evolution processes, such as convection, dredge up, wind mass loss, and nuclear reaction rates [25,92,93,94,95,96]. On the other hand, the limits also depend on other stellar parameters, such as rotation and chemical composition. These uncertainties affect the masses of stellar cores, which, in turn, have an impact on the nature and abundance of compact remnants that stars may form.
2.2. The Chandrasekhar Limit
The maximum mass of a WD is well constrained through theoretical arguments, which were firstly outlined by Chandrasekhar [100]. This limit exists because WDs are sustained against gravity by the pressure of electron degeneracy, which can be either non-relativistic or relativistic. Simple stellar polytropic models show that a star supported by a non-relativistic degenerate electron gas has a radius that is inversely proportional to the cube root of its mass, [100]. By looking at the scaling relation, one would expect that the WD radius becomes exceedingly small for exceedingly large masses. However, as the density increases, the electrons become relativistic, and the WD becomes supported by a relativistic degenerate electron gas. In such a state, the corresponding equation of state predicts the existence of a maximum sustainable mass: this is the maximum mass of a WD, also referred to as the Chandrasekhar mass limit. Its precise value depends on the average molecular weight per electron, which, in turn, depends on the chemical composition of the WD. For a typical CO or helium WD, the Chandrasekhar limit is .
2.3. The Tolman-Oppenheimer-Volkoff Limit
The maximum mass value for a NS, analogue to the Chandrasekhar limit, is the Tolman–Oppenheimer–Volkoff (TOV) limit [101,102]. In this case, support against gravity is provided by the degenerate pressure of a neutron gas. However, unlike in the case of the degenerate electron gas in WDs, neutron-neutron interactions become a crucial (but very uncertain) ingredient to include in the equation of state. Thus, the TOV limit reflects our uncertainties on the NS equation of state. In principle, depending on the adopted equation of state, the TOV limit can be anywhere from to [17,103,104,105,106,107,108,109,110,111,112,113,114]. The observations of NS masses ≳ (e.g., those in binary pulsars, such as PSR B1913 + 16) ruled out the softest equations of state, placing the TOV limit at –. The detection of the GW signal from merging NSs can also be used to constrain the maximum NS mass. In fact, tidal deformations during the last phase of the inspiral affect the properties of the gravitational waveform, which can then be linked to the NS equation of state. The analysis of GW170817 data constrains [115,116]. Stellar rotation may also play a role, with rigidly rotating NSs having about 25% larger allowed masses [117,118,119,120].
The secondary compact object of GW190814 (), if a NS, might challenge our understanding of the maximum mass of NSs. Because of the lack of a clear signature of tidal deformations in the GW190814 signal, and the poor constraints on the secondary’s spin, no definitive conclusions on the nature of the less massive component of GW190814 exist to date (see also Section 5.1).
2.4. The Role of Stellar Winds
The nature and final mass of a stellar remnant depends crucially on the final properties of the stellar core, which, in turn, depend on the amount of mass a star has lost during its life. Stellar winds have a central role in this picture since they drive mass loss over the lifetime of a star. Stellar winds, especially for massive stars, are uncertain, and even a factor of 2 uncertainty (typical for state-of-the-art models, e.g., [96]) might have important consequences on the nature and mass spectrum of compact objects.
Wind mass loss originates from the complex interaction between radiation and matter in stellar atmospheres. The idea that the outer layers of stars could expand was introduced already at the beginning of the 20th century by Saha [121]. Saha [121] suggested that radiation could be absorbed by matter in the solar atmosphere through an inelastic impact, with a resulting forward velocity of , where h is the Plank length, is the frequency of the photon and m the rest mass of matter. We now know that the strongly anisotropic and continuous component of photons from the innermost layers constantly exchanges energy and momentum with free electrons, ions, atoms and dust grains in stellar atmospheres. The momentum equation, considering only a radial direction of the radiation (1D problem), reads
where is the mass of the star, r is the distance from the center of the star, is the local wind velocity, is the local density, is the local pressure of gas, and the radiative acceleration. For the atmospheres of hot massive stars (), , where is the electron scattering acceleration, and is the selective acceleration caused by spectral line opacity. While is quite well established, the challenge is to estimate 4. The latter gained increasing importance over the years, especially after the discovery of blue-shifted resonance lines of carbon IV, silicon IV, and nitrogen V, in the OB supergiants , , and Orionis, which suggested expansion velocities and mass outflows of [122,123].
Castor et al. [124] introduced the idea to express through a force multiplier (CAK theory), that is
where is an optical-depth scale for the wind, assumed to depend only on the local conditions where the absorption occurs, including the wind velocity gradient [125], and . Castor et al. [124] showed that all spectral lines should be included in the calculation of , not only the resonance lines, and that , that is stellar winds in hot massive stars are line driven.
More and more spectral lines were included in the CAK theory over the years, and the contribution of metals—elements heavier than helium—to stellar winds became increasingly important. Indeed, hydrogen and helium have very few spectral lines in the UV (i.e., the radiation peak frequency of hot massive stars), thus their contribution is expected to be minimal compared to that coming from metals, which have crowded line spectra in the UV band. From CAK theory, it was already clear that stellar winds are quenched at low metallicity, that is the mass fraction of metals in a stellar layer. Denoting the mass loss by winds as and the metallicity as Z, with x ranging from [126] to [127].
It is nowadays understood that the amount and type of metals in the stellar atmosphere affect greatly the mass of the star prior to the SN explosion. Figure 2 shows the typical impact that different values of metallicity have on the final mass of the stars. It is apparent that stars at low Z retain significantly more mass than stars at higher Z, thus the former can collapse to significantly heavier BHs.
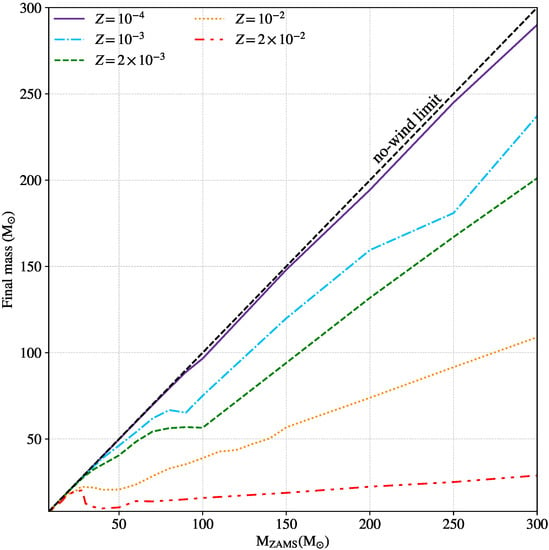
Figure 2.
Final mass of the stars as a function of their initial mass, for different values of metallicity. The dashed line at 45 degrees corresponds to the no-wind limit (i.e., final mass = initial mass). Plot obtained with the SEVN population-synthesis code [97] with look-up tables for single-star evolution from the PARSEC code [98].
The precise dependency of winds strength on the amount and kind of metals is still matter of debate. Abbott and Lucy [128] introduced an alternative approach to CAK based on a Monte Carlo method capable of tracking photon paths and includes the possibility of multiple photon scatterings. Vink et al. [129] used this improved approach to re-investigate the relation and found () for O (B) stars5. Vink et al. [129] pointed out that the dominant contribution to the inner (subsonic) stellar wind for O stars at high metallicity (Z∼) comes from the Fe-group elements, which are extremely efficient absorbers because their complex atomic structure allows for millions of different lines. At lower metallicity and in the outer (supersonic) wind, the main contribution comes from CNO elements. Furthermore, the recombination of Fe IV to Fe III for going from to gives a significant boost to mass loss, despite in this temperature range (bi-stability jump).
Mass loss is mainly driven by the Fe-group elements even for Wolf–Rayet (WR) stars, though the dependence on Z cannot be described as a single power-law. The atmospheres of WR stars are self-enriched with metals, (e.g., carbon), so the latter can sustain the mass loss of WR stars for , where, indeed, becomes insensitive to metallicity [130,131]. The mass loss prescriptions developed by Vink et al. [129] and Vink and de Koter [130] are the ones adopted by most state-of-the-art stellar evolution codes. A summary of the prescriptions is given in Section 4 of Vink [96].
Both the CAK theory and the Monte Carlo approach rely on the assumption that a photon with a specific frequency can only be absorbed in an infinitely narrow region of the stellar atmosphere [125]. This approximation breaks down if the wind is not supersonic (e.g., for the inner wind, where is set) and for clumpy winds. Recent works that do not adopt this assumption predict mass loss rates lower than [129], though the metallicity dependence is remarkably similar (e.g., [132]).
Another important aspect to consider is that the stars that approach the Eddington limit during their evolution might experience enhanced mass loss, which may even become insensitive to metallicity and occur in the form of pulsations [99,133,134,135,136,137,138]. Our knowledge of such continuum-driven winds is hampered by the uncertainties in modeling the interaction between winds and radiation-dominated envelopes.
Another main source of uncertainty is about the homogeneity of stellar winds. Several observations seem to suggest that winds are clumpy, though the clumps’ formation mechanism and evolution is still under debate [139,140]. The geometry, clumpiness level, and nature of clumps (i.e., optically thin or think) are also uncertain, but they might have a significant impact on stellar winds (e.g., [141]).
Finally, magnetic fields can quench winds and allow the formation of quite massive compact objects even at high metallicities (e.g., [142]), while stellar rotation affects the evolution of stars in many ways, but, overall, it tends to increase mass loss and to allow for the formation of larger stellar cores through enhanced mixing (e.g., [143,144]).
2.5. Core-Collapse Supernovae
As briefly described in Section 2.1, stars with mass ≳ end their life with a SN explosion, ejecting their outer layers in the interstellar medium and leaving a compact remnant behind (either a NS or a BH, depending on the progenitor’s mass and structure). The SN process starts with the collapse of the stellar structure, which, after the formation of the Fe-group elements, is not sustained anymore by either the core’s nuclear reactions or electron degeneracy pressure. Electron captures on nuclei accelerate core collapse, and when the temperature reaches the photodisintegration of the Fe-group elements becomes the dominant interaction mechanism (). This process requires very high energies ( per nucleon), thus the core-collapse accelerates and photons reach enough energies to even photodisintegrate particles (). At this stage, electrons have high enough energies () to collide with protons and forming neutrons and electron neutrinos (). Thus, it is apparent that there is a significant enrichment of neutrons, which eventually form a very compact degenerate structure that can halt the collapse.
The entire collapse process proceeds typically on the dynamical timescale which, for densities , might last a few milliseconds. The typical gravitational binding energy of the collapsed core is , more than enough to power a typical SN explosion, as long as an effective mechanism that transfers this energy to stellar layers exists.
The mechanism that triggers the actual explosion and, consequently, the link between progenitor stars and their compact remnants, are still matter of debate.
A possible scenario is the bounce-shock mechanism (e.g., [145]). During the collapse phase, the core contraction is not self-similar: only the innermost part of the core contracts all together (homologous core, ). When the density in the homologous core rises to , the neutron degeneracy pressure would be high enough to sustain the structure against collapse, though the core overshoots its equilibrium state and when the repulsive nuclear force makes the core bounce back, creating a shock wave. The latter might carry enough energy to eject the stellar envelope and power a prompt explosion. However, the shock dissipates most of its energy while travelling outwards, through the infalling material, until it stalls at about hundreds of kilometers from the center, well within the Fe core, failing to produce a successful SN.
Neutrinos play a crucial role in reviving the shock through the delayed neutrino-driven mechanism (e.g., [146]). At central densities , the mean free path of neutrinos is comparable to the dimension of the homologous core. At higher densities () neutrinos are basically trapped in the core and they start a congestion that results in the stall of the neutronization process at . The latter completes only seconds after the collapse, when most of the very high-energy neutrinos have had time to escape the core and to deposit part of their energy in the material behind the former shock wave. The rise in pressure in the layer between the proto-NS and the shock wave might revive the latter and power a successful explosion.
One-dimensional simulations of neutrino-driven explosions obtain successful SNe only for low-mass stars with naked O-Ne-Mg cores (ZAMS masses from to , electron-capture SNe—see Section 2.6). Two-dimensional simulations revealed that the layer where neutrinos deposit their energy experiences non-radial hydrodynamic instabilities, which (i) generate asymmetric explosions, and (ii) convert thermal energy into kinetic energy, further fueling the explosion (convection-enhanced neutrino-driven mechanism, e.g., [147,148,149]).
State-of-the-art, three-dimensional hydrodynamical simulations of neutrino-driven SNe predict successful explosions for stars up to . Such sophisticated multi-dimensional simulations are subject to major uncertainties and they are computationally intensive, but most state-of-the-art models seem to agree that blowing up massive stars (≳) is quite challenging (see [150,151,152] and references therein). For this reason, other explosion mechanisms have been proposed so far (e.g., magnetorotational-driven explosion explosions, [153,154,155,156,157,158,159,160,161]).
This does not necessarily undermine the foundations of the neutrino-driven mechanism. The detection of heavy stellar-mass BHs through GWs, the lack of observed SNe with massive progenitor stars (≳), and the fact that the observed SN energies are small compared to the energy reservoir of neutrinos (≲), provide clues towards an intrinsically inefficient SN mechanism.
2.6. Electron-Capture SNe
Stars with masses in the range ignite carbon and leave Oxygen-Neon-Magnesium cores. The central temperature and density in the core increase enough to reach electron degeneracy, but never enough to ignite Ne. The increasing electron degeneracy favors electron capture on and , which lowers pressure support, and initiates the core-collapse phase, which proceeds until the formation of a NS (e.g., [162,163], but see also [164]).
The steep density profile at the edge of O-Ne-Mg cores favors the propagation of the core-bounce shock, preventing its stagnation and the development of significant non-radial hydrodynamical asymmetries in the neutrino-heated layer. This explains why even one-dimensional neutrino-driven simulations produce successful explosions for low-mass progenitors (e.g., [165]). The resulting SN explosion is denoted as an electron-capture supernova (ECSN), and its lack of non-radial asymmetries has implication for the strength of SN kicks (see Section 2.10).
2.7. Compact Remnants and the Lower Mass Gap
The nature and mass of a compact remnant are close relatives of the SN explosion of the progenitor star. Depending on the energy of the explosion, a fraction of the star’s material may fall back onto the proto-compact object, which can eventually exceed the TOV limit and transform into a BH. Failed explosions are associated with the collapse of the entire stellar structure and the formation of a massive BH (i.e., , direct collapse). As such, fallback is a key ingredient to understand the mass spectrum of both NSs and BHs, but constraining it is very challenging.
On the one hand, large grids of self-consistent, multi-dimensional SN explosions are currently not feasible since they are computationally expensive and still require improvements in the implemented physics. On the other hand, one-dimensional simulations predict successful explosions only for low-mass progenitors (no convective engine). For these reasons, grids of SN explosions are generally constructed via one-dimensional models, where the explosion energy is artificially injected either directly into the convective region (energy-driven models) or modeled through the expansion of a hard surface placed at a specified mass-cut, generally at the outer border of the iron core (piston-driven). In both cases, the convective-enhanced neutrino energy becomes a parameter of the models, and it is generally calibrated using the observed SN luminosities and -yields. Following this approach, many authors tried to identify the key parameters of the stellar structure that drive the explodability of stars and the amount of fallback.
Fryer et al. [26] studied the outcome of several energy-driven SN explosions and introduced a model where the mass of compact remnants and fallback depend mainly on the final mass of the star and on the mass of the carbon-oxygen core (). Fryer et al. [26] considered two cases: (i) the explosion happens in the first ms and it is driven mainly by the Rayleigh–Taylor instability (rapid model), and (ii) the explosion is delayed (∼seconds) and its main engine becomes the standing accretion shock instability (delayed model). In both models, fallback has a huge impact on the masses of remnants from stars with . Both models predict direct collapse for , but the rapid model also for , which corresponds to The latter happens because the rapid mechanism occurs in ∼100 ms, i.e., when the infalling ram pressure can be still high enough to prevent a successful explosion. Thus, the rapid approach is more prone to a failed explosion than the delayed model, and it is more sensitive to the compactness of the innermost star’s regions. Specifically, in Fryer et al. [26], the stellar models with develop mixing instabilities and more compact structures during the latest evolutionary stages, causing a failed rapid SN and a gap in the remnants mass spectrum between and , a dearth which seems in agreement with observations (the lower mass gap [17,18,166]). While this argument might suggest a preference for the rapid model, the approach followed by Fryer et al. [26] is simplified and sensitive to the details of the stellar late-stage burning phases. Thus, the existence of the lower mass gap is still matter of debate and there are no conclusive results on the topic.
Figure 3 compares the mass spectrum of compact remnants obtained using the rapid and the delayed SN explosion models applied to the progenitor stars of the SEVN code [97], at (see also Figure 2 for the progenitors). From Figure 3, it is apparent that the rapid model creates a gap in the BH mass spectrum between and (shaded area), because stars with evolve through direct collapse, while the delayed model does not.
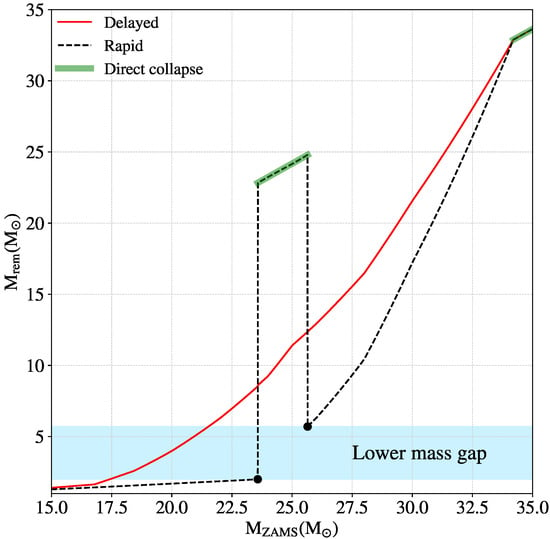
Figure 3.
Mass of the compact remnant as a function of the initial mass of its progenitor star obtained with the delayed (solid red line) and the rapid (dashed black line) SN explosion model. The progenitor stars come from the SEVN code [97] with look-up tables from PARSEC [98]. The shaded cyan area shows the location of the lower mass gap, while the semi-transparent green line highlights the region where direct collapse occurs. The two black points define the lower and the upper edge of the mass gap.
Ugliano et al. [167] adopted a more sophisticated model than [26], but still 1D, and showed that the compactness parameter, 6 [168], provides better insights than on the explodability of a star. Ugliano et al. [167] simulations revealed that BHs can form via direct collapse for and that successful SNe are possible for . This happens because stellar structure does not vary monotonically with , and the SN explosion is sensitive to such variations. Rather than a -threshold, it is the local maxima in the plane that increase the probability of failed SNe, thus, islands of explodability appear for , while direct collapse is dominant for . Specifically, stars with tend to have higher than neighboring stars and this creates a dearth of remnants with mass between and . While this finding qualitatively agrees with the rapid model of Fryer et al. [26], in Ugliano et al. [167] the gap is naturally produced through a wide range of explosion timescales (from 0.1 s to 1 s) that depend only on the structure of the progenitor at the onset of collapse.
Limongi and Chieffi [169] showed that there is a tight monotonic correlation between and , which can be expressed as , with given in units of [170]. This is in qualitative agreement with the simplified approach of Fryer et al. [26], but different assumptions on carbon nuclear reaction rates might significantly affect the correlation (e.g., [171]).
To capture the apparent stochasticity emerging from compactness-based studies, Clausen et al. [172] adopted a probabilistic description to model the NS and BH mass spectrum.
Ertl et al. [173] refined the compactness approach by introducing an even more sophisticated two-parameter model to predict the explodability of stars. The first parameter is the normalized enclosed mass for a dimensionless entropy per nucleon of , . This is a good proxy for the proto-NS mass, which corresponds roughly to the iron-core mass at the onset of collapse. The other parameter, , is the mass derivative at . The advantage of the two-parameter model is that the quantities and are strongly connected to the mass accretion rate of the stalling shock and to the neutrino luminosity, respectively, so they are expected to capture the physics of the neutrino-driven explosion better than . Ertl et al. [173] predicted successful (failed) SNe for (), where , and and , depending on the adopted set of progenitor stars. Ertl et al. [173] (see also [174]) confirmed the presence of islands of explodability, the prevalence of direct collapse for , and that fallback SNe are quite rare (i.e., a gap of compact objects with mass between and ).
Recently, Ertl et al. [175] investigated the explodability of a set of evolved naked-helium stars. They confirmed the presence of islands of explodability and the robustness of the two-parameter method to predict progenitors’ fate. Furthermore, they showed that the number of fallback SNe that form remnants between and is larger than that predicted by Ertl et al. [173] and Sukhbold et al. [174].
It is worth noting that all the features emerging through parametric (1D-based) approaches to the explodability of stars represent only the first step towards an exhaustive scenario for the SN mechanism and the masses of compact remnants. As such, they should be taken with a grain of salt, as all the features might be either confirmed or gone by the time we will have a realistic framework for 3D explosion models, which still need improvements and should be considered only as provisional (e.g., [176]).
2.8. Core-Collapse SNe in Population Synthesis Calculations
Performing accurate calculations of the internal structure of stars and sophisticated one-dimensional simulations of the SN mechanism is prohibitive for fast population-synthesis simulations of either single or binary stars.
To calculate the mass of compact remnants, the prescriptions of Fryer et al. [26] are easy to implement and do not require accurate calculations of the internal structure of stars. As such, while very simplified, they are still the most commonly used for fast population-synthesis simulations.
Ertl et al. [175] and Woosley et al. [177] provide tables and fitting formulas to calculate the remnant mass as a function of the initial and pre-SN helium core mass of the star, including also the effect of PISNe and pulsational pair-instability SNe (see Section 2.9). Such relations are expected to capture the physics behind the SN explosion mechanism better than [26].
A similar approach was followed by Patton and Sukhbold [178] who evolved a set of naked carbon-oxygen cores until the onset of collapse and provided values of and as a function of the initial and carbon abundance . The provided tables can be easily implemented in population-synthesis codes using a compactness- or a two-parameter based method for explodability.
Patton et al. [179] investigated the mass spectrum of NSs and BHs from population-synthesis simulations comparing the different approaches of Fryer et al. [26], Patton and Sukhbold [178], and Woosley et al. [177], for single and binary stars. They found qualitative agreement between the prescriptions of Patton and Sukhbold [178] and Woosley et al. [177], which give results roughly consistent with Ertl et al. [173] and Sukhbold et al. [174]. Significant differences emerge between Patton and Sukhbold [178] and Fryer et al. [26] for the mass distribution of NSs, and for the BH mass spectrum at low masses ().
2.9. Pair-Instability SNe and the Upper Mass Gap
Theoretical models of single-star evolution predict the existence of another gap in the mass spectrum of compact remnant, which extends from to . This is also known as the upper mass gap, as opposed to the lower mass gap which corresponds to a dearth of observations of compact objects with mass between and [17,18,166] (see also Section 2.7). The pulsational pair-instability supernova (PPISN) [180] and the PISN [181] are the main mechanisms behind the formation of the upper mass gap.
The relation that links the birth mass of a BH () to is complex because it reflects the uncertainties we have on the evolution of massive stars, on stellar winds, and on the SN explosion mechanism (e.g., [20,26]). Assuming that a progenitor star does not lose mass through stellar winds and that, at the end of its life, the entire stellar structure collapses into a BH without any ejecta, then ∼ (e.g., [22] and Figure 2). This is a continuous and monotonically increasing function, thus it predicts no gaps in the BH mass spectrum. Such a simplified relation would work reasonably well for massive stars () at low metallicity (), as long as PPISNe and PISNe are not effective. However, if stars’ core temperatures rise above , photons become energetic enough to create electron-positron pairs [180,182,183,184]. This process converts energy (gamma photons) into rest mass (electrons and positrons), thus it lowers radiation pressure and it triggers stellar collapse. In stars with helium core masses between and , the collapse is reversed by oxygen- or silicon- core burning, which shows up as a pulse and makes the core expand and cool. The flash is not energetic enough to disrupt the star and the core begins a series of contractions and expansions (stellar pulsations) that significantly enhance mass loss, especially from the outermost stellar layers, and continue until the entropy becomes low enough to avoid the pair instability and stabilize the core until the core-collapse SN explosion. Such pulsational instabilities are referred to as pulsational pair-instability supernova [180,181,185]. In contrast, in stars with helium core masses between and , the first pulse is energetic enough to completely disrupt the entire star (i.e., PISN [186,187,188])7. Stars with helium cores above experience a rapid pair instability-induced collapse but the energy released by nuclear burning is not enough to reverse the collapse before photodisintegration (endothermic) becomes the dominant photon-interaction mechanism [181]. Thus, the direct collapse to a massive BH (mass ) becomes unavoidable.
Stars with () will not evolve through the PISN (PPISN) phase, since their helium core masses cannot grow above () (e.g., [97]), though the metallicity limits are uncertain and depend on the prescriptions adopted to model several processes, including stellar winds, overshooting and stellar rotation.
The main consequence of PPISNe and PISNe is that they create a gap in the BH mass spectrum. At , the versus relation flattens out for stars with because of the enhanced mass loss caused by PPISNe, which removes all the hydrogen envelopes. Then, the BH mass continues to increase following the growth of the helium core until becomes large enough () to allow for the formation of helium cores ≳ , when stars evolve through the PISN and . This means that the versus relation has a local maximum which corresponds to the lower edge of the upper mass gap () [63,97,189,190,191,192,193]. Pair creation triggers direct collapse for stars with helium core masses ≳ (i.e., for ), thus these stars form massive (≳) BHs. This BH mass corresponds to a local minimum of the curve, for , and it is referred to as the upper edge of the upper mass gap () [97,194,195,196].
Figure 4 shows a typical example of a BH mass spectrum with the upper mass gap, obtained from a population of single stars, at various metallicities, through the SEVN population-synthesis code [97].
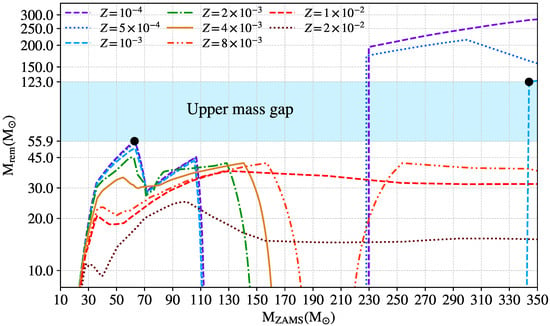
Figure 4.
Mass of the BH as a function of the initial mass of its progenitor star, for different values of metallicity . The shaded cyan area shows the location of the upper mass gap. The two black points set the lower edge () and the upper edge () of the gap. The plot has been adapted from Spera and Mapelli [97] and it has been obtained through the SEVN code coupled with look-up tables from PARSEC [98] and the delayed SN explosion model [26].
The values of and are highly uncertain because they strongly depend on metallicity, on the adopted stellar-wind models, on the boundaries of helium core masses for the occurrence of PPISNe and PISNe, on nuclear reaction rates, on stellar rotation, on the treatment of convection, and on the SN explosion mechanism. While most of these processes affect the value of and by a few percent [170,197,198,199], the two main sources of uncertainty are our understanding of the failed SN mechanism and of the 12C(, )16O reaction rate.
As concerns the failed SN mechanism, most theoretical models seem to agree on the occurrence of direct collapse for massive stars but we still do not know if the hydrogen envelope of the progenitor star is ejected during the collapse, leaving a remnant with the mass of about the helium core, or if it also contributes to the BH’s growth [172,174,200,201,202]. The collapse of the hydrogen envelope gives an uncertainty on of about [170].
The impact on is more difficult to quantify. As example, Spera and Mapelli [97] (see also Figure 4) show that stellar winds of massive stars with are likely strong enough to remove most of the hydrogen envelope during the main sequence phase, preventing the formation of helium cores with mass , even for extremely massive stars (≳). Very massive stars (≳) with might die as Wolf-Rayet stars with mass ≃, thus they might be the stars with the smallest to form BHs beyond the gap, setting the value of to . At , stars retain a significant fraction of their hydrogen envelope prior to collapse and the stars with the smallest to reach helium core masses above form BHs with masses above the gap. Indeed, at , the stars with the smallest to form BHs beyond the gap have and when the hydrogen envelope is accreted by the BH and when it is not. However, the uncertainties on the evolution of such extremely massive stars are significant and the discussed limits are uncertain. Following these arguments, Woosley [180] pointed out that the upper gap might be seen more as a cut off of BHs with mass , because BHs with masses can form only from the collapse of extremely massive stars, which are supposed to be exceedingly rare and live only for a few Myr (e.g., [203]).
Another significant source of uncertainty is given by our knowledge of the temperature dependence of the 12C(, )16O reaction rate (e.g., [204]). While changing the 12C(, )16O rate has no significant impact on the stellar structure, it governs the relative amount of oxygen with respect to carbon in the core. Low 12C(, )16O rates translate into large carbon reservoirs at the end of helium-core burning and into a prolonged carbon-burning phase, which contributes to suppress pair production, stabilize the oxygen core, and delay the latter ignition. In contrast, high 12C(, )16O rates imply significant carbon depletion in favor of oxygen, which ignites explosively just after the helium burning phase. This has a strong impact on the upper mass gap because low (high) 12C(, )16O rates push and towards higher (lower) values [192,193,198,205,206]. Furthermore, massive stars with low 12C(, )16O rates might experience significant dredge up which tends to stabilize the oxygen core even further. In this scenario, if very low () 12C(, )16O rates are considered together with the collapse of the hydrogen envelope, the upper mass gap might even disappear [206,207]. Conservatively, the impact of 12C(, )16O rates on both and is about .
It is also worth mentioning that the presence of physics beyond the standard model might also significantly affect the edges of the upper mass gap (e.g., [208]).
Overall, considering all the main known uncertainties so far, . As for , the scenario is more complex. A left endpoint of for the mass interval seems to be a quite robust prediction, while the right endpoint is more uncertain. For instance, considering only stars with and the collapse of the entire hydrogen envelope, might rise to . More conservative limits on (e.g., might even cause the mass gap to be seen as a cut off at . However, while rare, very massive stars might form from a series of stellar mergers, thus might be considered as a reasonable range for .
To model the enhanced mass loss predicted by PPISNe, population-synthesis codes generally adopt fitting formulas to detailed stellar evolution calculations (e.g., [97,209]).
2.9.1. Piling-Up BHs
A direct consequence of the enhanced mass loss caused by PPISNe is that most stars with initial mass die as naked helium cores, even at very low metallicity. The final helium cores of these stars have a mass , but pair-instability pulses are stronger for heavier cores, thus the helium cores left by PPISNe lie more likely in the range . Thus, we might expect an excess of BHs (pile-up) with masses in about the same range [97,177,189,210].
Constraining the extent of the BH bump and its mass limits is challenging. From a purely single stellar evolution perspective, the significance of the PPISNe bump depends primarily on the slope of the theoretical curve for (not affected by PPISNe) compared to that for (affected by PPISNe). With a standard initial mass function (e.g., Kroupa [203]), if the curve at is significantly flatter than the curve at , then the bump in the BH mass distribution will be more relevant and narrower, especially in correspondence of the kink between the two slopes. However, the relative slopes and the position of the kink in the curve are highly uncertain since they depend on many ingredients including metallicity, stellar winds, the details of the growth of helium cores inside massive stars, nuclear reaction rates (e.g., 12C(, )16O), and the collapse of the hydrogen envelope.
Figure 5 shows the BH mass spectrum (left panel) and the BH mass distribution (right panel) obtained from a population of single stars at . The progenitors follow a Kroupa [203] initial mass function with masses in the range . The black curve does not include the contribution of PPISNe, while the red does. It is apparent that the bumps in the BH mass distribution are close relatives of the kinks of the - curve. The pile-up of BHs through PPISNe happens at about , around the kinks B and C. However, the model we adopted to make Figure 5 has an additional kink in A, which also piles up BHs at , even without PPISNe. The pile-up at (kink D) disappears when PPISNe are considered because the latter force . Therefore, besides depending on metallicity, the existence and position of the kinks A, B, C, and D is strongly model-dependent.
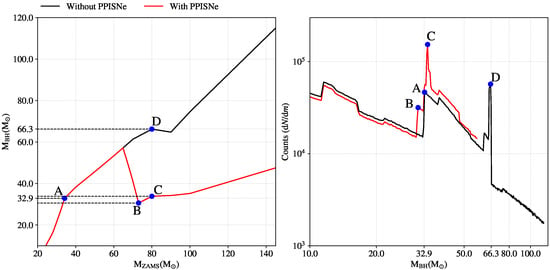
Figure 5.
Mass spectrum ( vs , left panel) and mass distribution ( vs , right panel) of BHs obtained evolving a population of single stars. The progenitors follow a power-law initial mass function that scales as [203] with masses between and . The black (red) curve shows the results without (with) PPISNe. The points A, B, C, and D represent the kinks of the – curve. The plot has been obtained for through the SEVN population-synthesis code [22] with PPISNe fitting formulas from [97], look-up tables for single stellar evolution from the PARSEC code [98], and the delayed SN explosion mechanism [26].
A pile-up of compact objects at mass in GW detections might suggest a PPISNe signature in the BH mass spectrum (e.g., [79,80]). However, the effect of piling up merging BHs at specific masses is not only model-dependent (e.g., Figure 5) but it might also have strong degeneracies with stellar dynamics and binary stellar evolution processes, thus disentangling the various contributions might be challenging.
2.9.2. Populating the Gap
The upper mass gap is a feature in the BH mass spectrum that comes from our theoretical knowledge of single stellar evolution processes. However, we know that stars are not born in isolation and, during their life, they may evolve through a series of events that can change their fate in many ways. Specifically, there are various (not exotic) astrophysical processes that can form BHs in the mass gap, without contradicting its existence (e.g., [52,56,58,207,211,212,213,214,215,216,217,218,219,220,221,222,223]).
For instance, a Nth-generation BH, which is a BH coming from a previous merger of two th-generation BHs, can easily fall into the upper mass gap. Furthermore, assuming that the hydrogen envelope participates in the BH formation process, stars with an oversized hydrogen envelope (gained through mass accretion from a companion star or even through a merger), but small enough helium cores to avoid the PISN, might form oversized BHs, with masses in the upper mass gap. The latter scenario is quite rare but possible for the isolated binary evolution channel (e.g., [222]).
Nth-generation BHs and oversized BHs coming from binary evolution can be retained, acquire a companion, and merge within a Hubble time in dense stellar environments. Therefore, they can become loud (and detectable) sources of GWs with at least one member in the upper mass gap (e.g., [214,215]).
Testing the presence of the upper mass gap and its underlying stellar astrophysics through GW detections might be challenging. The latest population analysis coming from the GWTC-3 shows a monotonically decreasing BH mass distribution at masses ≳ and an inconclusive evidence for the presence of the upper mass gap [80]. On the other hand, observing GW events with members in the upper mass gap might be the distinguishing feature of astrophysical formation channels other than single or isolated binary-star evolution, not necessarily contradicting the existence of the gap itself.
We will explore more scenarios on how to populate the upper mass gap in Section 5.
2.10. SNe Asymmetries and Kicks
Galactic pulsars are observed with fairly large spatial velocities, which can be as high as thousands of kilometers per second. Such values are too large to be explained through Blaauw kicks [224] from SN explosions in binary systems. Thus, some, if not all, compact objects should receive quite high kicks at birth [225]. Kicks have a huge impact on merging compact objects if they are members of isolated binaries (e.g., change of orbital parameters, unbinding the binary) or if they reside in dense stellar environments (e.g., ejections).
From the observational point of view, Hobbs et al. [226] presented an up-to-date catalogue of Galactic pulsars and showed that the mean three-dimensional velocity of young (age ) pulsars is . The three-dimensional speeds are well fit by a Maxwell-Boltzmann distribution with .
A more recent work [227] found that a double-Maxwell-Boltzmann distribution with , , and significantly improve the theoretical description of the pulsar data.
Analyses of a new dataset of proper motions and parallaxes [228] confirm the bi-modality feature of the velocity distribution with , , and .
From the theoretical point of view, asymmetries in the SN ejecta can impart high kicks to newly-born compact objects (e.g., [229]). The kicks can vary from to , depending mainly on the steepness of the density profile at the outer edge of the stellar core (i.e., compactness), and on the stochastic variations of non-radial instabilities associated with the SN engine. Shallow (steeper) density profiles are more (less) prone to SN shock stalling, thus neutrinos will be able to interact with more (less) material and produce more- (less-)asymmetric ejecta (e.g., [230]). As already discussed in Section 2.6, the progenitors of electron-capture SNe have very steep density profiles, so the explosion is expected to impart low kicks to NSs (tens of , e.g., [231]). Similar results have been obtained for ultra-stripped stars, which might form during mass transfer in close binaries [232,233,234].
Assuming that BHs share the same formation mechanism as NSs and that kicks are driven by the asymmetries in the SN ejecta, BH kicks are expected to be smaller than NSs’, with differences coming mainly from the heavier mass of BHs and the smaller amounts of ejecta. This theoretical argument cannot be supported by observations, because BH kicks lack strong observational constraints. Repetto et al. [235] and Repetto and Nelemans [236] showed that the large distances from the Galactic plane of some BH X-ray binaries can only be explained if BHs acquire high kicks at birth (as high as those of NSs), even though they cannot completely rule out smaller BH kicks (see also [237]).
For rapid population-synthesis calculations, most codes assign birth kicks assuming two velocity distributions that distinguish between electron-capture and ultra-stripped SNe from all the other core-collapse SNe. Following [26], compact-object kicks () are generally assumed to be the same as those coming from observations of pulsars (), but modulated by the fraction of fallback (), so that BHs that form via direct collapse (i.e., no SN ejecta) do not receive kicks:
where is the mass of the compact object, is the mass of the proto-compact object, and is the mass of the SN ejecta. A threshold of is assumed for distinguishing BHs from NSs.
Adopting small kicks for ECSNe and SNe from ultra-stripped progenitors is crucial to match the rates of merging NSs inferred by the LVK collaboration (e.g., [238,239]), but the simple model by Fryer et al. [26] fails to produce low kicks for compact objects from such channels, because the kick prescription is not very sensitive to (it appears in both the numerator and the denominator of Equation (4)). Here is an instructive example. Case 1: a progenitor star with , , and . The delayed SN prescription in Fryer et al. [26] predicts , , and . Case 2: same progenitor that becomes ultra-stripped via binary evolutionary processes. We will have , and the delayed SN prescription predicts , , and . This means that the birth-kick ratio between the two cases would be
that is, mostly the same kick for case 1 and case 2, despite the factor of ≃4 difference in . This is in contrast with both momentum-conserving arguments and with the low kicks obtained through multi-dimensional SN explosions from ultra-stripped progenitors.
Recently, Giacobbo and Mapelli [240] proposed a unified approach derived from momentum-conserving arguments, inspired by Bray and Eldridge [239], Bray and Eldridge [241]. Independent of the progenitor, the nature of compact remnant, and the SN explosion engine, the birth kick () is expressed as
where () is the average NS (ejecta) mass obtained from a population of isolated stars. This method naturally reproduces the bi-modal kick distribution obtained from observations: it predicts small kicks for compact objects from ECSNe and ultra-stripped progenitors (for which ), and the normalization ensures for isolated progenitors, so that kicks match those observed for Galactic pulsars.
Constraints on the kick magnitudes can be obtained through multi-dimensional simulations of SN explosions, though, as already discussed in Section 2.5, these sophisticated simulations are complex and highly uncertain, thus their results cannot be considered as conclusive.
2.11. Spins
The topic of spins of compact objects would deserve a review in its own right. Here, we discuss the main aspects that are relevant for the current catalog of GW detections, thus we focus mainly on BHs.
The spin rate of compact objects at birth is very uncertain, because it depends on the angular momentum transport mechanisms in the stellar interior, the efficiency of which is still matter of debate. Asteroseismic observations ([242,243,244,245,246,247]) have shown that the spin rates of red giant cores and WDs are slower than theoretically predicted by nearly all angular momentum transport mechanisms, such as meridional circulation, shear instabilities or propagation of gravity waves [248,249,250,251,252,253,254,255,256,257,258]. The magnetohydrodynamical instability known as the Tayler–Spruit dynamo [259,260] can provide more efficient angular momentum transport than other mechanisms, albeit early works predicted spin rates roughly an order of magnitude too large [252]. The typical BH natal spins predicted by the Tayler-Spruit dynamo are ∼–. Fuller et al. [261] and Fuller and Ma [262] (see also Heger et al. [263]) show that the Tayler–Spruit instability can persist in red giant branch stars despite the existence of strong composition gradients, and they argue that its growth will saturate in a different manner than proposed by Tayler [259] and Spruit [260]. In their formulation, sometimes referred to as the modified Tayler–Spruit dynamo, the instability can grow to larger amplitudes and produce stronger magnetic torques, which lead to an even more efficient angular momentum transport and lower natal spins (∼). The modified Tayler–Spruit instability proposed by Fuller et al. [261] may correctly explain the angular momentum contained in the core of stars, and hence the spin of the BH that is formed upon the collapse of massive stars. Eggenberger et al. [264] shows that the revised prescription for the transport by the Tayler–Spruit instability does not provide a complete solution to the missing angular-momentum transport revealed by asteroseismology of evolved stars. However, asteroseismic observations and new detailed theoretical models show that the angular momentum transport from the cores to the envelopes of massive stars may be very efficient, thus the first-born BH in a binary may form with low spin (e.g., [261,262,264,265,266]). The GW observations of low effective spins in most BBHs also hint at an efficient angular momentum transport in their progenitors [44,80,267,268].
Stars in binaries may spin up via tides, while compact objects in binaries may spin up though accretion. For instance, first-generation, highly spinning BHs can form if their progenitor stars become chemically homogeneous due to tides in close binaries, but BBHs originating from this channel have large and nearly equal masses [39,40,41]. BHs in X-ray binaries tend to spin faster than BHs observed through GWs, but whether these systems are distinct populations or two sides of the same coin is still matter of debate [19,269]. Spinning up first-born BHs in binaries would require a significant amount of accretion, which is unlikely to occur over the short evolutionary timescale of the massive, non-degenerate companion star or during a common-envelope phase (e.g., [270]). However, Olejak and Belczynski [271] find out that evolutionary sequences that do not involve a CE phase can still lead to an appreciable fraction () of systems that are spun up via tides, reaching , considering the classic Tayler-Spruit angular momentum transport. Bavera et al. [272] consider highly efficient angular momentum transport with the modified Tayler-Spruit dynamo, and obtain high spins for the second-born BH at low metallicity due to tidal spin-up. Conversely, they find that at high metallicity the second-born BH has a negligible spin because of wind mass-loss that spins down the progenitor and widens the binaries, weakening tidal interactions.
Finally, the merger remnants of coalescing BBHs will be spinning even if the progenitor BHs were non-spinning. As the two BHs merge, part of the angular momentum of the binary is converted into the spin of the final BH. This has important implications for the signatures of hierarchical mergers, wherein GW events are produced by second or higher-generation BHs formed from the coalescence of BBHs, rather than from SN explosions of their progenitor stars. Repeated mergers of BHs can thus produce higher and higher spinning remnants, and naively one might expect to achieve maximally spinning BHs, i.e., BHs with dimensionless spin . However, this is not the case, because the spin of the final remnant depends also also on the spin of the progenitor BHs and their relative orientation with respect to the binary angular momentum vector. Spins anti-aligned with the binary angular momentum will subtract from the total angular momentum budget of the final BH. Therefore, we expect hierarchical mergers to produce, after several generations of mergers, BHs with an average of [190,211,273,274,275,276,277]. The latter is true for nearly-equal mass mergers of higher generation BHs. On the other hand, if many first generation BHs coalesce into a single, massive merger product (as massive BH runaway formation scenarios, e.g., see [278]), the final BH spin will decrease on average. This is because, at next-to-leading order, the decrease in BH spin is proportional to the mass ratio of the binary, and thus on average the spin distribution of merger products will decrease after asymmetric mergers (e.g., [279]). Any hierarchical merger scenario, requires mechanisms to assemble higher-generation BHs into merging binaries, which will be described later in Section 4.
The spins of merging BBHs can be probed via GW observations. GWs carry information about the spin magnitude and orientation of the merging BHs into two phenomenological parameters: the effective inspiral spin parameter and the effective precession parameter [280,281,282,283]. The effective inspiral spin parameter relates to the component of the BHs’ spins aligned to angular momentum of the binary orbit, and can be expressed as:
where and are the masses of the two BHs, and are the two dimensionless spins, and and are the obliquities, i.e., the angle between the spin direction and the normal to the plane of the binary. The effective spin parameter remains approximatively constant during the inspiral, and it can be used to constrain the individual spins of the BHs. Note that the effective spin parameter is the mass-weighted average of the spin component parallel to the angular momentum vector. Consequently, high-mass-ratio inspirals will mostly carry information about the primary’s spin (e.g., GW190412, GW190814, Section 5.1 and Section 5.3).
The second phenomenological parameter, , relates to the orbital precession caused by the in-plane spin component, and is expressed as:
where the indices and refer to the primary and secondary BHs, so that , and is the mass ratio.
Correlations between and other parameters can be used to disentangle the formation scenarios of GW sources. For example, Zevin and Bavera [284] find that isolated binary evolution cannot produce BBHs with significant mass asymmetry and high spins in the primary BHs, unless either inefficient angular momentum transport or super-Eddington accretion are assumed [272]. The active galactic nuclei (AGN) scenario instead predicts values of that are anti-correlated with the mass ratio q, which is roughly consistent with the observed distribution [285,286]. We caution that these studies focus on a small region of the available parameter space of BBH mergers, and more systematic investigations will be required for a better understanding of the correlations between and the other observables.
3. Binary Stars
As briefly discussed in Section 1, two main mechanisms to pair compact objects have been proposed. The isolated binary evolution pathway, in which the GW progenitors evolve through various binary evolution processes in isolation, and the dynamical scenario, where the evolution of binaries is mediated by gravitational interactions with other bodies. Here we focus on the isolated binary mechanism, and leave the discussion of the dynamical scenarios for Section 4. We note, however, that some of the formation pathways that have been proposed so far blur the lines between these two categories, requiring elements of both binary stellar evolution and gravitational dynamics.
Many stars, especially the more massive ones, are born in binaries or higher multiple stellar systems. Moe and Di Stefano [287] showed that the multiplicity of stellar systems increases with the stellar mass. This crucial result suggests that most BH and NS progenitors are not isolated, but members of binaries, triples, and even quadruple stellar systems. Studying the interactions between close stars is crucial to understand the evolutionary histories of GW mergers.
The timescales of GW coalescence were derived analytically by Peters and Mathews [288], which showed that a circular BBH with masses , will coalesce in a time given by:
where a is the semimajor axis of the binary. Considering two BHs of , it follows that, in order to merge within , the separation must be smaller than . At solar metallicity, the stellar progenitors of BHs have about ZAMS mass and a radius of . It is apparent that such a binary could not have been born at a separation of , because the stars would have collided during the main-sequence phase, even without considering the following giant phase. Therefore, the progenitors of merging BBHs from isolated stellar evolution must have been born at wider separations, and subsequently brought to smaller separations by various mechanisms. Here, we begin by describing the evolutionary processes that can affect binary stars.
3.1. Stellar Tides
When a stellar binary is very tight, the point mass approximation is not enough to describe its motion, because finite-size effects (i.e., tidal forces) become significant. An elegant derivation of the equations of motion for a binary affected by tides can be found in [31,289]. The main idea behind these equations is that the star is deformed by its companion, generating a gravitational quadrupole moment. Due to dissipation sources in the stellar interior, the response of the quadrupole moment is not instantaneous with respect to the tidal field. This delay, called time-lag, allows the coupling between the rotational and orbital angular momenta, in addition to the dissipation of orbital energy in the stellar interior.
While the equations of [31] have been used to model a variety of different tidal dissipation mechanisms, the precise source of tidal dissipation depends on the stellar structure [290]. Tidal dissipation in convective layers occurs via the convective motion of large eddies. The convective flows counteracts the tidal flow, which gives rise to dissipation and the lag of the tidal bulges. This kind of tide is referred to as the equilibrium tide. For this reason, to quantify the tidal dissipation of evolved stars, we need to characterize the timescale of the convective motion, which is the eddie turnover timescale . This time scale can be calculated in several ways, either from the bulk properties of the star e.g., [35,291] or from the mixing length parameters adopted in the stellar models [292].
In stars with a radiative envelope, the source of tidal dissipation is the damping of low-frequency gravity waves near the surface of the star [293]. This kind of tide, called dynamical tide, is generally modeled following Hut [31], who relies on the ideas of quadrupole deformation and time lag, which are more suitable to describe the equilibrium tide. Nonetheless, just like the equilibrium tide, the tidal dissipation constants of the dynamical tide depend on the details of the stellar structure. The dissipation rate of the dynamical tide scales linearly with a dimensionless tidal torque constant, named , which must be calculated from the stellar density profile e.g., [294,295]. Tabulated values for were provided by Zahn [293], and were later fitted as a function of stellar mass by Hurley et al. [35], to use in population-synthesis codes. More recent fitting formulae can be found in Qin et al. [265], which, in turn, are based on the ones of Yoon and Cantiello [135]. An alternative formulation for the dynamical tide, which avoids entirely the tidal torque constant , was proposed by Kushnir et al. [296].
Compact stars (WDs, NSs) also experience tides, although their rates of tidal dissipation are poorly constrained [35,297,298,299].
The main effects of tides are the following. First, they tend to circularize eccentric binaries, shrinking their semimajor axis. Second, they tend to spin-up stars in close binaries, synchronizing their rotation period to the orbital period, and aligning the spin directions with the angular momentum vector of the binary. Both effects are especially important in the context of GWs. Specifically, tidal spin-up can change both magnitude and orientation of the spins of compact objects with respect to the orbital angular momentum vector, and GW observations may give us insights into these two parameters (see also Section 2.11).
Finally, another crucial consequence of tides is that they can radically change the structure and evolution of a star. Tidal spin-up in a close binary introduces rotational mixing of the stellar interior, which tends to flatten its chemical composition gradient. For very close massive binaries, rotational mixing drives large-scale Eddington–Sweet circulations [300,301], so that the entire star is fully mixed. These stars undergo chemical homogeneous evolution (CHE), which has been proposed as a formation pathway for BBHs [36,39,40,41,302,303]. Chemically-homogeneous stars skip entirely the evolved giant phase because they do not develop a core-envelope boundary. Since such stars remain compact even during the post-MS phases, they can evolve very close to each other without merging via unstable mass transfer (Section 3.2). Therefore, CHE can produce BBHs that merge within the age of the Universe. Because this scenario involves tight binaries with synchronized spins, it predicts BH mergers with large aligned spins. It also favors high BH masses (>20 ) and nearly equal mass ratios ().
3.2. Mass Loss, Mass Transfer and Accretion
As detailed in Section 2.4, stars lose mass through stellar winds. In binaries, such mass loss leads to changes in the orbit of the binary. If the mass loss by winds is isotropic (i.e., no net change in momentum) and adiabatic (slow with respect to the orbital period), the rate of change in orbital semimajor axis a is:
where and are the (negative) mass change rates of the two stars. If the mass loss is slow, the only effect of mass loss is the increase in size of the binary, while its eccentricity remains constant [304,305].
However, the wind lost by one star may be partially accreted by its companion, which introduces a positive rate of mass change. In addition, part of the accreted material may carry linear and angular momentum, further affecting the binary orbit. The wind accretion rate can be calculated using the Bondi and Hoyle [306] accretion model. Given a binary with eccentricity e, donor wind speed , and mean orbital velocity , Hurley et al. [35] approximate the mass accretion rate as:
where G is the gravitational constant, is an efficiency constant, and is the donor mass loss rate due to stellar winds. Understanding how the orbit responds to mass transfer is complex, because it depends not only on the amount of mass transferred or lost, but also on the linear and angular momentum that is carried out or accreted. Detailed equations for the orbital response including various mass transfer models were recently developed by Dosopoulou and Kalogera [305,307] and Hamers and Dosopoulou [308].
Another way to transfer mass from a star to its companion is via Roche lobe overflow. If the stellar radius is relatively large compared to the size of the binary, the external layers of the star may be stripped out by the gravity of the companion star and the centrifugal force of the binary motion. The region in space where this occurs is approximated by the Roche lobe, the equipotential surface shaped like two tear-drops that surround both stars, with the two lobes connected by a saddle point at the center (also known as the first Lagrangian point, ) [309,310,311]. In general, Roche-lobe overflow can be caused by either the primary star entering the giant phase and increasing in radius, or by the shrinking of the binary orbit due to tides.
Commonly, the Roche lobe is approximated as an equal-volume sphere of effective size , the Roche radius. A convenient analytic approximation for was given by Eggleton [312]:
where is the mass ratio, and corresponds to the Roche radius of the star of mass . If the radius of one of the stars exceeds its Roche radius, some material will flow through the saddle point. Part of the material will be accreted by the companion star, while some material will be dispersed in a circumbinary disk. If all the mass lost by one star is accreted by the other and no mass is dispersed, we are in the case of conservative mass transfer. The material that is lost during non-conservative mass transfer will carry out not only mass but also angular momentum from the binary.
The typical rate at which mass transfer proceeds through can be estimated, at order of magnitude, through Bernoulli’s equation, assuming an isentropic, adiabatic, and irrotational fluid, and that the velocity of the flow is parallel to the axis connecting the centers of the two stars. Under these assumptions, the mass transfer rate can be expressed as (e.g., Ge et al. [313])
where is the binary orbital period, is the Roche-lobe filling factor, and n and are the envelope’s polytropic index and the radius of the donor star, respectively.
Besides changing the binary orbit, mass loss and accretion via Roche lobe overflow will change the structure of both the donor and the accretor. Modeling the response of the donor star to mass transfer is crucial to predict the evolution of binary stars but it is also very challenging since it requires an in-depth knowledge of the internal structure of the star and possibly non-equilibrium solutions for it.
To assess the response of the star, we must carefully consider the relevant timescales of stellar evolution. The shortest characteristic time is the dynamical timescale, which is the time on which a star reacts to a perturbation to the hydrostatic equilibrium:
where is the gravitational acceleration at the stellar surface. The dynamical timescale can be also interpreted as the timescale for the star to collapse (or ‘free-fall’) if the gas pressure would suddenly disappear. For the Sun, this timescale is about , which means that main sequence stars are extremely close to hydrostatic equilibrium.
The thermal timescale, also known as the Kelvin-Helmholtz timescale, describes how fast the changes in the thermal structure of a star can be. A star without a nuclear energy source contracts by radiating away its internal energy content. The Kelvin-Helmholtz timescale is the timescale at which this gravitational contraction occurs:
where is the gravitational energy budget of the star, and L is the stellar luminosity. For the Sun, the Kelvin-Helmholtz timescale turns out to be .
Finally, the longest stellar timescale is the nuclear timescale, which is the timescale for the nuclear fuel to be exhausted. The energy source of nuclear fusion is the direct conversion of a small fraction of the rest mass of the reacting nuclei into energy. For hydrogen fusion, , while for helium fusion it is about 10 times smaller. The total nuclear energy supply can be then written as , where is the fraction of stellar mass that can serve as nuclear fuel (∼10%). The nuclear timescale can be written as
Using solar values, we obtain , which is consistent with the time the Sun will spend on the main sequence.
During mass transfer, stars continue their evolution in thermal equilibrium if the mass loss rate remains above the nuclear timescale but well below the thermal timescale for mass transfer, that is
where X is the initial hydrogen fraction, the mass of the stellar core, L the luminosity of the star, and c the speed of light. However, if the mass loss timescale becomes comparable or larger than the thermal timescale, but remains below the dynamical timescale, that is
the star cannot be considered in thermal equilibrium anymore and its response in terms of luminosity and radius variation can be significantly different. In the most extreme cases, mass transfer can reach values as high as the dynamical timescale, crucially altering the response of the donor.
The mass-loss rate depends on the Roche-filling factor (see Equation (13)), which, in turn, depends crucially on how the Roche-lobe radius (Equation (12)) and the donor’s radius respond to mass transfer/loss. Generally speaking, if during mass transfer the Roche lobe contracts more than the star does, then the Roche lobe filling factor increases and mass transfer accelerates. Such relative contractions/expansions are evaluated through the coefficients:
where , depending on whether the star is in equilibrium, out of thermal equilibrium, or out of both thermal and hydrodynamical equilibrium, respectively.
Approximate Solutions for Population Synthesis Simulations
The coefficient is a complex function that depends on many physical stellar parameters, including the star’s evolutionary phase. An on-the-fly, self-consistent calculation of such coefficients in population-synthesis simulations is prohibitive, considering also that and refer to non-equilibrium states.
The response of the star in population-synthesis codes is approximated considering the star always in both thermal and hydrodynamical equilibrium, thus the same fitting formulas or look-up tables for single stars apply to stripped/oversized stars in binaries. Furthermore, to predict whether the mass transfer will remain stable (say, at ∼constant ) or not (e.g., runaway Roche-lobe filling), such codes adopt a criterion based on a critical mass ratio, . Indeed, if we assume that mass transfer is conservative, i.e., , and that the total angular momentum of the binary (J) is conserved as well, then
and thus, the condition for unstable (hydrodynamical) mass transfer can be thought of as a condition that depends only on the mass ratio, that is
The values are generally approximated with simplified fitting formulas or constant values that depend on the stellar evolution phase, and they are generally calibrated to match the merger rate of compact objects inferred by the LVK and/or on other Galactic observations (e.g., Hurley et al. [35], Leiner and Geller [314], Neijssel et al. [315]).
The values of have a dramatic impact on merging compact-object binaries especially because, if the mass transfer is unstable, the binary orbit shrinks on a dynamical timescale, and the stars are destined to merge. However, if the donor is an evolved star, constituted by a massive core surrounded by a low-density envelope, the binary enters a further phase of binary evolution that has crucial consequences for compact objects: the CE phase.
Figure 6 is a cartoon that shows the normalized Roche-lobe radius (, see Equation (20)) and the donor’s radius response as a function of the mass of the donor star, under the assumptions and , with masses in arbitrary units. In the left panel, a donor with a very steep response to mass stripping () and mass fills its Roche lobe in correspondence to the blue point in the figure. As soon as mass transfer initiates, the star contracts significantly more (black arrow) than does (red arrow), i.e., . Thus, the star remains in thermal equilibrium, and mass transfer stops until nuclear reactions cause a further expansion of the donor. This is a typical case of (nuclear) stable mass transfer. In the right panel, a star with a shallower response () and is considered. In this case, shrinks more than (i.e., ), therefore increasing the Roche-lobe filling factor and the mass loss rate. This is a typical case of the beginning of a thermally unstable mass transfer, for which . By looking at the right panel of Figure 6, this configuration might last until , though, depending on the -filling factor, mass loss can become fast enough to drive the donor out of dynamical equilibrium, so that . For typical giant stars, mass loss easily evolves towards a very high rate. This happens because (e.g., [35]), thus, such donors easily initiate a runaway -filling process that likely leads to CE evolution.
Figure 6.
Normalized Roche-lobe radius (solid red line) and donor radius’s response (dashed black line) as a function of the donor mass in arbitrary units. Left (right) panel: donor star with steep (shallow) response to mass stripping, (), and mass (). The blue dot is where the donor fills its Roche lobe. The red (black) arrow shows the direction in which the Roche-lobe (donor) radius evolves after mass stripping. The shaded green area represents the amount of Roche-lobe filling. The total angular momentum and the total mass of the system are taken as constants.
3.3. Common Envelope
CE is the process by which one component of a binary gets engulfed in the envelope of its companion [32,37,38,316,317]. The gaseous envelope becomes gravitationally focused and exerts a drag force onto the secondary, which can be considered as a second core within the envelope of the primary. Because of the drag, the two cores begin an inspiral phase, during which orbital energy and angular momentum are transferred to the envelope, which heats up and expands. After the inspiral sets, only two outcomes are possible. If the envelope is too tightly bound, the inspiral continues until the two cores are tidally disrupted and the binary merges into a single star. If, instead, the envelope is ejected, a short-period binary forms.
The CE is a key process in the formation of GW events from isolated binary stars, because it can shrink binary separations by a factor of hundreds, decreasing the coalescence time of compact-object binaries [43,44,266,318,319,320,321]. In particular, Dominik et al. [37] found that the coalescence time distribution of post-CE compact object binaries approximately follows a log-uniform distribution, . The reason for this peculiar scaling comes from Equation (9), which imposes . If we assume that the distribution of semimajor axis of post-CE binaries follows a power-law as in
then, from Equation (9), the distribution of coalescence times can be written as
Therefore, even a moderately steep (–2) distribution of post-CE semimajor axes will result in a coalescence time distribution very close to a log-uniform distribution.
CE evolution is also important for explaining other astrophysical phenomena related to short period binaries, such as supernovae Ia, X-ray binaries and double neutron stars. In fact, the CE phase was first introduced to explain the existence of short-period dwarf binaries [29].
Due to the complexity of CE evolution, we are still lacking a complete theoretical picture to distinguish between its two possible outcomes—close binary formation or binary merger. Attempts at modeling the CE phase have been mostly limited to two approaches: hydrodynamic simulations [322,323,324,325,326,327,328,329,330] or analytic prescriptions [29,30,32,331,332,333,334]. The latter are particularly convenient because they can be applied to a wide sample of binaries with minimal computing effort.
Hydrodynamic simulations may appear as the best way to model CE evolution, however they come with their limitations. First, hydrodynamic codes can follow only the initial plunge-in stage of CE evolution, which advances on a dynamical timescale. However, the later stages of the CE phase, where the envelope is heated up and expands, proceed on a thermal timescale. In these later stages, the energy deposited by the inspiral is transported to the surface of the star and radiated away. Therefore, modeling this stage requires proper treatment of radiative and convective energy transfer and equation of state for the stellar layers. The pre-CE phase, wherein the binary undergoes unstable mass transfer or other structural instabilities, is also difficult to model with hydrodynamic codes. In fact, many hydrodynamic simulations place the companion stars on a grazing orbit, artificially triggering the plunge-in stage. This approach, however, misses important physics of the early CE stage, such as tidal effects and mass transfer, which can significantly change the stellar structure of the stars prior to the inspiral. Furthermore, hydrodynamic simulations are numerically expensive, which makes them impractical to use for fast population-synthesis calculations.
Analytic models of CE evolution are numerically inexpensive and easy to implement, but they also come with their drawbacks. The most commonly adopted formalism in fast population-synthesis codes is the – model [30,32,331], which is based on energy balance considerations. The main idea of this approach is to compare the orbital energy of the binary at the onset of CE with the binding energy of the envelope. By comparing these two energies, it is possible to determine whether or not the binary will survive the CE and to estimate the final size of the binary.
The model depends on two unknown parameters, and , which parametrize the CE efficiency (i.e., how efficienty orbital energy is used to unbind the envelope) and envelope binding energy, respectively. The binding energy of the envelope is parametrized through the parameter as [332]
where R is the stellar radius, and is the mass of the stellar envelope. When both stars are giants at the onset of CE, the binding energy of both envelopes is included in Equation (24). The parameter can be estimated from polytropic models or fit to detailed 1D stellar evolution models [35,335,336,337,338].
The envelope binding energy is then compared to the difference in orbital energy:
where and are the pre- and post-CE semimajor axes. is a dimensionless parameter that measures the efficiency of the CE phase, i.e., how much orbital energy is transferred to the envelope. By equating Equations (24) and (25) we can estimate the size of the final orbit :
In the above equation, the parameter appears as a fudge factor that determines how much gravitational binding energy is used up to unbind the binary. For , all the binary orbital energy is used to unbind the envelope, while for only a fraction of the orbital energy is transferred to the envelope. In other words, the parameter controls the efficiency of common envelope inspiral.
Because the and parameters appear multiplied together, and are both of order unity, they can be sometime dumped together into a single, unknown parameter. This however neglects differences in envelope binding energies between different stars, which can be instead measured from detailed stellar evolution models [35,335,336,337,338]. The parameter is mostly unconstrained. Some clues on its values can come from observations of post-CE binaries [339,340,341,342], and from 3D hydrodynamical simulations of low-mass giant donors (e.g., [343]). However, large values of the parameter in population-synthesis simulations (≳3) seem to be necessary to match the merger rate of BNSs inferred by LVK (e.g., [43]). Some recent one-dimensional hydrodynamic simulations also obtain high values for [344]. Values of greater than one deserve a particular attention, because according to Equation (26), they imply that more energy than available was used up during the inspiral, or in other words, energy was generated during CE phase. One important source of energy is the recombination energy, i.e., energy released during the recombination of the hydrogen plasma into atoms and molecules. Recombination energy has been suggested as a potential driving mechanism for the ejection of the envelope, once it has been expanded by viscous and gravitational drags. Other potential energy sources include nuclear and accretion energies.
The – model is a very simplistic approach, because it hides behind two parameters the complex physics processes that happen during CE evolution. One glaring issue is that it assumes that the entire envelope is ejected, while hydrodynamic simulations have shown that partial envelope ejection is possible. The envelope ejection is also fine-tuned to carry away zero kinetic energy at the infinity, which is not necessarily true. Finally, the – formalism neglects angular momentum transfer, tidal heating, and recombination energy of envelope material [317], all processes that can affect the outcome of CE evolution. Another shortcoming of the – is that it cannot reproduce the eccentricities of observed post-CE binaries, which were shown to deviate from a perfect circular orbit [345,346,347]. Finally, the – model does not follow the binary inspiral, but prescribes an instantaneous change of the binary orbital parameters. Therefore, it is difficult to incorporate such formalism in numerical models that follow the continuous time-evolution of multiple stellar systems. Recent works have been tackling some of these issues. Progress has been done to include the recombination energy into the description e.g., [336,337,338], and alternative models of CE inspiral that can follow the binary angular momentum are being investigated [348].
3.4. Supernovae: Blaauw and Velocity Kicks
SNe can change the binary orbit because they can impart significant natal kicks to compact objects. The natal kicks are caused by two main physical mechanisms.
The first is the impulsive mass loss caused by the (possible) ejection of mass during the SN explosion. The sudden loss of mass can change the orbit and even unbind the binary, and this process is sometimes referred to as the Blaauw kick. This unbinding mechanism was originally proposed to explain runaway O- and B-type stars, because the stars inherit a fraction of the binary orbital velocity following the breakup [224].
Unlike adiabatic mass loss (Section 3.2), the mass ejection during a SN explosion is an impulsive event. Mass loss decreases the gravitational potential, and can therefore even unbind a tight binary without the need of a velocity kick. A circular binary needs to lose half of its total mass during a SN explosion to become unbound, while for an eccentric binary this will depend on the binary phase at the explosion time [349]. If a binary of total mass M and semimajor axis , loses instantaneously a mass , the semimajor axis after the explosion is:
where r is the distance between the two bodies at the moment of the explosion ( for a circular binary).
The second physical mechanism is the velocity kick caused by the asymmetries in the SN ejecta (see Section 2.10). The asymmetries can also affect the spin of the newly-born compact remnant [151], by changing its magnitude and orientation.
Unlike the Blaauw kick, the velocity kicks can either tighten or unbind binaries, depending on the relative orientation of the velocity kick with respect to the orbital velocity. Besides changing the orbital energy, velocity kicks also alter the eccentricity of the binary, which can then trigger mass transfer episodes or tides.
Velocity kicks have multiple consequences for the formation of merging compact objects. Besides breaking binaries, they can re-align the binary orbital plane, or misalign it with respect to the stellar spin vectors. However, the velocity magnitude of velocity kicks is poorly constrained, especially those of BHs (see Section 2.10).
Strong velocity kicks are the only mechanism that can form merging BBHs with anti-aligned spins in isolated binary evolution [350,351,352]. In fact, SN kicks can even flip the orbital plane of the binary, resulting in anti-aligned spin-orbit vectors. On the other hand, extremely strong kicks are required to produce significantly misaligned and anti-aligned spins in isolated binary evolution. The reason is that BBHs that merge within a Hubble time have very short separations () and therefore high orbital velocities (). In order to significantly tilt the binary plane, SN kicks need to be comparable to the orbital velocity, but such extremely high BH natal kicks are in tension with the estimates obtained from the proper motion of X-ray binaries with BH companions [40,235,236] and GW observations (e.g., [353]).
An important consequence of natal kicks is that they can eject compact objects and binaries from their birth star clusters. This prevents them to pair with other compact objects through dynamical interactions, which are described in the next section.
We conclude Section 3 with Figure 7, which shows an example on how binary evolution processes reshape the mass spectrum of compact remnants compared to that obtained for isolated stars. The figure has been obtained by evolving a population of binary stars with the SEVN code, and it has been adapted from Spera et al. [222]. By looking at the left panel of Figure 7, we see that most primaries lose their envelopes through Roche-lobe overflow or CE evolution, thus they form much lighter remnants than those they would have formed as single stars (cfr. curve at in Figure 4). In contrast, the secondaries can acquire a significant amount of mass from the primary and they can either retain it and form a heavier compact remnant, or lose it through Roche-lobe mass transfer or CE evolution. The lower the metallicity, the larger the deviations from the mass spectrum from single stars: stellar winds are quenched at low Z, thus stars can donate/accrete more mass.
Figure 7.
Mass of the compact remnant as a function of the ZAMS mass of its progenitor. The figure has been obtained evolving a population of binary stars at with the SEVN code, as in Spera et al. [222]. The masses of the primary stars are drawn from a Kroupa initial mass function [203] while the secondary masses, initial orbital periods and eccentricities are distributed according to [354]. The left (right) panel refers to primary (secondary) stars, i.e., those that have the largest (smallest) in each binary. The color map represents the number of compact objects at each location of the plot, with counts that increase going from dark to light colors.
4. Stellar Dynamics
Another way to form merging compact-object binaries is through gravitational interactions. Usually, the dynamical scenario involves the formation and hardening of binaries through few-body encounters in stellar clusters. However, in recent years, other forms of dynamical scenarios have been proposed, which involve not only massive star clusters but also small multiple systems like triples and quadruples.
4.1. Dense Stellar Environments
Most, if not all, stars are born in stellar clusters: relatively dense ensembles of stars bound together by gravity. The evolution of star clusters is mainly driven by long-range gravitational interactions between individual stars, through a process called two-body relaxation. Two-body relaxation leads star clusters to develop a high density core surrounded by a low-density stellar halo. Given their relatively high central density () [355,356,357,358,359], the cores of star clusters are the ideal environments for extreme dynamical interactions between stars and binary stars, including stellar collisions, which are unlikely to occur in the galactic field [57,356].
Star clusters are distinguished according to their age, density and mass. globular clusters (GCs) are typically old systems (∼Universe’s age, ∼12 Gyr), very massive (≥10) and dense (central density ). They are evolved systems which do not contain gas, dust or young stars. Because of their mass and high central density, many studies for the dynamical formation of compact-object binaries focus on GCs [50,51,54,55,275,319,360,361,362,363,364,365,366,367,368,369]. young dense star clusters (YDSCs) are relatively young (<100 Myr) systems, thought to be the most common birthplace of massive stars [355,356]. The central density of YDSCs can be as high as that of GCs, although YDSCs have smaller sizes. Some YDSCs can have comparable masses to present-days GCs and, for this reason, they are thought to be close relatives of the ancient progenitors of GCs. However, because of the stellar mass loss during their evolution, YDSCs are not massive enough to evolve into present-day GCs. open clusters (OCs) are irregular star clusters composed of 10—a few stars. They are generally younger than GCs and they may still contain gas from the molecular cloud from which they formed. Studies of compact binary mergers in young and open clusters include [27,51,57,58,59,62,63,214,370,371,372,373,374]. Finally, nuclear star clusters (NSCs) reside in the nuclei of galaxies. Nuclear star clusters are rather common in galaxies, including our own [375,376]. NSCs are usually more massive and denser than GCs, and may host a super-massive black hole (SMBH) at their center. Regardless of the presence of a NSC, the environment close to SMBHs can also be a site for formation of GW progenitors. Cusps or disks of BHs may form around SMBHs, where they can interact with other compact objects [377,378,379,380,381]. In AGN, BHs can be trapped by the SMBH accretion disk, wherein they can migrate and merge [212,285,380,382,383,384,385,386,387,388,389,390,391,392].
YDSCs and OCs are not long-lived because they inevitably disrupt into the tidal field of their host galaxy as they lose mass during their evolution. Processes that contribute to their disruption include gas expulsion and stellar evaporation. The first may happen during the early life of gas-rich star clusters. Stellar winds and SNe can eject the remaining gas from the cluster, decreasing its gravitational binding and potentially causing its disruption, a process referred to as infant mortality. Stellar evaporation is instead the inevitable consequence of two-body relaxation.
4.2. Two-Body Relaxation and the Gravothermal Instability
Two-body relaxation is the consequence of small, but frequent deflections in stellar velocities due to long-range gravitational interactions. Over time, two-body relaxation causes the kinetic energy of stars to be redistributed across the clusters. This process occurs over the timescale [393]:
where is the velocity dispersion, G is the gravitational constant, the mean stellar mass, the stellar mass density, and is the Coulomb logarithm. This last term arises from the uncertain range in impact parameters for the interactions that drive the two-body relaxation, and it is generally assumed to be ∼. In simple terms, the two-body relaxation timescale is the time necessary for the system to “forget” its initial conditions through two-body gravitational interactions. The two-body relaxation of star clusters can range from 200 Myr to few Gyr, depending on clusters’ size and mass. For reference, the typical timescale for a star to traverse the cluster, called crossing time, is:
where R is the cluster size, and N is the number of stars. The crossing time is much shorter than the two-body relaxation timescale. For example, for a cluster of stars, the relaxation timescale is about times longer than the crossing time.
Two-body relaxation drives a flux of kinetic energy, carried by stars, from the center of the cluster to its outskirts. When stars move from the core of the cluster to the halo, they carry heat with them, i.e., kinetic energy. As the core loses energy to support against its gravity, it collapses, thus it increases its velocity dispersion. This causes even more stars to flow into the halo, which expands. As the stellar halo expands, some stars reach high enough velocities to escape the cluster, in a process called evaporation. In OCs and YDSCs, the expansion of the cluster accelerates the disruption of the cluster due to the tidal field of the galaxy. This runaway process is called gravothermal catastrophe, and in physical terms it is a consequence of the negative heat capacity typical of every self-gravitating system [394]. A system with negative heat capacity loses energy and becomes hotter. To become hotter, a self-gravitating system contracts so that its velocity dispersion (i.e., the average speed of the stars) increases.
In summary, the gravothermal catastrophe is a runaway process that triggers the collapse of the core and the expansion of the halo. This process is accelerated if the stars have a mass spectrum. In fact, massive stars are affected by two more physical processes: dynamical friction and energy equipartition.
4.3. Dynamical Friction, Energy Equipartition and Mass Segregation
Dynamical friction is a drag force that acts on massive bodies that travel through a medium of less massive objects. The gravity of the massive body attracts the lighter ones, which form a wake behind it. The overdensity of light bodies tends to decelerate the motion of the massive one via a gravitational drag. The massive body decelerates until it is finally at rest with respect to the lighter bodies. The timescale of dynamical friction for a body of mass M is [395,396,397]:
where is the mass density of the lighter bodies. The dynamical friction timescale is much shorter than the two-body relaxation time. In star clusters with a mass spectrum, the core collapse can occur on the dynamical friction timescale, rather than on the two-body relaxation one. The steeper the mass spectrum, the faster the core collapse [398]. The consequence of dynamical friction is that massive stars become slower and sink to the center of the cluster. This phenomenon, called mass segregation, is characterized by a varying mass spectrum across the cluster radius, with heavier stars sinking to the cluster’s core and the lighter ones crowding the halo. A more dramatic rearrangement of the massive stars in the cluster can be caused by energy equipartition, or rather, the lack of it.
Energy equipartition is the tendency for stars to equalize their average kinetic energy
where is the velocity dispersion of the stars of mass m. Therefore, two populations of masses will have a different velocity dispersion, in order to have the same kinetic energy
For > , , i.e., more massive stars will be on average slower. However, for typical initial mass functions (e.g., [399]), the pathway towards equipartition breaks, and the population of BHs (i.e., the most massive objects one can find in a cluster) decouples from the lightest objects. The BHs interact only among themselves and form an independent sub-cluster, which starts acting as an additional internal energy source for the whole system [362,400,401,402,403,404,405,406].
4.4. Halting Core Collapse with Binaries
The core collapse cannot proceed indefinitely. As the density of star increases, so does the chance that stars and binaries have a close gravitational interaction. The rate of encounter between a binary and a single of masses and m is [393]:
where n is the number density of single stars, m is their average mass, the velocity dispersion, and is the maximal closest approach distance. For the encounter to result in energy exchange between the single and the binary, the encounter distance needs to be of the order of the binary semimajor axis, e.g., . If in the core of the cluster there are no binaries, they can be formed via three-body encounters of single stars. These occur on a timescale given by [407]:
During a three-body encounter between a binary and a single star, a fraction of the internal energy of the binary can be redistributed as translational energy among the interacting bodies. This means that binaries can considered as a reservoir of kinetic energy. The kinetic energy released through three-body encounters can be used to reverse core collapse.
Statistically, three-body encounters can have different outcomes depending on the kinetic energy of the single,
and the internal energy of the binary
where, are the masses of the binary members and a the binary semimajor axis. In the context of stellar clusters, a binary is considered as hard if its internal energy is greater than the average kinetic energy of neighboring stars, while it is soft in the opposite case. On average, subsequent encounters make hard binaries harder (i.e., their semimajor axis shrinks), while soft binaries tend to become softer (i.e., wider semimajor axis) until they break up [45]. It is worth noting that hardness is a property of the binary relative to its environment. Due to the higher velocity dispersion, the same binary in the core of a cluster might be soft, whereas in the halo it would be hard.
4.5. Forming Merging Compact-Object Binaries
The process of binary hardening in stellar clusters is a direct consequence of the core collapse and the gravothermal catastrophe, and it is argued to be one of the most critical processes for the formation of BBHs. Shrinking the semimajor axis of compact object binaries can dramatically shorten the coalescence time of binaries, because the GW coalescence timescale scales as (Equation (9)). Another important consequence of three-body encounters is that they tend to excite the orbital eccentricity of binaries. In fact, the probability distribution of binary eccentricities after a three-body encounter is close to a thermal distribution (), and can be even super-thermal in the case of low angular momentum encounters [45,408,409,410,411,412,413]. The orbital eccentricity has an even greater impact on the GW coalescence timescale, because, for eccentricities close to 1, the coalescence timescale shortens as [414]. An example of the effects of three-body encounters on binary coalescence times is given in Figure 8. In this simulated three-body encounter, a binary and a single meet on a hyperbolic orbit with a small impact parameter and a velocity at infinity of , which is typical of small OCs. The initial binary is not close enough to merge within the age of the Universe. However, the outgoing binary has a shorter separation and a much higher eccentricity, which will cause the binary to coalesce in about 2 Myr after the encounter.
Figure 8.
Trajectories during a three-body encounter between a binary (1,2) and a single (3). After a brief chaotic interaction, the binary and the single undergo an exchange. The encounter is concluded by the ejection of the new binary (2,3) and the new single (1). The initial coalescence time of the binary is , much greater than a Hubble time. After the interaction, the coalescence time is . The initial approach of the binary-single is hyperbolic, with an impact parameter of and velocity at infinity of . All the bodies are BHs integrated with tsunami (Trani et al., in prep.), including post-Newtonian corrections of order 1PN, 2PN and 2.5PN to the equations of motion.
Due to dynamical friction and mass segregation, BHs sink to the core of star clusters [362], where they undergo three-body encounters during the core-collapse phase. A binary will keep undergoing three-body encounters in the core until (i) core collapse is reversed, i.e., the cluster’s core “bounces back” and the density in the core decreases, quenching the encounter rate, (ii) the recoil velocity of the binary becomes so high that it is ejected from the core, or (iii) the binary merges due to GW radiation.
The second outcome can happen because when the binary becomes harder, the difference between the initial and final internal binary energies is redistributed as kinetic energy . This kinetic energy is redistributed between the single and the binary following momentum conservation, i.e., a fraction is gained by the single, and a fraction is gained by the binary. In general, the binary recoil velocity is less than the ejection velocity of the single. However, if the injected kinetic energy is sufficiently high, the binary can be ejected from the core and even from the cluster itself. Early studies found that the dynamical formation of binaries occurs in star clusters, but most of the merger events happen from binaries that were hardened in the core and then ejected [27,51,54,55,369,415].
Only recently, attention has been brought to in-cluster mergers that can occur during few-body encounters in the core (e.g., [211,364,416]). These mergers result from the short pericenter passages that can happen during chaotic three-body encounters, which can trigger rapid gravitational wave coalescence. These kind of mergers can be extremely rapid, due to the initial short separation between the compact objects. For this reason, binaries formed through this scenario can retain detectable eccentricities in the LVK band [417,418]. Another possible scenario for producing eccentric mergers in the LIGO band are GW captures during hyperbolic single-single interactions [379,419,420]. Because the cross section for single-single captures is extremely small compared to binaries, hyperbolic captures are likely to happen only in the most dense environments, like NSCs and GCs.
During three-body encounters, one of the members of the binary might be swapped with the initially single body. Binaries formed through this process are referred to as exchanged binaries. Statistically, the lightest body has greater chances to be ejected. For this reason, binaries formed through three-body encounters tend to have higher masses and equal mass ratios. Furthermore, even if binaries formed through dynamical interactions tend to have high eccentricities [45,408], by the time they reach the LVK band, GW emission circularizes them. Therefore, most ejected binaries are not expected to have any residual eccentricity at Hz [13]. Figure 9 illustrates the impact of circularization of GW radiation on merging binaries. In the example, a binary with an initial eccentricity of will be completely circularized by the time it reaches a peak GW frequency of 10 Hz. Only binaries with an extreme eccentricity () can retain some eccentricity at 10 Hz, but their coalescence time will be extremely small (∼days).
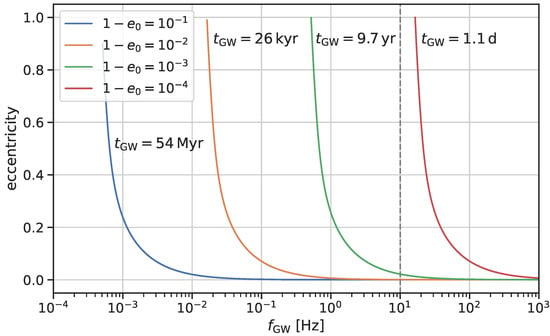
Figure 9.
Eccentricity as a function of peak GW frequency for inspiralling binaries. Each curve indicates a binary with the same semimajor axis (), but different initial eccentricity, as indicated in the legend. Coalescence timescales for each initial eccentricity are written next to the respective curves. The curves were calculated using the equations in Peters [414] and the fitting formula for the peak harmonic GW frequency in Hamers [421].
Furthermore, dynamically assembled binaries should not have any correlation between the orientation of BHs spins. Consequently, the predicted distribution of dynamically assembled binaries is symmetric and centered around ∼0 [211,285,422].
Finally, dense environments have an important consequence for hierarchical mergers, i.e., the GW coalescence of BHs formed from a prior BH coalescence. Asymmetric dissipation of linear momentum during the GW coalescence imparts a recoil kick to the final remnant. Depending on the mass ratio and spins of the merging BHs, these GW recoil kicks can be of the order of 100 km , which is much higher then the escape velocity of most clusters [423,424,425,426,427,428]. Therefore, it is expected that hierarchical mergers only occur in massive stellar environments such as GCs, NSCs, and close to SMBHs [275]. Runaway hierarchical mergers are also a proposed pathway to form intermediate mass BHs from stellar mass BHs [52,276,429,430,431,432]).
4.6. Small-N Systems
GW mergers can also be mediated by gravitational interactions in small-N systems, namely triples, quadruples and higher hierarchical systems. Hierarchical triple systems are constituted by a binary orbited by an outer object, in a stable configuration. Many stellar triple systems have been observeed so far, and it is reasonable to expect that in many triples the inner binary is composed of compact objects. In fact, massive stars are especially found in triples and higher multiples [433,434,435,436]. The fraction of stars found in multiples increases for more massive stars, up to % for B-type stars [287,437,438,439]. These multiple systems may be formed primordially as a natural outcome of star formation, or may also form dynamically from few-body encounters in stellar clusters.
Gravitational interactions can strongly affect the evolution of triple systems. If the outer object is sufficiently inclined with respect to the inner binary, the latter can exchange angular momentum with the outer orbit on a secular timescale, which is longer than the orbital period of the inner binary. These secular exchanges of angular momentum manifest themselves as the von Zeipel-Kozai-Lidov (ZKL) [440,441,442,443,444,445]. During such oscillations, the eccentricity of the inner binary can reach values very close to 1, inducing very close pericenter passages. If the inner binary is composed of compact objects, GW radiation can be efficiently emitted during these short pericenter passages, leading to the rapid coalescence of the binary. Figure 10 shows the typical evolution of a GW coalescence triggered by ZKL oscillations. There are two main effects of ZKL oscillations. First, they can accelerate the merging of compact object binaries, allowing them to merge within the age of the Universe. Secondly, they excite very high eccentricity in the inner compact binary, which can affect the GW emission waveform, and therefore can be potentially inferred by GW observations at different frequencies [446,447,448].
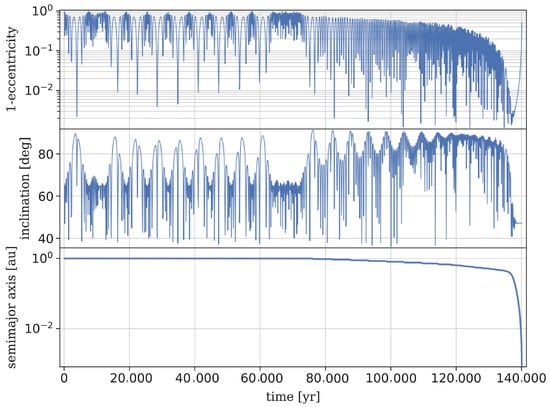
Figure 10.
Gravitational-wave merger induced by von Zeipel-Kozai-Lidov evolution in a triple system. Orbital parameters as a function of time for a triple system. Top panel: eccentricity of the inner orbit. Middle panel: inclination of the outer body’s orbit with respect to the inner binary. Bottom panel: semimajor axis of the inner binary. The initial orbital parameters of the triples are: mass of the outer body , mass of the inner bodies , , inner semimajor axis , outer semimajor axis , mutual inclination . Evolved with okinami, which solves the orbit-averaged equations of motion in Delaunay coordinates (Trani et al., in prep.).
The evolution in triple systems can also be affected by all the processes that occur in binary stars, and more. Mass can be lost by the tertiary star and transferred to the inner binary. The outer star could also be affected by tertiary tides [449] or become a giant and undergo a phase of triple CE [450]. In general, modeling the evolution of a triple system is quite complex, because of the strong interplay between dynamics and stellar evolution [451]. Due to the relative lower abundance of triples, the predicted merger rate of BBHs from triples is generally smaller by a factor of than that from dynamically assembled binaries [64,211,448,452,453,454,455,456,457,458,459,460].
The ZKL effect has applications also to triples in which the outer body is a massive BH. This may happen in NSCs hosting a SMBH, which can be orbited by a stellar BBH [461,462,463,464,465,466]. Just like in the case of a tertiary star, the massive BH can excite the eccentricity of the inner binary, causing the binary to merge.
Other forms of dynamical scenarios include dynamical perturbations of multiple stellar systems in the field [467,468,469], or interactions of binaries with the tidal fields of star clusters [470].
A few authors have recently started a systematic investigation of the evolution of hierarchical systems with [471,472]. Specifically, Vynatheya and Hamers [471] investigated compact-object mergers in quadruples, finding that the expected rates for BBHs are of the order of (see also [473]). Other studies on quadruples focused on specific GW events will be discussed in Section 5.
4.7. Hybrid Scenarios
Distinguishing between the isolated binary channel and the dynamical channel might not be straightforward. Stellar evolution and stellar dynamics are inseparable processes that are active at the same time. Indeed, besides evolving in complete isolation, stellar binaries can be found in star clusters as well, where they can be affected by close encounters just like compact-object binaries. These stellar binaries can therefore experience processes from both the binary evolution pathway (e.g., mass transfers, CEs) and the dynamical pathway (e.g., exchanges, excitation of eccentricity). For instance, in young star clusters, some BBHs are formed via CE evolution of dynamically-assembled main sequence binaries that, at some point of their life, are ejected from the cluster, and merge in the field, appearing as if they had evolved in complete isolation. They can contribute to the merger rate more than dynamically assembled BBHs [62,63,214,474]. These binaries undergo a CE phase, like in the isolated channel, but they also undergo dynamical interactions before and after collapsing to BHs. The CE phase might even be triggered by such dynamical interactions, so that the same binaries would not have merged without the crucial contribution of stellar dynamics. Some specific scenarios require elements from both channels. For example, three-body encounters of tidally spun-up, post-common-envelope binaries have been proposed as a mechanism to produce BBH with misaligned spins [64].
5. Astrophysical Insights from Exceptional Gravitational-Wave Events
In the previous sections, we presented the main astrophysical processes that can drive the formation of merging compact-object binaries. Despite the uncertainties and degeneracies in the astrophysical models, in this section we investigate whether some of the exceptional GW events have distinguishing features that may point us towards a specific formation scenario. An exhaustive analysis of all the exceptional GW events is beyond the scope of this review, which focuses mainly on the astrophysical processes behind merging compact-object binaries. Thus, in this section, we decided to restrict our analysis only to the events containing at least one BH and with physical properties that can be the smoking gun of a specific formation pathway: heavy BHs, as in GW190521, very asymmetric masses, as in GW190814 and GW190412, and mixed components, as in GW200105_162426 and GW200115_042309.
We stress that it is currently premature to make any kind of conclusive statements, especially on the origin of single GW events, though these exceptional events carry a number of astrophysical traces that are worth exploring here in some detail.
5.1. GW190814
GW190814 is a special LIGO-Virgo Collaboration (LVC) event detected during the first part of the third observing run and presented in Abbott et al. [81]. It is a coalescence with significantly unequal masses (mass ratio ). Furthermore, the secondary component of GW190814 is either the lightest BH or the heaviest NS ever discovered in a compact-object binary system, (secondary mass ). The mass of GW190814’s secondary falls into the range of the hypothesized lower mass gap (–), questioning the existence of this gap. GW190814 is also the GW event with the strongest constraint on the spin precession parameter () and on the spin of the primary component (), though both of these constraints are consistent with non-spinning components.
The secondary of GW190814 might be either a BH or a NS. The non-detection of any electromagnetic counterparts [475,476,477,478,479,480,481,482,483,484,485], the fact that there were neither clear signatures of tides or spin-induced quadrupole effects in the waveform [486,487], and the uncertainties on both the theoretical estimates of the maximum NS mass and the NS equation of state [488,489,490,491], prevent us to determine the nature of the compact object. Post-merger electromagnetic studies suggest that the merger product of GW170817 likely collapsed into a (highly-spinning) BH with a mass comparable to GW190814’s secondary () [492]. The latter result has been used by various authors as a starting point to constrain the NS equation of state and the maximum mass of a non-rotating NS, suggesting that the secondary of GW190814 is likely a BH [486,493,494]. However, the hypothesis of a rapidly rotating NS cannot be completely excluded [495,496,497,498,499,500,501,502,503,504,505], even in the context of extended theories of gravity (e.g., Astashenok et al. [506]).
The population analysis of GWTC-3 [80] shows that (i) the secondary of GW190814 is an outlier from the population of NSs of BNS and of the secondaries of NSBH systems detected so far through GWs, and that (ii) GW190814 is an outlier from the population of observed BBHs. These findings support the idea that GW190814 belongs to a distinct population of merging compact-object binaries.
Understanding the formation and evolutionary history of GW190814 is challenging for all current astrophysical models. The challenge is to find a theoretical model that can accommodate, at the same time, the GW190814 mass ratio, masses, and the LVC inferred merger rate. As already discussed in Section 2, most theoretical models do not have predictive power on the nature of compact objects and only a mass-threshold criterion is used to distinguish between NSs and BHs. Thus, depending on the adopted threshold, GW190814-like events might be marked as either NSBH or BBH mergers.
GW190814-like systems are outliers in terms of rates, masses, and mass ratios in most of the distributions of merging NSBH and merging BBH systems predicted by isolated binary evolution models [37,43,218,222,315,318,320,338,507,508,509,510]. Zevin et al. [507] identified two possible formation channels for GW190814-like systems, but (i) they form only if the delayed supernova explosion mechanism is adopted (see also Section 2.5), and (ii) their merger rates are at least one order of magnitude below the inferred LVC rates. Furthermore, Zevin et al. [507] showed that the mass of GW190814’s secondary is likely its birth mass, therefore GW190814 might give insights on the existence of the lower mass gap and, possibly, on the supernova explosion engine. It is worth mentioning that, in the isolated binary scenario, unlimited super-Eddington accretion onto compact objects might be the key to obtain significantly higher merger rates for GW190814-like systems, within the LVC inferred rate (see e.g., [511,512]).
GW190814 might be a second-generation merger event from a hierarchical triple system [61,439,447,457,513,514,515]. This is not an exotic formation pathway for GW190814, considering that most massive B-type stars, ≳, are in triples and the percentage tends to increase in low-metallicity environments (see also Section 4.6) [287,437,438,516,517,518,519,520,521]. Compared to the population of BH mergers from the isolated binary channel, mergers in triples tend to enhance the number of mergers with more unequal masses, resulting in a flatter mass-ratio distribution down to [61,457]. In this context, a possible formation pathway for GW190814 is that the members of the inner binary are two stars that evolve through the CE process and form a tight BNS system. The latter merges within a Hubble time, leaving a low-mass (∼), highly-spinning BH. The tertiary body is a star that turns into a ∼BH at its death. Lu et al. [513] show that there is a non-negligible chance that, at its formation, the low-mass BH is kicked into a low angular momentum orbit so that it can merge with the tertiary compact object within a Hubble time. The merger rate of GW190814-like sources obtained through this channel is consistent with the one inferred in Abbott et al. [81], provided that ≳ of BNS mergers occur in triples and that the tertiary orbital semi-major axis is less than a few au. A high spin of the low-mass BH would be a distinguishing feature of this scenario, but it cannot be corroborated through the analysis of the GW190814 signal because of the uninformative spin posterior of the secondary. Cholis et al. [515] investigated the same formation scenario and obtained similar results as Lu et al. [513], but they considered the possibility that the secondary of GW190814 is a Thorne–Zytkow object, i.e., a metastable object formed from the collision of a NS with a red giant star, possibly turning into a low-mass BH at the end if its life [522]. The local merger rate density from the latter channel can be as high as a few , which is within the LVC inferred rate.
Other authors investigated similar dynamical formation pathways for GW190814 involving systems with higher multiplicity, e.g., hierarchical quadruples [523,524,525,526], finding similar results.
GW190814-like systems might form in dense stellar environments through binary-single dynamical exchanges. However, the dynamical scenario favors the formation of compact-object binaries with similar masses (), pairing up the most massive objects (e.g., BHs and their stellar progenitors) in the dense cores of clusters, while low-mass objects (e.g., NSs) are likely ejected from the cluster during close three-body gravitational interactions (see also Section 4) [27,50,51,55,57,275,319,371,527,528]. In contrast, direct GW captures coming from single-single gravitational interactions seem to be exceedingly rare events [419]. Numerical simulations of GCs [529,530,531,532] and binary-single scattering experiments in GC-like environments [533,534,535] show that the local merger-rate density of GW190814-like systems is ≲, well below the single-event rate inferred by the LVC (). YDSCs might also have an impact in the formation of GW190814-like systems. In contrast to GCs, the dynamical evolution of YDSCs proceeds on much shorter timescales, and they are thought to be the nurseries of massive stars and the building blocks of galaxies. Furthermore, YDSCs form continuously in the Universe, at all redshifts, thus their contribution to the local merger-rate densities of merging compact-object binaries may potentially be higher than that of GCs [27,214,474,535,536]. Specifically, the N-body simulations of YDSCs presented in Rastello et al. [474] support a dynamical formation scenario for GW190814, with an estimated local merger-rate density of GW190814-like systems of . Most of the merging NSBH systems presented in Rastello et al. [474] come from dynamically-perturbed original binaries (i.e., from progenitor stars already bound in the initial conditions, but that would not have formed a merging NSBH if evolved in isolation). Furthermore, all mergers happened in the field because all the progenitor binaries were ejected from the star cluster before the binary members reach coalescence (i.e., hybrid scenario, see Section 1 and Section 4.7). In contrast, Fragione and Banerjee [431] performed direct N-body simulations of 65 YDSCs and estimated the local NSBH merger-rate density for these environments to be . However, Fragione and Banerjee [431] and Rastello et al. [474] consider different types of clusters with different initial masses and concentrations, different NS birth kick models, and different fractions of the cosmic star-formation rate that goes into clusters.
GW190814-like systems may also form in AGN. In such crowded environments, the gas-driven formation mechanisms and the hardening process of binaries are effective and gas accretion on compact objects with birth mass ≲ might be high enough to bring them in (or even beyond) the low-mass gap, before they merge with another compact objects [383,384,537]. Furthermore, the secondary of GW190814 might also be a compact object coming from a previous merger event in an AGN disk. This is not an exotic scenario because merger products are easily retained in AGN thanks to high escape speeds, thus next-generation compact objects can participate in additional mergers [537,538]. Specifically, McKernan et al. [383], McKernan et al. [384] show that the typical value for the mass ratio of the population of NSBH mergers in AGN disks is , with a corresponding local merger rate of about a few , both compatible with GW190814.
Bombaci et al. [539] discussed the hypothesis that the secondary of GW190814 is a strange quark star, which is a non-ordinary NS composed of a deconfined mixture of up, down and strange quarks. The authors showed that quark stars can reach masses comparable to the secondary of GW190814 while using physically motivated equations of state for hadrons and quarks, and without assuming an exceedingly large speed of sound.
Various authors investigated the hypothesis of the secondary component of GW190814 being a primordial BH, i.e., a BH formed from density fluctuations in the early Universe, a fraction of second after the big bang [540,541]. Vattis et al. [541] show that the member is rather unlikely to be a primordial BH because the typical time needed for a primordial BH to pair and then merge with a , stellar-origin BH is very close to (or even larger than) the age of the Universe, contradicting the GW190814 detection (but see also [542,543]).
It is apparent that the parameter space relevant for GW190814-like systems still needs to be fully explored and future GW detections will be crucial to shed light on the nature and formation channels of GW190814-like systems.
5.2. GW190521
GW190521 is currently the GW event with the heaviest BHs in the catalog [80]. The masses of the two BHs are and , respectively, and the mass of the merger product is [82,83]. The mass of the primary BH falls confidently into the hypothesized upper mass gap (–) and the merger product is the first strong observational evidence for the existence of intermediate-mass BHs (∼–).
Being the shortest-duration signal among the GW detections, GW190521 is a quite difficult event to analyze and measurements of spins and their in-plane components are quite uncertain. The data analysis presented in Abbott et al. [82] supports mild evidences for in-plane spin components with high spin magnitudes for both the BHs, but the values of the BH dimensionless spins remain uninformative at 90% credible intervals (i.e., ∼ 0.1–0.9). The hypotheses of a non-precessing signal with orbital eccentricity at 10 Hz [544] and of a precessing signal with orbital eccentricity [545] cannot be excluded, even though various authors suggest that GW190521-like binaries likely enter the 10 Hz-band with (e.g., [546]). Furthermore, subsequent analysis of the LVC data brought out the intriguing possibility of GW190521 being an intermediate-mass ratio inspiral, with and [195,547].
The formation channel of GW190521 is uncertain. The physical properties of the event seem to favor the dynamical formation pathway, while an explanation through the isolated binary channel is challenging.
Population-synthesis simulations of binary stars show that the most massive BBHs that can form at a given metallicity are unlikely to merge within a Hubble time, making it hard to even explain the formation of systems with lower masses, such as GW170729 [222]. In contrast, Belczynski [350] shows that if heavy () progenitor stars are considered and a very low 12C(, )16O rate is adopted ( with respect to the fiducial value of Farmer et al. [193]), the isolated-binary channel becomes a plausible formation pathway for GW190521. [219] found that GW190521-like systems can be formed from population III (Pop III) binaries, but only for stellar evolution models with a small convective overshooting parameter.
The hypothesis of repeated mergers in dense stellar systems seems to be a promising scenario to explain GW190521 [276,526,548,549,550,551,552,553].
The escape speed of GCs may be higher than the GW recoil kick imparted to some second-generation BHs, especially if BHs are born with low spins. Thus, second-generation BHs can be retained in GCs and Rodriguez et al. [275] show that the fraction of merging BBHs that have components formed from previous mergers in GCs can be ≳ ≳ for the detectable population. Kimball et al. [553] created a phenomenological population model for merging BBHs derived from [275], and they use that to infer the population properties of BH mergers in the second LVC catalog, finding that the members of GW190521 are likely second-generation (2 g) BHs. Triple systems in GCs may further enhance the retention probability of 2 g BHs, strengthening the Kimball et al. [553] and Rodriguez et al. [275] findings (e.g., [456]). Repeated minor mergers (>2 g) might also have formed the BHs of GW190521 but only in environments with escape velocities ≳ , such as the most massive GCs or nuclear star clusters (e.g., [448,548]).
The escape speed of YDSCs is significantly smaller than globular and nuclear star clusters, thus second-generation BH mergers are expected to be exceedingly rare in such environments [549,554]. However, [63,215,555,556] show that GW190521-like systems can still form in YDSCs via three-body encounters or multiple stellar mergers. In the latter scenario, a heavy BH can originate from the merger of an evolved star with a main-sequence star. If the helium core of the primary star is small enough to avoid PISN and the secondary star is still on the main-sequence, the merger product might be an evolved star with an oversized hydrogen envelope. If a significant fraction of the hydrogen envelope is retained and participate in the final collapse, a BH in the PISN mass gap can form [222]. Such heavy, single BHs can acquire a companion in dense stellar environments and explain the formation of GW190521-like systems. Furthermore, BHs born via this mechanism can preserve most of the spin of the progenitor star, leading to a high-spin BH even if they are 1 g BHs [170], in agreement with the properties of GW190521, even though the efficiency of angular momentum transport inside stars is matter of debate [197]. The same formation pathway has been identified also in GCs [223,557]. It is worth noting that, as in GCs, triple systems in YDSCs may enhance the overall retention probability of 2 g BHs, making the 2 g-channel for GW190521 a viable possibility also for such environments.
Palmese and Conselice [558] investigated the hypothesis that the two BHs of GW190521 were at the centers of two ultra-dwarf galaxies, assuming an extrapolation of the low-end of the central BH-galaxy mass relation (e.g., [559]). This scenario assumes that, after the merger of the two galaxies, the central BHs can merge, and the merger rates for GW190521-like systems from this channel match well those inferred by the LVC.
In AGN, Tagawa et al. [537] show that GW190521-like systems can form either via repeated mergers (>2 g at high metallicity, 2 g at low metallicity), or via mergers of 1g BHs that have grown via super-Eddington accretion. In such gas-rich environments, the interaction between the GW-recoiled merger product and the accretion disk of the active galactic nucleus might generate a delayed (∼days after the merger), off-center UV flare, potentially detectable as an electromagnetic transient counterpart of the GW event [560]. About 26 days after the merger of GW190521, the Zwicky transient facility [561] identified a flare from the AGN J124942.3 + 344929, the latter located at the 78% spatial contour and within from the peak marginal luminosity distance of GW190521. Graham et al. [562] identified the flare as a plausible electromagnetic counterpart to the BBH merger GW190521 (ZTF19abanrhr). While the possibility is intriguing and it is a possible distinguishing feature of the AGN formation scenario, the 90% localization area of GW190521 contains thousands of AGN and, currently, it is not possible to establish whether GW190521-ZTF19abanrhr is a real association or a chance coincidence [561,563]. Future high-mass detections and follow-up investigations will be crucial to shed light on this interesting possibility.
Various authors suggest Pop III stars as promising progenitors of the BHs members of GW190521 [207,220,221,321,564]. The key idea is that Pop III stars might retain most of their hydrogen envelope until the end of their life and might form heavy BHs via direct collapse, with masses up to ∼. Specifically, Liu and Bromm [221] investigated a simplified binary evolution scenario, with an initial binary population taken from N-body simulations of Pop III star clusters [565], and the dynamical hardening process of binaries in high-redshift () nuclear star clusters. The authors show that both the scenarios can explain the masses and merger rates of GW190521-like systems. In the same context, Safarzadeh and Haiman [218] developed an illustrative toy model showing that the collapse of relatively massive Pop III stars in high-redshift minihalos can form BH seeds that, in , can double their mass via gas accretion, reach the PISN mass gap, and then merge within a Hubble time, explaining the formation of GW190521. Similar results were obtained by Rice and Zhang [566], who investigated the growth of stellar BH seeds in dense molecular clouds.
De Luca et al. [567] studied the hypothesis of a primordial BH origin for GW190521. Their in-depth analysis shows that the primordial BH scenario is unlikely for GW190521 only if primordial BHs do not accrete mass during their cosmological evolution. In contrast, if accretion is efficient (see also [568]), the scenario can explain the properties of GW190521, including the mild evidence for high BH spins with non-zero in-plane components (see also [569]). A mixed scenario for GW190521-like systems, where primordial BHs coexist, interact and possibly merge with astrophysical (stellar-origin) BHs in dense stellar environments, is also a viable formation scenario [570].
More exotic explanations for the massive BHs of GW190521 are conceivable, and they have been investigated by various authors. They include horizonless vector boson stars, beyond-standard-model physics affecting the edges of the upper mass gap, and dark matter annihilation within stars to avoid PISNe (e.g., [208,571,572]).
5.3. GW190412
At the time of its detection, GW190412 was the first GW event with support for asymmetric masses, and the one with the strongest constraint on the individual spin magnitude of the primary BH [573]. The masses of the BHs are and , and the mass ratio is . The signal shows a mild evidence of precession coming from non-zero, in-plane spin components, with at 90% credibility. The LVC analysis reports a dimensionless spin of the primary BH of , at 90% credibility, obtained using uninformative priors for the spins of both the compact objects ().
In contrast, Mandel and Fragos [574] chose an informative spin prior, assuming that the event formed via the isolated binary channel, and they suggested an alternative interpretation of GW190412 as a merging BBH with a non-spinning primary and a rapidly spinning (tidally spun-up) secondary. Zevin et al. [575] studied the impact of different spin prior assumptions on the analysis of GW190412 and they found that the uninformative prior with both BHs spinning is preferred over other configurations.
Multiple scenarios can explain the formation of GW190412. As already discussed for GW190814, most of the merging BHs that originate from the isolated binary channel have mass ratios , but the tail of the mass-ratio distributions extends down to q∼, especially in low-metallicity environments [37,42,43,222,315,338,509]. Furthermore, the assumption of super-Eddington accretion onto compact objects might significantly increase the number of merging systems with [511,512]. Thus, GW190412 cannot be considered as an outlier for the isolated binary scenario in terms of masses and mass ratio. The moderately high spin of the primary BH may be difficult to reconcile with the isolated channel [218,284], but the uncertainties on the rotation speed and on the dominant mechanisms for angular momentum transport inside massive stars hamper our knowledge of the birth-spin distribution of stellar BHs.
First-generation, highly spinning BHs can form if their progenitor stars undergo CHE, but most of the BHs originating from this channel have large and nearly equal masses, making this scenario unlikely to explain GW190412 [39,40,41,576].
Repeated mergers of BHs in dense stellar environments might explain the mass ratio and the spin of the primary BH of GW190412. Assuming that BHs have negligible spins at birth, Rodriguez et al. [577] show that GW190412-like systems can form in super star clusters with central escape speeds of, at least, and that such events are consistent with a first-generation BH of ∼ merging with a BH formed from the subsequent merger of three ∼ BHs (i.e., a third-generation BH). Gerosa et al. [578] also support the hierarchical merger scenario in dynamical environments with central escape speeds ≳ , but they discussed the possibility of the primary of GW190412 being a second-generation BH.
The higher central escape speeds of NSCs and AGN can significantly enhance the retention fraction of >1-generation BH mergers, thus naturally producing hierarchical-merger events compatible with GW190412 [56,285,430,579].
On the other hand, Di Carlo et al. [63] and Rastello et al. [474] show that GW190412-like systems can also form in metal-poor YDSCs, but from merging first-generation BHs, because the central escape speed of such clusters is too low to allow for any retention of >1-generation BHs and most binaries are ejected from the cluster before they reach coalescence.
A first-generation origin for GW190412 is also supported by the phenomenological approach to mergers in dense stellar environments presented in Kimball et al. [580] and by von Zeipel-Kozai-Lidov induced mergers in isolated triples [61,457]. The moderately high spin of the primary of GW190412 may be difficult to reconcile with first-generation BHs, even though, as already discussed, the birth spin of BHs is uncertain (see also Section 2.11).
The high spin of the primary BH, the mass ratio, and the masses of GW190412 can also be explained through hierarchical mergers in isolated quadruples [524,581].
5.4. GW200105_162426 and GW200115_042309
GW200105_162426 and GW200115_042309 (hereafter GW200105 and GW200115) are the first two GW events that are consistent with merging NSBH systems. During the first part of the third observing run, GW190426_152155 and GW190814 were also reported as possible merging NSBH candidates. However, the false alarm rate of GW190426_152155 was too high to claim a confirmed detection and the uncertain nature of the secondary compact object prevents us from considering GW190814 as a NSBH merger (see Section 5.1). GW200105 consists of a BH with mass and a NS of , while GW200115 hosts a BH with mass and a NS of , using high-spin priors, i.e., . The effective inspiral spin parameter of GW200105 is peaked at zero () with , while GW200115 has a mild preference for misaligned spins with and , with .
Mandel and Smith [582] reanalyzed the GW200115 signal using astrophysically-motivated spin priors and they obtained better constrains on the masses of the compact objects (, ) and a BH spin close to zero ().
The spins of the secondaries are unconstrained and no electromagnetic counterpart has been identified for both the events, in agreement with theoretical expectations for mixed binaries with low-spinning primary BHs (e.g., [583,584], but see [585]).
Taking GW200105 and GW200115 as representative of the whole NSBH population, the inferred merger rate is [84].
As possible formation channels, very similar considerations as for GW190814 apply here. Indeed, in theoretical models, GW190814 may be identified as either a NSBH or a BBH, depending on the mass threshold adopted to distinguish between BHs and NSs. The main difference with GW190814 is that the masses, mass ratios, and inferred rates of GW200105/GW200115-like events are consistent also with the isolated binary formation channel [34,43,315,318,320,338,507,508,512,586,587,588,589,590,591,592,593].
6. Summary
Merging compact-object binaries, especially BBHs, have been among the main characters of the astrophysical scene over the last years. This happened mainly thanks to the discovery of GWs, which gave us access to a new information medium. While the GW catalog continues its inexorable growth, our theoretical knowledge of the formation channels of merging compact objects is still very limited, and most of the parameter space which is relevant for the astrophysical interpretation of GW detections is unexplored.
In this work, we reviewed the main astrophysical processes that may drive the formation of merging compact-object binaries and the lessons learned so far through some exceptional GW events (e.g., GW190814, GW190521). We discussed the degeneracies of the astrophysical models and we showed that some of the uncertainties are large enough to prevent any conclusive statements on merging compact objects.
The main sources of uncertainties come from: (i) our knowledge of the evolution of massive stars (e.g., clumpiness and porosity of stellar winds, energy transport in radiation-dominated envelopes, overshooting) – in the next decades, the James Webb Space Telescope and the Extremely Large Telescope will provide crucial insights on the evolution of massive stars, especially those at low metallicity; (ii) the SN explosion mechanism (e.g., explodability dependence on progenitor’s structure, fallback amount, lower mass gap, pulsational pair-instability SNe, asymmetries in the ejecta) – improvements in self-consistent, 3D simulations will help us to shed light on the SN engine and its byproducts (e.g., compact remnants, yields); (iii) binary evolution processes (especially common envelope and the response of donors/accretors to mass transfer) – comparisons with self-consistent, hydrodynamic simulations of binary stars will be crucial to calibrate the main (free) parameters in population-synthesis simulations; (iv) direct N-body simulations of star clusters (e.g., they inherit the uncertainties on single and binary stellar evolution processes, and they are computationally challenging) – new software, natively developed for state-of-the-art computing accelerators (e.g., Graphics Processing Units), and coupled with up-to-date population-synthesis codes, will give us the opportunity to accurately study merging compact objects in very dense stellar environments, possibly up to the regime of dwarf galaxies.
Meanwhile, detections will not stop, and a stunning collection of GW events will soon be available. The forth observing run (O4) of the LVK collaboration is planned to start later this year (December 2022) [594]. Furthermore, the next years will see the birth of new, next-generation, ground-based and space-born interferometers (e.g., Einsten Telescope, Cosmic Explorer, LISA) that promise to reveal merging compact objects throughout the entire cosmic history and across a much broader frequency range.
Thus, we are heading for exciting times in the field of GWs, with new facilities and detections that will help us to push current astrophysical models beyond the state-of-the-art. In the next decades, such a synergy will be crucial to shed light on the evolutionary histories of merging compact-object binaries across cosmic time.
Author Contributions
Conceptualization: M.S. and A.A.T.; data curation: M.S., A.A.T. and M.M; writing—original draft preparation: M.S. and A.A.T.; writing—review and editing, M.S., A.A.T. and M.M.; software: M.S. and A.A.T.; supervision: M.S. All authors have read and agreed to the published version of the manuscript.
Funding
A.A.T. received support from JSPS KAKENHI Grant Numbers 17H06360, 19K03907 and 21K13914.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We are indebted to Mike Zevin for his careful reading of the review and for providing comments that helped us to improve the manuscript. We thank the anonymous referees for their careful reading of our manuscript and their insightful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AGN | active galactic nuclei |
| BBH | binary black hole |
| BH | black hole |
| BNS | binary neutron star |
| CO | carbon-oxygen |
| CE | common envelope |
| CHE | chemical homogeneous evolution |
| GC | globular cluster |
| GW | gravitational wave |
| GWTC | Gravitational Wave Transient Catalog |
| ECSN | electron-capture supernova |
| LIGO | Laser Interferometer Gravitational-wave Observatory |
| LVC | LIGO-Virgo Collaboration |
| LVK | LIGO-Virgo-KAGRA |
| NS | neutron star |
| NSBH | neutron star-black hole binary |
| NSC | nuclear star cluster |
| OC | open cluster |
| PISN | pair-instability supernova |
| Pop III | population III |
| PPISN | pulsational pair-instability supernova |
| SMBH | super-massive black hole |
| SN | supernova |
| TOV | Tolman–Oppenheimer–Volkoff |
| WD | white dwarf |
| YDSC | young dense star cluster |
| ZAMS | zero age main sequence |
| ZKL | von Zeipel-Kozai-Lidov |
Notes
| 1 | Throughout this work, we will use the symbol to refer to the Sun’s mass. |
| 2 | LIGO-Virgo-KAGRA (LVK)-independent analyses have even found a few additional GW candidates (e.g., [76,77,78]). |
| 3 | . |
| 4 | In cool supergiants () the mechanism responsible for winds is the absorption of photons by dust grains, i.e., dust- (or continuum-) driven winds. |
| 5 | It is worth noting that wind mass loss does not depend only on metallicity, but also on luminosity, effective temperature, stellar mass, and the velocity of wind at infinity. |
| 6 | , where m is a threshold mass in and is the radius enclosing m, in units of 1000 km. |
| 7 | It is worth noting that a PISN is driven by a thermonuclear explosion, i.e., very different from neutrino-driven core-collapse SNe. |
References
- Zel’dovich, Y.B.; Podurets, M.A. The Evolution of a System of Gravitationally Interacting Point Masses. Sov. Astron. 1966, 9, 742. [Google Scholar]
- Rees, M.; Ruffini, R.; Wheeler, J.A. Black Holes, Gravitational Waves, and Cosmology: An Introduction to Current Research; Gordon and Breach: New York, NY, USA, 1974. [Google Scholar]
- Lattimer, J.M.; Schramm, D.N. Black-Hole-Neutron-Star Collisions. Astrophys. J. 1974, 192, L145. [Google Scholar] [CrossRef]
- Clark, J.P.A.; Eardley, D.M. Evolution of close neutron star binaries. Astrophys. J. 1977, 215, 311–322. [Google Scholar] [CrossRef]
- Clark, J.P.A.; van den Heuvel, E.P.J.; Sutantyo, W. Formation of neutron star binaries and their importance for gravitational radiation. Astron. Astrophys. 1979, 72, 120–128. [Google Scholar]
- Hils, D.; Bender, P.L.; Webbink, R.F. Gravitational Radiation from the Galaxy. Astrophys. J. 1990, 360, 75. [Google Scholar] [CrossRef]
- Narayan, R.; Piran, T.; Shemi, A. Neutron Star and Black Hole Binaries in the Galaxy. Astrophys. J. 1991, 379, L17. [Google Scholar] [CrossRef]
- Phinney, E.S. The Rate of Neutron Star Binary Mergers in the Universe: Minimal Predictions for Gravity Wave Detectors. Astrophys. J. 1991, 380, L17. [Google Scholar] [CrossRef]
- Tutukov, A.V.; Yungelson, L.R. The merger rate of neutron star and black hole binaries. Mon. Not. R. Astron. Soc. 1993, 260, 675–678. [Google Scholar] [CrossRef]
- Einstein, A. Über Gravitationswellen. In Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften (Berlin); Deutsche Akademie der Wissenschaften zu Berlin: Berlin, Germany, 1918; pp. 154–167. [Google Scholar]
- Hulse, R.A.; Taylor, J.H. Discovery of a pulsar in a binary system. Astrophys. J. 1975, 195, L51–L53. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Astrophysical implications of the binary black hole merger GW150914. Astrophys. J. 2016, 818, L22. [Google Scholar] [CrossRef]
- Klimenko, S.; Yakushin, I.; Mercer, A.; Mitselmakher, G. A coherent method for detection of gravitational wave bursts. Class. Quantum Gravity 2008, 25, 114029. [Google Scholar] [CrossRef]
- Lynch, R.; Vitale, S.; Essick, R.; Katsavounidis, E.; Robinet, F. An information-theoretic approach to the gravitational-wave burst detection problem. arXiv 2015, arXiv:1511.05955. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; et al. GW150914: First results from the search for binary black hole coalescence with Advanced LIGO. Phys. Rev. D 2016, 93, 122003. [Google Scholar] [CrossRef]
- Özel, F.; Psaltis, D.; Narayan, R.; McClintock, J.E. The Black Hole Mass Distribution in the Galaxy. Astrophys. J. 2010, 725, 1918–1927. [Google Scholar] [CrossRef]
- Farr, W.M.; Sravan, N.; Cantrell, A.; Kreidberg, L.; Bailyn, C.D.; Mandel, I.; Kalogera, V. The Mass Distribution of Stellar-mass Black Holes. Astrophys. J. 2011, 741, 103. [Google Scholar] [CrossRef]
- Fishbach, M.; Kalogera, V. Apples and Oranges: Comparing black holes in X-ray binaries and gravitational-wave sources. arXiv 2021, arXiv:2111.02935. [Google Scholar] [CrossRef]
- Heger, A.; Fryer, C.L.; Woosley, S.E.; Langer, N.; Hartmann, D.H. How Massive Single Stars End Their Life. Astrophys. J. 2003, 591, 288–300. [Google Scholar] [CrossRef]
- Mapelli, M.; Colpi, M.; Zampieri, L. Low metallicity and ultra-luminous X-ray sources in the Cartwheel galaxy. Mon. Not. R. Astron. Soc. 2009, 395, L71–L75. [Google Scholar] [CrossRef]
- Spera, M.; Mapelli, M.; Bressan, A. The mass spectrum of compact remnants from the PARSEC stellar evolution tracks. Mon. Not. R. Astron. Soc. 2015, 451, 4086–4103. [Google Scholar] [CrossRef]
- Mapelli, M.; Zampieri, L.; Ripamonti, E.; Bressan, A. Dynamics of stellar black holes in young star clusters with different metallicities—I. Implications for X-ray binaries. Mon. Not. R. Astron. Soc. 2013, 429, 2298–2314. [Google Scholar] [CrossRef]
- Belczynski, K.; Bulik, T.; Fryer, C.L.; Ruiter, A.; Valsecchi, F.; Vink, J.S.; Hurley, J.R. On the Maximum Mass of Stellar Black Holes. Astrophys. J. 2010, 714, 1217–1226. [Google Scholar] [CrossRef]
- Woosley, S.E.; Heger, A.; Weaver, T.A. The evolution and explosion of massive stars. Rev. Mod. Phys. 2002, 74, 1015–1071. [Google Scholar] [CrossRef]
- Fryer, C.L.; Belczynski, K.; Wiktorowicz, G.; Dominik, M.; Kalogera, V.; Holz, D.E. Compact Remnant Mass Function: Dependence on the Explosion Mechanism and Metallicity. Astrophys. J. 2012, 749, 91. [Google Scholar] [CrossRef]
- Ziosi, B.M.; Mapelli, M.; Branchesi, M.; Tormen, G. Dynamics of stellar black holes in young star clusters with different metallicities—II. Black hole-black hole binaries. Mon. Not. R. Astron. Soc. 2014, 441, 3703–3717. [Google Scholar] [CrossRef]
- Webbink, R.F. Evolution of Helium White Dwarfs in Close Binaries. Mon. Not. R. Astron. Soc. 1975, 171, 555–568. [Google Scholar] [CrossRef]
- Paczynski, B. Common Envelope Binaries. In Structure and Evolution of Close Binary Systems; Eggleton, P., Mitton, S., Whelan, J., Eds.; Springer: Dordrecht, The Netherlands, 1976; Volume 73, p. 75. [Google Scholar]
- van den Heuvel, E.P.J. Late Stages of Close Binary Systems. In Structure and Evolution of Close Binary Systems; Eggleton, P., Mitton, S., Whelan, J., Eds.; Springer: Dordrecht, The Netherlands, 1976; Volume 73, p. 35. [Google Scholar]
- Hut, P. Tidal evolution in close binary systems. Astron. Astrophys. 1981, 99, 126–140. [Google Scholar]
- Webbink, R.F. Double white dwarfs as progenitors of R Coronae Borealis stars and type I supernovae. Astrophys. J. 1984, 277, 355–360. [Google Scholar] [CrossRef]
- Bethe, H.A.; Brown, G.E. Evolution of Binary Compact Objects That Merge. Astrophys. J. 1998, 506, 780–789. [Google Scholar] [CrossRef]
- Belczynski, K.; Kalogera, V.; Bulik, T. A Comprehensive Study of Binary Compact Objects as Gravitational Wave Sources: Evolutionary Channels, Rates, and Physical Properties. Astrophys. J. 2002, 572, 407–431. [Google Scholar] [CrossRef]
- Hurley, J.R.; Tout, C.A.; Pols, O.R. Evolution of binary stars and the effect of tides on binary populations. Mon. Not. R. Astron. Soc. 2002, 329, 897–928. [Google Scholar] [CrossRef]
- de Mink, S.E.; Cantiello, M.; Langer, N.; Yoon, S.C.; Brott, I.; Glebbeek, E.; Verkoulen, M.; Pols, O.R. Rotational mixing in close binaries. In The Art of Modeling Stars in the 21st Century, Proceedings of the International Astronomical Union (IAU) Symposium, Sanya, China, 6–11 April 2008; Deng, L., Chan, K.L., Eds.; Cambridge University Press: Cambridge, UK, 2008; Volume 252, pp. 365–370. [Google Scholar] [CrossRef]
- Dominik, M.; Belczynski, K.; Fryer, C.; Holz, D.E.; Berti, E.; Bulik, T.; Mandel, I.; O’Shaughnessy, R. Double Compact Objects. I. The Significance of the Common Envelope on Merger Rates. Astrophys. J. 2012, 759, 52. [Google Scholar] [CrossRef]
- Postnov, K.A.; Yungelson, L.R. The Evolution of Compact Binary Star Systems. Living Rev. Relativ. 2014, 17, 3. [Google Scholar] [CrossRef] [PubMed]
- de Mink, S.E.; Mandel, I. The chemically homogeneous evolutionary channel for binary black hole mergers: Rates and properties of gravitational-wave events detectable by advanced LIGO. Mon. Not. R. Astron. Soc. 2016, 460, 3545–3553. [Google Scholar] [CrossRef]
- Mandel, I.; de Mink, S.E. Merging binary black holes formed through chemically homogeneous evolution in short-period stellar binaries. Mon. Not. R. Astron. Soc. 2016, 458, 2634–2647. [Google Scholar] [CrossRef]
- Marchant, P.; Langer, N.; Podsiadlowski, P.; Tauris, T.M.; Moriya, T.J. A new route towards merging massive black holes. Astron. Astrophys. 2016, 588, A50. [Google Scholar] [CrossRef]
- Stevenson, S.; Vigna-Gómez, A.; Mandel, I.; Barrett, J.W.; Neijssel, C.J.; Perkins, D.; de Mink, S.E. Formation of the first three gravitational-wave observations through isolated binary evolution. Nat. Commun. 2017, 8, 14906. [Google Scholar] [CrossRef]
- Giacobbo, N.; Mapelli, M. The progenitors of compact-object binaries: Impact of metallicity, common envelope and natal kicks. Mon. Not. R. Astron. Soc. 2018, 480, 2011–2030. [Google Scholar] [CrossRef]
- Zevin, M.; Bavera, S.S.; Berry, C.P.L.; Kalogera, V.; Fragos, T.; Marchant, P.; Rodriguez, C.L.; Antonini, F.; Holz, D.E.; Pankow, C. One Channel to Rule Them All? Constraining the Origins of Binary Black Holes Using Multiple Formation Pathways. Astrophys. J. 2021, 910, 152. [Google Scholar] [CrossRef]
- Heggie, D.C. Binary Evolution in Stellar Dynamics. Mon. Not. R. Astron. Soc. 1975, 173, 729–787. [Google Scholar] [CrossRef]
- Lightman, A.P.; Shapiro, S.L. The dynamical evolution of globular clusters. Rev. Mod. Phys. 1978, 50, 437–481. [Google Scholar] [CrossRef]
- Hills, J.G.; Fullerton, L.W. Computer simulations of close encounters between single stars and hard binaries. Astron. J. 1980, 85, 1281–1291. [Google Scholar] [CrossRef]
- McMillan, S.; Hut, P.; Makino, J. Star Cluster Evolution with Primordial Binaries. II. Detailed Analysis. Astrophys. J. 1991, 372, 111. [Google Scholar] [CrossRef]
- Hut, P.; McMillan, S.; Goodman, J.; Mateo, M.; Phinney, E.S.; Pryor, C.; Richer, H.B.; Verbunt, F.; Weinberg, M. Binaries in Globular Clusters. Publ. Astron. Soc. Pac. 1992, 104, 981. [Google Scholar] [CrossRef]
- Sigurdsson, S.; Hernquist, L. Primordial black holes in globular clusters. Nature 1993, 364, 423–425. [Google Scholar] [CrossRef]
- Zwart, S.F.P.; McMillan, S.L.W. Black Hole Mergers in the Universe. Astrophys. J. 2000, 528, L17–L20. [Google Scholar] [CrossRef]
- Miller, M.C.; Hamilton, D.P. Four-Body Effects in Globular Cluster Black Hole Coalescence. Astrophys. J. 2002, 576, 894–898. [Google Scholar] [CrossRef]
- O’Leary, R.M.; Rasio, F.A.; Fregeau, J.M.; Ivanova, N.; O’Shaughnessy, R. Binary Mergers and Growth of Black Holes in Dense Star Clusters. Astrophys. J. 2006, 637, 937–951. [Google Scholar] [CrossRef]
- Downing, J.M.B.; Benacquista, M.J.; Giersz, M.; Spurzem, R. Compact binaries in star clusters—I. Black hole binaries inside globular clusters. Mon. Not. R. Astron. Soc. 2010, 407, 1946–1962. [Google Scholar] [CrossRef]
- Rodriguez, C.L.; Morscher, M.; Pattabiraman, B.; Chatterjee, S.; Haster, C.J.; Rasio, F.A. Binary Black Hole Mergers from Globular Clusters: Implications for Advanced LIGO. Phys. Rev. Lett. 2015, 115, 051101. [Google Scholar] [CrossRef]
- Antonini, F.; Rasio, F.A. Merging Black Hole Binaries in Galactic Nuclei: Implications for Advanced-LIGO Detections. Astrophys. J. 2016, 831, 187. [Google Scholar] [CrossRef]
- Mapelli, M. Massive black hole binaries from runaway collisions: The impact of metallicity. Mon. Not. R. Astron. Soc. 2016, 459, 3432–3446. [Google Scholar] [CrossRef]
- Kimpson, T.O.; Spera, M.; Mapelli, M.; Ziosi, B.M. Hierarchical black hole triples in young star clusters: Impact of Kozai–Lidov resonance on mergers. Mon. Not. R. Astron. Soc. 2016, 463, 2443–2452. [Google Scholar] [CrossRef]
- Banerjee, S. Stellar-mass black holes in young massive and open stellar clusters and their role in gravitational-wave generation. Mon. Not. R. Astron. Soc. 2017, 467, 524–539. [Google Scholar] [CrossRef]
- Samsing, J.; Ramirez-Ruiz, E. On the Assembly Rate of Highly Eccentric Binary Black Hole Mergers. Astrophys. J. 2017, 840, L14. [Google Scholar] [CrossRef]
- Trani, A.A.; Rastello, S.; Carlo, U.N.D.; Santoliquido, F.; Tanikawa, A.; Mapelli, M. Compact object mergers in hierarchical triples from low-mass young star clusters. Mon. Not. R. Astron. Soc. 2022, 511, 1362–1372. [Google Scholar] [CrossRef]
- Kumamoto, J.; Fujii, M.S.; Tanikawa, A. Gravitational-wave emission from binary black holes formed in open clusters. Mon. Not. R. Astron. Soc. 2019, 486, 3942–3950. [Google Scholar] [CrossRef]
- Di Carlo, U.N.; Mapelli, M.; Giacobbo, N.; Spera, M.; Bouffanais, Y.; Rastello, S.; Santoliquido, F.; Pasquato, M.; Ballone, A.; Trani, A.A.; et al. Binary black holes in young star clusters: The impact of metallicity. Mon. Not. R. Astron. Soc. 2020, 498, 495–506. [Google Scholar] [CrossRef]
- Trani, A.A.; Tanikawa, A.; Fujii, M.S.; Leigh, N.W.C.; Kumamoto, J. Spin misalignment of black hole binaries from young star clusters: Implications for the origin of gravitational waves events. Mon. Not. R. Astron. Soc. 2021, 504, 910–919. [Google Scholar] [CrossRef]
- Arca Sedda, M.; Mapelli, M.; Benacquista, M.; Spera, M. Population synthesis of black hole mergers with B-POP: The impact of dynamics, natal spins, and intermediate-mass black holes on the population of gravitational wave sources. arXiv 2021, arXiv:2109.12119. [Google Scholar]
- Mikkola, S.; Aarseth, S.J. An efficient integration method for binaries in N-body simulations. New Astron. 1998, 3, 309–320. [Google Scholar] [CrossRef]
- Aarseth, S.J. Regularization tools for binary interactions. In Astrophysical Supercomputing Using Particle Simulations, Proceedings of the IAU Symposium n.208, Tokyo, Japan, 10–13 July 2001; Makino, J., Hut, P., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2003; Volume 208, p. 295. [Google Scholar]
- Konstantinidis, S.; Kokkotas, K.D. MYRIAD: A new N-body code for simulations of star clusters. Astron. Astrophys. 2010, 522, A70. [Google Scholar] [CrossRef][Green Version]
- Hypki, A.; Giersz, M. Mocca code for star cluster simulations—I. Blue stragglers, first results. Mon. Not. R. Astron. Soc. 2012, 429, 1221–1243. [Google Scholar] [CrossRef]
- Capuzzo-Dolcetta, R.; Spera, M.; Punzo, D. A fully parallel, high precision, N-body code running on hybrid computing platforms. J. Comput. Phys. 2013, 236, 580–593. [Google Scholar] [CrossRef]
- Capuzzo-Dolcetta, R.; Spera, M. A performance comparison of different graphics processing units running direct N-body simulations. Comput. Phys. Commun. 2013, 184, 2528–2539. [Google Scholar] [CrossRef][Green Version]
- Rodriguez, C.L.; Morscher, M.; Wang, L.; Chatterjee, S.; Rasio, F.A.; Spurzem, R. Million-body star cluster simulations: Comparisons between Monte Carlo and direct N-body. Mon. Not. R. Astron. Soc. 2016, 463, 2109–2118. [Google Scholar] [CrossRef]
- Maureira-Fredes, C.; Amaro-Seoane, P. GraviDy, a GPU modular, parallel direct-summation N-body integrator: Dynamics with softening. Mon. Not. R. Astron. Soc. 2017, 473, 3113–3127. [Google Scholar] [CrossRef]
- Wang, L.; Iwasawa, M.; Nitadori, K.; Makino, J. PETAR: A high-performance N-body code for modelling massive collisional stellar systems. Mon. Not. R. Astron. Soc. 2020, 497, 536–555. [Google Scholar] [CrossRef]
- Mencagli, M.; Nazarova, N.; Spera, M. ISTEDDAS: A new direct N-Body code to study merging compact-object binaries. J. Phys. Conf. Ser. 2022, 2207, 012051. [Google Scholar] [CrossRef]
- Nitz, A.H.; Capano, C.D.; Kumar, S.; Wang, Y.F.; Kastha, S.; Schäfer, M.; Dhurkunde, R.; Cabero, M. 3-OGC: Catalog of Gravitational Waves from Compact-binary Mergers. Astrophys. J. 2021, 922, 76. [Google Scholar] [CrossRef]
- Olsen, S.; Venumadhav, T.; Mushkin, J.; Roulet, J.; Zackay, B.; Zaldarriaga, M. New binary black hole mergers in the LIGO–Virgo O3a data. arXiv 2022, arXiv:2201.02252. [Google Scholar]
- Zackay, B.; Venumadhav, T.; Dai, L.; Roulet, J.; Zaldarriaga, M. Highly spinning and aligned binary black hole merger in the Advanced LIGO first observing run. Phys. Rev. D 2019, 100, 023007. [Google Scholar] [CrossRef]
- Abbott, R.; et al.; [The LIGO Scientific Collaboration]; [the Virgo Collaboration]; [the KAGRA Collaboration] GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run. arXiv 2021, arXiv:2111.03606. [Google Scholar]
- Abbott, R.; et al.; [The LIGO Scientific Collaboration]; [The Virgo Collaboration]; [The KAGRA Scientific Collaboration] The population of merging compact binaries inferred using gravitational waves through GWTC-3. arXiv 2021, arXiv:2111.03634. [Google Scholar]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. 2020, 896, L44. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190521: A Binary Black Hole Merger with a Total Mass of 150 M⊙. Phys. Rev. Lett. 2020, 125, 101102. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. Properties and Astrophysical Implications of the 150 M⊙ Binary Black Hole Merger GW190521. Astrophys. J. 2020, 900, L13. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Observation of Gravitational Waves from Two Neutron Star-Black Hole Coalescences. Astrophys. J. 2021, 915, L5. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Tiwari, V.; Fairhurst, S. The Emergence of Structure in the Binary Black Hole Mass Distribution. Astrophys. J. 2021, 913, L19. [Google Scholar] [CrossRef]
- Karathanasis, C.; Mukherjee, S.; Mastrogiovanni, S. Binary black holes population and cosmology in new lights: Signature of PISN mass and formation channel in GWTC-3. arXiv 2022, arXiv:2204.13495. [Google Scholar]
- Mukherjee, S. The redshift dependence of black hole mass distribution: Is it reliable for standard sirens cosmology? arXiv 2021, arXiv:2112.10256. [Google Scholar]
- Mapelli, M. Formation Channels of Single and Binary Stellar-Mass Black Holes. In Handbook of Gravitational Wave Astronomy; Springer: Singapore, 2021; p. 4. [Google Scholar] [CrossRef]
- Mandel, I.; Broekgaarden, F.S. Rates of compact object coalescences. Living Rev. Rel. 2022, 25, 1. [Google Scholar] [CrossRef]
- Eddington, A.S. On the relation between the masses and luminosities of the stars. Mon. Not. R. Astron. Soc. 1924, 84, 308–332. [Google Scholar] [CrossRef]
- Smartt, S.J. Progenitors of Core-Collapse Supernovae. Annu. Rev. Astron. Astrophys. 2009, 47, 63–106. [Google Scholar] [CrossRef]
- Horiuchi, S.; Beacom, J.F.; Kochanek, C.S.; Prieto, J.L.; Stanek, K.Z.; Thompson, T.A. The cosmic core-collapse supernova rate does not match the massive-star formation rate. Astrophys. J. 2011, 738, 154. [Google Scholar] [CrossRef]
- Smartt, S.J. Observational Constraints on the Progenitors of Core-Collapse Supernovae: The Case for Missing High-Mass Stars. Publ. Astron. Soc. Aust. 2015, 32, e016. [Google Scholar] [CrossRef]
- Aguirre, V.S. Stellar Evolution and Modelling Stars. Asteroseismology and Exoplanets: Listening to the Stars and Searching for New Worlds; Springer: Berlin/Heidelberg, Germany, 2017; pp. 3–25. [Google Scholar] [CrossRef]
- Vink, J.S. Theory and Diagnostics of Hot Star Mass Loss. arXiv 2021, arXiv:2109.08164. [Google Scholar] [CrossRef]
- Spera, M.; Mapelli, M. Very massive stars, pair-instability supernovae and intermediate-mass black holes with the sevn code. Mon. Not. R. Astron. Soc. 2017, 470, 4739–4749. [Google Scholar] [CrossRef]
- Bressan, A.; Marigo, P.; Girardi, L.; Salasnich, B.; Dal Cero, C.; Rubele, S.; Nanni, A. PARSEC: Stellar tracks and isochrones with the PAdova and TRieste Stellar Evolution Code. Mon. Not. R. Astron. Soc. 2012, 427, 127–145. [Google Scholar] [CrossRef]
- Chen, Y.; Bressan, A.; Girardi, L.; Marigo, P.; Kong, X.; Lanza, A. PARSEC evolutionary tracks of massive stars up to 350 M⊙ at metallicities 0.0001 ≤ Z ≤ 0.04. Mon. Not. R. Astron. Soc. 2015, 452, 1068–1080. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The highly collapsed configurations of a stellar mass (Second paper). Mon. Not. R. Astron. Soc. 1935, 95, 207–225. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Rhoades, C.E.; Ruffini, R. Maximum Mass of a Neutron Star. Phys. Rev. Lett. 1974, 32, 324–327. [Google Scholar] [CrossRef]
- Kalogera, V.; Baym, G. The Maximum Mass of a Neutron Star. Astrophys. J. 1996, 470, L61–L64. [Google Scholar] [CrossRef]
- Srinivasan, G. The maximum mass of neutron stars. Astron. Astrophys. Rev. 2002, 11, 67–96. [Google Scholar] [CrossRef]
- Margalit, B.; Metzger, B.D. Constraining the Maximum Mass of Neutron Stars from Multi-messenger Observations of GW170817. Astrophys. J. 2017, 850, L19. [Google Scholar] [CrossRef]
- Shibata, M.; Fujibayashi, S.; Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Sekiguchi, Y.; Tanaka, M. Modeling GW170817 based on numerical relativity and its implications. Phys. Rev. D 2017, 96, 123012. [Google Scholar] [CrossRef]
- Linares, M.; Shahbaz, T.; Casares, J. Peering into the Dark Side: Magnesium Lines Establish a Massive Neutron Star in PSR J2215 + 5135. Astrophys. J. 2018, 859, 54. [Google Scholar] [CrossRef]
- Alsing, J.; Silva, H.O.; Berti, E. Evidence for a maximum mass cut-off in the neutron star mass distribution and constraints on the equation of state. Mon. Not. R. Astron. Soc. 2018, 478, 1377–1391. [Google Scholar] [CrossRef]
- Rezzolla, L.; Most, E.R.; Weih, L.R. Using Gravitational-wave Observations and Quasi-universal Relations to Constrain the Maximum Mass of Neutron Stars. Astrophys. J. 2018, 852, L25. [Google Scholar] [CrossRef]
- Ruiz, M.; Shapiro, S.L.; Tsokaros, A. GW170817, general relativistic magnetohydrodynamic simulations, and the neutron star maximum mass. Phys. Rev. D 2018, 97, 021501. [Google Scholar] [CrossRef] [PubMed]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef]
- Li, Y.P.; Dempsey, A.M.; Li, S.; Li, H.; Li, J. Orbital Evolution of Binary Black Holes in Active Galactic Nucleus Disks: A Disk Channel for Binary Black Hole Mergers? Astrophys. J. 2021, 911, 124. [Google Scholar] [CrossRef]
- Li, A.; Miao, Z.; Han, S.; Zhang, B. Constraints on the Maximum Mass of Neutron Stars with a Quark Core from GW170817 and NICER PSR J0030 + 0451 Data. Astrophys. J. 2021, 913, 27. [Google Scholar] [CrossRef]
- Shibata, M.; Zhou, E.; Kiuchi, K.; Fujibayashi, S. Constraint on the maximum mass of neutron stars using GW170817 event. Phys. Rev. D 2019, 100, 023015. [Google Scholar] [CrossRef]
- Kashyap, R.; Das, A.; Radice, D.; Padamata, S.; Prakash, A.; Logoteta, D.; Perego, A.; Godzieba, D.A.; Bernuzzi, S.; Bombaci, I.E.A. Numerical relativity simulations of prompt collapse mergers: Threshold mass and phenomenological constraints on neutron star properties after GW170817. arXiv 2021, arXiv:2111.05183. [Google Scholar] [CrossRef]
- Friedman, J.L.; Ipser, J.R. On the Maximum Mass of a Uniformly Rotating Neutron Star. Astrophys. J. 1987, 314, 594. [Google Scholar] [CrossRef]
- Lasota, J.P.; Haensel, P.; Abramowicz, M.A. Fast Rotation of Neutron Stars. Astrophys. J. 1996, 456, 300. [Google Scholar]
- Lattimer, J.M.; Schutz, B.F. Constraining the Equation of State with Moment of Inertia Measurements. Astrophys. J. 2005, 629, 979–984. [Google Scholar] [CrossRef]
- Breu, C.; Rezzolla, L. Maximum mass, moment of inertia and compactness of relativistic stars. Mon. Not. R. Astron. Soc. 2016, 459, 646–656. [Google Scholar] [CrossRef]
- Saha, M.N. On Radiation-Pressure and the Quantum Theory. Astrophys. J. 1919, 50, 220. [Google Scholar] [CrossRef]
- Morton, D.C. Mass Loss from Three OB Supergiants in Orion. Astrophys. J. 1967, 150, 535. [Google Scholar] [CrossRef]
- Morton, D.C. The Far-Ultraviolet Spectra of Six Stars in Orion. Astrophys. J. 1967, 147, 1017. [Google Scholar] [CrossRef]
- Castor, J.I.; Abbott, D.C.; Klein, R.I. Radiation-driven winds in of stars. Astrophys. J. 1975, 195, 157–174. [Google Scholar] [CrossRef]
- Sobolev, V.V. Moving Envelopes of Stars; Harvard University Press: Cambridge, MA, USA, 1960. [Google Scholar]
- Kudritzki, R.P.; Pauldrach, A.; Puls, J. Radiation driven winds of hot luminous stars. II. Wind models for O-stars in the Magellanic clouds. Astron. Astrophys. 1987, 173, 293–298. [Google Scholar]
- Abbott, D.C. The theory of radiatively driven stellar winds. II. The line acceleration. Astrophys. J. 1982, 259, 282–301. [Google Scholar] [CrossRef]
- Abbott, D.C.; Lucy, L.B. Multiline transfer and the dynamics of stellar winds. Astrophys. J. 1985, 288, 679–693. [Google Scholar] [CrossRef]
- Vink, J.S.; de Koter, A.; Lamers, H.J.G.L.M. Mass-loss predictions for O and B stars as a function of metallicity. Astron. Astrophys. 2001, 369, 574–588. [Google Scholar] [CrossRef]
- Vink, J.S.; de Koter, A. On the metallicity dependence of Wolf-Rayet winds. Astron. Astrophys. 2005, 442, 587–596. [Google Scholar] [CrossRef]
- Sander, A.A.C.; Vink, J.S. On the nature of massive helium star winds and Wolf-Rayet-type mass-loss. Mon. Not. R. Astron. Soc. 2020, 499, 873–892. [Google Scholar] [CrossRef]
- Björklund, R.; Sundqvist, J.O.; Puls, J.; Najarro, F. New predictions for radiation-driven, steady-state mass-loss and wind-momentum from hot, massive stars. II. A grid of O-type stars in the Galaxy and the Magellanic Clouds. Astron. Astrophys. 2021, 648, A36. [Google Scholar] [CrossRef]
- Vink, J.S.; Muijres, L.E.; Anthonisse, B.; de Koter, A.; Gräfener, G.; Langer, N. Wind modelling of very massive stars up to 300 solar masses. Astron. Astrophys. 2011, 531, A132. [Google Scholar] [CrossRef]
- Vink, J.S.; de Koter, A. Predictions of variable mass loss for Luminous Blue Variables. Astron. Astrophys. 2002, 393, 543–553. [Google Scholar] [CrossRef]
- Yoon, S.C.; Cantiello, M. Evolution Of Massive Stars with Pulsation-Driven Superwinds during the Red Supergiant Phase. Astrophys. J. 2010, 717, L62–L65. [Google Scholar] [CrossRef]
- Tang, J.; Bressan, A.; Rosenfield, P.; Slemer, A.; Marigo, P.; Girardi, L.; Bianchi, L. New PARSEC evolutionary tracks of massive stars at low metallicity: Testing canonical stellar evolution in nearby star-forming dwarf galaxies. Mon. Not. R. Astron. Soc. 2014, 445, 4287–4305. [Google Scholar] [CrossRef]
- Gräfener, G.; Vink, J.S.; de Koter, A.; Langer, N. The Eddington factor as the key to understand the winds of the most massive stars. Evidence for a Γ-dependence of Wolf-Rayet type mass loss. Astron. Astrophys. 2011, 535, A56. [Google Scholar] [CrossRef]
- Gräfener, G.; Hamann, W.R. Mass loss from late-type WN stars and its Z-dependence. Very massive stars approaching the Eddington limit. Astron. Astrophys. 2008, 482, 945–960. [Google Scholar] [CrossRef]
- Davies, B.; Oudmaijer, R.D.; Vink, J.S. Asphericity and clumpiness in the winds of Luminous Blue Variables. Astron. Astrophys. 2005, 439, 1107–1125. [Google Scholar] [CrossRef]
- Puls, J.; Markova, N.; Scuderi, S.; Stanghellini, C.; Taranova, O.G.; Burnley, A.W.; Howarth, I.D. Bright OB stars in the Galaxy. III. Constraints on the radial stratification of the clumping factor in hot star winds from a combined Hα, IR and radio analysis. Astron. Astrophys. 2006, 454, 625–651. [Google Scholar] [CrossRef]
- Muijres, L.E.; de Koter, A.; Vink, J.S.; Krtička, J.; Kubát, J.; Langer, N. Predictions of the effect of clumping on the wind properties of O-type stars. Astron. Astrophys. 2011, 526, A32. [Google Scholar] [CrossRef]
- Petit, V.; Keszthelyi, Z.; MacInnis, R.; Cohen, D.H.; Townsend, R.H.D.; Wade, G.A.; Thomas, S.L.; Owocki, S.P.; Puls, J.; ud-Doula, A. Magnetic massive stars as progenitors of ‘heavy’ stellar-mass black holes. Mon. Not. R. Astron. Soc. 2017, 466, 1052–1060. [Google Scholar] [CrossRef]
- Heger, A.; Langer, N.; Woosley, S.E. Presupernova Evolution of Rotating Massive Stars. I. Numerical Method and Evolution of the Internal Stellar Structure. Astrophys. J. 2000, 528, 368–396. [Google Scholar] [CrossRef]
- Maeder, A.; Meynet, G. Stellar evolution with rotation. VI. The Eddington and Omega-limits, the rotational mass loss for OB and LBV stars. Astron. Astrophys. 2000, 361, 159–166. [Google Scholar]
- Colgate, S.A.; White, R.H. The Hydrodynamic Behavior of Supernovae Explosions. Astrophys. J. 1966, 143, 626. [Google Scholar] [CrossRef]
- Bethe, H.A.; Wilson, J.R. Revival of a stalled supernova shock by neutrino heating. Astrophys. J. 1985, 295, 14–23. [Google Scholar] [CrossRef]
- Janka, H.T.; Mueller, E. The First Second of a Type II Supernova: Convection, Accretion, and Shock Propagation. Astrophys. J. 1995, 448, L109. [Google Scholar] [CrossRef]
- Janka, H.T.; Mueller, E. Neutrino heating, convection, and the mechanism of Type-II supernova explosions. Astron. Astrophys. 1996, 306, 167. [Google Scholar]
- Burrows, A.; Hayes, J.; Fryxell, B.A. On the Nature of Core-Collapse Supernova Explosions. Astrophys. J. 1995, 450, 830. [Google Scholar] [CrossRef]
- Janka, H.T. Neutrino-Driven Explosions. In Handbook of Supernovae; Alsabti, A.W., Murdin, P., Eds.; Springer: Cham, Switzerland, 2017; p. 1095. [Google Scholar] [CrossRef]
- Janka, H.T. Explosion Mechanisms of Core-Collapse Supernovae. Annu. Rev. Nucl. Part. Sci. 2012, 62, 407–451. [Google Scholar] [CrossRef]
- Mezzacappa, A.; Endeve, E.; Messer, O.E.B.; Bruenn, S.W. Physical, numerical, and computational challenges of modeling neutrino transport in core-collapse supernovae. Living Rev. Comput. Astrophys. 2020, 6, 4. [Google Scholar] [CrossRef]
- LeBlanc, J.M.; Wilson, J.R. A Numerical Example of the Collapse of a Rotating Magnetized Star. Astrophys. J. 1970, 161, 541. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S. The Explosion of a Rotating Star As a Supernova Mechanism. Astron. Zhurnal 1970, 47, 813. [Google Scholar]
- Meier, D.L.; Epstein, R.I.; Arnett, W.D.; Schramm, D.N. Magnetohydrodynamic phenomena in collapsing stellar cores. Astrophys. J. 1976, 204, 869–878. [Google Scholar] [CrossRef]
- Mueller, E.; Hillebrandt, W. A magnetohydrodynamical supernova model. Astron. Astrophys. 1979, 80, 147–154. [Google Scholar]
- Fryer, C.L.; Warren, M.S. The Collapse of Rotating Massive Stars in Three Dimensions. Astrophys. J. 2004, 601, 391–404. [Google Scholar] [CrossRef]
- Kotake, K.; Sato, K.; Takahashi, K. Explosion mechanism, neutrino burst and gravitational wave in core-collapse supernovae. Rep. Prog. Phys. 2006, 69, 971–1143. [Google Scholar] [CrossRef]
- Nakamura, K.; Kuroda, T.; Takiwaki, T.; Kotake, K. Impacts of Rotation on Three-dimensional Hydrodynamics of Core-collapse Supernovae. Astrophys. J. 2014, 793, 45. [Google Scholar] [CrossRef]
- Takiwaki, T.; Kotake, K.; Suwa, Y. Three-dimensional simulations of rapidly rotating core-collapse supernovae: Finding a neutrino-powered explosion aided by non-axisymmetric flows. Mon. Not. R. Astron. Soc. 2016, 461, L112–L116. [Google Scholar] [CrossRef]
- Summa, A.; Janka, H.T.; Melson, T.; Marek, A. Rotation-supported Neutrino-driven Supernova Explosions in Three Dimensions and the Critical Luminosity Condition. Astrophys. J. 2018, 852, 28. [Google Scholar] [CrossRef]
- Miyaji, S.; Nomoto, K.; Yokoi, K.; Sugimoto, D. Supernova triggered by electron captures. Publ. Astron. Soc. Jpn. 1980, 32, 303–329. [Google Scholar]
- Nomoto, K.; Sparks, W.; Fesen, R.; Gull, T.R.; Miyaji, S.; Sugimoto, D. The Crab Nebula’s progenitor. Nature 1982, 299, 803–805. [Google Scholar] [CrossRef]
- Jones, S.; Röpke, F.K.; Pakmor, R.; Seitenzahl, I.R.; Ohlmann, S.T.; Edelmann, P.V.F. Do electron-capture supernovae make neutron stars? First multidimensional hydrodynamic simulations of the oxygen deflagration. Astron. Astrophys. 2016, 593, A72. [Google Scholar] [CrossRef]
- Kitaura, F.S.; Janka, H.T.; Hillebrandt, W. Explosions of O-Ne-Mg cores, the Crab supernova, and subluminous type II-P supernovae. Astron. Astrophys. 2006, 450, 345–350. [Google Scholar] [CrossRef]
- Özel, F.; Psaltis, D.; Narayan, R.; Santos Villarreal, A. On the Mass Distribution and Birth Masses of Neutron Stars. Astrophys. J. 2012, 757, 55. [Google Scholar] [CrossRef]
- Ugliano, M.; Janka, H.T.; Marek, A.; Arcones, A. Progenitor-explosion Connection and Remnant Birth Masses for Neutrino-driven Supernovae of Iron-core Progenitors. Astrophys. J. 2012, 757, 69. [Google Scholar] [CrossRef]
- O’Connor, E.; Ott, C.D. Black Hole Formation in Failing Core-Collapse Supernovae. Astrophys. J. 2011, 730, 70. [Google Scholar] [CrossRef]
- Limongi, M.; Chieffi, A. Presupernova Evolution and Explosive Nucleosynthesis of Rotating Massive Stars in the Metallicity Range −3 ≤ [Fe/H] ≤ 0. Astrophys. J. 2018, 237, 13. [Google Scholar] [CrossRef]
- Mapelli, M.; Spera, M.; Montanari, E.; Limongi, M.; Chieffi, A.; Giacobbo, N.; Bressan, A.; Bouffanais, Y. Impact of the Rotation and Compactness of Progenitors on the Mass of Black Holes. Astrophys. J. 2020, 888, 76. [Google Scholar] [CrossRef]
- Chieffi, A.; Roberti, L.; Limongi, M.; La Cognata, M.; Lamia, L.; Palmerini, S.; Pizzone, R.G.; Spartà, R.; Tumino, A. Impact of the New Measurement of the 12C + 12C Fusion Cross Section on the Final Compactness of Massive Stars. Astrophys. J. 2021, 916, 79. [Google Scholar] [CrossRef]
- Clausen, D.; Piro, A.L.; Ott, C.D. The Black Hole Formation Probability. Astrophys. J. 2015, 799, 190. [Google Scholar] [CrossRef]
- Ertl, T.; Janka, H.T.; Woosley, S.E.; Sukhbold, T.; Ugliano, M. A Two-parameter Criterion for Classifying the Explodability of Massive Stars by the Neutrino-driven Mechanism. Astrophys. J. 2016, 818, 124. [Google Scholar] [CrossRef]
- Sukhbold, T.; Ertl, T.; Woosley, S.E.; Brown, J.M.; Janka, H.T. Core-Collapse Supernovae from 9 to 120 Solar Masses Based on Neutrino-Powered Explosions. Astrophys. J. 2016, 821, 38. [Google Scholar] [CrossRef]
- Ertl, T.; Woosley, S.E.; Sukhbold, T.; Janka, H.T. The Explosion of Helium Stars Evolved with Mass Loss. Astrophys. J. 2020, 890, 51. [Google Scholar] [CrossRef]
- Burrows, A.; Radice, D.; Vartanyan, D.; Nagakura, H.; Skinner, M.A.; Dolence, J.C. The overarching framework of core-collapse supernova explosions as revealed by 3D FORNAX simulations. Mon. Not. R. Astron. Soc. 2020, 491, 2715–2735. [Google Scholar] [CrossRef]
- Woosley, S.E.; Sukhbold, T.; Janka, H.T. The Birth Function for Black Holes and Neutron Stars in Close Binaries. Astrophys. J. 2020, 896, 56. [Google Scholar] [CrossRef]
- Patton, R.A.; Sukhbold, T. Towards a realistic explosion landscape for binary population synthesis. Mon. Not. R. Astron. Soc. 2020, 499, 2803–2816. [Google Scholar] [CrossRef]
- Patton, R.A.; Sukhbold, T.; Eldridge, J.J. Comparing compact object distributions from mass- and presupernova core structure-based prescriptions. Mon. Not. R. Astron. Soc. 2022, 511, 903–913. [Google Scholar] [CrossRef]
- Woosley, S.E. Pulsational Pair-instability Supernovae. Astrophys. J. 2017, 836, 244. [Google Scholar] [CrossRef]
- Heger, A.; Woosley, S.E. The Nucleosynthetic Signature of Population III. Astrophys. J. 2002, 567, 532–543. [Google Scholar] [CrossRef]
- Fowler, W.A.; Hoyle, F. Neutrino Processes and Pair Formation in Massive Stars and Supernovae. Astrophys. J. Suppl. Ser. 1964, 9, 201. [Google Scholar] [CrossRef]
- Barkat, Z.; Rakavy, G.; Sack, N. Dynamics of Supernova Explosion Resulting from Pair Formation. Phys. Rev. Lett. 1967, 18, 379–381. [Google Scholar] [CrossRef]
- Rakavy, G.; Shaviv, G. Instabilities in Highly Evolved Stellar Models. Astrophys. J. 1967, 148, 803. [Google Scholar] [CrossRef]
- Woosley, S.E.; Blinnikov, S.; Heger, A. Pulsational pair instability as an explanation for the most luminous supernovae. Nature 2007, 450, 390–392. [Google Scholar] [CrossRef]
- Bond, J.R.; Arnett, W.D.; Carr, B.J. The evolution and fate of Very Massive Objects. Astrophys. J. 1984, 280, 825–847. [Google Scholar] [CrossRef]
- Fryer, C.L.; Woosley, S.E.; Heger, A. Pair-Instability Supernovae, Gravity Waves, and Gamma-Ray Transients. Astrophys. J. 2001, 550, 372–382. [Google Scholar] [CrossRef]
- Chatzopoulos, E.; Wheeler, J.C. Effects of Rotation on the Minimum Mass of Primordial Progenitors of Pair-Instability Supernovae. Astrophys. J. 2012, 748, 42. [Google Scholar] [CrossRef][Green Version]
- Belczynski, K.; Heger, A.; Gladysz, W.; Ruiter, A.J.; Woosley, S.; Wiktorowicz, G.; Chen, H.Y.; Bulik, T.; O’Shaughnessy, R.; Holz, D.E.; et al. The effect of pair-instability mass loss on black-hole mergers. Astron. Astrophys. 2016, 594, A97. [Google Scholar] [CrossRef]
- Fishbach, M.; Holz, D.E. Where Are LIGO’s Big Black Holes? Astrophys. J. 2017, 851, L25. [Google Scholar] [CrossRef]
- Stevenson, S.; Sampson, M.; Powell, J.; Vigna-Gómez, A.; Neijssel, C.J.; Szécsi, D.; Mandel, I. The Impact of Pair-instability Mass Loss on the Binary Black Hole Mass Distribution. Astrophys. J. 2019, 882, 121. [Google Scholar] [CrossRef]
- Farmer, R.; Renzo, M.; de Mink, S.E.; Marchant, P.; Justham, S. Mind the Gap: The Location of the Lower Edge of the Pair-instability Supernova Black Hole Mass Gap. Astrophys. J. 2019, 887, 53. [Google Scholar] [CrossRef]
- Farmer, R.; Renzo, M.; de Mink, S.E.; Fishbach, M.; Justham, S. Constraints from Gravitational-wave Detections of Binary Black Hole Mergers on the 12C(α, γ)16O Rate. Astrophys. J. 2020, 902, L36. [Google Scholar] [CrossRef]
- Mangiagli, A.; Bonetti, M.; Sesana, A.; Colpi, M. Merger Rate of Stellar Black Hole Binaries above the Pair-instability Mass Gap. Astrophys. J. 2019, 883, L27. [Google Scholar] [CrossRef]
- Fishbach, M.; Holz, D.E. Minding the Gap: GW190521 as a Straddling Binary. Astrophys. J. 2020, 904, L26. [Google Scholar] [CrossRef]
- Ezquiaga, J.N.; Holz, D.E. Jumping the Gap: Searching for LIGO’s Biggest Black Holes. Astrophys. J. Lett. 2021, 909, L23. [Google Scholar] [CrossRef]
- Marchant, P.; Moriya, T.J. The impact of stellar rotation on the black hole mass-gap from pair-instability supernovae. Astron. Astrophys. 2020, 640, L18. [Google Scholar] [CrossRef]
- Woosley, S.E.; Heger, A. The Pair-instability Mass Gap for Black Holes. Astrophys. J. 2021, 912, L31. [Google Scholar] [CrossRef]
- Renzo, M.; Farmer, R.J.; Justham, S.; de Mink, S.E.; Götberg, Y.; Marchant, P. Sensitivity of the lower edge of the pair-instability black hole mass gap to the treatment of time-dependent convection. Mon. Not. R. Astron. Soc. 2020, 493, 4333–4341. [Google Scholar] [CrossRef]
- Nadezhin, D.K. Some Secondary Indications of Gravitational Collapse. Astrophys. Space Sci. 1980, 69, 115–125. [Google Scholar] [CrossRef]
- Lovegrove, E.; Woosley, S.E. Very Low Energy Supernovae from Neutrino Mass Loss. Astrophys. J. 2013, 769, 109. [Google Scholar] [CrossRef]
- Kochanek, C.S. Constraints on core collapse from the black hole mass function. Mon. Not. R. Astron. Soc. 2015, 446, 1213–1222. [Google Scholar] [CrossRef][Green Version]
- Kroupa, P. On the variation of the initial mass function. Mon. Not. R. Astron. Soc. 2001, 322, 231–246. [Google Scholar] [CrossRef]
- deBoer, R.J.; Görres, J.; Wiescher, M.; Azuma, R.E.; Best, A.; Brune, C.R.; Fields, C.E.; Jones, S.; Pignatari, M.; Sayre, D.; et al. The 12C(α, γ )16O reaction and its implications for stellar helium burning. Rev. Mod. Phys. 2017, 89, 035007. [Google Scholar] [CrossRef]
- Takahashi, K.; Yoshida, T.; Umeda, H. Stellar Yields of Rotating First Stars. II. Pair-instability Supernovae and Comparison with Observations. Astrophys. J. 2018, 857, 111. [Google Scholar] [CrossRef]
- Costa, G.; Bressan, A.; Mapelli, M.; Marigo, P.; Iorio, G.; Spera, M. Formation of GW190521 from stellar evolution: The impact of the hydrogen-rich envelope, dredge-up, and 12C(α, γ)16O rate on the pair-instability black hole mass gap. Mon. Not. R. Astron. Soc. 2021, 501, 4514–4533. [Google Scholar] [CrossRef]
- Tanikawa, A.; Yoshida, T.; Kinugawa, T.; Trani, A.A.; Hosokawa, T.; Susa, H.; Omukai, K. Merger Rate Density of Binary Black Holes through Isolated Population I, II, III and Extremely Metal-poor Binary Star Evolution. Astrophys. J. 2022, 926, 83. [Google Scholar] [CrossRef]
- Sakstein, J.; Croon, D.; McDermott, S.D.; Straight, M.C.; Baxter, E.J. Beyond the Standard Model Explanations of GW190521. Phys. Rev. Lett. 2020, 125, 261105. [Google Scholar] [CrossRef]
- Marchant, P.; Renzo, M.; Farmer, R.; Pappas, K.M.W.; Taam, R.E.; de Mink, S.E.; Kalogera, V. Pulsational Pair-instability Supernovae in Very Close Binaries. Astrophys. J. 2019, 882, 36. [Google Scholar] [CrossRef]
- Spera, M.; Giacobbo, N.; Mapelli, M. Shedding light on the black hole mass spectrum. Mem. Soc. Astron. Ital. 2016, 87, 575. [Google Scholar]
- Rodriguez, C.L.; Amaro-Seoane, P.; Chatterjee, S.; Kremer, K.; Rasio, F.A.; Samsing, J.; Ye, C.S.; Zevin, M. Post-Newtonian dynamics in dense star clusters: Formation, masses, and merger rates of highly-eccentric black hole binaries. Phys. Rev. D 2018, 98, 123005. [Google Scholar] [CrossRef]
- Yang, Y.; Bartos, I.; Gayathri, V.; Ford, K.E.S.; Haiman, Z.; Klimenko, S.; Kocsis, B.; Márka, S.; Márka, Z.; McKernan, B.; et al. Hierarchical Black Hole Mergers in Active Galactic Nuclei. Phys. Rev. Lett. 2019, 123, 181101. [Google Scholar] [CrossRef] [PubMed]
- Arca Sedda, M. Birth, Life, and Death of Black Hole Binaries around Supermassive Black Holes: Dynamical Evolution of Gravitational Wave Sources. Astrophys. J. 2020, 891, 47. [Google Scholar] [CrossRef]
- Di Carlo, U.N.; Giacobbo, N.; Mapelli, M.; Pasquato, M.; Spera, M.; Wang, L.; Haardt, F. Merging black holes in young star clusters. Mon. Not. R. Astron. Soc. 2019, 487, 2947–2960. [Google Scholar] [CrossRef]
- Di Carlo, U.N.; Mapelli, M.; Bouffanais, Y.; Giacobbo, N.; Santoliquido, F.; Bressan, A.; Spera, M.; Haardt, F. Binary black holes in the pair instability mass gap. Mon. Not. R. Astron. Soc. 2020, 497, 1043–1049. [Google Scholar] [CrossRef]
- Roupas, Z.; Kazanas, D. Generation of massive stellar black holes by rapid gas accretion in primordial dense clusters. Astron. Astrophys. 2019, 632, L8. [Google Scholar] [CrossRef]
- Natarajan, P. A new channel to form IMBHs throughout cosmic time. Mon. Not. R. Astron. Soc. 2020, 501, 1413–1425. [Google Scholar] [CrossRef]
- Safarzadeh, M.; Haiman, Z. Formation of GW190521 via Gas Accretion onto Population III Stellar Black Hole Remnants Born in High-redshift Minihalos. Astrophys. J. 2020, 903, L21. [Google Scholar] [CrossRef]
- Tanikawa, A.; Susa, H.; Yoshida, T.; Trani, A.A.; Kinugawa, T. Merger Rate Density of Population III Binary Black Holes Below, Above, and in the Pair-instability Mass Gap. Astrophys. J. 2021, 910, 30. [Google Scholar] [CrossRef]
- Farrell, E.; Groh, J.H.; Hirschi, R.; Murphy, L.; Kaiser, E.; Ekström, S.; Georgy, C.; Meynet, G. Is GW190521 the merger of black holes from the first stellar generations? Mon. Not. R. Astron. Soc. 2021, 502, L40–L44. [Google Scholar] [CrossRef]
- Liu, B.; Bromm, V. The Population III Origin of GW190521. Astrophys. J. 2020, 903, L40. [Google Scholar] [CrossRef]
- Spera, M.; Mapelli, M.; Giacobbo, N.; Trani, A.A.; Bressan, A.; Costa, G. Merging black hole binaries with the SEVN code. Mon. Not. R. Astron. Soc. 2019, 485, 889–907. [Google Scholar] [CrossRef]
- Kremer, K.; Spera, M.; Becker, D.; Chatterjee, S.; Di Carlo, U.N.; Fragione, G.; Rodriguez, C.L.; Ye, C.S.; Rasio, F.A. Populating the Upper Black Hole Mass Gap through Stellar Collisions in Young Star Clusters. Astrophys. J. 2020, 903, 45. [Google Scholar] [CrossRef]
- Blaauw, A. On the origin of the O- and B-type stars with high velocities (the “run-away” stars), and some related problems. Bull. Astron. Inst. Neth. 1961, 15, 265. [Google Scholar]
- Gunn, J.E.; Ostriker, J.P. On the Nature of Pulsars. III. Analysis of Observations. Astrophys. J. 1970, 160, 979. [Google Scholar] [CrossRef]
- Hobbs, G.; Lorimer, D.R.; Lyne, A.G.; Kramer, M. A statistical study of 233 pulsar proper motions. Mon. Not. R. Astron. Soc. 2005, 360, 974–992. [Google Scholar] [CrossRef]
- Verbunt, F.; Igoshev, A.; Cator, E. The observed velocity distribution of young pulsars. Astron. Astrophys. 2017, 608, A57. [Google Scholar] [CrossRef]
- Igoshev, A.P. The observed velocity distribution of young pulsars-II. Analysis of complete PSRπ. Mon. Not. R. Astron. Soc. 2020, 494, 3663–3674. [Google Scholar] [CrossRef]
- Wongwathanarat, A.; Janka, H.T.; Müller, E. Three-dimensional neutrino-driven supernovae: Neutron star kicks, spins, and asymmetric ejection of nucleosynthesis products. Astron. Astrophys. 2013, 552, A126. [Google Scholar] [CrossRef]
- Janka, H.T. Neutron Star Kicks by the Gravitational Tug-boat Mechanism in Asymmetric Supernova Explosions: Progenitor and Explosion Dependence. Astrophys. J. 2017, 837, 84. [Google Scholar] [CrossRef]
- Gessner, A.; Janka, H.T. Hydrodynamical Neutron-star Kicks in Electron-capture Supernovae and Implications for the CRAB Supernova. Astrophys. J. 2018, 865, 61. [Google Scholar] [CrossRef]
- Tauris, T.M.; Langer, N.; Podsiadlowski, P. Ultra-stripped supernovae: Progenitors and fate. Mon. Not. R. Astron. Soc. 2015, 451, 2123–2144. [Google Scholar] [CrossRef]
- Müller, B.; Gay, D.W.; Heger, A.; Tauris, T.M.; Sim, S.A. Multidimensional simulations of ultrastripped supernovae to shock breakout. Mon. Not. R. Astron. Soc. 2018, 479, 3675–3689. [Google Scholar] [CrossRef]
- Suwa, Y.; Yoshida, T.; Shibata, M.; Umeda, H.; Takahashi, K. Neutrino-driven explosions of ultra-stripped Type Ic supernovae generating binary neutron stars. Mon. Not. R. Astron. Soc. 2015, 454, 3073–3081. [Google Scholar] [CrossRef]
- Repetto, S.; Davies, M.B.; Sigurdsson, S. Investigating stellar-mass black hole kicks. Mon. Not. R. Astron. Soc. 2012, 425, 2799–2809. [Google Scholar] [CrossRef]
- Repetto, S.; Nelemans, G. Constraining the formation of black holes in short-period black hole low-mass X-ray binaries. Mon. Not. R. Astron. Soc. 2015, 453, 3341–3355. [Google Scholar] [CrossRef]
- Mandel, I. Estimates of black hole natal kick velocities from observations of low-mass X-ray binaries. Mon. Not. R. Astron. Soc. 2016, 456, 578–581. [Google Scholar] [CrossRef]
- Giacobbo, N.; Mapelli, M. The impact of electron-capture supernovae on merging double neutron stars. Mon. Not. R. Astron. Soc. 2019, 482, 2234–2243. [Google Scholar] [CrossRef]
- Bray, J.C.; Eldridge, J.J. Neutron star kicks—II. Revision and further testing of the conservation of momentum ‘kick’ model. Mon. Not. R. Astron. Soc. 2018, 480, 5657–5672. [Google Scholar] [CrossRef]
- Giacobbo, N.; Mapelli, M. Revising Natal Kick Prescriptions in Population Synthesis Simulations. Astrophys. J. 2020, 891, 141. [Google Scholar] [CrossRef]
- Bray, J.C.; Eldridge, J.J. Neutron star kicks and their relationship to supernovae ejecta mass. Mon. Not. R. Astron. Soc. 2016, 461, 3747–3759. [Google Scholar] [CrossRef]
- Beck, P.G.; Montalban, J.; Kallinger, T.; De Ridder, J.; Aerts, C.; García, R.A.; Hekker, S.; Dupret, M.A.; Mosser, B.; Eggenberger, P.; et al. Fast core rotation in red-giant stars as revealed by gravity-dominated mixed modes. Nature 2012, 481, 55–57. [Google Scholar] [CrossRef] [PubMed]
- Mosser, B.; Goupil, M.J.; Belkacem, K.; Marques, J.P.; Beck, P.G.; Bloemen, S.; De Ridder, J.; Barban, C.; Deheuvels, S.; Elsworth, Y.; et al. Spin down of the core rotation in red giants. Astron. Astrophys. 2012, 548, A10. [Google Scholar] [CrossRef]
- Deheuvels, S.; Doğan, G.; Goupil, M.J.; Appourchaux, T.; Benomar, O.; Bruntt, H.; Campante, T.L.; Casagr, L.; Ceillier, T.; Davies, G.R.; et al. Seismic constraints on the radial dependence of the internal rotation profiles of six Kepler subgiants and young red giants. Astron. Astrophys. 2014, 564, A27. [Google Scholar] [CrossRef]
- Triana, S.A.; Corsaro, E.; De Ridder, J.; Bonanno, A.; Pérez Hernández, F.; García, R.A. Internal rotation of 13 low-mass low-luminosity red giants in the Kepler field. Astron. Astrophys. 2017, 602, A62. [Google Scholar] [CrossRef]
- Hermes, J.J.; Gänsicke, B.T.; Kawaler, S.D.; Greiss, S.; Tremblay, P.E.; Fusillo, N.G.; Raddi, R.; Fanale, S.M.; Bell, K.J.; Dennihy, E.; et al. White Dwarf Rotation as a Function of Mass and a Dichotomy of Mode Line Widths: Kepler Observations of 27 Pulsating DA White Dwarfs through K2 Campaign 8. Astrophys. J. Suppl. Ser. 2017, 232, 23. [Google Scholar] [CrossRef]
- Gehan, C.; Mosser, B.; Michel, E.; Samadi, R.; Kallinger, T. Core rotation braking on the red giant branch for various mass ranges. Astron. Astrophys. 2018, 616, A24. [Google Scholar] [CrossRef]
- Eggenberger, P.; Montalbán, J.; Miglio, A. Angular momentum transport in stellar interiors constrained by rotational splittings of mixed modes in red giants. Astron. Astrophys. 2012, 544, L4. [Google Scholar] [CrossRef]
- Marques, J.P.; Goupil, M.J.; Lebreton, Y.; Talon, S.; Palacios, A.; Belkacem, K.; Ouazzani, R.M.; Mosser, B.; Moya, A.; Morel, P.; et al. Seismic diagnostics for transport of angular momentum in stars. I. Rotational splittings from the pre-main sequence to the red-giant branch. Astron. Astrophys. 2013, 549, A74. [Google Scholar] [CrossRef]
- Ceillier, T.; Eggenberger, P.; García, R.A.; Mathis, S. Understanding angular momentum transport in red giants: The case of KIC 7341231. Astron. Astrophys. 2013, 555, A54. [Google Scholar] [CrossRef][Green Version]
- Tayar, J.; Pinsonneault, M.H. Implications of Rapid Core Rotation in Red Giants for Internal Angular Momentum Transport in Stars. Astrophys. J. 2013, 775, L1. [Google Scholar] [CrossRef]
- Cantiello, M.; Mankovich, C.; Bildsten, L.; Christensen-Dalsgaard, J.; Paxton, B. Angular Momentum Transport within Evolved Low-Mass Stars. Astrophys. J. 2014, 788, 93. [Google Scholar] [CrossRef]
- Fuller, J.; Lecoanet, D.; Cantiello, M.; Brown, B. Angular Momentum Transport via Internal Gravity Waves in Evolving Stars. Astrophys. J. 2014, 796, 17. [Google Scholar] [CrossRef]
- Belkacem, K.; Marques, J.P.; Goupil, M.J.; Mosser, B.; Sonoi, T.; Ouazzani, R.M.; Dupret, M.A.; Mathis, S.; Grosjean, M. Angular momentum redistribution by mixed modes in evolved low-mass stars. II. Spin-down of the core of red giants induced by mixed modes. Astron. Astrophys. 2015, 579, A31. [Google Scholar] [CrossRef]
- Fuller, J.; Cantiello, M.; Stello, D.; Garcia, R.A.; Bildsten, L. Asteroseismology can reveal strong internal magnetic fields in red giant stars. Science 2015, 350, 423–426. [Google Scholar] [CrossRef]
- Spada, F.; Gellert, M.; Arlt, R.; Deheuvels, S. Angular momentum transport efficiency in post-main sequence low-mass stars. Astron. Astrophys. 2016, 589, A23. [Google Scholar] [CrossRef]
- Eggenberger, P.; Lagarde, N.; Miglio, A.; Montalbán, J.; Ekström, S.; Georgy, C.; Meynet, G.; Salmon, S.; Ceillier, T.; García, R.A.; et al. Constraining the efficiency of angular momentum transport with asteroseismology of red giants: The effect of stellar mass. Astron. Astrophys. 2017, 599, A18. [Google Scholar] [CrossRef]
- Ouazzani, R.M.; Marques, J.P.; Goupil, M.J.; Christophe, S.; Antoci, V.; Salmon, S.J.A.J.; Ballot, J. γ Doradus stars as a test of angular momentum transport models. Astron. Astrophys. 2019, 626, A121. [Google Scholar] [CrossRef]
- Tayler, R.J. The adiabatic stability of stars containing magnetic fields—I.Toroidal fields. Mon. Not. R. Astron. Soc. 1973, 161, 365. [Google Scholar] [CrossRef]
- Spruit, H.C. Dynamo action by differential rotation in a stably stratified stellar interior. Astron. Astrophys. 2002, 381, 923–932. [Google Scholar] [CrossRef]
- Fuller, J.; Piro, A.L.; Jermyn, A.S. Slowing the spins of stellar cores. Mon. Not. R. Astron. Soc. 2019, 485, 3661–3680. [Google Scholar] [CrossRef]
- Fuller, J.; Ma, L. Most Black Holes Are Born Very Slowly Rotating. Astrophys. J. 2019, 881, L1. [Google Scholar] [CrossRef]
- Heger, A.; Woosley, S.E.; Spruit, H.C. Presupernova Evolution of Differentially Rotating Massive Stars Including Magnetic Fields. Astrophys. J. 2005, 626, 350–363. [Google Scholar] [CrossRef]
- Eggenberger, P.; den Hartogh, J.W.; Buldgen, G.; Meynet, G.; Salmon, S.J.A.J.; Deheuvels, S. Asteroseismology of evolved stars to constrain the internal transport of angular momentum. II. Test of a revised prescription for transport by the Tayler instability. Astron. Astrophys. 2019, 631, L6. [Google Scholar] [CrossRef]
- Qin, Y.; Fragos, T.; Meynet, G.; Andrews, J.; Sørensen, M.; Song, H.F. The spin of the second-born black hole in coalescing binary black holes. Astron. Astrophys. 2018, 616, A28. [Google Scholar] [CrossRef]
- Belczynski, K.; Klencki, J.; Fields, C.E.; Olejak, A.; Berti, E.; Meynet, G.; Fryer, C.L.; Holz, D.E.; O’Shaughnessy, R.; Brown, D.A.; et al. Evolutionary roads leading to low effective spins, high black hole masses, and O1/O2 rates for LIGO/Virgo binary black holes. Astron. Astrophys. 2020, 636, A104. [Google Scholar] [CrossRef]
- Miller, S.; Callister, T.A.; Farr, W.M. The Low Effective Spin of Binary Black Holes and Implications for Individual Gravitational-wave Events. Astrophys. J. 2020, 895, 128. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Population Properties of Compact Objects from the Second LIGO–Virgo Gravitational-Wave Transient Catalog. Astrophys. J. Lett. 2021, 913, L7. [Google Scholar] [CrossRef]
- Belczynski, K.; Done, C.; Lasota, J.P. All Apples: Comparing black holes in X-ray binaries and gravitational-wave sources. arXiv 2021, arXiv:2111.09401. [Google Scholar]
- MacLeod, M.; Ramirez-Ruiz, E. On the Accretion-Fed Growth of Neutron Stars during Common Envelope. Astrophys. J. 2014, 798, L19. [Google Scholar] [CrossRef]
- Olejak, A.; Belczynski, K. The Implications of High Black Hole Spins for the Origin of Binary Black Hole Mergers. Astrophys. J. Lett. 2021, 921, L2. [Google Scholar] [CrossRef]
- Bavera, S.S.; Fragos, T.; Zevin, M.; Berry, C.P.; Marchant, P.; Andrews, J.J.; Coughlin, S.; Dotter, A.; Kovlakas, K.; Misra, D.; et al. The impact of mass-transfer physics on the observable properties of field binary black hole populations. Astron. Astrophys. 2021, 647, A153. [Google Scholar] [CrossRef]
- Berti, E.; Volonteri, M. Cosmological Black Hole Spin Evolution by Mergers and Accretion. Astrophys. J. 2008, 684, 822–828. [Google Scholar] [CrossRef]
- Gerosa, D.; Berti, E. Are merging black holes born from stellar collapse or previous mergers? Phys. Rev. D 2017, 95, 124046. [Google Scholar] [CrossRef]
- Rodriguez, C.L.; Zevin, M.; Amaro-Seoane, P.; Chatterjee, S.; Kremer, K.; Rasio, F.A.; Ye, C.S. Black holes: The next generation—Repeated mergers in dense star clusters and their gravitational-wave properties. Phys. Rev. D 2019, 100, 043027. [Google Scholar] [CrossRef]
- Mapelli, M.; Dall’Amico, M.; Bouffanais, Y.; Giacobbo, N.; Arca Sedda, M.; Artale, M.C.; Ballone, A.; Di Carlo, U.N.; Iorio, G.; Santoliquido, F.; et al. Hierarchical black hole mergers in young, globular and nuclear star clusters: The effect of metallicity, spin and cluster properties. Mon. Not. R. Astron. Soc. 2021, 505, 339–358. [Google Scholar] [CrossRef]
- Tagawa, H.; Haiman, Z.; Bartos, I.; Kocsis, B.; Omukai, K. Signatures of hierarchical mergers in black hole spin and mass distribution. Mon. Not. R. Astron. Soc. 2021, 507, 3362–3380. [Google Scholar] [CrossRef]
- Ebisuzaki, T.; Makino, J.; Tsuru, T.G.; Funato, Y.; Portegies Zwart, S.; Hut, P.; McMillan, S.; Matsushita, S.; Matsumoto, H.; Kawabe, R. Missing Link Found? The “Runaway” Path to Supermassive Black Holes. Astrophys. J. 2001, 562, L19–L22. [Google Scholar] [CrossRef]
- Hughes, S.A.; Blandford, R.D. Black Hole Mass and Spin Coevolution by Mergers. Astrophys. J. 2003, 585, L101–L104. [Google Scholar] [CrossRef]
- Damour, T. Coalescence of two spinning black holes: An effective one-body approach. Phys. Rev. D 2001, 64, 124013. [Google Scholar] [CrossRef]
- Racine, É. Analysis of spin precession in binary black hole systems including quadrupole-monopole interaction. Phys. Rev. D 2008, 78, 044021. [Google Scholar] [CrossRef]
- Schmidt, P.; Hannam, M.; Husa, S. Towards models of gravitational waveforms from generic binaries: A simple approximate mapping between precessing and nonprecessing inspiral signals. Phys. Rev. D 2012, 86, 104063. [Google Scholar] [CrossRef]
- Schmidt, P.; Ohme, F.; Hannam, M. Towards models of gravitational waveforms from generic binaries: II. Modelling precession effects with a single effective precession parameter. Phys. Rev. D 2015, 91, 024043. [Google Scholar] [CrossRef]
- Zevin, M.; Bavera, S.S. Suspicious Siblings: The Distribution of Mass and Spin Across Component Black Holes in Isolated Binary Evolution. arXiv 2022, arXiv:2203.02515. [Google Scholar]
- Tagawa, H.; Haiman, Z.; Bartos, I.; Kocsis, B. Spin Evolution of Stellar-mass Black Hole Binaries in Active Galactic Nuclei. Astrophys. J. 2020, 899, 26. [Google Scholar] [CrossRef]
- McKernan, B.; Ford, K.E.S.; Callister, T.; Farr, W.M.; O’Shaughnessy, R.; Smith, R.; Thrane, E.; Vajpeyi, A. LIGO–Virgo correlations between mass ratio and effective inspiral spin: Testing the active galactic nuclei channel. arXiv 2021, arXiv:2107.07551. [Google Scholar]
- Moe, M.; Di Stefano, R. Mind Your Ps and Qs: The Interrelation between Period (P) and Mass-ratio (Q) Distributions of Binary Stars. Astrophys. J. Suppl. Ser. 2017, 230, 15. [Google Scholar] [CrossRef]
- Peters, P.C.; Mathews, J. Gravitational Radiation from Point Masses in a Keplerian Orbit. Phys. Rev. 1963, 131, 435–440. [Google Scholar] [CrossRef]
- Eggleton, P.P.; Kiseleva, L.G.; Hut, P. The Equilibrium Tide Model for Tidal Friction. Astrophys. J. 1998, 499, 853–870. [Google Scholar] [CrossRef]
- Zahn, J.P. Reprint of 1977A&A....57..383Z. Tidal friction in close binary stars. Astron. Astrophys. 1977, 500, 121–132. [Google Scholar]
- Rasio, F.A.; Tout, C.A.; Lubow, S.H.; Livio, M. Tidal Decay of Close Planetary Orbits. Astrophys. J. 1996, 470, 1187. [Google Scholar] [CrossRef]
- Brandenburg, A. Stellar Mixing Length Theory with Entropy Rain. Astrophys. J. 2017, 832, 6. [Google Scholar] [CrossRef]
- Zahn, J.P. The dynamical tide in close binaries. Astron. Astrophys. 1975, 41, 329–344. [Google Scholar]
- Claret, A.; Cunha, N.C.S. Circularization and synchronization times in Main-Sequence of detached eclipsing binaries II. Using the formalisms by Zahn. Astron. Astrophys. 1997, 318, 187–197. [Google Scholar]
- Siess, L.; Izzard, R.G.; Davis, P.J.; Deschamps, R. BINSTAR: A new binary stellar evolution code. Tidal interactions. Astron. Astrophys. 2013, 550, A100. [Google Scholar] [CrossRef]
- Kushnir, D.; Zaldarriaga, M.; Kollmeier, J.A.; Waldman, R. Dynamical tides reexpressed. Mon. Not. R. Astron. Soc. 2017, 467, 2146–2149. [Google Scholar] [CrossRef]
- Piran, T. Gamma-ray Bursts and Binary Neutron Star Mergers. In Compact Stars in Binaries; van Paradijs, J., van den Heuvel, E.P.J., Kuulkers, E., Eds.; The Astrophysics Spectator: Old Hickory, TN, USA, 1996; Volume 165, p. 489. [Google Scholar]
- Thorne, K.S.; Zytkow, A.N. Stars with degenerate neutron cores. I. Structure of equilibrium models. Astrophys. J. 1977, 212, 832–858. [Google Scholar] [CrossRef]
- Fryer, C.L.; Benz, W.; Herant, M. The Dynamics and Outcomes of Rapid Infall onto Neutron Stars. Astrophys. J. 1996, 460, 801. [Google Scholar] [CrossRef]
- Endal, A.S.; Sofia, S. The evolution of rotating stars. II. Calculations with time-dependent redistribution of angular momentum for 7 and 10 M sun stars. Astrophys. J. 1978, 220, 279–290. [Google Scholar] [CrossRef]
- Zahn, J.P. Circulation and turbulence in rotating stars. Astron. Astrophys. 1992, 265, 115–132. [Google Scholar]
- de Mink, S.E.; Cottaar, M.; Pols, O.R. Can Low-Metallicity Binaries Avoid Merging. In First Stars III; O’Shea, B.W., Heger, A., Eds.; American Institute of Physics Conference Series; American Institute of Physics: Santa Fe, NM, USA, 2008; Volume 990, pp. 217–219. [Google Scholar] [CrossRef]
- de Mink, S.E.; Cantiello, M.; Langer, N.; Pols, O.R.; Brott, I.; Yoon, S.C. Rotational mixing in massive binaries. Detached short-period systems. Astron. Astrophys. 2009, 497, 243–253. [Google Scholar] [CrossRef]
- Hadjidemetriou, J.D. Two-body problem with variable mass: A new approach. Icarus 1963, 2, 440–451. [Google Scholar] [CrossRef]
- Dosopoulou, F.; Kalogera, V. Orbital Evolution of Mass-transferring Eccentric Binary Systems. I. Phase-dependent Evolution. Astrophys. J. 2016, 825, 70. [Google Scholar] [CrossRef]
- Bondi, H.; Hoyle, F. On the mechanism of accretion by stars. Mon. Not. R. Astron. Soc. 1944, 104, 273. [Google Scholar] [CrossRef]
- Dosopoulou, F.; Kalogera, V. Orbital Evolution of Mass-transferring Eccentric Binary Systems. II. Secular Evolution. Astrophys. J. 2016, 825, 71. [Google Scholar] [CrossRef]
- Hamers, A.S.; Dosopoulou, F. An Analytic Model for Mass Transfer in Binaries with Arbitrary Eccentricity, with Applications to Triple-star Systems. Astrophys. J. 2019, 872, 119. [Google Scholar] [CrossRef]
- Sepinsky, J.F.; Willems, B.; Kalogera, V.; Rasio, F.A. Interacting Binaries with Eccentric Orbits: Secular Orbital Evolution Due to Conservative Mass Transfer. Astrophys. J. 2007, 667, 1170–1184. [Google Scholar] [CrossRef]
- Sepinsky, J.F.; Willems, B.; Kalogera, V.; Rasio, F.A. Interacting Binaries with Eccentric Orbits. II. Secular Orbital Evolution due to Non-conservative Mass Transfer. Astrophys. J. 2009, 702, 1387–1392. [Google Scholar] [CrossRef]
- Sepinsky, J.F.; Willems, B.; Kalogera, V.; Rasio, F.A. Interacting Binaries with Eccentric Orbits. III. Orbital Evolution due to Direct Impact and Self-Accretion. Astrophys. J. 2010, 724, 546–558. [Google Scholar] [CrossRef]
- Eggleton, P.P. Aproximations to the radii of Roche lobes. Astrophys. J. 1983, 268, 368–369. [Google Scholar] [CrossRef]
- Ge, H.; Hjellming, M.S.; Webbink, R.F.; Chen, X.; Han, Z. Adiabatic Mass Loss in Binary Stars. I. Computational Method. Astrophys. J. 2010, 717, 724–738. [Google Scholar] [CrossRef]
- Leiner, E.M.; Geller, A. A Census of Blue Stragglers in Gaia DR2 Open Clusters as a Test of Population Synthesis and Mass Transfer Physics. Astrophys. J. 2021, 908, 229. [Google Scholar] [CrossRef]
- Neijssel, C.J.; Vigna-Gómez, A.; Stevenson, S.; Barrett, J.W.; Gaebel, S.M.; Broekgaarden, F.S.; de Mink, S.E.; Szécsi, D.; Vinciguerra, S.; Mandel, I. The effect of the metallicity-specific star formation history on double compact object mergers. Mon. Not. R. Astron. Soc. 2019, 490, 3740–3759. [Google Scholar] [CrossRef]
- Vigna-Gómez, A.; Neijssel, C.J.; Stevenson, S.; Barrett, J.W.; Belczynski, K.; Justham, S.; de Mink, S.E.; Müller, B.; Podsiadlowski, P.; Renzo, M.; et al. On the formation history of Galactic double neutron stars. Mon. Not. R. Astron. Soc. 2018, 481, 4009–4029. [Google Scholar] [CrossRef]
- Ivanova, N.; Justham, S.; Chen, X.; De Marco, O.; Fryer, C.L.; Gaburov, E.; Ge, H.; Glebbeek, E.; Han, Z.; Li, X.D.; et al. Common envelope evolution: Where we stand and how we can move forward. Astron. Astrophys. Rev. 2013, 21, 59. [Google Scholar] [CrossRef]
- Dominik, M.; Berti, E.; O’Shaughnessy, R.; Mandel, I.; Belczynski, K.; Fryer, C.; Holz, D.E.; Bulik, T.; Pannarale, F. Double Compact Objects III: Gravitational-wave Detection Rates. Astrophys. J. 2015, 806, 263. [Google Scholar] [CrossRef]
- Rodriguez, C.L.; Chatterjee, S.; Rasio, F.A. Binary black hole mergers from globular clusters: Masses, merger rates, and the impact of stellar evolution. Phys. Rev. D 2016, 93, 084029. [Google Scholar] [CrossRef]
- Mapelli, M.; Giacobbo, N. The cosmic merger rate of neutron stars and black holes. Mon. Not. R. Astron. Soc. 2018, 479, 4391–4398. [Google Scholar] [CrossRef]
- Tanikawa, A.; Kinugawa, T.; Yoshida, T.; Hijikawa, K.; Umeda, H. Population III binary black holes: Effects of convective overshooting on formation of GW190521. Mon. Not. R. Astron. Soc. 2021, 505, 2170–2176. [Google Scholar] [CrossRef]
- Sandquist, E.L.; Taam, R.E.; Chen, X.; Bodenheimer, P.; Burkert, A. Double Core Evolution. X. Through the Envelope Ejection Phase. Astrophys. J. 1998, 500, 909–922. [Google Scholar] [CrossRef]
- Ricker, P.M.; Taam, R.E. An AMR Study of the Common-envelope Phase of Binary Evolution. Astrophys. J. 2012, 746, 74. [Google Scholar] [CrossRef]
- Passy, J.C.; De Marco, O.; Fryer, C.L.; Herwig, F.; Diehl, S.; Oishi, J.S.; Mac Low, M.M.; Bryan, G.L.; Rockefeller, G. Simulating the Common Envelope Phase of a Red Giant Using Smoothed-particle Hydrodynamics and Uniform-grid Codes. Astrophys. J. 2012, 744, 52. [Google Scholar] [CrossRef]
- Ivanova, N.; Nandez, J.L.A. Common envelope events with low-mass giants: Understanding the transition to the slow spiral-in. Mon. Not. R. Astron. Soc. 2016, 462, 362–381. [Google Scholar] [CrossRef]
- Ohlmann, S.T.; Röpke, F.K.; Pakmor, R.; Springel, V. Constructing stable 3D hydrodynamical models of giant stars. Astron. Astrophys. 2017, 599, A5. [Google Scholar] [CrossRef]
- Iaconi, R.; De Marco, O.; Passy, J.C.; Staff, J. The effect of binding energy and resolution in simulations of the common envelope binary interaction. Mon. Not. R. Astron. Soc. 2018, 477, 2349–2365. [Google Scholar] [CrossRef]
- Reichardt, T.A.; De Marco, O.; Iaconi, R.; Tout, C.A.; Price, D.J. Extending common envelope simulations from Roche lobe overflow to the nebular phase. Mon. Not. R. Astron. Soc. 2019, 484, 631–647. [Google Scholar] [CrossRef]
- Reichardt, T.A.; De Marco, O.; Iaconi, R.; Chamandy, L.; Price, D.J. The impact of recombination energy on simulations of the common-envelope binary interaction. Mon. Not. R. Astron. Soc. 2020, 494, 5333–5349. [Google Scholar] [CrossRef]
- Glanz, H.; Perets, H.B. Common envelope evolution of eccentric binaries. Mon. Not. R. Astron. Soc. 2021, 507, 2659–2670. [Google Scholar] [CrossRef]
- Livio, M.; Soker, N. The Common Envelope Phase in the Evolution of Binary Stars. Astrophys. J. 1988, 329, 764. [Google Scholar] [CrossRef]
- de Kool, M. Common Envelope Evolution and Double Cores of Planetary Nebulae. Astrophys. J. 1990, 358, 189. [Google Scholar] [CrossRef]
- Nelemans, G.; Verbunt, F.; Yungelson, L.R.; Portegies Zwart, S.F. Reconstructing the evolution of double helium white dwarfs: Envelope loss without spiral-in. Astron. Astrophys. 2000, 360, 1011–1018. [Google Scholar]
- Nelemans, G.; Tout, C.A. Reconstructing the evolution of white dwarf binaries: Further evidence for an alternative algorithm for the outcome of the common-envelope phase in close binaries. Mon. Not. R. Astron. Soc. 2005, 356, 753–764. [Google Scholar] [CrossRef]
- Dewi, J.D.M.; Tauris, T.M. On the energy equation and efficiency parameter of the common envelope evolution. Astron. Astrophys. 2000, 360, 1043–1051. [Google Scholar]
- Xu, X.J.; Li, X.D. On the Binding Energy Parameter λ of Common Envelope Evolution. Astrophys. J. 2010, 716, 114–121. [Google Scholar] [CrossRef]
- Claeys, J.S.W.; Pols, O.R.; Izzard, R.G.; Vink, J.; Verbunt, F.W.M. Theoretical uncertainties of the Type Ia supernova rate. Astron. Astrophys. 2014, 563, A83. [Google Scholar] [CrossRef]
- Kruckow, M.U.; Tauris, T.M.; Langer, N.; Kramer, M.; Izzard, R.G. Progenitors of gravitational wave mergers: Binary evolution with the stellar grid-based code COMBINE. Mon. Not. R. Astron. Soc. 2018, 481, 1908–1949. [Google Scholar] [CrossRef]
- Zorotovic, M.; Schreiber, M.R.; Gänsicke, B.T.; Nebot Gómez-Morán, A. Post-common-envelope binaries from SDSS. IX: Constraining the common-envelope efficiency. Astron. Astrophys. 2010, 520, A86. [Google Scholar] [CrossRef]
- Davis, P.J.; Kolb, U.; Willems, B. A comprehensive population synthesis study of post-common envelope binaries. Mon. Not. R. Astron. Soc. 2010, 403, 179–195. [Google Scholar] [CrossRef]
- Davis, P.J.; Kolb, U.; Knigge, C. Is the common envelope ejection efficiency a function of the binary parameters? Mon. Not. R. Astron. Soc. 2012, 419, 287–303. [Google Scholar] [CrossRef]
- De Marco, O.; Passy, J.C.; Moe, M.; Herwig, F.; Mac Low, M.M.; Paxton, B. On the α formalism for the common envelope interaction. Mon. Not. R. Astron. Soc. 2011, 411, 2277–2292. [Google Scholar] [CrossRef]
- Nandez, J.L.A.; Ivanova, N. Common envelope events with low-mass giants: Understanding the energy budget. Mon. Not. R. Astron. Soc. 2016, 460, 3992–4002. [Google Scholar] [CrossRef]
- Fragos, T.; Andrews, J.J.; Ramirez-Ruiz, E.; Meynet, G.; Kalogera, V.; Taam, R.E.; Zezas, A. The Complete Evolution of a Neutron-star Binary through a Common Envelope Phase Using 1D Hydrodynamic Simulations. Astrophys. J. 2019, 883, L45. [Google Scholar] [CrossRef]
- Lynch, R.S.; Freire, P.C.C.; Ransom, S.M.; Jacoby, B.A. The Timing of Nine Globular Cluster Pulsars. Astrophys. J. 2012, 745, 109. [Google Scholar] [CrossRef]
- Kawka, A.; Vennes, S.; O’Toole, S.; Németh, P.; Burton, D.; Kotze, E.; Buckley, D.A.H. New binaries among UV-selected, hot subdwarf stars and population properties. Mon. Not. R. Astron. Soc. 2015, 450, 3514–3548. [Google Scholar] [CrossRef]
- Kruckow, M.U.; Neunteufel, P.G.; Di Stefano, R.; Gao, Y.; Kobayashi, C. A Catalog of Potential Post-Common Envelope Binaries. Astrophys. J. 2021, 920, 86. [Google Scholar] [CrossRef]
- Trani, A.A.; Rieder, S.; Tanikawa, A.; Iorio, G.; Martini, R.; Karelin, G.; Glanz, H.; Portegies Zwart, S. Revisiting Common Envelope Evolution—A New Semi-Analytic Model for N-body and Population Synthesis Codes. arXiv 2022, arXiv:2205.13537. [Google Scholar]
- Hills, J.G. The effects of sudden mass loss and a random kick velocity produced in a supernova explosion on the dynamics of a binary star of arbitrary orbital eccentricity. Applications to X-ray binaries and to the binarypulsars. Astrophys. J. 1983, 267, 322–333. [Google Scholar] [CrossRef]
- Belczynski, K. The Most Ordinary Formation of the Most Unusual Double Black Hole Merger. Astrophys. J. 2020, 905, L15. [Google Scholar] [CrossRef]
- Callister, T.A.; Farr, W.M.; Renzo, M. State of the Field: Binary Black Hole Natal Kicks and Prospects for Isolated Field Formation after GWTC-2. Astrophys. J. 2021, 920, 157. [Google Scholar] [CrossRef]
- Steinle, N.; Kesden, M. Pathways for producing binary black holes with large misaligned spins in the isolated formation channel. Phys. Rev. D 2021, 103, 063032. [Google Scholar] [CrossRef]
- Wysocki, D.; Gerosa, D.; O’Shaughnessy, R.; Belczynski, K.; Gladysz, W.; Berti, E.; Kesden, M.; Holz, D.E. Explaining LIGO’s observations via isolated binary evolution with natal kicks. Phys. Rev. D 2018, 97, 043014. [Google Scholar] [CrossRef]
- Sana, H.; de Mink, S.E.; de Koter, A.; Langer, N.; Evans, C.J.; Gieles, M.; Gosset, E.; Izzard, R.G.; Le Bouquin, J.B.; Schneider, F.R.N. Binary Interaction Dominates the Evolution of Massive Stars. Science 2012, 337, 444. [Google Scholar] [CrossRef] [PubMed]
- Lada, C.J.; Lada, E.A. Embedded Clusters in Molecular Clouds. Annu. Rev. Astron. Astrophys. 2003, 41, 57–115. [Google Scholar] [CrossRef]
- Portegies Zwart, S.F.; McMillan, S.L.; Gieles, M. Young Massive Star Clusters. Annu. Rev. Astron. Astrophys. 2010, 48, 431–493. [Google Scholar] [CrossRef]
- Ward, J.L.; Kruijssen, J.M.D.; Rix, H.W. Not all stars form in clusters—Gaia-DR2 uncovers the origin of OB associations. Mon. Not. R. Astron. Soc. 2020, 495, 663–685. [Google Scholar] [CrossRef]
- Weidner, C.; Kroupa, P. The maximum stellar mass, star-cluster formation and composite stellar populations. Mon. Not. R. Astron. Soc. 2006, 365, 1333–1347. [Google Scholar] [CrossRef]
- Weidner, C.; Kroupa, P.; Bonnell, I.A.D. The relation between the most-massive star and its parental star cluster mass. Mon. Not. R. Astron. Soc. 2009, 401, 275–293. [Google Scholar] [CrossRef]
- Mapelli, M.; Colpi, M.; Possenti, A.; Sigurdsson, S. The fingerprint of binary intermediate-mass black holes in globular clusters: Suprathermal stars and angular momentum alignment. Mon. Not. R. Astron. Soc. 2005, 364, 1315–1326. [Google Scholar] [CrossRef]
- Tanikawa, A. Dynamical evolution of stellar mass black holes in dense stellar clusters: Estimate for merger rate of binary black holes originating from globular clusters. Mon. Not. R. Astron. Soc. 2013, 435, 1358–1375. [Google Scholar] [CrossRef]
- Breen, P.G.; Heggie, D.C. Dynamical evolution of black hole subsystems in idealized star clusters. Mon. Not. R. Astron. Soc. 2013, 432, 2779–2797. [Google Scholar] [CrossRef]
- Samsing, J.; MacLeod, M.; Ramirez-Ruiz, E. The Formation of Eccentric Compact Binary Inspirals and the Role of Gravitational Wave Emission in Binary-Single Stellar Encounters. Astrophys. J. 2014, 784, 71. [Google Scholar] [CrossRef]
- Samsing, J. Eccentric black hole mergers forming in globular clusters. Phys. Rev. D 2018, 97, 103014. [Google Scholar] [CrossRef]
- Askar, A.; Arca Sedda, M.; Giersz, M. MOCCA-SURVEY Database I: Galactic globular clusters harbouring a black hole subsystem. Mon. Not. R. Astron. Soc. 2018, 478, 1844–1854. [Google Scholar] [CrossRef]
- Arca Sedda, M.; Askar, A.; Giersz, M. MOCCA-Survey Database—I. Unravelling black hole subsystems in globular clusters. Mon. Not. R. Astron. Soc. 2018, 479, 4652–4664. [Google Scholar] [CrossRef]
- Kremer, K.; Rodriguez, C.L.; Amaro-Seoane, P.; Breivik, K.; Chatterjee, S.; Katz, M.L.; Larson, S.L.; Rasio, F.A.; Samsing, J.; Ye, C.S.; et al. Post-Newtonian dynamics in dense star clusters: Binary black holes in the LISA band. Phys. Rev. D 2019, 99, 063003. [Google Scholar] [CrossRef]
- Wang, L.; Fujii, M.S.; Tanikawa, A. Impact of initial mass functions on the dynamical channel of gravitational wave sources. Mon. Not. R. Astron. Soc. 2021, 504, 5778–5787. [Google Scholar] [CrossRef]
- Askar, A.; Szkudlarek, M.; Gondek-Rosińska, D.; Giersz, M.; Bulik, T. MOCCA-SURVEY Database—I. Coalescing binary black holes originating from globular clusters. Mon. Not. R. Astron. Soc. 2017, 464, L36–L40. [Google Scholar] [CrossRef]
- Banerjee, S.; Baumgardt, H.; Kroupa, P. Stellar-mass black holes in star clusters: Implications for gravitational wave radiation. Mon. Not. R. Astron. Soc. 2010, 402, 371–380. [Google Scholar] [CrossRef]
- Banerjee, S. Stellar-mass black holes in young massive and open stellar clusters and their role in gravitational-wave generation—II. Mon. Not. R. Astron. Soc. 2018, 473, 909–926. [Google Scholar] [CrossRef]
- Banerjee, S. Stellar-mass black holes in young massive and open stellar clusters—IV. Updated stellar-evolutionary and black hole spin models and comparisons with the LIGO-Virgo O1/O2 merger-event data. Mon. Not. R. Astron. Soc. 2020, 500, 3002–3026. [Google Scholar] [CrossRef]
- Fujii, M.S.; Tanikawa, A.; Makino, J. The detection rates of merging binary black holes originating from star clusters and their mass function. Publ. Astron. Soc. Jpn. 2017, 69, 94. [Google Scholar] [CrossRef]
- Kumamoto, J.; Fujii, M.S.; Tanikawa, A. Merger rate density of binary black holes formed in open clusters. Mon. Not. R. Astron. Soc. 2020, 495, 4268–4278. [Google Scholar] [CrossRef]
- Böker, T.; Laine, S.; van der Marel, R.P.; Sarzi, M.; Rix, H.W.; Ho, L.C.; Shields, J.C. A Hubble Space Telescope Census of Nuclear Star Clusters in Late-Type Spiral Galaxies. I. Observations and Image Analysis. Astron. J. 2002, 123, 1389–1410. [Google Scholar] [CrossRef]
- Graham, A.W.; Spitler, L.R. Quantifying the coexistence of massive black holes and dense nuclear star clusters. Mon. Not. R. Astron. Soc. 2009, 397, 2148–2162. [Google Scholar] [CrossRef]
- Bahcall, J.N.; Wolf, R.A. Star distribution around a massive black hole in a globular cluster. Astrophys. J. 1976, 209, 214–232. [Google Scholar] [CrossRef]
- Szölgyén, Á.; Kocsis, B. Black Hole Disks in Galactic Nuclei. Phys. Rev. Lett. 2018, 121, 101101. [Google Scholar] [CrossRef] [PubMed]
- Gondán, L.; Kocsis, B.; Raffai, P.; Frei, Z. Eccentric Black Hole Gravitational-wave Capture Sources in Galactic Nuclei: Distribution of Binary Parameters. Astrophys. J. 2018, 860, 5. [Google Scholar] [CrossRef]
- Leigh, N.W.C.; Geller, A.M.; McKernan, B.; Ford, K.E.S.; Mac Low, M.M.; Bellovary, J.; Haiman, Z.; Lyra, W.; Samsing, J.; O’Dowd, M.; et al. On the rate of black hole binary mergers in galactic nuclei due to dynamical hardening. Mon. Not. R. Astron. Soc. 2018, 474, 5672–5683. [Google Scholar] [CrossRef]
- Trani, A.A.; Spera, M.; Leigh, N.W.C.; Fujii, M.S. The Keplerian Three-body Encounter. II. Comparisons with Isolated Encounters and Impact on Gravitational Wave Merger Timescales. Astrophys. J. 2019, 885, 135. [Google Scholar] [CrossRef]
- McKernan, B.; Ford, K.E.S.; Bellovary, J.; Leigh, N.W.C.; Haiman, Z.; Kocsis, B.; Lyra, W.; Mac Low, M.M.; Metzger, B.; O’Dowd, M.; et al. Constraining Stellar-mass Black Hole Mergers in AGN Disks Detectable with LIGO. Astrophys. J. 2018, 866, 66. [Google Scholar] [CrossRef]
- McKernan, B.; Ford, K.E.S.; O’Shaugnessy, R.; Wysocki, D. Monte Carlo simulations of black hole mergers in AGN discs: Low χeff mergers and predictions for LIGO. Mon. Not. R. Astron. Soc. 2020, 494, 1203–1216. [Google Scholar] [CrossRef]
- McKernan, B.; Ford, K.E.S.; O’Shaughnessy, R. Black hole, neutron star, and white dwarf merger rates in AGN discs. Mon. Not. R. Astron. Soc. 2020, 498, 4088–4094. [Google Scholar] [CrossRef]
- Ford, K.E.S.; McKernan, B. Binary Black Hole Merger Rates in AGN Disks versus Nuclear Star Clusters: Loud beats Quiet. arXiv 2021, arXiv:2109.03212. [Google Scholar]
- McKernan, B.; Ford, K.E.S.; Lyra, W.; Perets, H.B. Intermediate mass black holes in AGN discs—I. Production and growth. Mon. Not. R. Astron. Soc. 2012, 425, 460–469. [Google Scholar] [CrossRef]
- McKernan, B.; Ford, K.E.S.; Kocsis, B.; Lyra, W.; Winter, L.M. Intermediate-mass black holes in AGN discs—II. Model predictions and observational constraints. Mon. Not. R. Astron. Soc. 2014, 441, 900–909. [Google Scholar] [CrossRef]
- Bellovary, J.M.; Low, M.M.M.; McKernan, B.; Ford, K.E.S. Migration Traps in Disks Around Supermassive Black Holes. Astrophys. J. 2016, 819, L17. [Google Scholar] [CrossRef]
- Bartos, I.; Kocsis, B.; Haiman, Z.; Márka, S. Rapid and Bright Stellar-mass Binary Black Hole Mergers in Active Galactic Nuclei. Astrophys. J. 2017, 835, 165. [Google Scholar] [CrossRef]
- Stone, N.C.; Metzger, B.D.; Haiman, Z. Assisted inspirals of stellar mass black holes embedded in AGN discs: Solving the ‘final au problem’. Mon. Not. R. Astron. Soc. 2016, 464, 946–954. [Google Scholar] [CrossRef]
- Secunda, A.; Bellovary, J.; Low, M.M.M.; Ford, K.E.S.; McKernan, B.; Leigh, N.W.C.; Lyra, W.; Sándor, Z. Orbital Migration of Interacting Stellar Mass Black Holes in Disks around Supermassive Black Holes. Astrophys. J. 2019, 878, 85. [Google Scholar] [CrossRef]
- Tagawa, H.; Haiman, Z.; Kocsis, B. Formation and Evolution of Compact-object Binaries in AGN Disks. Astrophys. J. 2020, 898, 25. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Lynden-Bell, D.; Wood, R. The gravo-thermal catastrophe in isothermal spheres and the onset of red-giant structure for stellar systems. Mon. Not. R. Astron. Soc. 1968, 138, 495. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Dynamical Friction. I. General Considerations: The Coefficient of Dynamical Friction. Astrophys. J. 1943, 97, 255. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Dynamical Friction. II. The Rate of Escape of Stars from Clusters and the Evidence for the Operation of Dynamical Friction. Astrophys. J. 1943, 97, 263. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Dynamical Friction. III. A More Exact Theory of the Rate of Escape of Stars from Clusters. Astrophys. J. 1943, 98, 54. [Google Scholar] [CrossRef]
- Fujii, M.S.; Portegies Zwart, S. The moment of core collapse in star clusters with a mass function. Mon. Not. R. Astron. Soc. 2014, 439, 1003–1014. [Google Scholar] [CrossRef]
- Salpeter, E.E. The Luminosity Function and Stellar Evolution. Astrophys. J. 1955, 121, 161. [Google Scholar] [CrossRef]
- Spitzer, L., Jr. Equipartition and the Formation of Compact Nuclei in Spherical Stellar Systems. Astrophys. J. 1969, 158, L139. [Google Scholar] [CrossRef]
- Merritt, D. Two-component stellar systems in thermal and dynamical equilibrium. Astron. J. 1981, 86, 318–324. [Google Scholar] [CrossRef]
- Inagaki, S.; Wiyanto, P. On equipartition of kinetic energies in two-component star clusters. Publ. Astron. Soc. Jpn. 1984, 36, 391–402. [Google Scholar]
- Bianchini, P.; van de Ven, G.; Norris, M.A.; Schinnerer, E.; Varri, A.L. A novel look at energy equipartition in globular clusters. Mon. Not. R. Astron. Soc. 2016, 458, 3644–3654. [Google Scholar] [CrossRef]
- Spera, M.; Mapelli, M.; Jeffries, R.D. Do open star clusters evolve towards energy equipartition? Mon. Not. R. Astron. Soc. 2016, 460, 317–328. [Google Scholar] [CrossRef]
- Webb, J.J.; Vesperini, E. On the link between energy equipartition and radial variation in the stellar mass function of star clusters. Mon. Not. R. Astron. Soc. 2017, 464, 1977–1983. [Google Scholar] [CrossRef]
- Kremer, K.; Ye, C.S.; Chatterjee, S.; Rodriguez, C.L.; Rasio, F.A. How Black Holes Shape Globular Clusters: Modeling NGC 3201. Astrophys. J. 2018, 855, L15. [Google Scholar] [CrossRef]
- Lee, H.M. Evolution of galactic nuclei with 10-M⊙ black holes. Mon. Not. R. Astron. Soc. 1995, 272, 605–617. [Google Scholar] [CrossRef]
- Jeans, J.H. The origin of binary systems. Mon. Not. R. Astron. Soc. 1919, 79, 408. [Google Scholar] [CrossRef]
- Monaghan, J.J. A statistical theory of the disruption of three-body systems—I. Low angular momentum. Mon. Not. R. Astron. Soc. 1976, 176, 63–72. [Google Scholar] [CrossRef]
- Monaghan, J.J. A statistical theory of the disruption of three-body systems—II. High angular momentum. Mon. Not. R. Astron. Soc. 1976, 177, 583–594. [Google Scholar] [CrossRef]
- Valtonen, M.; Karttunen, H. The Three-Body Problem; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Stone, N.C.; Leigh, N.W.C. A statistical solution to the chaotic, non-hierarchical three-body problem. Nature 2019, 576, 406–410. [Google Scholar] [CrossRef]
- Kol, B. Flux-based statistical prediction of three-body outcomes. Celest. Mech. Dyn. Astron. 2021, 133, 17. [Google Scholar] [CrossRef]
- Peters, P.C. Gravitational Radiation and the Motion of Two Point Masses. Phys. Rev. 1964, 136, 1224–1232. [Google Scholar] [CrossRef]
- Bae, Y.B.; Kim, C.; Lee, H.M. Compact binaries ejected from globular clusters as gravitational wave sources. Mon. Not. R. Astron. Soc. 2014, 440, 2714–2725. [Google Scholar] [CrossRef]
- Zevin, M.; Samsing, J.; Rodriguez, C.; Haster, C.J.; Ramirez-Ruiz, E. Eccentric Black Hole Mergers in Dense Star Clusters: The Role of Binary-Binary Encounters. Astrophys. J. 2019, 871, 91. [Google Scholar] [CrossRef]
- Lower, M.E.; Thrane, E.; Lasky, P.D.; Smith, R. Measuring eccentricity in binary black hole inspirals with gravitational waves. Phys. Rev. D 2018, 98, 083028. [Google Scholar] [CrossRef]
- Huerta, E.A.; Moore, C.J.; Kumar, P.; George, D.; Chua, A.J.; Haas, R.; Wessel, E.; Johnson, D.; Glennon, D.; Rebei, A.; et al. Eccentric, nonspinning, inspiral, Gaussian-process merger approximant for the detection and characterization of eccentric binary black hole mergers. Phys. Rev. D 2018, 97, 024031. [Google Scholar] [CrossRef]
- Samsing, J.; D’Orazio, D.J.; Kremer, K.; Rodriguez, C.L.; Askar, A. Single-single gravitational-wave captures in globular clusters: Eccentric deci-Hertz sources observable by DECIGO and Tian-Qin. Phys. Rev. D 2020, 101, 123010. [Google Scholar] [CrossRef]
- Hoang, B.M.; Naoz, S.; Kremer, K. Neutron Star-Black Hole Mergers from Gravitational-wave Captures. Astrophys. J. 2020, 903, 8. [Google Scholar] [CrossRef]
- Hamers, A.S. An Improved Numerical Fit to the Peak Harmonic Gravitational Wave Frequency Emitted by an Eccentric Binary. Res. Notes Am. Astron. Soc. 2021, 5, 275. [Google Scholar] [CrossRef]
- Safarzadeh, M.; Farr, W.M.; Ramirez-Ruiz, E. A Trend in the Effective Spin Distribution of LIGO Binary Black Holes with Mass. Astrophys. J. 2020, 894, 129. [Google Scholar] [CrossRef]
- Campanelli, M.; Lousto, C.; Zlochower, Y.; Merritt, D. Large Merger Recoils and Spin Flips from Generic Black Hole Binaries. Astrophys. J. 2007, 659, L5–L8. [Google Scholar] [CrossRef]
- Campanelli, M.; Lousto, C.O.; Zlochower, Y.; Merritt, D. Maximum Gravitational Recoil. Phys. Rev. Lett. 2007, 98, 231102. [Google Scholar] [CrossRef]
- Boyle, L.; Kesden, M.; Nissanke, S. Binary Black-Hole Merger: Symmetry and the Spin Expansion. Phys. Rev. Lett. 2008, 100, 151101. [Google Scholar] [CrossRef]
- Lousto, C.O.; Zlochower, Y. Modeling maximum astrophysical gravitational recoil velocities. Phys. Rev. D 2011, 83, 024003. [Google Scholar] [CrossRef]
- Lousto, C.O.; Zlochower, Y. Nonlinear gravitational recoil from the mergers of precessing black-hole binaries. Phys. Rev. D 2013, 87, 084027. [Google Scholar] [CrossRef]
- Lousto, C.O.; Zlochower, Y. Black hole binary remnant mass and spin: A new phenomenological formula. Phys. Rev. D 2014, 89, 104052. [Google Scholar] [CrossRef]
- Giersz, M.; Leigh, N.; Hypki, A.; Lützgendorf, N.; Askar, A. MOCCA code for star cluster simulations—IV. A new scenario for intermediate mass black hole formation in globular clusters. Mon. Not. R. Astron. Soc. 2015, 454, 3150–3165. [Google Scholar] [CrossRef]
- Antonini, F.; Gieles, M.; Gualandris, A. Black hole growth through hierarchical black hole mergers in dense star clusters: Implications for gravitational wave detections. Mon. Not. R. Astron. Soc. 2019, 486, 5008–5021. [Google Scholar] [CrossRef]
- Fragione, G.; Banerjee, S. Demographics of Neutron Stars in Young Massive and Open Clusters. Astrophys. J. 2020, 901, L16. [Google Scholar] [CrossRef]
- Mapelli, M.; Santoliquido, F.; Bouffanais, Y.; Arca Sedda, M.; Giacobbo, N.; Artale, M.C.; Ballone, A. Mass and rate of hierarchical black hole mergers in young, globular and nuclear star clusters. arXiv 2020, arXiv:2007.15022. [Google Scholar]
- Tokovinin, A. Comparative statistics and origin of triple and quadruple stars. Mon. Not. R. Astron. Soc. 2008, 389, 925–938. [Google Scholar] [CrossRef]
- Tokovinin, A. From Binaries to Multiples. I. Data on F and G Dwarfs within 67 pc of the Sun. Astron. J. 2014, 147, 86. [Google Scholar] [CrossRef]
- Tokovinin, A. From Binaries to Multiples. II. Hierarchical Multiplicity of F and G Dwarfs. Astron. J. 2014, 147, 87. [Google Scholar] [CrossRef]
- Tokovinin, A. The Updated Multiple Star Catalog. Astrophys. J. Suppl. Ser. 2018, 235, 6. [Google Scholar] [CrossRef]
- Duchêne, G.; Kraus, A. Stellar Multiplicity. Annu. Rev. Astron. Astrophys 2013, 51, 269–310. [Google Scholar] [CrossRef]
- Sana, H.; Le Bouquin, J.B.; Lacour, S.; Berger, J.P.; Duvert, G.; Gauchet, L.; Norris, B.; Olofsson, J.; Pickel, D.; Zins, G.; et al. Southern Massive Stars at High Angular Resolution: Observational Campaign and Companion Detection. Astrophys. J. Suppl. Ser. 2014, 215, 15. [Google Scholar] [CrossRef]
- Toonen, S.; Hamers, A.; Portegies Zwart, S. The evolution of hierarchical triple star-systems. Comput. Astrophys. Cosmol. 2016, 3, 6. [Google Scholar] [CrossRef]
- Lidov, M. The evolution of orbits of artificial satellites of planets under the action of gravitational perturbations of external bodies. Planet. Space Sci. 1962, 9, 719–759. [Google Scholar] [CrossRef]
- Kozai, Y. Secular perturbations of asteroids with high inclination and eccentricity. Astron. J. 1962, 67, 591–598. [Google Scholar] [CrossRef]
- Zeipel, H.V. Sur l’application des séries de M. Lindstedt à l’étude du mouvement des comètes périodiques. Astronom. Nachr. 1909, 183, 345–418. [Google Scholar] [CrossRef]
- Naoz, S. The Eccentric Kozai-Lidov Effect and Its Applications. Annu. Rev. Astron. Astrophys. 2016, 54, 441–489. [Google Scholar] [CrossRef]
- Shevchenko, I.I. The Lidov-Kozai Effect—Applications in Exoplanet Research and Dynamical Astronomy; Springer: Cham, Switzerland, 2017; Volume 441. [Google Scholar] [CrossRef]
- Ito, T.; Ohtsuka, K. The Lidov-Kozai Oscillation and Hugo von Zeipel. Monogr. Environ. Earth Planets 2019, 7, 1–113. [Google Scholar] [CrossRef]
- Hoang, B.M.; Naoz, S.; Kocsis, B.; Farr, W.M.; McIver, J. Detecting Supermassive Black Hole-induced Binary Eccentricity Oscillations with LISA. Astrophys. J. 2019, 875, L31. [Google Scholar] [CrossRef]
- Gupta, P.; Suzuki, H.; Okawa, H.; Maeda, K.i. Gravitational waves from hierarchical triple systems with Kozai-Lidov oscillation. Phys. Rev. D 2020, 101, 104053. [Google Scholar] [CrossRef]
- Arca-Sedda, M.; Rizzuto, F.P.; Naab, T.; Ostriker, J.; Giersz, M.; Spurzem, R. Breaching the Limit: Formation of GW190521-like and IMBH Mergers in Young Massive Clusters. Astrophys. J. 2021, 920, 128. [Google Scholar] [CrossRef]
- Gao, Y.; Toonen, S.; Grishin, E.; Comerford, T.; Kruckow, M.U. An empirical fit for viscoelastic simulations of tertiary tides. Mon. Not. R. Astron. Soc. 2020, 491, 264–271. [Google Scholar] [CrossRef]
- Glanz, H.; Perets, H.B. Simulations of common envelope evolution in triple systems: Circumstellar case. Mon. Not. R. Astron. Soc. 2021, 500, 1921–1932. [Google Scholar] [CrossRef]
- Toonen, S.; Portegies Zwart, S.; Hamers, A.S.; Bandopadhyay, D. The evolution of stellar triples. The most common evolutionary pathways. Astron. Astrophys. 2020, 640, A16. [Google Scholar] [CrossRef]
- Thompson, T.A. Accelerating Compact Object Mergers in Triple Systems with the Kozai Resonance: A Mechanism for “Prompt” Type Ia Supernovae, Gamma-Ray Bursts, and Other Exotica. Astrophys. J. 2011, 741, 82. [Google Scholar] [CrossRef]
- Antonini, F.; Toonen, S.; Hamers, A.S. Binary Black Hole Mergers from Field Triples: Properties, Rates, and the Impact of Stellar Evolution. Astrophys. J. 2017, 841, 77. [Google Scholar] [CrossRef]
- Antonini, F.; Chatterjee, S.; Rodriguez, C.L.; Morscher, M.; Pattabiraman, B.; Kalogera, V.; Rasio, F.A. Black Hole Mergers and Blue Stragglers from Hierarchical Triples Formed in Globular Clusters. Astrophys. J. 2016, 816, 65. [Google Scholar] [CrossRef]
- Grishin, E.; Perets, H.B.; Fragione, G. Quasi-secular evolution of mildly hierarchical triple systems: Analytics and applications for GW sources and hot Jupiters. Mon. Not. R. Astron. Soc. 2018, 481, 4907–4923. [Google Scholar] [CrossRef]
- Martinez, M.A.S.; Fragione, G.; Kremer, K.; Chatterjee, S.; Rodriguez, C.L.; Samsing, J.; Ye, C.S.; Weatherford, N.C.; Zevin, M.; Naoz, S.; et al. Black Hole Mergers from Hierarchical Triples in Dense Star Clusters. Astrophys. J. 2020, 903, 67. [Google Scholar] [CrossRef]
- Martinez, M.A.S.; Rodriguez, C.L.; Fragione, G. On the Mass Ratio Distribution of Black Hole Mergers in Triple Systems. arXiv 2021, arXiv:2105.01671. [Google Scholar]
- Silsbee, K.; Tremaine, S. Lidov-Kozai Cycles with Gravitational Radiation: Merging Black Holes in Isolated Triple Systems. Astrophys. J. 2017, 836, 39. [Google Scholar] [CrossRef]
- Toonen, S.; Perets, H.B.; Hamers, A.S. Rate of WD-WD head-on collisions in isolated triples is too low to explain standard type Ia supernovae. Astron. Astrophys. 2018, 610, A22. [Google Scholar] [CrossRef]
- Vigna-Gómez, A.; Toonen, S.; Ramirez-Ruiz, E.; Leigh, N.W.C.; Riley, J.; Haster, C.J. Massive Stellar Triples Leading to Sequential Binary Black Hole Mergers in the Field. Astrophys. J. 2021, 907, L19. [Google Scholar] [CrossRef]
- Antonini, F.; Perets, H.B. Secular Evolution of Compact Binaries near Massive Black Holes: Gravitational Wave Sources and Other Exotica. Astrophys. J. 2012, 757, 27. [Google Scholar] [CrossRef]
- VanLandingham, J.H.; Miller, M.C.; Hamilton, D.P.; Richardson, D.C. The Role of the Kozai–Lidov Mechanism in Black Hole Binary Mergers in Galactic Centers. Astrophys. J. 2016, 828, 77. [Google Scholar] [CrossRef]
- Fragione, G.; Grishin, E.; Leigh, N.W.C.; Perets, H.B.; Perna, R. Black hole and neutron star mergers in galactic nuclei. Mon. Not. R. Astron. Soc. 2019, 488, 47–63. [Google Scholar] [CrossRef]
- Hamers, A.S.; Bar-Or, B.; Petrovich, C.; Antonini, F. The Impact of Vector Resonant Relaxation on the Evolution of Binaries near a Massive Black Hole: Implications for Gravitational-wave Sources. Astrophys. J. 2018, 865, 2. [Google Scholar] [CrossRef]
- Hoang, B.M.; Naoz, S.; Kocsis, B.; Rasio, F.A.; Dosopoulou, F. Black Hole Mergers in Galactic Nuclei Induced by the Eccentric Kozai-Lidov Effect. Astrophys. J. 2018, 856, 140. [Google Scholar] [CrossRef]
- Trani, A.A. Do three-body encounters in galactic nuclei affect compact binary merger rates. In Star Clusters: From the Milky Way to the Early Universe; Bragaglia, A., Davies, M., Sills, A., Vesperini, E., Eds.; Cambridge University Press: Cambridge, UK, 2020; Volume 351, pp. 174–177. [Google Scholar] [CrossRef][Green Version]
- Michaely, E. From Ultra-wide Binaries to Interacting Binaries in the Field. In Proceedings of the AAS/Division of Dynamical Astronomy Meeting, Boulder, CO, USA, 10–13 June 2019; Volume 51, p. 202.07. [Google Scholar]
- Michaely, E.; Perets, H.B. High rate of gravitational waves mergers from flyby perturbations of wide black hole triples in the field. Mon. Not. R. Astron. Soc. 2020, 498, 4924–4935. [Google Scholar] [CrossRef]
- Grishin, E.; Perets, H.B. Chaotic dynamics of wide triples induced by galactic tides: A novel channel for producing compact binaries, mergers, and collisions. Mon. Not. R. Astron. Soc. 2022, 512, 4993–5009. [Google Scholar] [CrossRef]
- Hamilton, C.; Rafikov, R.R. Compact Object Binary Mergers Driven By Cluster Tides: A New Channel for LIGO/Virgo Gravitational-wave Events. Astrophys. J. 2019, 881, L13. [Google Scholar] [CrossRef]
- Vynatheya, P.; Hamers, A.S. How Important Is Secular Evolution for Black Hole and Neutron Star Mergers in 2 + 2 and 3 + 1 Quadruple-star Systems? Astrophys. J. 2022, 926, 195. [Google Scholar] [CrossRef]
- Hamers, A.S.; Fragione, G.; Neunteufel, P.; Kocsis, B. First- and second-generation black hole and neutron star mergers in 2 + 2 quadruples: Population statistics. Mon. Not. R. Astron. Soc. 2021, 506, 5345–5360. [Google Scholar] [CrossRef]
- Liu, B.; Lai, D. Enhanced black hole mergers in binary-binary interactions. Mon. Not. R. Astron. Soc. 2019, 483, 4060–4069. [Google Scholar] [CrossRef]
- Rastello, S.; Mapelli, M.; Di Carlo, U.N.; Giacobbo, N.; Santoliquido, F.; Spera, M.; Ballone, A.; Iorio, G. Dynamics of black hole-neutron star binaries in young star clusters. Mon. Not. R. Astron. Soc. 2020, 497, 1563–1570. [Google Scholar] [CrossRef]
- Dobie, D.; Stewart, A.; Murphy, T.; Lenc, E.; Wang, Z.; Kaplan, D.L.; Andreoni, I.; Banfield, J.; Brown, I.; Corsi, A.; et al. An ASKAP Search for a Radio Counterpart to the First High-significance Neutron Star–Black Hole Merger LIGO/Virgo S190814bv. Astrophys. J. 2019, 887, L13. [Google Scholar] [CrossRef]
- Gomez, S.; Hosseinzadeh, G.; Cowperthwaite, P.S.; Villar, V.A.; Berger, E.; Gardner, T.; Alexander, K.D.; Blanchard, P.K.; Chornock, R.; Drout, M.R.; et al. A Galaxy-targeted Search for the Optical Counterpart of the Candidate NS–BH Merger S190814bv with Magellan. Astrophys. J. 2019, 884, L55. [Google Scholar] [CrossRef]
- Ackley, K.; Amati, L.; Barbieri, C.; Bauer, F.E.; Benetti, S.; Bernardini, M.G.; Bhirombhakdi, K.; Botticella, M.T.; Branchesi, M.; Brocato, E.; et al. Observational constraints on the optical and near-infrared emission from the neutron star-black hole binary merger candidate S190814bv. Astron. Astrophys. 2020, 643, A113. [Google Scholar] [CrossRef]
- Andreoni, I.; Goldstein, D.A.; Kasliwal, M.M.; Nugent, P.E.; Zhou, R.; Newman, J.A.; Bulla, M.; Foucart, F.; Hotokezaka, K.; Nakar, E.; et al. GROWTH on S190814bv: Deep Synoptic Limits on the Optical/Near-infrared Counterpart to a Neutron Star-Black Hole Merger. Astrophys. J. 2020, 890, 131. [Google Scholar] [CrossRef]
- Antier, S.; Agayeva, S.; Aivazyan, V.; Alishov, S.; Arbouch, E.; Baransky, A.; Barynova, K.; Bai, J.M.; Basa, S.; Beradze, S.; et al. The first six months of the Advanced LIGO’s and Advanced Virgo’s third observing run with GRANDMA. Mon. Not. R. Astron. Soc. 2020, 492, 3904–3927. [Google Scholar] [CrossRef]
- Gompertz, B.P.; Levan, A.J.; Tanvir, N.R. A Search for Neutron Star-Black Hole Binary Mergers in the Short Gamma-Ray Burst Population. Astrophys. J. 2020, 895, 58. [Google Scholar] [CrossRef]
- Morgan, R.; Soares-Santos, M.; Annis, J.; Herner, K.; Garcia, A.; Palmese, A.; Drlica-Wagner, A.; Kessler, R.; García-Bellido, J.; Bachmann, T.; et al. Constraints on the Physical Properties of GW190814 through Simulations Based on DECam Follow-up Observations by the Dark Energy Survey. Astrophys. J. 2020, 901, 83. [Google Scholar] [CrossRef]
- Page, K.L.; Evans, P.A.; Tohuvavohu, A.; Kennea, J.A.; Klingler, N.J.; Cenko, S.B.; Oates, S.R.; Ambrosi, E.; Barthelmy, S.D.; Beardmore, A.; et al. Swift-XRT follow-up of gravitational wave triggers during the third aLIGO/Virgo observing run. Mon. Not. R. Astron. Soc. 2020, 499, 3459–3480. [Google Scholar] [CrossRef]
- Thakur, A.L.; Dichiara, S.; Troja, E.; Chase, E.A.; Sánchez-Ramírez, R.; Piro, L.; Fryer, C.L.; Butler, N.R.; Watson, A.M.; Wollaeger, R.; et al. A search for optical and near-infrared counterparts of the compact binary merger GW190814. Mon. Not. R. Astron. Soc. 2020, 499, 3868–3883. [Google Scholar] [CrossRef]
- Vieira, N.; Ruan, J.J.; Haggard, D.; Drout, M.R.; Nynka, M.C.; Boyce, H.; Spekkens, K.; Safi-Harb, S.; Carlberg, R.G.; Fernández, R.; et al. A Deep CFHT Optical Search for a Counterpart to the Possible Neutron Star–Black Hole Merger GW190814. Astrophys. J. 2020, 895, 96. [Google Scholar] [CrossRef]
- Watson, A.M.; Butler, N.R.; Lee, W.H.; Becerra, R.L.; Pereyra, M.; Angeles, F.; Farah, A.; Figueroa, L.; Gónzalez-Buitrago, D.; Quirós, F.; et al. Limits on the electromagnetic counterpart to S190814bv. Mon. Not. R. Astron. Soc. 2020, 492, 5916–5921. [Google Scholar] [CrossRef]
- Essick, R.; Landry, P. Discriminating between Neutron Stars and Black Holes with Imperfect Knowledge of the Maximum Neutron Star Mass. Astrophys. J. 2020, 904, 80. [Google Scholar] [CrossRef]
- Lackey, B.D.; Wade, L. Reconstructing the neutron-star equation of state with gravitational-wave detectors from a realistic population of inspiralling binary neutron stars. Phys. Rev. D 2015, 91. [Google Scholar] [CrossRef]
- Malik, T.; Ferreira, M.; Agrawal, B.K.; Providência, C. Relativistic description of dense matter equation of state and compatibility with neutron star observables: A Bayesian approach. arXiv 2022, arXiv:2201.12552. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; Van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-mass PSR J0740 + 6620. Astrophys. J. Lett. 2021, 915, L12. [Google Scholar] [CrossRef]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. PSR J1810+1744: Companion Darkening and a Precise High Neutron Star Mass. Astrophys. J. Lett. 2021, 908, L46. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Katerini, E.; Kurkela, A.; Nättilä, J.; Paschalidis, V.; Vuorinen, A. Multimessenger Constraints for Ultra-Dense Matter. Phys. Rev. X 2022, 12, 011058. [Google Scholar]
- Tews, I.; Pang, P.T.H.; Dietrich, T.; Coughlin, M.W.; Antier, S.; Bulla, M.; Heinzel, J.; Issa, L. On the Nature of GW190814 and Its Impact on the Understanding of Supranuclear Matter. Astrophys. J. 2021, 908, L1. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J.; Reed, B. GW190814: Impact of a 2.6 solar mass neutron star on the nucleonic equations of state. Phys. Rev. C 2020, 102, 065805. [Google Scholar] [CrossRef]
- Dexheimer, V.; Gomes, R.O.; Klähn, T.; Han, S.; Salinas, M. GW190814 as a massive rapidly rotating neutron star with exotic degrees of freedom. Phys. Rev. C 2021, 103, 025808. [Google Scholar] [CrossRef]
- Tsokaros, A.; Ruiz, M.; Shapiro, S.L. GW190814: Spin and Equation of State of a Neutron Star Companion. Astrophys. J. 2020, 905, 48. [Google Scholar] [CrossRef]
- Nathanail, A.; Most, E.R.; Rezzolla, L. GW170817 and GW190814: Tension on the Maximum Mass. Astrophys. J. 2021, 908, L28. [Google Scholar] [CrossRef]
- Most, E.R.; Papenfort, L.J.; Weih, L.R.; Rezzolla, L. A lower bound on the maximum mass if the secondary in GW190814 was once a rapidly spinning neutron star. Mon. Not. R. Astron. Soc. 2020, 499, L82–L86. [Google Scholar] [CrossRef]
- Biswas, B.; Nandi, R.; Char, P.; Bose, S.; Stergioulas, N. GW190814: On the properties of the secondary component of the binary. Mon. Not. R. Astron. Soc. 2021, 505, 1600–1606. [Google Scholar] [CrossRef]
- Zhang, N.B.; Li, B.A. GW190814’s Secondary Component with Mass 2.50–2.67 M⊙ as a Superfast Pulsar. Astrophys. J. 2020, 902, 38. [Google Scholar] [CrossRef]
- Tan, H.; Noronha-Hostler, J.; Yunes, N. Neutron Star Equation of State in Light of GW190814. Phys. Rev. Lett. 2020, 125, 261104. [Google Scholar] [CrossRef] [PubMed]
- Godzieba, D.A.; Radice, D.; Bernuzzi, S. On the Maximum Mass of Neutron Stars and GW190814. Astrophys. J. 2021, 908, 122. [Google Scholar] [CrossRef]
- Wu, X.; Bao, S.; Shen, H.; Xu, R. Effect of the symmetry energy on the secondary component of GW190814 as a neutron star. Phys. Rev. C 2021, 104, 015802. [Google Scholar] [CrossRef]
- Huang, K.; Hu, J.; Zhang, Y.; Shen, H. The Possibility of the Secondary Object in GW190814 as a Neutron Star. Astrophys. J. 2020, 904, 39. [Google Scholar] [CrossRef]
- Kanakis-Pegios, A.; Koliogiannis, P.S.; Moustakidis, C.C. Probing the Nuclear Equation of State from the Existence of a ∼2.6 M⊙ Neutron Star: The GW190814 Puzzle. Symmetry 2021, 13, 183. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D.; Oikonomou, V.K. Extended gravity description for the GW190814 supermassive neutron star. Phys. Lett. B 2020, 811, 135910. [Google Scholar] [CrossRef]
- Zevin, M.; Spera, M.; Berry, C.P.L.; Kalogera, V. Exploring the Lower Mass Gap and Unequal Mass Regime in Compact Binary Evolution. Astrophys. J. 2020, 899, L1. [Google Scholar] [CrossRef]
- Broekgaarden, F.S.; Berger, E.; Neijssel, C.J.; Vigna-Gómez, A.; Chattopadhyay, D.; Stevenson, S.; Chruslinska, M.; Justham, S.; de Mink, S.E.; Mandel, I. Impact of Massive Binary Star and Cosmic Evolution on Gravitational Wave Observations I: Black Hole—Neutron Star Mergers. Mon. Not. R. Astron. Soc. 2021. [Google Scholar] [CrossRef]
- Olejak, A.; Fishbach, M.; Belczynski, K.; Holz, D.E.; Lasota, J.P.; Miller, M.C.; Bulik, T. The Origin of Inequality: Isolated Formation of a 30 + 10 M⊙ Binary Black Hole Merger. Astrophys. J. 2020, 901, L39. [Google Scholar] [CrossRef]
- Mandel, I.; Müller, B.; Riley, J.; de Mink, S.E.; Vigna-Gómez, A.; Chattopadhyay, D. Binary population synthesis with probabilistic remnant mass and kick prescriptions. Mon. Not. R. Astron. Soc. 2021, 500, 1380–1384. [Google Scholar] [CrossRef]
- Eldridge, J.J.; Stanway, E.R. BPASS predictions for binary black hole mergers. Mon. Not. R. Astron. Soc. 2016, 462, 3302–3313. [Google Scholar] [CrossRef]
- Eldridge, J.J.; Stanway, E.R.; Xiao, L.; McClelland, L.A.S.; Taylor, G.; Ng, M.; Greis, S.M.L.; Bray, J.C. Binary Population and Spectral Synthesis Version 2.1: Construction, Observational Verification, and New Results. Publ. Astron. Soc. Aust. 2017, 34, e058. [Google Scholar] [CrossRef]
- Lu, W.; Beniamini, P.; Bonnerot, C. On the formation of GW190814. Mon. Not. R. Astron. Soc. 2021, 500, 1817–1832. [Google Scholar] [CrossRef]
- Samsing, J.; Ilan, T. Double gravitational wave mergers. Mon. Not. R. Astron. Soc. 2019, 482, 30–39. [Google Scholar] [CrossRef]
- Cholis, I.; Kritos, K.; Garfinkle, D. Can Thorne-Żytkow Objects source GW190814-type events? arXiv 2021, arXiv:2106.07662. [Google Scholar] [CrossRef]
- Jiménez-Esteban, F.M.; Solano, E.; Rodrigo, C. A Catalog of Wide Binary and Multiple Systems of Bright Stars from Gaia-DR2 and the Virtual Observatory. Astron. J. 2019, 157, 78. [Google Scholar] [CrossRef]
- Duquennoy, A.; Mayor, M. Multiplicity among solar-type stars in the solar neighbourhood. II—Distribution of the orbital elements in an unbiased sample. Astron. Astrophys. 1991, 500, 337–376. [Google Scholar]
- Sana, H. The multiplicity of massive stars: A 2016 view. In The Lives and Death-Throes of Massive Stars; Proceedings of the International Astronomical Union; Eldridge, J.J., Bray, J.C., McClelland, L.A.S., Xiao, L., Eds.; Cambridge University Press: Cambridge, UK, 2017; Volume 329, pp. 110–117. [Google Scholar] [CrossRef]
- Gao, S.; Liu, C.; Zhang, X.; Justham, S.; Deng, L.; Yang, M. The Binarity of Milky Way F,G,K Stars as a Function of Effective Temperature And Metallicity. Astrophys. J. 2014, 788, L37. [Google Scholar] [CrossRef]
- Yuan, H.; Liu, X.; Xiang, M.; Huang, Y.; Chen, B.; Wu, Y.; Hou, Y.; Zhang, Y. Stellar Loci II. A Model-Free Estimate of the Binary Fraction for Field FGK Stars. Astrophys. J. 2015, 799, 135. [Google Scholar] [CrossRef]
- Moe, M.; Kratter, K.M.; Badenes, C. The Close Binary Fraction of Solar-type Stars Is Strongly Anticorrelated with Metallicity. Astrophys. J. 2019, 875, 61. [Google Scholar] [CrossRef]
- Thorne, K.S.; Zytkow, A.N. Red giants and supergiants with degenerate neutron cores. Astrophys. J. 1975, 199, L19–L24. [Google Scholar] [CrossRef]
- Safarzadeh, M.; Hamers, A.S.; Loeb, A.; Berger, E. Formation and Merging of Mass Gap Black Holes in Gravitational-wave Merger Events from Wide Hierarchical Quadruple Systems. Astrophys. J. 2020, 888, L3. [Google Scholar] [CrossRef]
- Fragione, G.; Loeb, A.; Rasio, F.A. Merging Black Holes in the Low-mass and High-mass Gaps from 2 + 2 Quadruple Systems. Astrophys. J. 2020, 895, L15. [Google Scholar] [CrossRef]
- Fragione, G.; Kocsis, B. Black hole mergers from quadruples. Mon. Not. R. Astron. Soc. 2019, 486, 4781–4789. [Google Scholar] [CrossRef]
- Liu, B.; Lai, D. Hierarchical black hole mergers in multiple systems: Constrain the formation of GW190412-, GW190814-, and GW190521-like events. Mon. Not. R. Astron. Soc. 2021, 502, 2049–2064. [Google Scholar] [CrossRef]
- Sigurdsson, S.; Phinney, E.S. Dynamics and Interactions of Binaries and Neutron Stars in Globular Clusters. Astrophys. J. Suppl. Ser. 1995, 99, 609. [Google Scholar] [CrossRef]
- Fragione, G.; Kocsis, B. Black Hole Mergers from an Evolving Population of Globular Clusters. Phys. Rev. Lett. 2018, 121, 161103. [Google Scholar] [CrossRef]
- Clausen, D.; Sigurdsson, S.; Chernoff, D.F. Black hole-neutron star mergers in globular clusters. Mon. Not. R. Astron. Soc. 2013, 428, 3618–3629. [Google Scholar] [CrossRef]
- Clausen, D.; Sigurdsson, S.; Chernoff, D.F. Dynamically formed black hole + millisecond pulsar binaries in globular clusters. Mon. Not. R. Astron. Soc. 2014, 442, 207–219. [Google Scholar] [CrossRef]
- Devecchi, B.; Colpi, M.; Mapelli, M.; Possenti, A. Millisecond pulsars around intermediate-mass black holes in globular clusters. Mon. Not. R. Astron. Soc. 2007, 380, 691–702. [Google Scholar] [CrossRef]
- Ye, C.S.; Fong, W.F.; Kremer, K.; Rodriguez, C.L.; Chatterjee, S.; Fragione, G.; Rasio, F.A. On the Rate of Neutron Star Binary Mergers from Globular Clusters. Astrophys. J. 2020, 888, L10. [Google Scholar] [CrossRef]
- Kritos, K.; Cholis, I. Black holes merging with low mass gap objects inside globular clusters. Phys. Rev. D 2021, 104, 043004. [Google Scholar] [CrossRef]
- Arca Sedda, M. Dynamical Formation of the GW190814 Merger. Astrophys. J. 2021, 908, L38. [Google Scholar] [CrossRef]
- Arca Sedda, M. Dissecting the properties of neutron star-black hole mergers originating in dense star clusters. Commun. Phys. 2020, 3, 43. [Google Scholar] [CrossRef]
- Santoliquido, F.; Mapelli, M.; Bouffanais, Y.; Giacobbo, N.; Di Carlo, U.N.; Rastello, S.; Artale, M.C.; Ballone, A. The Cosmic Merger Rate Density Evolution of Compact Binaries Formed in Young Star Clusters and in Isolated Binaries. Astrophys. J. 2020, 898, 152. [Google Scholar] [CrossRef]
- Tagawa, H.; Kocsis, B.; Haiman, Z.; Bartos, I.; Omukai, K.; Samsing, J. Mass-gap Mergers in Active Galactic Nuclei. Astrophys. J. 2021, 908, 194. [Google Scholar] [CrossRef]
- Yang, Y.; Gayathri, V.; Bartos, I.; Haiman, Z.; Safarzadeh, M.; Tagawa, H. Black Hole Formation in the Lower Mass Gap through Mergers and Accretion in AGN Disks. Astrophys. J. 2020, 901, L34. [Google Scholar] [CrossRef]
- Bombaci, I.; Drago, A.; Logoteta, D.; Pagliara, G.; Vidaña, I. Was GW190814 a Black Hole–Strange Quark Star System? Phys. Rev. Lett. 2021, 126, 162702. [Google Scholar] [CrossRef] [PubMed]
- Jedamzik, K. Consistency of Primordial Black Hole Dark Matter with LIGO/Virgo Merger Rates. Phys. Rev. Lett. 2021, 126, 051302. [Google Scholar] [CrossRef] [PubMed]
- Vattis, K.; Goldstein, I.S.; Koushiappas, S.M. Could the 2.6 M⊙ object in GW190814 be a primordial black hole? Phys. Rev. D 2020, 102, 061301. [Google Scholar] [CrossRef]
- Carr, B.; Clesse, S.; García-Bellido, J.; Kühnel, F. Cosmic conundra explained by thermal history and primordial black holes. Phys. Dark Universe 2021, 31, 100755. [Google Scholar] [CrossRef]
- Clesse, S.; Garcia-Bellido, J. GW190425, GW190521 and GW190814: Three candidate mergers of primordial black holes from the QCD epoch. arXiv 2020, arXiv:2007.06481. [Google Scholar]
- Romero-Shaw, I.; Lasky, P.D.; Thrane, E.; Calderón Bustillo, J. GW190521: Orbital Eccentricity and Signatures of Dynamical Formation in a Binary Black Hole Merger Signal. Astrophys. J. 2020, 903, L5. [Google Scholar] [CrossRef]
- Gayathri, V.; Healy, J.; Lange, J.; O’Brien, B.; Szczepanczyk, M.; Bartos, I.; Campanelli, M.; Klimenko, S.; Lousto, C.; O’Shaughnessy, R. GW190521 as a Highly Eccentric Black Hole Merger. arXiv 2020, arXiv:2009.05461. [Google Scholar]
- Holgado, A.M.; Ortega, A.; Rodriguez, C.L. Dynamical Formation Scenarios for GW190521 and Prospects for Decihertz Gravitational-wave Astronomy with GW190521-like Binaries. Astrophys. J. 2021, 909, L24. [Google Scholar] [CrossRef]
- Nitz, A.H.; Capano, C.D. GW190521 May Be an Intermediate-mass Ratio Inspiral. Astrophys. J. 2021, 907, L9. [Google Scholar] [CrossRef]
- Fragione, G.; Loeb, A.; Rasio, F.A. On the Origin of GW190521-like Events from Repeated Black Hole Mergers in Star Clusters. Astrophys. J. 2020, 902, L26. [Google Scholar] [CrossRef]
- Fragione, G.; Kocsis, B.; Rasio, F.A.; Silk, J. Repeated mergers, mass-gap black holes, and formation of intermediate-mass black holes in nuclear star clusters. arXiv 2021, arXiv:2107.04639. [Google Scholar]
- Mapelli, M.; Santoliquido, F.; Bouffanais, Y.; Arca Sedda, M.A.; Artale, M.C.; Ballone, A. Mass and Rate of Hierarchical Black Hole Mergers in Young, Globular and Nuclear Star Clusters. Symmetry 2021, 13, 1678. [Google Scholar] [CrossRef]
- Baibhav, V.; Berti, E.; Gerosa, D.; Mould, M.; Wong, K.W.K. Looking for the parents of LIGO’s black holes. Phys. Rev. D 2021, 104, 084002. [Google Scholar] [CrossRef]
- Anagnostou, O.; Trenti, M.; Melatos, A. Hierarchical Formation Of An Intermediate Mass Black Hole Via Seven Mergers: Implications For GW190521. arXiv 2020, arXiv:2010.06161. [Google Scholar]
- Kimball, C.; Talbot, C.; Berry, C.P.L.; Zevin, M.; Thrane, E.; Kalogera, V.; Buscicchio, R.; Carney, M.; Dent, T.; Middleton, H.; et al. Evidence for Hierarchical Black Hole Mergers in the Second LIGO-Virgo Gravitational Wave Catalog. Astrophys. J. 2021, 915, L35. [Google Scholar] [CrossRef]
- Fragione, G.; Banerjee, S. Binary Black Hole Mergers from Young Massive and Open Clusters: Comparison to GWTC-2 Gravitational Wave Data. Astrophys. J. 2021, 913, L29. [Google Scholar] [CrossRef]
- Di Carlo, U.N.; Mapelli, M.; Pasquato, M.; Rastello, S.; Ballone, A.; Dall’Amico, M.; Giacobbo, N.; Iorio, G.; Spera, M.; Torniamenti, S.; et al. Intermediate-mass black holes from stellar mergers in young star clusters. Mon. Not. R. Astron. Soc. 2021, 507, 5132–5143. [Google Scholar] [CrossRef]
- Dall’Amico, M.; Mapelli, M.; Di Carlo, U.N.; Bouffanais, Y.; Rastello, S.; Santoliquido, F.; Ballone, A.; Arca Sedda, M. GW190521 formation via three-body encounters in young massive star clusters. Mon. Not. R. Astron. Soc. 2021, 508, 3045–3054. [Google Scholar] [CrossRef]
- González, E.; Kremer, K.; Chatterjee, S.; Fragione, G.; Rodriguez, C.L.; Weatherford, N.C.; Ye, C.S.; Rasio, F.A. Intermediate-mass Black Holes from High Massive-star Binary Fractions in Young Star Clusters. Astrophys. J. 2021, 908, L29. [Google Scholar] [CrossRef]
- Palmese, A.; Conselice, C.J. GW190521 from the Merger of Ultradwarf Galaxies. Phys. Rev. Lett. 2021, 126, 181103. [Google Scholar] [CrossRef]
- Reines, A.E.; Volonteri, M. Relations between Central Black Hole Mass and Total Galaxy Stellar Mass in the Local Universe. Astrophys. J. 2015, 813, 82. [Google Scholar] [CrossRef]
- McKernan, B.; Ford, K.E.S.; Bartos, I.; Graham, M.J.; Lyra, W.; Marka, S.; Marka, Z.; Ross, N.P.; Stern, D.; Yang, Y. Ram-pressure Stripping of a Kicked Hill Sphere: Prompt Electromagnetic Emission from the Merger of Stellar Mass Black Holes in an AGN Accretion Disk. Astrophys. J. 2019, 884, L50. [Google Scholar] [CrossRef]
- Ashton, G.; Ackley, K.; Hernandez, I.M.; Piotrzkowski, B. Current observations are insufficient to confidently associate the binary black hole merger GW190521 with AGN J124942.3 + 344929. Class. Quantum Gravity 2021, 38, 235004. [Google Scholar] [CrossRef]
- Graham, M.J.; Ford, K.E.S.; McKernan, B.; Ross, N.P.; Stern, D.; Burdge, K.; Coughlin, M.; Djorgovski, S.G.; Drake, A.J.; Duev, D.; et al. Candidate Electromagnetic Counterpart to the Binary Black Hole Merger Gravitational-Wave Event S190521g. Phys. Rev. Lett. 2020, 124, 251102. [Google Scholar] [CrossRef] [PubMed]
- Palmese, A.; Fishbach, M.; Burke, C.J.; Annis, J.; Liu, X. Do LIGO/Virgo Black Hole Mergers Produce AGN Flares? The Case of GW190521 and Prospects for Reaching a Confident Association. Astrophys. J. 2021, 914, L34. [Google Scholar] [CrossRef]
- Kinugawa, T.; Nakamura, T.; Nakano, H. Formation of binary black holes similar to GW190521 with a total mass of ∼150 M⊙ from Population III binary star evolution. Mon. Not. R. Astron. Soc. 2021, 501, L49–L53. [Google Scholar] [CrossRef]
- Liu, B.; Meynet, G.; Bromm, V. Dynamical evolution of population III stellar systems and the resulting binary statistics. Mon. Not. R. Astron. Soc. 2021, 501, 643–663. [Google Scholar] [CrossRef]
- Rice, J.R.; Zhang, B. Growth of Stellar-mass Black Holes in Dense Molecular Clouds and GW190521. Astrophys. J. 2021, 908, 59. [Google Scholar] [CrossRef]
- De Luca, V.; Desjacques, V.; Franciolini, G.; Pani, P.; Riotto, A. GW190521 Mass Gap Event and the Primordial Black Hole Scenario. Phys. Rev. Lett. 2021, 126, 051101. [Google Scholar] [CrossRef]
- Yang, Y. Influences of accreting primordial black holes on the global 21 cm signal in the dark ages. Mon. Not. R. Astron. Soc. 2021, 508, 5709–5715. [Google Scholar] [CrossRef]
- Cruz-Osorio, A.; Lora-Clavijo, F.D.; Herdeiro, C. GW190521 formation scenarios via relativistic accretion. J. Cosmol. Astropart. Phys. 2021, 2021, 032. [Google Scholar] [CrossRef]
- Kritos, K.; De Luca, V.; Franciolini, G.; Kehagias, A.; Riotto, A. The astro-primordial black hole merger rates: A reappraisal. J. Cosmol. Astropart. Phys. 2021, 2021, 039. [Google Scholar] [CrossRef]
- Bustillo, J.C.; Sanchis-Gual, N.; Torres-Forné, A.; Font, J.A.; Vajpeyi, A.; Smith, R.; Herdeiro, C.; Radu, E.; Leong, S.H.W. GW190521 as a Merger of Proca Stars: A Potential New Vector Boson of 8.7 × 10−13 eV. Phys. Rev. Lett. 2021, 126, 081101. [Google Scholar] [CrossRef] [PubMed]
- Ziegler, J.; Freese, K. Filling the black hole mass gap: Avoiding pair instability in massive stars through addition of nonnuclear energy. Phys. Rev. D 2021, 104, 043015. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190412: Observation of a binary-black-hole coalescence with asymmetric masses. Phys. Rev. D 2020, 102, 043015. [Google Scholar] [CrossRef]
- Mandel, I.; Fragos, T. An Alternative Interpretation of GW190412 as a Binary Black Hole Merger with a Rapidly Spinning Secondary. Astrophys. J. 2020, 895, L28. [Google Scholar] [CrossRef]
- Zevin, M.; Berry, C.P.L.; Coughlin, S.; Chatziioannou, K.; Vitale, S. You Can’t Always Get What You Want: The Impact of Prior Assumptions on Interpreting GW190412. Astrophys. J. 2020, 899, L17. [Google Scholar] [CrossRef]
- Riley, J.; Mandel, I.; Marchant, P.; Butler, E.; Nathaniel, K.; Neijssel, C.; Shortt, S.; Vigna-Gómez, A. Chemically homogeneous evolution: A rapid population synthesis approach. Mon. Not. R. Astron. Soc. 2021, 505, 663–676. [Google Scholar] [CrossRef]
- Rodriguez, C.L.; Kremer, K.; Grudić, M.Y.; Hafen, Z.; Chatterjee, S.; Fragione, G.; Lamberts, A.; Martinez, M.A.S.; Rasio, F.A.; Weatherford, N.; et al. GW190412 as a Third-generation Black Hole Merger from a Super Star Cluster. Astrophys. J. 2020, 896, L10. [Google Scholar] [CrossRef]
- Gerosa, D.; Vitale, S.; Berti, E. Astrophysical Implications of GW190412 as a Remnant of a Previous Black-Hole Merger. Phys. Rev. Lett. 2020, 125, 101103. [Google Scholar] [CrossRef]
- Miller, M.C.; Lauburg, V.M. Mergers of Stellar-Mass Black Holes in Nuclear Star Clusters. Astrophys. J. 2009, 692, 917–923. [Google Scholar] [CrossRef]
- Kimball, C.; Talbot, C.; Berry, C.P.L.; Carney, M.; Zevin, M.; Thrane, E.; Kalogera, V. Black Hole Genealogy: Identifying Hierarchical Mergers with Gravitational Waves. Astrophys. J. 2020, 900, 177. [Google Scholar] [CrossRef]
- Hamers, A.S.; Safarzadeh, M. Was GW190412 Born from a Hierarchical 3 + 1 Quadruple Configuration? Astrophys. J. 2020, 898, 99. [Google Scholar] [CrossRef]
- Mandel, I.; Smith, R.J.E. GW200115: A Nonspinning Black Hole-Neutron Star Merger. Astrophys. J. 2021, 922, L14. [Google Scholar] [CrossRef]
- Fragione, G. Black-hole-Neutron-star Mergers Are Unlikely Multimessenger Sources. Astrophys. J. 2021, 923, L2. [Google Scholar] [CrossRef]
- Hu, R.C.; Zhu, J.P.; Qin, Y.; Zhang, B.; Liang, E.W.; Shao, Y. A Channel to Form Fast-spinning Black Hole–Neutron Star Binary Mergers as Multi-messenger Sources. arXiv 2022, arXiv:2201.09549. [Google Scholar]
- D’Orazio, D.J.; Haiman, Z.; Levin, J.; Samsing, J.; Vigna-Gomez, A. Multi-Messenger Constraints on Magnetic Fields in Merging Black Hole-Neutron Star Binaries. arXiv 2021, arXiv:2112.01979. [Google Scholar]
- Sipior, M.S.; Sigurdsson, S. Nova Scorpii and Coalescing Low-Mass Black Hole Binaries as LIGO Sources. Astrophys. J. 2002, 572, 962–970. [Google Scholar] [CrossRef]
- Belczynski, K.; Perna, R.; Bulik, T.; Kalogera, V.; Ivanova, N.; Lamb, D.Q. A Study of Compact Object Mergers as Short Gamma-Ray Burst Progenitors. Astrophys. J. 2006, 648, 1110–1116. [Google Scholar] [CrossRef]
- Belczynski, K.; Repetto, S.; Holz, D.E.; O’Shaughnessy, R.; Bulik, T.; Berti, E.; Fryer, C.; Dominik, M. Compact Binary Merger Rates: Comparison with LIGO/Virgo Upper Limits. Astrophys. J. 2016, 819, 108. [Google Scholar] [CrossRef]
- Santoliquido, F.; Mapelli, M.; Giacobbo, N.; Bouffanais, Y.; Artale, M.C. The cosmic merger rate density of compact objects: Impact of star formation, metallicity, initial mass function, and binary evolution. Mon. Not. R. Astron. Soc. 2021, 502, 4877–4889. [Google Scholar] [CrossRef]
- Broekgaarden, F.S.; Berger, E. Formation of the First Two Black Hole-Neutron Star Mergers (GW200115 and GW200105) from Isolated Binary Evolution. Astrophys. J. 2021, 920, L13. [Google Scholar] [CrossRef]
- Kinugawa, T.; Nakamura, T.; Nakano, H. Neutron star black hole binaries in LIGO/Virgo O3b run were formed from Population I/II binaries. arXiv 2022, arXiv:2201.06713. [Google Scholar]
- Belczynski, K.; Romagnolo, A.; Olejak, A.; Klencki, J.; Chattopadhyay, D.; Stevenson, S.; Coleman Miller, M.; Lasota, J.P.; Crowther, P.A. The Uncertain Future of Massive Binaries Obscures the Origin of LIGO/Virgo Sources. Astrophys. J. 2022, 925, 69. [Google Scholar] [CrossRef]
- Zhu, J.P.; Wu, S.; Qin, Y.; Zhang, B.; Gao, H.; Cao, Z. Population Properties of Gravitational-Wave Neutron Star–Black Hole Mergers. arXiv 2021, arXiv:2112.02605. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Prospects for observing and localizing gravitational-wave transients with Advanced LIGO, Advanced Virgo and KAGRA. Living Rev. Relativ. 2018, 21, 3. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).