Status and Perspectives of Continuous Gravitational Wave Searches
Abstract
1. Introduction
2. Sources of Continuous GWs
2.1. Neutron Stars
Strain Amplitude Limits
2.2. Dark Matter Candidates
2.2.1. Boson Clouds
2.2.2. Ultralight Vector Bosons: Dark Photons
2.2.3. Compact Dark Objects and Primordial Black Holes
3. Searches for CWs Signals with Earth-Based Detectors
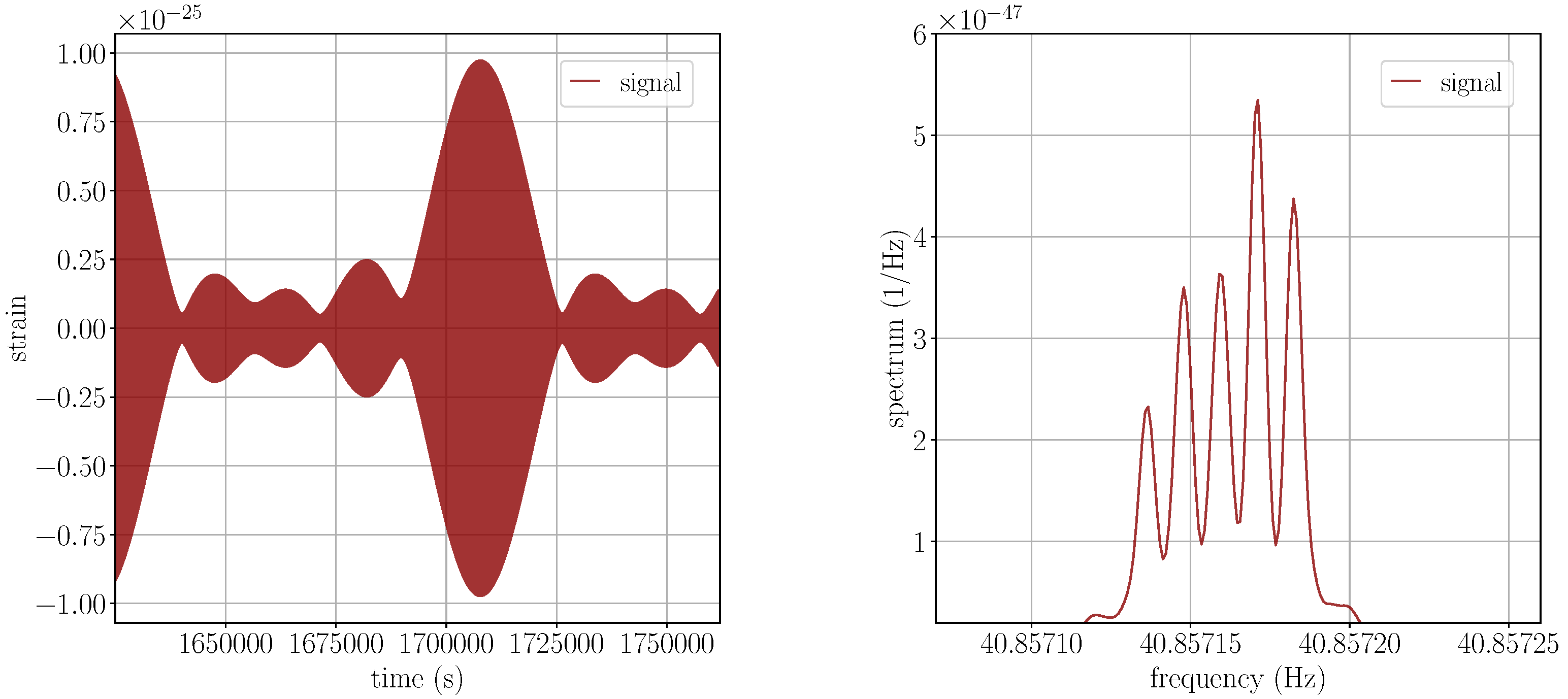
3.1. The Signal at the Detector
3.2. Search Methods
4. Recent Results
4.1. Results from Known Sources (Pulsars, LMXBs, Supernova Remnants)
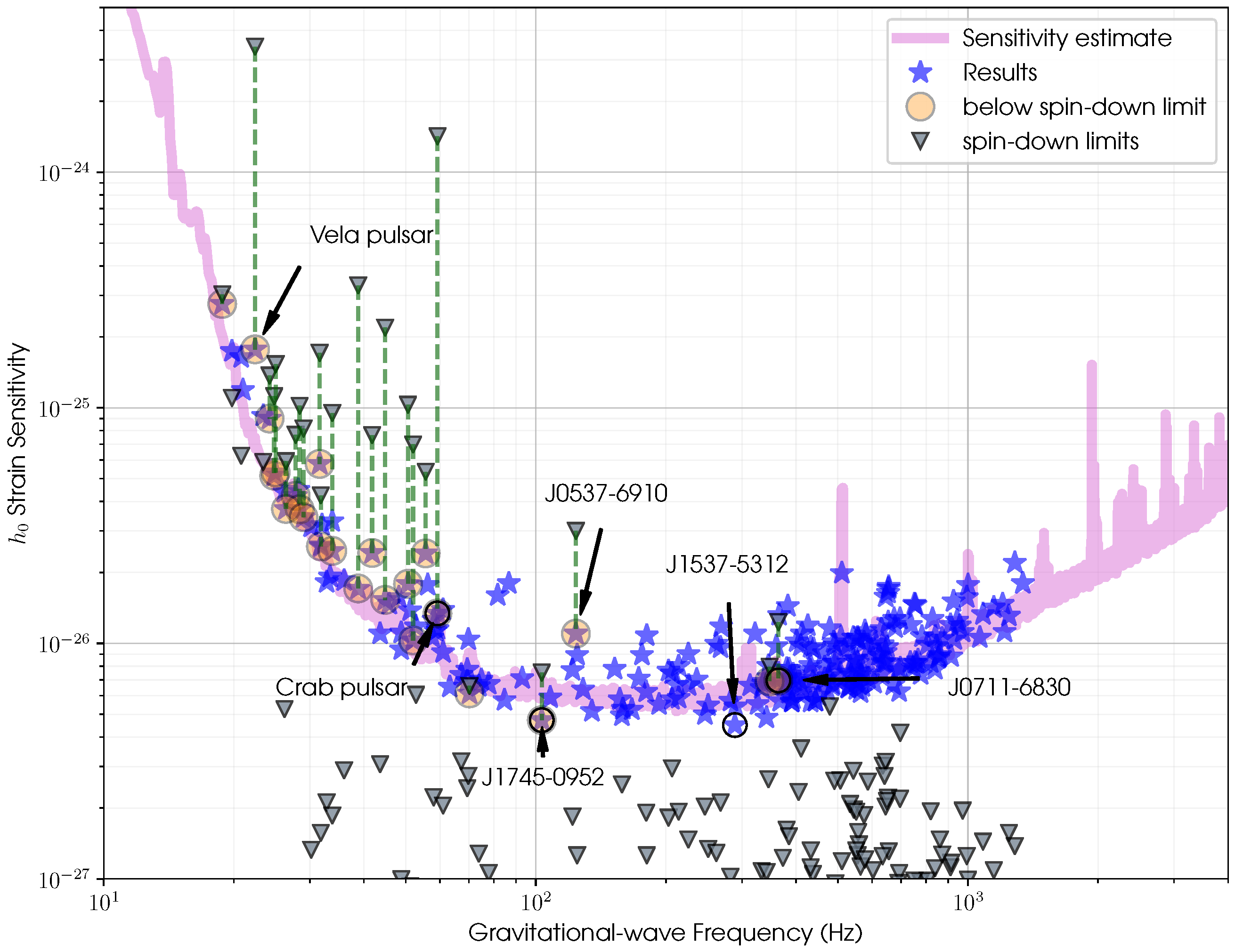
4.1.1. Known Pulsars
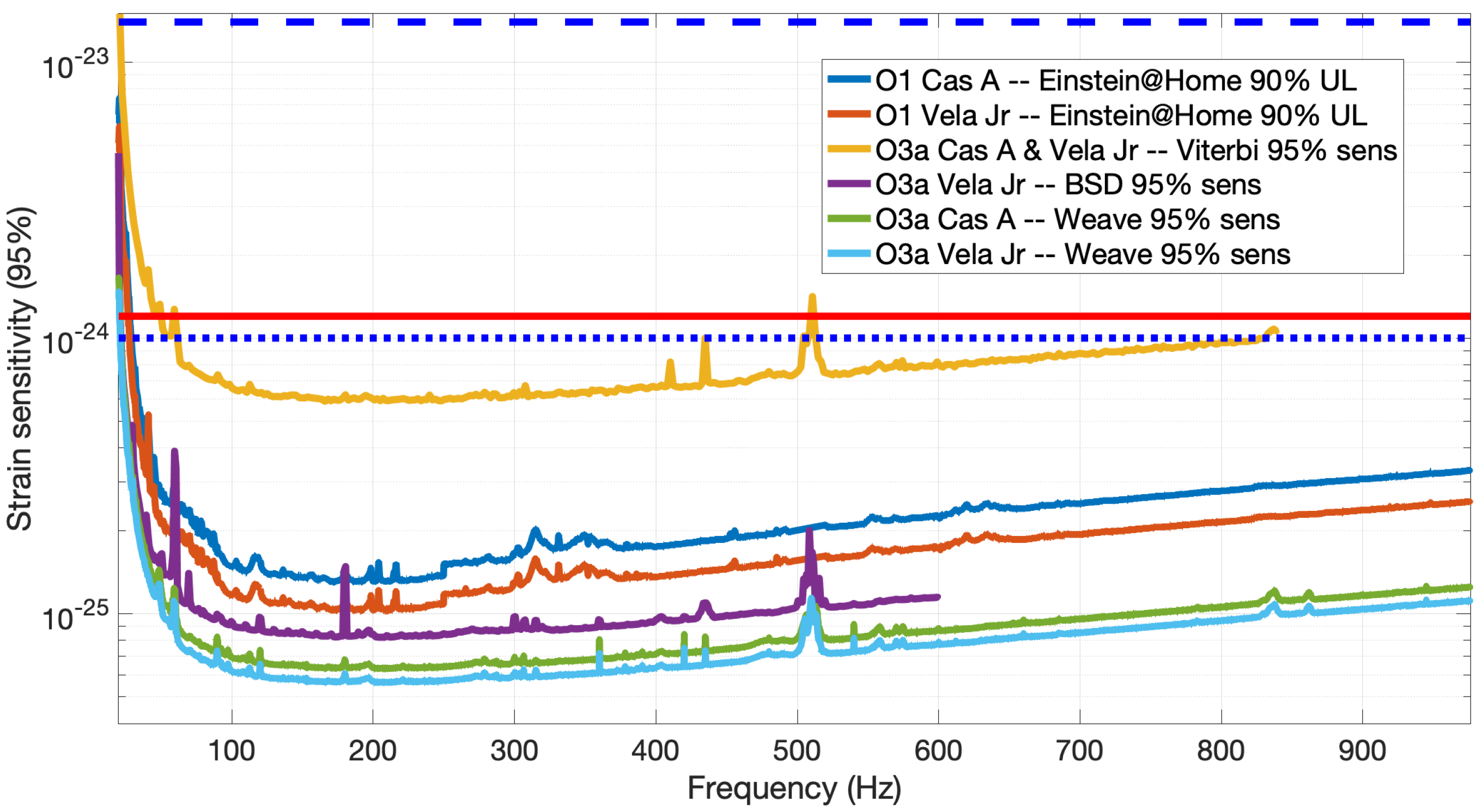
4.1.2. Supernova Remnants
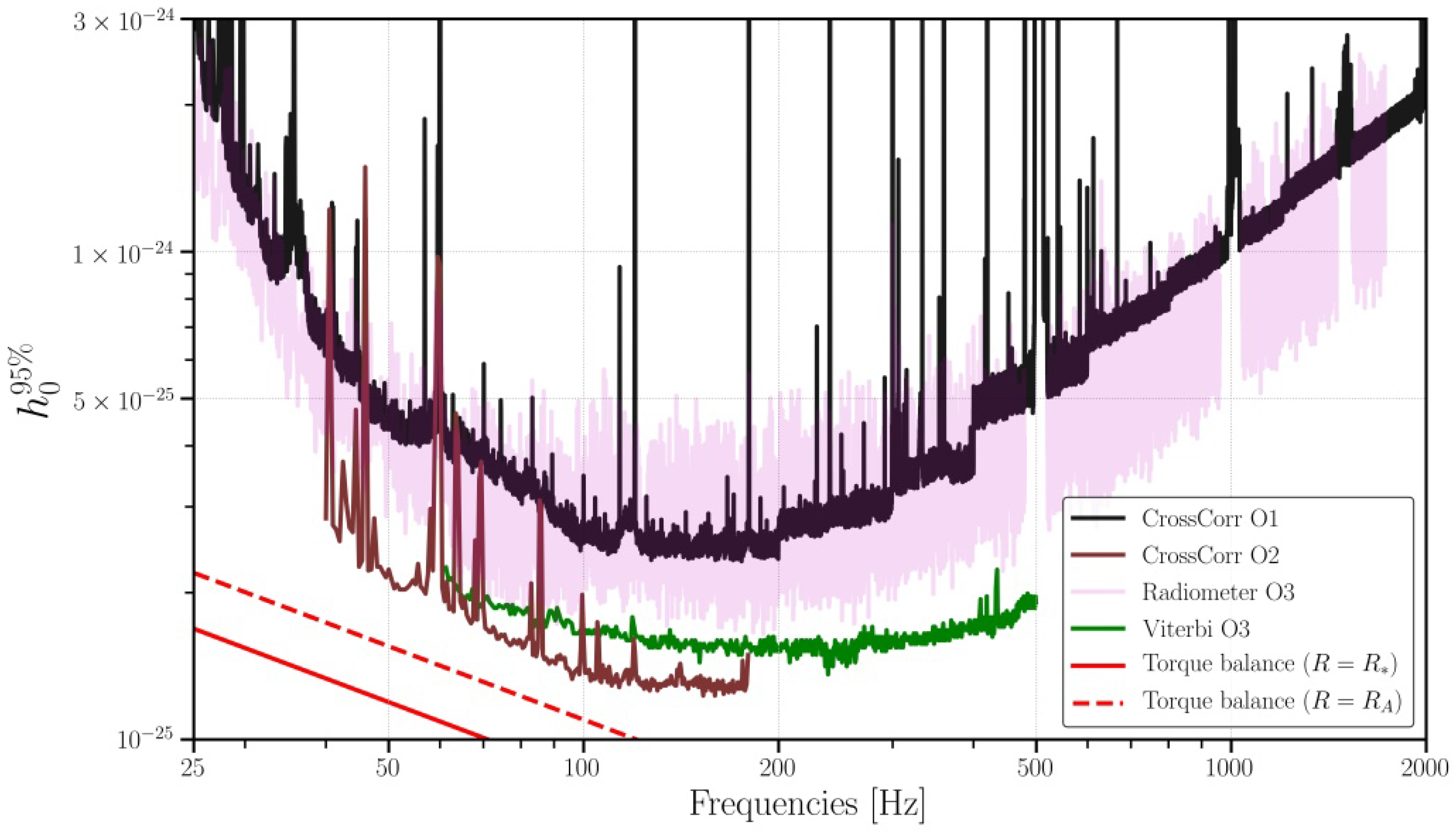
4.1.3. Low-Mass X-ray Binaries and Sco-X1
4.2. Results from Unknown Sources (All-Sky, Spotlight Surveys, Dark Matter Candidates)
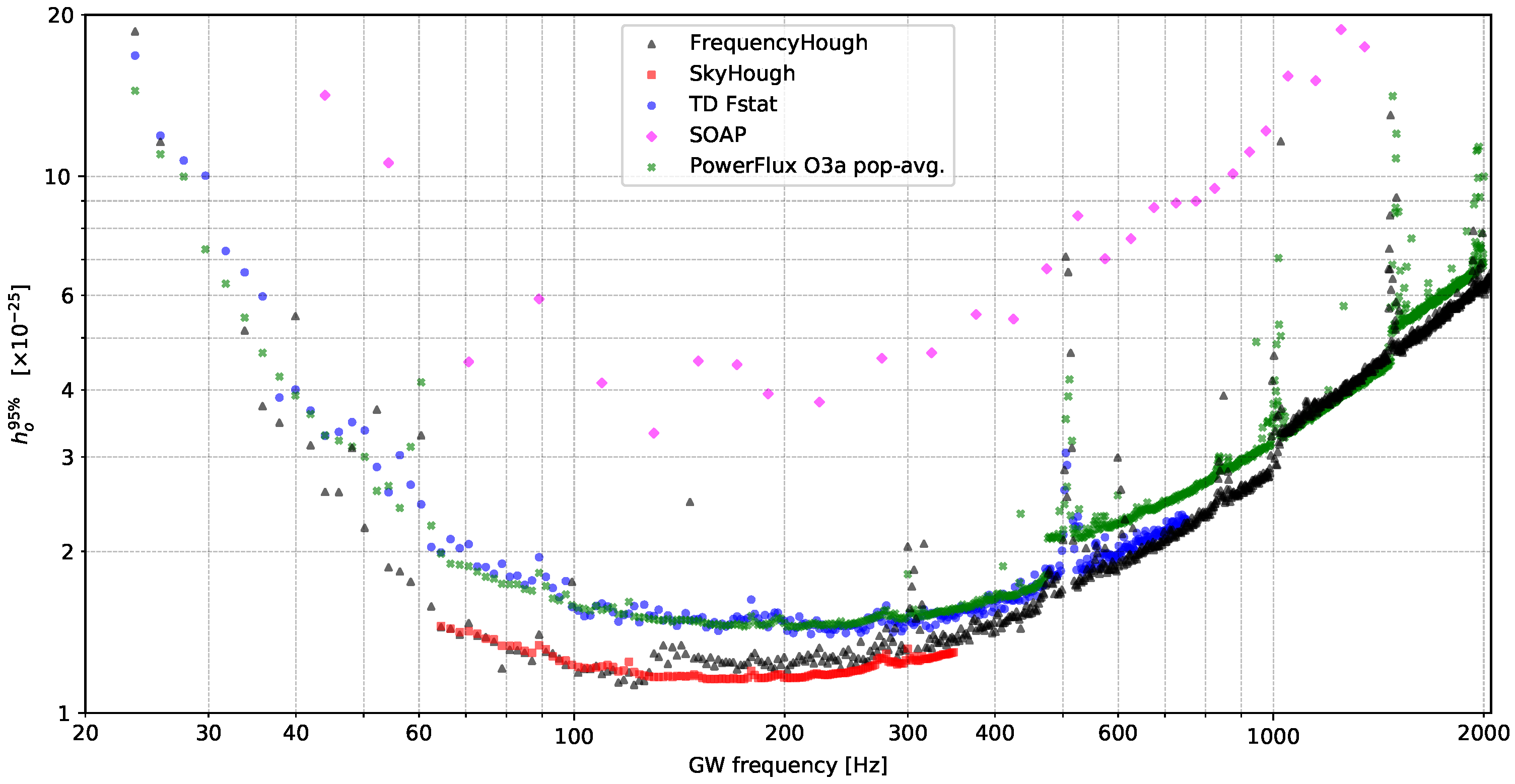
4.2.1. All-Sky Surveys
4.2.2. Spotlight Surveys: The Galactic Center and Terzan 5
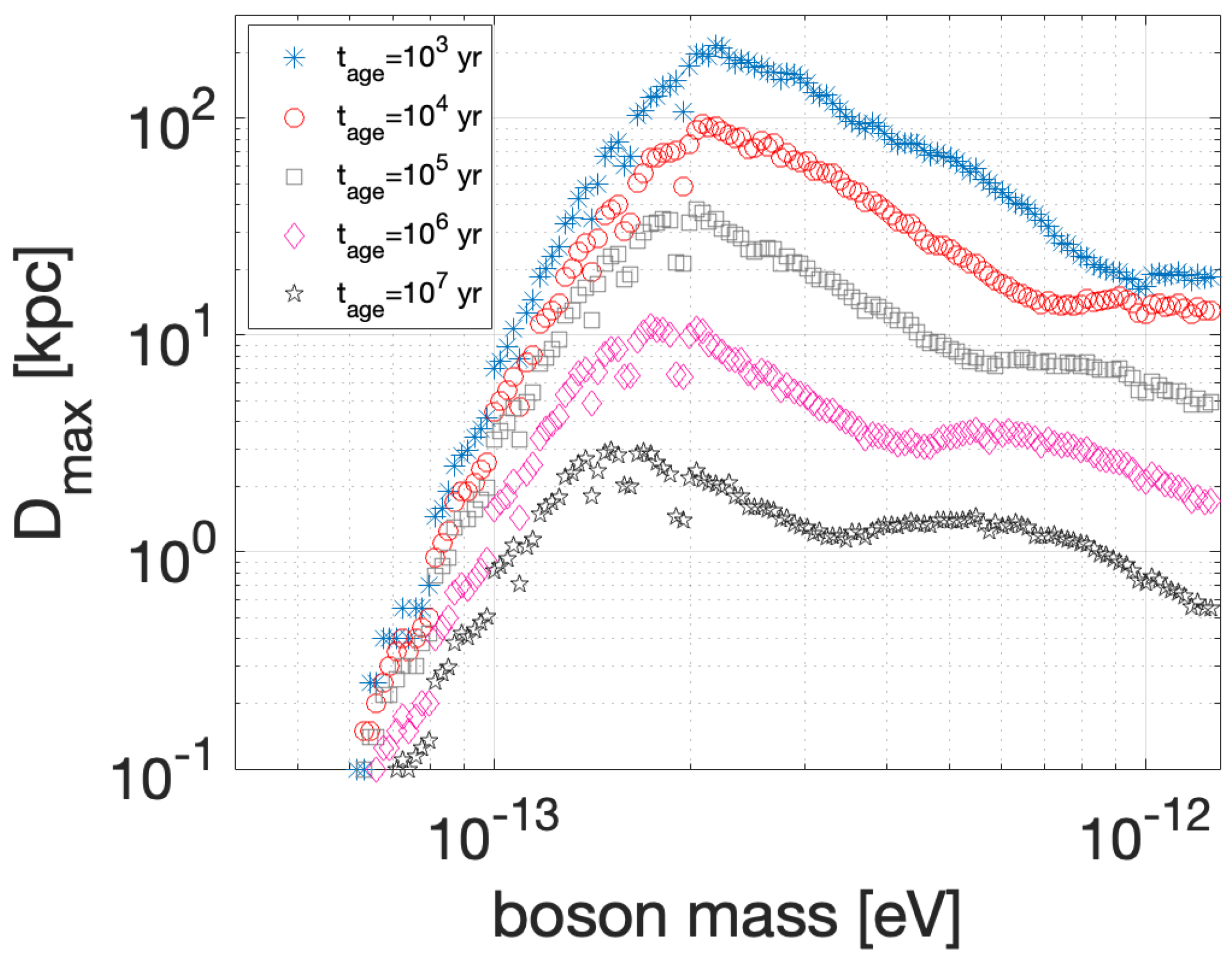
4.2.3. Dark Matter Candidates—Ultralight Bosons and CDOs
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
| 1 | Given the proportionality between and , here f can indicate any of the two frequencies. |
| 2 | for and for . |
| 3 | Hence, the time derivative of the time component of is negligible relative to . |
| 4 | Recycled pulsars are ordinary pulsars that have been spun up by accretion from a companion star in a binary system. |
| 5 | The ranges are due to fact that the coherence time used in [248] changes in each 10Hz frequency band. |
| 6 | except for the SOAP pipeline that covers the additional small region in frequency and in spin-up. |
References
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Advanced LIGO. Class. Quantum Gravity 2015, 32, 074001. [Google Scholar] [CrossRef]
- Acernese, F.; Agathos, M.; Agatsuma, K.; Aisa, D.; Allemandou, N.; Allocca, A.; Amarni, J.; Astone, P.; Balestri, G.; Ballardin, G.; et al. Advanced Virgo: A second-generation interferometric gravitational wave detector. Class. Quantum Gravity 2014, 32, 024001. [Google Scholar] [CrossRef]
- Nardecchia, I. Detecting Gravitational Waves with Advanced Virgo. Galaxies 2022, 10, 28. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. Phys. Rev. X 2019, 9, 031040. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GWTC-2: Compact Binary Coalescences Observed by LIGO and Virgo during the First Half of the Third Observing Run. Phys. Rev. X 2021, 11, 021053. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GWTC-2.1: Deep Extended Catalog of Compact Binary Coalescences Observed by LIGO and Virgo During the First Half of the Third Observing Run. arXiv 2021, arXiv:2108.01.45. [Google Scholar]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo during the Second Part of the Third Observing Run. arXiv 2021, arXiv:2111.03606. [Google Scholar] [CrossRef]
- Akutsu, T.; Ando, M.; Arai, K.; Arai, Y.; Araki, S.; Araya, A.; Aritomi, N.; Asada, H.; Aso, Y.; Atsuta, S.; et al. KAGRA: 2.5 generation interferometric gravitational wave detector. Nat. Astron. 2019, 3, 35–40. [Google Scholar] [CrossRef]
- Di Giovanni, F.; Sanchis-Gual, N.; Cerdá-Durán, P.; Zilhão, M.; Herdeiro, C.; Font, J.A.; Radu, E. Dynamical bar-mode instability in spinning bosonic stars. Phys. Rev. D 2020, 102, 124009. [Google Scholar] [CrossRef]
- Sanchis-Gual, N.; Di Giovanni, F.; Zilhão, M.; Herdeiro, C.; Cerdá-Durán, P.; Font, J.A.; Radu, E. Nonlinear Dynamics of Spinning Bosonic Stars: Formation and Stability. Phys. Rev. Lett. 2019, 123, 221101. [Google Scholar] [CrossRef]
- DeMarchi, L.; Sanders, J.R.; Levesque, E.M. Prospects for Multimessenger Observations of Thorne-Zytkow Objects. Astrophys. J. 2021, 911, 101. [Google Scholar] [CrossRef]
- Tenorio, R.; Keitel, D.; Sintes, A.M. Search Methods for Continuous Gravitational-Wave Signals from Unknown Sources in the Advanced-Detector Era. Universe 2021, 7, 474. [Google Scholar] [CrossRef]
- Jones, D.I. Learning from the Frequency Content of Continuous Gravitational Wave Signals. arXiv 2021, arXiv:2111.08561. [Google Scholar]
- Sieniawska, M.; Bejger, M. Continuous Gravitational Waves from Neutron Stars: Current Status and Prospects. Universe 2019, 5, 217. [Google Scholar] [CrossRef]
- Glampedakis, K.; Gualtieri, L. Gravitational Waves from Single Neutron Stars: An Advanced Detector Era Survey; Astrophysics and Space Science Library; Springer: Berlin/Heidelberg, Germany, 2018; pp. 673–736. [Google Scholar] [CrossRef]
- Riles, K. Recent searches for continuous gravitational waves. Mod. Phys. Lett. A 2017, 32, 1730035. [Google Scholar] [CrossRef]
- Lasky, P.D. Gravitational Waves from Neutron Stars: A Review. Publ. Astron. Soc. Aust. 2015, 32, e034. [Google Scholar] [CrossRef]
- Bersanetti, D.; Patricelli, B.; Piccinni, O.J.; Piergiovanni, F.; Salemi, F.; Sequino, V. Advanced Virgo: Status of the Detector, Latest Results and Future Prospects. Universe 2021, 7, 322. [Google Scholar] [CrossRef]
- Caudill, S.; Kandhasamy, S.; Lazzaro, C.; Matas, A.; Sieniawska, M.; Stuver, A.L. Gravitational-wave searches in the era of Advanced LIGO and Virgo. Mod. Phys. Lett. A 2021, 36, 2130022. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. The Physics of Neutron Stars. Science 2004, 304, 536–542. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars 1: Equation of State and Structure; Springer: New York, NY, USA, 2007; Volume 326. [Google Scholar] [CrossRef]
- Duncan, R.C.; Thompson, C. Formation of Very Strongly Magnetized Neutron Stars: Implications for Gamma-Ray Bursts. Astrophys. J. Lett. 1992, 392, L9. [Google Scholar] [CrossRef]
- Esposito, P.; Rea, N.; Israel, G.L. Magnetars: A Short Review and Some Sparse Considerations. In Timing Neutron Stars: Pulsations, Oscillations and Explosions; Astrophysics and Space Science Library; Springer: Berlin/Heidelberg, Germany, 2020; pp. 97–142. [Google Scholar] [CrossRef]
- Haskell, B.; Sedrakian, A. Superfluidity and Superconductivity in Neutron Stars. In The Physics and Astrophysics of Neutron Stars; Astrophysics and Space Science Library; Springer: Berlin/Heidelberg, Germany, 2018; pp. 401–454. [Google Scholar] [CrossRef]
- Chamel, N. Superfluidity and Superconductivity in Neutron Stars. J. Astrophys. Astron. 2017, 38, 43. [Google Scholar] [CrossRef]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rep. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef] [PubMed]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Stone, J.R. Nuclear Physics and Astrophysics Constraints on the High Density Matter Equation of State. Universe 2021, 7, 257. [Google Scholar] [CrossRef]
- Burgio, G.; Schulze, H.J.; Vidaña, I.; Wei, J.B. Neutron stars and the nuclear equation of state. Prog. Part. Nucl. Phys. 2021, 120, 103879. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Evidence for quark-matter cores in massive neutron stars. Nat. Phys. 2020, 16, 907–910. [Google Scholar] [CrossRef]
- Vidaña, I. Hyperons: The strange ingredients of the nuclear equation of state. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20180145. [Google Scholar] [CrossRef]
- Pethick, C.J.; Schaefer, T.; Schwenk, A. Bose-Einstein condensates in neutron stars. arXiv 2015, arXiv:1507.05839. [Google Scholar]
- Baym, G.; Flowers, E. Pion condensation in neutron star matter: Equilibrium conditions and model calculations. Nucl. Phys. A 1974, 222, 29–64. [Google Scholar] [CrossRef]
- Ramos, A.; Schaffner-Bielich, J.; Wambach, J. Kaon Condensation in Neutron Stars. In Physics of Neutron Star Interiors; Lecture Notes in Physics; Blaschke, D., Sedrakian, A., Glendenning, N.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 578. [Google Scholar] [CrossRef]
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Annu. Rev. Astron. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef]
- Watts, A.L.; Andersson, N.; Chakrabarty, D.; Feroci, M.; Hebeler, K.; Israel, G.; Lamb, F.K.; Miller, M.C.; Morsink, S.; Özel, F.; et al. Colloquium: Measuring the neutron star equation of state using X-ray timing. Rev. Mod. Phys. 2016, 88, 021001. [Google Scholar] [CrossRef]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. The neutron star mass-radius relation and the equation of state of dense matter. Astrophys. J. 2013, 765, L5. [Google Scholar] [CrossRef]
- Lattimer, J.M. Neutron star masses and radii. AIP Conf. Proc. 2019, 2127, 020001. [Google Scholar] [CrossRef]
- Llanes-Estrada, F.J.; Lope-Oter, E. Hadron matter in neutron stars in view of gravitational wave observations. Prog. Part. Nucl. Phys. 2019, 109, 103715. [Google Scholar] [CrossRef]
- Bogdanov, S.; Lamb, F.K.; Mahmoodifar, S.; Miller, M.C.; Morsink, S.M.; Riley, T.E.; Strohmayer, T.E.; Tung, A.K.; Watts, A.L.; Dittmann, A.J.; et al. Constraining the Neutron Star Mass–Radius Relation and Dense Matter Equation of State with NICER. II. Emission from Hot Spots on a Rapidly Rotating Neutron Star. Astrophys. J. 2019, 887, L26. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2019, 4, 72–76. [Google Scholar] [CrossRef]
- Guillot, S.; Rutledge, R.E. Rejecting proposed dense matter equations of state with Quiescent low-mass X-ray binaries. Astrophys. J. 2014, 796, L3. [Google Scholar] [CrossRef]
- Nattila, J.; Miller, M.C.; Steiner, A.W.; Kajava, J.J.E.; Suleimanov, V.F.; Poutanen, J. Neutron star mass and radius measurements from atmospheric model fits to X-ray burst cooling tail spectra. Astron. Astrophys. 2017, 608, A31. [Google Scholar] [CrossRef]
- Wei, J.B.; Figura, A.; Burgio, G.F.; Chen, H.; Schulze, H.J. Neutron star universal relations with microscopic equations of state. J. Phys. G Nucl. Part. Phys. 2019, 46, 034001. [Google Scholar] [CrossRef]
- Gendreau, K.; Arzoumanian, Z. Searching for a pulse. Nat. Astron. 2017, 1, 895. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. 2019, 887, L24. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. 2017, 848, L13. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. 2017, 848, L12. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GW190425: Observation of a Compact Binary Coalescence with Total Mass 3.4 M⊙. Astrophys. J. Lett. 2020, 892, L3. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Observation of Gravitational Waves from Two Neutron Star–Black Hole Coalescences. Astrophys. J. Lett. 2021, 915, L5. [Google Scholar] [CrossRef]
- Cerda-Duran, P.; Elias-Rosa, N. Neutron Stars Formation and Core Collapse Supernovae. In The Physics and Astrophysics of Neutron Stars; Astrophysics and Space Science Library; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–56. [Google Scholar] [CrossRef]
- Baiotti, L.; Rezzolla, L. Binary neutron star mergers: A review of Einstein’s richest laboratory. Rep. Prog. Phys. 2017, 80, 096901. [Google Scholar] [CrossRef]
- Haskell, B.; Schwenzer, K. Isolated Neutron Stars. In Handbook of Gravitational Wave Astronomy; Bambi, C., Katsanevas, S., Kokkotas, K.D., Eds.; Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; Wiley: Weinheim, Germany, 1983. [Google Scholar]
- Ushomirsky, G.; Cutler, C.; Bildsten, L. Deformations of accreting neutron star crusts and gravitational wave emission. Mon. Not. R. Astron. Soc. 2002, 319, 902–932. [Google Scholar] [CrossRef]
- Owen, B.J. Maximum Elastic Deformations of Compact Stars with Exotic Equations of State. Phys. Rev. Lett. 2005, 95, 211101. [Google Scholar] [CrossRef] [PubMed]
- Johnson-McDaniel, N.K.; Owen, B.J. Maximum elastic deformations of relativistic stars. Phys. Rev. D 2013, 88, 044004. [Google Scholar] [CrossRef]
- Woan, G.; Pitkin, M.D.; Haskell, B.; Jones, D.I.; Lasky, P.D. Evidence for a Minimum Ellipticity in Millisecond Pulsars. Astrophys. J. 2018, 863, L40. [Google Scholar] [CrossRef]
- Gittins, F.; Andersson, N.; Jones, D.I. Modelling neutron star mountains. Mon. Not. R. Astron. Soc. 2020, 500, 5570–5582. [Google Scholar] [CrossRef]
- Gittins, F.; Andersson, N. Modelling neutron star mountains in relativity. Mon. Not. R. Astron. Soc. 2021, 507, 116–128. [Google Scholar] [CrossRef]
- Haskell, B.; Jones, D.I.; Andersson, N. Mountains on Neutron Stars: Accreted versus Non-Accreted Crusts. Mon. Not. R. Astron. Soc. 2006, 373, 1423–1439. Available online: https://academic.oup.com/mnras/article-pdf/373/4/1423/11177018/mnras0373-1423.pdf (accessed on 2 May 2022). [CrossRef]
- Horowitz, C.J.; Kadau, K. Breaking Strain of Neutron Star Crust and Gravitational Waves. Phys. Rev. Lett. 2009, 102, 191102. [Google Scholar] [CrossRef]
- Mastrano, A.; Melatos, A.; Reisenegger, A.; Akgün, T. Gravitational Wave Emission from a Magnetically Deformed Non-Barotropic Neutron Star. Mon. Not. R. Astron. Soc. 2011, 417, 2288–2299. Available online: https://academic.oup.com/mnras/article-pdf/417/3/2288/3826519/mnras0417-2288.pdf (accessed on 2 May 2022). [CrossRef]
- Suvorov, A.G.; Mastrano, A.; Geppert, U. Gravitational Radiation from Neutron Stars Deformed by Crustal Hall Drift. Mon. Not. R. Astron. Soc. 2016, 459, 3407–3418. Available online: https://academic.oup.com/mnras/article-pdf/459/3/3407/8110424/stw909.pdf (accessed on 2 May 2022). [CrossRef]
- Haskell, B.; Samuelsson, L.; Glampedakis, K.; Andersson, N. Modelling Magnetically Deformed Neutron Stars. Mon. Not. R. Astron. Soc. 2008, 385, 531–542. Available online: https://academic.oup.com/mnras/article-pdf/385/1/531/3465601/mnras0385-0531.pdf (accessed on 2 May 2022). [CrossRef]
- Owen, B.J.; Lindblom, L.; Cutler, C.; Schutz, B.F.; Vecchio, A.; Andersson, N. Gravitational waves from hot young rapidly rotating neutron stars. Phys. Rev. D 1998, 58, 084020. [Google Scholar] [CrossRef]
- Lindblom, L.; Owen, B.J.; Morsink, S.M. Gravitational Radiation Instability in Hot Young Neutron Stars. Phys. Rev. Lett. 1998, 80, 4843–4846. [Google Scholar] [CrossRef]
- Kokkotas, K.D.; Schwenzer, K. r-mode astronomy. Eur. Phys. J. A 2016, 52, 38. [Google Scholar] [CrossRef]
- Owen, B.J. How to adapt broad-band gravitational-wave searches for r-modes. Phys. Rev. D 2010, 82, 104002. [Google Scholar] [CrossRef]
- Lockitch, K.H.; Friedman, J.L.; Andersson, N. Rotational modes of relativistic stars: Numerical results. Phys. Rev. D 2003, 68, 124010. [Google Scholar] [CrossRef]
- Idrisy, A.; Owen, B.J.; Jones, D.I. R-mode frequencies of slowly rotating relativistic neutron stars with realistic equations of state. Phys. Rev. D 2015, 91, 024001. [Google Scholar] [CrossRef]
- Caride, S.; Inta, R.; Owen, B.J.; Rajbhandari, B. How to search for gravitational waves from r-modes of known pulsars. Phys. Rev. D 2019, 100, 064013. [Google Scholar] [CrossRef]
- Watts, A.L.; Krishnan, B.; Bildsten, L.; Schutz, B.F. Detecting gravitational wave emission from the known accreting neutron stars. Mon. Not. R. Astron. Soc. 2008, 389, 839–868. [Google Scholar] [CrossRef]
- Haskell, B.; Zdunik, J.L.; Fortin, M.; Bejger, M.; Wijnands, R.; Patruno, A. Fundamental physics and the absence of sub-millisecond pulsars. Astron. Astrophys. 2018, 620, A69. [Google Scholar] [CrossRef]
- Gittins, F.; Andersson, N. Population synthesis of accreting neutron stars emitting gravitational waves. Mon. Not. R. Astron. Soc. 2019, 488, 99–110. [Google Scholar] [CrossRef]
- Andersson, N.; Glampedakis, K.; Haskell, B.; Watts, A.L. Modelling the Spin Equilibrium of Neutron Stars in Low-Mass X-ray Binaries without Gravitational Radiation. Mon. Not. R. Astron. Soc. 2005, 361, 1153–1164. Available online: https://academic.oup.com/mnras/article-pdf/361/4/1153/3885817/361-4-1153.pdf (accessed on 2 May 2022). [CrossRef]
- Mukherjee, A.; Messenger, C.; Riles, K. Accretion-induced spin-wandering effects on the neutron star in Scorpius X-1: Implications for continuous gravitational wave searches. Phys. Rev. D 2018, 97, 043016. [Google Scholar] [CrossRef]
- Leaci, P.; Astone, P.; D’Antonio, S.; Frasca, S.; Palomba, C.; Piccinni, O.; Mastrogiovanni, S. Novel directed search strategy to detect continuous gravitational waves from neutron stars in low- and high-eccentricity binary systems. Phys. Rev. D 2017, 95, 122001. [Google Scholar] [CrossRef]
- Yim, G.; Jones, D.I. Transient Gravitational Waves from Pulsar Post-Glitch Recoveries. Mon. Not. R. Astron. Soc. 2020, 498, 3138–3152. Available online: https://academic.oup.com/mnras/article-pdf/498/3/3138/33780576/staa2534.pdf (accessed on 2 May 2022). [CrossRef]
- Palomba, C. Simulation of a population of isolated neutron stars evolving through the emission of gravitational waves. Mon. Not. R. Astron. Soc. 2005, 359, 1150–1164. [Google Scholar] [CrossRef]
- Jones, D.I. Gravitational wave emission from rotating superfluid neutron stars. Mon. Not. R. Astron. Soc. 2010, 402, 2503–2519. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s Principle and a Relativistic Theory of Gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Isi, M.; Weinstein, A.J.; Mead, C.; Pitkin, M. Detecting beyond-Einstein polarizations of continuous gravitational waves. Phys. Rev. D 2015, 91, 082002. [Google Scholar] [CrossRef]
- Isi, M.; Pitkin, M.; Weinstein, A.J. Probing dynamical gravity with the polarization of continuous gravitational waves. Phys. Rev. D 2017, 96, 042001. [Google Scholar] [CrossRef]
- Verma, P. Probing Gravitational Waves from Pulsars in Brans–Dicke Theory. Universe 2021, 7, 235. [Google Scholar] [CrossRef]
- Schutz, B.F. Networks of gravitational wave detectors and three figures of merit. Class. Quantum Gravity 2011, 28, 125023. [Google Scholar] [CrossRef]
- Wette, K.; Owen, B.J.; Allen, B.; Ashley, M.; Betzwieser, J.; Christensen, N.; Creighton, T.D.; Dergachev, V.; Gholami, I.; Goetz, E.; et al. Searching for gravitational waves from Cassiopeia A with LIGO. Class. Quantum Gravity 2008, 25, 235011. [Google Scholar] [CrossRef]
- Bildsten, L.; Chakrabarty, D.; Chiu, J.; Finger, M.H.; Koh, D.T.; Nelson, R.W.; Prince, T.A.; Rubin, B.C.; Scott, D.M.; Stollberg, M.; et al. Observations of Accreting Pulsars. Astrophys. J. Suppl. Ser. 1997, 113, 367–408. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D. History of dark matter. Rev. Mod. Phys. 2018, 90, 045002. [Google Scholar] [CrossRef]
- Bertone, G.; Croon, D.; Amin, M.; Boddy, K.K.; Kavanagh, B.; Mack, K.J.; Natarajan, P.; Opferkuch, T.; Schutz, K.; Takhistov, V.; et al. Gravitational wave probes of dark matter: Challenges and opportunities. SciPost Phys. Core 2020, 3, 7. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Dimopoulos, S.; Dubovsky, S.; Kaloper, N.; March-Russell, J. String axiverse. Phys. Rev. D 2010, 81, 123530. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Dubovsky, S. Exploring the string axiverse with precision black hole physics. Phys. Rev. D 2011, 83, 044026. [Google Scholar] [CrossRef]
- Brito, R.; Cardoso, V.; Pani, P. Superradiance; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Instantons. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Baryakhtar, M.; Huang, X. Discovering the QCD axion with black holes and gravitational waves. Phys. Rev. D 2015, 91, 084011. [Google Scholar] [CrossRef]
- Baryakhtar, M.; Galanis, M.; Lasenby, R.; Simon, O. Black hole superradiance of self-interacting scalar fields. Phys. Rev. D 2021, 103, 095019. [Google Scholar] [CrossRef]
- Palomba, C.; D’Antonio, S.; Astone, P.; Frasca, S.; Intini, G.; La Rosa, I.; Leaci, P.; Mastrogiovanni, S.; Miller, A.; Muciaccia, F.; et al. Direct Constraints on the Ultralight Boson Mass from Searches of Continuous Gravitational Waves. Phys. Rev. Lett. 2019, 123, 171101. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.J.; Baryakhtar, M.; Papa, M.A.; Tsuna, D.; Kawanaka, N.; Eggenstein, H.B. Characterizing the continuous gravitational-wave signal from boson clouds around Galactic isolated black holes. Phys. Rev. D 2020, 102, 063020. [Google Scholar] [CrossRef]
- Cardoso, V.; Pani, P.; Yu, T.T. Superradiance in rotating stars and pulsar-timing constraints on dark photons. Phys. Rev. D 2017, 95, 124056. [Google Scholar] [CrossRef]
- Day, F.V.; McDonald, J.I. Axion superradiance in rotating neutron stars. J. Cosmol. Astropart. Phys. 2019, 2019, 051. [Google Scholar] [CrossRef]
- Graham, M.; Hearty, C.; Williams, M. Searches for dark photons at accelerators. arXiv 2021, arXiv:2104.10280. [Google Scholar] [CrossRef]
- Fabbrichesi, M.; Gabrielli, E.; Lanfranchi, G. The Physics of the Dark Photon; SpringerBriefs in Physics; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Pierce, A.; Riles, K.; Zhao, Y. Searching for Dark Photon Dark Matter with Gravitational-Wave Detectors. Phys. Rev. Lett. 2018, 121, 061102. [Google Scholar] [CrossRef]
- Graham, P.W.; Kaplan, D.E.; Mardon, J.; Rajendran, S.; Terrano, W.A. Dark matter direct detection with accelerometers. Phys. Rev. D 2016, 93, 075029. [Google Scholar] [CrossRef]
- Carney, D.; Hook, A.; Liu, Z.; Taylor, J.M.; Zhao, Y. Ultralight dark matter detection with mechanical quantum sensors. New J. Phys. 2021, 23, 023041. [Google Scholar] [CrossRef]
- Armaleo, J.M.; López Nacir, D.; Urban, F.R. Searching for spin-2 ULDM with gravitational waves interferometers. J. Cosmol. Astropart. Phys. 2021, 2021, 053. [Google Scholar] [CrossRef]
- Raggi, M.; Kozhuharov, V. Results and perspectives in dark photon physics. Riv. Nuovo Cim. 2015, 38, 449–505. [Google Scholar] [CrossRef]
- Co, R.T.; Hall, L.J.; Harigaya, K. QCD Axion Dark Matter with a Small Decay Constant. Phys. Rev. Lett. 2018, 120, 211602. [Google Scholar] [CrossRef] [PubMed]
- Co, R.T.; Pierce, A.; Zhang, Z.; Zhao, Y. Dark photon dark matter produced by axion oscillations. Phys. Rev. D 2019, 99, 075002. [Google Scholar] [CrossRef]
- Guo, H.K.; Ma, Y.; Shu, J.; Xue, X.; Yuan, Q.; Zhao, Y. Detecting dark photon dark matter with Gaia-like astrometry observations. J. Cosmol. Astropart. Phys. 2019, 2019, 015. [Google Scholar] [CrossRef]
- Xue, X.; Xia, Z.Q.; Zhu, X.; Zhao, Y.; Shu, J.; Yuan, Q.; Bhat, N.D.R.; Cameron, A.D.; Dai, S.; Feng, Y.; et al. High-precision search for dark photon dark matter with the Parkes Pulsar Timing Array. arXiv 2021, arXiv:2112.07687. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Huang, J.; Van Tilburg, K. Searching for dilaton dark matter with atomic clocks. Phys. Rev. D 2015, 91, 015015. [Google Scholar] [CrossRef]
- Morisaki, S.; Fujita, T.; Michimura, Y.; Nakatsuka, H.; Obata, I. Improved sensitivity of interferometric gravitational-wave detectors to ultralight vector dark matter from the finite light-traveling time. Phys. Rev. D 2021, 103, L051702. [Google Scholar] [CrossRef]
- Guo, H.K.; Riles, K.; Yang, F.W.; Zhao, Y. Searching for dark photon dark matter in LIGO O1 data. Commun. Phys. 2019, 2, 155. [Google Scholar] [CrossRef]
- Michimura, Y.; Fujita, T.; Morisaki, S.; Nakatsuka, H.; Obata, I. Ultralight vector dark matter search with auxiliary length channels of gravitational wave detectors. Phys. Rev. D 2020, 102, 102001. [Google Scholar] [CrossRef]
- Vermeulen, S.M.; Relton, P.; Grote, H.; Raymond, V.; Affeldt, C.; Bergamin, F.; Bisht, A.; Brinkmann, M.; Danzmann, K.; Doravari, S.; et al. Direct limits for scalar field dark matter from a gravitational-wave detector. Nature 2021, 600, 424–428. [Google Scholar] [CrossRef]
- Stadnik, Y.V.; Flambaum, V.V. Enhanced effects of variation of the fundamental constants in laser interferometers and application to dark-matter detection. Phys. Rev. A 2016, 93, 063630. [Google Scholar] [CrossRef]
- Stadnik, Y.V.; Flambaum, V.V. Searching for Dark Matter and Variation of Fundamental Constants with Laser and Maser Interferometry. Phys. Rev. Lett. 2015, 114, 161301. [Google Scholar] [CrossRef] [PubMed]
- Grote, H.; Stadnik, Y.V. Novel signatures of dark matter in laser-interferometric gravitational-wave detectors. Phys. Rev. Res. 2019, 1, 033187. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. Constraints on dark photon dark matter using data from LIGO’s and Virgo’s third observing run. arXiv 2021, arXiv:2105.13085. [Google Scholar] [CrossRef]
- Horowitz, C.; Papa, M.; Reddy, S. Search for compact dark matter objects in the solar system with LIGO data. Phys. Lett. B 2020, 800, 135072. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Widmer-Schnidrig, R. Gravimeter Search for Compact Dark Matter Objects Moving in the Earth. Phys. Rev. Lett. 2020, 124, 051102. [Google Scholar] [CrossRef]
- Carr, B.; Kuhnel, F. Primordial Black Holes as Dark Matter Candidates. arXiv 2021, arXiv:2110.02821. [Google Scholar] [CrossRef]
- Carr, B.; Kohri, K.; Sendouda, Y.; Yokoyama, J. Constraints on primordial black holes. Rep. Prog. Phys. 2021, 84, 116902. [Google Scholar] [CrossRef]
- Green, A.M.; Kavanagh, B.J. Primordial black holes as a dark matter candidate. J. Phys. G Nucl. Part. Phys. 2021, 48, 043001. [Google Scholar] [CrossRef]
- Carr, B.; Kühnel, F. Primordial Black Holes as Dark Matter: Recent Developments. Annu. Rev. Nucl. Part. Sci. 2020, 70, 355–394. [Google Scholar] [CrossRef]
- Kouvaris, C.; Tinyakov, P.; Tytgat, M.H.G. NonPrimordial Solar Mass Black Holes. Phys. Rev. Lett. 2018, 121, 221102. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Maggiore, M. Gravitational Waves: Volume 1: Theory and Experiments; Gravitational Waves; OUP Oxford: Oxford, UK, 2008. [Google Scholar]
- Creighton, J.; Anderson, W. Gravitational-Wave Physics and Astronomy: An Introduction to Theory, Experiment and Data Analysis. In Gravitational-Wave Physics and Astronomy: An Introduction to Theory, Experiment and Data Analysis; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Peters, P.C. Gravitational Radiation and the Motion of Two Point Masses. Phys. Rev. 1964, 136, B1224–B1232. [Google Scholar] [CrossRef]
- Tiwari, V.; Klimenko, S.; Necula, V.; Mitselmakher, G. Reconstruction of chirp mass in searches for gravitational wave transients. Class. Quantum Gravity 2015, 33, 01LT01. [Google Scholar] [CrossRef]
- Miller, A.L.; Clesse, S.; De Lillo, F.; Bruno, G.; Depasse, A.; Tanasijczuk, A. Probing planetary-mass primordial black holes with continuous gravitational waves. Phys. Dark Universe 2021, 32, 100836. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Gravitational-wave Constraints on the Equatorial Ellipticity of Millisecond Pulsars. Astrophys. J. Lett. 2020, 902, L21. [Google Scholar] [CrossRef]
- Astone, P.; D’Antonio, S.; Frasca, S.; Palomba, C. A method for detection of known sources of continuous gravitational wave signals in non-stationary data. Class. Quantum Gravity 2010, 27, 194016. [Google Scholar] [CrossRef]
- Astone, P.; Colla, A.; D’Antonio, S.; Frasca, S.; Palomba, C. Coherent search of continuous gravitational wave signals: Extension of the 5-vectors method to a network of detectors. J. Phys. Conf. Ser. 2012, 363, 012038. [Google Scholar] [CrossRef]
- Jaranowski, P.; Królak, A.; Schutz, B.F. Data analysis of gravitational-wave signals from spinning neutron stars: The signal and its detection. Phys. Rev. D 1998, 58, 063001. [Google Scholar] [CrossRef]
- Prix, R.; Krishnan, B. Targeted search for continuous gravitational waves: Bayesian versus maximum-likelihood statistics. Class. Quantum Gravity 2009, 26, 204013. [Google Scholar] [CrossRef]
- Prix, R. Search for continuous gravitational waves: Metric of the multidetector F-statistic. Phys. Rev. D 2007, 75, 023004. [Google Scholar] [CrossRef]
- Jaranowski, P.; Królak, A. Searching for gravitational waves from known pulsars using the F and G statistics. Class. Quantum Gravity 2010, 27, 194015. [Google Scholar] [CrossRef]
- Cutler, C.; Schutz, B.F. Generalized F-statistic: Multiple detectors and multiple gravitational wave pulsars. Phys. Rev. D 2005, 72, 063006. [Google Scholar] [CrossRef]
- Dupuis, R.J.; Woan, G. Bayesian estimation of pulsar parameters from gravitational wave data. Phys. Rev. D 2005, 72, 102002. [Google Scholar] [CrossRef]
- Pitkin, M.; Isi, M.; Veitch, J.; Woan, G. A nested sampling code for targeted searches for continuous gravitational waves from pulsars. arXiv 2017, arXiv:1705.08978. [Google Scholar]
- Piccinni, O.J.; Astone, P.; D’Antonio, S.; Frasca, S.; Intini, G.; Leaci, P.; Mastrogiovanni, S.; Miller, A.; Palomba, C.; Singhal, A. A new data analysis framework for the search of continuous gravitational wave signals. Class. Quantum Gravity 2018, 36, 015008. [Google Scholar] [CrossRef]
- Brady, P.R.; Creighton, T.; Cutler, C.; Schutz, B.F. Searching for periodic sources with LIGO. Phys. Rev. D 1998, 57, 2101–2116. [Google Scholar] [CrossRef]
- Brady, P.R.; Creighton, T. Searching for periodic sources with LIGO. II. Hierarchical searches. Phys. Rev. D 2000, 61, 082001. [Google Scholar] [CrossRef]
- Cutler, C.; Gholami, I.; Krishnan, B. Improved stack-slide searches for gravitational-wave pulsars. Phys. Rev. D 2005, 72, 042004. [Google Scholar] [CrossRef]
- Astone, P.; Colla, A.; D’Antonio, S.; Frasca, S.; Palomba, C. Method for all-sky searches of continuous gravitational wave signals using the frequency-Hough transform. Phys. Rev. D 2014, 90, 042002. [Google Scholar] [CrossRef]
- Palomba, C.; Astone, P.; Frasca, S. Adaptive Hough transform for the search of periodic sources. Class. Quant. Grav. 2005, 22, S1255–S1264. [Google Scholar] [CrossRef]
- Antonucci, F.; Astone, P.; D’Antonio, S.; Frasca, S.; Palomba, C. Detection of periodic gravitational wave sources by Hough transform in the f versus plane. Class. Quantum Gravity 2008, 25, 184015. [Google Scholar] [CrossRef]
- Krishnan, B.; Sintes, A.M.; Papa, M.A.; Schutz, B.F.; Frasca, S.; Palomba, C. Hough transform search for continuous gravitational waves. Phys. Rev. D 2004, 70, 082001. [Google Scholar] [CrossRef]
- Sintes, A.M.; Krishnan, B. Improved Hough search for gravitational wave pulsars. J. Phys. Conf. Ser. 2006, 32, 206–211. [Google Scholar] [CrossRef]
- Jordana, L.S.d.l.; Collaboration, t.L.S.C.a. Hierarchical Hough all-sky search for periodic gravitational waves in LIGO S5 data. J. Phys. Conf. Ser. 2010, 228, 012004. [Google Scholar] [CrossRef]
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Accadia, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; et al. Implementation of an F-statistic all-sky search for continuous gravitational waves in Virgo VSR1 data. Class. Quantum Gravity 2014, 31, 165014. [Google Scholar] [CrossRef]
- Pisarski, A.; Jaranowski, P. Banks of templates for all-sky narrow-band searches of gravitational waves from spinning neutron stars. Class. Quantum Gravity 2015, 32, 145014. [Google Scholar] [CrossRef][Green Version]
- Wette, K.; Walsh, S.; Prix, R.; Papa, M. Implementing a semicoherent search for continuous gravitational waves using optimally constructed template banks. Phys. Rev. D 2018, 97, 123016. [Google Scholar] [CrossRef]
- Dergachev, V.; Description of PowerFlux Algorithms and Implementation. In LIGO Document T050186. 2005. Available online: https://dcc.ligo.org/LIGO-T050186/public (accessed on 2 May 2022).
- Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.; Adya, V.; Affeldt, C.; et al. All-sky search for continuous gravitational waves from isolated neutron stars in the early O3 LIGO data. Phys. Rev. D 2021, 104, 082004. [Google Scholar] [CrossRef]
- Pletsch, H.J. Parameter-space correlations of the optimal statistic for continuous gravitational-wave detection. Phys. Rev. D 2008, 78, 102005. [Google Scholar] [CrossRef]
- Pletsch, H.J.; Allen, B. Exploiting Large-Scale Correlations to Detect Continuous Gravitational Waves. Phys. Rev. Lett. 2009, 103, 181102. [Google Scholar] [CrossRef]
- Pletsch, H.J. Parameter-space metric of semicoherent searches for continuous gravitational waves. Phys. Rev. D 2010, 82, 042002. [Google Scholar] [CrossRef]
- Walsh, S.; Pitkin, M.; Oliver, M.; D’Antonio, S.; Dergachev, V.; Krolak, A.; Astone, P.; Bejger, M.; Di Giovanni, M.; Dorosh, O.; et al. Comparison of methods for the detection of gravitational waves from unknown neutron stars. Phys. Rev. D 2016, 94, 124010. [Google Scholar]
- Dergachev, V. On blind searches for noise dominated signals: A loosely coherent approach. Class. Quantum Gravity 2010, 27, 205017. [Google Scholar] [CrossRef]
- Dergachev, V. Loosely coherent searches for sets of well-modeled signals. Phys. Rev. D 2012, 85, 062003. [Google Scholar] [CrossRef]
- Dergachev, V. Loosely coherent searches for medium scale coherence lengths. arXiv 2019, arXiv:1807.02351. [Google Scholar]
- Wette, K.; Dunn, L.; Clearwater, P.; Melatos, A. Deep exploration for continuous gravitational waves at 171–172 Hz in LIGO second observing run data. Phys. Rev. D 2021, 103, 083020. [Google Scholar] [CrossRef]
- Suvorova, S.; Sun, L.; Melatos, A.; Moran, W.; Evans, R. Hidden Markov model tracking of continuous gravitational waves from a neutron star with wandering spin. Phys. Rev. D 2016, 93, 123009. [Google Scholar] [CrossRef]
- Sun, L.; Melatos, A.; Lasky, P.D. Tracking continuous gravitational waves from a neutron star at once and twice the spin frequency with a hidden Markov model. Phys. Rev. D 2019, 99, 123010. [Google Scholar] [CrossRef]
- Sun, L.; Melatos, A.; Suvorova, S.; Moran, W.; Evans, R.J. Hidden Markov model tracking of continuous gravitational waves from young supernova remnants. Phys. Rev. D 2018, 97, 043013. [Google Scholar] [CrossRef]
- D’Antonio, S.; Palomba, C.; Frasca, S.; Astone, P.; La Rosa, I.; Leaci, P.; Mastrogiovanni, S.; Piccinni, O.J.; Pierini, L.; Rei, L. Sidereal filtering: A novel robust method to search for continuous gravitational waves. Phys. Rev. D 2021, 103, 063030. [Google Scholar] [CrossRef]
- Romano, J.D.; Cornish, N.J. Detection methods for stochastic gravitational-wave backgrounds: A unified treatment. Living Rev. Relativ. 2017, 20, 2. [Google Scholar] [CrossRef]
- Thrane, E.; Kandhasamy, S.; Ott, C.D.; Anderson, W.G.; Christensen, N.L.; Coughlin, M.W.; Dorsher, S.; Giampanis, S.; Mandic, V.; Mytidis, A.; et al. Long gravitational-wave transients and associated detection strategies for a network of terrestrial interferometers. Phys. Rev. D 2011, 83, 083004. [Google Scholar] [CrossRef]
- Bayley, J.; Messenger, C.; Woan, G. Generalized application of the Viterbi algorithm to searches for continuous gravitational-wave signals. Phys. Rev. D 2019, 100, 023006. [Google Scholar] [CrossRef]
- Mitra, S.; Dhurandhar, S.; Souradeep, T.; Lazzarini, A.; Mandic, V.; Bose, S.; Ballmer, S. Gravitational wave radiometry: Mapping a stochastic gravitational wave background. Phys. Rev. D 2008, 77, 042002. [Google Scholar] [CrossRef]
- Whelan, J.T.; Sundaresan, S.; Zhang, Y.; Peiris, P. Model-based cross-correlation search for gravitational waves from Scorpius X-1. Phys. Rev. D 2015, 91, 102005. [Google Scholar] [CrossRef]
- Suvorova, S.; Clearwater, P.; Melatos, A.; Sun, L.; Moran, W.; Evans, R. Hidden Markov model tracking of continuous gravitational waves from a binary neutron star with wandering spin. II. Binary orbital phase tracking. Phys. Rev. D 2017, 96, 102006. [Google Scholar] [CrossRef]
- Singhal, A.; Leaci, P.; Astone, P.; D’Antonio, S.; Frasca, S.; Intini, G.; Rosa, I.L.; Mastrogiovanni, S.; Miller, A.; Muciaccia, F.; et al. A resampling algorithm to detect continuous gravitational-wave signals from neutron stars in binary systems. Class. Quantum Gravity 2019, 36, 205015. [Google Scholar] [CrossRef]
- Covas, P.; Sintes, A.M. New method to search for continuous gravitational waves from unknown neutron stars in binary systems. Phys. Rev. D 2019, 99, 124019. [Google Scholar] [CrossRef]
- Goetz, E.; Riles, K. An all-sky search algorithm for continuous gravitational waves from spinning neutron stars in binary systems. Class. Quantum Gravity 2011, 28, 215006. [Google Scholar] [CrossRef]
- Oliver, M.; Keitel, D.; Sintes, A.M. Adaptive transient Hough method for long-duration gravitational wave transients. Phys. Rev. D 2019, 99, 104067. [Google Scholar] [CrossRef]
- Miller, A.; Astone, P.; D’Antonio, S.; Frasca, S.; Intini, G.; La Rosa, I.; Leaci, P.; Mastrogiovanni, S.; Muciaccia, F.; Palomba, C.; et al. Method to search for long duration gravitational wave transients from isolated neutron stars using the generalized frequency-Hough transform. Phys. Rev. D 2018, 98, 102004. [Google Scholar] [CrossRef]
- Prix, R.; Giampanis, S.; Messenger, C. Search method for long-duration gravitational-wave transients from neutron stars. Phys. Rev. D 2011, 84, 023007. [Google Scholar] [CrossRef]
- Sun, L.; Melatos, A. Application of hidden Markov model tracking to the search for long-duration transient gravitational waves from the remnant of the binary neutron star merger GW170817. Phys. Rev. D 2019, 99, 123003. [Google Scholar] [CrossRef]
- Banagiri, S.; Sun, L.; Coughlin, M.W.; Melatos, A. Search strategies for long gravitational-wave transients: Hidden Markov model tracking and seedless clustering. Phys. Rev. D 2019, 100, 024034. [Google Scholar] [CrossRef]
- Keitel, D. Robust semicoherent searches for continuous gravitational waves with noise and signal models including hours to days long transients. Phys. Rev. D 2016, 93, 084024. [Google Scholar] [CrossRef]
- Keitel, D.; Ashton, G. Faster search for long gravitational-wave transients: GPU implementation of the transient F-statistic. Class. Quantum Gravity 2018, 35, 205003. [Google Scholar] [CrossRef]
- Ashton, G.; Prix, R.; Jones, D. A semicoherent glitch-robust continuous-gravitational-wave search method. Phys. Rev. D 2018, 98, 063011. [Google Scholar] [CrossRef]
- Ashton, G.; Prix, R.; Jones, D. Statistical characterization of pulsar glitches and their potential impact on searches for continuous gravitational waves. Phys. Rev. D 2017, 96, 063004. [Google Scholar] [CrossRef]
- Pitkin, M.; Messenger, C.; Fan, X. Hierarchical Bayesian method for detecting continuous gravitational waves from an ensemble of pulsars. Phys. Rev. D 2018, 98, 063001. [Google Scholar] [CrossRef]
- Buono, M.; De Rosa, R.; D’Onofrio, L.; Errico, L.; Palomba, C.; Piccinni, O.J.; Sequino, V. A method for detecting continuous gravitational wave signals from an ensemble of known pulsars. Class. Quantum Gravity 2021, 38, 135021. [Google Scholar] [CrossRef]
- D’Antonio, S.; Palomba, C.; Astone, P.; Frasca, S.; Intini, G.; La Rosa, I.; Leaci, P.; Mastrogiovanni, S.; Miller, A.; Muciaccia, F.; et al. Semicoherent analysis method to search for continuous gravitational waves emitted by ultralight boson clouds around spinning black holes. Phys. Rev. D 2018, 98, 103017. [Google Scholar] [CrossRef]
- Isi, M.; Sun, L.; Brito, R.; Melatos, A. Directed searches for gravitational waves from ultralight bosons. Phys. Rev. D 2019, 99, 084042. [Google Scholar] [CrossRef]
- Miller, A.L.; Astone, P.; Bruno, G.; Clesse, S.; D’Antonio, S.; Depasse, A.; De Lillo, F.; Frasca, S.; La Rosa, I.; Leaci, P.; et al. Probing new light gauge bosons with gravitational-wave interferometers using an adapted semicoherent method. Phys. Rev. D 2021, 103, 103002. [Google Scholar] [CrossRef]
- Morawski, F.; Bejger, M.; Ciecieląg, P. Convolutional neural network classifier for the output of the time-domain F-statistic all-sky search for continuous gravitational waves. Mach. Learn. Sci. Technol. 2020, 1, 025016. [Google Scholar] [CrossRef]
- Yamamoto, T.S.; Tanaka, T. Use of an excess power method and a convolutional neural network in an all-sky search for continuous gravitational waves. Phys. Rev. D 2021, 103, 084049. [Google Scholar] [CrossRef]
- Miller, A.L.; Astone, P.; D’Antonio, S.; Frasca, S.; Intini, G.; La Rosa, I.; Leaci, P.; Mastrogiovanni, S.; Muciaccia, F.; Mitidis, A.; et al. How effective is machine learning to detect long transient gravitational waves from neutron stars in a real search? Phys. Rev. D 2019, 100, 062005. [Google Scholar] [CrossRef]
- Beheshtipour, B.; Papa, M.A. Deep learning for clustering of continuous gravitational wave candidates. Phys. Rev. D 2020, 101, 064009. [Google Scholar] [CrossRef]
- Dreissigacker, C.; Sharma, R.; Messenger, C.; Zhao, R.; Prix, R. Deep-Learning Continuous Gravitational Waves. Phys. Rev. D 2019, 100, 044009. [Google Scholar] [CrossRef]
- Dreissigacker, C.; Prix, R. Deep-Learning Continuous Gravitational Waves: Multiple detectors and realistic noise. Phys. Rev. D 2020, 102, 022005. [Google Scholar] [CrossRef]
- Bayley, J.; Messenger, C.; Woan, G. Robust machine learning algorithm to search for continuous gravitational waves. Phys. Rev. D 2020, 102, 083024. [Google Scholar] [CrossRef]
- Leaci, P. Methods to filter out spurious disturbances in continuous-wave searches from gravitational-wave detectors. Phys. Scr. 2015, 90, 125001. [Google Scholar] [CrossRef]
- Tenorio, R.; Keitel, D.; Sintes, A.M. Application of a hierarchical MCMC follow-up to Advanced LIGO continuous gravitational-wave candidates. Phys. Rev. D 2021, 104, 084012. [Google Scholar] [CrossRef]
- Tenorio, R.; Keitel, D.; Sintes, A.M. Time-frequency track distance for comparing continuous gravitational wave signals. Phys. Rev. D 2021, 103, 064053. [Google Scholar] [CrossRef]
- Intini, G.; Leaci, P.; Astone, P.; Antonio, S.D.; Frasca, S.; Rosa, I.L.; Miller, A.; Palomba, C.; Piccinni, O. A Doppler-modulation based veto to discard false continuous gravitational-wave candidates. Class. Quantum Gravity 2020, 37, 225007. [Google Scholar] [CrossRef]
- Zhu, S.J.; Papa, M.A.; Walsh, S. New veto for continuous gravitational wave searches. Phys. Rev. D 2017, 96, 124007. [Google Scholar] [CrossRef]
- Keitel, D. Distinguishing transient signals and instrumental disturbances in semi-coherent searches for continuous gravitational waves with line-robust statistics. J. Phys. Conf. Ser. 2016, 716, 012003. [Google Scholar] [CrossRef]
- Ashton, G.; Prix, R. Hierarchical multistage MCMC follow-up of continuous gravitational wave candidates. Phys. Rev. D 2018, 97, 103020. [Google Scholar] [CrossRef]
- Isi, M.; Mastrogiovanni, S.; Pitkin, M.; Piccinni, O.J. Establishing the significance of continuous gravitational-wave detections from known pulsars. Phys. Rev. D 2020, 102, 123027. [Google Scholar] [CrossRef]
- Behnke, B.; Papa, M.A.; Prix, R. Postprocessing methods used in the search for continuous gravitational-wave signals from the Galactic Center. Phys. Rev. D 2015, 91, 064007. [Google Scholar] [CrossRef]
- Keitel, D.; Prix, R.; Papa, M.A.; Leaci, P.; Siddiqi, M. Search for continuous gravitational waves: Improving robustness versus instrumental artifacts. Phys. Rev. D 2014, 89, 064023. [Google Scholar] [CrossRef]
- Tenorio, R.; Modafferi, L.M.; Keitel, D.; Sintes, A.M. Empirically estimating the distribution of the loudest candidate from a gravitational-wave search. arXiv 2021, arXiv:2111.12032. [Google Scholar] [CrossRef]
- Covas, P.; Effler, A.; Goetz, E.; Meyers, P.; Neunzert, A.; Oliver, M.; Pearlstone, B.; Roma, V.; Schofield, R.; Adya, V.; et al. Identification and mitigation of narrow spectral artifacts that degrade searches for persistent gravitational waves in the first two observing runs of Advanced LIGO. Phys. Rev. D 2018, 97, 082002. [Google Scholar] [CrossRef]
- Dreissigacker, C.; Prix, R.; Wette, K. Fast and accurate sensitivity estimation for continuous-gravitational-wave searches. Phys. Rev. D 2018, 98, 084058. [Google Scholar] [CrossRef]
- Dergachev, V. Novel universal statistic for computing upper limits in an ill-behaved background. Phys. Rev. D 2013, 87, 062001. [Google Scholar] [CrossRef]
- Feldman, G.J.; Cousins, R.D. Unified approach to the classical statistical analysis of small signals. Phys. Rev. D 1998, 57, 3873–3889. [Google Scholar] [CrossRef]
- Treves, A.; Turolla, R.; Zane, S.; Colpi, M. Isolated Neutron Stars: Accretors and Coolers. Publ. Astron. Soc. Pac. 2000, 112, 297–314. [Google Scholar] [CrossRef]
- Rajwade, K.; Chennamangalam, J.; Lorimer, D.; Karastergiou, A. The Galactic halo pulsar population. Mon. Not. R. Astron. Soc. 2018, 479, 3094–3100. [Google Scholar] [CrossRef]
- Manchester, R.N.; Hobbs, G.B.; Teoh, A.; Hobbs, M. The Australia Telescope National Facility Pulsar Catalogue. Astron. J. 2005, 129, 1993–2006. [Google Scholar] [CrossRef]
- Abbott, R.; Abe, H.; Acernese, F.; Ackley, K.; Adhikari, N.; Adhikari, R.X.; Adkins, V.K.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. Searches for Gravitational Waves from Known Pulsars at Two Harmonics in the Second and Third LIGO-Virgo Observing Runs. arXiv 2021, arXiv:2111.13106. [Google Scholar]
- Pitkin, M.; Gill, C.; Jones, D.I.; Woan, G.; Davies, G.S. First results and future prospects for dual-harmonic searches for gravitational waves from spinning neutron stars. Mon. Not. R. Astron. Soc. 2015, 453, 4399–4420. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Searches for Gravitational Waves from Known Pulsars at Two Harmonics in 2015–2017 LIGO Data. Astrophys. J. 2019, 879, 10. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. First Search for Gravitational Waves from Known Pulsars with Advanced LIGO. Astrophys. J. 2017, 839, 12. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. First Search for Nontensorial Gravitational Waves from Known Pulsars. Phys. Rev. Lett. 2018, 120, 031104. [Google Scholar] [CrossRef] [PubMed]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Diving below the Spin-down Limit: Constraints on Gravitational Waves from the Energetic Young Pulsar PSR J0537-6910. Astrophys. J. Lett. 2021, 913, L27. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Espinoza, C.M.; Arzoumanian, Z.; Enoto, T.; Tamba, T.; Antonopoulou, D.; Bejger, M.; Guillot, S.; Haskell, B.; Ray, P.S. Return of the Big Glitcher: NICER timing and glitches of PSR J0537-6910. Mon. Not. R. Astron. Soc. 2020, 498, 4605–4614. [Google Scholar] [CrossRef] [PubMed]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Constraints from LIGO O3 Data on Gravitational-wave Emission Due to R-modes in the Glitching Pulsar PSR J0537–6910. Astrophys. J. 2021, 922, 71. [Google Scholar] [CrossRef]
- Fesik, L.; Papa, M.A. First Search for r-mode Gravitational Waves from PSR J0537-6910. Astrophys. J. 2020, 895, 11. [Google Scholar] [CrossRef]
- Andersson, N.; Antonopoulou, D.; Espinoza, C.M.; Haskell, B.; Ho, W.C.G. The Enigmatic Spin Evolution of PSR J0537–6910: R-modes, Gravitational Waves, and the Case for Continued Timing. Astrophys. J. 2018, 864, 137. [Google Scholar] [CrossRef]
- Antonopoulou, D.; Espinoza, C.M.; Kuiper, L.; Andersson, N. Pulsar spin-down: The glitch-dominated rotation of PSR J0537-6910. Mon. Not. R. Astron. Soc. 2017, 473, 1644–1655. [Google Scholar] [CrossRef]
- Rajbhandari, B.; Owen, B.J.; Caride, S.; Inta, R. First searches for gravitational waves from r-modes of the Crab pulsar. Phys. Rev. D 2021, 104, 122008. [Google Scholar] [CrossRef]
- Mastrogiovanni, S.; Astone, P.; D’Antonio, S.; Frasca, S.; Intini, G.; Leaci, P.; Miller, A.; Palomba, C.; Piccinni, O.J.; Singhal, A. An improved algorithm for narrow-band searches of continuous gravitational waves. Class. Quantum Gravity 2017, 34, 135007. [Google Scholar] [CrossRef]
- Astone, P.; Colla, A.; D’Antonio, S.; Frasca, S.; Palomba, C.; Serafinelli, R. Method for narrow-band search of continuous gravitational wave signals. Phys. Rev. D 2014, 89, 062008. [Google Scholar] [CrossRef]
- Ashok, A.; Beheshtipour, B.; Papa, M.A.; Freire, P.C.C.; Steltner, B.; Machenschalk, B.; Behnke, O.; Allen, B.; Prix, R. New Searches for Continuous Gravitational Waves from Seven Fast Pulsars. Astrophys. J. 2021, 923, 85. [Google Scholar] [CrossRef]
- Nieder, L.; Clark, C.J.; Bassa, C.G.; Wu, J.; Singh, A.; Donner, J.Y.; Allen, B.; Breton, R.P.; Dhillon, V.S.; Eggenstein, H.B.; et al. Detection and Timing of Gamma-Ray Pulsations from the 707 Hz Pulsar J0952-0607. Astrophys. J. 2019, 883, 42. [Google Scholar] [CrossRef]
- Nieder, L.; Clark, C.J.; Kandel, D.; Romani, R.W.; Bassa, C.G.; Allen, B.; Ashok, A.; Cognard, I.; Fehrmann, H.; Freire, P.; et al. Discovery of a Gamma-Ray Black Widow Pulsar by GPU-accelerated Einstein@Home. Astrophys. J. Lett. 2020, 902, L46. [Google Scholar] [CrossRef]
- Beniwal, D.; Clearwater, P.; Dunn, L.; Melatos, A.; Ottaway, D. Search for continuous gravitational waves from ten H.E.S.S. sources using a hidden Markov model. Phys. Rev. D 2021, 103, 083009. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. Narrowband searches for continuous and long-duration transient gravitational waves from known pulsars in the LIGO-Virgo third observing run. arXiv 2021, arXiv:2112.10990. [Google Scholar]
- Modafferi, L.M.; Moragues, J.; Keitel, D.; Collaboration, L.S.; Collaboration, V.; Collaboration, K. Search setup for long-duration transient gravitational waves from glitching pulsars during LIGO-Virgo third observing run. arXiv 2022, arXiv:2201.08785. [Google Scholar]
- Keitel, D.; Woan, G.; Pitkin, M.; Schumacher, C.; Pearlstone, B.; Riles, K.; Lyne, A.G.; Palfreyman, J.; Stappers, B.; Weltevrede, P. First search for long-duration transient gravitational waves after glitches in the Vela and Crab pulsars. Phys. Rev. D 2019, 100, 064058. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.; Adya, V.; Affeldt, C.; et al. Narrow-band search for gravitational waves from known pulsars using the second LIGO observing run. Phys. Rev. D 2019, 99, 122002. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. First narrow-band search for continuous gravitational waves from known pulsars in advanced detector data. Phys. Rev. D 2017, 96, 122006. [Google Scholar] [CrossRef]
- Ming, J.; Krishnan, B.; Papa, M.A.; Aulbert, C.; Fehrmann, H. Optimal directed searches for continuous gravitational waves. Phys. Rev. D 2016, 93, 064011. [Google Scholar] [CrossRef]
- Ming, J.; Papa, M.A.; Krishnan, B.; Prix, R.; Beer, C.; Zhu, S.J.; Eggenstein, H.B.; Bock, O.; Machenschalk, B. Optimally setting up directed searches for continuous gravitational waves in Advanced LIGO O1 data. Phys. Rev. D 2018, 97, 024051. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. Search of the Early O3 LIGO Data for Continuous Gravitational Waves from the Cassiopeia A and Vela Jr. Supernova Remnants. arXiv 2021, arXiv:2111.15116. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Searches for Continuous Gravitational Waves from Young Supernova Remnants in the Early Third Observing Run of Advanced LIGO and Virgo. Astrophys. J. 2021, 921, 80. [Google Scholar] [CrossRef]
- Papa, M.A.; Ming, J.; Gotthelf, E.V.; Allen, B.; Prix, R.; Dergachev, V.; Eggenstein, H.B.; Singh, A.; Zhu, S.J. Search for Continuous Gravitational Waves from the Central Compact Objects in Supernova Remnants Cassiopeia A, Vela Jr., and G347.3–0.5. Astrophys. J. 2020, 897, 22. [Google Scholar] [CrossRef]
- Ming, J.; Papa, M.A.; Singh, A.; Eggenstein, H.B.; Zhu, S.J.; Dergachev, V.; Hu, Y.; Prix, R.; Machenschalk, B.; Beer, C.; et al. Results from an Einstein@Home search for continuous gravitational waves from Cassiopeia A, Vela Jr., and G347.3. Phys. Rev. D 2019, 100, 024063. [Google Scholar] [CrossRef]
- Ming, J.; Papa, M.A.; Eggenstein, H.B.; Machenschalk, B.; Steltner, B.; Prix, R.; Allen, B.; Behnke, O. Results From an Einstein@Home Search for Continuous Gravitational Waves From G347.3 at Low Frequencies in LIGO O2 Data. Astrophys. J. 2022, 925, 8. [Google Scholar] [CrossRef]
- Lindblom, L.; Owen, B.J. Directed searches for continuous gravitational waves from twelve supernova remnants in data from Advanced LIGO’s second observing run. Phys. Rev. D 2020, 101, 083023. [Google Scholar] [CrossRef]
- Millhouse, M.; Strang, L.; Melatos, A. Search for gravitational waves from 12 young supernova remnants with a hidden Markov model in Advanced LIGO’s second observing run. Phys. Rev. D 2020, 102, 083025. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Searches for Continuous Gravitational Waves from 15 Supernova Remnants and Fomalhaut b with Advanced LIGO. Astrophys. J. 2019, 875, 122. [Google Scholar] [CrossRef]
- Jones, D.; Sun, L. Search for continuous gravitational waves from Fomalhaut b in the second Advanced LIGO observing run with a hidden Markov model. Phys. Rev. D 2021, 103, 023020. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.; Adya, V.; Affeldt, C.; Agarwal, D.; et al. Search for continuous gravitational waves from 20 accreting millisecond x-ray pulsars in O3 LIGO data. Phys. Rev. D 2022, 105, 022002. [Google Scholar] [CrossRef]
- Middleton, H.; Clearwater, P.; Melatos, A.; Dunn, L. Search for gravitational waves from five low mass x-ray binaries in the second Advanced LIGO observing run with an improved hidden Markov model. Phys. Rev. D 2020, 102, 023006. [Google Scholar] [CrossRef]
- Haskell, B.; Patruno, A. Are Gravitational Waves Spinning Down PSR J1023+0038? Phys. Rev. Lett. 2017, 119, 161103. [Google Scholar] [CrossRef]
- Zhang, Y.; Papa, M.A.; Krishnan, B.; Watts, A.L. Search for Continuous Gravitational Waves from Scorpius X-1 in LIGO O2 Data. Astrophys. J. Lett. 2021, 906, L14. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. Search for gravitational waves from Scorpius X-1 in the first Advanced LIGO observing run with a hidden Markov model. Phys. Rev. D 2017, 95, 122003. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.; Adya, V.; Affeldt, C.; et al. Search for gravitational waves from Scorpius X-1 in the second Advanced LIGO observing run with an improved hidden Markov model. Phys. Rev. D 2019, 100, 122002. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Upper Limits on Gravitational Waves from Scorpius X-1 from a Model-based Cross-correlation Search in Advanced LIGO Data. Astrophys. J. 2017, 847, 47. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. Search for gravitational waves from Scorpius X-1 with a hidden Markov model in O3 LIGO data. arXiv 2022, arXiv:2201.10104. [Google Scholar]
- Bildsten, L. Gravitational Radiation and Rotation of Accreting Neutron Stars. Astrophys. J. 1998, 501, L89–L93. [Google Scholar] [CrossRef]
- Wagoner, R.V. Gravitational radiation from accreting neutron stars. Astrophys. J. 1984, 278, 345–348. [Google Scholar] [CrossRef]
- Wang, L.; Steeghs, D.; Galloway, D.K.; Marsh, T.; Casares, J. Precision Ephemerides for Gravitational-wave Searches—III. Revised system parameters of Sco X-1. Mon. Not. R. Astron. Soc. 2018, 478, 5174–5183. [Google Scholar] [CrossRef]
- Meadors, G.D.; Krishnan, B.; Papa, M.A.; Whelan, J.T.; Zhang, Y. Resampling to accelerate cross-correlation searches for continuous gravitational waves from binary systems. Phys. Rev. D 2018, 97, 044017. [Google Scholar] [CrossRef]
- Fomalont, E.B.; Geldzahler, B.J.; Bradshaw, C.F. Scorpius X-1: The Evolution and Nature of the Twin Compact Radio Lobes. Astrophys. J. 2001, 558, 283–301. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.; Adya, V.; Affeldt, C.; et al. Search for anisotropic gravitational-wave backgrounds using data from Advanced LIGO and Advanced Virgo’s first three observing runs. Phys. Rev. D 2021, 104, 022005. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. All-sky search for continuous gravitational waves from isolated neutron stars using Advanced LIGO and Advanced Virgo O3 data. arXiv 2022, arXiv:2201.00697. [Google Scholar]
- Miller, A.L.; Aggarwal, N.; Clesse, S.; Lillo, F.D. Constraints on planetary and asteroid-mass primordial black holes from continuous gravitational-wave searches. arXiv 2021, arXiv:2110.06188. [Google Scholar] [CrossRef]
- Dergachev, V.; Papa, M.A. Results from the First All-Sky Search for Continuous Gravitational Waves from Small-Ellipticity Sources. Phys. Rev. Lett. 2020, 125, 171101. [Google Scholar] [CrossRef]
- Dergachev, V.; Papa, M.A. Results from high-frequency all-sky search for continuous gravitational waves from small-ellipticity sources. Phys. Rev. D 2021, 103, 063019. [Google Scholar] [CrossRef]
- Dergachev, V.; Papa, M.A. Search for continuous gravitational waves from small-ellipticity sources at low frequencies. Phys. Rev. D 2021, 104, 043003. [Google Scholar] [CrossRef]
- Steltner, B.; Papa, M.A.; Eggenstein, H.B.; Allen, B.; Dergachev, V.; Prix, R.; Machenschalk, B.; Walsh, S.; Zhu, S.J.; Behnke, O.; et al. Einstein@Home All-sky Search for Continuous Gravitational Waves in LIGO O2 Public Data. Astrophys. J. 2021, 909, 79. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.; Adya, V.; Affeldt, C.; et al. All-sky search for continuous gravitational waves from isolated neutron stars using Advanced LIGO O2 data. Phys. Rev. D 2019, 100, 024004. [Google Scholar] [CrossRef]
- Dergachev, V.; Papa, M.A. Results from an extended Falcon all-sky survey for continuous gravitational waves. Phys. Rev. D 2020, 101, 022001. [Google Scholar] [CrossRef]
- Dergachev, V.; Papa, M.A. Sensitivity Improvements in the Search for Periodic Gravitational Waves Using O1 LIGO Data. Phys. Rev. Lett. 2019, 123, 101101. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. First low-frequency Einstein@Home all-sky search for continuous gravitational waves in Advanced LIGO data. Phys. Rev. D 2017, 96, 122004. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.E.A. All-sky search in early O3 LIGO data for continuous gravitational-wave signals from unknown neutron stars in binary systems. Phys. Rev. D 2021, 103, 064017. [Google Scholar] [CrossRef]
- Tenorio, R.; The LIGO Scientific Collaboration; Virgo Collaboration. An all-sky search in early O3 LIGO data for continuous gravitational-wave signals from unknown neutron stars in binary systems. arXiv 2021, arXiv:2105.07455. [Google Scholar]
- Covas, P.; Sintes, A.M. First All-Sky Search for Continuous Gravitational-Wave Signals from Unknown Neutron Stars in Binary Systems Using Advanced LIGO Data. Phys. Rev. Lett. 2020, 124, 191102. [Google Scholar] [CrossRef]
- Singh, A.; Papa, M.A.; Dergachev, V. Characterizing the sensitivity of isolated continuous gravitational wave searches to binary orbits. Phys. Rev. D 2019, 100, 024058. [Google Scholar] [CrossRef]
- Rajwade, K.M.; Lorimer, D.R.; Anderson, L.D. Detecting Pulsars in the Galactic Centre. Mon. Not. R. Astron. Soc. 2017, 471, 730–739. Available online: https://academic.oup.com/mnras/article-pdf/471/1/730/19376227/stx1661.pdf (accessed on 2 May 2022). [CrossRef]
- Kim, C.; Davies, M.B. Neutron Stars in the Galactic Center. J. Korean Astron. Soc. 2018, 51, 165–170. [Google Scholar] [CrossRef]
- Ajello, M.; Albert, A.; Atwood, W.B.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; Bissaldi, E.; Blandford, R.D.; Bloom, E.D.; et al. Fermi-lat observations of high-energy γ-ray emission toward the galactic center. Astrophys. J. 2016, 819, 44. [Google Scholar] [CrossRef]
- Di Mauro, M. Characteristics of the Galactic Center excess measured with 11 years of Fermi -LAT data. Phys. Rev. D 2021, 103, 063029. [Google Scholar] [CrossRef]
- Collaboration, H.E.S.S.; Abramowski, A.; Aharonian, F. Acceleration of petaelectronvolt protons in the Galactic Centre. Nature 2016, 531, 476–479. [Google Scholar] [CrossRef]
- Bartels, R.; Krishnamurthy, S.; Weniger, C. Strong Support for the Millisecond Pulsar Origin of the Galactic Center GeV Excess. Phys. Rev. Lett. 2016, 116, 051102. [Google Scholar] [CrossRef]
- Calore, F.; Mauro, M.D.; Donato, F.; Hessels, J.W.T.; Weniger, C. Radio detection prospects for a bulge population of millisecond pulsars as suggested by fermi-lat observations of the inner galaxy. Astrophys. J. 2016, 827, 143. [Google Scholar] [CrossRef]
- Grégoire, T.; Knödlseder, J. Constraining the Galactic millisecond pulsar population using Fermi Large Area Telescope. Astron. Astrophys. 2013, 554, A62. [Google Scholar] [CrossRef]
- Hooper, D.; Linden, T. Millisecond pulsars, TeV halos, and implications for the Galactic Center gamma-ray excess. Phys. Rev. D 2018, 98, 043005. [Google Scholar] [CrossRef]
- Buschmann, M.; Rodd, N.L.; Safdi, B.R.; Chang, L.J.; Mishra-Sharma, S.; Lisanti, M.; Macias, O. Foreground mismodeling and the point source explanation of the Fermi Galactic Center excess. Phys. Rev. D 2020, 102, 023023. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. Search for continuous gravitational wave emission from the Milky Way center in O3 LIGO–Virgo data. arXiv 2022, arXiv:2204.04523. [Google Scholar] [CrossRef]
- Piccinni, O.J.; Astone, P.; D’Antonio, S.; Frasca, S.; Intini, G.; La Rosa, I.; Leaci, P.; Mastrogiovanni, S.; Miller, A.; Palomba, C. Directed search for continuous gravitational-wave signals from the Galactic Center in the Advanced LIGO second observing run. Phys. Rev. D 2020, 101, 082004. [Google Scholar] [CrossRef]
- Dergachev, V.; Papa, M.A.; Steltner, B.; Eggenstein, H.B. Loosely coherent search in LIGO O1 data for continuous gravitational waves from Terzan 5 and the Galactic Center. Phys. Rev. D 2019, 99, 084048. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. All-sky search for gravitational wave emission from scalar boson clouds around spinning black holes in LIGO O3 data. arXiv 2021, arXiv:2111.15507. [Google Scholar] [CrossRef]
- Sun, L.; Brito, R.; Isi, M. Search for ultralight bosons in Cygnus X-1 with Advanced LIGO. Phys. Rev. D 2020, 101, 063020. [Google Scholar] [CrossRef]
- Schlamminger, S.; Choi, K.Y.; Wagner, T.A.; Gundlach, J.H.; Adelberger, E.G. Test of the Equivalence Principle Using a Rotating Torsion Balance. Phys. Rev. Lett. 2008, 100, 041101. [Google Scholar] [CrossRef]
- Bergé, J.; Brax, P.; Métris, G.; Pernot-Borràs, M.; Touboul, P.; Uzan, J.P. MICROSCOPE Mission: First Constraints on the Violation of the Weak Equivalence Principle by a Light Scalar Dilaton. Phys. Rev. Lett. 2018, 120, 141101. [Google Scholar] [CrossRef]
- Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. The Einstein Telescope: A third-generation gravitational wave observatory. Class. Quantum Gravity 2010, 27, 194002. [Google Scholar] [CrossRef]
- Reitze, D.; Adhikari, R.X.; Ballmer, S.; Barish, B.; Barsotti, L.; Billingsley, G.; Brown, D.A.; Chen, Y.; Coyne, D.; Eisenstein, R.; et al. Contribution to Gravitational-Wave Astronomy beyond LIGO. arXiv 2019, arXiv:1907.04833. [Google Scholar]
- Danzmann, K.; The LISA Pathfinder Team; The eLISA Consortium. LISA and its pathfinder. Nat. Phys. 2015, 11, 613–615. [Google Scholar] [CrossRef]
- Kalogera, V.; Sathyaprakash, B.S.; Bailes, M.; Bizouard, M.A.; Buonanno, A.; Burrows, A.; Colpi, M.; Evans, M.; Fairhurst, S.; Hild, S.; et al. The Next Generation Global Gravitational Wave Observatory: The Science Book. arXiv 2021, arXiv:2111.06990. [Google Scholar]
- Kawamura, S.; Ando, M.; Seto, N.; Sato, S.; Musha, M.; Kawano, I.; Yokoyama, J.I.; Tanaka, T.; Ioka, K.; Akutsu, T.; et al. Current status of space gravitational wave antenna DECIGO and B-DECIGO. arXiv 2020, arXiv:2006.13545. [Google Scholar] [CrossRef]
- Luo, J.; Chen, L.S.; Duan, H.Z.; Gong, Y.G.; Hu, S.; Ji, J.; Liu, Q.; Mei, J.; Milyukov, V.; Sazhin, M.; et al. TianQin: A space-borne gravitational wave detector. Class. Quantum Gravity 2016, 33, 035010. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piccinni, O.J. Status and Perspectives of Continuous Gravitational Wave Searches. Galaxies 2022, 10, 72. https://doi.org/10.3390/galaxies10030072
Piccinni OJ. Status and Perspectives of Continuous Gravitational Wave Searches. Galaxies. 2022; 10(3):72. https://doi.org/10.3390/galaxies10030072
Chicago/Turabian StylePiccinni, Ornella Juliana. 2022. "Status and Perspectives of Continuous Gravitational Wave Searches" Galaxies 10, no. 3: 72. https://doi.org/10.3390/galaxies10030072
APA StylePiccinni, O. J. (2022). Status and Perspectives of Continuous Gravitational Wave Searches. Galaxies, 10(3), 72. https://doi.org/10.3390/galaxies10030072





