Non-Thermal Emission from Radio-Loud AGN Jets: Radio vs. X-rays

Abstract

We consider the sample of 55 blazars and Seyferts cross-correlated from the Planck all-sky survey based on the Early Release Compact Source Catalog (ERCSC) and Swift BAT 105-Month Hard X-ray Survey. The radio Planck spectra vs. X-ray Swift/XRT+BAT spectra of the active galactic nuclei (AGN) sample were fitted with the simple and broken power law (for the X-ray spectra taking into account also the Galactic neutral absorption) to test the dependencies between the photon indices of synchrotron emission (in radio range) and synchrotron self-Compton (SSC) or inverse-Compton emission (in X-rays). We show that for the major part of the AGN in our sample there is a correspondence between synchrotron and SSC photon indices (one of two for broken power-law model) compatible within the error levels. For such objects, this can give a good perspective for the task of distinguishing between the jet base counterpart from that one emitted in the disk+corona AGN “central engine”.

1. Introduction

The blazars are the radio-loud AGN with one jet directed along the line-of-sight to the observer (i.e., AGN type 0). Due to the jet alignment, an observer can see near pure jet base emission at the AGN center, as the emission of the disk+corona «central engine» is usually significantly weaker than the jet base one, and almost not visible in the blazar’s X-ray spectrum. This makes blazars especially interesting when we intend to investigate the properties of the jet base emission. Here, we consider the dependence between the direct synchrotron emission of a jet base in the radio wave range and its inverse Compton (IC) or synchrotron self-Compton (SSC) emission in X-rays. Taking into account that non-blazar radio loud (RL) AGN have the same non-thermal component in their spectra, this dependence can open some possibilities to distinguish between nuclear (disk+corona) and jet base components in their high energy spectra extrapolating some parameters of the jet base synchrotron radio spectra to IC/SSC ones.

The jet base is of the order of a percent of pc in size. It is composed of ultra-relativistic plasma, either electron-positron (usually referred to as leptonic) or electron-proton (referred to as hadronic); the composition of this plasma is still being debated. Plasma particles are ejected at relativistic bulk velocity from an AGN central region and being accelerated at shock fronts inside the jet, emit synchrotron radiation visible at a wide range of wavelengths from radio to ultraviolet or even higher.

Depending on the peak frequency ${\nu }_S$ of the Synchrotron power (of peak intensity) ${\nu }_S$F(${\nu }_S)$ two classes of BL Lacs were introduced in [1]: low-frequency peaked BL Lacs (LBL) and high-frequency peaked BL Lacs (HBL). In [2], similar classification was introduced to the sample of all blazars: low Synchrotron peaked blazars (LSP, ${\nu }_S\le {10}^{14}$ Hz), intermediate Synchrotron peaked blazars (ISP, ${10}^{14}\le {\nu }_S\le {10}^{15}$ Hz), and high Synchrotron peaked blazars (HSP, ${\nu }_S>{10}^{15}$ Hz) (see also discussion in [3,4,5]).

In addition to the dominant non-thermal jet-driven emission, accretion-driven thermal disk radiation, Comptonised by a hot ∼100 keV corona to power-law X-ray emission, can also make a significant contribution to the overall X-ray flux in some cases (3C120, 3C273, etc.) [2,6,7]. Signatures of such a disk+corona contribution in X-ray spectra are expected from LSP blazars in which IC/SSC jet components are dominant. Some ISP blazars with the intersection of falling synchrotron and rising IC/SSC spectra in the X-ray band (similarly to IBL S5 0716+714) are also promising candidates for the investigation of a jet-disk+corona interplay in X-ray band [2,8].

As it was shown in [9], the jet synchrotron and X-ray IC/SSC spectra are interconnected because they are produced by the same leptonic cosmic ray population. In particular, there is a relationship between photon indices in radio-band ${\Gamma }_R$ and X-ray band ${\Gamma }_X$.

In our work, we investigate how this dependency manifest itself in radio and X-ray spectra of the sample of radio loud AGN created from the cross-correlation of the Swift BAT 105-Month Hard X-ray Survey (https://swift.gsfc.nasa.gov/results/bs105mon/ Accessed on 10 June 2020) and the Planck Early Release Compact Source Catalog (ERCSC, [10]) (http://www.sciops.esa.int/index.php?project=planck&page=Planck_Legacy_Archive Accessed on 15 June 2020). For this purpose, we use the 24–240 GHz Planck spectra and the Swift/XRT+BAT spectra of the same objects in X-rays and compare the photon indices.

The organisation of this paper is as follows. In the Section 2, we analyse the non-thermal MWL emission of AGN jets. In Section 3, we describe our AGN sample and spectral fitting procedure. In Section 4, we discuss an interconnection of radio and X-ray spectra of considered AGN and in Section 5 we draw out our conclusions.

2. Spectral Energy Distribution of Radio Loud AGN

Accelerated particles—cosmic-ray electrons and positrons (hereafter electrons)—of the jet in the most cases are distributed over the energies $E>E_m$ (Lorentz factor $\gamma =E/m_e{c}^2>{\gamma }_m$) following a single power-law dependency $N\left(E\right)\propto E^{-p}exp(-E/E_{cut})$ of the injected electron spectrum with the spectral index p and an exponential cut-off at $E\sim E_{cut}$ [9,11]. Such distribution of ultra-relativistic electrons (${\gamma }_m\gg 1$) generates a two-hump spectrum consisting of the low-frequency synchrotron component and the high-frequency component due to inverse-Compton scattering (IC) of synchrotron photons (synchrotron-self-Compton SSC) or external low energy photons (CMB and other background radiation) by the same electron population [12]. In Figure 1, the two-hump spectra of two LSPs (3C279 and 3C273) and two HSPs (Mrk 421 ans Mrk 501) blazars are presented. In 3C273 case, the thermal contribution of the accretion disk in the optical-UV band is also visible.

The fast radiation cooling of the high energy relativistic electrons (if present) results in the broken power law spectrum of the final emitting electrons with the spectral index $p+1$ for $\gamma >{\gamma }_c$. For such a two-segment power law electron spectrum the corresponding synchrotron spectrum for the slow cooling case (${\gamma }_c>{\gamma }_m$) is the four-segment power law $F_{\nu }\propto {\nu }^{-\alpha }$ with the spectral indices ${\alpha }_s$ (the photon index ${\Gamma }_s={\alpha }_s+1$) equal to −2.0, −1/3, $(p-1)/2$, and $p/2$ for $\nu <{\nu }_a$, ${\nu }_a<\nu <{\nu }_m$, ${\nu }_m<\nu <{\nu }_c$, and $\nu >{\nu }_c$, correspondingly. Here ${\nu }_a$ is the self-absorption frequency, ${\nu }_m$ is the frequency of synchrotron emission of electrons with minimum Lorenz factor $\gamma ={\gamma }_m$, ${\nu }_c$ is the same for electrons at the edge of fast cooling with $\gamma ={\gamma }_c$ and the typical case ${\nu }_a<{\nu }_m<{\nu }_c$ with the weak self-absorption regime ${\nu }_a<{\nu }_c$ is considered [9]. Synchrotron frequencies ${\nu }_i$ ($i=a,m,c$) are radiated by electrons with ${\gamma }_i$ via ${\gamma }^2$-scattering of virtual photons with gyrofrequency ${\nu }_g={\omega }_g/2\pi =eB/\left(2\pi m_{e}c\right)$ in magnetic field B: ${\nu }_i\sim {\gamma }_i^2{\nu }_g$.

In the case of IC/SSC emission, the real photons of background (IC) or newly generated synchrotron (SSC) radiation are ${\gamma }^2$-scattered by the relativistic electrons and characteristic frequencies of the SSC spectra are dependent on ones of synchrotron spectra ${\nu }_{ij}^{IC}\sim {\gamma }_i^2{\nu }_j$. Therefore, the profiles of the SSC spectra are similar to the synchrotron ones and for the considered above case ${\nu }_a<{\nu }_m<{\nu }_c$ the four-segment power law spectrum has the spectral indices ${\alpha }_{IC}$ (the photon index ${\Gamma }_{IC}={\alpha }_{IC}+1$) equal to −1.0, −1/3, $(p-1)/2$, and $p/2$ for $\nu <{\nu }_{ma}^{IC}$, ${\nu }_{ma}^{IC}<\nu <{\nu }_{mm}^{IC}$, ${\nu }_{mm}^{IC}<\nu <{\nu }_{cc}^{IC}$, and $\nu >{\nu }_{cc}^{IC}$, correspondingly [9].

The multi-wavelength spectral energy distributions of blazars (BL Lacs and FSRQs) clearly demonstrates the two-hump shape (Figure 2, taken from [4]). As it is discussed in detail in [4], at low frequencies $\nu <{\nu }_t$ up to the self-absorption frequency ${10}^{11}\le {\nu }_t/Hz\le {10}^{12}$ in the radio band a reasonable approximation of all observable spectra corresponds to power law with ${\alpha }_R=-0.1$ or photon index ${\Gamma }_R=0.9$. In $log\left(\nu L_{\nu }\right)-log\nu$ representation where $L_{\nu }$ is the spectral luminosity, the peak frequency ${\nu }_S$ of the synchrotron emission determines the mentioned above classes (LSP, ISP, and HSP) of blazars. At frequency ${\nu }_{cut,S}$ the transition to the IC-dominated emission takes place. In a similar way, the peak frequency ${\nu }_C$ determines Compton-dominated hump and at ${\nu }_{cut,C}$ Compton-dominated emission decays. Between limiting frequencies ${\nu }_t$ and ${\nu }_{cut,C}$, the two-segment power law approximations for synchrotron humps (photon indices ${\Gamma }_1$ and ${\Gamma }_2$) and for IC/SSC humps (photon indices ${\Gamma }_3$ and ${\Gamma }_4={\Gamma }_2$) are presented and analysed in [4]. In Figure 2, the hump parameters are indicated for the FSRQs with $44<log(L_{\gamma }/erg{s}^{-1})<45$. From Table 1, in [4], it follows that interconnection between synchrotron radio-spectra at frequencies ${\nu }_t<\nu <{\nu }_S$ and IC/SSC X-ray spectra at frequencies $\nu >{\nu }_{cut,S}$ as signatures of emission produced by common cosmic-ray electron population is visible in some cases. Namely, in the cases of FSRQs with $44<log(L_{\gamma }/erg{s}^{-1})<47$ the photon indices ${\Gamma }_1\approx 1.5$, while $1.4<{\Gamma }_3<1.75$ and IC/SSC X-ray emission dominates for $\nu >{\nu }_{cut,S}\approx {10}^{16}$ Hz. There are also promising sources among BL Lacs with $46<log(L_{\gamma }/erg{s}^{-1})<48$ for which $1.5<{\Gamma }_1<1.65$ while $1.45<{\Gamma }_3<1.62$ and IC/SSC X-ray emission dominates for $\nu >{\nu }_{cut,S}\approx 6\times {10}^{15}$ Hz.

3. The AGN Sample and Spectral Fitting

This research includes all the Swift/XRT+BAT datasets available in public data archive HEASARC for the objects of the sample identified as beamed AGN 1.

However, other sources identified these objects as BL Lacs (

Table 1. Sub-sample of BL Lac type blazars.

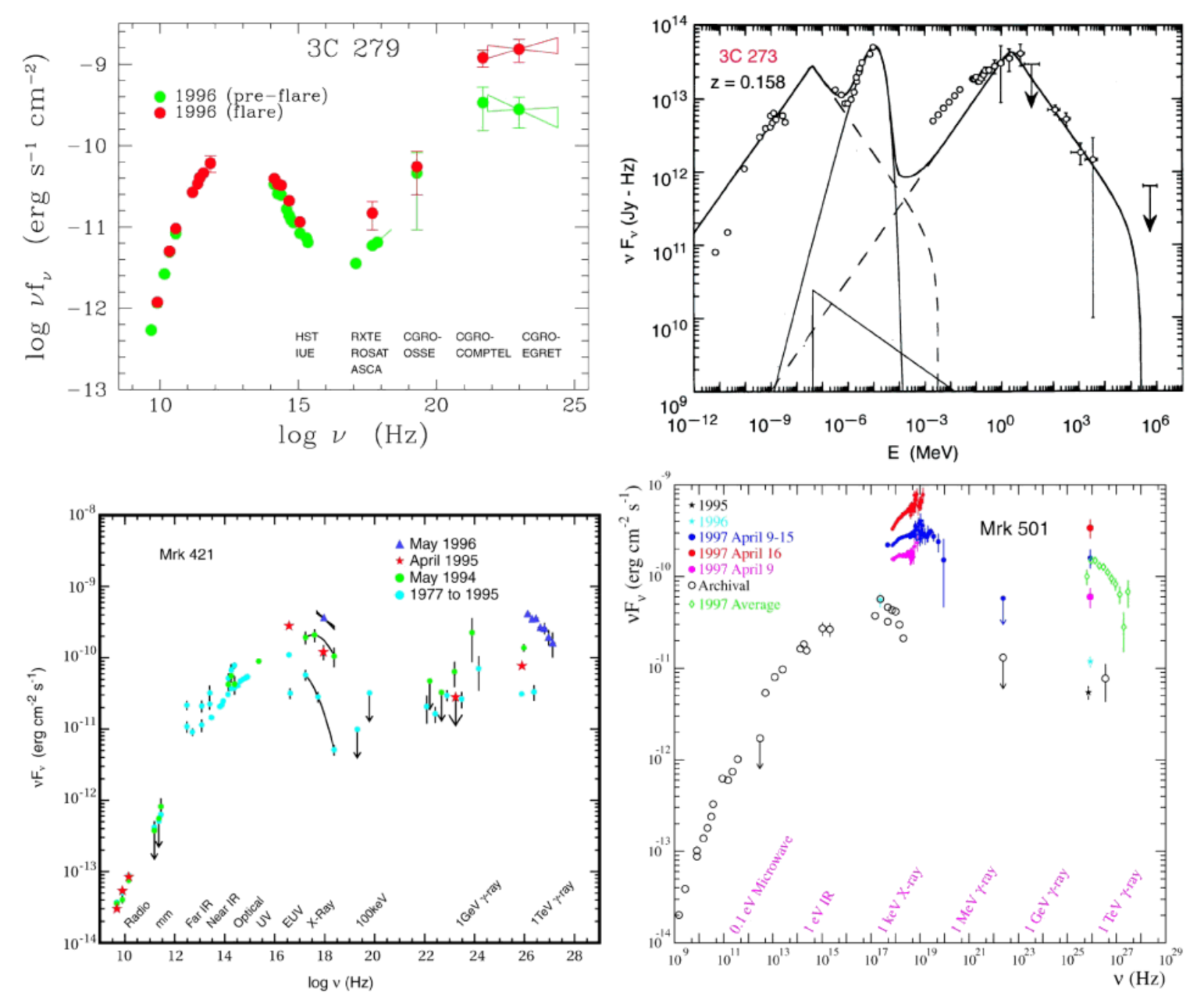
Object	Type	RA [h, m, s]	Dec [o, ${}^{\prime }$, ${}^{\prime \prime }$]	z	${\mathit{N}}_{\mathit{H}}$ [cm${}^{-2}$]
PKS 0426-380	LSP	04 28 40.42	−37 56 19.58	1.11	$2.3\times {10}^{20}$
PKS 0521-36	LSP	05 22 57.98	−36 27 30.84	0.05	$4.1\times {10}^{20}$
PKS 0537-441	LSP	05 38 50.36	−44 05 08.93	0.89	$3.5\times {10}^{20}$
S5 0716+714	ISP	07 21 53.44	+71 20 36.36	0.3	$3.5\times {10}^{20}$
Mrk 501	HSP	16 53 52.21	+39 45 36.6	0.03	$3.5\times {10}^{20}$
S5 1803+784	LSP	18 00 45.68	+78 28 04.01	0.68	$4.1\times {10}^{20}$
PKS 2005-489	HSP	20 09 25.39	−48 49 53.72	0.07	$4.1\times {10}^{20}$
PKS 2331-240	ISP	23 33 55.23	−23 43 40.65	0.05	$1.7\times {10}^{20}$

), FSRQs (

Table 2. Sub-sample of FSRQ type blazars.

Object	Type	RA [h, m, s]	Dec [o, ${}^{\prime }$, ${}^{\prime \prime }$]	z	${\mathit{N}}_{\mathit{H}}$ [cm${}^{-2}$]
S5 0212+735	FSRQ-LSP	02 17 30.81	+73 49 32.61	2.36	$3.9\times {10}^{21}$
PKS 0312-770	FSRQ	03 11 55.25	−76 51 50.84	0.22	$8.0\times {10}^{20}$
4C +32.14	FSRQ	03 36 30.1	+32 18 29.34	1.26	$2.7\times {10}^{21}$
4C +50.11	FSRQ	03 59 29.74	+50 57 50.16	1.52	$2.7\times {10}^{21}$
PKS 0402-362	FSRQ	04 03 53.74	−36 05 01.91	1.42	$6.1\times {10}^{19}$
PMN J0525-2338	FSRQ	05 25 06.50	−23 38 10.8	3.1	$2.4\times {10}^{20}$
PKS 0528+134	FSRQ-LSP	05 30 56.46	+13 31 55.14	2.07	$2.4\times {10}^{20}$
PKS 0537-286	FSRQ	05 39 54.28	−28 39 55.94	3.1	$2.4\times {10}^{20}$
B2 0552+39A	FSRQ	05 55 30.80	+39 48 49.16	2.37	$2\times {10}^{21}$
PMN J0623-6436	FSRQ	06 23 07.69	−64 36 20.71	0.12	$4.7\times {10}^{20}$
PKS 0723-008	FSRQ	07 25 50.63	-00 54 56.54	0.12	$1.7\times {10}^{21}$
4C +71.078	FSRQ	08 41 24.35	+70 53 42.28	2.21	$3.1\times {10}^{20}$
S5 1039+81	FSRQ	10 44 23.06	+80 54 39.44	1.26	$2.7\times {10}^{20}$
PKS 1127-14	FSRQ-LSP	11 30 07.05	−14 49 27.38	1.18	$3.8\times {10}^{20}$
4C +49.22	FSRQ-LSP	11 53 24.46	+49 31 08.83	0.33	$3.8\times {10}^{20}$
FBQS J1159+2914	FSRQ-LSP	11 59 31.83	+29 14 43.82	0.72	$3.8\times {10}^{20}$
PG 1222+216	FSRQ	12 24 54.45	+21 22 46.38	0.43	$2.3\times {10}^{20}$
3C 273	FSRQ-LSP	12 29 06.69	+02 03 08.59	0.15	$2.3\times {10}^{20}$
3C 279	FSRQ-LSP	12 56 11.16	−05 47 21.53	0.53	$2.3\times {10}^{20}$
PKS 1329-049	FSRQ	13 32 04.46	−05 09 43.3	2.15	$2.4\times {10}^{20}$
PKS 1335-127	FSRQ	13 37 39.78	−12 57 24.69	0.54	$6.5\times {10}^{20}$
PMN J1508-4953	FSRQ	15 08 38.94	−49 53 02.32	-	$3.4\times {10}^{21}$
PKS 1510-08	FSRQ	15 12 50.53	−09 05 59.82	0.36	$9.3\times {10}^{20}$
PKS 1622-29	FSRQ	16 26 06	−29 51 26.97	0.81	$2.6\times {10}^{21}$
3C 345	FSRQ-LSP	16 42 58.81	+39 48 36.99	0.59	$2.6\times {10}^{21}$
PKS 1830-21	FSRQ-LSP	18 33 39.92	−21 03 39	2.5	$2.6\times {10}^{21}$
B1921-293	FSRQ	19 24 51.05	−29 14 30.12	0.35	$2\times {10}^{21}$
4C +73.18	FSRQ	19 27 48.49	+73 58 01.57	0.3	$1.1\times {10}^{21}$
PKS 2008-159	FSRQ	20 11 15.71	−15 46 40.25	1.18	$2\times {10}^{21}$
QSO B2013+370	FSRQ	20 15 28.72	+37 10 59.51	0.85	$1.3\times {10}^{22}$
B2 2023+33	FSRQ	20 25 10.84	+33 43	0.22	$7.7\times {10}^{21}$
PKS 2052-47	FSRQ	20 56 16.35	−47 14 47.62	1.49	$3.2\times {10}^{20}$
[HB 89] 2142-758	FSRQ	21 48	−75.575	1.13	$7.7\times {10}^{21}$
PKS 2145+06	FSRQ	21 48 05.45	+06 57 38.6	1	$5.6\times {10}^{20}$
PKS 2149-306	FSRQ-LSP	21 51 55.52	−30 27 53.69	2.35	$1.8\times {10}^{20}$
4C +31.63	FSRQ-LSP	22 03 14.97	+31 45 38.26	0.29	$1.2\times {10}^{21}$
II Zw 171	FSRQ	22 11 53.88	+18 41 49.85	0.06	$5.1\times {10}^{20}$
[HB 89] 2230+114	FSRQ	22 31 48	+11.721	1.03	$5.1\times {10}^{20}$
PKS 2227-088	FSRQ-LSP	22 29 40.08	−08 32 54.43	1.55	$5.0\times {10}^{20}$
3C 454.3	FSRQ	22 53 57	+16 08 53	0.85	$8.6\times {10}^{20}$

), and Seyferts 1 (

Table 3. Sub-sample of Seyfert 1 type AGN.

Object	Type	RA [h, m, s]	Dec [o, ${}^{\prime }$, ${}^{\prime \prime }$]	z	${\mathit{N}}_{\mathit{H}}$ [cm${}^{-2}$]
Mrk 1501	Seyfert 1	00 10 31.00	+10 58 29.5	0.09	$7.1\times {10}^{20}$
QSO B0309+411	Seyfert 1	03 13 01.96	+41 20 01.18	0.13	$1.7\times {10}^{21}$
PKS 0405-12	Seyfert 1	04 07 48.43	−12 11 36.66	0.57	$4.2\times {10}^{20}$
PKS 1143-696	Seyfert 1	11 45 53.62	−69 54 01.79	0.24	$2.8\times {10}^{21}$
3C 309.1	Seyfert 1	14 59 07.58	+71 40 19.86	0.9	$2.4\times {10}^{20}$
3C 380	Seyfert 1	18 29 31.78	+48 44 46.15	0.69	$2.4\times {10}^{20}$
8C 1849+670	Seyfert 1	18 49 16.07	+67 05 41.68	0.66	$6.0\times {10}^{20}$
NGC 7213	Seyfert 1	22 09 16.21	−47 10 00.08	0.005	$1.1\times {10}^{20}$

). In these Tables we show the source type, coordinates, and redshift following the SIMBAD data2 and the neutral hydrogen absorbing column in the Galaxy following [13].

The Planck spectra within the frequency range 24 to 240 GHz were taken from the Early Release Compact Source Catalog (ERCSC) of compact sources observed by Planck during the 2009–2010 whole sky coverage. These Planck spectra are publicly available on the HEAVENS webpage3.

The Swift/XRT spectra were obtained using the observations made by UK Swift Science Data Centre (UKSSDC) at the University of Leicester4. We have used single-pass centroid with the maximum of 10 attempts and 6 arcmin search radius.

The Swift/BAT spectra were obtained from the Swift BAT 105-Month Hard X-ray Survey official webpage5.

To perform the spectra fitting the XSPEC package of the NASA HeaSoft version 6.27.2 software for astronomical data processing and analysis6 was applied.

To fit the spectra in the both radio and X-ray range (here we include also the neutral hydrogen absorption in our model) we use the simple or broken power-law model taking into account that the flattering frequency ${\nu }_t$ due to the self-absorption may be located in the Planck range and the dip frequency ${\nu }_{cut,S}$ of the transition from synchrotron to IC component may be located in the Swift range or higher (Figure 2). So, if the self-absorption frequency ${\nu }_t$ falls into the Planck range 24 GHz $<{\nu }_t<$ 240 GHz, the two-segment power law approximation results in two photon indices: ${\Gamma }_{1,l}<1$ for $\nu <{\nu }_t$ and ${\Gamma }_{1,h}>1$ for $\nu >{\nu }_t$.

In a similar way, simple power law X-ray Swift spectra with $2>{\Gamma }_3\approx {\Gamma }_1>1$ are expected for the LSP and some IPS blazars with ${\nu }_{cut,S}\le {10}^{17}$ Hz, i.e., below the Swift range. Otherwise, the two-segment power law approximation of X-ray spectra will results in two photon indices: ${\Gamma }_{3,l}>2$ for $\nu <{\nu }_{cut,S}$ and $2>{\Gamma }_{3,h}>1$ for $\nu >{\nu }_{cut,S}$. If $h{\nu }_{cut,S}$ exceeds the Swift/BAT range (175 keV) two photon indices: ${\Gamma }_{3,l}\ge 2$ for $E<E_{br}$ and ${\Gamma }_{3,h}\ge {\Gamma }_{3,l}$ for $E>E_{br}$ describe the falling part of the synchrotron spectra of HPS blazars.

In

Table 4. The best-fit model parameters for the Planck and Swift/XRT+BAT spectra.

Object	Radio			X-rays
Parameter ->	${\Gamma }_{\mathbf{1},\mathbf{l}}$	E${}_{\mathbf{b}}$, 10${}^{-\mathbf{4}}$ eV	${\Gamma }_{\mathbf{1},\mathbf{h}}$	${\Gamma }_{\mathbf{3},\mathbf{l}}$	E${}_{\mathbf{b}}$, keV	${\Gamma }_{\mathbf{3},\mathbf{h}}$
Mrk 1501	0.4 ± 0.8	1.6 ± 0.4	1.47 ± 0.09	1.62 ± 0.03	74 ± 69	2.91 ± 0.16
S5 0212+735	1.57 ± 0.08	4.0 ± 0.6	2.0 ± 0.3	1.41 ± 0.08	-	-
PKS 0312-770	0.4 ± 0.3	2.0 ± 0.2	1.95 ± 0.15	2.15 ± 0.08	2.7 ± 0.3	1.41 ± 0.09
QSO B0309+411	1.0 ± 0.2	-	-	2.7 ± 0.6	1.2 ± 0.2	1.8 ± 0.07
4C +32.14	1.62 ± 0.14	-	-	1.47 ± 0.07	25 ± 4	1.8 ± 0.3
4C +50.11	1.60 ± 0.05	-	-	1.66$\pm 0.07$	-	-
PKS 0402-362	1.13 ± 0.08	6.0 ± 0.6	1.45 ± 0.05	1.58 ± 0.04	9.5 ± 9.3	2.0 ± 0.5
PKS 0405-12	1.64 ± 0.09	-	-	1.79 ± 0.15	21 ± 4	2.7 ± 0.3
PKS 0426-380	0.7 ± 0.4	2.0 ± 0.6	1.57 ± 0.08	1.66 ± 0.07	4.1 ± 1.9	1.35 ± 0.07
PKS 0521-36	1.11 ± 0.09	4.1 ± 0.7	1.32 ± 0.03	1.58 ± 0.03	4.8 ± 1.8	1.86 ± 0.06
PMN J0525-2338	0.6 ± 0.6	2.5 ± 0.3	2.5 ± 0.5	1.5 ± 0.8	-	-
PKS 0528+134	1.9 ± 0.1	-	-	0.9 ± 0.3	1.5 ± 0.9	1.49 ± 0.07
PKS 0537-441	2.0 ± 0.4	-	-	2.0 ± 0.2	0.9 ± 0.2	1.68 ± 0.03
PKS 0537-286	1.10 ± 0.08	4.1 ± 0.8	1.43 ± 0.03	1.20 ± 0.06	10.9 ± 5.2	1.36 ± 0.04
B2 0552+39A	2.5 ± 0.3	1.9 ± 0.5	1.78 ± 0.10	1.45 ± 0.11	-	-
PMN J0623-6436	0.87${}_{-0.23}^{+0.17}$	2.1 ± 0.1	1.59 ± 0.08	1.63 ± 0.11	-	-
S5 0716+714	0.75 ± 0.29	3.4 ± 0.6	1.28 ± 0.07	2.02 ± 0.09	6.1 ± 0.4	1.13 ± 0.06
PKS 0723-008	0.85 ± 0.06	3.7 ± 0.6	1.48 ± 0.06	1.62 ± 0.05	-	-
S5 1039+81	1.38 ± 0.15	-	-	1.25 ± 0.35	2.7 ± 1.8	1.65 ± 0.12
PKS 1127-14	0.6 ± 0.4	2.9 ± 0.6	1.70 ± 0.08	1.49 ± 0.06	18.4 ± 9.9	2.7 ± 1.6
PKS 1143-696	1.12 ± 0.35	3.3 ± 1.5	1.85 ± 0.27	2.5 ± 1.4	unc.	1.79 ± 0.14
4C +49.22	1.29 ± 0.05	-	-	1.68 ± 0.05	5.4 ± 2.8	1.84 ± 0.04
FBQS J1159+2914	1.17 ± 0.06	-	-	1.53 ± 0.04	47${}_{-19}^{+90}$	>1.6
PG 1222+216	0.28 ± 0.22	2.4 ± 0.6	1.62 ± 0.12	2.16 ± 0.17	1.1 ± 0.1	1.43 ± 0.03
3C 273	0.96 ± 0.01	3.8 ± 0.2	1.76 ± 0.03	1.52 ± 0.03	2.5 ± 0.3	1.72$\pm 0.01$
3C 279	1.12 ± 0.08	4 ± 1	1.60 ± 0.03	1.49 ± 0.05	2.5 ± 0.3	1.67 ± 0.03
PKS 1329-049	1.22 ± 0.09	-	-	1.33 ± 0.09	-	-
PKS 1335-127	1.13 ± 0.04	3.5 ± 0.8	1.64 ± 0.06	1.42 ± 0.02	6.4 ± 0.7	2.1 ± 0.3
3C 309.1	1.41 ± 0.13	-	-	1.48 ± 0.07	-	-
PMN J1508-4953	0.6 ± 0.5	3.5 ± 0.7	1.5 ± 0.3	1.32 ± 0.07	-	-
PKS 1510-08	$1.13\pm 0.06$	3.3 ± 0.4	1.85 ± 0.09	1.31 ± 0.02	10.7 ± 6.5	1.39 ± 0.05
PKS 1622-29	1.08 ± 0.08	-	-	1.39 ± 0.03	7.1 ± 0.9	1.91${}_{-0.2}^{+0.4}$
3C 345	1.33 ± 0.02	3.8 ± 0.8	1.80 ± 0.04	1.97 ± 0.22	1.2 ± 0.2	1.64 ± 0.04
Mrk 501	1.57 ± 0.10	-	-	2.09 ± 0.01	21 ± 14	2.46 ± 0.13
S5 1803+784	1.17 ± 0.04	4.0 ± 0.8	1.51 ± 0.06	1.52 ± 0.04	-	-
3C 380	1.53 ± 0.09	3.7 ± 0.5	1.95 ± 0.15	1.67 ± 0.17	2.3 ± 0.9	2.1 ± 0.3
PKS 1830-21	1.74 ± 0.04	-	-	1.40 ± 0.03	5.3 ± 0.7	1.21 ± 0.05
8C 1849+670	1.26 ± 0.19	3.7 ± 1.6	1.53 ± 0.11	1.72 ± 0.10	6.3 ± 5.3	1.49 ± 0.1
B1921-293	1.32 ± 0.01	4.9 ± 0.3	1.72 ± 0.03	1.82 ± 0.10	-	-
4C +73.18	1.04 ± 0.55	2.2 ± 0.7	1.75 ± 0.08	1.76 ± 0.05	-	-
PKS 2005-489	1.13 ± 0.12	5.5 ± 0.9	1.9 ± 0.3	1.42 ± 0.02	7.1 ± 0.6	2.4 ± 0.3
PKS 2008-159	1.64 ± 0.14	-	-	1.40 ± 0.02	6.4 ± 0.9	2.0${}_{-0.3}^{+0.5}$
QSO B2013+370	1.51 ± 0.20	-	-	1.16 ± 0.20	22 ± 18	2.2 ± 0.8
PKS 2052-47	1.39 ± 0.04	4.5 ± 1.5	1.41 ± 0.07	1.38 ± 0.02	11.0 ± 0.4	2.2${}_{-0.4}^{+0.5}$
PKS 2145+06	1.35 ± 0.04	3.9 ± 0.4	1.97 ± 0.05	1.28 ± 0.06	2.0 ± 0.5	1.43 ± 0.01
[HB 89] 2142-758	0.7 ± 0.2	2.0 ± 0.2	1.46 ± 0.05	0.8 ± 0.3	1.8 ± 0.3	1.49 ± 0.11
4C +31.63	1.0 ± 0.4	3.0 ± 0.9	1.49 ± 0.154	1.62 ± 0.06	-	-
II Zw 171	1.27 ± 0.16	-	-	1.81 ± 0.05	-	-
PKS 2149-306	1.12 ± 0.09	-	-	1.22 ± 0.03	14 ± 5	1.61 ± 0.13
NGC 7213	−1.67 ± 0.15	-	-	1.69 ± 0.03	-	-
PKS 2227-088	0.97 ± 0.06	4.2 ± 0.9	1.61 ± 0.08	1.3 ± 1.5	<85	1.69 ± 0.32
[HB 89] 2230+114	1.39 ± 0.04	5.7 ± 0.8	2.0 ± 0.2	1.40 ± 0.02	7.1 ± 2.1	1.96 ± 0.11
3C 454.3	0.37 ± 0.05	3.0 ± 0.2	1.21 ± 0.03	1.92 ± 0.20	1.2 ± 0.3	1.62 ± 0.03
PKS 2331-240	0.9 ± 0.07	3.6 ± 0.3	1.57 ± 0.12	1.64 ± 0.04	7.6 ± 2.2	2.4 ± 0.3
4C +71.078	0.73 ± 0.05	3.2 ± 0.5	1.20 ± 0.15	1.33 ± 0.03	6.7 ± 1.8	1.73 ± 0.07
B2 2023+33	1.37 ± 0.15	7.4 ± 0.8	-0.2 ± 0.8	1.46 ± 0.17	-	-

, we show the best-fit model parameters to the Planck and Swift/XRT+BAT spectra of the sample of 55 blazars and Seyferts. The models used to fit them were:

• po (simple power-law, for the Planck spectra);
• bknpo (broken power-law, for the Planck spectra);
• po*tbabs (absorbed power-law, for the Swift/XRT+BAT spectra);
• bknpo*tbabs (absorbed broken power-law, for the Swift/XRT+BAT spectra).

We explain the details of our Planck spectra fitting and data statistics in the Appendix A.

In columns 2–4 of the Table 4, we show the best-fit photon indices and break energies for the Planck spectra of the objects shown in the first column; in the last three columns we show the photon indices and the break energies for the X-ray (Swift/XRT+BAT) spectra. If the difference between the simple power-law and broken power-law is statistically significant (i.e., the null-hypothesis probability P${}_{null}<10\%$ where the null-hypothesis corresponds to the simple power-law model) we show the best-fit broken power-law model parameters. If there is not such difference between these two models in sense of $\chi$-statistics and values of parameters, we show the simple power-law photon index only.

4. AGN Sample: Interconnection of Radio and X-ray Spectra

As we can see from the Table 4 33 of 55 AGN have at least one of the photon indices in the model of Planck spectrum coincident with one of the photon indices of the X-ray spectral model. In total, 23 AGN of this subsample follow the pattern when the single ${\Gamma }_1$ or the upper ${\Gamma }_{1,h}$ photon index of the Planck spectrum coincides within the error levels with the single ${\Gamma }_3$ or lower ${\Gamma }_{3,l}$ photon index of the X-ray spectrum, i.e., in both radio and X-ray ranges we see the lower segments of the synchrotron and IC/SSC components.

Such a situation we observe for S5 0212+735, PKS0312-770, PKS 2331-240, PKS0537-441, PMN J0623-6436, 3C 309.1, 4C +31.63, 4C +32.14, 4C +50.11, 4C +73.18, PKS 1329-049, PKS 2005-489, PKS 2227-088, PKS 0405-12, PKS 0426-380, PKS 0528+134, PKS 0723-008, B2 0552+39A, S5 1039+81, S5 1803+784, B1921-293, B2 2023+33, PMN J1508-4953, and others. In total, 8 objects of this subsample follow the pattern when the single ${\Gamma }_1$ or the upper ${\Gamma }_{1,h}$ photon index of the Planck spectrum coincides within the error levels with the upper ${\Gamma }_{3,h}$ photon index of the X-ray spectrum, i.e., PKS 1143-696, PG1222+216, 3C 273, 3C 279, and others. Three objects have both upper and lower photon indices of the Planck spectrum coincident with the X-rays ones: PKS 0537-286, [HB 89] 2230+114 and 3C 380; such a situation can be interpreted as if we can see the ${\Gamma }_{1,l,h}$ and ${\Gamma }_{3,l,h}$ segments in the both Planck and Swift spectra. However, for some of them, namely 3C 273, [HB 89] 2142-758, etc., the values of the lower photon indices are below 1, what can be interpreted for the radio range as a sign of the self-absorption (see Figure 1 for the 3C273 case).

The subsample with no correspondence between the photon indices is also quite significant and consists of 22 blazars. There can be different explanations for each of these objects. For instance, as shown in [14], the single synchrotron zone model is inappropriate for 3C 454.3. Mrk 501 is the HSP blazar for which we see the lower part of synchrotron hump in the Planck spectrum and the upper one in X-rays. The IC/SSC spectrum of Mrk 501 is situated above the energies we consider here (see Figure 1). Similarly, to explain the 4C +49.22 spectral properties the two-zone SSC model is needed [15]. PKS 1830-21 is a gravitationally lensed blazar and its spectra thus can be distorted by the influence of a lensing object [16]. The classification type of PKS 0521-36 is not surely BL Lac, there are some signs of a Broad Line Radio Galaxy (BLRG) also [17], and thus the accretion disk/corona counterpart in its X-ray spectrum can be quite significant. S5 0716+714 is an ISP blazar for which the significant part of the Planck spectrum lies in the self-absorbed zone and in X-rays we see a dip-like intersection of synchrotron and SSC spectra at $E_b\approx 6$ keV [8].

5. Conclusions

In the simple one-zone model of multi-wavelength radiation of radio-loud AGN the observable two-hump spectra with $\nu L_{\nu }$-maxima in low-energy (∼${10}^{-1}-{10}^4$ eV) and high-energy ($\ge {10}^7$ eV) bands can be naturally explained by the non-thermal synchrotron and IC/SSC emission of relativistic leptons, accelerated at relativistic shocks, and during magnetic field reconnections in relativistic jets. Typical power-law spectra of accelerated leptonic cosmic-rays result in similar predicted slopes or photon indices of low-energy radio and high energy X-ray and $\gamma$-ray emission. Meantime, in some radio-loud AGN Comptonised thermal X-ray luminosity of accretion disk+corona complex can be comparable to the non-thermal X-ray jet luminosity. Joint analysis of radio and X-ray spectra of such AGN open a possibility to disentangle jet and disk+corona contributions and to clarify the radiative processes in AGN. We carry out a comparative analysis of Planck radio spectra and Swift /XRT+BAT X-ray spectra for the sample of 55 beamed AGN (Blazars and Seyferts 1) from the Swift BAT 105-Month Hard X-ray Survey. For 33 of 55 AGN we confirm predicted by one-zone model coincidences of the photon indices of radio and X-ray spectra. As expected, comparison of radio and X-ray data can help to disentangle jet and disk+corona contribution in case of LSP and some of ISP radio-loud AGN, in which transition from synchrotron to IC/SSC dominant contribution take place in sub-keV region.