1. Introduction
On 14 September 2015, the Advanced LIGO detectors made the first direct detection of gravitational waves (GWs) from a binary black hole merger [
1]. The detectors had just achieved full operation after a five-year hiatus while they were upgraded from initial to Advanced LIGO. The Advanced LIGO detectors featured new technologies and new optical configuration, designed to improve the signal-to-noise ratio of GW signals across the audio frequency spectrum [
2,
3,
4]. The upgraded detectors drastically improved the sensitivity to intermediate mass black hole merger GW signals, enabling the detection of GW150914 [
5].
On 17 August 2017, the Advanced LIGO and Virgo detectors discovered gravitational waves from a binary neutron star merger with a gamma-ray-burst counterpart [
6]. This event triggered telescopes to point in the direction of the merger, in order to catch electromagnetic radiation from across the energy spectrum [
7].
Today, the detectors have progressed significantly toward the goal of achieving design sensitivity [
8]. Through the third observing run (O3), 90 confident gravitational wave detections from astrophysical compact binary mergers have been reported, along with many more low-confidence detections [
9].
Now, in the period between observing runs three and four, major infrastructure improvements known as the A+ upgrades are being installed at the LIGO detectors [
10,
11]. These upgrades are focused on lowering the fundamental noise limit of the Advanced LIGO detectors, making higher levels of sensitivity to gravitational waves possible.
Here we will review the design and performance of the Advanced LIGO detectors leading into to observing run four (O4), scheduled to begin in December 2022.
Section 2 will briefly overview the gravitational wave signals we expect.
Section 3 will overview the Advanced LIGO optical configuration and lock acquisition process.
Section 4 will review the fundamental limits of the Advanced LIGO detectors’ sensitivity, as well as the current achieved sensitivity.
Section 5 will discuss the current performance of the detectors, introducing the topics of point absorbers on optics and squeezed states of light.
Section 6 will overview the upgrades currently being installed in preparation for O4.
Section 7 will comment on future avenues for increasing detector sensitivity. Appendices
Appendix A and
Appendix B will overview the basics of the Michelson and Fabry–Pérot interferometric configurations, the fundamental building blocks of the full Advanced LIGO interferometer.
2. Gravitational Waves
A gravitational wave can be described as a small perturbation
on a flat spacetime metric
[
12,
13]:
In the transverse–traceless gauge, a gravitational wave propagating in the
z direction can be expressed as
where
is the plus-polarization gravitational wave strain,
is the cross-polarization strain, and
and
k are the frequency and wavenumber of the GW. In Equation (
2), we have defined the usual coordinate system
for the Greek indices ranging from 0 to 3. In this gauge choice, the trace of the matrix in Equation (
2) is zero, and the spacetime strain is only in the
x and
y directions, transverse to the
z direction of propagation.
Next, we will show that a gravitational wave modulates the spacetime interval
, and show how this can be interpreted as a change in length
[
14,
15]. In general, the spacetime interval between any two points is
where we have set our coordinate vector
.
Gravitational wave detectors use laser light to sense spacetime. Light always has a spacetime interval
. If we set up a test particle on the
x-axis a length
from the origin, and look at the spacetime interval
for a light wave traveling between the origin and particle when only a
wave is incident, assuming
, we obtain
Equation (8) emphasizes that, in the chosen gauge and coordinates, the passing gravitational wave modulates the light travel time between the two stationary points and . Equivalently, the GW strain can be said to modulate the x length: . Along the y-axis between the points and , the sign of the GW modulation is flipped, as seen from Equation (5): .
The differential length
in the
x- and
y-axis, assuming
, yields
Equation (10) is the usual strain-to-length relation used in GW detection based on Michelson interferometers, which feature two orthogonal optical cavities filled with laser light. This motivates the choice for extremely long interferometer arms: generally, the longer the arms, the larger the differential length change
will be. This holds as long as the long-wavelength approximation
is true: if not, Equation (10) breaks down because the GW oscillates spacetime faster than the light can complete a round trip in the optical cavities [
16].
3. Advanced LIGO Detectors
Each Advanced LIGO detector is a long-baseline laser interferometer with two 4 km-long orthogonal arms. The interferometer acts as a transducer, transforming the GW signal into observable laser power fluctuations at the antisymmetric port.
The interferometer is supported by several auxiliary subsystems required to detect gravitational waves. Auxiliary subsystems include the core optics length controls [
17,
18,
19,
20,
21,
22,
23], angular controls [
24,
25,
26,
27,
28,
29,
30,
31], high-powered stabilized laser [
32,
33,
34], vacuum system [
35,
36,
37], optics suspensions [
38,
39,
40], seismic isolation [
41,
42,
43,
44], and electronics and data acquisition systems [
45,
46,
47,
48]. This review will focus on the optical configuration and operation of the interferometers.
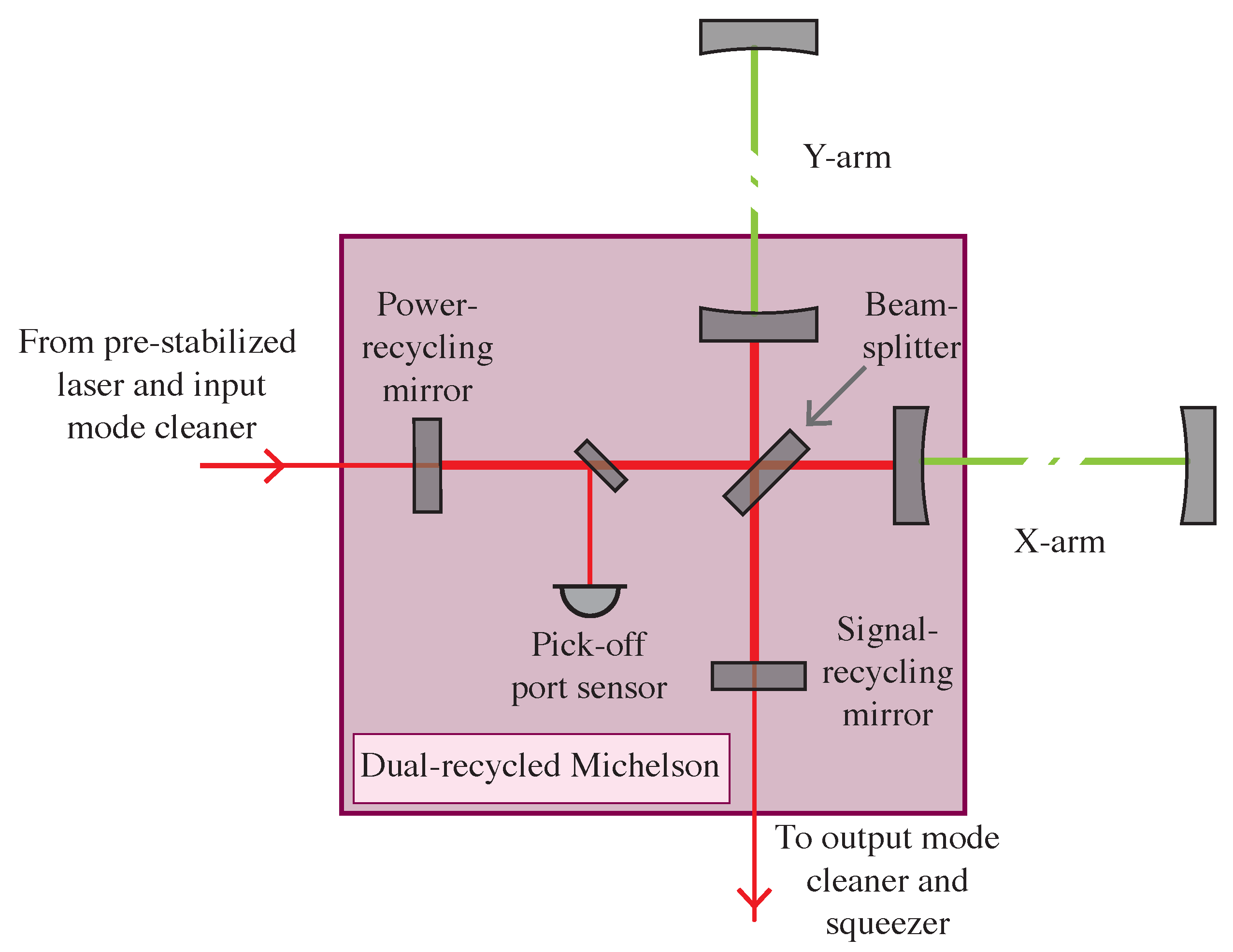
The core of the Advanced LIGO detectors are dual-recycled, Fabry–Pérot, Michelson interferometers [
2,
3], enhanced with an input and an output mode cleaner [
49,
50], and filled with pre-stabilized laser light [
32]. The entire LIGO optomechanical control system is based on the Pound–Drever–Hall frequency stabilization technique [
17].
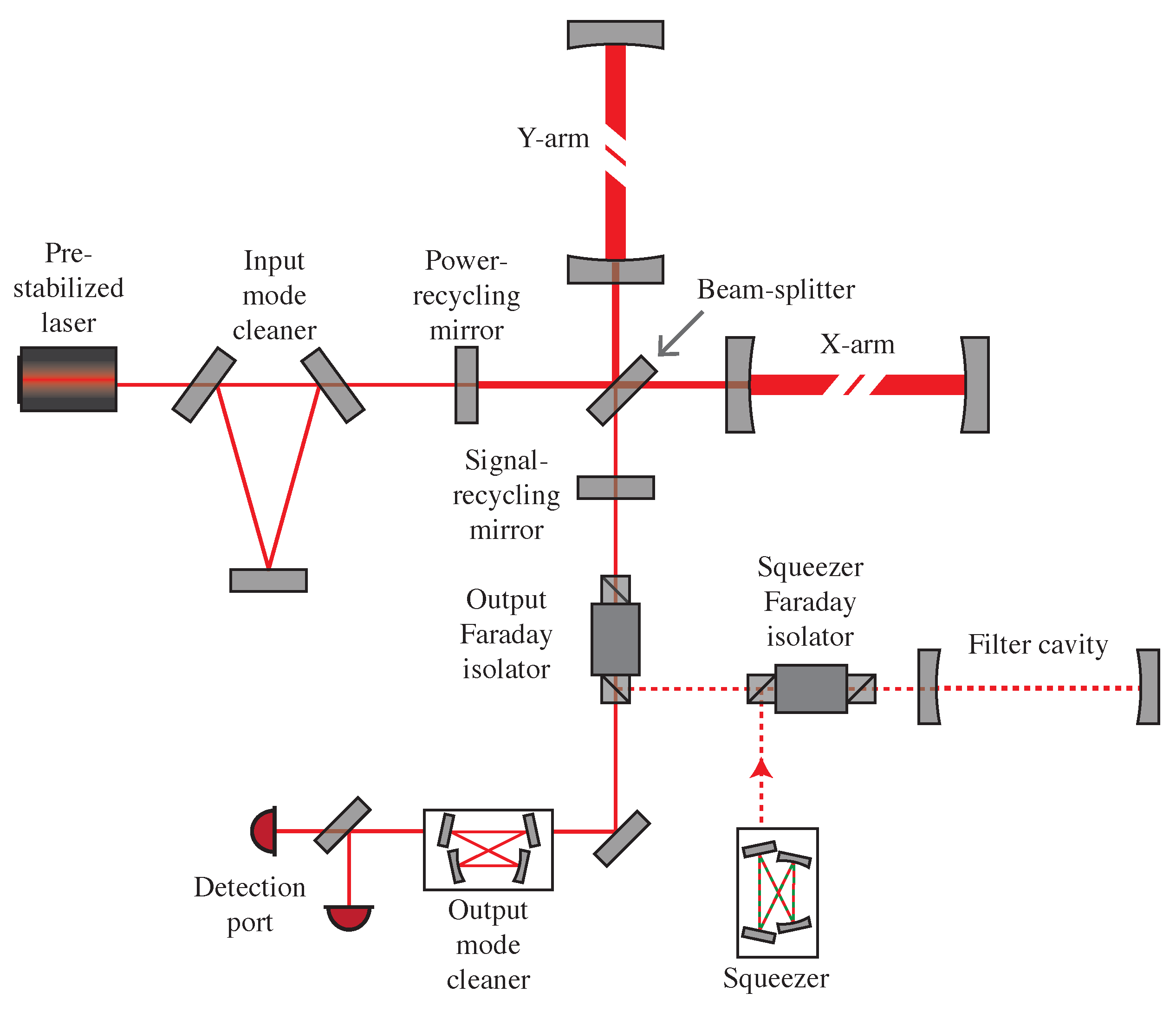
Figure 1 shows a simplified optical configuration planned for O4. The optical configuration is the same as O3, except for the addition of the 300 m filter cavity [
51,
52,
53].
In this section, we will overview the Advanced LIGO optical configuration and the lock acquisition process.
Appendix A overviews the optical components that make up the Advanced LIGO design.
3.1. Main Interferometer
The main interferometer consists of seven core optics, shown in
Figure 1: the power-recycling mirror, the signal-recycling mirror, the beamsplitter, and the four arm cavity optics known as input test masses (ITMs) and end test masses (ETMs).
The main interferometer relies on
constructive interference to build up high levels of laser power inside the 4 km Fabry–Pérot arm cavities (see
Appendix B). With more laser power built up in the interferometer, more light is modulated by a passing GW, creating a stronger detected response to GWs at the detection port.
In the Michelson interferometer formed by the two arms and the beamsplitter,
destructive interference occurs at the antisymmetric (detection) port, where the the beams from the two arms are recombined out of phase, so no light appears. At the input port, constructive interference occurs, so all the light input is reflected back toward the laser in the Michelson interferometer (see
Appendix A).
Differential phase changes in the light in each arm, such as those caused by gravitational waves, will cause light to exit out the Michelson detection port. Common phase changes, on the other hand, will have no effect on the light levels at either the input or detection port. Thus, the Michelson detection port is said to have high common mode rejection, as both frequency and intensity fluctuations in the input laser light are largely rejected from the detection port.
3.1.1. Basic Signal
The gravitational wave
signal-to-noise ratio (SNR) at the antisymmetric port is formed by the laser power signal due to GWs
, as well as the laser power noise
, i.e., fluctuations not due to GWs. The gravitational wave
for the shot-noise-dominated regime can be approximately written as
where
L is the length of the Fabry–Pérot arm cavities,
is the full power buildup in the arms,
is the duration of the GW signal in the detector bandwidth,
is the laser wavelength, and
h is the GW strain amplitude. The full detector response is derived in [
54,
55], and expanded upon in [
23,
56,
57,
58]. A more complete understanding of detector signal and noise processing can be found in [
59,
60].
Several major considerations in detector design are captured in Equation (
11). First, the simplest way to amplify the signal is to extend the arm length
L. The main limit on making detectors longer is the cost of the facility, particularly the evacuated beamtube, which currently limits the LIGO detectors to the 4 km scale. Maximizing the arm power
increases the detectable laser signal created by GWs, and is limited by input power and losses in the interferometer from absorption and scatter. Reducing the detector wavelength
would naïvely increase sensitivity to GWs, but would require all major detector infrastructure, such as the source laser, optical coatings, substrates, and photodetectors, to perform at or better than the current noise levels.
3.1.2. Dual-Recycling
Dual-recycling refers to the two recycling cavities formed by the mirrors at the input and output of the main interferometer [
61,
62,
63,
64]. The mirror at the input is the
power-recycling mirror, and is used to reflect light back into the main interferometer, enabling greater levels of light circulating inside the interferometer [
55,
65,
66]. The mirror at the output is the
signal-recycling mirror, and is used to broaden the detector bandwidth [
54].
The Advanced LIGO recycling cavities are designed to be geometrically stable to better control spatial mode of the beam entering and exiting the Michelson [
67], although point absorbers on the mirrors are suspected of polluting the main spatial mode (see
Section 5.3.2). Control schemes for the interferometer degrees of freedom associated with the recycling cavities have been designed and implemented for length [
18,
19,
20,
21,
23] and angular controls [
26,
29,
30,
68].
3.1.3. Squeezer
Heisenberg uncertainty in the form of shot noise and radiation pressure noise (
Section 4.2) limits the sensitivity of the interferometer [
69,
70]. The
squeezer is a squeezed vacuum source, and refers to the optics producing entangled photons for injection into the antisymmetric port of the interferometer [
71,
72,
73,
74]. The ensemble of entangled photons produce a quantum
squeezed-vacuum electromagnetic field. By squeezing the quantum vacuum, quantum shot noise can be lowered across the bandwidth of the detector. This is known as
frequency-independent squeezing.
The filter cavity shown in
Figure 1 will enable
frequency-dependent squeezed light injection. The results of squeezing in O3 are explained in
Section 5.4. The filter cavity is explained further in
Section 6.3.
3.1.4. Detector Bandwidth and Linewidth
The LIGO
detector bandwidth refers to the frequency at which the differential arm (DARM) frequency response begins falling off. This value is also known as the
DARM coupled-cavity pole or simply the
DARM pole. This frequency is defined primarily by the DARM coupled cavity, which is formed by the arm cavities and the signal-recycling cavity [
23]. As mentioned in
Section 3.1.2, the signal recycling mirror is locked exactly off-resonance to broaden the detector bandwidth, in a scheme known as
resonant-sideband extraction [
54,
56]. During mid-2021 locking, the detector bandwidth at LIGO Hanford was about
.
Similarly, the
detector linewidth refers to the full-width half-maximum of the laser frequency noise when the detector is locked. With a long-baseline, high-finesse interferometer such as Advanced LIGO, this is identical to twice the frequency at which the common arm (CARM) frequency response begins falling off. This is known as the
CARM coupled-cavity pole or the
CARM pole. The CARM coupled cavity is formed by the arm cavities and the power-recycling cavity, which in this case is locked on-resonance to enhance the resonating power [
23]. This, paired with the
-long baseline, makes the linewidth very small, and the laser ultrastable in the detector bandwidth [
75]. The detector linewidth is estimated to be about
.
3.1.5. Calibration
Calibration is the process of converting the detector output
into gravitational wave units of strain
h [
76,
77,
78,
79,
80,
81,
82]. The calibration reference is the
photon calibrator, which uses an auxiliary laser to apply a known force on the optics via radiation pressure [
83,
84]. The O3 calibration response upper limit on systematic error and associated uncertainty is ∼11% in magnitude and ∼9
in phase (
confidence interval) in the sensitive frequency band 20–2000 Hz [
78,
79]. The systematic error alone is estimated at levels of <2% in magnitude and <4
in phase [
79].
Newtonian calibrators, which employ rapidly spinning masses near the optics, are also under development [
85,
86,
87]. During O3, a Newtonian calibrator with a quadrupole and hexapole was installed at Hanford, and successfully induced motion on the X-end test mass (ETMX) [
88]. Due to problems with precision installation and distance uncertainty analysis, the Newtonian calibrator will not be pursued by LIGO as a precision calibration instrument in O4.
3.2. Input Mode Cleaner
The input mode cleaner is a three-mirror, 33 m round trip triangular cavity used to further stabilize the frequency, intensity, and spatial mode content of the input laser before it enters the main interferometer [
49]. The RMS laser frequency noise is limited by the linewidth of the interferometer, which is extremely low (1.2 Hz). The laser frequency is locked to the input mode cleaner length, providing high-gain high-bandwidth feedback (∼100 kHz) to massively suppress frequency noise intrinsic to the NPRO laser [
20,
75,
89]. A small sample of the transmission through the input mode cleaner is used to stabilize the intensity of the laser input into the main interferometer.
3.3. Output Mode Cleaner
The output mode cleaner is a four-mirror, 1.1 m round trip bowtie cavity used to transmit only the main interferometer GW signal [
50,
90,
91,
92].
The GW readout scheme is known as
DC readout [
22,
93]. A picometer-scale offset in the differential arm length is deliberately introduced and is controlled to let 20 mW of light leak out to the detection port. This light used as a local oscillator, beating against the GW signal light, rendering it detectable on a photodetector.
The radio-frequency sidebands used for controlling interferometer degrees of freedom, and higher-order modes from the main interferometer, are both reflected away from the detection port by the output mode cleaner. Backscatter, i.e. reflection from the output mode cleaner along the main beam path, is rejected by the output Faraday isolator.
3.4. Lock Acquisition
The lock acquisition process is a sequence of steps taken to bring the interferometer from a free-swinging uncontrolled state to an observation-ready state [
2,
21,
94,
95]. The optical cavities shown in
Figure 1 must be held on resonance (locked) and in the correct alignment. This section will review the lock acquisition process used during O3, which was also described in [
8].
Each cavity is locked using the Pound–Drever–Hall (PDH) technique [
17]. Four sets of radio-frequency (RF) phase-modulated sidebands are added to the input laser using an electro-optic modulator (9 MHz, 24 MHz, 45 MHz, 118 MHz). The RF sideband frequencies are chosen to be resonant in some cavities and antiresonant in others. The RF beat notes are detected on reflection of the interferometer, at the antisymmetric (detection) port, or through a pick-off on transmission of the power-recycling cavity. RF photodetectors at each port are then used to sense the length and angular degrees of freedom.
The lock acquisition process is coded using the Guardian finite state machine [
47]. During O3, the lock acquisition sequence took roughly 25 min, but depends strongly on environmental factors including seismic activity and wind speed [
8]. The lock acquisition sequence is always undergoing improvements in speed and versatility.
3.4.1. Prestabilized Laser and Input Optics
The first step of the lock process is to ensure a laser stabilized in frequency, intensity, and spatial mode is entering the main interferometer. Inside a clean room, several important optical components reside on an optical table, making up a full system known as the
pre-stabilized laser, or PSL [
32]. Included in the pre-stabilized laser is a 2-Watt NPRO 1064 nm laser source, a high-powered amplifier to increase the input laser power, a pre-mode cleaner to clean the the laser beam spatial mode, a reference cavity to stabilize the laser frequency, and two photodetectors on a pickoff to stabilize the laser intensity.
Next, the pre-stabilized laser beam is input onto the first in-vacuum, suspended cavity, the input mode cleaner [
49]. The beam is further cleaned and stabilized by the input mode cleaner (
Section 3.2), and traverses the
input Faraday isolator which prevents the formation of a parasitic interferometer and provides access to the interferometer reflected beam. Finally, the beam is incident on the first mirror of the main interferometer, the power-recycling mirror.
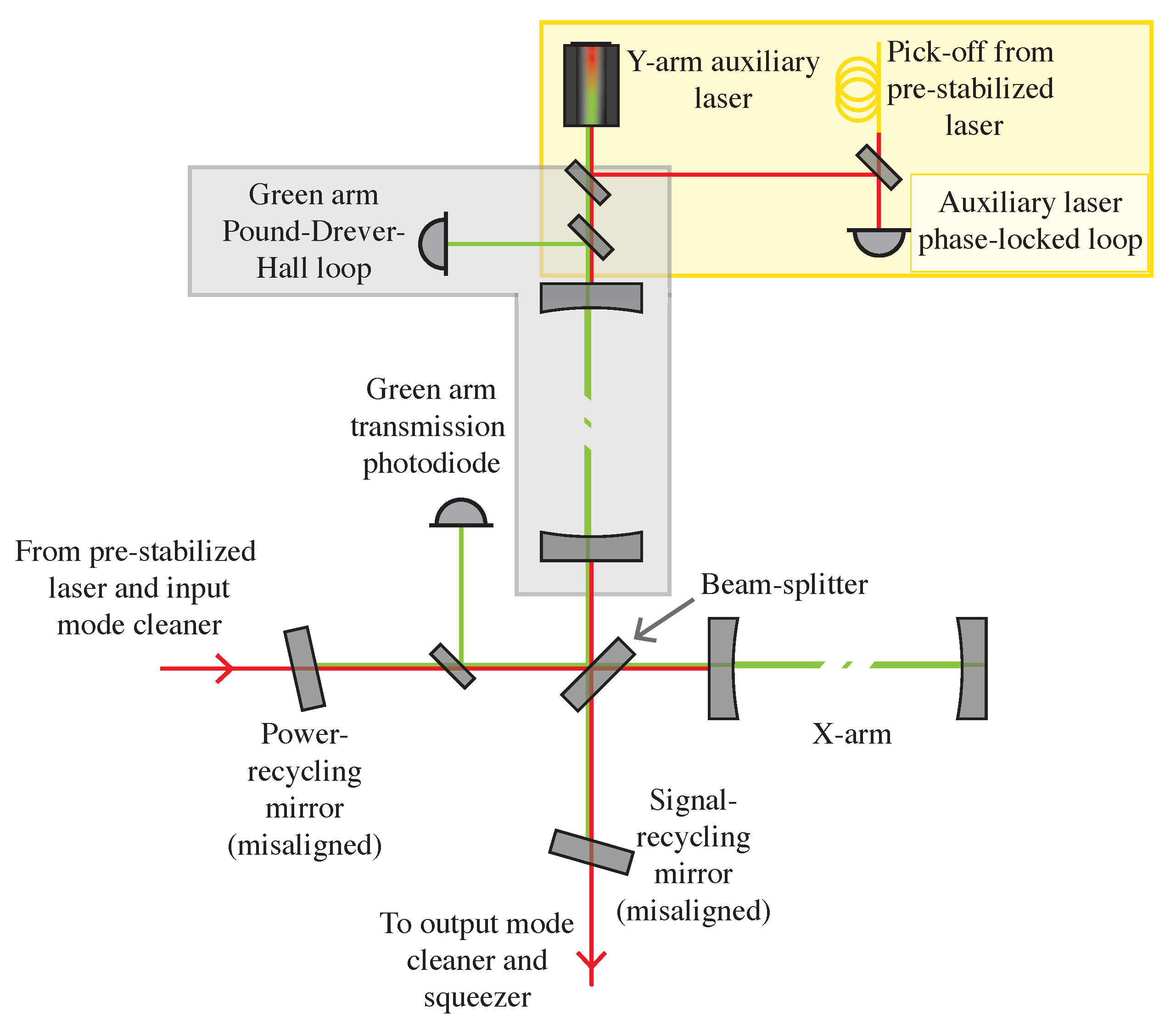
3.4.2. Arm-Length Stabilization
Next, the arms are brought under control using green light, known as the
arm-length stabilization system [
96,
97,
98]. Green light is used so that the arm lengths can be independently controlled while infrared is used to lock the corner.
Figure 2 shows the interferometer configuration during arm-length stabilization.
The ALS system consists of two auxiliary green laser sources at each end station. The end station lasers are phase-locked to the main laser, then frequency-doubled to generate 532 nm (green) light which is injected into the arm cavities. Each ALS laser is then locked to their respective arm lengths.
3.4.3. Dual-Recycled Michelson Locking
The next step in the lock acquisition is to lock the dual-recycled Michelson interferometer (DRMI) with infrared light. The dual-recycled Michelson interferometer is formed by the five optics in the corner: the power- and signal-recycling mirror, beamsplitter, and input test masses to the arm cavities. Crucially, the end test masses are
not included.
Figure 3 shows the interferometer configuration during dual-recycled Michelson locking.
During the green locking of the arms, the corner optics are purposely misaligned. Then, the arms are purposely held off-resonance for infrared using the information from the green lock. Finally, the three corner degrees of freedom (the Michelson length, power-recycling length, and signal-recycling length) are brought under control simultaneously using the
3f-PDH locking technique [
96,
99]. As the interferometer arms are brought onto resonance for infrared, the usual 1f PDH locking signals flip sign, which would cause the interferometer corner to lose control. The 3f locking signals do not suffer from the sign flip, and are used to maintain control while the arms are brought onto resonance.
3.4.4. Full Interferometer Locking
Having locked the dual-recycled Michelson with infrared light, the arms are brought onto resonance for infrared light. As the arms move into resonance, ∼10 of infrared laser power begins resonating in each interferometer arm.
In O3, the noise in the arm length stabilization system is around ∼2
[
100,
101]. However, the linewidth of the interferometer is ∼1
. This renders it impossible to directly transition from ALS to full interferometer PDH locking [
94,
96].
Therefore, the infrared transmission through the arms is used as an error signal to sense the common arm length as it is brought to full power. Once full power is very nearly reached, the common and differential arm length error signal is transitioned to the PDH error signal.
Once the full interferometer is fully locked on infrared, the corner degrees of freedom are switched from 3f to 1f PDH error signals, differential arm control is switched to DC readout [
22], and all the angular controls are turned and allowed to converged on the best alignment in preparation for high power.
3.4.5. High-Power, Low-Noise Lock
Until this point, the laser input power is kept at 2 W. Once full lock is achieved, the input power is increased to the highest achievable power.
At this point, the suspension actuators are brought from acquisition mode—with high range and high noise—to low-noise mode, and the control loop bandwidths for the length and angular controls are cut off to achieve the lowest noise state.
Finally, squeezed light is injected to further reduce quantum shot noise; the squeezer subsystem is further discussed in
Section 3.1.3 and
Section 5.4. The interferometer is now ready to observe gravitational waves.
During full lock, the circulating power in the interferometer heats the optics until the heat absorbed and emitted reaches a steady state. This heating process is known as
thermalization, and takes about 30 minutes after full lock to reach a steady-state. Thermalization affects many aspects of the interferometer, most notably the radius of curvature of the main optics, which affects the scattering of laser light out of the laser’s fundamental spatial mode [
102]. The optical gain of the interferometer is also affected, although this is tracked via calibration lines [
81].
The
thermal compensation system is a subsystem dedicated to monitoring and controlling negative changes in the interferometer at full power [
103]. The thermal compensation system is comprised of ring heater actuators to adjust the test mass optics radii of curvature, spatially tunable
laser projectors to heat optical surfaces, and Hartmann wavefront sensors to monitor optic surface changes. This system is primarily used to repair spatial distortions in the main beam, enabling higher power buildup inside the interferometer. It is also used to minimize measured noise couplings to the gravitational wave data channel.
4. Detector Sensitivity to Gravitational Waves
Detector sensitivity refers to the gravitational wave signal-to-noise ratio. The GW signal is imprinted on the laser light resonating in the detector, and sensed by photodetectors at the detection port.
Noise is any laser power fluctuations sensed at the detection port that are not due to gravitational waves. The are two main types of noise: fundamental and technical.
Fundamental noise is intrinsic to the design of the detector. Fundamental noises include quantum uncertainty, thermal noise in the optics, seismic noise, and Newtonian noise. These often cannot be improved without major upgrades to the detector, such as increasing the arm length or replacing the optical coatings.
Technical noise is not intrinsic to the detector design, but can limit the performance of the detectors. Technical noises are wide in variety, and most detector work is dedicated to eliminating it. Important examples of technical noise include
Length and angular controls noise;
Laser frequency and intensity noise;
Scattered light;
Residual gas noise;
Photodetector dark noise;
Electromagnetic noise.
All of these noise sources and more are considered carefully in [
8], but controls noise is the main technical limit to gravitational wave detectors at low frequencies.
A
noise budget is a way of quantifying the contributions to the measured noise curve [
104].
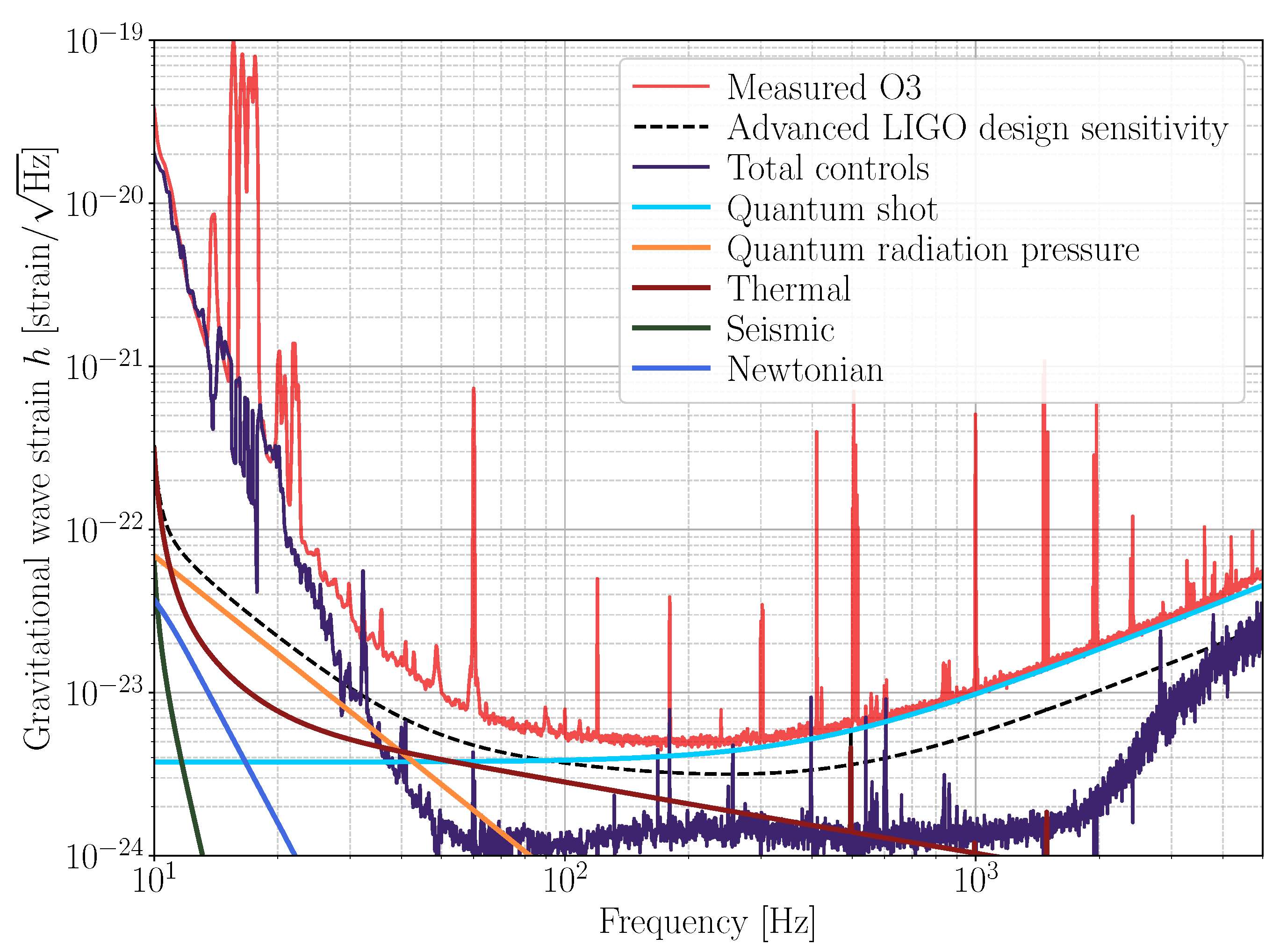
Figure 4 shows a simplified noise budget of the O3 LIGO Hanford interferometer. To produce the measured noise curve in
Figure 4, the time series of the detector output is Fourier-transformed to represent the frequency content of the noise as an amplitude spectral density (ASD), then calibrated into units of gravitational wave strain
h.
4.1. Design Sensitivity
Design sensitivity is the ultimate sensitivity Advanced LIGO is expected to achieve given the detector configuration and estimated performance. It is formed by the sum of all fundamental noises. Design sensitivity has not yet been achieved by the current detectors, due to technical noises and insufficient power buildup.
Figure 4 shows the Advanced LIGO design sensitivity as the black dashed curve [
2,
105]. No squeezing is included in the design sensitivity curve. This affects the quantum noise, lowering the design’s strain-referenced quantum shot noise but increasing the quantum radiation pressure noise (
Section 4.2).
For design sensitivity, 125 W of laser input power is assumed, resulting in of circulating power in the arm cavities. The O3 input power was much lower, ∼34 W at Hanford and ∼38 W at Livingston.
4.2. Quantum Noise
Fluctuations of the vacuum electric field at the interferometer readout port impose the main fundamental limit to the interferometer sensitivity [
54,
69,
70,
106]. Quantum noise appears as
shot noise and
quantum radiation pressure noise.
4.2.1. Shot Noise
In general, shot noise arises from Poisson fluctuations in the arrival time of discrete objects. In the case of interferometers, the discrete objects are photons at the detection port.
Heisenberg uncertainty in the measured laser amplitude at the detection port cannot be distinguished from actual mirror motion due to GWs. The power detected on the photodetector is made up of a finite number of photons which arrive randomly and independently of one another, leading to a detected white noise amplitude spectral density
proportional to the total power
on the photodetector:
where
is the fundamental angular frequency of the laser.
Equation (
12) is white noise in units of
, meaning it has no frequency dependence. However, when this noise is referenced against the GW detector response to yield units
, it begins to rise above the detector bandwidth of around 450 Hz. In
Figure 4, the cyan curve shows the estimated GW-referenced quantum shot noise.
4.2.2. Radiation Pressure Noise
Quantum radiation pressure noise (QRPN) is displacement noise arising from amplitude fluctuations of the electric field in the arms. These amplitude fluctuations, again due to Heisenberg uncertainty, mean the arm power is spontaneously increasing and decreasing. This induces forces on the optics via radiation pressure, moving the optics in the arm [
69].
For a Michelson interferometer with Fabry–Pérot arms, the displacement amplitude spectral density due to QRPN
can be described as [
55]
where
is power on the beamsplitter,
m is the mirror mass,
L is the arm length,
is the laser frequency,
is the arm pole describing the number of reflections inside the Fabry–Pérot cavity, and
f is the GW signal frequency. Equation (
13) is plotted in
Figure 4 as the orange curve.
4.3. Thermal Noise
Thermal noise refers to the actual displacement in the mirrors induced by thermal fluctuations in the atoms making up the test mass suspension, substrate, and optical coatings [
107,
108,
109,
110]. In general, thermal noise increases with mechanical loss in the materials making up the optics, as described by the fluctuation-dissipation theorem [
111,
112,
113].
For LIGO test masses, the observable fluctuation is the optic displacement due to dissipation from thermal excitations. The dominant source of mechanical loss, and thus thermal noise, is the optical coatings deposited on the optical surface. For a single coating with thickness
d, the dissipated power and coating displacement noise
due to thermal fluctuations can be calculated [
114,
115]:
where
T is temperature,
is the coating Poisson ratio,
d is the coating thickness,
E is the Young’s modulus,
w is the beam radius, and
is the mechanical loss angle of the coating.
The actual LIGO coatings have more than a single layer, and their thermal noise properties are measured directly in the lab [
116,
117]. Other thermal noise contributions include thermal noise vibrations in the optic suspensions [
113,
118]. The total thermal noise estimate, largely from coatings at high frequency and suspensions at low frequency, are plotted as the maroon line in
Figure 4.
4.4. Seismic Noise
Seismic noise is optical displacement due to the motion of the Earth physically shaking the mirrors resting on the Earth’s surface. Unmitigated, the vibrations of the Earth are much larger than LIGO optics can tolerate. Enormous effort is put into isolating the core optics from the ground vibrations, particularly in the GW-sensitive range. Additionally, earthquakes and windy conditions can make holding the detector lock impossible.
The main LIGO optics are suspended from a quadruple-stage pendulum chain to passively isolate them from ground motion [
39]. These pendulums are suspended from active seismic isolation platforms [
43] which themselves are supported by hydraulically actuated pre-isolation structures [
42].
Ultimately, the linear coupling due to seismic motion is largely suppressed in the GW-detection band, as seen by the green trace in
Figure 4. This curve comes from the measured differential displacement of the seismic isolation platforms, multiplied by the isolation of the suspensions which hang from those platforms.
However, at very low frequencies (<1
), below the pendulum resonance frequencies, seismic motion still dominates. Worse, high motion at very low frequencies can couple to higher frequencies via bilinear or nonlinear coupling mechanisms. Work continues to suppress seismic motion further, via monitoring systems and more advanced control schemes [
44].
4.5. Newtonian Noise
Newtonian noise, or gravity-gradient noise, is from fluctuations in the ground creating changes in the local gravitational potential around the optics, moving them [
119,
120,
121]. Newtonian noise is related to seismic noise, but the coupling mechanism is not from ground motion propagating down a pendulum chain, but changes in ground density due to seismic activity. Therefore, Newtonian noise cannot be isolated away with longer pendulums, but can be monitored and actively subtracted [
122,
123,
124].
Upper limits have been placed on Newtonian noise contributions to LIGO, but have never been directly observed [
125]. The blue trace in
Figure 4 represents an estimate of Newtonian noise coupling to the GW spectrum given local seismic activity, but is highly uncertain.
4.6. Controls Noise
Controls noise is the noise associated with the sensor and feedback system required to hold the interferometer optics on resonance. This includes both length control loops, which manage the optic’s position [
18,
19,
20,
21,
22,
23,
75,
93], and angular control loops, which point the optics at each other [
24,
25,
26,
27,
28,
29,
30,
31,
68].
Controls noise is the result of multiple effects. The control loops are required to suppress real motion in the optics, known as
displacement noise. The controllers must be strong enough to hold the optics in place. To hold the optics in place, electromagnetic coil actuators or electrostatic drives are employed [
39,
40].
However, the controllers must know where to hold the optics. The Pound–Drever–Hall error signals hold the information about where each optic must be held [
2,
3,
17]. The PDH error signals are detected with radio-frequency photodetectors (RFPDs). These RFPD sensors are limited by sources of
sensor noise, largely shot noise, but also potentially “dark” noise and analog-to-digital conversion noise. Sensor noise is indistinguishable from actual displacement noise, and dominates most control loop noise floors above ∼50
.
4.6.1. Tradeoff
This sets up the fundamental tradeoff involved in LIGO control loop design. Make the controllers too strong, and sensor noise will be reinjected into the controller actuators, creating true, unintended displacement. Make the controllers too weak, and excess displacement noise will pollute the spectrum and make it difficult to hold the interferometer on resonance.
LIGO controllers are designed to be overtly strong during the locking phase, in order to hold the optics on resonance and avoid lock losses. This injects excess sensor noise. Near the end of the locking process, the loop bandwidths are reduced, weakening the hold but avoiding sensor noise injection.
4.6.2. Feedforward
Even with loop bandwidth reduction, optical cross-couplings cause controllers to inject noise into other loops [
23]. In fact, sensor noise in the auxiliary length degrees of freedom is injected into the GW spectrum, causing a major limitation.
However, we have information on this sensor noise, since we are constantly measuring it. Therefore, we can
feedforward the sensor noise, with a negative sign, to the interferometer optics [
8]. This creates an optic displacement which counteracts the displacement caused by auxiliary length sensor noise.
4.6.3. Results
Controls noise dominates the GW spectrum at low frequencies, as seen by the purple curve in
Figure 4. This curve represents the sum of the noise measured via excess power injection into each length, angular, and laser control loop [
8].
The problem is more difficult than summarized above. Optical cross-couplings affect not just the GW spectrum, but all degrees of freedom. Bilinear and nonlinear couplings can be hard to fully quantify, even with excess power injections. Damping loops on suspensions and seismic isolation platforms that reduce large low-frequency seismic motion can leak noise into higher frequencies [
15].
Work to lower controls noise further is the highest priority of the commissioning team. A more advanced feedforward scheme is under consideration to reduce angle-to-length coupling. Multiple-input multiple-output controls models are under development. Controls noise for the output mode cleaner are being analyzed. Efforts to better quantify important interferometer parameters, such as optical losses and beam mode matching, are being implemented.
5. Current Performance of the Advanced LIGO Detectors
The performance of the detectors is their overall sensitivity and uptime to astrophysical gravitational wave events. There are currently 90 gravitational wave candidate detections, consisting of binary mergers across the universe from the first three observing runs (O1, O2, and O3) [
9].
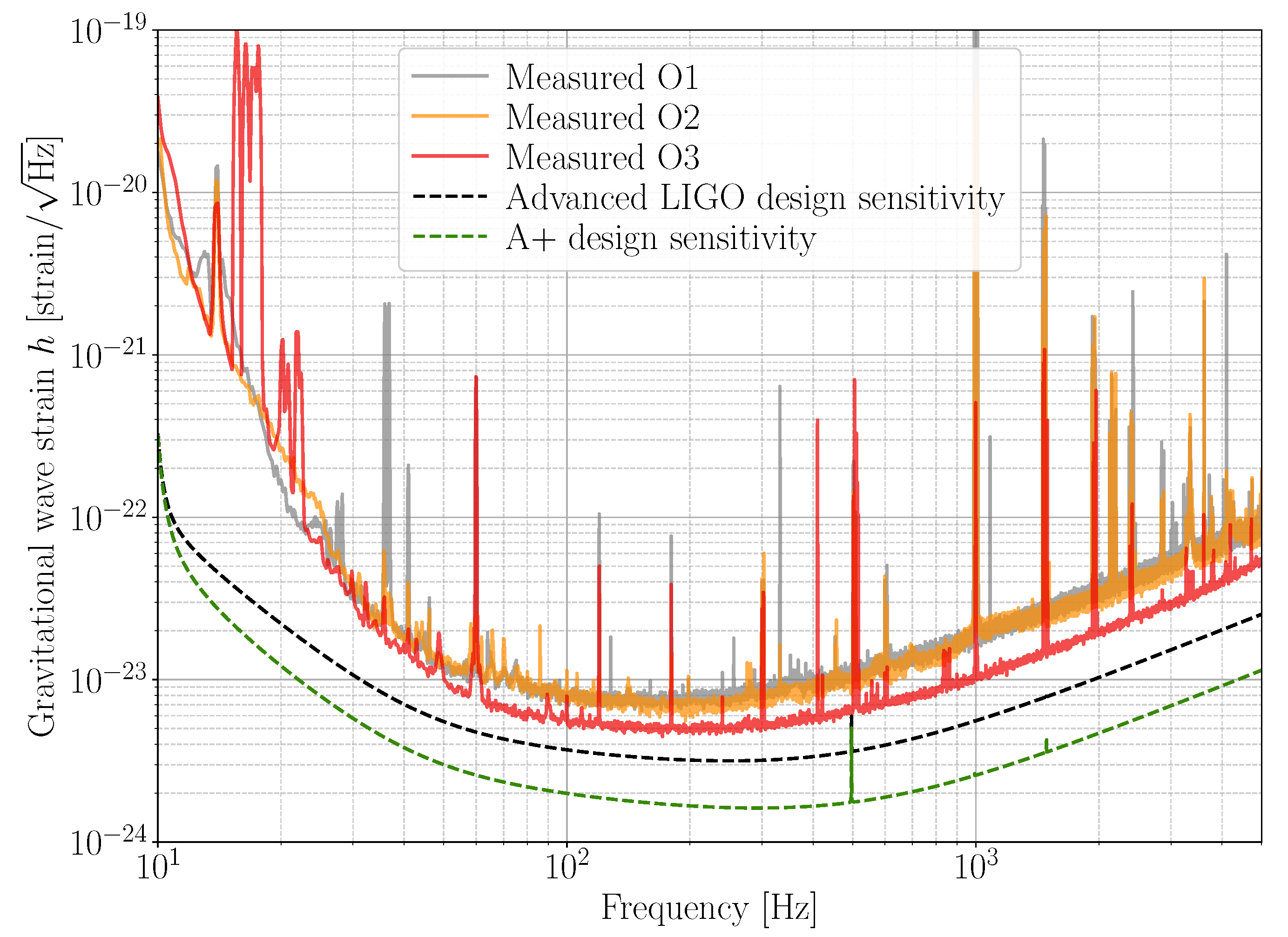
Figure 5 shows representative GW sensitivity spectra for each observing run.
In this section, we will review the astrophysical range and duty cycle of the detectors, discuss the power budget and major technical limitations involved with high power interferometry, the status of squeezing in LIGO interferometers, and environmental disturbance sources and mitigation efforts.
5.1. Astrophysical Range
A common performance gauge for the LIGO interferometers is the
binary neutron star inspiral range, or simply the
range [
128,
129,
130]. The range refers to the luminosity distance at which the detector is sensitive to a
neutron star merger with an SNR of 8, averaged over sky location and GW polarization.
During O3, the LIGO Livingston Observatory achieved a median binary neutron star range of 134 Mpc, while the LIGO Hanford Observatory achieved a median range of 111 Mpc [
8]. The detector sensitivity to heavier binary black holes extends much further than binary neutron stars, since the signals produced by black hole mergers are stronger.
5.2. Duty Cycle
The duty cycle is the uptime of the detectors, in other words, how often the detectors are sensitive to GWs. Also important is coincident observation time, where both the Hanford and Livingston detectors are online at the same time. Coincident observation is critical for extracting maximum information from detections, particularly, verifying the detection is not a false positive and generating sky location data [
10].
During O3, both detectors were operational for a greater percentage of the time compared to the previous two observing runs, with Hanford and Livingston achieving observation duty cycles of 74.6% and 77.0%, respectively, with coincident observation 62.2% of the time [
8].
5.3. High-Power Interferometry
Gravitational wave observatories are dedicated to pushing the limits on maximum circulating laser power. In Equation (
11), we see that as power in the arms
increases, so does the detector response to gravitational waves.
The biggest limit on power buildup in the interferometer is imposed by the presence of small, absorbing defects in the test mass optical coatings, known as point absorbers [
131]. In this section, we will review how we quantify the power budget in the interferometer, what point absorbers are and how we can mitigate their effect, and other technical problems with high power, including parametric instability and radiation pressure-based optomechanics.
5.3.1. Power Budget
Laser power must be conserved inside the interferometer, i.e.
. A
power budget is a record of where the input power of an interferometer is lost in the interferometer steady-state at full lock. Losses can be from absorption by the optics themselves, or scattered off imperfections in the mirror surfaces into higher-order modes [
102,
132].
For the carrier laser light, thanks to the common-mode rejection of the Michelson, we can model the interferometer power buildup using a simple plane–wave
coupled cavity, i.e. three-mirror cavity [
65,
66]. The three mirrors are the power-recycling mirror, an input test mass, and an end test mass.
The laser resonates inside the coupled cavity, building up power until losses exactly equal the input power. In the coupled-cavity model, there are two main sources of power losses: power-recycling losses
and round-trip arm cavity losses
. There is also the promptly reflected power
and transmitted power through the arms
. The transmission of the power-recycling mirror
must be strategically selected to be
impedance-matched with the overall interferometer losses, or else too much carrier light will be promptly reflected [
2,
3,
61,
65,
66].
A convenient proxy for power buildup in the interferometer is the
power-recycling gain, or PRG. The power-recycling gain
can be expressed as [
131],
where
is the power-recycling mirror amplitude transmission,
is the power-recycling mirror amplitude reflectivity,
is the end test mass amplitude transmission,
is the arm power gain ∼265,
is the round-trip arm cavity loss,
is the power-recycling cavity loss. Equation (
15) shows how losses in the arms matter more than losses in the power-recycling cavity, because the arm gain
scales the arm loss to account for the multiple reflections inside the arm cavity.
For LIGO Hanford in mid-2021, preliminary results suggest that interferometer round-trip losses
may now be lower than assumed for Advanced LIGO design [
2,
133,
134]. There are metrics other than the PRG for measuring the power buildup in the interferometer, including the total interferometer reflection measurement and direct radiation-pressure-based arm power measurement [
8,
135]. These provide more information on the true power budget, and indicate that the simple plane-wave coupled-cavity model is not sufficient to fully explain power in the interferometer.
5.3.2. Point Absorbers
When the beam circulating in the interferometer encounters the test mass it uniformly heats an area of the test mass across its Gaussian profile. The absorber power in this uniform cross section is determined by the power in the beam and the properties of the fused silica and the optical coating.
Point absorbers are submillimeter points of nonuniform, anomalously high optical absorption found on the test masses. A full discussion of the point absorbers in LIGO can be found in Brooks et. al. [
131]. Point absorbers have been identified on multiple test masses in LIGO during the first three observing runs. Their deformation is visible on Hartmann wavefront sensors, an auxiliary sensing system which measures the test mass surface and substrate deformation during power up. Point absorbers have also been imaged on test masses which have been removed from the interferometers, using dark-field microscopy.
The origin of point absorbers is under active investigation. Point absorbers have been observed in the lab on spare test masses which have never been exposed to high optical power. They appear to be embedded in the optical coating and are thought to originate during the coating deposition process. Initial elemental analysis of some point absorbers show high concentrations of aluminum.
The circulating optical power in the interferometer heats up a point absorber, causing light to be scattered out of the arm cavity or into higher-order cavity modes. Depending on the geometry of the cavity, the higher-order modes may be resonantly enhanced, causing additional loss to the fundamental mode and coupling unwanted modes to the GW detection port. As the input power to the interferometer increases, the power scattered into higher-order modes increases, as does the optical loss. Point absorbers on the input test mass affect the arm cavity gain and power-recycling cavity gain, while the end test mass point absorbers only affect the arm cavity. The thermal timescale of losses due to point absorbers are roughly an order or magnitude faster than that of uniform absorption. Point absorbers have been observed to increase coupling of scattered light, laser frequency noise, and laser intensity noise to the gravitational wave readout [
8].
To avoid the negative effects of point absorbers, the interferometer alignment can be adjusted such that the beam spot overlap with the point absorbers is minimized. In O3, both Hanford and Livingston operated with the spot position offset from center by ∼10 s of millimeters for certain test masses with known point absorbers [
131,
136]. However, beam spot position offsets cannot exceed the size of the optic itself (
diameter for test masses), and even small offsets risk scattering excess light out of the fringe of the main Gaussian beam (∼12
diameter).
5.3.3. Parametric Instability
Parametric instabilities (PIs) are mechanical modes of the test masses that sap energy from the fundamental mode, putting it into higher-order optical modes of the resonating laser [
137,
138]. As the mechanical modes begin to oscillate, more laser light is scattered into the higher-order optical mode, further increasing the mechanical oscillations in runaway positive feedback loop.
Mitigation of PIs is essential to avoid runaway mechanical oscillations causing locklosses. Ring-heaters on the core optics can change the radius of curvature of the optic, which in turn changes the eigenfrequency of the cavity higher-order modes, eliminating the overlap between the optical and mechanical mode frequencies. The electrostatic drive can be used to directly damp parametric instabilities that ring up at high circulating power [
139,
140,
141].
During O1 and O2, the ring-heaters and electrostatic drive damping were the only ways to combat PI ringups. However, with the higher circulating laser power in O3, dozens to hundreds of potential PIs were expected.
Therefore, acoustic mode dampers (AMDs) were installed on all core test masses [
142]. AMDs are mechanical tuned mass dampers glued to the sides of the test mass, with a piezoelectric transducer and shunt resistor designed to dissipate mechanical energy by converting it to electric charge and running it through the resistor. The AMDs passively damp the mechanical oscillations, making it far more difficult for PIs to ring up.
Parametric instabilities have been observed even with the AMDs installed, as expected, but the overall parametric gain of all PIs is drastically reduced. This makes the problem far more tractable to solve with the ring-heaters and electrostatic drive damping. This work enables the higher circulating laser power seen in O3 and beyond (
Section 5.3.1).
5.3.4. Radiation Pressure Optomechanics
With the advent of high-power interferometry comes a new era of radiation-pressure-based optomechanics, particularly optical springs and optical torques for suspended optical cavities. The laser power in the interferometer arm cavities couples the optic suspensions together such that the length and angular degrees of freedom must be considered together. As circulating laser power increases, the dynamics of the optomechanical plants also change, presenting an additional challenge to high-powered interferometry.
Optical springs occur when the radiation pressure in a cavity creates a non-negligible restoring force (or non-restoring force) that affects the usual pendulum response [
143,
144,
145,
146]. The differential arm degree of freedom at Hanford has exhibited an optical spring effect since O1 [
57,
77,
78,
82].
Optical torques refer to radiation pressure causing additional torques on the mirrors that affect the usual pendulum angular response [
27]. The
hard modes refer to the angular modes where the torsional stiffness increases due to the laser power torques. Likewise, the
soft modes are angular modes where the torsional stiffness decreases due to the laser power torques. One set of these modes must be statically unstable.
The radius of curvature of the test masses plays a strong role in governing the stability of the angular modes. In Advanced LIGO, the soft modes have been chosen to be statically unstable, as they have a lower stiffness parameter and are easier to manage with a feedback control loop. Optical torques have been observed in initial LIGO [
28,
30], and accounted for in Advanced LIGO design [
29].
5.4. Quantum Squeezing
As explained in
Section 3.1.3, quantum shot noise limits the sensitivity of interferometers to GWs. A squeezed light source reflected off the output port of the interferometer can decrease quantum shot noise, increasing the detector sensitivity.
Frequency-independent squeezing was injected into both LIGO detectors for the duration of O3, reducing quantum shot noise and increasing the expected gravitational wave detection rate by the cube of the range increase (40% at LIGO Hanford Observatory and 50% at LIGO Livingston Observatory) [
71]. Though the squeezer subsystems at both LIGO sites are identical, small differences in the optical loss in their beam paths result in slightly different squeezer performance. During O3, LIGO Hanford Observatory measured 2.0 dB of shot noise improvement from squeezing and LIGO Livingston Observatory measured 2.7 dB in the 1.1–1.4
regime [
71]. At LIGO Livingston, additional squeezing injection was possible, but would cause a measurable increase in radiation pressure noise and worsen detector range. In addition to improved range, squeezed state injection facilitated interesting investigations into the quantum nature of the LIGO interferometers [
73,
74,
147].
A filter cavity is being installed at both LIGO sites to improve the quantum noise limit. The filter cavity is discussed in
Section 6.3. A full review of the current status of squeezing in LIGO detectors will be published alongside this review [
148].
5.5. Environmental Disturbances
Every effort is made to isolate the LIGO optics from environmental noise. Environmental disturbances such as ground motion, acoustic noise, and magnetic noise can couple to the interferometer and cause excess noise in the gravitational wave readout, masking gravitational wave signals and limiting sensitivity. The physical environment monitoring system includes of a variety of sensors and noise injection tools around the main interferometer and is used to monitor environmental noise and characterize coupling to gravitational readout [
149]. Sensors include seismometers, accelerometers, thermometers, microphones, magnetometers, electrometers, radio receivers, infrasound microphones, tilt meters, anemometers, voltage monitors, and hygrometers. In this section we discuss some egregious environmental disturbances and their coupling to the interferometer.
5.5.1. Earthquakes
In general, the gravitational wave detector sensitivity is not limited by seismic noise, see
Figure 4 and
Section 4.4. However, when the seismic waves generated by an earthquake pass through the detector site, the ground motion can become so high that the active seismic control system [
42,
43] cannot sufficiently suppress the motion.
Earthquakes and large seismic motion accounted for 5% of the unplanned downtime of the LIGO detectors during O1 and O2. For O3, a new seismic controls mode was implemented during earthquakes, aimed at reducing actuator saturation and gain peaking to maintain interferometer lock during earthquakes [
150]. When the detector is taken to earthquake mode, two major seismic configuration changes occur: the seismic loops are set to have reduced gain in the 50–60 mHz band, and the common motion measured by seismometers in the corner and end stations is subtracted from the feedback signal. Earthquake mode has allowed the LIGO detectors to remain locked through large earthquakes causing ground velocities up to 3.9
RMS.
5.5.2. Wind
High-velocity wind can cause the corner and end station buildings to tilt, confusing seismometers and making it difficult (or impossible) to maintain lock. This has been a problem particularly at LIGO Hanford, where gusts over 60 mph have been measured. Between O1 and O2, tilt meters (or ground-rotation sensors) were installed at LIGO Hanford, and used to subtract ground tilt from seismometer signals [
151]. More recently, wind fences have been installed at LIGO Hanford, and their effectiveness is under study.
5.5.3. Anthropogenic Noise
Anthropogenic ground motion, caused by human activity near the site, typically occurs in the 1–5 Hz frequency band and is particularly problematic at the LIGO Livingston observatory. At LIGO Livingston, trains passing near the Y-arm, as well as elevated anthropogenic noise during the daytime, which cause scattering noise to be visible in the gravitational wave data in the 10–50 Hz band (see
Section 5.5.4).
5.5.4. Scattered Light
The sources of ground motion discussed above can couple to the gravitational wave readout through scattered light. Tiny imperfections in the main and auxiliary optics can cause light to scatter out of the main interferometer beam. This scattered light can then reflect off surfaces in the vacuum system, such as the suspension cages, chamber walls, or viewports. If the light then couples back into the main interferometer beam, it will carry phase modulation from ground motion, and inject noise into the gravitational wave readout. The characteristic morphology of scattering noise in the gravitational wave stain data is arches in the time–frequency domain—see examples in References [
149,
152]. Low-frequency ground motion caused by earthquakes (0.03–0.1 Hz) or microseism (0.1–0.3 Hz) cause excess noise in the gravitational wave readout in the 10–100 Hz band. In O3, scattered light coupling to the gravitational wave readout was improved compared to previous runs, thanks to a suite of stray light baffles, and improved vibration isolation in the pre-stabilized laser room improved test mass suspension control techniques.
6. Upgrades for Observing Run Four
Observing run three ended in March 2020, and observing run four is scheduled to begin in December 2022. Between these runs, there are several key upgrades being made to the LIGO detectors to improve sensitivity as part of the A+ upgrades [
10,
11].
6.1. Y-Arm Input Test Mass Replacement at Hanford
During O3, a significant point absorber was identified on the Y-arm input test mass (ITMY) at LIGO Hanford (see
Section 5.3.2). In December 2020, during the first part of the break between O3 and O4, the old ITMY was removed and a new test mass installed. Preliminary results from the mid-2021 commissioning period showed no significant absorbers on the new ITMY and improvement in power buildups (see
Section 5.3.1).
6.2. End Test Mass Replacements at Livingston
The end test masses at Livingston exhibit strong point absorbers limiting the overall circulating power. In order to achieve the O4 circulating power goal of 400 kW, new end test masses (ETMs) are planned to be installed at LIGO Livingston in 2022.
LIGO Hanford also has exhibited point absorbers on its end test masses, but preliminary results from mid-2021 locking suggest these do not limit power buildup as much as those at Livingston. The possibility for replacing Hanford’s ETMs remains open, depending on commissioning results with the higher input powers from the PSL (see
Section 6.4).
6.3. Filter Cavity
One side effect of frequency-independent squeezing is that quantum radiation pressure noise increases [
54,
55,
73]. This can be mitigated by reflecting the squeezed light off of a
filter cavity [
51,
52,
53,
153,
154,
155] before injecting it into the interferometer, as shown in
Figure 1.
In short, the filter cavity rotates the quadrature of the squeezed light for frequencies below the filter cavity pole frequency, but leaves unrotated the squeezed light quadrature above the filter cavity pole frequency. This is known as frequency-dependent squeezing, since the squeezing uncertainty ellipse rotates about the filter cavity pole frequency. This can lower quantum uncertainty across the entire detector bandwidth, not just the shot noise dominated regime.
Currently, the facilities infrastructure for the filter cavity is under construction at both Hanford and Livingston. The filter cavity is expected to be fully built and commissioned in time for O4, starting in December 2022.
6.4. Higher Input Laser Power
While commissioning the LIGO detectors, the input laser power is maximized to reduce shot noise, while maintaining stable operation. During O3, the pre-stabilized laser (PSL) was able to generate ∼50 W of optical power at the input mode cleaner, and the detectors operated with 34–38 W input power [
8]. Higher power operations were limited by point absorbers.
The goal for O4 is to double the power in the interferometer, from ∼200 to in the arms. Higher input powers are expected to be possible, especially after the test mass replacements. Therefore, the pre-stabilized laser is being upgraded to produce more power.
The new PSL configuration features two NeoLASE NeoVAN-4s-HP solid-state amplifiers in series, amplifying a seed beam from 2 W to 125 W [
156]. The seed laser is the same as previous runs: a nonplanar ring oscillator (NPRO) Nd-YAG 1064 nm infrared laser [
89].
6.5. Output Path Active Mode Matching
When the squeezed vacuum state encounters any imperfect optical interface, the squeezed state is degraded slightly. Additionally, mode mismatch is when the spacial mode of the squeezed state is not exactly matched to the spacial mode of the interferometer. The squeezing improvement to quantum noise is limited by total optical losses from mode mismatch and imperfect optical surfaces.
Of the budgeted sources of loss in O3, mode mismatch was the largest, estimated at 10% loss [
71]. Further modeling and analysis of the squeezing over the full detection band has revealed that mode mismatch within the detector itself also induces frequency-dependent loss [
74]. For O4, active mode matching elements are being installed between the elements of the squeezer and the interferometer to improve the mode matching.
In the O4 interferometer layout, problematic mode mismatch can occur in several locations. The squeezer mode must match the cavity modes of the output mode cleaner, the filter cavity and the interferometer mode (i.e. the mode circulating in the signal-recycling cavity). While the layout is designed such that these cavity modes are matched, in reality there is some uncertainty in the signal-recycling cavity mode, as well as uncertainty in the placement of optics as they are installed in vacuum. The active mode-matching elements will allow for changes to the spacial modes propagating between these optical cavities.
Two types of active mode-matching element are being installed. A thermally-actuated mirror with large actuation range (200 millidiopters) and slower response time is being installed on the path between the interferometer and the output mode cleaner [
157]. Three piezoelectric deformable mirrors, with reduced actuation range (120 millidiopters) but faster response time, are being installed between the squeezer and the filter cavity, and between the filter cavity and the interferometer [
158].
7. Conclusions
Powerful black hole and neutron star mergers are now revealed by their imprint on spacetime itself, traveling to the Earth from the distant past, carrying a wealth of information about the events that created them. Advanced LIGO has already revolutionized our understanding of astrophysics and astronomy, with 90 detections of gravitational waves. More detections and higher SNR detections from a more sensitive detector will make new results in astrophysics, general relativity, and cosmology possible.
The Advanced LIGO detectors switch between periods of upgrades and installs, commissioning those upgrades to work as intended, and observation runs. O4 is scheduled to run for one year of coincident observation time between the LIGO detectors, starting in December 2022 with
circulating power and ∼175 Mpc binary neutron star range. O5 is when we plan to achieve the A+ sensitivity shown in
Figure 5.
Advanced LIGO’s success would not have been possible if not for the lessons learned and support from the first generation of long-baseline interferometers from around the world, including initial LIGO [
159,
160,
161], Virgo [
162,
163], GEO600 [
164,
165], and TAMA [
166].
Advanced Virgo [
167] currently runs alongside Advanced LIGO, and is the only detector other than LIGO Hanford and LIGO Livingston to have sensed gravitational waves. KAGRA is anticipated to join O4 in observations [
168,
169,
170]. LIGO India is expected to begin constructing a new observatory soon [
171].
More ambitious upgrades to the current facilities are possible for LIGO Voyager, including a new laser wavelength (
) and cryogenically cooled optics [
172]. Third-generation detector designs are currently being proposed based on results and designs from Advanced LIGO and A+, including Einstein Telescope [
173] in Europe and Cosmic Explorer in the United States [
174]. Space-based interferometers with very long baselines are also being designed and constructed. The LISA mission is anticipated to detect much lower frequency GWs than LIGO [
175], with the initial LISA Pathfinder results being extremely promising [
176].
The technological achievements made with Advanced LIGO will reverberate into the future, just as the knowledge gained by first generation detectors paved the way for Advanced LIGO. Every step toward design sensitivity brings the furthest reaches of the universe closer.
Author Contributions
Both authors have researched and wrote significant portions of this review. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation grant number PHY-1764464 and PHY-1834382.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the vast amount of work that goes into designing, building, operating, and maintaining the LIGO Laboratory and facilities. For locking the interferometer, bringing it to its lowest-noise state, and characterizing the noise sources, we acknowledge the 2021 LIGO Hanford commissioning team, including Sheila Dwyer, Jenne Driggers, Anamaria Effler, Valary Frolov, Keita Kawabe, Jeff Kissel, Robert Schofield, Daniel Sigg, and Varun Srivastava. We acknowledge the calibration working group for producing the infrastructure to calibrate the interferometer data. We acknowledge the LIGO lab operations teams for locking, running, and managing the detector. We acknowledge the LIGO lab detector engineers for fabricating and installing the new Y-arm input test mass that was critical for removing point absorbers from the interferometer core optics. We acknowledge the LIGO facilities crew for building the facility, including the new filter cavity infrastrucuture. This material is based upon work supported by NSF’s LIGO Laboratory which is a major facility fully funded by the National Science Foundation.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GW | gravitational waves |
| LIGO | laser interferometer gravitational wave observatory |
| O1 | observing run one |
| O2 | observing run two |
| O3 | observing run three |
| O4 | observing run four |
| SNR | signal-to-noise ratio |
| PDH | Pound–Drever–Hall |
| RF | radio-frequency |
| PSL | pre-stabilized laser |
| ALS | arm-length stabilization |
| DRMI | dual-recycled Michelson interferometer |
| DARM | differential arm (length) |
| ASD | amplitude spectral density |
| QRPN | quantum radiation pressure noise |
| MICH | Michelson length |
| PRCL | power-recycling cavity length |
| SRCL | signal-recycling cavity length |
| RFPD | radio-frequency photodetectors |
| PRG | power-recycling gain |
| PI | parametric instability |
| ITMY | input test mass (Y-arm) |
| ETM | end test mass |
Appendix A. Michelson Interferometer
Gravitational waves produce differential motion in orthogonal directions of spacetime (
Section 2). Michelson interferometers were originally created to precisely measure differential light velocity in each arm [
177]. Today, a Michelson interferometer forms the core of the Advanced LIGO detector, and is used to detect differential motion in the arms [
146]. This section will overview how a Michelson is sensitive to differential motion.
First, we will assume the plane-wave approximation is valid, so all electric fields will be simplified into a single complex number . Second, we will assume our mirrors are thin mirrors with no losses, so where r and t are the amplitude reflection and transmission coefficients of the mirrors and R and T are the power reflection and transmission coefficients of the mirrors. Third, we will use the “” mirror reflection convention based on the Fresnel relations, which states that a beam reflected off the back of the mirror suffers a phase flip, but a beam reflected off the front suffers no phase flip.
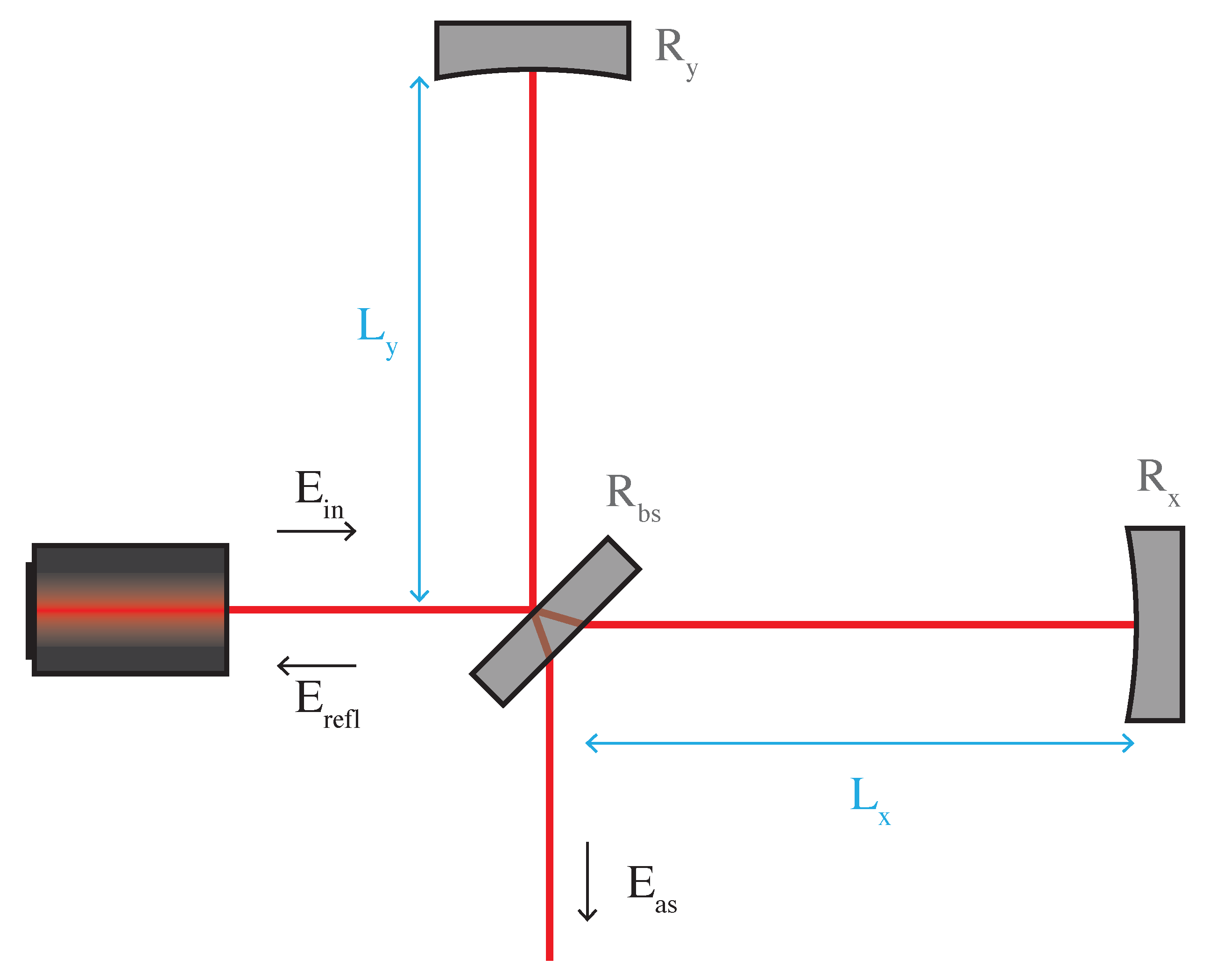
Appendix A.1. Basics
Figure A1 shows a Michelson interferometer, which consists of an input laser, a 50:50 beamsplitter, and two “arms” of laser light with highly reflective mirrors at the end. The laser input amplitude
is split into the arms equally by the beamsplitter
. The light in each arm
propagates the length of its arm
, is reflected off the end mirrors
accruing different amounts of phase
:
Figure A1.
Optical layout of a Michelson interferometer. The input laser electric field is , the field reflected from the Michelson is , and the field transmitter through the Michelson antisymmetric port is . The 50:50 beamsplitter reflects half the laser power to the Y-arm and transmits half to the X-arm. The highly reflecting end mirrors send most of the light directly back to the beamsplitter.
Figure A1.
Optical layout of a Michelson interferometer. The input laser electric field is , the field reflected from the Michelson is , and the field transmitter through the Michelson antisymmetric port is . The 50:50 beamsplitter reflects half the laser power to the Y-arm and transmits half to the X-arm. The highly reflecting end mirrors send most of the light directly back to the beamsplitter.
The light from each arm is then recombined at the beamsplitter, producing the reflected beam
and transmitted, or antisymmetric, beam
:
where between Equations (A4) and (A5) we have defined the common length
and differential length
.
Calculating the power at the reflected and antisymmetric ports
:
where
is the input power. The power at the antisymmetric port in Equation (A7) depends on the static differential length
.
Appendix A.2. Transfer Function
Suppose we inject a small differential length oscillation
into the Michelson, such that
. The
transfer function from the differential length to antisymmetric power at the frequency of injection
is
The transfer function Equation (
A8) defines the frequency response of antisymmetric power to length motion of the Michelson interferometer. In this case, the transfer function is flat for all
.
The easiest way to see the effect of the length oscillation
on
is to think about the derivative of Equation (A7) with respect to
. The small oscillation will vary
at the same frequency as
,
. The derivative of Equation (A7) is a slight simplification, as it would be missing a factor of two compared to Equation (
A8).
The transfer function of a gravitational wave
h to power at the antisymmetric port is more complicated, as seen in [
14]:
Equation (
A9) is not flat: when the signal
where the
free spectral range , the transfer function dips to zero. This is from the laser in the Michelson integrating over one full period of the gravitational wave from Equation (
2), yielding zero overall phase change at that frequency. For the full derivation, see either [
14,
146] or Appendix B of [
58].
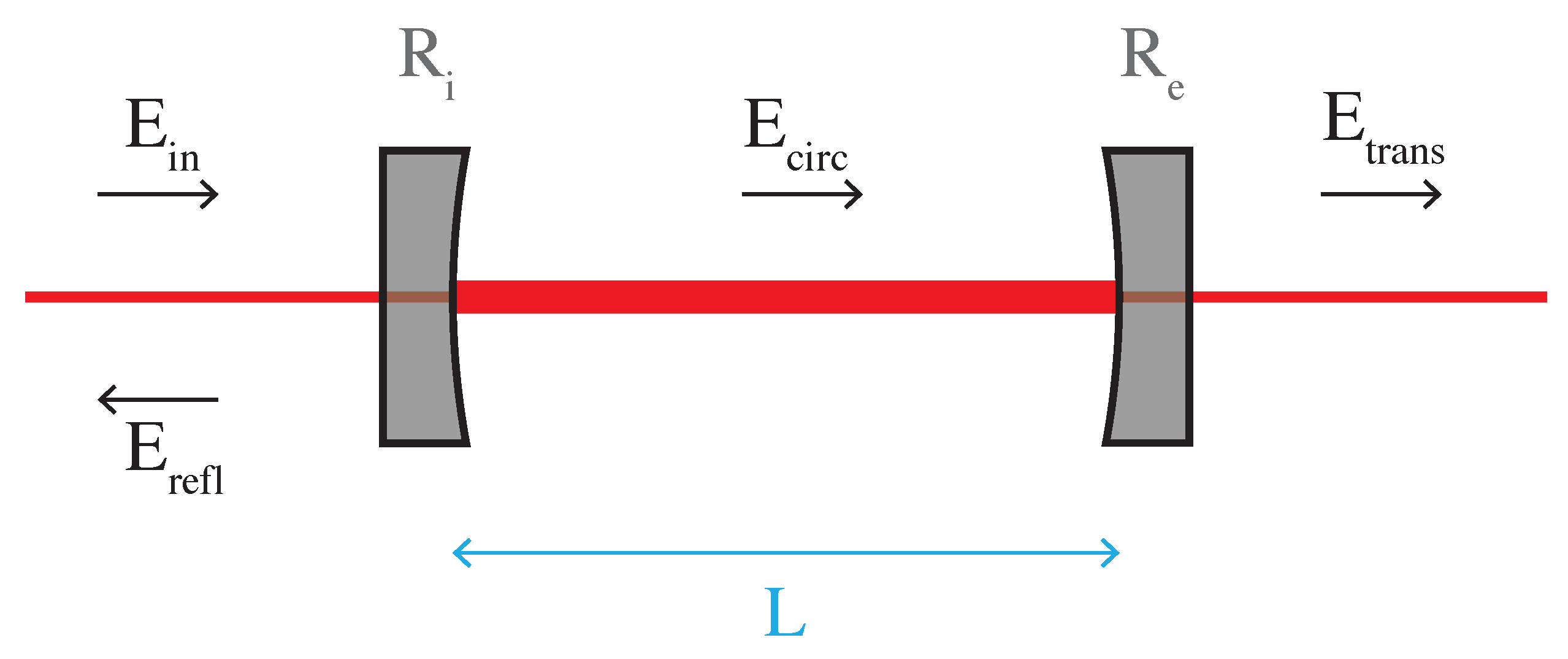
Appendix B. Fabry–Pérot Interferometer
The Fabry–Pérot interferometer forms a core optomechanical technology in LIGO, with its resonantly enhanced sensitivity to length motion. The beam reflected from the Fabry–Pérot
has a phase strongly dependent on the cavity length
L. Combined with a Michelson interferometer, the Fabry–Pérot phase shift can be preferentially “picked-off” and sent out the antisymmetric port, enhancing a normal Michelson’s sensitivity to differential motion, and gravitational waves. In the below sections, we will make the same assumptions as
Appendix A.
Appendix B.3. Basics
Figure A2 shows a Fabry–Pérot interferometer, which is just a two-mirror aligned optical cavity. The input mirror has reflectivity
, and the end mirror has reflectivity
.
The input beam is partially reflected into , and partially transmitted into the cavity . The circulating beam makes round trips in the cavity with length L, accruing a phase with every round trip, but also partially transmits through the end mirror and back through the input mirror .
We can write out the equations for the plane-wave Fabry–Pérot beams as
where
are the amplitude transmission and reflection coefficients of the input mirror,
are the same for the end mirror, and
k is the laser wavenumber. In Equation (A11),
has a negative sign due to the “
” convention, where we have chosen the left side of the input mirror to suffer a phase flip.
Figure A2.
Optical layout of a Fabry–Pérot interferometer.
Figure A2.
Optical layout of a Fabry–Pérot interferometer.
Using Equation (
A10), we can solve for
, and use that result for Equations (A11) and (A12):
From Equation (
A13), we can examine how the resonant buildup works for
. Normally, the product
in the denominator is selected to be very close to one. This leaves the phasor
, which can make the resonant power very large when it equals one. The phasor can equal one when
, where
n is any positive integer. Simplifying yields the
resonance condition for the cavity length
L:
where
is the laser wavelength.
One important quantity is the
cavity pole , which can be derived by setting the denominator of Equations (
A13)–(A15) to zero:
The cavity pole is the frequency at which the Fabry–Pérot frequency response to length motion falls by half, see Equation (A20).
Now we examine Equation (A14), the reflection from the Fabry–Pérot. First, we’ll assume
, which is true for a lossless mirror. Next, we’ll assume that we are near resonance except for a small deviation
such that
, then
. A first-order series expansion of Equation (A14) about
yields
The key of Equation (
A18) is the term that depends on
is entirely imaginary and very large. This means that the phase of the reflected light
is strongly responding to small changes in length
.
Appendix B.4. Transfer Function
Here, we report the frequency response from end mirror displacement modulation
to the reflected light
. Assuming the cavity is resonant per Equation (
A16), we can write the length to reflected field transfer function as
where
is the ideal cavity power gain, and
is the cavity pole from Equation (
A17). Between Equations (
A19) and (A20) we have assumed the end mirror length modulation
is small.
Again, it is easiest to think of the frequency response in Equations (
A19) and (A20) as the derivative of Equation (A14) with respect to
L. In reality, we must consider the full audio sideband picture to obtain the more accurate Equation (
A19). More complete derivations of the Fabry–Pérot frequency response can be found in [
57,
146,
178,
179,
180].
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Advanced LIGO. Class. Quantum Gravity 2015, 32, 074001. [Google Scholar] [CrossRef]
- Abbott, R.; Adhikari, R.; Ballmer, S.; Barsotti, L.; Evans, M.; Fritschel, P.; Frolov, V.; Mueller, G.; Slagmolen, B.; Waldman, S. Advanced LIGO Length Sensing and Control Final Design. Tech. Rep. 2010, 1000298, 2010. [Google Scholar]
- Martynov, D.V.; Hall, E.D.; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Adams, C.; Adhikari, R.X.; Anderson, R.A.; Anderson, S.B.; Arai, K.; et al. Sensitivity of the Advanced LIGO detectors at the beginning of gravitational wave astronomy. Phys. Rev. D 2016, 93, 112004. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW150914: The Advanced LIGO Detectors in the Era of First Discoveries. Phys. Rev. Lett. 2016, 116, 131103. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Bloemen, S.; Canizares, P.; Falcke, H.; Fender, R.P.; Ghosh, S.; Groot, P.; Hinderer, T.; Hörandel, J.R.; Jonker, P.G.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Buikema, A.; Cahillane, C.; Mansell, G.L.; Blair, C.D.; Abbott, R.; Adams, C.; Adhikari, R.X.; Ananyeva, A.; Appert, S.; Arai, K.; et al. Sensitivity and performance of the Advanced LIGO detectors in the third observing run. Phys. Rev. D 2020, 102, 062003. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run. arXiv 2021, arXiv:2111.03606. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. Prospects for observing and localizing gravitational-wave transients with Advanced LIGO, Advanced Virgo and KAGRA. Living Rev. Relativ. 2020, 23, 1–69. [Google Scholar] [CrossRef]
- Fritschel, P.; Reid, S.; Vajente, G.; Hammond, G.; Miao, H.; Brown, D.; Quetschke, V.; Steinlechner, J. Instrument Science White Paper 2021; Technical Report LIGO-T2100298; LIGO Scientific Collaboration: Pasadena, CA, USA, 2021. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Macmillan: Basingstoke, UK, 1973. [Google Scholar]
- Sathyaprakash, B.S.; Schutz, B.F. Physics, Astrophysics and Cosmology with Gravitational Waves. Living Rev. Relativ. 2009, 12, 2. [Google Scholar] [CrossRef] [PubMed]
- Saulson, P.R. Fundamentals of Interferometric Gravitational Wave Detectors; World Scientific: Singapore, 1994. [Google Scholar]
- Adhikari, R.X. Gravitational radiation detection with laser interferometry. Rev. Mod. Phys. 2014, 86, 121–151. [Google Scholar] [CrossRef]
- Rakhmanov, M.; Romano, J.D.; Whelan, J.T. High-frequency corrections to the detector response and their effect on searches for gravitational waves. Class. Quantum Gravity 2008, 25, 184017. [Google Scholar] [CrossRef]
- Drever, R.W.; Hall, J.L.; Kowalski, F.V.; Hough, J.; Ford, G.M.; Munley, A.J.; Ward, H. Laser phase and frequency stabilization using an optical resonator. Appl. Phys. Photophysics Laser Chem. 1983, 31, 97–105. [Google Scholar] [CrossRef]
- Regehr, M.W.; Raab, F.J.; Whitcomb, S.E. Demonstration of a power-recycled Michelson interferometer with Fabry–Perot arms by frontal modulation. Opt. Lett. 1995, 20, 1507–1509. [Google Scholar] [CrossRef]
- Sigg, D.; Mavalvala, N.; Giaime, J.; Fritschel, P.; Shoemaker, D. Signal extraction in a power-recycled Michelson interferometer with Fabry-Perot arm cavities by use of a multiple-carrier frontal modulation scheme. Appl. Opt. 1998, 37, 5687–5693. [Google Scholar] [CrossRef]
- Fritschel, P.; Bork, R.; González, G.; Mavalvala, N.; Ouimette, D.; Rong, H.; Sigg, D.; Zucker, M. Readout and control of a power-recycled interferometric gravitational-wave antenna. Appl. Opt. 2001, 40, 4988–4998. [Google Scholar] [CrossRef]
- Strain, K.A.; Müller, G.; Delker, T.; Reitze, D.H.; Tanner, D.B.; Mason, J.E.; Willems, P.A.; Shaddock, D.A.; Gray, M.B.; Mow-Lowry, C.; et al. Sensing and control in dual-recycling laser interferometer gravitational-wave detectors. Appl. Opt. 2003, 42, 1244–1256. [Google Scholar] [CrossRef][Green Version]
- Fricke, T.T.; Smith-Lefebvre, N.D.; Abbott, R.; Adhikari, R.; Dooley, K.L.; Evans, M.; Fritschel, P.; Frolov, V.V.; Kawabe, K.; Kissel, J.S.; et al. DC readout experiment in Enhanced LIGO. Class. Quantum Gravity 2012, 29, 065005. [Google Scholar] [CrossRef]
- Izumi, K.; Sigg, D. Advanced LIGO: Length sensing and control in a dual recycled interferometric gravitational wave antenna. Class. Quantum Gravity 2017, 34, 015001. [Google Scholar] [CrossRef]
- Anderson, D.Z. Alignment of resonant optical cavities. Appl. Opt. 1984, 23, 2944–2949. [Google Scholar] [CrossRef] [PubMed]
- Morrison, E.; Meers, B.J.; Robertson, D.I.; Ward, H. Automatic alignment of optical interferometers. Appl. Opt. 1994, 33, 5041–5049. [Google Scholar] [CrossRef] [PubMed]
- Mavalvala, N.; Sigg, D.; Shoemaker, D. Experimental test of an alignment-sensing scheme for a gravitational-wave interferometer. Appl. Opt. 1998, 37, 7743–7746. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sidles, J.A.; Sigg, D. Optical torques in suspended Fabry—Perot interferometers. Phys. Lett. A 2006, 354, 167–172. [Google Scholar] [CrossRef]
- Hirose, E.; Kawabe, K.; Sigg, D.; Adhikari, R.; Saulson, P.R. Angular instability due to radiation pressure in the LIGO gravitational-wave detector. Appl. Opt. 2010, 49, 3474–3484. [Google Scholar] [CrossRef]
- Barsotti, L.; Evans, M.; Fritschel, P. Alignment sensing and control in advanced LIGO. Class. Quantum Gravity 2010, 27, 084026. [Google Scholar] [CrossRef]
- Dooley, K.L.; Barsotti, L.; Adhikari, R.X.; Evans, M.; Fricke, T.T.; Fritschel, P.; Frolov, V.; Kawabe, K.; Smith-Lefebvre, N. Angular control of optical cavities in a radiation-pressure-dominated regime: The Enhanced LIGO case. J. Opt. Soc. Am. A 2013, 30, 2618–2626. [Google Scholar] [CrossRef]
- Enomoto, Y.; Nagano, K.; Kawamura, S. Standard quantum limit of angular motion of a suspended mirror and homodyne detection of a ponderomotively squeezed vacuum field. Phys. Rev. A 2016, 94, 012115. [Google Scholar] [CrossRef]
- Kwee, P.; Bogan, C.; Danzmann, K.; Frede, M.; Kim, H.; King, P.; Pöld, J.; Puncken, O.; Savage, R.L.; Seifert, F.; et al. Stabilized high-power laser system for the gravitational wave detector advanced LIGO. Opt. Express 2012, 20, 10617–10634. [Google Scholar] [CrossRef]
- Seifert, F.; Kwee, P.; Heurs, M.; Willke, B.; Danzmann, K. Laser power stabilization for second-generation gravitational wave detectors. Opt. Lett. 2006, 31, 2000–2002. [Google Scholar] [CrossRef]
- Kwee, P.; Willke, B.; Danzmann, K. Shot-noise-limited laser power stabilization with a high-power photodiode array. Opt. Lett. 2009, 34, 2912–2914. [Google Scholar] [CrossRef] [PubMed]
- Zucker, M.E.; Whitcomb, S.E. Measurement of optical path fluctuations due to residual gas in the LIGO 40 meter interferometer. In Proceedings of the Seventh Marcel Grossman Meeting on Recent Developments in Theoretical and Experimental General Relativity, Gravitation, and Relativistic Field Theories, Stanford, CA, USA, 24–30 July 1994; World Scientific: Singapore, 1996; pp. 1434–1436. [Google Scholar]
- Dolesi, R.; Hueller, M.; Nicolodi, D.; Tombolato, D.; Vitale, S.; Wass, P.J.; Weber, W.J.; Evans, M.; Fritschel, P.; Weiss, R.; et al. Brownian force noise from molecular collisions and the sensitivity of advanced gravitational wave observatories. Phys. Rev. D 2011, 84, 063007. [Google Scholar] [CrossRef]
- Phelps, M.H.; Gushwa, K.E.; Torrie, C.I. Optical contamination control in the Advanced LIGO ultra-high vacuum system. Int. Soc. Opt. Photonics 2013, 8885, 314–327. [Google Scholar] [CrossRef]
- Robertson, N.A.; Cagnoli, G.; Crooks, D.R.; Elliffe, E.; Faller, J.E.; Fritschel, P.; Goßler, S.; Grant, A.; Heptonstall, A.; Hough, J.; et al. Quadruple suspension design for Advanced LIGO. Class. Quantum Gravity 2002, 19, 4043. [Google Scholar] [CrossRef]
- Aston, S.M.; Barton, M.A.; Bell, A.S.; Beveridge, N.; Bl, B.; Brummitt, A.J.; Cagnoli, G.; Cantley, C.A.; Carbone, L.; Cumming, A.V.; et al. Update on quadruple suspension design for Advanced LIGO. Class. Quantum Gravity 2012, 29, 235004. [Google Scholar] [CrossRef]
- Carbone, L.; Aston, S.M.; Cutler, R.M.; Freise, A.; Greenhalgh, J.; Heefner, J.; Hoyl, D.; Lockerbie, N.A.; Lodhia, D.; Robertson, N.A.; et al. Sensors and actuators for the Advanced LIGO mirror suspensions. Class. Quantum Gravity 2012, 29, 115005. [Google Scholar] [CrossRef]
- Daw, E.J.; Giaime, J.A.; Lormand, D.; Lubinski, M.; Zweizig, J. Long-term study of the seismic environment at LIGO. Class. Quantum Gravity 2004, 21, 2255–2273. [Google Scholar] [CrossRef]
- Wen, S.; Mittleman, R.; Mason, K.; Giaime, J.; Abbott, R.; Kern, J.; O’Reilly, B.; Bork, R.; Hammond, M.; Hardham, C.; et al. Hydraulic external pre-isolator system for LIGO. Class. Quantum Gravity 2014, 31, 235001. [Google Scholar] [CrossRef]
- Matichard, F.; Lantz, B.; Mittleman, R.; Mason, K.; Kissel, J.; Abbott, B.; Biscans, S.; McIver, J.; Abbott, R.; Abbott, S.; et al. Seismic isolation of Advanced LIGO: Review of strategy, instrumentation and performance. Class. Quantum Gravity 2015, 32, 185003. [Google Scholar] [CrossRef]
- Biscans, S.; Warner, J.; Mittleman, R.; Buchanan, C.; Coughlin, M.; Evans, M.; Gabbard, H.; Harms, J.; Lantz, B.; Mukund, N.; et al. Control strategy to limit duty cycle impact of earthquakes on the LIGO gravitational-wave detectors. Class. Quantum Gravity 2018, 35, 055004. [Google Scholar] [CrossRef]
- Bork, R.; Abbott, R.; Barker, D.; Heefner, J. An Overview of the LIGO Control and Data Acquisition System. arXiv 2001, arXiv:0111077. [Google Scholar]
- Bartos, I.; Bork, R.; Factourovich, M.; Heefner, J.; Mrka, S.; Mrka, Z.; Raics, Z.; Schwinberg, P.; Sigg, D. The Advanced LIGO timing system. Class. Quantum Gravity 2010, 27, 084025. [Google Scholar] [CrossRef]
- Rollins, J.G. Distributed state machine supervision for long-baseline gravitational-wave detectors. Rev. Sci. Instrum. 2016, 87, 094502. [Google Scholar] [CrossRef] [PubMed]
- Bork, R.; Hanks, J.; Barker, D.; Betzwieser, J.; Rollins, J.; Thorne, K.; von Reis, E. advligorts: The Advanced LIGO real-time digital control and data acquisition system. SoftwareX 2021, 13, 100619. [Google Scholar] [CrossRef]
- Mueller, C.L.; Arain, M.A.; Ciani, G.; Derosa, R.T.; Effler, A.; Feldbaum, D.; Frolov, V.V.; Fulda, P.; Gleason, J.; Heintze, M.; et al. The advanced LIGO input optics. Rev. Sci. Instrum. 2016, 87, 014502. [Google Scholar] [CrossRef] [PubMed]
- Arai, K.; Barnum, S.; Fritschel, P.; Lewis, J.; Waldman, S. Output Mode Cleaner Design; Technical Report LIGO-T1000276-v5; LIGO Scientific Collaboration: Pasadena, CA, USA, 2013. [Google Scholar]
- Evans, M.; Barsotti, L.; Kwee, P.; Harms, J.; Miao, H. Realistic filter cavities for advanced gravitational wave detectors. Phys. Rev. D 2013, 88, 022002. [Google Scholar] [CrossRef]
- McCuller, L.; Whittle, C.; Ganapathy, D.; Komori, K.; Tse, M.; Fernandez-Galiana, A.; Barsotti, L.; Fritschel, P.; MacInnis, M.; Matichard, F.; et al. Frequency-Dependent Squeezing for Advanced LIGO. Phys. Rev. Lett. 2020, 124, 171102. [Google Scholar] [CrossRef]
- McCuller, L.; Barsotti, L. Design Requirement Document of the A+ Filter Cavity and Relay Optics for Frequency Dependent Squeezing; Technical Report T1800447-v7; Massachusetts Institute of Technology: Cambridge, MA, USA, 2020. [Google Scholar]
- Buonanno, A.; Chen, Y. Quantum noise in second generation, signal-recycled laser interferometric gravitational-wave detectors. Phys. Rev. D 2001, 64, 042006. [Google Scholar] [CrossRef]
- Kimble, H.J.; Levin, Y.; Matsko, A.B.; Thorne, K.S.; Vyatchanin, S.P. Conversion of conventional gravitational-wave interferometers into quantum nondemolition interferometers by modifying their input and/or output optics. Phys. Rev. D 2001, 65, 022002. [Google Scholar] [CrossRef]
- Ward, R.L. Length Sensing and Control of a Prototype Advanced Interferometric Gravitational Wave Detector. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2010. [Google Scholar] [CrossRef]
- Hall, E.D. Long-Baseline Laser Interferometry for the Detection of Binary Black-Hole Mergers. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2017. [Google Scholar] [CrossRef]
- Cahillane, C. Controlling and Calibrating Interferometric Gravitational Wave Detectors. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2021. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. A guide to LIGO–Virgo detector noise and extraction of transient gravitational-wave signals. Class. Quantum Gravity 2020, 37, 055002. [Google Scholar] [CrossRef]
- Allen, B.; Anderson, W.G.; Brady, P.R.; Brown, D.A.; Creighton, J.D.E. FINDCHIRP: An algorithm for detection of gravitational waves from inspiraling compact binaries. Phys. Rev. D 2012, 85, 122006. [Google Scholar] [CrossRef]
- Meers, B.J. Recycling in laser-interferometric gravitational-wave detectors. Phys. Rev. D 1988, 38, 2317. [Google Scholar] [CrossRef]
- Strain, K.A.; Meers, B.J. Experimental demonstration of dual recycling for interferometric gravitational-wave detectors. Phys. Rev. Lett. 1991, 66, 1391. [Google Scholar] [CrossRef] [PubMed]
- Heinzel, G.; Strain, K.A.; Mizuno, J.; Skeldon, K.D.; Willke, B.; Winkler, W.; Schilling, R.; Rüdiger, A.; Danzmann, K. Experimental demonstration of a suspended dual recycling interferometer for gravitational wave detection. Phys. Rev. Lett. 1998, 81, 5493–5496. [Google Scholar] [CrossRef]
- Grote, H.; Freise, A.; Malec, M.; Heinzel, G.; Willke, B.; Lück, H.; Strain, K.A.; Hough, J.; Danzmann, K. Dual recycling for GEO 600. Class. Quantum Gravity 2004, 21, S473. [Google Scholar] [CrossRef]
- Fritschel, P.; Shoemaker, D.; Weiss, R. Demonstration of light recycling in a Michelson interferometer with Fabry-Perot cavities. Appl. Opt. 1992, 31, 1412–1418. [Google Scholar] [CrossRef] [PubMed]
- Ando, M. Power Recycling for an Interferometric Gravitational Wave Detector. Ph.D. Thesis, University of Tokyo, Tokyo, Japan, 1998. [Google Scholar]
- Arain, M.A.; Mueller, G. Design of the Advanced LIGO Recycling Cavities. Optics Express 2008, 16, 10018–10032. [Google Scholar] [CrossRef]
- Fritschel, P.; Mavalvala, N.; Shoemaker, D.; Sigg, D.; Zucker, M.; González, G. Alignment of an interferometric gravitational wave detector. Appl. Opt. 1998, 37, 6734–6747. [Google Scholar] [CrossRef]
- Caves, C.M. Quantum-Mechanical Radiation-Pressure Fluctuations in an Interferometer. Phys. Rev. Lett. 1980, 45, 75–79. [Google Scholar] [CrossRef]
- Caves, C.M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 1981, 23, 1693–1708. [Google Scholar] [CrossRef]
- Tse, M.; Yu, H.; Kijbunchoo, N.; Fernandez-Galiana, A.; Dupej, P.; Barsotti, L.; Blair, C.; Brown, D.; Dwyer, S.; Effler, A.; et al. Quantum-Enhanced Advanced LIGO Detectors in the Era of Gravitational-Wave Astronomy. Phys. Rev. Lett. 2019, 123, 231107. [Google Scholar] [CrossRef]
- Oelker, E.; Mansell, G.; Tse, M.; Miller, J.; Matichard, F.; Barsotti, L.; Fritschel, P.; McClelland, D.E.; Evans, M.; Mavalvala, N. Ultra-low phase noise squeezed vacuum source for gravitational wave detectors. Optica 2016, 3, 682–685. [Google Scholar] [CrossRef]
- Yu, H.; McCuller, L.; Tse, M.; Kijbunchoo, N.; Barsotti, L.; Mavalvala, N. Quantum correlations between light and the kilogram-mass mirrors of LIGO. Nature 2020, 583, 43–47. [Google Scholar] [CrossRef] [PubMed]
- McCuller, L.; Dwyer, S.E.; Green, A.C.; Yu, H.; Kuns, K.; Barsotti, L.; Blair, C.D.; Brown, D.D.; Effler, A.; Evans, M.; et al. LIGO’s quantum response to squeezed states. Phys. Rev. D 2021, 104, 062006. [Google Scholar] [CrossRef]
- Cahillane, C.; Sigg, D.; Mansell, G.L.; Sigg, D. Laser frequency noise in next generation gravitational-wave detectors. Opt. Express 2021, 29, 42144–42161. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Ackley, K.; Adams, C.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Calibration of the Advanced LIGO detectors for the discovery of the binary black-hole merger GW150914. Phys. Rev. D 2017, 95, 062003. [Google Scholar] [CrossRef]
- Cahillane, C.; Betzwieser, J.; Brown, D.A.; Goetz, E.; Hall, E.D.; Izumi, K.; Kandhasamy, S.; Karki, S.; Kissel, J.S.; Mendell, G.; et al. Calibration uncertainty for Advanced LIGO’s first and second observing runs. Phys. Rev. D 2017, 96, 102001. [Google Scholar] [CrossRef]
- Sun, L.; Goetz, E.; Kissel, J.S.; Betzwieser, J.; Karki, S.; Viets, A.; Wade, M.; Bhattacharjee, D.; Bossilkov, V.; Covas, P.B.; et al. Characterization of systematic error in Advanced LIGO calibration. Class. Quantum Gravity 2020, 37, 225008. [Google Scholar] [CrossRef]
- Sun, L.; Goetz, E.; Kissel, J.S.; Betzwieser, J.; Karki, S.; Bhattacharjee, D.; Covas, P.B.; Datrier, L.E.H.; Kandhasamy, S.; Lecoeuche, Y.K.; et al. Characterization of systematic error in Advanced LIGO calibration in the second half of O3. arXiv 2021, arXiv:2107.00129. [Google Scholar]
- Lindblom, L. Optimal calibration accuracy for gravitational-wave detectors. Phys. Rev. D 2009, 80, 042005. [Google Scholar] [CrossRef]
- Tuyenbayev, D.; Karki, S.; Betzwieser, J.; Cahillane, C.; Goetz, E.; Izumi, K.; Kandhasamy, S.; Kissel, J.S.; Mendell, G.; Wade, M.; et al. Improving LIGO calibration accuracy by tracking and compensating for slow temporal variations. Class. Quantum Gravity 2017, 34, 015002. [Google Scholar] [CrossRef]
- Vitale, S.; Haster, C.J.; Sun, L.; Farr, B.; Goetz, E.; Kissel, J.; Cahillane, C. Physical approach to the marginalization of LIGO calibration uncertainties. Phys. Rev. D 2021, 103, 063016. [Google Scholar] [CrossRef]
- Karki, S.; Tuyenbayev, D.; Kandhasamy, S.; Abbott, B.P.; Abbott, T.D.; Anders, E.H.; Berliner, J.; Betzwieser, J.; Cahillane, C.; Canete, L.; et al. The Advanced LIGO photon calibrators. Rev. Sci. Instrum. 2016, 87, 114503. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharjee, D.; Lecoeuche, Y.; Karki, S.; Betzwieser, J.; Bossilkov, V.; Kandhasamy, S.; Payne, E.; Savage, R.L. Fiducial displacements with improved accuracy for the global network of gravitational wave detectors. Class. Quantum Gravity 2020, 38, 015009. [Google Scholar] [CrossRef]
- Estevez, D.; Lieunard, B.; Marion, F.; Mours, B.; Rolland, L.; Verkindt, D. First tests of a Newtonian calibrator on an interferometric gravitational wave detector. Class. Quantum Gravity 2018, 35, 235009. [Google Scholar] [CrossRef]
- Inoue, Y.; Haino, S.; Kanda, N.; Ogawa, Y.; Suzuki, T.; Tomaru, T.; Yamanmoto, T.; Yokozawa, T. Improving the absolute accuracy of the gravitational wave detectors by combining the photon pressure and gravity field calibrators. Phys. Rev. D 2018, 98, 022005. [Google Scholar] [CrossRef]
- Estevez, D.; Mours, B.; Pradier, T. Newtonian calibrator tests during the Virgo O3 data taking. Class. Quantum Gravity 2021, 38, 075012. [Google Scholar] [CrossRef]
- Ross, M.P.; Mistry, T.; Datrier, L.; Kissel, J.; Venkateswara, K.; Weller, C.; Kumar, K.; Hagedorn, C.; Adelberger, E.; Lee, J.; et al. Initial Results from the LIGO Newtonian Calibrator. arXiv 2021, arXiv:2107.00141. [Google Scholar] [CrossRef]
- Kane, T.J.; Byer, R.L. Monolithic, unidirectional single-mode Nd:YAG ring laser. Opt. Lett. 1985, 10, 65–67. [Google Scholar] [CrossRef]
- Korth, Z. Mitigating Noise in Interferometric Gravitational Wave Detectors. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2019. [Google Scholar] [CrossRef]
- Hoak, D. Gravitational Wave Astrophysics: Instrumentation, Detector Characterization, and a Search for Gravitational Signals from Gamma-ray Bursts. Ph.D. Thesis, University of Massachusetts Amherst, Amherst, MA, USA, 2015. [Google Scholar] [CrossRef]
- Venugopalan, G. Prototype Interferometry in the Era of Gravitational Wave Astronomy. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2021. [Google Scholar] [CrossRef]
- Hild, S.; Grote, H.; Degallaix, J.; Chelkowski, S.; Danzmann, K.; Freise, A.; Hewitson, M.; Hough, J.; Lück, H.; Prijatelj, M.; et al. DC-readout of a signal-recycled gravitational wave detector. Class. Quantum Gravity 2009, 26, 055012. [Google Scholar] [CrossRef]
- Martynov, D.V. Lock Acquisition and Sensitivity Analysis of Advanced LIGO Interferometers. Ph.D Thesis, California Institute of Technology, Pasadena, CA, USA, 2015. [Google Scholar] [CrossRef]
- Staley, A.N. Locking the Advanced LIGO Gravitational Wave Detector: With a focus on the Arm Length Stabilization Technique. Ph.D. Thesis, Columbia University, New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Staley, A.; Martynov, D.; Abbott, R.; Adhikari, R.X.; Arai, K.; Ballmer, S.; Barsotti, L.; Brooks, A.F.; Derosa, R.T.; Dwyer, S.; et al. Achieving resonance in the Advanced LIGO gravitational-wave interferometer. Class. Quantum Gravity 2014, 31, 245010. [Google Scholar] [CrossRef]
- Izumi, K.; Arai, K.; Barr, B.; Betzwieser, J.; Brooks, A.; Dahl, K.; Doravari, S.; Driggers, J.C.; Korth, W.Z.; Miao, H.; et al. Multicolor cavity metrology. J. Opt. Soc. Am. A 2012, 29, 2092–2103. [Google Scholar] [CrossRef] [PubMed]
- Mullavey, A.J.; Slagmolen, B.J.J.; Miller, J.; Evans, M.; Fritschel, P.; Sigg, D.; Waldman, S.J.; Shaddock, D.A.; McClelland, D.E. Arm-length stabilisation for interferometric gravitational-wave detectors using frequency-doubled auxiliary lasers. Opt. Express 2012, 20, 81–89. [Google Scholar] [CrossRef] [PubMed]
- Arai, K.; Ando, M.; Moriwaki, S.; Kawabe, K.; Tsubono, K. New signal extraction scheme with harmonic demodulation for power-recycled Fabry-Perot-Michelson interferometers. Phys. Lett. A 2000, 273, 15–24. [Google Scholar] [CrossRef]
- Cahillane, C.; Sigg, D. Out of Loop ALS COMM Frequency Measurement via IR. LHO alog 43119. Available online: https://alog.ligo-wa.caltech.edu/aLOG/index.php?callRep=43119 (accessed on 29 July 2018).
- Cahillane, C.; Dwyer, S.; Sigg, D. Out of Loop ALS COMM Frequency Measurement—Take Two. LHO alog 43214. Available online: https://alog.ligo-wa.caltech.edu/aLOG/index.php?callRep=43214 (accessed on 2 August 2018).
- Vajente, G. In situ correction of mirror surface to reduce round-trip losses in Fabry-Perot cavities. Appl. Opt. 2014, 53, 1459–1465. [Google Scholar] [CrossRef]
- Brooks, A.F.; Heptonstall, A.; Lynch, A.; Cole, A.; Abbott, B.; Vorvick, C.; Guido, C.; Ottaway, D.; King, E.; Gustafson, E.; et al. Overview of Advanced LIGO adaptive optics. Appl. Opt. 2016, 55, 8256–8265. [Google Scholar] [CrossRef]
- Weiss, R. Electronically Coupled Broadband Gravitational Antenna; Massachusetts Institute of Technology: Cambridge, MA, USA, 1972; p. 54. [Google Scholar]
- Barsotti, L.; Fritschel, P.; Evans, M.; Gras, S. Updated Advanced LIGO Sensitivity Design Curve; Technical Report LIGO-T1800044; LIGO Scientific Collaboration: Cambridge, MA, USA, 2018. [Google Scholar]
- Braginsky, V.B.; Khalili, F.Y.; Thorne, K.S. Quantum Measurement; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar] [CrossRef]
- Braginsky, V.; Vyatchanin, S. Thermodynamical fluctuations in optical mirror coatings. Phys. Lett. A 2003, 312, 244–255. [Google Scholar] [CrossRef][Green Version]
- Levin, Y. Internal thermal noise in the LIGO test masses: A direct approach. Phys. Rev. D 1998, 57, 659–663. [Google Scholar] [CrossRef]
- Hong, T.; Yang, H.; Gustafson, E.K.; Adhikari, R.X.; Chen, Y. Brownian thermal noise in multilayer coated mirrors. Phys. Rev. D 2013, 87, 082001. [Google Scholar] [CrossRef]
- Yam, W.; Gras, S.; Evans, M. Multimaterial coatings with reduced thermal noise. Phys. Rev. D 2015, 91, 042002. [Google Scholar] [CrossRef]
- Callen, H.; Greene, R. On a Theorem of Irreversible Thermodynamics. Phys. Rev. 1952, 86, 702–710. [Google Scholar] [CrossRef]
- Kubo, R. The fluctuation-dissipation theorem. Rep. Prog. Phys. 1966, 29, 255–284. [Google Scholar] [CrossRef]
- Saulson, P.R. Thermal noise in mechanical experiments. Phys. Rev. D 1990, 42, 2437–2445. [Google Scholar] [CrossRef] [PubMed]
- Nakagawa, N.; Gretarsson, A.M.; Gustafson, E.K.; Fejer, M.M. Thermal noise in half-infinite mirrors with nonuniform loss: A slab of excess loss in a half-infinite mirror. Phys. Rev. D 2002, 65, 102001. [Google Scholar] [CrossRef]
- Chalermsongsak, T.; Seifert, F.; Hall, E.D.; Arai, K.; Gustafson, E.K.; Adhikari, R.X. Broadband measurement of coating thermal noise in rigid Fabry–Pérot cavities. Metrologia 2014, 52, 17–30. [Google Scholar] [CrossRef]
- Gras, S.; Yu, H.; Yam, W.; Martynov, D.; Evans, M. Audio-band coating thermal noise measurement for Advanced LIGO with a multimode optical resonator. Phys. Rev. D 2017, 95, 022001. [Google Scholar] [CrossRef]
- Gras, S.; Evans, M. Direct measurement of coating thermal noise in optical resonators. Phys. Rev. D 2018, 98, 122001. [Google Scholar] [CrossRef]
- Cagnoli, G.; Hough, J.; DeBra, D.; Fejer, M.M.; Gustafson, E.; Rowan, S.; Mitrofanov, V. Damping dilution factor for a pendulum in an interferometric gravitational waves detector. Phys. Lett. A 2000, 272, 39–45. [Google Scholar] [CrossRef]
- Saulson, P.R. Terrestrial gravitational noise on a gravitational wave antenna. Phys. Rev. D 1984, 30, 732–736. [Google Scholar] [CrossRef]
- Hughes, S.A.; Thorne, K.S. Seismic gravity-gradient noise in interferometric gravitational-wave detectors. Phys. Rev. D 1998, 58, 122002. [Google Scholar] [CrossRef]
- Harms, J. Terrestrial Gravity Fluctuations. Living Rev. Relativ. 2015, 18, 3. [Google Scholar] [CrossRef] [PubMed]
- Driggers, J.C.; Harms, J.; Adhikari, R.X. Subtraction of Newtonian noise using optimized sensor arrays. Phys. Rev. D 2012, 86, 102001. [Google Scholar] [CrossRef]
- Coughlin, M.; Mukund, N.; Harms, J.; Driggers, J.; Adhikari, R.; Mitra, S. Towards a first design of a Newtonian-noise cancellation system for Advanced LIGO. Class. Quantum Gravity 2016, 33, 244001. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Harms, J.; Driggers, J.; McManus, D.J.; Mukund, N.; Ross, M.P.; Slagmolen, B.J.J.; Venkateswara, K. Implications of Dedicated Seismometer Measurements on Newtonian-Noise Cancellation for Advanced LIGO. Phys. Rev. Lett. 2018, 121, 221104. [Google Scholar] [CrossRef]
- Harms, J.; Bonilla, E.L.; Coughlin, M.W.; Driggers, J.; Dwyer, S.E.; McManus, D.J.; Ross, M.P.; Slagmolen, B.J.J.; Venkateswara, K. Observation of a potential future sensitivity limitation from ground motion at LIGO Hanford. Phys. Rev. D 2020, 101, 102002. [Google Scholar] [CrossRef]
- Driggers, J.C.; Vitale, S.; Lundgren, A.P.; Evans, M.; Kawabe, K.; Dwyer, S.E.; Izumi, K.; Schofield, R.M.; Effler, A.; Sigg, D.; et al. Improving astrophysical parameter estimation via offline noise subtraction for Advanced LIGO. Phys. Rev. D 2019, 99, 042001. [Google Scholar] [CrossRef]
- Barsotti, L.; McCuller, L.; Evans, M.; Fritschel, P. The A+ Design Curve; Technical Report T1800042-v5; LIGO Scientific Collaboration: Cambridge, MA, USA, 2018. [Google Scholar]
- Finn, L.S.; Chernoff, D.F. Observing binary inspiral in gravitational radiation: One interferometer. Phys. Rev. D 1993, 47, 2198. [Google Scholar] [CrossRef]
- Finn, L.S. Binary inspiral, gravitational radiation, and cosmology. Phys. Rev. D 1996, 53, 2878–2894. [Google Scholar] [CrossRef]
- Chen, H.Y.; Holz, D.E.; Miller, J.; Evans, M.; Vitale, S.; Creighton, J. Distance measures in gravitational-wave astrophysics and cosmology. Class. Quantum Gravity 2021, 38, 055010. [Google Scholar] [CrossRef]
- Brooks, A.F.; Vajente, G.; Yamamoto, H.; Abbott, R.; Adams, C.; Adhikari, R.X.; Ananyeva, A.; Appert, S.; Arai, K.; Areeda, J.S.; et al. Point absorbers in Advanced LIGO. Appl. Opt. 2021, 60, 4047–4063. [Google Scholar] [CrossRef]
- Isogai, T.; Miller, J.; Kwee, P.; Barsotti, L.; Evans, M.; Hinkley, N.; Sherman, J.A.; Phillips, N.B.; Schioppo, M.; Lemke, N.D.; et al. Loss in long-storage-time optical cavities. Opt. Express 2013, 21, 30114–30125. [Google Scholar] [CrossRef] [PubMed]
- Cahillane, C. Power Trend of Latest High Power Lock. LHO alog 58772. Available online: https://alog.ligo-wa.caltech.edu/aLOG/index.php?callRep=58772 (accessed on 28 April 2021).
- Cahillane, C. Power Trends for a Lock Today. LHO alog 58794. Available online: https://alog.ligo-wa.caltech.edu/aLOG/index.php?callRep=58794 (accessed on 29 April 2021).
- Cahillane, C. Power in the Interferometer—Pre-O4. LHO alog 59142. Available online: https://alog.ligo-wa.caltech.edu/aLOG/index.php?callRep=59142 (accessed on 4 June 2021).
- Martynov, D. PRG and Optical Gain Increase. LLO alog 43121. Available online: https://alog.ligo-la.caltech.edu/aLOG/index.php?callRep=43121 (accessed on 3 February 2019).
- Evans, M.; Barsotti, L.; Fritschel, P. A general approach to optomechanical parametric instabilities. Phys. Lett. A 2010, 374, 665–671. [Google Scholar] [CrossRef]
- Green, A.C.; Brown, D.D.; Dovale-Alvarez, M.; Collins, C.; Miao, H.; Mow-Lowry, C.M.; Freise, A. The influence of dual-recycling on parametric instabilities at Advanced LIGO. Class. Quantum Gravity 2017, 34, 205004. [Google Scholar] [CrossRef]
- Miller, J.; Evans, M.; Barsotti, L.; Fritschel, P.; MacInnis, M.; Mittleman, R.; Shapiro, B.; Soto, J.; Torrie, C. Damping parametric instabilities in future gravitational wave detectors by means of electrostatic actuators. Phys. Lett. A 2011, 375, 788–794. [Google Scholar] [CrossRef]
- Blair, C.; Gras, S.; Abbott, R.; Aston, S.; Betzwieser, J.; Blair, D.; Derosa, R.; Evans, M.; Frolov, V.; Fritschel, P.; et al. First Demonstration of Electrostatic Damping of Parametric Instability at Advanced LIGO. Phys. Rev. Lett. 2017, 118, 151102. [Google Scholar] [CrossRef] [PubMed]
- Hardwick, T. High Power and Optomechanics in Advanced LIGO Detectors. Ph.D. Thesis, Louisiana State University, Baton Rouge, LA, USA, 2019. [Google Scholar]
- Biscans, S.; Gras, S.; Blair, C.D.; Driggers, J.; Evans, M.; Fritschel, P.; Hardwick, T.; Mansell, G. Suppressing parametric instabilities in LIGO using low-noise acoustic mode dampers. Phys. Rev. D 2019, 100, 122003. [Google Scholar] [CrossRef]
- Buonanno, A.; Chen, Y. Signal recycled laser-interferometer gravitational-wave detectors as optical springs. Phys. Rev. D 2002, 65, 042001. [Google Scholar] [CrossRef]
- Sheard, B.S.; Gray, M.B.; Mow-Lowry, C.M.; McClelland, D.E.; Whitcomb, S.E. Observation and characterization of an optical spring. Phys. Rev. A 2004, 69, 051801. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Bond, C.; Brown, D.; Freise, A.; Strain, K.A. Interferometer techniques for gravitational-wave detection. Living Rev. Relativ. 2017, 19, 1–217. [Google Scholar] [CrossRef]
- Whittle, C.; Hall, E.D.; Dwyer, S.; Mavalvala, N.; Sudhir, V.; Abbott, R.; Ananyeva, A.; Austin, C.; Barsotti, L.; Betzwieser, J.; et al. Approaching the motional ground state of a 10-kg object. Science 2021, 372, 1333–1336. [Google Scholar] [CrossRef] [PubMed]
- Dwyer, S.; Mansell, G.; McCuller, L. Squeezing in gravitational wave detectors. Galaxies, 2022; under review. [Google Scholar]
- Nguyen, P.; Schofield, R.M.; Effler, A.; Austin, C.; Adya, V.; Ball, M.; Banagiri, S.; Banowetz, K.; Billman, C.; Blair, C.D.; et al. Environmental noise in advanced LIGO detectors. Class. Quantum Gravity 2021, 38, 14500. [Google Scholar] [CrossRef]
- Schwartz, E.; Pele, A.; Warner, J.; Lantz, B.; Betzwieser, J.; Dooley, K.L.; Biscans, S.; Coughlin, M.; Mukund, N.; Abbott, R.; et al. Improving the robustness of the advanced LIGO detectors to earthquakes. Class. Quantum Gravity 2020, 37, 235007. [Google Scholar] [CrossRef]
- Ross, M.P.; Venkateswara, K.; Mow-Lowry, C.; Cooper, S.; Warner, J.; Lantz, B.; Kissel, J.; Radkins, H.; Shaffer, T.; Mittleman, R.; et al. Towards windproofing LIGO: Reducing the effect of wind-driven floor tilt by using rotation sensors in active seismic isolation. Class. Quantum Gravity 2020, 37, 185018. [Google Scholar] [CrossRef]
- Soni, S.; Austin, C.; Effler, A.; Schofield, R.M.S.; González, G.; Frolov, V.V.; Driggers, J.C.; Pele, A.; Urban, A.L.; Valdes, G.; et al. Reducing scattered light in LIGO’s third observing run. Class. Quantum Gravity 2021, 38, 025016. [Google Scholar] [CrossRef]
- Kwee, P.; Miller, J.; Isogai, T.; Barsotti, L.; Evans, M. Decoherence and degradation of squeezed states in quantum filter cavities. Phys. Rev. D 2014, 90, 062006. [Google Scholar] [CrossRef]
- Whittle, C.; Komori, K.; Ganapathy, D.; McCuller, L.; Barsotti, L.; Mavalvala, N.; Evans, M. Optimal detuning for quantum filter cavities. Phys. Rev. D 2020, 102, 102002. [Google Scholar] [CrossRef]
- Komori, K.; Ganapathy, D.; Whittle, C.; McCuller, L.; Barsotti, L.; Mavalvala, N.; Evans, M. Demonstration of an amplitude filter cavity at gravitational-wave frequencies. Phys. Rev. D 2020, 102, 102003. [Google Scholar] [CrossRef]
- Bode, N.; Meylahn, F.; Willke, B. Sequential high power laser amplifiers for gravitational wave detection. Opt. Express 2020, 28, 29469–29478. [Google Scholar] [CrossRef]
- Cao, H.T.; Brooks, A.; Ng, S.W.S.; Ottaway, D.; Perreca, A.; Richardson, J.W.; Chaderjian, A.; Veitch, P.J. High dynamic range thermally actuated bimorph mirror for gravitational wave detectors. Appl. Opt. 2020, 59, 2784–2790. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, V.; Mansell, G.; Makarem, C.; Noh, M.; Abbott, R.; Ballmer, S.; Billingsley, G.; Brooks, A.; Cao, H.T.; Fritschel, P.; et al. Piezo-deformable Mirrors for Active Mode Matching in Advanced LIGO. arXiv 2021, arXiv:2110.00674. [Google Scholar]
- Sigg, D. Status of the LIGO detectors. Class. Quantum Gravity 2008, 25, 114041. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Adhikari, R.; Ajith, P.; Allen, B.; Allen, G.; Amin, R.S.; Anderson, S.B.; Anderson, W.G.; Arain, M.A.; et al. LIGO: The Laser Interferometer Gravitational-Wave Observatory. Rep. Prog. Phys. 2009, 72, 076901. [Google Scholar] [CrossRef]
- Aasi, J.; Abadie, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Accadia, T.; Acernese, F.; Adams, C.; Adams, T.; et al. Characterization of the LIGO detectors during their sixth science run. Class. Quantum Gravity 2015, 32, 115012. [Google Scholar] [CrossRef]
- Caron, B.; Dominjon, A.; Drezen, C.; Flaminio, R.; Grave, X.; Marion, F.; Massonnet, L.; Mehmel, C.; Morand, R.; Mours, B.; et al. The VIRGO interferometer for gravitational wave detection. Nucl. Phys. B Proc. Suppl. 1997, 54, 167–175. [Google Scholar] [CrossRef]
- Acernese, F.; Alshourbagy, M.; Amico, P.; Antonucci, F.; Aoudia, S.; Astone, P.; Avino, S.; Baggio, L.; Ballardin, G.; Barone, F.; et al. Status of Virgo. Class. Quantum Gravity 2008, 25, 114045. [Google Scholar] [CrossRef][Green Version]
- Grote, H.; Allen, B.; Aufmuth, P.; Aulbert, C.; Babak, S.; Balasubramanian, R.; Barr, B.W.; Berukoff, S.; Bunkowski, A.; Cagnoli, G.; et al. The status of GEO 600. Class. Quantum Gravity 2005, 22, S193–S198. [Google Scholar] [CrossRef]
- Grote, H.; LIGO Scientific Collaboration. The GEO 600 status. Class. Quantum Gravity 2010, 27, 084003. [Google Scholar] [CrossRef]
- Ando, M.; Collaboration, t.T. Current status of TAMA. Class. Quantum Gravity 2002, 19, 1409. [Google Scholar] [CrossRef]
- Acernese, F.; Agathos, M.; Agatsuma, K.; Aisa, D.; Allemandou, N.; Allocca, A.; Amarni, J.; Astone, P.; Balestri, G.; Ballardin, G.; et al. Advanced Virgo: A second-generation interferometric gravitational wave detector. Class. Quantum Gravity 2015, 32, 024001. [Google Scholar] [CrossRef]
- Somiya, K. Detector configuration of KAGRA–the Japanese cryogenic gravitational-wave detector. Class. Quantum Gravity 2012, 29, 124007. [Google Scholar] [CrossRef]
- Aso, Y.; Michimura, Y.; Somiya, K.; Ando, M.; Miyakawa, O.; Sekiguchi, T.; Tatsumi, D.; Yamamoto, H. Interferometer design of the KAGRA gravitational wave detector. Phys. Rev. D 2013, 88, 043007. [Google Scholar] [CrossRef]
- Akutsu, T.; Ando, M.; Arai, K.; Arai, Y.; Araki, S.; Araya, A.; Aritomi, N.; Aso, Y.; Bae, S.; Bae, Y.; et al. Overview of KAGRA: Detector design and construction history. Prog. Theor. Exp. Phys. 2021, 2021, 49. [Google Scholar] [CrossRef]
- Padma, T. India’s LIGO gravitational-wave observatory gets green light. Nature. 22 January 2019. [CrossRef]
- Adhikari, R.X.; Arai, K.; Brooks, A.F.; Wipf, C.; Aguiar, O.; Altin, P.; Barr, B.; Barsotti, L.; Bassiri, R.; Bell, A.; et al. A cryogenic silicon interferometer for gravitational-wave detection. Class. Quantum Gravity 2020, 37, 165003. [Google Scholar] [CrossRef]
- Hild, S.; Abernathy, M.; Acernese, F.; Amaro-Seoane, P.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. Sensitivity studies for third-generation gravitational wave observatories. Class. Quantum Gravity 2011, 28, 094013. [Google Scholar] [CrossRef]
- Evans, M.; Adhikari, R.X.; Afle, C.; Ballmer, S.W.; Biscoveanu, S.; Borhanian, S.; Brown, D.A.; Chen, Y.; Eisenstein, R.; Gruson, A.; et al. A Horizon Study for Cosmic Explorer: Science, Observatories, and Community. arXiv 2021, arXiv:2109.09882. [Google Scholar]
- Baker, J.; Bellovary, J.; Bender, P.L.; Berti, E.; Caldwell, R.; Camp, J.; Conklin, J.W.; Cornish, N.; Cutler, C.; DeRosa, R.; et al. The Laser Interferometer Space Antenna: Unveiling the Millihertz Gravitational Wave Sky. arXiv 2019, arXiv:1907.06482. [Google Scholar]
- Sumner, T.J.; Mueller, G.; Conklin, J.W. LISA Pathfinder: First steps to observing gravitational waves from space. J. Phys. Conf. Ser. 2017, 840, 012001. [Google Scholar] [CrossRef]
- Michelson, A.A.; Morley, E.W. On the Relative Motion of the Earth and the Luminiferous Ether. Am. J. Sci. 1887, 34, 333–345. [Google Scholar] [CrossRef]
- Willke, B.; Gustafson, E.K.; Husman, M.E.; Lawrence, M.J.; Byer, R.L. Dynamic response of a Fabry-Perot interferometer. JOSA B 1999, 16, 523–532. [Google Scholar] [CrossRef]
- Rakhmanov, M.; Savage, R.; Reitze, D.; Tanner, D. Dynamic resonance of light in Fabry-Perot cavities. Phys. Lett. A 2002, 305, 239–244. [Google Scholar] [CrossRef]
- Bondu, F.; Debieu, O. Accurate measurement method of Fabry-Perot cavity parameters via optical transfer function. Appl. Opt. 2007, 46, 2611–2614. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).