Stochastic Gravitational-Wave Backgrounds: Current Detection Efforts and Future Prospects
Abstract
1. Introduction
2. Theory of Stochastic Backgrounds
2.1. Gravitational-Wave Strain and Stokes Parameters
2.2. The Energy Density of Gravitational Waves
3. Sources of Stochastic Backgrounds
3.1. Astrophysical Backgrounds
3.2. Primordial Backgrounds
3.3. Anisotropies in Stochastic Backgrounds
3.4. Observational Properties of Stochastic Backgrounds
4. Detection Approaches and Methodologies
4.1. Interdetector and Spatial Correlations
4.2. Isotropic Background Search Methods
4.2.1. Ground-Based Detectors
4.2.2. Pulsar Timing Arrays
4.3. Anisotropic Background Detection Methods
4.4. The Approach towards Non-Gaussian Backgrounds
5. Current Detection Efforts of SGWBs
5.1. Searches with Ground-Based Laser Interferometers
5.1.1. Search Results for an Isotropic Background by LVK
5.1.2. Search Results for an Anisotropic Background by LVK
5.2. Stochastic Searches with Pulsar Timing Arrays
5.2.1. Search Results for an Isotropic Nanohertz Background
5.2.2. Challenges in GWB Searches with PTAs
5.2.3. Search Results for an Anisotropic Nanohertz Background
5.2.4. Search Results for a Nanohertz Background Not Related to Supermassive Black Hole Binaries
5.3. Other Stochastic Background Searches
6. Stochastic Background Detection Prospects with Future Gravitational-Wave Detectors
6.1. Stochastic Searches with Third Generation Interferometers
6.2. Stochastic Searches with the Laser Interferometer Space Antenna
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | There are several theories that postulate modifications to this statement, but these modifications are strongly constrained by multimessenger observations of the binary neutron star merger GW170817 [36]. |
| 2 | Strictly speaking, GWs with wavelengths larger than the size of the cosmological horizon are frozen out by Hubble friction and, thus, do not contribute to the effective energy density. As a result, the density parameter appearing on the left-hand side of Equation (14) should be interpreted as an integral over from a minimum frequency of , which corresponds to the size of the horizon at the epoch when the CMB photons were emitted. |
| 3 | Often in the literature, the letter is used to denote a different spectral index, hereby denoted , of the characteristic strain spectrum of the stochastic gravitational wave background , where is the power spectral density of the background. This leads to the power-law index of for in Equation (25) instead of . |
| 4 | |
| 5 | As mentioned in the footnote 3, the energy density spectral index is related to the strain amplitude spectral index such that . Therefore , which is the quantity often referred to as in publications. Due to the parametric choices made in the different search pipelines, is most frequently used in LVK literature, while is most frequently used in the PTA literature. |
| 6 | There are, in fact, sources of spatially correlated noise. They can be distinguished from SGWBs by either a deterministic component or by an overlap reduction function different to those of SGWBs. We provide more details in Section 5. |
| 7 | Time segments with non-stationary noise are removed from analyses of real data [56], the stationarity is usually determined empirically. Note that when applying a non-trivial windowing function to time-domain data, e.g., for computing a discrete Fourier transform, we introduce correlations between frequency bins. This effect and the methods to mitigate it are described in [130]. |
| 8 | |
| 9 | Note that directly interfering laser beams in the case of LISA is impossible due to energy dispersion along the arm [29]. |
| 10 | Note that this is no longer the case in the presence of temporal shot noise, e.g., for the astrophysical GWB from compact binary coalescences [122]. In this case, each time segment will have random GWB intensity fluctuations due to the finite number of sources. The statistical independence of these fluctuations at different times can be leveraged to mitigate the impact of shot noise on measurements of the angular power spectrum [123]. |
| 11 | Note that in these two cases and have different units because in (114) the basis function carry units . |
| 12 | In fact, in [215] the authors discuss the extension of their optimal search method in the presence of non-Gaussian noise as well. The implementation of the method becomes substantially more involved, however practical considerations about the nature and behaviour of the non-Gaussian noise can simplify it considerably. |
| 13 | |
| 14 | Often used in the literature to quantify noise in a given pulsar. For rms of Gaussian white noise, the power spectral density of residuals , where is the time between observations, which is typically a couple of weeks. Note, rms residuals may increase with longer data spans due to more sources of noise becoming prominent at longer time scales. Sometimes rms residuals are provided for a particular source of noise. |
References
- Davis, D.; Walker, M. Detector Characterization and Mitigation of Noise in Ground-Based Gravitational-Wave Interferometers. Galaxies 2022, 10, 12. [Google Scholar] [CrossRef]
- Sun, L.; Goetz, E.; Kissel, J.S.; Betzwieser, J.; Karki, S.; Viets, A.; Wade, M.; Bhattacharjee, D.; Bossilkov, V.; Covas, P.B.; et al. Characterization of systematic error in Advanced LIGO calibration. Class. Quant. Grav. 2020, 37, 225008. [Google Scholar] [CrossRef]
- Sun, L.; Goetz, E.; Kissel, J.S.; Betzwieser, J.; Karki, S.; Bhattacharjee, D.; Covas, P.B.; Datrier, L.E.; Kandhasamy, S.; Lecoeuche, Y.K.; et al. Characterization of systematic error in Advanced LIGO calibration in the second half of O3. arXiv 2021, arXiv:2107.00129. [Google Scholar]
- Acernese, F.; Agathos, M.; Ain, A.; Albanesi, S.; Allocca, A.; Amato, A.; Andrade, T.; Andres, N.; Andrić, T.; Ansoldi, S.; et al. Calibration of Advanced Virgo and reconstruction of detector strain h(t) during the Observing Run O3. Class. Quant. Grav. 2022, 39, 045006. [Google Scholar] [CrossRef]
- Akutsu, T.; Ando, M.; Arai, K.; Arai, Y.; Araki, S.; Araya, A.; Aritomi, N.; Asada, H.; Aso, Y.; Bae, S.; et al. Overview of KAGRA: Calibration, detector characterization, physical environmental monitors, and the geophysics interferometer. PTEP 2021, 2021, 05A102. [Google Scholar] [CrossRef]
- Verbiest, J.P.W.; Osłowski, S.; Burke-Spolaor, S. Pulsar Timing Array Experiments. In Handbook of Gravitational Wave Astronomy; Bambi, C., Katsanevas, S., Kokkotas, K.D., Eds.; Springer: Singapore, 2020; pp. 1–42. [Google Scholar] [CrossRef]
- Tiburzi, C. Pulsars Probe the Low-Frequency Gravitational Sky: Pulsar Timing Arrays Basics and Recent Results. PASA 2018, 35, e013. [Google Scholar] [CrossRef]
- Hobbs, G.; Dai, S. Gravitational wave research using pulsar timing arrays. Natl. Sci. Rev. 2017, 4, 707–717. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW150914: The Advanced LIGO Detectors in the Era of First Discoveries. Phys. Rev. Lett. 2016, 116, 131103. [Google Scholar] [CrossRef]
- Accadia, T.; Acernese, F.; Antonucci, F.; Astone, P.; Ballardin, G.; Barone, F.; Barsuglia, M.; Basti, A.; Bauer, T.S.; Bebronne, M.; et al. Status of the Virgo project. Class. Quantum Gravity 2011, 28, 114002. [Google Scholar] [CrossRef]
- Affeldt, C.; Danzmann, K.; Dooley, K.L.; Grote, H.; Hewitson, M.; Hild, S.; Hough, J.; Leong, J.; Lück, H.; Prijatelj, M.; et al. Advanced techniques in GEO 600. Class. Quantum Gravity 2014, 31, 224002. [Google Scholar] [CrossRef]
- Castelvecchi, D. Japan’s pioneering detector set to join hunt for gravitational waves. Nature 2019, 562, 9–10. [Google Scholar] [CrossRef] [PubMed]
- LIGO-India, Proposal of the Consortium for Indian Initiative in Gravitational-Wave Observations (IndIGO). Available online: https://dcc.ligo.org/LIGO-M1100296/public (accessed on 1 November 2021).
- Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. The Einstein Telescope: A third-generation gravitational wave observatory. Class. Quant. Grav. 2010, 27, 194002. [Google Scholar] [CrossRef]
- Sathyaprakash, B.; Abernathy, M.; Acernese, F.; Amaro-Seoane, P.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. Scientific Potential of Einstein Telescope. In Proceedings of the 46th Rencontres de Moriond on Gravitational Waves and Experimental Gravity, La Thuile, Italy, 20–27 March 2011; pp. 127–136. [Google Scholar]
- Abadie, J.; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.; Accadia, T.; Acernese, F.; Adams, C.; Adhikari, R.; Affeldt, C.; et al. Upper limits on a stochastic gravitational-wave background using LIGO and Virgo interferometers at 600–1000 Hz. Phys. Rev. D 2012, 85, 122001. [Google Scholar] [CrossRef]
- Reitze, D.; Adhikari, R.X.; Ballmer, S.; Barish, B.; Barsotti, L.; Billingsley, G.; Brown, D.A.; Chen, Y.; Coyne, D.; Eisenstein, R.; et al. Cosmic Explorer: The U.S. Contribution to Gravitational-Wave Astronomy beyond LIGO. Bull. Am. Astron. Soc. 2019, 51, 035. [Google Scholar]
- Hall, E.D.; Kuns, K.; Smith, J.R.; Bai, Y.; Wipf, C.; Biscans, S.; Adhikari, R.X.; Arai, K.; Ballmer, S.; Barsotti, L.; et al. Gravitational-wave physics with Cosmic Explorer: Limits to low-frequency sensitivity. Phys. Rev. D 2021, 103, 122004. [Google Scholar] [CrossRef]
- McLaughlin, M.A. The North American Nanohertz Observatory for Gravitational Waves. Class. Quantum Gravity 2013, 30, 224008. [Google Scholar] [CrossRef]
- Manchester, R.N.; Hobbs, G.; Bailes, M.; Coles, W.A.; van Straten, W.; Keith, M.J.; Shannon, R.M.; Bhat, N.D.R.; Brown, A.; Burke-Spolaor, S.G.; et al. The Parkes Pulsar Timing Array Project. PASA 2013, 30, e017. [Google Scholar] [CrossRef]
- Kramer, M.; Champion, D.J. The European Pulsar Timing Array and the Large European Array for Pulsars. Class. Quantum Gravity 2013, 30, 224009. [Google Scholar] [CrossRef]
- Desvignes, G.; Caballero, R.N.; Lentati, L.; Verbiest, J.P.W.; Champion, D.J.; Stappers, B.W.; Janssen, G.H.; Lazarus, P.; Osłowski, S.; Babak, S.; et al. High-precision timing of 42 millisecond pulsars with the European Pulsar Timing Array. Mon. Not. R. Astron. Soc. 2016, 458, 3341–3380. [Google Scholar] [CrossRef]
- Hobbs, G.; Archibald, A.; Arzoumanian, Z.; Backer, D.; Bailes, M.; Bhat, N.D.R.; Burgay, M.; Burke-Spolaor, S.; Champion, D.; Cognard, I.; et al. The International Pulsar Timing Array project: Using pulsars as a gravitational wave detector. Class. Quantum Gravity 2010, 27, 084013. [Google Scholar] [CrossRef]
- Verbiest, J.P.W.; Lentati, L.; Hobbs, G.; van Haasteren, R.; Demorest, P.B.; Janssen, G.H.; Wang, J.B.; Desvignes, G.; Caballero, R.N.; Keith, M.J.; et al. The International Pulsar Timing Array: First data release. MNRAS 2016, 458, 1267–1288. [Google Scholar] [CrossRef]
- Joshi, B.C.; Arumugasamy, P.; Bagchi, M.; Bandyopadhyay, D.; Basu, A.; Dhanda Batra, N.; Bethapudi, S.; Choudhary, A.; De, K.; Dey, L.; et al. Precision pulsar timing with the ORT and the GMRT and its applications in pulsar astrophysics. J. Astrophys. Astron. 2018, 39, 51. [Google Scholar] [CrossRef]
- Goncharov, B.; Shannon, R.M.; Reardon, D.J.; Hobbs, G.; Zic, A.; Bailes, M.; Curyło, M.; Dai, S.; Kerr, M.; Lower, M.E.; et al. On the Evidence for a Common-spectrum Process in the Search for the Nanohertz Gravitational-wave Background with the Parkes Pulsar Timing Array. ApJ 2021, 917, L19. [Google Scholar] [CrossRef]
- Dewdney, P.E.; Hall, P.J.; Schilizzi, R.T.; Lazio, T.J.L.W. The Square Kilometre Array. IEEE Proc. 2009, 97, 1482–1496. [Google Scholar] [CrossRef]
- Nan, R.; Li, D.; Jin, C.; Wang, Q.; Zhu, L.; Zhu, W.; Zhang, H.; Yue, Y.; Qian, L. The Five-Hundred Aperture Spherical Radio Telescope (fast) Project. Int. J. Mod. Phys. D 2011, 20, 989–1024. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Wald, R.M. General Relativity; University of Chicago Press: Chicago, IL, USA, 1984. [Google Scholar]
- Cornish, N.J. Mapping the gravitational-wave background. Class. Quantum Gravity 2001, 18, 4277–4291. [Google Scholar] [CrossRef]
- Allen, B.; Ottewill, A.C. Detection of Anisotropies in the Gravitational-Wave Stochastic Background. Phys. Rev. D 1996, 56, 545–563. [Google Scholar] [CrossRef]
- Romano, J.D.; Cornish, N.J. Detection methods for stochastic gravitational-wave backgrounds: A unified treatment. Living Rev. Relativ. 2017, 20, 1–223. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Renzini, A.I. Mapping the Gravitational-Wave Background. Ph.D. Thesis, Imperial College London, London, UK, 2020. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Kolb, E.W.; Turner, M.S. The Early Universe; Addison-Wesley: Boston, MA, USA, 1990; Volume 69. [Google Scholar]
- Pagano, L.; Salvati, L.; Melchiorri, A. New constraints on primordial gravitational waves from Planck 2015. Phys. Lett. B 2016, 760, 823–825. [Google Scholar] [CrossRef]
- Christensen, N. Stochastic Gravitational Wave Backgrounds. Rep. Prog. Phys. 2019, 82, 016903. [Google Scholar] [CrossRef] [PubMed]
- Phinney, E.S. A Practical Theorem on Gravitational Wave Backgrounds. arXiv 2001, arXiv:0108028. [Google Scholar]
- Isaacson, R.A. Gravitational Radiation in the Limit of High Frequency. I. The Linear Approximation and Geometrical Optics. Phys. Rev. 1968, 166, 1263–1271. [Google Scholar] [CrossRef]
- Isaacson, R.A. Gravitational Radiation in the Limit of High Frequency. II. Nonlinear Terms and the Ef fective Stress Tensor. Phys. Rev. 1968, 166, 1272–1279. [Google Scholar] [CrossRef]
- Renzini, A.I.; Romano, J.D.; Contaldi, C.R.; Cornish, N.J. A comparison of maximum likelihood mapping methods for gravitational-wave backgrounds. Phys. Rev. D 2022, 105, 023519. [Google Scholar] [CrossRef]
- Grishchuk, L. Amplification of gravitational waves in an isotropic universe. Sov. J. Exp. Theor. Phys. 1975, 40, 409. [Google Scholar]
- Maggiore, M. Gravitational wave experiments and early universe cosmology. Phys. Rep. 2000, 331, 283–367. [Google Scholar] [CrossRef]
- Hogan, C.J. Gravitational radiation from cosmological phase transitions. Mon. Not. R. Astron. Soc. 1986, 218, 629–636. [Google Scholar] [CrossRef]
- Battye, R.A.; Caldwell, R.R.; Shellard, E.P.S. Gravitational waves from cosmic strings. In Topological Defects in Cosmology; World Scientific Pub. Co. Inc.: Singapore, 1997; pp. 11–31. [Google Scholar]
- Vilenkin, A.; Shellard, E.S. Cosmic Strings and Other Topological Defects; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bartolo, N.; De Luca, V.; Franciolini, G.; Lewis, A.; Peloso, M.; Riotto, A. Primordial Black Hole Dark Matter: LISA Serendipity. Phys. Rev. Lett. 2019, 122, 211301. [Google Scholar] [CrossRef]
- Bartolo, N.; Bertacca, D.; De Luca, V.; Franciolini, G.; Matarrese, S.; Peloso, M.; Ricciardone, A.; Riotto, A.; Tasinato, G. Gravitational wave anisotropies from primordial black holes. J. Cosmol. Astropart. Phys. 2020, 02, 028. [Google Scholar] [CrossRef]
- Margalit, A.; Contaldi, C.R.; Pieroni, M. Phase Decoherence of Gravitational Wave Backgrounds. Phys. Rev. D 2020, 102, 083506. [Google Scholar] [CrossRef]
- Maggiore, M. Gravitational Waves. Vol. 2: Astrophysics and Cosmology; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Auclair, P.; Blanco-Pillado, J.J.; Figueroa, D.G.; Jenkins, A.C.; Lewicki, M.; Sakellariadou, M.; Sanidas, S.; Sousa, L.; Steer, D.A.; Wachter, J.M.; et al. Probing the gravitational wave background from cosmic strings with LISA. J. Cosmol. Astropart. Phys. 2020, 04, 034. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Baker, P.T.; Blumer, H.; Bécsy, B.; Brazier, A.; Brook, P.R.; Burke-Spolaor, S.; Chatterjee, S.; Chen, S.; Cordes, J.M.; et al. The NANOGrav 12.5 yr Data Set: Search for an Isotropic Stochastic Gravitational-wave Background. ApJ 2020, 905, L34. [Google Scholar] [CrossRef]
- Caprini, C.; Hindmarsh, M.; Huber, S.; Konstandin, T.; Kozaczuk, J.; Nardini, G.; No, J.M.; Petiteau, A.; Schwaller, P.; Servant, G.; et al. Science with the space-based interferometer eLISA. II: Gravitational waves from cosmological phase transitions. JCAP 2016, 04, 001. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Upper limits on the isotropic gravitational-wave background from Advanced LIGO and Advanced Virgo’s third observing run. Phys. Rev. D 2021, 104, 022004. [Google Scholar] [CrossRef]
- Kalogera, V.; Baym, G. The maximum mass of a neutron star. Astrophys. J. Lett. 1996, 470, L61–L64. [Google Scholar] [CrossRef]
- Bailyn, C.D.; Jain, R.K.; Coppi, P.; Orosz, J.A. The Mass Distribution of Stellar Black Holes. ApJ 1998, 499, 367–374. [Google Scholar] [CrossRef]
- Özel, F.; Psaltis, D.; Narayan, R.; McClintock, J.E. The Black Hole Mass Distribution in the Galaxy. ApJ 2010, 725, 1918–1927. [Google Scholar] [CrossRef]
- Gupta, A.; Gerosa, D.; Arun, K.G.; Berti, E.; Farr, W.M.; Sathyaprakash, B.S. Black holes in the low mass gap: Implications for gravitational wave observations. Phys. Rev. D 2020, 101, 103036. [Google Scholar] [CrossRef]
- Celotti, A.; Miller, J.C.; Sciama, D.W. Astrophysical evidence for the existence of black holes. Class. Quantum Gravity 2000, 16, A3. [Google Scholar] [CrossRef]
- Cooray, A.R. Gravitational wave background of neutron star-white dwarf binaries. Mon. Not. R. Astron. Soc. 2004, 354, 25–30. [Google Scholar] [CrossRef][Green Version]
- Korol, V.; Belokurov, V.; Moore, C.J.; Toonen, S. Weighing Milky Way Satellites with LISA. Mon. Not. R. Astron. Soc. 2021, 502, L55–L60. [Google Scholar] [CrossRef]
- Regimbau, T. The astrophysical gravitational wave stochastic background. Res. Astron. Astrophys. 2011, 11, 369. [Google Scholar] [CrossRef]
- Callister, T.; Fishbach, M.; Holz, D.; Farr, W. Shouts and Murmurs: Combining Individual Gravitational-Wave Sources with the Stochastic Background to Measure the History of Binary Black Hole Mergers. Astrophys. J. Lett. 2020, 896, L32. [Google Scholar] [CrossRef]
- Fishbach, M.; Holz, D.E.; Farr, W.M. Does the Black Hole Merger Rate Evolve with Redshift? Astrophys. J. Lett. 2018, 863, L41. [Google Scholar] [CrossRef]
- Madau, P.; Dickinson, M. Cosmic Star Formation History. Annu. Rev. Astron. Astrophys. 2014, 52, 415–486. [Google Scholar] [CrossRef]
- Boco, L.; Lapi, A.; Goswami, S.; Perrotta, F.; Baccigalupi, C.; Danese, L. Merging Rates of Compact Binaries in Galaxies: Perspectives for Gravitational Wave Detections. Astrophys. J. 2019, 881, 157. [Google Scholar] [CrossRef]
- Boco, L.; Lapi, A.; Chruslinska, M.; Donevski, D.; Sicilia, A.; Danese, L. Evolution of Galaxy Star Formation and Metallicity: Impact on Double Compact Objects Mergers. Astrophys. J. 2021, 907, 110. [Google Scholar] [CrossRef]
- Callister, T.; Sammut, L.; Qiu, S.; Mandel, I.; Thrane, E. The limits of astrophysics with gravitational-wave backgrounds. Phys. Rev. X 2016, 6, 031018. [Google Scholar] [CrossRef]
- Sesana, A.; Vecchio, A.; Colacino, C.N. The stochastic gravitational-wave background from massive black hole binary systems: Implications for observations with Pulsar Timing Arrays. Mon. Not. R. Astron. Soc. 2008, 390, 192–209. [Google Scholar] [CrossRef]
- Thorne, K.; Hawking, S.; Israel, W. Three Hundred Years of Gravitation; Cambridge University Press: Cambridge, UK, 1987; p. 330. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Implications for the Stochastic Gravitational-Wave Background from Compact Binary Coalescences. Phys. Rev. Lett. 2018, 120, 091101. [Google Scholar] [CrossRef] [PubMed]
- LIGO Scientific Collaboration; Virgo Collaboration; KAGRA Scientific Collaboration. The population of merging compact binaries inferred using gravitational waves through GWTC-3. arXiv 2021, arXiv:2111.03634. [Google Scholar]
- LIGO Scientific Collaboration; Virgo Collaboration; KAGRA Collaboration. The Population of Merging Compact Binaries Inferred Using Gravitational Waves through GWTC-3—Data Release. 2021. Available online: https://zenodo.org/record/5655785 (accessed on 1 November 2021).
- Caprini, C.; Figueroa, D.G. Cosmological backgrounds of gravitational waves. Class. Quantum Gravity 2018, 35, 163001. [Google Scholar] [CrossRef]
- Guzzetti, M.C.; Bartolo, N.; Liguori, M.; Matarrese, S. Gravitational waves from inflation. Riv. Nuovo Cim. 2016, 39, 399–495. [Google Scholar] [CrossRef]
- Contaldi, C.R.; Magueijo, J. Unsqueezing of standing waves due to inflationary domain structure. Phys. Rev. D 2018, 98, 043523. [Google Scholar] [CrossRef]
- Kamionkowski, M.; Kosowsky, A.; Stebbins, A. A Probe of primordial gravity waves and vorticity. Phys. Rev. Lett. 1997, 78, 2058–2061. [Google Scholar] [CrossRef]
- COrE Collaboration; Bouchet, F.R. COrE (Cosmic Origins Explorer) A White Paper. arXiv 2011, arXiv:1102.2181. [Google Scholar]
- Matsumura, T.; Akiba, Y.; Borrill, J.; Chinone, Y.; Dobbs, M.; Fuke, H.; Ghribi, A.; Hasegawa, M.; Hattori, K.; Hattori, M.; et al. Mission design of LiteBIRD. J. Low Temp. Phys. 2014, 176, 733. [Google Scholar] [CrossRef]
- Abazajian, K.N.; Adshead, P.; Ahmed, Z.; Allen, S.W.; Alonso, D.; Arnold, K.S.; Baccigalupi, C.; Bartlett, J.G.; Battaglia, N.; Benson, B.A.; et al. CMB-S4 Science Book, First Edition. arXiv 2016, arXiv:1610.02743. [Google Scholar]
- Ade, P.; Aguirre, J.; Ahmed, Z.; Aiola, S.; Ali, A.; Alonso, D.; Alvarez, M.A.; Arnold, K.; Ashton, P.; Austermann, J.; et al. The Simons Observatory: Science goals and forecasts. JCAP 2019, 02, 056. [Google Scholar] [CrossRef]
- Kuroyanagi, S.; Chiba, T.; Sugiyama, N. Precision calculations of the gravitational wave background spectrum from inflation. Phys. Rev. D 2009, 79, 103501. [Google Scholar] [CrossRef]
- Chung, D.J.H.; Kolb, E.W.; Riotto, A.; Tkachev, I.I. Probing Planckian physics: Resonant production of particles during inflation and features in the primordial power spectrum. Phys. Rev. D 2000, 62, 043508. [Google Scholar] [CrossRef]
- Ananda, K.N.; Clarkson, C.; Wands, D. The Cosmological gravitational wave background from primordial density perturbations. Phys. Rev. D 2007, 75, 123518. [Google Scholar] [CrossRef]
- Clesse, S.; García-Bellido, J.; Orani, S. Detecting the Stochastic Gravitational Wave Background from Primordial Black Hole Formation. arXiv 2018, arXiv:1812.11011. [Google Scholar]
- Garcia-Bellido, J.; Peloso, M.; Unal, C. Gravitational Wave signatures of inflationary models from Primordial Black Hole Dark Matter. JCAP 2017, 09, 013. [Google Scholar] [CrossRef]
- Khlebnikov, S.Y.; Tkachev, I.I. Relic gravitational waves produced after preheating. Phys. Rev. D 1997, 56, 653–660. [Google Scholar] [CrossRef]
- Easther, R.; Lim, E.A. Stochastic gravitational wave production after inflation. JCAP 2006, 04, 010. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Figueroa, D.G. A stochastic background of gravitational waves from hybrid preheating. Phys. Rev. Lett. 2007, 98, 061302. [Google Scholar] [CrossRef]
- Easther, R.; Giblin, J.T.; Lim, E.A. Gravitational Wave Production at the End of Inflation. Phys. Rev. Lett. 2007, 99, 221301. [Google Scholar] [CrossRef]
- Bartolo, N.; Caprini, C.; Domcke, V.; Figueroa, D.G.; Garcia-Bellido, J.; Guzzetti, M.C.; Liguori, M.; Matarrese, S.; Peloso, M.; Petiteau, A.; et al. Science with the space-based interferometer LISA. IV: Probing inflation with gravitational waves. J. Cosmol. Astropart. Phys. 2016, 12, 026. [Google Scholar] [CrossRef]
- Jeannerot, R.; Rocher, J.; Sakellariadou, M. How generic is cosmic string formation in SUSY GUTs. Phys. Rev. D 2003, 68, 103514. [Google Scholar] [CrossRef]
- García-Bellido, J.; Jaraba, S.; Kuroyanagi, S. The stochastic gravitational wave background from close hyperbolic encounters of primordial black holes in dense clusters. arXiv 2021, arXiv:2109.11376. [Google Scholar]
- Alexander, S.; Marciano, A.; Smolin, L. Gravitational origin of the weak interaction’s chirality. Phys. Rev. D 2014, 89, 065017. [Google Scholar] [CrossRef]
- Freidel, L.; Minic, D.; Takeuchi, T. Quantum gravity, torsion, parity violation and all that. Phys. Rev. D 2005, 72, 104002. [Google Scholar] [CrossRef]
- Alexander, S.H. Isogravity: Toward an Electroweak and Gravitational Unification. arXiv 2007, arXiv:0706.4481. [Google Scholar]
- Smolin, L. The Plebanski action extended to a unification of gravity and Yang-Mills theory. Phys. Rev. D 2009, 80, 124017. [Google Scholar] [CrossRef]
- Contaldi, C.R. Anisotropies of Gravitational Wave Backgrounds: A Line Of Sight Approach. Phys. Rev. Lett. 2017, B771, 9–12. [Google Scholar] [CrossRef]
- Jenkins, A.C.; Sakellariadou, M. Anisotropies in the stochastic gravitational-wave background: Formalism and the cosmic string case. Phys. Rev. D 2018, 98, 063509. [Google Scholar] [CrossRef]
- Jenkins, A.C.; O’Shaughnessy, R.; Sakellariadou, M.; Wysocki, D. Anisotropies in the astrophysical gravitational-wave background: The impact of black hole distributions. Phys. Rev. Lett. 2019, 122, 111101. [Google Scholar] [CrossRef]
- Durrer, R. The Cosmic Microwave Background; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Peebles, P.J.E. The Large-Scale Structure of the Universe; Princeton University Press: Princeton, NJ, USA, 2020. [Google Scholar]
- Sachs, R.; Wolfe, A. Perturbations of a cosmological model and angular variations of the microwave background. Astrophys. J. 1967, 147, 73–90. [Google Scholar] [CrossRef]
- Bartolo, N.; Bertacca, D.; Matarrese, S.; Peloso, M.; Ricciardone, A.; Riotto, A.; Tasinato, G. Anisotropies and non-Gaussianity of the Cosmological Gravitational Wave Background. Phys. Rev. D 2019, 100, 121501. [Google Scholar] [CrossRef]
- Cusin, G.; Dvorkin, I.; Pitrou, C.; Uzan, J.P. First predictions of the angular power spectrum of the astrophysical gravitational wave background. Phys. Rev. Lett. 2018, 120, 231101. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, A.C.; Sakellariadou, M.; Regimbau, T.; Slezak, E. Anisotropies in the astrophysical gravitational-wave background: Predictions for the detection of compact binaries by LIGO and Virgo. Phys. Rev. D 2018, 98, 063501. [Google Scholar] [CrossRef]
- Capurri, G.; Lapi, A.; Baccigalupi, C.; Boco, L.; Scelfo, G.; Ronconi, T. Intensity and anisotropies of the stochastic gravitational wave background from merging compact binaries in galaxies. JCAP 2021, 11, 032. [Google Scholar] [CrossRef]
- Geller, M.; Hook, A.; Sundrum, R.; Tsai, Y. Primordial Anisotropies in the Gravitational Wave Background from Cosmological Phase Transitions. Phys. Rev. Lett. 2018, 121, 201303. [Google Scholar] [CrossRef]
- Bertacca, D.; Ricciardone, A.; Bellomo, N.; Jenkins, A.C.; Matarrese, S.; Raccanelli, A.; Regimbau, T.; Sakellariadou, M. Projection effects on the observed angular spectrum of the astrophysical stochastic gravitational wave background. Phys. Rev. D 2020, 101, 103513. [Google Scholar] [CrossRef]
- Bellomo, N.; Bertacca, D.; Jenkins, A.C.; Matarrese, S.; Raccanelli, A.; Regimbau, T.; Ricciardone, A.; Sakellariadou, M. CLASS_GWB: Robust modeling of the astrophysical gravitational wave background anisotropies. arXiv 2021, arXiv:2110.15059. [Google Scholar]
- Cusin, G.; Dvorkin, I.; Pitrou, C.; Uzan, J.P. Comment on the article “Anisotropies in the astrophysical gravitational-wave background: The impact of black hole distributions” by A.C. Jenkins et al. [arXiv:1810.13435]. arXiv 2018, arXiv:1811.03582. [Google Scholar]
- Jenkins, A.C.; Sakellariadou, M.; Regimbau, T.; Slezak, E.; O’Shaughnessy, R.; Wysocki, D. Response to Cusin et al’s comment on arXiv:1810.13435. arXiv 2019, arXiv:1901.01078. [Google Scholar]
- Pitrou, C.; Cusin, G.; Uzan, J.P. Unified view of anisotropies in the astrophysical gravitational-wave background. Phys. Rev. D 2020, 101, 081301. [Google Scholar] [CrossRef]
- Alonso, D.; Contaldi, C.R.; Cusin, G.; Ferreira, P.G.; Renzini, A.I. The Nℓ of gravitational wave background experiments. arXiv 2020, arXiv:2005.03001. [Google Scholar]
- Regimbau, T.; Dent, T.; Del Pozzo, W.; Giampanis, S.; Li, T.G.F.; Robinson, C.; Van Den Broeck, C.; Meacher, D.; Rodriguez, C.; Sathyaprakash, B.S.; et al. Mock data challenge for the Einstein Gravitational-Wave Telescope. Phys. Rev. D 2012, 86, 122001. [Google Scholar] [CrossRef]
- Regimbau, T.; Meacher, D.; Coughlin, M. Second Einstein Telescope mock science challenge: Detection of the gravitational-wave stochastic background from compact binary coalescences. Phys. Rev. D 2014, 89, 084046. [Google Scholar] [CrossRef]
- Cornish, N.J.; Romano, J.D. When is a gravitational-wave signal stochastic? Phys. Rev. D 2015, 92, 042001. [Google Scholar] [CrossRef]
- Rosado, P.A.; Sesana, A.; Gair, J. Expected properties of the first gravitational wave signal detected with pulsar timing arrays. Mon. Not. R. Astron. Soc. 2015, 451, 2417–2433. [Google Scholar] [CrossRef]
- Meacher, D.; Thrane, E.; Regimbau, T. Statistical properties of astrophysical gravitational-wave backgrounds. Phys. Rev. D 2014, 89, 084063. [Google Scholar] [CrossRef]
- Jenkins, A.C.; Sakellariadou, M. Shot noise in the astrophysical gravitational-wave background. Phys. Rev. D 2019, 100, 063508. [Google Scholar] [CrossRef]
- Jenkins, A.C.; Romano, J.D.; Sakellariadou, M. Estimating the angular power spectrum of the gravitational-wave background in the presence of shot noise. Phys. Rev. D 2019, 100, 083501. [Google Scholar] [CrossRef]
- Alonso, D.; Cusin, G.; Ferreira, P.G.; Pitrou, C. Detecting the anisotropic astrophysical gravitational wave background in the presence of shot noise through cross-correlations. Phys. Rev. D 2020, 102, 023002. [Google Scholar] [CrossRef]
- Canas-Herrera, G.; Contigiani, O.; Vardanyan, V. Cross-correlation of the astrophysical gravitational-wave background with galaxy clustering. Phys. Rev. D 2020, 102, 043513. [Google Scholar] [CrossRef]
- Dvorkin, I.; Uzan, J.P.; Vangioni, E.; Silk, J. Exploring stellar evolution with gravitational-wave observations. Mon. Not. R. Astron. Soc. 2018, 479, 121–129. [Google Scholar] [CrossRef]
- Mukherjee, S.; Silk, J. Time-dependence of the astrophysical stochastic gravitational wave background. Mon. Not. R. Astron. Soc. 2020, 491, 4690–4701. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. Constraints on dark photon dark matter using data from LIGO’s and Virgo’s third observing run. arXiv 2021, arXiv:2105.13085. [Google Scholar]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Constraints on Cosmic Strings Using Data from the Third Advanced LIGO–Virgo Observing Run. Phys. Rev. Lett. 2021, 126, 241102. [Google Scholar] [CrossRef] [PubMed]
- Talbot, C.; Thrane, E.; Biscoveanu, S.; Smith, R. Inference with finite time series: Observing the gravitational Universe through windows. Phys. Rev. Res. 2021, 3, 043049. [Google Scholar] [CrossRef]
- Matas, A.; Romano, J.D. Frequentist versus Bayesian analyses: Cross-correlation as an approximate sufficient statistic for LIGO-Virgo stochastic background searches. Phys. Rev. D 2021, 103, 062003. [Google Scholar] [CrossRef]
- Littenberg, T.; Cornish, N.; Lackeos, K.; Robson, T. Global Analysis of the Gravitational Wave Signal from Galactic Binaries. Phys. Rev. D 2020, 101, 123021. [Google Scholar] [CrossRef]
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Advanced LIGO. Class. Quantum Gravity 2015, 32, 074001. [Google Scholar] [CrossRef]
- Armstrong, J.W.; Estabrook, F.B.; Tinto, M. Time-Delay Interferometry for Space-based Gravitational Wave Searches. Astrophys. J. 1999, 527, 814–826. [Google Scholar] [CrossRef]
- Tinto, M.; Armstrong, J.W. Cancellation of laser noise in an unequal-arm interferometer detector of gravitational radiation. Phys. Rev. D 1999, 59, 102003. [Google Scholar] [CrossRef]
- Seto, N.; Taruya, A. Measuring a parity-violation signature in the early universe via ground-based laser interferometers. Phys. Rev. Lett. 2007, 99, 121101. [Google Scholar] [CrossRef] [PubMed]
- Seto, N.; Taruya, A. Polarization analysis of gravitational-wave backgrounds from the correlation signals of ground-based interferometers: Measuring a circular-polarization mode. Phys. Rev. D Part. Fields, Gravit. Cosmol. 2008, 77, 1–27. [Google Scholar] [CrossRef]
- Bayle, J.B.; Hartwig, O.; Staab, M. Adapting time-delay interferometry for LISA data in frequency. Phys. Rev. D 2021, 104, 023006. [Google Scholar] [CrossRef]
- Bayle, J.B.; Lilley, M.; Petiteau, A.; Halloin, H. Effect of filters on the time-delay interferometry residual laser noise for LISA. PRD 2019, 99, 084023. [Google Scholar] [CrossRef]
- Vallisneri, M.; Bayle, J.B.; Babak, S.; Petiteau, A. Time-delay interferometry without delays. Phys. Rev. D 2021, 103, 082001. [Google Scholar] [CrossRef]
- Bayle, J.B.; Vallisneri, M.; Babak, S.; Petiteau, A. On the matrix formulation of time-delay interferometry. arXiv 2021, arXiv:2106.03976. [Google Scholar]
- Tinto, M.; Dhurandhar, S.; Joshi, P. Matrix representation of time-delay interferometry. PRD 2021, 104, 044033. [Google Scholar] [CrossRef]
- Page, J.; Littenberg, T.B. Bayesian time delay interferometry. PRD 2021, 104, 084037. [Google Scholar] [CrossRef]
- Baghi, Q.; Thorpe, J.I.; Slutsky, J.; Baker, J. Statistical inference approach to time-delay interferometry for gravitational-wave detection. PRD 2021, 103, 042006. [Google Scholar] [CrossRef]
- LISA Data Challenge Manual. 2018. Available online: https://lisa-ldc.lal.in2p3.fr/static/data/pdf/LDC-manual-001.pdf (accessed on 1 November 2021).
- Tinto, M.; Dhurandhar, S.V. TIME DELAY. Living Rev. Relativ. 2005, 8, 4. [Google Scholar] [CrossRef] [PubMed]
- Adams, M.R.; Cornish, N.J. Discriminating between a stochastic gravitational wave background and instrument noise. Phys. Rev. D 2010, 82, 022002. [Google Scholar] [CrossRef]
- Adams, M.R.; Cornish, N.J. Detecting a stochastic gravitational wave background in the presence of a galactic foreground and instrument noise. Phys. Rev. D 2014, 89, 022001. [Google Scholar] [CrossRef]
- Anholm, M.; Ballmer, S.; Creighton, J.D.E.; Price, L.R.; Siemens, X. Optimal strategies for gravitational wave stochastic background searches in pulsar timing data. PRD 2009, 79, 084030. [Google Scholar] [CrossRef]
- Hellings, R.W.; Downs, G.S. Upper limits on the isotropic gravitational radiation background from pulsar timing analysis. ApJ 1983, 265, L39–L42. [Google Scholar] [CrossRef]
- Allen, B.; Romano, J.D. Detecting a stochastic background of gravitational radiation: Signal processing strategies and sensitivities. Phys. Rev. D 1999, 59, 102001. [Google Scholar] [CrossRef]
- Renzini, A.I.; Contaldi, C.R. Mapping Incoherent Gravitational Wave Backgrounds. Mon. Not. R. Astron. Soc. 2018, 481, 4650–4661. [Google Scholar] [CrossRef]
- Renzini, A.I.; Contaldi, C.R. Gravitational Wave Background Sky Maps from Advanced LIGO O1 Data. Phys. Rev. Lett. 2019, 122, 081102. [Google Scholar] [CrossRef]
- Renzini, A.; Contaldi, C. Improved limits on a stochastic gravitational-wave background and its anisotropies from Advanced LIGO O1 and O2 runs. Phys. Rev. 2019, D100, 063527. [Google Scholar] [CrossRef]
- Chatziioannou, K.; Haster, C.J.; Littenberg, T.B.; Farr, W.M.; Ghonge, S.; Millhouse, M.; Clark, J.A.; Cornish, N. Noise spectral estimation methods and their impact on gravitational wave measurement of compact binary mergers. Phys. Rev. D 2019, 100, 104004. [Google Scholar] [CrossRef]
- Cornish, N.J.; Romano, J.D. Towards a unified treatment of gravitational-wave data analysis. Phys. Rev. D 2013, 87, 122003. [Google Scholar] [CrossRef]
- Cornish, N.J. Detecting a stochastic gravitational wave background with the Laser Interferometer Space Antenna. Phys. Rev. D 2002, 65, 022004. [Google Scholar] [CrossRef]
- Coughlin, M.; Christensen, N.; Gair, J.; Kandhasamy, S.; Thrane, E. Method for estimation of gravitational-wave transient model parameters in frequency–time maps. Class. Quantum Gravity 2014, 31, 165012. [Google Scholar] [CrossRef]
- Mandic, V.; Thrane, E.; Giampanis, S.; Regimbau, T. Parameter Estimation in Searches for the Stochastic Gravitational-Wave Background. Phys. Rev. Lett. 2012, 109, 171102. [Google Scholar] [CrossRef]
- Callister, T.; Biscoveanu, A.S.; Christensen, N.; Isi, M.; Matas, A.; Minazzoli, O.; Regimbau, T.; Sakellariadou, M.; Tasson, J.; Thrane, E. Polarization-based Tests of Gravity with the Stochastic Gravitational-Wave Background. Phys. Rev. X 2017, 7, 041058. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. Search for the isotropic stochastic background using data from Advanced LIGO’s second observing run. Phys. Rev. D 2019, 100, 061101. [Google Scholar] [CrossRef]
- Tsukada, L.; Callister, T.; Matas, A.; Meyers, P. First search for a stochastic gravitational-wave background from ultralight bosons. Phys. Rev. D 2019, 99, 103015. [Google Scholar] [CrossRef]
- Tsukada, L.; Brito, R.; East, W.E.; Siemonsen, N. Modeling and searching for a stochastic gravitational-wave background from ultralight vector bosons. Phys. Rev. D 2021, 103, 083005. [Google Scholar] [CrossRef]
- Romero, A.; Martinovic, K.; Callister, T.A.; Guo, H.K.; Martínez, M.; Sakellariadou, M.; Yang, F.W.; Zhao, Y. Implications for First-Order Cosmological Phase Transitions from the Third LIGO-Virgo Observing Run. Phys. Rev. Lett. 2021, 126, 151301. [Google Scholar] [CrossRef]
- Romero-Rodriguez, A.; Martinez, M.; Pujolàs, O.; Sakellariadou, M.; Vaskonen, V. Search for a scalar induced stochastic gravitational wave background in the third LIGO-Virgo observing run. Phys. Rev. Lett. 2022, 128, 051301. [Google Scholar] [CrossRef]
- Martinovic, K.; Badger, C.; Sakellariadou, M.; Mandic, V. Searching for parity violation with the LIGO-Virgo-KAGRA network. Phys. Rev. D 2021, 104, L081101. [Google Scholar] [CrossRef]
- Meyers, P.M.; Martinovic, K.; Christensen, N.; Sakellariadou, M. Detecting a stochastic gravitational-wave background in the presence of correlated magnetic noise. PRD 2020, 102, 102005. [Google Scholar] [CrossRef]
- Martinovic, K.; Meyers, P.M.; Sakellariadou, M.; Christensen, N. Simultaneous estimation of astrophysical and cosmological stochastic gravitational-wave backgrounds with terrestrial detectors. Phys. Rev. D 2021, 103, 043023. [Google Scholar] [CrossRef]
- Parida, A.; Suresh, J.; Mitra, S.; Jhingan, S. Component separation map-making for stochastic gravitational wave background. arXiv 2019, arXiv:1904.05056. [Google Scholar]
- Meacher, D.; Coughlin, M.; Morris, S.; Regimbau, T.; Christensen, N.; Kandhasamy, S.; Mandic, V.; Romano, J.D.; Thrane, E. Mock data and science challenge for detecting an astrophysical stochastic gravitational-wave background with Advanced LIGO and Advanced Virgo. Phys. Rev. D 2015, 92, 063002. [Google Scholar] [CrossRef]
- Biwer, C.; Barker, D.; Batch, J.C.; Betzwieser, J.; Fisher, R.P.; Goetz, E.; Kandhasamy, S.; Karki, S.; Kissel, J.S.; Lundgren, A.P.; et al. Validating gravitational-wave detections: The Advanced LIGO hardware injection system. Phys. Rev. D 2017, 95, 062002. [Google Scholar] [CrossRef]
- van Haasteren, R.; Levin, Y.; McDonald, P.; Lu, T. On measuring the gravitational-wave background using Pulsar Timing Arrays. MNRAS 2009, 395, 1005–1014. [Google Scholar] [CrossRef]
- van Haasteren, R.; Levin, Y.; Janssen, G.H.; Lazaridis, K.; Kramer, M.; Stappers, B.W.; Desvignes, G.; Purver, M.B.; Lyne, A.G.; Ferdman, R.D.; et al. Placing limits on the stochastic gravitational-wave background using European Pulsar Timing Array data. MNRAS 2011, 414, 3117–3128. [Google Scholar] [CrossRef]
- Lentati, L.; Alexander, P.; Hobson, M.P.; Taylor, S.; Gair, J.; Balan, S.T.; van Haasteren, R. Hyper-efficient model-independent Bayesian method for the analysis of pulsar timing data. PRD 2013, 87, 104021. [Google Scholar] [CrossRef]
- van Haasteren, R.; Vallisneri, M. New advances in the Gaussian-process approach to pulsar-timing data analysis. PRD 2014, 90, 104012. [Google Scholar] [CrossRef]
- Lentati, L.; Alexander, P.; Hobson, M.P.; Feroz, F.; van Haasteren, R.; Lee, K.J.; Shannon, R.M. TEMPONEST: A Bayesian approach to pulsar timing analysis. MNRAS 2014, 437, 3004–3023. [Google Scholar] [CrossRef]
- Hobbs, G.; Jenet, F.; Lee, K.J.; Verbiest, J.P.W.; Yardley, D.; Manchester, R.; Lommen, A.; Coles, W.; Edwards, R.; Shettigara, C. TEMPO2: A new pulsar timing package—III. Gravitational wave simulation. MNRAS 2009, 394, 1945–1955. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.J.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crowter, K.; Demorest, P.B.; et al. The NANOGrav Nine-year Data Set: Limits on the Isotropic Stochastic Gravitational Wave Background. ApJ 2016, 821, 13. [Google Scholar] [CrossRef]
- Taylor, S.R.; Lentati, L.; Babak, S.; Brem, P.; Gair, J.R.; Sesana, A.; Vecchio, A. All correlations must die: Assessing the significance of a stochastic gravitational-wave background in pulsar timing arrays. PRD 2017, 95, 042002. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Baker, P.T.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.J.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crawford, F.; et al. The NANOGrav 11 Year Data Set: Pulsar-timing Constraints on the Stochastic Gravitational-wave Background. ApJ 2018, 859, 47. [Google Scholar] [CrossRef]
- Chamberlin, S.J.; Creighton, J.D.E.; Siemens, X.; Demorest, P.; Ellis, J.; Price, L.R.; Romano, J.D. Time-domain implementation of the optimal cross-correlation statistic for stochastic gravitational-wave background searches in pulsar timing data. PRD 2015, 91, 044048. [Google Scholar] [CrossRef]
- Vigeland, S.J.; Islo, K.; Taylor, S.R.; Ellis, J.A. Noise-marginalise optimal statistic: A robust hybrid frequentist-Bayesian statistic for the stochastic gravitational-wave background in pulsar timing arrays. PRD 2018, 98, 044003. [Google Scholar] [CrossRef]
- Cornish, N.J.; Sampson, L. Towards robust gravitational wave detection with pulsar timing arrays. PRD 2016, 93, 104047. [Google Scholar] [CrossRef]
- Bécsy, B.; Cornish, N.J. Joint search for isolated sources and an unresolved confusion background in pulsar timing array data. Class. Quantum Gravity 2020, 37, 135011. [Google Scholar] [CrossRef]
- Prix, R.; Itoh, Y. Global parameter-space correlations of coherent searches for continuous gravitational waves. Class. Quantum Gravity 2005, 22, S1003–S1012. [Google Scholar] [CrossRef]
- Ain, A.; Dalvi, P.; Mitra, S. Fast gravitational wave radiometry using data folding. Phys. Rev. D Part. Fields, Gravit. Cosmol. 2015, 92, 022003. [Google Scholar] [CrossRef]
- Ain, A.; Suresh, J.; Mitra, S. Very fast stochastic gravitational wave background map making using folded data. PRD 2018, 98, 024001. [Google Scholar] [CrossRef]
- Goncharov, B.; Thrane, E. All-sky radiometer for narrowband gravitational waves using folded data. PRD 2018, 98, 064018. [Google Scholar] [CrossRef]
- Mitra, S.; Dhurandhar, S.; Souradeep, T.; Lazzarini, A.; Mandic, V.; Bose, S.; Ballmer, S. Gravitational wave radiometry: Mapping a stochastic gravitational wave background. Phys. Rev. D 2008, 77, 042002. [Google Scholar] [CrossRef]
- Thrane, E.; Ballmer, S.; Romano, J.D.; Mitra, S.; Talukder, D.; Bose, S.; Mandic, V. Probing the anisotropies of a stochastic gravitational-wave background using a network of ground-based laser interferometers. Phys. Rev. D Part. Fields, Gravit. Cosmol. 2009, 80, 122002. [Google Scholar] [CrossRef]
- Mingarelli, C.M.F.; Sidery, T.; Mandel, I.; Vecchio, A. Characterizing gravitational wave stochastic background anisotropy with pulsar timing arrays. PRD 2013, 88, 062005. [Google Scholar] [CrossRef]
- Taylor, S.R.; Gair, J.R. Searching for anisotropic gravitational-wave backgrounds using pulsar timing arrays. PRD 2013, 88, 084001. [Google Scholar] [CrossRef]
- Contaldi, C.R.; Pieroni, M.; Renzini, A.I.; Cusin, G.; Karnesis, N.; Peloso, M.; Ricciardone, A.; Tasinato, G. Maximum likelihood map-making with the Laser Interferometer Space Antenna. Phys. Rev. D 2020, 102, 043502. [Google Scholar] [CrossRef]
- Banagiri, S.; Criswell, A.; Kuan, T.; Mandic, V.; Romano, J.D.; Taylor, S.R. Mapping the gravitational-wave sky with LISA: A Bayesian spherical harmonic approach. MNRAS 2021, 507, 5451–5462. [Google Scholar] [CrossRef]
- Bond, J.R.; Jaffe, A.H.; Knox, L. Estimating the power spectrum of the cosmic microwave background. Phys. Rev. 1998, D57, 2117–2137. [Google Scholar] [CrossRef]
- Rocha, G.; Contaldi, C.; Bond, J.; Gorski, K. Application of XFaster power spectrum and likelihood estimator to Planck. Mon. Not. R. Astron. Soc. 2011, 414, 823–846. [Google Scholar] [CrossRef][Green Version]
- Cornish, N.J.; van Haasteren, R. Mapping the nano-Hertz gravitational wave sky. arXiv 2014, arXiv:1406.4511. [Google Scholar]
- Ballmer, S.W. A radiometer for stochastic gravitational waves. Class. Quantum Gravity 2006, 23, S179–S185. [Google Scholar] [CrossRef]
- Gair, J.; Romano, J.D.; Taylor, S.; Mingarelli, C.M.F. Mapping gravitational-wave backgrounds using methods from CMB analysis: Application to pulsar timing arrays. PRD 2014, 90, 082001. [Google Scholar] [CrossRef]
- Gair, J.R.; Romano, J.D.; Taylor, S.R. Mapping gravitational-wave backgrounds of arbitrary polarisation using pulsar timing arrays. PRD 2015, 92, 102003. [Google Scholar] [CrossRef]
- Romano, J.D.; Taylor, S.R.; Cornish, N.J.; Gair, J.; Mingarelli, C.M.F.; van Haasteren, R. Phase-coherent mapping of gravitational-wave backgrounds using ground-based laser interferometers. PRD 2015, 92, 042003. [Google Scholar] [CrossRef]
- Taylor, S.R.; Mingarelli, C.M.F.; Gair, J.R.; Sesana, A.; Theureau, G.; Babak, S.; Bassa, C.G.; Brem, P.; Burgay, M.; Caballero, R.N.; et al. Limits on Anisotropy in the Nanohertz Stochastic Gravitational Wave Background. PRL 2015, 115, 041101. [Google Scholar] [CrossRef]
- Ali-Haïmoud, Y.; Smith, T.L.; Mingarelli, C.M.F. Fisher formalism for anisotropic gravitational-wave background searches with pulsar timing arrays. PRD 2020, 102, 122005. [Google Scholar] [CrossRef]
- Ali-Haïmoud, Y.; Smith, T.L.; Mingarelli, C.M.F. Insights into searches for anisotropies in the nanohertz gravitational-wave background. PRD 2021, 103, 042009. [Google Scholar] [CrossRef]
- Suresh, J.; Agarwal, D.; Mitra, S. Jointly setting upper limits on multiple components of an anisotropic stochastic gravitational-wave background. PRD 2021, 104, 102003. [Google Scholar] [CrossRef]
- Gorski, K.M.; Hivon, E.; Banday, A.J.; Wandelt, B.D.; Hansen, F.K.; Reinecke, M.; Bartelman, M. HEALPix—A Framework for high resolution discretization, and fast analysis of data distributed on the sphere. Astrophys. J. 2005, 622, 759–771. [Google Scholar] [CrossRef]
- Hotinli, S.C.; Kamionkowski, M.; Jaffe, A.H. The search for statistical anisotropy in the gravitational-wave background with pulsar timing arrays. Open J. Astrophys. 2019, 2, 8. [Google Scholar] [CrossRef]
- Ivezić, Ž.; Connolly, A.; VanderPlas, J.; Gray, A. Statistics, Data Mining, and Machine Learning in Astronomy: A Practical Python Guide for the Analysis of Survey Data; Princeton Series in Modern Observational Astronomy; Princeton University Press: Princeton, NJ, USA, 2014. [Google Scholar]
- Suresh, J.; Ain, A.; Mitra, S. Unified mapmaking for an anisotropic stochastic gravitational wave background. PRD 2021, 103, 083024. [Google Scholar] [CrossRef]
- Myers, S.T.; Contaldi, C.R.; Bond, J.R.; Pen, U.L.; Pogosyan, D.; Prunet, S.; Sievers, J.L.; Mason, B.S.; Pearson, T.J.; Readhead, A.C.S.; et al. A fast gridded method for the estimation of the power spectrum of the CMB from interferometer data with application to the cosmic background imager. Astrophys. J. 2003, 591, 575–598. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Search for anisotropic gravitational-wave backgrounds using data from Advanced LIGO and Advanced Virgo’s first three observing runs. Phys. Rev. D 2021, 104, 022005. [Google Scholar] [CrossRef]
- Drasco, S.; Flanagan, E.E. Detection methods for non-Gaussian gravitational wave stochastic backgrounds. Phys. Rev. 2003, D67, 082003. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run. arXiv 2021, arXiv:2111.03606. [Google Scholar]
- Thrane, E. Measuring the non-Gaussian stochastic gravitational-wave background: A method for realistic interferometer data. Phys. Rev. D 2013, 87, 043009. [Google Scholar] [CrossRef]
- Smith, R.; Thrane, E. Optimal Search for an Astrophysical Gravitational-Wave Background. Phys. Rev. X 2018, 8, 021019. [Google Scholar] [CrossRef]
- Lawrence, J.; Turbang, K.; Matas, A.; Renzini, A.; Van Remortel, N.; Romano, J. A stochastic-signal-based search for intermittent gravitational-wave backgrounds. 2022; in preparation. [Google Scholar]
- Banagiri, S.; Mandic, V.; Scarlata, C.; Yang, K.Z. Measuring angular N-point correlations of binary black hole merger gravitational-wave events with hierarchical Bayesian inference. Phys. Rev. D 2020, 102, 063007. [Google Scholar] [CrossRef]
- Barsotti, L.; Fritschel, P.; Evans, M.; Gras, S. Advanced LIGO Design Sensitivity Curve. 2018. Available online: https://dcc.ligo.org/LIGO-T1800044/public (accessed on 1 November 2021).
- Thrane, E.; Romano, J.D. Sensitivity curves for searches for gravitational-wave backgrounds. Phys. Rev. 2013, D88, 124032. [Google Scholar] [CrossRef]
- Coughlin, M.; Harms, J. Constraining the gravitational wave energy density of the Universe using Earth’s ring. Phys. Rev. D 2014, 90, 042005. [Google Scholar] [CrossRef]
- Armstrong, J.W.; Iess, L.; Tortora, P.; Bertotti, B. Stochastic gravitational wave background: Upper limits in the 10**-6-Hz 10**-3-Hz band. Astrophys. J. 2003, 599, 806–813. [Google Scholar] [CrossRef][Green Version]
- Lasky, P.D.; Mingarelli, C.M.; Smith, T.L.; Giblin, J.T., Jr.; Thrane, E.; Reardon, D.J.; Caldwell, R.; Bailes, M.; Bhat, N.R.; Burke-Spolaor, S.; et al. Gravitational-wave cosmology across 29 decades in frequency. Phys. Rev. X 2016, 6, 011035. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef]
- Badurina, L.; Bentine, E.; Blas, D.; Bongs, K.; Bortoletto, D.; Bowcock, T.; Bridges, K.; Bowden, W.; Buchmueller, O.; Burrage, C.; et al. AION: An Atom Interferometer Observatory and Network. JCAP 2020, 05, 011. [Google Scholar] [CrossRef]
- Blas, D.; Jenkins, A.C. Detecting stochastic gravitational waves with binary resonance. arXiv 2021, arXiv:2107.04063. [Google Scholar]
- Blas, D.; Jenkins, A.C. Bridging the μHz gap in the gravitational-wave landscape with binary resonance. arXiv 2021, arXiv:2107.04601. [Google Scholar]
- Janssen, G.H.; Hobbs, G.; McLaughlin, M.; Bassa, C.G.; Deller, A.T.; Kramer, M.; Lee, K.J.; Mingarelli, C.M.F.; Rosado, P.A.; Sanidas, S.; et al. Gravitational wave astronomy with the SKA. PoS 2015, AASKA14, 037. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Adhikari, R.; Ageev, A.; Allen, B.; Amin, R.; Anderson, S.B.; Anderson, W.G.; Araya, M.; Armandula, H.; et al. Analysis of first LIGO science data for stochastic gravitational waves. Phys. Rev. D 2004, 69, 122004. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Adhikari, R.; Agresti, J.; Ajith, P.; Allen, B.; Allen, J.; Amin, R.; Anderson, S.B.; Anderson, W.G.; et al. Upper limits on a stochastic background of gravitational waves. Phys. Rev. Lett. 2005, 95, 221101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.; Abbott, R.; Adhikari, R.; Agresti, J.; Ajith, P.; Allen, B.; Amin, R.; Anderson, S.B.; Anderson, W.G.; Araya, M.; et al. Searching for a Stochastic Background of Gravitational Waves with LIGO. Astrophys. J. 2007, 659, 918–930. [Google Scholar] [CrossRef]
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Accadia, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; et al. Improved Upper Limits on the Stochastic Gravitational-Wave Background from 2009–2010 LIGO and Virgo Data. Phys. Rev. Lett. 2014, 113, 231101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Upper Limits on the Stochastic Gravitational-Wave Background from Advanced LIGO’s First Observing Run. Phys. Rev. Lett. 2017, 118, 121101, Erratum on 2017, 119, 029901. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Adhikari, R.; Agresti, J.; Ajith, P.; Allen, B.; Amin, R.; Anderson, S.B.; Anderson, W.G.; Arain, M.; et al. Upper limit map of a background of gravitational waves. Phys. Rev. D 2007, 76, 082003. [Google Scholar] [CrossRef]
- Abadie, J.; Abbott, B.P.; Abbott, R.; Abernathy, M.; Accadia, T.; Acernese, F.; Adams, C.; Adhikari, R.; Ajith, P.; Allen, B.; et al. Directional Limits on Persistent Gravitational Waves Using LIGO S5 Science Data. Phys. Rev. Lett. 2011, 107, 271102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Directional Limits on Persistent Gravitational Waves from Advanced LIGO’s First Observing Run. Phys. Rev. Lett. 2017, 118, 121102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Directional limits on persistent gravitational waves using data from Advanced LIGO’s first two observing runs. Phys. Rev. D 2019, 100, 062001. [Google Scholar] [CrossRef]
- Aasi, J.; Abadie, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Accadia, T.; Acernese, F.; Adams, C.; Adams, T.; et al. Constraints on Cosmic Strings from the LIGO-Virgo Gravitational-Wave Detectors. Phys. Rev. Lett. 2014, 112, 131101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Constraints on cosmic strings using data from the first Advanced LIGO observing run. Phys. Rev. D 2018, 97, 102002. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Search for Tensor, Vector, and Scalar Polarizations in the Stochastic Gravitational-Wave Background. Phys. Rev. Lett. 2018, 120, 201102. [Google Scholar] [CrossRef]
- Agarwal, D.; Suresh, J.; Mitra, S.; Ain, A. Upper limits on persistent gravitational waves using folded data and the full covariance matrix from Advanced LIGO’s first two observing runs. PRD 2021, 104, 123018. [Google Scholar] [CrossRef]
- Yang, K.Z.; Mandic, V.; Scarlata, C.; Banagiri, S. Searching for Cross-Correlation Between Stochastic Gravitational Wave Background and Galaxy Number Counts. Mon. Not. R. Astron. Soc. 2020, 500, 1666–1672. [Google Scholar] [CrossRef]
- Kapadia, S.J.; Lal Pandey, K.; Suyama, T.; Kandhasamy, S.; Ajith, P. Search for the Stochastic Gravitational-wave Background Induced by Primordial Curvature Perturbations in LIGO’s Second Observing Run. Astrophys. J. Lett. 2021, 910, L4. [Google Scholar] [CrossRef]
- Covas, P.B.; Effler, A.; Goetz, E.; Meyers, P.M.; Neunzert, A.; Oliver, M.; Pearlstone, B.L.; Roma, V.J.; Schofield, R.M.; Adya, V.B.; et al. Identification and mitigation of narrow spectral artifacts that degrade searches for persistent gravitational waves in the first two observing runs of Advanced LIGO. Phys. Rev. D 2018, 97. [Google Scholar] [CrossRef]
- LIGO Document T2000384-v4. Available online: https://dcc.ligo.org/T2000384/public (accessed on 1 November 2021).
- Matas, A.; Dvorkin, I.; Regimbau, T.; Romero, A. Applying Gating to Stochastic Searches in O3. 2021. Available online: https://dcc.ligo.org/P2000546/public (accessed on 1 November 2021).
- LIGO Scientific Collaboration; Virgo Collaboration; KAGRA Scientific Collaboration. Data for Upper Limits on the Isotropic Gravitational-Wave Background from Advanced LIGO’s and Advanced Virgo’s Third Observing Run. 2021. Available online: https://dcc.ligo.org/LIGO-G2001287 (accessed on 1 November 2021).
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Relativ. 2014, 17, 4. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. Prospects for observing and localizing gravitational-wave transients with Advanced LIGO, Advanced Virgo and KAGRA. Living Rev. Relativ. 2020, 23, 3. [Google Scholar] [CrossRef]
- Mukherjee, S.; Broadhurst, T.; Diego, J.M.; Silk, J.; Smoot, G.F. Inferring the lensing rate of LIGO-Virgo sources from the stochastic gravitational wave background. Mon. Not. R. Astron. Soc. 2021, 501, 2451–2466. [Google Scholar] [CrossRef]
- Buscicchio, R.; Moore, C.J.; Pratten, G.; Schmidt, P.; Bianconi, M.; Vecchio, A. Constraining the lensing of binary black holes from their stochastic background. Phys. Rev. Lett. 2020, 125, 141102. [Google Scholar] [CrossRef]
- Buscicchio, R.; Moore, C.J.; Pratten, G.; Schmidt, P.; Vecchio, A. Constraining the lensing of binary neutron stars from their stochastic background. Phys. Rev. D 2020, 102, 081501. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GWTC-2: Compact Binary Coalescences Observed by LIGO and Virgo During the First Half of the Third Observing Run. Phys. Rev. X 2021, 11, 021053. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XXV. Searches for cosmic strings and other topological defects. Astron. Astrophys. 2014, 571, A25. [Google Scholar] [CrossRef]
- Vaskonen, V.; Veermäe, H. Lower bound on the primordial black hole merger rate. Phys. Rev. D 2020, 101, 043015. [Google Scholar] [CrossRef]
- Carr, B.; Kohri, K.; Sendouda, Y.; Yokoyama, J. Constraints on Primordial Black Holes. Rep. Prog. Phys. 2021, 84, 116902. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration; Virgo Collaboration; KAGRA Scientific Collaboration. Data Products and Supplemental Information for O3 Stochastic Directional Paper. 2021. Available online: https://dcc.ligo.org/LIGO-G2002165 (accessed on 1 November 2021).
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. Search for gravitational waves from Scorpius X-1 in the first Advanced LIGO observing run with a hidden Markov model. Phys. Rev. D 2017, 95, 122003. [Google Scholar] [CrossRef]
- Sun, L.; Melatos, A.; Lasky, P.D.; Chung, C.T.Y.; Darman, N.S. Cross-correlation search for continuous gravitational waves from a compact object in SNR 1987A in LIGO Science run 5. Phys. Rev. D 2016, 94, 082004. [Google Scholar] [CrossRef]
- Aasi, J.; Abadie, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Accadia, T.; Acernese, F.; Adams, C.; Adams, T.; et al. Directed search for continuous gravitational waves from the Galactic center. Phys. Rev. D 2013, 88, 102002. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. All-sky, all-frequency directional search for persistent gravitational-waves from Advanced LIGO’s and Advanced Virgo’s first three observing runs. arXiv 2021, arXiv:2110.09834. [Google Scholar]
- Tenorio, R.; Keitel, D.; Sintes, A.M. Application of a hierarchical MCMC follow-up to Advanced LIGO continuous gravitational-wave candidates. Phys. Rev. D 2021, 104, 084012. [Google Scholar] [CrossRef]
- Burke-Spolaor, S.; Taylor, S.R.; Charisi, M.; Dolch, T.; Hazboun, J.S.; Holgado, A.M.; Kelley, L.Z.; Lazio, T.J.W.; Madison, D.R.; McMann, N.; et al. The astrophysics of nanohertz gravitational waves. A&A Rev. 2019, 27, 5. [Google Scholar] [CrossRef]
- Taylor, S.R. The Nanohertz Gravitational Wave Astronomer. arXiv 2021, arXiv:2105.13270. [Google Scholar]
- Sazhin, M.V. Opportunities for detecting ultralong gravitational waves. Sov. Astron. 1978, 22, 36–38. [Google Scholar]
- Detweiler, S. Pulsar timing measurements and the search for gravitational waves. ApJ 1979, 234, 1100–1104. [Google Scholar] [CrossRef]
- Siemens, X.; Ellis, J.; Jenet, F.; Romano, J.D. The stochastic background: Scaling laws and time to detection for pulsar timing arrays. Class. Quantum Gravity 2013, 30, 224015. [Google Scholar] [CrossRef]
- Bailes, M.; Jameson, A.; Abbate, F.; Barr, E.D.; Bhat, N.D.R.; Bondonneau, L.; Burgay, M.; Buchner, S.J.; Camilo, F.; Champion, D.J.; et al. The MeerKAT telescope as a pulsar facility: System verification and early science results from MeerTime. PASA 2020, 37, e028. [Google Scholar] [CrossRef]
- Jonas, J.L. MeerKAT - The South African Array With Composite Dishes and Wide-Band Single Pixel Feeds. IEEE Proc. 2009, 97, 1522–1530. [Google Scholar] [CrossRef]
- Jenet, F.A.; Hobbs, G.B.; van Straten, W.; Manchester, R.N.; Bailes, M.; Verbiest, J.P.W.; Edwards, R.T.; Hotan, A.W.; Sarkissian, J.M.; Ord, S.M. Upper Bounds on the Low-Frequency Stochastic Gravitational Wave Background from Pulsar Timing Observations: Current Limits and Future Prospects. ApJ 2006, 653, 1571–1576. [Google Scholar] [CrossRef]
- Demorest, P.B.; Ferdman, R.D.; Gonzalez, M.E.; Nice, D.; Ransom, S.; Stairs, I.H.; Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.J.; et al. Limits on the Stochastic Gravitational Wave Background from the North American Nanohertz Observatory for Gravitational Waves. ApJ 2013, 762, 94. [Google Scholar] [CrossRef]
- Shannon, R.M.; Ravi, V.; Coles, W.A.; Hobbs, G.; Keith, M.J.; Manchester, R.N.; Wyithe, J.S.B.; Bailes, M.; Bhat, N.D.R.; Burke-Spolaor, S.; et al. Gravitational-wave limits from pulsar timing constrain supermassive black hole evolution. Science 2013, 342, 334–337. [Google Scholar] [CrossRef]
- Lentati, L.; Taylor, S.R.; Mingarelli, C.M.F.; Sesana, A.; Sanidas, S.A.; Vecchio, A.; Caballero, R.N.; Lee, K.J.; van Haasteren, R.; Babak, S.; et al. European Pulsar Timing Array limits on an isotropic stochastic gravitational-wave background. MNRAS 2015, 453, 2576–2598. [Google Scholar] [CrossRef]
- NANOGrav Collaboration; Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.; Crowter, K.; et al. The NANOGrav Nine-year Data Set: Observations, Arrival Time Measurements, and Analysis of 37 Millisecond Pulsars. ApJ 2015, 813, 65. [Google Scholar] [CrossRef]
- Shannon, R.M.; Ravi, V.; Lentati, L.T.; Lasky, P.D.; Hobbs, G.; Kerr, M.; Manchester, R.N.; Coles, W.A.; Levin, Y.; Bailes, M.; et al. Gravitational waves from binary supermassive black holes missing in pulsar observations. Science 2015, 349, 1522–1525. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Caballero, R.N.; Guo, Y.J.; Chalumeau, A.; Liu, K.; Shaifullah, G.; Lee, K.J.; Babak, S.; Desvignes, G.; Parthasarathy, A.; et al. Common-red-signal analysis with 24-yr high-precision timing of the European Pulsar Timing Array: Inferences in the stochastic gravitational-wave background search. MNRAS 2021, 508, 4970–4993. [Google Scholar] [CrossRef]
- Antoniadis, J.; Arzoumanian, Z.; Babak, S.; Bailes, M.; Bak Nielsen, A.S.; Baker, P.T.; Bassa, C.G.; Bécsy, B.; Berthereau, A.; Bonetti, M.; et al. The International Pulsar Timing Array second data release: Search for an isotropic gravitational wave background. MNRAS 2022, 510, 4873–4887. [Google Scholar] [CrossRef]
- Shannon, R.M.; Osłowski, S.; Dai, S.; Bailes, M.; Hobbs, G.; Manchester, R.N.; van Straten, W.; Raithel, C.A.; Ravi, V.; Toomey, L.; et al. Limitations in timing precision due to single-pulse shape variability in millisecond pulsars. MNRAS 2014, 443, 1463–1481. [Google Scholar] [CrossRef]
- Lam, M.T.; McLaughlin, M.A.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; Cromartie, H.T.; Demorest, P.B.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. The NANOGrav 12.5 yr Data Set: The Frequency Dependence of Pulse Jitter in Precision Millisecond Pulsars. ApJ 2019, 872, 193. [Google Scholar] [CrossRef]
- Kerr, M.; Reardon, D.J.; Hobbs, G.; Shannon, R.M.; Manchester, R.N.; Dai, S.; Russell, C.J.; Zhang, S.; van Straten, W.; Osłowski, S.; et al. The Parkes Pulsar Timing Array project: Second data release. PASA 2020, 37, e020. [Google Scholar] [CrossRef]
- Lentati, L.; Shannon, R.M.; Coles, W.A.; Verbiest, J.P.W.; van Haasteren, R.; Ellis, J.A.; Caballero, R.N.; Manchester, R.N.; Arzoumanian, Z.; Babak, S.; et al. From spin noise to systematics: Stochastic processes in the first International Pulsar Timing Array data release. MNRAS 2016, 458, 2161–2187. [Google Scholar] [CrossRef]
- Goncharov, B.; Zhu, X.J.; Thrane, E. Is there a spectral turnover in the spin noise of millisecond pulsars? MNRAS 2020, 497, 3264–3272. [Google Scholar] [CrossRef]
- Chalumeau, A.; Babak, S.; Petiteau, A.; Chen, S.; Samajdar, A.; Caballero, R.N.; Theureau, G.; Guillemot, L.; Desvignes, G.; Parthasarathy, A.; et al. Noise analysis in the European Pulsar Timing Array data release 2 and its implications on the gravitational-wave background search. MNRAS 2022, 509, 5538–5558. [Google Scholar] [CrossRef]
- Haskell, B.; Melatos, A. Models of pulsar glitches. Int. J. Mod. Phys. D 2015, 24, 1530008. [Google Scholar] [CrossRef]
- Hazboun, J.S.; Simon, J.; Siemens, X.; Romano, J.D. Model Dependence of Bayesian Gravitational-wave Background Statistics for Pulsar Timing Arrays. ApJ 2020, 905, L6. [Google Scholar] [CrossRef]
- Goncharov, B.; Reardon, D.J.; Shannon, R.M.; Zhu, X.J.; Thrane, E.; Bailes, M.; Bhat, N.D.R.; Dai, S.; Hobbs, G.; Kerr, M.; et al. Identifying and mitigating noise sources in precision pulsar timing data sets. MNRAS 2021, 502, 478–493. [Google Scholar] [CrossRef]
- Meyers, P.M.; O’Neill, N.J.; Melatos, A.; Evans, R.J. Rapid parameter estimation of a two-component neutron star model with spin wandering using a Kalman filter. MNRAS 2021, 506, 3349–3363. [Google Scholar] [CrossRef]
- Tiburzi, C.; Hobbs, G.; Kerr, M.; Coles, W.A.; Dai, S.; Manchester, R.N.; Possenti, A.; Shannon, R.M.; You, X.P. A study of spatial correlations in pulsar timing array data. MNRAS 2016, 455, 4339–4350. [Google Scholar] [CrossRef]
- Guo, Y.J.; Li, G.Y.; Lee, K.J.; Caballero, R.N. Studying the Solar system dynamics using pulsar timing arrays and the LINIMOSS dynamical model. MNRAS 2019, 489, 5573–5581. [Google Scholar] [CrossRef]
- Vallisneri, M.; Taylor, S.R.; Simon, J.; Folkner, W.M.; Park, R.S.; Cutler, C.; Ellis, J.A.; Lazio, T.J.W.; Vigeland, S.J.; Aggarwal, K.; et al. Modeling the Uncertainties of Solar System Ephemerides for Robust Gravitational-wave Searches with Pulsar-timing Arrays. ApJ 2020, 893, 112. [Google Scholar] [CrossRef]
- Hazboun, J.S.; Romano, J.D.; Smith, T.L. Realistic sensitivity curves for pulsar timing arrays. PRD 2019, 100, 104028. [Google Scholar] [CrossRef]
- Hazboun, J.; Romano, J.; Smith, T. Hasasia: A Python package for Pulsar Timing Array Sensitivity Curves. J. Open Source Softw. 2019, 4, 1775. [Google Scholar] [CrossRef]
- Verbiest, J.P.W.; Shaifullah, G.M. Measurement uncertainty in pulsar timing array experiments. Class. Quantum Gravity 2018, 35, 133001. [Google Scholar] [CrossRef]
- Lommen, A.N. Pulsar timing arrays: The promise of gravitational wave detection. Rep. Prog. Phys. 2015, 78, 124901. [Google Scholar] [CrossRef] [PubMed]
- Sesana, A.; Vecchio, A. Measuring the parameters of massive black hole binary systems with pulsar timing array observations of gravitational waves. PRD 2010, 81, 104008. [Google Scholar] [CrossRef]
- Mingarelli, C.M.F.; Lazio, T.J.W.; Sesana, A.; Greene, J.E.; Ellis, J.A.; Ma, C.P.; Croft, S.; Burke-Spolaor, S.; Taylor, S.R. The local nanohertz gravitational-wave landscape from supermassive black hole binaries. Nat. Astron. 2017, 1, 886–892. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Baker, P.T.; Blumer, H.; Bécsy, B.; Brazier, A.; Brook, P.R.; Burke-Spolaor, S.; Charisi, M.; Chatterjee, S.; Chen, S.; et al. Searching for Gravitational Waves from Cosmological Phase Transitions with the NANOGrav 12.5-Year Dataset. PRL 2021, 127, 251302. [Google Scholar] [CrossRef] [PubMed]
- Xue, X.; Bian, L.; Shu, J.; Yuan, Q.; Zhu, X.; Bhat, N.D.R.; Dai, S.; Feng, Y.; Goncharov, B.; Hobbs, G.; et al. Constraining Cosmological Phase Transitions with the Parkes Pulsar Timing Array. PRL 2021, 127, 251303. [Google Scholar] [CrossRef] [PubMed]
- Moore, C.J.; Vecchio, A. Ultra-low-frequency gravitational waves from cosmological and astrophysical processes. Nat. Astron. 2021, 5, 1268–1274. [Google Scholar] [CrossRef]
- Chen, Z.C.; Yuan, C.; Huang, Q.G. Non-tensorial gravitational wave background in NANOGrav 12.5-year data set. Sci. China Physics, Mech. Astron. 2021, 64, 120412. [Google Scholar] [CrossRef]
- Chen, Z.C.; Wu, Y.M.; Huang, Q.G. Searching for Isotropic Stochastic Gravitational-Wave Background in the International Pulsar Timing Array Second Data Release. arXiv 2021, arXiv:2109.00296. [Google Scholar]
- Wu, Y.M.; Chen, Z.C.; Huang, Q.G. Constraining the Polarization of Gravitational Waves with the Parkes Pulsar Timing Array Second Data Release. arXiv 2021, arXiv:2108.10518. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Baker, P.T.; Blumer, H.; Bécsy, B.; Brazier, A.; Brook, P.R.; Burke-Spolaor, S.; Charisi, M.; Chatterjee, S.; Chen, S.; et al. The NANOGrav 12.5-year Data Set: Search for Non-Einsteinian Polarization Modes in the Gravitational-wave Background. ApJ 2021, 923, L22. [Google Scholar] [CrossRef]
- Aggarwal, N.; Aguiar, O.D.; Bauswein, A.; Cella, G.; Clesse, S.; Cruise, A.M.; Domcke, V.; Figueroa, D.G.; Geraci, A.; Goryachev, M.; et al. Challenges and opportunities of gravitational-wave searches at MHz to GHz frequencies. Living Rev. Relativ. 2021, 24, 4. [Google Scholar] [CrossRef]
- Weber, J. Detection and Generation of Gravitational Waves. Phys. Rev. 1960, 117, 306–313. [Google Scholar] [CrossRef]
- Weber, J. Evidence for discovery of gravitational radiation. Phys. Rev. Lett. 1969, 22, 1320–1324. [Google Scholar] [CrossRef]
- Aguiar, O.D. The Past, Present and Future of the Resonant-Mass Gravitational Wave Detectors. Res. Astron. Astrophys. 2011, 11, 1–42. [Google Scholar] [CrossRef]
- Harms, J.; Ambrosino, F.; Angelini, L.; Braito, V.; Branchesi, M.; Brocato, E.; Cappellaro, E.; Coccia, E.; Coughlin, M.; Della Ceca, R.; et al. Lunar Gravitational-wave Antenna. Astrophys. J. 2021, 910, 1. [Google Scholar] [CrossRef]
- Jani, K.; Loeb, A. Gravitational-Wave Lunar Observatory for Cosmology. J. Cosmol. Astropart. Phys. 2021, 2021, 044. [Google Scholar] [CrossRef]
- Sesana, A.; Korsakova, N.; Sedda, M.A.; Baibhav, V.; Barausse, E.; Barke, S.; Berti, E.; Bonetti, M.; Capelo, P.R.; Caprini, C.; et al. Unveiling the gravitational universe at μ-Hz frequencies. Exper. Astron. 2021, 51, 1333–1383. [Google Scholar] [CrossRef]
- Book, L.G.; Flanagan, E.E. Astrometric Effects of a Stochastic Gravitational Wave Background. Phys. Rev. D 2011, 83, 024024. [Google Scholar] [CrossRef]
- Moore, C.J.; Mihaylov, D.P.; Lasenby, A.; Gilmore, G. Astrometric Search Method for Individually Resolvable Gravitational Wave Sources with Gaia. Phys. Rev. Lett. 2017, 119, 261102. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Murayama, H.; White, G. Exploring the Early Universe with Gaia and THEIA. J. Cosmol. Astropart. Phys. 2021, 2021, 023. [Google Scholar] [CrossRef]
- Graham, P.W.; Hogan, J.M.; Kasevich, M.A.; Rajendran, S.; Romani, R.W. Mid-band gravitational wave detection with precision atomic sensors. arXiv 2017, arXiv:1711.02225. [Google Scholar]
- Abe, M.; Adamson, P.; Borcean, M.; Bortoletto, D.; Bridges, K.; Carman, S.P.; Chattopadhyay, S.; Coleman, J.; Curfman, N.M.; DeRose, K.; et al. Matter-wave Atomic Gradiometer Interferometric Sensor (MAGIS-100). Quantum Sci. Technol. 2021, 6, 044003. [Google Scholar] [CrossRef]
- Vitale, S.; Farr, W.M.; Ng, K.K.Y.; Rodriguez, C.L. Measuring the Star Formation Rate with Gravitational Waves from Binary Black Holes. ApJ 2019, 886, L1. [Google Scholar] [CrossRef]
- Regimbau, T.; Evans, M.; Christensen, N.; Katsavounidis, E.; Sathyaprakash, B.; Vitale, S. Digging deeper: Observing primordial gravitational waves below the binary black hole produced stochastic background. Phys. Rev. Lett. 2017, 118, 151105. [Google Scholar] [CrossRef] [PubMed]
- Ackley, K.; Adya, V.B.; Agrawal, P.; Altin, P.; Ashton, G.; Bailes, M.; Baltinas, E.; Barbuio, A.; Beniwal, D.; Blair, C.; et al. Neutron Star Extreme Matter Observatory: A kilohertz-band gravitational-wave detector in the global network. Publ. Astron. Soc. Austral. 2020, 37, e047. [Google Scholar] [CrossRef]
- Maggiore, M.; Van Den Broeck, C.; Bartolo, N.; Belgacem, E.; Bertacca, D.; Bizouard, M.A.; Branchesi, M.; Clesse, S.; Foffa, S.; García-Bellido, J.; et al. Science Case for the Einstein Telescope. JCAP 2020, 03, 050. [Google Scholar] [CrossRef]
- Cutler, C.; Harms, J. BBO and the neutron-star-binary subtraction problem. Phys. Rev. D 2006, 73, 042001. [Google Scholar] [CrossRef]
- Sachdev, S.; Regimbau, T.; Sathyaprakash, B.S. Subtracting compact binary foreground sources to reveal primordial gravitational-wave backgrounds. PRD 2020, 102, 024051. [Google Scholar] [CrossRef]
- Sharma, A.; Harms, J. Searching for cosmological gravitational-wave backgrounds with third-generation detectors in the presence of an astrophysical foreground. PRD 2020, 102, 063009. [Google Scholar] [CrossRef]
- Raidal, M.; Spethmann, C.; Vaskonen, V.; Veermäe, H. Formation and evolution of primordial black hole binaries in the early universe. J. Cosmol. Astropart. Phys. 2019, 2019, 018. [Google Scholar] [CrossRef]
- Mandic, V.; Bird, S.; Cholis, I. Stochastic Gravitational-Wave Background due to Primordial Binary Black Hole Mergers. Phys. Rev. Lett. 2016, 117, 201102. [Google Scholar] [CrossRef] [PubMed]
- Ali-Haïmoud, Y.; Kovetz, E.D.; Kamionkowski, M. Merger rate of primordial black-hole binaries. Phys. Rev. D 2017, 96, 123523. [Google Scholar] [CrossRef]
- De Luca, V.; Franciolini, G.; Pani, P.; Riotto, A. The Minimum Testable Abundance of Primordial Black Holes at Future Gravitational-Wave Detectors. J. Cosmol. Astropart. Phys. 2021, 2021, 039. [Google Scholar] [CrossRef]
- Ng, K.K.Y.; Chen, S.; Goncharov, B.; Dupletsa, U.; Borhanian, S.; Branchesi, M.; Harms, J.; Maggiore, M.; Sathyaprakash, B.S.; Vitale, S. On the single-event-based identification of primordial black hole mergers at cosmological distances. arXiv 2021, arXiv:2108.07276. [Google Scholar]
- Biscoveanu, S.; Talbot, C.; Thrane, E.; Smith, R. Measuring the primordial gravitational-wave background in the presence of astrophysical foregrounds. Phys. Rev. Lett. 2020, 125, 241101. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, S.; Silk, J. Can we distinguish astrophysical from primordial black holes via the stochastic gravitational wave background? Mon. Not. R. Astron. Soc. 2021, 506, 3977–3985. [Google Scholar] [CrossRef]
- Mukherjee, S.; Meinema, M.S.P.; Silk, J. Prospects of discovering sub-solar primordial black holes using the stochastic gravitational wave background from third-generation detectors. arXiv 2021, arXiv:2107.02181. [Google Scholar]
- Mukherjee, S.; Silk, J. Fundamental physics using the temporal gravitational wave background. Phys. Rev. D 2021, 104, 063518. [Google Scholar] [CrossRef]
- Schumann, W.O. Über die strahlungslosen Eigenschwingungen einer leitenden Kugel, die von einer Luftschicht und einer Ionosphärenhülle umgeben ist. Z. Naturforschung Teil A 1952, 7, 149–154. [Google Scholar] [CrossRef]
- Schumann, W.O.; König, H. Über die Beobachtung von “atmospherics” bei geringsten Frequenzen. Naturwissenschaften 1954, 41, 183–184. [Google Scholar] [CrossRef]
- Christensen, N. Measuring the stochastic gravitational radiation background with laser interferometric antennas. Phys. Rev. D 1992, 46, 5250–5266. [Google Scholar] [CrossRef] [PubMed]
- Thrane, E.; Christensen, N.; Schofield, R.M.S. Correlated magnetic noise in global networks of gravitational-wave detectors: Observations and implications. PRD 2013, 87, 123009. [Google Scholar] [CrossRef]
- Thrane, E.; Christensen, N.; Schofield, R.M.S.; Effler, A. Correlated noise in networks of gravitational-wave detectors: Subtraction and mitigation. PRD 2014, 90, 023013. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Christensen, N.L.; De Rosa, R.; Fiori, I.; Gołkowski, M.; Guidry, M.; Harms, J.; Kubisz, J.; Kulak, A.; Mlynarczyk, J.; et al. Subtraction of correlated noise in global networks of gravitational-wave interferometers. Class. Quantum Gravity 2016, 33, 224003. [Google Scholar] [CrossRef]
- Himemoto, Y.; Taruya, A. Impact of correlated magnetic noise on the detection of stochastic gravitational waves: Estimation based on a simple analytical model. PRD 2017, 96, 022004. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Cirone, A.; Meyers, P.; Atsuta, S.; Boschi, V.; Chincarini, A.; Christensen, N.L.; De Rosa, R.; Effler, A.; Fiori, I.; et al. Measurement and subtraction of Schumann resonances at gravitational-wave interferometers. PRD 2018, 97, 102007. [Google Scholar] [CrossRef]
- Himemoto, Y.; Taruya, A. Correlated magnetic noise from anisotropic lightning sources and the detection of stochastic gravitational waves. PRD 2019, 100, 082001. [Google Scholar] [CrossRef]
- Himemoto, Y.; Nishizawa, A.; Taruya, A. Impacts of overlapping gravitational-wave signals on the parameter estimation: Toward the search for cosmological backgrounds. PRD 2021, 104, 044010. [Google Scholar] [CrossRef]
- Janssens, K.; Martinovic, K.; Christensen, N.; Meyers, P.M.; Sakellariadou, M. Impact of Schumann resonances on the Einstein Telescope and projections for the magnetic coupling function. PRD 2021, 104, 122006. [Google Scholar] [CrossRef]
- Saulson, P.R. Terrestrial gravitational noise on a gravitational wave antenna. PRD 1984, 30, 732–736. [Google Scholar] [CrossRef]
- Hughes, S.A.; Thorne, K.S. Seismic gravity-gradient noise in interferometric gravitational-wave detectors. PRD 1998, 58, 122002. [Google Scholar] [CrossRef]
- Harms, J. Terrestrial gravity fluctuations. Living Rev. Relativ. 2019, 22, 6. [Google Scholar] [CrossRef]
- Amann, F.; Bonsignorio, F.; Bulik, T.; Bulten, H.J.; Cuccuru, S.; Dassargues, A.; DeSalvo, R.; Fenyvesi, E.; Fidecaro, F.; Fiori, I.; et al. Site-selection criteria for the Einstein Telescope. Rev. Sci. Instruments 2020, 91, 094504. [Google Scholar] [CrossRef] [PubMed]
- Driggers, J.C.; Harms, J.; Adhikari, R.X. Subtraction of Newtonian noise using optimized sensor arrays. PRD 2012, 86, 102001. [Google Scholar] [CrossRef]
- Coughlin, M.; Harms, J.; Christensen, N.; Dergachev, V.; DeSalvo, R.; Kandhasamy, S.; Mandic, V. Wiener filtering with a seismic underground array at the Sanford Underground Research Facility. Class. Quantum Gravity 2014, 31, 215003. [Google Scholar] [CrossRef]
- Coughlin, M.; Mukund, N.; Harms, J.; Driggers, J.; Adhikari, R.; Mitra, S. Towards a first design of a Newtonian-noise cancellation system for Advanced LIGO. Class. Quantum Gravity 2016, 33, 244001. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Harms, J.; Driggers, J.; McManus, D.J.; Mukund, N.; Ross, M.P.; Slagmolen, B.J.J.; Venkateswara, K. Implications of Dedicated Seismometer Measurements on Newtonian-Noise Cancellation for Advanced LIGO. PRL 2018, 121, 221104. [Google Scholar] [CrossRef]
- Badaracco, F.; Harms, J.; Bertolini, A.; Bulik, T.; Fiori, I.; Idzkowski, B.; Kutynia, A.; Nikliborc, K.; Paoletti, F.; Paoli, A.; et al. Machine learning for gravitational-wave detection: Surrogate Wiener filtering for the prediction and optimized cancellation of Newtonian noise at Virgo. Class. Quantum Gravity 2020, 37, 195016. [Google Scholar] [CrossRef]
- Harms, J.; Hild, S. Passive Newtonian noise suppression for gravitational-wave observatories based on shaping of the local topography. Class. Quantum Gravity 2014, 31, 185011. [Google Scholar] [CrossRef]
- Badaracco, F.; Harms, J. Optimization of seismometer arrays for the cancellation of Newtonian noise from seismic body waves. Class. Quantum Gravity 2019, 36, 145006. [Google Scholar] [CrossRef]
- Harms, J.; Venkateswara, K. Newtonian-noise cancellation in large-scale interferometric GW detectors using seismic tiltmeters. Class. Quantum Gravity 2016, 33, 234001. [Google Scholar] [CrossRef]
- Creighton, T. Tumbleweeds and airborne gravitational noise sources for LIGO. Class. Quantum Gravity 2008, 25, 125011. [Google Scholar] [CrossRef]
- Fiorucci, D.; Harms, J.; Barsuglia, M.; Fiori, I.; Paoletti, F. Impact of infrasound atmospheric noise on gravity detectors used for astrophysical and geophysical applications. PRD 2018, 97, 062003. [Google Scholar] [CrossRef]
- Muratore, M.; Vetrugno, D.; Vitale, S. Revisitation of time delay interferometry combinations that suppress laser noise in LISA. Class. Quantum Gravity 2020, 37, 185019. [Google Scholar] [CrossRef]
- Estabrook, F.B.; Tinto, M.; Armstrong, J.W. Time-delay analysis of LISA gravitational wave data: Elimination of spacecraft motion effects. Phys. Rev. D 2000, 62, 042002. [Google Scholar] [CrossRef]
- Prince, T.A.; Tinto, M.; Larson, S.L.; Armstrong, J. The LISA optimal sensitivity. Phys. Rev. D 2002, 66, 122002. [Google Scholar] [CrossRef]
- Sylvestre, J.; Tinto, M. Noise characterization for LISA. Phys. Rev. D 2003, 68, 102002. [Google Scholar] [CrossRef]
- Crowder, J.; Cornish, N.J. LISA source confusion. Phys. Rev. D 2004, 70, 082004. [Google Scholar] [CrossRef]
- Chen, Z.C.; Huang, F.; Huang, Q.G. Stochastic Gravitational-wave Background from Binary Black Holes and Binary Neutron Stars and Implications for LISA. Astrophys. J. 2019, 871, 97. [Google Scholar] [CrossRef]
- Caprini, C.; Chala, M.; Dorsch, G.C.; Hindmarsh, M.; Huber, S.J.; Konstandin, T.; Kozaczuk, J.; Nardini, G.; No, J.M.; Rummukainen, K.; et al. Detecting gravitational waves from cosmological phase transitions with LISA: An update. JCAP 2020, 03, 024. [Google Scholar] [CrossRef]
- Boileau, G.; Jenkins, A.C.; Sakellariadou, M.; Meyer, R.; Christensen, N. Ability of LISA to detect a gravitational-wave background of cosmological origin: The cosmic string case. Phys. Rev. D 2022, 105, 023510. [Google Scholar] [CrossRef]
- Crowder, J.; Cornish, N. A Solution to the Galactic Foreground Problem for LISA. Phys. Rev. D 2007, 75, 043008. [Google Scholar] [CrossRef]
- LISA Data Challenge Manual. Available online: https://lisa-ldc.lal.in2p3.fr/static/data/pdf/LDC-manual-Sangria.pdf (accessed on 1 November 2021).
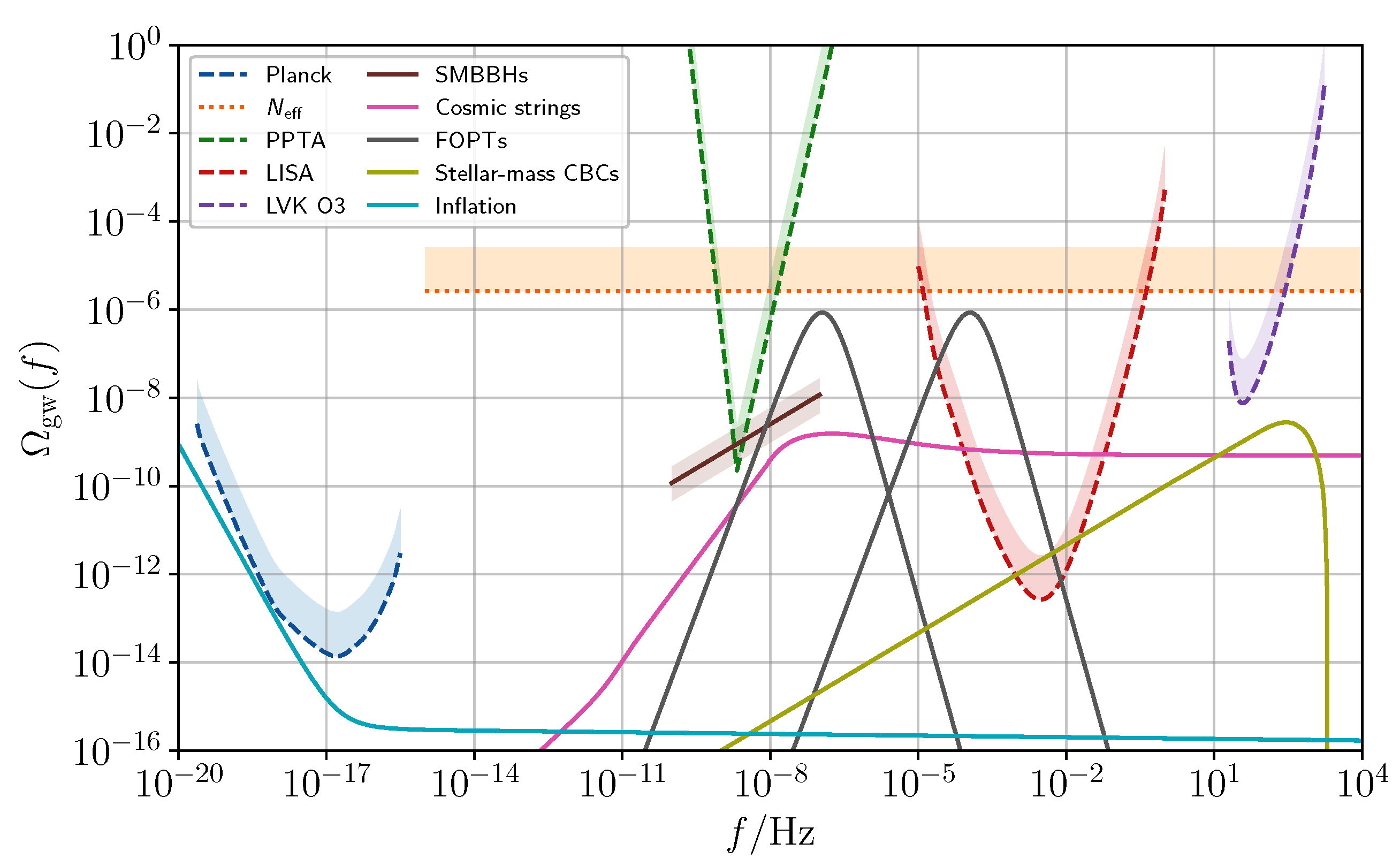
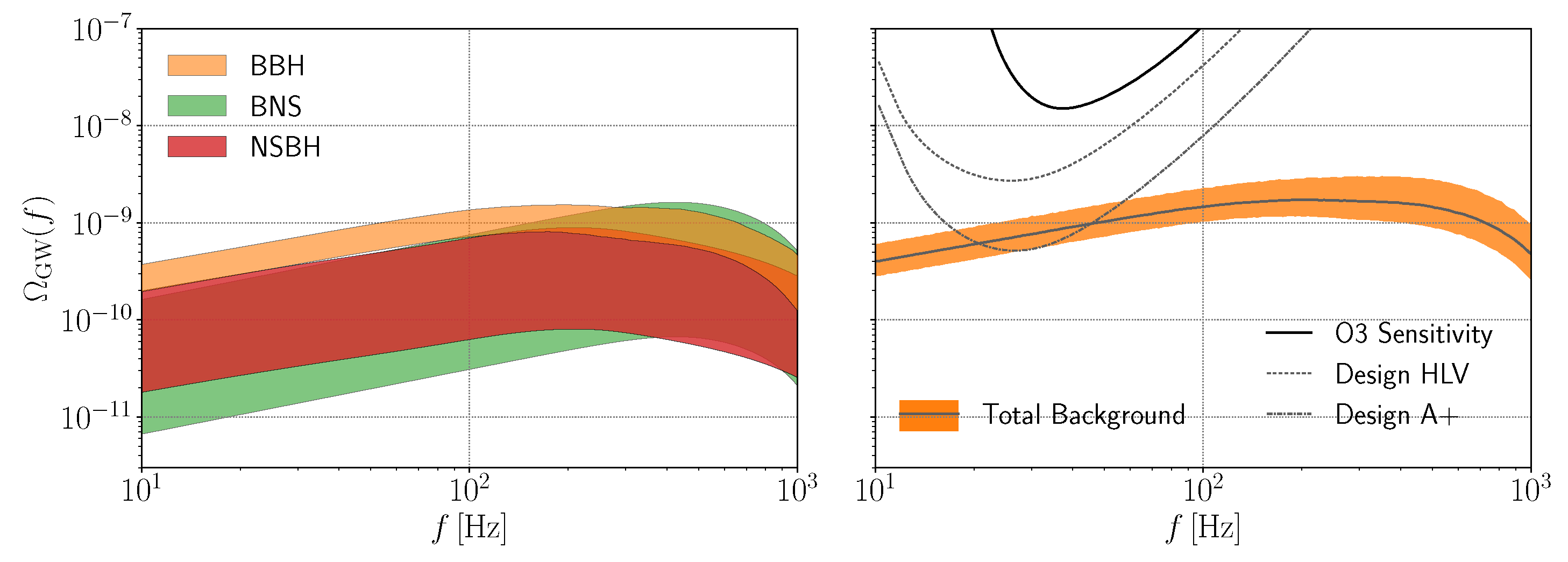
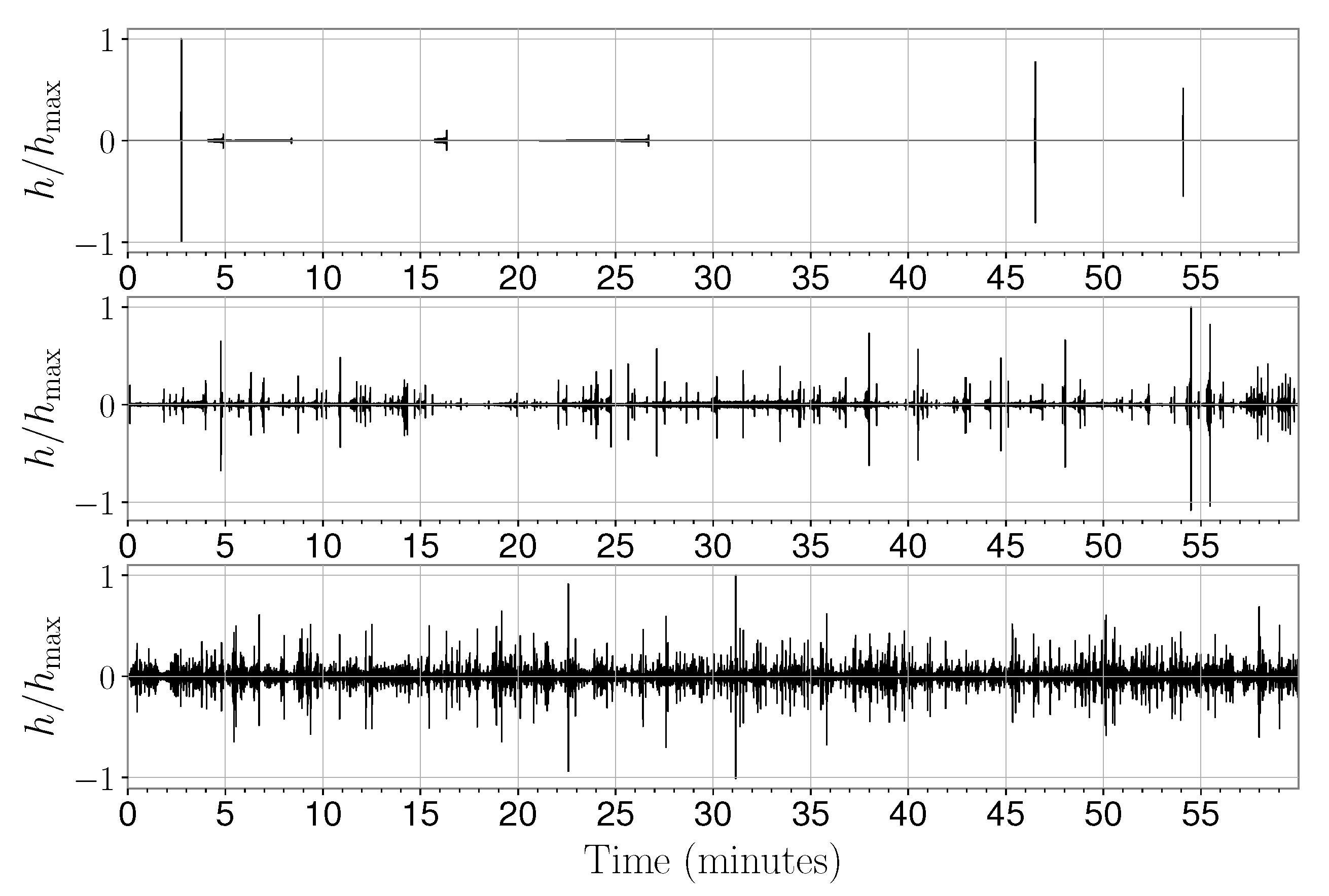
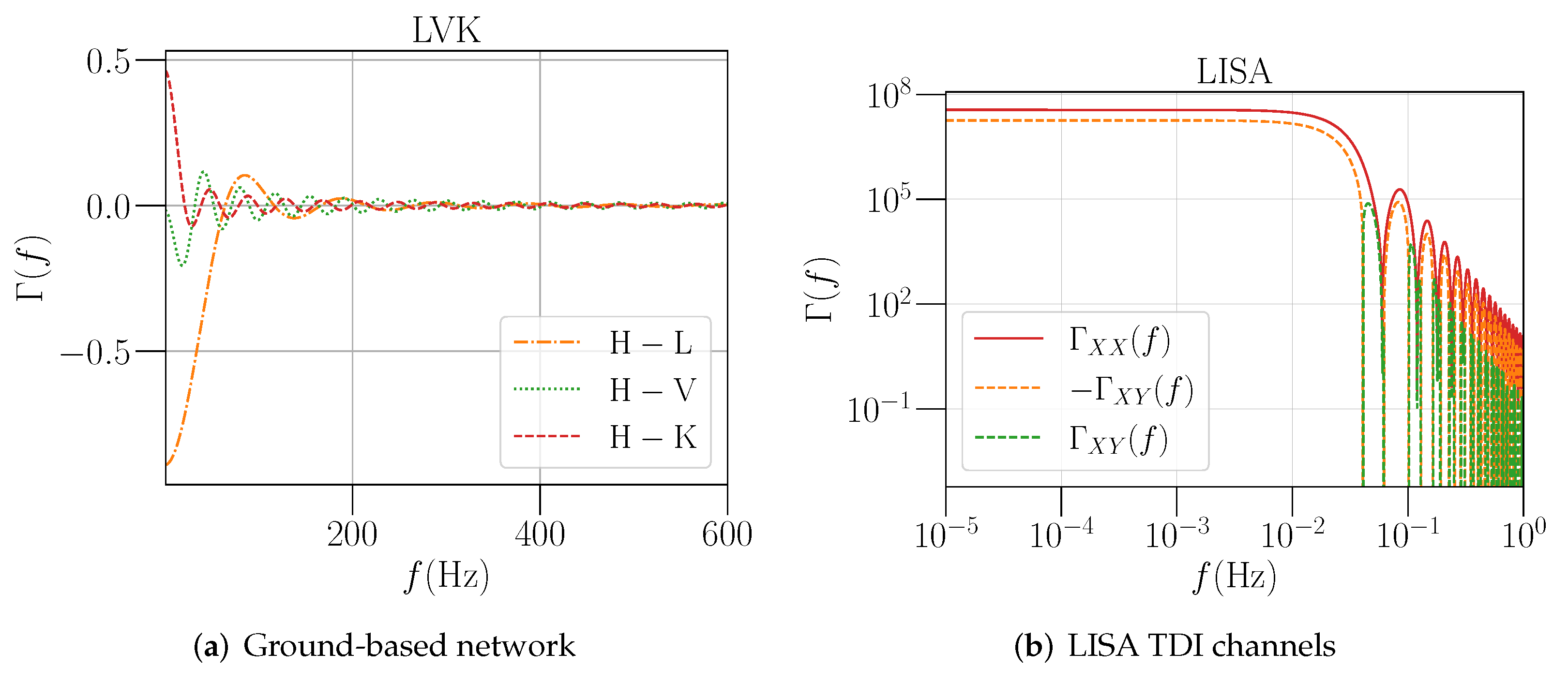
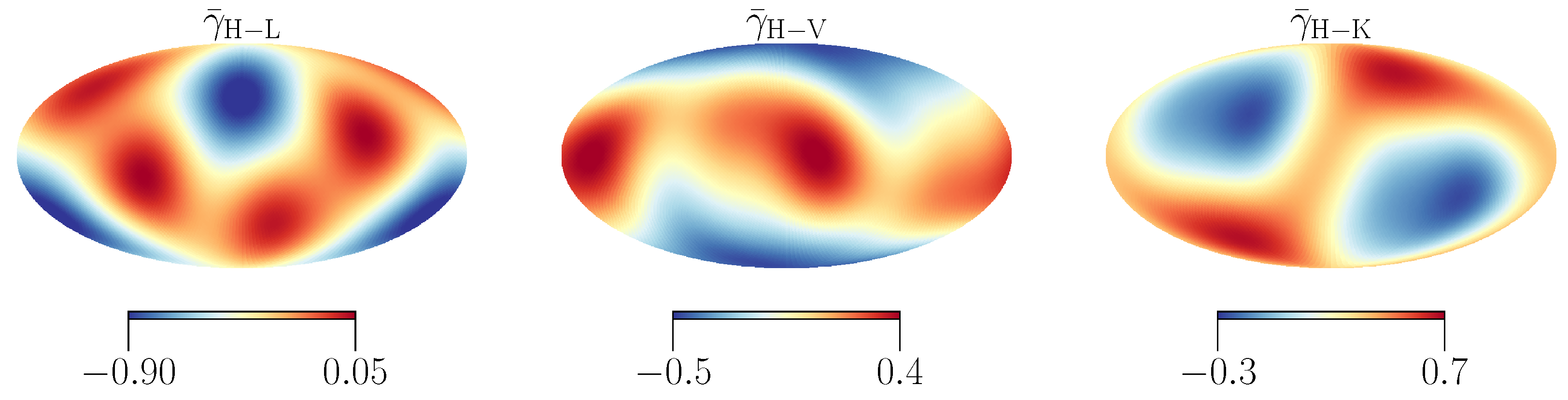
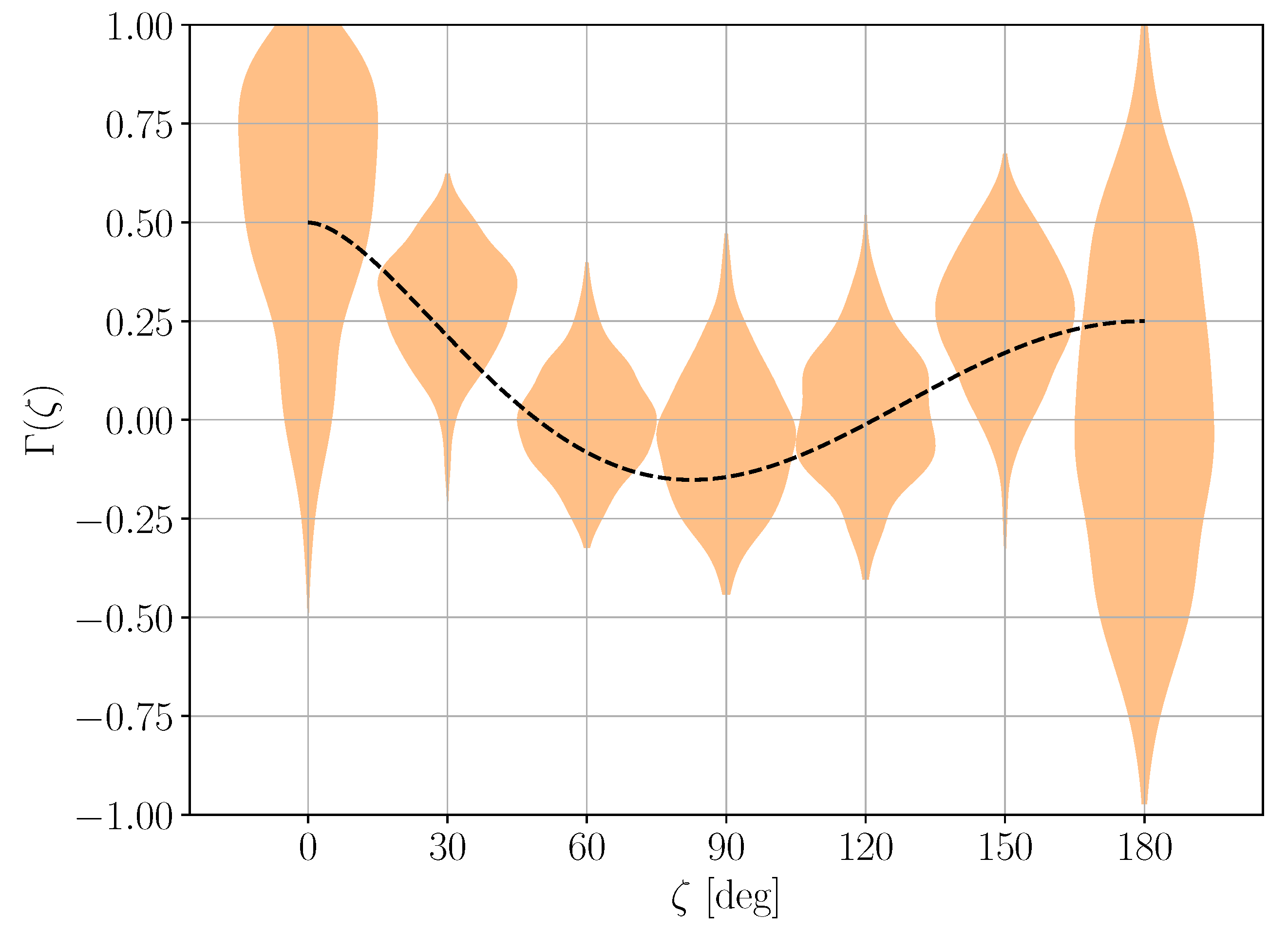
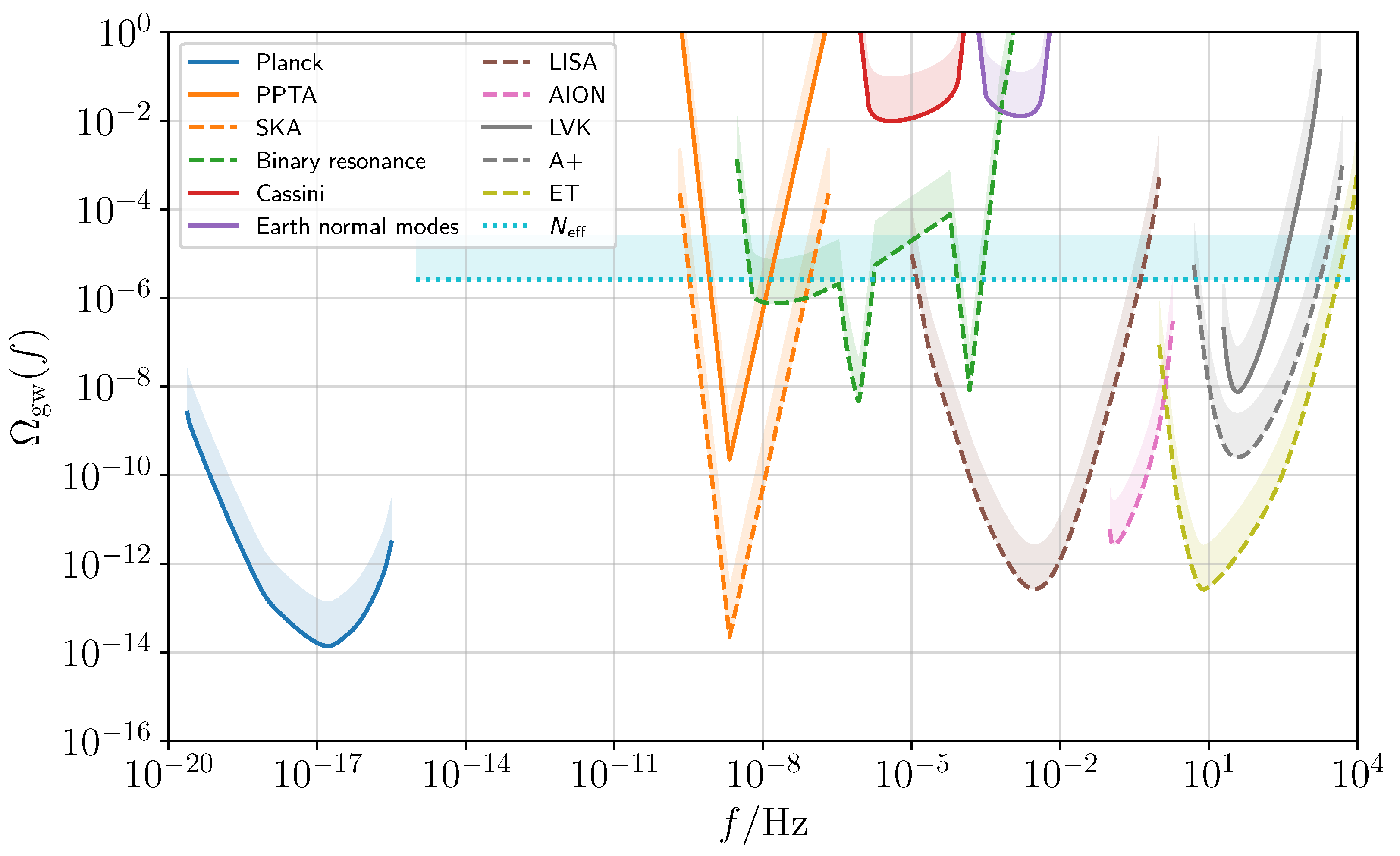
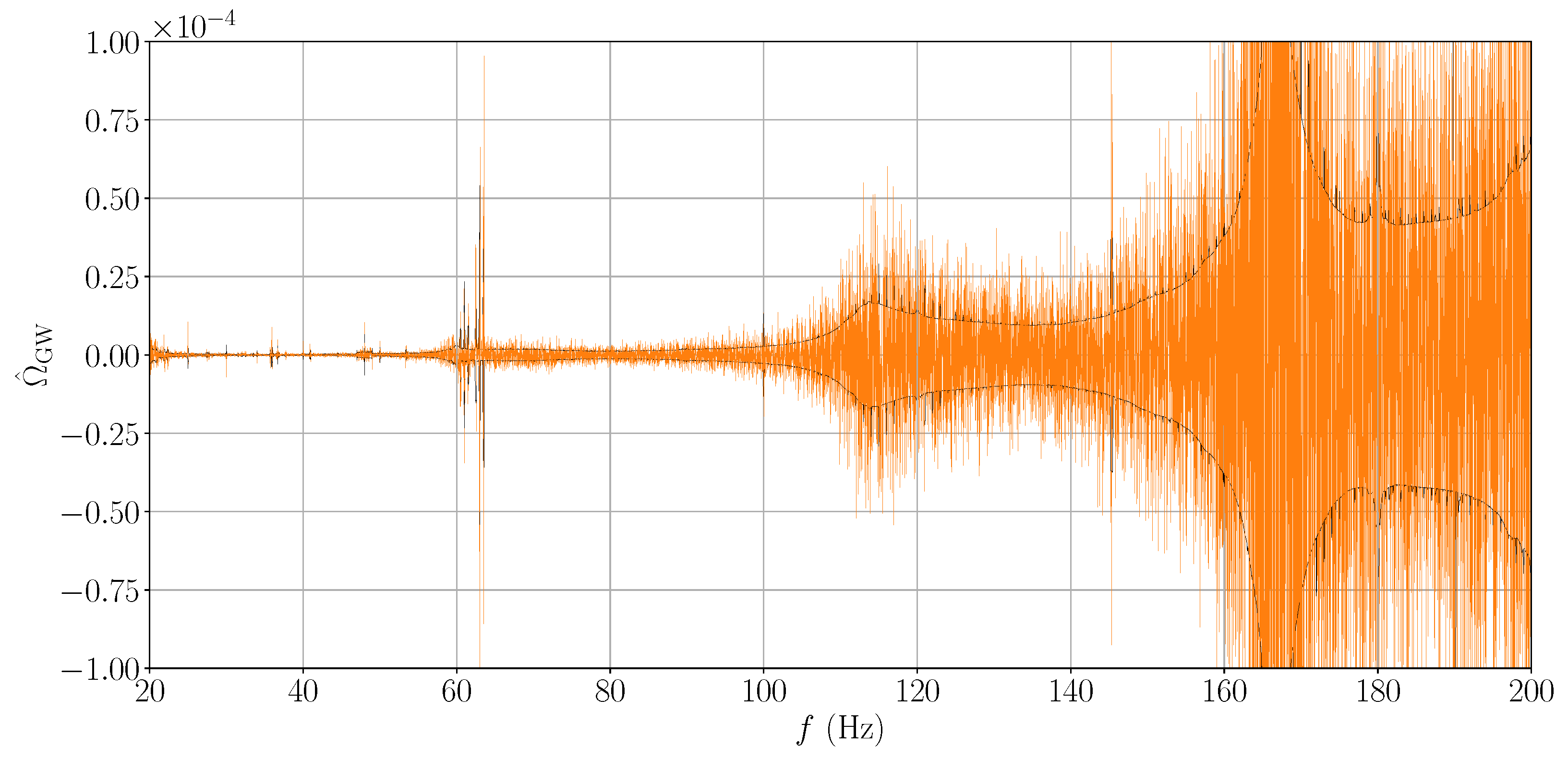
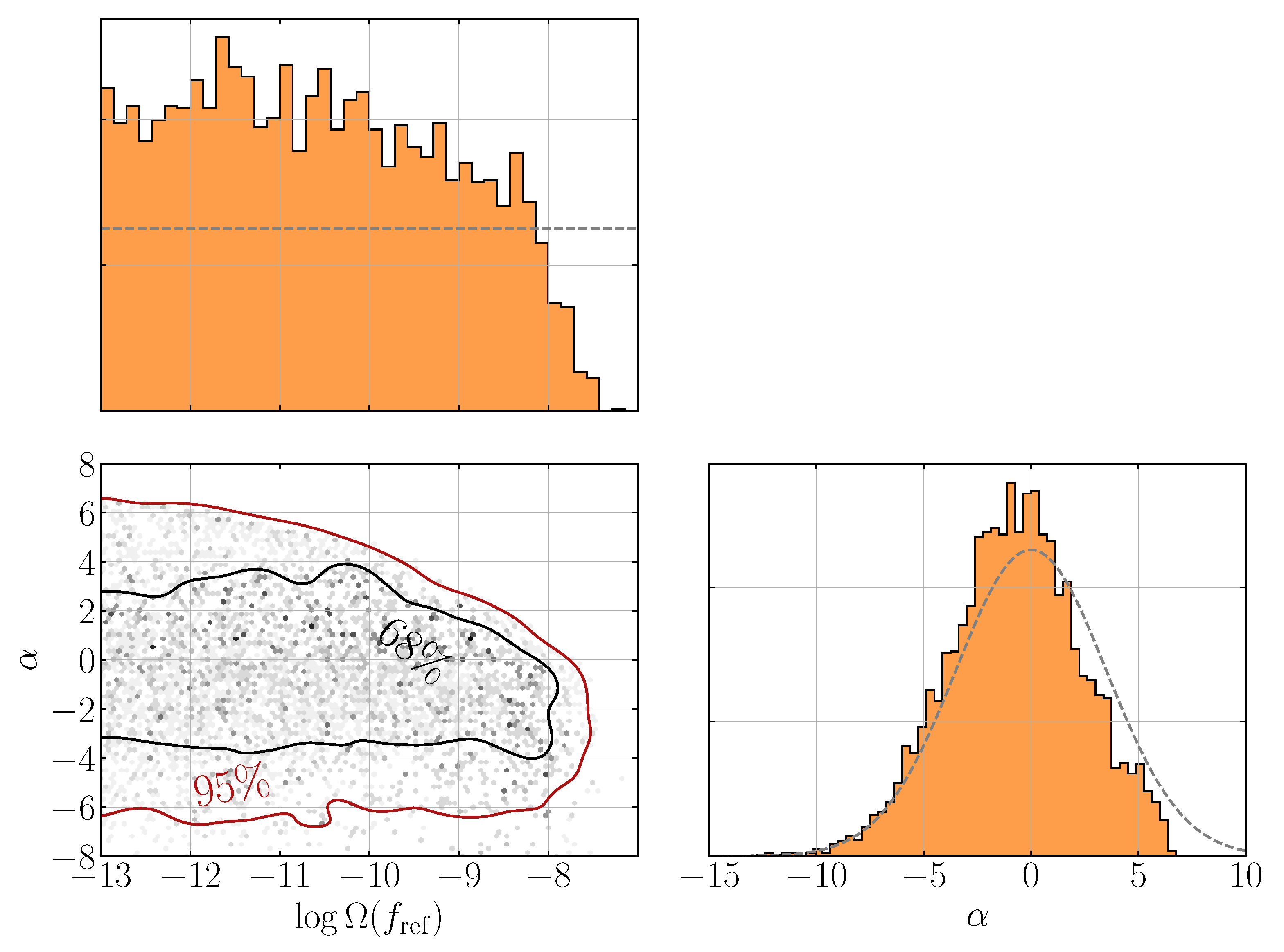
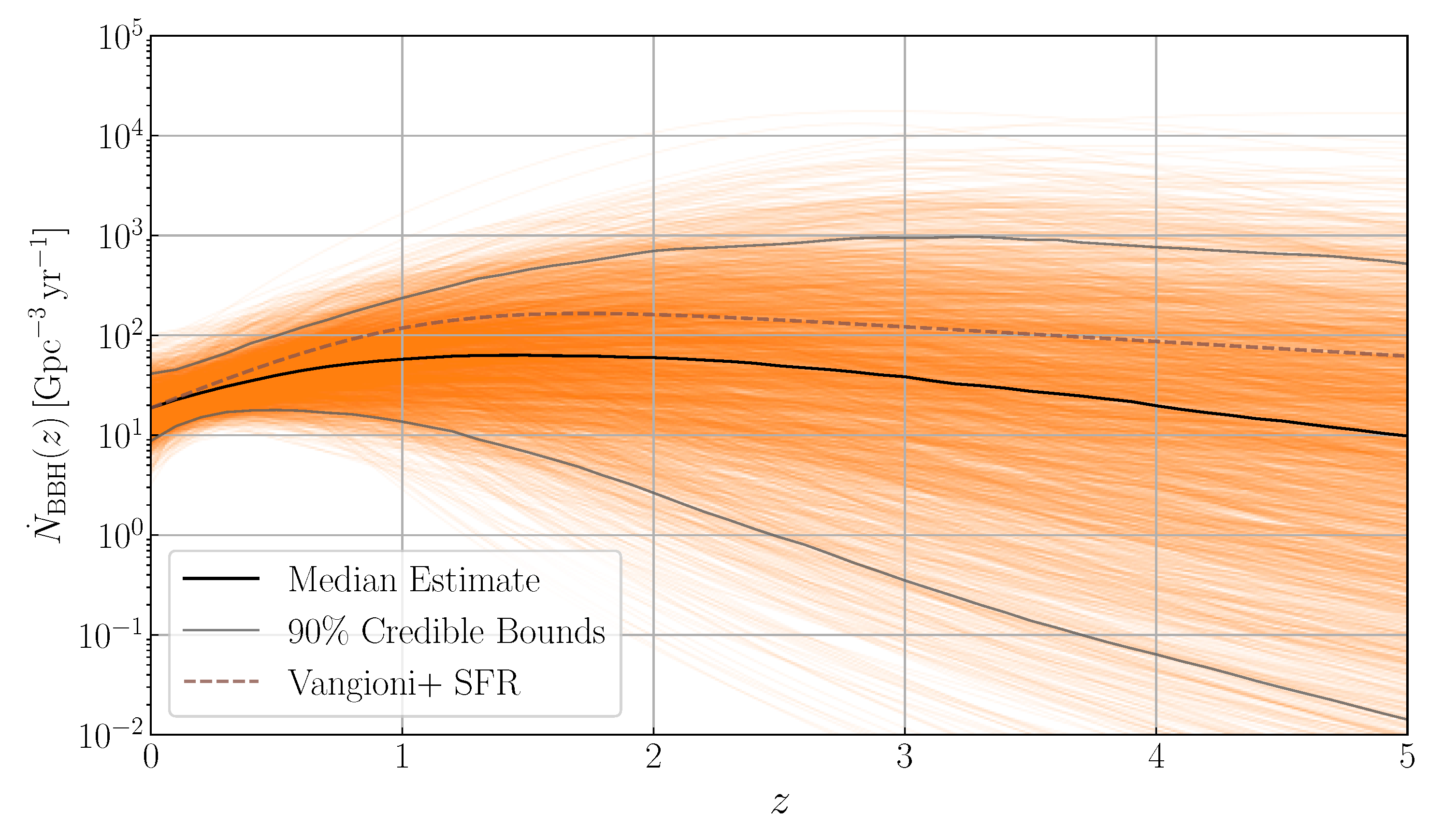
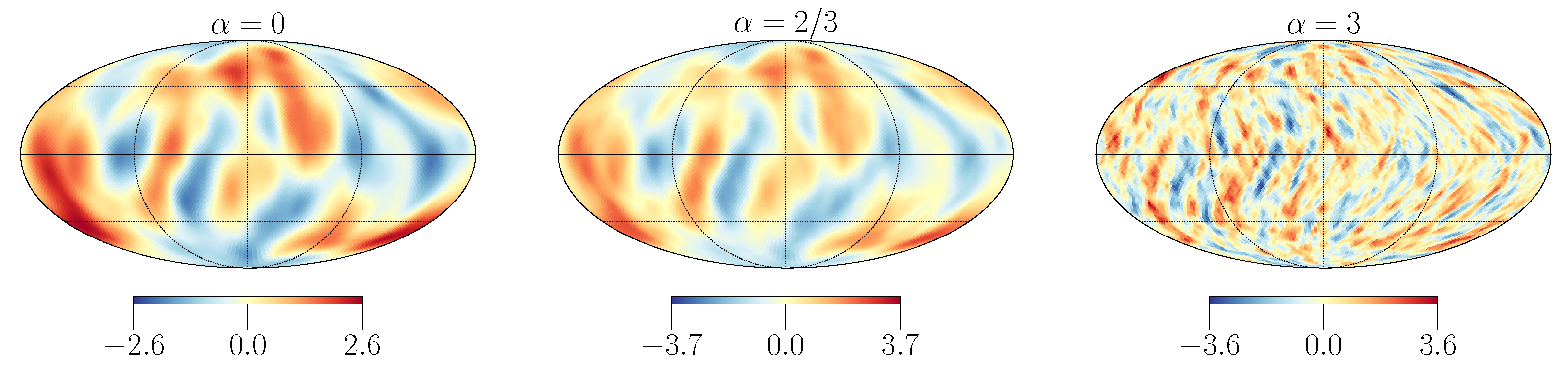
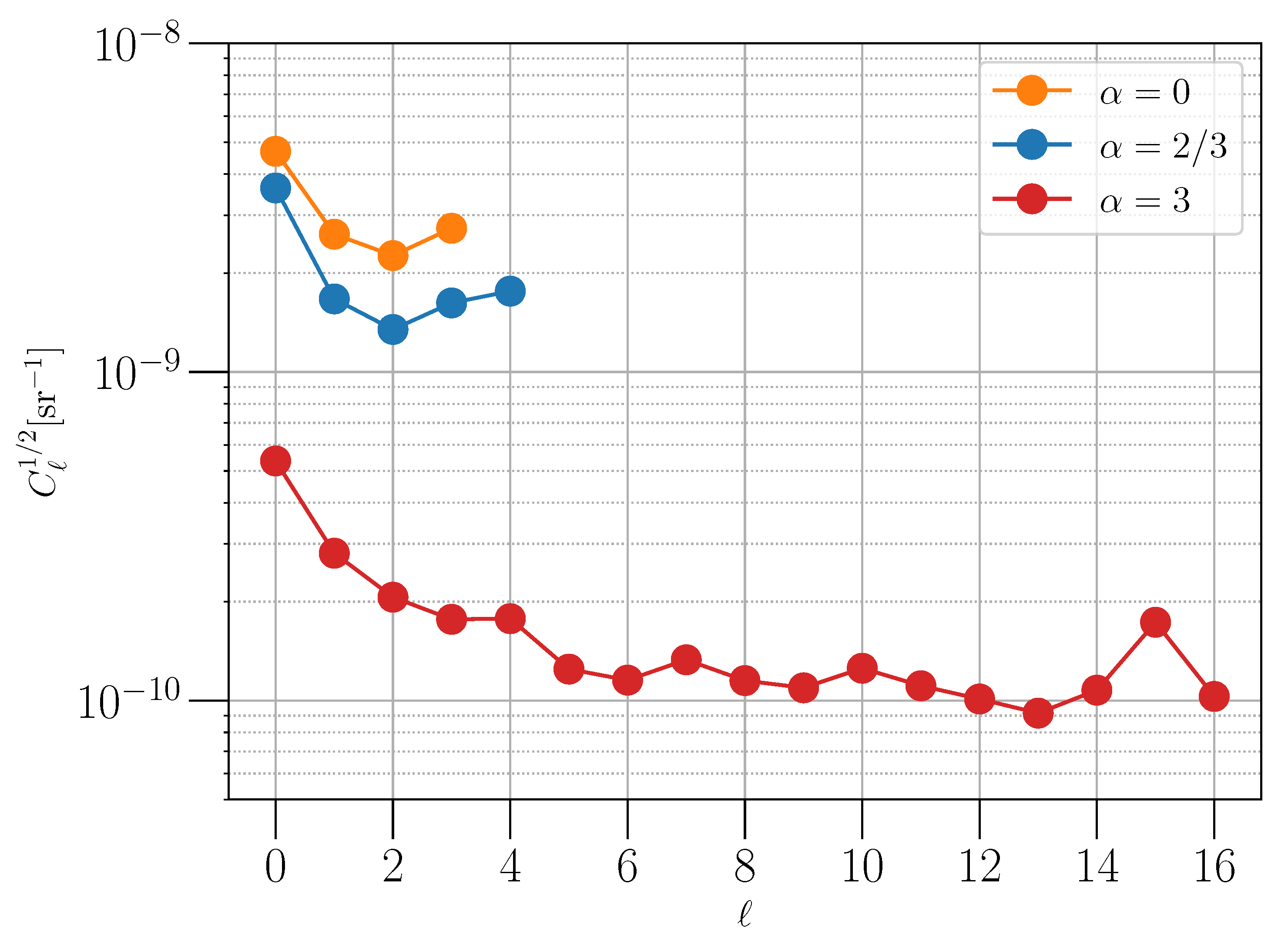
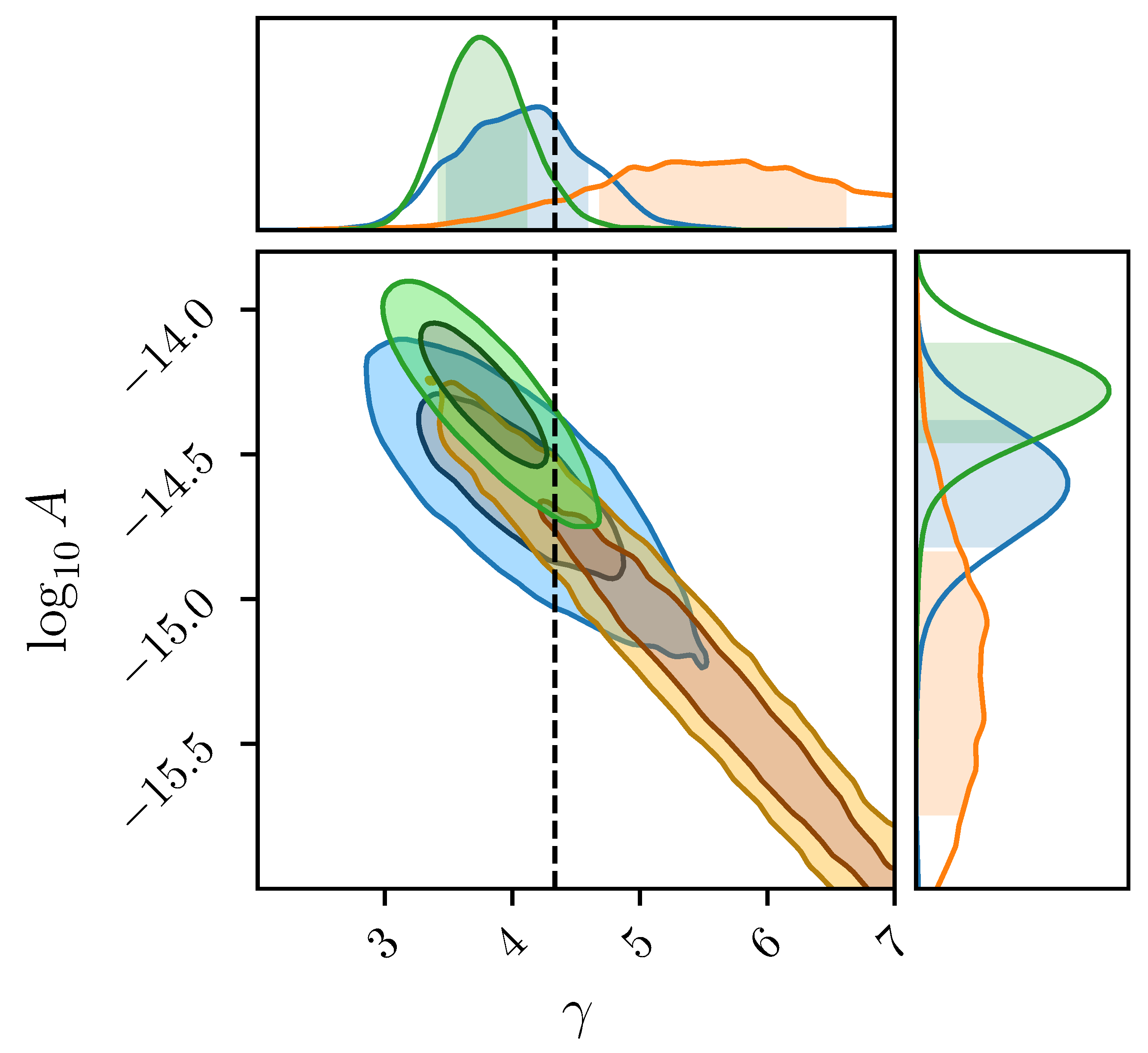
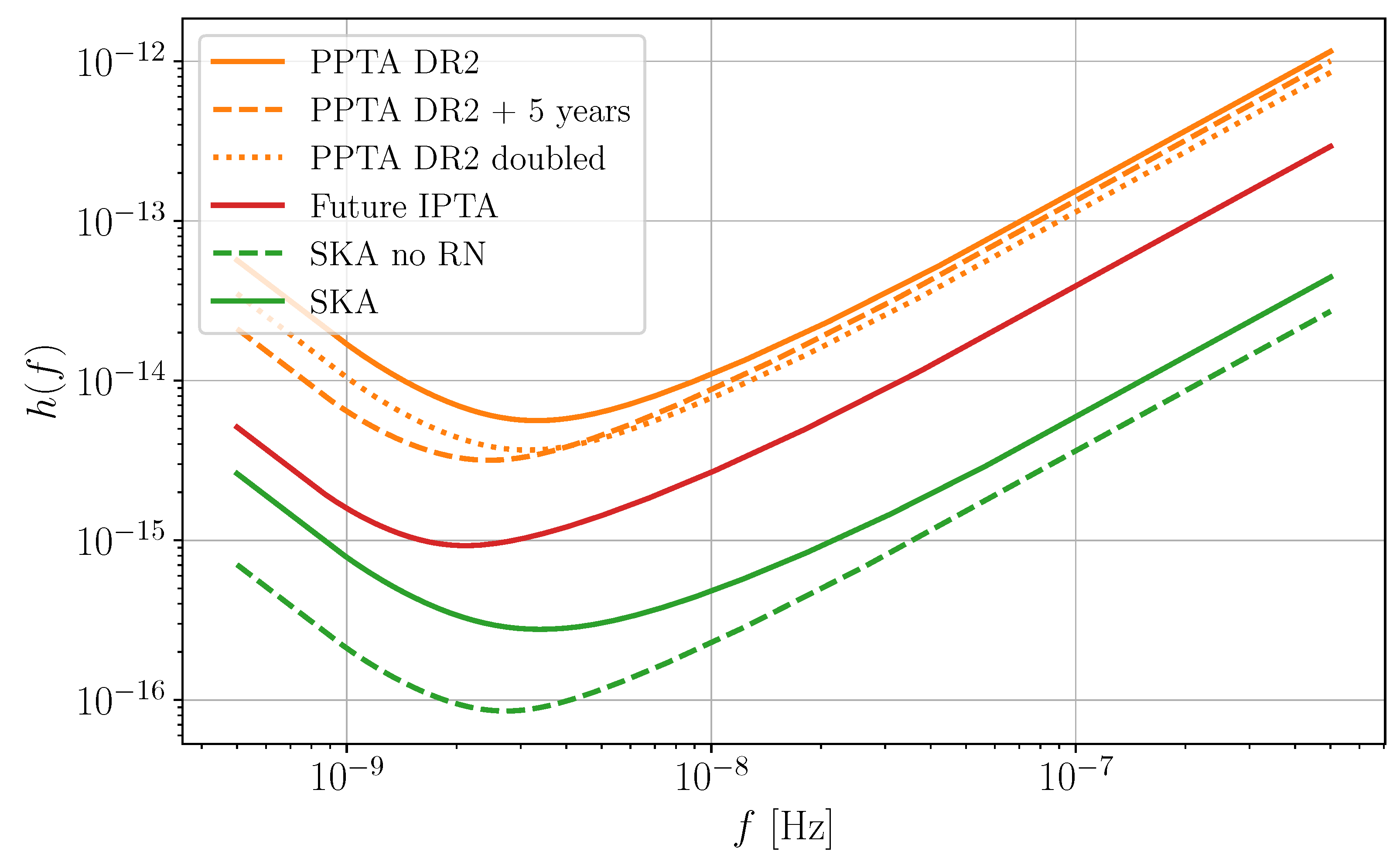
| Publication | Collaboration | Year | |||
|---|---|---|---|---|---|
| Jenet et al. [269] | PPTA | 2006 | <11 | 20 | 7 |
| van Haasteren et al. [173] | EPTA | 2011 | <6 | 11 | 5 |
| Demorest et al. [270] | NANOGrav | 2013 | <7 | 5 | 17 |
| Shannon et al. [271] | PPTA | 2013 | <2.4 | 25 | 6 |
| Lentati et al. [272] | EPTA | 2015 | <3.0 | 18 | 6 |
| * Arzoumanian et al. [178] | NANOGrav | 2015 | <1.5 | 9 | 37 |
| Shannon et al. [274] | PPTA | 2015 | <1.0 | 11 | 4 |
| Verbiest et al. [24] | IPTA | 2016 | <1.7 | 21 | 4 |
| * Arzoumanian et al. [180] | NANOGrav | 2018 | <1.45 | 11.4 | 45 |
| * Arzoumanian et al. [54] | NANOGrav | 2020 | CP: | 12.5 | 45 |
| Goncharov et al. [26] | PPTA | 2021 | CP: | 15.0 | 26 |
| Chen et al. [275] | EPTA | 2021 | CP: | 24.0 | 6 |
| * Antoniadis et al. [276] | IPTA | 2022 | CP: | 30.2 | 53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Renzini, A.I.; Goncharov, B.; Jenkins, A.C.; Meyers, P.M. Stochastic Gravitational-Wave Backgrounds: Current Detection Efforts and Future Prospects. Galaxies 2022, 10, 34. https://doi.org/10.3390/galaxies10010034
Renzini AI, Goncharov B, Jenkins AC, Meyers PM. Stochastic Gravitational-Wave Backgrounds: Current Detection Efforts and Future Prospects. Galaxies. 2022; 10(1):34. https://doi.org/10.3390/galaxies10010034
Chicago/Turabian StyleRenzini, Arianna I., Boris Goncharov, Alexander C. Jenkins, and Patrick M. Meyers. 2022. "Stochastic Gravitational-Wave Backgrounds: Current Detection Efforts and Future Prospects" Galaxies 10, no. 1: 34. https://doi.org/10.3390/galaxies10010034
APA StyleRenzini, A. I., Goncharov, B., Jenkins, A. C., & Meyers, P. M. (2022). Stochastic Gravitational-Wave Backgrounds: Current Detection Efforts and Future Prospects. Galaxies, 10(1), 34. https://doi.org/10.3390/galaxies10010034






