Detecting Gravitational Waves with Advanced Virgo

Abstract

Advanced Virgo is the European gravitational-wave detector that, along with the American ones, is part of the global network of detectors that have been pinpointing gravitational waves since 2015. These kilometer-scale laser interferometers, measuring the distance between quasi-free-falling mirrors, represent the suitable detectors to explore the Universe through gravitational radiation. The initial Virgo experiment completed several runs of scientific data between 2007 and 2011, establishing the upper limits on the gravitational-wave rate expected for several astrophysical sources. The Advanced Virgo project led this instrument to unprecedented sensitivities making gravitational wave detections a routine occurrence. In this review, the basic techniques to build gravitational-waves interferometers and the upgrades needed to boost their sensitivities, even beyond the classical limit, are presented. The particular case of Advanced Virgo will be described hinting at its future developments, as well.

1. Introduction

Almost one hundred years ago, Albert Einstein predicted the existence of gravitational waves [1], ripples in the fabric of space-time set off by extremely violent, cosmic cataclysms in the early Universe, supernovae explosions, colliding black holes and neutron stars. With the technology available in 1916, Einstein assumed that such ripples would be vanishingly small and nearly impossible to detect. The technological advancements over the past century have changed those prospects and, on 14 September 2015, the LIGO-Virgo Collaboration detected for the first time the ripples in space-time caused by two coalescing black holes (GW150914) [2].

Six years after the first observation, about one hundred detections have followed [3,4]. Among them, the Gravitational Wave (GW) signal detected by two colliding neutron stars in August 2017 (GW170817) [5], marked the first time a cosmic event has been viewed in both gravitational and electromagnetic windows.

These impressive results have been achieved thanks to the global network of second generation of kilometer-scale Micheleson laser interferometers Advanced LIGO and Advanced Virgo [6,7].

The purpose of this review is to provide the operating principles of gravitational-wave detectors discussing in details the Advanced Virgo case: Section 2 provides an overview of the main techniques used in GW interferometers, and in Section 3 the main noise sources affecting the performances of the GW detectors are described. In Section 4, the implementation in Advanced Virgo of all the techniques described in the previous sections will be detailed, portraying the interferometer configuration during the latest observing run. Finally, in Section 5 the future instrument upgrades for Advanced Virgo to push the detector sensitivity towards the maximum achievable limit will be described.

2. Gravitational Wave Interferometric Detectors

The effect of a gravitational wave is a change in the local space–time metric, which can be considered equivalent to a change in the distance measured between free-falling test masses.

The GW polarization implies that the distance variation is intrinsically differential: two measurements performed along orthogonal directions provide opposite results.

If the test masses are mirrors, one could reflect laser light off them and observe this GW-induced stretching and compressing of space-time by measuring the light travel time. Interferometric GW detectors are based on this principle.

GW detection is so hard since they are expected to be extremely weak when they finally reach the Earth. The amount by which a distance L would shrink or stretch due to a GW is proportional to the strain amplitude h, that is [8]:

$$\Delta L=\frac{hL}{2}.$$

(1)

Since the expected strain amplitudes are of the order of ${10}^{-22}$, we are faced with the prospect of measuring changes in separation of ${10}^{-19}$ m even for a 1 km scale interferometer.

In a Michelson interferometer, laser light is incident on a beam splitter that reflects one half of it and transmits the other half. Each light beam travels some distance before being reflected back by a mirror towards the beam splitter where the two beams interfere. The interference provides an output beam, whose power carries information about the difference of the path traveled by the two beams. The GW passage causes one arm of the interferometer to grow longer while the other grows shorter, then vice versa, back and forth as long as the wave is passing.

It can be considered as a transducer which converts a length variation to a variation of the phase of a laser field.

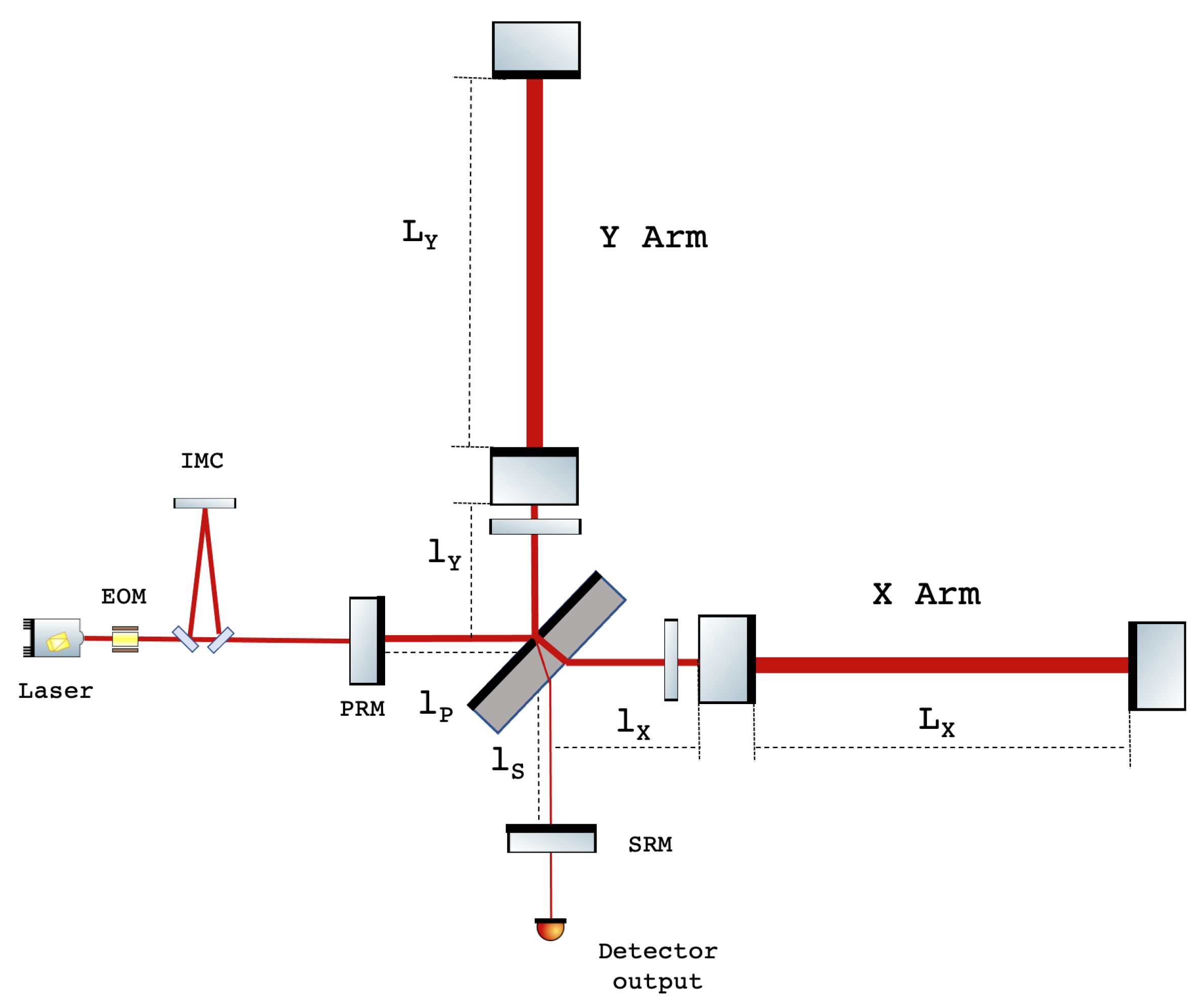
The simple Michelson configuration is not enough to make the detector sensitive to expected GW signals, thus many techniques need to be employed to make possible the GW detection.

The main differences with respect to the simple Michelson scheme are related to the mirrors defining the light paths: they are hang freely on pendula instead of being fixed to a rigid structure and they are several kilometers apart, instead of a few meters.

Despite this improvement, the arms would still be too short to enable the detection of gravitational waves. Thus, an additional mirror is placed into each arm, near the beam splitter, at about a few km from the mirror at the end of that arm forming a Fabry–Perot (FP) optical cavity. As result, the laser into each arm bounces between its two mirrors about 300 times before being merged with the beam from the other arm. These reflections build up the laser power within the interferometer and increase the distance traveled by each laser beam from a few to thousands of km. GW interferometers reach their maximum sensitivity operating at dark fringe so that most of the light is reflected back towards the laser, the so called bright port.

At this point quantum physics enters in the GW detection. First of all, the light’s energy can only be absorbed in discrete quanta (photons), resulting in photon-counting noise or shot noise. The GW signal-to-shot-noise ratio can be improved by detecting more photons.

Consequently, GW detectors use high-power laser systems and optical resonators to maximize their shot noise limited sensitivity.

The dark fringe working point allows to increase the laser power circulating into the detector by introducing an additional mirror, called Power Recycling Mirror (PRM). It is located between the laser source and the beam splitter continuously reflecting back into the interferometer the laser light that has traveled through the instrument.

Thanks to this recycling mechanism, the power circulating into the detector can reach values of the order of MW starting from a Nd:YAG laser source delivering only few hundred watts of power. Thus, the power recycling cavity greatly boosts the power of the laser beam inside the FP cavities without the need to generate such a powerful laser beam at the outset.

Moreover, the quantum noise of light disturbs a GW detector. The quantum nature of light produces a fluctuating radiation pressure force on the test-mass mirrors. The mirrors are displaced by the light, an effect that cannot be distinguished from a GW signal. In order to reduce this effect, GW detectors use test masses of up to 40 kg.

With the addition of the power recycling cavity, first generation GW detectors are known as Power Recycled, Fabry–Perot Michelson interferometers.

To date, the basic scheme of a GW interferometer is described, but many other techniques are applied to minimize all the noises affecting its performance.

One of the major obstacles to reach the desired detector sensitivity at frequencies around 10 Hz is the effect of local environmental disturbances causing the motion of the interferometer optics, coupled as noise in the gravitational wave data output.

In the interferometer’s most sensitive frequency band (few Hz-300 Hz), the main limitation of the sensitivity is represented by the thermal noise. The mirrors and their suspensions are built from materials having exquisitely high mechanical quality factors. They are made of very pure fused silica glass absorbing only just one in 3-million photons hitting them, making the mirrors not prone to heating. Fused silica exhibits very low thermal noise making it a natural choice to realize the interferometer optics.

The technological enhancement of noise reduction techniques led to the upgrade of the first generation of GW detectors to the second one, the so-called advanced, whose main features are the replacement of steel wires with fused silica fibers to suspend the mirrors, the installation of another partially reflecting mirror, i.e., Signal Recycling Mirror (SRM), placed between the beam splitter and the detector output port to improve the GW signal [9], the injection of squeezed states of light into the dark port of the interferometer to reduce the quantum noise and the implementation of more performing thermal compensation system to cope with the power increase.

Due to the combination of power and signal recycling techniques, the second generation of GW detectors are known as Double Recycled, Fabry–Perot Michelson interferometers (Figure 1).

These so-called advanced detectors replaced the existing interferometers, aiming for a 10 times increased sensitivity.

The GW detectors combine a number of advanced technologies to push the limits of precision length measurement even beyond the classic one. The simple Michelson topology integrates additional optical elements, which significantly change the properties of the optical system. In the next paragraphs, an overview of the aforementioned techniques, adopted to make the simple Michelson interferometer a gravitational-wave detector, will be described.

2.1. Free-Falling Mirrors

The optical and mechanical properties of the mirrors play a crucial role to detect GW. Their spherical shape matches the fundamental Gaussian mode of the main laser beam propagating into the detector, their diameter is dimensioned accordingly to the current technology and, finally, their thickness and, consequently their weight, are optimized to cope with the radiation pressure depending on the power circulating into the detector. The mirror aspect ratio is properly chosen to minimize the thermal noise contribution. The advanced GW detector glass mirrors have the same diameter as the first generation ones (around 35 cm) but are twice as thick (20 cm) and, consequently, twice as heavy (around 42 kg).

According to the General Relativity [1], these mirrors are designed to be quasi-free falling in the direction of propagation of the laser beam to respond to the GW, thereby acting as test masses that probe space-time [11]. This is achieved by suspending the mirrors as sophisticated pendula through four tiny fibers of 0.4 mm of diameter. Above the pendulum’s resonant frequency, typically around 1 Hz, the suspension system isolates the mirror from vibrations of the ground and the structures on which it is mounted, making it quasi-free. The targeted detection band of earth-based detectors is therefore restricted to the audio band in the range 10 Hz–10 kHz. At lower frequencies, disturbances from the environment are too high, at higher frequencies no strong GW signals are expected [12].

2.2. Michelson Interferometer

In a Michelson interferometer, laser light is incident on a beam splitter that reflects half of it and transmits the other half. Each light beam travels some distance before it is reflected back by a mirror towards the beam splitter where the two beams interfere. The interference provides an output beam, the power of which carries information about the laser path difference. The power measured at the output of the detector, after the recombination of the two beams, is proportional to [8]:

$$\begin{array}{c}\hfill P_{out}\propto P_{in}{sin}^2\left[k(L_y-L_x)\right]=P_{in}{sin}^2\delta \varphi ,\end{array}$$

(2)

where $P_{in}$ is the input power, k is the wavenumber of the laser light defined as $k=2\pi /\lambda$ with $\lambda$ the wavelength of the laser and $L_x$ and $L_y$ are the lengths of the two arms. Therefore, any variation in the length of the two arms causes a variation of the phase $\delta \varphi$, resulting in a variation of the power measured at the output of the detector.

2.3. Fabry-Perot Optical Cavity

Each arm of gravitational-wave Michelson interferometers hosts a linear two-mirror cavity formed by the input mirror, partially reflective, and the end mirror, almost completely reflective. The behaviour of the cavity is described by its length L, the wavelength of the laser $\lambda$ and the reflectivity and transmissivity of both mirrors $r_1$, $r_2$, $t_1$ and $t_2$, respectively. The power circulating inside the cavity is given by:

$$P_{circ}=P_{in}\frac{t_1^2}{{(1-r_1{r}_2)}^2+4r_1{r}_2{sin}^2\left(kL\right)}$$

(3)

with $k=2\pi /\lambda$ and $P_{in}$ the power injected into the cavity.

The maximum power, obtained when the sine function becomes equal to zero, i.e., at $kL=N\lambda$ with N an integer, corresponds to the cavity resonance condition and the power circulating in the cavity is:

$$\begin{array}{c}\hfill P_{res}=P_{in}\frac{t_1^2}{{(1-r_1{r}_2)}^2}.\end{array}$$

(4)

Multiple resonant peaks are present, spaced in length by half wavelength and in frequency by the cavity free spectral range, defined as:

$$\Delta f_{FSR}=\frac{c}{2L}.$$

(5)

Another characteristic parameter of a cavity is its linewidth, usually defined as the Full Width at Half Maximum (FWHM) of the resonance peak:

$$FWHM=\frac{2\Delta f_{FSR}}{\pi }arcsin\left(\frac{1-r_1{r}_2}{2\sqrt{r_1{r}_2}}\right),$$

(6)

that indicates the frequency range resonating inside the cavity. The ratio of the linewidth to the FSR defines the $finesse$ (F) of the cavity:

$$F=\frac{\Delta f_{FSR}}{FWHM}=\frac{\pi }{2arcsin\left(\frac{1-r_1{r}_2}{2\sqrt{r_1{r}_2}}\right)}.$$

(7)

In the case of high finesse ($F>100$), as for GW detectors, i.e., $r_1$ and $r_2$ are close to 1, the argument of the arcsin function is small, so:

$$\begin{array}{c}\hfill F\approx \frac{\pi \sqrt{r_1{r}_2}}{1-r_1{r}_2}.\end{array}$$

(8)

and Equation (3) can be approximated as:

$$P_{res}=P_{in}\frac{t_1^2}{{(1-r_1{r}_2)}^2}\approx P_{in}\frac{2F}{\pi }.$$

(9)

The build-up factor $2F/\pi$ can be interpreted as the number of round-trips inside the cavity. The average time spent by the photons inside the cavity is related to the finesse by the expression:

$${\tau }_s=\frac{L}{c}\frac{F}{\pi }$$

(10)

and the pole frequency of the cavity is given by:

$$f_p=\frac{1}{4\pi {\tau }_s}.$$

(11)

Thus, in the limit of high finesse, the effective storage time of the light, which in the arm of a Michelson interferometer is $2L/\mathrm{c}$, is enhanced by a factor $F/\left(2\pi \right)$.

The use of FP cavities not only allows to increase the circulating power in the detector but also provides an important help to improve the sensitivity of gravitational-wave detectors.

The field reflected by the FP cavity is described by:

$$E_{ref}=-\frac{r_1-r_2(1-L_1)e^{2ikL}}{1-r_1{r}_2{e}^{2ikL}}{E}_{in}$$

(12)

where $L_1$ are the losses of the input mirror1. When the over-coupled cavity condition is satisfied, i.e., $r_1<r_2$, the phase of the reflected beam rotates by $2\pi$, changing sign between resonance and anti-resonance conditions. It can be demonstrated that, expanding at first order the cavity displacement $\delta L$, assuming L${}_1$ = 0 and solving for the resonance condition $e^{2ikL}=1$, Equation (12) can be written in first approximation as [13]:

$$\begin{array}{c}\hfill E_{ref}^{res}\left(\delta L\right)=\frac{r_2-r_1}{1-r_1{r}_2}(1+i2k\delta L\frac{r_2{(1-r_1)}^2}{(1-r_1{r}_2)(r_2-r_1)})=E_{ref}^{res}{e}^{i{\varphi }_{FP}\left(\delta L\right)},\end{array}$$

(13)

where $E_{ref}^{res}=\frac{r_2-r_1}{1-r_1{r}_2}$ is the reflected field at resonance and ${\varphi }_{FP}\left(\delta L\right)$ is the phase of the field reflected by the Fabry–Perot cavity due to $\delta L$. Considering r${}_2\approx 1$, ${\varphi }_{FP}\left(\delta L\right)$ can be written as:

$${\varphi }_{FP}\left(\delta L\right)=2k\frac{2F}{\pi }\delta L,$$

(14)

showing that the phase variation due to a length change is directly proportional to the cavity finesse. Away from the resonances, the phase of the reflected beam is almost flat, so it is insensitive to the changes of the cavity length. The phase of the reflected field changes rapidly when the length is close to resonance. When the reflectivity of the input mirror is close to unit, the sensitivity to a change in the phase term $2kL$ is enhanced by a factor $2F/\pi$ compared to the arm of the simple Michelson interferometer.

Thus, the use of the Fabry–Perot cavities at the resonance condition allows to build up the laser power within the interferometer and amplifies the phase change induced by GW by the same factor $2F/\pi$.

2.4. Interaction of Fabry–Perot Michelson Interferometer with Gravitational Waves

The response of laser interferometers to gravitational waves has been calculated in different ways, particularly in the transverse–traceless (TT) gauge and in the proper detector frame. In the TT gauge, the proper distance between the two test masses changes as a consequence of the GW passage while the coordinate position of the mirrors, initially at rest, does not vary. In the detector frame, the effect of the passage of GW is a displacement of the test masses from their original position and, if the distance between the FP mirrors L is small compared to the GW wavelength, this displacement can be derived using the geodesic deviation equation [8].

In the following, the phase shift induced by GW in the FP cavity will be derived in the proper detector frame.

Consider a FP cavity oriented along the x axis and a GW with only the plus polarization whose amplitude is $h_0$ and frequency $f_{gw}$, propagating perpendicularly to the x-y plane of the detector. In the proper detector frame, the distance variation $\delta L_x$ between the two mirrors induced by the GW derived by the geodesic deviation equation is:

$$\delta L_x=\frac{L{h}_0}{2}cos\left(2\pi f_{gw}t\right).$$

(15)

This induces a change $\delta {\varphi }_x$ of the field reflected from the cavity along the X arm equal to:

$$\delta {\varphi }_{FP,x}\approx \frac{4F}{\pi }k\delta L_x.$$

(16)

The phase shift of the FP cavity along the Y direction is obtained by reversing the sign of $h_0$: $\delta {\varphi }_{FP,y}=-\delta {\varphi }_{FP,x}$. Thus, the total shift in the Michelson FP interferometer is:

$$\delta {\varphi }_{M-FP}=\delta {\varphi }_{FP,x}-\delta {\varphi }_{FP,y}=2\delta {\varphi }_{FP,x}\approx \frac{8F}{\pi }k\delta L_x.$$

(17)

By replacing Equation (15) into Equation (17), it becomes:

$$\Delta {\varphi }_{M-FP}=\frac{4F}{\pi }kL{h}_{0}cos\left(2\pi f_{gw}t\right).$$

(18)

This result is exhaustive only when the period of GW is higher than the cavity storage time ${\tau }_s$. To evaluate the response of the detector when the period of the incoming GW is comparable to the cavity round-trip time, the TT gauge frame must be considered2. In this reference system the phase shift of the Michelson FP interferometer becomes:

$$\delta {\varphi }_{M-FP}=\frac{4F}{\pi }kL{h}_{0}cos\left(2\pi f_{gw}t\right)\frac{1}{\sqrt{1+{(f_{gw}/f_p)}^2}}.$$

(19)

Thus, for $f_{gw}<<f_p$, the detector response to the GW passage is maximum (Equation (19) reduced to Equation (18) in the proper detector frame), when $f_{gw}=f_p$ the cavity response decreases by factor $\sqrt{2}$ with respect to its maximum and, if $f_{gw}>>f_p$, the detector response decreases linearly with $f_{gw}$.

Summarizing, the power stored inside the cavity is amplified with respect to the input power by a factor $G_{FP}=2F/\pi$. The same amplification applies to the phase response of the reflected beam to GWs, but only for frequencies below the cavity pole:

$$\delta {\varphi }_{FP,x}\approx 2k\delta L_x{G}_{FP}\frac{1}{\sqrt{1+{(f_{gw}/f_p)}^2}}.$$

(20)

The effect of a GW on the field propagating through the FP cavity can be also described in terms of signal sidebands generated in each arm cavity as a consequence result of the GW passage. Their amplitude is proportional to the power circulating inside the arm, and to a frequency-dependent component related to the FP cavity pole. Since the GW effect is differential, the signal sidebands generated in the two orthogonal arms have opposite sign. Thus, once reached the beam splitter, they interfere in the opposite way with respect to the main laser beam: they are maximized propagating toward the anti-symmetric port, and minimized toward the power recycling mirror.

2.5. Detection at the Dark Fringe

In a Michelson interferometer, any variation in the length of the two arms causes a variation of the phase $\delta \varphi$, resulting in a variation of the power measured at the output of the detector. This is described by Equation (2) where $\delta \varphi$ can be written as $\delta \varphi ={\varphi }_0+{\varphi }_{gw}$ where ${\varphi }_{gw}$ contains the GW phase shift contribution and ${\varphi }_0$ is the Michelson interferometer working point chosen to maximize the performance of the detector. The choice of tuning the interferometer in dark fringe to detect GW may seem counterintuitive but, is a consequence of use of real devices that are, therefore, affected by noise. The presence of the so-called technical noises3, makes the dark fringe configuration the one with the highest sensitivity [8].

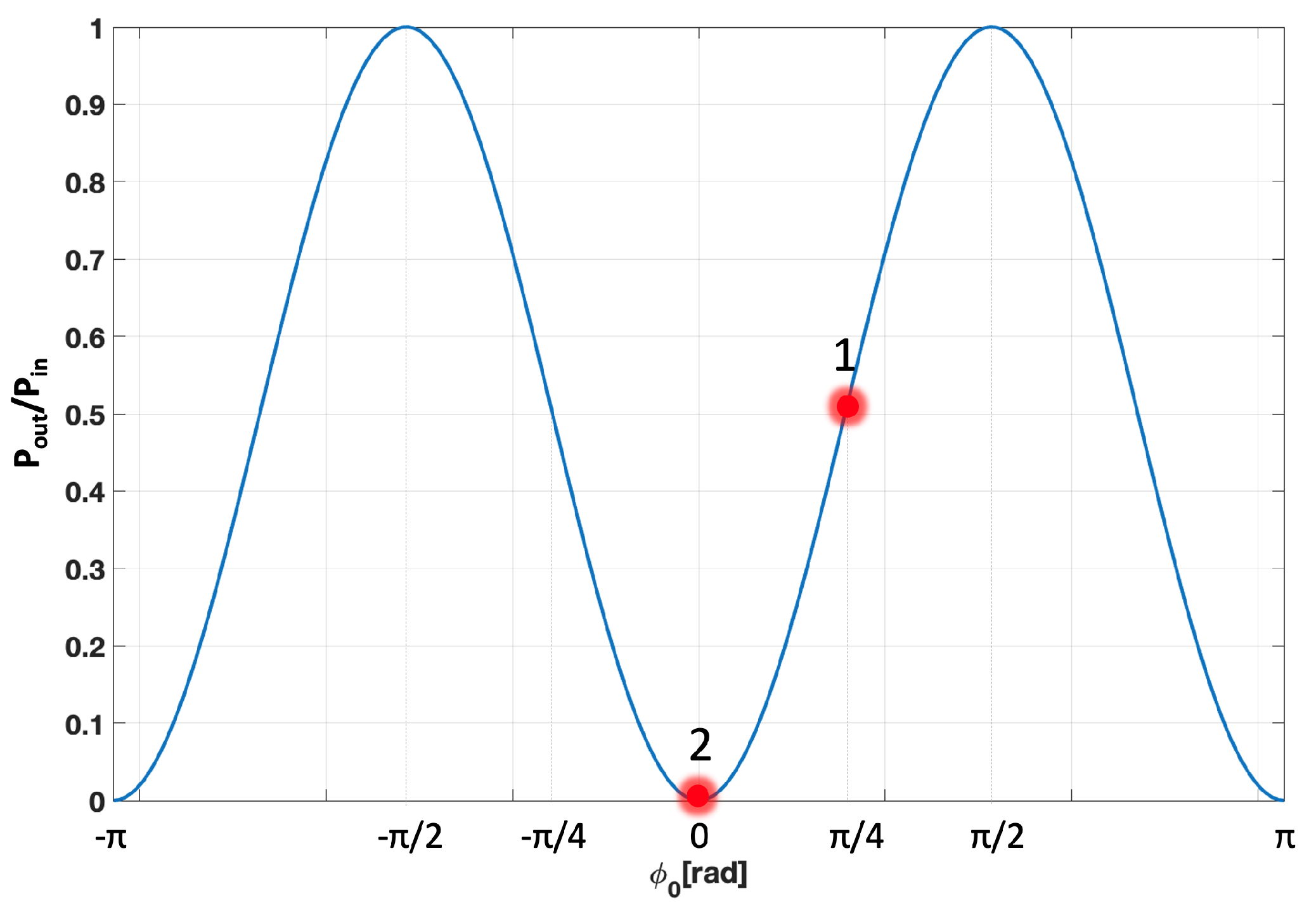
The sinusoidal detector response, shown in Figure 2, indicates the half fringe (${\varphi }_0=\pi /4$) as the best working point for the detector since the derivative $\partial P/\partial {\varphi }_0$ is maximum and the sensitivity to a small displacement is the highest. Nevertheless, in this point, any fluctuation in the laser power $P_{in}$ causes a variation of the power measured at the output of the instrument, which can be mistakenly interpreted as the consequence of a GW passage.

Bringing the detector at the dark fringe, it results insensitive to the laser power fluctuations and, in absence of GW, the output power is null. However, it has to be considered that, in this configuration, also the derivative $\partial P/\partial {\varphi }_0$ is zero. Thus, for an incoming GW, the power variation measured at the dark fringe would be of the order of $h^2$.

Such a signal is of course invisible.

To overcome this issue, the laser light is modulated through an Electro Optical Modulator (EOM) before being injected into the interferometer. A variable refractive index crystal placed inside the EOM introduces a phase shift on the beam proportional to the applied voltage, generating some sidebands.

The incident electromagnetic field of the laser, passing through the modulator, acquires a time-varying phase and the electromagnetic field becomes:

$$\begin{array}{c}\hfill \psi \left(t\right)={\psi }_0{e}^{-i({\omega }_{0}t+msin(\Omega t))},\end{array}$$

(21)

where ${\psi }_0$ is the amplitude of the input beam, ${\omega }_0$ is the laser frequency, m is the modulation index and $\Omega$ is the modulation frequency.

Equation (21) can be expanded in Fourier modes as:

$$\begin{array}{c}\hfill \psi \left(t\right)={\psi }_0\sum _{n=-\infty }^{+\infty }{J}_n\left(m\right)e^{-i({\omega }_0+n\Omega )t},\end{array}$$

(22)

where $J_n\left(m\right)$ are the Bessel functions. For $m<<1$, only three terms of the expansion can be considered:

$$\begin{array}{c}\hfill \psi \left(t\right)\approx {\psi }_0\left[J_0\left(m\right)e^{-i{\omega }_{0}t}+J_1\left(m\right)e^{-i({\omega }_0+\Omega )t}+J_{-1}\left(m\right)e^{-i({\omega }_0-\Omega )t}\right],\end{array}$$

(23)

where the first term represents the carrier, and the other two terms correspond to the first upper and lower sidebands with frequencies ${\omega }_{\pm }={\omega }_0\pm \Omega$. Equation (23) describes the beam impinging on the Fabry–Perot resonant cavity as composed of three independent fields: the carrier and the sideband ones.

If the distance between the beam splitter and the input mirror of the FP cavity along X and Y arms is the same, carrier and sidebands are both on the dark fringe. However, introducing a macroscopic arm length difference of several centimeter equal to an integer number of laser wavelength, called Schnupp asymmetry ($l_X-l_Y$ in Figure 1), the sidebands are no longer on the dark fringe, allowing to be transferred through the interferometer to the output port even if the carrier is at the dark fringe.

When a GW propagates through the interferometer, the term of the electromagnetic field at the dark port containing the contributions of beats of the carrier with the sidebands, encodes the GW signal, which is linear in h and oscillates at frequency $\Omega$ [8]. In a second demodulation process the photo-current is then electronically demodulated at $\Omega$ in order to finally derive the GW signal stream at $f_{gw}$.

In conclusion, operating at dark fringe and introducing a small asymmetry in the distance between the beam splitter and the input mirrors of the FP cavities, make the signal insensitive to the laser power fluctuations and allow the extraction of the GW signal from the component demodulated at $\Omega$ which is linear (and not quadratic) in h.

This technique, based on the use of the sidebands as optical local oscillator to extract the gravitational wave signal, called heterodyne readout, was commonly used in the first generation of gravitational wave detectors. However, the experience gained running these interferometers indicates several limitations connected to the heterodyne readout, mainly related to the arise of thermal effects in the core optics, due to the high power circulating into the detector, that spoils the quality of the sidebands. Thus, the second generation of gravitational wave detectors uses a detection scheme known as DC readout [14], where a small differential detuning is introduced in the interferometer so that it is no longer locked on a dark fringe. This allows a small amount of carrier light to exit the interferometer to be used as a local oscillator field. A crucial element in the DC readout detection scheme is the Output Mode Cleaner (OMC), which is an optical cavity that transmits only the fundamental Gaussian mode at the carrier frequency. The purpose is to keep only light which leaves the interferometer due to a gravitational wave signal and remove Higher-Order Modes (HOM) caused by interferometer mirror defects and radio-frequency sidebands.

2.6. Power Recycling Cavity

The Power Recycling Cavity (PRC) greatly boosts the power of the laser beam inside the Fabry–Perot cavities without the need to generate such a powerful laser beam at the outset.

It is composed of the power recycling mirror and the compound mirror formed by the Michelson FP interferometer. At resonance, the power circulating into the detector is built up with respect to the input power by the so-called gain that is:

$$\begin{array}{c}\hfill G_{PRC}=\frac{1-r_{PR}^2}{[1-r_{PR}(1-\frac{F}{\pi }{L}_{RT}){]}^2},\end{array}$$

(24)

where $r_{PR}$ is the reflectivity of the power recycling mirror and $L_{RT}$ are the round trip losses obtained by summing those of the mirrors forming the FP cavity.

2.7. Signal Recycling Cavity

For a power recycled high-finesse Fabry–Perot–Michelson interferometer, when $f_{gw}>>f_p$, the measurable phase shift decreases linearly with $f_{gw}$ limiting the detector bandwidth of the detectors (Equation (19)). The installation of another partially reflecting mirror between the beam splitter and the output port to form the Signal Recycling Cavity (SRC) allows to move the pole frequency of the cavity at higher frequency, extending the frequency range where the response of the detector to the passage of the gravitational wave is maximized [13].

The effect induced by GW on the laser beam is to generate differential signal sidebands in the light propagating in the two arms, having the same amplitude but opposite sign. Once constructively recombined at the beam splitter, they are transmitted toward the signal recycling mirror. The differential sidebands see an equivalent input mirror formed by the FP input mirror and the signal recycling one. The reflection and transmission coefficients, $r_{SRC}$ and $t_{SRC}$, of the equivalent mirror depends on the microscopic tuning of the signal recycling cavity length $l_S$, that is the distance between the signal recycling mirror and the input mirror. The beam phase propagating through the signal recycling cavity is:

$$\begin{array}{c}\hfill {\varphi }_{SRC}=k{l}_{SRC}=k[l_S+\frac{l_X+l_Y}{2}],\end{array}$$

(25)

where $l_X$ and $l_Y$ are the distances of the two input mirrors of the Fabry-Perot cavities from the beam splitter (Figure 1) and the reflection and transmission coefficients can be written as:

$$\begin{array}{c}\hfill r_{SRC}=\frac{r_i-r_s{e}^{2i{\varphi }_{SRC}}}{1-r_i{r}_s{e}^{2i{\varphi }_{SRC}}},t_{SRC}=\frac{t_i{t}_s{e}^{i{\varphi }_{SRC}}}{1-r_i{r}_s{e}^{2i{\varphi }_{SRC}}},\end{array}$$

(26)

where $r_i$, $r_s$, $t_i$ and $t_s$ are the input mirror and the signal recycling reflectiviy and transmissivity. When ${\varphi }_{SRC}=0$, the signal recycling cavity is tuned to be resonant for the carrier field. In this configuration the reflectivity of the equivalent input mirror is lower than the FP input mirror decreasing the finesse of the FP cavity seen by the GW sideband signals by the quantity:

$$\begin{array}{c}\hfill \frac{F_{{\varphi }_{SRC}=0}}{F_{FP}}=\frac{1-r_i{r}_s}{1+r_s}.\end{array}$$

(27)

Consequently, the pole frequency of the cavity is moved toward high frequency increasing the detector bandwith sensitivity. This signal recycling cavity working point, defined broad-band, is currently implemented in all the advanced GW detectors.

2.8. Laser Source and Injection System

The laser source is an ultra-stable, high-power continuous-wave Nd:YAG laser system. GW detectors set highly demanding requirements in their laser light sources. None of the laser parameters as delivered have adequate stability to allow direct injection of the laser beam into the interferometer [15]. Hence, the beam is injected into the detector after propagating through an extremely complex optical system, installed both in air and in vacuum, to stabilize important laser observables like the power, the frequency, the beam pointing and the spatial filtering. In all GW detectors the high power laser generation and its stabilization are conceptually similar.

The beam is produced by a low power stable laser (master laser), and then a multi-stage amplification scheme is implemented to deliver hundreds watts of input power. Passive stabilization methods, based on the use of a hierarchical scheme of three optical cavities in cascade composed of the pre-mode cleaner (PMC), the Input Mode Cleaner (IMC) and the Reference Frequency Cavity (RFC), concur to stabilize the laser frequency and power in synergy with nested feedback control acting to minimize the beam jitter and to preserve the beam pointing into the detector. Finally, the laser beam geometrical properties, needed to be matched with the interferometer optical cavities, are defined through the Mode Matching Telescope (MMT).

2.9. Thermal Effects

The FP cavities boost the power circulating by a factor around 300 with respect to simple Michelson configuration. The absorptions of the optical power by the coating of the core optics, albeit of the order of ppm (parts per milion), result in a radial temperature gradient within the mirrors [16] causing thermo-refractive substrate lenses in the recycling cavities (due to the dependence of the refractive index on the temperature) and thermo-elastic surface deformation in the Fabry–Perot mirrors. Both these mechanisms induce wavefront aberrations in the sideband and the carrier fields4 triggering HOMs that, depending on the stability of the cavity, could be scattered out from the cavity losing circulating power or could become resonant inside it spoiling the control signals.

The optical aberrations are not induced only by thermal effects but also by the cold defects coming from the residual imperfections due to the state of the art of the mirror production procedure.

The Thermal Compensation System (TCS) [17] is conceived to tackle the aberrations coming both from cold defects and thermally driven effects. The thermal compensation strategy is to induce in the optics a complementary distortion with respect to the main laser one restoring the nominal optical configuration of the interferometer. The complex system of thermal actuators and sensors composing the TCS is fundamental to guarantee the operation at high power of the GW detector. Moving from the first generation of gravitational-wave detectors to the second one, new high-performance sensors and actuators have been included in the TCS making it a dynamical adaptive optical system. Wavefront aberrations on each core optics are sensed by the Hartmann Wavefront Sensors (HWSs) [18], probing the optics through an auxiliary beam, usually a SLED (SuperLuminescent Light Emitting Diode), which accumulates wavefront distortions after being transmitted through or reflected from the deformed optics.

The wavefront aberration local sensing provided by HWSs is complementary to the global one measured by the phase camera encoding the amplitude and phase of the main beam circulating into the detector [19]. This sensor scans over a photodiode the beam resulting from the recombination of the pick off of the main laser beam with the one picked up at the strategical ports of the detector. The heterodyne technique is used to independently assess the information in the carrier, upper and lower sidebands at different frequencies.

Two different actuators are designed to cope with thermal effects and cold defects: the CO${}_2$ lasers5 to correct both cold and thermal lenses and the ring heaters to decrease the radii of curvature of the mirrors. The formers project the suitably shaped heating pattern on an additional transmissive fused silica plate, the so-called Compensation Plate (CP), installed between the beam splitter and the input mirrors.

Ring heaters are thermal actuators conceived to precisely tune the radius of curvature of the highly reflective surface of the mirrors. They are provided by heating elements radiatively coupled to the mirror barrel that induce a thermal gradient in the optics reducing its Radius of Curvature (RoC).

The requested accuracy for the TCS sensors and actuators is strictly dependent from the peculiar design of the interferometer optical cavities.

2.10. Working Point

Length sensing and control is vital to ensure the operation of GW detectors: the carrier must resonate in all the optical cavities and the two beams reflected back by the FP cavities must destructively interfere. The achievement of this configuration, from the uncontrolled mirrors to the final working point, takes place through a complex procedure called lock acquisition. The mirrors are free to swing along the optical axis and to rotate around the horizontal (pitch angle) and vertical (yaw angle) axes in the mirror plane. The former is the longitudinal Degree of Freedom (DoF) which must be controlled within a precision of about $[{10}^{-12}$–${10}^{-10}]$ m to ensure the carrier resonance condition in the optical cavities, the latters define the angulars DoFs to be controlled with nano-radian accuracy.

The working point of a power recycled Fabry–Perot–Michelson interferometer can be described by four longitudinal degrees of freedom6 (cf. Figure 1):

• the length difference between the two input mirrors of the FP cavities from the beam splitter, MICH: $l_X-l_Y$;
• the differential length of the Fabry–Perot arms, DARM: $(L_X-L_Y)/2$. This is the most important DoF, since it contains the GW signal;
• the average (Common) length of the Fabry–Perot arms, CARM: $(L_X+L_Y)/2$;
• the length of the power recycling cavity, PRCL: $l_P+(l_X+l_Y)/2$, where $l_P$ is the distance between the power recycling mirror and the beam splitter.

The FP and power-recycling cavities (CARM, DARM and PRCL) need to be kept on resonance to maximize the optical path traveled by the light inside the interferometer. In addition, the Michelson interferometer is brought to the dark fringe and the working point is achieved. The longitudinal DoFs are controlled by using the Pound-Drever-Hall (PDH) technique [22,23]: the output of different photodiodes located in strategical part of the detector are used to extract the error signals for each DoF by measuring the beating between the carrier, resonating in all the optical cavities, and the radio-frequency sidebands, anti-resonant in the FP cavities and resonant in the recycling cavities.

Once the longitudinal DoFs controls are engaged, different angular controls act to overlap the input laser beam to the optical cavity axis (the straight line that intersects the centers of curvature of the two spherical mirrors forming the cavity). At the first stage, the angular motions in pitch and yaw of every single mirror are controlled using optical lever signals provided by an auxiliary probe beam reflected by the mirror surface impinging on a positioning sensing device. This type of control is defined local since it is independent from the main laser beam pointing and from the mutual position of the optics.

The noise performance of the local controls is not enough to meet the noise and accuracy requirements. Therefore, during the last steps of the lock acquisition sequence, such control is replaced with an angular global control scheme reaching the nano-radian accuracy, based on error signals provided by quadrant photodiodes (QPD) installed in strategical places of the laser beam path, encoding tilt and shift information about the cavity angular DoFs.

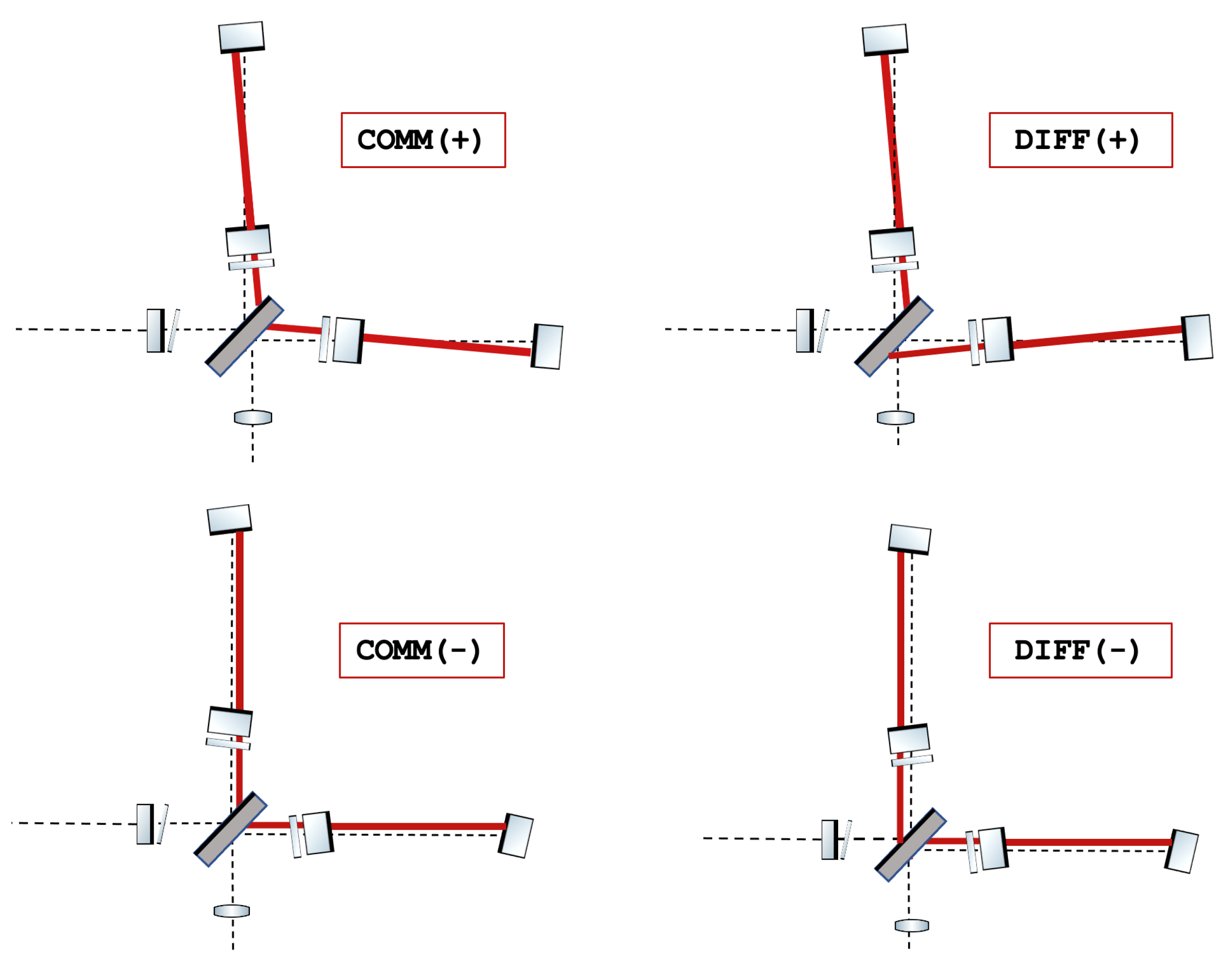
Once the dark fringe configuration is achieved, the effects induced by radiation pressure arise in the FP arm cavities inducing an optical spring between the cavity mirrors. Thus, in this condition, a basis of Common and Differential DoFs, both (+) and (−), are introduced to describe the global misalignment of the optical cavities (Figure 3):

• Common tilt of the arm cavities, COMM(+): the two beams recombine in the same spot on the BS mirror;
• Differential tilt of the arm cavities, DIFF(+): the two beams recombine on the two opposite sides of the BS mirror;
• Common shift of the arm cavities, COMM(−): the effect is two beams recombining in the same spot on the BS mirror;
• Differential shift of the arm cavities, DIFF(−): the effect is two beams recombining on the two opposite sides of the BS mirror.

The error signals associated with these DoFs satisfy the required accuracy for the control of the orientation of the optics needed to ensure a robust and reliable working point to acquire scientific data.

3. Noises

As described before, GWs are detected by looking at a small transient fluctuation in the amount of power emerging from the output of the detector, but there can be other reasons for the power to fluctuate besides the passage of a gravitational wave through the apparatus. In this section, several of the most important reasons for a false indication of a GW passage, the so-called noises, will be discussed. In a GW interferometer, each noise manifests itself as an apparent or real variation of the position of the mirrors, simulating the effect of the incidence of a GW. In order to distinguish the noise source from the gravitational signal, the amplitude spectral sensitivity $h\left(f\right)$ is defined for each noise:

$$\begin{array}{c}\hfill h\left(f\right)=\frac{\sqrt{{\tilde{x}}^2\left(f\right)}}{L},\end{array}$$

(28)

where L is the arm length of the interferometer and ${\tilde{x}}^2\left(f\right)$ is the power spectral density of the displacement due to the noise source. The quantity $h\left(f\right)$, which has dimension $1/\sqrt{\mathrm{Hz}}$, indicates the amplitude of the gravitational wave signal that would produce the displacement caused by the noise.

The sensitivity of a GW detector is expressed in terms of the strain sensitivity obtained by summing quadratically the amplitude spectral densities of the noises affecting the detector:

$$\begin{array}{c}\hfill h\left(f\right)=\sqrt{\sum _{i=1}^n{h}_i^2\left(f\right)},\end{array}$$

(29)

where i runs on the total number of the noises.

The sensitivity curve represents the minimum intensity of the gravitational signal detectable by an interferometer.

3.1. Quantum Noise

Quantum noise limits the ability to read out the arm length difference in an interferometer. It comes from the quantum nature of light, which reveals itself through two fundamental mechanisms: photon counting noise (shot noise), arising from statistical fluctuations in the arrival time of photons at the interferometer output; and radiation pressure noise, which is the recoil of the mirrors due to the quantum fluctuations in the photon flux.

The spectral density of the shot noise for a power recycled, Fabry–Perot–Michelson interferometer is given by:

$$\begin{array}{c}\hfill h_{shot}\left(f\right)=\frac{1}{8FL}(\frac{4\pi \hslash \lambda c}{P_{bs}}{)}^{1/2}\sqrt{1+{(f/f_p)}^2},\end{array}$$

(30)

where $\lambda$ is the wavelength of the main laser and $P_{bs}$ is the power on the beam splitter after the recycling. The radiation pressure noise spectral density is described by:

$$\begin{array}{c}\hfill h_{rp}\left(f\right)=\frac{16\sqrt{2}F}{ML{\left(2\pi f\right)}^2}(\frac{\hslash P_{bs}}{2\pi \lambda c}{)}^{1/2}\frac{1}{\sqrt{1+{(f/f_p)}^2}},\end{array}$$

(31)

where M is the mass of each of the interferometer’s four test masses. At low frequencies, the radiation pressure noise term, proportional to $1/f^2$, dominates, while at high frequencies the shot noise is the major contribution. The radiation pressure amplitude spectral density is proportional to the square root of the laser light power while the shot noise amplitude spectral density is inversely proportional to the same quantity. Therefore, while it is possible to improve the strain sensitivity of an interferometer at high frequencies by increasing the circulating light power, inevitably at the same time the sensitivity will worsen at low frequencies, as the radiation pressure increases with the light power.

The so-called optical readout noise is given by the quadrature sum of these two noises:

$$\begin{array}{c}\hfill h_{opr}=\sqrt{h_{shot}^2+h_{rp}^2}.\end{array}$$

(32)

By equalizing the contributions of $h_{shot}$ (Equation (30)) and $h_{rp}$ (Equation (31)), an optimal power, which results in identical magnitude contributions from shot noise and quantum radiation pressure noise for each observation frequency f, can be evaluated:

$$\begin{array}{c}\hfill P_{opt}=\frac{{\pi }^{3}c\lambda M{f}^2}{16F^2}[1+(\frac{f}{f_p}{)}^2].\end{array}$$

(33)

By replacing Equation (33) into Equation (30) (or Equation (31)), the optical readout noise (Equation (32)) corresponding to the the Standard Quantum Limit (SQL) can be evaluated:

$$\begin{array}{c}\hfill h_{SQL}=\frac{1}{2\pi fL}\sqrt{\frac{8\hslash }{M}}.\end{array}$$

(34)

The SQL is defined as the lower bound envelope of the quantum noise spectra for all the optical powers circulating in the interferometer with arm length L and mirror mass M. However, it is possible to beat the SQL by applying quantum techniques [24]. An intuitive understanding of quantum noise can be given through the quadrature pictures in the realm of quantum mechanics, where the uncertainty of the amplitude and phase of the light beam are encoded in the amplitude and phase quadratures, respectively. Both quadratures obey to the Heisenberg Uncertainty principle that imposes a limit on the precision achievable when they are measured simultaneously. The so-called Quantum-Non-Demolition techniques [25,26] allow to redistribute the quadrature uncertainty, reducing the variance in one quadrature at the expense of increased variance in the orthogonal quadrature. A squeezed state can be represented in the quadrature plane as an ellipse, characterized by two frequency-dependent parameters: the squeezing magnitude (the ratio of the ellipse axes with respect to the unsqueezed state) and the squeezing angle (the ellipse orientation).

The first proposal to use the quantum entanglement to improve the measurement precision beyond the limit set by measurement-counting noise, was made by Caves in 1981 [27], when he suggested the use of squeezed states of light as an additional input for laser interferometric GW detectors.

Their sensitivity is limited by the interference caused by the quantum-level creation and annihilation of photons in the vacuum, the so-called vacuum noise that is all-pervasive in space at every frequency.

The vacuum noise introduces noise fluctuations at the output port of the detector imposing the classical-limit of the detector sensitivity. To overcome this limit, a squeezed beam, with the same size, shape and frequency of the main interferometer beam, is injected into the detector and overimposed to the main laser. By replacing the classic vacuum with the squeezed light, the quantum noise contributions can be manipulated. In the GW advanced detectors operating up to date, the radiation pressure did not limit the low frequency range, thus a purely phase-squeezed has been applied to minimize the phase quadrature and therefore the shot noise.

This configuration is defined frequency-independent squeezing. Clearly, the improvement of the current sensitivity at low frequency, could make the radiation pressure noise the dominant contribution. Thus, to simultaneously reduce shot noise and quantum radiation pressure noise in the entire detection frequency range, the squeezed quadrature must be rotated as a function of frequency producing the so-called frequency-dependent squeezing.

The interaction of a frequency-independent squeezed state with an optical Fabry-Perot resonator, referred to as filter cavity, is able to induce such rotation of the squeeze ellipse [28]. The first demonstration of a squeezing source able to reduce quantum noise in the whole spectrum of advanced gravitational-wave detectors is reported in [29].

3.2. Thermal Noise

The thermal excitation of the mechanical degrees of freedom of the test masses, as well as those of their suspension system, results in a spurious contribution to the output of an interferometric detector, setting up a limit to the sensitivity of GW interferometers in a wide frequency band between few Hz and 300 Hz. Thermal noise is intrinsic to all bodies at thermodynamic equilibrium: in a body at steady-state temperature T, the energy equipartition theorem assigns to each degree of freedom a mean energy of $k_{B}T/2$ where $k_B$ is the Boltzmann constant. Due to the interactions among the microscopic elements, this energy is subject to time fluctuations that generate random oscillations of macroscopic observables mimicking the effect of the GW passage. This phenomenon is described by the Fluctuation–Dissipation Theorem [30], which identifies the link between a generic dissipative mechanism inside a mechanical system and its thermal fluctuations. This theorem asserts that the thermal noise power spectral density is given by:

$$\begin{array}{c}\hfill {\tilde{x}}^2\left(\omega \right)=\frac{4k_{B}T}{{\omega }^2}\mathbb{R}\left[\frac{1}{Z\left(\omega \right)}\right],\end{array}$$

(35)

where $Z\left(\omega \right)$ is the impedance of the system whose real part represents the dissipative mechanism due to the internal friction in the material quantified by the so called loss angle parameter $\varphi$. In the GW detectors, the thermal noise has two different origins: the first one is due to dissipation in the wires used to suspend the optics and it is dominant up to 30 Hz; the so-called suspension thermal noise. The second one is due to dissipation processes inside the mirrors themselves; the so-called mirror thermal noise.

The suspension thermal noise is given by three contributions, the horizontal and the vertical oscillations due to the pendulum configuration and the violin modes of the fibers suspending the mirrors. The suspension mechanical losses $\varphi$ result from the combination of losses of different nature: the material intrinsic losses, the thermo-elastic ones, deriving from the expansion coefficient of the material, the surfaces losses due to external pollution, and, finally, the losses due to the coupling system between mirror and fibers.

According to the fluctuation–dissipation theorem, thermal noise can be reduced by minimizing the amount of mechanical loss in the suspensions. When a pendulum is displaced in the horizontal direction from its rest position, a restoring force is exerted mainly by the lossless gravitational field acting as a constant spring. Therefore, the total losses of the suspension could be lower than the ones of the material of which it is composed, by the ratio of the elastic energy to the gravitational energy, the so-called dilution factor [11]. The mechanism in the vertical direction is different, if the mass is displaced vertically, the restoring elastic force of the fiber acts on the mirror as a simple harmonic oscillator motion with a frequency determined by the elastic spring constant associated with the elongation of the wire. Finally, the suspension wires, subjected to tension, behave like vibrating ropes shaping the violin modes that appear as a nearly harmonic sequence.

The fused silica has a very low loss angle ($\varphi \approx {10}^{-9}$) making it the natural choice to realize the mirrors. In the first gravitational wave detectors the suspension fibers were of stainless steel, but the high structural losses of steel ($\varphi \approx {10}^{-4}$) made this solution unsuitable for the second generation detectors. Therefore, fused silica was also employed to produce the suspension fibers forming with the mirror, the so-called monolithic payload [31,32]. This upgrade allowed to reduce the suspension thermal noise contribution by factor up to 10 at 30 Hz. Thus, it was used in all the advanced GW detectors to suspend the FP cavity mirrors.

In the frequency band from 30 Hz to 300 Hz, the sensitivity of the detector is limited by the thermal noise of the coating layers deposited on the surfaces of the core optics to make them highly reflective7. A HR coating is made of a stack of alternate layers of two materials with high and low refractive index. The reflectivity improves by increasing the refractive index difference between the employed materials and by enhancing the number of layers.

The thermal noise power spectral density of the mirrors coating is proportional to:

$$\begin{array}{c}\hfill {\tilde{x}}^2\left(\omega \right)\propto \frac{k_{B}T}{\omega }\frac{d}{w^2}{\varphi }_{coat},\end{array}$$

(36)

where w is the radius of the laser beam impinging on the mirror, ${\varphi }_{coat}$ is the coating loss angle and d is the coating thickness. Thus, besides lowering the temperature of the mirrors, the thermal noise could be minimized by reducing the coating thickness, by identifying new materials with lower losses and by increasing the laser beam size. Various numbers of different dielectric material pairs for reflective coatings have been investigated. It has been found that a coating made by alternating layers of titania doped tantala (TiO${}_2$:Ta${}_2$O${}_5$) and silica (SiO${}_2$) gives the desired reflectivity satisfying the strict limits on the thermal noise and on the optical absorption [33]. The laser beam radius on the mirrors is set around 60 mm according to the technology limitations for the realization of mirrors having a diameter greater than 35 cm.

3.3. Seismic and Newtonian Noise

Another source of displacement noise to deal with is the vibration of the terrestrial environment known as seismic noise. In the region 1–10 Hz, it is mostly due to human activity, natural phenomena in the atmosphere, and many other forms of ground born oscillations. Furthermore, there is a micro-seismic background, which affects a GW interferometer mostly in the form of surface waves that shake the suspension mechanisms and the mirrors. This noise is strongly dependent on the geographical localization of the detector. In general, the amplitude spectral density is of the order of ${10}^{-11}1/\sqrt{\mathrm{Hz}}$ at 10 Hz, 10 order of magnitudes larger than the expected GW amplitude. Therefore, to build a GW detector it is crucial to implement techniques for the vibration isolation of the test masses able to adequately attenuate this noise.

The vibration isolation system is obtained using a set of pendula in cascade. A single pendulum with resonance frequency $f_0$ attenuates the vibrations transferred to the mirror by a factor $f_0^2/f^2$. Thus, a multistage filter made by N pendula provides an attenuation factor ${(f_0^2/f^2)}^N$.

The Newtonian noise, also known as gravity gradient noise, is due to the time-varying Newtonian gravitational forces acting on the mirrors as a consequence of density fluctuations to density fluctuations caused by seismic activity as well as acoustic and turbulent phenomena in the Earth’s atmosphere [34,35]. Given the direct coupling of gravitational fields to the mirrors, they cannot be shielded from this noise. The approach identified to minimize this noise is based on the use of algorithms to process the data acquired by arrays of seismic sensors located near the vacuum chambers hosting the mirrors and, then to subtract its contribution from the ouput data of the interferometer [36]. This noise did not limit the sensitivity of the first generation interferometers, since its magnitude, expected to be ${10}^{-21}1/\sqrt{\mathrm{Hz}}$ at 10 Hz, was much lower than the radiation pressure one. Its contribution will become non-negligible in the next generations of detectors.

3.4. Technical Noise Sources

Besides these fundamental noises, other disturbances, the so-called technical noises, affect the detector performance requiring advanced technologies to be minimized. The largest contribution to technical noises are the control noises related to the lock and the alignment of the interferometer. Another of the most limiting noise at low-medium frequency range is the scattered light, i.e., diffused light due to the imperfections on the optics surfaces that is scattered out along the main laser beam path introducing additional noise in the detector signals [37]. In order to reduce this spurious light, the optical benches hosting the optical systems devoted to inject the beam into the detector, to monitor its performance and to extract the GW signals, are isolated from the ground replicating the same operating principle of the core optics suspensions. Moreover, the optical benches are studded by light dumpers to suppress spurious beams and some baffles, made of absorbing materials, surrounding the core optics [7]. The reduction of the diffused light is also one of the main reason why GW detectors are placed inside the largest vacuum chambers in the world. Indeed, the light propagates through the interferometer into ultra high-vacuum pipes, in order to reduce the refractive index fluctuation caused by the presence of residual air molecules.

4. Advanced Virgo Interferometer

Advanced Virgo is the European gravitational-wave interferometric detector, being part of the global network of interferometers built to detect GW [7]. The Virgo project takes its name from the Virgo cluster, a group of 2000 galaxies 15 Mpc distant from the Earth. Its target sensitivity was ${10}^{-21}1/\sqrt{\mathrm{Hz}}$ according to the gravitational wave amplitude h $\approx [{10}^{-21}-{10}^{-22}]1/\sqrt{\mathrm{Hz}}$ expected for the coalescence of two neutron stars of masses $1.4M_{\odot }$ at distance of 15 Mpc from the Earth. The history of this experiment begins about 30 years ago, the approval by the scientific community dates back to 1994 and its construction started in 1996, two years later, in Italy, in the countryside around Pisa.

The Virgo experiment acquired scientific data between 2007 and 2011 in four different observing runs. Before the beginning of the third one, the monolithic suspensions have been integrated in the instrument, and Virgo became Virgo plus, an intermediate configuration between the first and second generation of gravitational-wave detectors. Once the last scientific run was over, it was switched off in order to upgrade the experiment to the second generation project, called Advanced Virgo.

This detector joined the second observing run O2 with Advanced LIGO in August 2017, contributing to the first detection of GW emitted by a Binary Neutron Star (BNS) coalescence, GW170817 [5].

After a time break of about two years to upgrade the instruments, Advanced Virgo started the observation period O3 together with Advanced LIGO in April 2019. It should have ended on 30 April 2020 but, due to the COVID-19 pandemic, the conclusion of the observational period was changed to 27 March 2020.

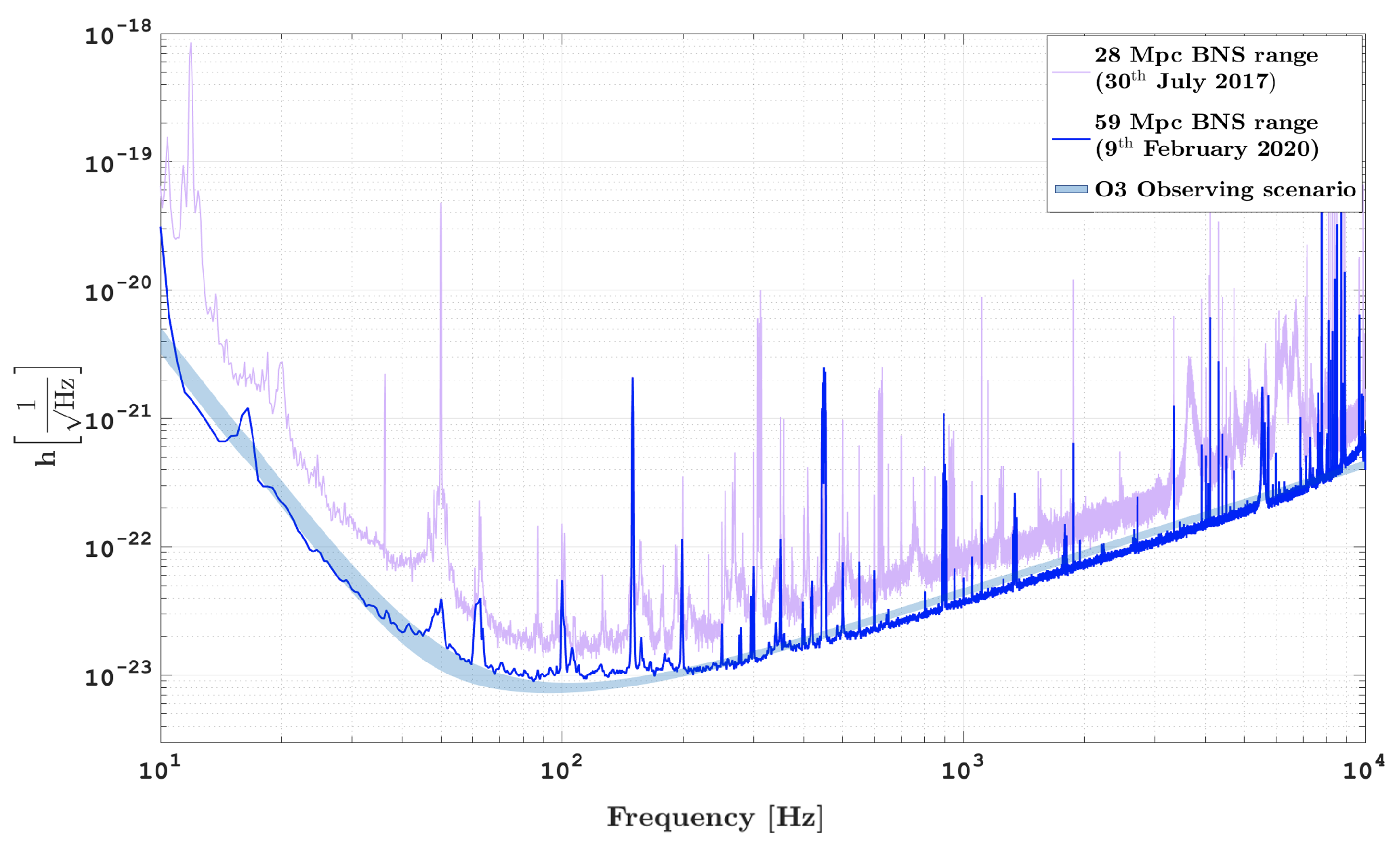
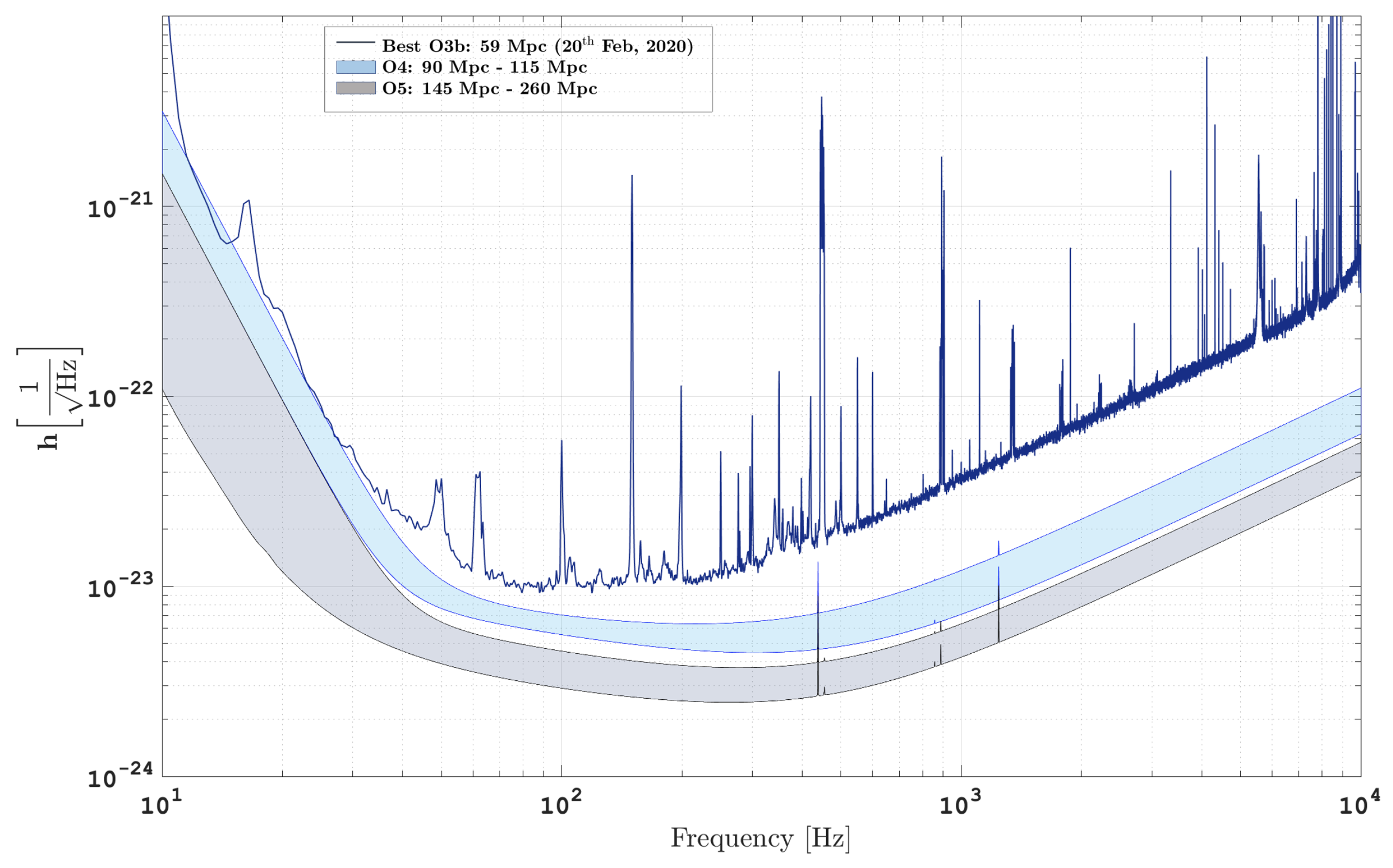
Despite the early closure, the sensitivity of Advanced Virgo and Advanced LIGO in O3 enabled to increase the number of gravitational wave detections more than three-fold over the O2 observing run.

At the end of O3, Advanced Virgo increased its BNS range up to 60 Mpc8 from the Earth, doubling the best sensitivity achieved during O2.

In Figure 4, the best sensitivity curves during O2 and during O3 are shown compared to the design sensitivity target.

In the following, the instrument configuration during the last part of O3, that made achievable 60 Mpc BNS range, will be described.

4.1. Mirrors and Their Suspensions

The core optics of Advanced Virgo, 20 cm thick, with diameter of 35 cm and weight of 42 kg, are high-purity fused silica cylinders, ultra-fine polished to achieve sub-nanometric roughness, and properly coated to reach the desired reflectivity.

They are suspended by four fused silica fibers to the last stage of the Superattenuator (SA) [40], to make them quasi-free and to reduce the seismic noise by ten order of magnitudes above 2 Hz. SA suppresses the seismic horizontal vibrations through a chain of five mechanical filters 8 m-long supported by a three-leg elastic structure (inverted pendulum), connected to ground through flexible joints at the base of each leg. The vertical seismic movements are attenuated by replacing each mass of the multi-stage pendulum by a cylindrical mechanical filter with a set of blade springs with low stiffness. The blades support the next mechanical filter through 1 m-long steel wire, forming a chain of low frequency oscillators. The blades act in parallel to a magnetic anti-spring system, assembled on each filter, to reduce its fundamental vertical frequency from about 1.5 Hz down to below 0.5 Hz [41]. The mirror’s suspension wires are anchored to the marionette, a rigid plate suspended to the last filter of the SA, through a single steel cable, hosting the magnets faced to the coils attached to the last filter of the SA. This coil–magnet system allows to steer the payload in four degrees of freedom: the translation along the beam and the rotations around the vertical axis and around the horizontal ones, perpendicular and parallel to the beam. Finally, the mirror is enfolded in the actuator cage fixed to the last steering filter of the SA, providing the support frame for the baffles, the compensation plate on the input payloads and ring heaters. On the actuator cage, a further set of coils are installed faced on the magnets glued to the anti-reflective surface of the mirror. The SA is the same for both recycling and FP mirrors, while the last stage of suspension is different depending on the mirror and its position in the interferometer.

The lateral surface of each mirror is machined to make flat two small areas to allow the bonding of the ears, rectangular silica pieces, hosting the end part of the fibers properly shaped to be anchored. The suspension wires of the recycling cavity mirrors and the beam splitter are made of steel and not of fused silica since they are outside the FP cavities and, therefore, the coupling of the noise to the detector sensitivity is reduced by factor $2F/\pi$ where F is the finesse of the FP cavity. For these mirrors, four triangular silica spacers are glued to the two flat areas allowing the steel fibers to envelop the mirror like a cradle. The same approach has been applied to suspend the beam splitter, the largest optics ever suspended in an interferometric gravitational-wave detector, having a diameter of 550 mm and thickness of 65 mm. The suspension systems of all mirrors are described in details in [42].

4.2. Optical Layout

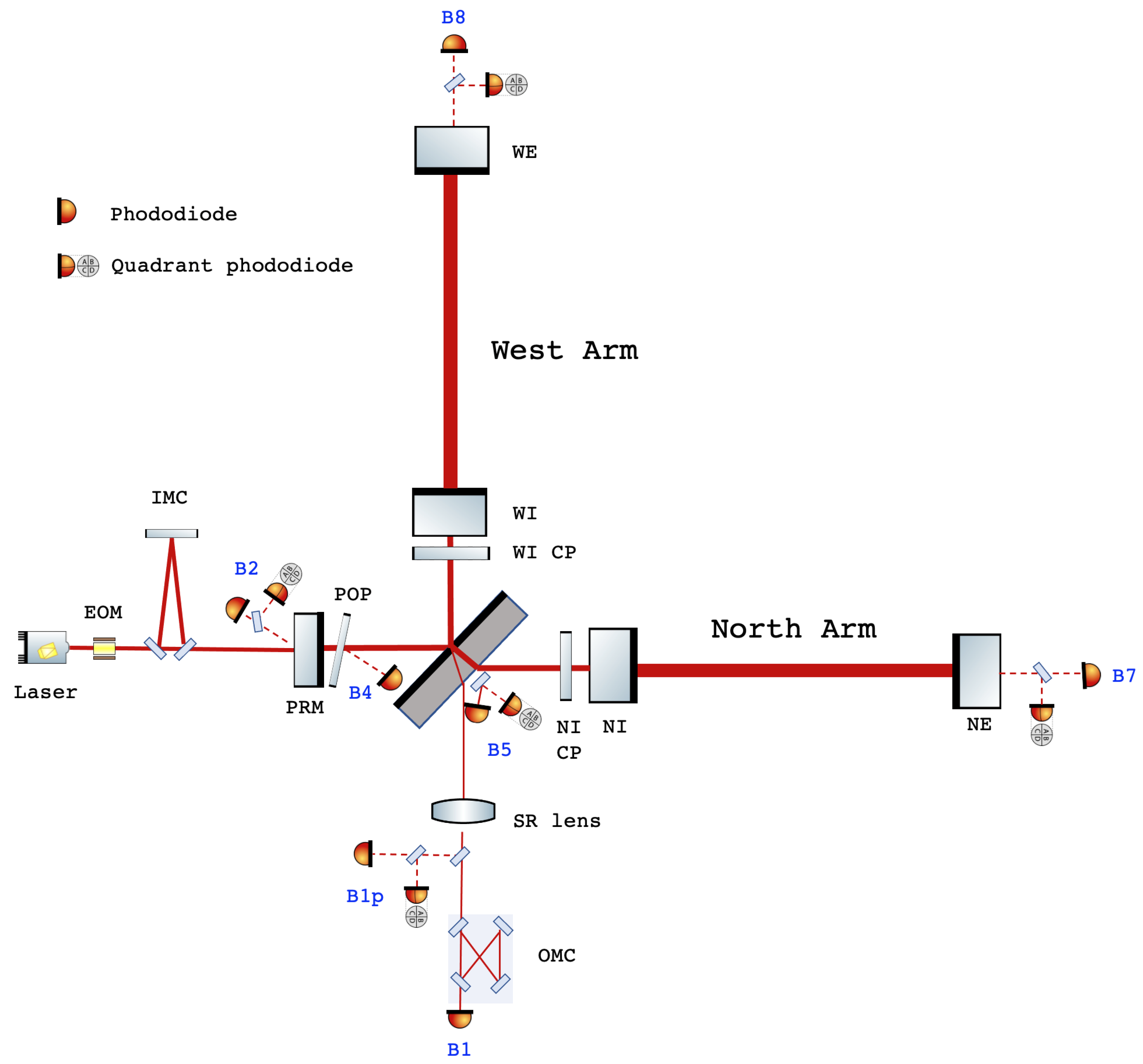
The two 3 km-long FP cavities are identified as North and West, following their geographical orientation. The beam transmitted and reflected by the beam splitter propagates through the North and West arms, respectively. In the North arm, Input and End mirrors are called North Input (NI) and North End (NE). Similarly, in the West arm, the two mirrors are identified as West Input (WI) and West End (WE). The FP cavities, have a bi-concave geometry. The nominal mirror’s radii of curvature are 1420 m and 1683 m for the input and end mirrors, respectively. With this type of topology, the cavity waist is near the middle of the cavity and the beam radius is about 49 mm on the input test mass and 58 mm on the end one.

The reflectivities of the input and the end mirrors are 98.6 % and 99.9995%. Therefore the finesse is 450 and the pole frequency is at 55 Hz. The FP mirror radii of curvature have been defined in order to maximize the beam size on the FP end mirrors to reduce as much as possible the mirror coating thermal noise. This choice imposed the power recycling mirror radius of curvature of 1430 m for the length of the cavity equal to 11.952 m, pushing the power recycling cavity stability condition very close to the instability limit ($g=0.9999885$).

The power recycling mirror reflectivity is 95%, thus the finesse of the power recycling cavity is 48.

The distances between the beam splitter and the two input mirrors differ of the Schnupp asymmetry, equal to 0.23 m.

During O3, the signal recycling mirror has been used as a lens, thus Advanced Virgo runned in the power-recycled Michelson configuration.

4.3. High Power Laser and Injection System

During O3, the high power continuous wave laser could deliver about 100 W at the input of the injection system whose role is to further stabilize the laser frequency, to improve the beam shape, to match and to steer the laser beam toward the interferometer core optics.

The laser system was based on a high power oscillator (HPO) configuration: a 500 mW non-planar ring oscillator laser, the master one, is amplified up to 100 W by two medium power solid state amplifiers, the first one called slave laser that amplifies the seeder up to 20 W and the second one, the NeoVan, providing about 100 W at the output.

The optical amplifier is based on four Nd3${}^{+}$:YVO4 crystals, each longitudinally pumped with 50 W at 878.7 nm emitted by Bragg grating diode lasers. The amplified laser beam propagates through a bow-tie pre-mode cleaner cavity 308 mm-long, which cleans the spatial profile and reduce the jitter of the laser beam [43].

Then, the pre-stabilized high power beam propagates through electro-optical modulators providing the radio frequency sidebands used to control the interferometer: the 6,270,777 Hz and 56,433,933 Hz sidebands are anti-resonant in the FP arms and resonant in the power recycling cavity, the 8,361,036 Hz sidebands are anti-resonant in all optical cavities and, finally, the 22.38 MHz sidebands are used to control the input mode cleaner, the in-vacuum 144 m-long triangular cavity with finesse of 1200.

Then, about 30 mW of the laser beam transmitted by the IMC are picked up to feed the monolithic RFC providing the reference to pre-stabilize the master laser frequency. Indeed, the IMC is locked on the reference cavity and the master laser frequency is locked on the IMC length by tuning the temperature and, consequently, the refractive index of its laser crystal. Finally, the PMC is locked on the master laser by tuning the length of the PMC cavity itself. These optical cavities operate in a hierarchical configuration allowing to reduce the frequency noise at the level of ${10}^{-6}\mathrm{Hz}/\sqrt{\mathrm{Hz}}$ between 10 Hz and 10 kHz.

Finally, the beam propagates through the Mode Matching Telescopes before being injected into the power recycling cavity. It is used to match the beam onto the detector at the best of 99%. This telescope consists of an afocal off-axis parabolic telescope made of two mirrors that increases the beam size by a factor 8.5 (from 2.6 to 22 mm) [44]. Then, a diverging lens is used in combination with the PR mirror to match the beam to the interferometer.

The power available to be injected inside the detector after the propagation through the injection system was more than 65 W. After some commissioning activities at different power values, the input laser power was set to 19 W during the first part of O3 observing run and increased up to 26 W during the second half.

4.4. Detection System

After the recombination on the beam splitter, the beam propagates through the SR lens and the second MMT, another afocal off-axis parabolic telescope, that reduces the beam size from 49 mm to 1.3 mm to adapt the beam itself to the output mode cleaner cavity. As anticipated in Section 2.5, the goal of the OMC is to clean the dark fringe beam from the spurious light not carrying information on the differential arm displacement. Thus, the OMC filters out the main beam HOMs as well as the 6.27 MHz and 56.44 MHz sidebands transmitted at the dark port.

The OMC is composed of two fused-silica monolithic cavities in series in the bow-tie configuration with finesse 120 [42].

The beam filtered out by OMC encodes only the valuable information about the gravitational wave signal.

4.5. Thermal Compensation System

The marginally stable geometry of the power recycling cavity makes it extremely sensitive to the HOMs occurring in presence of optical aberrations that degrade the quality of the error signals, making the interferometer global working point not reliable. The Advanced Virgo Thermal Compensation System is conceived to tackle the aberrations coming both from cold defects and thermally driven effects (Section 2.9) so that the residual optical path length increase in the recycling cavities is below 2 nm Gaussian weighted RMS, and the RoCs of the FP cavity mirrors are within ±2 m from their design values [42]. These requirements ensure the quality of the sidebands used to control the detector, the optimization of the circulating power into the FP cavities and the improvement of the destructive interference at the output port of the detector.

TCS features both wavefront sensors and actuators, so that it can be operated as a control loop keeping the detector at the optimal working point.

The CO${}_2$ actuation optical systems are hosted on two optical benches, acoustically isolated from the environment, installed in the two corners between the vacuum chambers of the beam splitter and of each input mirror.

The projectors have been designed to produce two different actuation patterns on the CPs: the Double Axicon System (DAS) and the Central Heating (CH). The first one is obtained by superimposing two annular beams with different sizes and radii in order to shape a donut. The name of this actuator derives from axicon, an optic with a conical surface, used to convert the CO${}_2$ Gaussian beam into an annular one. The DAS is used mainly to correct the thermal lensing due to uniform coating absorption in the input mirrors and the cold defects showing a high degree of spherical aberration. The CH actuator, having a Gaussian shape of the same size of the main laser beam, is used to mitigate the thermal transients when the interferometer loses lock.

The laser beam induces a bump on the mirror high-reflectivity surfaces making their profiles non-spherical. To compensate this deformation, a ring heater surrounds each FP mirror. The Advanced Virgo RH consists of two parallel, thin o-rings made of borosilicateglass (Pyrex), that encircle the mirror. Each ring is powered by Joule heating through a Nickel Crome conductive wire tightly wrapped in helical coils around it, then acting as a radiator. To increase the efficiency of the system, the heat that radiates away is gathered and conveyed toward the mirror barrel by a copper shield enclosing the rings. The same shield provides, in addition, a stable and protective support for holding the rings around the TM. The shield has a c-shaped rectangular cross section and it is internally polished to enhance its reflectivity.

The TCS actuators require error signals for their optimized operation.

In Advanced Virgo six HWSs are used to measure the optical aberrations on the FP mirrors. In particular, two of them measure the thermal lens on the two input mirrors crossed by the laser beam, the so-called HWS in transmission, while four wavefront sensing setups, identified as HWS in reflection, have been designed to measure the thermoelastic deformation on the input and end mirrors. The two HWSs in trasmission and their probe beam SLEDs at 790 nm are hosted on the injection (HWS-INJ) and detection (HWS-DET) areas to sense the thermal lenses on the WI and NI mirrors, respectively. They propagate overimposed to the main laser beam, through the power recycling and signal recycling cavities up to the high reflectivity mirror surfaces of the input mirrors that reflect the beams toward the HWSs allowing for double pass measurement. An afocal telescope with magnification 11 is used to increase the SLED beam size to probe the optics area of around 100 mm-radius and then to reduce it to 9 mm to be matched with the HWS size.

The HWS in reflection are conceptually similar but the probe beam at 880 nm is magnified by a factor of 7 and impinges on the mirror with an angle of 45${}^{\circ }$, then, it is reflected by the high-reflectivity mirror surface on an auxiliary mirror installed in the same vacuum chamber and it is reflected back towards the wavefront sensor hosted on an in-air optical optical bench installed outside of the mirrors’ vacuum chamber.

Two high-performance phase cameras are also installed in the power recycling cavity and on the dark port to sense the real-time status of the phases and amplitudes of the carrier and the sidebands used to control the interferometer. The reference signal is picked up before the IMC and brought to the desired positions through two polarization maintaining fibers. The pickoff beam in the power recycling cavity is extracted by using the Pickoff Plate (POP) placed in front of the PR mirror.

The detailed description of these sensors are addressed in [45,46].

As a reference, a scheme of the TCS sensors and actuators integrated in Advanced Virgo is shown in Figure 5.

During O3, the DAS shined the CPs to compensate the thermal lensing induced by the main laser beam at 26 W, stabilizing the power recycling cavity and increasing the robusteness of the detector. The CH actuator has been switched on during the lock acquisition sequence to avoid thermal transients which slowed down the whole procedure. Finally, the end mirror’s RH have been used to tune the RoC in order to maximize the intra-cavity power and minimize the power at the anti-symmetric port. As result, the FP circulating power increased of about 15% and the power exiting the interferometer decreased by factor 2.

4.6. Interferometer Read-Out

The output of several photodiodes located in strategical parts of the detector are used to extract the gravitational wave strain and the error signals needed to control the interferometer. The read-out scheme of all photodiodes (PDs) installed in Advanced Virgo is shown in Figure 6.

The photodiodes located at the output port of the detector, B1p and B1 before and after the output mode cleaner, respectively, carry the information about the DARM DoF and, they are sensitive to the GW passage. At the symmetric port, B2 PD senses the beam reflected from the interferometer towards the laser source. The photodiode B4 measures the pickoff beam in the PRC reflected by the POP and B5 measures the pickoff beam originating from the reflection coming from the North arm on the anti-reflective surface of the beam splitter. Finally, the photodiodes B7 and B8 measure the powers transmitted by the North and West arm cavities, respectively.

In parallel to aforementioned PDs, quadrant photodiodes are used to provide the error signals needed to control the cavity angular degrees of freedom.

4.7. Interferometer Sensing and Control

The Interferometer Sensing and Control (ISC) allows to achieve and maintain the correct working point of the detector through the lock acquisition procedure (Section 2.10). At the starting point of the lock acquisition, the power recycling mirror is misaligned and FP mirrors are kept in place by optical lever signals. During the first phase of the locking sequence, the two FP cavities are brought to the resonance by using the PDH signals demodulated at 6 MHz provided by B7 and B8 PDs. Then, the MICH DoF is settled at half fringe by using the DC signal measured by B1p normalized by the sum of B4 and B1p DC signals, their ratio is 1 in the bright fringe configuration and 0 in the dark fringe, so when it is equal to 0.5, half of power is reflected toward the symmetric port and the other half toward the antisymmetric port.

During this phase, the dithering control technique [38] is applied in order to overlap the cavity axis to the mirror center minimizing the coupling between longitudinal and angular DoFs: the error signals are provided by mechanically exciting both angular DoFs of each test mass at a specific frequency once the longitudinal DoFs have been fixed. When the beam impinges far from the optics center, the two DoFs are strongly coupled. On the contrary, this coupling is minimized in the mirror center. The mirror angular position which minimize this coupling is chosen. Then, the same strategy is implemented to align the input beam on the cavity axes acting on the PRM and BS. Since the PR rear surface is a strong converging lens (RoC = 3.62 m), its translational DoFs are mechanically exciting at specific frequency to steer the input beam along the North cavity. The error signal, encoding the mutual tilt between the input beam and the cavity axis, is obtained by demodulating the excitation line in the North arm transmitted power. The same purpose is reached for the West Arm by moving the beam splitter in the two angular DoFs. When the powers transmitted by the FP cavities are maximized, the input beam and the cavity axis are overlapped.

During the second phase of the lock acquisition, the power recycling mirror is aligned to achieve the resonance position and MICH is reduced to attain the destructive interference working point [47,48]. During this phase, the power circulating into the detector increases significantly, making very critical the alignment of the power recycling mirror. Thus, during this phase, the PR mirror angular control is performed by using the B2 QPD signal reflected by the power recycling cavity looking at the signal demodulated at 8 MHz.

Once the dark fringe condition is achieved, the error signals associated with the Common and Differential DoFs (Section 2.10) are used to improve the accuracy of the working point. In particular, the B1p QPD demodulated at 56 MHz provides the errors signals for the most critical DoFs, i.e., COMM(+) and DIFF(+), improving the FP mirror angular DoFs accuracy at the nano-radian level.

The last steps of the lock acquisition are the control of the OMC cavity and the engagement of the DC read-out by adding a DARM offset to have few mW on B1 PD that becomes the final error signal for DARM. Once the procedure is concluded, the squeezing beam is injected and aligned in the interferometer. The duration of the whole looking procedure is about twenty minutes and it is completely automatized on the Metatron environment [49]. The detailed description of the whole acquisition sequence can be found in [38,50].

Thanks to the combined action between ISC and TCS, the longest lock (132 h) has been achieved in the week between 1 and 7 January 2020 [38]9.

4.8. Squeezed Light Injection

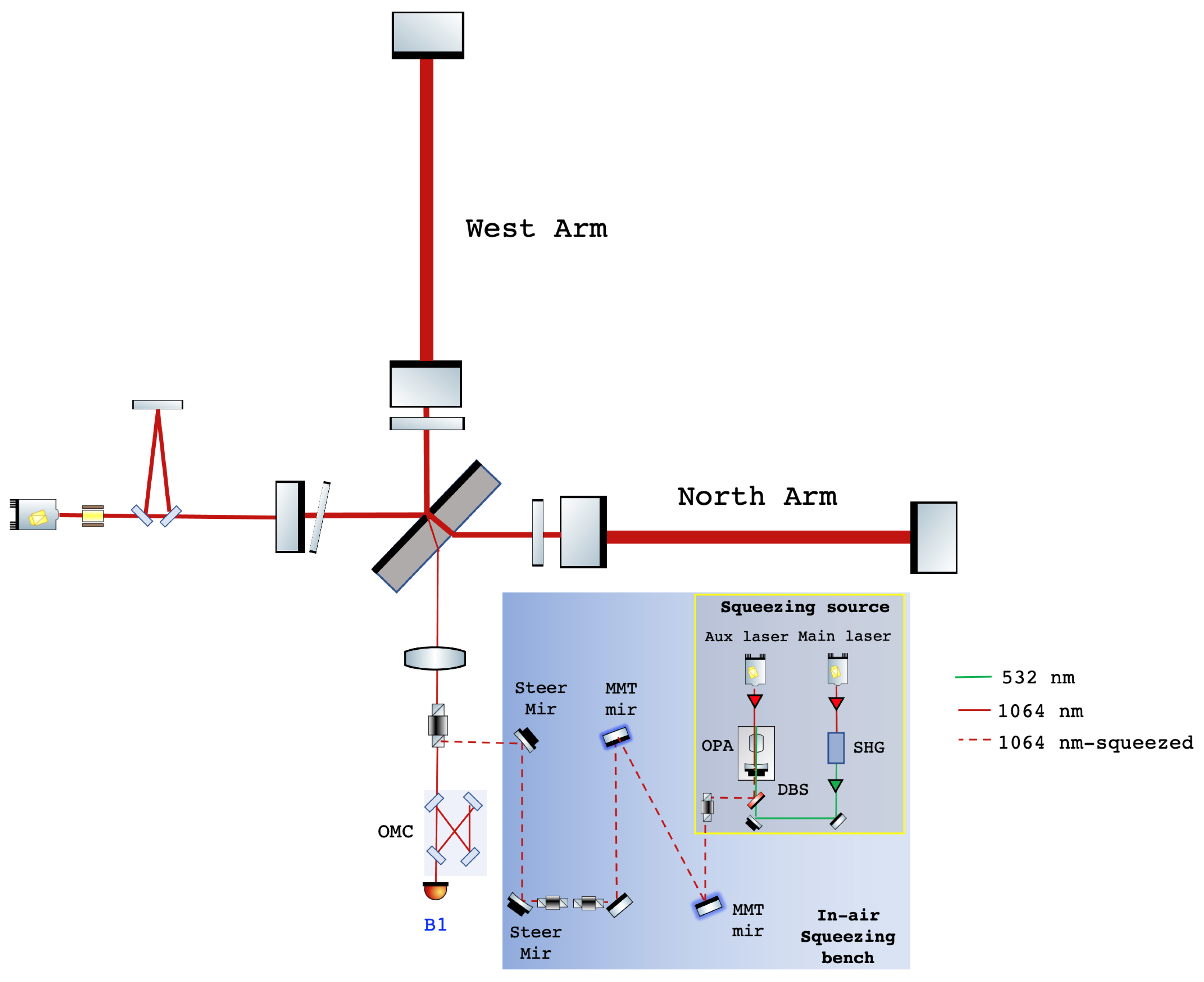
The routinely injection of the frequency-independent squeezing in Advanced Virgo to reduce its quantum noise at high frequency was one of the major upgrade implemented before O3. The two optical systems needed to generate squeezed light and to inject it into the dark port of the interferometer are installed in-air, on a single optical bench close to the vacuum chambers hosting the output system. The squeezing light generation is a stand-alone system developed at Albert Einstein Institute (AEI) in Hannover [51] that mainly includes two commercial lasers at 1064 nm. The main one, locked to the Virgo laser frequency, is used to produce the beam at 532 nm (pump beam), that seeds the squeezing generation. The auxiliary laser, locked to the main laser frequency one, shifted by 7 MHz, is used to perform the coherent control needed to produce squeezing at the audio frequencies. The squeezing light at 1064 nm is produced by the green beam pumping the OPA, a linear doubly resonant cavity consisting of a piezo-actuated coupling mirror and a periodically poled potassium titanyl phosphate (PPKTP) nonlinear crystal whose temperature is stabilized to mK to simultaneously ensure phase matching and co-resonance of both wavelengths. The cavity length is controlled via PDH technique using the green beam reflected by the OPA.

A mode matching telescope, made by two spherical mirrors, shapes the squeezing beam size to be equal to the interferometer’s one and a pair of piezo-actuated tip-tilt mirrors are used to steer the squeezed beam into the Faraday isolator installed between the detection mode matching telescope and the output mode cleaner where the squeezed and the interferometer beams overlap (Figure 7).

The squeezing system has its own hierarchical locking scheme, independent of the interferometer one, that takes care of the working point of the squeezed light source and of the injection of the squeezed states into the interferometer.

During O3, the injection of phase-squeezed vacuum states reduced the shot noise level by about 3 dB improving the binary neutron star range by 8% [52].

5. Advanced Virgo + Phase I and II

After the end of O3 run, both Advanced LIGO and Advanced Virgo implemented mid-scale upgrades, designated as A+ and AdV+, aiming to improve their sensitivities by more than two times the current levels [53].

The Advanced Virgo short-term planned upgrades included the installation of the signal recycling mirror, the installation of a more powerful laser and the construction of a filter cavity to provide frequency dependent squeezed light to reduce and reshape the impact of quantum noise. The goal of these upgrades, identified as Phase I, is to detect gravitational waves from the coalescence of binary neutron stars at distances of the order of 100 Mpc. Now the instrument is being prepared for the fourth data taking O4 that should start by the end of 2022. After the end of O4, in view of the fifth observing run O5, a new installation phase, called Phase II, including larger mirrors with lower thermal noise optical coatings, will start. The target will be to detect gravitational waves from the coalescence of binary neutron stars at distances of the order of 200 Mpc.

The detector sensitivities expected for the next observing runs are shown in Figure 8 [54].

6. Conclusions

A network of worldwide distributed interferometers operating as a unified detector allowed to detect gravitational waves challenging the most established astrophysical and cosmological scenarios. The Advanced LIGO and Advanced Virgo detectors have actively searched GWs in a highly coordinated campaign during a series of observing runs carried out from 2015.

This overview covers the basic physics behind the gravitational wave interferometers involving the combination of relatively simple optical systems into more and more complex assemblies. The current generation of GW interferometer, such as Advanced Virgo and Advanced LIGO, operates in high-power and quantum regime configuration.

In this paper, the Advanced Virgo experiment is described focusing on the hardware features that allowed to reach a BNS range of 60 Mpc.

Advanced Virgo shut down on 27 March 2020 together with Advanced LIGO, earlier than planned owing to the COVID-19 pandemic, and have been undergoing major upgrades in order to improve the BNS range at distances about 100 Mpc during O4 and as far as more than 200 Mpc during O5.

[custom] References