Fusing Multiview Functional Brain Networks by Joint Embedding for Brain Disease Identification
Abstract
1. Introduction
2. Related Work
2.1. Pearson’s Correlation
2.2. Sparse Representation
2.3. Mutual Information
2.4. Correlation’s Correlation
3. Materials and Methods
3.1. Data Preparation
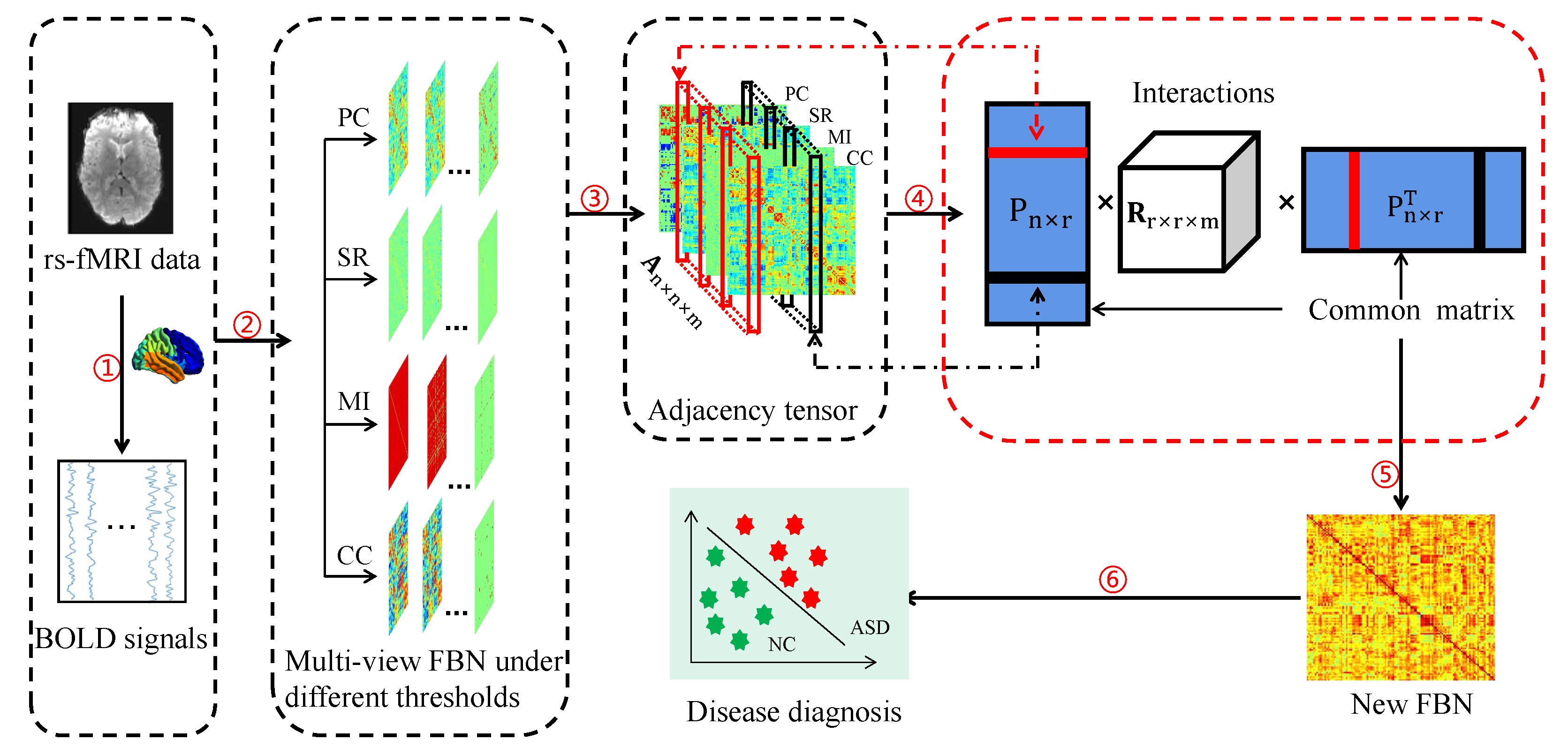
3.2. Proposed Method
3.2.1. Motivation
3.2.2. General Framework
3.2.3. Proposed Joint Embedding
3.2.4. Theoretical Explanation
3.2.5. Optimization
- (a)
- Update P:
- (b)
- Update:
| Algorithm 1: Algorithm of MJE |
| Input: × n × m: adjacency tensor; : regularization parameter; r: rank of the latent representation; : the maximum number of iterations, THIS Initialize: P with the r largest eigenvectors of the Eigen decomposition of ; is initialized byany random matrices While not converged or do Update P according to Equation (11); Update according to Equation (14); t = t + 1; check the convergence conditions: or end Reconstruct the FBN with PC for the potential representation of each ROI by Output: Restructuring the FBN: W |
3.2.6. Classification
4. Experiments
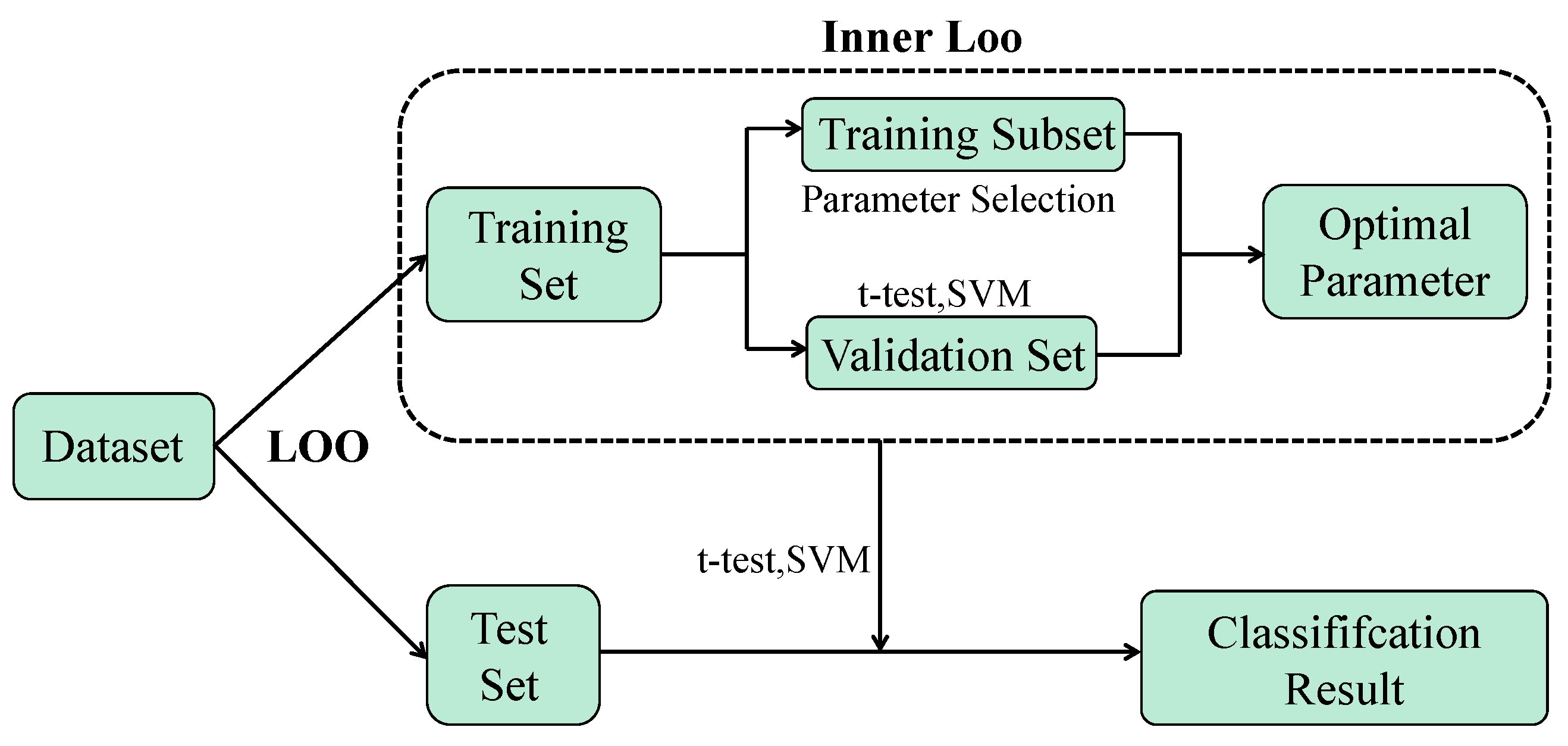
4.1. Experimental Setting
4.2. Comparison Methods
- •
- MNER [26]: This method uses the sparse regression model with group constraints to generate multiple sparse FBNs with different sparsity levels, followed by multiview FBN fusion via a multiview learning method.
- •
- LORTA [46]: This method assumes that FBNs have similar but not necessarily the same topology across subjects. It is implemented in a two-step learning framework. First, the FBNs are estimated according to conventional methods. Then, the estimated FCNs of all subjects are stacked into a tensor and refined by low-rank tensor approximation.
- •
- BMGF [27]: This method aims to fuse a fully connected FBN and a 1-nearest neighbor (1NN) FCN, taking into account the effects of intersubject variability and cross-subject heterogeneity.
- •
- GraphCGC-Net [51]: This method is a unified three-stage graph learning framework for brain disease diagnosis. First, it constructs a coarsened graph to obtain a critical graph structure using supervised multigraph clustering. A graph GAN is then used to generate the realistic brain networks based on the coarsened graph. It further finetunes the pretrained GCN by combining the generated and original graphs into a mixed training dataset.
- •
- MVS-GCN [30]: This method is a prior brain structure learning-guided multiview graph convolution network framework. It first constructs multiview coarsened brain network structures that are consistent for all the subjects and then implements multitask graph embedding learning to capture the intrinsic correlations among different views.
- •
- MFC-PL [52]: This method trains DNN models through unsupervised and supervised training steps to learn abstract feature representations of low-order and high-order FC patterns. Then, the learned multilevel abstract FC features are combined, and an ensemble classifier is trained on the fused features for brain disease classification.
- •
- BrainGC-Net [53]: This method improves the classification performance of the graph through three mechanisms. First, a priori subnetwork structure regularization is proposed to guide the pooling process and ensure accurate subnetwork identification. Then, a graph GAN model that focuses on both embedding and graph space is proposed based on the structure of -GAN. In addition, a domain-consistent GCN model is proposed to alleviate the gap that exists between the real graph and the domain of the generated graph.
4.3. Results
4.3.1. Initial FBN Parameter Selection
4.3.2. Results of ASD Identification
5. Discussion
5.1. Sensitivity to Parameters
5.2. Influence of Proposed Fusion Strategy
5.3. Influence of Number of FBNs
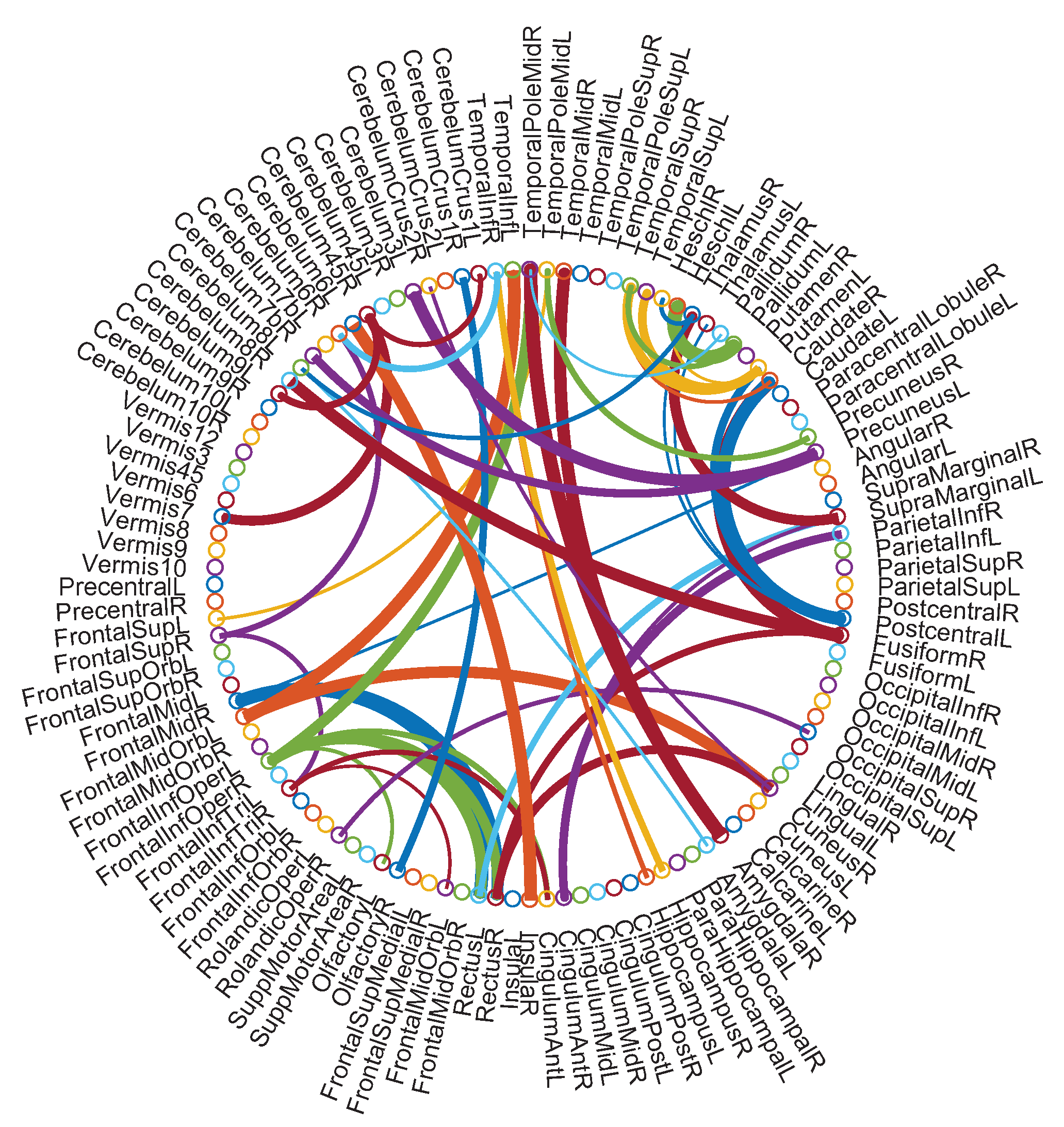
5.4. Identified Discriminative Features
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Uno, Y.; Uchiyama, T.; Kurosawa, M.; Aleksic, B.; Ozaki, N. The combined measles, mumps, and rubella vaccines and the total number of vaccines are not associated with development of autism spectrum disorder: The first case-control study in asia. Vaccine 2012, 30, 28. [Google Scholar] [CrossRef] [PubMed]
- Pierce, K.; Courchesne, E.; Bacon, E. To screen or not to screen universally for autism is not the question: Why the task force got it wrong. J. Pediatr. 2016, 176, 182–194. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Zhang, Y.; Zhai, W.; Wang, H.; Zhang, J.; Jin, H.; Feng, J.; Qin, Q.; Xu, H.; Li, B.; et al. Attenuated effective connectivity of large-scale brain networks in children with autism spectrum disorders. Front. Neurosci. 2022, 16, 2031. [Google Scholar] [CrossRef] [PubMed]
- Riddiford, J.A.; Enticott, P.G.; Lavale, A.; Gurvich, C. Gaze and social functioning associations in autism spectrum disorder: A systematic review and meta-analysis. Autism Res. 2022, 15, 1380–1446. [Google Scholar] [CrossRef]
- Geschwind, D.H.; Levitt, P. Autism spectrum disorders: Developmental disconnection syndromes. Curr. Opin. Neurobiol. 2007, 17, 103–111. [Google Scholar] [CrossRef]
- Rossi, J.; Newschaffer, C.; Yudell, M. Autism spectrum disorders, risk communication, and the problem of inadvertent harm. Kennedy Inst. Ethics J. 2013, 23, 105–138. [Google Scholar] [CrossRef]
- Courchesne, E.; Gazestani, V.H.; Lewis, N.E. Prenatal origins of ASD: The when, what, and how of ASD development. Trends Neurosci. 2020, 43, 326–342. [Google Scholar] [CrossRef]
- Lombardo, M.V.; Chakrabarti, B.; Bullmore, E.T.; Baron-Cohen, S.; MRC AIMS Consortium. Specialization of right temporo-parietal junction for mentalizing and its relation to social impairments in autism. Neuroimage 2011, 56, 1832–1838. [Google Scholar] [CrossRef]
- Elsabbagh, M.; Holmboe, K.; Gliga, T.; Mercure, E.; Hudry, K.; Charman, T.; BASIS team. Social and attention factors during infancy and the later emergence of autism characteristics. Prog. Brain Res. 2011, 189, 195–207. [Google Scholar]
- Pierce, K.; Marinero, S.; Hazin, R.; McKenna, B.; Barnes, C.C.; Malige, A. Eye tracking reveals abnormal visual preference for geometric images as an early biomarker of an autism spectrum disorder subtype associated with increased symptom severity. Biol. Psychiatry 2016, 79, 657–666. [Google Scholar] [CrossRef]
- Ullah, Z.; Farooq, M.U.; Lee, S.H.; An, D. A hybrid image enhancement based brain MRI images classification technique. Med. Hypotheses 2020, 143, 109922. [Google Scholar] [CrossRef]
- Lin, K.; Jie, B.; Dong, P.; Ding, X.; Bian, W.; Liu, M. Convolutional recurrent neural network for dynamic functional mri analysis and brain disease identification. Front. Neurosci. 2022, 16, 933660. [Google Scholar] [CrossRef]
- Eslami, T.; Mirjalili, V.; Fong, A.; Laird, A.R.; Saeed, F. ASD-DiagNet: A hybrid learning approach for detection of autism spectrum disorder using fMRI data. Front. Neuroinform. 2019, 13, 70. [Google Scholar] [CrossRef]
- Subah, F.Z.; Deb, K.; Dhar, P.K.; Koshiba, T. A deep learning approach to predict autism spectrum disorder using multisite resting-state fMRI. Appl. Sci. 2021, 11, 3636. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, L.; Yu, J.; Li, J.; Yu, X. Identification of autism spectrum disorder using multi-regional resting-state data through an attention learning approach. Biomed. Signal Process. Control. 2021, 69, 102833. [Google Scholar] [CrossRef]
- Liu, F.; Wang, Y.; Li, M.; Wang, W.; Li, R.; Zhang, Z.; Chen, H. Dynamic functional network connectivity in idiopathic generalized epilepsy with generalized tonic–clonic seizure. Hum. Brain Mapp. 2017, 38, 957–973. [Google Scholar] [CrossRef]
- Li, K.; Guo, L.; Nie, J.; Li, G.; Liu, T. Review of methods for functional brain connectivity detection using fMRI. Comput. Med Imaging Graph. 2009, 33, 131–139. [Google Scholar] [CrossRef]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef]
- Wang, H.E.; Bénar, C.G.; Quilichini, P.P.; Friston, K.J.; Jirsa, V.K.; Bernard, C. A systematic framework for functional connectivity measures. Front. Neurosci. 2014, 8, 405. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, L.; Chen, S.; Shen, D. Data-driven graph construction and graph learning: A review. Neurocomputing 2018, 312, 336–351. [Google Scholar] [CrossRef]
- Lee, H.; Lee, D.S.; Kang, H.; Kim, B.N.; Chung, M.K. Sparse brain network recovery under compressed sensing. IEEE Trans. Med Imaging 2011, 30, 1154–1165. [Google Scholar] [PubMed]
- Gómez-Verdejo, V.; Martínez-Ramón, M.; Florensa-Vila, J.; Oliviero, A. Analysis of fMRI time series with mutual information. Med Image Anal. 2012, 16, 451–458. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Alahmadi, A.; Zhu, D.; Li, T. Brain functional connectivity analysis using mutual information. In Proceedings of the 2015 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Orlando, FL, USA, 14–16 December 2015; pp. 542–546. [Google Scholar]
- Zhang, H.; Chen, X.; Shi, F.; Li, G.; Kim, M.; Giannakopoulos, P.; Shen, D. Topographical information-based high-order functional connectivity and its application in abnormality detection for mild cognitive impairment. J. Alzheimer’s Dis. 2016, 54, 1095–1112. [Google Scholar] [CrossRef] [PubMed]
- Jie, B.; Zhang, D.; Wee, C.Y.; Shen, D. Topological graph kernel on multiple thresholded functional connectivity networks for mild cognitive impairment classification. Hum. Brain Mapp. 2014, 35, 2876–2897. [Google Scholar] [CrossRef]
- Huang, H.; Liu, X.; Jin, Y.; Lee, S.W.; Wee, C.Y.; Shen, D. Enhancing the representation of functional connectivity networks by fusing multi-view information for autism spectrum disorder diagnosis. Hum. Brain Mapp. 2019, 40, 833–854. [Google Scholar] [CrossRef]
- Gan, J.; Peng, Z.; Zhu, X.; Hu, R.; Ma, J.; Wu, G. Brain functional connectivity analysis based on multi-graph fusion. Med Image Anal. 2021, 71, 102057. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, H.; Huang, J.; Xu, X.; Guan, D.; Zhang, D. Hybrid functional brain network with first-order and second-order information for computer-aided diagnosis of schizophrenia. Front. Neurosci. 2019, 13, 603. [Google Scholar] [CrossRef]
- Yang, X.; Jin, Y.; Chen, X.; Zhang, H.; Li, G.; Shen, D. Functional connectivity network fusion with dynamic thresholding for MCI diagnosis. In International Workshop on Machine Learning in Medical Imaging; Springer: Cham, Switzerland, 2016; pp. 246–253. [Google Scholar]
- Wen, G.; Cao, P.; Bao, H.; Yang, W.; Zheng, T.; Zaiane, O. MVS-GCN: A prior brain structure learning-guided multiview graph convolution network for autism spectrum disorder diagnosis. Comput. Biol. Med. 2022, 142, 105239. [Google Scholar] [CrossRef]
- Nickel, M.; Tresp, V.; Kriegel, H.P. A three-way model for collective learning on multi-relational data. Icml 2011, 11, 3104482–3104584. [Google Scholar]
- Bonacich, P. Factoring and weighting approaches to status scores and clique identification. J. Math. Sociol. 1972, 2, 113–120. [Google Scholar] [CrossRef]
- Li, W.; Wang, Z.; Zhang, L.; Qiao, L.; Shen, D. Remodeling Pearson’s correlation for functional brain network estimation and autism spectrum disorder identification. Front. Neuroinform. 2017, 11, 55. [Google Scholar] [CrossRef]
- Zhou, Y.; Qiao, L.; Li, W.; Zhang, L.; Shen, D. Simultaneous estimation of low-and high-order functional connectivity for identifying mild cognitive impairment. Front. Neuroinform. 2018, 12, 3. [Google Scholar] [CrossRef]
- Li, W.; Zhang, L.; Qiao, L.; Shen, D. Toward a better estimation of functional brain network for mild cognitive impairment identification: A transfer learning view. IEEE J. Biomed. Health Inform. 2019, 24, 1160–1168. [Google Scholar] [CrossRef]
- Li, W.; Qiao, L.; Zhang, L.; Wang, Z.; Shen, D. Functional brain network estimation with time series self-scrubbing. IEEE J. Biomed. Health Inform. 2019, 23, 2494–2504. [Google Scholar] [CrossRef]
- Fornito, A.; Zalesky, A.; Bullmore, E. Fundamentals of Brain Network Analysis; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Craddock, C.; Benhajali, Y.; Chu, C.; Chouinard, F.; Evans, A.; Jakab, A.; Bellec, P. The neuro bureau preprocessing initiative: Open sharing of preprocessed neuroimaging data and derivatives. Front. Neuroinform. 2013, 7, 27. [Google Scholar]
- Chen, X.; Zhang, H.; Gao, Y.; Wee, C.Y.; Li, G.; Shen, D. Alzheimer’s Disease Neuroimaging Initiative. High-order resting-state functional connectivity network for MCI classification. Hum. Brain Mapp. 2016, 37, 3282–3296. [Google Scholar] [CrossRef]
- Plis, S.M.; Sui, J.; Lane, T.; Roy, S.; Clark, V.P.; Potluru, V.K.; Calhoun, V.D. High-order interactions observed in multi-task intrinsic networks are dominant indicators of aberrant brain function in schizophrenia. NeuroImage 2014, 102, 35–48. [Google Scholar] [CrossRef]
- Macke, J.H.; Opper, M.; Bethge, M. Common input explains higher-order correlations and entropy in a simple model of neural population activity. Phys. Rev. Lett. 2011, 106, 208102. [Google Scholar] [CrossRef]
- Friston, K.J.; Williams, S.; Howard, R.; Frackowiak, R.S.; Turner, R. Movement-related effects in fMRI time-series. Magn. Reson. Med. 1996, 35, 346–355. [Google Scholar] [CrossRef]
- Tzourio-Mazoyer, N.; Landeau, B.; Papathanassiou, D.; Crivello, F.; Etard, O.; Delcroix, N.; Joliot, M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 2002, 15, 273–289. [Google Scholar] [CrossRef]
- Al-Sharoa, E.; Al-Khassaweneh, M.; Aviyente, S. Tensor based temporal and multilayer community detection for studying brain dynamics during resting state fMRI. IEEE Trans. Biomed. Eng. 2018, 66, 695–709. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Cao, P.; Xu, M.; Yang, J.; Zaiane, O. Hi-GCN: A hierarchical graph convolution network for graph embedding learning of brain network and brain disorders prediction. Comput. Biol. Med. 2020, 127, 104096. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Zhang, L.; Qiao, L.; Shen, D. Estimating functional connectivity networks via low-rank tensor approximation with applications to MCI identification. IEEE Trans. Biomed. Eng. 2019, 67, 1912–1920. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhang, Y.; Zhang, L.; Qiao, L.; Shen, D. Estimating brain functional networks based on adaptively-weighted fMRI signals for MCI identification. Front. Aging Neurosci. 2021, 12, 595322. [Google Scholar] [CrossRef]
- Tang, W.; Lu, Z.; Dhillon, I.S. Clustering with multiple graphs. In Proceedings of the 2009 Ninth IEEE International Conference on Data Mining, Miami Beach, FL, USA, 6–9 December 2009. [Google Scholar]
- Verma, A.; Bharadwaj, K.K. Identifying community structure in a multi-relational network employing non-negative tensor factorization and GA k-means clustering. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2017, 7, e1196. [Google Scholar] [CrossRef]
- Nickel, M.; Tresp, V. Logistic tensor factorization for multi-relational data. arXiv 2013, arXiv:1306.2084. [Google Scholar]
- Yang, W.; Wen, G.; Cao, P.; Yang, J.; Zaiane, O.R. Collaborative learning of graph generation, clustering and classification for brain networks diagnosis. Comput. Methods Programs Biomed. 2022, 219, 106772. [Google Scholar] [CrossRef]
- Liang, Y.; Xu, G. Multi-level Functional Connectivity Fusion Classification Framework for Brain Disease Diagnosis. IEEE J. Biomed. Health Inform. 2022, 26, 2714–2725. [Google Scholar] [CrossRef]
- Cao, P.; Wen, G.; Yang, W.; Liu, X.; Yang, J.; Zaiane, O. A unified framework of graph structure learning, graph generation and classification for brain network analysis. Appl. Intell. 2022, 1–14. [Google Scholar] [CrossRef]
- Bi, X.A.; Liu, Y.; Jiang, Q.; Shu, Q.; Sun, Q.; Dai, J. The diagnosis of autism spectrum disorder based on the random neural network cluster. Front. Hum. Neurosci. 2018, 12, 257. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Q.; Zhang, H.; Chen, J.; Wang, S.; Shen, D. Sparse multiview task-centralized ensemble learning for ASD diagnosis based on age-and sex-related functional connectivity patterns. IEEE Trans. Cybern. 2018, 49, 3141–3154. [Google Scholar] [CrossRef]
- Shao, L.; Fu, C.; You, Y.; Fu, D. Classification of ASD based on fMRI data with deep learning. Cogn. Neurodynamics 2021, 15, 961–974. [Google Scholar] [CrossRef]


| Dataset | Class | Gender (M/F) | Age (Years) | FIQ | VIQ | PIQ |
|---|---|---|---|---|---|---|
| ABIDE | ASD | |||||
| NC |
| Method | PC | SR | MI | CC | Aver | Min | Max | Ours |
|---|---|---|---|---|---|---|---|---|
| Interclass FBN Distance | 9.20 | 2.52 | 6.41 | 12.26 | 5.88 | 6.87 | 6.02 | 13.24 |
| Method | ACC (%) | SEN (%) | SPE (%) | BAC (%) | PPV (%) | NPV (%) | AUC (%) |
|---|---|---|---|---|---|---|---|
| MNER [26] | 70.65 | 58.82 | 74.29 | 66.66 | 61.98 | 74.29 | 73.32 |
| LORTA [46] | 68.48 | 71.70 | 64.10 | 67.90 | 64.93 | 74.29 | 74.29 |
| BMGF [27] | 66.30 | 60.76 | 70.48 | 65.62 | 60.76 | 70.48 | 70.56 |
| GraphCGC-Net [51] | 71.74 | 63.83 | 78.26 | 71.05 | 75.00 | 78.26 | 77.42 |
| MVS-GCN [30] | 67.93 | 58.23 | 75.24 | 66.73 | 63.89 | 70.54 | 71.14 |
| MFC-PL [52] | 66.74 | 56.54 | 74.95 | 65.75 | 63.10 | 63.10 | 69.70 |
| BrainGC-Net [53] | 77.43 | 59.30 | 51.20 | 58.52 | 59.17 | 64.30 | 74.83 |
| Ours | 74.46 | 64.56 | 81.90 | 73.23 | 72.86 | 75.44 | 81.72 |
| CV | p-Value | Method | ACC (%) | SEN (%) | SPE (%) | BAC (%) | PPV (%) | NPV (%) | AUC (%) |
|---|---|---|---|---|---|---|---|---|---|
| LOOCV | p = 0.01 | PC | 66.85 | 65.82 | 67.62 | 66.72 | 60.47 | 72.45 | 74.56 |
| SR | 66.31 | 49.37 | 79.05 | 64.21 | 63.93 | 67.48 | 71.78 | ||
| MI | 57.07 | 36.71 | 72.38 | 54.54 | 50.00 | 60.32 | 57.18 | ||
| CC | 65.76 | 58.23 | 71.43 | 64.83 | 60.53 | 69.44 | 72.68 | ||
| Ours | 73.91 | 65.82 | 80.00 | 72.91 | 71.23 | 75.68 | 75.68 | ||
| p = 0.05 | PC | 67.39 | 59.49 | 73.33 | 66.41 | 62.67 | 70.64 | 71.79 | |
| SR | 59.78 | 46.84 | 69.52 | 58.18 | 53.62 | 63.48 | 58.64 | ||
| MI | 55.43 | 41.77 | 65.71 | 53.74 | 47.83 | 60.00 | 62.69 | ||
| CC | 66.85 | 58.23 | 73.33 | 65.78 | 62.16 | 70.00 | 69.99 | ||
| Ours | 66.30 | 60.76 | 70.48 | 65.62 | 60.76 | 70.48 | 70.56 | ||
| p = 0.001 | PC | 66.30 | 65.82 | 66.67 | 66.24 | 59.77 | 72.16 | 70.17 | |
| SR | 63.04 | 51.90 | 71.43 | 61.66 | 57.75 | 66.37 | 64.48 | ||
| MI | 64.13 | 62.03 | 65.71 | 63.87 | 57.65 | 69.70 | 72.56 | ||
| CC | 70.11 | 64.56 | 74.29 | 69.42 | 65.38 | 73.58 | 78.52 | ||
| Ours | 74.46 | 64.56 | 81.90 | 73.23 | 72.86 | 75.44 | 81.72 | ||
| p = 0.005 | PC | 69.02 | 68.35 | 69.52 | 68.94 | 62.79 | 74.49 | 73.25 | |
| SR | 67.39 | 48.10 | 81.90 | 65.00 | 66.67 | 67.72 | 70.61 | ||
| MI | 55.43 | 41.77 | 65.71 | 53.74 | 47.83 | 60.00 | 62.69 | ||
| CC | 69.57 | 63.29 | 74.29 | 68.79 | 64.94 | 72.90 | 77.37 | ||
| Ours | 74.46 | 68.35 | 79.05 | 73.70 | 71.05 | 76.85 | 76.85 |
| Method | Number of FBNs | ||
|---|---|---|---|
| Two-View FBNs | Three-View FBNs | Four-View FBNs | |
| Averaging Fusion | 62.74% | 63.99% | 64.77% |
| Ours | 71.73% | 72.14% | 74.41% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Zhang, L.; Zhang, J.; Qiao, L.; Liu, M. Fusing Multiview Functional Brain Networks by Joint Embedding for Brain Disease Identification. J. Pers. Med. 2023, 13, 251. https://doi.org/10.3390/jpm13020251
Wang C, Zhang L, Zhang J, Qiao L, Liu M. Fusing Multiview Functional Brain Networks by Joint Embedding for Brain Disease Identification. Journal of Personalized Medicine. 2023; 13(2):251. https://doi.org/10.3390/jpm13020251
Chicago/Turabian StyleWang, Chengcheng, Limei Zhang, Jinshan Zhang, Lishan Qiao, and Mingxia Liu. 2023. "Fusing Multiview Functional Brain Networks by Joint Embedding for Brain Disease Identification" Journal of Personalized Medicine 13, no. 2: 251. https://doi.org/10.3390/jpm13020251
APA StyleWang, C., Zhang, L., Zhang, J., Qiao, L., & Liu, M. (2023). Fusing Multiview Functional Brain Networks by Joint Embedding for Brain Disease Identification. Journal of Personalized Medicine, 13(2), 251. https://doi.org/10.3390/jpm13020251










