Transparent Quality Optimization for Machine Learning-Based Regression in Neurology
Abstract
:1. Introduction
1.1. Background
1.2. Motivation for Transparent Optimization Design
- Is it possible to create working ML-based prediction prototypes for specific medical use cases with only few data of low/medium quality?
- What are the best possible prediction results for these kinds of approaches?
- What are the influencing factors for the quality of medical ML prototypes, especially for prediction quality?
2. Methods and Materials
2.1. State of the Art
2.1.1. Data-Based Prediction Approaches
2.1.2. Software Technologies
2.2. Dataset
2.3. ML-Based Software Approach
2.3.1. Machine-Learning Setup Design
2.3.2. Setup Optimization
2.4. Analysis Strategy for the Prediction Quality
2.5. Reliability and Validity of the Optimized Algorithm
3. Results
3.1. Software Execution
3.2. Fractional Factorial Benchmark Results
3.2.1. Definition of the Number of Epochs
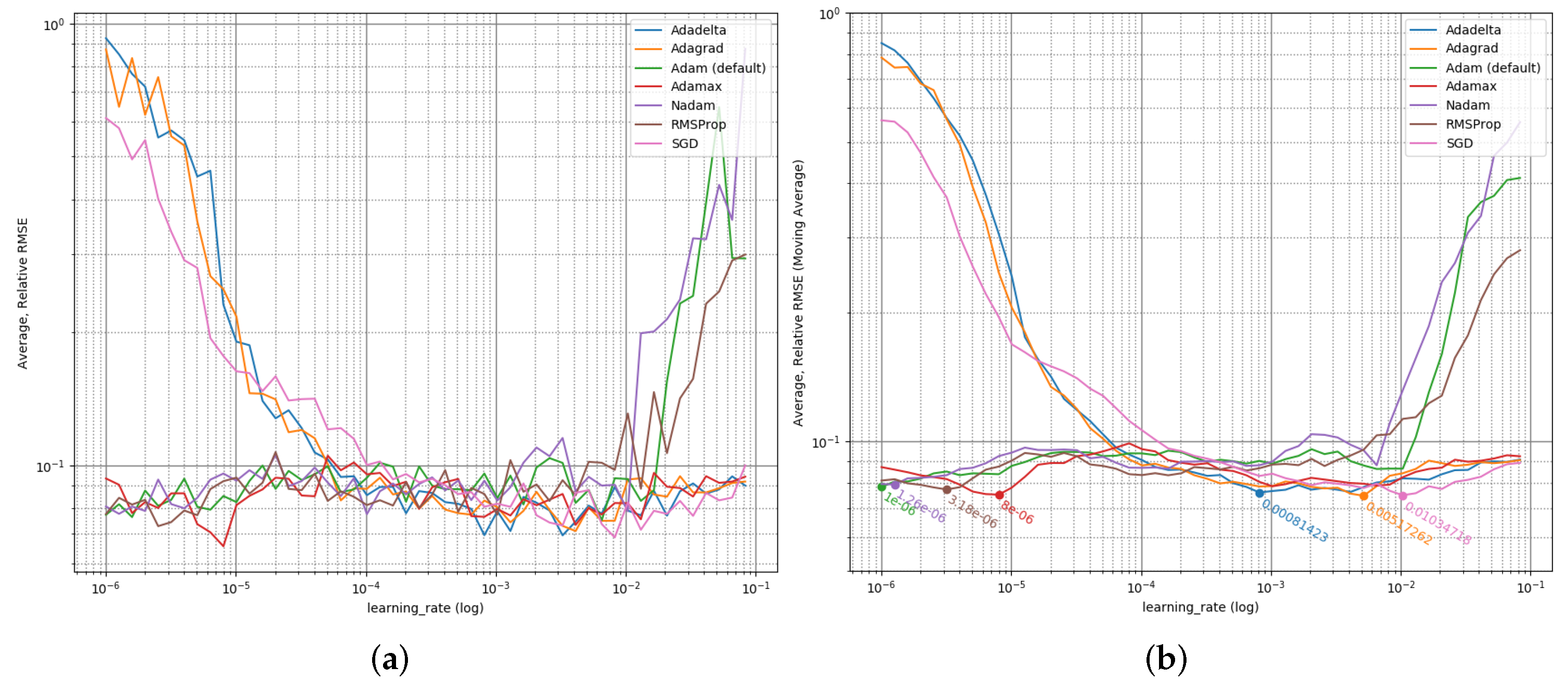
3.2.2. Learning Rate Optimization
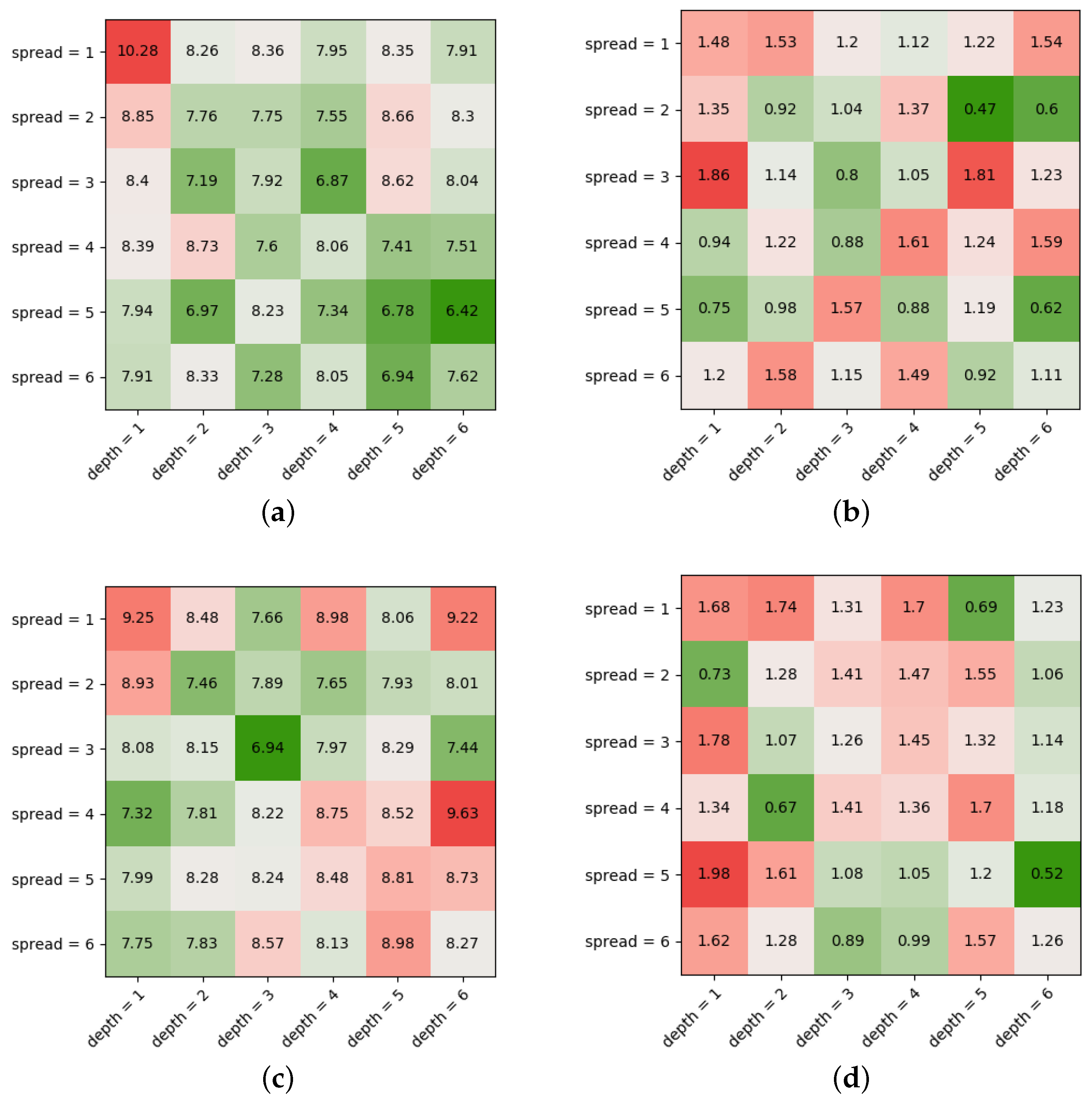
3.2.3. Model Optimization
3.2.4. Optimization Algorithm Comparison
3.2.5. Best Prediction Result
3.2.6. Sanity Check
3.3. Reliability Check
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, L.; Pan, S.; Wang, J.; Vasilakos, A.V. Machine learning on big data: Opportunities and challenges. Neurocomputing 2017, 237, 350–361. [Google Scholar] [CrossRef] [Green Version]
- L’heureux, A.; Grolinger, K.; Elyamany, H.F.; Capretz, M.A.M. Machine learning with big data: Challenges and approaches. IEEE Access 2017, 5, 7776–7797. [Google Scholar] [CrossRef]
- Franch, X.; Ayala, C.; López, L.; Martinez-Fernández, S.; Rodriguez, P.; Gómez, C.; Jedlitschka, A.; Oivo, M.; Partanen, J.; Räty, T.; et al. Data-driven requirements engineering in agile projects: The Q-rapids approach. In Proceedings of the 2017 IEEE 25th International Requirements Engineering Conference Workshops (REW), Lisbon, Portugal, 4–8 September 2017; pp. 411–414. [Google Scholar] [CrossRef] [Green Version]
- Chitnis, T.; Glanz, B.I.; Gonzalez, C.; Healy, B.C.; Saraceno, T.J.; Sattarnezhad, N.; Diaz-Cruz, C.; Polgar-Turcsanyi, M.; Tummala, S.; Bakshi, R.; et al. Quantifying neurologic disease using biosensor measurements in-clinic and in free-living settings in multiple sclerosis. Npj Digit. Med. 2019, 2, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reich, D.S.; Lucchinetti, C.F.; Calabresi, P.A. Multiple Sclerosis. N. Engl. J. Med. 2018, 378, 169–180. [Google Scholar] [CrossRef]
- Lindner, M.; Klotz, L.; Wiendl, H. Mechanisms underlying lesion development and lesion distribution in CNS autoimmunity. J. Neurochem. 2018, 146, 122–132. [Google Scholar] [CrossRef] [PubMed]
- Heesen, C.; Böhm, J.; Reich, C.; Kasper, J.; Goebel, M.; Gold, S.M. Patient perception of bodily functions in multiple sclerosis: Gait and visual function are the most valuable. Mult. Scler. J. 2008, 14, 988–991. [Google Scholar] [CrossRef] [PubMed]
- Cameron, M.H.; Wagner, J.M. Gait Abnormalities in Multiple Sclerosis: Pathogenesis, Evaluation, and Advances in Treatment. Curr. Neurol. Neurosci. Rep. 2011, 11, 507. [Google Scholar] [CrossRef]
- Sosnoff, J.J.; Sandroff, B.M.; Motl, R.W. Quantifying gait abnormalities in persons with multiple sclerosis with minimal disability. Gait Posture 2012, 36, 154–156. [Google Scholar] [CrossRef]
- Trentzsch, K.; Weidemann, M.L.; Torp, C.; Inojosa, H.; Scholz, M.; Haase, R.; Schriefer, D.; Akgün, K.; Ziemssen, T. The Dresden Protocol for Multidimensional Walking Assessment (DMWA) in Clinical Practice. Front. Neurosci. 2020, 14, 582046. [Google Scholar] [CrossRef]
- Créange, A.; Serre, I.; Levasseur, M.; Audry, D.; Nineb, D.; Boërio, D.; Moreau, T.; Maison, P. Walking capacities in multiple sclerosis measured by global positioning system odometer. Mult. Scler. 2007, 13, 220–223. [Google Scholar] [CrossRef]
- Donovan, K.; Lord, S.E.; McNaughton, H.K.; Weatherall, M. Mobility beyond the clinic: The effect of environment on gait and its measurement in community-ambulant stroke survivors. Clin. Rehabil. 2008, 22, 556–563. [Google Scholar] [CrossRef] [PubMed]
- Storm, F.A.; Cesareo, A.; Reni, G.; Biffi, E. Wearable inertial sensors to assess gait during the 6-minute walk test: A systematic review. Sensors 2020, 20, 2660. [Google Scholar] [CrossRef] [PubMed]
- Trentzsch, K.; Melzer, B.; Stölzer-Hutsch, H.; Haase, R.; Bartscht, P.; Meyer, P.; Ziemssen, T. Automated analysis of the two-minute walk test in clinical practice using accelerometer data. Brain Sci. 2021, 11, 1507. [Google Scholar] [CrossRef] [PubMed]
- ISO/IEC 25000:2014; Systems and Software Engineering: Systems and Software Quality Requirements and Evaluation (SQuaRE): Guide to SQuaRE. ISO/IEC: Geneva, Switzerland, 2014; p. 27.
- Fabijan, A.; Dmitriev, P.; Olsson, H.H.; Bosch, J. The evolution of continuous experimentation in software product development: From data to a data-driven organization at scale. In Proceedings of the 2017 IEEE/ACM 39th International Conference on Software Engineering (ICSE), Buenos Aires, Argentina, 20–28 May 2017; pp. 770–780. [Google Scholar] [CrossRef]
- Demšar, J.; Curk, T.; Erjavec, A.; Gorup, Č.; Hočevar, T.; Milutinovič, M.; Možina, M.; Polajnar, M.; Toplak, M.; Starič, A.; et al. Orange: Data mining toolbox in Python. J. Mach. Learn. Res. 2013, 14, 2349–2353. [Google Scholar]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef] [Green Version]
- Chatterjee, S.; Hadi, A.S. Regression Analysis by Example; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Kerschke, P.; Hoos, H.H.; Neumann, F.; Trautmann, H. Automated algorithm selection: Survey and perspectives. Evol. Comput. 2019, 27, 3–45. [Google Scholar] [CrossRef]
- Osisanwo, F.Y.; Akinsola, J.E.T.; Awodele, O.; Hinmikaiye, J.O.; Olakanmi, O.; Akinjobi, J. Supervised machine learning algorithms: Classification and comparison. Int. J. Comput. Trends Technol. (IJCTT) 2017, 48, 128–138. [Google Scholar]
- Fatima, M.; Pasha, M. Survey of machine learning algorithms for disease diagnostic. J. Intell. Learn. Syst. Appl. 2017, 9, 1. [Google Scholar] [CrossRef] [Green Version]
- Kather, J.N.; Pearson, A.T.; Halama, N.; Jäger, D.; Krause, J.; Loosen, S.H.; Marx, A.; Boor, P.; Tacke, F.; Neumann, U.P.; et al. Deep learning can predict microsatellite instability directly from histology in gastrointestinal cancer. Nat. Med. 2019, 25, 1054–1056. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design And Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283, ISBN 978-1-931971-33-1. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Feurer, M.; Hutter, F. Hyperparameter optimization. In Automated Machine Learning; Springer: Cham, Switzerland, 2019; pp. 3–33. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar] [CrossRef]
- Thornton, C.; Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Auto-WEKA: Combined selection and hyperparameter optimization of classification algorithms. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; pp. 847–855. [Google Scholar] [CrossRef]
- Da Silva, I.N.; Spatti, D.H.; Flauzino, R.A.; Liboni, L.H.B.; dos Reis Alves, S.F. Artificial neural network architectures and training processes. In Artificial Neural Networks; Springer: Cham, Switzerland, 2017; pp. 21–28. [Google Scholar] [CrossRef]
- Rojas-Dominguez, A.; Padierna, L.C.; Valadez, J.M.C.; Puga-Soberanes, H.J.; Fraire, H.J. Optimal hyper-parameter tuning of SVM classifiers with application to medical diagnosis. IEEE Access 2017, 6, 7164–7176. [Google Scholar] [CrossRef]
- Goldman, M.D.; Motl, R.W.; Scagnelli, J.; Pula, J.H.; Sosnoff, J.J.; Cadavid, D. Clinically meaningful performance benchmarks in MS:Timed 25-Foot Walk and the real world. Neurology 2013, 81, 1856–1863. [Google Scholar] [CrossRef] [PubMed]
- Andersen, L.K.; Knak, K.L.; Witting, N.; Vissing, J. Two- and 6-minute walk tests assess walking capability equally in neuromuscular diseases. Neurology 2016, 86, 442–445. [Google Scholar] [CrossRef] [PubMed]
- Retory, Y.; David, P.; Niedzialkowski, P.; de Picciotto, C.; Bonay, M.; Petitjean, M. Gait monitoring and walk distance estimation with an accelerometer during 6-minute walk test. Respir. Care 2019, 64, 923–930. [Google Scholar] [CrossRef]
- Vienne-Jumeau, A.; Oudre, L.; Moreau, A.; Quijoux, F.; Edmond, S.; Dandrieux, M.; Legendre, E.; Vidal, P.P.; Ricard, D. Personalized Template-Based Step Detection From Inertial Measurement Units Signals in Multiple Sclerosis. Front. Neurol. 2020, 11, 261. [Google Scholar] [CrossRef] [Green Version]
- Moon, Y.; McGinnis, R.S.; Seagers, K.; Motl, R.W.; Sheth, N.; Wright, J.A.; Ghaffari, R.; Sosnoff, J.J. Monitoring gait in multiple sclerosis with novel wearable motion sensors. PLoS ONE 2017, 12, e0171346. [Google Scholar] [CrossRef]
- Voigt, I.; Inojosa, H.; Dillenseger, A.; Haase, R.; Akgün, K.; Ziemssen, T. Digital twins for multiple sclerosis. Front. Immunol. 2021, 12, 1556. [Google Scholar] [CrossRef]


| Quality | Description |
|---|---|
| Prediction quality | The results should be as good as achievable |
| Reliability | A statement about the results’ steadiness should be available |
| Robustness | The results should be tolerant w.r.t. new or other data |
| Transparency, explainability | The prediction approach should be as transparent and explainable as possible w.r.t. the selected ML technologies |
| Recoverability | The setup, as well as the result should be recoverable |
| Accessibility | The prototype should be usable by physicians |
| Interoperability, modularity, reusability | The prototype should not be restricted to specific software technologies and designed in a way to allow functionality replacement or the adaption to other (medical) use cases |
| Leanness | The prototype should base on a small specific code base to reduce dependencies and achieve the result as fast as possible |
| Aspect | Description |
|---|---|
| Technical environment | PC with sufficient hardware; no grid of GPU or HPC system |
| Data format requirements | Table based, e.g., CSV format |
| Data import | Use case specific; manual import; standard normalization and error handling |
| ML technology | TensorFlow [24]; no hyperparameter optimization framework |
| Model | DFFNN [29] of different shapes as regressor |
| Quality metrics | based on [19], see Formula (1); SD of |
| Sanity check | , see Formula (2) |
| Result optimization objective | Minimize , respectively |
| Optimization space | , , , |
| Factor | Actions |
|---|---|
| nepoch = 1000 | Small initial LR (<default) test all ML optimization algorithms fixed: LR, fModelSpread, nModelDepth |
| LR = 10−6..10−1 (exp. step size) | Increase LR step-wisely test all ML optimization algorithms with different LR fixed: nepoch, fModelSpread, nModelDepth |
| fModelSpread = 1..6 nModelDepth = 1..6 | Increase fModelSpread and fModelSpread step-wisely test all ML optimization algorithms for different model sizes fixed: nepoch, LR |
| talg | Test all ML optimization algorithms fixed: nepoch, LR, fModelSpread, nModelDepth |
| Feature | Reverse Weight |
|---|---|
| Lower Limb - Cadence R (steps/min) | |
| Lower Limb - Gait Speed R (m/s) | |
| Lower Limb - Gait Speed L (m/s) | |
| Lower Limb - Stride Length L (m) | |
| Lower Limb - Cadence L (steps/min) | |
| … | … |
| Upper Limb - Arm Range of Motion L (degrees) | |
| Lower Limb - Step Duration L (s) | |
| Lower Limb - Swing L (%GCT) | |
| Lower Limb - Terminal Double Support L | |
| Lower Limb - Double Support L (%GCT) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wendt, K.; Trentzsch, K.; Haase, R.; Weidemann, M.L.; Weidemann, R.; Aßmann, U.; Ziemssen, T. Transparent Quality Optimization for Machine Learning-Based Regression in Neurology. J. Pers. Med. 2022, 12, 908. https://doi.org/10.3390/jpm12060908
Wendt K, Trentzsch K, Haase R, Weidemann ML, Weidemann R, Aßmann U, Ziemssen T. Transparent Quality Optimization for Machine Learning-Based Regression in Neurology. Journal of Personalized Medicine. 2022; 12(6):908. https://doi.org/10.3390/jpm12060908
Chicago/Turabian StyleWendt, Karsten, Katrin Trentzsch, Rocco Haase, Marie Luise Weidemann, Robin Weidemann, Uwe Aßmann, and Tjalf Ziemssen. 2022. "Transparent Quality Optimization for Machine Learning-Based Regression in Neurology" Journal of Personalized Medicine 12, no. 6: 908. https://doi.org/10.3390/jpm12060908
APA StyleWendt, K., Trentzsch, K., Haase, R., Weidemann, M. L., Weidemann, R., Aßmann, U., & Ziemssen, T. (2022). Transparent Quality Optimization for Machine Learning-Based Regression in Neurology. Journal of Personalized Medicine, 12(6), 908. https://doi.org/10.3390/jpm12060908








