A PDE Model of Breast Tumor Progression in MMTV-PyMT Mice
Abstract
1. Introduction
2. Materials and Methods
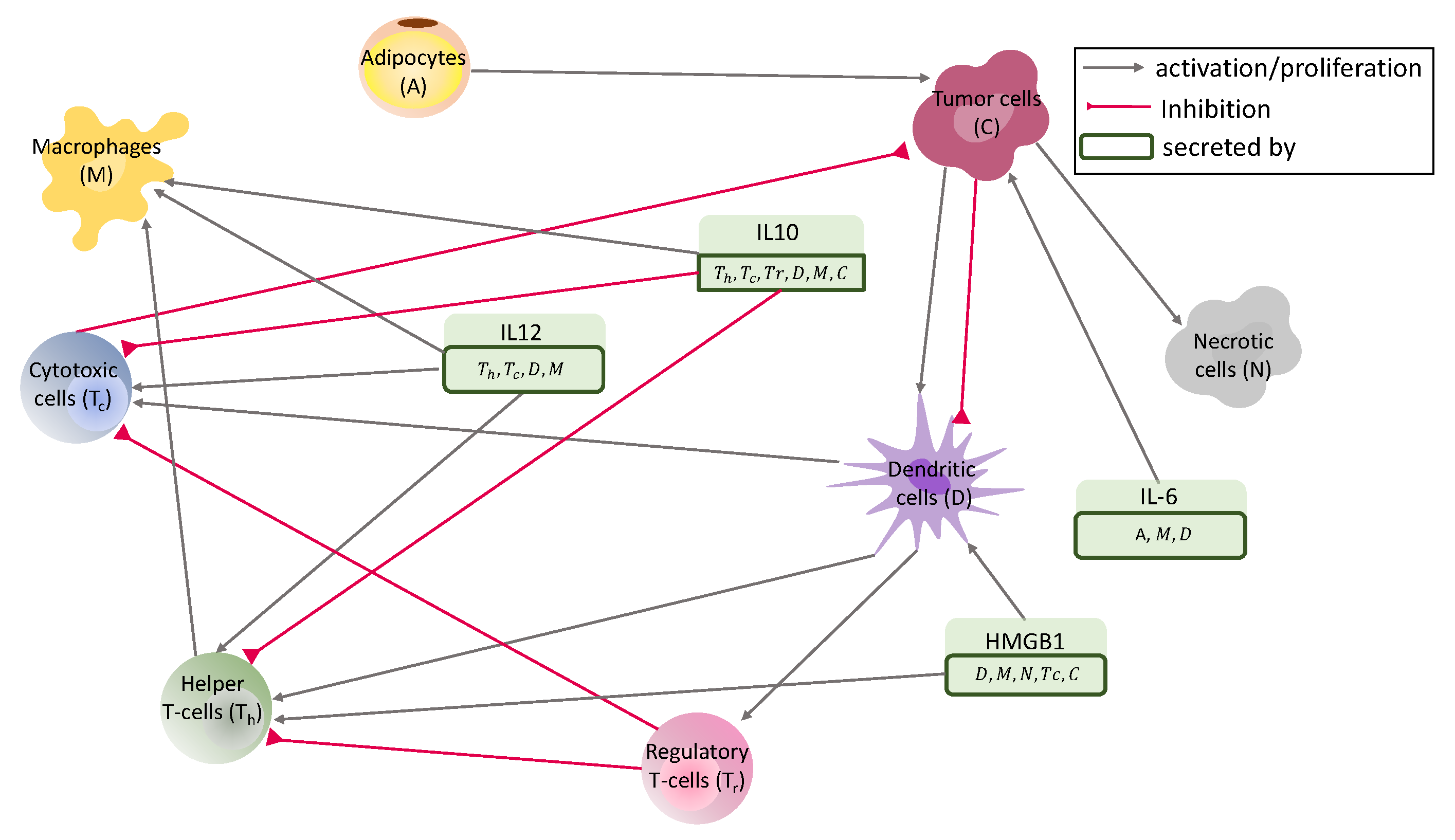
2.1. PDE System
Boundary Conditions
2.2. Mechanical Model
2.3. Data of the Model
2.3.1. Mouse Model and Experiments
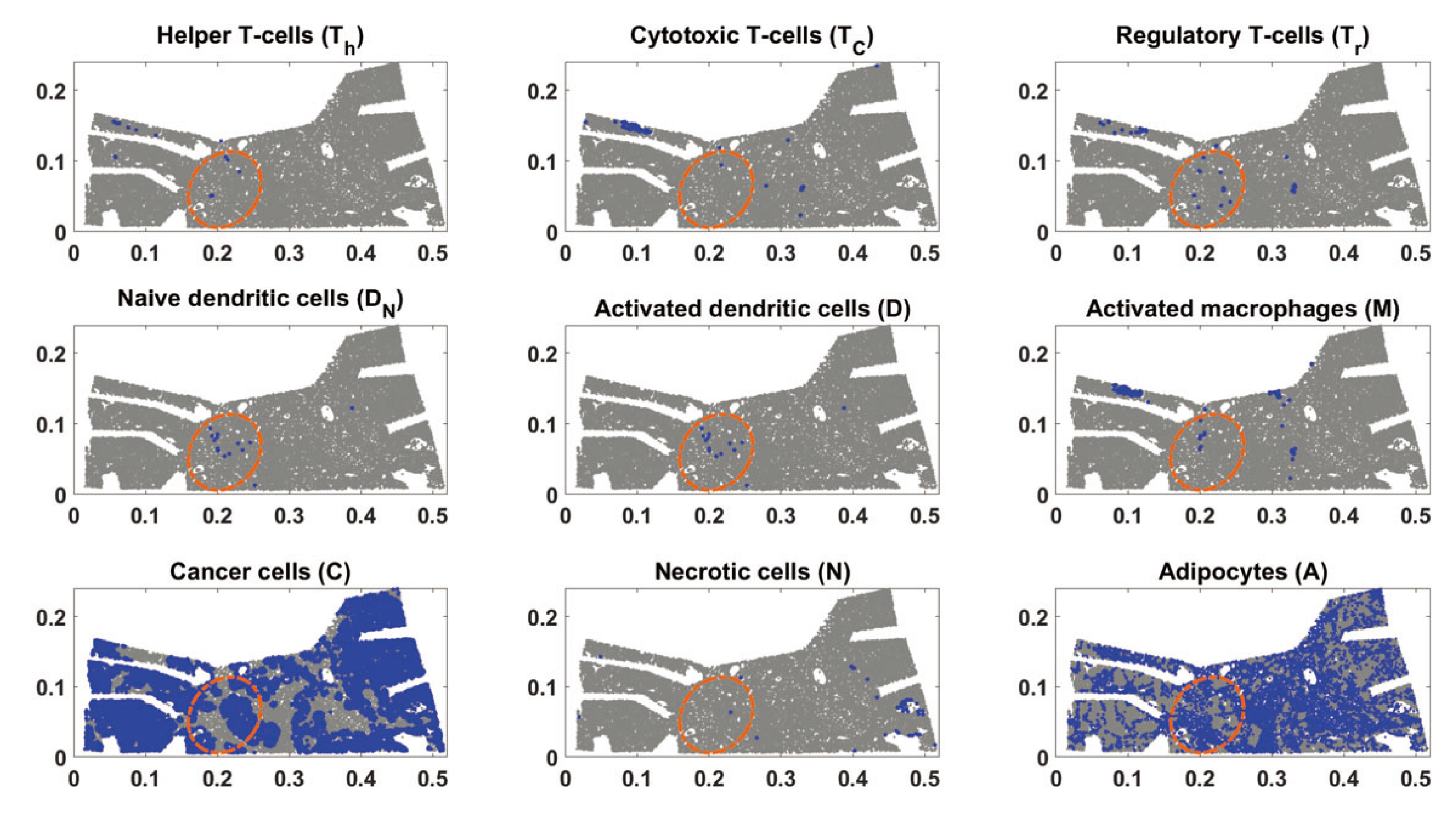
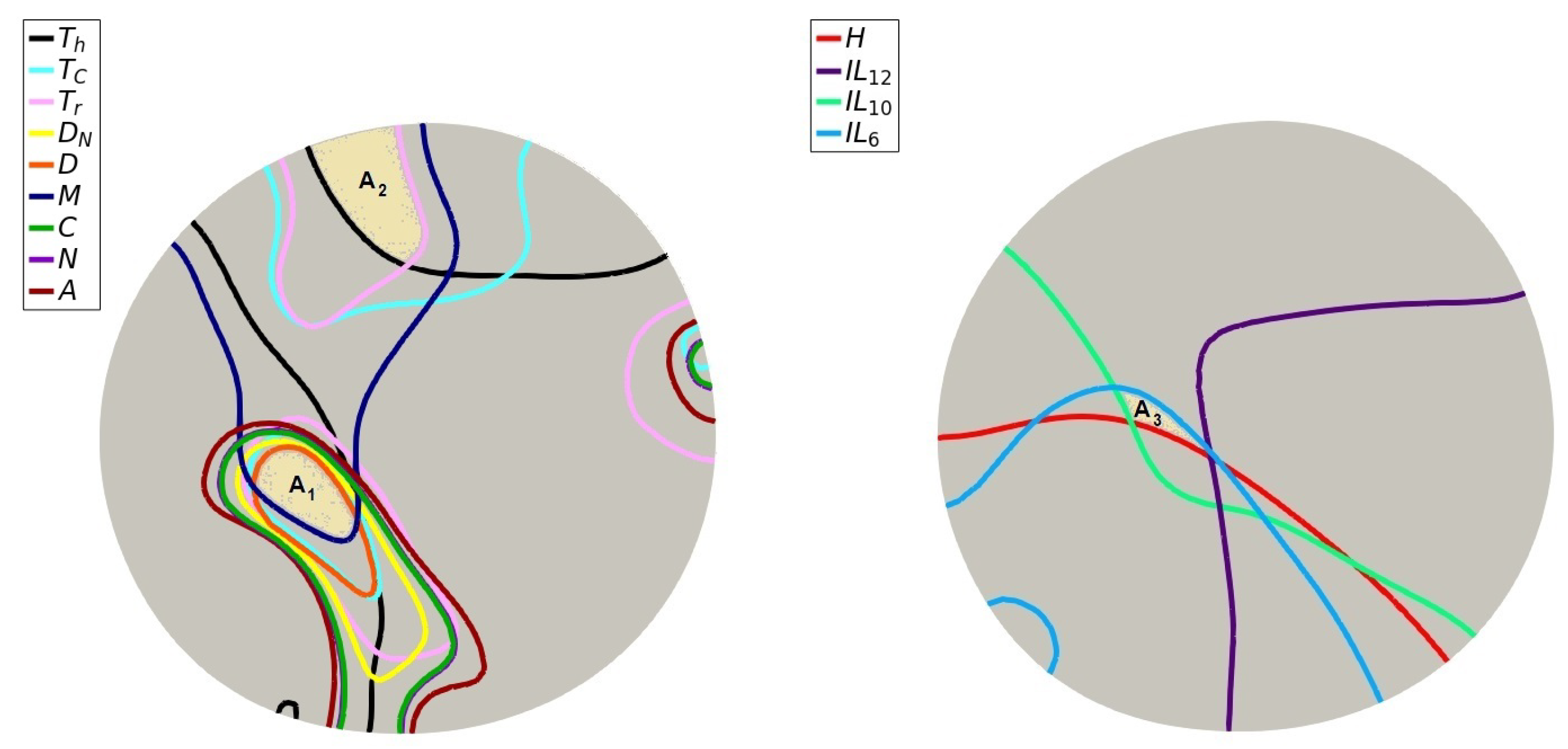
2.3.2. Preparation of Initial Conditions
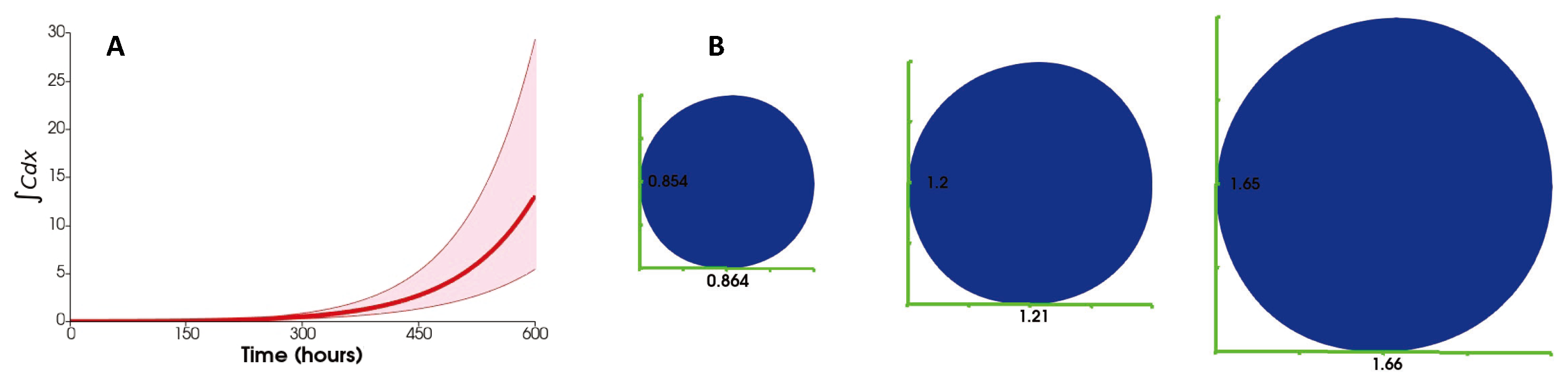
3. Results
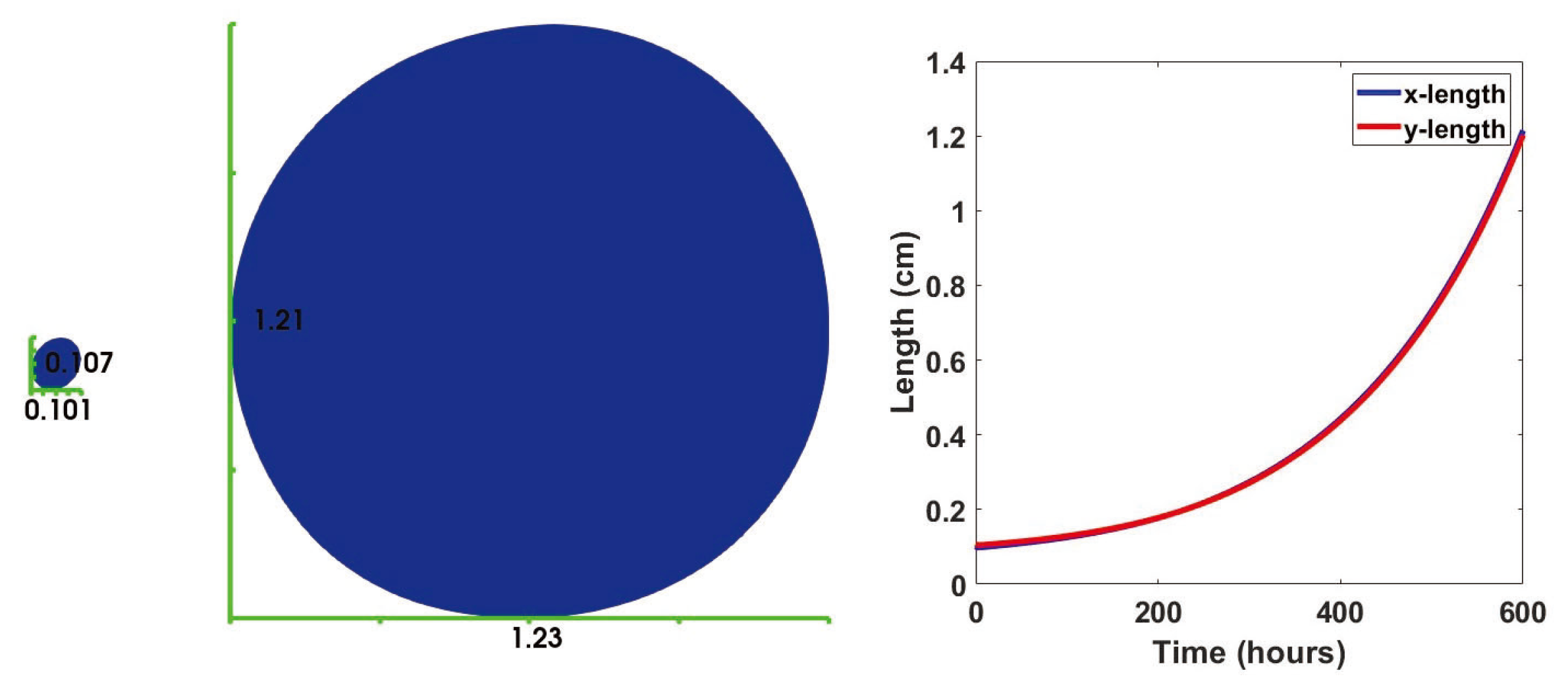
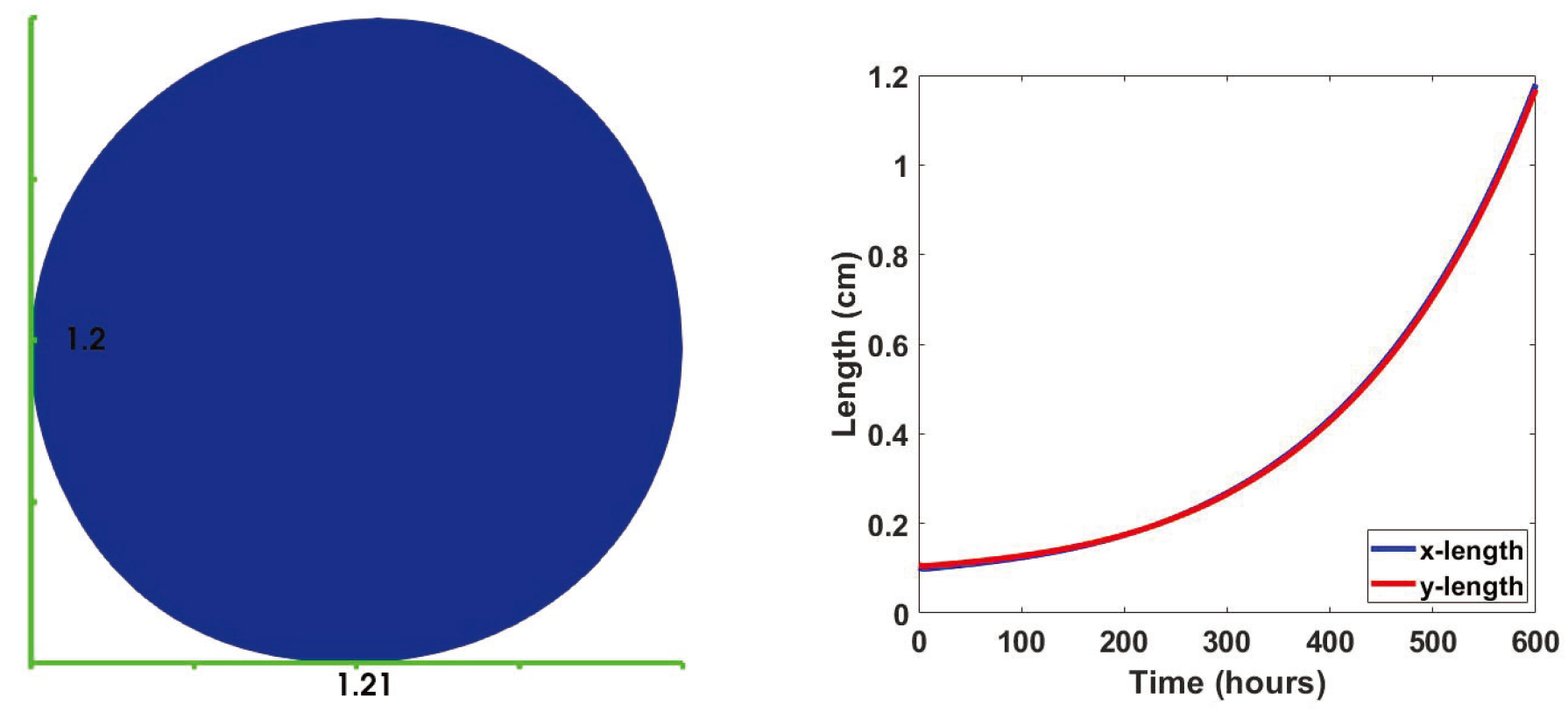
3.1. No Influx
3.2. Immune Cell Influx
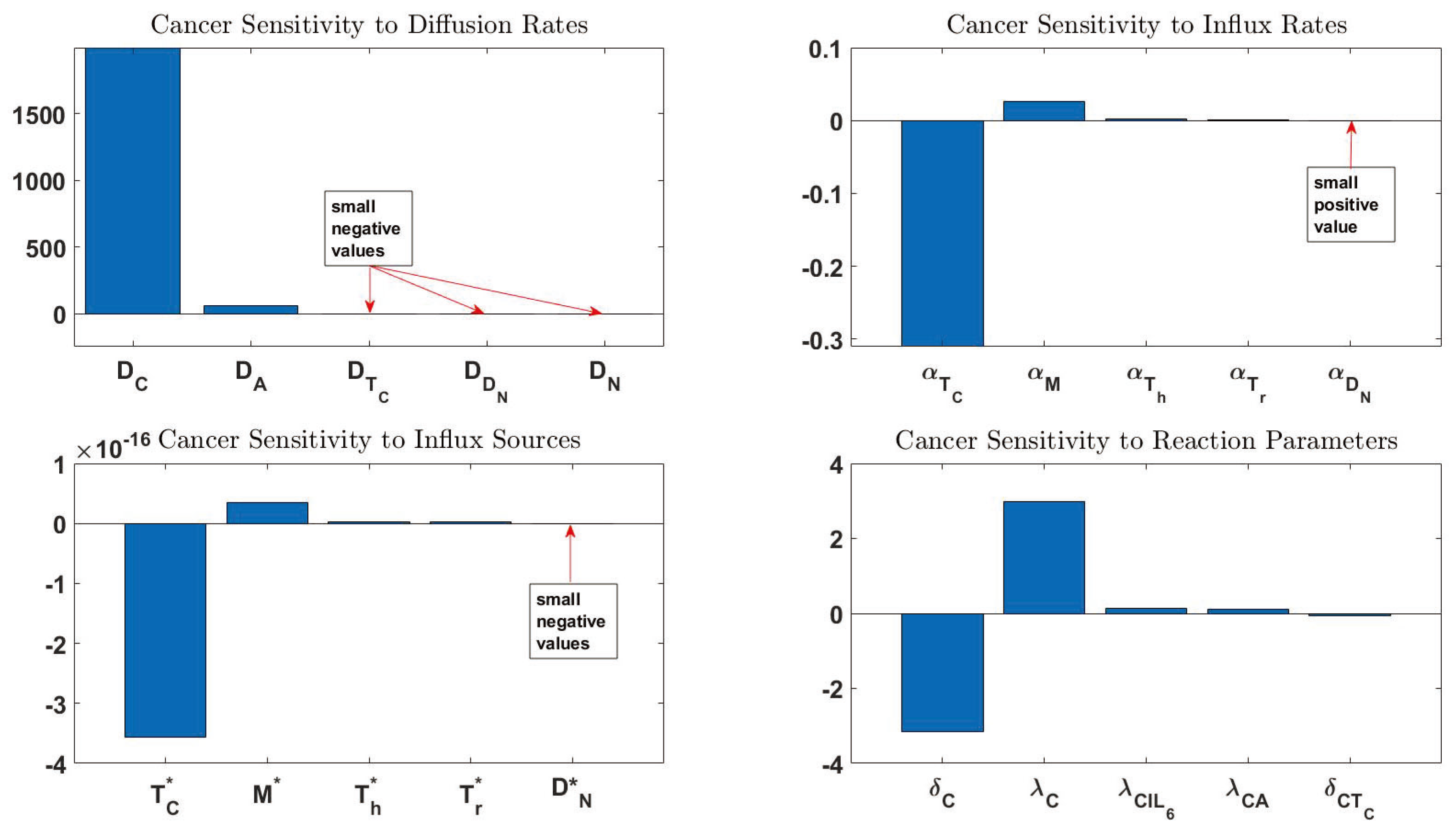
3.3. Sensitivity Analysis
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
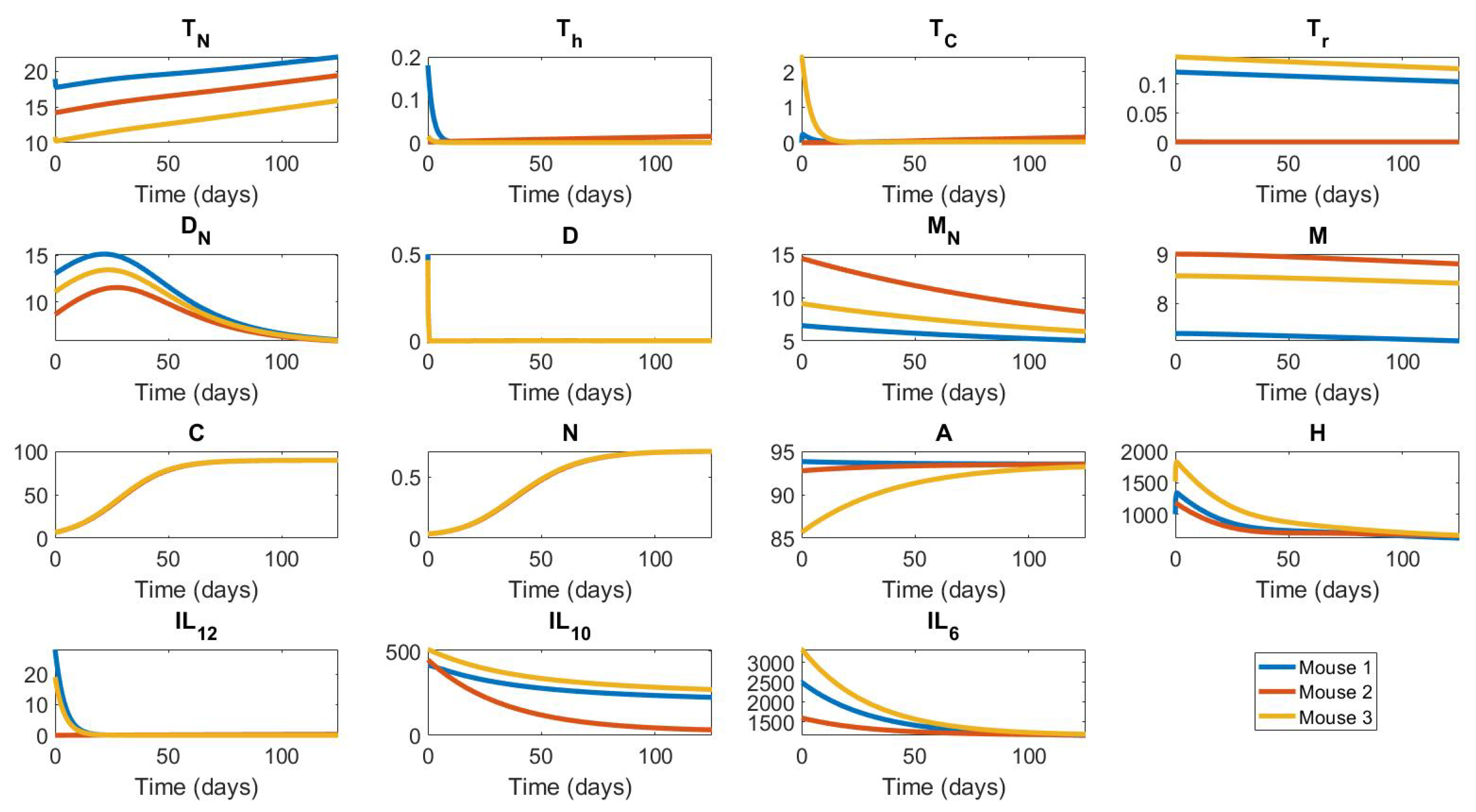
Appendix B
Appendix C
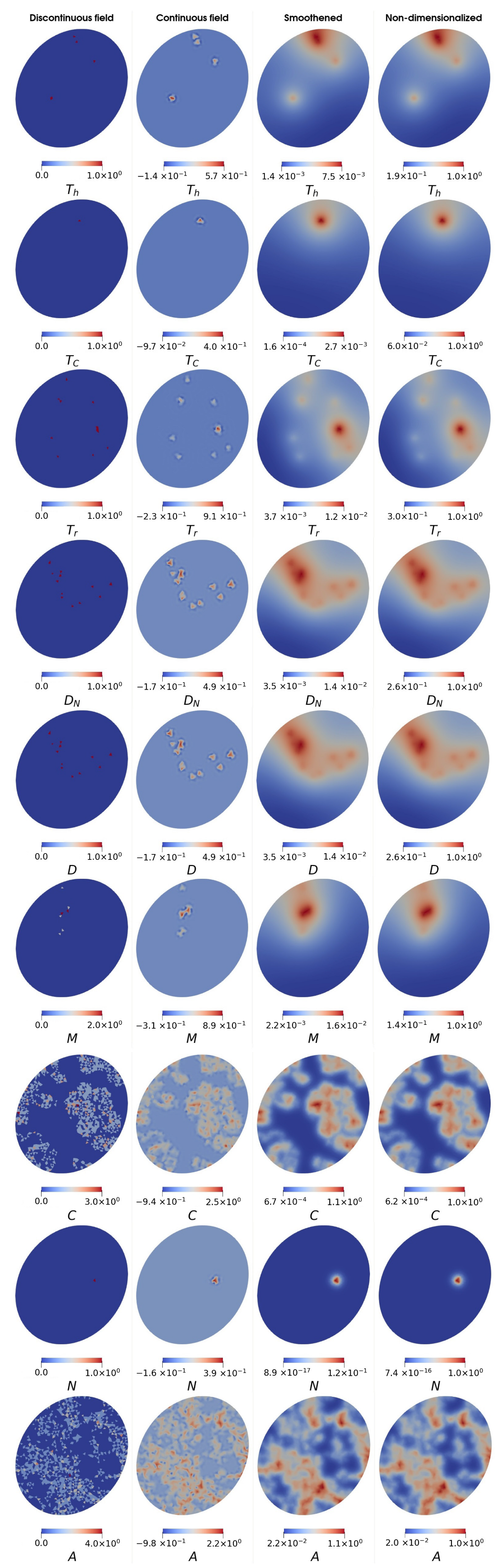
Appendix D
Appendix D.1. Weak Formulation and Discretization
Appendix D.2. Simulation
Appendix E
| Order | Notation | Sensitivity | Definition | Order | Notation | Sensitivity | Definition |
|---|---|---|---|---|---|---|---|
| 1 | 2242.835 | Diffusion coefficient of C | 44 | − | Death rate of | ||
| 2 | 56.46447 | Diffusion coefficient of A | 45 | Activation rate of M by | |||
| 3 | −3.16066 | Death rate of C | 46 | − | Independent production rate of | ||
| 4 | 2.989047 | Proliferation rate of C | 47 | Death rate of | |||
| 5 | −0.31011 | Influx rate of | 48 | Activation rate of by H | |||
| 6 | −0.2628 | Diffusion coefficient of | 49 | − | Activation rate of D by C | ||
| 7 | 0.138431 | Proliferation rate of C by | 50 | Activation rate of by | |||
| 8 | 0.107539 | Proliferation rate of C by A | 51 | Independent production rate of | |||
| 9 | −0.06665 | Inhibition rate of C by | 52 | − | Activation rate of by D | ||
| 10 | −0.03611 | Death rate of A | 53 | Death rate of | |||
| 11 | 0.03531 | Proliferation rate of A | 54 | Production rate of by D | |||
| 12 | 0.025664 | Influx rate of M | 55 | − | Inhibition rate of by | ||
| 13 | −0.01152 | Decay rate of | 56 | − | Inhibition rate of by | ||
| 14 | 0.009239 | Production rate of by A | 57 | − | Activation rate of D by H | ||
| 15 | 0.007813 | Production rate of by M | 58 | Carrying capacity of A | |||
| 16 | 0.002154 | Influx rate of | 59 | − | Death rate of | ||
| 17 | 0.001508 | Death rate of | 60 | − | Production rate of by M | ||
| 18 | 0.001441 | Influx rate of | 61 | Decay rate of | |||
| 19 | −0.00094 | Diffusion coefficient of | 62 | − | Production rate of by | ||
| 20 | −0.00094 | Diffusion coefficient of N | 63 | − | Production rate of by | ||
| 21 | 0.000541 | Carrying capacity of C | 64 | Diffusion coefficient of | |||
| 22 | −0.00044 | Diffusion coefficient of | 65 | Activation rate of by D | |||
| 23 | −0.00039 | Decay rate of | 66 | Activation rate of by D | |||
| 24 | 0.000386 | Production rate of by C | 67 | − | Death rate of D | ||
| 25 | −0.00035 | Activation rate of by | 68 | − | Decay rate of H | ||
| 26 | −0.00034 | Diffusion coefficient of M | 69 | Production rate of H by M | |||
| 27 | 0.000319 | Production rate of by | 70 | Production rate of H by | |||
| 28 | −0.00029 | Death rate of M | 71 | Production rate of H by C | |||
| 29 | 0.00024 | Production rate of by M | 72 | Activation rate of D by C | |||
| 30 | 0.00018 | Production rate of by | 73 | − | Production rate of by D | ||
| 31 | 0.000153 | Production rate of IL10 by | 74 | Production rate of H by N | |||
| 32 | −0.00015 | Diffusion coefficient of | 75 | Production rate of H by D | |||
| 33 | 0.000126 | Diffusion coefficient of | 76 | Death rate of N | |||
| 34 | − | Independent production rate of | 77 | Diffusion coefficient of H | |||
| 35 | Influx rate of | 78 | C to N conversion fraction | ||||
| 36 | Inhibition rate of by | 79 | − | influx source | |||
| 37 | Diffusion coefficient of D | 80 | M influx source | ||||
| 38 | Inhibition rate of by | 81 | influx source | ||||
| 39 | Production rate of by D | 82 | influx source | ||||
| 40 | − | Diffusion coefficient of | 83 | − | influx source | ||
| 41 | Activation rate of M by | ||||||
| 42 | − | Death rate of | |||||
| 43 | Activation rate of M by |
References
- Harbeck, N.; Penault-Llorca, F.; Cortes, J.; Gnant, M.; Houssami, N.; Poortmans, P.; Ruddy, K.; Tsang, J.; Cardoso, F. Breast cancer. Nat. Rev. Dis. Prim. 2019, 5, 66. [Google Scholar] [CrossRef] [PubMed]
- Ferlay, J.; Soerjomataram, I.; Dikshit, R.; Eser, S.; Mathers, C.; Rebelo, M.; Parkin, D.M.; Forman, D.; Bray, F. Cancer incidence and mortality worldwide: Sources, methods and major patterns in GLOBOCAN 2012. Int. J. Cancer 2015, 136, E359–E386. [Google Scholar] [CrossRef] [PubMed]
- Siegel, R.L.; Miller, K.D.; Fuchs, H.E.; Jemal, A. Cancer statistics, 2021. CA Cancer J. Clin. 2021, 71, 7–33. [Google Scholar] [CrossRef] [PubMed]
- Waks, A.G.; Winer, E.P. Breast cancer treatment: A review. JAMA 2019, 321, 288–300. [Google Scholar] [CrossRef] [PubMed]
- Maughan, K.L.; Lutterbie, M.A.; Ham, P. Treatment of breast cancer. Am. Fam. Phys. 2010, 81, 1339–1346. [Google Scholar]
- Joyce, J.A. Therapeutic targeting of the tumor microenvironment. Cancer Cell 2005, 7, 513–520. [Google Scholar] [CrossRef]
- Meenakshi Upreti, A.J.; Sethi, P. Tumor microenvironment and nanotherapeutics. Transl. Cancer Res. 2013, 2, 309. [Google Scholar]
- Natrajan, R.; Sailem, H.; Mardakheh, F.K.; Arias Garcia, M.; Tape, C.J.; Dowsett, M.; Bakal, C.; Yuan, Y. Microenvironmental heterogeneity parallels breast cancer progression: A histology–genomic integration analysis. PLoS Med. 2016, 13, e1001961. [Google Scholar] [CrossRef]
- Yuan, Y. Spatial heterogeneity in the tumor microenvironment. Cold Spring Harb. Perspect. Med. 2016, 6, a026583. [Google Scholar] [CrossRef]
- Burlingame, E.A.; Eng, J.; Thibault, G.; Chin, K.; Gray, J.W.; Chang, Y.H. Toward reproducible, scalable, and robust data analysis across multiplex tissue imaging platforms. Cell Rep. Methods 2021, 1, 100053. [Google Scholar] [CrossRef]
- Parker, T.M.; Gupta, K.; Palma, A.M.; Yekelchyk, M.; Fisher, P.B.; Grossman, S.R.; Won, K.J.; Madan, E.; Moreno, E.; Gogna, R. Cell competition in intratumoral and tumor microenvironment interactions. EMBO J. 2021, 40, e107271. [Google Scholar] [CrossRef] [PubMed]
- Lyssiotis, C.A.; Kimmelman, A.C. Metabolic interactions in the tumor microenvironment. Trends Cell Biol. 2017, 27, 863–875. [Google Scholar] [CrossRef] [PubMed]
- Lampreht Tratar, U.; Horvat, S.; Cemazar, M. Transgenic mouse models in cancer research. Front. Oncol. 2018, 8, 268. [Google Scholar] [CrossRef] [PubMed]
- Hursting, S.D.; Slaga, T.J.; Fischer, S.M.; DiGiovanni, J.; Phang, J.M. Mechanism-based cancer prevention approaches: Targets, examples, and the use of transgenic mice. J. Natl. Cancer Inst. 1999, 91, 215–225. [Google Scholar] [CrossRef] [PubMed]
- Hurwitz, A.A.; Foster, B.A.; Kwon, E.D.; Truong, T.; Choi, E.M.; Greenberg, N.M.; Burg, M.B.; Allison, J.P. Combination immunotherapy of primary prostate cancer in a transgenic mouse model using CTLA-4 blockade. Cancer Res. 2000, 60, 2444–2448. [Google Scholar] [PubMed]
- Gingrich, J.; Greenberg, N. A transgenic mouse prostate cancer model. Toxicol. Pathol. 1996, 24, 502–504. [Google Scholar] [CrossRef]
- Korac-Prlic, J.; Degoricija, M.; Vilović, K.; Haupt, B.; Ivanišević, T.; Franković, L.; Grivennikov, S.; Terzić, J. Targeting Stat3 signaling impairs the progression of bladder cancer in a mouse model. Cancer Lett. 2020, 490, 89–99. [Google Scholar] [CrossRef]
- Floc’h, N.; Kinkade, C.W.; Kobayashi, T.; Aytes, A.; Lefebvre, C.; Mitrofanova, A.; Cardiff, R.D.; Califano, A.; Shen, M.M.; Abate-Shen, C. Dual targeting of the Akt/mTOR signaling pathway inhibits castration-resistant prostate cancer in a genetically engineered mouse model. Cancer Res. 2012, 72, 4483–4493. [Google Scholar] [CrossRef]
- Zhao, H.; Richardson, R.; Talebloo, N.; Mukherjee, P.; Wang, P.; Moore, A. uMUC1-targeting magnetic resonance imaging of therapeutic response in an orthotropic mouse model of colon cancer. Mol. Imaging Biol. 2019, 21, 852–860. [Google Scholar] [CrossRef]
- Zeng, H.; Wei, W.; Xu, X. Chemokine (CXC motif) receptor 4 RNA interference inhibits bone metastasis in breast cancer. Oncol. Lett. 2014, 8, 77–81. [Google Scholar] [CrossRef][Green Version]
- Chang, A.; Le, C.P.; Walker, A.K.; Creed, S.J.; Pon, C.K.; Albold, S.; Carroll, D.; Halls, M.L.; Lane, J.R.; Riedel, B.; et al. β2-Adrenoceptors on tumor cells play a critical role in stress-enhanced metastasis in a mouse model of breast cancer. Brain Behav. Immun. 2016, 57, 106–115. [Google Scholar] [CrossRef] [PubMed]
- Ling, X.; Arlinghaus, R.B. Knockdown of STAT3 expression by RNA interference inhibits the induction of breast tumors in immunocompetent mice. Cancer Res. 2005, 65, 2532–2536. [Google Scholar] [CrossRef] [PubMed]
- Welm, A.L.; Sneddon, J.B.; Taylor, C.; Nuyten, D.S.; van de Vijver, M.J.; Hasegawa, B.H.; Bishop, J.M. The macrophage-stimulating protein pathway promotes metastasis in a mouse model for breast cancer and predicts poor prognosis in humans. Proc. Natl. Acad. Sci. USA 2007, 104, 7570–7575. [Google Scholar] [CrossRef] [PubMed]
- Pollard, J.W. Macrophages define the invasive microenvironment in breast cancer. J. Leukoc. Biol. 2008, 84, 623–630. [Google Scholar] [CrossRef] [PubMed]
- Kitamura, T.; Doughty-Shenton, D.; Cassetta, L.; Fragkogianni, S.; Brownlie, D.; Kato, Y.; Carragher, N.; Pollard, J.W. Monocytes differentiate to immune suppressive precursors of metastasis-associated macrophages in mouse models of metastatic breast cancer. Front. Immunol. 2018, 8, 2004. [Google Scholar] [CrossRef] [PubMed]
- Coffelt, S.B.; Kersten, K.; Doornebal, C.W.; Weiden, J.; Vrijland, K.; Hau, C.S.; Verstegen, N.J.; Ciampricotti, M.; Hawinkels, L.J.; Jonkers, J.; et al. IL-17-producing γδ T cells and neutrophils conspire to promote breast cancer metastasis. Nature 2015, 522, 345–348. [Google Scholar] [CrossRef]
- Lin, E.Y.; Li, J.F.; Gnatovskiy, L.; Deng, Y.; Zhu, L.; Grzesik, D.A.; Qian, H.; Xue, X.N.; Pollard, J.W. Macrophages regulate the angiogenic switch in a mouse model of breast cancer. Cancer Res. 2006, 66, 11238–11246. [Google Scholar] [CrossRef]
- He, H.; Wang, X.; Chen, J.; Sun, L.; Sun, H.; Xie, K. High-mobility group box 1 (HMGB1) promotes angiogenesis and tumor migration by regulating hypoxia-inducible factor 1 (HIF-1α) expression via the phosphatidylinositol 3-kinase (PI3K)/AKT signaling pathway in breast cancer cells. Med. Sci. Monit. Int. Med. J. Exp. Clin. Res. 2019, 25, 2352. [Google Scholar] [CrossRef]
- Lewis, B.C.; Klimstra, D.S.; Varmus, H.E. The c-myc and PyMT oncogenes induce different tumor types in a somatic mouse model for pancreatic cancer. Genes Dev. 2003, 17, 3127–3138. [Google Scholar] [CrossRef]
- Lin, E.Y.; Jones, J.G.; Li, P.; Zhu, L.; Whitney, K.D.; Muller, W.J.; Pollard, J.W. Progression to malignancy in the polyoma middle T oncoprotein mouse breast cancer model provides a reliable model for human diseases. Am. J. Pathol. 2003, 163, 2113–2126. [Google Scholar] [CrossRef]
- Boyle, S.T.; Faulkner, J.W.; McColl, S.R.; Kochetkova, M. The chemokine receptor CCR6 facilitates the onset of mammary neoplasia in the MMTV-PyMT mouse model via recruitment of tumor-promoting macrophages. Mol. Cancer 2015, 14, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Hollern, D.P.; Honeysett, J.; Cardiff, R.D.; Andrechek, E.R. The E2F transcription factors regulate tumor development and metastasis in a mouse model of metastatic breast cancer. Mol. Cell. Biol. 2014, 34, 3229–3243. [Google Scholar] [CrossRef] [PubMed]
- Cowen, S.; McLaughlin, S.L.; Hobbs, G.; Coad, J.; Martin, K.H.; Olfert, I.M.; Vona-Davis, L. High-fat, high-calorie diet enhances mammary carcinogenesis and local inflammation in MMTV-PyMT mouse model of breast cancer. Cancers 2015, 7, 1125–1142. [Google Scholar] [CrossRef] [PubMed]
- Sancho-Araiz, A.; Mangas-Sanjuan, V.; F Trocóniz, I. The Role of Mathematical Models in Immuno-Oncology: Challenges and Future Perspectives. Pharmaceutics 2021, 13, 1016. [Google Scholar] [CrossRef] [PubMed]
- de Pillis, L.G.; Gu, W.; Radunskaya, A.E. Mixed immunotherapy and chemotherapy of tumors: Modeling, applications and biological interpretations. J. Theor. Biol. 2006, 238, 841–862. [Google Scholar] [CrossRef]
- Kareva, I.; Berezovskaya, F. Cancer immunoediting: A process driven by metabolic competition as a predator–prey–shared resource type model. J. Theor. Biol. 2015, 380, 463–472. [Google Scholar] [CrossRef]
- Renardy, M.; Jilkine, A.; Shahriyari, L.; Chou, C.S. Control of cell fraction and population recovery during tissue regeneration in stem cell lineages. J. Theor. Biol. 2018, 445, 33–50. [Google Scholar] [CrossRef]
- Mehdizadeh, R.; Shariatpanahi, S.P.; Goliaei, B.; Peyvandi, S.; Rüegg, C. Dormant Tumor Cell Vaccination: A Mathematical Model of Immunological Dormancy in Triple-Negative Breast Cancer. Cancers 2021, 13, 245. [Google Scholar] [CrossRef]
- Oke, S.I.; Matadi, M.B.; Xulu, S.S. Optimal control analysis of a mathematical model for breast cancer. Math. Comput. Appl. 2018, 23, 21. [Google Scholar]
- Mohammad Mirzaei, N.; Su, S.; Sofia, D.; Hegarty, M.; Abdel-Rahman, M.H.; Asadpoure, A.; Cebulla, C.M.; Chang, Y.H.; Hao, W.; Jackson, P.R.; et al. A Mathematical Model of Breast Tumor Progression Based on Immune Infiltration. J. Pers. Med. 2021, 11, 1031. [Google Scholar] [CrossRef]
- Shahriyari, L.; Komarova, N.L. The role of the bi-compartmental stem cell niche in delaying cancer. Phys. Biol. 2015, 12, 055001. [Google Scholar] [CrossRef] [PubMed]
- Shahriyari, L.; Mahdipour-Shirayeh, A. Modeling dynamics of mutants in heterogeneous stem cell niche. Phys. Biol. 2017, 14. [Google Scholar] [CrossRef] [PubMed]
- Shahriyari, L. Cell dynamics in tumour environment after treatments. J. R. Soc. Interface 2017, 14, 20160977. [Google Scholar] [CrossRef]
- Kirshtein, A.; Akbarinejad, S.; Hao, W.; Le, T.; Su, S.; Aronow, R.A.; Shahriyari, L. Data Driven Mathematical Model of Colon Cancer Progression. J. Clin. Med. 2020, 9, 3947. [Google Scholar] [CrossRef]
- Budithi, A.; Su, S.; Kirshtein, A.; Shahriyari, L. Data Driven Mathematical Model of FOLFIRI Treatment for Colon Cancer. Cancers 2021, 13, 2632. [Google Scholar] [CrossRef] [PubMed]
- Le, T.; Su, S.; Kirshtein, A.; Shahriyari, L. Data-Driven Mathematical Model of Osteosarcoma. Cancers 2021, 13, 2367. [Google Scholar] [CrossRef]
- Le, T.; Su, S.; Shahriyari, L. Investigating Optimal Chemotherapy Options for Osteosarcoma Patients through a Mathematical Model. Cells 2021, 10, 2009. [Google Scholar] [CrossRef]
- Hao, W.; Friedman, A. The LDL-HDL profile determines the risk of atherosclerosis: A mathematical model. PLoS ONE 2014, 9, e90497. [Google Scholar]
- Mohammad Mirzaei, N.; Weintraub, W.S.; Fok, P.W. An integrated approach to simulating the vulnerable atherosclerotic plaque. Am. J. Physiol.-Heart Circ. Physiol. 2020, 319, H835–H846. [Google Scholar] [CrossRef]
- Hao, W.; Friedman, A. Mathematical model on Alzheimer’s disease. BMC Syst. Biol. 2016, 10, 108. [Google Scholar] [CrossRef]
- Weickenmeier, J.; Jucker, M.; Goriely, A.; Kuhl, E. A physics-based model explains the prion-like features of neurodegeneration in Alzheimer’s disease, Parkinson’s disease, and amyotrophic lateral sclerosis. J. Mech. Phys. Solids 2019, 124, 264–281. [Google Scholar] [CrossRef]
- Viguerie, A.; Veneziani, A.; Lorenzo, G.; Baroli, D.; Aretz-Nellesen, N.; Patton, A.; Yankeelov, T.E.; Reali, A.; Hughes, T.J.; Auricchio, F. Diffusion–reaction compartmental models formulated in a continuum mechanics framework: Application to COVID-19, mathematical analysis, and numerical study. Comput. Mech. 2020, 66, 1131–1152. [Google Scholar] [CrossRef] [PubMed]
- Iwata, K.; Kawasaki, K.; Shigesada, N. A dynamical model for the growth and size distribution of multiple metastatic tumors. J. Theor. Biol. 2000, 203, 177–186. [Google Scholar] [CrossRef]
- Barbolosi, D.; Benabdallah, A.; Hubert, F.; Verga, F. Mathematical and numerical analysis for a model of growing metastatic tumors. Math. Biosci. 2009, 218, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Friedman, A. Interaction of tumor with its micro-environment: A mathematical model. Bull. Math. Biol. 2010, 72, 1029–1068. [Google Scholar] [CrossRef]
- Friedman, A.; Jain, H.V. A partial differential equation model of metastasized prostatic cancer. Math. Biosci. Eng. 2013, 10, 591. [Google Scholar]
- Liu, J.; Wang, X.S. Numerical optimal control of a size-structured PDE model for metastatic cancer treatment. Math. Biosci. 2019, 314, 28–42. [Google Scholar] [CrossRef]
- Knútsdóttir, H.; Pálsson, E.; Edelstein-Keshet, L. Mathematical model of macrophage-facilitated breast cancer cells invasion. J. Theor. Biol. 2014, 357, 184–199. [Google Scholar] [CrossRef]
- Bretti, G.; De Ninno, A.; Natalini, R.; Peri, D.; Roselli, N. Estimation Algorithm for a Hybrid PDE–ODE Model Inspired by Immunocompetent Cancer-on-Chip Experiment. Axioms 2021, 10, 243. [Google Scholar] [CrossRef]
- Lai, X.; Stiff, A.; Duggan, M.; Wesolowski, R.; Carson, W.E.; Friedman, A. Modeling combination therapy for breast cancer with BET and immune checkpoint inhibitors. Proc. Natl. Acad. Sci. USA 2018, 115, 5534–5539. [Google Scholar] [CrossRef]
- Fung, Y.C. Biomechanics; Springer: New York, NY, USA, 1993. [Google Scholar] [CrossRef]
- Fung, Y.C. Biomechanics: Motion, Flow, Stress, and Growth; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Fung, Y.C. Biomechanics: Circulation; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Fung, Y.C. Biomechanics: Mechanical Properties of Living Tissues; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Prevost, T.P.; Balakrishnan, A.; Suresh, S.; Socrate, S. Biomechanics of brain tissue. Acta Biomater. 2011, 7, 83–95. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A. Biomechanics of soft tissue. Handb. Mater. Behav. Model. 2001, 3, 1049–1063. [Google Scholar]
- Holzapfel, G.A.; Ogden, R.W. Biomechanics of Soft Tissue in Cardiovascular Systems; Springer: Berlin, Germany, 2014; Volume 441. [Google Scholar]
- Rajagopal, V.; Nielsen, P.M.; Nash, M.P. Modeling breast biomechanics for multi-modal image analysis—Successes and challenges. Wiley Interdiscip. Rev. Syst. Biol. Med. 2010, 2, 293–304. [Google Scholar] [CrossRef] [PubMed]
- Frieboes, H.B.; Edgerton, M.E.; Fruehauf, J.P.; Rose, F.R.; Worrall, L.K.; Gatenby, R.A.; Ferrari, M.; Cristini, V. Prediction of drug response in breast cancer using integrative experimental/computational modeling. Cancer Res. 2009, 69, 4484–4492. [Google Scholar] [CrossRef] [PubMed]
- Friedman, A.; Hu, B. Bifurcation for a free boundary problem modeling tumor growth by Stokes equation. SIAM J. Math. Anal. 2007, 39, 174–194. [Google Scholar] [CrossRef]
- Pham, K.; Frieboes, H.B.; Cristini, V.; Lowengrub, J. Predictions of tumour morphological stability and evaluation against experimental observations. J. R. Soc. Interface 2011, 8, 16–29. [Google Scholar] [CrossRef] [PubMed]
- Hao, W.; Hauenstein, J.D.; Hu, B.; McCoy, T.; Sommese, A.J. Computing steady-state solutions for a free boundary problem modeling tumor growth by Stokes equation. J. Comput. Appl. Math. 2013, 237, 326–334. [Google Scholar] [CrossRef][Green Version]
- Huang, Y.; Zhang, Z.; Hu, B. Bifurcation for a free-boundary tumor model with angiogenesis. Nonlinear Anal. Real World Appl. 2017, 35, 483–502. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, F. Asymptotic behavior of solutions of a free boundary problem modeling tumor spheroid with Gibbs–Thomson relation. J. Differ. Equ. 2017, 262, 4907–4930. [Google Scholar] [CrossRef]
- Mohammad Mirzaei, N.; Changizi, N.; Asadpoure, A.; Su, S.; Sofia, D.; Tatarova, Z.; Zervantonakis, I.K.; Chang, Y.H.; Shahriyari, L. Investigating key cell types and molecules dynamics in PyMT mice model of breast cancer through a mathematical model. PLoS Comput. Biol. 2022, 18, e1009953. [Google Scholar] [CrossRef]
- Buzby, G.P.; Mullen, J.L.; Stein, T.P.; Miller, E.E.; Hobbs, C.L.; Rosato, E.F. Host-tumor interaction and nutrient supply. Cancer 1980, 45, 2940–2948. [Google Scholar] [CrossRef]
- Blagih, J.; Hennequart, M.; Zani, F. Tissue nutrient environments and their effect on regulatory T cell biology. Front. Immunol. 2021, 12, 908. [Google Scholar] [CrossRef]
- Zeng, H.; Combs, G.F., Jr. Selenium as an anticancer nutrient: Roles in cell proliferation and tumor cell invasion. J. Nutr. Biochem. 2008, 19, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Balkwill, F.R.; Capasso, M.; Hagemann, T. The tumor microenvironment at a glance. J. Cell Sci. 2012, 125, 5591–5596. [Google Scholar] [CrossRef]
- Franks, S.; Byrne, H.; King, J.; Underwood, J.; Lewis, C. Modelling the early growth of ductal carcinoma in situ of the breast. J. Math. Biol. 2003, 47, 424–452. [Google Scholar] [CrossRef] [PubMed]
- Hao, W.; Friedman, A. Serum upar as biomarker in breast cancer recurrence: A mathematical model. PLoS ONE 2016, 11, e0153508. [Google Scholar] [CrossRef]
- Liao, K.L.; Bai, X.F.; Friedman, A. Mathematical modeling of interleukin-27 induction of anti-tumor T cells response. PLoS ONE 2014, 9, e91844. [Google Scholar] [CrossRef]
- Liao, K.L.; Bai, X.F.; Friedman, A. The role of CD200–CD200R in tumor immune evasion. J. Theor. Biol. 2013, 328, 65–76. [Google Scholar] [CrossRef]
- Hao, W.; Gong, S.; Wu, S.; Xu, J.; Go, M.R.; Friedman, A.; Zhu, D. A mathematical model of aortic aneurysm formation. PLoS ONE 2017, 12, e0170807. [Google Scholar] [CrossRef]
- Lee, C.H.; Espinosa, I.; Vrijaldenhoven, S.; Subramanian, S.; Montgomery, K.D.; Zhu, S.; Marinelli, R.J.; Peterse, J.L.; Poulin, N.; Nielsen, T.O.; et al. Prognostic significance of macrophage infiltration in leiomyosarcomas. Clin. Cancer Res. 2008, 14, 1423–1430. [Google Scholar] [CrossRef]
- Zhang, J.; Endres, S.; Kobold, S. Enhancing tumor T cell infiltration to enable cancer immunotherapy. Immunotherapy 2019, 11, 201–213. [Google Scholar] [CrossRef] [PubMed]
- Teng, M.W.; Ngiow, S.F.; Ribas, A.; Smyth, M.J. Classifying cancers based on T-cell infiltration and PD-L1. Cancer Res. 2015, 75, 2139–2145. [Google Scholar] [CrossRef] [PubMed]
- Ono, M.; Torisu, H.; Fukushi, J.i.; Nishie, A.; Kuwano, M. Biological implications of macrophage infiltration in human tumor angiogenesis. Cancer Chemother. Pharmacol. 1999, 43, S69–S71. [Google Scholar] [CrossRef] [PubMed]
- Treilleux, I.; Blay, J.Y.; Bendriss-Vermare, N.; Ray-Coquard, I.; Bachelot, T.; Guastalla, J.P.; Bremond, A.; Goddard, S.; Pin, J.J.; Barthelemy-Dubois, C.; et al. Dendritic cell infiltration and prognosis of early stage breast cancer. Clin. Cancer Res. 2004, 10, 7466–7474. [Google Scholar] [CrossRef]
- Friedman, A.; Hao, W. The role of exosomes in pancreatic cancer microenvironment. Bull. Math. Biol. 2018, 80, 1111–1133. [Google Scholar] [CrossRef]
- Szomolay, B.; Eubank, T.D.; Roberts, R.D.; Marsh, C.B.; Friedman, A. Modeling the inhibition of breast cancer growth by GM-CSF. J. Theor. Biol. 2012, 303, 141–151. [Google Scholar] [CrossRef]
- Kremheller, J.; Vuong, A.T.; Yoshihara, L.; Wall, W.A.; Schrefler, B.A. A monolithic multiphase porous medium framework for (a-) vascular tumor growth. Comput. Methods Appl. Mech. Eng. 2018, 340, 657–683. [Google Scholar] [CrossRef]
- Chapman, S.J.; Shipley, R.J.; Jawad, R. Multiscale modeling of fluid transport in tumors. Bull. Math. Biol. 2008, 70, 2334–2357. [Google Scholar] [CrossRef]
- Sciume, G.; Shelton, S.; Gray, W.G.; Miller, C.T.; Hussain, F.; Ferrari, M.; Decuzzi, P.; Schrefler, B. A multiphase model for three-dimensional tumor growth. New J. Phys. 2013, 15, 015005. [Google Scholar] [CrossRef]
- Govindaraju, K.; Kamangar, S.; Badruddin, I.A.; Viswanathan, G.N.; Badarudin, A.; Ahmed, N.S. Effect of porous media of the stenosed artery wall to the coronary physiological diagnostic parameter: A computational fluid dynamic analysis. Atherosclerosis 2014, 233, 630–635. [Google Scholar] [CrossRef]
- Karagiannis, G.S.; Pastoriza, J.M.; Borriello, L.; Jafari, R.; Coste, A.; Condeelis, J.S.; Oktay, M.H.; Entenberg, D. Assessing tumor microenvironment of metastasis doorway-mediated vascular permeability associated with cancer cell dissemination using intravital imaging and fixed tissue analysis. JoVE (J. Vis. Exp.) 2019, 148, e59633. [Google Scholar] [CrossRef] [PubMed]
- Franks, S.; Byrne, H.; Underwood, J.; Lewis, C. Biological inferences from a mathematical model of comedo ductal carcinoma in situ of the breast. J. Theor. Biol. 2005, 232, 523–543. [Google Scholar] [CrossRef] [PubMed]
- Johnson, T.; Ding, H.; Le, H.Q.; Ducote, J.L.; Molloi, S. Breast density quantification with cone-beam CT: A post-mortem study. Phys. Med. Biol. 2013, 58, 8573. [Google Scholar] [CrossRef][Green Version]
- Byrne, H.M.; Chaplain, M.A. Modelling the role of cell-cell adhesion in the growth and development of carcinomas. Math. Comput. Model. 1996, 24, 1–17. [Google Scholar] [CrossRef]
- Byrne, H. The importance of intercellular adhesion in the development of carcinomas. Math. Med. Biol. J. IMA 1997, 14, 305–323. [Google Scholar] [CrossRef]
- Friedman, A. A free boundary problem for a coupled system of elliptic, hyperbolic, and Stokes equations modeling tumor growth. Interfaces Free Boundaries 2006, 8, 247–261. [Google Scholar] [CrossRef]
- Rianna, C.; Radmacher, M. Comparison of viscoelastic properties of cancer and normal thyroid cells on different stiffness substrates. Eur. Biophys. J. 2017, 46, 309–324. [Google Scholar] [CrossRef]
- Sancho, A.; Vandersmissen, I.; Craps, S.; Luttun, A.; Groll, J. A new strategy to measure intercellular adhesion forces in mature cell-cell contacts. Sci. Rep. 2017, 7, 1–14. [Google Scholar] [CrossRef]
- Talari, A.C.S.; Raza, A.; Rehman, S.; Rehman, I.U. Analyzing normal proliferating, hypoxic and necrotic regions of T-47D human breast cancer spheroids using Raman spectroscopy. Appl. Spectrosc. Rev. 2017, 52, 909–924. [Google Scholar] [CrossRef]
- Gallaher, J.A.; Brown, J.S.; Anderson, A.R. The impact of proliferation-migration tradeoffs on phenotypic evolution in cancer. Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef]
- Datta, P.; Dey, M.; Ataie, Z.; Unutmaz, D.; Ozbolat, I.T. 3D bioprinting for reconstituting the cancer microenvironment. NPJ Precis. Oncol. 2020, 4, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Zhang, C.; Song, Y.; Wang, Z.; Wang, Y.; Luo, F.; Xu, Y.; Zhao, Y.; Wu, Z.; Xu, Y. Mechanism of immune evasion in breast cancer. OncoTargets Ther. 2017, 10, 1561. [Google Scholar] [CrossRef] [PubMed]
- Vesely, M.D.; Kershaw, M.H.; Schreiber, R.D.; Smyth, M.J. Natural innate and adaptive immunity to cancer. Annu. Rev. Immunol. 2011, 29, 235–271. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, R.D.; Old, L.J.; Smyth, M.J. Cancer immunoediting: Integrating immunity’s roles in cancer suppression and promotion. Science 2011, 331, 1565–1570. [Google Scholar] [CrossRef]
- Soysal, S.D.; Tzankov, A.; Muenst, S.E. Role of the tumor microenvironment in breast cancer. Pathobiology 2015, 82, 142–152. [Google Scholar] [CrossRef]
- Bertram, C.A.; Aubreville, M.; Gurtner, C.; Bartel, A.; Corner, S.M.; Dettwiler, M.; Kershaw, O.; Noland, E.L.; Schmidt, A.; Sledge, D.G.; et al. Computerized calculation of mitotic count distribution in canine cutaneous mast cell tumor sections: Mitotic count is area dependent. Vet. Pathol. 2020, 57, 214–226. [Google Scholar] [CrossRef]
- Li, S.; Petzold, L. Adjoint sensitivity analysis for time-dependent partial differential equations with adaptive mesh refinement. J. Comput. Phys. 2004, 198, 310–325. [Google Scholar] [CrossRef]
- Mitusch, S.K.; Funke, S.W.; Dokken, J.S. dolfin-adjoint 2018.1: Automated adjoints for FEniCS and Firedrake. J. Open Source Softw. 2019, 4, 1292. [Google Scholar] [CrossRef]
- Qian, B.Z.; Pollard, J.W. Macrophage diversity enhances tumor progression and metastasis. Cell 2010, 141, 39–51. [Google Scholar] [CrossRef]
- Nielsen, S.R.; Schmid, M.C. Macrophages as key drivers of cancer progression and metastasis. Mediat. Inflamm. 2017, 2017, 9624760. [Google Scholar] [CrossRef]
- Doak, G.R.; Schwertfeger, K.L.; Wood, D.K. Distant relations: Macrophage functions in the metastatic niche. Trends Cancer 2018, 4, 445–459. [Google Scholar] [CrossRef] [PubMed]
- Ma, R.Y.; Zhang, H.; Li, X.F.; Zhang, C.B.; Selli, C.; Tagliavini, G.; Lam, A.D.; Prost, S.; Sims, A.H.; Hu, H.Y.; et al. Monocyte-derived macrophages promote breast cancer bone metastasis outgrowth. J. Exp. Med. 2020, 217, e20191820. [Google Scholar] [CrossRef] [PubMed]
- Palmer, T.D.; Ashby, W.J.; Lewis, J.D.; Zijlstra, A. Targeting tumor cell motility to prevent metastasis. Adv. Drug Deliv. Rev. 2011, 63, 568–581. [Google Scholar] [CrossRef] [PubMed]
- Yamazaki, D.; Kurisu, S.; Takenawa, T. Regulation of cancer cell motility through actin reorganization. Cancer Sci. 2005, 96, 379–386. [Google Scholar] [CrossRef] [PubMed]
- Gregory, A.D.; Houghton, A.M. Tumor-associated neutrophils: New targets for cancer therapy. Cancer Res. 2011, 71, 2411–2416. [Google Scholar] [CrossRef]
- Raskov, H.; Orhan, A.; Christensen, J.P.; Gögenur, I. Cytotoxic CD8+ T cells in cancer and cancer immunotherapy. Br. J. Cancer 2021, 124, 359–367. [Google Scholar] [CrossRef]
- Farhood, B.; Najafi, M.; Mortezaee, K. CD8+ cytotoxic T lymphocytes in cancer immunotherapy: A review. J. Cell. Physiol. 2019, 234, 8509–8521. [Google Scholar] [CrossRef]
- Johar, D.; Roth, J.C.; Bay, G.H.; Walker, J.N.; Kroczak, T.J.; Los, M. Inflammatory response, reactive oxygen species, programmed (necrotic-like and apoptotic) cell death and cancer. Rocz. Akad. Med. Bialymst. 2004, 49, 31–39. [Google Scholar]
- Bredholt, G.; Mannelqvist, M.; Stefansson, I.M.; Birkeland, E.; Bø, T.H.; Øyan, A.M.; Trovik, J.; Kalland, K.H.; Jonassen, I.; Salvesen, H.B.; et al. Tumor necrosis is an important hallmark of aggressive endometrial cancer and associates with hypoxia, angiogenesis and inflammation responses. Oncotarget 2015, 6, 39676. [Google Scholar] [CrossRef]
- Ferreira, S., Jr.; Martins, M.; Vilela, M. Reaction-diffusion model for the growth of avascular tumor. Phys. Rev. E 2002, 65, 021907. [Google Scholar] [CrossRef]
- Cassim, S.; Pouyssegur, J. Tumor microenvironment: A metabolic player that shapes the immune response. Int. J. Mol. Sci. 2019, 21, 157. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Nogales-Cadenas, R.; Zhang, Q.; Lin, J.R.; Zhang, W.; O’Brien, K.; Montagna, C.; Zhang, Z.D. Transcriptomic dynamics of breast cancer progression in the MMTV-PyMT mouse model. BMC Genom. 2017, 18, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Brezzi, F.; Russo, A. Choosing bubbles for advection-diffusion problems. Math. Model. Methods Appl. Sci. 1994, 4, 571–587. [Google Scholar] [CrossRef]
- Franca, L.P.; Nesliturk, A.; Stynes, M. On the stability of residual-free bubbles for convection-diffusion problems and their approximation by a two-level finite element method. Comput. Methods Appl. Mech. Eng. 1998, 166, 35–49. [Google Scholar] [CrossRef]
- Sendur, A. A Comparative Study on Stabilized Finite Element Methods for the Convection-Diffusion-Reaction Problems. J. Appl. Math. 2018, 2018, 4259634. [Google Scholar] [CrossRef]
- Logg, A.; Mardal, K.A.; Wells, G. Automated Solution of Differential Equations by the Finite Element Method: The FEniCS Book; Springer Science & Business Media: Berlin, Germany, 2012; Volume 84. [Google Scholar]





| Variable in PDE | Variable in ODE | Name |
|---|---|---|
| Naive T cells | ||
| Helper T cells | ||
| Cytotoxic cells | ||
| Regulatory T cells | ||
| Naive dendritic cells | ||
| D | Activated dendritic cells | |
| Naive macrophages | ||
| M | Activated macrophages | |
| C | Cancer cells | |
| N | Necrotic cells | |
| A | Cancer associated Adipocytes | |
| H | HMGB1 | |
| IL-12 | ||
| IL-10 | ||
| IL-6 |
| Cell Type | Biomarker Combination |
|---|---|
| Helper T cells () | Epcam(−) CD45(+) CD3(+) CD4(+) CD8(−) |
| Cytotoxic T cells () | Epcam(−) CD45(+) CD3(+) CD4(−) CD8(+) |
| Naive dendritic cells () | Epcam(−) CD45(+) F4/80(−) CD11C(+) |
| Dendritic cells (D) | Epcam(−) CD45(+) F4/80(−) CD11C(+) MHC-II(+) |
| Activated macrophages (M) | Epcam(−) CD45(+) F4/80(+) CD11C(−) CSF1R(+) or Epcam(−) CD45(+) F4/80(+) CD11C(−) CSF1R(−) MHC-II(+) |
| Cancer cells (C) | Epcam(+) CD45(−) |
| Necrotic cells (N) | CC3(+) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammad Mirzaei, N.; Tatarova, Z.; Hao, W.; Changizi, N.; Asadpoure, A.; Zervantonakis, I.K.; Hu, Y.; Chang, Y.H.; Shahriyari, L. A PDE Model of Breast Tumor Progression in MMTV-PyMT Mice. J. Pers. Med. 2022, 12, 807. https://doi.org/10.3390/jpm12050807
Mohammad Mirzaei N, Tatarova Z, Hao W, Changizi N, Asadpoure A, Zervantonakis IK, Hu Y, Chang YH, Shahriyari L. A PDE Model of Breast Tumor Progression in MMTV-PyMT Mice. Journal of Personalized Medicine. 2022; 12(5):807. https://doi.org/10.3390/jpm12050807
Chicago/Turabian StyleMohammad Mirzaei, Navid, Zuzana Tatarova, Wenrui Hao, Navid Changizi, Alireza Asadpoure, Ioannis K. Zervantonakis, Yu Hu, Young Hwan Chang, and Leili Shahriyari. 2022. "A PDE Model of Breast Tumor Progression in MMTV-PyMT Mice" Journal of Personalized Medicine 12, no. 5: 807. https://doi.org/10.3390/jpm12050807
APA StyleMohammad Mirzaei, N., Tatarova, Z., Hao, W., Changizi, N., Asadpoure, A., Zervantonakis, I. K., Hu, Y., Chang, Y. H., & Shahriyari, L. (2022). A PDE Model of Breast Tumor Progression in MMTV-PyMT Mice. Journal of Personalized Medicine, 12(5), 807. https://doi.org/10.3390/jpm12050807







