Logarithmic Scaling of Loss Functions for Enhanced Self-Supervised Accelerated MRI Reconstruction
Abstract
1. Introduction
2. Theory
2.1. Parallel Imaging Problem
2.2. Deep Learning-Based MRI Reconstruction
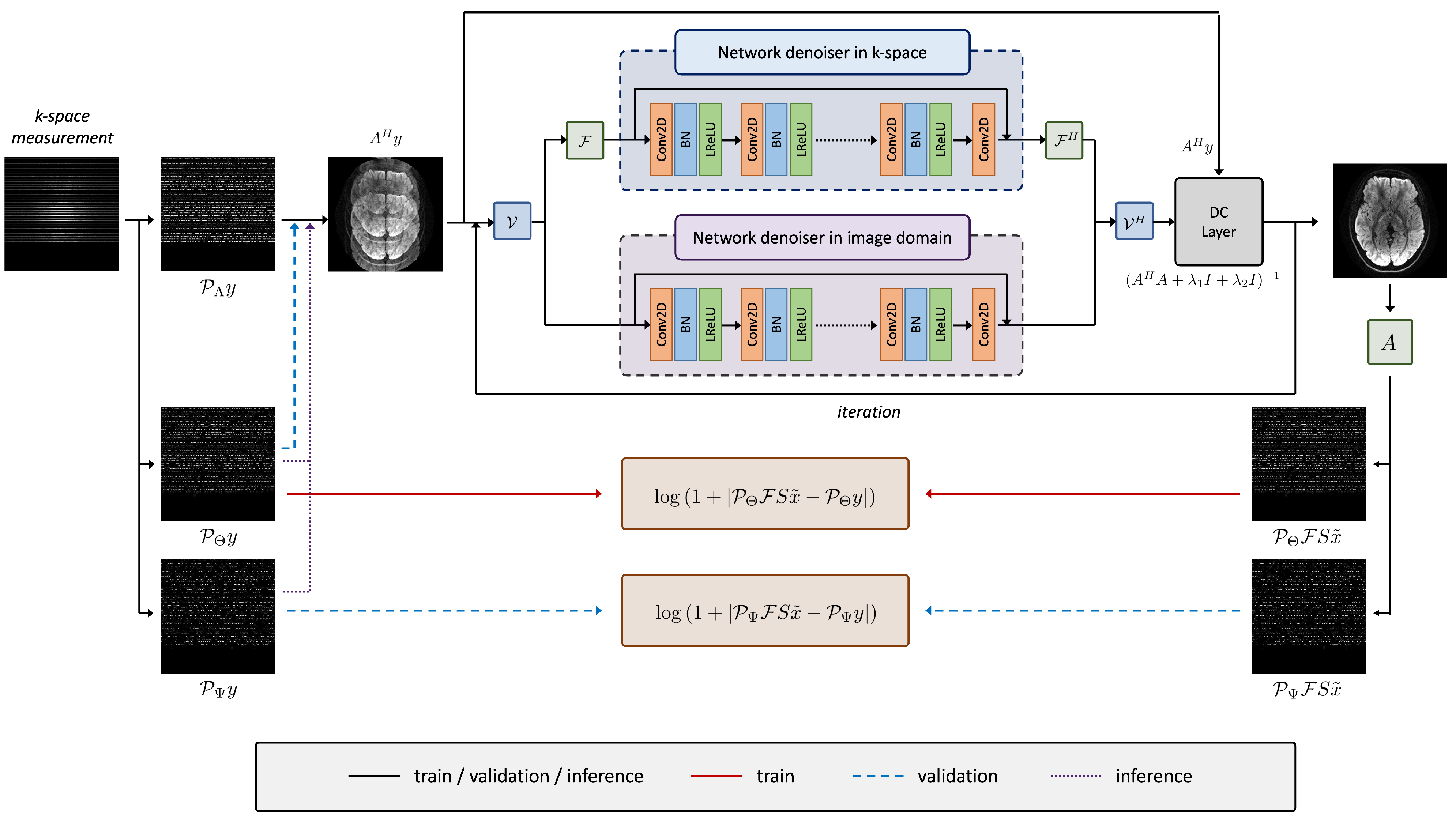
2.3. Self-Supervised Learning for MRI Reconstruction
2.4. Logarithmic Scaling of the Loss
3. Materials and Methods
3.1. Network Architecture
3.2. Experiment Details
3.2.1. 1D Subsampling
3.2.2. 2D Subsampling
4. Results and Discussion
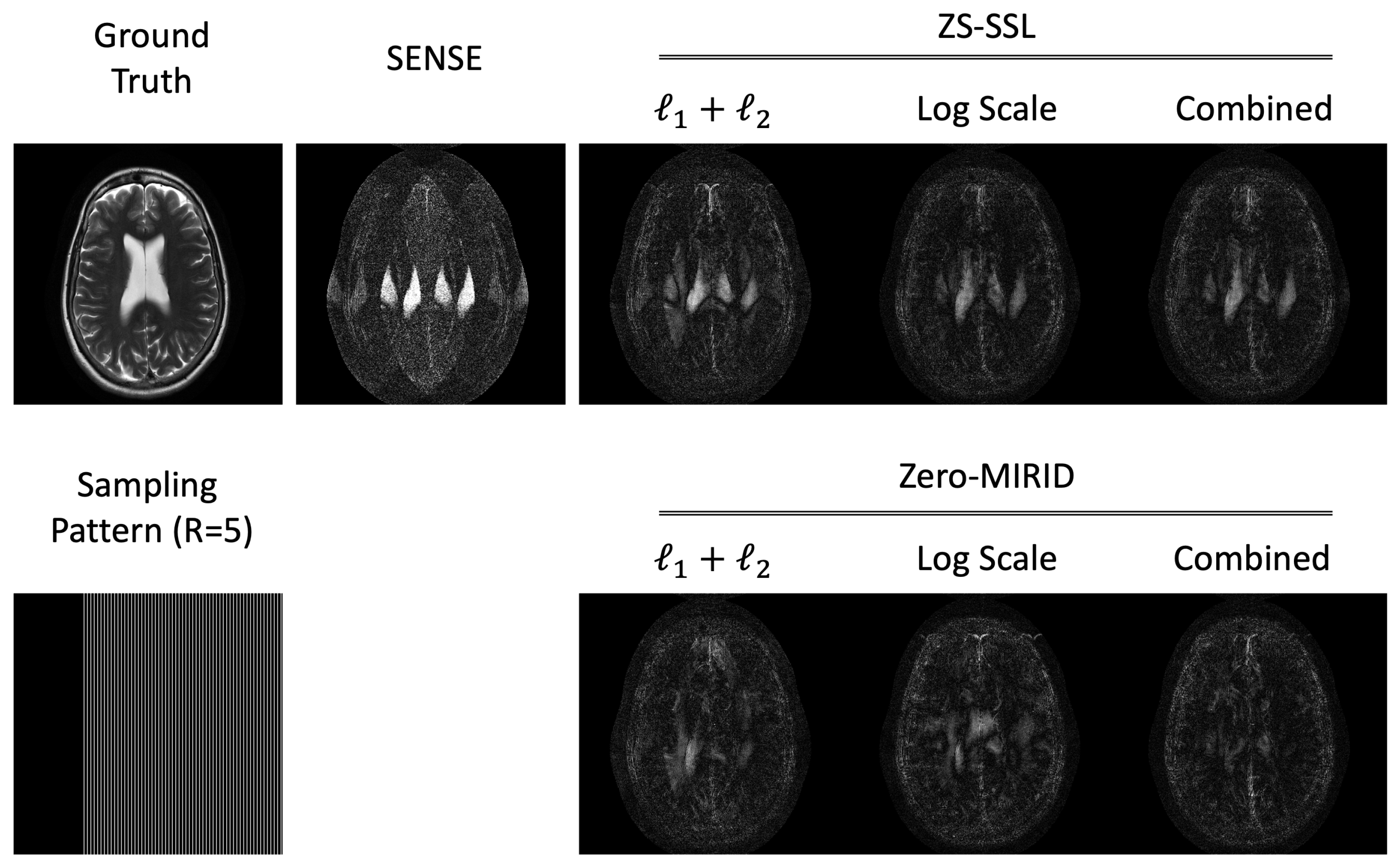
4.1. 1D Subsampling
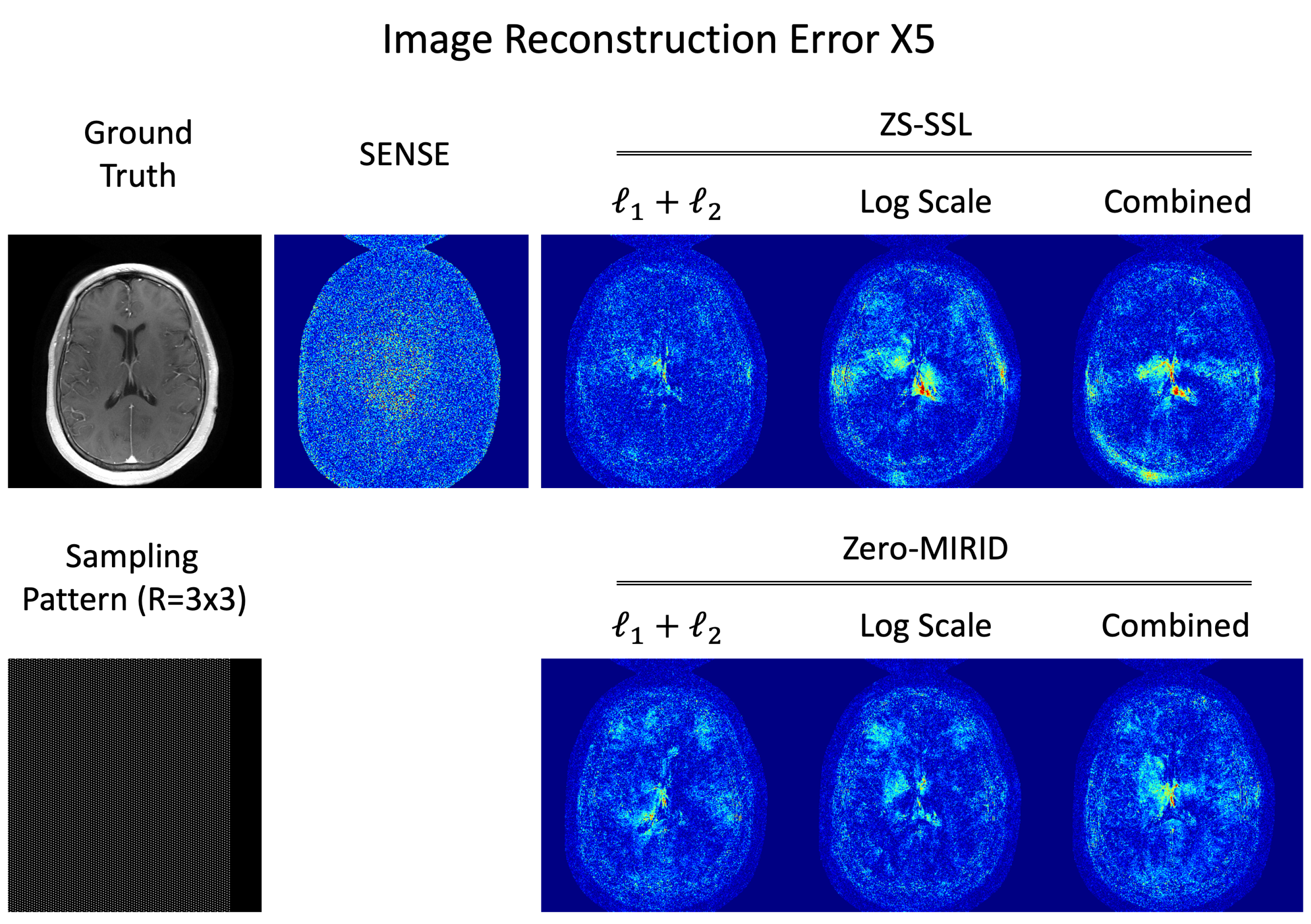
4.2. 2D Subsampling
4.3. Residual Error Analysis
4.4. Key Findings and Analysis
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CAIPI | Controlled Aliasing in Parallel Imaging |
| CS | Compressed Sensing |
| DC | Data Consistency |
| FSIM | Feature Similarity Index Measure |
| GRAPPA | Generalized Autocalibrating Partially Parallel Acquisition |
| HFEN | High-Frequency Error Norm |
| LPIPS | Learned Perceptual Image Patch Similarity |
| MoDL | Model-Based Deep Learning |
| MRI | Magnetic Resonance Imaging |
| NRMSE | Normalized Root Mean Square Error |
| PF | Partial Fourier |
| PI | Parallel Imaging |
| PSNR | Peak Signal-to-Noise Ratio |
| SENSE | Sensitivity Encoding |
| SSIM | Structural Similarity Index Measure |
| ZS-SSL | Zero-Shot Self-Supervised Learning |
| Zero-MIRID | Zero-shot Multi-shot Image Reconstruction for Improved Diffusion MRI |
References
- Lauterbur, P.C. Image formation by induced local interactions: Examples employing nuclear magnetic resonance. Nature 1973, 242, 190–191. [Google Scholar] [CrossRef]
- Zaitsev, M.; Maclaren, J.; Herbst, M. Motion artifacts in MRI: A complex problem with many partial solutions. J. Magn. Reson. Imaging 2015, 42, 887–901. [Google Scholar] [CrossRef]
- Pruessmann, K.P.; Weiger, M.; Scheidegger, M.B.; Boesiger, P. SENSE: Sensitivity encoding for fast MRI. Magn. Reson. Med. 1999, 42, 952–962. [Google Scholar] [CrossRef]
- Griswold, M.A.; Jakob, P.M.; Heidemann, R.M.; Nittka, M.; Jellus, V.; Wang, J.; Kiefer, B.; Haase, A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn. Reson. Med. 2002, 47, 1202–1210. [Google Scholar] [CrossRef] [PubMed]
- Haldar, J.P.; Setsompop, K. Linear Predictability in MRI Reconstruction: Leveraging Shift-Invariant Fourier Structure for Faster and Better Imaging. IEEE Signal Process. Mag. 2020, 37, 69–82. [Google Scholar] [CrossRef] [PubMed]
- Lustig, M.; Donoho, D.; Pauly, J.M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007, 58, 1182–1195. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.L.; Santos, J.M.; Pauly, J.M. Compressed sensing MRI. IEEE Signal Process. Mag. 2008, 25, 72–82. [Google Scholar] [CrossRef]
- Haldar, J.P. Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI. IEEE Trans. Med Imaging 2013, 33, 668–681. [Google Scholar] [CrossRef]
- Lee, D.; Jin, K.H.; Kim, E.Y.; Park, S.H.; Ye, J.C. Acceleration of MR parameter mapping using annihilating filter-based low rank hankel matrix (ALOHA). Magn. Reson. Med. 2016, 76, 1848–1864. [Google Scholar] [CrossRef]
- Trzasko, J.; Manduca, A.; Borisch, E. Local versus global low-rank promotion in dynamic MRI series reconstruction. Proc. Int. Symp. Magn. Reson. Med. 2011, 19, 4371. [Google Scholar]
- Zhao, B.; Lu, W.; Hitchens, T.K.; Lam, F.; Ho, C.; Liang, Z.P. Accelerated MR parameter mapping with low-rank and sparsity constraints. Magn. Reson. Med. 2015, 74, 489–498. [Google Scholar] [CrossRef]
- Heckel, R.; Jacob, M.; Chaudhari, A.; Perlman, O.; Shimron, E. Deep learning for accelerated and robust MRI reconstruction. Magn. Reson. Mater. Phys. Biol. Med. 2024, 37, 335–368. [Google Scholar] [CrossRef]
- Jin, K.H.; McCann, M.T.; Froustey, E.; Unser, M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans. Image Process. 2017, 26, 4509–4522. [Google Scholar] [CrossRef] [PubMed]
- Hammernik, K.; Klatzer, T.; Kobler, E.; Recht, M.P.; Sodickson, D.K.; Pock, T.; Knoll, F. Learning a variational network for reconstruction of accelerated MRI data. Magn. Reson. Med. 2018, 79, 3055–3071. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, H.K.; Mani, M.P.; Jacob, M. MoDL: Model-based deep learning architecture for inverse problems. IEEE Trans. Med Imaging 2018, 38, 394–405. [Google Scholar] [CrossRef] [PubMed]
- Lehtinen, J.; Munkberg, J.; Hasselgren, J.; Laine, S.; Karras, T.; Aittala, M.; Aila, T. Noise2Noise: Learning image restoration without clean data. arXiv 2018, arXiv:1803.04189. [Google Scholar] [CrossRef]
- Aali, A.; Arvinte, M.; Kumar, S.; Arefeen, Y.I.; Tamir, J.I. Robust multi-coil MRI reconstruction via self-supervised denoising. Magn. Reson. Med. 2025, 94, 1859–1877. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, Z.; Xie, Y.; Li, D.; Christodoulou, A.G. Repeatability-encouraging self-supervised learning reconstruction for quantitative MRI. Magn. Reson. Med. 2025, 94, 797–809. [Google Scholar] [CrossRef]
- Yaman, B.; Hosseini, S.A.H.; Moeller, S.; Ellermann, J.; Uğurbil, K.; Akçakaya, M. Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data. Magn. Reson. Med. 2020, 84, 3172–3191. [Google Scholar] [CrossRef]
- Yaman, B. Zero-Shot Self-Supervised Learning for MRI Reconstruction. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Cho, J.; Jun, Y.; Wang, X.; Kobayashi, C.; Bilgic, B. Improved multi-shot diffusion-weighted mri with zero-shot self-supervised learning reconstruction. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Vancouver, BC, Canada, 8–12 October 2023; Springer: Cham, Switzerland, 2023; pp. 457–466. [Google Scholar]
- Eo, T.; Jun, Y.; Kim, T.; Jang, J.; Lee, H.J.; Hwang, D. KIKI-net: Cross-domain convolutional neural networks for reconstructing undersampled magnetic resonance images. Magn. Reson. Med. 2018, 80, 2188–2201. [Google Scholar] [CrossRef]
- Aggarwal, H.K.; Mani, M.P.; Jacob, M. MoDL-MUSSELS: Model-based deep learning for multishot sensitivity-encoded diffusion MRI. IEEE Trans. Med Imaging 2019, 39, 1268–1277. [Google Scholar] [CrossRef]
- Blaimer, M.; Gutberlet, M.; Kellman, P.; Breuer, F.A.; Köstler, H.; Griswold, M.A. Virtual coil concept for improved parallel MRI employing conjugate symmetric signals. Magn. Reson. Med. 2009, 61, 93–102. [Google Scholar] [CrossRef]
- Kim, T.H.; Setsompop, K.; Haldar, J.P. LORAKS makes better SENSE: Phase-constrained partial fourier SENSE reconstruction without phase calibration. Magn. Reson. Med. 2017, 77, 1021–1035. [Google Scholar] [CrossRef]
- Knoll, F.; Zbontar, J.; Sriram, A.; Muckley, M.J.; Bruno, M.; Defazio, A.; Parente, M.; Geras, K.J.; Katsnelson, J.; Chandarana, H.; et al. fastMRI: A publicly available raw k-space and DICOM dataset of knee images for accelerated MR image reconstruction using machine learning. Radiol. Artif. Intell. 2020, 2, e190007. [Google Scholar] [CrossRef]
- Breuer, F.A.; Blaimer, M.; Mueller, M.F.; Seiberlich, N.; Heidemann, R.M.; Griswold, M.A.; Jakob, P.M. Controlled aliasing in volumetric parallel imaging (2D CAIPIRINHA). Magn. Reson. Med. 2006, 55, 549–556. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 586–595. [Google Scholar]
- Xue, W.; Zhang, L.; Mou, X.; Bovik, A.C. Gradient magnitude similarity deviation: A highly efficient perceptual image quality index. IEEE Trans. Image Process. 2013, 23, 684–695. [Google Scholar] [CrossRef]


| SENSE | ZS-SSL | Zero-MIRID | |||||
|---|---|---|---|---|---|---|---|
| - | Log Scale | Combined | Log Scale | Combined | |||
| NRMSE | 13.74 | 10.28 | 7.58 | 7.47 | 8.83 | 8.84 | 8.36 |
| PSNR | 29.80 | 32.32 | 34.96 | 35.08 | 33.64 | 33.63 | 34.11 |
| SSIM | 0.8585 | 0.9154 | 0.9477 | 0.9485 | 0.9302 | 0.9496 | 0.9465 |
| FSIM | 0.9683 | 0.9848 | 0.9889 | 0.9891 | 0.9878 | 0.9884 | 0.9878 |
| HFEN | 0.1571 | 0.1185 | 0.0765 | 0.0700 | 0.0843 | 0.1017 | 0.0879 |
| LPIPS | 0.1229 | 0.0810 | 0.0602 | 0.0588 | 0.0684 | 0.0599 | 0.0596 |
| GMSD | 0.1932 | 0.1525 | 0.1328 | 0.1321 | 0.1428 | 0.1310 | 0.1332 |
| SENSE | ZS-SSL | Zero-MIRID | |||||
|---|---|---|---|---|---|---|---|
| - | Log Scale | Combined | Log Scale | Combined | |||
| NRMSE | 11.78 | 6.77 | 7.64 | 7.32 | 7.81 | 6.66 | 7.65 |
| PSNR | 31.71 | 36.52 | 35.47 | 35.83 | 35.28 | 36.65 | 35.46 |
| SSIM | 0.7896 | 0.9288 | 0.9472 | 0.9470 | 0.9421 | 0.9485 | 0.9508 |
| FSIM | 0.9637 | 0.9929 | 0.9934 | 0.9935 | 0.9939 | 0.9942 | 0.9940 |
| HFEN | 0.1107 | 0.0731 | 0.0994 | 0.0882 | 0.0885 | 0.0882 | 0.0836 |
| LPIPS | 0.1822 | 0.0966 | 0.0776 | 0.0827 | 0.0805 | 0.0758 | 0.0741 |
| GMSD | 0.2471 | 0.1655 | 0.1494 | 0.1514 | 0.1529 | 0.1489 | 0.1479 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, J. Logarithmic Scaling of Loss Functions for Enhanced Self-Supervised Accelerated MRI Reconstruction. Diagnostics 2025, 15, 2993. https://doi.org/10.3390/diagnostics15232993
Cho J. Logarithmic Scaling of Loss Functions for Enhanced Self-Supervised Accelerated MRI Reconstruction. Diagnostics. 2025; 15(23):2993. https://doi.org/10.3390/diagnostics15232993
Chicago/Turabian StyleCho, Jaejin. 2025. "Logarithmic Scaling of Loss Functions for Enhanced Self-Supervised Accelerated MRI Reconstruction" Diagnostics 15, no. 23: 2993. https://doi.org/10.3390/diagnostics15232993
APA StyleCho, J. (2025). Logarithmic Scaling of Loss Functions for Enhanced Self-Supervised Accelerated MRI Reconstruction. Diagnostics, 15(23), 2993. https://doi.org/10.3390/diagnostics15232993





