Impact of Voxel Normalization on a Machine Learning-Based Method: A Study on Pulmonary Nodule Malignancy Diagnosis Using Low-Dose Computed Tomography (LDCT)
Abstract
:1. Introduction
2. Materials and Methods
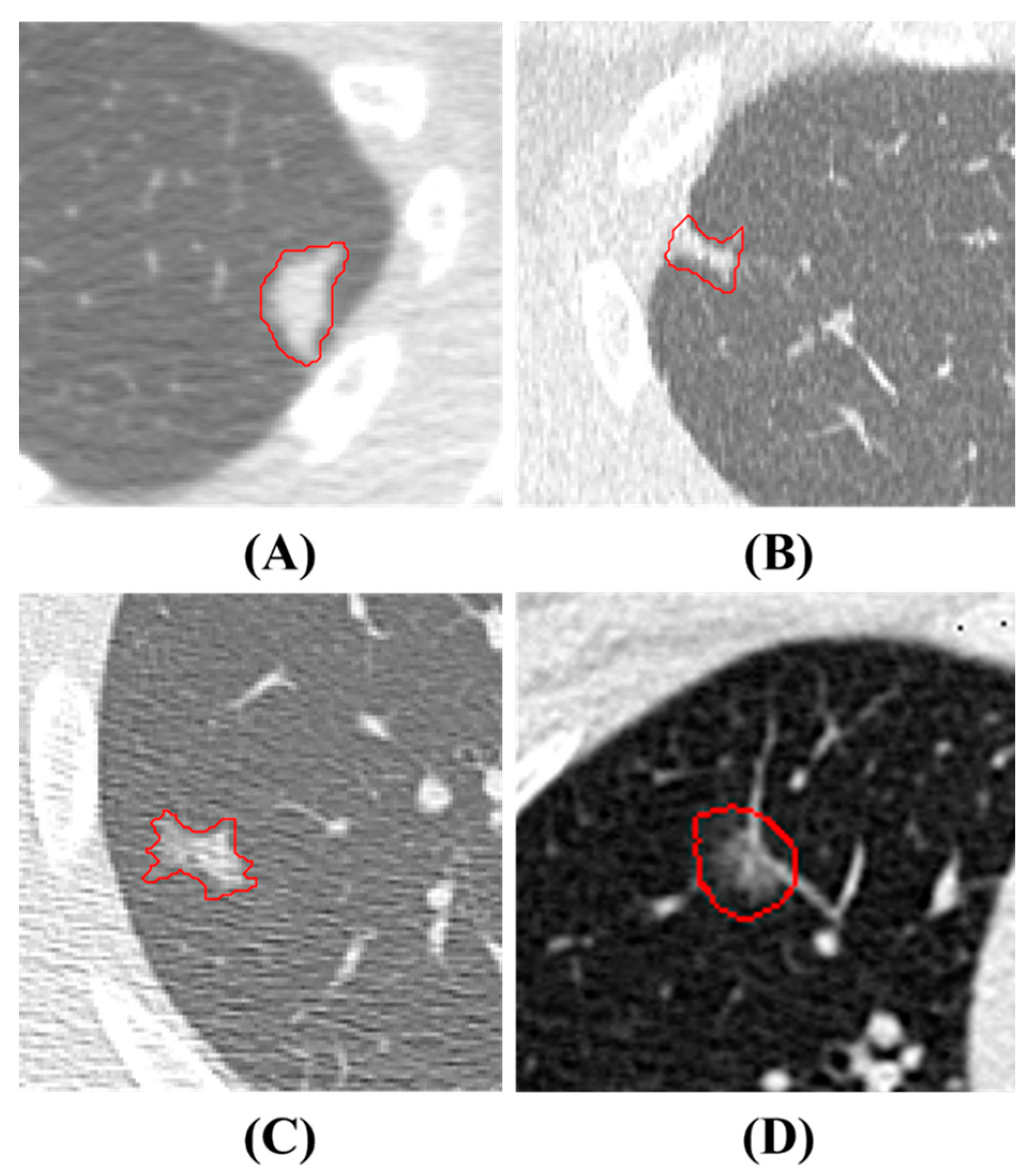
2.1. Dataset in House and Annotation
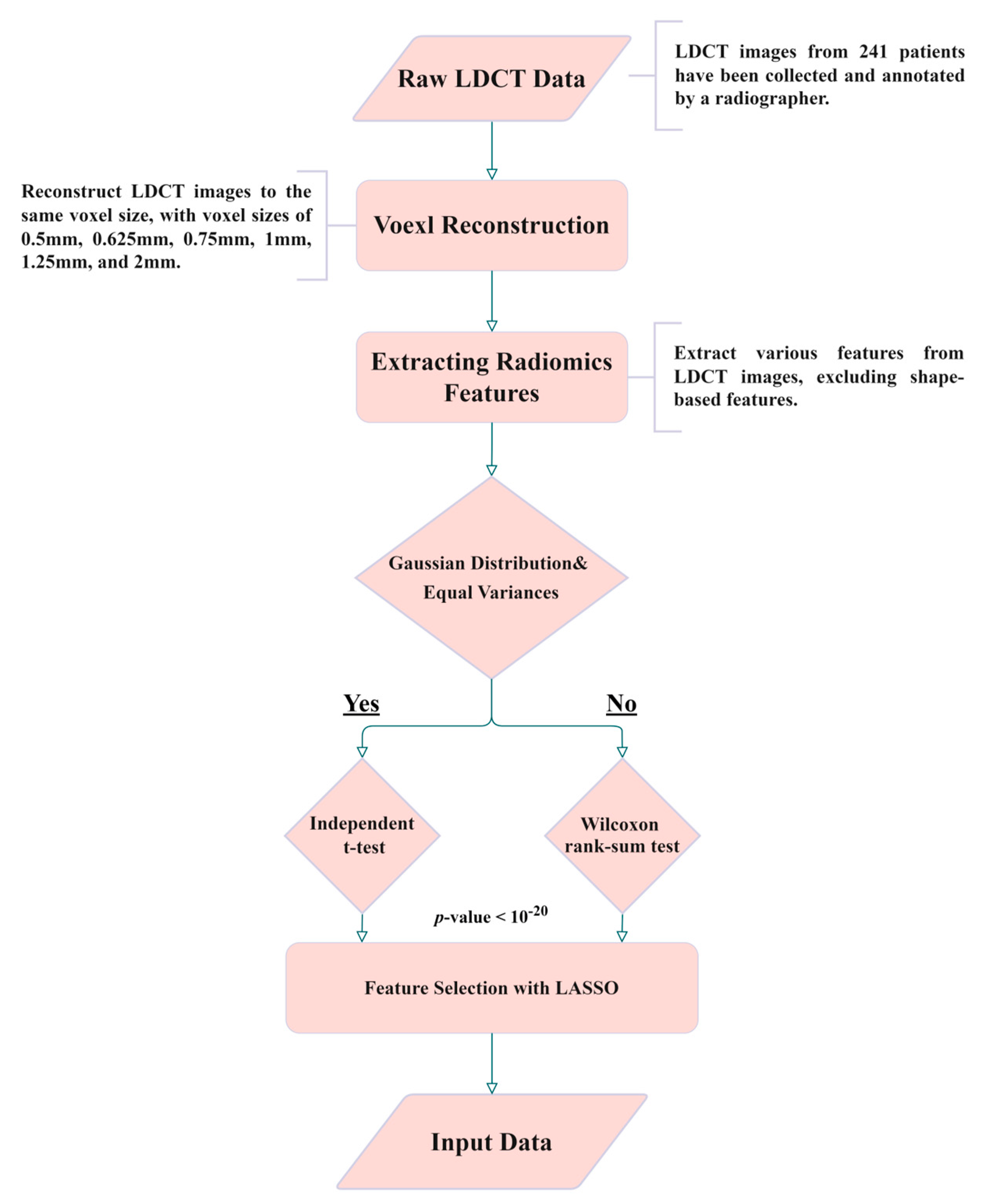
2.2. Isotropic Voxel Normalization and Image Reconstruction
2.3. Radiomics and Feature Selection
2.4. Support Vector Machine (SVM) and Hyperparameter Optimization
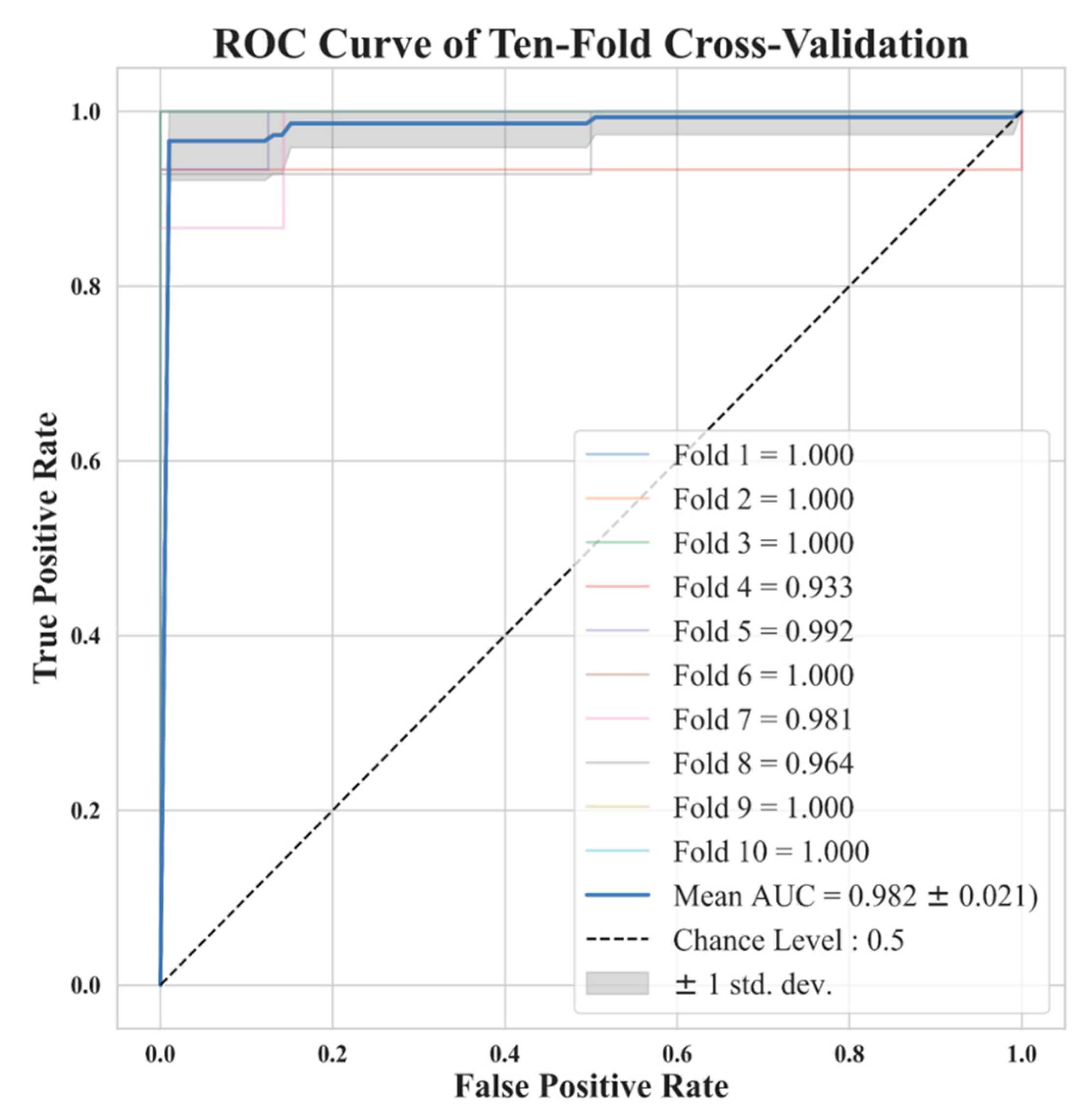
2.5. K-Fold Cross-Validation and Model Performance Evaluation
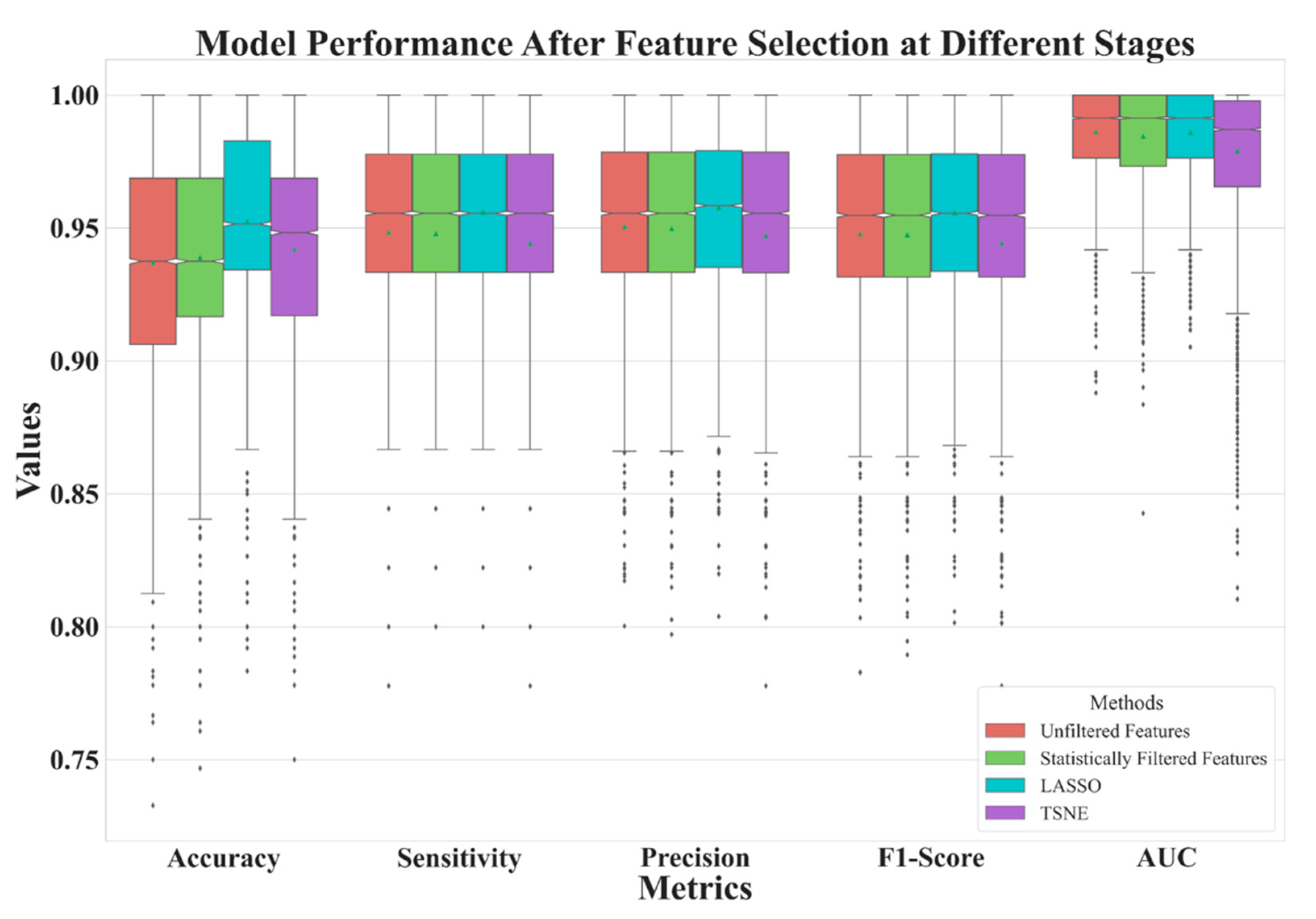
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Feature Description | Types |
|---|---|
| original_shape_Elongation | Shape-Based |
| original_shape_Flatness | Shape-Based |
| original_shape_LeastAxisLength | Shape-Based |
| original_shape_MajorAxisLength | Shape-Based |
| original_shape_Maximum2DDiameterColumn | Shape-Based |
| original_shape_Maximum2DDiameterRow | Shape-Based |
| original_shape_Maximum2DDiameterSlice | Shape-Based |
| original_shape_Maximum3DDiameter | Shape-Based |
| original_shape_MeshVolume | Shape-Based |
| original_shape_MinorAxisLength | Shape-Based |
| original_shape_Sphericity | Shape-Based |
| original_shape_SurfaceArea | Shape-Based |
| original_shape_SurfaceVolumeRatio | Shape-Based |
| original_shape_VoxelVolume | Shape-Based |
Appendix B
References
- Siegel, R.L.; Miller, K.D.; Wagle, N.S.; Jemal, A. Cancer statistics, 2023. CA Cancer J. Clin. 2023, 73, 17–48. [Google Scholar] [CrossRef] [PubMed]
- Herbst, R.S.; Morgensztern, D.; Boshoff, C. The biology and management of non-small cell lung cancer. Nature 2018, 553, 446–454. [Google Scholar] [CrossRef] [PubMed]
- Knight, S.B.; Crosbie, P.; Balata, H.; Chudziak, J.; Hussell, T.; Dive, C. Progress and prospects of early detection in lung cancer. Open Biol. 2017, 7, 170070. [Google Scholar]
- Jemal, A.; Fedewa, S.A. Lung cancer screening with low-dose computed tomography in the United States—2010 to 2015. JAMA Oncol. 2017, 3, 1278–1281. [Google Scholar] [CrossRef] [PubMed]
- Armato III, S.G.; McLennan, G.; Bidaut, L.; McNitt-Gray, M.F.; Meyer, C.R.; Reeves, A.P.; Zhao, B.; Aberle, D.R.; Henschke, C.I.; Hoffman, E.A. The lung image database consortium (LIDC) and image database resource initiative (IDRI): A completed reference database of lung nodules on CT scans. Med. Phys. 2011, 38, 915–931. [Google Scholar] [CrossRef] [PubMed]
- Cha, M.J.; Lee, K.S.; Kim, H.S.; Lee, S.W.; Jeong, C.J.; Kim, E.Y.; Lee, H.Y. Improvement in imaging diagnosis technique and modalities for solitary pulmonary nodules: From ground-glass opacity nodules to part-solid and solid nodules. Expert Rev. Respir. Med. 2016, 10, 261–278. [Google Scholar] [CrossRef] [PubMed]
- Swensen, S.J.; Viggiano, R.W.; Midthun, D.E.; Müller, N.L.; Sherrick, A.; Yamashita, K.; Naidich, D.P.; Patz, E.F.; Hartman, T.E.; Muhm, J.R. Lung nodule enhancement at CT: Multicenter study. Radiology 2000, 214, 73–80. [Google Scholar] [CrossRef]
- Chelala, L.; Hossain, R.; Kazerooni, E.A.; Christensen, J.D.; Dyer, D.S.; White, C.S. Lung-RADS version 1.1: Challenges and a look ahead, from the AJR special series on radiology reporting and data systems. Am. J. Roentgenol. 2021, 216, 1411–1422. [Google Scholar] [CrossRef]
- Swensen, S.J.; Silverstein, M.D.; Edell, E.S.; Trastek, V.F.; Aughenbaugh, G.L.; Ilstrup, D.M.; Schleck, C.D. Solitary pulmonary nodules: Clinical prediction model versus physicians. Mayo Clin. Proc. 1999, 74, 319–329. [Google Scholar] [CrossRef]
- Khan, T.; Usman, Y.; Abdo, T.; Chaudry, F.; Keddissi, J.I.; Youness, H.A. Diagnosis and management of peripheral lung nodule. Ann. Transl. Med. 2019, 7, 348. [Google Scholar] [CrossRef]
- Gillies, R.J.; Kinahan, P.E.; Hricak, H. Radiomics: Images are more than pictures, they are data. Radiology 2016, 278, 563–577. [Google Scholar] [CrossRef] [PubMed]
- Doi, K. Current status and future potential of computer-aided diagnosis in medical imaging. Br. J. Radiol. 2005, 78 (Suppl. S1), s3–s19. [Google Scholar] [CrossRef] [PubMed]
- Dey, R.; Lu, Z.; Hong, Y. Diagnostic classification of lung nodules using 3D neural networks. In Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018; IEEE: New York, NY, USA, 2018; pp. 774–778. [Google Scholar]
- Huang, H.; Wu, R.; Li, Y.; Peng, C. Self-supervised transfer learning based on domain adaptation for benign-malignant lung nodule classification on thoracic CT. IEEE J. Biomed. Health Inform. 2022, 26, 3860–3871. [Google Scholar] [CrossRef] [PubMed]
- Kang, G.; Liu, K.; Hou, B.; Zhang, N. 3D multi-view convolutional neural networks for lung nodule classification. PLoS ONE 2017, 12, e0188290. [Google Scholar] [CrossRef]
- Kumar, D.; Wong, A.; Clausi, D.A. Lung nodule classification using deep features in CT images. In Proceedings of the 2015 12th Conference on Computer and Robot Vision, Halifax, NS, Canada, 3–5 June 2015; IEEE: New York, NY, USA, 2015; pp. 133–138. [Google Scholar]
- Liu, K.; Kang, G. Multiview convolutional neural networks for lung nodule classification. Int. J. Imaging Syst. Technol. 2017, 27, 12–22. [Google Scholar] [CrossRef]
- Lu, X.; Nanehkaran, Y.A.; Karimi Fard, M. A method for optimal detection of lung cancer based on deep learning optimized by marine predators algorithm. Comput. Intell. Neurosci. 2021, 2021, 3694723. [Google Scholar] [CrossRef] [PubMed]
- Mehta, K.; Jain, A.; Mangalagiri, J.; Menon, S.; Nguyen, P.; Chapman, D.R. Lung nodule classification using biomarkers, volumetric radiomics, and 3D CNNs. J. Digit. Imaging 2021, 34, 647–666. [Google Scholar] [CrossRef] [PubMed]
- Saihood, A.; Karshenas, H.; Nilchi, A.R.N. Deep fusion of gray level co-occurrence matrices for lung nodule classification. PLoS ONE 2022, 17, e0274516. [Google Scholar] [CrossRef]
- Shen, W.; Zhou, M.; Yang, F.; Yang, C.; Tian, J. Multi-scale convolutional neural networks for lung nodule classification. In Proceedings of the 24th International Conference, Information Processing in Medical Imaging IPMI 2015, Isle of Skye, UK, 28 June–3 July 2015; Springer: Cham, Switzerland, 2015; pp. 588–599. [Google Scholar]
- Shen, W.; Zhou, M.; Yang, F.; Yu, D.; Dong, D.; Yang, C.; Zang, Y.; Tian, J. Multi-crop convolutional neural networks for lung nodule malignancy suspiciousness classification. Pattern Recognit. 2017, 61, 663–673. [Google Scholar] [CrossRef]
- Tomassini, S.; Falcionelli, N.; Sernani, P.; Burattini, L.; Dragoni, A.F. Lung nodule diagnosis and cancer histology classification from computed tomography data by convolutional neural networks: A survey. Comput. Biol. Med. 2022, 146, 105691. [Google Scholar] [CrossRef]
- Halder, A.; Chatterjee, S.; Dey, D. Adaptive morphology aided 2-pathway convolutional neural network for lung nodule classification. Biomed. Signal Process. Control 2022, 72, 103347. [Google Scholar] [CrossRef]
- Kim, H.; Goo, J.M.; Ohno, Y.; Kauczor, H.-U.; Hoffman, E.A.; Gee, J.C.; Van Beek, E.J. Effect of reconstruction parameters on the quantitative analysis of chest computed tomography. J. Thorac. Imaging 2019, 34, 92–102. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Fontaine, K.; Germino, M.; Mulnix, T.; Casey, M.E.; Carson, R.E.; Liu, C. Investigation of sub-centimeter lung nodule quantification for low-dose PET. IEEE Trans. Radiat. Plasma Med. Sci. 2017, 2, 41–50. [Google Scholar] [CrossRef]
- Tonekaboni, S.; Joshi, S.; McCradden, M.D.; Goldenberg, A. What clinicians want: Contextualizing explainable machine learning for clinical end use. In Proceedings of the Machine Learning for Healthcare Conference (PMLR), Ann Arbor, MI, USA, 8–10 August 2019; pp. 359–380. [Google Scholar]
- Nioche, C.; Orlhac, F.; Boughdad, S.; Reuzé, S.; Goya-Outi, J.; Robert, C.; Pellot-Barakat, C.; Soussan, M.; Frouin, F.; Buvat, I. LIFEx: A freeware for radiomic feature calculation in multimodality imaging to accelerate advances in the characterization of tumor heterogeneity. Cancer Res. 2018, 78, 4786–4789. [Google Scholar] [CrossRef] [PubMed]
- Heeren, T.; D’Agostino, R. Robustness of the two independent samples t-test when applied to ordinal scaled data. Stat. Med. 1987, 6, 79–90. [Google Scholar] [CrossRef] [PubMed]
- Rosner, B.; Glynn, R.J.; Ting Lee, M.L. Incorporation of clustering effects for the Wilcoxon rank sum test: A large-sample approach. Biometrics 2003, 59, 1089–1098. [Google Scholar] [CrossRef] [PubMed]
- Das, K.R.; Imon, A. A brief review of tests for normality. Am. J. Theor. Appl. Stat. 2016, 5, 5–12. [Google Scholar]
- Schultz, B.B. Levene’s test for relative variation. Syst. Zool. 1985, 34, 449–456. [Google Scholar] [CrossRef]
- Fonti, V.; Belitser, E. Feature selection using lasso. VU Amst. Res. Pap. Bus. Anal. 2017, 30, 1–25. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Suthaharan, S.; Suthaharan, S. Support vector machine. In Machine Learning Models and Algorithms for Big Data Classification: Thinking with Examples for Effective Learning; Springer: Boston, MA, USA, 2016; pp. 207–235. [Google Scholar]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Frazier, P.I. A tutorial on Bayesian optimization. arXiv 2018, arXiv:1807.02811. [Google Scholar]
- Abdulkareem, N.K.; Hajee, S.I.; Hassan, F.F.; Ibrahim, I.K.; Al-Khalidi, R.E.H.; Abdulqader, N.A. Investigating the slice thickness effect on noise and diagnostic content of single-source multi-slice computerized axial tomography. J. Med. Life 2023, 16, 862. [Google Scholar] [CrossRef] [PubMed]
- LUng Nodule Analysis (LUNA) 2016, Grand Challenges. Available online: https://luna16.grand-challenge.org/Data/ (accessed on 20 November 2023).
- Huang, C.H.; Cheng, D.C. Lung Nodule Detection Method on Low-Dose Chest Computer Tomography Images Using Deep Learning and Its Computer Program Product. Invention Patent I733627, 11 July 2021. [Google Scholar]
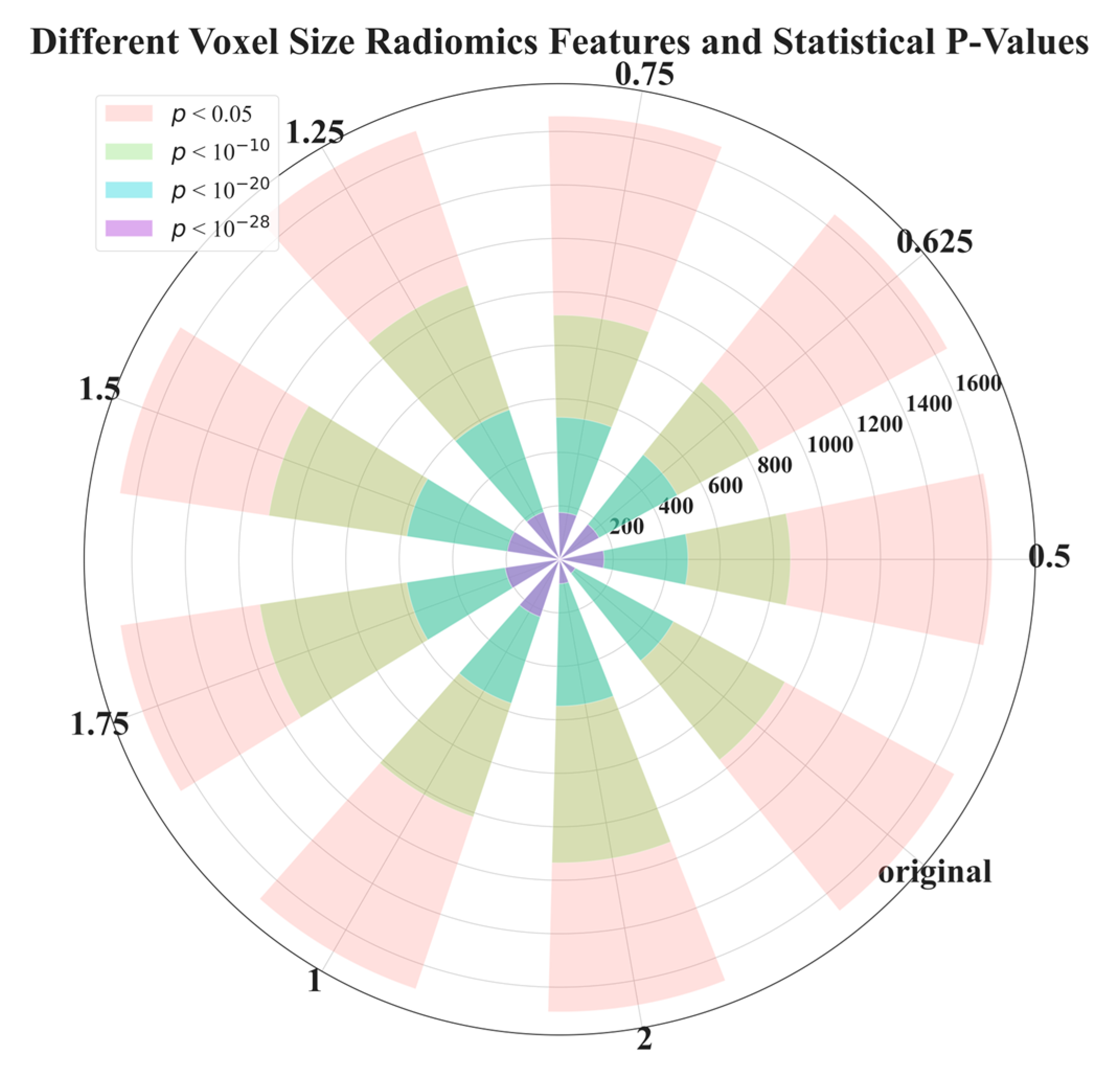
| Voxel Size | 0.5 | 0.625 | 0.75 | 1 | 1.25 | 1.5 | 1.75 | 2 | Original |
|---|---|---|---|---|---|---|---|---|---|
| p < 0.05 | 1617 | 1650 | 1657 | 1694 | 1690 | 1663 | 1661 | 1692 | 1680 |
| p < 1 × 10−10 | 863 | 850 | 913 | 1016 | 1081 | 1100 | 1134 | 1135 | 959 |
| p < 1 × 10−20 | 480 | 501 | 531 | 568 | 590 | 578 | 578 | 549 | 485 |
| p < 1 × 10−28 | 166 | 168 | 175 | 227 | 187 | 198 | 206 | 91 | 67 |
| Unfiltered Features | Statistically Filtered Features | LASSO | t-SNE | |
|---|---|---|---|---|
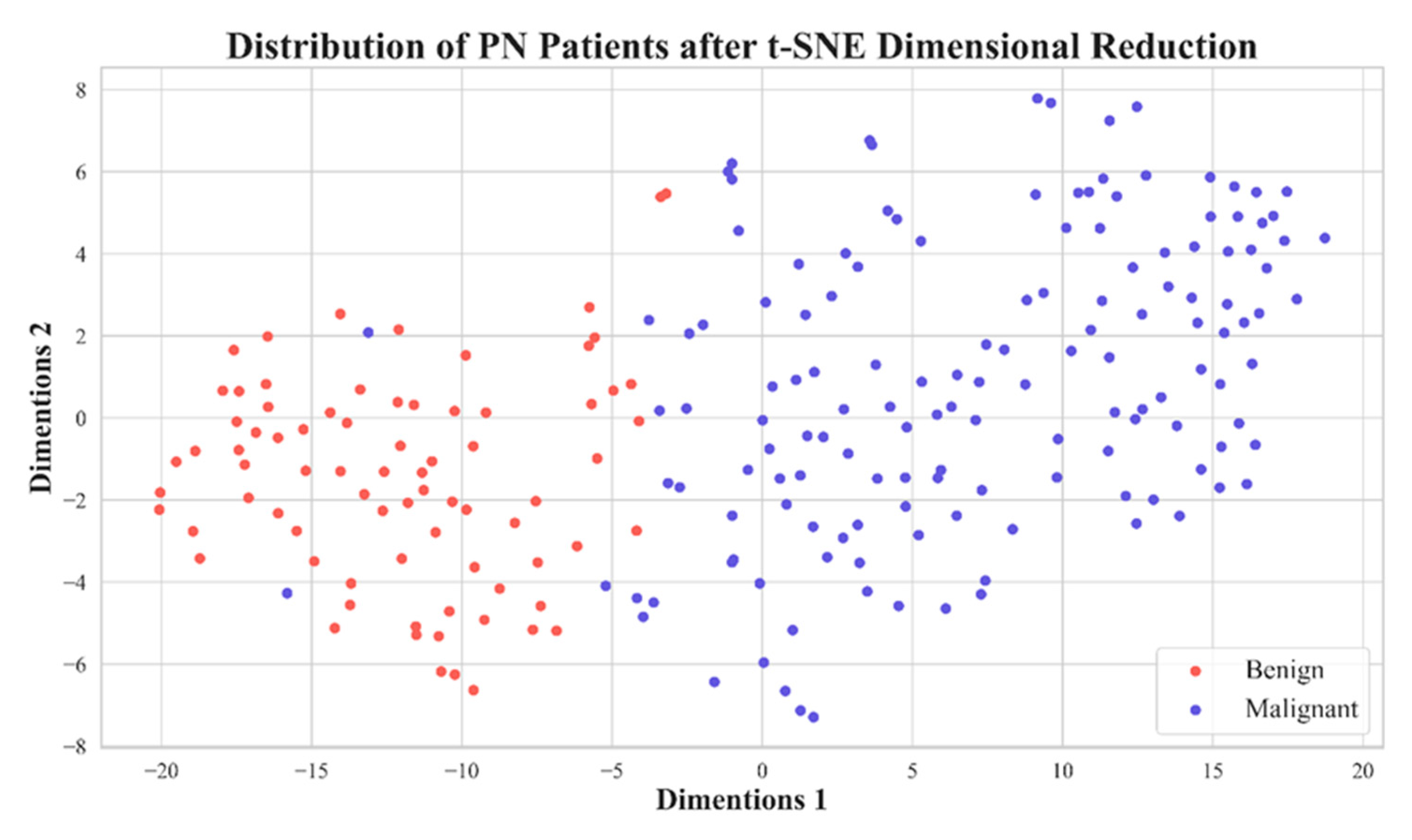
| Feature Number | 2061 | 480 | 11 | 2 |
| Accuracy | AUC | Sensitivity | Precision | F1 Score | |
|---|---|---|---|---|---|
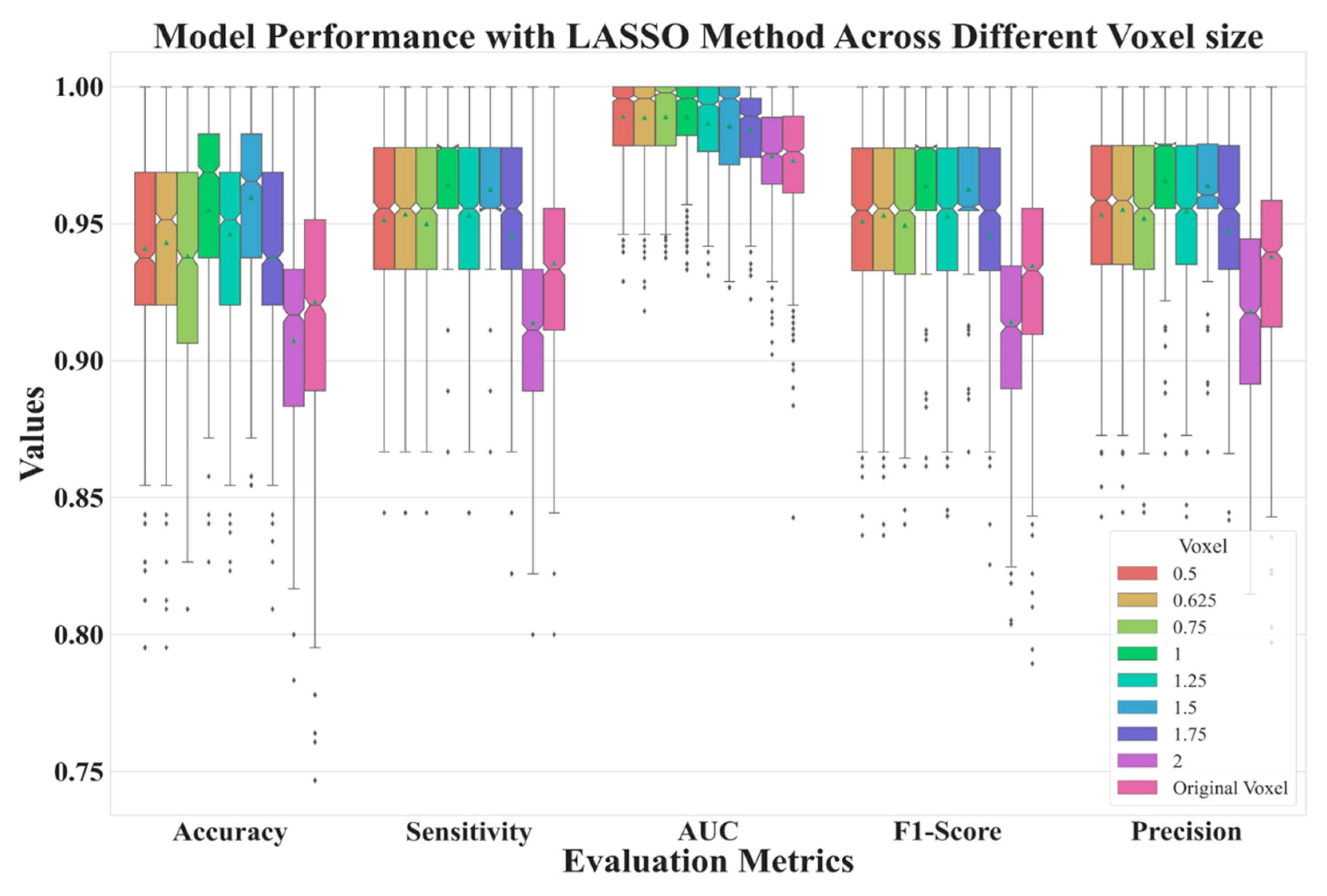
| 0.5 | 0.9409 | 0.9891 | 0.9514 | 0.9533 | 0.9509 |
| 0.625 | 0.9431 | 0.9887 | 0.9535 | 0.9551 | 0.9530 |
| 0.75 | 0.9350 | 0.9890 | 0.9481 | 0.9501 | 0.9473 |
| 1 | 0.9531 | 0.9890 | 0.9624 | 0.9640 | 0.9620 |
| 1.25 | 0.9467 | 0.9866 | 0.9532 | 0.9548 | 0.9530 |
| 1.5 | 0.9596 | 0.9855 | 0.9619 | 0.9633 | 0.9619 |
| 1.75 | 0.9371 | 0.9844 | 0.9452 | 0.9468 | 0.9449 |
| 2 | 0.9073 | 0.9747 | 0.9156 | 0.9197 | 0.9159 |
| Original | 0.9223 | 0.9731 | 0.9357 | 0.9381 | 0.9349 |
| Halder et al., 2021 [24] | 0.9610 | 0.9936 | 0.9685 | - | - |
| Mehta et al., 2021 [19] | - | 0.8659 | - | - | - |
| Shen et al., 2017 [22] | 0.8612 | - | - | - | - |
| Lu et al., 2021 [18] | 0.934 | 0.984 | - | - |
| Feature Description | Types |
|---|---|
| original_gldm_SmallDependenceLowGrayLevelEmphasis | Texture |
| log-sigma-2-0-mm-3D_glcm_DifferenceEntropy | Texture |
| log-sigma-2-0-mm-3D_gldm_SmallDependenceEmphasis | Texture |
| log-sigma-3-0-mm-3D_glszm_ZonePercentage | Texture |
| lbp-2D_gldm_DependenceNonUniformityNormalized | Texture |
| lbp-3D-m1_gldm_DependenceNonUniformityNormalized | Texture |
| lbp-3D-m2_gldm_DependenceNonUniformityNormalized | Texture |
| log-sigma-2-0-mm-3D_firstorder_Mean | First order |
| lbp-3D-m1_firstorder_Skewness lbp-3D- | First order |
| wavelet-LLH_firstorder_Mean | First order |
| wavelet-LHL_firstorder_Mean | First order |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsiao, C.-C.; Peng, C.-H.; Wu, F.-Z.; Cheng, D.-C. Impact of Voxel Normalization on a Machine Learning-Based Method: A Study on Pulmonary Nodule Malignancy Diagnosis Using Low-Dose Computed Tomography (LDCT). Diagnostics 2023, 13, 3690. https://doi.org/10.3390/diagnostics13243690
Hsiao C-C, Peng C-H, Wu F-Z, Cheng D-C. Impact of Voxel Normalization on a Machine Learning-Based Method: A Study on Pulmonary Nodule Malignancy Diagnosis Using Low-Dose Computed Tomography (LDCT). Diagnostics. 2023; 13(24):3690. https://doi.org/10.3390/diagnostics13243690
Chicago/Turabian StyleHsiao, Chia-Chi, Chen-Hao Peng, Fu-Zong Wu, and Da-Chuan Cheng. 2023. "Impact of Voxel Normalization on a Machine Learning-Based Method: A Study on Pulmonary Nodule Malignancy Diagnosis Using Low-Dose Computed Tomography (LDCT)" Diagnostics 13, no. 24: 3690. https://doi.org/10.3390/diagnostics13243690
APA StyleHsiao, C.-C., Peng, C.-H., Wu, F.-Z., & Cheng, D.-C. (2023). Impact of Voxel Normalization on a Machine Learning-Based Method: A Study on Pulmonary Nodule Malignancy Diagnosis Using Low-Dose Computed Tomography (LDCT). Diagnostics, 13(24), 3690. https://doi.org/10.3390/diagnostics13243690








