Development of “Mathematical Technology for Cytopathology,” an Image Analysis Algorithm for Pancreatic Cancer
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Design
2.2. Procedure of EUS-FNA/EUS-FNB and Diagnosis
2.3. Automatic Diagnosis Assistance System
2.4. The Mathematical Method
2.4.1. The Reaction–Diffusion System
2.4.2. Numerical Computations
2.5. Calculating the Quantitative Index
2.6. Classifying Tissues as Normal or Adenocarcinoma Tissues
2.7. Evaluating the Classification Accuracy
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2019. CA Cancer J. Clin. 2019, 69, 7–34. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bray, F.; Ferlay, J.; Soerjomataram, I.; Siegel, R.L.; Torre, L.A.; Jemal, A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2018, 68, 394–424. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Halperin, D.M.; Varadhachary, G.R. Resectable, borderline resectable, and locally advanced pancreatic cancer: What does it matter? Curr. Oncol. Rep. 2014, 16, 366. [Google Scholar] [CrossRef] [PubMed]
- ASGE Standards of Practice Committee; Eloubeidi, M.A.; Decker, G.A.; Chandrasekhara, V.; Chathadi, K.V.; Early, D.S.; Evans, J.A.; Fanelli, R.D.; Fisher, D.A.; Foley, K.; et al. The role of endoscopy in the evaluation and management of patients with solid pancreatic neoplasia. Gastrointest. Endosc. 2016, 83, 17–28. [Google Scholar] [CrossRef]
- Jenssen, C.; Hocke, M.; Fusaroli, P.; Gilja, O.H.; Buscarini, E.; Havre, R.F.; Ignee, A.; Saftoiu, A.; Vilmann, P.; Burmester, E.; et al. EFSUMB guidelines on interventional ultrasound (INVUS), part IV-EUS-guided interventions: General aspects and EUS-guided sampling (short version). Ultraschall Med. 2016, 37, 157–169. [Google Scholar] [CrossRef] [Green Version]
- Iwashita, T.; Uemura, S.; Mita, N.; Iwasa, Y.; Ichikawa, H.; Senju, A.; Yasuda, I.; Shimizu, M. Utility of endoscopic ultrasound and endoscopic ultrasound-guided fine-needle aspiration for the diagnosis and management of pancreatic cystic lesions: Differences between the guidelines. Dig. Endosc. 2020, 32, 251–262. [Google Scholar] [CrossRef]
- Yang, F.; Liu, E.; Sun, S. Rapid on-site evaluation (ROSE) with EUS-FNA: The ROSE looks beautiful. Endosc. Ultrasound 2019, 8, 283–287. [Google Scholar]
- Klapman, J.B.; Logrono, R.; Dye, C.E.; Waxman, I. Clinical impact of on-site cytopathology interpretation on endoscopic ultrasound-guided fine needle aspiration. Am. J. Gastroenterol. 2003, 98, 1289–1294. [Google Scholar] [CrossRef]
- Polkowski, M.; Jenssen, C.; Kaye, P.; Carrara, S.; Deprez, P.; Gines, A.; Fernández-Esparrach, G.; Eisendrath, P.; Aithal, G.P.; Arcidiacono, P.; et al. Technical aspects of endoscopic ultrasound (EUS)-guided sampling in gastroenterology: European Society of Gastrointestinal Endoscopy (ESGE) Technical Guideline—March 2017. Endoscopy 2017, 49, 989–1006. [Google Scholar] [CrossRef] [Green Version]
- Dey, P. The emerging role of deep learning in cytology. Cytopathology 2021, 32, 154–160. [Google Scholar] [CrossRef]
- McAlpine, E.D.; Pantanowitz, L.; Michelow, P.M. Challenges developing deep learning algorithms in cytology. Acta Cytol. 2021, 65, 301–309. [Google Scholar] [CrossRef] [PubMed]
- Qaiser, T.; Taniyama, D.; Epstein, D.; Sakamoto, N.; Nakane, K.; Epstein, D.; Rajpoot, N. Fast and accurate tumor segmentation of histology images using persistent homology and deep convolutional features. Med. Image Anal. 2019, 55, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, C.; Nakane, K.; Wang, X.; Fu, Y.; Lu, H.; Fan, X.; Feldman, M.D.; Madabhushi, A.; Xu, J. Automated Gleason grading on prostate biopsy slides by statistical representations of homology Profile. Comput. Methods Programs Biomed. 2020, 194, 105528. [Google Scholar] [CrossRef] [PubMed]
- Nishio, M.; Nishio, M.; Jimbo, N.; Nakane, K. Homology-based image processing for automatic classification of histopathological images of lung tissue. Cancers 2021, 13, 1192. [Google Scholar] [CrossRef]
- Nakane, K.; Takiyama, A.; Mori, S.; Matsuura, N. Homology-based method for detecting regions of interest in colonic digital images. Diagn. Pathol. 2015, 10, 36. [Google Scholar] [CrossRef] [Green Version]
- Edelsbrunner, H.; Harer, J. Persistent homology—A survey. Contemp. Math. 2008, 453, 257–282. [Google Scholar]
- Qaiser, T.; Sirinukunwattana, K.; Nakane, K.; Tsang, Y.W.; Epstein, D.; Rajpoot, N. Persistent homology for fast tumor segmentation in whole slide histology images. Procedia Comput. Sci. 2016, 90, 119–124. [Google Scholar] [CrossRef] [Green Version]
- Epstein, I.R.; Pojman, J.A. An Introduction to Nonlinear Chemical Dynamics—Oscillations, Waves, Patterns and Chaos; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Nomura, A.; Ichikawa, M.; Sianipar, R.H.; Miike, H. Edge detection with reaction-diffusion equations having a local average threshold. Pattern Recognit. Image Anal. 2008, 18, 289–299. [Google Scholar] [CrossRef]
- Mahara, H.; Mizobe, K.; Kida, K.; Nakane, K. Image analyzing method to detect vague boundaries by using reaction-diffusion system. Appl. Numer. Math. 2017, 114, 124–131. [Google Scholar] [CrossRef]
- FitzHugh, R. Impulses and physiological states in theoretical models of nerve membrane. Biophys. J. 1961, 1, 445–466. [Google Scholar] [CrossRef] [Green Version]
- Kondo, S.; Asal, R. A reaction-diffusion wave on the skin of the marine angelfish Pomacanthus. Nature 1995, 376, 765–768. [Google Scholar] [CrossRef] [PubMed]
- Nagumo, J.; Arimoto, S.; Yoshizawa, S. An active pulse transmission line simulating nerve axon. Proc. IRE 1962, 50, 2061–2070. [Google Scholar] [CrossRef]
- Naito, Y.; Tsuneki, M.; Fukushima, N.; Koga, Y.; Higashi, M.; Notohara, K.; Aishima, S.; Ohike, N.; Tajiri, T.; Yamaguchi, H.; et al. A deep learning model to detect pancreatic ductal adenocarcinoma on endoscopic ultrasound-guided fine-needle biopsy. Sci. Rep. 2021, 11, 8454. [Google Scholar] [CrossRef] [PubMed]
- Rimbaş, M.; Crino, S.F.; Gasbarrini, A.; Costamagna, G.; Scarpa, A.; Larghi, A. EUS-guided fine-needle tissue acquisition for solid pancreatic lesions: Finally moving from fine-needle aspiration to fine-needle biopsy? Endosc. Ultrasound 2018, 7, 137–140. [Google Scholar]
- Chen, Y.I.; Chatterjee, A.; Berger, R.; Kanber, Y.; Wyse, J.M.; Lam, E.; Gan, S.I.; Auger, M.; Kenshil, S.; Telford, J.; et al. Endoscopic ultrasound (EUS)-guided fine needle biopsy alone vs. EUS-guided fine needle aspiration with rapid onsite evaluation in pancreatic lesions: A multicenter randomized trial. Endoscopy 2022, 54, 4–12. [Google Scholar] [CrossRef] [PubMed]
- Crinò, S.F.; Di Mitri, R.; Nguyen, N.Q.; Tarantino, I.; de Nucci, G.; Deprez, P.H.; Carrara, S.; Kitano, M.; Shami, V.M.; Fernández-Esparrach, G.; et al. Endoscopic ultrasound-guided fine-needle biopsy with or without rapid on-site evaluation for diagnosis of solid pancreatic lesions: A randomized controlled non-inferiority trial. Gastroenterology 2021, 16, 899–909. [Google Scholar] [CrossRef]
- Crinò, S.F.; Le Grazie, M.; Manfrin, E.; Bellocchi, M.C.C.; Bernardoni, L.; Granato, A.; Locatelli, F.; Parisi, A.; Di Stefano, S.; Frulloni, L.; et al. Randomized trial comparing fork-tip and side-fenestrated needles for EUS-guided fine-needle biopsy of solid pancreatic lesions. Gastrointest. Endosc. 2020, 92, 648–658. [Google Scholar] [CrossRef]
- Gkolfakis, P.; Crinò, S.F.; Tziatzios, G.; Ramai, D.; Papaefthymiou, A.; Papanikolaou, I.S.; Triantafyllou, K.; Arvanitakis, M.; Lisotti, A.; Fusaroli, P.; et al. Comparative diagnostic performance of end-cutting fine-needle biopsy needles for endoscopic ultrasound tissue sampling of solid pancreatic masses: A network meta-analysis. Gastrointest. Endosc. 2022; ahead of print. [Google Scholar] [CrossRef]
- Mie, T.; Sasaki, T.; Kanata, R.; Furukawa, T.; Takeda, T.; Kasuga, A.; Matsuyama, M.; Ozaka, M.; Sasahira, N. Diagnostic yield of endoscopic ultrasound-guided tissue acquisition for small solid pancreatic lesions. Endosc. Int. Open 2020, 8, E1359–E1364. [Google Scholar]
- Fitzpatrick, M.J.; Hernandez-Barco, Y.G.; Krishnan, K.; Casey, B.; Pitman, M.B. Evaluating triage protocols for endoscopic ultrasound-guided fine needle biopsies of the pancreas. J. Am. Soc. Cytopathol. 2020, 9, 396–404. [Google Scholar] [CrossRef]
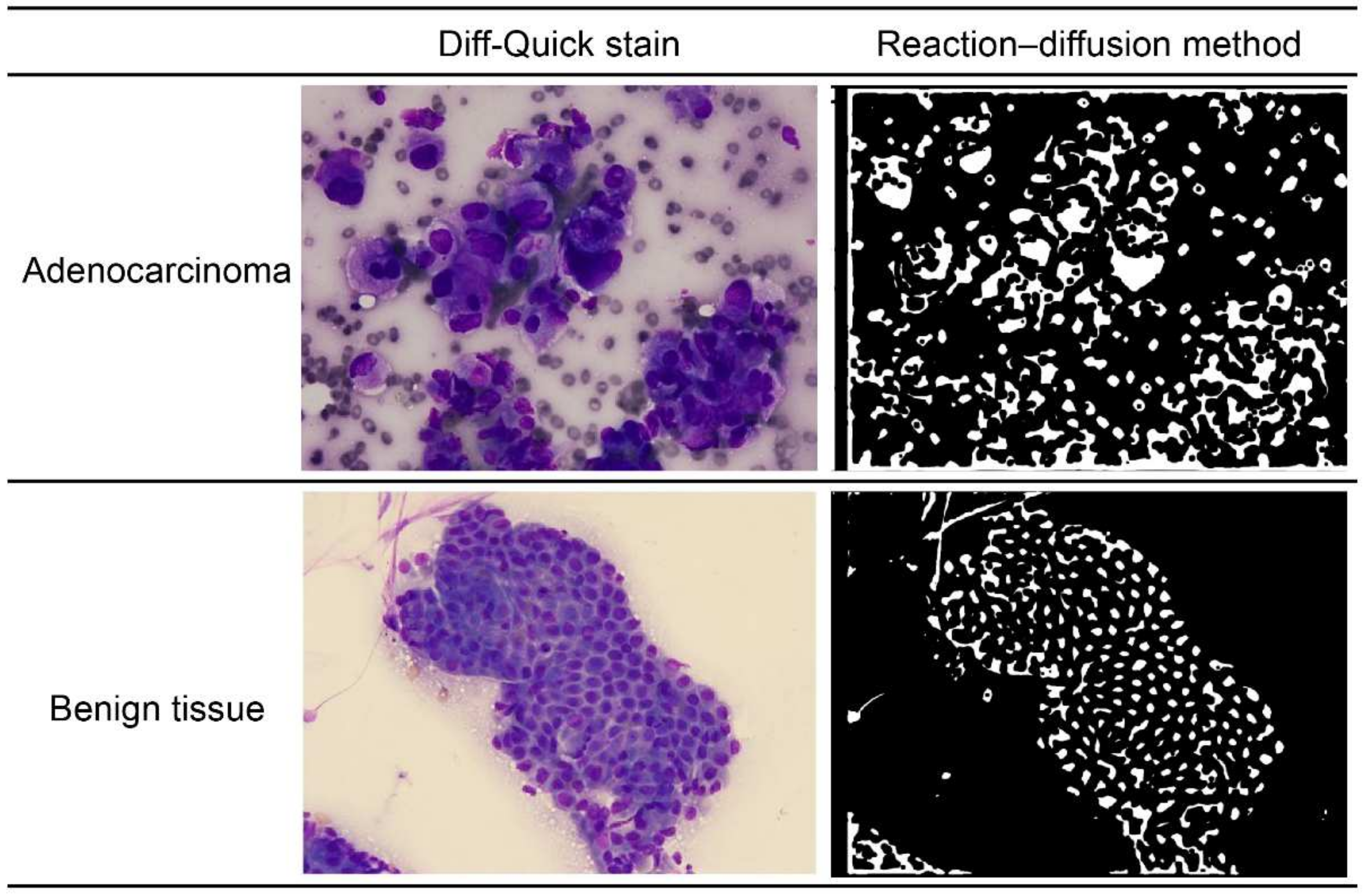

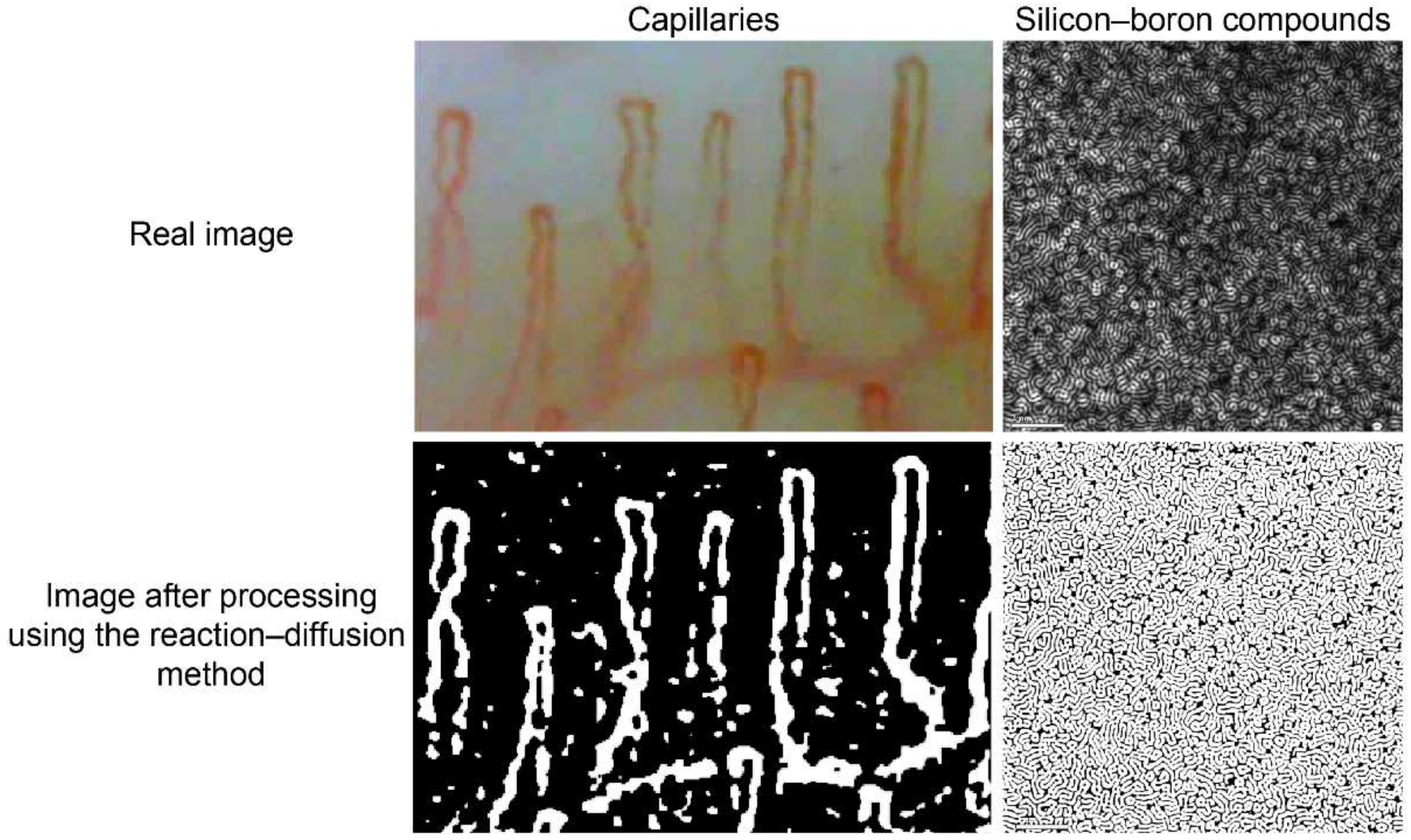

| Quantitative Index | Accuracy (%) | Sensitivity (%) | Specificity (%) | |
|---|---|---|---|---|
| Univariate analysis | Number of pixels | 71 | 75 | 65 |
| Area | 39 | 47 | 28 | |
| Interquartile area range | 67 | 71 | 61 | |
| Area/pixel | 68 | 72 | 63 | |
| Average perimeter of the connected components | 57 | 64 | 48 | |
| Average circularity of the connected components | 46 | 53 | 36 | |
| Interquartile circularity range of the connected components | 43 | 50 | 33 | |
| Multivariate analysis | Number of pixels + interquartile area range + average perimeter of the connected components | 75 | 78 | 70 |
| Quantitative Index | Accuracy (%) | Sensitivity (%) | Specificity (%) | |
|---|---|---|---|---|
| Univariate analysis | Number of pixels | 68 | 72 | 62 |
| Area | 42 | 49 | 31 | |
| Interquartile area range | 67 | 71 | 61 | |
| Area/pixel | 66 | 71 | 60 | |
| Average perimeter of the connected components | 40 | 49 | 27 | |
| Average circularity of the connected components | 24 | 34 | 10 | |
| Interquartile circularity range of the connected components | 69 | 74 | 64 | |
| Multivariate analysis | Number of pixels + interquartile area range | 70 | 74 | 65 |
| Quantitative Index | Accuracy (%) | Sensitivity (%) | Specificity (%) | |
|---|---|---|---|---|
| Univariate analysis | Number of pixels | 56 | 62 | 48 |
| Area | 52 | 58 | 44 | |
| Interquartile area range | 69 | 73 | 64 | |
| Area/pixel | 55 | 61 | 48 | |
| Average perimeter of the connected components | 46 | 54 | 34 | |
| Average circularity of the connected components | 23 | 33 | 9 | |
| Interquartile circularity range of the connected components | 74 | 78 | 69 | |
| Multivariate analysis | Area/pixel + interquartile circularity range of the connected components | 74 | 77 | 70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamada, R.; Nakane, K.; Kadoya, N.; Matsuda, C.; Imai, H.; Tsuboi, J.; Hamada, Y.; Tanaka, K.; Tawara, I.; Nakagawa, H. Development of “Mathematical Technology for Cytopathology,” an Image Analysis Algorithm for Pancreatic Cancer. Diagnostics 2022, 12, 1149. https://doi.org/10.3390/diagnostics12051149
Yamada R, Nakane K, Kadoya N, Matsuda C, Imai H, Tsuboi J, Hamada Y, Tanaka K, Tawara I, Nakagawa H. Development of “Mathematical Technology for Cytopathology,” an Image Analysis Algorithm for Pancreatic Cancer. Diagnostics. 2022; 12(5):1149. https://doi.org/10.3390/diagnostics12051149
Chicago/Turabian StyleYamada, Reiko, Kazuaki Nakane, Noriyuki Kadoya, Chise Matsuda, Hiroshi Imai, Junya Tsuboi, Yasuhiko Hamada, Kyosuke Tanaka, Isao Tawara, and Hayato Nakagawa. 2022. "Development of “Mathematical Technology for Cytopathology,” an Image Analysis Algorithm for Pancreatic Cancer" Diagnostics 12, no. 5: 1149. https://doi.org/10.3390/diagnostics12051149
APA StyleYamada, R., Nakane, K., Kadoya, N., Matsuda, C., Imai, H., Tsuboi, J., Hamada, Y., Tanaka, K., Tawara, I., & Nakagawa, H. (2022). Development of “Mathematical Technology for Cytopathology,” an Image Analysis Algorithm for Pancreatic Cancer. Diagnostics, 12(5), 1149. https://doi.org/10.3390/diagnostics12051149






