Autocatalytic Networks at the Basis of Life’s Origin and Organization
Abstract
1. Life’s Organization
2. Formal Models
- hypercycles (Eigen & Schuster, Germany),
- chemotons (Gánti, Hungary),
- autopoietic systems (Maturana & Varela, Chile),
- (M,R) systems (Rosen, USA/Canada),
- collectively autocatalytic sets (Kauffman, USA).
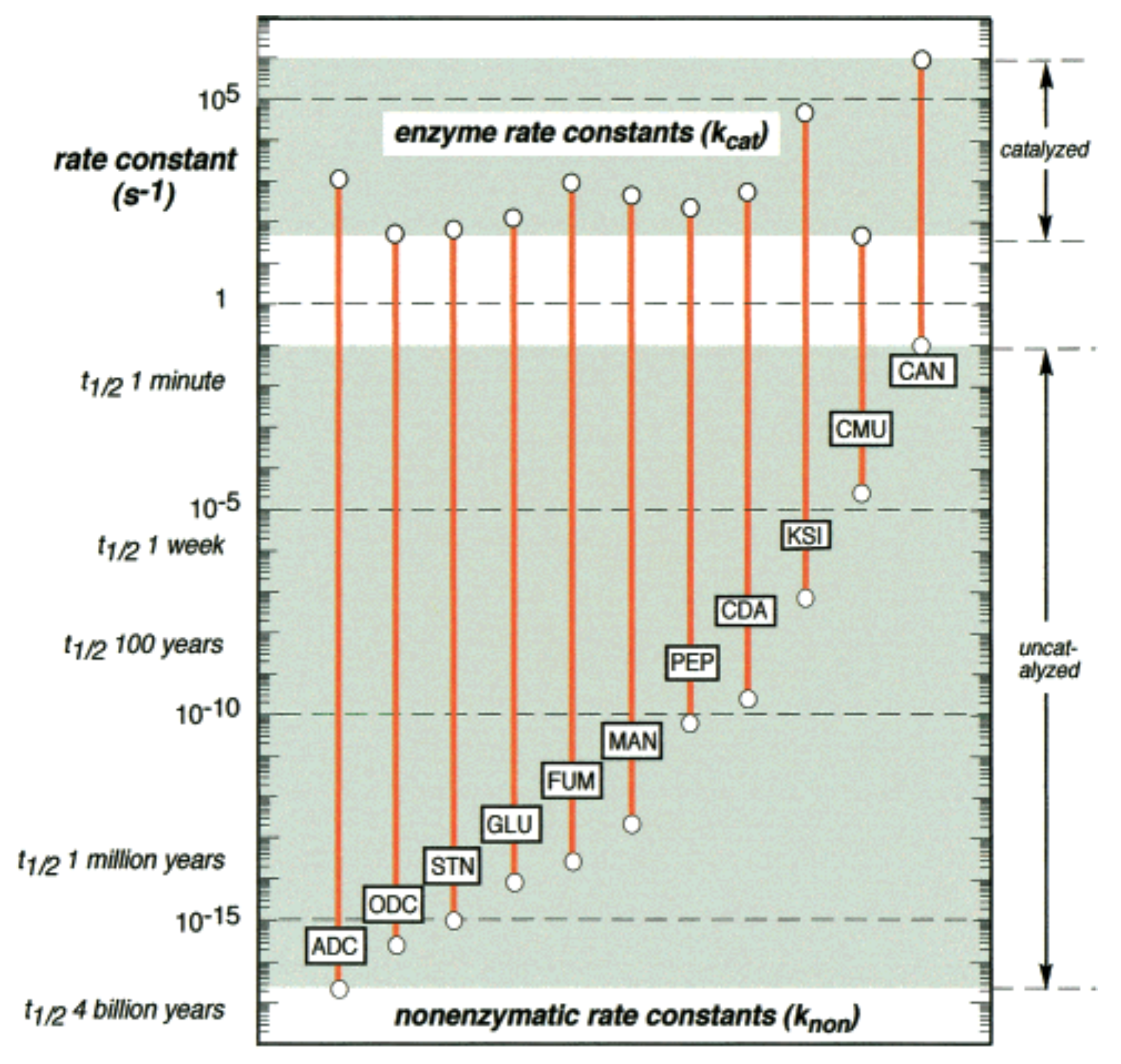
3. Catalysis: The Secret to Life?
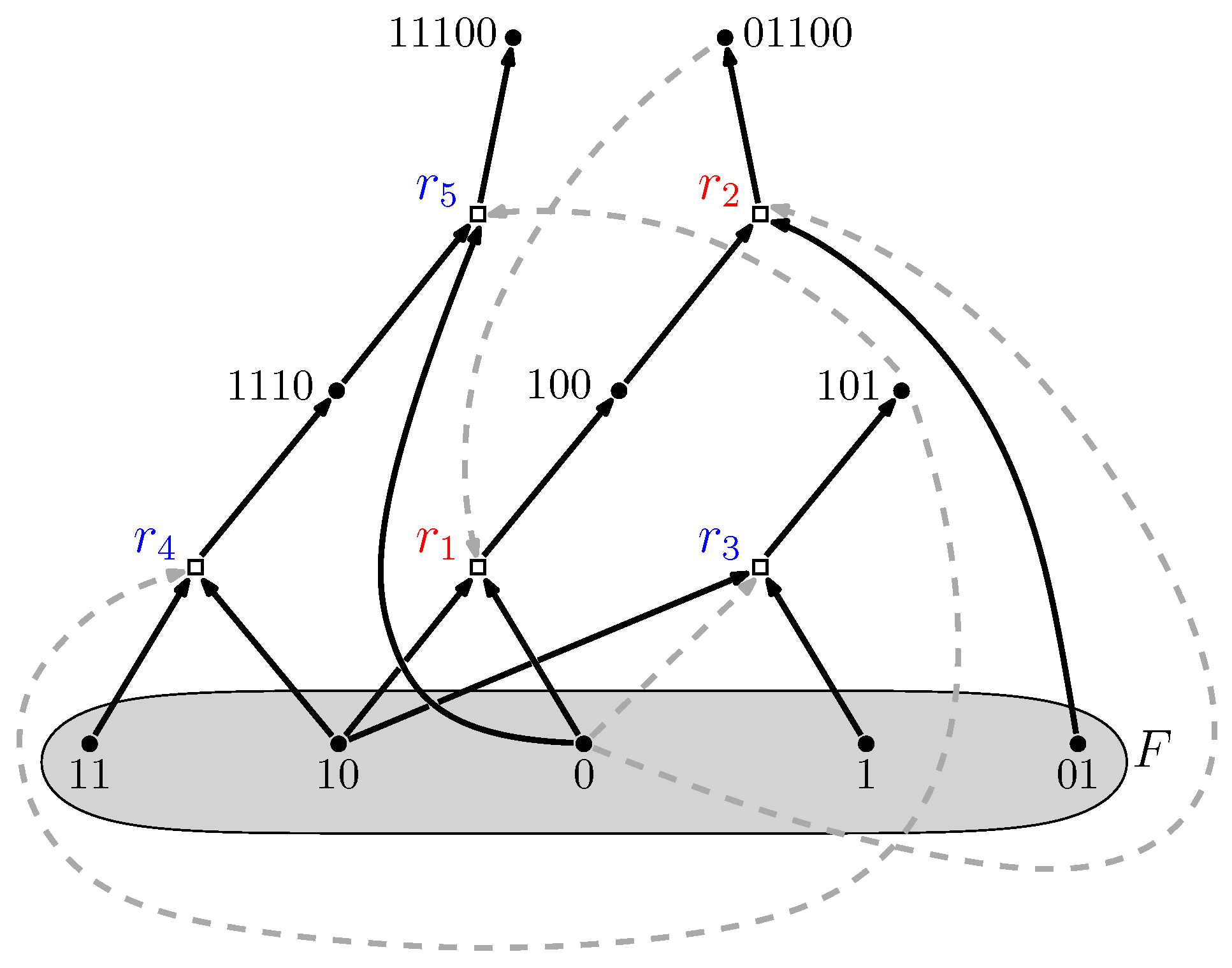
4. Autocatalytic Sets
- Reflexively Autocatalytic (RA): Each reaction is catalyzed by at least one molecule type that is either a product of or is present in the food set F; and
- F-generated (F): All reactants involved in reactions in can be created from the food set F by using a series of reactions only from itself.
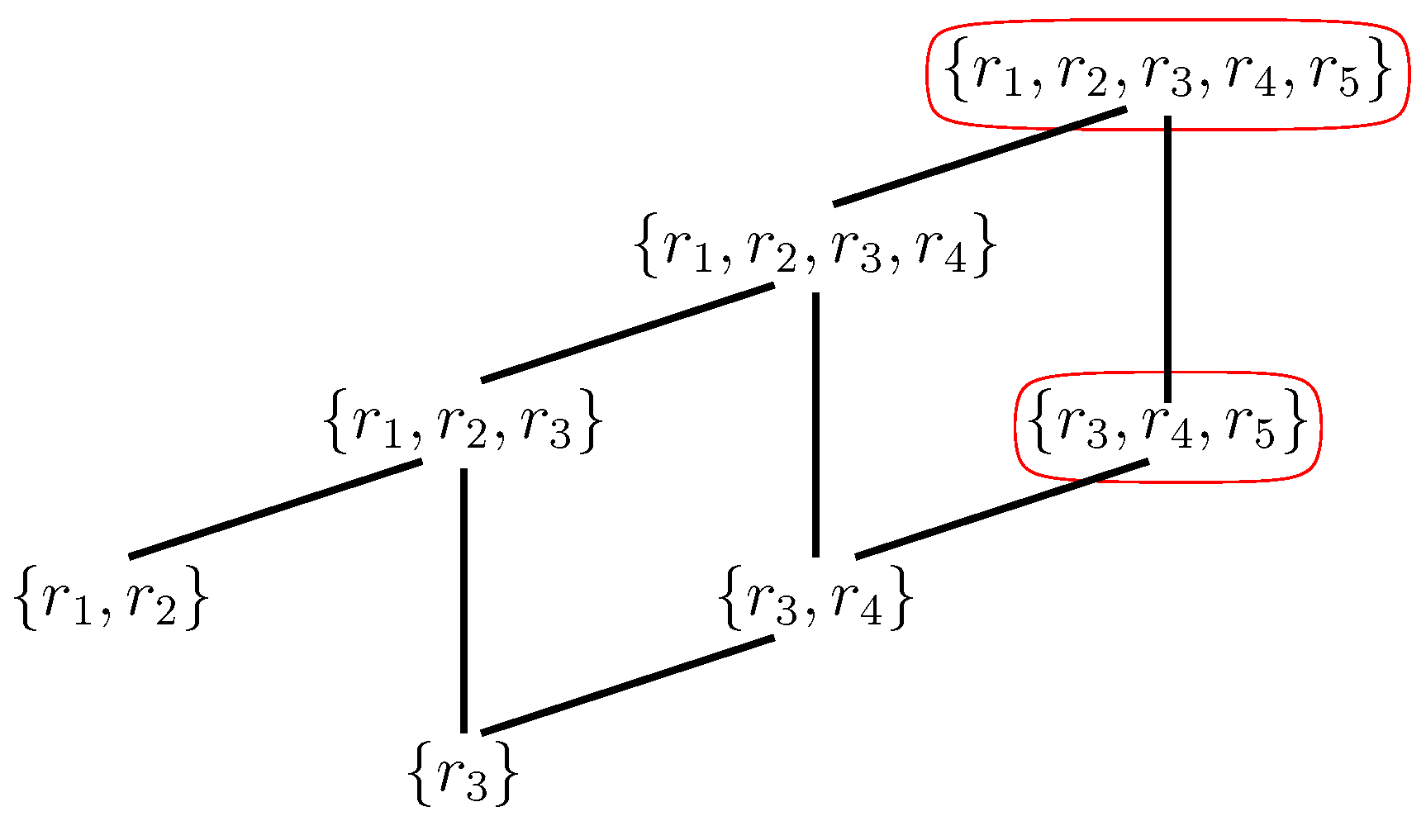
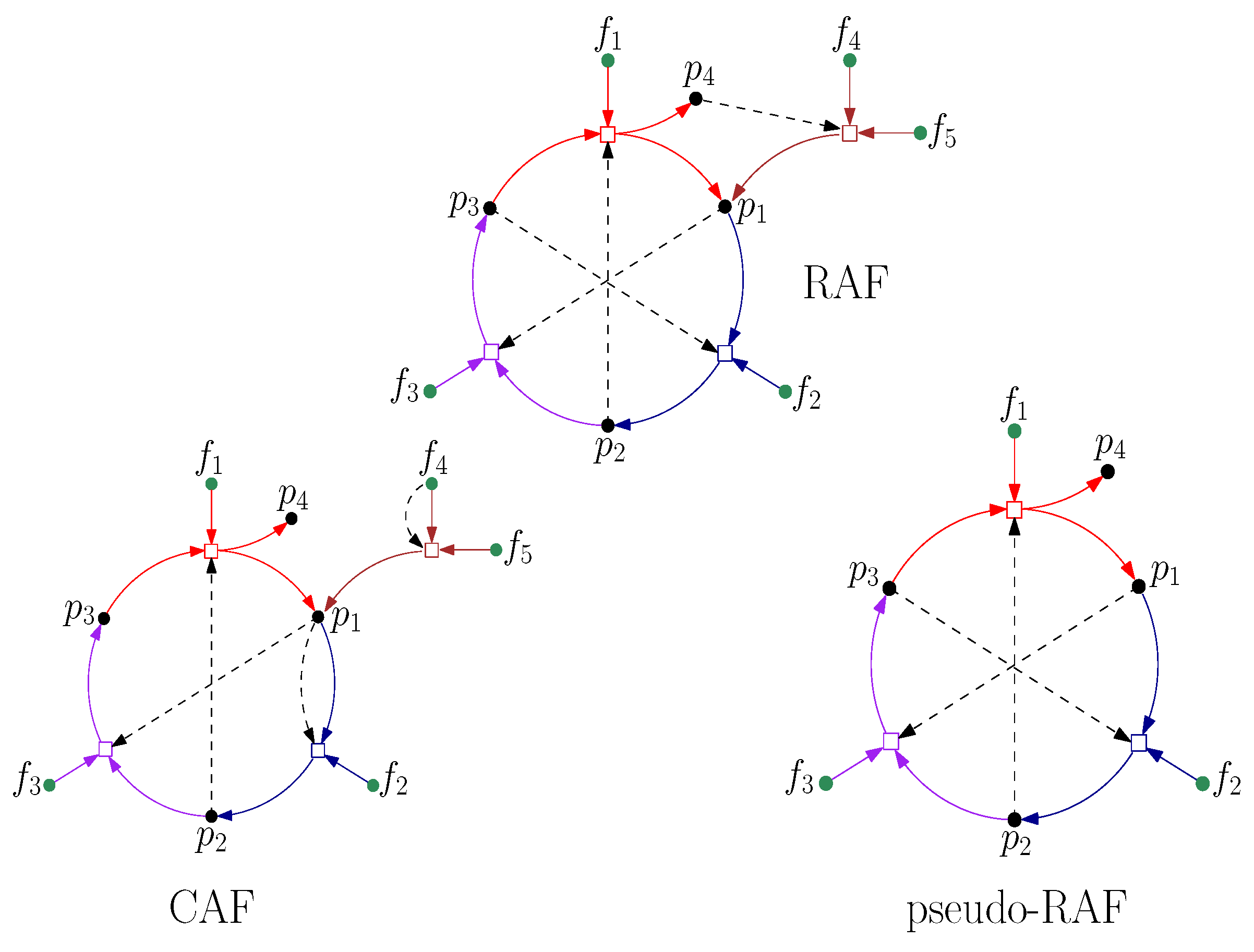
5. RAF Theory
6. Cofactors and Coevolution
7. Beyond Chemistry
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Skoultchi, A.I.; Morowitz, H.J. Information storage and survival of biological systems at temperatures near absolute zero. Yale J. Biol. Med. 1964, 37, 158–163. [Google Scholar] [PubMed]
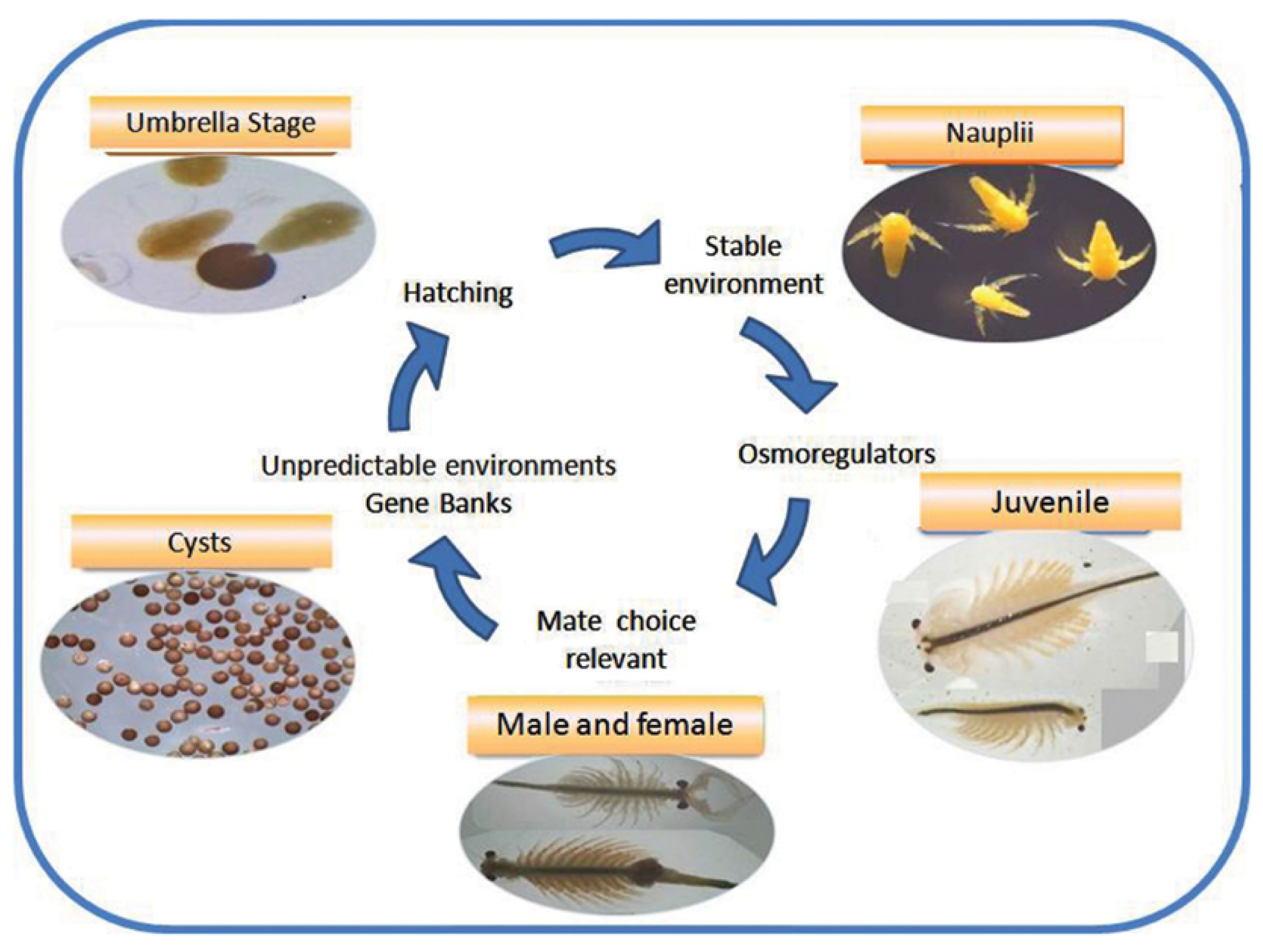
- Gajardo, G.M.; Beardmore, J.A. The brine shrimp Artemia: Adapted to critical life conditions. Front. Physiol. 2012, 3, 185. [Google Scholar] [CrossRef] [PubMed]
- Eigen, M. Selforganization of matter and the evolution of biological macromolecules. Naturwissenschaften 1971, 58, 465–523. [Google Scholar] [CrossRef] [PubMed]
- Eigen, M.; Schuster, P. The Hypercycle; Springer: Berlin/Heidelberg, Germany, 1979. [Google Scholar]
- Boerlijst, M.C.; Hogeweg, P. Spiral wave structure in pre-biotic evolution: Hypercycles stable against parasites. Phys. D 1991, 48, 17–28. [Google Scholar] [CrossRef]
- Boerlijst, M.C.; Hogeweg, P. Spatial gradients enhance persistence of hypercycles. Phys. D 1995, 88, 29–39. [Google Scholar] [CrossRef]
- Maynard Smith, J. Hypercycles and the origin of life. Nature 1979, 280, 445–446. [Google Scholar] [CrossRef]
- Gánti, T. Organization of chemical reactions into dividing and metabolizing units: The chemotons. BioSystems 1975, 7, 15–21. [Google Scholar] [CrossRef]
- Gánti, T. The Principles of Life; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Varela, F.J.; Maturana, H.R.; Uribe, R. Autopoiesis: The organization of living systems, its characterization and a model. BioSystems 1974, 5, 187–196. [Google Scholar] [CrossRef]
- Rosen, R. Life Itself; Columbia University Press: New York, NY, USA, 1991. [Google Scholar]
- Letelier, J.C.; Marín, G.; Mpodozis, J. Autopoietic and (M,R) systems. J. Theor. Biol. 2003, 222, 261–272. [Google Scholar] [CrossRef]
- Walde, P.; Wick, R.; Fresta, M.; Mangone, A.; Luigi Luisi, P. Autopoietic Self-Reproduction of Fatty Acid Vesicles. J. Am. Chem. Soc. 1994, 116, 11649–11654. [Google Scholar] [CrossRef]
- Kauffman, S.A. Cellular homeostasis, epigenesis and replication in randomly aggregated macromolecular systems. J. Cybern. 1971, 1, 71–96. [Google Scholar] [CrossRef]
- Kauffman, S.A. Autocatalytic sets of proteins. J. Theor. Biol. 1986, 119, 1–24. [Google Scholar] [CrossRef]
- Kauffman, S.A. The Origins of Order; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Farmer, J.D.; Kauffman, S.A.; Packard, N.H. Autocatalytic replication of polymers. Phys. D 1986, 22, 50–67. [Google Scholar] [CrossRef]
- Bagley, R.J.; Farmer, J.D. Spontaneous emergence of a metabolism. In Artificial Life II; Langton, C.G., Taylor, C., Farmer, J.D., Rasmussen, S., Eds.; Addison-Wesley: Boston, MA, USA, 1991; pp. 93–140. [Google Scholar]
- Bagley, R.J.; Farmer, J.D.; Fontana, W. Evolution of a metabolism. In Artificial Life II; Langton, C.G., Taylor, C., Farmer, J.D., Rasmussen, S., Eds.; Addison-Wesley: Boston, MA, USA, 1991; pp. 141–158. [Google Scholar]
- Sievers, D.; von Kiedrowski, G. Self-replication of complementary nucleotide-based oligomers. Nature 1994, 369, 221–224. [Google Scholar] [CrossRef]
- Kim, D.E.; Joyce, G.F. Cross-catalytic replication of an RNA ligase ribozyme. Chem. Biol. 2004, 11, 1505–1512. [Google Scholar] [CrossRef]
- Ashkenasy, G.; Jegasia, R.; Yadav, M.; Ghadiri, M.R. Design of a directed molecular network. Proc. Natl. Acad. Sci. USA 2004, 101, 10872–10877. [Google Scholar] [CrossRef] [PubMed]
- Vaidya, N.; Manapat, M.L.; Chen, I.A.; Xulvi-Brunet, R.; Hayden, E.J.; Lehman, N. Spontaneous network formation among cooperative RNA replicators. Nature 2012, 491, 72–77. [Google Scholar] [CrossRef] [PubMed]
- Arsène, S.; Ameta, S.; Lehman, N.; Griffiths, A.D.; Nghe, P. Coupled catabolism and anabolism in autocatalytic RNA sets. Nucleic Acids Res. 2018, 46, 9660–9666. [Google Scholar] [CrossRef]
- Hordijk, W.; Steel, M. Chasing the tail: The emergence of autocatalytic networks. BioSystems 2017, 152, 1–10. [Google Scholar] [CrossRef]
- Szöke, A.; Scott, W.G.; Hajdu, J. Catalysis, evolution and life. FEBS Lett. 2003, 553, 18–20. [Google Scholar] [CrossRef]
- Wolfenden, R.; Snider, M.J. The depth of chemical time and the power of enzymes as catalysts. Acc. Chem. Res. 2001, 34, 938–945. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Steel, M. Detecting autocatalytic, self-sustaining sets in chemical reaction systems. J. Theor. Biol. 2004, 227, 451–461. [Google Scholar] [CrossRef]
- Hordijk, W.; Kauffman, S.A.; Steel, M. Required levels of catalysis for emergence of autocatalytic sets in models of chemical reaction systems. Int. J. Mol. Sci. 2011, 12, 3085–3101. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Steel, M. Predicting template-based catalysis rates in a simple catalytic reaction model. J. Theor. Biol. 2012, 295, 132–138. [Google Scholar] [CrossRef]
- Steel, M. The emergence of a self-catalysing structure in abstract origin-of-life models. Appl. Math. Lett. 2000, 3, 91–95. [Google Scholar] [CrossRef]
- Mossel, E.; Steel, M. Random biochemical networks: The probability of self-sustaining autocatalysis. J. Theor. Biol. 2005, 233, 327–336. [Google Scholar] [CrossRef]
- Hordijk, W.; Hasenclever, L.; Gao, J.; Mincheva, D.; Hein, J. An investigation into irreducible autocatalytic sets and power law distributed catalysis. Nat. Comput. 2014, 13, 287–296. [Google Scholar] [CrossRef]
- Hordijk, W.; Wills, P.R.; Steel, M. Autocatalytic sets and biological specificity. Bull. Math. Biol. 2014, 76, 201–224. [Google Scholar] [CrossRef]
- Smith, J.; Steel, M.; Hordijk, W. Autocatalytic sets in a partitioned biochemical network. J. Syst. Chem. 2014, 5, 2. [Google Scholar] [CrossRef]
- Hordijk, W.; Steel, M. Autocatalytic sets in polymer networks with variable catalysis distributions. J. Math. Chem. 2016, 54, 1997–2021. [Google Scholar] [CrossRef]
- Hordijk, W.; Steel, M.; Kauffman, S. The structure of autocatalytic sets: Evolvability, enablement, and emergence. Acta Biotheor. 2012, 60, 379–392. [Google Scholar] [CrossRef]
- Hordijk, W.; Smith, J.I.; Steel, M. Algorithms for detecting and analysing autocatalytic sets. Algorithms Mol. Biol. 2015, 10, 15. [Google Scholar] [CrossRef] [PubMed]
- Vasas, V.; Fernando, C.; Santos, M.; Kauffman, S.; Sathmáry, E. Evolution before genes. Biol. Direct 2012, 7, 1. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Steel, M. Conditions for evolvability of autocatalytic sets: A formal example and analysis. Orig. Life Evol. Biosph. 2014, 44, 111–124. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W. Evolution of autocatalytic sets in computational models of chemical reaction networks. Orig. Life Evol. Biosph. 2016, 46, 233–245. [Google Scholar] [CrossRef]
- Hordijk, W.; Naylor, J.; Krasnogor, N.; Fellermann, H. Population dynamics of autocatalytic sets in a compartmentalized spatial world. Life 2018, 8, 33. [Google Scholar] [CrossRef] [PubMed]
- Wills, P.R.; Henderson, L. Self-organisation and information-carrying capacity of collectively autocatalytic sets of polymers: Ligation systems. In Unifying Themes in Complex Systems: Proceedings of the First International Conference on Complex Systems; Bar-Yam, Y., Ed.; Perseus Books: New York, NY, USA, 2000; pp. 613–623. [Google Scholar]
- Filisetti, A.; Graudenzi, A.; Serra, R.; Villani, M.; De Lucrezia, D.; Fuchslin, R.M.; Kauffman, S.A.; Packard, N.; Poli, I. A stochastic model of the emergence of autocatalytic cycles. J. Syst. Chem. 2011, 2, 2. [Google Scholar] [CrossRef]
- Filisetti, A.; Villani, M.; Damiani, C.; Graudenzi, A.; Roli, A.; Hordijk, W.; Serra, R. On RAF sets and autocatalytic cycles in random reaction networks. Commun. Comput. Inf. Sci. 2014, 445, 113–126. [Google Scholar]
- Serra, R.; Villani, M. Modelling Protocells; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Jain, S.; Krishna, S. Autocatalytic sets and the growth of complexity in an evolutionary model. Phys. Rev. Lett. 1998, 81, 5684–5687. [Google Scholar] [CrossRef]
- Jain, S.; Krishna, S. A model for the emergence of cooperation, interdependence, and structure in evolving networks. Proc. Natl. Acad. Sci. USA 2001, 98, 543–547. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.; Krishna, S. Large extinctions in an evolutionary model: The role of innovation and keystone species. Proc. Natl. Acad. Sci. USA 2002, 99, 2055–2060. [Google Scholar] [CrossRef] [PubMed]
- Segre, D.; Lancet, D.B.E.D. Compositional genomes: Prebiotic information transfer in mutually catalytic noncovalent assemblies. Proc. Natl. Acad. Sci. USA 2001, 97, 219–230. [Google Scholar] [CrossRef]
- Markovitch, O.; Lancet, D. Excess mutual catalysis is required for effective evolvability. Artif. Life 2012, 18, 243–266. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Steel, M. A formal model of autocatalytic sets emerging in an RNA replicator system. J. Syst. Chem. 2013, 4, 3. [Google Scholar] [CrossRef]
- Hordijk, W.; Vaidya, N.; Lehman, N. Serial transfer can aid the evolution of autocatalytic sets. J. Syst. Chem. 2014, 5, 4. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Shichor, S.; Ashkenasy, G. The influence of modularity, seeding, and product inhibition on peptide autocatalytic network dynamics. ChemPhysChem 2018, 19, 2437–2444. [Google Scholar] [CrossRef]
- Sousa, F.L.; Hordijk, W.; Steel, M.; Martin, W.F. Autocatalytic sets in E. coli metabolism. J. Syst. Chem. 2015, 6, 4. [Google Scholar] [CrossRef]
- Ruiz-Mirazo, K.; Briones, C.; de la Escosura, A. Chemical roots of biological evolution: The origins of life as a process of development of autonomous functional systems. Open Biol. 2017, 7, 170050. [Google Scholar] [CrossRef]
- Steel, M.; Hordijk, W.; Smith, J. Minimal autocatalytic networks. J. Theor. Biol. 2013, 332, 96–107. [Google Scholar] [CrossRef]
- Dittrich, P.; Speroni di Fenizio, P. Chemical Organization Theory. Bull. Math. Biol. 2007, 69, 1199–1231. [Google Scholar] [CrossRef]
- Hordijk, W.; Steel, M.; Dittrich, P. Autocatalytic sets and chemical organizations: Modeling self-sustaining reaction networks at the origin of life. New J. Phys. 2018, 20, 015011. [Google Scholar] [CrossRef]
- Steel, M.; Hordijk, W.; Xavier, J.C. Autocatalytic networks in biology: Structural theory and algorithms. J. R. Soc. Interface 2018. under review. [Google Scholar]
- Gillespie, D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Schwartz, A.W.; de Graaf, R.M. The prebiotic synthesis of carbohydrates: A reassessment. J. Mol. Evol. 1993, 36, 101–106. [Google Scholar] [CrossRef]
- Zhang, X.V.; Martin, S.T. Driving parts of Krebs cycle in reverse through mineral photochemistry. J. Am. Chem. Soc. 2006, 128, 16032–16033. [Google Scholar] [CrossRef] [PubMed]
- Muchowska, K.B.; Varma, S.J.; Chevallot-Beroux, E.; Lethuillier-Karl, L.; Li, G.; Moran, J. Metals promote sequences of the reverse Krebs cycle. Nat. Ecol. Evol. 2017, 1, 1716–1721. [Google Scholar] [CrossRef] [PubMed]
- Varma, S.J.; Muchowska, K.B.; Chatelain, P.; Moran, J. Native iron reduces CO2 to intermediates and end-products of the acetyl-CoA pathway. Nat. Ecol. Evol. 2018, 2, 1019–1024. [Google Scholar] [CrossRef]
- Christen, P.; Mehta, P.K. From cofactor to enzymes: The molecular evolution of pyridoxal-5′-phosphate-dependent enzymes. Chem. Rec. 2001, 1, 436–447. [Google Scholar] [CrossRef]
- Rees, D.C.; Howard, J.B. The interface between the biological and inorganic worlds: Iron-sulfur metalloclusters. Science 2003, 300, 929–931. [Google Scholar] [CrossRef]
- Goldford, J.E.; Segrè, D. Modern views of ancient metabolic networks. Curr. Opin. Syst. Biol. 2018, 8, 117–124. [Google Scholar] [CrossRef]
- Weiss, M.C.; Sousa, F.L.; Mrnjavac, N.; Neukirchen, S.; Roettger, M.; Nelson-Sathi, S.; Martin, W.F. The physiology and habitat of the last universal common ancestor. Nat. Microbiol. 2016, 1, 16116. [Google Scholar] [CrossRef] [PubMed]
- Carter, C.W., Jr.; Wills, P.R. Did Gene Expression Co-evolve with Gene Replication? In Origin and Evolution of Biodiversity; Pontarotti, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 293–313. [Google Scholar]
- Hordijk, W.; Steel, M. Autocatalytic sets and boundaries. J. Syst. Chem. 2015, 6, 1. [Google Scholar] [CrossRef] [PubMed]
- Cazzolla Gatti, R.; Hordijk, W.; Kauffman, S. Biodiversity is autocatalytic. Ecol. Model. 2017, 346, 70–76. [Google Scholar] [CrossRef]
- Cazzolla Gatti, R.; Fath, B.; Hordijk, W.; Kauffman, S.; Ulanowicz, R. Niche emergence as an autocatalytic process in the evolution of ecosystems. J. Theor. Biol. 2018, 454, 110–117. [Google Scholar] [CrossRef] [PubMed]
- Kauffman, S.A. Economics and the Collectively Autocatalytic Structure of the Real Economy. 2011. Available online: http://www.npr.org/blogs/13.7/2011/11/21/142594308/economics-and-the-collectively-autocatalytic-structure-of-the-real-economy (accessed on 28 November 2018).
- Gabora, L.; Steel, M. Autocatalytic networks in cognition and the origin of culture. J. Theor. Biol. 2017, 431, 87–95. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hordijk, W.; Steel, M. Autocatalytic Networks at the Basis of Life’s Origin and Organization. Life 2018, 8, 62. https://doi.org/10.3390/life8040062
Hordijk W, Steel M. Autocatalytic Networks at the Basis of Life’s Origin and Organization. Life. 2018; 8(4):62. https://doi.org/10.3390/life8040062
Chicago/Turabian StyleHordijk, Wim, and Mike Steel. 2018. "Autocatalytic Networks at the Basis of Life’s Origin and Organization" Life 8, no. 4: 62. https://doi.org/10.3390/life8040062
APA StyleHordijk, W., & Steel, M. (2018). Autocatalytic Networks at the Basis of Life’s Origin and Organization. Life, 8(4), 62. https://doi.org/10.3390/life8040062




