Prebiotic RNA Network Formation: A Taxonomy of Molecular Cooperation
Abstract
1. Introduction
2. Results
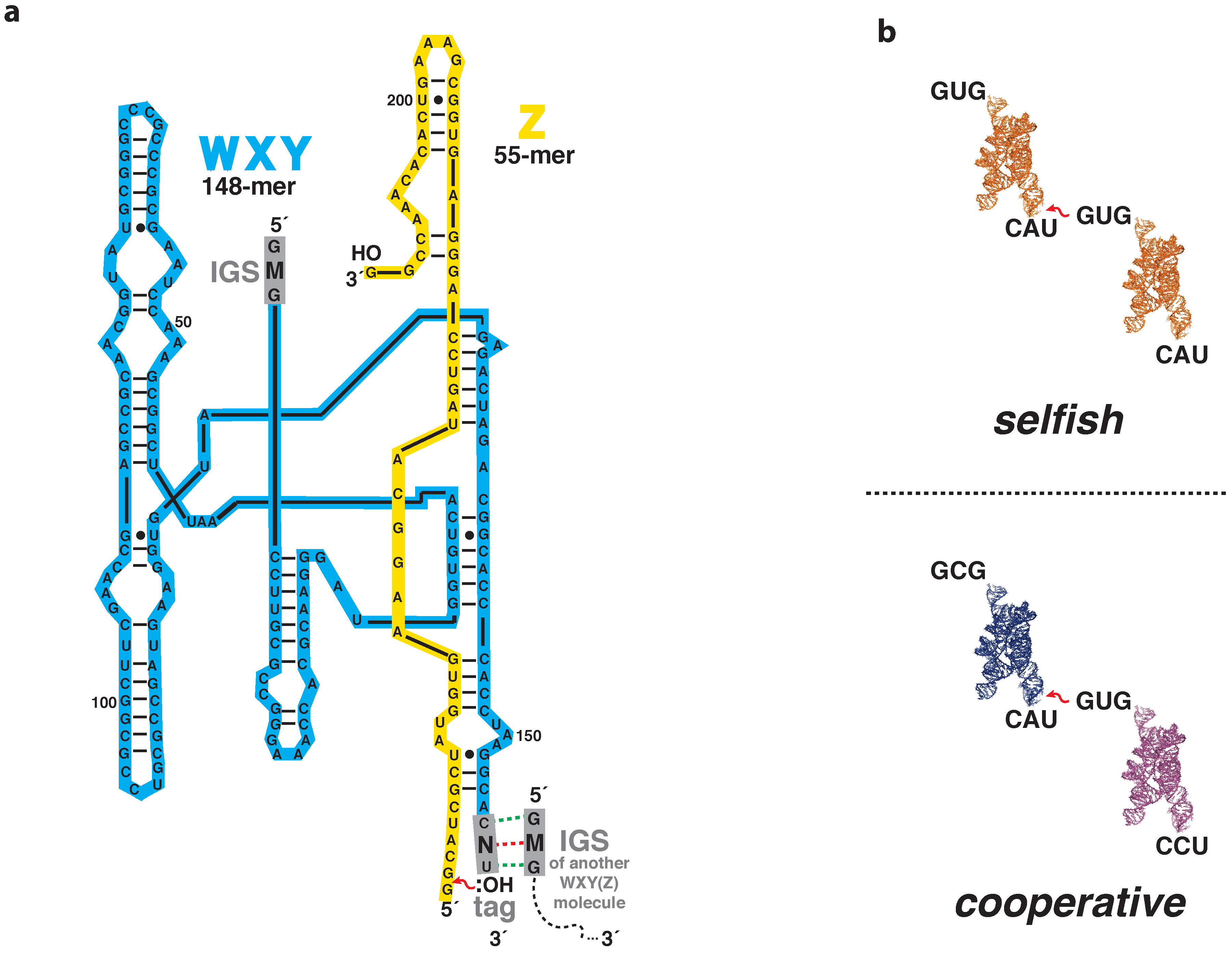
2.1. Nomenclature and Chemistry
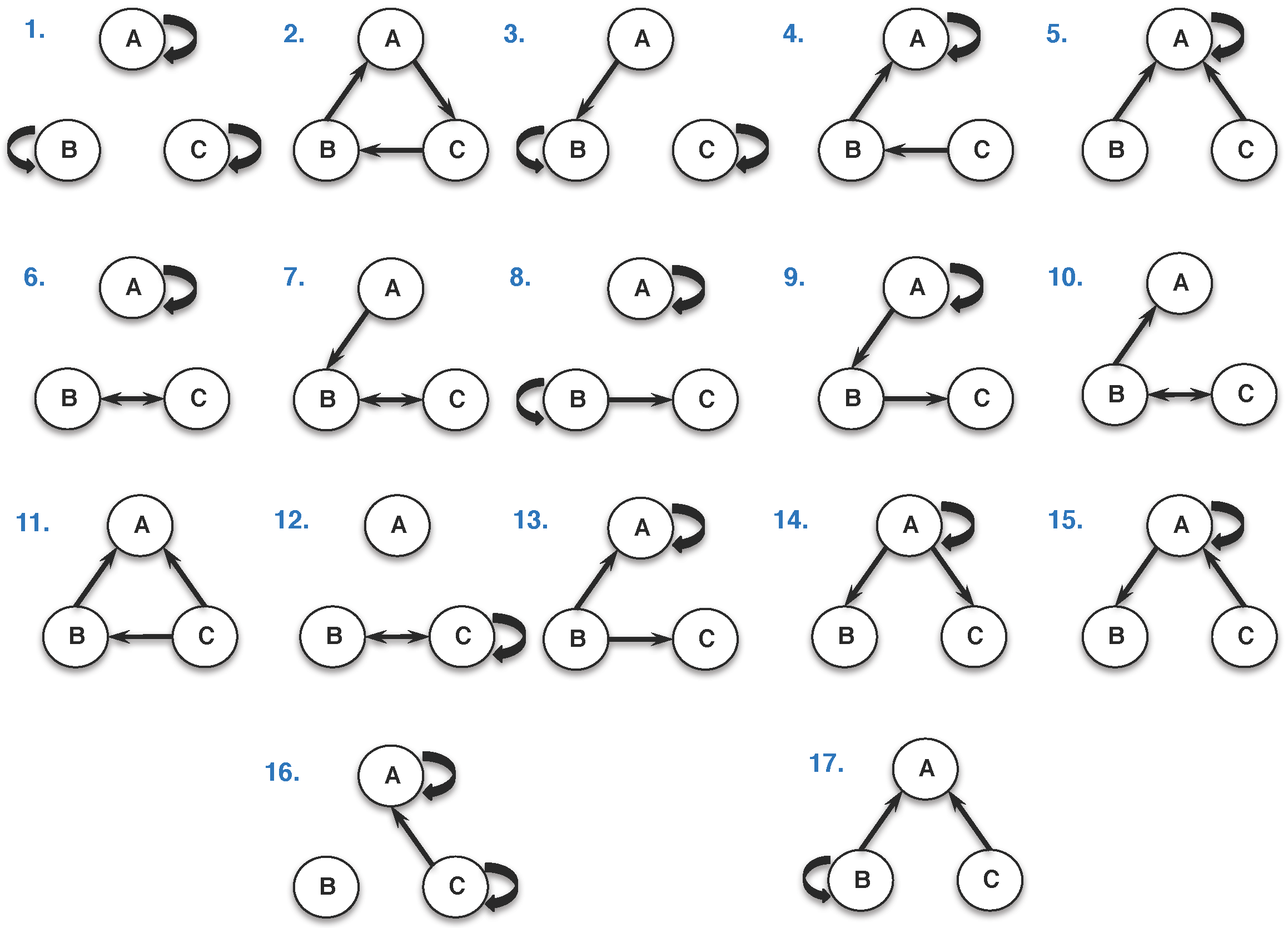
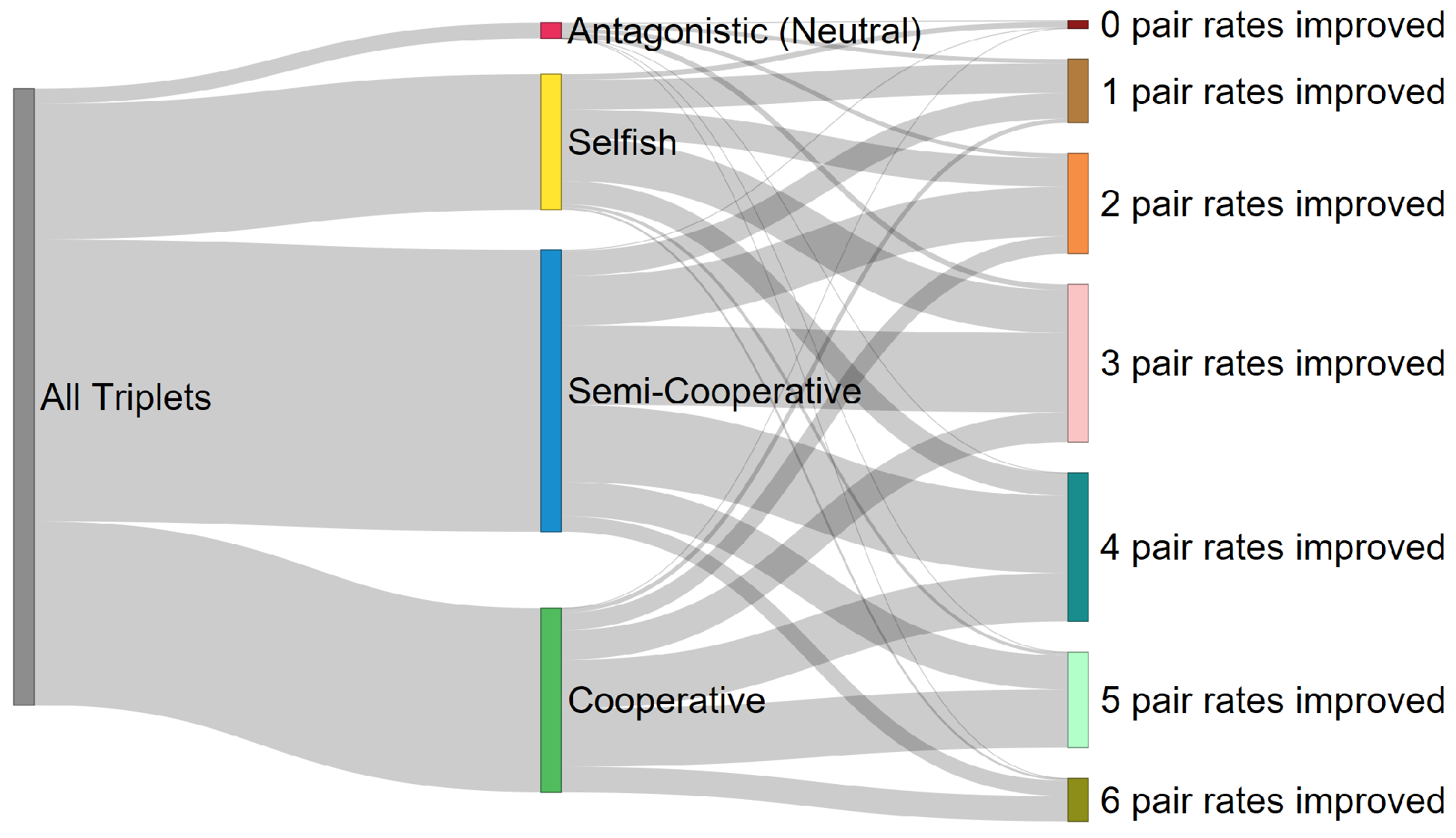
2.2. Classification and Taxonomy
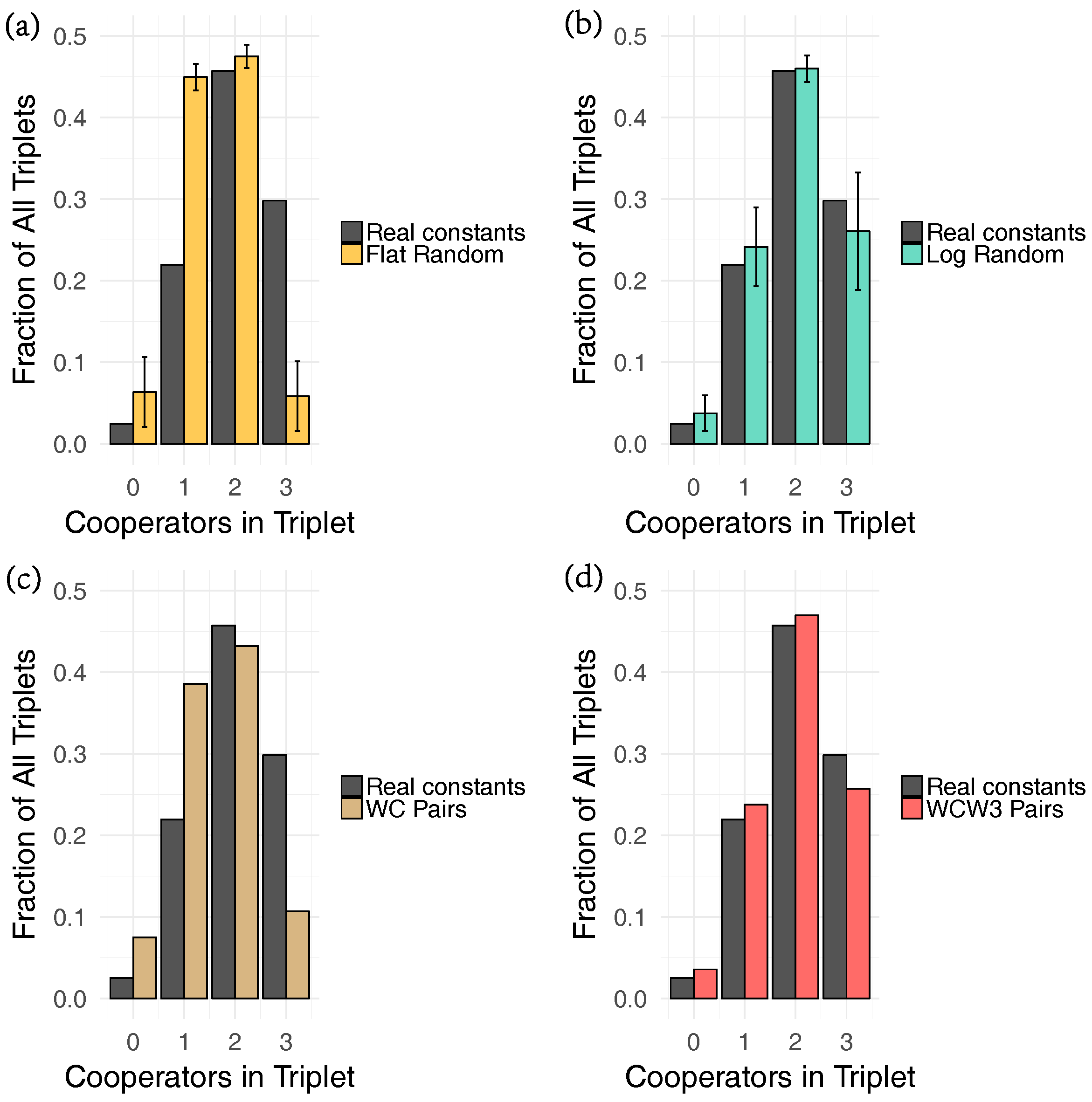
3. Discussion
4. Materials and Methods
4.1. Kinetic Simulations
4.2. Fitting Growth Constants
4.3. Randomization Experiments
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| RNA | Ribonucleic acid |
| IGS | Internal guide sequence |
| RPS | Rock-paper-scissors |
| G | guanosine |
| A | adenosine |
| C | cytidine |
| U | uridine |
| WC | Watson–Crick |
| WCW3 | Watson–Crick 3 Wobble Pairs |
References
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.; Highfield, R. Supercooperators: Altruism, Evolution, and Why We Need Each Other to Succeed; Simon and Schuster: New York, NY, USA, 2011. [Google Scholar]
- Higgs, P.G.; Lehman, N. The RNA World: Molecular cooperation at the origins of life. Nat. Rev. Genet. 2015, 16, 7–17. [Google Scholar] [CrossRef] [PubMed]
- Chen, I.A.; Nowak, M.A. From prelife to life: How chemical kinetics become evolutionary dynamics. Acc. Chem. Res. 2012, 45, 2088–2096. [Google Scholar] [CrossRef] [PubMed]
- Bohl, K.; Hummert, S.; Werner, S.; Basanta, D.; Deutsch, A.; Schuster, S.; Theißen, G.; Schroeter, A. Evolutionary game theory: Molecules as players. Mol. BioSyst. 2014, 10, 3066–3074. [Google Scholar] [CrossRef] [PubMed]
- Yeates, J.A.; Hilbe, C.; Zwick, M.; Nowak, M.A.; Lehman, N. Dynamics of Prebiotic RNA Reproduction Illuminated by Chemical Game Theory. Proc. Natl. Acad. Sci. USA 2016, 113, 5030–5035. [Google Scholar] [CrossRef] [PubMed]
- Smith, E.; Morowitz, H.J. The Origin and Nature of Life on Earth: The Emergence of the Fourth Geosphere; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Hayden, E.J.; Lehman, N. Self-assembly of a group I intron from inactive oligonucleotide fragments. Chem. Biol. 2006, 13, 909–918. [Google Scholar] [CrossRef] [PubMed]
- Yeates, J.A.; Nghe, P.; Lehman, N. Topological and thermodynamic factors that influence the evolution of small networks of catalytic RNA species. RNA 2017, 23, 1088–1096. [Google Scholar] [CrossRef] [PubMed]
- Vaidya, N.; Manapat, M.L.; Chen, I.A.; Xulvi-Brunet, R.; Hayden, E.J.; Lehman, N. Spontaneous network formation among cooperative RNA replicators. Nature 2012, 491, 72–77. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Sigmund, K. Evolutionary dynamics of biological games. Science 2004, 303, 793–799. [Google Scholar] [CrossRef] [PubMed]
- Nghe, P.; Hordijk, W.; Kauffman, S.A.; Walker, S.I.; Schmidt, F.J.; Kemble, H.; Yeates, J.A.; Lehman, N. Prebiotic network evolution: Six key parameters. Mol. BioSyst. 2015, 11, 3206–3217. [Google Scholar] [CrossRef] [PubMed]
- Sinervo, B.; Lively, C.M. The rock-paper-scissors game and the evolution of alternative male strategies. Nature 1996, 380, 240–243. [Google Scholar] [CrossRef]
- Turner, P.E.; Chao, L. Escape from prisoner’s dilemma in RNA phage Φ6. Am. Nat. 2003, 161, 497–505. [Google Scholar] [CrossRef] [PubMed]
- Satterwhite, L.E.; Yeates, J.A.; Lehman, N. Group I intron internal guide sequence binding strength as a component of ribozyme network formation. Molecules 2016, 21, 1293. [Google Scholar] [CrossRef] [PubMed]
- Reinhold-Hurek, B.; Shub, D.A. Self-splicing introns in tRNA genes of widely divergent bacteria. Nature 1992, 357, 173–176. [Google Scholar] [CrossRef] [PubMed]
- Kuo, L.Y.; Davidson, L.A.; Pico, S. Characterization of the Azoarcus ribozyme: Tight binding to guanosine and substrate by an unusually small group I ribozyme. Biochim. Biophys. Acta (BBA) Gene Struct. Expr. 1999, 1489, 281–292. [Google Scholar] [CrossRef]
- Guo, F.; Cech, T.R. In vivo selection of better self-splicing introns in Escherichia coli: The role of the P1 extension helix of the Tetrahymena intron. RNA 2002, 8, 647–658. [Google Scholar] [CrossRef] [PubMed]
- Draper, W.E.; Hayden, E.J.; Lehman, N. Mechanisms of covalent self-assembly of the Azoarcus ribozyme from four fragment oligonucleotides. Nucleic Acids Res. 2007, 36, 520–531. [Google Scholar] [CrossRef] [PubMed]
- Filisetti, A.; Graudenzi, A.; Serra, R.; Villani, M.; De Lucrezia, D.; Füchslin, R.M.; Kauffman, S.A.; Packard, N.; Poli, I. A stochastic model of the emergence of autocatalytic cycles. J. Syst. Chem. 2011, 2, 2. [Google Scholar] [CrossRef]
- Hordijk, W.; Steel, M. A formal model of autocatalytic sets emerging in an RNA replicator system. J. Syst. Chem. 2013, 4, 3. [Google Scholar] [CrossRef]
- Eschenmoser, A. Chemical etiology of nucleic acid structure. Science 1999, 284, 2118–2124. [Google Scholar] [CrossRef] [PubMed]
- Walker, S.I.; Davies, P.C. The algorithmic origins of life. J. R. Soc. Interface 2013, 10. [Google Scholar] [CrossRef] [PubMed]
- Flack, J. 12 Life’s Information Hierarchy. In From Matter to Life: Information and Causality; The MIT Press: Cambridge, MA, USA; London, UK, 2017; p. 283. [Google Scholar]
- Szathmáry, E. Toward Major Evolutionary Transitions Theory 2.0. Proc. Natl. Acad. Sci. USA 2015, 112, 10104–10111. [Google Scholar] [CrossRef] [PubMed]
- Kawamura, K. A Hypothesis: Life Initiated from Two Genes, as Deduced from the RNA World Hypothesis and the Characteristics of Life-Like Systems. Life 2016, 6, 29. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Davies, P.; Walker, S.I. New scaling relation for information transfer in biological networks. J. R. Soc. Interface 2015, 12. [Google Scholar] [CrossRef] [PubMed]
- Walker, S.I.; Kim, H.; Davies, P.C. The informational architecture of the cell. Philos. Trans. R. Soc. A 2016, 374. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Vasas, V.; Fernando, C.; Santos, M.; Kauffman, S.; Szathmáry, E. Evolution before genes. Biol. Direct 2012, 7, 1. [Google Scholar] [CrossRef] [PubMed]
- Szathmáry, E. The origin of replicators and reproducers. Philos. Trans. R. Soc. B Biol. Sci. 2006, 361, 1761–1776. [Google Scholar] [CrossRef] [PubMed]
- Lane, N.; Martin, W.F. The origin of membrane bioenergetics. Cell 2012, 151, 1406–1416. [Google Scholar] [CrossRef] [PubMed]
| WXY Genotype | Self-Assembly Rates (); min−1 | Nucleotide Pair Type |
|---|---|---|
| C•G | 0.0415 | |
| A•U | 0.0319 | strong (Watson–Crick) |
| U•A | 0.0197 | |
| G•C | 0.0125 | |
| G•U | 0.0091 | |
| A•C | 0.0069 | intermediate (wobble) |
| U•G | 0.0049 | |
| U•C | 0.0038 | |
| U•U | 0.0022 | |
| C•A | 0.0020 | |
| C•C | 0.0016 | |
| G•G | 0.0006 | weak |
| G•A | 0.0005 | |
| A•A | 0.0004 | |
| C•U | 0.0004 | |
| A•G | 0.0001 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mathis, C.; Ramprasad, S.N.; Walker, S.I.; Lehman, N. Prebiotic RNA Network Formation: A Taxonomy of Molecular Cooperation. Life 2017, 7, 38. https://doi.org/10.3390/life7040038
Mathis C, Ramprasad SN, Walker SI, Lehman N. Prebiotic RNA Network Formation: A Taxonomy of Molecular Cooperation. Life. 2017; 7(4):38. https://doi.org/10.3390/life7040038
Chicago/Turabian StyleMathis, Cole, Sanjay N. Ramprasad, Sara Imari Walker, and Niles Lehman. 2017. "Prebiotic RNA Network Formation: A Taxonomy of Molecular Cooperation" Life 7, no. 4: 38. https://doi.org/10.3390/life7040038
APA StyleMathis, C., Ramprasad, S. N., Walker, S. I., & Lehman, N. (2017). Prebiotic RNA Network Formation: A Taxonomy of Molecular Cooperation. Life, 7(4), 38. https://doi.org/10.3390/life7040038






