Dry/Wet Cycling and the Thermodynamics and Kinetics of Prebiotic Polymer Synthesis
Abstract
:1. Introduction
2. Background and Approach
3. Results
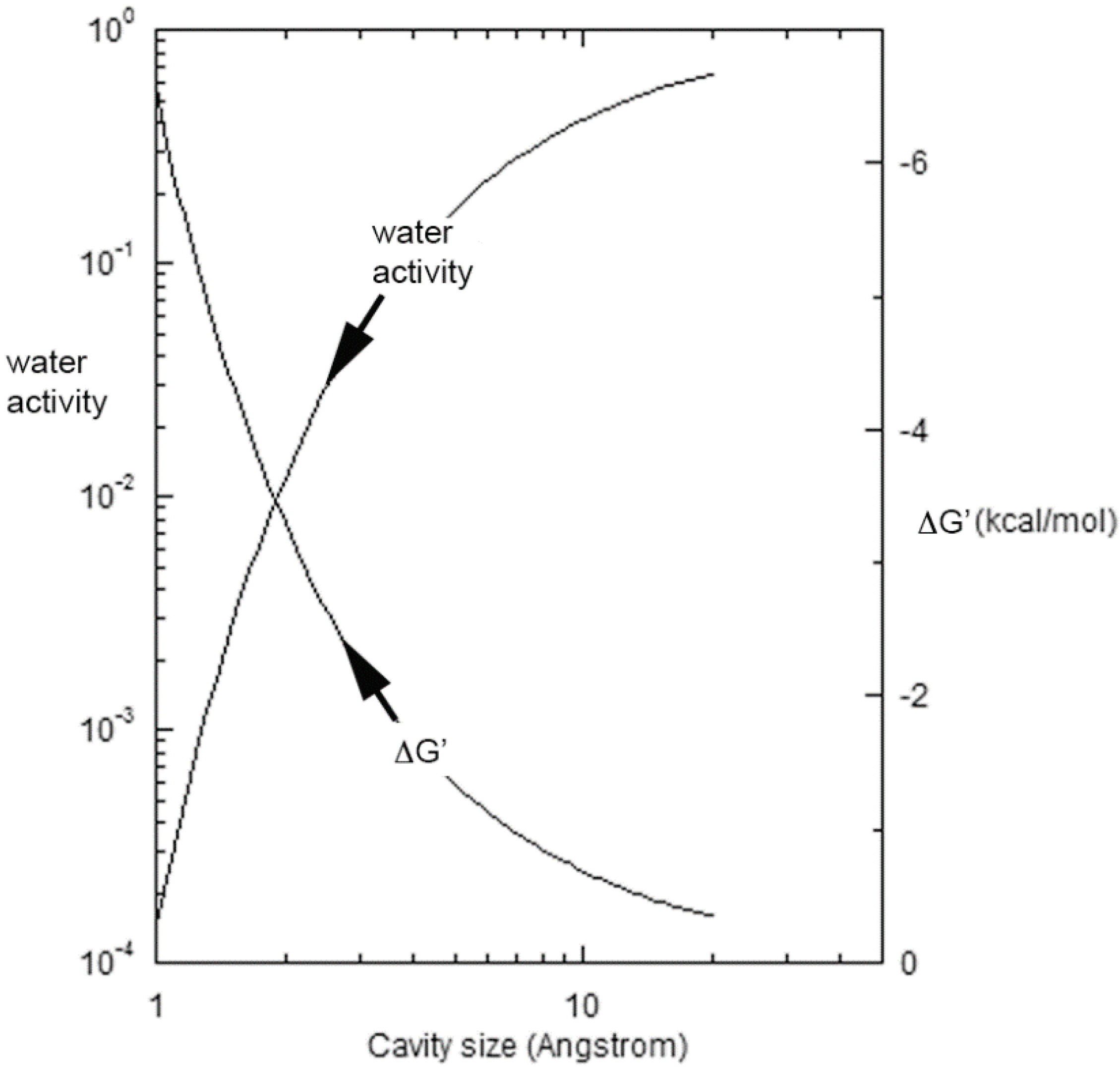
3.1. Evaporation
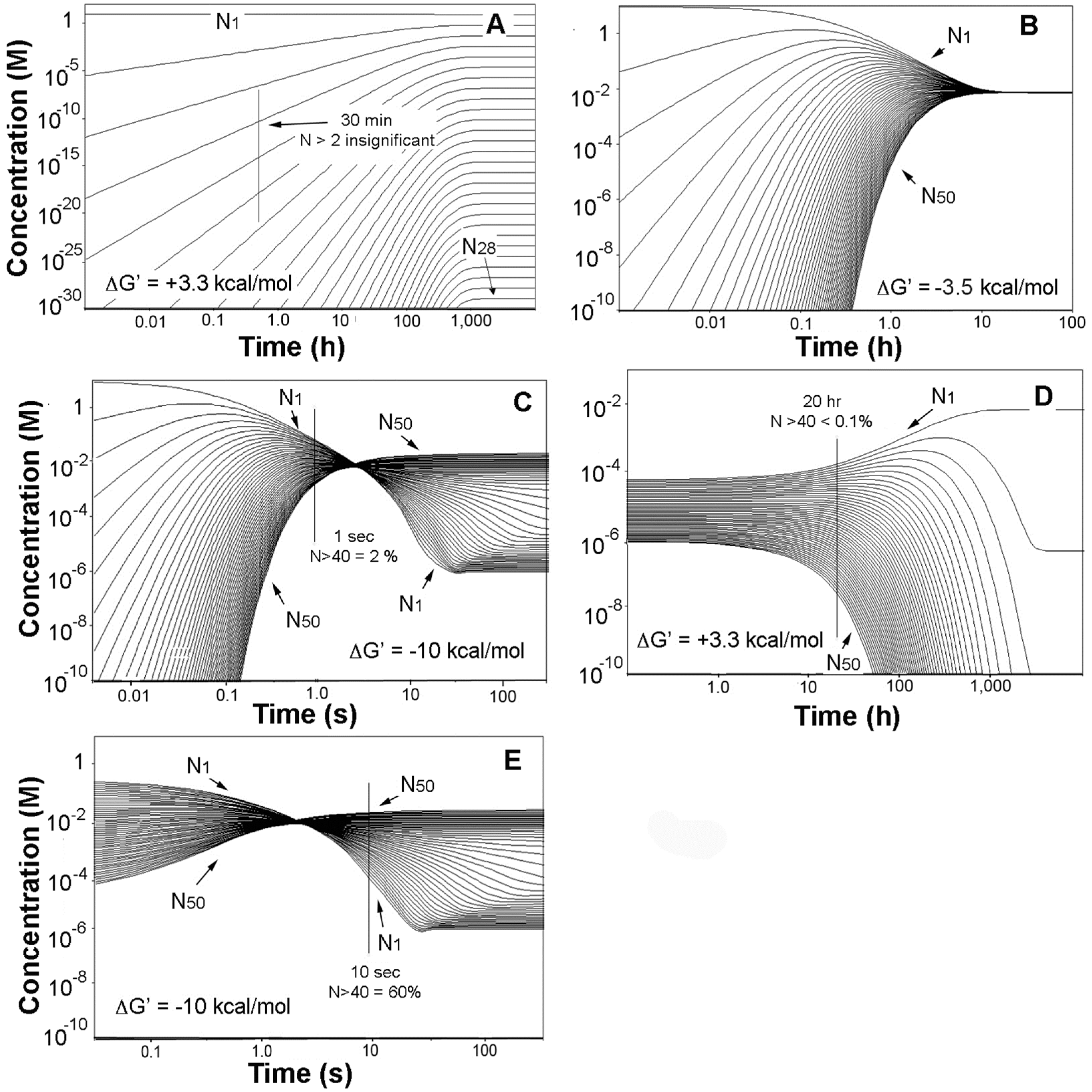
3.2. Rehydration, Disaggregation, and Kinetic Traps
4. Discussion
4.1. Polymer Synthesis and the RNA World Scenario
4.2. Competition between Synthetic and Degradative Processes
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bada, J.L.; Lazcano, A. Some like it hot, but not the first biomolecules. Science 2002, 296, 1982–1983. [Google Scholar] [CrossRef] [PubMed]
- Steinman, G.; Lemmon, R.M.; Calvin, M. Cyanamide: A possible key compound in chemical evolution. Proc. Natl. Acad. Sci. USA 1964, 52, 27–30. [Google Scholar] [CrossRef] [PubMed]
- Ponnamperuma, C.; Peterson, E. Peptide synthesis from amino acids in aqueous solution. Science 1965, 147, 1572–1574. [Google Scholar] [CrossRef] [PubMed]
- Rabinowitz, J.; Flores, J.; Kresbach, R.; Rogers, G. Peptide formation in the presence of linear or cyclic polyphosphates. Nature 1969, 224, 795–796. [Google Scholar] [CrossRef] [PubMed]
- Yamagata, Y.; Inomata, K. Condensation of glycylglycine to oligoglycines with trimetaphosphate in aqueous solution. II: Catalytic effect of magnesium ion. Orig. Life Evol. Biosph. 1997, 27, 339–344. [Google Scholar] [CrossRef] [PubMed]
- Hill, A.; Orgel, L. Trimetaphosphate-induced addition of aspartic acid to oligo(glutamic acid)s. Helv. Chim. Acta 2002, 85, 4111–4578. [Google Scholar] [CrossRef]
- Taillades, J.; Boiteau, L.; Beuzelin, I.; Lagrille, O.; Biron, J.; Vayaboury, W.; Vandenabeele-Trambouze, O.; Giani, O.; Commeyras, A. A pH-dependent cyanate reactivity model: Application to preparative n-carbamoylation of amino acids. J. Chem. Soc. Perkin Trans. 2001, 2, 1247–1254. [Google Scholar] [CrossRef]
- Leman, L.; Orgel, L.; Ghadiri, M.R. Carbonyl sulfide-mediated prebiotic formation of peptides. Science 2004, 306, 283–286. [Google Scholar] [CrossRef] [PubMed]
- Ferris, J.P. Montmorillonite-catalysed formation of RNA oligomers: The possible role of catalysis in the origins of life. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2006, 361, 1777–1786. [Google Scholar] [CrossRef] [PubMed]
- Danger, G.B.L.; Cottet, H.; Pascal, R. The peptide formation mediated by cyanate revisited. N-carboxyanhydrides as accessible intermediates in the decomposition of n-carbamoylamino acids. J. Am. Chem. Soc. 2006, 128, 7412–7413. [Google Scholar] [PubMed]
- Mungi, C.V.; Rajamani, S. Characterization of RNA-like oligomers from lipid-assisted nonenzymatic synthesis: Implications for origin of informational molecules on early earth. Life 2015, 5, 65–84. [Google Scholar] [CrossRef] [PubMed]
- Knauth, L.P. Temperature and salinity history of the precambrian ocean: Implications for the course of microbial evolution. Paleogeogr. Paleoclimatol. Paleoecol. 2005, 219, 53–69. [Google Scholar] [CrossRef]
- Lahav, N.; White, D.; Chang, S. Peptide formation in the prebiotic era: Thermal condensation of glycine in fluctuating clay environments. Science 1978, 201, 67–69. [Google Scholar] [CrossRef] [PubMed]
- Varfolomeev, S.D.; Lushchekina, S.V. Prebiotic synthesis and selection of macromolecules. Thermal cycling as a condition for synthesis and combinatorial selection. Geochem. Int. 2014, 52, 1197–1206. [Google Scholar] [CrossRef]
- DeGuzman, V.; Vercoutere, W.; Shenasa, H.; Deamer, D. Generation of oligonucleotides under hydrothermal conditions by non-enzymatic polymerization. J. Mol. Evol. 2014, 78, 251–262. [Google Scholar] [CrossRef] [PubMed]
- Rajamani, S.; Vlassov, A.; Benner, S.; Coombs, A.; Olasagasti, F.; Deamer, D. Lipid-assisted synthesis of RNA-like polymers from mononucleotides. Orig. Life Evol. Biosph. 2008, 38, 57–74. [Google Scholar] [CrossRef] [PubMed]
- Da Silva, L.; Maurel, M.C.; Deamer, D. Salt-promoted synthesis of RNA-like molecules in simulated hydrothermal conditions. J. Mol. Evol. 2015, 80, 86–97. [Google Scholar] [CrossRef] [PubMed]
- Spitzer, J.; Poolman, B. The role of biomacromolecular crowding, ionic strength, and physicochemical gradients in the complexities of life’s emergence. Microbiol. Mol. Biol. Rev. 2009, 73, 371–388. [Google Scholar] [CrossRef] [PubMed]
- Saha, R.; Pohorille, A.; Chen, I.A. Molecular crowding and early evolution. Orig. Life Evol. Biosph. 2014, 44, 319–324. [Google Scholar] [CrossRef] [PubMed]
- Hansma, H. The power of crowding for the origins of life. Orig. Life Evol. Biosph. 2015, 44, 307–311. [Google Scholar] [CrossRef] [PubMed]
- Minton, A.P. The influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media. J. Biol. Chem. 2001, 276, 10577–10580. [Google Scholar] [CrossRef] [PubMed]
- Nakano, S.; Miyoshi, D.; Sugimoto, N. Effects of molecular crowding on the structures, interactions, and functions of nucleic acids. Chem. Rev. 2014, 114, 2733–2758. [Google Scholar] [CrossRef] [PubMed]
- Elllis, R. Macromolecular crowding: Obvious but underappreciated. Trends Biochem. Sci. 2001, 26, 597–604. [Google Scholar] [CrossRef]
- Nelson, D.; Cox, M. Lehninger Principles of Biochemistry, 4th ed.; WH Freeman and Co.: New York, NY, USA, 2005; p. 493. [Google Scholar]
- Wolfenden, R.; Snider, M.J. The depth of chemical time and the power of enzymes as catalysts. Accts. Chem. Res. 2001, 34, 938–945. [Google Scholar] [CrossRef]
- Mabey, W.; Mill, T. Critical review of hydrolysis of organic compounds in water under environmental conditions. J. Phys. Chem. Ref. Data 1978, 7, 383–415. [Google Scholar] [CrossRef]
- Wolfenden, R.; Yuan, Y. Rates of Spontaneous Cleavage of Glucose, Fructose, Sucrose, and Trehalose in Water, and the Catalytic Proficiencies of Invertase and Trehalas. J. Am. Chem. Soc. 2008, 130, 7548–7549. [Google Scholar] [CrossRef] [PubMed]
- Oivanen, M.; Kuusela, S.; Lonnberg, H. Kinetics and mechanisms for the cleavage and isomerization of the phosphodiester bonds of RNA by bronsted acids and bases. Chem. Rev. 1998, 98, 961–990. [Google Scholar] [CrossRef] [PubMed]
- Stetter, K.O. Hyperthermophiles in the history of life. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2006, 361, 1837–1842. [Google Scholar] [CrossRef] [PubMed]
- Persson, E.; Halle, B. Nanosecond to microsecond protein dynamics probed by magnetic relaxation dispersion of buried water molecules. J. Am. Chem. Soc. 2008, 130, 1774–1787. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.S.; Yethiraj, A. Effect of macromolecular crowding on reaction rates: A computational and theoretical study. Biophys. J. 2009, 96, 1333–1340. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, O.; Riul, A.; Leite, V.B.P. Water at interfaces and its influence on the electrical properties of adsorbed films. Braz. J. Phys. 2004, 34, 73–83. [Google Scholar] [CrossRef]
- Tinoco, J.I.; Sauer, K.; Wang, J. Physical Chemistry—Principles and Applications in Biological Sciences; Prentice Hall: Upper Saddle River, New Jersey, USA, 1995; p. 141. [Google Scholar]
- Hall, D.; Minton, A.P. Macromolecular crowding: Qualitative and semiquantitative successes, quantitative challenges. Biochim. Biophys. Acta 2003, 1649, 127–139. [Google Scholar] [CrossRef]
- Moore, W. Physical Chemistry; Prentice-Hall, Inc.: Englewood Cliffs, New Jersey, USA, 1956; pp. 504–505. [Google Scholar]
- Toppozini, L.; Dies, H.; Deamer, D.W.; Rheinstädter, M.C. Adenosine monophosphate forms ordered arrays in multilamellar lipid matrices: Insights into assembly of nucleic acid for primitive life. PLoS ONE 2013, 8, e62810. [Google Scholar] [CrossRef] [PubMed]
- Freier, S.M.; Kierzek, R.; Jaeger, J.A.; Sugimoto, N.; Caruthers, M.H.; Neilson, T.; Turner, D.H. Improved free-energy parameters for predictions of RNA duplex stability. Proc. Natl. Acad. Sci. USA 1986, 83, 9373–9377. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, J.A.; Turner, D.H.; Zuker, M. Improved predictions of secondary structures for RNA. Proc. Natl. Acad. Sci. USA 1989, 86, 7706–7710. [Google Scholar] [CrossRef] [PubMed]
- Butcher, S.E.; Pyle, A.M. The molecular interactions that stabilize RNA tertiary structure: Rna motifs, patterns, and networks. Acc. Chem. Res. 2011, 44, 1302–1311. [Google Scholar] [CrossRef] [PubMed]
- Ianni, J. Comparison of the Bader-Deuflhard and the Cash-Karp Runge-Kutta Integrators for the Gri-Mech 3.0 Model Based on the Chemical Kinetics Code Kintecus; Elsevier Science Ltd.: Oxford, UK, 2003. [Google Scholar]
- Dauty, E.; Verkman, A.S. Molecular crowding reduces to a similar extent the diffusion of small solutes and macromolecules: Measurement by fluorescence correlation spectroscopy. J. Mol. Recognit. 2004, 17, 441–447. [Google Scholar] [CrossRef] [PubMed]
- Goodner, M.; DeSimone, J.; Kiserow, D.; Roberts, G. An equilibrium model for diffusion-limited solid-state polycondensation. Ind. Eng. Chem. Res. 2000, 39, 2797–2806. [Google Scholar] [CrossRef]
- Laidler, K. Chemical Kinetics, 2nd ed.; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Damer, B.; Deamer, D. Coupled phases and combinatorial selection in fluctuating hydrothermal pools: A scenario to guide experimental approaches to the origin of cellular life. Life 2015, 5, 872–887. [Google Scholar] [CrossRef] [PubMed]
- Robertson, M.; Joyce, G. The origins of the RNA world. Cold Spring Harb. Perspect. Biol. 2010, 4. [Google Scholar] [CrossRef] [PubMed]
- Benner, S.; Kim, H.-J.; Yang, Z. Setting the stage: The history, chemistry, and geobiology behind RNA. Cold Spring Harb. Perspect. Biol. 2010, 2, a003541. [Google Scholar] [CrossRef] [PubMed]
- Benson, S. Thermochemical Kinetics; John Wiley and Sons: New York, NY, USA, 1998. [Google Scholar]
- Mathews, D.H.; Moss, W.N.; Turner, D.H. Folding and finding RNA secondary structure. Cold Spring Harb. Perspect. Biol. 2010, 2, a003665. [Google Scholar] [CrossRef] [PubMed]
- Stull, D.; Sinke, G.; Westrum, E., Jr. The Chemical Thermodynamics of Organic Compounds; John Wiley and Sons Inc.: New York, NY, USA, 1969. [Google Scholar]
- Brown, J.W. The ribonuclease p database. Nucl. Acids Res. 1999, 27, 314. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, R.; Bernhart, S.H.; Honer Zu Siederdissen, C.; Tafer, H.; Flamm, C.; Stadler, P.F.; Hofacker, I.L. ViennaRNA package 2.0. Algorithms Mol. Biol. 2011, 6, 26. [Google Scholar] [CrossRef] [PubMed]
- Higgs, P.G. Rna secondary structure: A comparison of real and random sequences. J. Phys. I France 1993, 3, 43–59. [Google Scholar] [CrossRef]
- Moore, J.; Pearson, R.; New, S. Kinetics and Mechanism, 3rd ed.; Wiley: New York, NY, USA, 1981; pp. 358–359. [Google Scholar]
- Larralde, R.; Robertson, M.P.; Miller, S.L. Rates of decomposition of ribose and other sugars: Implications for chemical evolution. Proc. Natl. Acad. Sci. USA 1995, 92, 8158–8160. [Google Scholar] [CrossRef] [PubMed]
- Ott, A.; van Rossum, C.T.; van Harskamp, F.; van de Mheen, H.; Hofman, A.; Breteler, M.M. Education and the incidence of dementia in a large population-based study: The rotterdam study. Neurology 1999, 52, 663–666. [Google Scholar] [CrossRef] [PubMed]
- Lindahl, T. Instability and decay of the primary structure of DNA. Nature 1993, 362, 709–715. [Google Scholar] [CrossRef] [PubMed]
- Eigen, M.; Schuster, P. The hypercycle. A principle of natural self-organization. Part A: Emergence of the hypercycle. Naturwissenschaften 1977, 64, 541–565. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Hein, J. Mike steel, Autocatalytic sets and the origin of life. Entropy 2010, 12, 1733–1742. [Google Scholar] [CrossRef]
| Thermochemical and Kinetic Factors | Protein, Amide | Polysacch., Glycoside | RNA, Phosphate Ester | DNA, Phosphate Ester | |
|---|---|---|---|---|---|
| ΔG°′ formation/kcal/mol a | 2.2 | 3.8 | 3.3 | ||
| Arrhenius parameters, hydrolysis, pH 7 b | log A/year−1 | 15.5 | 16.0 | 10.5 | 14.1 |
| Ea/kcal·mol−1 | 25.2 | 31.5 | 15.6 | 26.8 | |
| Hydrolytic half-lives, linking functionality | 25 °C, pH 7 | 385 years | 4 M years | 5 years | 0.2 M years |
| 85 °C, pH 2.5 | 7 min c | 250 h c | 8 days d | 876 years e | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ross, D.S.; Deamer, D. Dry/Wet Cycling and the Thermodynamics and Kinetics of Prebiotic Polymer Synthesis. Life 2016, 6, 28. https://doi.org/10.3390/life6030028
Ross DS, Deamer D. Dry/Wet Cycling and the Thermodynamics and Kinetics of Prebiotic Polymer Synthesis. Life. 2016; 6(3):28. https://doi.org/10.3390/life6030028
Chicago/Turabian StyleRoss, David S., and David Deamer. 2016. "Dry/Wet Cycling and the Thermodynamics and Kinetics of Prebiotic Polymer Synthesis" Life 6, no. 3: 28. https://doi.org/10.3390/life6030028
APA StyleRoss, D. S., & Deamer, D. (2016). Dry/Wet Cycling and the Thermodynamics and Kinetics of Prebiotic Polymer Synthesis. Life, 6(3), 28. https://doi.org/10.3390/life6030028






