Abstract
Extant core metabolic cycles such as the TCA cycle and its related analog pathways utilize carboxylic acids as metabolites, with thioesters playing a key role. We examine if sugars from the potentially autocatalytic formose reaction can be converted to carboxylic acids in the absence of enzymes by calculating the thermodynamics and kinetics of such pathways. We zero in on a mechanism involving the addition of a thiol to an aldehyde, followed by intramolecular disproportionation to form a thioester that can be hydrolyzed into its carboxylic acid. This route is thermodynamically favorable but can have kinetic bottlenecks. We find that elimination of H2O or H2S is often the rate-determining step, and that alpha di-carbonyl reactants that do not require such a step are more feasible in the absence of catalysts.
1. Introduction
The core of extant metabolism essentially involves metabolites containing just carbon, hydrogen and oxygen; in the tricarboxylic acid (TCA) cycle and its closely related analog pathways (such as the 3HP/4HB cycle), these metabolites are carboxylic acids [1]. When run in the oxidative direction, these metabolic cycles are catalytic and feature highly evolved enzymes that lower the otherwise high reaction barriers. However, if run in the reverse direction, the cycle is potentially autocatalytic, and the net overall reaction formally converts two CO2 into an acetate analog, i.e., C1 + C1 → C2. While autocatalytic cycles are common in extant metabolism [2], they are rarely observed in simple benchtop chemistry. One rare example, often invoked in discussions on the chemical origins of life and prebiotic chemistry, is the formose reaction. Starting from formaldehyde (CH2O) as the C1 species, a plethora of sugars is produced in a complex messy reaction [3] that also includes carboxylic acids and polyols as side-products.
The mechanisms of the formose reaction have been well-studied [4,5,6]. The smallest cycle involves just three reactions: (1) C2 + C1 → C3 aldol addition, (2) C3 + C1 → C4 aldol addition, and (3) C4 → C2 + C2 retro-aldol reaction, as shown schematically in the lefthand side of Figure 1. If only C1 is present, the reaction is very slow. The direct addition of two C1 species to form C2 is kinetically very challenging because there is no umpolung species to favor C–C bond formation. (This is true for CH2O in the formose reaction with its partially positive carbon, and even more so for CO2 in extant metabolism.) The presence of even a small amount of the key C2 molecule, glycolaldehyde, is sufficient to trigger the autocatalytic cycle, because the aldol additions have significantly lower barriers with enolizable aldehydes present. (A small amount of the C3 or C4 species is also sufficient to bypass the unfavorable direct C1 + C1 → C2 reaction.) As shown in Figure 1, the complexity of the formose reaction with its wide suite of products is because larger sugars can be formed by further aldol additions (especially as C1 “food” runs out). Furthermore, the Cannizzaro reaction that disproportionates aldehydes into carboxylic acids and alcohols is always present. Changing the reaction conditions can lead to different suites of products, as shown by the Huck group in a series of systematic studies [7,8,9].
How might the formose cycle involving sugars transition into a proto-metabolic cycle with carboxylic acids as proto-metabolites? Why is acetate the key C2 species in extant metabolic cycles? Why are thioester species such as acetyl-CoA part of such cycles? The salient presence of thioesters led De Duve to propose a prebiotic “thioester world” [10] whereby thioesters may have played an early role in energy transduction when phosphate species were locked up in minerals and not easily available in solution [11,12], although there are recent suggestions that dissolved Fe2+ may increase phosphate availability [13], or that reduced phosphorus compounds may have been the precursors [14,15]. Analysis of biochemical networks suggests that the most ancient metabolic pathways may have been phosphate-free, and intriguingly organosulfur compounds are featured in their place [16,17]. Sulfur’s role at the origin of life has been spotlighted in Wachterhauser’s “pyrite world” [18] and Sutherland’s “cyanosulfidic world” [19]. Sulfur’s broad role in prebiotic chemistry was recently reviewed by Vallee et al. [20] and earlier this year Devaraj et al. published work utilizing thioesters to create protocells [21].
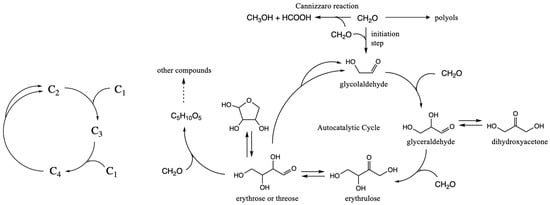
Figure 1.
Core autocatalytic cycle of the formose reaction. Reproduced from ref. [22] with permission from the authors.
Our group is interested in the role of sulfur at the origin-of-life. In generating a thermodynamic map of the free energies of small CHOS compounds, we found that thiols are stabilized compared to their hydroxyl counterparts [22]. We followed up with a detailed analysis of the formose reaction with mercaptoaldehyde (rather than glycolaldehyde) as the key C2 species [23], finding that the presence of thiol groups lowered crucial kinetic barriers leading to a thermodynamically more favorable C4 → C2 + C2 retro-aldol reaction. Thus, a formose-like core autocatalytic cycle containing sulfur analogs with a higher turnover rate could potentially outcompete one that lacked sulfur. Our results also suggested that high H2S concentrations (and therefore higher thiol concentration) kinetically disfavored the parasitic Cannizzaro reaction.
The current work investigates if the presence of thiols could facilitate the transition from sugars to acids. Thioesters are a key intermediate in this pathway, and their formation is significantly exergonic providing a driving force for this reaction. We took inspiration from work by Weber and co-workers in the 1980s that unfortunately was not followed-up by other experimental groups. Weber had proposed the formation of “energy-rich thioesters” by reacting glyceraldehyde with N-acetylcysteine [24]. Experimentally, the synthesis led to a lactic acid thioester suggesting that an intramolecular disproportionation is a crucial step in the transformation [25]; although Cannizzaro side-products are also observed under their reaction conditions.
Utilizing computational chemistry, we calculate the thermodynamics and kinetics for transforming small sugars (CH2O)n for n = 2–4 into their corresponding thioesters. We find that hydrolysis of the thioesters is exergonic by 5–7 kcal/mol; intriguingly, this value is similar to ATP hydrolysis and may support De Duve’s thioester world hypothesis. Weber had also shown that formation of pyrophosphate is facilitated by thioesters providing a direct link between the two energy “currencies” [26,27]. Our chosen sugar reactants come from the core of the formose cycle and its corresponding sulfur analogs. We find that elimination of H2O or H2S is often the rate-determining step; and reactants such as alpha di-carbonyl compounds do not require such a step as part of the intramolecular disproportionation are kinetically more feasible.
Before getting into the results and discussion, we describe our computational protocol and its limitations. Our current work examines in detail the reaction pathways analogous to Weber’s reaction (albeit with CH3SH as the thiol in our computations rather than a cysteine analog) but goes beyond it by explicitly connecting formose sugars (and their dicarbonyl analogs) to thioesters that when hydrolyzed lead to extant metabolic compounds. Our proposed intramolecular disproportionation mechanism fleshes out in detail what is hinted at by Weber, including multiple intermediates not easily isolated experimentally, and proposes where the bottlenecks might be. The scope of our study does not include other recent experimental work on thioesters in prebiotic chemistry; and we would like to point readers interested in the scope of thioesters at the origin of life to work by the Vallee lab [28,29] and Frenkel-Pinter et al. [30]. Nor have we included thioester-facilitated carboxylation mechanisms proposed by De Duve, which will be the subject of a future investigation.
2. Computational Methods
We use the same computational protocol as our recent work on CHOS molecules and sulfur analogs of the formose cycle. This allows us to make direct comparisons and extend our free energy map. Here, we provide a brief description of that protocol for the convenience of our readers. Much of the text in this section (and the first two paragraphs of the next section) is reproduced from those two articles (published in this journal) [22,23] since we think the description is both clear and succinct. Our calculated free energies using this quantum chemistry protocol showed good agreement with available experimental results for CHO systems [31,32,33,34].
Here are the computational details: The geometry of each molecule is optimized and its electronic energy calculated at the B3LYP (Becke3-Lee-Yang-Parr) [35,36,37,38] flavor of density functional theory with the 6-311G** basis set. To maximize the probability of finding global minima, multiple conformers are generated using molecular mechanics (MMFFs force field [39]). The optimized structures are embedded in a continuum dielectric to calculate the aqueous solvation contribution to the free energy. While this does not provide a specific concentration, it assumes a dilute solution such that the electrostatic field generated by a neighboring solute molecule is effectively screened by the water solvent. One can consider all solutes to have the same relative concentrations in our calculations. Since our previous work [23] found a handful of transition states, for uniformity, we used the SMD (Solvation Model based on Density) implicit solvent [40] in all transition state calculations. (There was practically no difference in the solvation free energy for minima).
Zero-point energy corrections are included, and we apply the standard temperature-dependent enthalpy correction term (for 298.15 K) from statistical mechanics by assuming translational and rotational corrections are a constant times kT, and that low frequency vibrational modes generally cancel out when calculating enthalpy differences. However, entropic corrections in aqueous solution are problematic [41,42,43]. Changes in free energy terms for translation and rotation are poorly defined in solution due to restricted complex motion, particularly as the size of the molecule increases (thus increasing its conformational entropy). Free energy corrections come from two different sources: thermal corrections and implicit solvent. Neither of these parameters is easily separable, nor do they constitute all the required parts of the free energy. We follow the approach of Deubel & Lau [44], assigning the solvation entropy of each species as half its gas-phase entropy (calculated using standard statistical mechanics approximations similar to the enthalpy calculations described above), based on proposals by Wertz [45] and Abraham [46] that upon dissolving in water, molecules lose a constant fraction (~0.5) of their entropy.
To estimate activation energies, transition states were optimized by including several explicit water and/or catalytic molecules to aid transferring H moieties. All calculated transition states have one significant negative eigenvalue corresponding to the reaction coordinate, and each was checked to ensure it had the correct eigenvectors for bond breaking/forming connecting the transition state to its reactants and products. Several conformers built by hand are tested in each case and we only report the lowest calculated barriers with the optimum number of solvent molecules added to assist in proton transfer.
Our protocol performs well comparing the equilibrium concentrations in a self-oligomerizing solution of 1 M glycolaldehyde at 298 K to subsequent NMR measurements [33]. Our relative Gibbs free energies in aqueous solution are typically within 0.5 kcal/mol compared to experiment. That being said, our protocol has systematic errors of 2–3 kcal/mol when calculating barriers involving carbonyl chemistry when compared to experimental results. Going to a higher level of theory does not reduce this error [47]; nor does using anionic species and our protocol actually does better when carboxylic acids are calculated in their neutral COOH form [34]. While protonation may vary with pH, we expect thermodynamic trends not to vary significantly within plausibly prebiotic conditions of pH 5–9 from our reference state, since almost all the compounds in our pathways remain in their neutral form in this pH range, with the exception of the final carboxylic acids (not part of the route from sugar to thioester). The kinetics however may change. There are also specific computational problems with including cations in our protocol as discussed in previous work [48,49] which also showed how to capture systematic changes in activation energies using a range of neutral catalysts in our protocol. Quantum chemistry is about error cancelation, and our protocol (with its foibles, including the simplistic entropy correction) has worked well even with a systematic error for activation barriers.
3. Results and Discussion
To connect this work to our prior CHOS thermodynamic maps [22,23], we use the same set of reference compounds: CO2, H2, H2O and H2S are assigned a relative free energy, Grel of 0.0 kcal/mol. The Grel values of all other species can be determined by calculating the change in free energy for forming the species, analogous to a free energy of formation. For example, the formation reaction of mercaptoaldehyde (C2H4OS) is written as
2 CO2 + 4 H2 + H2S → C2H4OS + 3 H2O
Since ΔG of this reaction is −6.2 kcal/mol, we assign Grel(C2H4OS) = −6.2 kcal. For the rest of this paper, we will use the unit kcal as shorthand to signify kcal/mol. The Grel values for all compounds parsed into their separate enthalpic, entropic, and solvation free energy are provided in Supplementary Information.
A consistent set of reference compounds allows us to globally compare energies. In the Figures, Grel values are found next to each compound for local minima and in square brackets next to an arrow for transition states. We use ΔG to designate the change in free energy when focusing on a particular reaction, where ΔG = Grel(products) − Grel(reactants). Similarly, when we refer to the barrier of a specific reaction, we designate this ΔG‡ which compares Grel of the transition state to either the reactants or products depending on whether the forward or reverse reaction is being discussed. Note that several reactions involve the non-reference compound CH3SH which has a Grel of −19.2 kcal.
3.1. Glycolaldehyde and Mercaptoaldehyde
In the formose reaction, glycolaldehyde (1a) is the linchpin C2 species regenerated in the C4 → C2 + C2 retro-aldol reaction. Figure 2 shows the free energy changes for conversion of glycolaldehyde to its thioester (and subsequent hydrolysis) with CH3SH as the reacting thiol. Relevant transition states along the pathway are shown in Figure 3. The first step is adding CH3SH (Grel = −19.2 kcal) to 1a (Grel = −0.5 kcal) to form 2a (Grel = −19.2 kcal). In the potential energy curve of Figure 2, the starting point includes both CH3SH and 1a, and the sum of their Grel values is −19.7 kcal. Thus, this reaction is marginally endergonic with ΔG = −19.2 − (−19.7) = +0.5 kcal. Since the transition state has Grel = −0.3 kcal, the forward reaction barrier is ΔG‡ = −0.3 − (−19.7) = 19.4 kcal. The optimal eight-center transition state (1a↔2a) includes two explicit solvent (water) molecules. The O…H distances for proton transfers are in the 1.05 to 1.45 Å range; the forming C…S distance is 2.37 Å and the breaking S…H distance is 1.74 Å; these are 20–40% longer than the typical C–S and S–H single covalent bonds as expected. For the remainder of this paper, we will not explicitly show the calculation of ΔG and ΔG‡ from Grel values; since our Figures provide all the Grel values. Key ΔG and ΔG‡ values are also explicitly shown in the potential energy curves.
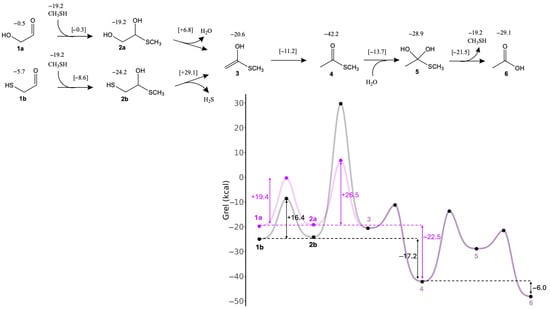
Figure 2.
Formation of acetic acid and thioester from C2 aldehyde (Grel in kcal).
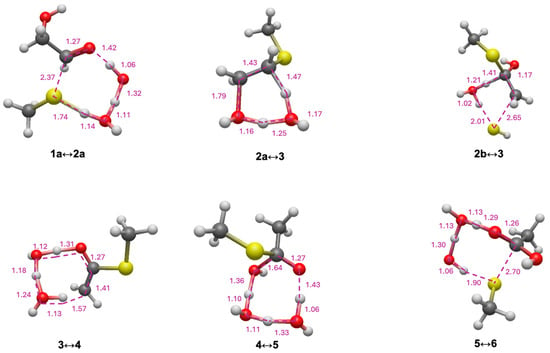
Figure 3.
Transition state structures for C2 pathway (bond distances in Å).
Dehydration of 2a to 3 is mildly exergonic (ΔG = −1.4 kcal), and is the rate-determining step (highest Grel in the pathway) with a barrier of ΔG‡ = +26.0 kcal. The optimal six-center transition state (2a↔3) has one additional solvent molecule. The breaking C…O and C…H distances are 1.79 Å and 1.47 Å, respectively, in the expected range.
Enol-to-keto isomerization of 3 leads to the thioester 4; this reaction is highly exergonic (ΔG = −21.6 kcal) with a low barrier (ΔG‡ = +9.4 kcal). The C…H forming bond of 1.57 Å in transition state 3↔4 is a little long but still reasonable (other distances are as expected). Comparing the thioester 4 to glycolaldehyde 1a, we see that intramolecular disproportionation has taken place. 1a has carbon oxidation numbers of +1 and +2 while 4 has carbon oxidation numbers of 0 and +3. This redox disproportionation is the thermodynamic driving force for converting a sugar into a thioester. The net change in ΔG from 1a to 4 is −22.5 kcal (as indicated in Figure 2).
Hydrolysis of thioester to carboxylic acid proceeds in two steps. First, a nucleophilic addition of water to 4 forms the tetrahedral intermediate 5, followed by elimination of CH3SH to form acetic acid 6. The conversion of 4 to 6 is exergonic (ΔG = −6.1 kcal); this is the first of several examples where the exergonicity of thioester hydrolysis under standard conditions is not too different from ATP hydrolysis (at pH 7, Keq’ = 6.3 × 104, ΔG’ ° = −6.5 kcal, from eQuilibrator [50]). Note that because CH3SH is a separate product, the energy curve in Figure 2 includes this value and the total Grel of the combined final products is −48.2 kcal. (The same will be true for energy curves in subsequent Figures). In Figure 3, Transition state 4↔5 involving the addition of water has a shorter C…O forming bond at 1.64 Å but still reasonable. For the elimination of CH3SH (transition state 5↔6), the C…S bond is noticeably longer than expected (2.70 Å) but we verified that this breaking bond is one of the eigenvectors in the transition state.
In the sulfur analog of the formose reaction [23], the C2 linchpin species is mercaptoaldehyde (1b). As shown in Figure 2, starting from 1b, adding CH3SH to form 2b is similarly mildly endergonic (ΔG = +0.7 kcal), while the barrier is 3 kcal lower (ΔG‡ = +16.3 kcal) compared to starting from glycolaldehyde 1a. This is similar to what we found in our previous study; several of the formose reaction thiol analogs had barriers lowered by 2–3 kcal compared to the non-sulfur counterparts. However, forming the enol 3 from 2b requires elimination of H2S which is kinetically very unfavorable with a very high barrier (ΔG‡ = +53.3 kcal). This step is also endergonic (ΔG = +3.6 kcal) but not hugely so. The transition state has a slightly longer C…S breaking bond (2.65 Å). The remainder of the pathway to the thioester and subsequent hydrolysis to form acetic acid is similar.
Since the transition state with the highest energies either involves the removal of water (from glycolaldehyde hemithioacetal 2a) or removal of H2S (from mercaptoaldehyde hemithioacetal 2b), a pathway that avoids this step would be kinetically more feasible. Having a carbonyl group alpha to the hemithioacetal avoids this difficult step, since only keto-enol isomerization is needed to form the thioester. The smallest molecule that can do this is glyoxal.
3.2. Glyoxal
While most studies of the formose reaction focus on the sugar product distribution, others have noted the presence of oxidized and reduced species formed in this complex reaction. Starting with glycolaldehyde aldol reactions, glyoxal was observed in a detailed study tracking the carbonyl migrations and epimerizations in sugars [51]. Thus, we expect glyoxal to be present in messy formose systems.
As shown in Figure 4, starting from glyoxal (7), the addition of CH3SH to produce hemithioacetal 8 is exergonic (ΔG = −7.1 kcal) with a low barrier (ΔG‡ = +10.4 kcal). This first addition reaction is more favorable compared to glycolaldehyde, because glyoxal is a higher-energy (or “activated”) species in the thermodynamic landscape [34]. Enolization of 8 to 9 is endergonic (ΔG = +7.9 kcal) with a moderately high barrier (ΔG‡ = +28.0 kcal); this is the rate-determining step. A second enolization to form the thioester 10 is highly exergonic (ΔG = −19.2 kcal) with a modest barrier (ΔG‡ = +19.7 kcal); the thermodynamic favorability is driven by the intramolecular disproportionation as expected. While there may be a possible direct route from 8 to 10 avoiding the transient enol 9, we were not able to find a suitable transition state that involves moving four hydrogens in a single step. Once thioester 10 is formed, it can be hydrolyzed in a two-step reaction going through the tetrahedral intermediate 11 before forming the final product glycolic acid 12. The hydrolysis is overall exergonic by 4.7 kcal. All transition states along this pathway look similar to their analogs in Figure 3 with distances of breaking and forming bonds in the expected range. (Cartesian coordinates of all transition states are provided in the Supplementary Materials.)

Figure 4.
Formation of glycolic acid thioester from glyoxal (Grel in kcal).
3.3. Glyceraldehyde and Its Sulfur Analogs
As discussed in the Introduction, glyceraldehyde 13a is the sugar used in Weber’s experiments; we use CH3SH as the representative thiol in our computations instead of N-acetylcysteine [24]. The pathway and its energetics are shown in Figure 5. Adding CH3SH to glyceraldehyde to form 14a is energetically break-even (ΔG = +0.1 kcal) with a barrier (ΔG‡) of 19.4 kcal; these values are similar to what we found for the addition of CH3SH to glycolaldehyde discussed earlier. Alternatively, glyceraldehyde could first dehydrate to the enol of methylglyoxal 15a (the enol is favored because of the conjugated π-system); this reaction is exergonic (ΔG = −6.8 kcal) but it has a relatively high barrier (ΔG‡ = +31.1 kcal). Subsequent addition of CH3SH and 15a to form 16a is slightly endothermic (ΔG = +4.8 kcal) with a modest barrier (ΔG‡ = +21.5 kcal). The pathway 13a → 15a → 16a is kinetically preferred over 13a → 14a → 16a which has a prohibitively high dehydration barrier (ΔG‡ = +55.4 kcal). While 14a → 16a does not lead to a stabilizing conjugated π-system (compared to 13a → 15a), it is unclear why our calculated barrier for the 14a↔16a transition state is so much larger even though the transition states look quite similar.
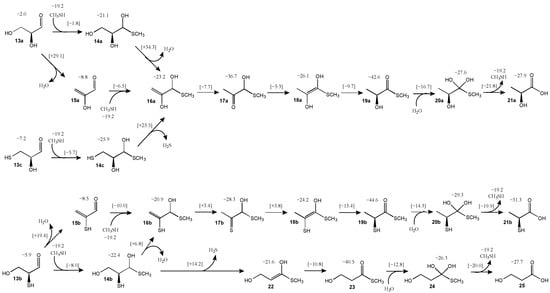
Figure 5.
Pathways for formation of thioesters from C3 aldehydes (Grel in kcal).
Progressing along the pathway, tautomerization of enol 16a to the ketone 17a is significantly exergonic (ΔG = −13.5 kcal) with a relatively low barrier (ΔG‡ = +15.5 kcal). Getting to the thioester stepwise requires two more tautomerization steps. Converting 17a to the enol 18a is endergonic (ΔG = +10.5 kcal). Compared to 16a, enol 18a is more stable by 3.0 kcal, although its transition state 17a↔18a (Grel = −5.3 kcal) is higher in energy than 16a↔17a (Grel = −7.7 kcal).
The transition states for 13a → 15a → 16a → 17a → 18a are shown in Figure 6. As with the C2 system starting with glycolaldehyde, the optimal transition state for dehydration (13a↔15a) is a six-center state; the breaking C…O and C…H distances are 1.62 Å and 1.66 Å, respectively, indicating that breaking the C–H bond proceeds ahead of the C–O bond. For addition of CH3SH, the optimal transition state 15a↔16a) is eight-center; the forming C…S distance is 2.61 Å and the breaking S…H distance is 1.87 Å, both a little longer than the C2 case, but still within the expected range. The two subsequent enolization steps have transition state bond distances as expected: In 16a↔17a the forming C…H bond is 1.54 Å; and in 17a↔18a the breaking C…H bond is 1.63 Å.
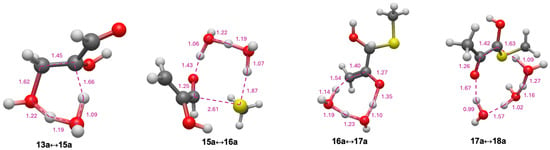
Figure 6.
First four transition state structures for glycolaldehyde pathway (bond distances in Å).
Tautomerization of enol 18a to the thioester 19a is significantly exergonic (ΔG = −16.5 kcal) with a relatively low barrier (ΔG‡ = +16.4 kcal). The overall exergonicity from sugar to thioester for the C3 (13a to 19a) is 21.4 kcal, similar to its C2 analog (1a to 4) of 22.5 kcal. We attempted to find pathways that bypass 17a (for example a 1,3-H-shift of 16a to 18a) but the transition states were all higher in energy. Once the thioester 19a is formed, it can undergo hydrolysis to lactic acid 21a (via tetrahedral intermediate 20a); this reaction is overall exergonic by 4.5 kcal. The transition states converting 18a to 21a are analogous to the ones from 3 to 6, with no surprises in the bond distances of the breaking and forming bonds. The overall energy pathway of 13a to 21a can be seen in Figure 7 by following the green curve with the green dots.
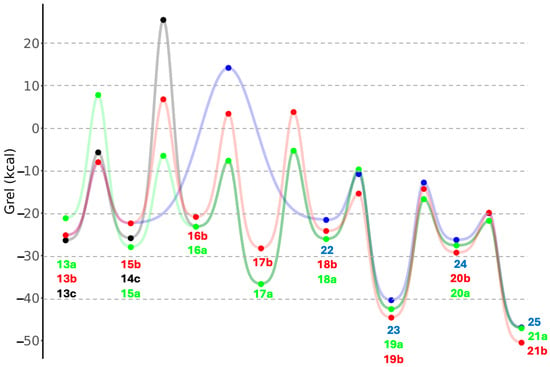
Figure 7.
Energy diagram for C3 pathways superimposed (Grel in kcal).
We now examine the sulfur analogs. Starting from 2-thioglyceraldehyde 13b, dehydration leads to 15b. The reaction is exergonic (ΔG = −2.6 kcal) although less so than the dehydration of 13a to 15a. The barrier for 13b → 15b is 25.3 kcal, which interestingly is noticeably lower than the 33.1 kcal for 13a → 15a. Addition of CH3SH to 15b to form 16b is endergonic (ΔG = +6.8 kcal) due to the loss of the π-conjugated system, although the barrier is relatively low (ΔG‡ = +17.7 kcal). An alternative route to 16b is to first add CH3SH to 13b to form 14b (ΔG = +2.7 kcal, ΔG‡ = +17.1 kcal) followed by the dehydration of 14b to 16b (ΔG = −1.5 kcal, ΔG‡ = +29.2 kcal).
Tautomerization of thioenol 16b to the thione 17b is exergonic (ΔG = −7.4 kcal) with a modest barrier (ΔG‡ = +24.3 kcal). Tautomerizing 17b to 18b is slightly endergonic (ΔG = +4.1 kcal) and the transition state 17b↔18b (Grel = +3.8 kcal) has a similar relative energy to 16b↔17b (Grel = +3.3 kcal). Tautomerization of enol 18b to the thioester 19b is significantly exergonic (ΔG = −20.4 kcal), very similar to its non-sulfur analog, and has a low barrier (ΔG‡ = +8.8 kcal). Hydrolysis of the thioester 19b to its acid 21b (via tetrahedral intermediate 20b) is exergonic by 5.9 kcal, once again, not too different from ATP hydrolysis. This overall energy pathway of 13b to 21b is indicated by the red curve in Figure 7.
Starting from 2-thioglyceraldehyde, another possible route is to eliminate H2S which converts 14b to 22. This reaction is barely endergonic (ΔG = +0.8 kcal) although it has a high barrier (ΔG‡ = +36.6 kcal); thus we expect this pathway to be less feasible. However, if a small amount of enol 22 is formed, it very favorably tautomerizes into the thioester 23 (ΔG = −18.9 kcal, ΔG‡ = +10.8 kcal). Hydrolysis of the thioester 23 (going through tetrahedral intermediate 24) leads to 3-hydroxypropanoic (3HP) acid 25, an isomer of lactic acid. 3HP is a metabolite in the 3HP/4HB cycle, an analog of the rTCA cycle. The hydrolysis of 23 to 25 is exergonic by 6.4 kcal, very similar to ATP hydrolysis. This overall energy pathway of 13b to 25 in Figure 7 begins with the red curve and branches to the blue curve.
Another possible starting analog is 3-thioglyceraldehyde 13c. Addition of CH3SH leads to 14c (ΔG = +0.5 kcal, ΔG‡ = +20.7 kcal) but the subsequent elimination of H2S to form 16a has a prohibitively high barrier of 50.4 kcal, so we expect this pathway not to be favored (initial gray curve in Figure 7). Alternatively, 14c could dehydrate to the thiol analog of 22 and the subsequent pathway might proceed to eventually form 3-thiopropanoic acid, the sulfur analog of 3HP. We did not pursue this pathway although we expect the energetics to be similar.
3.4. Intramolecular Disproportionation with a C4 Sugar
For the C2 and C3 starting sugars, the thiol (CH3SH) is added intermolecularly. Since we had previously explored thiol analogs of the formose reaction [23], we thought it would be interesting to consider a possible intramolecular addition and disproportionation starting from a 4-thioaldose. We chose 4-thiothreose 26 as our starting structure (slightly more stable than 4-thioerythrose) as a prototypical test case. The reaction pathway and energetics are shown in Figure 8. Forming the cyclic hemithioacetal 27 in an intramolecular nucleophilic addition is marginally exothermic (ΔG = −1.5 kcal) and kinetically very feasible with a barrier of ΔG‡ = +14.1 kcal. The transition state 26↔27 is shown in Figure 9. The ring closing C…S is 2.23 Å while the breaking S…H is 1.75 Å (with O…H distances as expected).
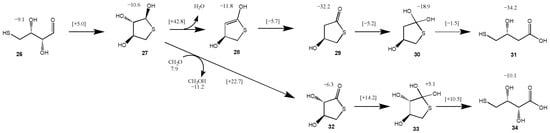
Figure 8.
Two pathways for converting 4-thiothreose to thioesters (Grel in kcal).
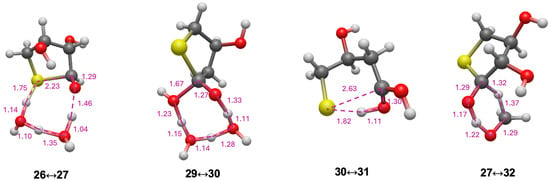
Figure 9.
Selected transition states for converting 4-thiothreose to thioesters.
However, the dehydration of 27 to 28, while marginally exothermic (ΔG = −1.2 kcal) has a prohibitively high barrier (ΔG‡ = +53.4 kcal), similar to our 14a↔16a transition state. If dehydrating conditions or a suitable catalyst allowed this reaction to proceed, tautomerization of 28 to the thioester 29 is very exergonic (ΔG = −20.4 kcal) with a very low barrier (ΔG‡ = +6.1 kcal). Hydrolysis of 29 (going through tetrahedral intermediate 30) leads to the acid 31. The hydrolysis reaction is only slightly exergonic (ΔG = −2.0 kcal). This final product, 2-deoxy-4-thiothreonic acid, is much more stable than its reactant isomer 4-thiothreose (by 25.1 kcal). Intramolecular redox disproportionation is the driving force. The optimal 29↔30 transition-state is eight-center with all bond distances in the expected range. Interestingly, the optimal 30↔31 transition-state did not require additional explicit water molecules; the C…S breaking bond is 2.63 Å.
We explored a second disproportionation pathway since we had previously found Cannizzaro reactions to be thermodynamically favored albeit with relatively high barriers [23]. Using the reduction of CH2O to CH3OH as a coupling agent, we calculate the oxidation of 27 to form the thioester 32 to be thermodynamically favorable (ΔG = [(−6.3) + (−11.2)] − [(−10.6) + (+7.9)] = −14.8 kcal); the barrier is 25.4 kcal, very similar to the Cannizzaro disproportionation of formaldehyde. Hydrolysis of the thioester 32 leads to 4-thiothreonic acid 34 (via tetrahedral intermediate 33) and is overall exergonic by 4.8 kcal. The optimal transition state is six-center, very similar to the Cannizzaro reaction transition states in our previous work [23]. Thus, depending on what else is present in the system, a sugar thiol could form different thioesters (and subsequently acids) depending on whether it undergoes inter or intra-molecular disproportionation.
4. Conclusions
Our calculated free energies suggest that the overall pathway converting sugars to thioesters is feasible and thermodynamically favorable. The driving force for this reaction is an intramolecular disproportionation redox reaction, oxidizing an aldehyde to a thioester while concomitantly reducing a neighboring alcohol group. The standard half-cell reduction potential for a carboxylic acid to an aldehyde is significantly more negative than the reduction of alcohol to alkyl; representative values for the reduction potentials have been tabulated by Weber [52]. The exergonicity of the internal disproportionation was also reflected in our thermodynamic map of CHO compounds [34]; sugars were 22–28 kcal less stable than their isomeric dihydroxy-acid counterparts. Since the thioester is 5–7 kcal less stable than its acid, we expect sugar to thioester conversion to be exergonic by 15–23 kcal; this is indeed what we observe in our calculations.
With regard to the kinetics, dehydration of sugar to enol was typically the rate-determining step with relatively high barriers of ~30 kcal. (For the sulfur analog, removal of H2S had a prohibitively high barrier of over 50 kcal, and we expect not to observe such reactions.) This suggests that dehydrating environmental conditions could facilitate the reaction, or an appropriate catalyst could accelerate thioester formation from its parent sugar. In a recent study where we utilized HCOOH and NH3 as simple proxy catalysts for the formose reaction [49], barriers could be lowered by 4–10 kcal compared to the baseline uncatalyzed values. The challenge for dehydrating conditions is that it would also promote other competing oligomerization reactions of sugars.
The dehydration step can be avoided if the starting compound is an alpha-keto aldehyde. Glyoxal is the smallest such example, although it is not usually considered a sugar. In this case, an enolization step is rate-determining. This is also true for the C3 compound methylglyoxal, which is one of two isomers of dehydrated glyceraldehyde. (The other isomer is malondialdehyde.) In this work, we have not looked at the possibility of starting with an alpha-keto acid, the smallest example being glyoxilic acid, given that it is thermodynamically a high-energy or “activated” species [34], although we are actively investigating this possibility because of recent interesting results on a glyoxylose system as a proto-metabolic precursor [53].
Our current work does not directly address if thioesters could have been precursors to phosphates in energy transduction of a protometabolic system; however, it is intriguing that our calculated free energies of thioester hydrolysis are very similar to ATP hydrolysis under standard conditions. Future work includes addressing this issue, and examining the possible compounds within this system that could act as prebiotic catalysts and facilitate thioester formation. This includes possible Cannizzaro-like reactions which have barriers in the ~30 kcal range but are also thermodynamically favorable through redox disproportionation, although this would be intermolecular rather than intramolecular.
We hope our work encourages others to revisit the “sugar system” first proposed by Weber. While Weber’s experiments only considered glyceraldehyde as the starting sugar, our work suggests that a wider range of aldehydes could be tested experimentally to examine if our proposed mechanisms are reasonable. In particular, wet-dry cycles may lead to dehydrated sugars with an alpha-carbonyl adjacent to the aldehyde facilitating thioester formation. Using thiols that are prebiotically plausible forerunners to glutathione, along with simple prebiotic catalysts, may also shed light on the metabolic origins of the glyoxalase enzyme. In future computational work, we plan to expand this system and explore if it can lead to a model of robust proto-metabolism with the inclusion of nitrogen-containing species and a wider range of prebiotically plausible compounds.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/life15081189/s1, Table S1: Energy breakdown of molecules and transition state Cartesian coordinates.
Author Contributions
J.K. was responsible for conceptualization, methodology, writing (original draft and subsequent edits), supervision, and project administration; J.K. and J.D.K. both contributed to formal analysis, investigation, data curation, visualization. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by NASA-Exobiology under Award 80NSSC24K0679.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in Supplementary Materials.
Acknowledgments
This research was supported by the University of San Diego and a research grant from NASA-Exobiology (award # 80NSSC24K0679). Shared computing facilities were provided by the saber3 computing cluster at the University of San Diego.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Braakman, R.; Smith, E. The compositional and evolutionary logic of metabolism. Phys. Biol. 2013, 10, 11001. [Google Scholar] [CrossRef]
- Xavier, J.C.; Hordijk, W.; Kauffman, S.; Steel, M.; Martin, W.F. Autocatalytic chemical networks at the origin of metabolism. Proc. Biol. Sci. 2020, 287, 20192377. [Google Scholar] [CrossRef]
- Omran, A.; Menor-Salvan, C.; Springsteen, G.; Pasek, M. The Messy Alkaline Formose Reaction and Its Link to Metabolism. Life 2020, 10, 125. [Google Scholar] [CrossRef]
- Breslow, R. On the Mechanism of the Formose Reaction. Tetrahedron Lett. 1959, 1, 22–26. [Google Scholar] [CrossRef]
- Appayee, C.; Breslow, R. Deuterium studies reveal a new mechanism for the formose reaction involving hydride shifts. J. Am. Chem. Soc. 2014, 136, 3720–3723. [Google Scholar] [CrossRef]
- Ricardo, A.; Frye, F.; Carrigan, M.A.; Tipton, J.D.; Powell, D.H.; Benner, S.A. 2-Hydroxymethylboronate as a reagent to detect carbohydrates: Application to the analysis of the formose reaction. J. Org. Chem. 2006, 71, 9503–9505. [Google Scholar] [CrossRef]
- Robinson, W.E.; Daines, E.; van Duppen, P.; de Jong, T.; Huck, W.T.S. Environmental conditions drive self-organization of reaction pathways in a prebiotic reaction network. Nat. Chem. 2022, 14, 623–631. [Google Scholar] [CrossRef]
- van Duppen, P.; Daines, E.; Robinson, W.E.; Huck, W.T.S. Dynamic Environmental Conditions Affect the Composition of a Model Prebiotic Reaction Network. J. Am. Chem. Soc. 2023, 145, 7559–7568. [Google Scholar] [CrossRef]
- Briš, A.; Baltussen, M.G.; Tripodi, G.L.; Huck, W.T.; Franceschi, P.; Roithová, J. Direct Analysis of Complex Reaction Mixtures: Formose Reaction. Angew. Chem. Int. Ed. 2024, 63, e202316621. [Google Scholar] [CrossRef]
- de Duve, C. The Beginnings of Life on Earth. Am. Sci. 1995, 83, 428–437. [Google Scholar]
- Gulick, A. Phosphorus as a factor in the origin of life. Am. Sci. 1955, 43, 479–489. [Google Scholar]
- Keefe, A.D.; Miller, S.L. Are polyphosphates or phosphate esters prebiotic reagents? J. Mol. Evol. 1995, 41, 693–702. [Google Scholar] [CrossRef]
- Brady, M.P.; Tostevin, R.; Tosca, N.J. Marine phosphate availability and the chemical origins of life on Earth. Nat. Commun. 2022, 13, 5162. [Google Scholar] [CrossRef]
- Gull, M.; Feng, T.; Cruz, H.A.; Krishnamurthy, R.; Pasek, M.A. Prebiotic Chemistry of Phosphite: Mild Thermal Routes to Form Condensed-P Energy Currency Molecules Leading Up to the Formation of Organophosphorus Compounds. Life 2023, 13, 920. [Google Scholar] [CrossRef]
- Gull, M.; Feng, T.; Smith, B.; Calcul, L.; Pasek, M.A. Prebiotic Syntheses of Organophosphorus Compounds from Reduced Source of Phosphorus in Non-Aqueous Solvents. Life 2023, 13, 2134. [Google Scholar] [CrossRef]
- Goldford, J.E.; Hartman, H.; Marsland, R., 3rd; Segre, D. Environmental boundary conditions for the origin of life converge to an organo-sulfur metabolism. Nat. Ecol. Evol. 2019, 3, 1715–1724. [Google Scholar] [CrossRef]
- Goldford, J.E.; Hartman, H.; Smith, T.F.; Segre, D. Remnants of an Ancient Metabolism without Phosphate. Cell 2017, 168, 1126–1134 e1129. [Google Scholar] [CrossRef]
- Wachtershauser, G. Before enzymes and templates: Theory of surface metabolism. Microbiol. Rev. 1988, 52, 452–484. [Google Scholar] [CrossRef]
- Patel, B.H.; Percivalle, C.; Ritson, D.J.; Duffy, C.D.; Sutherland, J.D. Common origins of RNA, protein and lipid precursors in a cyanosulfidic protometabolism. Nat. Chem. 2015, 7, 301–307. [Google Scholar] [CrossRef]
- Youssef-Saliba, S.; Vallee, Y. Sulfur Amino Acids: From Prebiotic Chemistry to Biology and Vice Versa. Synthesis 2021, 53, 2798–2808. [Google Scholar] [CrossRef]
- Cho, C.J.; An, T.; Lai, Y.C.; Vazquez-Salazar, A.; Fracassi, A.; Brea, R.J.; Chen, I.A.; Devaraj, N.K. Protocells by spontaneous reaction of cysteine with short-chain thioesters. Nat. Chem. 2025, 17, 148–155. [Google Scholar] [CrossRef]
- Kua, J.; Miller, N.A. Preliminary Free Energy Map of Prebiotic Compounds Formed from CO2, H2 and H2S. Life 2022, 12, 1763. [Google Scholar] [CrossRef]
- Kua, J.; Peña, M.T.; Cotter, S.N.; Leca, J. Sulfur Analogs of the Core Formose Cycle: A Free Energy Map. Life 2025, 15, 1. [Google Scholar] [CrossRef]
- Weber, A.L. Prebiotic formation of ‘energy-rich’ thioesters from glyceraldehyde and N-acetylcysteine. Orig. Life Evol. Biosph. 1984, 15, 17–27. [Google Scholar] [CrossRef]
- Weber, A.L. Nonenzymatic formation of “energy-rich” lactoyl and glyceroyl thioesters from glyceraldehyde and a thiol. J. Mol. Evol. 1984, 20, 157–166. [Google Scholar] [CrossRef]
- Weber, A.L. Formation of pyrophosphate, tripolyphosphate, and phosphorylimidazole with the thioester, n, s-diacetyl-cysteamine, as the condensing agent. J. Mol. Evol. 1981, 18, 24–29. [Google Scholar] [CrossRef]
- Weber, A.L. Formation of pyrophosphate on hydroxyapatite with thioesters as condensing agents. Biosystems 1982, 15, 183–189. [Google Scholar] [CrossRef]
- El Qami, A.; Hilari, J.I.; Blandin, V.; Gayraud, O.; Milet, A.; Vallee, Y. Prebiotic formation of thioesters via cyclic anhydrides as a key step in the emergence of metabolism. Sci. Rep. 2025, 15, 7039. [Google Scholar] [CrossRef]
- Leqraa, N.; Nicolet, Y.; Milet, A.; Vallee, Y. A way to thioacetate esters compatible with non-oxidative prebiotic conditions. Sci. Rep. 2020, 10, 14488. [Google Scholar] [CrossRef]
- Frenkel-Pinter, M.; Bouza, M.; Fernandez, F.M.; Leman, L.J.; Williams, L.D.; Hud, N.V.; Guzman-Martinez, A. Thioesters provide a plausible prebiotic path to proto-peptides. Nat. Commun. 2022, 13, 2569. [Google Scholar] [CrossRef]
- Kua, J.; Hanley, S.W.; De Haan, D.O. Thermodynamics and Kinetics of Glyoxal Dimer Formation: A Computational Study. J. Phys. Chem. A 2008, 112, 66–72. [Google Scholar] [CrossRef]
- Kua, J.; Avila, J.E.; Lee, C.G.; Smith, W.D. Mapping the Kinetic and Thermodynamic Landscape of Formaldehyde Oligomerization under Neutral Conditions. J. Phys. Chem. A 2013, 117, 12658–12667. [Google Scholar] [CrossRef]
- Kua, J.; Galloway, M.M.; Millage, K.D.; Avila, J.E.; De Haan, D.O. Glycolaldehyde Monomer and Oligomer Equilibria in Aqueous Solution: Comparing Computational Chemistry and NMR Data. J. Phys. Chem. A 2013, 117, 2997–3008. [Google Scholar] [CrossRef]
- Kua, J.; Hernandez, A.L.; Velasquez, D.N. Thermodynamics of Potential CHO Metabolites in a Reducing Environment. Life 2021, 11, 1025. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Halgren, T.A. MMFF VII. Characterization of MMFF94, MMFF94s, and other widely available force fields for conformational energies and for intermolecular-interaction energies and geometries. J. Comput. Chem. 1999, 20, 730–748. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Warshel, A.; Florian, J. Computer simulations of enzyme catalysis: Finding out what has been optimized by evolution. Proc. Natl. Acad. Sci. USA 1998, 95, 5950–5955. [Google Scholar] [CrossRef]
- Wiberg, K.B.; Bailey, W.F. Chiral diamines 4: A computational study of the enantioselective deprotonation of Boc-pyrrolidine with an alkyllithium in the presence of a chiral diamine. J. Am. Chem. Soc. 2001, 123, 8231–8238. [Google Scholar] [CrossRef]
- Nielsen, R.J.; Keith, J.M.; Stoltz, B.M.; Goddard, W.A., 3rd. A computational model relating structure and reactivity in enantioselective oxidations of secondary alcohols by (-)-sparteine-Pd(II) complexes. J. Am. Chem. Soc. 2004, 126, 7967–7974. [Google Scholar] [CrossRef]
- Deubel, D.V.; Lau, J.K. In silico evolution of substrate selectivity: Comparison of organometallic ruthenium complexes with the anticancer drug cisplatin. Chem. Commun. 2006, 23, 2451–2453. [Google Scholar] [CrossRef]
- Wertz, D.H. Relationship between the gas-phase entropies of molecules and their entropies of solvation in water and 1-octanol. J. Am. Chem. Soc. 1980, 102, 5316–5322. [Google Scholar] [CrossRef]
- Abraham, M.H. Relationship between solution entropies and gas phase entropies of nonelectrolytes. J. Am. Chem. Soc. 1981, 103, 6742–6744. [Google Scholar] [CrossRef]
- Krizner, H.E.; De Haan, D.O.; Kua, J. Thermodynamics and Kinetics of Methylglyoxal Dimer Formation: A Computational Study. J. Phys. Chem. A 2009, 113, 6994–7001. [Google Scholar] [CrossRef]
- Kua, J.; Miller, A.S.; Wallace, C.E.; Loli, H. Role of Acid in the Co-oligomerization of Formaldehyde and Pyrrole. ACS Omega 2019, 4, 22251–22259. [Google Scholar] [CrossRef]
- Kua, J.; Tripoli, L.P. Exploring the Core Formose Cycle: Catalysis and Competition. Life 2024, 14, 933. [Google Scholar] [CrossRef]
- eQuilbrator. Available online: http://equilibrator.weizmann.ac.il (accessed on 15 April 2025).
- Yi, R.; Kern, R.; Pollet, P.; Lin, H.; Krishnamurthy, R.; Liotta, C.L. Erythrose and Threose: Carbonyl Migrations, Epimerizations, Aldol, and Oxidative Fragmentation Reactions under Plausible Prebiotic Conditions. Chemistry 2023, 29, e202202816. [Google Scholar] [CrossRef]
- Weber, A.L. Chemical constraints governing the origin of metabolism: The thermodynamic landscape of carbon group transformations under mild aqueous conditions. Orig. Life Evol. Biosph. 2002, 32, 333–357. [Google Scholar] [CrossRef]
- Krishnamurthy, R.; Liotta, C.L. The potential of glyoxylate as a prebiotic source molecule and a reactant in protometabolic pathways-The glyoxylose reaction. Chem 2023, 9, 784–797. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).