Patterns of Variation and Coordination in Shoot Traits Across Four Branching Orders of Larix principis-rupprechtii
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Species
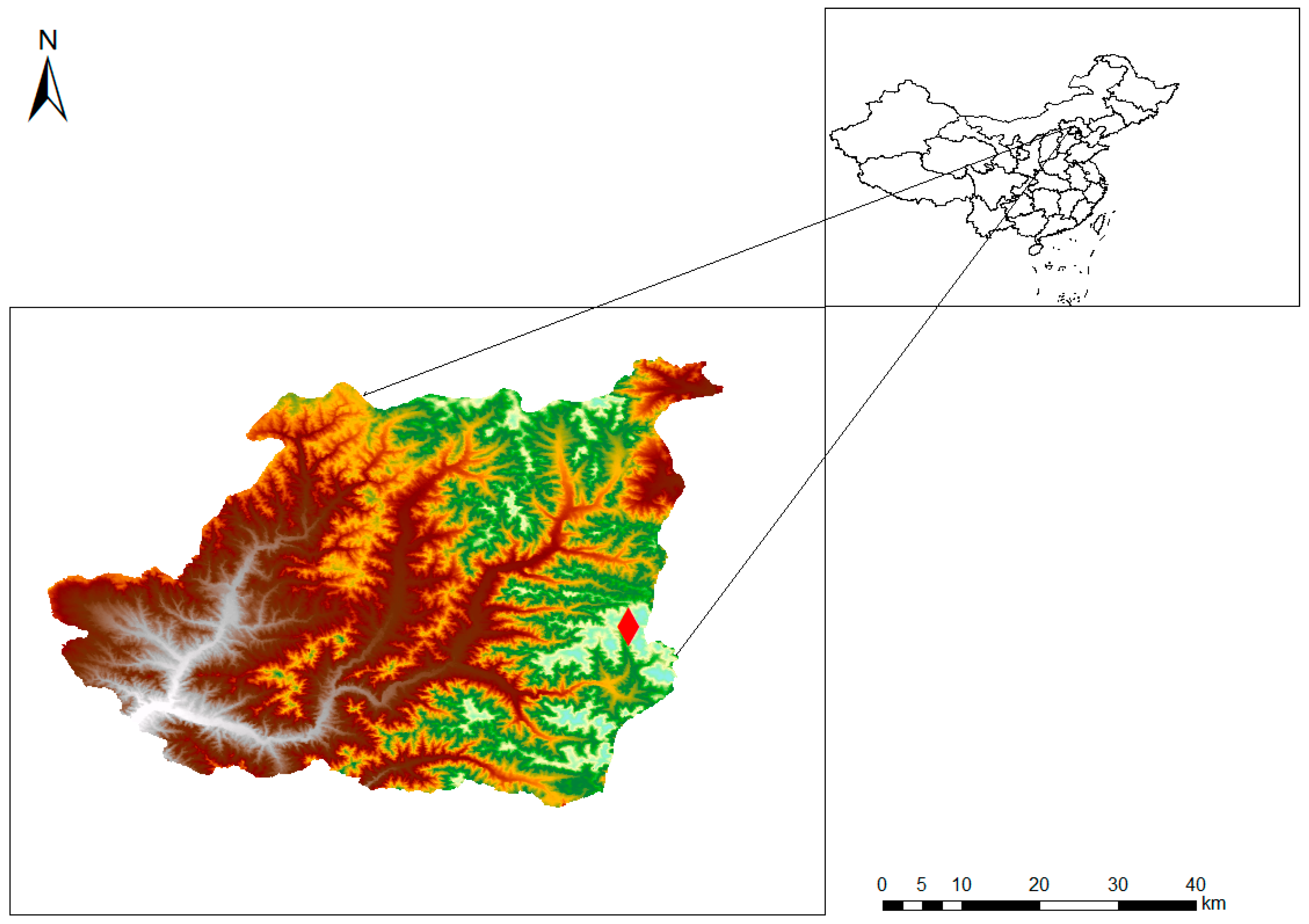
2.2. Study Area
2.3. Sample Collection
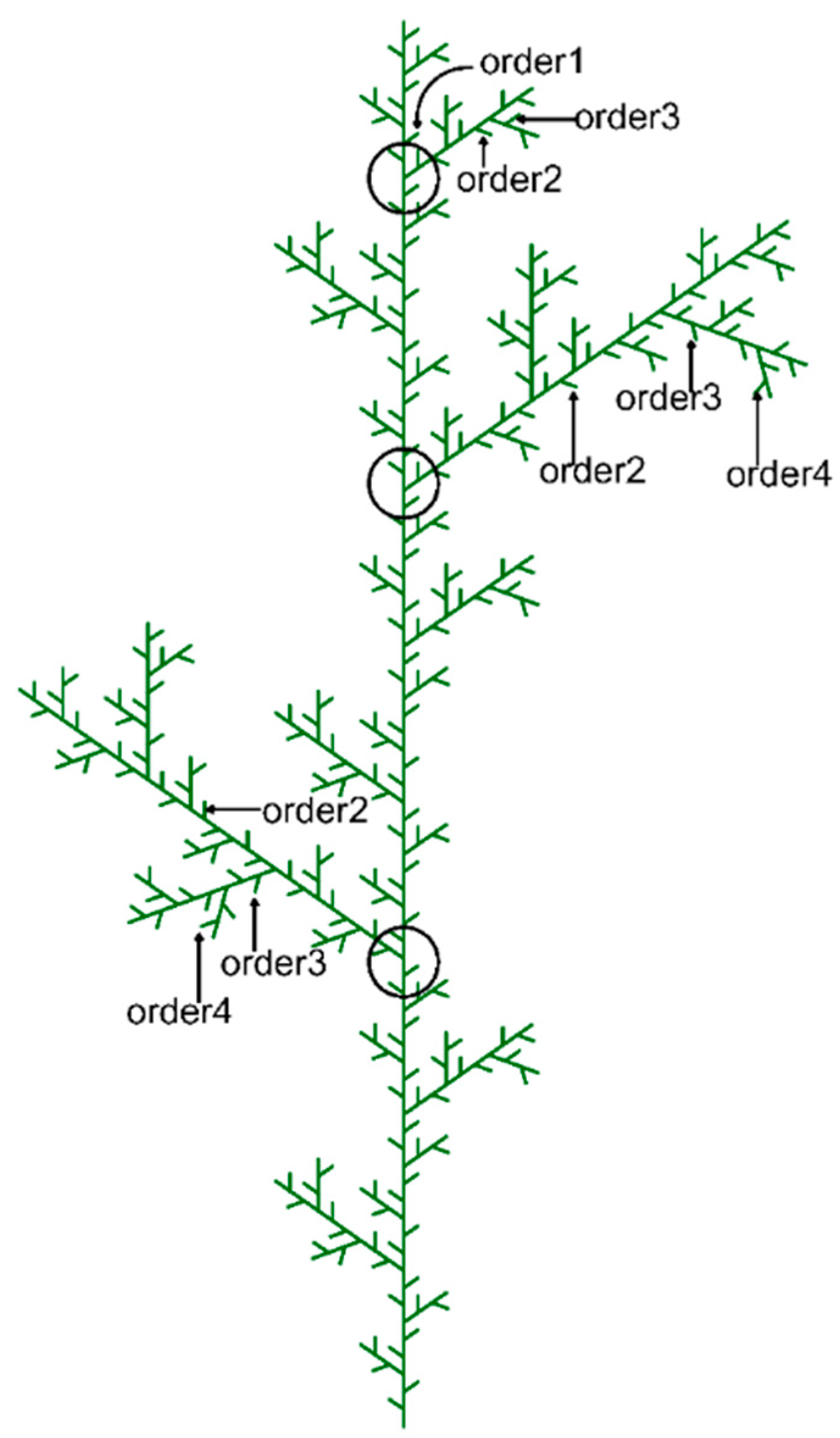
2.4. Shoot Trait Measurements
2.5. Data Analysis
3. Results
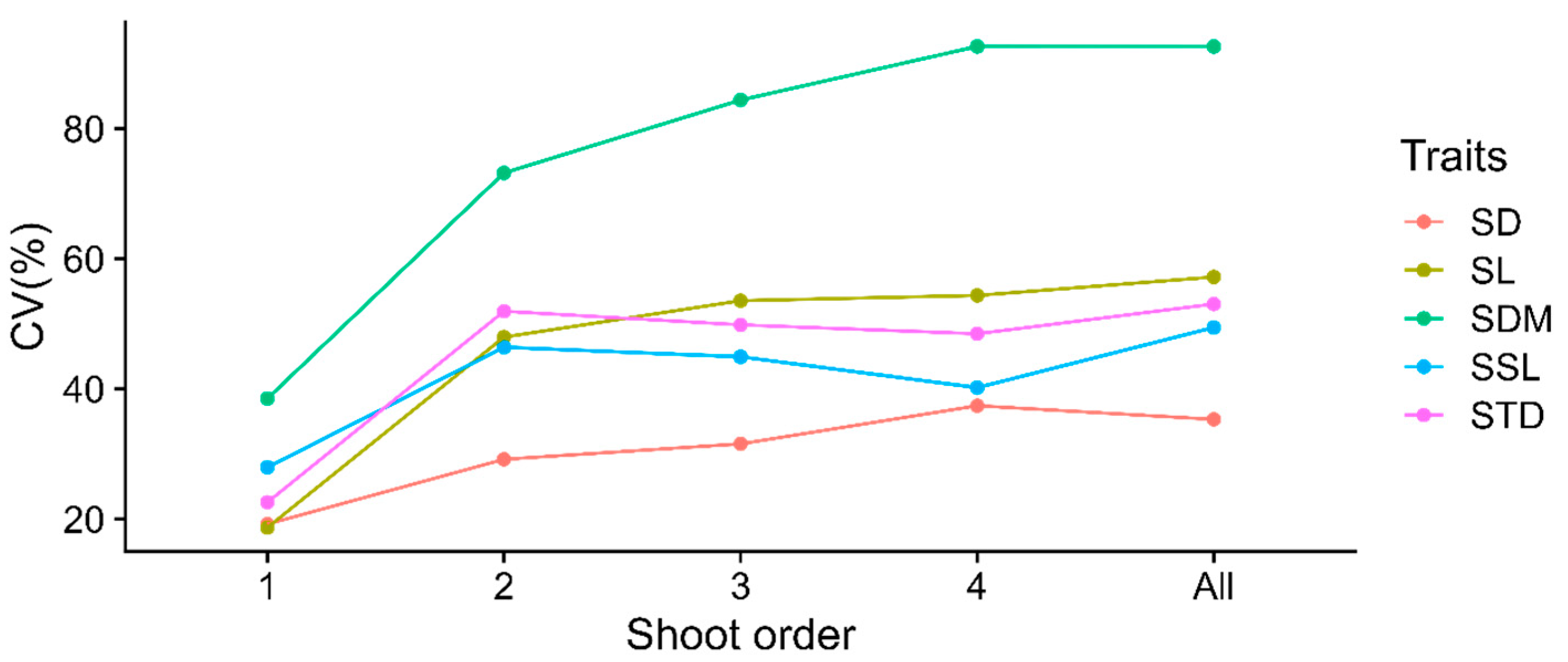
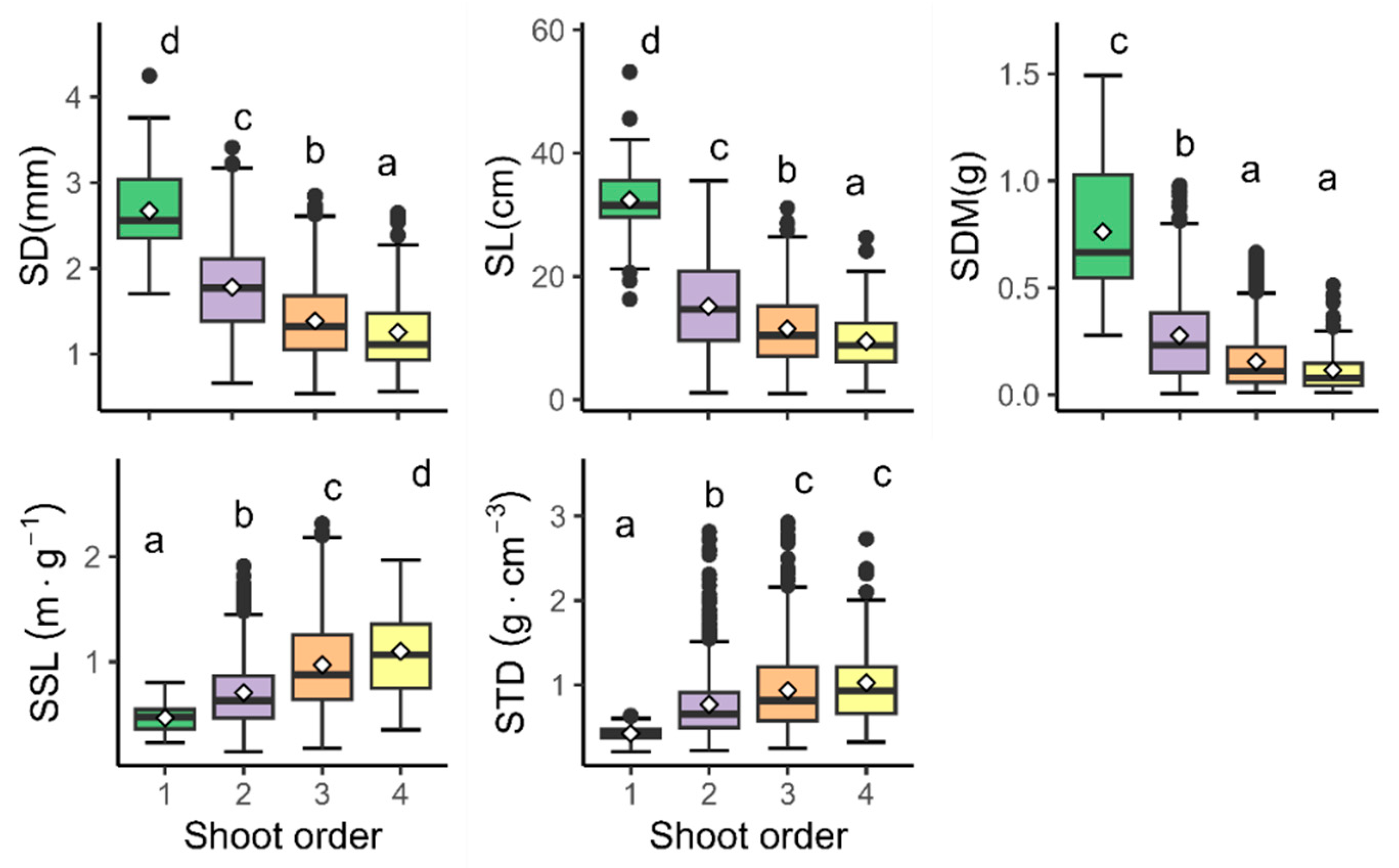
3.1. Variations in Shoot Traits by Branching Orders
3.2. Trait Correlations in the Shoot
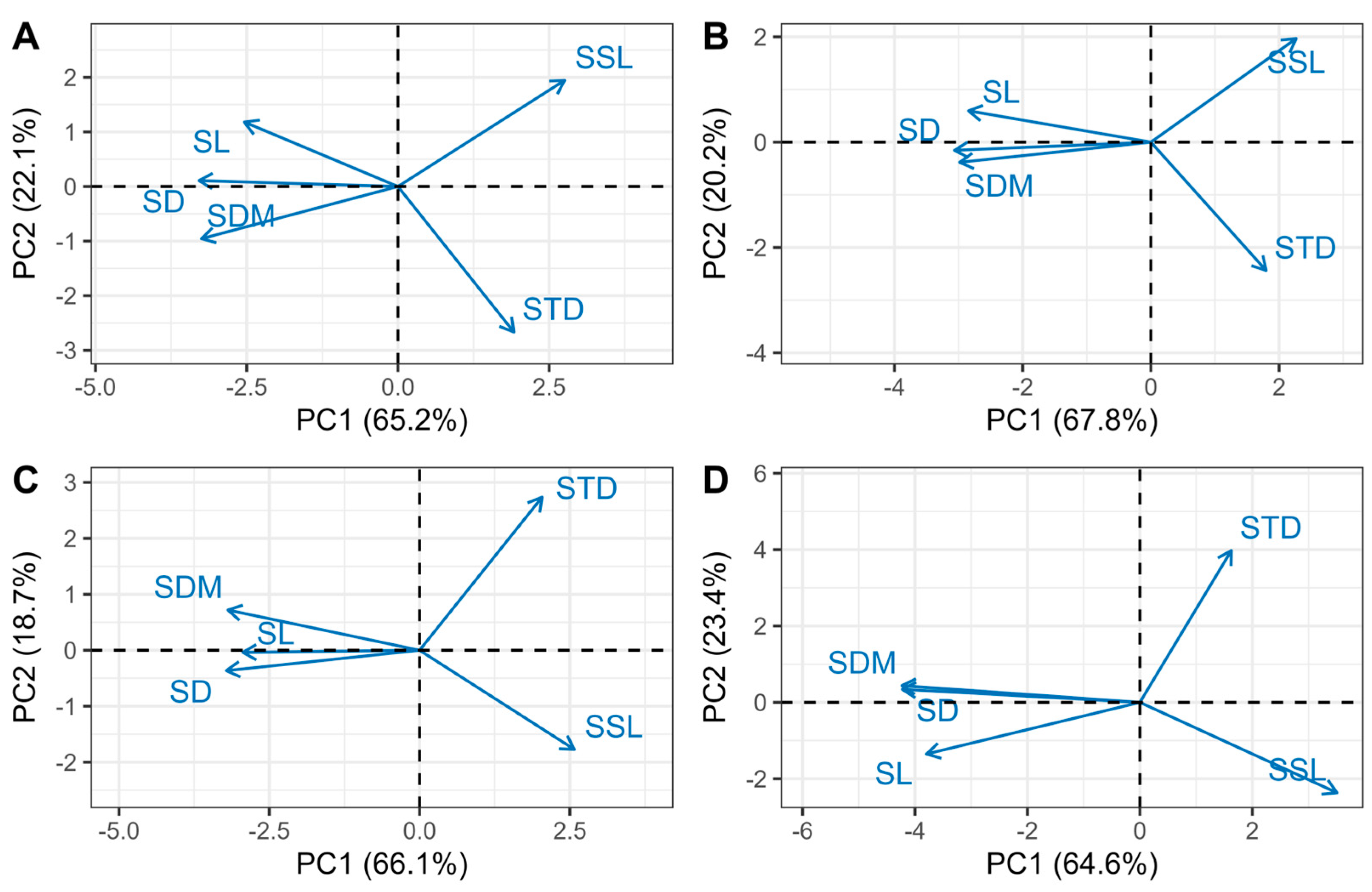
3.3. Multivariate Coordination
4. Discussion
4.1. The Relative Importance of Acclimation at the Level of Allocation and Morphology
4.2. Bivariate Relationships Among Shoot Traits
4.3. Leading Dimensions of Shoot Trait Variation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diaz, S.; Hodgson, J.G.; Thompson, K.; Cabido, M.; Cornelissen, J.H.C.; Jalili, A.; Montserrat-Martí, G.; Grime, J.P.; Zarrinkamar, F.; Asri, Y.; et al. The Plant Traits That Drive Ecosystems: Evidence from Three Continents. J. Veg. Sci. 2004, 15, 295–304. [Google Scholar] [CrossRef]
- Shipley, B.; De Bello, F.; Cornelissen, J.H.C.; Laliberté, E.; Laughlin, D.C.; Reich, P.B. Reinforcing Loose Foundation Stones in Trait-Based Plant Ecology. Oecologia 2016, 180, 923–931. [Google Scholar] [CrossRef] [PubMed]
- Violle, C.; Navas, M.-L.; Vile, D.; Kazakou, E.; Fortunel, C.; Hummel, I.; Garnier, E. Let the Concept of Trait Be Functional! Oikos 2007, 116, 882–892. [Google Scholar] [CrossRef]
- Cope, O.L.; Keefover-Ring, K.; Kruger, E.L.; Lindroth, R.L. Growth–Defense Trade-Offs Shape Population Genetic Composition in an Iconic Forest Tree Species. Proc. Natl. Acad. Sci. USA 2021, 118, e2103162118. [Google Scholar] [CrossRef] [PubMed]
- Funk, J.L.; Larson, J.E.; Ames, G.M.; Butterfield, B.J.; Cavender-Bares, J.; Firn, J.; Laughlin, D.C.; Sutton-Grier, A.E.; Williams, L.; Wright, J. Revisiting the Holy Grail: Using Plant Functional Traits to Understand Ecological Processes. Biol. Rev. 2017, 92, 1156–1173. [Google Scholar] [CrossRef]
- Kovenock, M.; Koven, C.D.; Knox, R.G.; Fisher, R.A.; Swann, A.L.S. Leaf Trait Plasticity Alters Competitive Ability and Functioning of Simulated Tropical Trees in Response to Elevated Carbon Dioxide. Glob. Biogeochem. Cycles 2021, 35, e2020GB006807. [Google Scholar] [CrossRef]
- Bjorkman, A.D.; Myers-Smith, I.H.; Elmendorf, S.C.; Normand, S.; Rüger, N.; Beck, P.S.A.; Blach-Overgaard, A.; Blok, D.; Cornelissen, J.H.C.; Forbes, B.C.; et al. Plant Functional Trait Change across a Warming Tundra Biome. Nature 2018, 562, 57–62. [Google Scholar] [CrossRef]
- Poorter, H.; Ryser, P. The Limits to Leaf and Root Plasticity: What Is so Special about Specific Root Length? New Phytol. 2015, 206, 1188–1190. [Google Scholar] [CrossRef]
- Poorter, H.; Niklas, K.J.; Reich, P.B.; Oleksyn, J.; Poot, P.; Mommer, L. Biomass Allocation to Leaves, Stems and Roots: Meta-Analyses of Interspecific Variation and Environmental Control. New Phytol. 2012, 193, 30–50. [Google Scholar] [CrossRef]
- Violle, C.; Enquist, B.J.; McGill, B.J.; Jiang, L.; Albert, C.H.; Hulshof, C.; Jung, V.; Messier, J. The Return of the Variance: Intraspecific Variability in Community Ecology. Trends Ecol. Evol. 2012, 27, 244–252. [Google Scholar] [CrossRef]
- Goto, T.; Osada, N. Geographic Variation in Shoot Structure in Association with Fruit Size in an Evergreen Woody Species. AoB Plants 2021, 13, plab023. [Google Scholar] [CrossRef] [PubMed]
- Yao, F.; Chen, Y.; Yan, Z.; Li, P.; Han, W.; Fang, J. Biogeographic Patterns of Structural Traits and C:N:P Stoichiometry of Tree Twigs in China’s Forests. PLoS ONE 2015, 10, e0116391. [Google Scholar] [CrossRef] [PubMed]
- Taugourdeau, O.; Delagrange, S.; Lecigne, B.; Sousa-Silva, R.; Messier, C. Sugar Maple (Acer saccharum Marsh.) Shoot Architecture Reveals Coordinated Ontogenetic Changes between Shoot Specialization and Branching Pattern. Trees 2019, 33, 1615–1625. [Google Scholar] [CrossRef]
- Wang, Z.; Niklas, K.J.; Ma, Z.; Jiang, D.; Deng, J. The 2/3 Scaling of Twig Nitrogen to Phosphorus in Woody Plants. For. Ecosyst. 2022, 9, 100049. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, G.; Xian, J.; Yang, K.; Wang, L.; Yang, Q. Complex Dynamics of Twig Elements and Stoichiometric Ratios with Altitude Changes in the Typical Dry Valley, Eastern Qinghai-Tibet Plateau. Ecol. Indic. 2022, 144, 109484. [Google Scholar] [CrossRef]
- Siefert, A.; Violle, C.; Chalmandrier, L.; Albert, C.H.; Taudiere, A.; Fajardo, A.; Aarssen, L.W.; Baraloto, C.; Carlucci, M.B.; Cianciaruso, M.V.; et al. A Global Meta-Analysis of the Relative Extent of Intraspecific Trait Variation in Plant Communities. Ecol. Lett. 2015, 18, 1406–1419. [Google Scholar] [CrossRef]
- Albert, C.H.; Thuiller, W.; Yoccoz, N.G.; Soudant, A.; Boucher, F.; Saccone, P.; Lavorel, S. Intraspecific Functional Variability: Extent, Structure and Sources of Variation. J. Ecol. 2010, 98, 604–613. [Google Scholar] [CrossRef]
- Messier, J.; McGill, B.J.; Enquist, B.J.; Lechowicz, M.J. Trait Variation and Integration across Scales: Is the Leaf Economic Spectrum Present at Local Scales? Ecography 2017, 40, 685–697. [Google Scholar] [CrossRef]
- Moran, E.V.; Hartig, F.; Bell, D.M. Intraspecific Trait Variation across Scales: Implications for Understanding Global Change Responses. Glob. Change Biol. 2016, 22, 137–150. [Google Scholar] [CrossRef]
- Remphrey, W.R.; Powell, G.R. Crown Architecture of Larix laricina Saplings: An Analysis of Higher Order Branching. Can. J. Bot. 1987, 65, 268–279. [Google Scholar] [CrossRef]
- Qiu, X.; Wang, H.; Peng, D.; Liu, X.; Yang, F.; Li, Z.; Cheng, S. Thinning Drives C:N:P Stoichiometry and Nutrient Resorption in Larix principis-rupprechtii Plantations in North China. For. Ecol. Manag. 2020, 462, 117984. [Google Scholar] [CrossRef]
- Xue, F.; Jiang, Y.; Dong, M.; Wang, M.; Ding, X.; Yang, X.; Cui, M.; Xu, H.; Kang, M. Seasonal and Daily Variations in Stem Water Relations between Co-Occurring Larix principis-rupprechtii and Picea meyeri at Different Elevations. For. Ecol. Manag. 2022, 504, 119821. [Google Scholar] [CrossRef]
- Zhang, Y.-P.; Jiang, Y.; Wang, B.; Jiao, L.; Wang, M. Seasonal Water Use by Larix principis-rupprechtii in an Alpine Habitat. For. Ecol. Manag. 2018, 409, 47–55. [Google Scholar] [CrossRef]
- Cai, K.; Zhou, X.; Li, X.; Kang, Y.; Yang, X.; Cui, Y.; Li, G.; Pei, X.; Zhao, X. Insight Into the Multiple Branches Traits of a Mutant in Larix olgensis by Morphological, Cytological, and Transcriptional Analyses. Front. Plant Sci. 2021, 12, 787661. [Google Scholar] [CrossRef] [PubMed]
- Díaz, S.; Kattge, J.; Cornelissen, J.H.C.; Wright, I.J.; Lavorel, S.; Dray, S.; Reu, B.; Kleyer, M.; Wirth, C.; Colin Prentice, I.; et al. The Global Spectrum of Plant Form and Function. Nature 2016, 529, 167–171. [Google Scholar] [CrossRef]
- Wright, I.J.; Reich, P.B.; Westoby, M.; Ackerly, D.D.; Baruch, Z.; Bongers, F.; Cavender-Bares, J.; Chapin, T.; Cornelissen, J.H.C.; Diemer, M.; et al. The Worldwide Leaf Economics Spectrum. Nature 2004, 428, 821–827. [Google Scholar] [CrossRef]
- Osada, N. Crown Development in a Pioneer Tree, Rhus Trichocarpa, in Relation to the Structure and Growth of Individual Branches. New Phytol. 2006, 172, 667–678. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, A. Influence of Shoot Architectural Position on Shoot Growth and Branching Patterns in Cleyera japonica. Tree Physiol. 2002, 22, 885–889. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, A. Patterns of Vegetative Growth and Reproduction in Relation to Branch Orders: The Plant as a Spatially Structured Population. Trees 2000, 14, 329–333. [Google Scholar] [CrossRef]
- Suzuki, A.A. Shoot Growth Patterns in Saplings of Cleyera Japonica in Relation to Light and Architectural Position. Tree Physiol. 2003, 23, 67–71. [Google Scholar] [CrossRef]
- Anderegg, L.D.L.; Berner, L.T.; Badgley, G.; Sethi, M.L.; Law, B.E.; HilleRisLambers, J. Within-Species Patterns Challenge Our Understanding of the Leaf Economics Spectrum. Ecol. Lett. 2018, 21, 734–744. [Google Scholar] [CrossRef]
- Anderson, J.T.; Gezon, Z.J. Plasticity in Functional Traits in the Context of Climate Change: A Case Study of the Subalpine Forb Boechera stricta (Brassicaceae). Glob. Change Biol. 2015, 21, 1689–1703. [Google Scholar] [CrossRef] [PubMed]
- Osada, N.; Tateno, R.; Mori, A.; Takeda, H. Changes in Crown Development Patterns and Current-Year Shoot Structure with Light Environment and Tree Height in Fagus crenata (Fagaceae). Am. J. Bot. 2004, 91, 1981–1989. [Google Scholar] [CrossRef]
- Sone, K.; Noguchi, K.; Terashima, I. Mechanical and Ecophysiological Significance of the Form of a Young Acer Rufinerve Tree: Vertical Gradient in Branch Mechanical Properties. Tree Physiol. 2006, 26, 1549–1558. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Enquist, B.J.; West, G.B.; Charnov, E.L.; Brown, J.H. Allometric Scaling of Production and Life-History Variation in Vascular Plants. Nature 1999, 401, 907–911. [Google Scholar] [CrossRef]
- Reich, P.B. Do Plants Increase Resource Acquisition Potential in the Face of Resource Shortfalls, and If so, How? New Phytol. 2018, 219, 1142–1144. [Google Scholar] [CrossRef] [PubMed]
- Freschet, G.T.; Pagès, L.; Iversen, C.M.; Comas, L.H.; Rewald, B.; Roumet, C.; Klimešová, J.; Zadworny, M.; Poorter, H.; Postma, J.A.; et al. A Starting Guide to Root Ecology: Strengthening Ecological Concepts and Standardising Root Classification, Sampling, Processing and Trait Measurements. New Phytol. 2021, 232, 973–1122. [Google Scholar] [CrossRef]
- Liu, R.; Yang, X.; Gao, R.; Huang, Z.; Cornelissen, J.H.C. Coordination of Economics Spectra in Leaf, Stem and Root within the Genus Artemisia along a Large Environmental Gradient in China. Glob. Ecol. Biogeogr. 2023, 32, 324–338. [Google Scholar] [CrossRef]
- McCulloh, K.A.; Meinzer, F.C.; Sperry, J.S.; Lachenbruch, B.; Voelker, S.L.; Woodruff, D.R.; Domec, J.-C. Comparative Hydraulic Architecture of Tropical Tree Species Representing a Range of Successional Stages and Wood Density. Oecologia 2011, 167, 27–37. [Google Scholar] [CrossRef]
- Poorter, L.; McDonald, I.; Alarcón, A.; Fichtler, E.; Licona, J.-C.; Peña-Claros, M.; Sterck, F.; Villegas, Z.; Sass-Klaassen, U. The Importance of Wood Traits and Hydraulic Conductance for the Performance and Life History Strategies of 42 Rainforest Tree Species. New Phytol. 2010, 185, 481–492. [Google Scholar] [CrossRef]
- Chave, J.; Coomes, D.; Jansen, S.; Lewis, S.L.; Swenson, N.G.; Zanne, A.E. Towards a Worldwide Wood Economics Spectrum. Ecol. Lett. 2009, 12, 351–366. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Li, X.; Ji, X.; Zhang, Z.; Zhang, H.; Zha, T.; Jiang, L. Elevation and Total Nitrogen Are the Critical Factors That Control the Spatial Distribution of Soil Organic Carbon Content in the Shrubland on the Bashang Plateau, China. Catena 2021, 204, 105415. [Google Scholar] [CrossRef]
- Borchert, R.; Slade, N.A. Bifurcation Ratios and the Adaptive Geometry of Trees. Bot. Gaz. 1981, 142, 394–401. [Google Scholar] [CrossRef]
- Pregitzer, K.S. Fine Roots of Trees—A New Perspective. New Phytol. 2002, 154, 267–270. [Google Scholar] [CrossRef] [PubMed]
- Gaaliche, B.; Aїachi-Mezghani, M.; Trad, M.; Costes, E.; Lauri, P.-E.; Mars, M. Shoot Architecture and Morphology of Different Branch Orders in Fig Tree (Ficus carica L.). Int. J. Fruit Sci. 2016, 16, 378–394. [Google Scholar] [CrossRef]
- Suzuki, A.A.; Suzuki, M. Why Do Lower Order Branches Show Greater Shoot Growth than Higher Order Branches? Considering Space Availability as a Factor Affecting Shoot Growth. Trees 2009, 23, 69–77. [Google Scholar] [CrossRef]
- Ryser, P.; Eek, L. Consequences of Phenotypic Plasticity vs. Interspecific Differences in Leaf and Root Traits for Acquisition of Aboveground and Belowground Resources. Am. J. Bot. 2000, 87, 402–411. [Google Scholar] [CrossRef]
- Ostonen, I.; Truu, M.; Helmisaari, H.-S.; Lukac, M.; Borken, W.; Vanguelova, E.; Godbold, D.L.; Lõhmus, K.; Zang, U.; Tedersoo, L.; et al. Adaptive Root Foraging Strategies along a Boreal–Temperate Forest Gradient. New Phytol. 2017, 215, 977–991. [Google Scholar] [CrossRef]
- Muller-Landau, H.C. Interspecific and Inter-Site Variation in Wood Specific Gravity of Tropical Trees. Biotropica 2004, 36, 20–32. [Google Scholar] [CrossRef]
- Chao, K.-J.; Phillips, O.L.; Gloor, E.; Monteagudo, A.; Torres-Lezama, A.; Martínez, R.V. Growth and Wood Density Predict Tree Mortality in Amazon Forests. J. Ecol. 2008, 96, 281–292. [Google Scholar] [CrossRef]
- King, D.A.; Davies, S.J.; Tan, S.; Noor, N.S.M. The Role of Wood Density and Stem Support Costs in the Growth and Mortality of Tropical Trees. J. Ecol. 2006, 94, 670–680. [Google Scholar] [CrossRef]
- Kong, D.; Ma, C.; Zhang, Q.; Li, L.; Chen, X.; Zeng, H.; Guo, D. Leading Dimensions in Absorptive Root Trait Variation across 96 Subtropical Forest Species. New Phytol. 2014, 203, 863–872. [Google Scholar] [CrossRef] [PubMed]
- Roumet, C.; Birouste, M.; Picon-Cochard, C.; Ghestem, M.; Osman, N.; Vrignon-Brenas, S.; Cao, K.-F.; Stokes, A. Root Structure-Function Relationships in 74 Species: Evidence of a Root Economics Spectrum Related to Carbon Economy. New Phytol. 2016, 210, 815–826. [Google Scholar] [CrossRef] [PubMed]
- Mommer, L.; Weemstra, M. The Role of Roots in the Resource Economics Spectrum. New Phytol. 2012, 195, 725–727. [Google Scholar] [CrossRef] [PubMed]
- Valverde-Barrantes, O.J.; Smemo, K.A.; Blackwood, C.B. Fine Root Morphology Is Phylogenetically Structured, but Nitrogen Is Related to the Plant Economics Spectrum in Temperate Trees. Funct. Ecol. 2015, 29, 796–807. [Google Scholar] [CrossRef]
- Kong, D.; Wang, J.; Wu, H.; Valverde-Barrantes, O.J.; Wang, R.; Zeng, H.; Kardol, P.; Zhang, H.; Feng, Y. Nonlinearity of Root Trait Relationships and the Root Economics Spectrum. Nat. Commun. 2019, 10, 2203. [Google Scholar] [CrossRef]
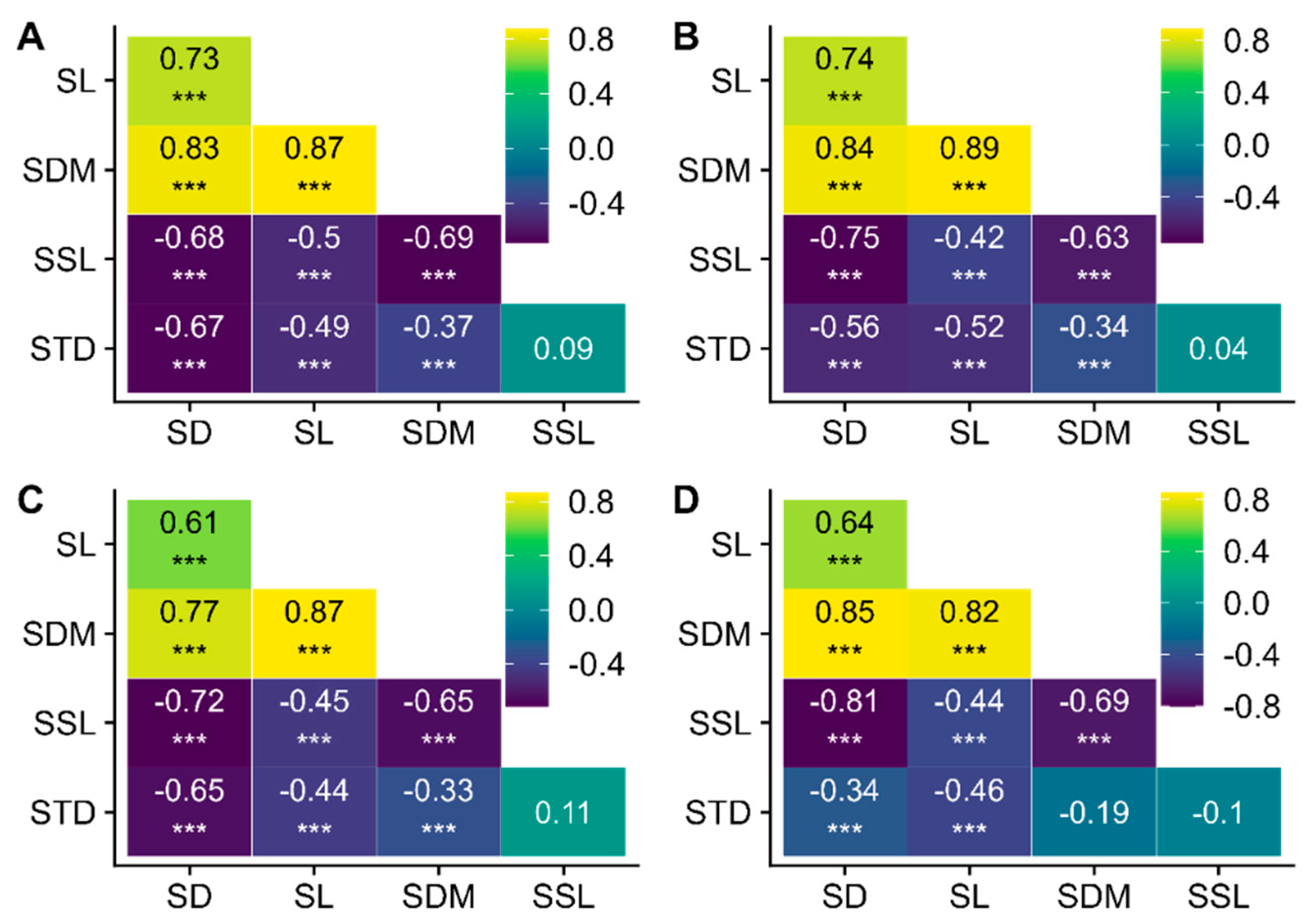
| Traits | df | Χ2 | p |
|---|---|---|---|
| SD | 3 | 371.48 | <0.001 |
| SL | 3 | 296.38 | <0.001 |
| SDM | 3 | 350.74 | <0.001 |
| SSL | 3 | 261.93 | <0.001 |
| STD | 3 | 187.10 | <0.001 |
| Branch Orders | KMO Test | Bartlett’s Test | ||
|---|---|---|---|---|
| df | Χ2 | p | ||
| Order 1 | 0.46 | 10 | 434.04 | <0.001 |
| Order 2 | 0.52 | 10 | 3186.681 | <0.001 |
| Order 3 | 0.49 | 10 | 2813.344 | <0.001 |
| Order 4 | 0.60 | 10 | 516.61 | <0.001 |
| Overall | 0.54 | 10 | 7299.953 | <0.001 |
| Traits | Order | n | Mean | SD | Median | Min | Max | CV% |
|---|---|---|---|---|---|---|---|---|
| 1 | 69 | 2.67 | 0.51 | 2.56 | 1.70 | 4.25 | 19.24 | |
| 2 | 713 | 1.78 | 0.52 | 1.77 | 0.66 | 3.41 | 29.20 | |
| SD (mm) | 3 | 658 | 1.39 | 0.44 | 1.32 | 0.54 | 2.85 | 31.57 |
| 4 | 111 | 1.25 | 0.47 | 1.11 | 0.56 | 2.65 | 37.43 | |
| all | 1551 | 1.61 | 0.57 | 1.54 | 0.54 | 4.25 | 35.34 | |
| 1 | 69 | 32.41 | 6.06 | 31.50 | 16.29 | 53.2 | 18.71 | |
| 2 | 713 | 15.15 | 7.27 | 14.66 | 1.10 | 35.5 | 47.98 | |
| SL (cm) | 3 | 658 | 11.47 | 6.15 | 10.40 | 1.02 | 31.1 | 53.57 |
| 4 | 111 | 9.42 | 5.12 | 8.80 | 1.30 | 26.3 | 54.38 | |
| all | 1551 | 13.95 | 7.98 | 12.49 | 1.02 | 53.2 | 57.21 | |
| 1 | 69 | 0.76 | 0.29 | 0.67 | 0.28 | 1.49 | 38.53 | |
| 2 | 713 | 0.28 | 0.2 | 0.23 | 0.01 | 0.98 | 73.20 | |
| SDM (g) | 3 | 658 | 0.16 | 0.13 | 0.11 | 0.01 | 0.66 | 84.40 |
| 4 | 111 | 0.12 | 0.11 | 0.08 | 0.01 | 0.51 | 92.64 | |
| all | 1551 | 0.24 | 0.22 | 0.16 | 0.01 | 1.49 | 92.63 | |
| 1 | 69 | 0.47 | 0.13 | 0.48 | 0.23 | 0.80 | 27.97 | |
| 2 | 713 | 0.71 | 0.33 | 0.63 | 0.15 | 1.91 | 46.42 | |
| SSL (m/g) | 3 | 658 | 0.97 | 0.44 | 0.88 | 0.17 | 2.31 | 44.95 |
| 4 | 111 | 1.10 | 0.44 | 1.06 | 0.35 | 1.97 | 40.21 | |
| all | 1551 | 0.84 | 0.41 | 0.74 | 0.15 | 2.31 | 49.46 | |
| 1 | 69 | 0.42 | 0.10 | 0.41 | 0.21 | 0.64 | 22.59 | |
| 2 | 713 | 0.77 | 0.40 | 0.65 | 0.22 | 2.82 | 51.95 | |
| STD (g/cm3) | 3 | 658 | 0.94 | 0.47 | 0.81 | 0.25 | 2.93 | 49.86 |
| 4 | 111 | 1.02 | 0.50 | 0.93 | 0.32 | 2.73 | 48.49 | |
| all | 1551 | 0.84 | 0.45 | 0.72 | 0.21 | 2.93 | 53.06 |
| Traits | df | SS | MS | F | p |
|---|---|---|---|---|---|
| SD | 3 | 144.36 | 48.121 | 206.75 | <0.001 |
| SL | 3 | 30,851 | 10,283.8 | 234.51 | <0.001 |
| SDM | 3 | 26.051 | 8.6837 | 281.95 | <0.001 |
| SSL | 3 | 40.734 | 13.578 | 93.745 | <0.001 |
| STD | 3 | 25.36 | 8.4533 | 46.053 | <0.001 |
| All | Order 1 | Order 2 | Order 3 | Order 4 | |
|---|---|---|---|---|---|
| Variation explained (%) | 67.3 | 65.2 | 67.8 | 66.1 | 64.6 |
| Shoot traits | Loadings | ||||
| SD | −0.52 | −0.53 | −0.52 | −0.51 | −0.52 |
| SL | −0.48 | −0.41 | −0.48 | −0.47 | −0.47 |
| SDM | −0.50 | −0.52 | −0.51 | −0.50 | −0.52 |
| SSL | 0.39 | 0.44 | 0.38 | 0.41 | 0.43 |
| STD | 0.32 | 0.31 | 0.30 | 0.32 | 0.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Zhang, H.; Wang, Z.; Liu, Z. Patterns of Variation and Coordination in Shoot Traits Across Four Branching Orders of Larix principis-rupprechtii. Life 2025, 15, 927. https://doi.org/10.3390/life15060927
Yu Y, Zhang H, Wang Z, Liu Z. Patterns of Variation and Coordination in Shoot Traits Across Four Branching Orders of Larix principis-rupprechtii. Life. 2025; 15(6):927. https://doi.org/10.3390/life15060927
Chicago/Turabian StyleYu, Yang, Huayong Zhang, Zhongyu Wang, and Zhao Liu. 2025. "Patterns of Variation and Coordination in Shoot Traits Across Four Branching Orders of Larix principis-rupprechtii" Life 15, no. 6: 927. https://doi.org/10.3390/life15060927
APA StyleYu, Y., Zhang, H., Wang, Z., & Liu, Z. (2025). Patterns of Variation and Coordination in Shoot Traits Across Four Branching Orders of Larix principis-rupprechtii. Life, 15(6), 927. https://doi.org/10.3390/life15060927







