Biological, Equilibrium and Photochemical Signatures of C, N and S Isotopes in the Early Earth and Exoplanet Atmospheres

Abstract

The unambiguous detection of biosignatures in exoplanet atmospheres is a primary objective for astrobiologists and exoplanet astronomers. The primary methodology is the observation of combinations of gases considered unlikely to coexist in an atmosphere or individual gases considered to be highly biogenic. Earth-like examples of the former include CH₄ and O₃, and the latter includes dimethyl sulfide (DMS). To improve the plausibility of the detection of life, I argue that the isotope ratios of key atmospheric species are needed. The C isotope ratios of CO₂ and CH₄ are especially valuable. On Earth, thermogenesis and volcanism result in a substantial difference in δ¹³C between atmospheric CH₄ and CO₂ of ~−25‰. This difference could have changed significantly, perhaps as large as −95‰ after the evolution of hydrogenotrophic methanogens. In contrast, nitrogen fixation by nitrogenase results in a relatively small difference in δ¹⁵N between N₂ and NH₃. Isotopic biosignatures on ancient Earth and rocky exoplanets likely coexist with much larger photochemical signatures. Extreme δ¹⁵N enrichment in HCN may be due to photochemical self-shielding in N₂, a purely abiotic process. Spin-forbidden photolysis of CO₂ produces CO with δ¹³C < −200‰, as has been observed in the Venus mesosphere. Self-shielding in SO₂ may generate detectable ³⁴S enrichment in SO in atmospheres similar to that of WASP-39b. Sufficiently precise isotope ratio measurements of these and related gases in terrestrial-type exoplanet atmospheres will require instruments with significantly higher spectral resolutions and light-collecting areas than those currently available.

1. Introduction

Stable isotope ratios are used as terrestrial biosignatures in all epochs of Earth history, from the present to the Archean, and are essential tools in astrobiology [1]. Most of these data are in situ measurements from ancient rocks. Here, my focus is on possible atmospheric isotope signatures. Models of Earth’s ancient atmosphere [2] carefully consider the evolution of atmospheric composition over time but generally do not consider the possible evolution of atmospheric isotope ratios. One of my objectives here is to estimate a plausible range of C isotope histories for the Earth’s early atmosphere. The geochemical record of C and N isotopes in ancient rocks will serve as a baseline to guide these estimates for early Earth and provide a possible framework for predicting isotopic biosignatures in the atmospheres of Earth-like exoplanets.

Several studies have been conducted on the detectability of isotope ratios in exoplanet atmospheres [3,4], including rocky planets in the Trappist-1 system [5]. Measurements have been reported for a young, directly imaged, super-Jupiter [6], and also for WASP-77b, which is a hot Jupiter [7]. In both cases, the C isotope ratio was determined for atmospheric CO, and these objects were found to be extremely enriched in ¹³C compared to Earth. Given the equilibrium temperatures of these two objects, they are not likely abodes for life, but their high ¹³C enrichment may suggest an accumulation of ¹³C-rich ices during formation beyond the CO snow line [6]. In addition to CO, Glidden et al. [8] have pointed out the favorability of using CO₂ to determine C isotope ratios in exoplanet atmospheres.

Superimposed on any biological isotope fractionation in atmospheric molecules are photochemically induced isotope effects, with sometimes quite large isotope fractionation drive by UV photodissociation. Self-shielding is believed to be important in protoplanetary disks [9,10] and molecular cloud core [11,12] environments and is a likely mechanism for explaining the differences in C, N, and O isotope ratios for inner solar system planets compared to those of the Sun [11,13]. Self-shielding in N₂ has been demonstrated to be important for ¹⁵N enrichment in nitriles in Titan’s atmosphere [14] and very likely occurred in Earth’s ancient atmosphere.

Photochemical self-shielding is an example of an abundance-dependent isotope fractionation process. Biological isotope fractionation is an example of a kinetic fractionation process driven by the mass dependence of relatively rapid biochemical reactions. In addition to these two mechanisms, equilibrium isotope fractionation is driven by differences in zero-point energies among isotopologues [15]. Equilibrium fractionation has its roots in the quantum mechanics of the harmonic oscillator for molecular bonds. These three isotope fractionation processes, equilibrium, kinetic, and abundance-dependent, encompass the majority of isotopic processes relevant to exoplanet atmospheres.

The remainder of this paper is organized as follows. I first discuss C and N isotope ratios in the modern Earth atmosphere. This is followed by model predictions for the equilibrium isotope ratios among pairs of C-containing and N-containing gases from [15]. Equilibrium isotope ratios are most relevant to warm and hot exoplanet atmospheres, but they serve as a useful benchmark for atmospheres with isotope ratios determined by photochemical or biological processes. Next, I examine how UV photochemical self-shielding in small molecules can dramatically alter C and especially N isotope ratios in photochemical products such as HCN. I also apply these ideas to S isotopes in warm Jupiters. I then address the evolution of C and N isotopes in Earth’s early atmosphere, allowing for terrestrial biological processes such as methanogenesis and nitrogen fixation. Finally, I present IR spectra of key atmospheric molecules and their isotopologues and briefly discuss the detectability of isotope ratios in exoplanet atmospheres with respect to the needed spectral resolution.

The objective of this paper is to consider the prospects of using stable isotope ratios as biosignatures in exoplanet atmospheres. The technical difficulty of astronomically observing isotope ratios is well appreciated [3,4,5,6,7], and it is unlikely that they will be useful as biosignatures on rocky worlds in the JWST era [16]. Nevertheless, isotopes offer a view of biological processes that is distinct from and complements the more usual atmospheric chemical composition arguments for biosignatures in atmospheres [17]. High-resolution spectral measurements with large telescopes will eventually make such measurements feasible, even for rocky planets.

2. C and N Isotope Ratios in the Modern Earth Atmosphere

As an example of how isotope ratios vary among molecules in the present-day atmosphere, I will first consider carbon in CO₂ and CH₄. Ignoring anthropogenic input, the CO₂ mixing ratio is determined by the balance of CO₂ emitted by volcanism and the sequestration of CO₂ in marine carbonates, primarily by biological organisms. Rather than compute CO₂ I will focus on the geochemcial processes that alter its isotope composition. The δ¹³C ratio of CO₂ is determined primarily by CO₂ exchange with the oceans. The massive reservoir of HCO₃⁻ in the oceans and the high exchange flux between the atmosphere and oceanic mixed layer fix the C isotope ratios in the ocean. Neglecting CO₂ photolysis in the upper atmosphere, a process that is not important for tropospheric isotope ratios, δ¹³C for CO₂ is −8.4 permil today and was about −6.5 permil in the pre-industrial atmosphere [18]. The pre-industrial δ¹³C value for CO₂ is close to the mantle value of −5 to −8‰ [19]. Photosynthesis, respiration, and air-sea exchange all contribute to the fractionation of C isotopes. Fractionation during photosynthesis creates fixed C with δ¹³C values 18 and 4‰ lower than those of atmospheric CO₂ for C₃ and C₄ plants, respectively [20]. The predominance of C₃ plants (about 85%) yields a terrestrial bulk biosphere with δ¹³C ~−22% relative to VPDB.

Expressing the δ¹³C of atmospheric CO₂ in terms of its sources, we have

$${\mathsf{\delta }}^{13}\mathrm{C}({\mathrm{C}\mathrm{O}}_2)={\displaystyle \frac{{\mathsf{\delta }}^{13}\mathrm{C}\left({\mathrm{C}}_{\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{t}}\right){\phi }_{plant resp}+{\mathsf{\delta }}^{13}\mathrm{C}\left({\mathrm{C}\mathrm{O}}_{2,\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f} \mathrm{o}\mathrm{c}\mathrm{e}\mathrm{a}\mathrm{n}}\right){\phi }_{ocean exch}}{{\phi }_{plant resp}+{\phi }_{ocean exch}}}$$

(1)

where φ is the CO₂ flux due to either plant respiration or emissions associated with air-ocean exchange. The fluxes of C are φ_{plant resp} = 60 Gt C yr⁻¹ and φ_{ocean exch} = 90 Gt C yr⁻¹, and the representative δ-values are −22‰ for plants and +2.5‰ for surface dissolved inorganic carbon (DIC). Air-sea exchange results in kinetic and equilibrium isotope enrichment in HCO₃⁻ relative to atmospheric CO₂ of ~7–10‰ [21]. From Equation (1), the above values yield δ¹³C = −7.5‰ for the atmospheric CO₂. Anthropogenic CO₂ must also be included when computing δ¹³C values for the modern atmosphere [20].

To estimate the δ¹³C value for CH₄ in the modern atmosphere, it is necessary to consider the production and loss processes. Methane is primarily a biogenic gas with a substantial anthropogenic contribution. The total source CH₄ flux to the atmosphere is ${\phi }_{{CH}_4}$ = 540 Tg CH₄ yr⁻¹, with 2/3 due to microbial activity (wetlands, rice paddies, animals, and termites) and 1/3 due to anthropogenic activity (biomass burning, landfills, coal mining, and natural gas) [22]. The sink flux of CH₄ is almost entirely oxidation in the atmosphere via the reaction

OH + CH₄ → CH₃ + H₂O

(2)

with a rate constant

$$k_2=1.36\times {10}^{-13}{\left({\displaystyle \frac{T}{298}}\right)}^{3.04}{e}^{-{\displaystyle \frac{920}{T}}}$$

(3)

The rate constant k₂ has units of cm³ molec⁻¹ s⁻¹ and is valid from 195–1234 K [23].

Equating the sources and sinks yields

$${\phi }_{{CH}_4}=\underset{0}{\overset{top}{\int }}{k}_1\left[\mathrm{O}\mathrm{H}\right]\left[{\mathrm{C}\mathrm{H}}_4\right]dz$$

(4)

OH and, to a lesser extent, CH₄ have complicated vertical profiles, which I will approximate as following the barometric law. The vertical integral in Equation (4) may then be approximated as multiplication by the atmospheric scale height

$$H_a={\displaystyle \frac{kT}{mg}}$$

(5)

where k is the Boltzmann constant, T is the atmospheric temperature, m is the mean molecular mass, and g is the acceleration of gravity. For the modern troposphere, H_a = 8 km. Solving for the steady-state CH₄ concentration yields

$$[\mathrm{C}{\mathrm{H}}_4]={\displaystyle \frac{{\phi }_{{CH}_4}}{k_2\left[\mathrm{O}\mathrm{H}\right]H_a}}$$

(6)

Most of the CH₄ oxidation occurs in the troposphere. For a representative lower troposphere temperature of 280 K, $k_2=4.2\times {10}^{-15}$ cm³ s⁻¹. The CH₄ source flux is 540 Tg CH₄ yr⁻¹ circa 1990 [22], which corresponds to $1.3\times {10}^{11}$ molec cm⁻² s⁻¹. For a maximum OH number density in the troposphere of ~1 × 10⁶ cm⁻³, the CH₄ number density is 3.9 × 10¹³ cm^−3, corresponding to a surface mole fraction of 1.5 ppm. This compares well with the 1991 atmospheric value of 1.7 ppm [24].

To compute the C isotope ratio for atmospheric CH₄, I rewrite Equation (6) for ¹³C-specific processes. Most CH₄ sources are either directly biogenic or involve the combustion of biogenic materials and will therefore produce a ¹³C-depleted CH₄ flux compared to oceanic carbon. Additionally, oxidation reaction 2 has a rate constant that varies with the isotope. For the ¹³C isotopologue Equation (6) becomes

$$[{}^{13}\mathrm{CH}_4]={\displaystyle \frac{{\phi }_{{}^{13}\mathit{CH}_4}}{{}^{13}{k}_2[OH]H_a}}$$

(7)

The global bulk source flux of CH₄ has a δ¹³C of ~−53‰ [25]. This value is the weighted average of biogenic sources (wetlands, rice fields, and ruminants) with δ¹³C ~−70 to −50‰ and thermogenic/pyrogenic sources (biomass burning) with δ¹³C ~15‰ [25]. There is a kinetic isotope effect in reaction 2 that causes slower oxidation of ¹³CH₄ by about 4‰ at 296 K [26]. The resulting CH₄ isotopologue ratio is

$${\displaystyle \frac{\left[{}^{13}\mathrm{CH}_4\right]}{\left[{\mathrm{CH}}_4\right]}}={\displaystyle \frac{{\phi }_{{}^{13}\mathit{CH}_4}}{{\phi }_{{CH}_4}}}{\displaystyle \frac{k_2}{{}^{13}{k}_2}}$$

(8)

From the definition of the geochemical δ-value for the C flux, δ¹³C, the ratio of fluxes may be expressed as

$${\displaystyle \frac{{\phi }_{{}^{13}\mathit{CH}_4}}{{\phi }_{{CH}_4}}}=\left({\delta }^{13}\mathrm{C}\left({\phi }_{source}\right)+1\right){\left({\displaystyle \frac{{}^{13}\mathrm{C}}{{}^{12}\mathrm{C}}}\right)}_{VPDB}$$

(9)

In Equation (9), δ¹³C has a fractional rather than permil value, δ¹³C(φ) + 1 = 0.9470, and VPDB is the Vienna Peedee Belemnite isotope standard with ¹³C/¹²C = 0.011180 [27]. For ${\displaystyle \frac{k_2}{{}^{13}{k}_2}}$ = 1.0039 [26], Equations (8) and (9) yield δ¹³C(CH₄) = −49‰, which is in good agreement with the measured tropospheric value of −47‰ [28]. There is additional isotope fractionation in the stratosphere due to the oxidation of CH₄ by O(¹D) and Cl [29,30], which I will neglect here. Aerobic methane oxidation by methanotrophs also produces a very large positive ¹³C enrichment in unoxidized CH₄; however, this does not significantly affect the δ¹³C of the large reservoir of CH₄ in the modern atmosphere [31].

In both ancient and modern Earth atmospheres, the primary nitrogen species is N₂. In the modern atmosphere, the next most abundant N-containing compounds are nitrogen oxides (N₂O, NO, NO₂, and HNO₃), whereas in the ancient Earth atmosphere, HCN and possibly NH₃ were important species. For Archean CH₄ ~1000 ppm, photochemical models predict HCN concentrations of ~100 ppm [2]. NH₃ is rapidly lost by photolysis in early Earth atmosphere models unless a haze (probably hydrocarbon) is present to block near-UV radiation. In the modern Earth atmosphere, N isotope variability is predicted and observed in nitrogen oxide species due to photolysis and isotope exchange reactions. Rather than discussing this in detail here, I refer the reader to a paper by Michalski et al. [32]. Both HCN and NH₃ are present in the atmosphere today, but at mixing ratios of ~200 ppt [33] and ~1–10 ppb [34], respectively. Nitrogen isotope measurements of NH₃ indicate two primary sources, agriculture and livestock and fossil fuel-related activities. Agriculture and livestock produce NH₃ with δ¹⁵N ~−40 to −10‰ and fossil fuel sources produce NH₃ with δ¹⁵N ~−20 to +10‰ [34]. Marine values for NH₃ are ~+5 to +13‰. All δ¹⁵N values are reported relative to an atmospheric N₂ standard.

3. Equilibrium C, N and S Isotope Ratios

Isotopic equilibrium is an important end-member for the isotope ratios in planetary atmospheres. For an equilibrium reaction involving isotope exchange among gas-phase species, the equilibrium constant can be defined in terms of the partition functions of the reactants and products. Following Richet et al. [15], I write an isotope equilibrium reaction as

$$\mathrm{A}{\mathrm{X}}_{\mathrm{n}}+\mathrm{B}{\mathrm{X}}_{\mathrm{m}}^{\mathrm{\prime }}=\mathrm{A}{\mathrm{X}}_{\mathrm{n}}^{\mathrm{\prime }}+\mathrm{B}{\mathrm{X}}_{\mathrm{m}}$$

(10)

where X’ is an isotope of X, and n and m are integers. A fractionation factor α is defined as

$$\mathsf{\alpha }(\mathrm{A}{\mathrm{X}}_{\mathrm{n}},\mathrm{B}{\mathrm{X}}_{\mathrm{m}})={\displaystyle \frac{\mathrm{R}\left(\mathrm{A}{\mathrm{X}}_{\mathrm{n}}\right)}{\mathrm{R}\left(\mathrm{B}{\mathrm{X}}_{\mathrm{m}}\right)}}$$

(11)

where the ratio R is

$$\mathrm{R}(\mathrm{A}{\mathrm{X}}_{\mathrm{n}})={\displaystyle \frac{\left[\mathrm{A}{\mathrm{X}}_{\mathrm{n}}^{\mathrm{\prime }}\right]}{\left[\mathrm{A}{\mathrm{X}}_{\mathrm{n}}\right]}}$$

(12)

For relatively small delta-values (<100‰), the fractionation factor and δ’s are related by

$$1000\mathrm{l}\mathrm{n}\mathsf{\alpha }\left(\mathrm{A}{\mathrm{X}}_{\mathrm{n}},\mathrm{B}{\mathrm{X}}_{\mathrm{m}}\right)=\mathsf{\delta }\left(\mathrm{A}{\mathrm{X}}_{\mathrm{n}}\right)-\mathsf{\delta }\left(\mathrm{B}{\mathrm{X}}_{\mathrm{m}}\right)$$

(13)

where $\mathsf{\delta }\left(\mathrm{A}{\mathrm{X}}_{\mathrm{n}}\right)={10}^3\left({\mathrm{R}}_{\mathrm{X}}\left(\mathrm{A}{\mathrm{X}}_{\mathrm{n}}\right)/{\mathrm{R}}_{\mathrm{X}}\left(\mathrm{s}\mathrm{t}\mathrm{d}\right)-1\right)$. For n = m = 1, the fractionation factor becomes the equilibrium constant for the reaction. For more general cases, the fractionation factor may be expressed as [15]

$$\mathsf{\alpha }(\mathrm{A}{\mathrm{X}}_{\mathrm{n}},\mathrm{B}{\mathrm{X}}_{\mathrm{m}})=\mathrm{K}{\left(\mathrm{A}{\mathrm{X}}_{\mathrm{n}},\mathrm{B}{\mathrm{X}}_{\mathrm{m}}\right)}^{{\displaystyle \frac{1}{\mathrm{m}\mathrm{n}}}}{\displaystyle \frac{\mathsf{\epsilon }\left(\mathrm{A}{\mathrm{X}}_{\mathrm{n}}\right)}{\mathsf{\epsilon }\left(\mathrm{B}{\mathrm{X}}_{\mathrm{m}}\right)}}$$

(14)

where ε is an ‘excess factor’ and K is the equilibrium constant for the reaction $\mathrm{m}\mathrm{A}{\mathrm{X}}_{\mathrm{n}}+\mathrm{n}\mathrm{B}{\mathrm{X}}_{\mathrm{m}}^{\mathrm{\prime }}=\mathrm{m}\mathrm{A}{\mathrm{X}}_{\mathrm{n}}^{\mathrm{\prime }}+\mathrm{n}\mathrm{B}{\mathrm{X}}_{\mathrm{m}}$. The formulation of the equilibrium constants and excess factors is in terms of the partition functions that are a function of the vibrational and rotational energy levels available to the primary and rare isotopologues, as determined from the Schrodinger equation. Richet et al. [15] give a more detailed description of the excess factor ε.

To tabulate results it is convenient to define an additional fractionation factor β, which is the fractionation factor between AX_n and X and may be written as [15]

$$\mathsf{\beta }(\mathrm{A}{\mathrm{X}}_{\mathrm{n}},\mathrm{X})={\displaystyle \frac{{\left[\frac{{\mathrm{X}}^{\mathrm{\prime }}}{\mathrm{X}}\right]}_{\mathrm{A}{\mathrm{X}}_{\mathrm{n}}}}{\left[\frac{{\mathrm{X}}^{\mathrm{\prime }}}{\mathrm{X}}\right]}}={\displaystyle \frac{\mathrm{R}\left(\mathrm{A}{\mathrm{X}}_{\mathrm{n}}\right)}{\mathrm{R}\left(\mathrm{X}\right)}}$$

(15)

The two fractionation factors are then related by

$$\mathsf{\alpha }(\mathrm{A}{\mathrm{X}}_{\mathrm{n}},\mathrm{B}{\mathrm{X}}_{\mathrm{m}})={\displaystyle \frac{\mathsf{\beta }(\mathrm{A}{\mathrm{X}}_{\mathrm{n}},\mathrm{X})}{\mathsf{\beta }(\mathrm{B}{\mathrm{X}}_{\mathrm{m}},\mathrm{X})}}$$

(16)

In terms of partition functions, β is given by

$$\mathsf{\beta }(\mathrm{A}{\mathrm{X}}_{\mathrm{n}},\mathrm{X})={\left[{\displaystyle \frac{\mathrm{Q}\left(\mathrm{A}\mathrm{X}\right)}{\mathrm{Q}\left(\mathrm{A}{\mathrm{X}}_{\mathrm{n}}\right)}}\right]}^{{\displaystyle \frac{1}{\mathrm{n}}}}{\left[{\displaystyle \frac{{\mathrm{m}}^{\mathrm{\prime }}}{\mathrm{m}}}\right]}^{-{\displaystyle \frac{3}{2}}}\mathsf{\epsilon }(\mathrm{A}{\mathrm{X}}_{\mathrm{n}})$$

(17)

where m and m’ are the masses of the isotopes X and X’. The partition function Q has its usual form

$$\mathrm{Q}={\mathrm{Q}}_{\mathrm{t}\mathrm{r}}{\mathrm{Q}}_{\mathrm{e}}{\mathrm{Q}}_{\mathrm{v}\mathrm{i}\mathrm{b}}{\mathrm{Q}}_{\mathrm{a}\mathrm{n}\mathrm{h}}{\mathrm{Q}}_{\mathrm{r}\mathrm{o}\mathrm{t}}{\mathrm{Q}}_{\mathrm{r}\mathrm{o}\mathrm{t}-\mathrm{v}\mathrm{i}\mathrm{b}}$$

(18)

which accounts for the population of translational, electronic, vibrational, and rotational states, including the effects of anharmonicity and rotational-vibrational coupling. The vibrational partition function is of particular importance because it accounts for most of the temperature dependence of equilibrium isotope fractionation.

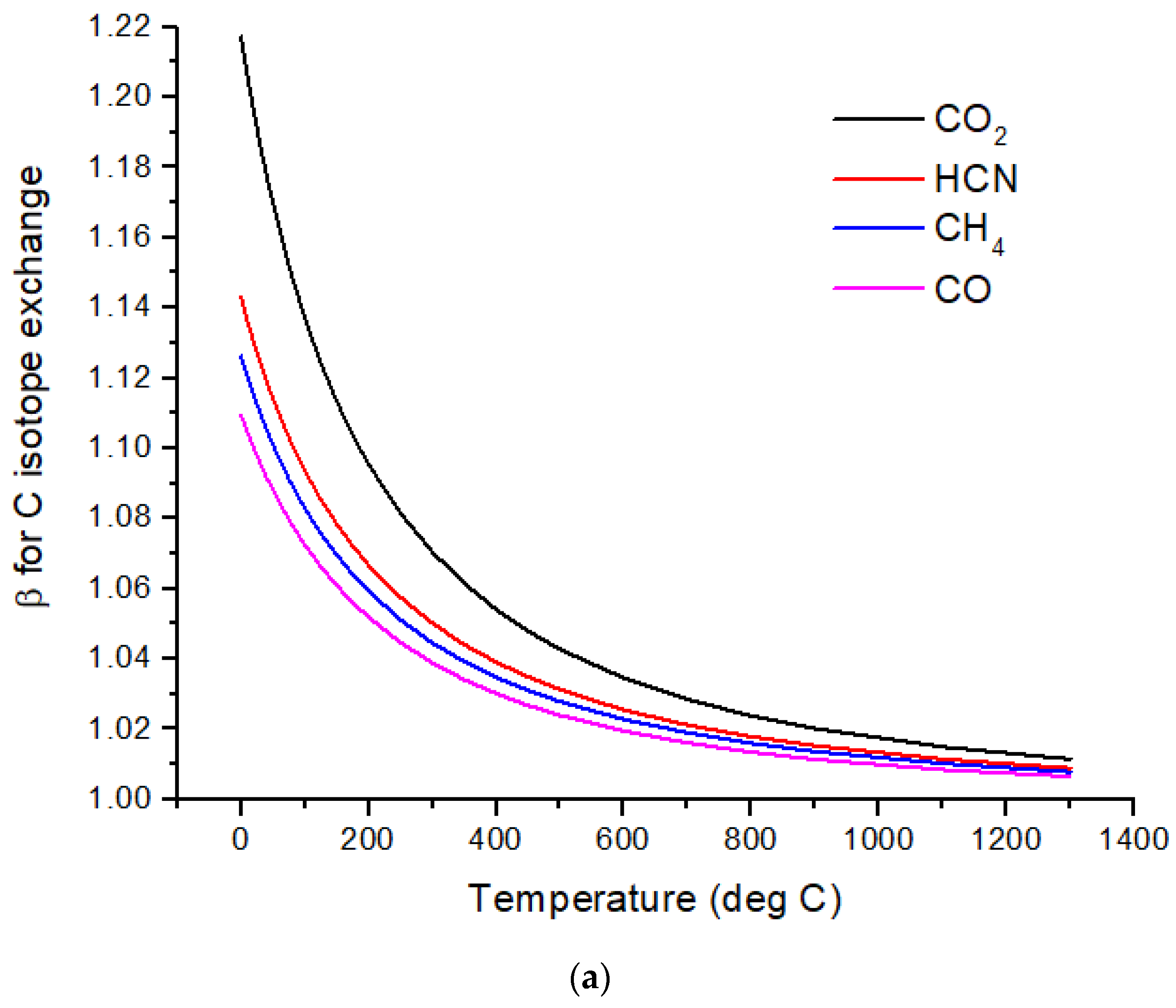
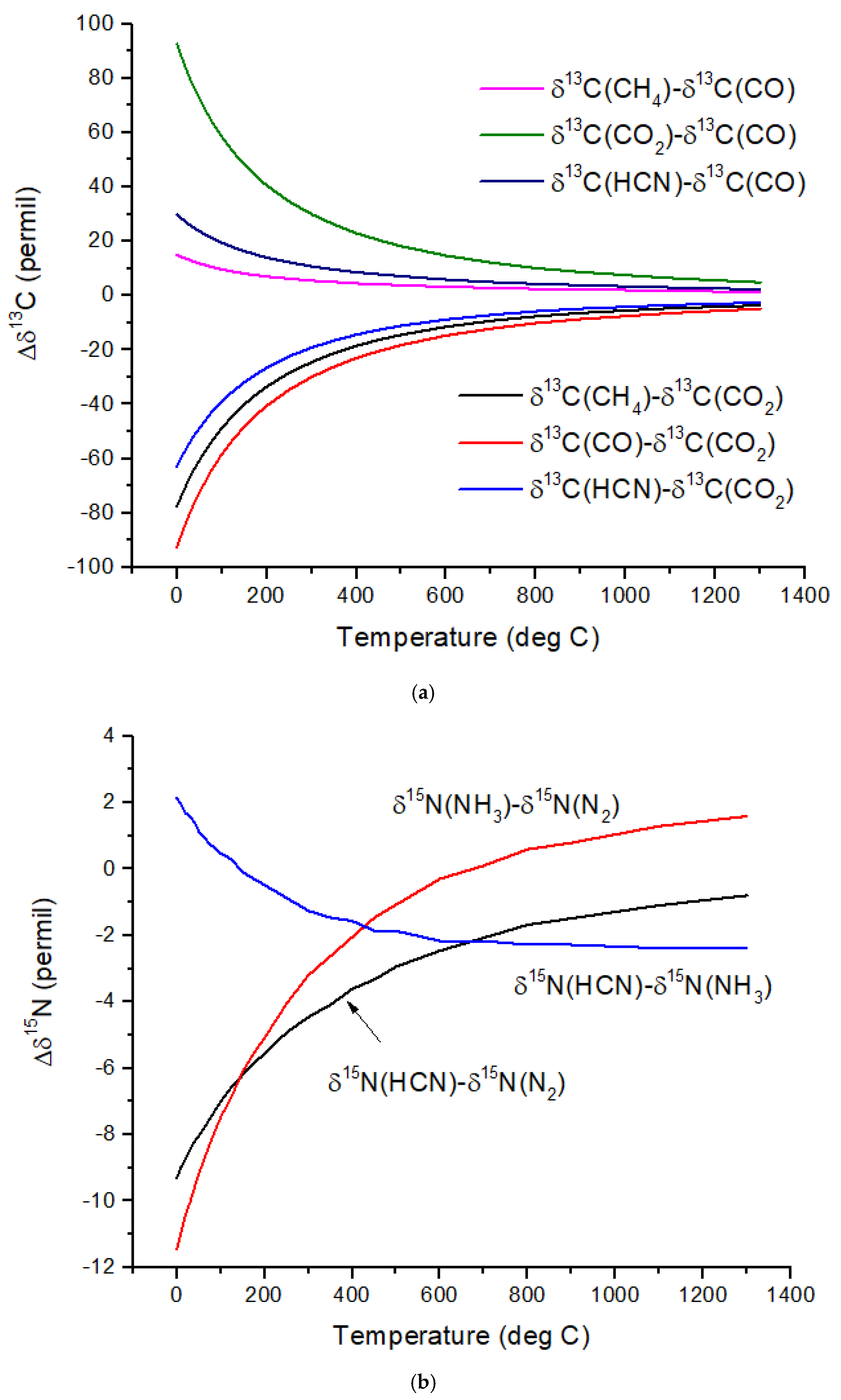
The computed β-factors for C exchange as a function of temperature for CO, CO₂, CH_4, and HCN are shown in Figure 1a, and the β-factors for N exchange for N₂, NH_3, and HCN are shown in Figure 1b. The difference in δ¹³C values, Δδ¹³C, for several pairs of molecules illustrates the expected range of C isotope ratios under conditions of isotopic chemical equilibrium (Figure 2a). At temperatures above 700 °C, the magnitude of Δδ¹³C < 15‰ and decreases with increasing temperature. For hot Jupiters, where CO and to a lesser extent, CO₂ [35] are the primary carbon-bearing molecules, Δδ¹³C is likely to be too small to detect. Isotope-selective photodissociation of CO (i.e., self-shielding) and/or CO₂ will produce non-equilibrium isotope ratios. For hot Jupiters, these effects are primarily in the upper atmosphere. CO self-shielding will produce ¹³C-depleted CO and ¹³C-enriched C atoms. If the ¹³C-rich C atoms are sequestered in a C-rich haze layer, a detectable depletion of ¹³C in CO may be detectable. If the ¹³C-rich C is ionized to C⁺, rapid isotope exchange with CO will occur, erasing the self-shielding signature. Isotope fractionation due to CO₂ photolysis will occur at longer wavelengths and greater depths in the atmosphere. At greater depths in the atmosphere, C isotope exchange between CO and CO₂ will occur as a result of reactions with H and OH that efficiently inter-convert CO and CO_2.

Cooler, rocky exoplanets (T < 500 K) are likely to have N₂ atmospheres with CO₂ or CH₄ as the primary C-bearing molecules [36]. For temperatures below 400 °C, the magnitude of Δδ¹³C > 20‰ relative to CO₂ and increases with decreasing temperature. This well-known equilibrium isotope effect arises from the preference of the heavier isotopes for the higher bond strength compound. For CH₄ in the most common habitable temperature range of 0 to ~50°C, Δδ¹³C ~−60 to −80‰ relative to CO₂ at equilibrium. For gases to reach isotopic equilibrium at low temperatures, a catalyst must be present. Life may play the role of a catalyst, although biochemical reactions are generally dominated by kinetic isotope effects.

Nitrogen isotopes do not show as large a range of equilibrium isotope fractionation as the C isotopes (Figure 2b). At hot Jupiter temperatures, Δδ¹⁵N of only a few permil is predicted for HCN and NH₃ relative to N₂. Even at habitable temperatures, where N₂ is plausibly the primary atmospheric gas (for an Earth-sized planet), Δδ¹⁵N for HCN relative to NH₃ is only ~2‰. These are both astronomically observable molecules, but remotely measuring such a small difference in δ-values is difficult due to the large uncertainties expected for isotope ratio measurements. A small Δδ¹⁵N is consistent with the magnitude of the fractionation that occurs during N₂ fixation by nitrogenase. Measurements by [37] of δ¹⁵N of biomass produced by diazotrophic growth of several bacterial strains yielded ~−1 to −3‰ relative to air N₂ for traditional bacteria using the most common Mo-Fe nitrogenase. Bacteria using either V-Fe or pure Fe nitrogenase show larger fractionation of −3 to −7‰, but this is still quite small compared to biogenic C isotope fractionation.

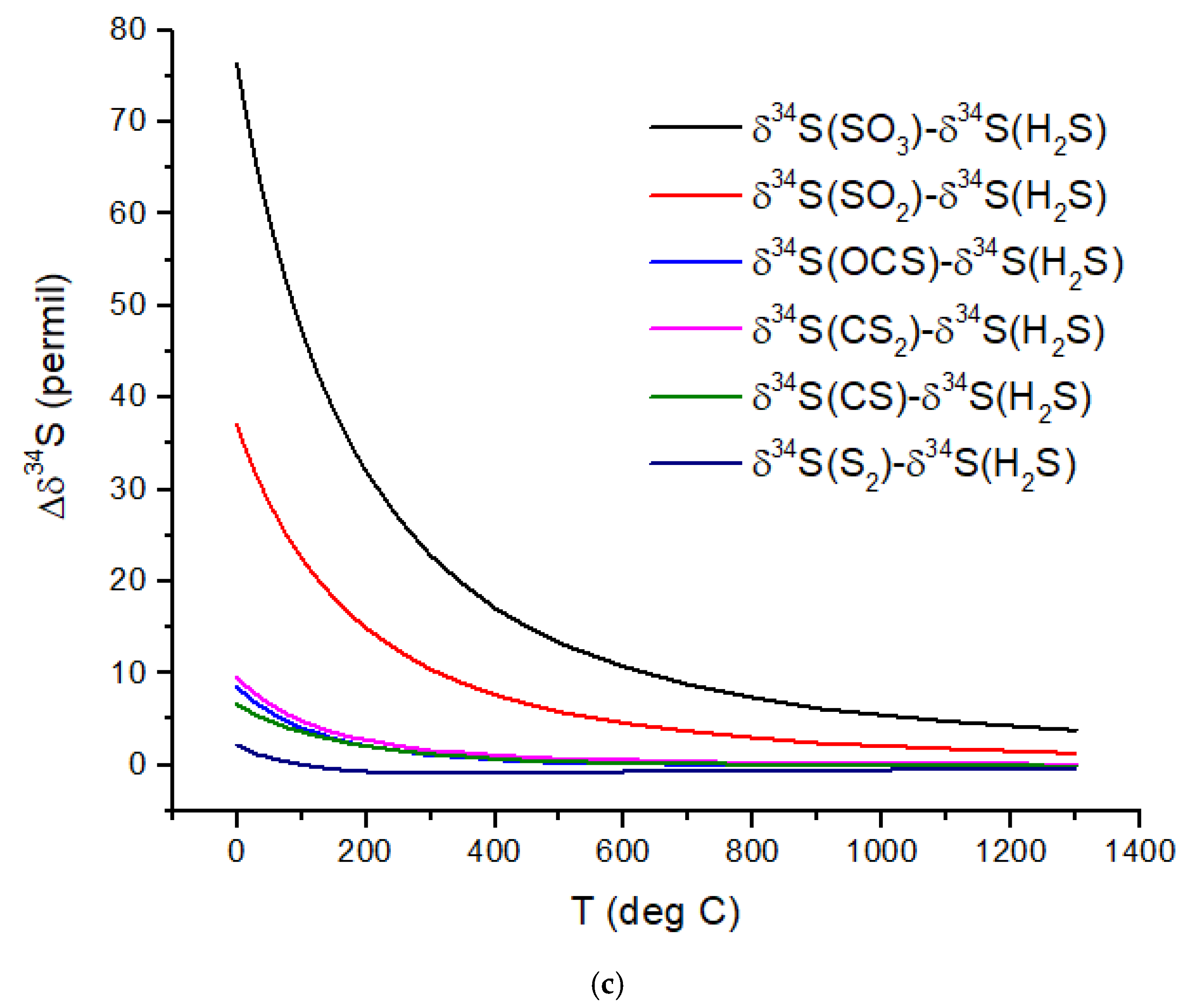
Sulfur isotopes exhibit equilibrium fractionation intermediate between the C and N isotopes (Figure 2c). Motivated by the photochemical models of Tsai et al. [37] for WASP-39b, SO₂, H₂S, and S₂ are considered. Other high-temperature S-species include OCS and CS. Of possible relevance to cooler rocky planets, SO₃ and CS₂ δ³⁴S values are also computed. I have not considered biological fractionation of S isotopes. With an atmospheric temperature of ~900 °C, WASP-39b will have a Δδ³⁴S ~3‰ for SO₂ relative to H₂S. However, photochemical self-shielding is likely to substantially modify these values, as discussed in the following section.

4. Photochemical Signatures of C, N and S Isotopes

Any assessment of biosignatures in isotope ratios must consider the possibility of photochemically generated signatures. Photochemistry drives atmospheric chemistry away from the thermodynamic equilibrium. If the UV photon flux, atmospheric temperature, and pressure are sufficiently stable, a steady-state photochemical composition will be reached. I consider here how photochemistry can alter the C, N, and S isotope ratios in planetary atmospheres. This is most applicable to terrestrial-type exoplanets, but may have relevance to warm Neptunes and the lower temperature range of hot Jupiters. It is not my intent to exhaustively cover this topic but rather to consider a few specific cases in a qualitative or semi-quantitative manner.

For high-temperature exoplanets, C and N will be present in the IR-detectable region of the atmosphere as primarily CO and N₂. These two diatomic molecules are isoelectronic with the ground states of X¹Σ⁺ and X¹Σ_g⁺, respectively. Both molecules undergo photodissociation in the far-ultraviolet (FUV) region, from 91 to 108 nm for CO and from 91 to 100 nm for N₂ molecules. They are also photodissociated and photoionized at wavelengths <91 nm; however, for H₂-rich environments, the onset of H ionization at 91 nm absorbs most FUV photons, as would be expected for warm Neptunes and hot Jupiters. Both CO and N₂ undergo predissociation, which means that the absorption of a sufficiently energetic FUV photon creates a bound electronically excited state that then either relaxes by fluorescence or crosses to an unbound dissociating state, resulting in atomic products. Again, for both CO and N_2, the bound excited states have relatively long lifetimes (e.g., ~10 psec to 1 nsec), resulting in narrow transition line widths (~0.5 to 0.005 cm⁻¹). Isotope substitution in these molecules, for example, ¹³CO and ²⁹N₂, yields an absorption spectrum very similar to the main isotopologues (¹²CO and ²⁸N₂) but offset by several to several 10’s of cm⁻¹. This means that the photodissociation of a column of either CO or N₂ will result in a process termed self-shielding, in which the most abundant isotopologue (¹²CO or ²⁸N₂) will become optically thick and cease to dissociate, while the rare isotopologue (¹³CO or ²⁹N₂) will continue to undergo photodissociation. The result is a massive enrichment of the rare isotopes of the dissociation products, i.e., ¹³C, ¹⁵N, or ¹⁷O and ¹⁸O when considering self-shielding by N₂ or CO, together with a depletion of the rare isotopes in the parent molecules. These isotope effects occur downstream of the region where the primary isotopologues become optically thick in the FUV. Self-shielding is a specific case of isotope-selective photodissociation in which isotope substitution induces changes in the absorption spectrum of a molecule due to changes in the coupling of electronic states. There are numerous examples of molecular clouds, protoplanetary disks [9,38,39], and planetary atmospheres [14,40].

I first consider N isotope fractionation due to N₂ self-shielding in the early Earth atmosphere. Photodissociation of N₂ and CH₄ likely produces substantial quantities of HCN [41,42], and the self-shielding of N₂ could produce a large ¹⁵N enrichment in HCN. As demonstrated by Oro [43], HCN is an essential ingredient in the prebiotic formation of adenine. To assess this possibility, I use model results from [42] for the early Earth (0–100 km) combined with an estimate of the downward flux of ²⁸N₂ and ²⁹N₂ from a model of Earth’s upper atmosphere (120–1000 km) (Lyons and Bondoc, in prep). Self-shielding of N₂ occurs primarily at altitudes of 150–300 km. Rather than use the high-resolution cross sections for N₂, I use shielding functions as described in [38] for CO. Assuming a 45° solar zenith angle and a pure N₂ atmosphere, shielding functions have been determined for self-shielding by ²⁸N₂ and ²⁹N₂, and for mutual shielding by ²⁸N₂ and ²⁹N₂ (on ²⁹N₂ and ²⁸N₂, respectively) [39]. The photodissociation rate coefficients for ²⁸N₂ and ²⁹N₂ are written as

$$J_{28}(z)=J_0{\mathsf{\Theta }}_{ss}(N_{{}^{28}{N}_2}){\mathsf{\Theta }}_{ms}(N_{{}^{29}{N}_2})$$

(19)

$$J_{29}(z)=J_0{\mathsf{\Theta }}_{ss}(N_{{}^{29}{N}_2}){\mathsf{\Theta }}_{ms}(N_{{}^{28}{N}_2})$$

(20)

where Θ_ss and Θ_ms are the self-shielding and mutual-shielding functions, N is the column density of ²⁸N₂ or ²⁹N₂ from the top of the atmosphere to altitude z, and J₀ is the N₂ dissociation rate at the top of the atmosphere. Equations (19) and (20) only account for self-shielding from 91 to 100 nm. Although N₂ dissociates down to 80 nm, line broadening makes the self-shielding effect less significant. For the modern atmosphere, J₀ ~2 × 10⁻⁷ s⁻¹, and for the early Earth atmosphere, it is ~10³ times higher [42]. The shielding functions for N₂ are not given here (they are lengthy polynomial expressions) but will be described elsewhere. 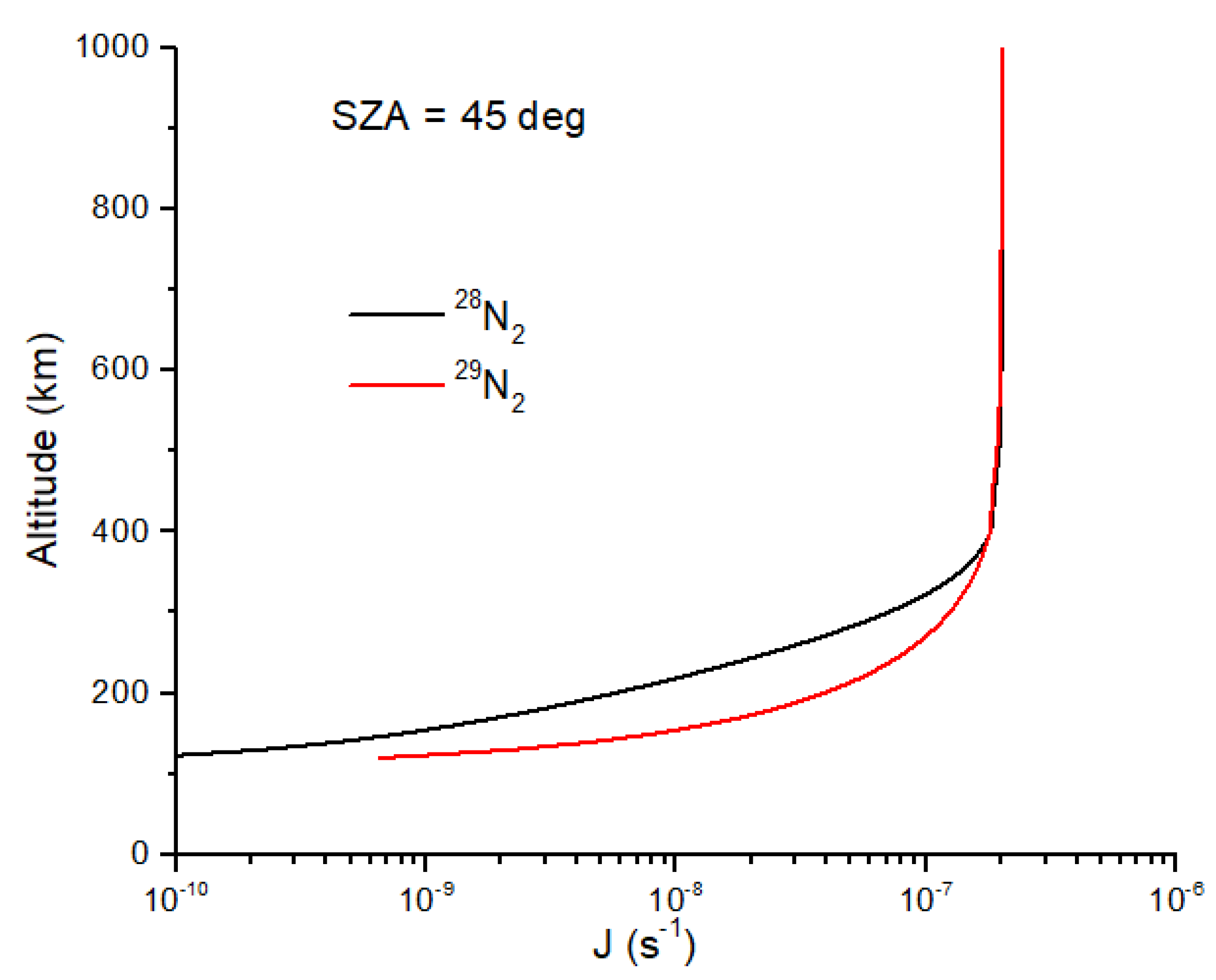The photodissociation rate coefficients for ²⁸N₂ and ²⁹N₂ illustrate the self-shielding effect (Figure 3). At a given altitude between 350 and 120 km, J₂₉ > J₂₈ due to self-shielding by ²⁸N₂. The shielding functions in Equations (19) and (20) capture the effects of line saturation in ²⁸N₂ without having to integrate the high-resolution cross sections over wavelength. The decrease in the photolysis rate coefficient for ²⁸N₂ is nearly a factor of 10 at maximal self-shielding altitudes (Figure 3), yielding ¹⁵N enrichment in N atoms of ~1000 permil. In addition to a much higher solar EUV flux, the solar wind particle flux was also much higher, with implications for atmospheric erosion for small, weakly magnetized planets such as Mars [44], a scenario I will not consider here.

Line broadening will diminish the self-shielding effect. For planetary atmospheres both Doppler and pressure broadening need to be considered. The Doppler linewidth is given by

$$\mathrm{\Delta }{\mathsf{\nu }}_{\mathrm{D}}={\mathsf{\nu }}_0{\displaystyle \frac{v_{\mathrm{t}\mathrm{h}}}{\mathrm{c}}}$$

(21)

For the modern Earth thermosphere, the thermospheric temperature is ~1000 K, and the thermal gas velocity (most probable speed) is v_th = 7.7 × 10⁴ cm s⁻¹. At a wavelength of 100 nm, the Doppler linewidth is Δν_D = 0.26 cm⁻¹. This linewidth is much smaller than the typical spacing between the rotational lines for N₂ and CO and does not impact self-shielding. Pressure broadening derives from the decoherence time due to molecular collisions, and is given by

$$\mathrm{\Delta }{\mathsf{\nu }}_{\mathrm{p}}~{\displaystyle \frac{1}{4\mathsf{\pi }}}{\mathsf{\sigma }}_{\mathrm{c}}{nv}_{\mathrm{t}\mathrm{h}}$$

(22)

where σ_c ~3 × 10⁻¹⁵ cm² is the molecular collision cross-section, and n is the atmospheric number density. At low pressures (<1 microbar), where self-shielding occurs for N₂ in Earth’s atmosphere (Figure 3), Δν_p ~10⁻⁸ cm^−1, which is negligible.

Photolysis of N₂ produces ground state and excited state atoms in approximately an equal mixture as

$${\mathrm{N}}_2+\mathrm{h}\mathsf{\nu }\to \mathrm{N}\left({}^4\mathrm{S}\right)+\mathrm{N}\left({}^2\mathrm{D}\right)$$

(23)

N(²D) decays to N(⁴S) with a radiative lifetime of 6.1 × 10⁴ s (17 h). It undergoes quenching to N(⁴S) by collisions with N₂ and CO on timescales of ~60 s at 100 km in the model from [42]. N(²D) can also react with species such as H₂ via the reaction

$$\mathrm{N}\left({}^2\mathrm{D}\right)+{\mathrm{H}}_2\to \mathrm{N}\mathrm{H}+\mathrm{H}$$

(24)

The model of Tian et al. [42] has an H₂ mixing ratio of 2 × 10⁻³ at 100 km, which implies a loss timescale for N(²D) by reaction 22 of ~1400 s for a thermosphere temperature of 180 K. All of these timescales are much shorter than the model eddy transport timescale at 100 km of ~3 × 10⁵ s. The recombination of N atoms via $\mathrm{N}+\mathrm{N}\mathrm{H}\to {\mathrm{N}}_2+\mathrm{H}$ acts to reverse the effects of N₂ self-shielding.

A maximum downward flux of ¹⁴N and ¹⁵N at altitude z can be estimated by ignoring N loss due to N + NH recombination, which yields

$${\phi }_{14}=2{\int }_z^{top}{J}_{28}\left[{}^{28}{\mathrm{N}}_2\right]dz$$

(25)

$${\phi }_{15}={\int }_z^{top}{J}_{29}\left[{}^{29}{\mathrm{N}}_2\right]dz$$

(26)

For the modern Earth upper atmosphere model used here, φ₁₄ = 7.45 × 10⁸ cm⁻² s⁻¹ and φ₁₅ = 1.76 × 10⁷ cm⁻² s⁻¹ at 120 km. Zahnle [41] estimates a download N flux of ~1 × 10¹⁰ cm⁻² s⁻¹ for wavelengths from 79.6 to 91.2 nm. Relative to the modern Earth atmosphere N₂ with ¹⁵N/¹⁴N = 1/272.0, the N atom downward flux due to 91–100 nm photons has δ¹⁵N(φ_N) = 5400‰. Making the end-member assumption of no self-shielding for 80–91 nm photons, the overall (80–100 nm) δ¹⁵N(φ_N) = 370‰. The true value will be between 370 and 5400‰.

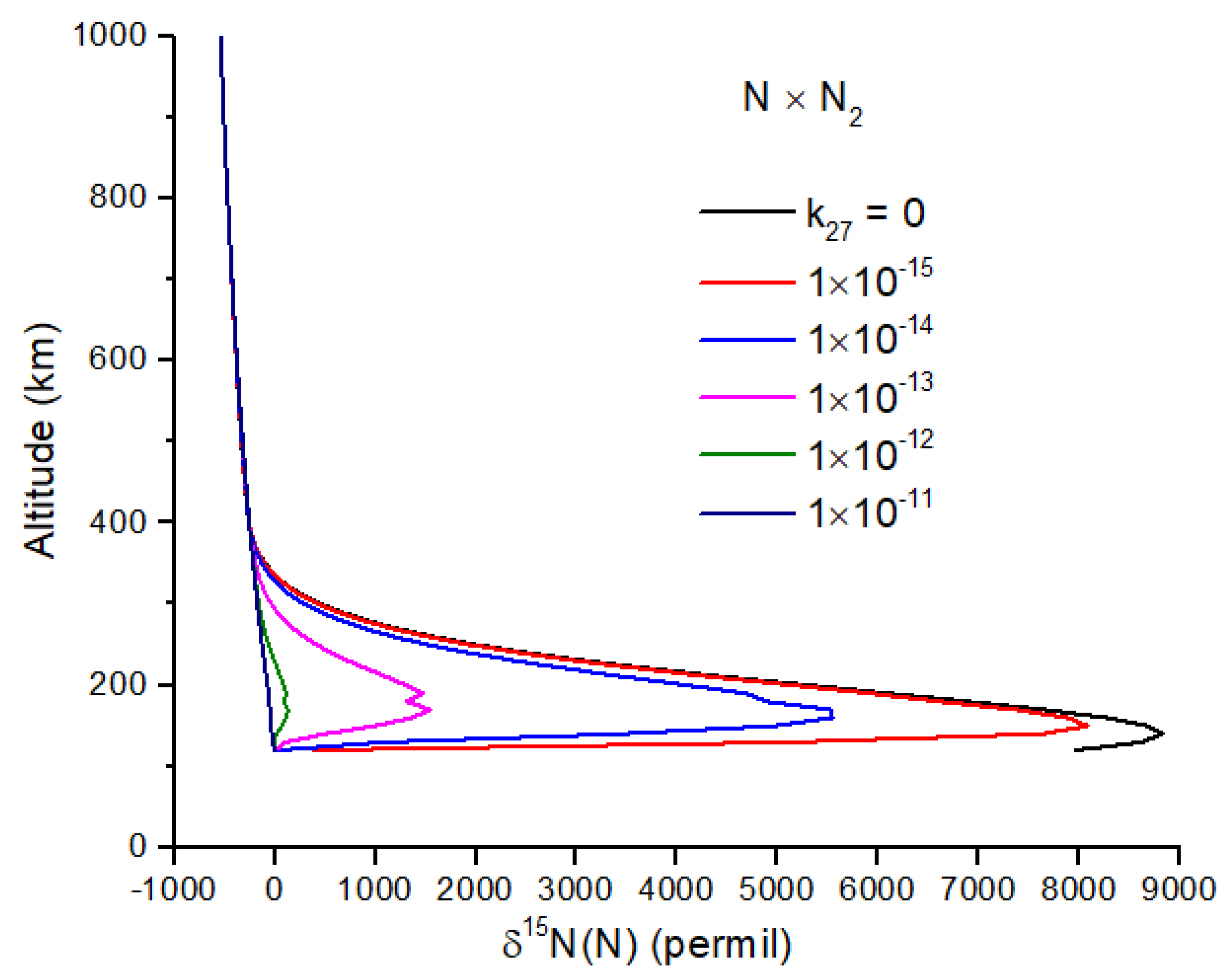
Exchange reactions can also be very important and may include the reactions

$${}^{15}\mathrm{N}+{}^{28}\mathrm{N}_2\leftrightarrow {}^{15}\mathrm{N}+{}^{29}\mathrm{N}_2$$

(27)

$${}^{15}\mathrm{N}\left({}^2\mathrm{D}\right)+{}^{28}\mathrm{N}_2\leftrightarrow {}^{14}\mathrm{N}\left({}^2\mathrm{D}\right)+{}^{28}\mathrm{N}_2$$

(28)

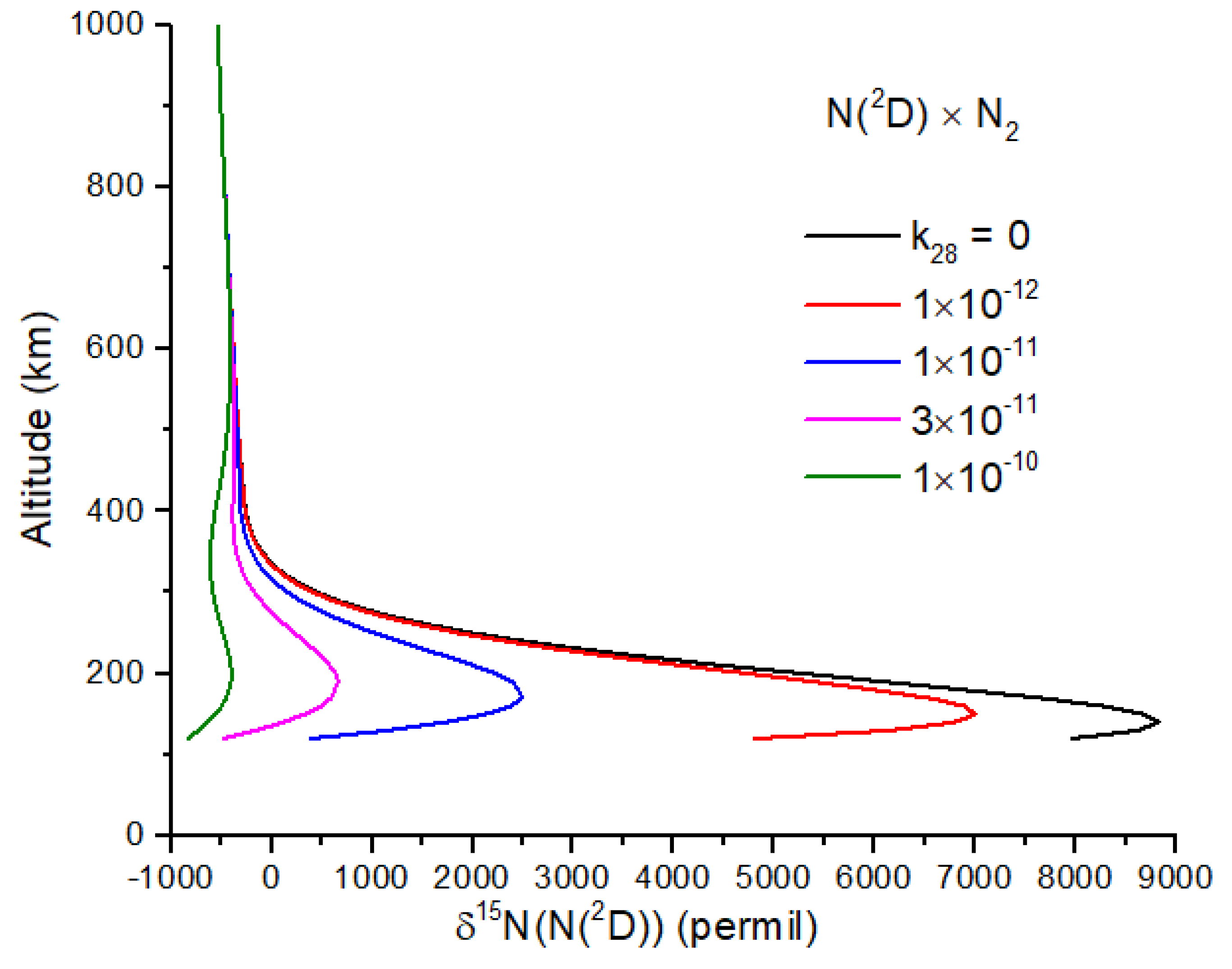
For both reactions, the intermediate N₃ is a doublet, and therefore, reaction 27 is spin-forbidden. From the work of [45], I infer a rate constant of $k_{27}<2.6 {\times 10}^{-13}{e}^{-{\displaystyle \frac{\mathrm{12,600}}{T}}}$, which makes reaction 27 negligibly slow at temperatures < 1000 K. If this is not the case, and reaction 27 is important, it will greatly reduce the δ¹⁵N enrichment of N atoms (Figure 4). Reaction 28 is spin-allowed but does not appear to have a measured rate coefficient. At 100 km, the timescale for the loss of ¹⁵N(²D) by reaction 28 is comparable to the timescale for loss by quenching by N₂ for k₂₈ ~2 × 10⁻¹⁴ cm⁻³ s⁻¹, a plausible value for a spin-allowed reaction. Further work on reaction 28 is needed, as it too can reduce the N atom δ¹⁵N enrichment (Figure 5).

HCN is produced by two pathways [41,42]

$$\mathrm{N}+{}^3\mathrm{C}{\mathrm{H}}_2\to \mathrm{H}\mathrm{C}\mathrm{N}+\mathrm{H}$$

(29)

$$\mathrm{N}+\mathrm{C}{\mathrm{H}}_3\to {\mathrm{H}}_2\mathrm{C}\mathrm{N}+\mathrm{H}\stackrel{\mathrm{H}}{\to }\mathrm{H}\mathrm{C}\mathrm{N}+{\mathrm{H}}_2+\mathrm{H}$$

(30)

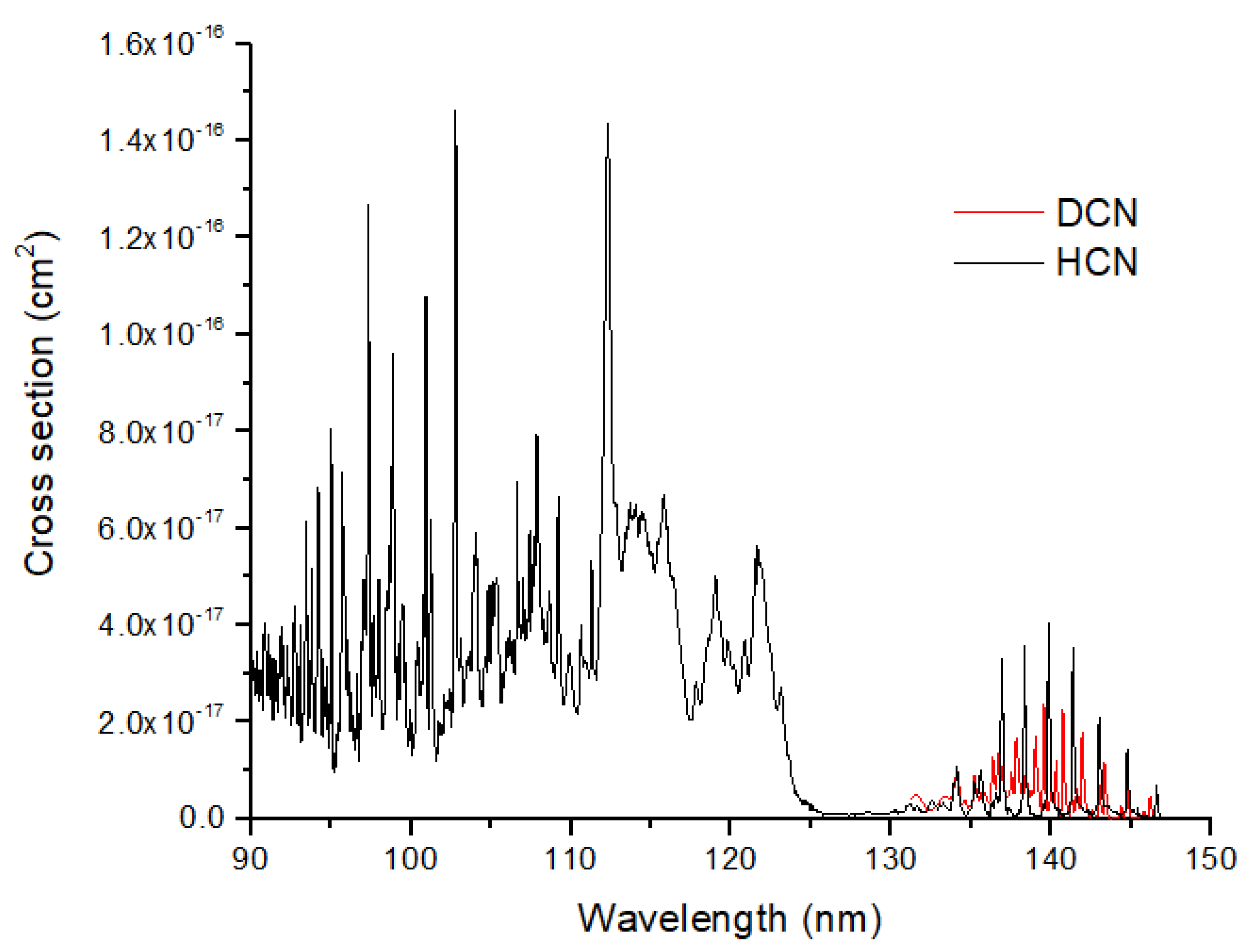
Both of these pathways, which peak at ~70 km in the Tian et al. model [42], will impart a large ¹⁵N enrichment to HCN, specifically δ¹⁵N(HCN) ~370–5400‰ from the results for φ_N above. N₂ self-shielding occurs at considerably higher altitudes (~120–350 km) than does HCN formation. The loss of HCN occurs primarily by photolysis at Ly α (121.6 nm) to make products H + CN. The UV absorption cross sections for HCN show significant structure both near Ly α and in a vibrational progression from 130–150 nm (Figure 6). The photolysis of HCN is likely to modify the isotope ratios in HCN, as suggested by the large vibrational peak shifts between HCN and DCN. If HCN is optically thick, its ¹⁵N enrichment from formation would be reduced. In summary, a significant isotopic photosignature of HCN is a strong possibility for terrestrial-type exoplanets. Because this signature would be enriched in ¹⁵N, it should be distinct from any biogenic HCN in the atmosphere. Finally, I note that there is some evidence for ¹⁵N enriched Archean organic sediments (e.g., +15‰, ref. [46]), but these data are from metamorphosed sediments that likely preferentially lost ¹⁴N during burial and heating.

Carbon isotopes are also affected by photolysis reactions. The spin-forbidden photolysis of CO₂

$$\mathrm{C}{\mathrm{O}}_2+\mathrm{h}\mathsf{\nu }(>167\mathrm{n}\mathrm{m})\to \mathrm{C}\mathrm{O}+\mathrm{O}\left({}^3\mathrm{P}\right)$$

(31)

was predicted [47] and experimentally demonstrated [48] to produce CO with a large depletion of ¹³C. The large fractionation arises from a small redshift in the absorption spectrum at longer wavelengths for the ¹³CO₂ isotopologue. The shift occurs in a region of the spectrum that is rapidly decreasing in absorption strength with wavelength, which enhances the effects of the spectral shift. This is also a region of the spectrum populated by hot bands (bands with a lower level vibrational quantum number v > 0), which makes the isotope fractionation strongly temperature-dependent. There is evidence for this process occurring in the present-day atmosphere of Mars from occultation measurements of CO by the ExoMars spacecraft at Mars, which show that CO has a δ¹³C of ~−250 to −150‰ [49,50], consistent with CO₂ photolysis as the primary source of CO gas in the Martian atmosphere and consistent with photochemical models [40].

In Earth’s atmosphere today, CO has a concentration of ~100 ppb and is produced from biomass burning, CH₄ oxidation, and as a byproduct of anthropogenic combustion reactions. ACE-FTS solar occultation measurements of CO in the Earth’s mesosphere reveal isotopically depleted CO at altitudes of ~50–80 km with δ¹³C ~−160‰ [51]. This isotope signature exhibits seasonal and transport-related variations in the mesosphere and upper stratosphere but not in the lower stratosphere and troposphere.

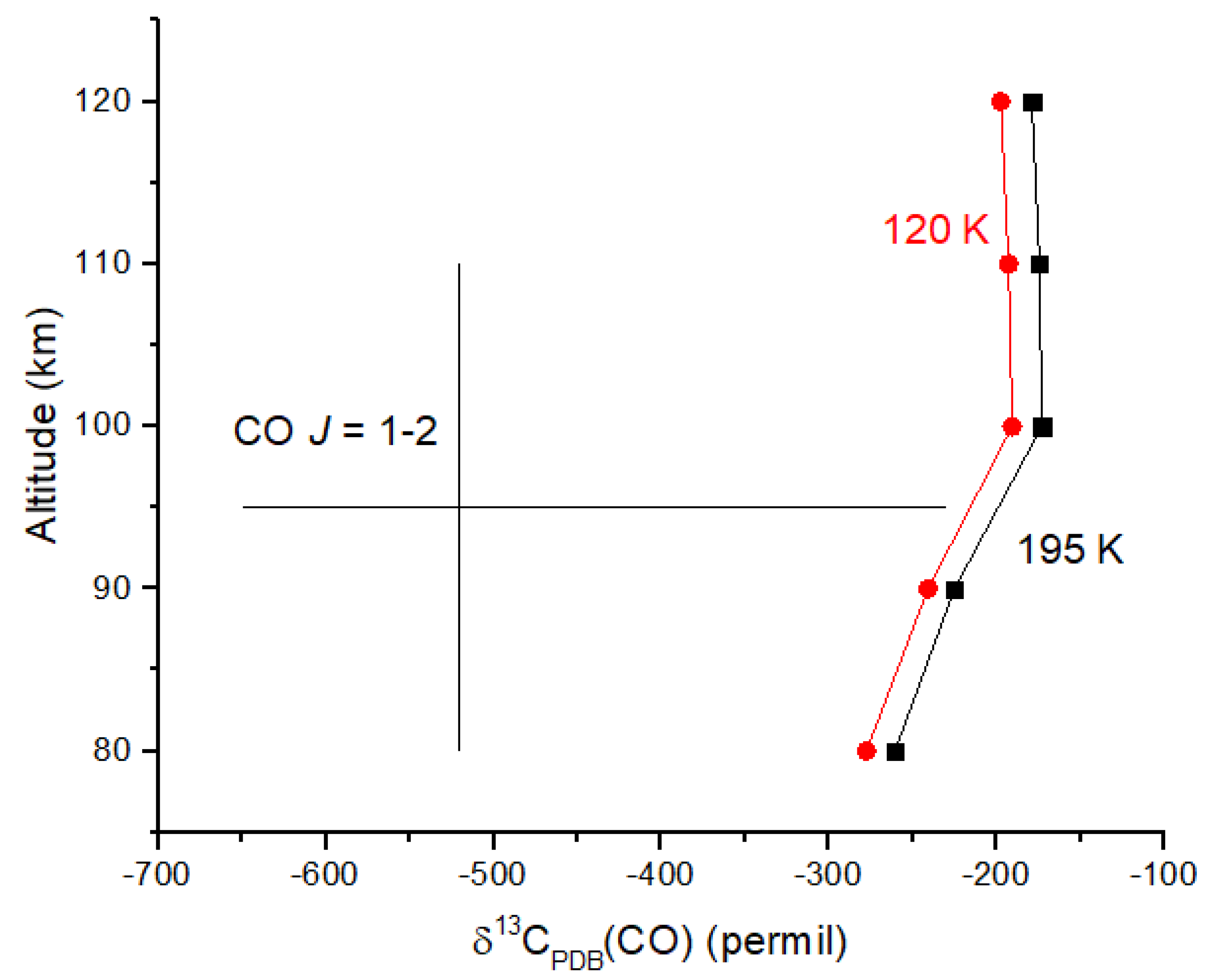
Venus provides another example of a very low δ¹³C value for CO in the upper atmosphere. Observations of the J = 1 → 2 transition for ¹²CO and ¹³CO at 230 and 220 GHz in the 80–110 km region of the atmosphere revealed ¹²CO/¹³CO = 185 ± 69 [52]. Converting this ratio to δ-values relative to the PDB standard yields δ¹³C(CO) = ${-520}_{-130}^{+290}$‰. The high end of this range (−230‰) is comparable to those observed on Earth and Mars. I calculated the photodissociation rate coefficients for ¹²CO₂ and ¹³CO₂ using equations analogous to Equations (19) and (20) and the ab initio cross sections of [47] (rather than shielding functions) together with CO₂ number densities from [53]. Although the measurement uncertainties are large, the ¹³C depletion in CO is certainly due, at least in part, to reaction 31 (Figure 7). Ueno et al. [48] suggest that the cross sections in [47] overestimate C isotope fractionation by 30%, suggesting that the computed δ¹³C values may be too small in magnitude to account for the observations. CO is optically thick up to ~110 km in the Venus mesosphere; therefore, it is possible that ¹²CO self-shielding at wavelengths <108 nm contributes to the ¹³C depletion in CO. CO₂ would shield CO at these wavelengths; therefore, CO self-shielding should be diminished. Venus provides an excellent example of a photochemical-derived isotope signature that we can expect in other rocky planets with CO₂ atmospheres.

Of more relevance here is the early Earth atmosphere with a high CO₂ partial pressure and a correspondingly high CO abundance. For the early Earth, ref. [41] predicts a CO mixing ratio of 2 × 10⁻⁵ at the ground and 1 × 10⁻³ at 100 km. The primary source of CO is the photolysis of CO₂ by reaction 31 and at higher altitudes by spin-allowed photolysis of CO₂ at wavelengths <167 nm (which does not cause large isotope fractionation). As CO₂ photolysis is the primary source of CO, a large negative δ¹³C signature is expected to be present in the middle atmosphere. The reaction $\mathrm{C}\mathrm{O}+\mathrm{O}\mathrm{H}\to \mathrm{C}{\mathrm{O}}_2+\mathrm{H}$, a primary loss pathway for CO, will act to decrease the ¹³C enrichment in CO. The net result is a low δ¹³C value (~−100 to −200‰) for CO in the middle atmosphere, which may eventually be detectable in analogous rocky exoplanets using cross-correlation techniques.

I next briefly consider C isotope fractionation due to CO self-shielding in the early Earth atmosphere and in an H₂-rich exoplanet atmosphere. CO will be optically thick and, therefore, undergo self-shielding at a lower altitude than N₂ because of its lower abundance. Because both molecules have long-lived predissociation states, the mutual shielding of N₂ on CO will occur but will not significantly diminish the self-shielding in CO. I therefore expect large ¹³C and ¹⁷O and ¹⁸O enrichments in product C and O atoms. The fates of C and O atoms differ. C is likely to react with OH to reform CO via C + OH → CO + H, which would act to reverse the effects of CO self-shielding. If an organic haze is present, ¹³C-enriched C could be sequestered in the haze, leaving measurable ¹³C-depleted CO in the atmosphere. Isotopically enriched O atoms are likely to eventually form H₂O, although the initiating reaction, O + H₂ → OH + H, is strongly temperature-dependent. Exchange reactions between O and O₂ and OH and H₂O will diminish the self-shielding signature in O isotopes, but a positive δ¹⁷O and δ¹⁸O in atmospheric H₂O is possible, although it is likely to be diluted by H₂O already in the atmosphere.

I next consider CO self-shielding in a warm Neptune/hot Jupiter. At very high temperatures, isotopically enriched O will rapidly form OH and H₂O, and the reaction OH + CO → CO₂ + H and the reverse reaction will act to erase the self-shielding signature in O-containing species. In addition, the exchange reaction

$${}^{\mathrm{x}}\mathrm{O}+\mathrm{C}{}^{16}\mathrm{O}\leftrightarrow {}^{16}\mathrm{O}+\mathrm{C}{}^{\mathrm{x}}\mathrm{O}$$

(32)

which has an activation energy of 6.9 kcal mole⁻¹ (activation temperature of 3470 K), will also reduce the self-shielding signature. The fate of the ¹³C-enriched C atoms is less clear. C may react with H₂ to form CH₂ in the 3-body reaction $\mathrm{C}+{\mathrm{H}}_2\stackrel{\mathrm{M}}{\to }{}^3{\mathrm{C}\mathrm{H}}_2$ where M is a 3rd-body molecule (H₂ most likely). The rate constant is 6.9 × 10⁻³² cm⁶ s⁻¹ at 300 K [54], and is likely somewhat slower at higher temperatures. This reaction is too slow at CO self-shielding altitudes, which are likely to be ~microbars of total pressure. Radiative recombination, $\mathrm{C}+{\mathrm{H}}_2\to {}^3{\mathrm{C}\mathrm{H}}_2+\mathrm{h}\mathsf{\nu }$, is likely a faster pathway with a typical rate constant of ~1 × 10⁻¹² cm³ s⁻¹, and thus a loss timescale for C of ~1 s. The formation of ³CH₂ would lead to CO reformation via reactions such as ${}^3{\mathrm{C}\mathrm{H}}_2+\mathrm{O}\to \mathrm{C}\mathrm{O}+{\mathrm{H}}_2 \mathrm{o}\mathrm{r} \mathrm{C}\mathrm{O}+2\mathrm{H}$, or more indirectly by ${}^3{\mathrm{C}\mathrm{H}}_2+\mathrm{O}\to \mathrm{C}\mathrm{H}+\mathrm{O}\mathrm{H},$ followed by the reaction of CH with O to form CO. Reformation of CO by any of these reactions will decrease the magnitude of the self-shielding signature in C. Another possible mechanism for erasing a CO self-shielding signature is the exchange of C with CO via

$${}^{13}\mathrm{C}+{}^{12}\mathrm{C}\mathrm{O}\leftrightarrow {}^{12}\mathrm{C}+{}^{13}\mathrm{C}\mathrm{O}$$

(33)

This reaction should proceed through a C₂O intermediate with a triplet ground state, which is spin-allowed. I did not find a 2-body exchange rate coefficient for reaction 33; however, there is a measured 3-body rate coefficient for C₂O formation of 6.31 × 10⁻³² cm⁶ s⁻¹ [55].

If C produced from CO photolysis under self-shielding conditions avoids recombination to CO, one possible fate for it would be to form a haze layer, either by contributing to an existing organic haze layer or by forming a solid carbon haze layer at high altitudes via the reaction $\mathrm{C}\to \mathrm{C}$(s). Depending on the temperature, C particles can condense as either amorphous carbon or graphite. The haze particles would be ¹³C-enriched, and the CO would be ¹³C-depleted at altitudes in the vicinity of the CO self-shielding. The latter may be detectable at infrared wavelengths, as a low ¹³C/¹²C ratio.

Finally, I briefly consider the sulfur isotopes in hot Jupiters. The detection of photochemically produced SO₂ in the hot Jupiter WASP-39b [37] provides the prospect of measuring the exoplanet ³²S/³⁴S isotope ratio modified by UV self-shielding. Self-shielding in SO₂ has been investigated as a mechanism for explaining Archean S isotope signatures in sedimentary rocks [56,57]. SO₂ undergoes predissociation in the C-X band from about 180–220 nm and has an absorption spectrum with resolved lines in a vibronic progression. Sulfur isotope substitution creates a redshift in this spectrum, which generates a large isotope enrichment of the less abundant stable isotopes (³⁴S, ³³S, and ³⁶S) in the dissociation product SO. Although this mechanism does not explain the early Earth rock record, it has been verified experimentally [58]. The key requirement is an optically thick column of SO₂.

For WASP-39b, the peak mixing ratio for SO₂ is ~5 × 10⁻⁵ at ~0.1 mbar on the morning terminator and ~2 × 10⁻⁵ at ~0.03 mbar on the evening terminator [37]. For a scale height of 890 km, these correspond to vertical column densities of 2.9 × 10¹⁸ cm⁻² and 3.9 × 10¹⁷ cm⁻² in the morning and evening, respectively. The peak cross-section for SO₂ near 200 nm is ~3 × 10⁻¹⁷ cm² at room temperature and ~2 × 10⁻¹⁷ cm² at ~1000 K. (It should be noted that the absorption lines are narrow; therefore, accurate UV cross sections require high-resolution laboratory measurements). Peak vertical optical depths are ~58 and 7.8, morning and evening. The tangential optical depths along the terminators are ~25 times the vertical optical depths. Thus, at the peak SO₂ mixing ratios, SO₂ is strongly optically thick under all conditions. Self-shielding by ³²SO₂ will produce a large enrichment in ³⁴SO during photolysis

$${}^2\mathrm{SO}_{\mathrm{x}}+\mathrm{h}\mathsf{\nu }\to {}^{\mathrm{x}}\mathrm{SO}+\mathrm{O}$$

(34)

where x = 32 or 34 (and also 33 and 36, but these are much less abundant). Self-shielding by ³²SO₂ means that J₃₄ >> J₃₂, so the instantaneous number density of ³⁴SO will be highly enriched compared to the standard isotope ratios. (The sulfur isotope standard is a meteorite mineral, the Canyon Diablo troilite or CDT). Models [56] and measurements [57,58] suggest δ³⁴S ~100 to 200‰ enrichments in SO. The steady-state enrichment of ³⁴SO and the corresponding depletion of ³⁴SO₂ depend on subsequent and concurrent reactions. SO and SO₂ are produced by oxidation reactions with OH, which is produced by the photolysis of H₂O [37]. Although photolysis is the primary loss process for SO₂ in WASP-39b, the continual reformation of SO and SO₂ will act to reduce the self-shielding signature. Additionally, S exchange with SO,

$${}^{\mathrm{x}}\mathrm{SO}+\mathrm{S}\leftrightarrow \mathrm{S}\mathrm{O}+{}^{\mathrm{x}}\mathrm{S}$$

(35)

may also reduce the self-shielding enrichment of ³⁴SO unless SO photolysis is the primary source of S atoms. Detailed photochemical modeling is required to address these issues.

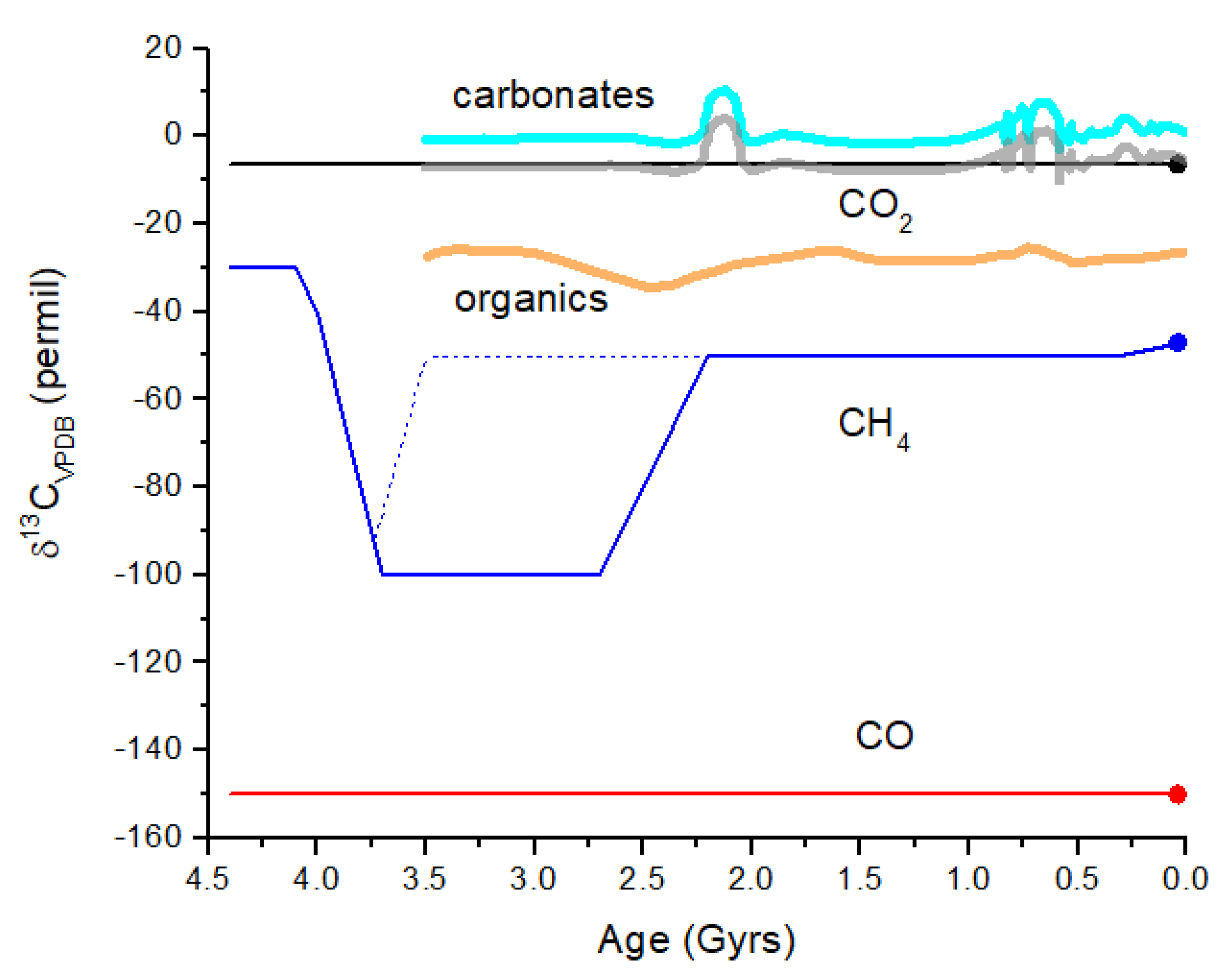
5. Evolution of C and N Isotopes in Earth’s Early Atmosphere

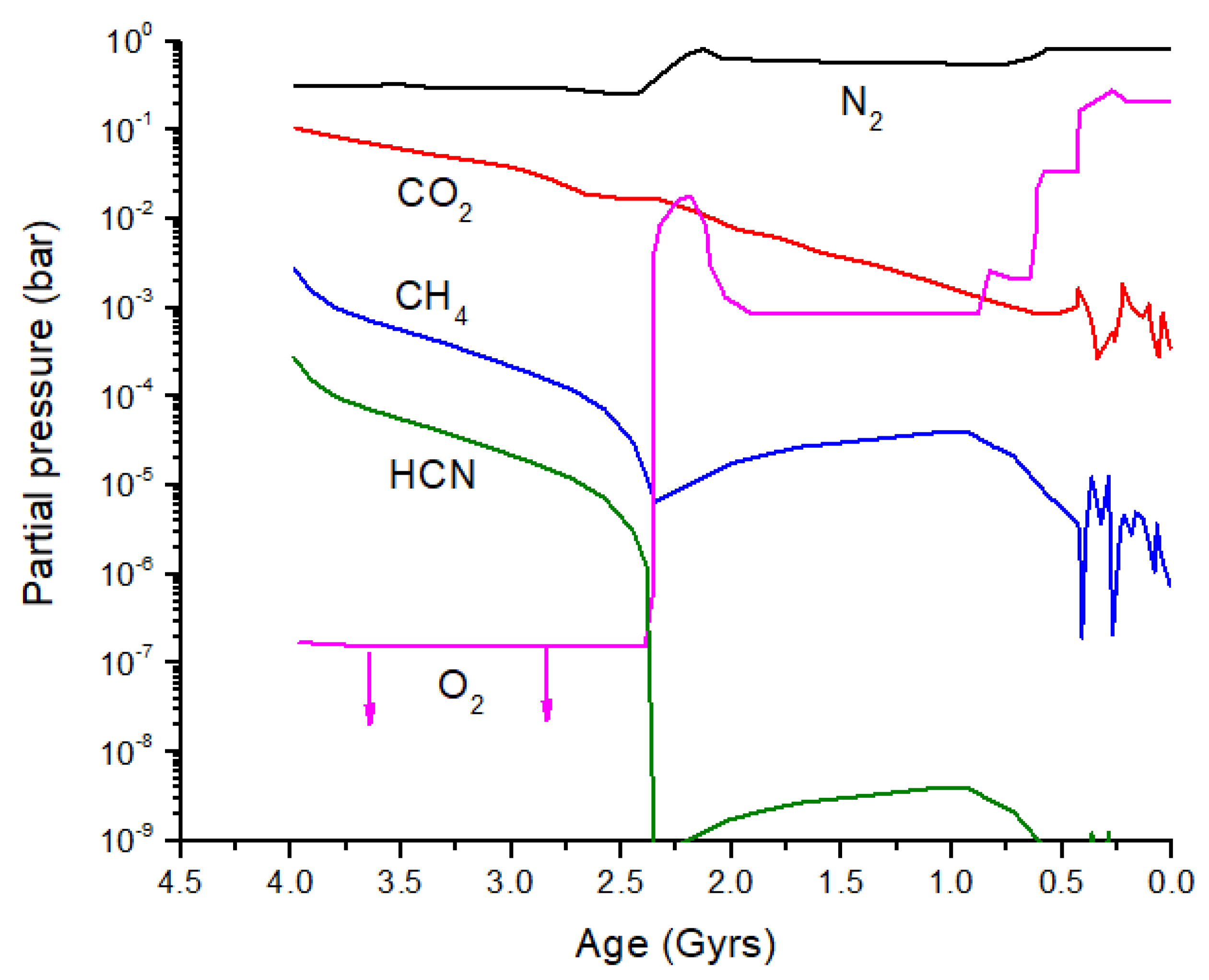
From the discussion above, it is clear that significant isotope fractionation is possible in exoplanet atmospheres. Is it possible to see biosignatures against this backdrop of equilibrium and photo-induced isotope fractionation, and what might this have looked like in early Earth? Catling and Zahnle [2] produced an evolution diagram of the composition of Earth’s atmosphere over the past 4 billion years (Figure 8). I have added HCN to this diagram by scaling HCN relative to CH₄ before and after the atmospheric Great Oxidation Event (GOE): 10⁻¹$P_{{CH}_4}$ prior to the GOE and 10⁻⁴$P_{{CH}_4}$ after the GOE. More accurate HCN evolution calculations can be performed. Prior to the GOE, the primary loss process for HCN is photolysis; after the GOE, loss by OH dominates, although the rate of this loss reaction will vary depending on the O₃ partial pressure.

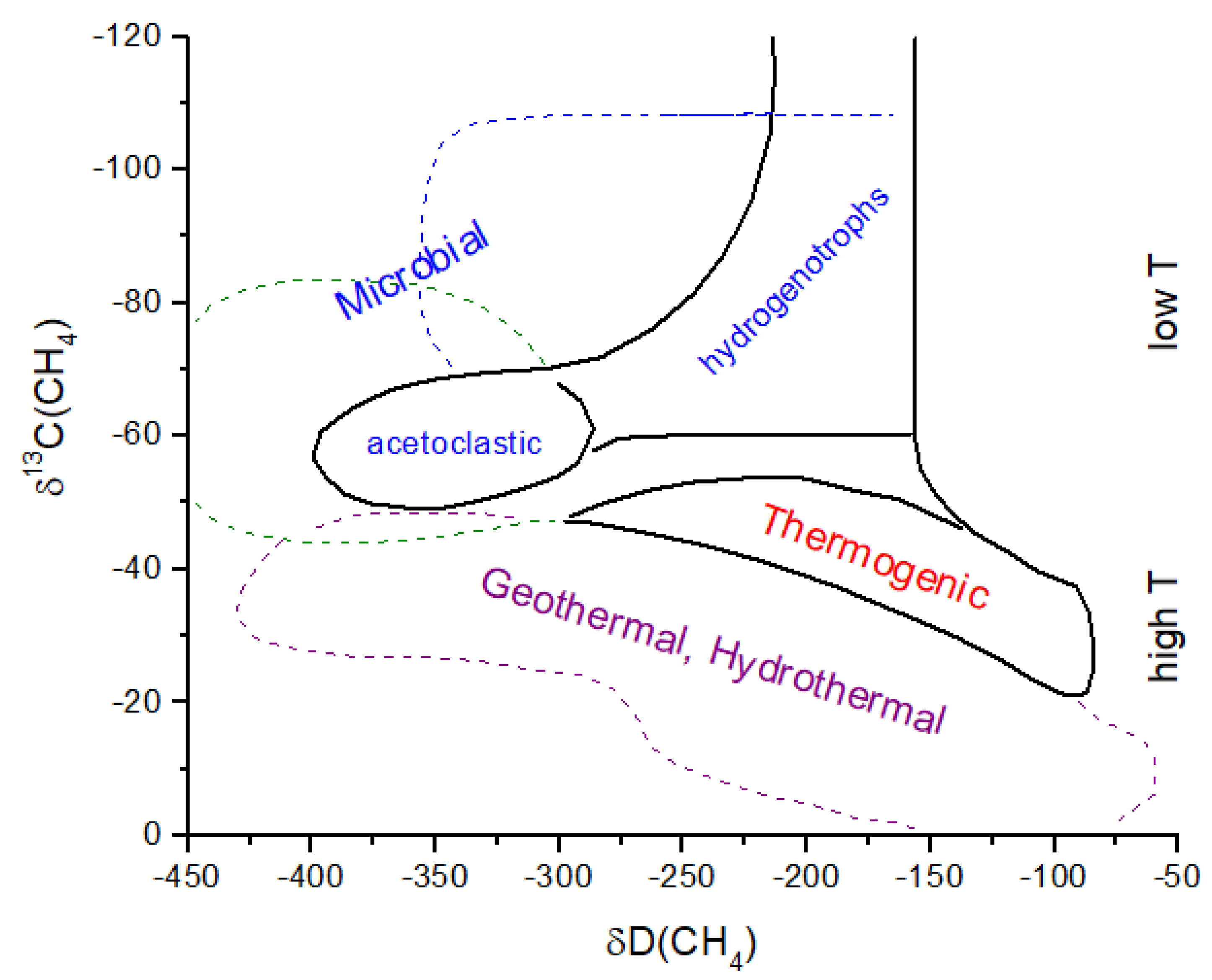
Catling and Zahnle [2] assumed a gradual onset of methanogenesis at ~4.0 Gyr and a gradual onset of photosynthesis at ~3.0 Gyr. Thus, in their model, the high CH₄ partial pressure (2000 ppm) at 4.0 Gyrs may be mostly biogenic. Prior to the onset of methanogenesis, but after the short-lived massive impact-generated reduced atmospheres, CH₄ is primarily thermogenic and/or derived from geothermal and hydrothermal reactions. Thermogenic refers to CH₄ produced by the high-temperature decomposition of buried organic compounds. Today and during the Phanerozoic, most buried organics are biogenic in origin; therefore, the δ¹³C values for atmospheric CH₄ are relatively low at ~−20 to −50‰ (Figure 9) [59]. Prior to 4.0 Gyrs, most buried organics were either derived from the original delivery of chondritic materials or from the burial of material produced by the UV processing of impact-reduced atmospheres. Bulk insoluble organic matter (IOM) in carbonaceous chondrites has δ¹³C ~−35 to −10‰ and in ordinary chondrites has δ¹³C ~−24 to −10‰ [60], coincidentally similar to the range for C₃ and C₄ plants. It is therefore likely that thermogenic CH₄ produced from 4.4 to 4.0 Gyr would have a similar range of δ¹³C values to what we see today (Figure 9).

Geothermal and hydrothermal CH₄ differ from thermogenic CH₄ in that the former is derived from inorganic reactions in the Earth’s crust. The general form of the reaction responsible for the geothermal/hydrothermal production of CH₄, known as the Sabatier reaction, is $\mathrm{C}{\mathrm{O}}_2+4{\mathrm{H}}_2\leftrightarrow \mathrm{C}{\mathrm{H}}_4+2{\mathrm{H}}_2\mathrm{O}$ [61]. Serpentinization, which generates H₂ in the crust via a redox reaction between Fe(II) and H₂O, also falls into this category of reactions. I will not assess the possible flux of CH₄ prior to methanogenesis, but I will assume that the flux of CH₄ available from crustal sources was sufficient to maintain a substantial CH₄ partial pressure.

Following Catling and Zahnle [2], I assume that methanogenesis becomes the dominant CH₄ source by ~4.0 Gyr. If hydrogenotrophic methanogenesis is the primary initial methanogenic process (Figure 9), then substantial ¹³C depletion is likely to be present in atmospheric CH₄ (Figure 10). If acetoclastic methanogenesis was the primary source of CH₄, then atmospheric CH₄ would have been less strongly fractionated. Carbon isotope analysis of organics in ancient rocks yields a mean of δ¹³C ~−30‰ with a large variation [62] (Figure 10). If hydrogenotrophic methanogenesis was the predominant source of CH₄ in the ancient atmosphere, then the organics in rocks have δ¹³C values decoupled from atmospheric CH₄. Anaerobic methane oxidation by methanotrophs, which is known to produce extremely light δ¹³C in lipids (<−100‰) and leave correpsondingly ¹³C-enriched CH₄, could also modify the CH₄ δ¹³C history, as shown in Figure 10. In the modern atmosphere, anaerobic methanotrophy does not significantly alter δ¹³C for atmospheric CH₄ (see Section 2). For the early Earth, it has been argued that anaerobic methanotrophs can explain Tumbiana Formation organics with δ¹³C ~−60‰ at 2.8 Gyr ago [63] (not shown in Figure 10). This event could have produced atmospheric CH₄ with δ¹³C values of >>−50‰. Given the above considerations, the evolution of methanogenesis and δ¹³C for atmospheric CH₄ in Figure 10 must be treated as an approximation of the actual values.

The reservoir of dissolved inorganic carbon (DIC) in the oceans today is ~38,000 Pg C, vastly larger than the sum of atmosphere, land plants, and soil C, which is ~2800 Pg C [22]. Even for a slightly more acidic early ocean, C would be present primarily as HCO₃⁻ and CO₃²⁻, and I assume that δ¹³C of early DIC is approximately the same as modern DIC. I make this assumption because air-sea exchange is the primary source of equilibrium fractionation between atmospheric CO₂ and DIC [21]. Photosynthesis in surface waters creates additional ¹³C enrichment in DIC and yields δ¹³C(DIC) ~+1 to + 3‰ [64]. The majority of carbonates in sedimentary rocks are believed to be biogenic, and the δ¹³C of carbonates has generally been fairly close to 0‰ over the past 3.5 Gyrs, with occasional deviations of ±10‰ [65]. I will further assume that abiotic carbonate formation on the prebiotic Earth did not strongly affect the C isotope ratios in atmospheric CO₂, while CO₂ mostly tracked marine carbonate formation over the past 3.5 Gyrs with a roughly constant fractionation due to air-sea exchange. Figure 10 illustrates the evolution of δ¹³C for CO₂ over the past 4.4 Gyrs, with the constant value of −6.5‰ [64] prior to 3.5 Gyr ago supplanted by the curve (thick gray line) that tracks the carbonates. The CO curve represents the minimum δ¹³C expected due to CO₂ photolysis. This minimum occurs at a high altitude in the mesosphere or even the lower thermosphere for a high pCO₂ case. In the lower atmosphere, the δ¹³C of CO is closer to that of CO₂.

Figure 10. Schematic representation of δ¹³C evolution in the Earth’s atmosphere. In the simplest scenario, CO₂ is derived from volcanism and has δ¹³C ~−6.5‰ as for mantle C. CO₂ undergoes gas exchange with the surface ocean throughout Earth history since 4.4 Gyr ago (black line). More likely, CO₂ tracked the carbonates. The carbonates curve (thick cyan line) is a smoothed version of measurements of δ¹³C for marine carbonates over the past 3.5 Gyr [65]. The curve illustrates the approximate range of variation seen in marine carbonates, which would likely be present in atmospheric CO₂. Atmospheric CO₂ will track carbonates but will be displaced by about −6.5‰ (thick gray curve). The CO curve illustrates the effect of isotope fractionation during CO₂ photolysis in the upper atmosphere. Although δ¹³C for CO is constant over time, the CO mixing ratio decreases by many orders of magnitude from ~10⁻³ at 4 Gyr to ~10⁻¹⁰ today. The CH₄ curve (blue line) illustrates abiogenic sources prior to 4.0 Gyr ago, followed by hydrogenotrophic methanogenesis for the next ~1.5 Gyr, and then CH₄ with modern δ¹³C values after the GOE at 2.4 Gyr ago. The mean δ¹³C for organics recorded from rocks (thick orange line) [62] does not exhibit highly negative δ¹³C, indicating that either the rock record does not entirely correlate with atmospheric CH₄ or that methanogenesis was not a major biochemical process (dotted blue line). The δ¹³C difference between CO₂ and abiogenic CH₄ is ~25‰ versus ~95‰ between CO₂ and hydrogenotrophic methanogen CH₄. This comparison of CO₂ and CH₄ may represent a viable biosignature in a given terrestrial exoplanet atmosphere.

Figure 10. Schematic representation of δ¹³C evolution in the Earth’s atmosphere. In the simplest scenario, CO₂ is derived from volcanism and has δ¹³C ~−6.5‰ as for mantle C. CO₂ undergoes gas exchange with the surface ocean throughout Earth history since 4.4 Gyr ago (black line). More likely, CO₂ tracked the carbonates. The carbonates curve (thick cyan line) is a smoothed version of measurements of δ¹³C for marine carbonates over the past 3.5 Gyr [65]. The curve illustrates the approximate range of variation seen in marine carbonates, which would likely be present in atmospheric CO₂. Atmospheric CO₂ will track carbonates but will be displaced by about −6.5‰ (thick gray curve). The CO curve illustrates the effect of isotope fractionation during CO₂ photolysis in the upper atmosphere. Although δ¹³C for CO is constant over time, the CO mixing ratio decreases by many orders of magnitude from ~10⁻³ at 4 Gyr to ~10⁻¹⁰ today. The CH₄ curve (blue line) illustrates abiogenic sources prior to 4.0 Gyr ago, followed by hydrogenotrophic methanogenesis for the next ~1.5 Gyr, and then CH₄ with modern δ¹³C values after the GOE at 2.4 Gyr ago. The mean δ¹³C for organics recorded from rocks (thick orange line) [62] does not exhibit highly negative δ¹³C, indicating that either the rock record does not entirely correlate with atmospheric CH₄ or that methanogenesis was not a major biochemical process (dotted blue line). The δ¹³C difference between CO₂ and abiogenic CH₄ is ~25‰ versus ~95‰ between CO₂ and hydrogenotrophic methanogen CH₄. This comparison of CO₂ and CH₄ may represent a viable biosignature in a given terrestrial exoplanet atmosphere.

From Figure 10, the maximum difference in δ¹³C for atmospheric CH₄ and CO₂ is Δδ¹³C = δ¹³C(CH₄) − δ¹³C(CO₂) ~−95‰ during an era when hydrogenotrophic methanogenesis was dominant. In the modern atmosphere, this difference is about −40‰, and in the prebiotic atmosphere, this difference may have been ~−25 to −30‰. For Earth-like exoplanets (i.e., rocky planets with oceans), the value of Δδ¹³C may serve as a biosignature, assuming similar microbial evolution. Δδ¹³C is an entirely internal measure, meaning that a comparison with the δ¹³C of the parent star or other objects in the planetary system is not necessary. The feasibility of measuring Δδ¹³C in an exoplanet atmosphere is considered in the following section.

6. Spectral Signatures of Isotopic Gases

Here, I briefly consider the HITRAN line intensities [66] for the relevant isotopologues discussed above to illustrate the magnitude of the isotope-induced band shifts. A complete analysis of the detectability of the isotope ratios discussed above should include isotopologue cross sections, line broadening, and detection in a noisy spectrum [4,67], which will be discussed elsewhere.

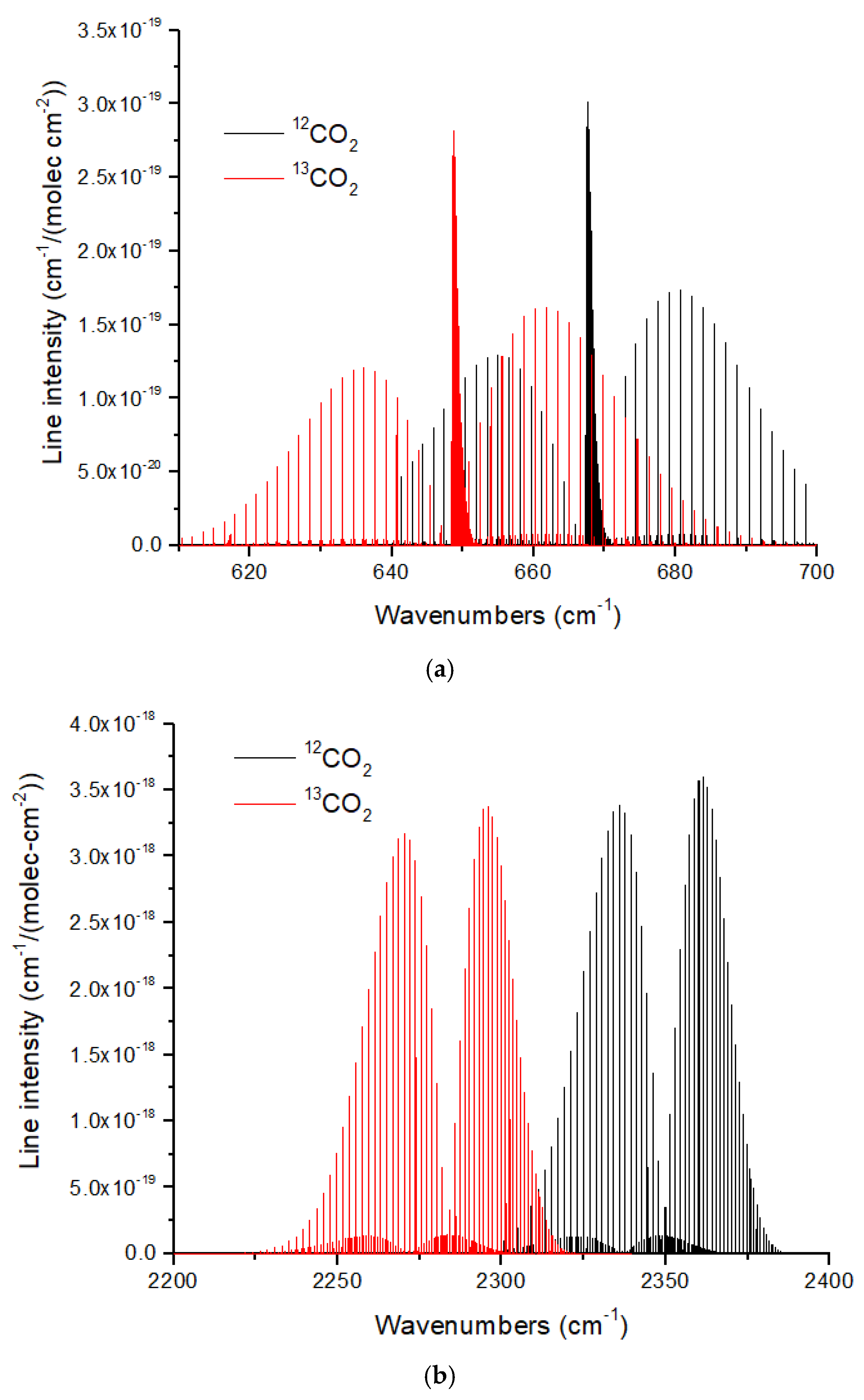
The ν₂ and ν₃ bands of CO₂ show redshifts of 19 cm⁻¹ and 70 cm⁻¹, respectively, for the ¹³CO₂ isotopologue (Figure 11). These large redshifts reflect the large displacement of the C atom in the bending and asymmetric stretch modes of CO₂. As discussed in [16], the large band shifts in CO₂ make isotopologue ratio measurements possible in exoplanet atmospheres with large atmospheric scale heights using JWST MIRI or NIRSpec at medium spectral resolution (R ~1000–3000). The CO molecule [66] also exhibits large isotopic band shifts of ~50 cm⁻¹ and ~95 cm⁻¹ for the fundamental (4.7 microns) and first overtone (2.35 microns). CO is especially useful for measuring isotope ratios in hot Jupiters [6] and brown dwarfs [7], and is essential for determining the C isotope ratio of the solar photosphere [13]. In addition, CO is the molecule of choice for measuring the C and O isotope ratios in exoplanet parent stars.

Figure 11. (a) Normalized line intensities at 296 K for the ν₂ band (bending mode) of ¹²CO₂ and ¹³CO₂. The redshift of the ¹³CO₂ spectrum is ~19 cm⁻¹. (b) For the CO₂ ν₃ band (asymmetric stretch) the redshift is larger at ~70 cm⁻¹. For both figures, the ¹³CO₂ line intensity has been normalized by the ¹³C fraction (0.011057) given in HITRAN. Data were obtained from HITRANonline [66].

Figure 11. (a) Normalized line intensities at 296 K for the ν₂ band (bending mode) of ¹²CO₂ and ¹³CO₂. The redshift of the ¹³CO₂ spectrum is ~19 cm⁻¹. (b) For the CO₂ ν₃ band (asymmetric stretch) the redshift is larger at ~70 cm⁻¹. For both figures, the ¹³CO₂ line intensity has been normalized by the ¹³C fraction (0.011057) given in HITRAN. Data were obtained from HITRANonline [66].

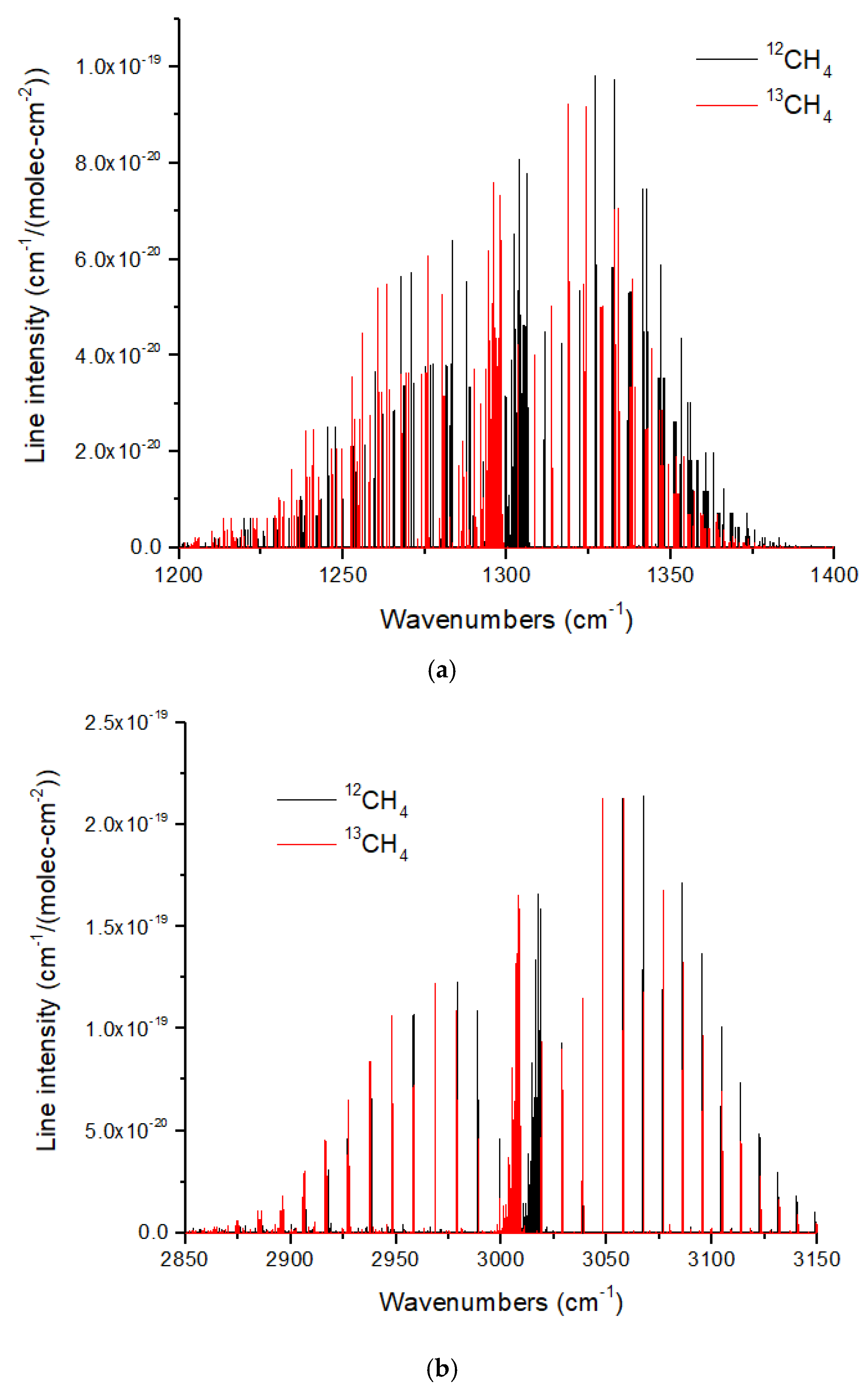
The ν₃ (3.3 microns) and ν₄ (7.7 microns) bands of CH₄ also show redshifts upon ¹³C substitution. However, these redshifts are ~8–10 cm⁻¹ (Figure 12), which are smaller than those for CO and CO₂. In addition, there is an occasional overlap in the ν₄ band. This means that some ¹³CH₄ lines will be masked by lines from the ~100 times more abundant ¹²CH₄. This problem is more acute for the ν₃ band, for which there is a coincidental overlap of the P and R branch lines adjacent to the Q-branch, such that pressure broadening will cause increased line overlap and masking of ¹³CH₄. The Q branches of both bands are a complex cluster of lines with a typical line spacing of ~0.05–0.10 cm⁻¹. Resolving these lines would require a high spectral resolution of R ~30,000–60,000, far beyond the JWST capability. Resolving the Q-branch envelopes is easier, requiring a minimum R ~160 and 380 for ν₄ and ν_3, respectively.

As discussed above, HCN photochemically produced in a N₂-CO₂-CH₄ atmosphere, as proposed for the Archean Earth, is expected to have a massive ¹⁵N enrichment (δ¹⁵N ~300 to several 1000‰) due to N₂ self-shielding at wavelengths <100 nm. HCN is a linear molecule with a C-H stretch mode (ν₁), a doubly degenerate bending mode (ν₂), and a C-N stretch mode (ν₃). Only the ν₃ mode has substantial N displacement, but it is a very weak band. The much stronger ν₁ and ν₂ bands have substantial C displacement but only slight N displacement (Figure 13a). The result is a very small ν₂ band shift of ~1–1.5 cm⁻¹ for HC¹⁵N, causing overlap between the Q branches (Figure 13b). To resolve these Q branches requires a minimum resolution of R ~700, and to resolve individual lines requires R ~3500–7000. Hydrogen isocyanide, HNC, with a central N atom, will exhibit larger band shifts for H¹⁵NC, although it is generally less abundant than HCN.

As a final spectroscopic example, I consider ³²SO₂ and ³⁴SO₂. The SO₂ ν₃ band at 1360 cm⁻¹ is strong and exhibits a band shift of 18 cm⁻¹ (Figure 14a). The spectrum is densely populated with transitions, which means that the line overlap from ³²SO₂ may shield some of the ³⁴SO₂ lines. Line overlap is an important consideration when retrieving the isotope ratios. Significant line overlap by the more abundant isotopologue will create an artificially low abundance for the rare isotopes in this case, ³⁴SO₂. This could give the impression of a stronger self-shielding signature in SO₂ than is actually present. The typical spacing between the lines can be assessed from Figure 14b. The line spacing for a given isotopologue for ν₃ is ~0.03 to 0.2 cm⁻¹, which requires a spectral resolution of R ~6700–45,000.

Model calculations by Tsai et al. [37] suggest that SO may also be observable in WASP-39b or similar atmospheres. HITRAN does not have line intensity data for ³⁴SO, but estimating the fundamental vibrational frequency from the ³²SO fundamental gives

$${\nu }_{34}={\nu }_{32}\sqrt{{\displaystyle \frac{{\mu }_{32}}{{\mu }_{34}}}}$$

(36)

where μ is the reduced mass of each isotopologue. For ν₃₂ ~1125 cm⁻¹, ν₃₄ ~1114 cm⁻¹ for a red shift of 11 cm⁻¹. Reaction 34 will result in a significant enhancement of ³⁴SO, which, together with the less dense SO spectrum, suggests that it may be easier to obtain a S isotope ratio from SO than from SO₂.

7. Discussion

The study of isotopes in exoplanet atmospheres is still in its early stages. The few measurements made thus far have been in hot Jupiter (or brown dwarf) atmospheres. These have yielded surprising results for C isotope ratios, with evidence for extreme enrichment of ¹³CO, interpreted as the input of a high fraction of ¹³C-enriched ices during planet formation [6]. Confirmation of high ¹⁸O enrichment would support this interpretation. It is clear that exoplanet isotope ratio data can contribute to understanding the formation environment of exoplanets, just as they do in understanding the formation of our solar system [9,11]. The measurement of the C and O isotope ratios of CO in parent stars would be a valuable contribution to this effort. A careful assessment of line overlap and dipole moment functions is essential, as was found for the solar photosphere [13,68].

A recent review of isotope ratios as biosignatures in exoplanet atmospheres concluded that the prospects are bleak, given the current technology [16]. Obtaining quality isotope ratios for cooler terrestrial-type exoplanets is not possible with the JWST (insufficient resolution) or ground-based telescopes (insufficient number of photons at high resolution). I entirely agree with Glidden et al.’s [16] assessment of rocky planets. However, technology and analysis methods will improve, and it is important to establish the range of fractionation possible for various isotope systems. This includes both photochemically produced isotope signatures and potential biologically generated isotope signatures.

Glidden et al. [16] argue that an evaluation of exoplanet isotope biosignatures requires a context such as the isotope ratios of the parent star or the parent molecular cloud. Our own solar system argues against this suggestion. The solar photosphere is 400‰ depleted in ¹⁵N compared to the Earth’s atmosphere [69], yet this appears to have minimal implications with respect to N₂ fixation, the key nitrogen biochemical process on Earth.

Table 1. Summary of possible photochemical and biological isotopic signatures of exoplanets.

Exoplanet Type	Isotope Ratio	Fractionation Process	Molecule (s)	δ-Values a,b (‰)	IR Bands	Spectral Resolution e
Exo-Venus	13C/12C	CO2 + hν CO self-shielding	CO mesosphere CO mesosphere	δ13C ~−200 probably small	CO 4.7 μm f CO 4.7 μm	3000–5000 3000–5000
Exo-Earth	15N/14N 13C/12C 13C/12C	N2 self-shielding H. methanogens CO2 + hν	HCN or HNC CH4 vs. CO2 CO mesosphere	δ15N ~370–5400 Δδ13C ~−95 δ13C ~−200	HCN ν3 see text CO 4.7 μm	700–7000 400–60,000 3000–5000
Super-Earth (rock)	13C/12C 15N/14N 13C/12C	CO2 + hν CO self-shielding N2 self-shielding H. methanogens c	CO mesosphere CO mesosphere HCN or HNC CH4 vs. CO2	δ13C ~−200 probably small δ15N ~370–5400 Δδ13C ~−95	CO 4.7 μm CO 4.7 μm HCN ν3 see text	3000–5000 3000–5000 700–7000 400–60,000
Sub-Neptune Warm Neptune d	13C/12C 15N/14N	CO2 + hν CO self-shielding N2 self-shielding (low NH3)	CO stratosphere CO stratosphere HCN or HNC	δ13C ~−200 probably small δ15N < 370–5400 at high temps	CO 4.7 μm CO 4.7 μm HCN ν3	3000–5000 3000–5000 700–7000
Hot Jupiter	34S/32S 13C/12C	SO2 self-shielding CO self-shielding	SO2 stratosphere SO stratosphere CO stratosphere	δ34S ~−10 to −50 δ34S ~100 to 200 probably small	SO2 ν3 SO CO 4.7 μm	6700–47,000 >1000 3000–5000

^a For photochemical reactions, δ-values are relative to the parent molecule (e.g., CO₂, N₂, SO₂). ^b For hydrogenotrophic methanogens Δδ¹³C = δ¹³C(CH₄) − δ¹³C(CO₂). ^c For low-temperature super-Earth (~300 K). ^d Assuming that hazes do not substantially block UV. ^e When the spectra have Q branches, low values are for Q-branch envelopes and high values are for individual Q-branch lines. ^f The first overtone at 2.35 µm is also useful.

presents a summary of the isotopic results obtained here for several types of exoplanet atmospheres, from rocky planets to hot Jupiters. Exo-Venus objects imply CO₂ rich atmospheres with depleted H₂O, while exo-Earths are similar to a pre-oxygenated early Earth. Oxygenated exo-Earths would likely have lower mixing ratios of CH₄ and HCN, making it more difficult to measure the isotope ratios of these molecules. The category of super-Earths covers a very broad range of compositions from essentially Earth-like at ~300 K to much higher temperatures with a retained, primary atmosphere. I will use the term super-Earth for a strictly rocky object, and for a super-Earth-sized object that has retained its primary atmosphere, I will use the term sub-Neptune [70]. The range of atmospheric compositions possible for super-Earths/sub-Neptunes is vast [71]. Here, I will treat rocky super-Earths as exo-Earths in terms of atmospheric composition, with the recognition that many super-Earths have equilibrium temperatures far above that expected to be capable of supporting life. Sub-Neptunes and warm Neptunes are H₂-rich objects with substantial H₂O and possibly CH₄, NH_3, or N₂. If NH₃ is the primary form of nitrogen, then HCN will not have a significant ¹⁵N enrichment. Photochemical hazes, including organic hazes, will diminish the magnitude of photochemically-derived isotope signatures. CO and CO₂ in the presence of substantial OH from H₂O photolysis will have diminished C isotope signatures due to interconversion mediated by OH. HCN produced photochemically from N₂ will have a reduced δ¹⁵N signature at higher temperatures due to weaker self-shielding and a lower mixing ratio of CH₄. For hot Jupiters, SO₂ self-shielding presents the interesting possibility of ³⁴S depletion in SO₂ and large ³⁴S enrichment in SO. At shorter wavelengths, CO self-shielding could produce a detectable δ¹³C signature in CO if the photochemical product C is sequestered in a C-rich haze. I have not included the photochemical signature of CO₂ due to CO₂ photolysis in Table 1. It might have a detectable ¹³C enrichment, but this will generally be much smaller in magnitude than that of CO for rocky exoplanets.

The next steps in the analysis presented here are twofold. First, the infrared cross sections for the isotopologues discussed are computed with a complete treatment of line broadening for relevant atmospheric conditions. Second, to evaluate the ability of cross-correlation with absorption templates, with and without isotopes, to detect isotope ratios in simulated exoplanet transit data. Simulated data must include appropriate observational noise [68].

8. Conclusions

For photochemically-derived isotope signatures, far-UV self-shielding produces some of the largest isotopic enrichments known outside of nuclear reactions. Some of the most important molecules with respect to self-shielding are N₂, CO, and SO₂, all of which have either been detected in hot Jupiter atmospheres or are expected to be present. N₂ self-shielding will yield ¹⁵N-enriched N atoms that can be sequestered in HCN or its tautomer HNC. In early Earth-like N₂-CO₂-CH₄ atmospheres, HCN formation is likely to be efficient, and we can expect significant ¹⁵N enrichment (δ¹⁵N ~370 to 5400‰) in HCN, especially in the prebiotic atmosphere. Such high enrichments increase the likelihood of detecting the rare isotopologue. More detailed photochemical modeling is needed to evaluate the production of highly ¹⁵N-enriched HCN or HNC in warm Neptune or hot Jupiter atmospheres. Spectroscopic measurement of the ¹⁵N/¹⁴N ratio is complicated by the small band shift (~1.5 cm⁻¹) of the ν₂ band of HC¹⁵N. Hydrogen isocyanide, H¹⁵NC, will have a larger red shift in the ν₂ band. The measurement of δ¹⁵N in these molecules for Earth-like exoplanets awaits future instrumentation.

A photochemically-derived signature in C isotopes is especially likely to be found in CO produced from CO₂ spin-forbidden photodissociation. For a CO₂ dominated atmosphere, highly depleted ¹³CO will be present in the mesosphere or lower thermosphere, as is well demonstrated by CO in the mesosphere (80–110 km) of Venus, which I argue is a result of reaction 31. Venus can serve as a model exoplanet for photochemical C isotope signatures.

Sulfur isotopes present an interesting scenario because of the presence of photochemically produced SO₂ in the hot Jupiter WASP-39b. The morning and evening terminator column densities for SO₂ are optically thick in the C-X dissociation band around 200 nm. SO₂ self-shielding will produce SO that is highly enriched in ³⁴S. Either ³⁴S-enriched SO or possibly ³⁴S-depleted SO₂ may be observable in hot Jupiter atmospheres with the JWST. For the ν₃ band of SO₂, line overlap among isotopologues must be carefully evaluated due to the high density of rovibrational lines.

Isotopic biosignatures in general exhibit much smaller isotope fractionation than does photochemical self-shielding, but this fractionation is of far greater significance. I argue here that what matters most are the isotopic differences in pairs of atmospheric molecules involved in key biochemical processes. Important pairs include CO₂/CH₄ and N₂/NH₃. Isotope equilibrium argues that a significant difference in isotope ratios is expected for CO₂ and CH₄ at low (~300 K) temperatures, but not for N₂ and NH_3.. On prebiotic Earth, a typical difference in δ¹³C for CH₄ and CO₂ is ~−25‰. After the advent of hydrogenotrophic methanogenesis, the difference could be as large as Δδ¹³C = δ¹³C(CH₄) − δ¹³C(CO₂) ~−95‰. Living systems are not in chemical equilibrium; however, life processes may act to bring isotope ratios closer to isotopic equilibrium in low-temperature biological systems. Alternatively, biochemical kinetic isotope effects could produce isotope fractionation similar to equilibrium isotope fractionation at low temperatures.

This δ¹³C difference between atmospheric CH₄ and CO₂ is the isotopic biosignature that we seek. It is an internal measure independent of the δ¹³C of the parent star or other objects in the planetary system. It assumes a planetary surface that carries out photosynthesis, methanogenesis, and probably N₂ fixation. The technology to measure isotope ratios with an accuracy of ~50‰ or better on an Earth-like exoplanet does not presently exist. However, it will eventually exist, and this internal comparison of isotope ratios will be a valuable biosignature.