An Analysis of the Kinetic Energy in the Basket to Handstand on Parallel Bars: A Case Study of an Elite Gymnast
Abstract
1. Introduction
2. Materials and Methods
2.1. Participant
2.2. Study Design
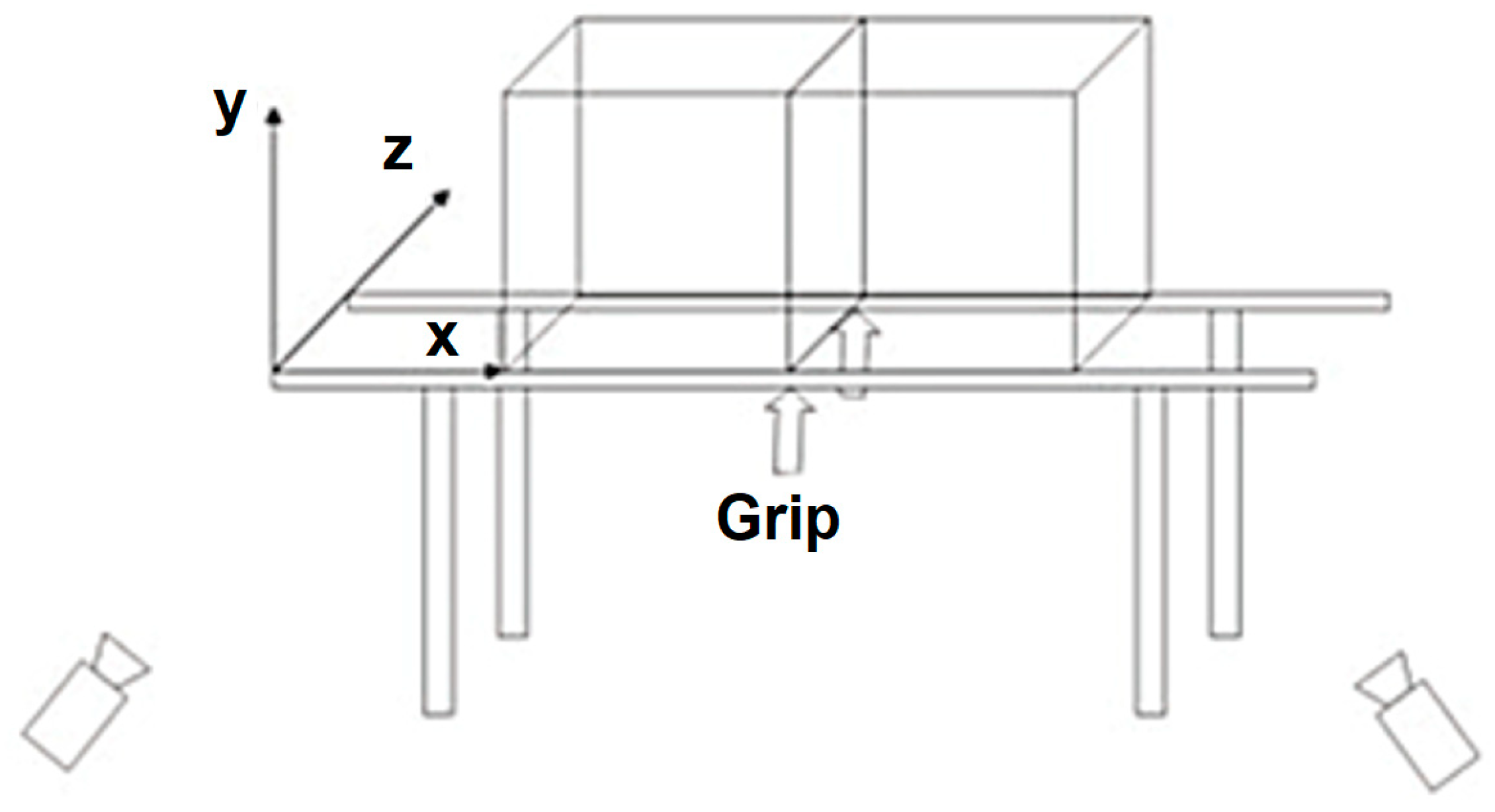
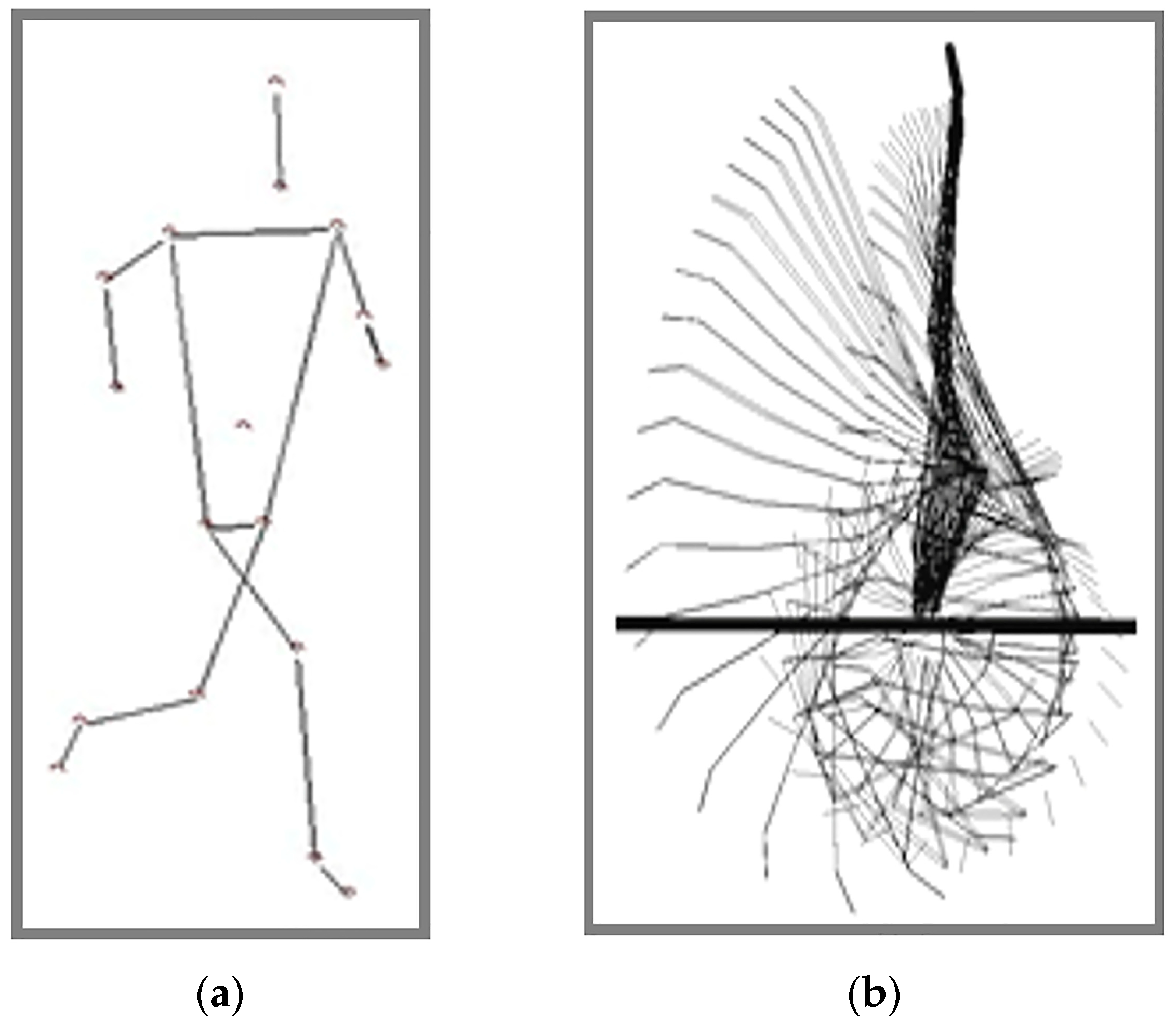
2.3. Procedures
2.4. Statistical Analysis
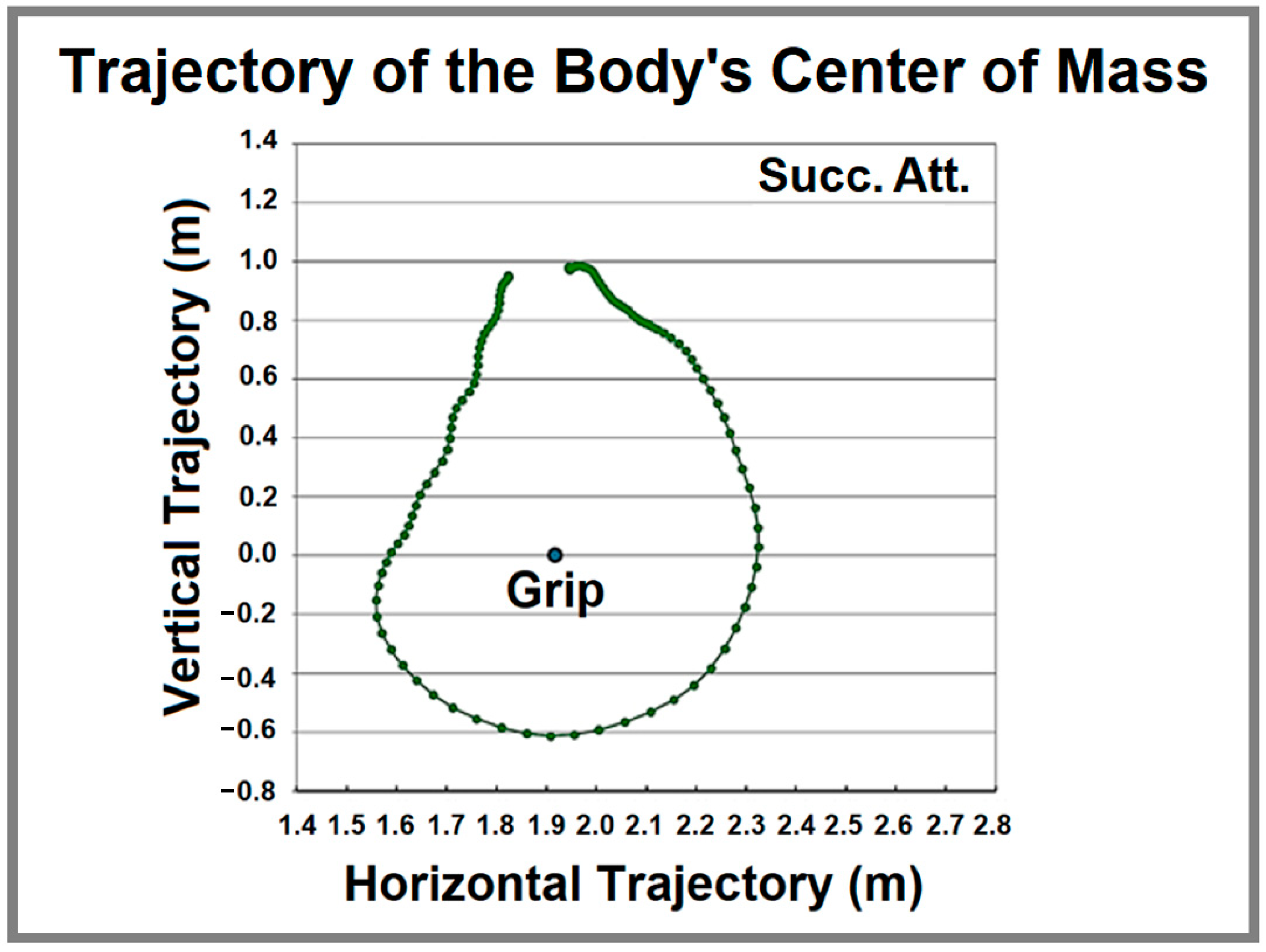
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- FIG Rules. Men’s Artistic Gymnastics; Fédération Internationale de Gymnastique: Lausanne, Switzerland, 2024; Available online: https://www.gymnastics.sport/site/rules/#2 (accessed on 26 November 2024).
- Rohleder, J.; Pizzera, A.; Breuer, J.; Vogt, T. Performance rating in men’s world elite artistic gymnastics: A status-quo study on scoring tendencies at Olympic Games following rule changes. Int. J. Perform. Anal. Sport 2023, 23, 413–427. [Google Scholar] [CrossRef]
- Hernández-Beltrán, V.; Espada, M.C.; Muñoz-Jiménez, J.; León, K.; Ferreira, C.C.; Parraca, J.A.; Gamonales, J.M. Evolution of documents related to biomechanics research in gymnastics. Biomechanics 2023, 3, 477–492. [Google Scholar] [CrossRef]
- Kolimechkov, S.; Yanev, I.; Kiuchukov, I.; Petrov, L. Kinematic analysis of double back straight somersault and double back straight somersault with full twist on rings. Sci. Gymnast. J. 2021, 13, 191–202. [Google Scholar] [CrossRef]
- Mellos, V.; Dallas, G.; Kirialanis, P.; Fiorilli, G.; Di Cagno, A. Comparison between physical conditioning status and improvement in artistic gymnasts and non-athletes peers. Sci. Gymnast. J. 2014, 6, 33–43. [Google Scholar]
- Schärer, C.; Tacchelli, L.; Göpfert, B.; Gross, M.; Lüthy, F.; Taube, W.; Hübner, K. Specific eccentric-isokinetic cluster training improves static strength elements on rings for elite gymnasts. Int. J. Environ. Res. Public Health 2019, 16, 4571. [Google Scholar] [CrossRef] [PubMed]
- Hoareau, D.; Jodin, G.; Laaraibi, A.-R.A.; Prioux, J.; Razan, F. Available kinetic energy sources on the human body during sports activities: A numerical approach based on accelerometers for cantilevered piezoelectric harvesters. Energies 2023, 16, 2695. [Google Scholar] [CrossRef]
- Wasserberger, K.W.; Giordano, K.A.; de Swart, A.; Barfield, J.W.; Oliver, G.D. Energy generation, absorption, and transfer at the shoulder and elbow in youth baseball pitchers. Sports Biomech. 2021, 23, 1160–1175. [Google Scholar] [CrossRef]
- Priest, J.W.; Jones, J.N.; Conger, B.; Marble, D.K. Performance measures of NCAA baseball tryouts obtained from the new 60-yd run-shuttle. J. Strength Cond. Res. 2011, 25, 2872–2878. [Google Scholar] [CrossRef]
- Jones, J.N.; Priest, J.W.; Marble, D.K. Kinetic energy factors in evaluation of athletes. J. Strength Cond. Res. 2008, 22, 2050–2055. [Google Scholar] [CrossRef] [PubMed]
- Schärer, C.; Gross, M.; Lorenzetti, S.; Hübner, K. Energy transformation on vault in elite artistic gymnastics: Comparisons between simple and difficult Tsukahara and Yurchenko vaults. Appl. Sci. 2021, 11, 9484. [Google Scholar] [CrossRef]
- World Medical Association. World Medical Association Declaration of Helsinki—Ethical principles for medical research involving human subjects. Bull. World Health Organ. 2001, 79, 373. [Google Scholar]
- Kolar, E.; Samardžija Pavletič, M.; Veličković, S. Importance of biomechanical modelling for technical preparation of a gymnast. In Proceedings of the 2nd International Scientific Congress—Slovenian Gymnastics Federation, Portorož, Slovenia, 23 January 2015. [Google Scholar]
- Veličković, S.; Kolar, E.; Kugovnik, O.; Petković, D.; Petković, E.; Bubanj, S.; Bubanj, R.; Stanković, R. The kinematic model of the basket to handstand on the parallel bars. Facta Univ. Ser. Phys. Educ. Sport 2011, 9, 55–68. [Google Scholar]
- Skof, B.; Stuhec, S. Kinematic analysis of Jolanda Ceplak’s running technique. New Stud. Athl. 2004, 19, 23–31. [Google Scholar]
- Veličković, S.; Kolar, E.; Kugovnik, O.; Madić, D.; Aleksić-Veljković, A.; Paunović, M. Prediction of the success of the basket to handstand on parallel bars based on kinematic parameters—A case study. Facta Univ. Ser. Phys. Educ. Sport 2013, 11, 9–21. [Google Scholar]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Miranda-Oliveira, P.; Branco, M.; Fernandes, O.J.; Santos-Rocha, R. Comparison of the accuracy of a free 3D camera system with the Ariel performance system. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2021, 9, 670–677. [Google Scholar] [CrossRef]
- Abernethy, B.; Kippers, V.; Hanrahan, S.J.; Pandy, M.G.; McManus, A.M.; Mackinnon, L.T. Biophysical Foundations of Human Movement, 3rd ed.; Human Kinetics: Champaign, IL, USA, 2013; pp. 81–92. [Google Scholar]
- Hopkins, W.; Marshall, S.; Batterham, A.; Hanin, J. Progressive statistics for studies in sports medicine and exercise science. Med. Sci. Sports Exerc. 2009, 41, 3–12. [Google Scholar] [CrossRef] [PubMed]
- Mkaouer, B.; Jemni, M.; Amara, S.; Chaabène, H.; Tabka, Z. Kinematic and kinetic analysis of two gymnastics acrobatic series to performing the backward stretched somersault. J. Hum. Kinet. 2013, 37, 17–26. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Leite, I.; Fonseca, P.; Ávila-Carvalho, L.; Vilas-Boas, J.P.; Goethel, M.; Mochizuki, L.; Conceição, F. Biomechanical research methods used in acrobatic gymnastics: A systematic review. Biomechanics 2023, 3, 52–68. [Google Scholar] [CrossRef]
- Prassas, S.; Kwon, Y.; Sands, W.A. Biomechanical research in artistic gymnastics: A review. Sports Biomech. 2006, 5, 261–291. [Google Scholar] [CrossRef]
- Nyman, E. Biomechanics of Gymnastics. In Gymnastics Medicine; Sweeney, E., Ed.; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Russo, L.; Palermi, S.; Dhahbi, W.; Kalinski, S.D.; Bragazzi, N.L.; Padulo, J. Selected components of physical fitness in rhythmic and artistic youth gymnast. Sport Sci. Health 2021, 17, 415–421. [Google Scholar] [CrossRef]
- Gervais, P.; Dunn, J. Gymnastics: The double back salto dismount from the parallel bars. Sports Biomech. 2003, 2, 85–101. [Google Scholar] [CrossRef]
- Liu, W.; Lu, Z.; Li, X.; Gao, Z.; Xu, Y.; Mei, Q.; Fekete, G.; Gu, Y. Biomechanical analysis of gymnastics movements using wearable motion capture systems and linear sensors: A case study of the kipping bar muscle-up. In Material Strength and Applied Mechanics; Khotsianovsky, A., Chen, Y., Eds.; IOS Press: Amsterdam, The Netherlands, 2024. [Google Scholar] [CrossRef]
- Kolar, E.; Kolar, K.A.; Štuhec, S. Gymnastics. Sports Biomech. 2002, 1, 69–78. [Google Scholar] [CrossRef]
- Cronin, J.; Lawton, T.; Harris, N.; Kilding, A.; McMaster, D.T. A brief review of handgrip strength and sport performance. J. Strength Cond. Res. 2017, 31, 3187–3217. [Google Scholar] [CrossRef] [PubMed]
- Cuk, I. Handgrip in artistic gymnastics. Sci. Gymnast. J. 2015, 7, 128. [Google Scholar]
- Das, A.; Dutta, M. Correlation between body mass index and handgrip strength and handgrip endurance among young healthy adults. J. Evid.-Based Med. Healthc. 2015, 2, 3995–4001. [Google Scholar] [CrossRef] [PubMed]
- Nipp, H.; Debeliso, M.; Lawrence, M. The relationship between handgrip strength and performance scores in North American collegiate Division I women’s artistic gymnasts. Turk. J. Kinesiol. 2022, 8, 56–66. [Google Scholar] [CrossRef]
- Paunović, M.; Đorđević, D.; Marinković, D.; Veličković, S.; Veličković, P.; Čović, N.; Žilić Fišer, S. Is the handgrip strength an influential factor on the competition result in elite male artistic gymnasts? J. Men’s Health 2023, 19, 8–14. [Google Scholar] [CrossRef]

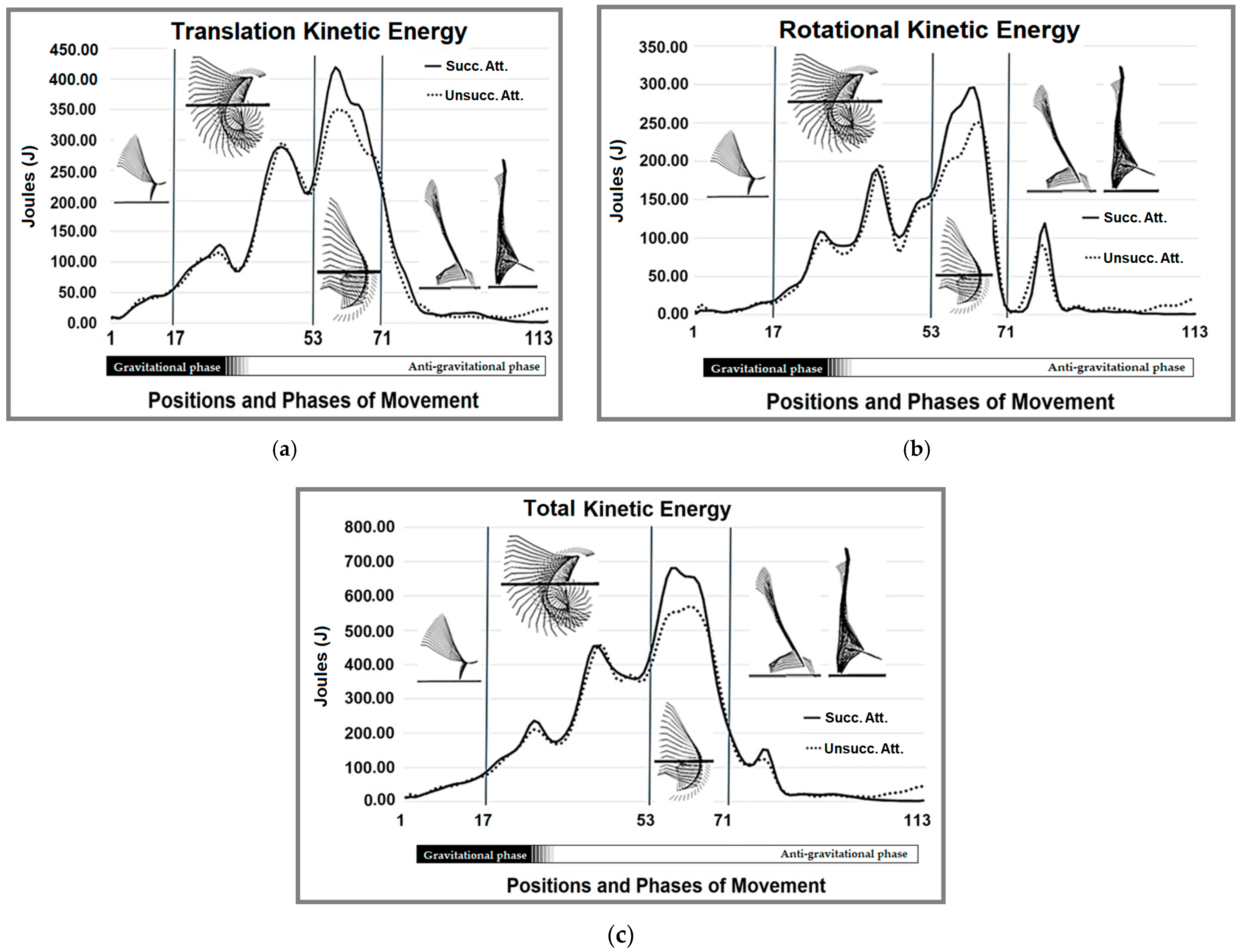
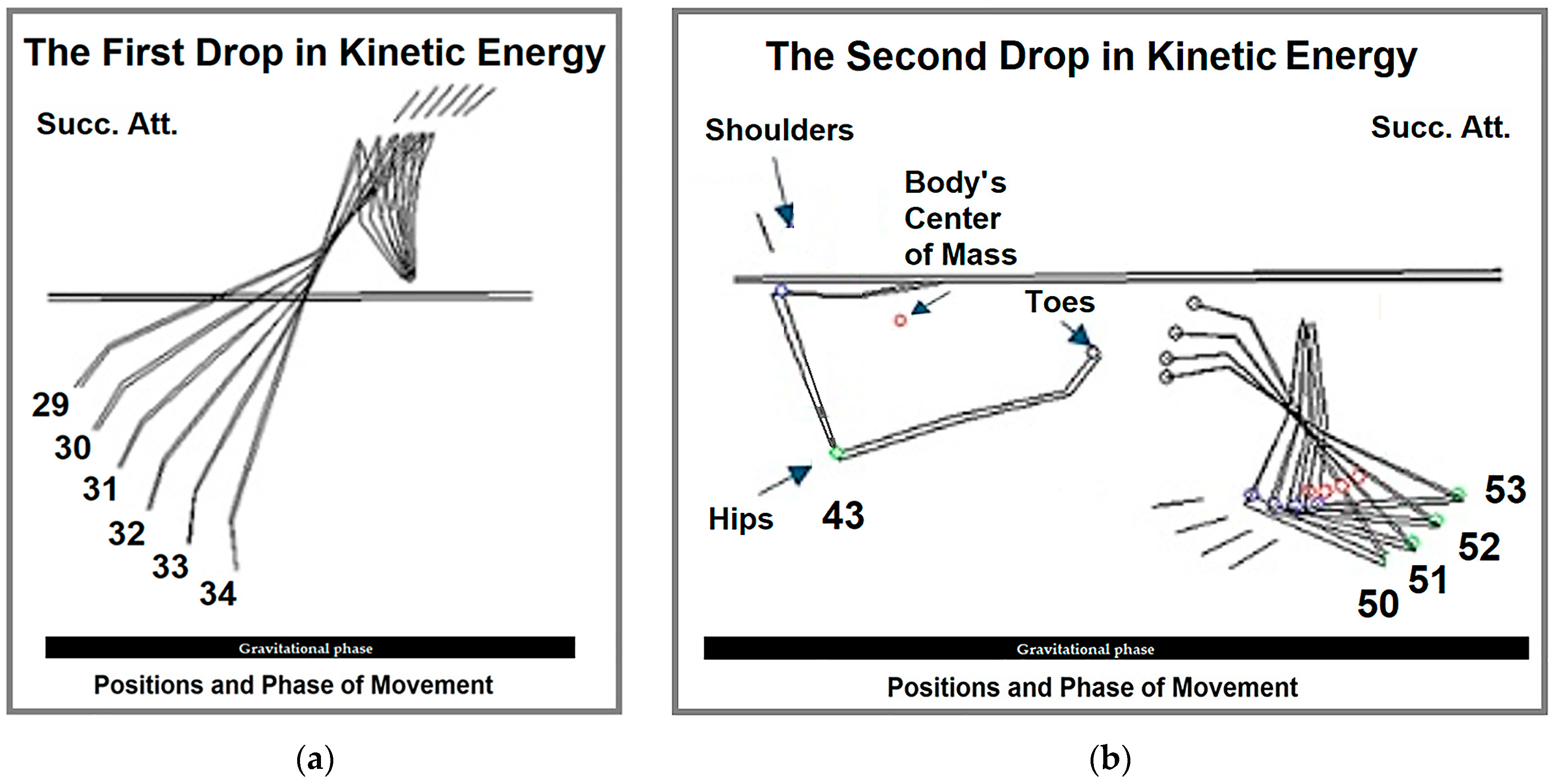
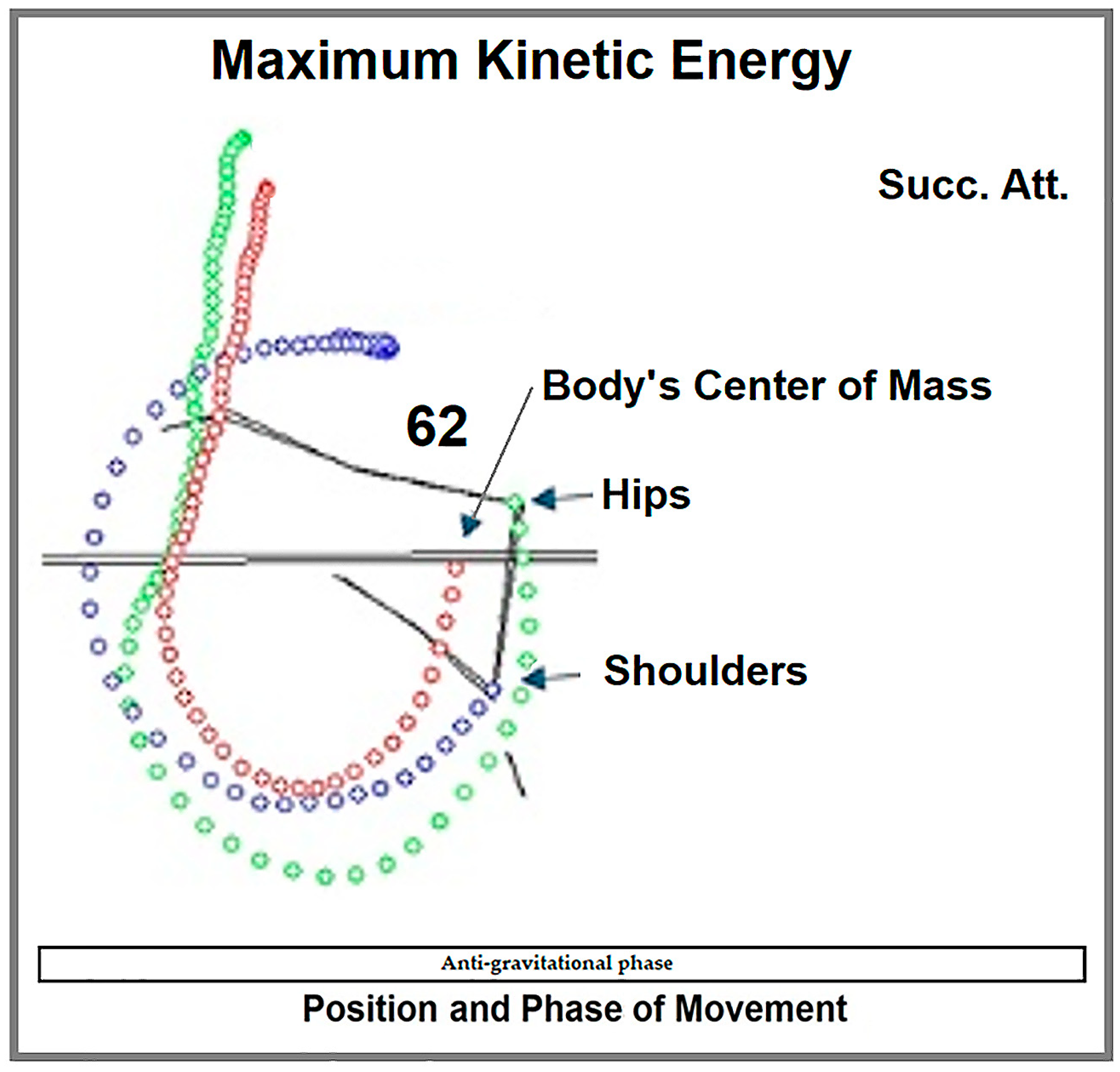
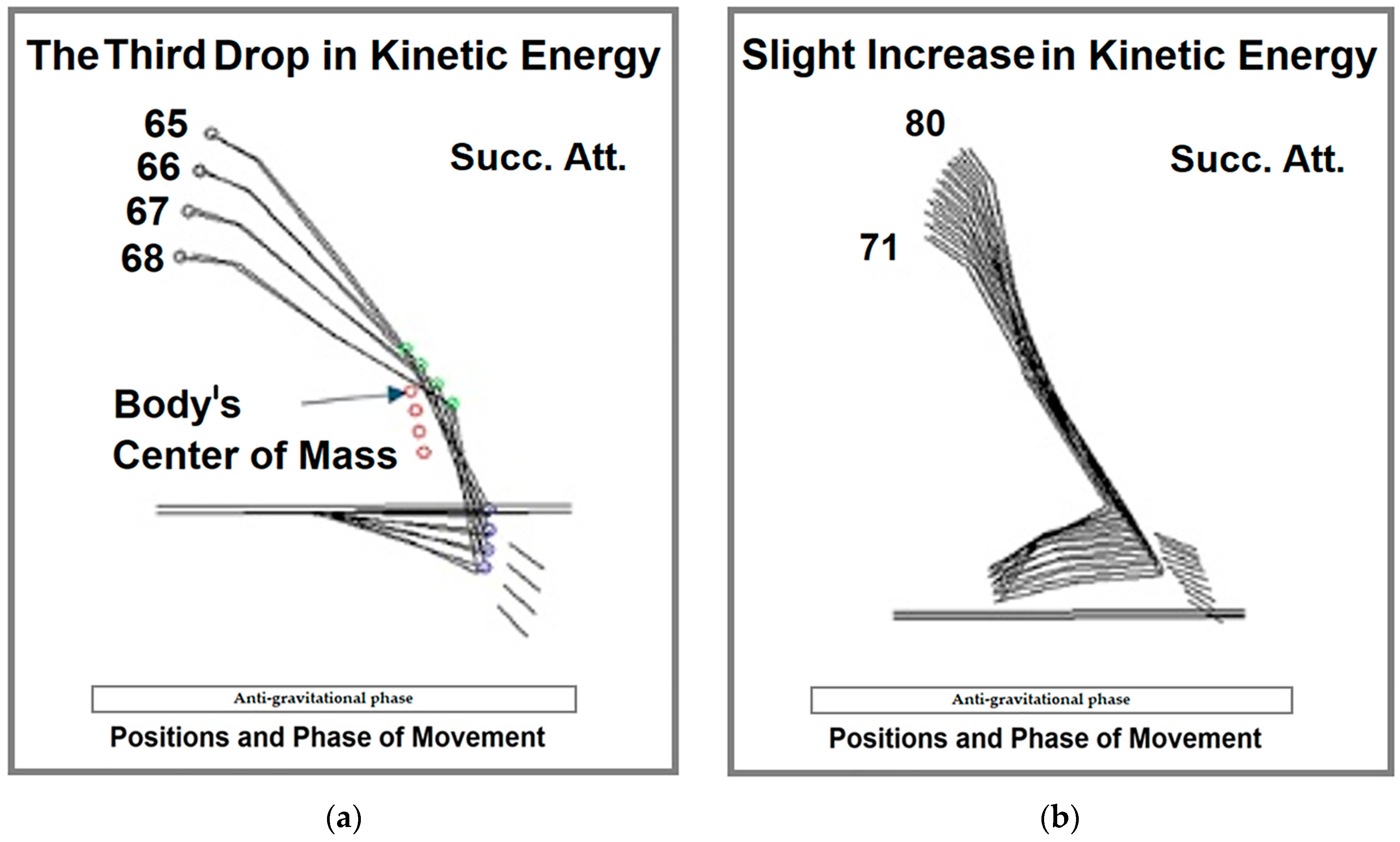
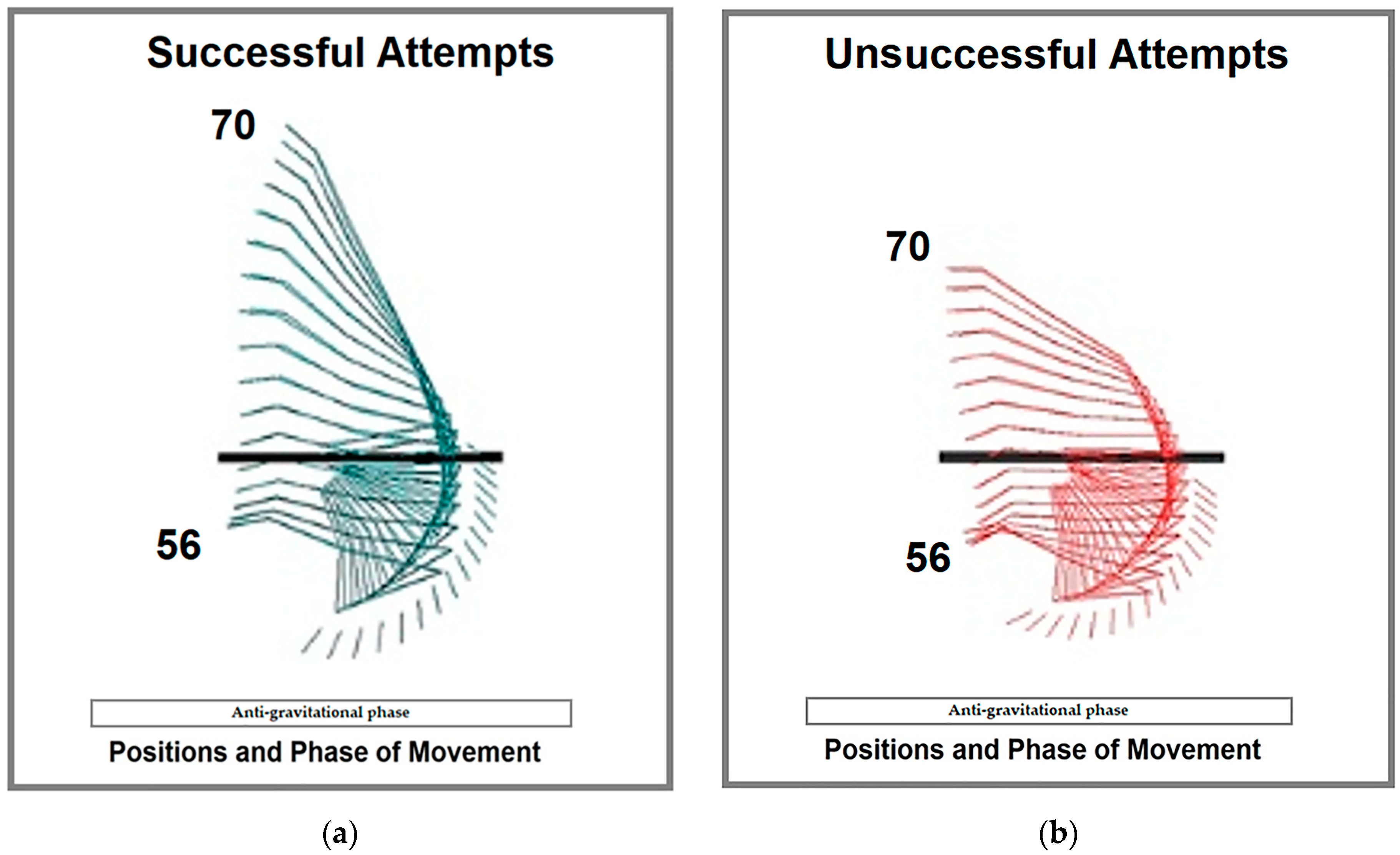
| Variable | KP | Successful [J] | Unsuccessful [J] | Diff [J] | t-Test | p | ∆ (%) | ES |
|---|---|---|---|---|---|---|---|---|
| KEtrans | 56 | 338.640 | 293.616 | 45.024 | 2.412 | 0.03 | 15% | 1.37 *** |
| KErot | 57 | 218.593 | 186.177 | 32.416 | 2.222 | 0.04 | 17% | 1.24 *** |
| KEtotal | 57 | 596.541 | 508.694 | 87.847 | 2.636 | 0.02 | 17% | 1.53 *** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veličković, S.; Đorđević, D.; Veličković, P.; Možnik, M.; Kolar, E.; Stoica, C.-E.; Cristuță, A.-M.; Voinea, N.-L.; Vulpe, A.-M.; Bubanj, S.; et al. An Analysis of the Kinetic Energy in the Basket to Handstand on Parallel Bars: A Case Study of an Elite Gymnast. Life 2025, 15, 172. https://doi.org/10.3390/life15020172
Veličković S, Đorđević D, Veličković P, Možnik M, Kolar E, Stoica C-E, Cristuță A-M, Voinea N-L, Vulpe A-M, Bubanj S, et al. An Analysis of the Kinetic Energy in the Basket to Handstand on Parallel Bars: A Case Study of an Elite Gymnast. Life. 2025; 15(2):172. https://doi.org/10.3390/life15020172
Chicago/Turabian StyleVeličković, Saša, Dušan Đorđević, Petar Veličković, Marijo Možnik, Edvard Kolar, Cristina-Elena Stoica, Alina-Mihaela Cristuță, Nicolae-Lucian Voinea, Ana-Maria Vulpe, Saša Bubanj, and et al. 2025. "An Analysis of the Kinetic Energy in the Basket to Handstand on Parallel Bars: A Case Study of an Elite Gymnast" Life 15, no. 2: 172. https://doi.org/10.3390/life15020172
APA StyleVeličković, S., Đorđević, D., Veličković, P., Možnik, M., Kolar, E., Stoica, C.-E., Cristuță, A.-M., Voinea, N.-L., Vulpe, A.-M., Bubanj, S., Stanković, D., Bjelica, B., Aksović, N., & Dobrescu, T. (2025). An Analysis of the Kinetic Energy in the Basket to Handstand on Parallel Bars: A Case Study of an Elite Gymnast. Life, 15(2), 172. https://doi.org/10.3390/life15020172










