Abstract
This study examined lateral wedge insoles and altered foot progression angles on medial tibiofemoral loading and long-term cartilage failure risk. Fifteen healthy male participants walked under four conditions: neutral gait, lateral wedge insoles, toe-in and toe-out gait. Three-dimensional kinematics were captured using an eight-camera system, and ground reaction forces were measured via a piezoelectric force plate. Musculoskeletal simulation analysis quantified tibiofemoral compressive forces, cartilage stresses, strains, and whole-body metabolic power. Probabilistic modelling was employed to estimate the probability of cartilage failure. Comparisons across the four gait conditions employed linear mixed-effects models with repeated measures. Peak compressive forces, stresses and strains were significantly larger in the neutral (force = 2.68 BW, stress = 2.61 MPa & strain = 0.22), compared to toe-in (force = 2.51 BW, stress 2.47 MPa & strain = 0.21) and toe-out (force = 2.43 BW, stress 2.40 MPa & strain = 0.21) conditions. Medial tibiofemoral cartilage failure probability was also significantly larger in the neutral condition (14.04%) compared to toe-in (10.66%) and toe-out (7.89%) conditions. Whole-body metabolic power was also significantly greater in the toe-out (9.74 W/kg) condition compared to neutral (9.32 W/kg) and lateral insoles (9.36 W/kg). The findings suggest that toe-in or toe-out walking may reduce medial tibiofemoral osteoarthritis risk. However, the greater metabolic demand of toe-out walking may limit its long-term feasibility and practicality as a preventive intervention.
1. Introduction
Knee osteoarthritis (OA) is the most prevalent form of lower-limb OA and a leading contributor to disability worldwide [1], imposing substantial economic burdens on healthcare systems [2]. The condition is progressive and degenerative and is characterised by a gradual loss of articular cartilage within the knee joint [3]. Those affected frequently experience persistent ongoing pain and stiffness [4].
Epidemiological data indicate that approximately 10% of people over 55 years of age have knee OA [5], with more than 90% of cases affecting the medial tibiofemoral compartment [6]. Although the mechanisms underlying disease onset and progression are complex, excessive mechanical stress on tibiofemoral cartilage during gait and daily movement is considered a central factor [7]. Susceptibility is further increased by risk factors such as ageing, genetic predisposition, obesity, and previous injury [7].
Given the substantial prevalence of medial tibiofemoral OA and its link to abnormal joint loading, several conservative strategies have been developed to reduce medial joint stresses. Because direct measurement of tibiofemoral contact forces is difficult, the external knee adduction moment is widely used as a surrogate for medial compartment loading [8,9]. A common intervention is the application of lateral wedge insoles [10], which aim to medially displace the centre of pressure (CoP) and shorten the knee adduction moment lever arm [11]. The literature, however, reports mixed outcomes: many studies have shown that lateral wedges reduce the knee adduction moment during walking [12,13,14,15,16,17,18,19] and stair ascent [20], whereas others have observed no reduction [21,22]. Similarly, while some clinical trials have reported improvements in pain and function [23,24,25], others found limited or no benefit [26,27,28,29].
In addition to insoles, gait modification has been explored as a means of attenuating the knee adduction moment [30]. The most common approach is altering the foot progression angle, by either externally (toe-out) or internally (toe-in) rotating the foot [30]. Both strategies seek to influence the mediolateral CoP location and thereby alter knee joint loading [31]. Previous investigations indicate that toe-out gait [31,32,33,34,35] and toe-in gait [36] can reduce the magnitude of the knee adduction moment. Direct comparisons between the two strategies remain scarce, with Lynn and Costigan [37] demonstrating reductions in knee adduction moment with toe-out walking but not toe-in. Conversely, Van den Noort et al. [38] and Khan et al. [30] reported that toe-in gait reduced loading in early stance, while toe-out was more effective during late stance. These studies also showed that toe-in walking reduced the adduction moment impulse, capturing both magnitude and duration of medial loading. Simic et al. [39] found reductions at both early and late stance with toe-in gait, but in their study, toe-out gait produced a significant decrease in adduction moment impulse. Beyond biomechanical analyses, intervention studies suggest that toe-out gait can reduce pain and improve function in individuals with medial tibiofemoral OA [31,40], though no long-term clinical evaluation has been performed for toe-in gait. Nevertheless, as these strategies alter habitual gait patterns, they may increase metabolic and neuromuscular demands [31]. Since humans are evolutionarily optimized to minimize energy expenditure during locomotion, even small increases in metabolic cost could impede daily adoption and limit long-term sustainability outside the laboratory.
It is important to note that the knee adduction moment, although widely used, provides only an indirect approximation of medial tibiofemoral joint loading [41]. While it has been associated with medial knee cartilage degeneration [8,9], it does not directly measure tibiofemoral contact forces [42]. Data from instrumented prostheses indicate only weak to moderate associations between the knee adduction moment and actual medial tibiofemoral contact forces [43]. Herzog et al. [42] demonstrated that muscle forces play the dominant role in determining joint loading. Recent advances in musculoskeletal simulation now allow muscle-driven estimates not only of joint contact forces but also of whole-body metabolic power [44], providing a more comprehensive assessment of gait interventions. To date, such simulation approaches have not yet been adopted to examine the effects of lateral insoles and foot progression modifications on the metabolic demands of walking and medial tibiofemoral joint contact loading.
Challenges also persist in quantifying how different gait strategies and joint loading conditions contribute to the onset and progression of OA [45]. Computational probabilistic modelling of cartilage mechanics has emerged as a promising method for estimating the lifetime risk of OA under repeated loading conditions [46]. The principal advantage of this approach is its ability to estimate long-term risk of OA, allowing the effects of prophylactic interventions to be evaluated in young and healthy individuals, prior to the onset of pathological changes. However, this approach has not yet been used to investigate the influence of lateral wedge insoles or foot progression angle alterations on medial tibiofemoral cartilage failure probability.
Accordingly, the present study aimed to examine whether toe-in gait, toe-out gait, and lateral wedge insoles reduce medial tibiofemoral cartilage loading mechanics and lifetime failure probability compared with natural gait. Furthermore, this investigation also aimed to examine the metabolic demands of walking in the aforementioned conditions. It was hypothesized firstly that all three interventions would decrease medial tibiofemoral loading and probability of failure compared to natural gait, with no significant differences between them and secondly that toe-in and toe-out gait would increase the metabolic demands of walking.
2. Materials and Methods
2.1. Participants
Fifteen healthy male volunteers (mean ± SD: age 31.73 ± 4.96 years, stature 172 ± 6.0 cm, body mass 69.31 ± 9.92 kg, BMI 23.45 ± 2.78 kg/m2) were recruited through advertisements distributed across the university campus and surrounding community areas. A priori power analysis, informed by data from previous work [47] that identified a mean ± SD difference of 0.28 ± 0.60 BW in peak compressive medial tibiofemoral force across conditions, indicated that a sample size of 15 would achieve α = 0.05 and β = 0.80. Participants were eligible if they were aged 18–45 years, reported no knee pain or history of OA, had no known allergy or sensitivity to adhesive tape required for retroreflective marker placement, and were free from any other musculoskeletal pathology at the time of testing. Written informed consent was obtained in line with the Declaration of Helsinki, and the protocol received approval from the institutional ethics committee (STEMH 1013).
2.2. Experimental Insoles
The intervention involved commercially available full-length insoles (Slimflex Simple, High Density, Full Length, Algeos UK, Liverpool, UK). These were manufactured from ethylene-vinyl acetate with a shore A hardness of 65 and incorporated an 11 mm heel thickness, inclusive of the wedge. Each insole was designed with a continuous 5° lateral wedge spanning the full length.
2.3. Foot Progression Angles
To examine the effect of altered foot progression, target angles of 15° toe-in and 15° toe-out during stance were prescribed [30]. To aid consistency, the force plate was initially marked with two reference lines: one corresponding to 15° toe-out and the other to 15° toe-in for the right foot. These markers were removed before data collection, after which participants were instructed to reproduce the designated angles independently. This was considered an ecologically valid approach, since individuals adopting gait modifications in real-world walking would not ordinarily receive visual guidance or feedback [30].
The actual foot progression angles achieved were derived from force plate data by tracking the CoP trajectory. Angles were computed as the line connecting the CoP at initial contact and toe-off relative to the anterior (forward) direction, with positive values representing toe-out and negative values toe-in [48].
2.4. Procedure
Participants walked along a 22 m laboratory, ensuring contact with an embedded piezoelectric force plate (Kistler Instruments Ltd., Winterthur, Switzerland) using their right, dominant foot. The force plate captured data at 1000 Hz. Walking was performed at each participant’s self-selected velocity to maximise ecological validity and better reflect the long-term loading patterns produced by the gait conditions. Enforcing a fixed speed across trials was avoided, as this would not align with everyday walking behaviour; moreover, the probabilistic cartilage failure model described later in this section accounts for the total number of loading cycles.
Each participant completed five valid trials (one gait cycle per trial) in four gait conditions: (1) natural gait with self-selected foot angle, (2) toe-out progression, (3) toe-in progression, and (4) lateral wedge insoles with self-selected foot angle. A trial was accepted when the right foot made complete contact with the force plate and gait remained unaffected by the experimental setup. All participants wore the same footwear (Asics Gel Patriot 6) and were given a five-minute familiarisation period for each of the three intervention conditions [47]. The shoes had a mean mass of 0.265 kg, with a 22 mm heel thickness and 10 mm heel-toe drop. Ground reaction forces (GRFs) and motion data were collected concurrently. Kinematics were captured at 250 Hz with an eight-camera motion system (Qualisys Medical AB, Gothenburg, Sweden), and dynamic calibration was conducted prior to each session.
Body segments were modelled with six degrees of freedom using the calibrated anatomical systems technique [49]. Anatomical reference frames for the thorax, pelvis, thighs, shanks, and feet were established through placement of retroreflective markers on C7, T12, and the xiphoid process, along with bilateral markers on the acromion processes, iliac crests, anterior and posterior superior iliac spines (ASIS, PSIS), medial and lateral femoral epicondyles, medial and lateral malleoli, greater trochanters, calcanei, and the first and fifth metatarsals (Figure 1a). Marker placement was carried out by a researcher with previously demonstrated excellent intra-rater reliability [50]. Knee and ankle joint centres were defined as the midpoints between the epicondyle and malleolar markers, respectively [51,52], while hip joint centres were estimated using a regression method based on ASIS marker positions [53]. Segment tracking was achieved with carbon-fibre clusters containing four non-collinear markers on the thighs and shanks, while the feet were tracked via markers placed on the calcaneus, first metatarsal, and fifth metatarsal. The pelvis was tracked using ASIS and PSIS markers, and the thorax using markers on C7, T12, and the xiphoid process. Static calibration trials were performed to establish anatomical marker positions relative to the tracking clusters. Segment coordinate systems were oriented following the right-hand rule: the Z-axis (transverse plane) aligned vertically from distal to proximal, the Y-axis (coronal plane) extended posterior to anterior, and the X-axis (sagittal plane) ran medial to lateral (Figure 1b).
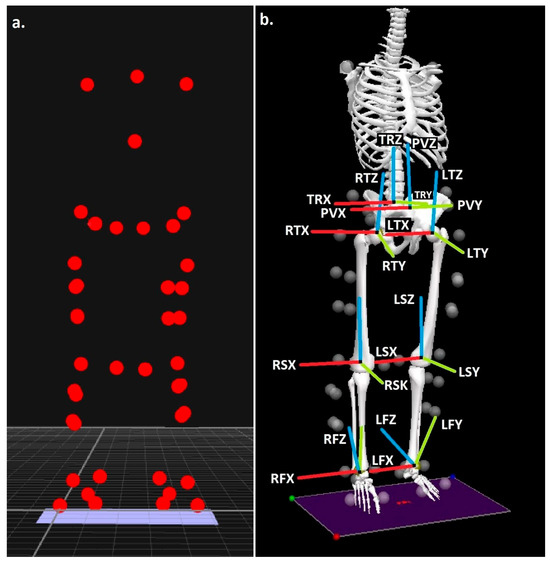
Figure 1.
(a) Anatomical landmark locations and (b) modelled segments, with segment co-ordinate axes (R = right & L = left), (TR = trunk, P = pelvis, T= thigh, S = shank & F = foot), (X = sagittal, Y = coronal & Z = transverse planes).
2.5. Processing
The walking biomechanics dataset underwent four sequential stages of processing to estimate long-term medial tibiofemoral cartilage failure risk: (1) kinematic and temporal data, (2) simulation modelling, (3) medial tibiofemoral contact mechanics, and (4) probabilistic modelling of tibiofemoral cartilage.
2.5.1. Kinematic and Temporal Data
Dynamic walking trials were first handled in Qualisys Track Manager (Qualisys Medical AB, Gothenburg, Sweden), where anatomical and tracking markers were identified and labelled. The resulting datasets were exported as C3D files into Visual 3D (C-Motion, Germantown, MD, USA) for subsequent analysis. The stance phase was defined duration over which the vertical GRF exceeded 20 N [54]. GRF signals were filtered with a 4th-order, zero-lag Butterworth filter with a 50 Hz cut-off, while marker trajectories were filtered at 6 Hz. These cut-off frequencies for kinetic and kinematic data were selected based on residual analysis [55]. Walking velocity was calculated within Visual 3D as the anterior linear velocity of the model’s centre of mass [56], and stride length was obtained as the change in anterior displacement of the foot’s centre of mass between consecutive ipsilateral footstrikes [56]. For each condition, the estimated number of daily loading cycles was computed by dividing the modelled daily walking distance by stride length.
The gait interventions (toe-in, toe-out, and lateral insoles) were designed to alter the mediolateral positioning of the CoP. Therefore, to evaluate their effect, the mediolateral location of the CoP relative to the foot’s centre of mass (mm) was calculated at the time of peak medial tibiofemoral contact force, determined by the subsequent analysis [57]. Positive values indicate that the CoP lies lateral to the foot’s centre of mass.
2.5.2. Simulation Modelling
Kinematic and kinetic data from the stance phase were exported from Visual 3D into OpenSim v3.3 (Simtk.org). A validated musculoskeletal model was first scaled to each participant’s anthropometry. The model consisted of 12 body segments, 19 degrees of freedom, and 92 musculotendon actuators [58], enabling estimation of lower-limb muscle and joint loading. To minimise dynamic inconsistencies between measured GRFs and model kinematics, a residual reduction algorithm [44] was first applied. Muscle forces were then computed using the static optimization framework described by Steele et al. [59]. Since compressive tibiofemoral loads are primarily governed by muscle forces [42], the peak medial compressive tibiofemoral force (normalized to body weight, BW) was extracted via OpenSim’s joint reaction analysis, which used the outputs of static optimization as inputs [58]. Cumulative medial tibiofemoral loading was subsequently estimated by dividing the mean contact force by stride length, following the approach of Miller and Krupenevich [46].
Previous research has shown that, at the point of peak compressive tibiofemoral force, the vastus intermedius, vastus lateralis, and vastus medialis are the primary contributors to medial joint loading during walking [47]. To examine potential differences in peak medial tibiofemoral kinetics across gait conditions, muscle forces (BW) obtained through static optimization were extracted at the time of peak joint loading. These included the three aforementioned quadriceps muscles as well as other knee-crossing muscles: rectus femoris, biceps femoris long and short heads, semimembranosus, semitendinosus, and the medial and lateral gastrocnemius, which were subsequently entered into statistical analyses.
Metabolic cost minimization is a fundamental principle underlying the neural control of locomotion [60], with humans naturally favoring movement patterns that reduce metabolic energy expenditure [61]. Whole-body energy minimization is widely recognized as a key determinant of gait behavior, influencing both efficiency and sustainability [62]. Given that both toe-out and toe-in gait modifications have been shown to alter muscle force distributions in major lower extremity musculature [47], these strategies may lead to unsustainable walking patterns, potentially offsetting their intended benefits and reducing long-term adherence. Therefore, to fully understand the implications of these gait modifications, it was essential to also examine whole-body metabolic power using musculoskeletal simulation, providing a comprehensive assessment of their energetic efficiency and feasibility.
To accomplish this, the Computed Muscle Control (CMC) tool was applied within OpenSim [63,64]. The outputs from CMC were used as inputs to a modified version of the muscle energetics model described by Umberger et al. [65]. This implementation incorporated muscle-specific parameters, including proportions of slow- and fast-twitch fibers obtained from Johnson et al. [66], Garrett et al. [67], and Alway [68]. Muscle mass for each individual muscle was estimated from physiological cross-sectional area, optimal fiber length, and the fiber length associated with maximal isometric force capacity [69]. To maintain physiological validity, whole-muscle metabolic rate was constrained to remain non-negative, reflecting the principle that negative mechanical work does not contribute to ATP resynthesis [70]. Physiological cross-sectional area was calculated using a skeletal muscle density of 1059.7 kg/m3, consistent with mammalian muscle tissue [65], and maximal isometric force was estimated using muscle-specific tensions reported by Hamner and Delp [71] applied to measured cross-sectional areas [69].
Normalized whole-body metabolic power (W/kg) was obtained by adding a basal rate of 1.13 W/kg [72,73] to that generated from the Umberger et al. [65] probe in OpenSim. For statistical purposes, whole-body metabolic power was determined by integrating the estimated whole-body metabolic rate across the step duration using a trapezoidal approach [56].
In addition to whole-body values, muscle-level metabolic power (W/kg) was evaluated to examine the effects of the four gait modification conditions. Analysis was limited to the 21 muscles previously identified as the largest contributors to metabolic cost [74]: extensor digitorum longus, gluteus minimus, gluteus medius, gluteus maximus, psoas major, iliacus, rectus femoris, vastus intermedius, vastus lateralis, vastus medialis, adductor magnus, biceps femoris long and short heads, semitendinosus, semimembranosus, sartorius, adductor longus, tibialis anterior, medial and lateral gastrocnemius, and soleus. For muscles represented by multiple lines of action within OpenSim (gluteus minimus, gluteus medius, gluteus maximus, adductor magnus), outputs were combined for simplicity [58,74]. Muscle-level metabolic power was calculated by integrating each muscle’s metabolic rate across the step duration [56].
2.5.3. Medial Tibiofemoral Contact Mechanics
Peak medial tibiofemoral compressive forces during the stance phase were applied to a medial knee contact mechanics model to estimate corresponding stress and strain within the tibiofemoral cartilage. This analysis was conducted in MATLAB (R2023b) using scripts adapted from the method of Miller and Krupenevich [46]. The modelling framework was based on the approach originally introduced by Nuño and Ahmed [75].
Within the model, the medial femoral condyle was represented by two convex arcs in the sagittal plane (anterior and posterior regions) and a single arc in the posterior coronal plane, while the tibial plateau was represented as a concave curve. The tibial arc radius in the frontal plane was fixed at 21 mm, and the sagittal radii of the femoral arcs were 35.0 mm (anterior) and 18.9 mm (posterior). The tibial component was held fixed, whereas the femoral component included two adjustable parameters: the vertical location of the knee flexion axis relative to the tibia and the knee flexion angle itself, consistent with Nuño and Ahmed [75]. Tibiofemoral cartilage was represented by an array of spring elements distributed across the tibial plateau, each with an unloaded thickness of 5.0 mm [76]. These elements were assumed to exhibit nonlinear elastic stress–strain properties [77]. Medial tibiofemoral contact stress (σ) and strain (ε) were then determined using Equations (1) and (2).
σ = −Mean tibiofemoral cartilage modulus * Log(1 − ε)
ε = Cartilage element compression/modelled cartilage height
Peak compressive stresses (MPa) and strains within the tibiofemoral joint were estimated using three key parameters: the elastic modulus of the loaded cartilage, the deformation of the contact elements under compression, and the total number of elements included in the model. The mesh comprised 7326 elements, corresponding to a 0.5 mm spacing and consistent with the defined tibial and femoral arc radii. The elastic modulus values assigned to the cartilage differed depending on meniscal coverage, with 8.6 MPa for femoral cartilage, 4.0 MPa for uncovered tibial cartilage, and 10.1 MPa for tibial cartilage beneath the meniscus [78]. The medial meniscus itself was given a modulus of 1.3 MPa and modelled as covering 46% of the tibial plateau surface [79,80]. A Poisson’s ratio of 0.45 was applied to both cartilage and meniscal tissues.
The knee flexion angle incorporated into the model was taken from the initial kinematic analysis at the instant of peak medial tibiofemoral contact force, derived from the joint force calculations. To establish loading, the vertical position of the knee flexion axis was first adjusted so that the cartilage elements were unloaded, and then gradually lowered until the predicted force matched the medial tibiofemoral contact force input. Because different radii were assigned to the anterior and posterior aspects of the medial femur, the proportion of cartilage engaged in loading varied as a function of flexion angle [81]. Translational mechanics were excluded from the model, in line with evidence that the medial femoral surface typically remains centered on the tibial plateau across knee flexion [82].
2.5.4. Probabilistic Modelling of Tibiofemoral Cartilage
In line with the framework of Miller & Krupenevich [46], cartilage failure in the medial tibiofemoral compartment was defined as the onset of macroscopic plastic deformation, a hallmark of early osteoarthritic degeneration [83]. Since the median age of knee OA diagnosis is approximately 55 years, with 9.29% of the U.S. population affected symptomatically by that age [5], the modelling window extended across 37 years, representing the period from skeletal maturity at 18 years through to age 55 [84]. Failure probability was estimated using a probabilistic damage-repair approach [85,86,87], where compressive cartilage strain acted as the surrogate variable for cumulative tissue damage. Our prior analyses [88] have examined the sensitivity of peak compressive tibiofemoral strain, the principal predictor of cartilage failure in this model, by systematically varying each parameter within biologically and anthropometrically realistic ranges, while holding all others constant.
The probability of cartilage failure at the 37-year target point was determined as a cumulative outcome of cyclic loading, based on the modelled cartilage experiencing repeated stresses over a daily travel distance. Stride length values extracted from the kinematic and temporal data were incorporated into this calculation, as formalised in Equation (3).
Probability of cartilage failure = 1 − Exp − [(Volume of stressed cartilage/Reference stressed cartilage volume) (time/time until failure) Weibull exponent/Power law exponent]
In Equation (3), constant values were specified for the reference stressed cartilage volume (78.5 mm3), the Weibull exponent (14.3), and the power law exponent (12.9). The estimated time to cartilage failure was subsequently obtained from Equation (4).
Time to failure = (Power law coefficient * Stride length/Distance per day) (Weibull coefficient * ε) –Power law exponent
In Equation (4), the predicted time to failure reflects the point at which 63.2% of simulated samples would be expected to fail under the imposed magnitude and frequency of cartilage strain. The model assumed a daily travel distance of 6.0 km, approximating the distance covered by completing 7000 steps per day, a value now widely regarded as beneficial for overall health [89]. For each gait condition, the daily number of loading cycles (steps) was calculated by dividing this distance by the stride length obtained from the kinematic and temporal data analysis. In the time-to-failure calculations, the Weibull coefficient (1.03), the power law coefficient (1.0), and the power law exponent (12.9) were applied as fixed constants. Parameter values for the Weibull and power law functions were adopted from Miller & Krupenevich [46], who fitted a power-law model for cycles to failure based on data from Riemenschneider et al. [90].
Equation (3) outlines the probability of cartilage failure in vitro. To account for the ability of living cartilage to partially repair strain-induced damage over time [91], the probability of recovery within the medial tibiofemoral cartilage was incorporated into the framework through Equation (5).
Probability of repair = 1 − Exp − [ − (time/time until repair) Cartilage repair exponent]
In Equation (5), the time to repair (fixed at 5.0 years) and the repair exponent (5.2) were specified based on values reported by Miller & Krupenevich [46]. The repair time was defined as the duration at which 63.2% of damaged cartilage cases would be expected to show recovery. Following the method outlined by Miller & Krupenevich [46], this repair mechanism was incorporated into Equation (3) by generating a probability density function that represents the instantaneous likelihood of failure across time. This approach is formalised in Equation (6).
Probability density function = (Volume of stressed cartilage * Weibull exponent/power law exponent * Reference stressed cartilage volume * time until failure) (time/time until failure) Weibull exponent/Power law exponent − 1 exp [−(Volume of stressed cartilage/Reference stressed cartilage volume) (time/time until failure) Weibull exponent/Power law exponent]
To account for both failure and repair, the probability density function was multiplied by the cumulative likelihood that repair had not yet taken place (1 − probability of repair) and then integrated across time. This procedure is shown in Equation (7).
Probability of failure with repair = ∫ (time 0) [Probability density function * (1 − Probability of repair)] modelled distance between contact elements * time.
Miller & Krupenevich [46] noted that this repair modelling approach may overestimate recovery in cartilage, since it assumes that damage occurring at any time point is fully restored after a duration equal to the sum of the damage and repair periods, thereby implying near-complete recovery of all damage.
2.6. Statistical Analyses
Mean values and standard deviations (SDs) were calculated for all biomechanical and cartilage failure outcomes. Differences between the four gait conditions were assessed using linear mixed-effects models with repeated measures [92]. The restricted maximum likelihood estimation was applied alongside compound symmetry, with gait condition specified as a fixed effect and participant-level random intercepts included [88]. Effect sizes (Cohen’s d) were reported and interpreted as small (d = 0.2), medium (d = 0.5), or large (d = 0.8) according to accepted guidelines [93]. Statistical analyses were performed in SPSS version 29 (IBM, SPSS, New York, NY, USA), with significance set at p ≤ 0.05.
3. Results
3.1. Kinematic and Temporal Data
Walking speed was greater in the neutral gait (p = 0.002, d = 0.97) and with lateral insoles (p = 0.007, d = 0.81) compared with toe-out. The CoP was shifted more laterally during toe-in relative to neutral (p = 0.001, d = 1.06), toe-out (p = 0.002, d = 0.95), and lateral insoles (p < 0.001, d = 1.58). Additionally, the neutral gait exhibited a more lateral CoP than both lateral insoles (p = 0.018, d = 0.69) and toe-out (p = 0.019, d = 0.69) (Table 1).

Table 1.
Initial kinematic processing values (mean and standard deviations).
3.2. Simulation Modelling
Peak medial tibiofemoral compressive force was greater under the neutral condition compared with toe-in (p = 0.005, d = 0.85) and toe-out (p = 0.001, d = 1.09). Similarly, lateral insoles produced greater values than toe-in (p = 0.006, d = 0.84) and toe-out (p < 0.001, d = 1.64) (Table 2). Peak cumulative compressive force was also greater in the neutral condition relative to toe-in (p = 0.023, d = 0.66) and toe-out (p < 0.001, d = 1.78), while lateral insoles exceeded toe-out (p = 0.001, d = 1.11) (Table 2).

Table 2.
Musculoskeletal simulation values (mean and standard deviations).
For muscle forces, vastus intermedius was greater in neutral compared to toe-in (p = 0.01, d = 0.76) and toe-out (p = 0.001, d = 1.06), in lateral insoles compared to toe-out (p < 0.001, d = 1.43), and in toe-in compared to toe-out (p = 0.038, d = 0.59). Vastus lateralis was greater in neutral compared to toe-in (p = 0.004, d = 0.89) and toe-out (p = 0.001, d = 1.03), and in lateral insoles compared to toe-out (p < 0.001, d = 1.21). Vastus medialis was greater in neutral compared to toe-out (p = 0.001, d = 1.05), in lateral insoles compared to toe-out (p < 0.001, d = 1.63), and in toe-in compared to toe-out (p = 0.001, d = 1.02). Rectus femoris was greater in toe-out compared to neutral (p = 0.041, d = 0.58), lateral insoles (p < 0.001, d = 1.36), and toe-in (p < 0.001, d = 1.62), with lateral insoles also exceeding toe-in (p = 0.018, d = 0.69) (Table 2).
Whole-body metabolic power was greater during toe-out walking compared to both neutral (p = 0.033, d = 0.61) and lateral insoles (p = 0.015, d = 0.72) (Figure 2). Muscle-level metabolic outputs are reported in the Supplementary Material (S1).
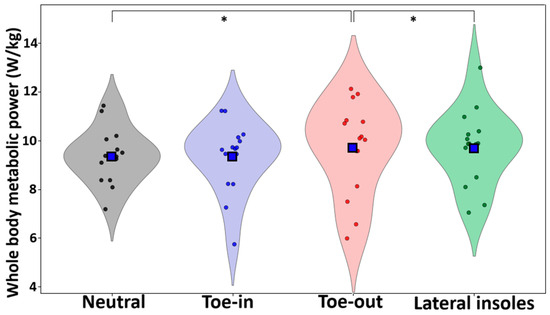
Figure 2.
Violin plots for each condition. Blue squares represent the mean and * denotes significant differences at the p < 0.05 level.
3.3. Medial Tibiofemoral Contact Mechanics
Peak medial tibiofemoral compressive stress was greater in the neutral gait compared with toe-in (p = 0.01, d = 0.76) and toe-out (p = 0.001, d = 1.08). Lateral insoles also produced greater stresses than toe-in (p = 0.005, d = 0.86) and toe-out (p < 0.001, d = 1.35) (Table 3). Similarly, peak medial tibiofemoral compressive strain was greater during neutral gait compared to toe-in (p = 0.01, d = 0.77) and toe-out (p = 0.001, d = 1.09), with lateral insoles again exceeding both toe-in (p = 0.005, d = 0.85) and toe-out (p < 0.001, d = 1.53) (Table 3).

Table 3.
Medial tibiofemoral contact mechanics (mean and standard deviations).
3.4. Probabilistic Modelling of Tibiofemoral Cartilage
When considering repair, the probability of medial tibiofemoral cartilage failure was greater in the neutral condition compared to both toe-in (p = 0.046, d = 0.56) and toe-out (p = 0.05, d = 0.55) (Table 4, Figure 3).

Table 4.
Medial tibiofemoral cartilage failure probabilistic values (mean and standard deviations).
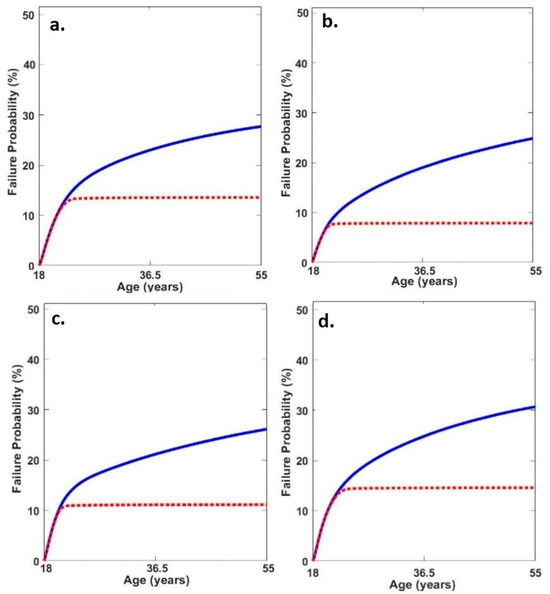
Figure 3.
Average medial tibiofemoral cartilage failure time series probabilities in (a) neutral, (b) toe-out, (c) toe-in and (d) lateral insoles (red line = failure probability with adaptation and blue line = failure probability without adaptation).
4. Discussion
Medial tibiofemoral OA is a common condition that imposes substantial economic burdens on healthcare systems and is frequently accompanied by persistent pain and stiffness. Our understanding of how altered gait mechanics and lateral insoles influence cartilage loading, long-term probability of OA and the energetic consequences of gait modifications remains poorly understood. The aim of this investigation was therefore to evaluate how toe-in gait, toe-out gait, and lateral wedge insoles affect medial tibiofemoral cartilage loading and the projected lifetime probability of cartilage failure. In addition, concurrent analysis of whole-body metabolic power was undertaken to provide insight into the potential long-term sustainability of these gait modifications. Together, these results are intended to provide new perspectives on the potential preventative and therapeutic roles of these strategies in supporting medial tibiofemoral cartilage integrity.
In line with the original hypothesis, both toe-in and toe-out gait patterns produced statistically significant reductions in medial tibiofemoral forces, stresses, and strains relative to a neutral walking pattern. By contrast, the lack of any significant reductions in cartilage loading with lateral wedge insoles was contrary to expectations. The findings with respect to toe-in and toe-out walking are consistent with prior work [31,32,33,34,35,36], which used the knee adduction moment as a principal outcome, whereas the findings for lateral insoles diverge from several earlier reports [12,13,14,15,16,17,18,19].
Although the precise mechanisms explaining these discrepancies remain uncertain, earlier research [47] identified vasti muscle forces as the strongest contributors to medial tibiofemoral joint loading during gait. This implies that the differences observed across the present experimental conditions may be attributable to alterations in vasti muscle activity. As vasti forces were significantly reduced during both toe-in and toe-out gait, it seems probable that the reductions in medial tibiofemoral loading arose from these kinetic adjustments. Despite all three interventions shifting the CoP location, only the toe-in and toe-out gait modifications demonstrated an ability to reduce the mechanical factors associated with medial knee OA risk.
Walking velocity was larger in the neutral condition, and given that medial tibiofemoral joint loading is affected by gait speed [94], some portion of the observed differences may reflect velocity-related influences. This also suggests that toe-out modifications may constrain preferred walking speed compared with unmodified gait. Moreover, cumulative medial tibiofemoral loading was significantly reduced under both toe-in and toe-out conditions, further supporting the initial hypothesis. Since stride length and daily loading cycles were not significantly altered, the observed reduction in cumulative load likely reflects reduced medial tibiofemoral loads per step.
Consistent in part with our original hypotheses, the present study found that the probability of cartilage failure was significantly decreased in the toe-in and toe-out gait conditions compared to the neutral gait. Given that the number of daily loading cycles did not differ between conditions, interpretation of the probabilistic failure framework [46] indicates that these reductions were likely driven by decreases in cartilage strain under the modified gait patterns. Altering the foot progression angle can improve pain and functional outcomes in individuals with established knee OA [31,40], and the current findings extend this evidence, suggesting that such gait modifications may also hold preventative potential, helping to reduce the risk of symptom onset. Considering the disabling pain, reduced mobility, and considerable healthcare costs associated with knee OA [1,2], toe-in and toe-out gait strategies may warrant inclusion as part of long-term musculoskeletal management aimed at preventing medial tibiofemoral OA.
In partial agreement with our hypothesis, the findings demonstrate that although both toe-in and toe-out gait modifications reduced medial tibiofemoral cartilage failure probability compared to the neutral condition, whole-body metabolic power was significantly greater in the toe-out condition. The muscle-level metabolic outcomes presented in S1 reveal distinct redistributions of muscular workload in response to the experimental gait modifications. Specifically, the toe-out gait condition was characterized by increased metabolic demands in the gluteal musculature, with a concurrent reduction in the energetic contribution of the vasti muscles. Conversely, the toe-in gait condition resulted in elevated metabolic activity within the adductor and the semimembranosus, coupled with a relative unloading of the gluteal muscles. As previous analyses have demonstrated that the hip adductors are the predominant contributors to the metabolic cost of walking [95], it is proposed that the elevated metabolic power observed in the toe-out gait condition may be attributable to increased metabolic demand placed on these muscles (i.e., gluteal muscles) during this condition. Given that metabolic cost minimization is a fundamental principle guiding the neural control of human locomotion [60], the metabolic penalty associated with toe-out gait may render this gait modification less sustainable over time, potentially diminishing the clinical utility of the toe-out gait as a preventative strategy for medial tibiofemoral OA.
The plausibility of the medial tibiofemoral mechanical outcomes observed in this work was evaluated by comparison with previous computational and in vivo investigations. Given the walking speeds tested, the peak medial tibiofemoral forces were consistent with those reported for participant K8L (2.59 BW at 1.39 m/s) from in vivo datasets [96]. Likewise, the cartilage strain values (0.23 at 1.52 m/s) and longitudinal failure probability for medial tibiofemoral cartilage in the neutral condition aligned closely with those reported by Miller & Krupenevich [46] (13.4%) and correspond with epidemiological incidence rates for medial tibiofemoral OA at age 55 [5].
Sex is a recognized independent risk factor for knee OA, with females exhibiting increased prevalence [97], and established sex-related differences in walking mechanics have also been reported [98]. Therefore, the generalizability of our findings to females remains uncertain; and future studies should therefore evaluate toe-in gait, toe-out gait, and lateral wedge insoles using probabilistic modelling in female cohorts. It is important to note that OA is recognised as a multifactorial disorder [99], with chronic, low-grade inflammation alongside mechanical loading, proposed as a key factor in its pathogenesis [100]. The computational framework applied in the present study did not incorporate potential influences from circulating adipokines, which could be considered a limitation. Future refinement of this modelling approach should aim to integrate both mechanical and biological determinants of OA into a pathophysiologically relevant probabilistic model, thereby enabling more comprehensive assessment of potential disease-modifying interventions. Moreover, directed by the present findings, future research should include longitudinal investigations to now provide the direct evidence necessary to substantiate the prophylactic potential of gait modification strategies. Finally, though familiarization was undertaken [47] alongside a repeated measures study design; a potential drawback is the novel exposure to different walking modalities. Neuromuscular demand of novel tasks can decline with repeated exposure, as motor recruitment becomes more efficient [101]; emphasizing the need for further longitudinal research.
5. Conclusions
Whilst previous studies have examined the biomechanical consequences of toe-in and toe-out gait adjustments and the use of lateral wedge insoles, their long-term influence has not previously been explored within an integrated musculoskeletal simulation and probabilistic modelling framework. The present work extends current knowledge by assessing how these gait strategies and lateral insoles influence the likelihood of medial tibiofemoral cartilage failure when compared with a neutral walking pattern. The analyses showed that cartilage forces, stresses, and strains were greater during neutral gait than under toe-in or toe-out conditions. Importantly, both toe-in and toe-out walking reduced the estimated probability of cartilage failure, although the toe-out pattern was accompanied by greater metabolic cost. These results indicate that altering foot progression to a toe-in or toe-out position may reduce medial tibiofemoral OA risk, though the additional metabolic burden of toe-out gait may limit its practicality as a long-term preventive strategy.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/life15111677/s1.
Author Contributions
Conceptualization, J.S. and. G.Z.; methodology J.S. and. G.Z.; data curation, J.S.; formal analysis, J.S. and. G.Z.; project administration, J.S.; writing—original draft preparation, J.S. and. G.Z.; writing—review and editing J.S. and. G.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study was granted ethical approval by the University Lancashire Science, Technology, Engineering, Math and Health Ethics Committee (STEMH 1013 and 11 April 2022 of approval).
Informed Consent Statement
All participants provided written informed consent in accordance with the Declaration of Helsinki and the Oviedo Convention.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Heidari, B. Knee osteoarthritis prevalence, risk factors, pathogenesis and features: Part I. Casp. J. Intern. Med. 2011, 2, 205–212. [Google Scholar]
- Martins, R.; Kotsopoulos, N.; Kließ, M.K.; Beck, C.; Abraham, L.; Large, S.; Connolly, M.P. Comparing the fiscal consequences of controlled and uncontrolled osteoarthritis pain applying a UK public economic perspective. J. Health Econ. Outcomes Res. 2021, 8, 127–136. [Google Scholar] [CrossRef]
- Chen, D.I.; Shen, J.; Zhao, W.; Wang, T.; Han, L.; Hamilton, J.L.; Im, H.J. Osteoarthritis: Toward a comprehensive understanding of pathological mechanism. Bone Res. 2017, 5, 16044. [Google Scholar] [CrossRef]
- Alshami, A.M. Knee osteoarthritis related pain: A narrative review of diagnosis and treatment. Int. J. Health Sci. 2014, 8, 85–104. [Google Scholar] [CrossRef]
- Losina, E.; Weinstein, A.M.; Reichmann, W.M.; Burbine, S.A.; Solomon, D.H.; Daigle, M.E.; Katz, J.N. Lifetime risk and age at diagnosis of symptomatic knee osteoarthritis in the US. Arthritis Care Res. 2013, 65, 703–711. [Google Scholar] [CrossRef]
- Wise, B.L.; Niu, J.; Yang, M.; Lane, N.E.; Harvey, W.; Felson, D.T.; Multicenter Osteoarthritis (MOST) Group. Patterns of compartment involvement in tibiofemoral osteoarthritis in men and women and in whites and African Americans. Arthritis Care Res. 2012, 64, 847–852. [Google Scholar] [CrossRef]
- Eitner, A.; Hofmann, G.O.; Schaible, H.G. Mechanisms of osteoarthritic pain. Studies in humans and experimental models. Front. Mol. Neurosci. 2017, 10, 349. [Google Scholar] [CrossRef] [PubMed]
- Miyazaki, T.; Wada, M.; Kawahara, H.; Sato, M.; Baba, H.; Shimada, S. Dynamic load at baseline can predict radiographic disease progression in medial compartment knee osteoarthritis. Ann. Rheum. Dis. 2002, 61, 617–622. [Google Scholar] [CrossRef] [PubMed]
- Morgenroth, D.C.; Medverd, J.R.; Seyedali, M.; Czerniecki, J.M. The relationship between knee joint loading rate during walking and degenerative changes on magnetic resonance imaging. Clin. Biomech. 2014, 29, 664–670. [Google Scholar] [CrossRef] [PubMed]
- Xing, F.; Lu, B.; Kuang, M.J.; Wang, Y.; Zhao, Y.L.; Zhao, J.; Ma, X.L. A systematic review and meta-analysis into the effect of lateral wedge arch support insoles for reducing knee joint load in patients with medial knee osteoarthritis. Medicine 2017, 96, e7168. [Google Scholar] [CrossRef] [PubMed]
- Sinclair, J. Mechanical effects of medial and lateral wedged orthoses during running. Phys. Ther. Sport 2018, 32, 48–53. [Google Scholar] [CrossRef]
- Jones, R.K.; Nester, C.J.; Richards, J.D.; Kim, W.Y.; Johnson, D.S.; Jari, S.; Tyson, S.F. A comparison of the biomechanical effects of valgus knee braces and lateral wedged insoles in patients with knee osteoarthritis. Gait Posture 2013, 37, 368–372. [Google Scholar] [CrossRef]
- Hsu, W.C.; Jhong, Y.C.; Chen, H.L.; Lin, Y.J.; Chen, L.F.; Hsieh, L.F. Immediate and long-term efficacy of laterally-wedged insoles on persons with bilateral medial knee osteoarthritis during walking. Biomed. Eng. Online 2015, 14, 43. [Google Scholar] [CrossRef] [PubMed]
- Hinman, R.S.; Payne, C.; Metcalf, B.R.; Wrigley, T.V.; Bennell, K.L. Lateral wedges in knee osteoarthritis: What are their immediate clinical and biomechanical effects and can these predict a three—Month clinical outcome? Arthritis Care Res. 2008, 59, 408–415. [Google Scholar] [CrossRef]
- Hinman, R.S.; Bowles, K.A.; Metcalf, B.B.; Wrigley, T.V.; Bennell, K.L. Lateral wedge insoles for medial knee osteoarthritis: Effects on lower limb frontal plane biomechanics. Clin. Biomech. 2012, 27, 27–33. [Google Scholar] [CrossRef] [PubMed]
- Sawada, T.; Tanimoto, K.; Tokuda, K.; Iwamoto, Y.; Ogata, Y.; Anan, M.; Shinkoda, K. Rear foot kinematics when wearing lateral wedge insoles and foot alignment influence the effect of knee adduction moment for medial knee osteoarthritis. Gait Posture 2017, 57, 177–181. [Google Scholar] [CrossRef]
- Shimada, S.; Kobayashi, S.; Wada, M.; Uchida, K.; Sasaki, S.; Kawahara, H.; Baba, H. Effects of disease severity on response to lateral wedged shoe insole for medial compartment knee osteoarthritis. Arch. Phys. Med. Rehabil. 2006, 87, 1436–1441. [Google Scholar] [CrossRef] [PubMed]
- Kerrigan, D.C.; Lelas, J.L.; Goggins, J.; Merriman, G.J.; Kaplan, R.J.; Felson, D.T. Effectiveness of a lateral-wedge insole on knee varus torque in patients with knee osteoarthritis. Arch. Phys. Med. Rehabil. 2002, 83, 889–893. [Google Scholar] [CrossRef]
- Dessery, Y.; Belzile, É.; Turmel, S.; Corbeil, P. Effects of foot orthoses with medial arch support and lateral wedge on knee adduction moment in patients with medial knee osteoarthritis. Prosthet. Orthot. Int. 2017, 41, 356–363. [Google Scholar] [CrossRef]
- Alshawabka, A.Z.; Liu, A.; Tyson, S.F.; Jones, R.K. The use of a lateral wedge insole to reduce knee loading when ascending and descending stairs in medial knee osteoarthritis patients. Clin. Biomech. 2014, 29, 650–656. [Google Scholar] [CrossRef]
- Maly, M.R.; Culham, E.G.; Costigan, P.A. Static and dynamic biomechanics of foot orthoses in people with medial compartment knee osteoarthritis. Clin. Biomech. 2002, 17, 603–610. [Google Scholar] [CrossRef]
- Nester, C.J.; Van Der Linden, M.L.; Bowker, P. Effect of foot orthoses on the kinematics and kinetics of normal walking gait. Gait Posture 2003, 17, 180–187. [Google Scholar] [CrossRef]
- Hatef, M.R.; Mirfeizi, Z.; Sahebari, M.; Jokar, M.H.; Mirheydari, M. Superiority of laterally elevated wedged insoles to neutrally wedged insoles in medial knee osteoarthritis symptom relief. Int. J. Rheum. Dis. 2014, 17, 84–88. [Google Scholar] [CrossRef]
- Hsieh, R.L.; Lee, W.C. Clinical effects of lateral wedge arch support insoles in knee osteoarthritis: A prospective double-blind randomized study. Medicine 2016, 95, e3952. [Google Scholar] [CrossRef]
- Skou, S.T.; Hojgaard, L.; Simonsen, O.H. Customized foot insoles have a positive effect on pain, function, and quality of life in patients with medial knee osteoarthritis. J. Am. Podiatr. Med. Assoc. 2013, 103, 50–55. [Google Scholar] [CrossRef]
- Sasaki, T.; Yasuda, K. Clinical evaluation of the treatment of osteoarthritic knees using a newly designed wedged insole. Clin. Orthop. Relat. Res. 1987, 221, 181–187. [Google Scholar] [CrossRef]
- Baker, K.; Goggins, J.; Xie, H.; Szumowski, K.; LaValley, M.; Hunter, D.J.; Felson, D.T. A randomized crossover trial of a wedged insole for treatment of knee osteoarthritis. Arthritis Rheum. 2007, 56, 1198–1203. [Google Scholar] [CrossRef] [PubMed]
- Bennell, K.L.; Bowles, K.A.; Payne, C.; Cicuttini, F.; Williamson, E.; Forbes, A.; Hinman, R.S. Lateral wedge insoles for medial knee osteoarthritis: 12 month randomised controlled trial. BMJ 2011, 342, d2912. [Google Scholar] [CrossRef] [PubMed]
- Pham, T.; Maillefert, J.F.; Hudry, C.; Kieffert, P.; Bourgeois, P.; Lechevalier, D.; Dougados, M. Laterally elevated wedged insoles in the treatment of medial knee osteoarthritis: A two-year prospective randomized controlled study. Osteoarthr. Cartil. 2004, 12, 46–55. [Google Scholar] [CrossRef]
- Khan, S.S.; Khan, S.J.; Usman, J. Effects of toe-out and toe-in gait with varying walking speeds on knee joint mechanics and lower limb energetics. Gait Posture 2017, 53, 185–192. [Google Scholar] [CrossRef]
- Hunt, M.A.; Takacs, J. Effects of a 10-week toe-out gait modification intervention in people with medial knee osteoarthritis: A pilot, feasibility study. Osteoarthr. Cartil. 2014, 22, 904–911. [Google Scholar] [CrossRef]
- Guo, M.; Axe, M.J.; Manal, K. The influence of foot progression angle on the knee adduction moment during walking and stair climbing in pain free individuals with knee osteoarthritis. Gait Posture 2007, 26, 436–441. [Google Scholar] [CrossRef] [PubMed]
- Lynn, S.K.; Kajaks, T.; Costigan, P.A. The effect of internal and external foot rotation on the adduction moment and lateral–medial shear force at the knee during gait. J. Sci. Med. Sport 2008, 11, 444–451. [Google Scholar] [CrossRef] [PubMed]
- Rutherford, D.J.; Hubley-Kozey, C.L.; Deluzio, K.J.; Stanish, W.D.; Dunbar, M. Foot progression angle and the knee adduction moment: A cross-sectional investigation in knee osteoarthritis. Osteoarthr. Cartil. 2008, 16, 883–889. [Google Scholar] [CrossRef]
- Jenkyn, T.R.; Hunt, M.A.; Jones, I.C.; Giffin, J.R.; Birmingham, T.B. Toe-out gait in patients with knee osteoarthritis partially transforms external knee adduction moment into flexion moment during early stance phase of gait: A tri-planar kinetic mechanism. J. Biomech. 2008, 41, 276–283. [Google Scholar] [CrossRef] [PubMed]
- Shull, P.B.; Shultz, R.; Silder, A.; Dragoo, J.L.; Besier, T.F.; Cutkosky, M.R.; Delp, S.L. Toe-in gait reduces the first peak knee adduction moment in patients with medial compartment knee osteoarthritis. J. Biomech. 2013, 46, 122–128. [Google Scholar] [CrossRef]
- Lynn, S.K.; Costigan, P.A. Effect of foot rotation on knee kinetics and hamstring activation in older adults with and without signs of knee osteoarthritis. Clin. Biomech. 2008, 23, 779–786. [Google Scholar] [CrossRef]
- Van den Noort, J.C.; Schaffers, I.; Snijders, J.; Harlaar, J. The effectiveness of voluntary modifications of gait pattern to reduce the knee adduction moment. Hum. Mov. Sci. 2013, 32, 412–424. [Google Scholar] [CrossRef]
- Simic, M.; Wrigley, T.V.; Hinman, R.S.; Hunt, M.A.; Bennell, K.L. Altering foot progression angle in people with medial knee osteoarthritis: The effects of varying toe-in and toe-out angles are mediated by pain and malalignment. Osteoarthr. Cartil. 2013, 21, 1272–1280. [Google Scholar] [CrossRef]
- Deo, M.; Jain, S. Effect of toe-out gait modification on pain and quality of life in patients with knee osteoarthritis: A randomised controlled pilot trial. MOJ Orthop. Rheumatol. 2022, 14, 139–145. [Google Scholar] [CrossRef]
- Sinclair, J.K.; Ingram, J.; Taylor, P.J.; Chockalingam, N. Acute effects of different orthoses on lower extremity kinetics and kinematics during running; a musculoskeletal simulation analysis. Acta Bioeng. Biomech. 2019, 21, 13–25. [Google Scholar] [CrossRef]
- Herzog, W.; Clark, A.; Wu, J. Resultant and local loading in models of joint disease. Arthritis Care Res.—Off. J. Am. Coll. Rheumatol. 2003, 49, 239–247. [Google Scholar] [CrossRef] [PubMed]
- Kutzner, I.; Trepczynski, A.; Heller, M.O.; Bergmann, G. Knee adduction moment and medial contact force–facts about their correlation during gait. PLoS ONE 2013, 8, e81036. [Google Scholar] [CrossRef] [PubMed]
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Thelen, D.G. OpenSim: Open-source software to create and analyze dynamic simulations of movement. IEEE Trans. Biomed. Eng. 2007, 54, 1940–1950. [Google Scholar] [CrossRef]
- Sinclair, J.; Lynch, H.; Chockalingam, N.; Taylor, P.J. Effects of Obesity on Medial Tibiofemoral Cartilage Mechanics in Females—An Exploration Using Musculoskeletal Simulation and Probabilistic Cartilage Failure Modelling. Life 2023, 13, 270. [Google Scholar] [CrossRef] [PubMed]
- Miller, R.H.; Krupenevich, R.L. Medial knee cartilage is unlikely to withstand a lifetime of running without positive adaptation: A theoretical biomechanical model of failure phenomena. PeerJ 2020, 8, e9676. [Google Scholar] [CrossRef]
- Sinclair, J.; Brooks, D.; Taylor, P.J.; Liles, N. Effects of toe-in/out toe-in gait and lateral wedge orthoses on lower extremity joint kinetics; an exploration using musculoskeletal simulation and Bayesian contrasts. Sport Sci. Health 2021, 17, 781–795. [Google Scholar] [CrossRef]
- Chang, A.; Hurwitz, D.; Dunlop, D.; Song, J.; Cahue, S.; Hayes, K.; Sharma, L. The relationship between toe-out angle during gait and progression of medial tibiofemoral osteoarthritis. Ann. Rheum. Dis. 2007, 66, 1271–1275. [Google Scholar] [CrossRef]
- Cappozzo, A.; Catani, F.; Della Croce, U.; Leardini, A. Position and orientation in space of bones during movement: Anatomical frame definition and determination. Clin. Biomech. 1995, 10, 171–178. [Google Scholar] [CrossRef]
- Sinclair, J.; Hebron, J.; Taylor, P.J. The influence of tester experience on the reliability of 3D kinematic information during running. Gait Posture 2014, 40, 707–711. [Google Scholar] [CrossRef]
- Graydon, R.; Fewtrell, D.J.; Atkins, S.J.; Sinclair, J.K. The test-retest reliability of different ankle joint center location techniques. Foot Ankle Online J. 2015, 8, 26–31. [Google Scholar]
- Sinclair, J.; Hebron, J.; Taylor, P.J. The test-retest reliability of knee joint center location techniques. J. Appl. Biomech. 2015, 31, 117–121. [Google Scholar] [CrossRef] [PubMed]
- Sinclair, J.; Taylor, P.J.; Currigan, G.; Hobbs, S.J. The test-retest reliability of three different hip joint centre location techniques. Mov. Sport Sci.—Sci. Mot. 2014, 83, 31–39. [Google Scholar] [CrossRef]
- Sinclair, J.K.; Edmundson, C.J.; Brooks, D.; Hobbs, S.J. Evaluation of kinematic methods of identifying gait Events during running. Int. J. Sports Sci. Eng. 2011, 5, 188–192. [Google Scholar]
- Sinclair, J.; Taylor, P.J.; Hobbs, S.J. Digital filtering of three-dimensional lower extremity kinematics: An assessment. J. Hum. Kinet. 2013, 39, 25–36. [Google Scholar] [CrossRef]
- Sinclair, J.; Chockalingam, N.; Taylor, P.J. Lower Extremity Kinetics and Kinematics in Runners with Patellofemoral Pain: A Retrospective Case–Control Study Using Musculoskeletal Simulation. Appl. Sci. 2022, 12, 585. [Google Scholar] [CrossRef]
- Sinclair, J.; Taylor, P.J.; Shadwell, G.; Stone, M.; Booth, N.; Jones, B.; Edmundson, C.J. Two-Experiment Examination of Habitual and Manipulated Foot Placement Angles on the Kinetics, Kinematics, and Muscle Forces of the Barbell Back Squat in Male Lifters. Sensors 2022, 22, 6999. [Google Scholar] [CrossRef]
- Lerner, Z.F.; DeMers, M.S.; Delp, S.L.; Browning, R.C. How tibiofemoral alignment and contact locations affect predictions of medial and lateral tibiofemoral contact forces. J. Biomech. 2015, 48, 644–650. [Google Scholar] [CrossRef]
- Steele, K.M.; DeMers, M.S.; Schwartz, M.H.; Delp, S.L. Compressive tibiofemoral force during crouch gait. Gait Posture 2012, 35, 556–560. [Google Scholar] [CrossRef] [PubMed]
- McDonald, K.A.; Cusumano, J.P.; Hieronymi, A.; Rubenson, J. Humans trade off whole-body energy cost to avoid overburdening muscles while walking. Proc. R. Soc. B 2022, 289, 20221189. [Google Scholar] [CrossRef]
- McNeill, A.R. Energetics and optimization of human walking and running: The 2000 Raymond Pearl memorial lecture. Am. J. Hum. Biol. 2002, 14, 641–648. [Google Scholar] [CrossRef]
- McAllister, M.J.; Chen, A.; Selinger, J.C. Behavioural energetics in human locomotion: How energy use influences how we move. J. Exp. Biol. 2025, 228 (Suppl. 1), JEB248125. [Google Scholar] [CrossRef]
- Thelen, D.G.; Anderson, F.C. Using computed muscle control to generate forward dynamic simulations of human walking from experimental data. J. Biomech. 2006, 39, 1107–1115. [Google Scholar] [CrossRef]
- Thelen, D.G.; Anderson, F.C.; Delp, S.L. Generating dynamic simulations of movement using computed muscle control. J. Biomech. 2003, 36, 321–328. [Google Scholar] [CrossRef] [PubMed]
- Umberger, B.R.; Gerritsen, K.G.; Martin, P.E. A model of human muscle energy expenditure. Comput. Methods Biomech. Biomed. Eng. 2003, 6, 99–111. [Google Scholar] [CrossRef]
- Johnson, M.; Polgar, J.; Weightman, D.; Appleton, D. Data on the distribution of fibre types in thirty-six human muscles: An autopsy study. J. Neurol. Sci. 1973, 18, 111–129. [Google Scholar] [CrossRef] [PubMed]
- Garrett, W.E., Jr.; Califf, J.C.; Bassett, F.H. Histochemical correlates of hamstring injuries. Am. J. Sports Med. 1984, 12, 98–103. [Google Scholar] [CrossRef] [PubMed]
- Alway, S.E. Is fiber mitochondrial volume density a good indicator of muscle fatigability to isometric exercise? J. Appl. Physiol. 1991, 70, 2111–2119. [Google Scholar] [CrossRef]
- Uchida, T.K.; Hicks, J.L.; Dembia, C.L.; Delp, S.L. Stretching your energetic budget: How tendon compliance affects the metabolic cost of running. PLoS ONE 2016, 11, e0150378. [Google Scholar] [CrossRef]
- Gonabadi, M.A.; Antonellis, P.; Malcolm, P. Differences between joint-space and musculoskeletal estimations of metabolic rate time profiles. PLoS Comput. Biol. 2020, 16, e1008280. [Google Scholar]
- Hamner, S.R.; Delp, S.L. Muscle contributions to fore-aft and vertical body mass center accelerations over a range of running speeds. J. Biomech. 2013, 46, 780–787. [Google Scholar] [CrossRef]
- Miller, R.H. A comparison of muscle energy models for simulating human walking in three dimensions. J. Biomech. 2014, 47, 1373–1381. [Google Scholar] [CrossRef]
- Waters, R.L.; Mulroy, S. The energy expenditure of normal and pathologic gait. Gait Posture 1999, 9, 207–231. [Google Scholar] [CrossRef] [PubMed]
- Pimentel, R.E.; Pieper, N.L.; Clark, W.H.; Franz, J.R. Muscle metabolic energy costs while modifying propulsive force generation during walking. Comput. Methods Biomech. Biomed. Eng. 2021, 24, 1552–1565. [Google Scholar] [CrossRef] [PubMed]
- Nuno, N.; Ahmed, A.M. Sagittal profile of the femoral condyles and its application to femorotibial contact analysis. J. Biomechical Eng. 2001, 123, 18–26. [Google Scholar] [CrossRef]
- Liu, F.; Kozanek, M.; Hosseini, A.; Van de Velde, S.K.; Gill, T.J.; Rubash, H.E.; Li, G. In vivo tibiofemoral cartilage deformation during the stance phase of gait. J. Biomech. 2010, 43, 658–665. [Google Scholar] [CrossRef]
- Blankevoort, L.; Kuiper, J.H.; Huiskes, R.; Grootenboer, H.J. Articular contact in a three-dimensional model of the knee. J. Biomech. 1991, 24, 1019–1031. [Google Scholar] [CrossRef] [PubMed]
- Shepherd, D.E.; Seedhom, B.B. The instantaneous’ compressive modulus of human articular cartilage in joints of the lower limb. Rheumatology 1999, 38, 124–132. [Google Scholar] [CrossRef]
- Danso, E.K.; Mäkelä, J.T.A.; Tanska, P.; Mononen, M.E.; Honkanen, J.T.J.; Jurvelin, J.S.; Korhonen, R.K. Characterization of site-specific biomechanical properties of human meniscus—Importance of collagen and fluid on mechanical nonlinearities. J. Biomech. 2015, 48, 1499–1507. [Google Scholar] [CrossRef]
- Blöcker, K.; Guermazi, A.; Wirth, W.; Benichou, O.; Kwoh, C.K.; Hunter, D.J.; Englund, M.; Resch, H.; Eckstein, F.; OAI investigators. Tibial coverage, meniscus position, size and damage in knees discordant for joint space narrowing–data from the Osteoarthritis Initiative. Osteoarthr. Cartil. 2013, 21, 419–427. [Google Scholar] [CrossRef]
- Henderson, C.E.; Higginson, J.S.; Barrance, P.J. Comparison of MRI-based estimates of articular cartilage contact area in the tibiofemoral joint. J. Biomech. Eng. 2011, 133, 014502. [Google Scholar] [CrossRef]
- DeFrate, L.E.; Sun, H.; Gill, T.J.; Rubash, H.E.; Li, G. In vivo tibiofemoral contact analysis using 3D MRI-based knee models. J. Biomech. 2004, 37, 1499–1504. [Google Scholar] [CrossRef]
- Weightman, B.O.; Freeman, M.A.R.; Swanson, S.A.V. Fatigue of articular cartilage. Nature 1973, 244, 303–304. [Google Scholar] [CrossRef] [PubMed]
- Johnson, W.; Stovitz, S.D.; Choh, A.C.; Czerwinski, S.A.; Towne, B.; Demerath, E.W. Patterns of linear growth and skeletal maturation from birth to 18 years of age in overweight young adults. Int. J. Obes. 2012, 36, 535–541. [Google Scholar] [CrossRef]
- Taylor, D. Fatigue of bone and bones: An analysis based on stressed volume. J. Orthop. Res. 1998, 16, 163–169. [Google Scholar] [CrossRef]
- Taylor, D.; Kuiper, J.H. The prediction of stress fractures using a ‘stressed volume’concept. J. Orthop. Res. 2001, 19, 919–926. [Google Scholar] [CrossRef] [PubMed]
- Taylor, D.; Casolari, E.; Bignardi, C. Predicting stress fractures using a probabilistic model of damage, repair and adaptation. J. Orthop. Res. 2004, 22, 487–494. [Google Scholar] [CrossRef]
- Sinclair, J.; Huang, G.; Taylor, P.J.; Chockalingam, N.; Fan, Y. Effects of Running in Minimal and Conventional Footwear on Medial Tibiofemoral Cartilage Failure Probability in Habitual and Non-Habitual Users. J. Clin. Med. 2022, 11, 7335. [Google Scholar] [CrossRef] [PubMed]
- Paluch, A.E.; Gabriel, K.P.; Fulton, J.E.; Lewis, C.E.; Schreiner, P.J.; Sternfeld, B.; Carnethon, M.R. Steps per day and all-cause mortality in middle-aged adults in the coronary artery risk development in young adults study. JAMA Netw. Open 2021, 4, e2124516. [Google Scholar] [CrossRef]
- Riemenschneider, P.E.; Rose, M.D.; Giordani, M.; McNary, S.M. Compressive fatigue and endurance of juvenile bovine articular cartilage explants. J. Biomech. 2019, 95, 109304. [Google Scholar] [CrossRef]
- Nakamura, N.; Horibe, S.; Toritsuka, Y.; Mitsuoka, T.; Natsuume, T.; Yoneda, K.; Shino, K. The location-specific healing response of damaged articular cartilage after ACL reconstruction: Short-term follow-up. Knee Surg. Sports Traumatol. Arthrosc. 2008, 16, 843–848. [Google Scholar] [CrossRef]
- Schielzeth, H.; Dingemanse, N.J.; Nakagawa, S.; Westneat, D.F.; Allegue, H.; Teplitsky, C.; Araya-Ajoy, Y.G. Robustness of linear mixed--effects models to violations of distributional assumptions. Methods Ecol. Evol. 2020, 11, 1141–1152. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1988. [Google Scholar]
- Ismailidis, P.; Egloff, C.; Hegglin, L.; Pagenstert, G.; Kernen, R.; Eckardt, A.; Nüesch, C. Kinematic changes in patients with severe knee osteoarthritis are a result of reduced walking speed rather than disease severity. Gait Posture 2020, 79, 256–261. [Google Scholar] [CrossRef]
- Rao, K. Understanding Elevated Metabolic Cost of Asymmetric Walking. Ph.D. Thesis, Johns Hopkins University, Baltimore, MD, USA, 2019. [Google Scholar]
- Bergmann, G.; Bender, A.; Graichen, F.; Dymke, J.; Rohlmann, A.; Trepczynski, A.; Kutzner, I. Standardized loads acting in knee implants. PLoS ONE 2014, 9, e86035. [Google Scholar] [CrossRef]
- Cho, H.J.; Chang, C.B.; Kim, K.W.; Park, J.H.; Yoo, J.H.; Koh, I.J.; Kim, T.K. Gender and prevalence of knee osteoarthritis types in elderly Koreans. J. Arthroplast. 2011, 26, 994–999. [Google Scholar] [CrossRef]
- Clément, J.; Toliopoulos, P.; Hagemeister, N.; Desmeules, F.; Fuentes, A.; Vendittoli, P.A. Healthy 3D knee kinematics during gait: Differences between women and men, and correlation with X-ray alignment. Gait Posture 2018, 64, 198–204. [Google Scholar] [CrossRef] [PubMed]
- Coaccioli, S.; Sarzi-Puttini, P.; Zis, P.; Rinonapoli, G.; Varrassi, G. Osteoarthritis: New insight on its pathophysiology. J. Clin. Med. 2022, 11, 6013. [Google Scholar] [CrossRef]
- Ouchi, N.; Parker, J.L.; Lugus, J.J.; Walsh, K. Adipokines in inflammation and metabolic disease. Nat. Rev. Immunol. 2011, 11, 85–97. [Google Scholar] [CrossRef]
- Caldwell, L.K.; Laubach, L.L.; Barrios, J.A. Effect of specific gait modifications on medial knee loading, metabolic cost and perception of task difficulty. Clin. Biomech. 2013, 28, 649–654. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).