Dispersal Kernel Type Highly Influences Projected Relationships for Plant Disease Epidemic Severity When Outbreak and At-Risk Populations Differ in Susceptibility
Abstract
1. Introduction
2. Materials and Methods
2.1. Wheat Stripe Rust
2.2. Wheat Stripe Rust Disease Spread Simulations
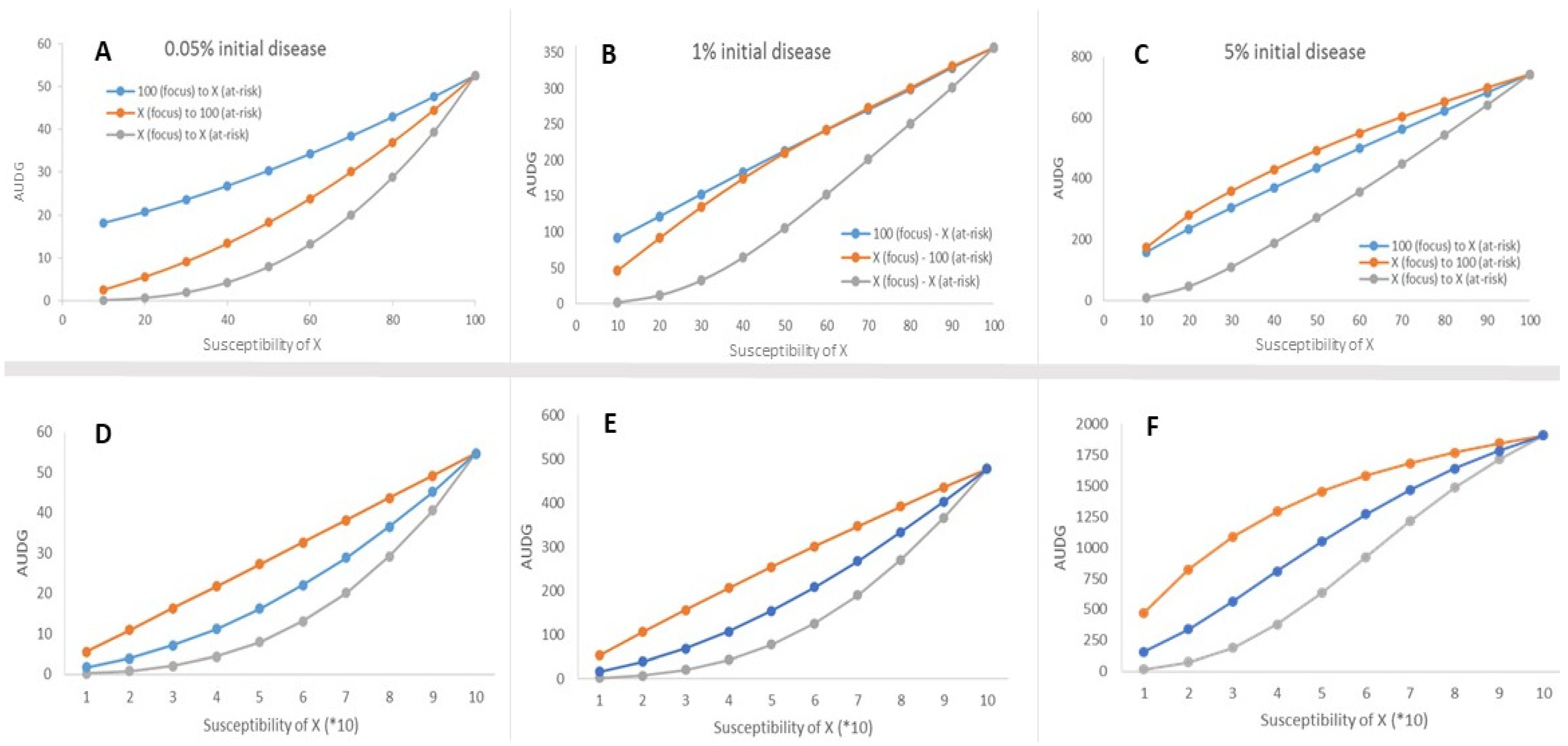
3. Results
4. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Keeling, M.J.; Woolhouse, M.E.J.; May, R.M.; Davies, G.; Grenfell, B.T. Modelling vaccination strategies against foot-and-mouth disease. Nature 2003, 421, 136–142. [Google Scholar] [CrossRef] [PubMed]
- Grimm, V.; Revilla, E.; Berger, U.; Jeltsch, F.; Mooij, W.M.; Railsback, S.F.; Thulke, H.H.; Weiner, J.; Wiegand, T.; DeAngelis, D.L. Pattern-oriented modeling of agent-based complex systems: Lessons from ecology. Science 2005, 310, 987–991. [Google Scholar] [CrossRef]
- Bzdok, D.; Altman, N.; Krzywinski, M. Statistics versus machine learning. Nat. Methods 2018, 15, 233–234. [Google Scholar] [CrossRef] [PubMed]
- Sardain, A.; Sardain, E.; Leung, B. Global forecasts of shipping traffic and biological invasions to 2050. Nat. Sustain. 2019, 2, 274–282. [Google Scholar] [CrossRef]
- Manzoor, S.A.; Griffiths, G.; Lukac, M. Land use and climate change interaction triggers contrasting trajectories of biological invasion. Ecol. Indic. 2021, 120, 106936. [Google Scholar] [CrossRef]
- Pili, A.N.; Tingley, R.; Chapple, D.G.; Schumaker, N.H. VirToad: Simulating the spatiotemporal population dynamics and management of a global invader. Landsc. Ecol. 2022, 37, 2273–2292. [Google Scholar] [CrossRef]
- Clobert, J.; Baguette, M.; Benton, T.G.; Bullock, J.M. Dispersal Ecology and Evolution; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Simberloff, D. The role of propagule pressure in biological invasions. Annu. Rev. Ecol. Evol. Syst. 2009, 40, 81–102. [Google Scholar] [CrossRef]
- Holle, B.V.; Simberloff, D. Ecological resistance to biological invasion overwhelmed by propagule pressure. Ecology 2005, 86, 3212–3218. [Google Scholar] [CrossRef]
- Severns, P.M.; Sackett, K.; Mundt, C.C. Outbreak propagule pressure influences the landscape spread of a wind-dispersed, epidemic-causing, plant pathogen. Landsc. Ecol. 2015, 30, 2111–2119. [Google Scholar] [CrossRef]
- Howard, P.L. Human adaptation to invasive species: A conceptual framework based on a case study metasynthesis. Ambio 2019, 48, 1401–1430. [Google Scholar] [CrossRef]
- Espinoza, B.; Castillo-Chavez, C.; Perrings, C. Mobility restrictions for the control of epidemics: When do they work? PLoS ONE 2020, 15, e0235731. [Google Scholar] [CrossRef]
- Lucardi, R.D.; Bellis, E.S.; Cunard, C.E.; Gravesande, J.K.; Hughes, S.C.; Whitehurst, L.E.; Worthy, S.J.; Burgess, K.S.; Marsico, T.D. Seeds attached to refrigerated shipping containers represent a substantial risk of nonnative plant species introduction and establishment. Sci. Rep. 2020, 10, 15017. [Google Scholar] [CrossRef] [PubMed]
- Kot, M.; Lewis, M.A.; van den Driessche, P. Dispersal data and the spread of invading organisms. Ecology 1996, 77, 2027–2042. [Google Scholar] [CrossRef]
- Frantzen, J.; Van den Bosch, F. Spread of organisms: Can travelling and dispersive waves be distinguished? Basic Appl. Ecol. 2000, 1, 83–92. [Google Scholar] [CrossRef]
- Ferrandino, F.J. Dispersive epidemic waves: I. Focus expansion within a linear planting. Phytopathology 1993, 83, 795–802. [Google Scholar] [CrossRef]
- Sackett, K.E.; Mundt, C.C. Primary disease gradients of wheat stripe rust in large field plots. Phytopathology 2005, 95, 983–991. [Google Scholar] [CrossRef]
- Mundt, C.C.; Sackett, K.E.; Wallace, L.D.; Cowger, C.; Dudley, J.P. Long-distance dispersal and accelerating waves of disease: Empirical relationships. Am. Nat. 2009, 173, 456–466. [Google Scholar] [CrossRef] [PubMed]
- Lindström, T.; Håkansson, N.; Wennergren, U. The shape of the spatial kernel and its implications for biological invasions in patchy environments. Proc. R. Soc. B Biol. Sci. 2011, 278, 1564–1571. [Google Scholar] [CrossRef] [PubMed]
- Byrne, A.W.; Quinn, J.L.; O’Keeffe, J.J.; Green, S.; Paddy Sleeman, D.; Wayne Martin, S.; Davenport, J. Large-scale movements in European badgers: Has the tail of the movement kernel been underestimated? J. Anim. Ecol. 2014, 83, 991–1001. [Google Scholar] [CrossRef]
- Sullivan, L.L.; Michalska-Smith, M.J.; Sperry, K.P.; Moeller, D.A.; Shaw, A.K. Consequences of ignoring dispersal variation in network models for landscape connectivity. Conserv. Biol. 2021, 35, 944–954. [Google Scholar] [CrossRef]
- Wan, A.; Zhao, Z.; Chen, X.; He, Z.; Jin, S. Wheat stripe rust epidemic and virulence of Puccinia striiformis f. sp. tritici in China in 2002. Plant Dis. 2004, 88, 896–904. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.M. Epidemiology and control of stripe rust on wheat. Can. J. Plant Pathol. 2005, 27, 314–337. [Google Scholar] [CrossRef]
- Wellings, C.R. Puccinia stiiformis in Australia: A review of the incursion, evolution and adaptation of stripe rust in the period 1979–2006. Aust. J. Agric. Res. 2007, 58, 567–575. [Google Scholar] [CrossRef]
- Milus, E.A.; Kristensen, K.; Hovmøller, M.S. Evidence for increased aggressiveness in a recent widespread strain of Puccinia striiformis f. sp. tritici causing stripe rust of wheat. Phytopathology 2009, 99, 89–94. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.N.; Chen, X.M. First report of Oregon grape (Mahonia aquifolium) as an alternate host for the wheat stripe rust pathogen (Puccinia striiformis f. sp. tritici) under artificial inoculation. Plant Dis. 2013, 97, 839. [Google Scholar] [CrossRef]
- Rodriguez-Algaba, J.; Walter, S.; Sørensen, C.K.; Hovmøller, M.S.; Justesen, A.F. Sexual structures and recombination of the wheat rust fungus Puccinia striiformis on Berberis vulgaris. Fungal Genet. Biol. 2014, 70, 77–78. [Google Scholar] [CrossRef]
- Zeng, S.M.; Luo, Y. Long-distance spread and interregional epidemics of wheat stripe rust in China. Plant Dis. 2006, 90, 980–988. [Google Scholar] [CrossRef]
- Maddison, A.C.; Manners, J.G. Lethal effects of artificial ultraviolet radiation on cereal rust uredospores. Trans. Br. Mycol. Soc. 1973, 60, 471–494. [Google Scholar] [CrossRef]
- Papastamati, K.; van den Bosch, F. The sensitivity of epidemic growth rate to weather variables, with an application to yellow rust on wheat. Phytopathology 2006, 97, 202–210. [Google Scholar] [CrossRef][Green Version]
- Farber, D.H.; Medlock, J.; Mundt, C.C. Local dispersal of Puccinia striiformis f. sp. tritici from isolated source lesions. Plant Pathol. 2017, 66, 28–37. [Google Scholar] [CrossRef]
- Farber, D.H.; De Leenheer, P.; Mundt, C.C. Dispersal kernels may be scalable: Implications from a plant pathogen. J. Biogeogr. 2019, 46, 2042–2055. [Google Scholar] [CrossRef] [PubMed]
- Brown, J.K.; Hovmøller, M.S. Aerial dispersal of pathogens on the global and continental scales and its impact on plant disease. Science 2002, 297, 537–541. [Google Scholar] [CrossRef] [PubMed]
- Carmona, M.; Sautua, F.; Pérez-Hérnandez, O.; Reis, M. Role of fungicide applications on the integrated management of wheat stripe rust. Front. Plant Sci. 2020, 11, 733. [Google Scholar] [CrossRef]
- Figueroa, M.; Hammond-Kosack, K.E.; Solomon, P.S. A review of wheat diseases-a field perspective. Mol. Plant Pathol. 2018, 19, 1523–1536. [Google Scholar] [CrossRef]
- Cook, N.M.; Chang, S.; Woodman, T.L.; Warren, R.; Oliver, R.P.; Saunders, D.G. High frequency of fungicide resistance-associated mutations in the wheat yellow rust pathogen Puccinia striiformis f. sp. tritici. Pest Manag. Sci. 2021, 77, 3358–3371. [Google Scholar] [CrossRef]
- Hawkins, N.J.; Fraaije, B.A. Fitness penalties in the evolution of fungicide resistance. Annu. Rev. Phytopathol. 2018, 56, 339–360. [Google Scholar] [CrossRef]
- Sykes, E.M.; Sackett, K.E.; Severns, P.M.; Mundt, C.C. Sensitivity variation and cross-resistance of Zymoseptoria tritici to azole fungicides in North America. Eur. J. Plant Pathol. 2018, 151, 269–274. [Google Scholar] [CrossRef]
- McDonald, M.C.; Renkin, M.; Spackman, M.; Orchard, B.; Croll, D.; Solomon, P.S.; Milgate, A. Rapid parallel evolution of azole fungicide resistance in Australian populations of the wheat pathogen Zymoseptoria tritici. Appl. Environ. Microbiol. 2019, 85, e01908-18. [Google Scholar] [CrossRef]
- Garnault, M.; Duplaix, C.; Leroux, P.; Couleaud, G.; David, O.; Walker, A.S.; Carpentier, F. Large-scale study validates that regional fungicide applications are major determinants of resistance evolution in the wheat pathogen Zymoseptoria tritici in France. New Phytol. 2021, 229, 3508–3521. [Google Scholar] [CrossRef]
- Leroux, P.; Gredt, M.; Remuson, F.; Micoud, A.; Walker, A.S. Fungicide resistance status in French populations of the wheat eyespot fungi Oculimacula acuformis and Oculimacula yallundae. Pest Manag. Sci. 2013, 69, 15–26. [Google Scholar] [CrossRef]
- Castroagudín, V.L.; Ceresini, P.C.; de Oliveira, S.C.; Reges, J.T.; Maciel, J.L.; Bonato, A.L.; McDonald, B.A. Resistance to QoI fungicides is widespread in Brazilian populations of the wheat blast pathogen Magnaporthe oryzae. Phytopathology 2015, 105, 284–294. [Google Scholar] [CrossRef] [PubMed]
- Mundt, C.C. Pyramiding for resistance durability: Theory and practice. Phytopatology 2018, 108, 792–802. [Google Scholar] [CrossRef] [PubMed]
- Kampmeijer, P.; Zadocks, J.C. EPIMUL, a Simulator of Foci and Epidemics in Mixtures of Resistant and Susceptible Plants, Mosaics and Multilines; Centre for Agricultural Publishing and Documentation: Wageningen, The Netherlands, 1977. [Google Scholar]
- Severns, P.M.; Mundt, C.C. Delays in epidemic outbreak control cost disproportionately large treatment footprints to offset. Pathogens 2022, 11, 393. [Google Scholar] [CrossRef] [PubMed]
- Diekmann, O.; Heesterbeek, J.A.P. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Severns, P.M.; Estep, L.K.; Sackett, K.E.; Mundt, C.C. Degree of host susceptibility in the initial disease outbreak influences subsequent epidemic spread. J. Appl. Ecol. 2014, 51, 1622–1630. [Google Scholar] [CrossRef]
- Madden, L.V.; Hughes, G.; van den Bosch, F. The Study of Plant Disease Epidemics; American Phytopathological Society: St. Paul, MN, USA, 2007. [Google Scholar]
- Aylor, D.E. Aerial Dispersal of Pollen and Spores; APS Press: St. Paul, MN, USA, 2017; 418p. [Google Scholar]
- Neubert, M.G.; Parker, I.M. Projecting rates of spread for invasive species. Risk Anal. 2004, 24, 817–831. [Google Scholar] [CrossRef]
- Srivastava, V.; Lafond, V.; Griess, V.C. Species distribution models (SDM): Applications, benefits and challenges in invasive species management. CABI Rev. 2019, 24, 7. [Google Scholar] [CrossRef]
- Atallah, S.S.; Gómez, M.I.; Conrad, J.M.; Nyrop, J.P. A plant-level, spatial, bioeconomic model of plant disease diffusion and control: Grapevine leafroll disease. Am. J. Agric. Econ. 2015, 97, 199–218. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. The invasion, persistence and spread of infectious diseases within animal and plant communities. Phil. Trans. R. Soc. Lond. B Biol. Sci. 1986, 314, 533–570. [Google Scholar] [CrossRef]
- Shearer, F.M.; Moyes, C.L.; Pigott, D.M.; Brady, O.J.; Marinho, F.; Deshpande, A.; Longbottom, J.; Browne, A.J.; Kraemer, M.U.; O’Reilly, K.M.; et al. Global yellow fever vaccination coverage from 1970 to 2016: An adjusted retrospective analysis. Lancet Infect. Dis. 2017, 17, 1209–1217. [Google Scholar] [CrossRef]
- Ogden, N.H.; Wilson, J.R.; Richardson, D.M.; Hui, C.; Davies, S.J.; Kumschick, S.; Le Roux, J.J.; Measey, J.; Saul, W.C.; Pulliam, J.R. Emerging infectious diseases and biological invasions: A call for a One Health collaboration in science and management. R. Soc. Open Sci. 2019, 6, 181577. [Google Scholar] [CrossRef]
- Zadoks, J.C.; van den Bosch, F. On the spread of plant disease: A theory on foci. Annu. Rev. Phytopathol. 1994, 32, 503–521. [Google Scholar] [CrossRef] [PubMed]
- Isard, S.A.; Chamecki, M. A physically based theoretical model of spore deposition for predicting spread of plant diseases. Phytopathology 2016, 106, 244–253. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Severns, P.M. Dispersal Kernel Type Highly Influences Projected Relationships for Plant Disease Epidemic Severity When Outbreak and At-Risk Populations Differ in Susceptibility. Life 2022, 12, 1727. https://doi.org/10.3390/life12111727
Severns PM. Dispersal Kernel Type Highly Influences Projected Relationships for Plant Disease Epidemic Severity When Outbreak and At-Risk Populations Differ in Susceptibility. Life. 2022; 12(11):1727. https://doi.org/10.3390/life12111727
Chicago/Turabian StyleSeverns, Paul M. 2022. "Dispersal Kernel Type Highly Influences Projected Relationships for Plant Disease Epidemic Severity When Outbreak and At-Risk Populations Differ in Susceptibility" Life 12, no. 11: 1727. https://doi.org/10.3390/life12111727
APA StyleSeverns, P. M. (2022). Dispersal Kernel Type Highly Influences Projected Relationships for Plant Disease Epidemic Severity When Outbreak and At-Risk Populations Differ in Susceptibility. Life, 12(11), 1727. https://doi.org/10.3390/life12111727






