A Theoretical Approach for the Electrochemical Characterization of Ciliary Epithelium
Abstract
1. Introduction
- the flow of ions through ion transporters and the combined effect of channels and pumps (membrane scale level);
- the overall contribution to AH production by a single cell of the ciliary epithelium (cellular scale level);
- the hydrostatic and oncotic pressure effects (eye scale level).
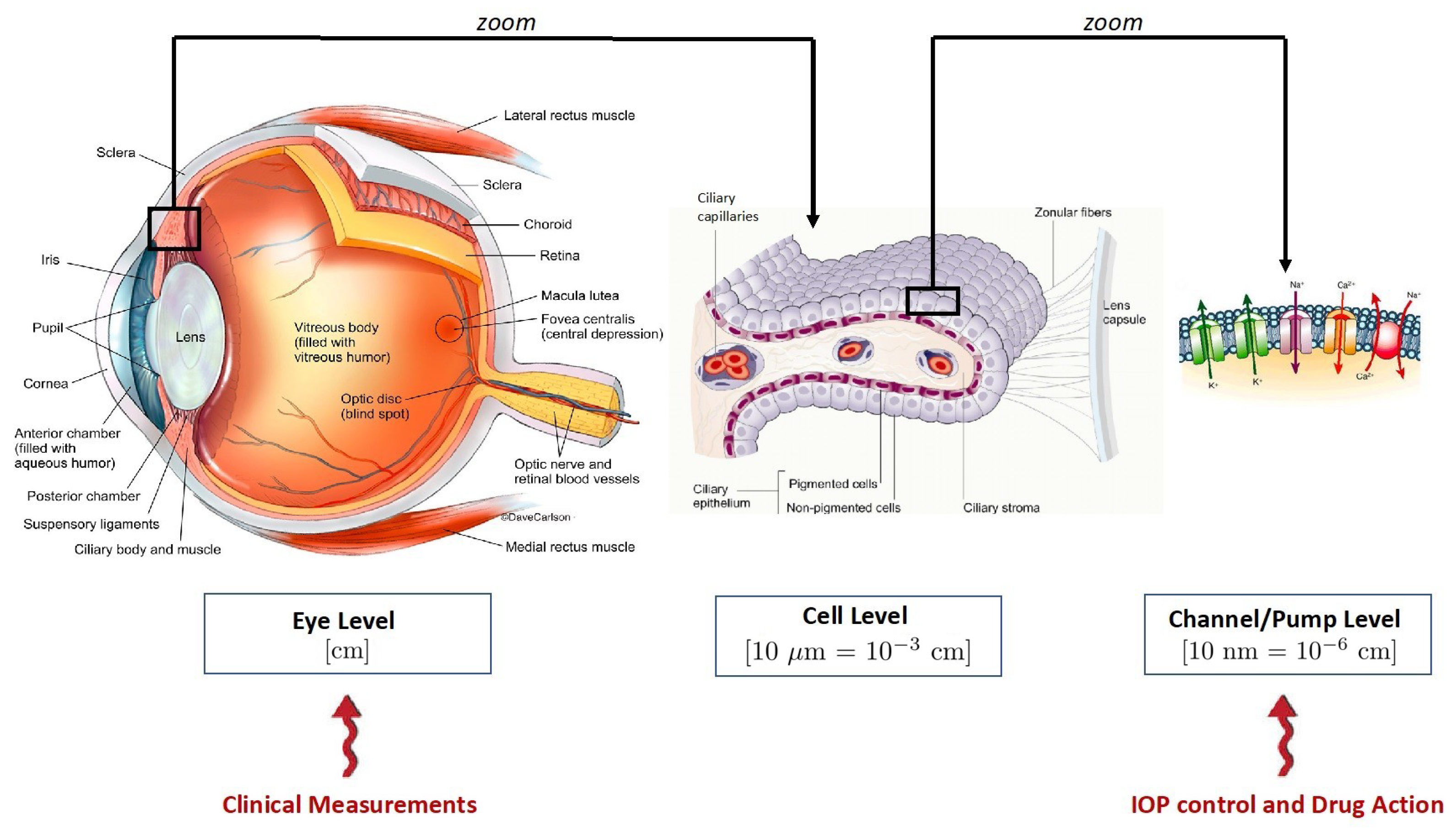
1.1. The Multiscale Architecture of Aqueous Humor Production
- (a)
- the macroscopic scale. This is the level of observation corresponding to the eye globe and its characteristic length is in the order of centimeters;
- (b)
- the cellular scale. This is the level of observation corresponding to the PEC/NPEC couplet and its characteristic length is in the order of tens of microns (i.e., );
- (c)
- the membrane scale. This is the level of observation corresponding to the membrane of the NPEC and its characteristic length is in the order of tens of nanometers (i.e., ).
1.2. Ciliary Epithelium and Aqueous Humor Production
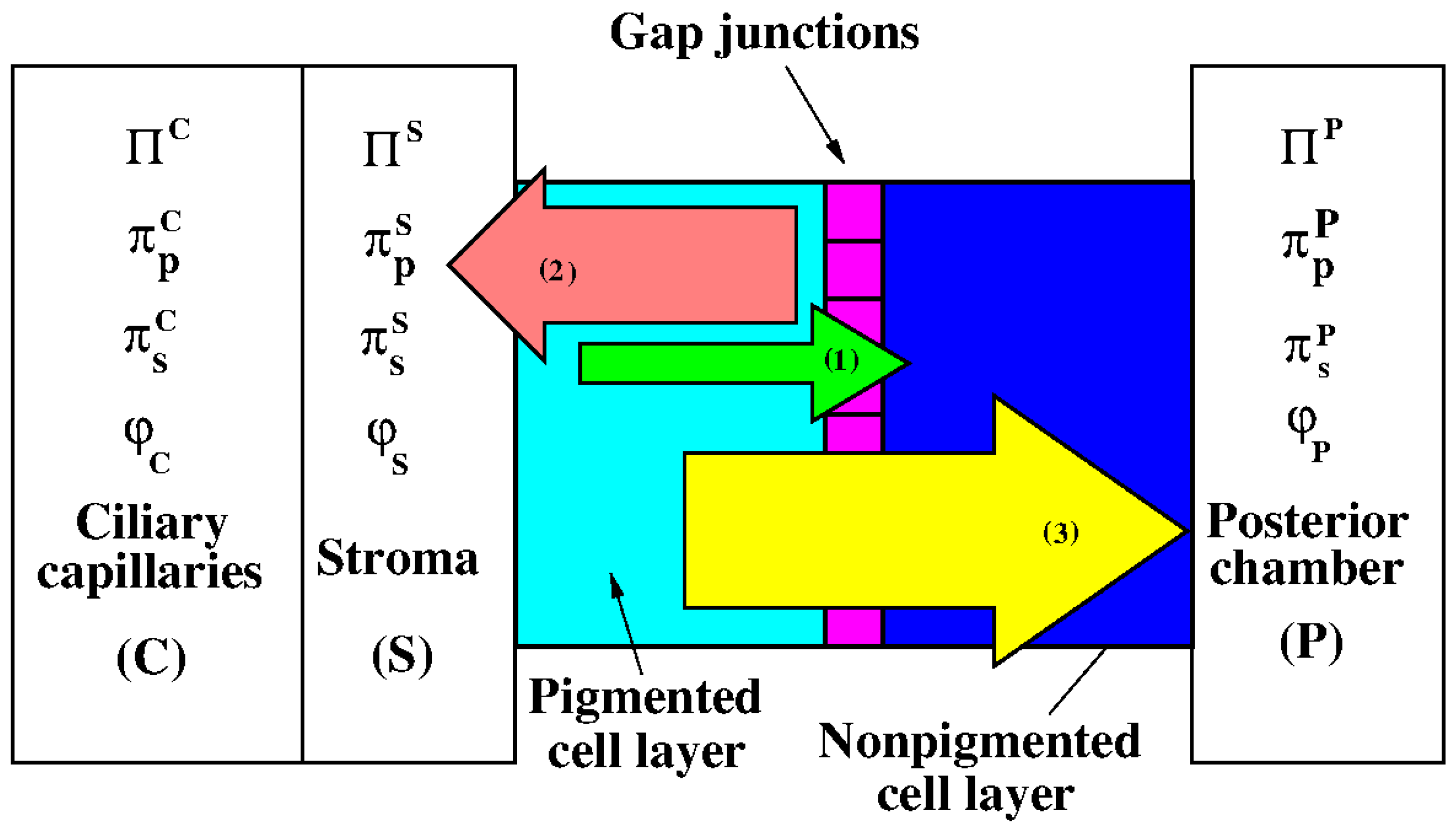
- Convective delivery of water, ions, proteins, and metabolic fuel by the ciliary circulation;
- Ultrafiltration of water and ions (driven by oncotic and hydrostatic pressure gradients) and diffusion of larger molecules from the capillaries into the stroma (driven by concentration gradients);
- Active ionic secretion into the basolateral space between the NPE cells which promotes water flow down the resulting osmotic gradient.
- : volumetric flow rate of aqueous humor due to the difference between the hydrostatic pressure in the ciliary capillaries and the hydrostatic pressure in the posterior chamber assumed to be equal to the intraocular pressure (IOP)
- : volumetric flow rate of aqueous humor due to the difference between the oncotic pressure in the ciliary capillaries and the oncotic pressure in the posterior chamber
1.3. Active Secretion of Aqueous Humor
- Proteins are practically absent inside the CE cells. As a consequence, HCO is the main responsible for maintaining the pH of the cells within physiological values (between 7.21 and 7.4, see [27]);
- The Na/K-ATPase pump (shortly, Na/K pump) is essential to set the cell off its electrochemical balance and create a driving force for the secretion of AH. Studies show that inhibiting this pump results in blocking AH secretion (see [28])
1.4. Connecting AH Flow, Ocular Physiology, and Pathology: The Role of Mathematical Modeling
- A1
- verify that the value of the predicted transepithelial potential difference is physiologically correct;
- A2
- verify that the values of the predicted intracellular ion concentrations are physiologically correct;
- A3
- verify that the value of the predicted NPE transmembrane potential difference is physiologically correct.
2. Results
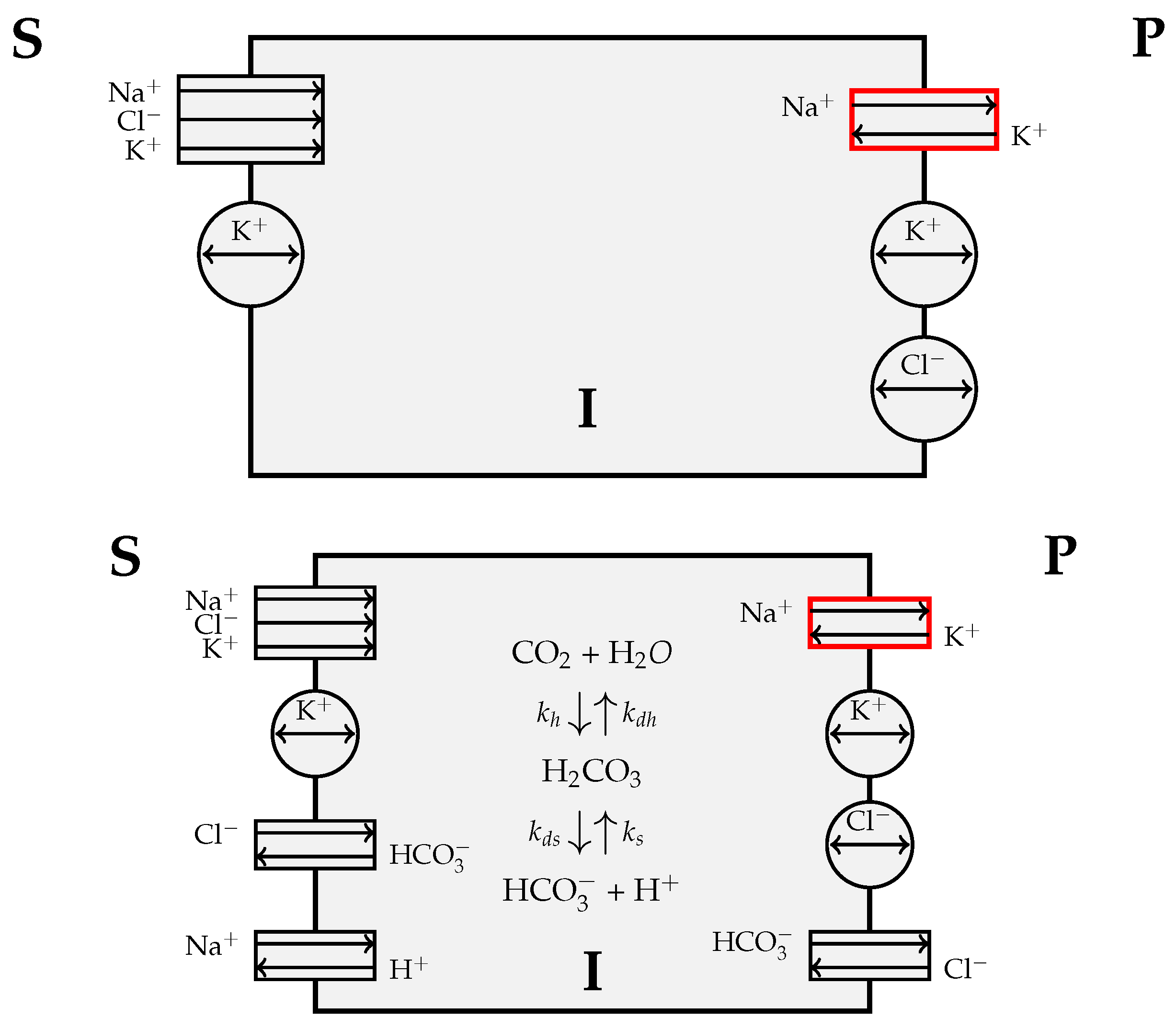
2.1. Model 0
- Na-K-Cl symporter;
- K uniporter.
- Na-K pump;
- K uniporter;
- Cl uniporter.
2.2. Model 1
- Na-K-Cl symporter;
- K uniporter;
- Cl-HCO antiporter;
- Na-H antiporter.
- Na-K pump;
- K uniporter;
- Cl uniporter;
- Cl-HCO antiporter.
2.3. Verification of Model Predictions against Experimental Data
- transepithelial potential difference (in mV);
- intracellular concentrations of Na, K, and Cl (in mM);
- NPE transmembrane potential difference (in mV).
2.3.1. Results for Model 0
2.3.2. Results for Model 1
3. Discussion
3.1. Discussion of the Predictions of Model 0
3.2. Discussion of the Predictions of Model 1
3.3. Comparison between Model 0 and Model 1
- the configuration of ion exchangers and the biochemical reactions mediated by the carbonic anhydrase enzyme strongly influence the prediction of intracellular ion concentrations and transmembrane potentials;
- Model 1 provides better estimates of intracellular concentrations than predicted by Model 0;
- the transmembrane potentials estimated by Models 0 and 1 are both within the same order of magnitude as those measured experimentally, but not exactly within the experimental range.
4. Materials and Methods
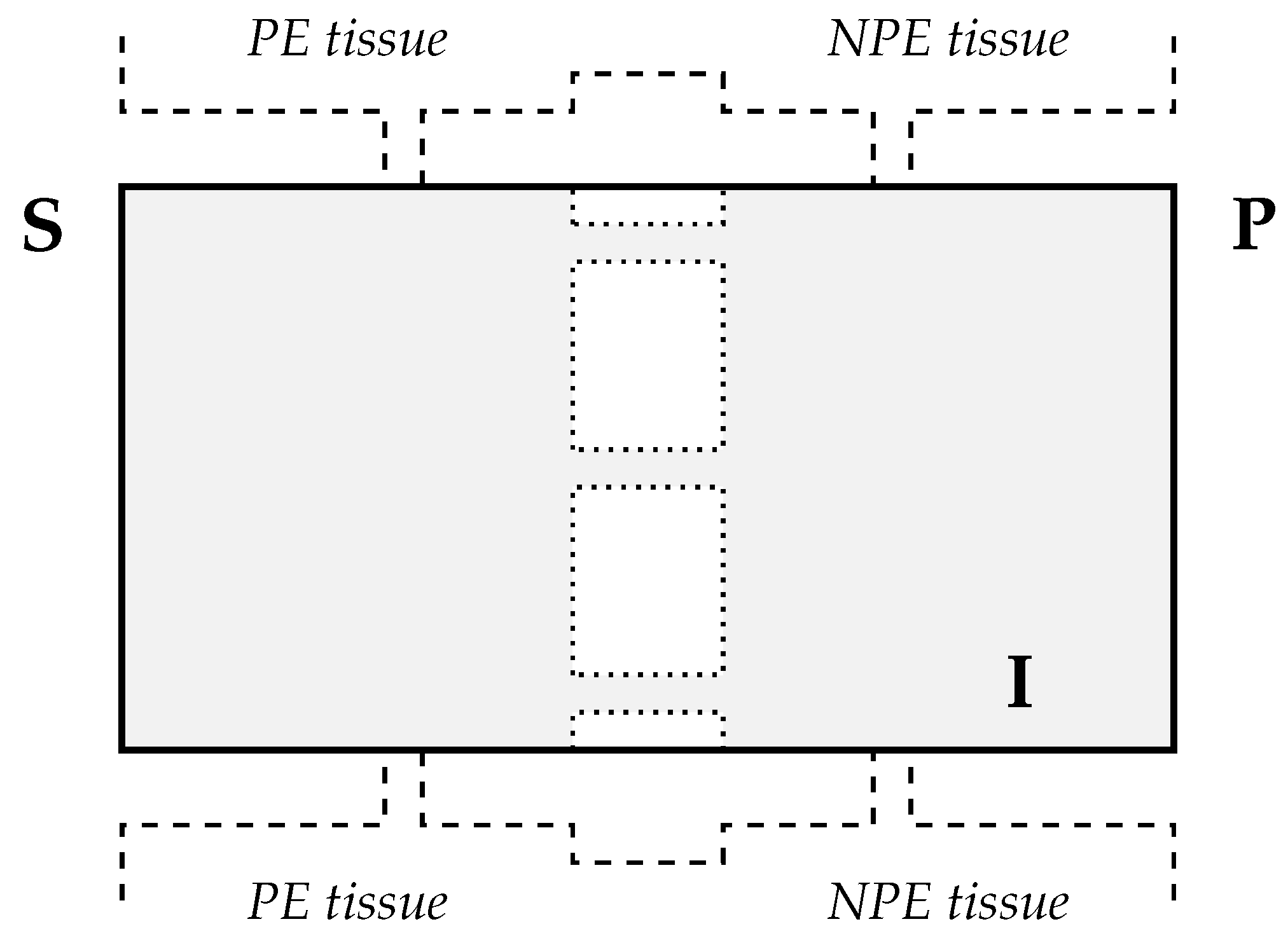
4.1. Model Assumptions
- each pair of neighboring PE and NPE cells are considered as a single unit (referred to as the PE–NPE cell couplet) rather than two distinct compartments;
- ion transporters have uniform spatial distribution along the CE;
- the unit has a fixed volume;
- gap junctions within PE and NPE cells are neglected.
4.2. Mathematical Model
- electric potential at the S side and in the I region;
- ion concentrations in the I region,
- the electric potentials and ;
- the ion concentrations , , and .
- the electric potentials and ;
- the ion concentrations , , , , and ;
- the concentrations and .
4.3. Numerical Solution and the Issue of Electroneutrality
4.4. Models for Ion Fluxes
4.4.1. Uniporters
4.4.2. Antiporters and Symporters
4.4.3. Pumps
4.5. Model for Water Flux
5. Conclusions and Perspectives
- ion exchanger configuration and intracellular biochemical reactions strongly influence the model prediction of intracellular ion concentrations and transmembrane potentials;
- one of the two configurations predicts sodium and potassium intracellular concentrations and transmembrane potential much more accurately than the other;
- predicted transmembrane potentials are within the same order of magnitude as those measured experimentally, but not exactly within the experimental range.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CE | Ciliary Epithelium |
| AH | Aqueous Humor |
| IOP | Intraocular Pressure |
| PE | Pigmented Epithelial Cells |
| NPE | Nonpigmented Epithelial Cells |
| S | Stroma |
| P | Posterior Chamber |
| I | Intracellular region of cell couplet |
| cAMP | Cyclic adenosine monophosphate |
References
- Ocular Fluid Dynamics. Anatomy, Physiology, Imaging Techniques, and Mathematical Modeling; Modeling and Simulation in Science, Engineering, and Technology; Springer-Birkhauser: New York, NY, USA, 2019.
- Sala, L.; Prud’homme, C.; Prada, D.; Salerni, F.; Trophime, C.; Chabannes, V.; Szopos, M.; Repetto, R.; Bertoluzza, S.; Sacco, R.; et al. Patient-specific virtual simulator of tissue perfusion in the lamina cribrosa. Investig. Ophthalmol. Vis. Sci. 2017, 58, 727. [Google Scholar]
- Sala, L.; Prud’homme, C.; Guidoboni, G.; Szopos, M. Towards a full model for ocular biomechanics, fluid dynamics, and hemodynamics. J. Model. Ophtalmol. 2018, 2, 7–13. [Google Scholar]
- Sala, L.; Prud’homme, C.; Guidoboni, G.; Szopos, M. Ocular mathematical virtual simulator: A hemodynamical and biomechanical study towards clinical applications. J. Coupled Syst. Multiscale Dyn. 2018, 6, 241–247. [Google Scholar] [CrossRef]
- Moses, R.A. Intraocular pressure. In Adler’s Physiology of the Eye: Clinical Application; Moses, R.A., Hart, W.M., Eds.; C. V. Mosby Co.: St Louis, MO, USA, 1987; pp. 223–245. [Google Scholar]
- Kiel, J.W. Physiology of the intraocular pressure. In Pathophysiology of the Eye; Feher, J., Ed.; Number 4 in Glaucoma; Akademiai Kiadò: Budapest, Hungary, 1998; pp. 79–107. [Google Scholar]
- Guidoboni, G.; Harris, A.; Arciero, J.C.; Siesky, B.A.; Amireskandari, A.; Gerber, A.L.; Huck, A.H.; Kim, N.J.; Cassani, S.; Carichino, L. Mathematical modeling approaches in the study of glaucoma disparities among people of african and european descents. J. Coupled Syst. Multiscale Dyn. 2013, 1, 1–21. [Google Scholar] [CrossRef]
- Wojcik-Gryciuk, A.; Skup, M.; Waleszczyk, W. Glaucoma-state of the art and perspectives on treatment. Restor. Neurol Neurosci. 2015, 34, 107–123. [Google Scholar] [CrossRef]
- Szopos, M.; Cassani, S.; Guidoboni, G.; Prud’homme, C.; Sacco, R.; Siesky, B.; Harris, A. Mathematical modeling of aqueous humor flow and intraocular pressure under uncertainty: Towards individualized glaucoma management. J. Model. Ophthalmol. 2016, 2, 29–39. [Google Scholar]
- Kiel, J.W. Physiology of the intraocular pressure. In Pathophysiology of the Eye, 4. Glaucoma; Akademiai Kiado: Budapest, Hungary, 1998; Chapter III. [Google Scholar]
- Fonseca, B.; Martinez-Aguila, A.; de Lara, M.J.P.; Miras-Portugal, M.T.; Gomez-Villafuertes, R.; Pintor, J. Changes in P2Y Purinergic Receptor Expression in the Ciliary Body in a Murine Model of Glaucoma. Front. Pharmacol. 2017, 8, 719. [Google Scholar] [CrossRef]
- Shahidullah, M.; Wilson, W.S. Atriopeptin, sodium azide and cyclic GMP reduce secretion of aqueous humour and inhibit intracellular calcium release in bovine cultured ciliary epithelium. Br. J. Pharmacol. 1999, 127, 1438–1446. [Google Scholar] [CrossRef]
- Carlson Stock Art: Life Science Illustration and More. Available online: https://www.carlsonstockart.com/ (accessed on 23 January 2020).
- Vaajanen, A. Expression and Function of Angiotensins in the Regulation of Intraocular Pressure—An Experimental Study. Ph.D. Thesis, University of Helsinki, Helsinki, Finland, 2009. [Google Scholar]
- Marbán, E. Cardiac channelopathies. Nature 2002, 415, 213–218. [Google Scholar] [CrossRef]
- Mauri, A.G.; Sala, L.; Airoldi, P.; Novielli, G.; Sacco, R.; Cassani, S.; Guidoboni, G.; Siesky, B.A.; Harris, A. Electro-fluid dynamics of aqueous humor production: simulations and new directions. J. Model. Ophthalmol. 2016, 2, 48–58. [Google Scholar]
- Bonifazi, G. Electrochemical and Fluid Dynamical Characterization of Ciliary Epithelium Physiology: A Multiscale Approach. Master’s Thesis, Politecnico di Milano, Milan, Italy, 2018. [Google Scholar]
- Sala, L.; Mauri, A.G.; Sacco, R.; Messenio, D.; Guidoboni, G.; Harris, A. A Theoretical Study of Aqueous Humor Secretion Based on a Continuum Model Coupling Electrochemical and Fluid-Dynamical Transmembrane Mechanisms. Commun. Appl. Math. Comput. Sci. 2019, 14, 65–103. [Google Scholar] [CrossRef]
- Kiel, J.; Hollingsworth, M.; Rao, R.; Chen, M.; Reitsamer, H. Ciliary blood flow and aqueous humor production. Progr. Retin. Eye Res. 2011, 30, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Brubaker, R.F. Flow of aqueous humor in humans [The Friedenwald Lecture]. Investig. Ophthalmol. Vis. Sci. 1991, 32, 3145–3166. [Google Scholar]
- Civan, M. The Eye’s Aqueous Humor; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- McLaughlin, C.W.; Zellhuber-McMillan, S.; Macknight, A.D.C.; Civan, M.M. Electron microprobe analysis of ouabain-exposed ciliary epithelium: PE-NPE cell couplets form the functional units. Am. J. Physiol.-Cell Physiol. 2004, 286, C1376–C1389. [Google Scholar] [CrossRef] [PubMed]
- McLaughlin, C.W.; Zellhuber-McMillan, S.; Peart, D.; Purves, R.D.; Macknight, A.D.C.; Civan, M.M. Regional Differences in Ciliary Epithelial Cell Transport Properties. J. Membr. Biol. 2001, 182, 213–222. [Google Scholar] [CrossRef] [PubMed]
- Shahidullah, M.; Al-Malki, W.H.; Delamere, N.A. Mechanism of Aqueous Humor Secretion, Its Regulation and Relevance to Glaucoma. In Glaucoma; Rumelt, S., Ed.; IntechOpen: Rijeka, Croatia, 2011; Chapter 1. [Google Scholar] [CrossRef]
- Sacco, R.; Guidoboni, G.; Mauri, A.G. A Comprehensive Physically Based Approach to Modeling in Bioengineering and Life Sciences, 1st ed.; Elsevier Inc.: Cambridge, MA, USA, 2019. [Google Scholar]
- Civan, M.M.; Macknight, A.D. The ins and outs of aqueous humour secretion. Exp. Eye Res. 2004, 78, 625–631. [Google Scholar] [CrossRef]
- To, C.H.; Kong, C.W.; Chan, C.Y.; Shahidullah, M.; Do, C.W. The mechanism of aqueous humour formation. Clin. Exp. Optom. 2002, 85, 335–349. [Google Scholar]
- Bonting, S.L.; Becker, B. Studies on Sodium-Potassium Activated Adenosinetriphosphatase: XIV. Inhibition of Enzyme Activity and Aqueous Humor flow in the Rabbit Eye after Intravitreal Injection of Ouabain. Investig. Ophthalmol. Vis. Sci. 1964, 3, 523–533. [Google Scholar]
- Wiederholt, M.; Zadunaisky, J. Membrane potentials and intracellular chloride activity in the ciliary body of the shark. Pflugers Arch. 1986, 407 (Suppl. 2), S112–S115. [Google Scholar] [CrossRef]
- Lindskog, S. Structure and mechanism of carbonic anhydrase. Pharmacol. Ther. 1997, 74, 1–20. [Google Scholar] [CrossRef]
- Reale, E. Freeze-fracture analysis of junctional complexes in human ciliary epithelia. Albrecht Von Graefes Arch. Klin. Exp. Ophthalmol. 1975, 195, 1–16. [Google Scholar] [CrossRef]
- Helbig, H.; Korbmacher, C.; Wohlfarth, J.; Coca-Prados, M.; Wiederholt, M. Electrical membrane properties of a cell clone derived from human nonpigmented ciliary epithelium. Investig. Ophthalmol. Vis. Sci. 1989, 30, 882–889. [Google Scholar]
- Han, Z.B.; Yang, J.B.; Wax, M.B.; Patil, R.V. Molecular identification of functional water channel protein in cultured human nonpigmented ciliary epithelial cells. Curr. Eye Res. 2000, 20, 242–247. [Google Scholar] [CrossRef]
- Crook, R.B.; Riese, K. Beta-adrenergic stimulation of Na+, K+, Cl− cotransport in fetal nonpigmented ciliary epithelial cells. Investig. Ophthalmol. Vis. Sci. 1996, 37, 1047–1057. [Google Scholar]
- Krueger, B.; Schloetzer-Schrehardt, U.; Haerteis, S.; Zenkel, M.; Chankiewitz, V.E.; Amann, K.U.; Kruse, F.E.; Korbmacher, C. Four subunits (αβγδ) of the epithelial sodium channel (ENaC) are expressed in the human eye in various locations. Investig. Ophthalmol. Vis. Sci. 2012, 53, 596–604. [Google Scholar] [CrossRef] [PubMed]
- Helbig, H.; Korbmacher, C.; Kuhner, D.; Berweck, S.; Wiederholt, M. Characterization of Cl−/HCO3− exchange in cultured bovine pigmented ciliary epithelium. Exp. Eye Res. 1988, 47, 515–523. [Google Scholar] [CrossRef]
- Edelman, J.L.; Loo, D.D.; Sachs, G. Characterization of potassium and chloride channels in the basolateral membrane of bovine nonpigmented ciliary epithelial cells. Investig. Ophthalmol. Vis. Sci. 1995, 36, 2706–2716. [Google Scholar]
- Helbig, H.; Korbmacher, C.; Nawrath, M.; Erb, C.; Wiederholt, M. Sodium bicarbonate cotransport in cultured pigmented ciliary epithelial cells. Curr. Eye Res. 1989, 8, 595–598. [Google Scholar] [CrossRef]
- Helbig, H.; Korbmacher, C.; Stumpff, F.; Coca-Prados, M.; Wiederholt, M. Na+/H+ exchange regulates intracellular pH in a cell clone derived from bovine pigmented ciliary epithelium. J. Cell Physiol. 1988, 137, 384–389. [Google Scholar] [CrossRef]
- Ghosh, S.; Freitag, A.C.; Martin-Vasallo, P.; Coca-Prados, M. Cellular distribution and differential gene expression of the three alpha subunit isoforms of the Na,K-ATPase in the ocular ciliary epithelium. J. Biol. Chem. 1990, 265, 2935–2940. [Google Scholar]
- Ghosh, S.; Hernando, N.; Martin-Alonso, J.M.; Martin-Vasallo, P.; Coca-Prados, M. Expression of multiple Na+,K+-ATPase genes reveals a gradient of isoforms along the nonpigmented ciliary epithelium: functional implications in aqueous humor secretion. J. Cell Physiol. 1991, 149, 184–194. [Google Scholar] [CrossRef] [PubMed]
- Dunn, J.J.; Lytle, C.; Crook, R.B. Immunolocalization of the Na-K-Cl cotransporter in bovine ciliary epithelium. Investig. Ophthalmol. Vis. Sci. 2001, 42, 343–353. [Google Scholar]
- Counillon, L.; Touret, N.; Bidet, M.; Peterson-Yantorno, K.; Coca-Prados, M.; Stuart-Tilley, A.; Wilhelm, S.; Alper, S.L.; Civan, M.M. Na+/H+ and Cl−/HCO3−-antiporters of bovine pigmented ciliary epithelial cells. Pflugers Arch. 2000, 440, 667–678. [Google Scholar] [CrossRef] [PubMed]
- Shahidullah, M.; Mandal, A.; Delamere, N.A. Responses of sodium-hydrogen exchange to nitric oxide in porcine cultured nonpigmented ciliary epithelium. Investig. Ophthalmol. Vis. Sci. 2009, 50, 5851–5858. [Google Scholar] [CrossRef][Green Version]
- Kong, C.W.; Li, K.K.; To, C.H. Chloride secretion by porcine ciliary epithelium: New insight into species similarities and differences in aqueous humor formation. Investig. Ophthalmol. Vis. Sci. 2006, 47, 5428–5436. [Google Scholar] [CrossRef]
- Takahira, M.; Sakurai, M.; Sakurada, N.; Sugiyama, K. Swelling-activated potassium channel in porcine pigmented ciliary epithelial cells. Investig. Ophthalmol. Vis. Sci. 2011, 52, 5928–5932. [Google Scholar] [CrossRef]
- Shahidullah, M.; Delamere, N.A. Connexins form functional hemichannels in porcine ciliary epithelium. Exp. Eye Res. 2014, 118, 20–29. [Google Scholar] [CrossRef]
- Shahidullah, M.; To, C.H.; Pelis, R.M.; Delamere, N.A. Studies on bicarbonate transporters and carbonic anhydrase in porcine nonpigmented ciliary epithelium. Investig. Ophthalmol. Vis. Sci. 2009, 50, 1791–1800. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Watanabe, T.; Hirakata, A.; Hida, T. Localization and ontogeny of aquaporin-1 and -4 expression in iris and ciliary epithelial cells in rats. Cell Tissue Res. 2006, 325, 101–109. [Google Scholar] [CrossRef]
- Hu, R.G.; Lim, J.C.; Kalloniatis, M.; Donaldson, P.J. Cellular localization of glutamate and glutamine metabolism and transport pathways in the rat ciliary epithelium. Investig. Ophthalmol. Vis. Sci. 2011, 52, 3345–3353. [Google Scholar] [CrossRef][Green Version]
- Jo, A.O.; Lakk, M.; Frye, A.M.; Phuong, T.T.; Redmon, S.N.; Roberts, R.; Berkowitz, B.A.; Yarishkin, O.; Krizaj, D. Differential volume regulation and calcium signaling in two ciliary body cell types is subserved by TRPV4 channels. Proc. Natl. Acad. Sci. USA 2016, 113, 3885–3890. [Google Scholar] [CrossRef]
- Burgos, J.; Villanueva, S.; Ojeda, M.; Cornejo, I.; Cid, L.P.; Sepulveda, F.V. Kir7.1 inwardly rectifying K+ channel is expressed in ciliary body non pigment epithelial cells and might contribute to intraocular pressure regulation. Exp. Eye Res. 2019, 186, 107723. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.; Delamere, N.A. Protein kinase C inhibits Na(+)-K(+)-2Cl− cotransporter activity in cultured rabbit nonpigmented ciliary epithelium. Am. J. Physiol. 1994, 267, C1553–C1560. [Google Scholar] [CrossRef] [PubMed]
- Katz, A.; Tal, D.M.; Heller, D.; Habeck, M.; Ben Zeev, E.; Rabah, B.; Bar Kana, Y.; Marcovich, A.L.; Karlish, S.J.D. Digoxin derivatives with selectivity for the 3b123b23 isoform of Na,K-ATPase potently reduce intraocular pressure. Proc. Natl. Acad. Sci. USA 2015, 112, 13723–13728. [Google Scholar] [CrossRef] [PubMed]
- Li, S.K.L.; Shan, S.W.; Li, H.L.; Cheng, A.K.W.; Pan, F.; Yip, S.P.; Civan, M.M.; To, C.H.; Do, C.W. Characterization and Regulation of Gap Junctions in Porcine Ciliary Epithelium. Investig. Ophthalmol. Vis. Sci. 2018, 59, 3461–3468. [Google Scholar] [CrossRef] [PubMed]
- Katz, A.; Tal, D.M.; Heller, D.; Haviv, H.; Rabah, B.; Barkana, Y.; Marcovich, A.L.; Karlish, S.J.D. Digoxin derivatives with enhanced selectivity for the α2 isoform of Na,K-ATPase: Effects on intraocular pressure in rabbits. J. Biol. Chem. 2014, 289, 21153–21162. [Google Scholar] [CrossRef]
- Do, C.W.; To, C.H. Chloride Secretion by Bovine Ciliary Epithelium: A Model of Aqueous Humor Formation. Investig. Ophthalmol. Vis. Sci. 2000, 41, 1853–1860. [Google Scholar]
- Crook, R.B.; Takahashi, K.; Mead, A.; Dunn, J.J.; Sears, M.L. The Role of NaKCl Cotransport in Blood-to-Aqueous Chloride Fluxes across Rabbit Ciliary Epithelium. Investig. Ophthalmol. Vis. Sci. 2000, 41, 2574–2583. [Google Scholar]
- Shahidullah, M.; Tamiya, S.; Delamere, N.A. Primary culture of porcine nonpigmented ciliary epithelium. Curr. Eye Res. 2007, 32, 511–522. [Google Scholar] [CrossRef]
- Quigley, H.A.; Broman, A.T. The number of people with glaucoma worldwide in 2010 and 2020. Br. J. Ophthalmol. 2006, 90, 262–267. [Google Scholar] [CrossRef]
- Heijl, A.; Leske, M.C.; Bengtsson, B.; Hyman, L.; Bengtsson, B.; Hussein, M. Reduction of intraocular pressure and glaucoma progression: results from the early manifest glaucoma trial. Arch. Ophthalmol. 2002, 120, 1268–1279. [Google Scholar] [CrossRef] [PubMed]
- Stumm, W.; Morgan, J. Aquatic Chemistry; Wiley: Hoboken, NJ, USA, 1996. [Google Scholar]
- Wu, R.; Flammer, J.; Haefliger, I. Transepithelial Short Circuit Currents in Human and Porcine Isolated Ciliary Bodies: Effect of Acetazolamide and Epinephrine. Klin. Monbl. Augenheilkd. 2003, 220, 156–160. [Google Scholar] [CrossRef] [PubMed]
- Bowler, J.M.; Peart, D.; Purves, R.D.; Carré, D.A.; Macknight, A.D.; Civan, M.M. Electron Probe X-Ray Microanalysis of Rabbit Ciliary Epithelium. Exp. Eye Res. 1996, 62, 131–140. [Google Scholar] [CrossRef] [PubMed]
- Raviola, E.; Raviola, G. Intercellular junctions in the ciliary epithelium. Investig. Ophthalmol. Vis. Sci. 1978, 17, 958–981. [Google Scholar]
- Layton, A.T.; Edwards, A. Mathematical Modeling in Renal Physiology; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Fraser, J.A.; Huang, C.L. A quantitative analysis of cell volume and resting potential determination and regulation in excitable cells. J. Physiol. 2004, 559 Pt 2, 459–478. [Google Scholar] [CrossRef]
- Mori, Y. A Three-Dimensional Model of Cellular Electrical Activity. Ph.D. Thesis, New York University, New York, NY, USA, 2006. [Google Scholar]
- MathWorks®. Constrained Nonlinear Optimization Algorithms. Available online: https://it.mathworks.com/help/optim/ug/constrained-nonlinear-optimization-algorithms.html (accessed on 23 January 2020).
- Weinstein, A. Nonequilibrium thermodynamic model of the rat proximal tubule epithelium. Biophys. J. 1983, 44, 153–170. [Google Scholar] [CrossRef]
- Lyubimov, G.A.; Moiseeva, I.N.; Stein, A.A. Dynamics of the Intraocular Fluid: Mathematical Model and Its Main Consequences. Fluid Dyn. 2007, 42, 684–694. [Google Scholar] [CrossRef]
| Parameter | Value | Units |
|---|---|---|
| 25 | ||
| 15 | ||
| − | ||
| 20 | ||
| 147 | ||
| 145 |
| Study | Species | Transporter/Channel | Localization |
|---|---|---|---|
| [31] | Human | Gap junctions | Lateral surface of PE/NPE |
| Apical junction of PE/NPE | |||
| [32] | Human | Na/K ATPase | Basolateral membrane of NPE |
| K channel | Basolateral membrane of NPE | ||
| [33] | Human | AQP1 | NPE |
| [34] | Human | Na/K/2Cl cotransporter | Basolateral membrane of NPE |
| [35] | Human | ENaC | Unspecified |
| [36] | Bovine | Cl/HCO exchanger | Basolateral membrane of PE |
| [37] | Bovine | Ca dependent K channel | Basolateral membrane of NPE |
| cAMP activated Cl channel | Basolateral membrane of NPE | ||
| [38] | Bovine | Cl dependent Na/HCO cotransporter | Basolateral membrane of PE |
| [39] | Bovine | Na/H+ exchanger | Basolateral membrane of PE |
| [40] | Bovine | Na/K ATPase (alpha 1, 2, and 3 isoforms) | Basolateral membrane of NPE |
| [41] | Bovine | Na/K ATPase (alpha 1 and beta 1 isoforms) | Basolateral membrane of PE |
| [42] | Bovine | Na/K/2Cl cotransporter | Basolateral surface of PE |
| [43] | Bovine | Na/H+ exchanger | Basolateral membrane of PE |
| Cl/HCO exchanger | Basolateral membrane of PE | ||
| [44] | Porcine | Na/K ATPase (alpha 1, 2, and 3 isoforms) | Basolateral membrane of NPE |
| Tight junctions | Lateral membrane of NPE | ||
| [45] | Porcine | Na/K/2Cl cotransporter | Basolateral membrane of PE |
| Cl/HCO exchanger | Basolateral membrane of PE | ||
| Cl channel | Basolateral membrane of NPE | ||
| [46] | Porcine | Swelling activated K channel | PE basolateral membrane |
| [47] | Porcine | Hemichannels | Basolateral membrane of NPE |
| [48] | Porcine | Na/K exchanger | Basolateral membrane of NPE |
| [49] | Murine | APQ4 | Basolateral membrane of NPE |
| [50] | Murine | Glutamate transporter | Basolateral membrane of NPE |
| Glutamine transporter | Basolateral membrane of NPE | ||
| [51] | Murine | TRPV4 channel | NPE |
| [52] | Murine | Inwardly rectifying K channel | NPE |
| [53] | Leporine | Na/K/2Cl cotransporter | Basolateral membrane of NPE |
| [54] | Rabbit | Na/K ATPase (alpha 2 and beta 3 isoforms) | Basolateral membrane of NPE |
| [55] | Porcine | Cx isoforms | Gap junctions between PE and NPE cells |
| [56] | Rabbits | Na/K ATPase (alpha 2 isoform) | Basolateral membrane of NPE |
| [57] | Bovine | Na/K/2Cl cotransporter | Basolateral membrane of PE |
| Cl/HCO and Na/H+ exchangers | Basolateral membrane of PE | ||
| Cl Channel | Basolateral membrane of NPE | ||
| [58] | Rabbits | Na/K/2Cl cotransporter | Basolateral membrane of PE |
| Cl/HCO exchanger | Basolateral membrane of PE | ||
| Cl channel | Basolateral membrane of NPE |
| Quantity | Model Prediction | Reference Range | Species | Bibliographical Source |
|---|---|---|---|---|
| mV | mV | Humans | [63] | |
| 75 mM | mM | Rabbit | [64] | |
| 55 mM | mM | Rabbit | [64] | |
| 10 mM | mM | Rabbit | [64] | |
| mV | mV | Shark | [29] |
| Quantity | Model Prediction | Reference Range | Species | Bibliographical Source |
|---|---|---|---|---|
| mV | mV | Humans | [63] | |
| 15.59 mM | mM | Rabbit | [64] | |
| 132.09 mM | mM | Rabbit | [64] | |
| 3.97 mM | mM | Rabbit | [64] | |
| mV | mV | Shark | [29] |
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| species | Na | K | Cl | H | HCO | CO | HCO |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sacco, R.; Guidoboni, G.; Jerome, J.W.; Bonifazi, G.; Marazzi, N.M.; Verticchio Vercellin, A.C.; Lang, M.S.; Harris, A. A Theoretical Approach for the Electrochemical Characterization of Ciliary Epithelium. Life 2020, 10, 8. https://doi.org/10.3390/life10020008
Sacco R, Guidoboni G, Jerome JW, Bonifazi G, Marazzi NM, Verticchio Vercellin AC, Lang MS, Harris A. A Theoretical Approach for the Electrochemical Characterization of Ciliary Epithelium. Life. 2020; 10(2):8. https://doi.org/10.3390/life10020008
Chicago/Turabian StyleSacco, Riccardo, Giovanna Guidoboni, Joseph W. Jerome, Giulio Bonifazi, Nicholas M. Marazzi, Alice C. Verticchio Vercellin, Matthew S. Lang, and Alon Harris. 2020. "A Theoretical Approach for the Electrochemical Characterization of Ciliary Epithelium" Life 10, no. 2: 8. https://doi.org/10.3390/life10020008
APA StyleSacco, R., Guidoboni, G., Jerome, J. W., Bonifazi, G., Marazzi, N. M., Verticchio Vercellin, A. C., Lang, M. S., & Harris, A. (2020). A Theoretical Approach for the Electrochemical Characterization of Ciliary Epithelium. Life, 10(2), 8. https://doi.org/10.3390/life10020008






