Operator-Based Nonlinear Control of Calorimetric System Actuated by Peltier Device
Abstract
:1. Introduction
2. Presentation of the System and Control System Design
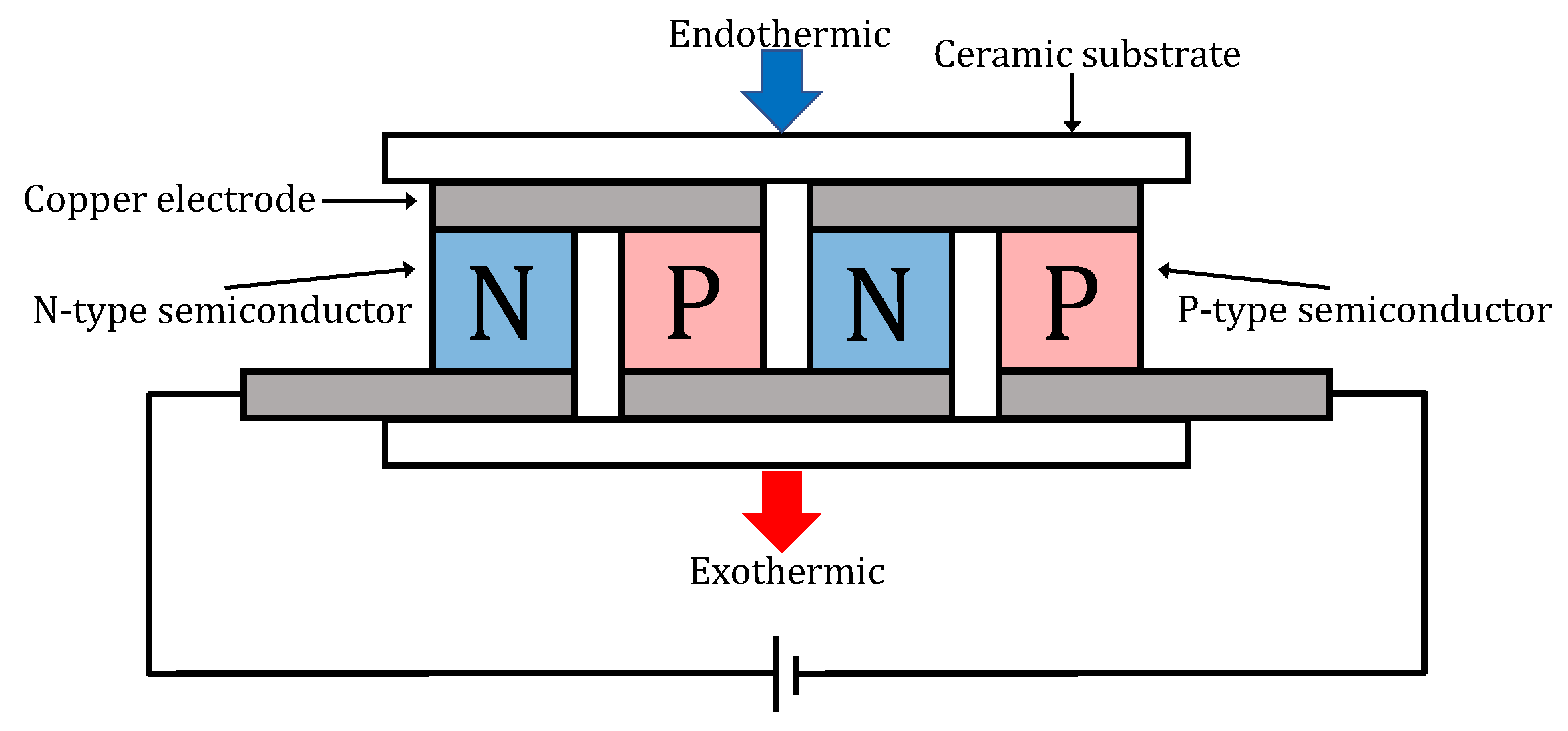
2.1. The Structure of the Peltier Device
2.2. Principles of the Calorimetric System Using the Peltier Device
2.3. Modeling of the System
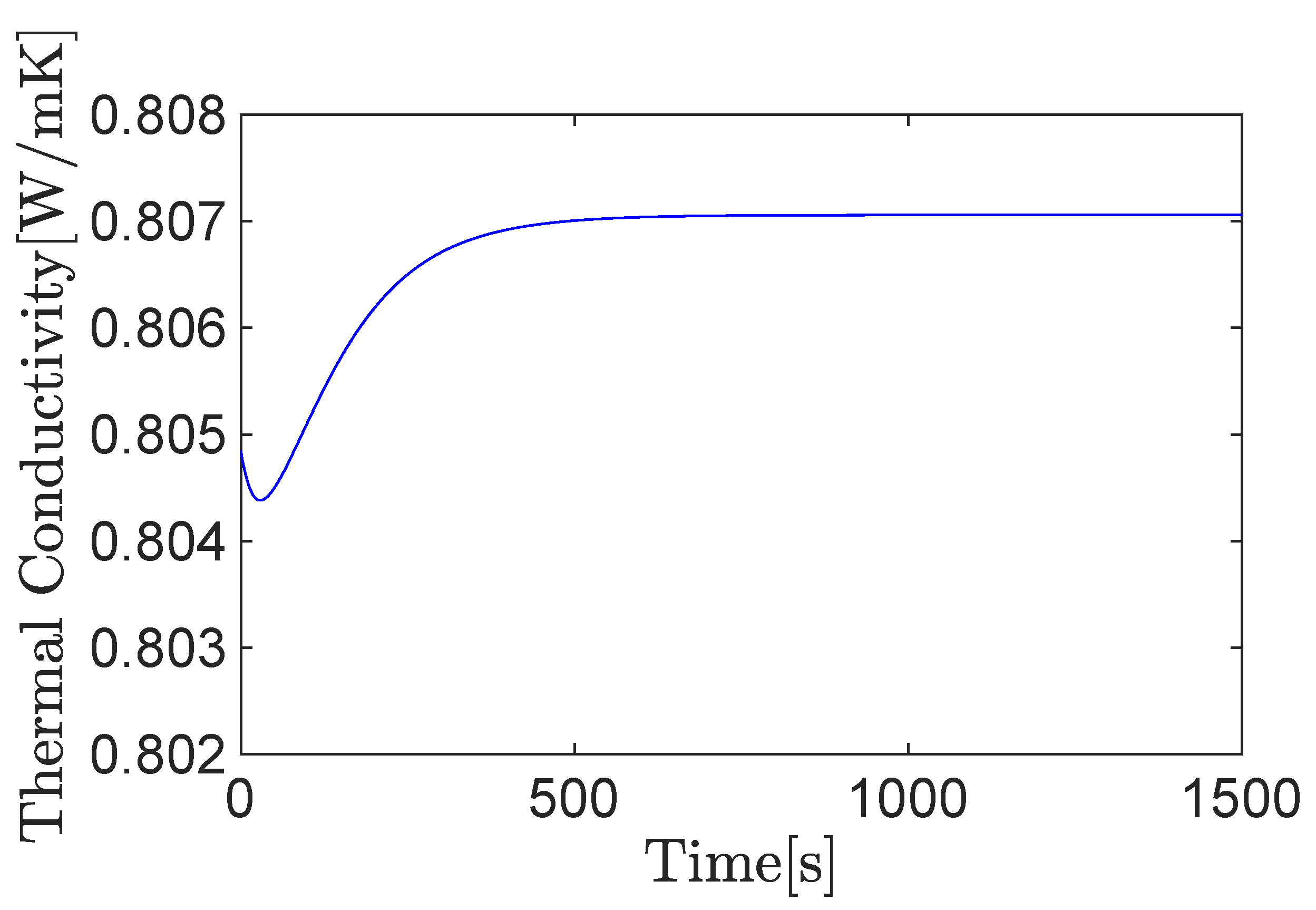
2.4. Temperature Dependence of Thermal Conductivity
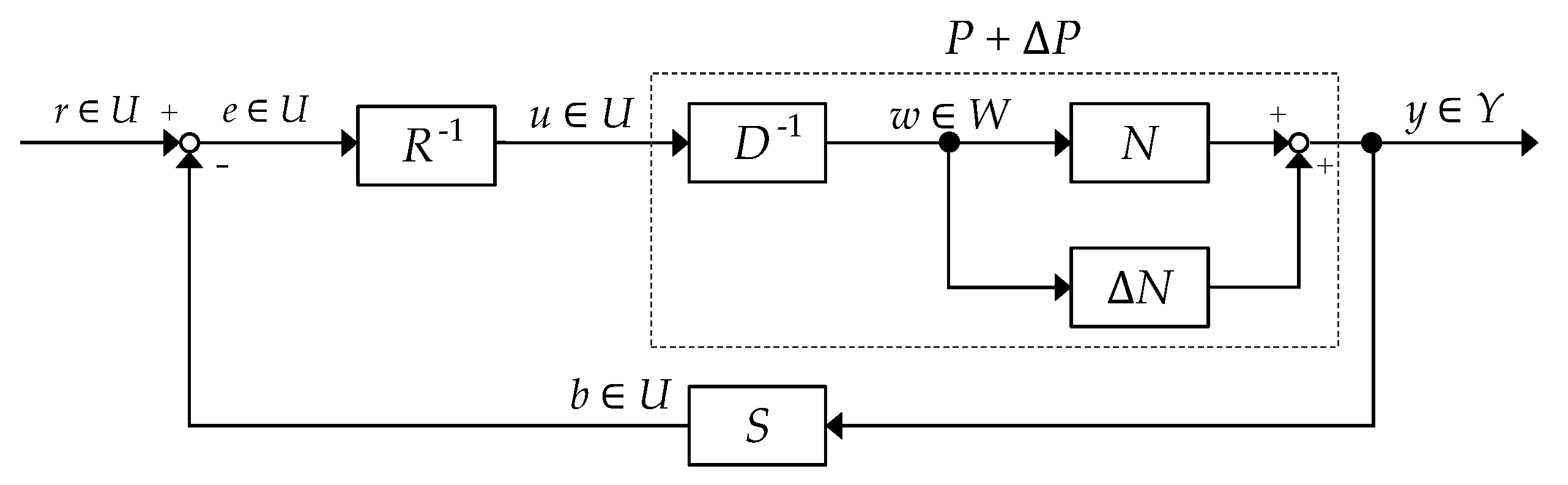
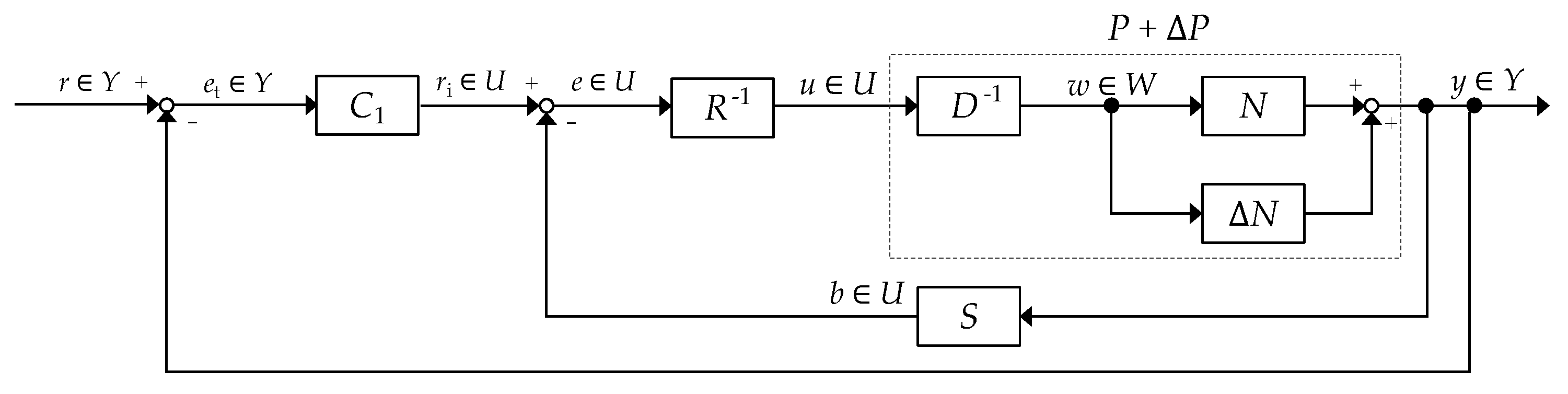
2.5. Operator-Based Nonlinear Control Feedback System Design
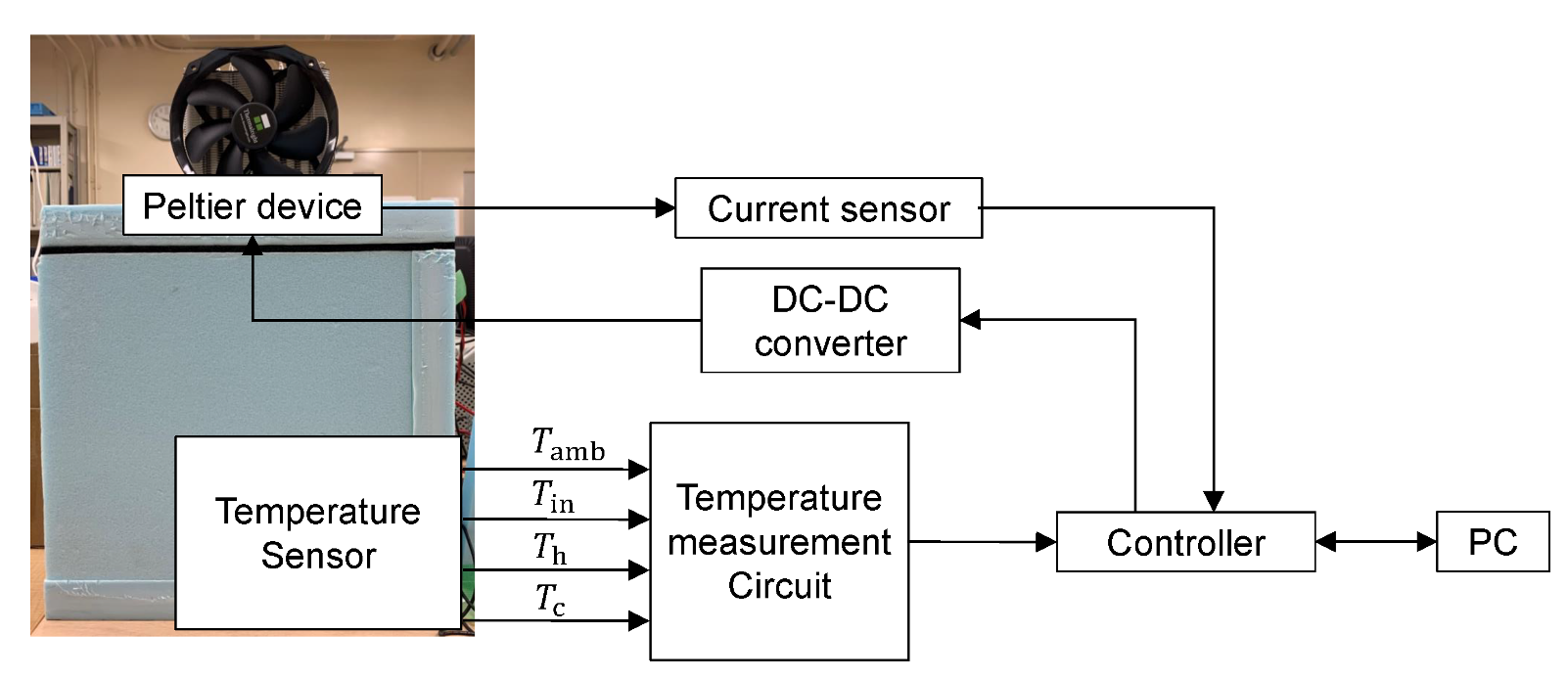
2.6. Experimental System
3. Results and Discussion
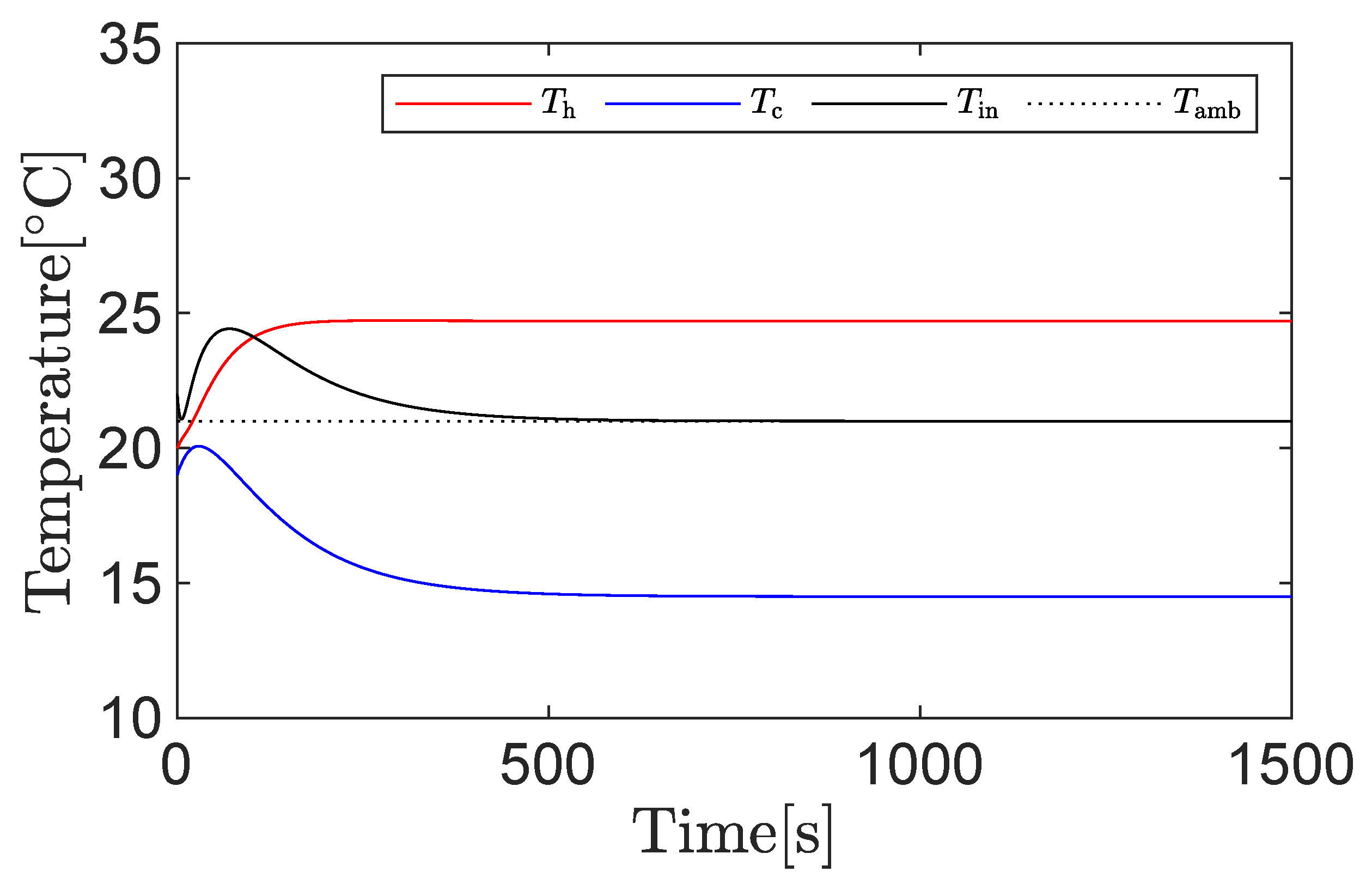
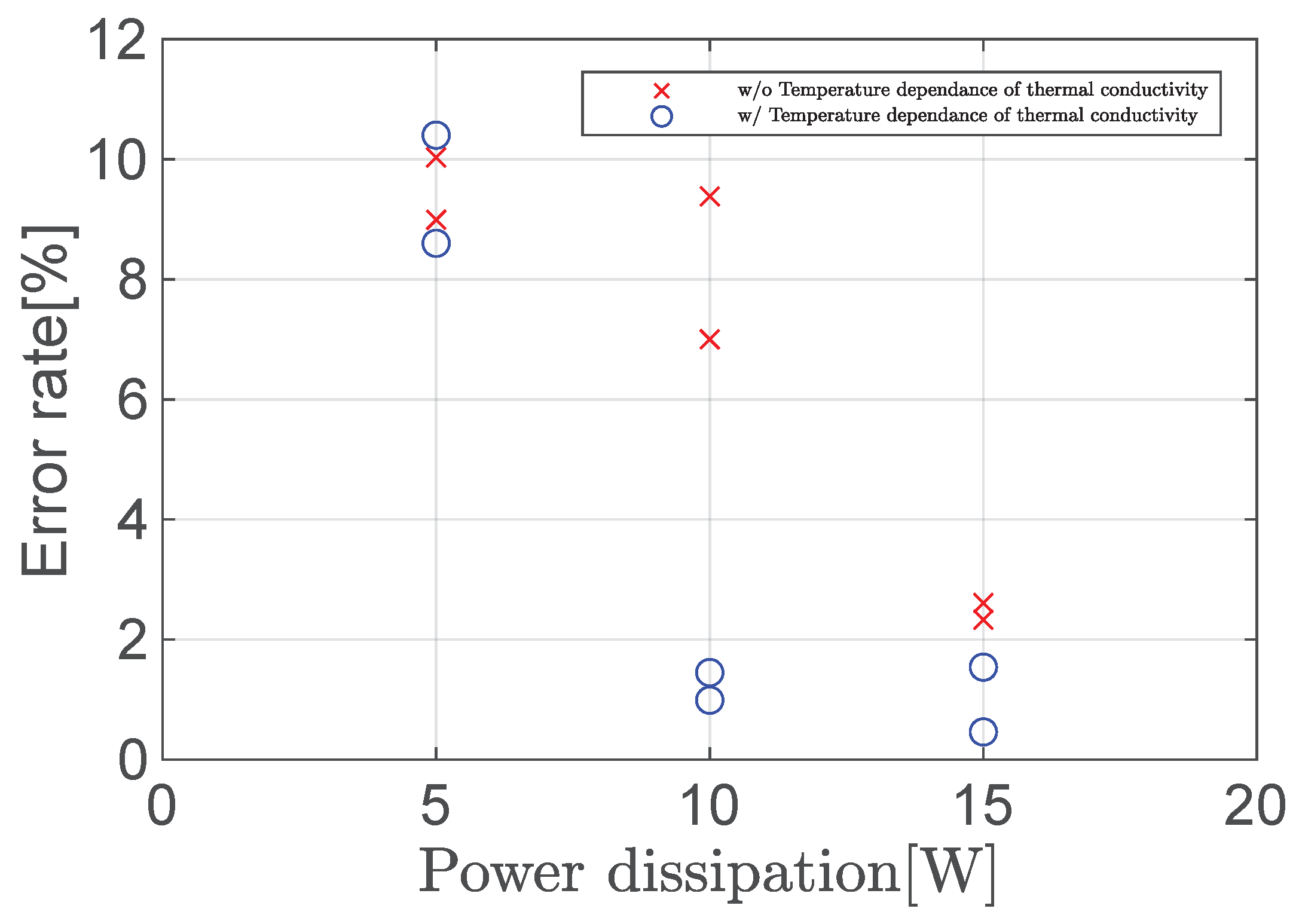
3.1. Simulation Results
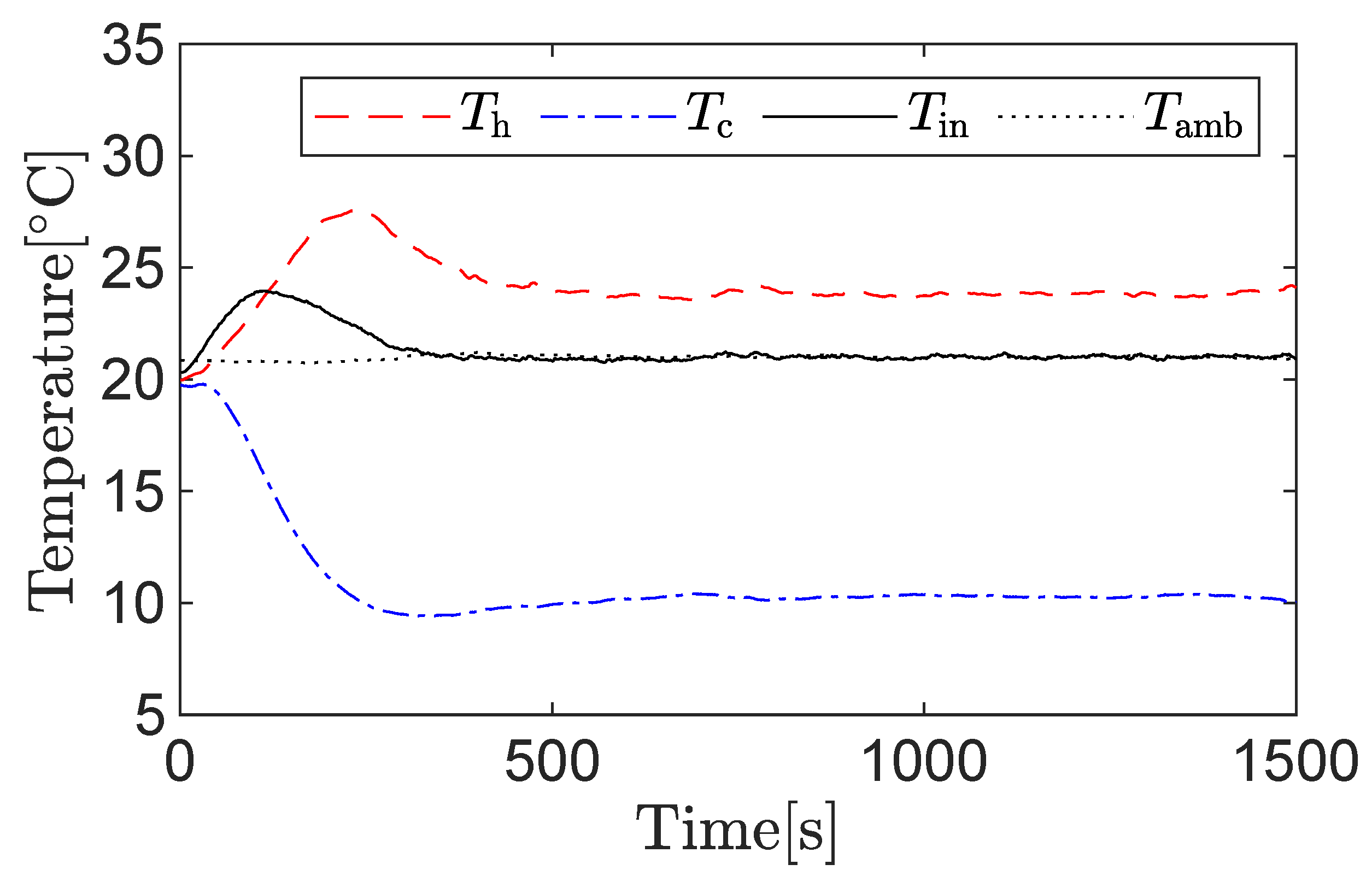
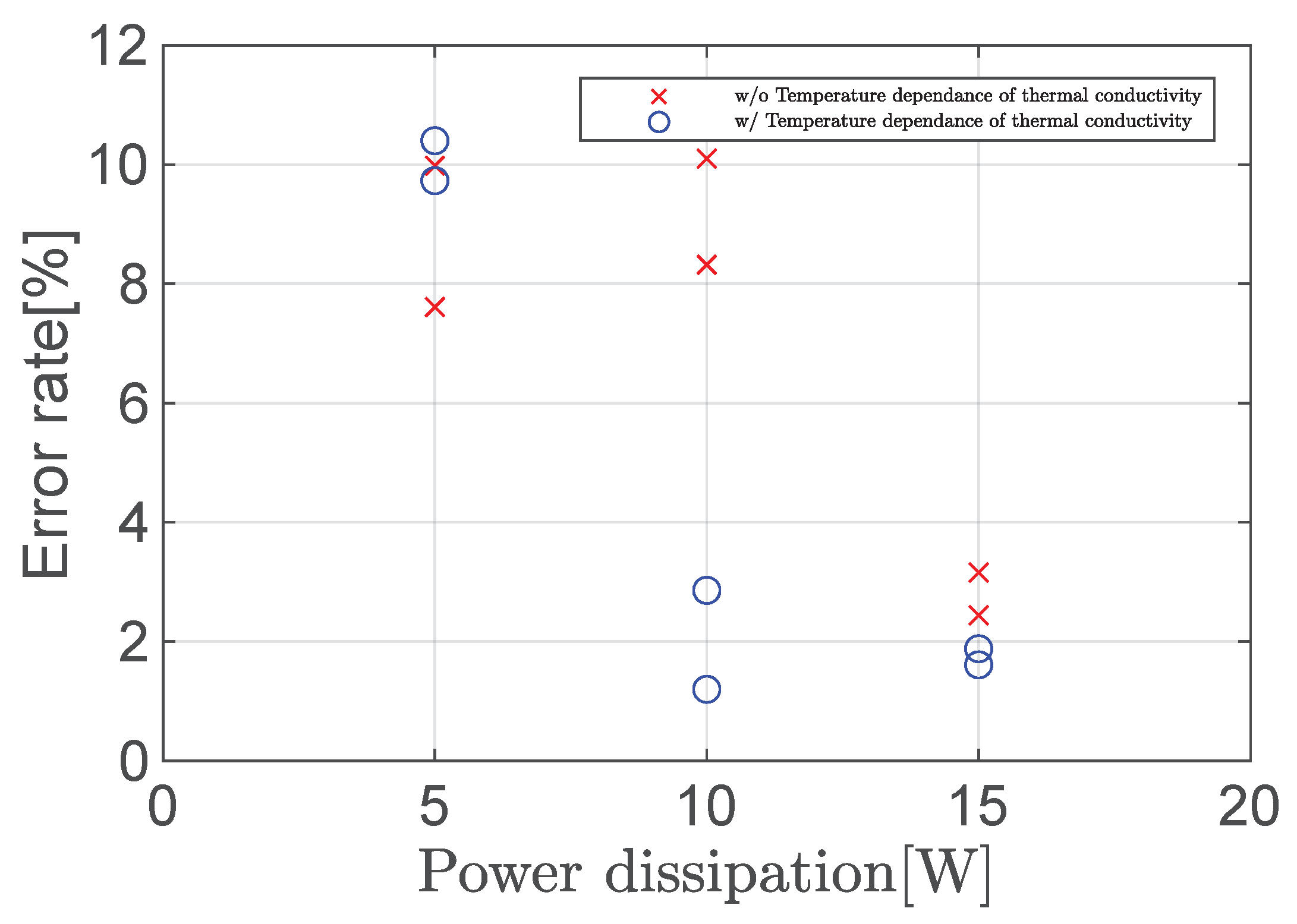
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DUT | Device under test |
References
- Kamei, R.; Kawamura, A.; Kim, T. Discussion on highly accurate calorimetric for power loss measurement. In Proceedings of the Annual Conference of IEEE of Japan, Kyoto, Japan, 5–9 June 2011; pp. 363–366. [Google Scholar]
- Peretto, L.; Sasdelli, R.; Serra, G. Measurement of harmonic losses in transformers supplying nonsinusoidal load currents. IEEE Trans. Instrum. Meas. 2000, 49, 315–319. [Google Scholar] [CrossRef]
- Szabados, B.; Mihalcea, A. Design and implementation of a calorimetric measurement facility for determining losses in electrical machines. IEEE Trans. Instrum. Meas. 2002, 51, 902–907. [Google Scholar] [CrossRef]
- Xiao, C.; Chen, G.; Odendaal, W.G. Overview of power loss measurement techniques in power electronics systems. IEEE Trans. Ind. Appl. 2007, 43, 657–664. [Google Scholar] [CrossRef]
- Mitsugi, K.; Deng, M. Operator-based robustnonlinear control for calorimet-ric power loss measurement system using Peltier device. In Proceedings of the 2nd International Conference on Industrial Artificial Intelligence, Shenyang, China, 23–25 October 2020; pp. 1–6. [Google Scholar]
- Qian, D.; Liu, X.; Li, L. Adaptive hierarchical sliding mode control for ball-beam systems. Int. J. Adv. Mechatron. Syst. 2012, 4, 205–211. [Google Scholar] [CrossRef]
- Sato, T.; Fujita, K.; Kawaguchi, N.; Takagi, T.; Mizumoto, I. Null-space-based steady-state tracking error compensation of simple adaptive control with parallel feedforward compensator and its application to rotation control. Contr. Eng. Pract. 2012, 105, 104651. [Google Scholar] [CrossRef]
- Yu, J.; Bi, S.; Wen, S. Modelling and adaptive control of NAO robot arm. Int. J. Adv. Mechatron. Syst. 2021, 9, 102–108. [Google Scholar] [CrossRef]
- Deng, M.; Inoue, A.; Ishikawa, K. Operator-based nonlinear feedback control design using robust right coprime factorization. IEEE Trans. Autom. Contr. 2006, 51, 645–648. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Han, Z. Robust right coprime factorization and robust stabilization of nonlinear feedback control systems. IEEE Trans. Autom. Contr. 1998, 43, 1505–1509. [Google Scholar] [CrossRef]
- Deng, M.; Kawashima, T. Adaptive nonlinear sensorless control for an uncertain miniature pneumatic curling rubber actuator using passivity and robust right coprime factorization. IEEE Trans. Control Syst. Technol. 2015, 24, 318–324. [Google Scholar] [CrossRef]
- Wandg, A.; Ma, Z.; Wen, S. Operator-Based Robust Nonlinear Control Design and Analysis of a Semiconductor Refrigeration Device. J. Robot. Mechatron. 2017, 29, 1065–1072. [Google Scholar] [CrossRef]
- Wen, S.; Yu, J.; Guo, G.; Bi, S.; Wang, A.; Wang, D. Fractional order based robust right coprime factorization control for an inverted pendulum. In Proceedings of the 2016 International Conference on Advanced Mechatronic Systems, Melbourne, VIC, Australia, 30 November–3 December 2016; pp. 159–163. [Google Scholar]
- Deng, M.; Wang, A. Robust non-linear control design to an ionic polymer metal composite with hysteresis using operator-based approach. IET Contr. Theory Appl. 2012, 6, 2667–2675. [Google Scholar] [CrossRef]
- Bi, S.; Han, C.; Wamg, L. Operator-based robust control for nonlinear system with input and output nonlinearities. In Proceedings of the 2016 International Conference on Advanced Mechatronic Systems, Melbourne, VIC, Australia, 30 November–3 December 2016; pp. 50–55. [Google Scholar]
- Bu, N.; Liu, H.; Li, W. Robust passive tracking control for an uncertain soft actuator using robust right coprime factorization. Int. J. Robust Nonlinear Contr. 2021. [Google Scholar] [CrossRef]
- Bu, N.; Chen, W.; Jin, L.; Zhao, Y. Robust control for uncertain nonlinear feedback system using operator-based right coprime factorization. IEEE/CAA J. Autom. Sin. 2019, 6, 824–829. [Google Scholar] [CrossRef]
- Hu, X.; Takazawa, H.; Nagase, K.; Ohta, M.; Yamamoto, A. Three-dimensionalnite-element simulation for a thermoelectric generator module. J. Electron. Mater. 2015, 44, 3637–3645. [Google Scholar] [CrossRef]
- Yamakita, A.; Deng, M. Nonlinear control considering temperature dependenceof thermal conductivity for a cooling and heating system based on the concept ofsliding mode. In Proceedings of the 2018 International Conference on Advanced Mechatronic Systems, Zhengzhou, China, 30 August–2 September 2018; pp. 162–165. [Google Scholar]
- Osawa, Y.; Katsura, S. Variable heat disturbance observer for control of Peltier device. IEEJ J. Ind. Appl. 2019, 8, 185–191. [Google Scholar] [CrossRef] [Green Version]
- Christen, D.; Badstuebner, U.; Biela, J.; Kolar, J.W. Calorimetric power loss measurement for highly efficient converters. In Proceedings of the Power Electronics Conference, 2010 International, Sapporo, Japan, 21–24 June 2010; pp. 1438–1445. [Google Scholar]
- Deng, M.; Saijo, N.; Gomi, H.; Inoue, A. A robust real time method for estimating human multijoint arm viscoelasticity. Int. J. Innov. Comput. Inf. Contr. 2006, 2, 705–721. [Google Scholar]
- Jiang, L.; Deng, M.; Inoue, A. Obstacle avoidance and motion control of a two wheeled mobile robot using SVR technique. Int. J. Innov. Comput. Inf. Contr. 2009, 5, 253–262. [Google Scholar]
- Zhang, K.; Cocquempot, V.; Jiang, B. Adjustable parameter-based multi-objective fault estimation observer design for continuous-time/discrete-time dynamic systems. Int. J. Contr. Autom. Syst. 2017, 15, 1077–1088. [Google Scholar] [CrossRef]








| Parameter | Definition | Value |
|---|---|---|
| Seebeck coefficient | (V/K) | |
| Thermal conductivity | (W/mK) | |
| A | Area of the Peltier device | |
| d | Thickness of the Peltier device | (m) |
| Internal resistance of the Peltier device | ||
| Hot side temperature | (K) | |
| Cold side temperature | (K) | |
| I | Current | (A) |
| Parameter | Definition | Value |
|---|---|---|
| q | Heat flux | (K/m) |
| Temperature gradient inside solid | (K/m) | |
| Thermal conductivity | (W/mK) | |
| Heat transfer coefficient | ||
| T | Temperature of solid | (K) |
| Temperature of fluid | (K) |
| Parameter | Definition | Value |
|---|---|---|
| Thermopower | 0.0411 V/K | |
| Resistance of Peltier device | 1.51 | |
| Outside temperature | 21 C | |
| Thermal resistance of internal air | 166.7 K/W | |
| Thermal resistance of cold-side cooler | 0.4 K/W | |
| Thermal resistance of hot-side cooler | 0.15 K/W | |
| Thermal resistance of DUT | 3 K/W | |
| Thermal resistance of chamber | 2 K/W | |
| Heat capacity of internal air | 15.98 J/K | |
| Heat capacity of cold-side cooler | 100 J/K | |
| Heat capacity of hot-side cooler | 70 J/K | |
| Heat capacity of DUT | 10 J/K | |
| Power dissipation of DUT | 15 W | |
| Power dissipation of hot-side cooler | 1.25 W | |
| Power dissipation of cold-side cooler | 1.25 W | |
| Area of Peltier device | 1.6 | |
| Thickness of ceramic plate | 1 mm | |
| Thickness of semiconductor | 2 mm | |
| Thermal conductivity of alumina | 32 W/mK | |
| Proportional gain | 0.05 | |
| Integral gain | 0.0005 | |
| Proportional gain | 0.4398 | |
| Integral gain | 197.4 | |
| B | Design parameter | 0.992 |
| Parameter | Definition | Value |
|---|---|---|
| N | Number of atoms in a crystal | 2 |
| V | Volume of the unit lattice | 1.065 × |
| Effective sound velocity | 1790 m/s | |
| Lorentz number | 2.44 × W/ | |
| Electrical conductivity | 5.13 × 1/m | |
| c | Heat capacity of phonon | 25 J/molK |
| a | Dimensionless parameter | 0.95 × |
| b | Dimensionless parameter | 0.5 |
| Boltzmann’s constant | 1.38 × J/K | |
| ℏ | Dirac’s constant | 1.054 × Js |
| Debye temperature | 660.9 K |
| Peltier device | TEC1-12706: Cooling capacity 50 W | |
| Dimensions: 40 mm × 40 mm × 3.9 mm | ||
| Sensors | Temperature | Pt100: Accuracy ±0.01 C |
| Current | CASR 6-NP: Accuracy 0.8% | |
| Chamber | Expanded polystyrene: | |
| Dimensions: 300 mm × 300 mm × 300 mm, Wall thickness: 30 mm | ||
| DUT | Aluminum resistor: Resistance 3.3 | |
| Dimensions: 148 mm × 210 mm × 0.5 mm | ||
| Coolers | Hot side | TY-140: |
| Dimensions: 152 mm × 140 mm × 26.5 mm | ||
| Cold side | CC-Siberian-01: | |
| Dimensions: 120 mm × 96 mm × 66 mm | ||
| Parameter | Definition | Value |
|---|---|---|
| Experiment time | 1500 s | |
| Power dissipation of DUT | 5, 10, 15 W | |
| Sampling time of temperature | 1 s | |
| Proportional gain (w/o operator theory) | 0.5 | |
| Integral gain (w/o operator theory) | 0.05 | |
| Proportional gain (w/ operator theory) | 0.05 | |
| Integral gain (w/ operator theory) | 0.0005 |
| w/o Operator Theory | w/ Operator Theory | |
|---|---|---|
| w/o Temperature dependence of thermal conductivity | 700 s | 600 s |
| w/ Temperature dependence of thermal conductivity | 600 s | 500 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chikaraishi, R.; Deng, M. Operator-Based Nonlinear Control of Calorimetric System Actuated by Peltier Device. Machines 2021, 9, 174. https://doi.org/10.3390/machines9080174
Chikaraishi R, Deng M. Operator-Based Nonlinear Control of Calorimetric System Actuated by Peltier Device. Machines. 2021; 9(8):174. https://doi.org/10.3390/machines9080174
Chicago/Turabian StyleChikaraishi, Ryo, and Mingcong Deng. 2021. "Operator-Based Nonlinear Control of Calorimetric System Actuated by Peltier Device" Machines 9, no. 8: 174. https://doi.org/10.3390/machines9080174
APA StyleChikaraishi, R., & Deng, M. (2021). Operator-Based Nonlinear Control of Calorimetric System Actuated by Peltier Device. Machines, 9(8), 174. https://doi.org/10.3390/machines9080174







