PFC-Based Control of Friction-Induced Instabilities in Drive Systems
Abstract
1. Introduction
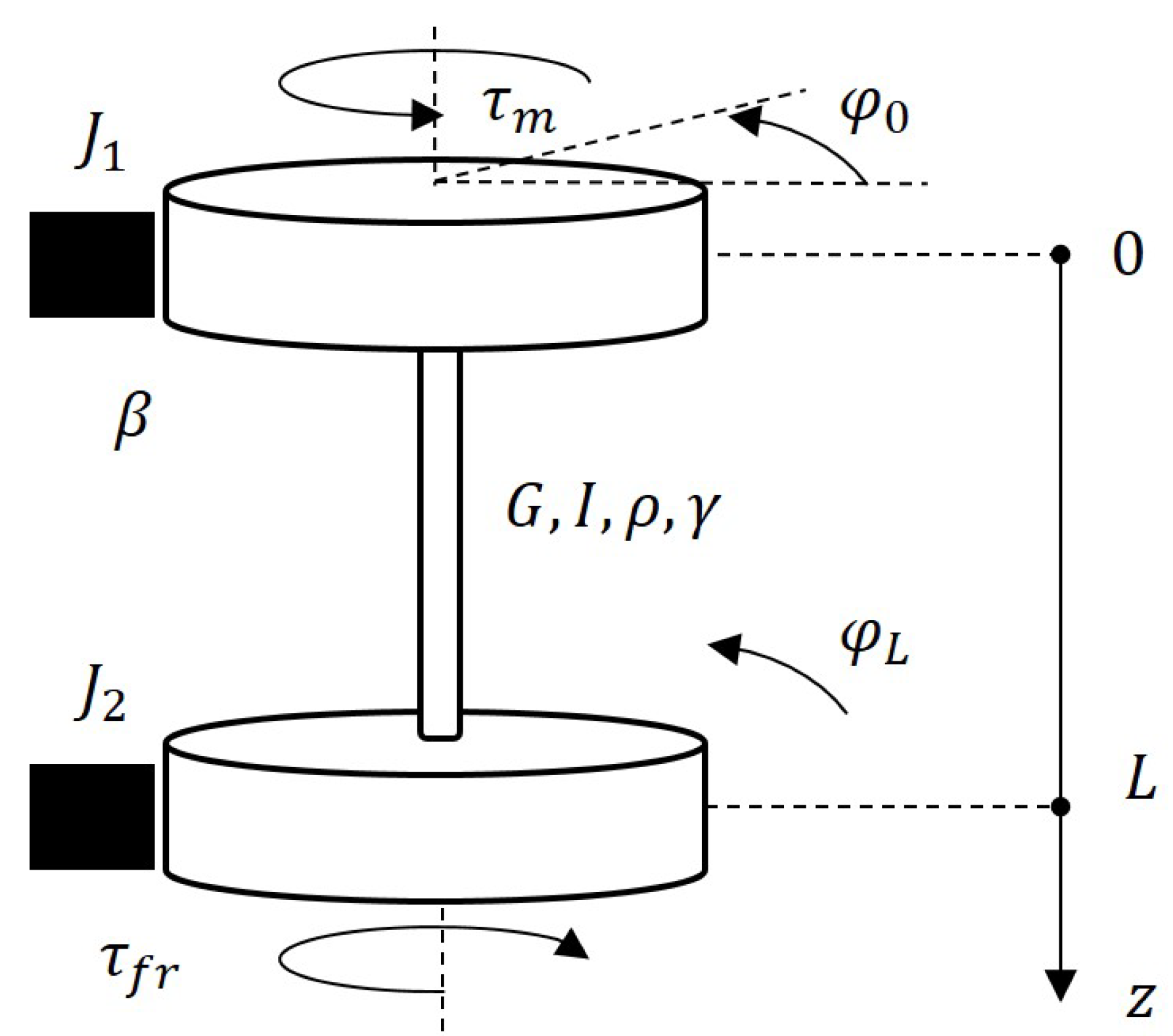
2. Modeling
2.1. Mathematical Model
2.2. Model Discretization
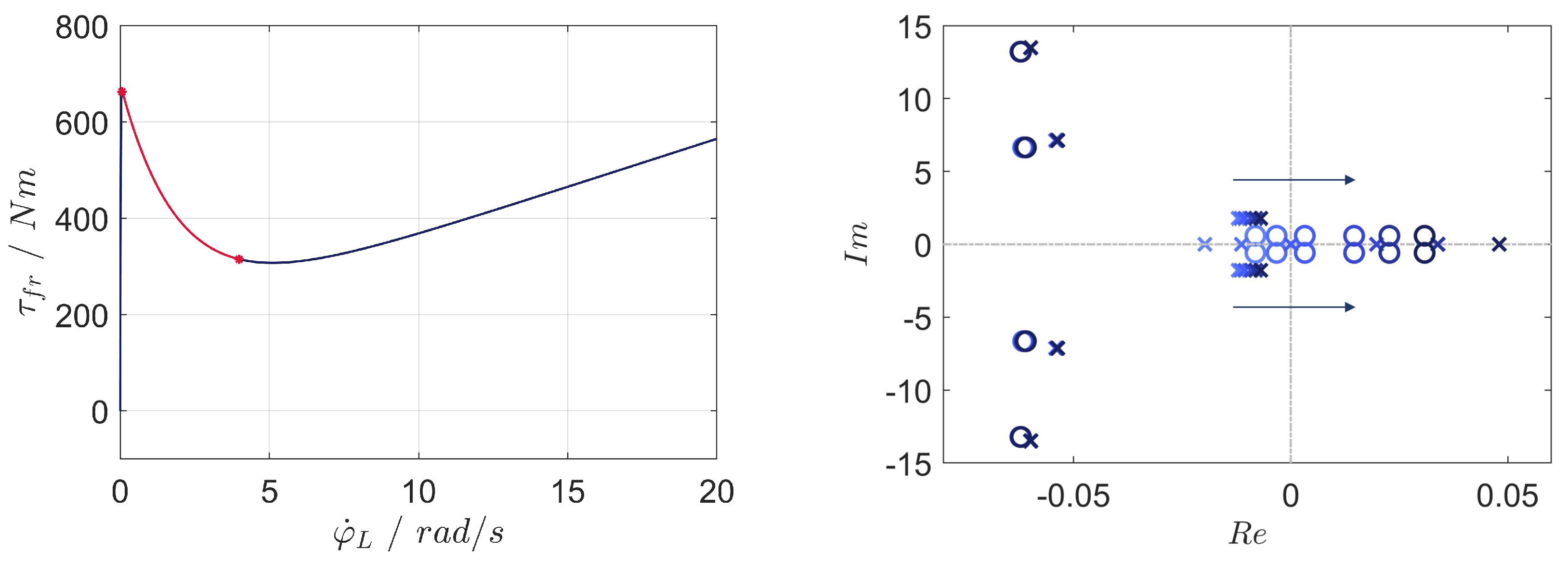
3. Friction-Induced Self-Excited Oscillations
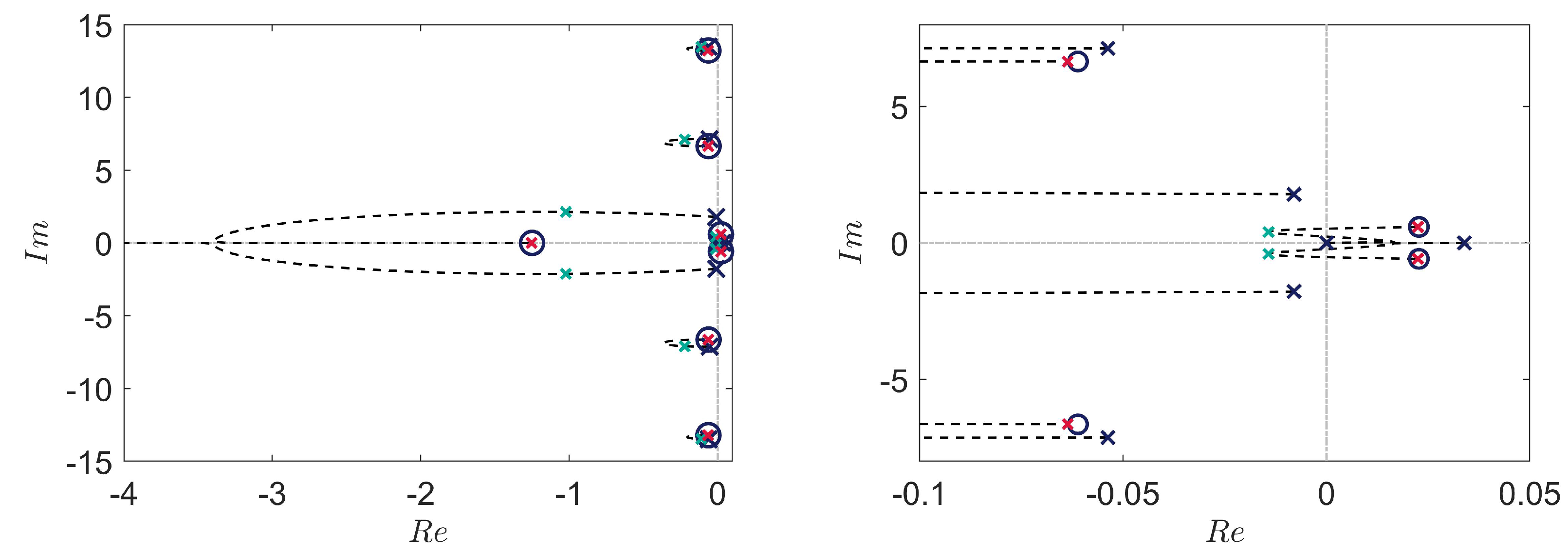
3.1. Stability and Zero Dynamics
3.2. Conventional Velocity Control
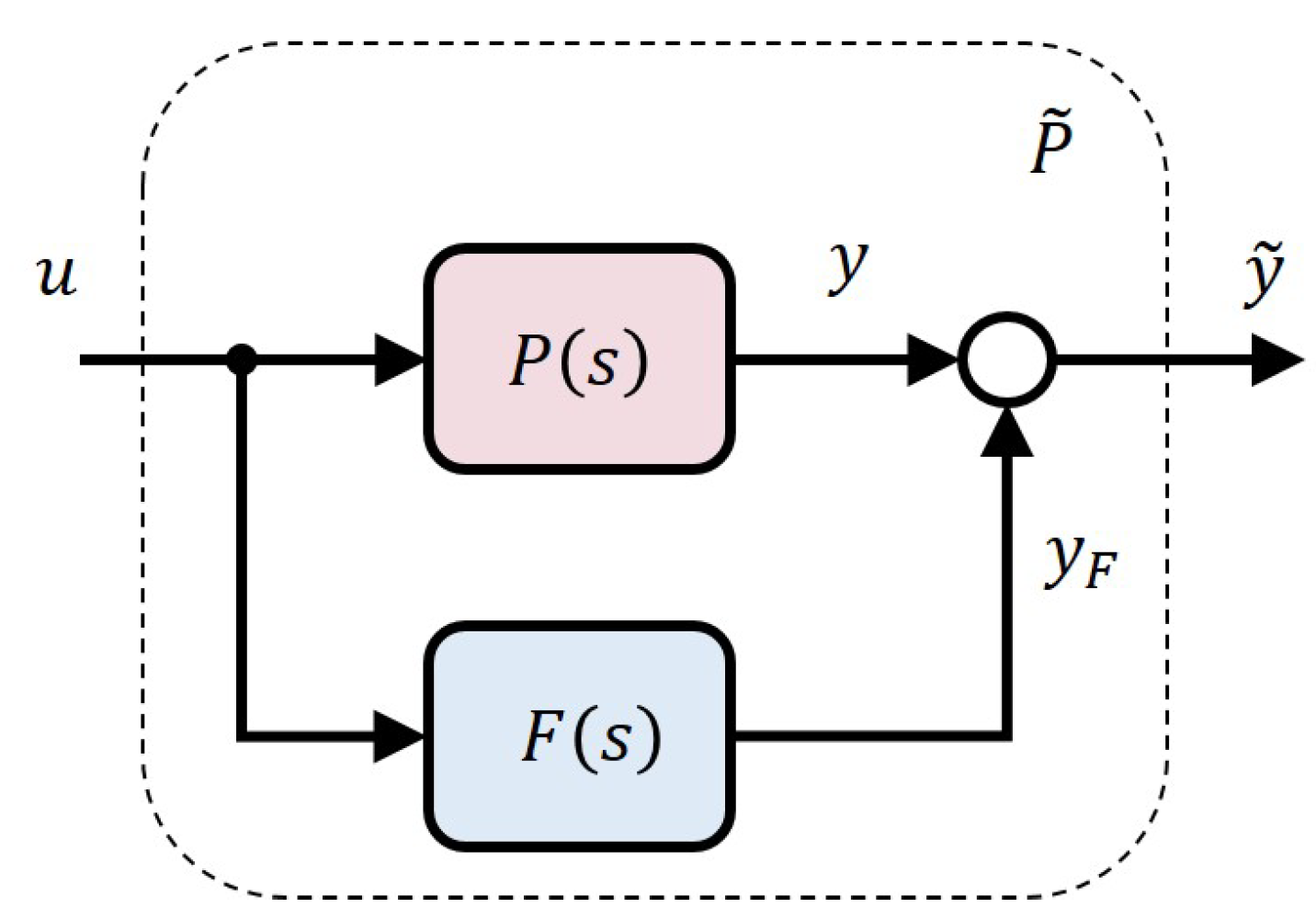
4. PFC-Based Control
4.1. Motivation
- is strictly the minimum phase, i.e., zeros of are in the LHP ;
- the relative degree of the system is 0 or 1.
4.2. PFC Design
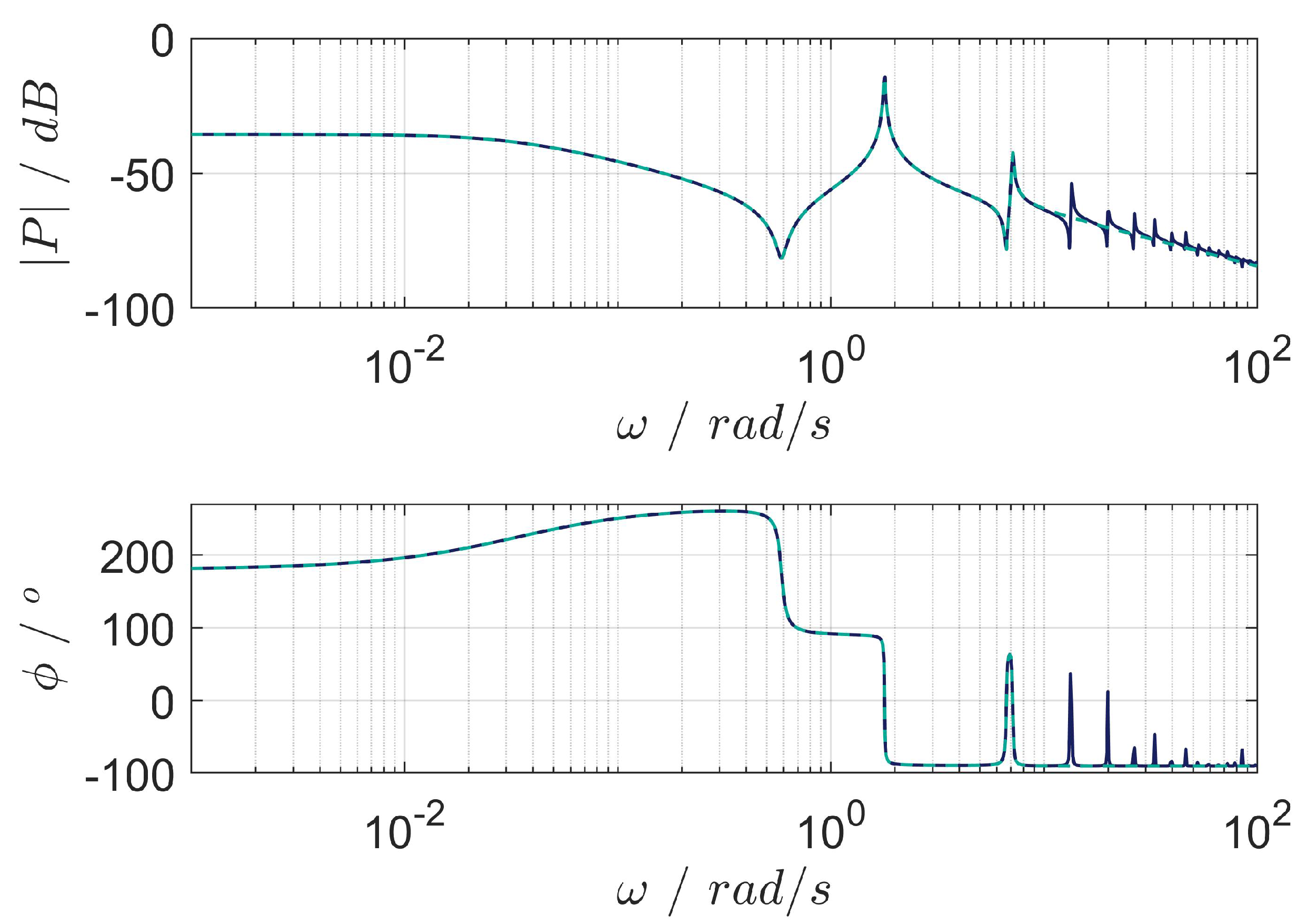
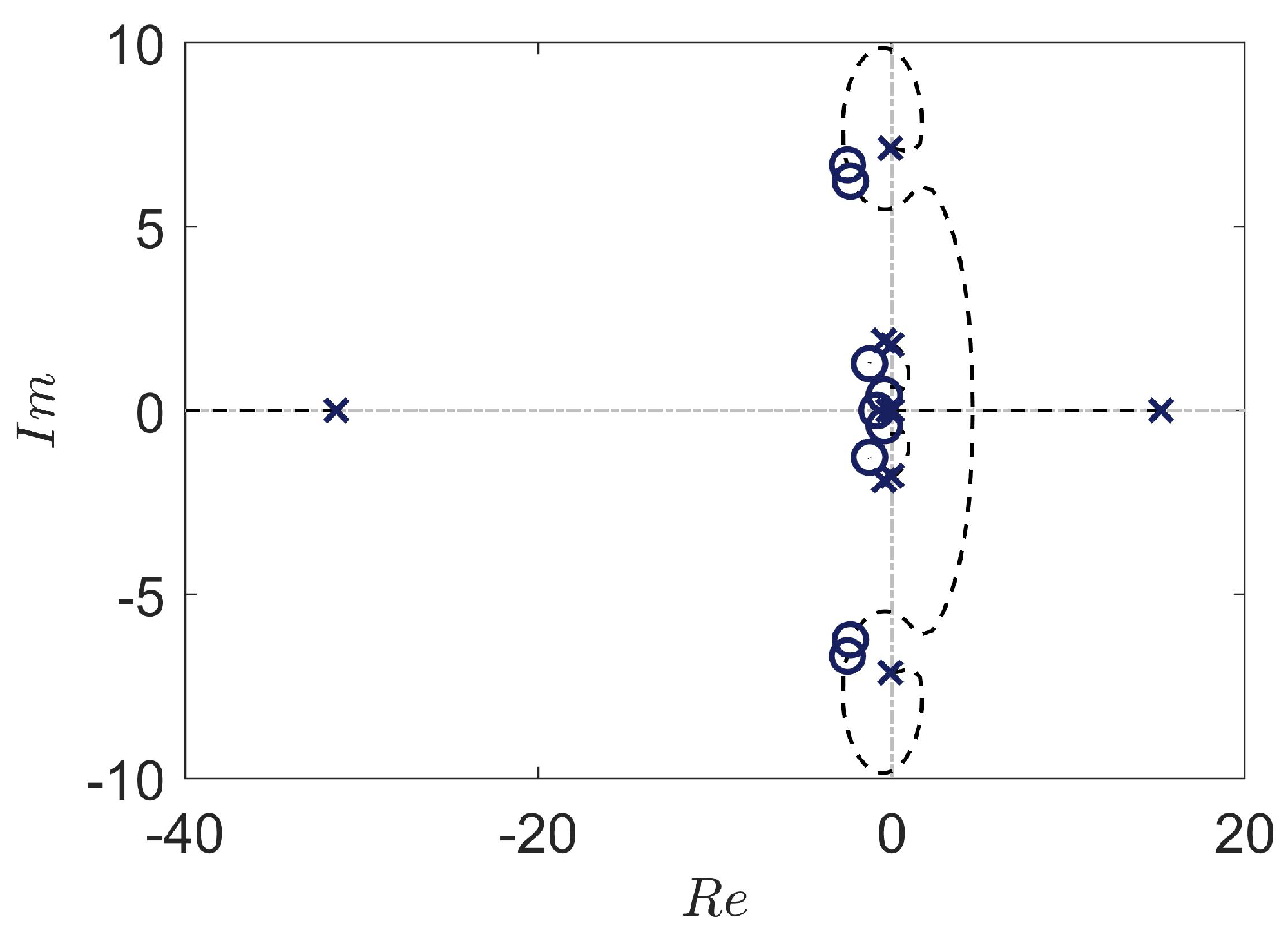
4.3. Stability of the Augmented Plant
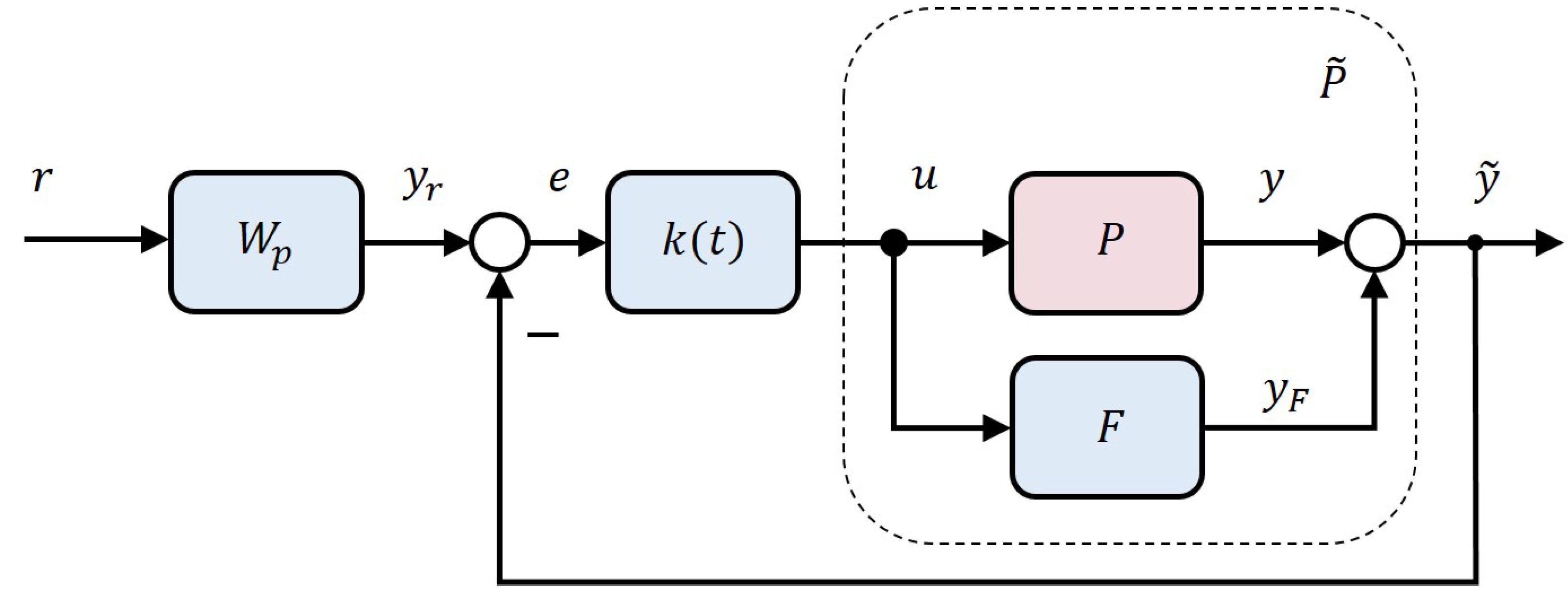
4.4. PFC-Based Adaptive Feedback Control
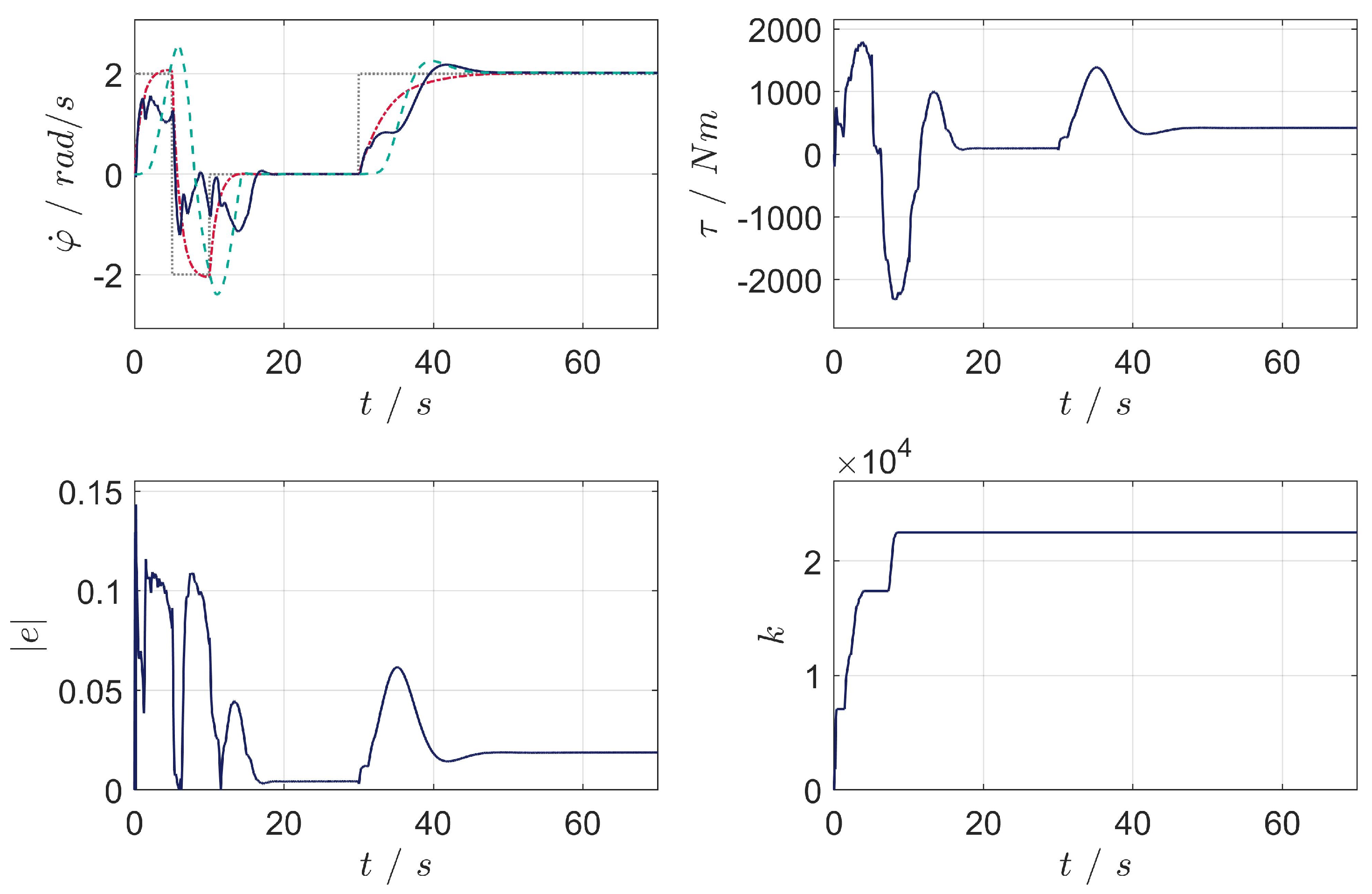
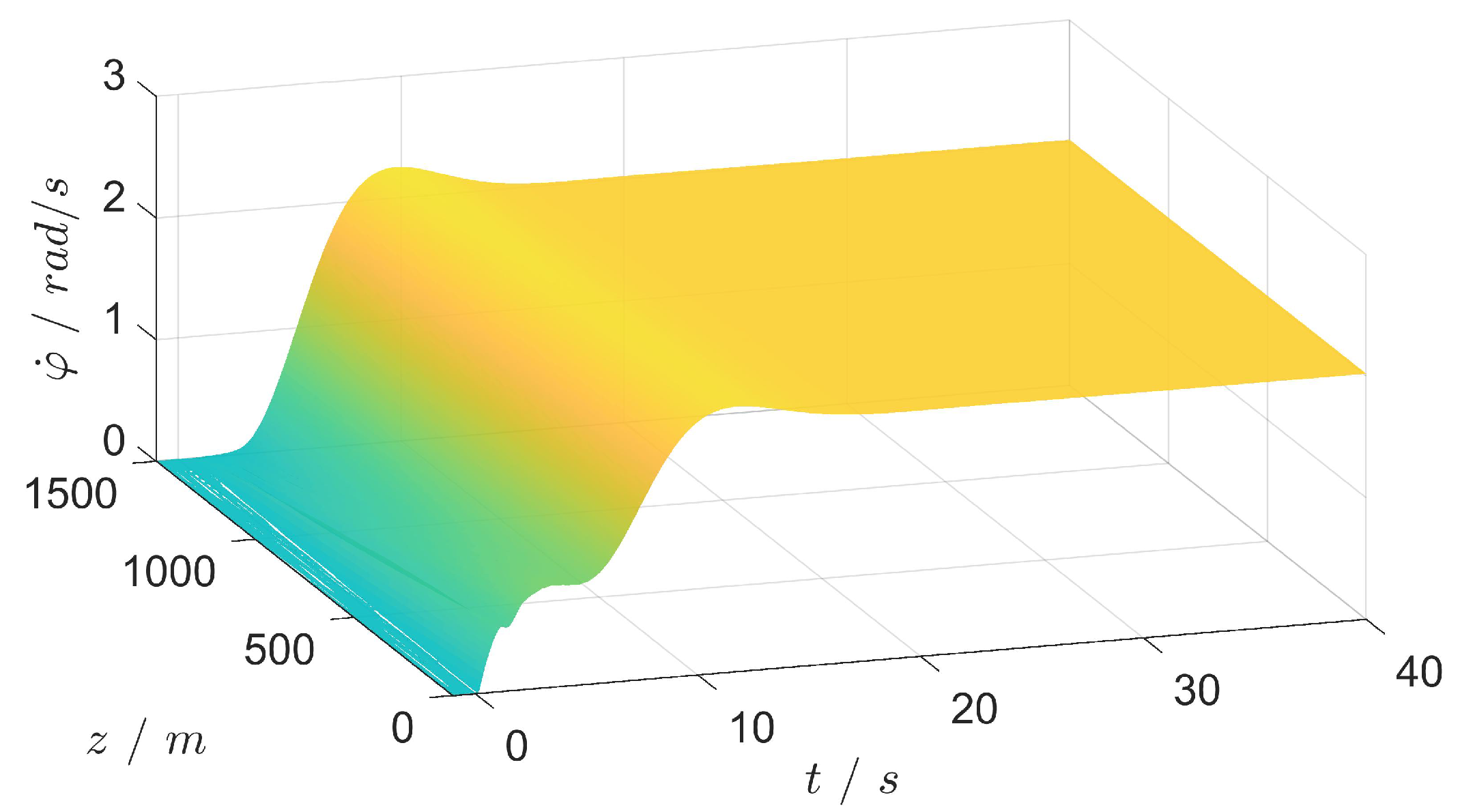
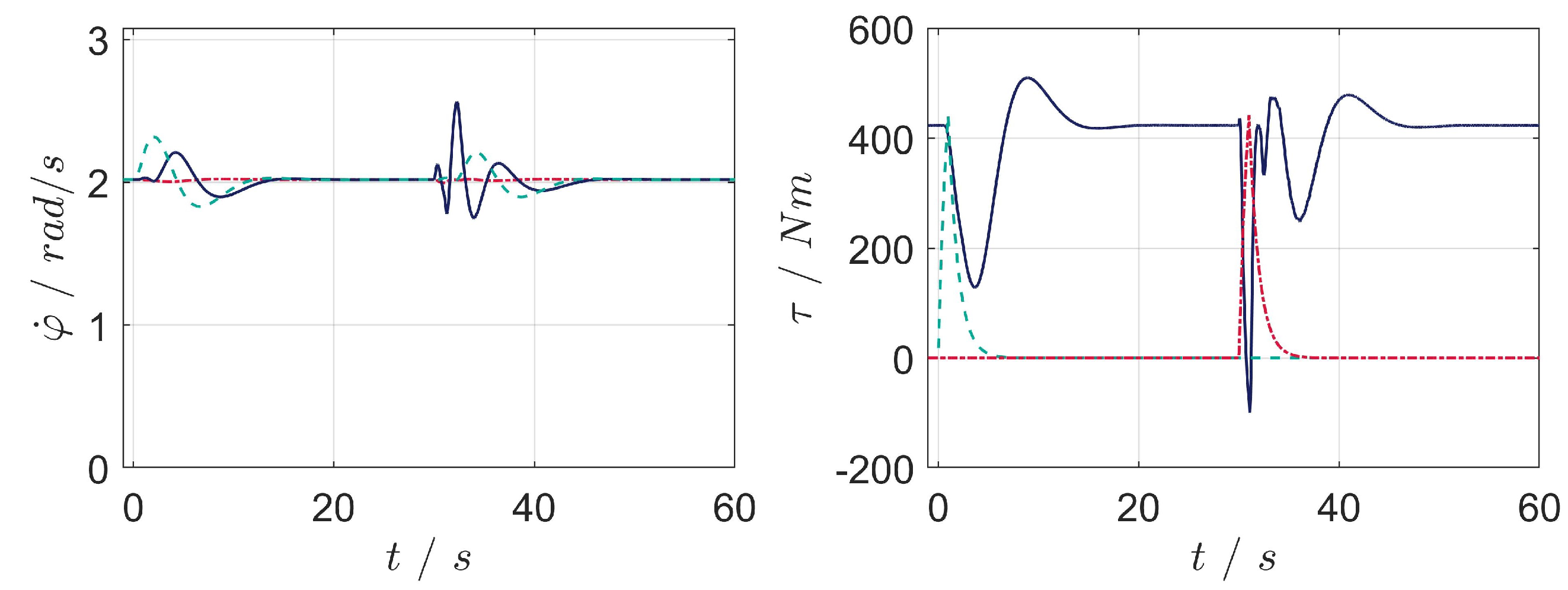
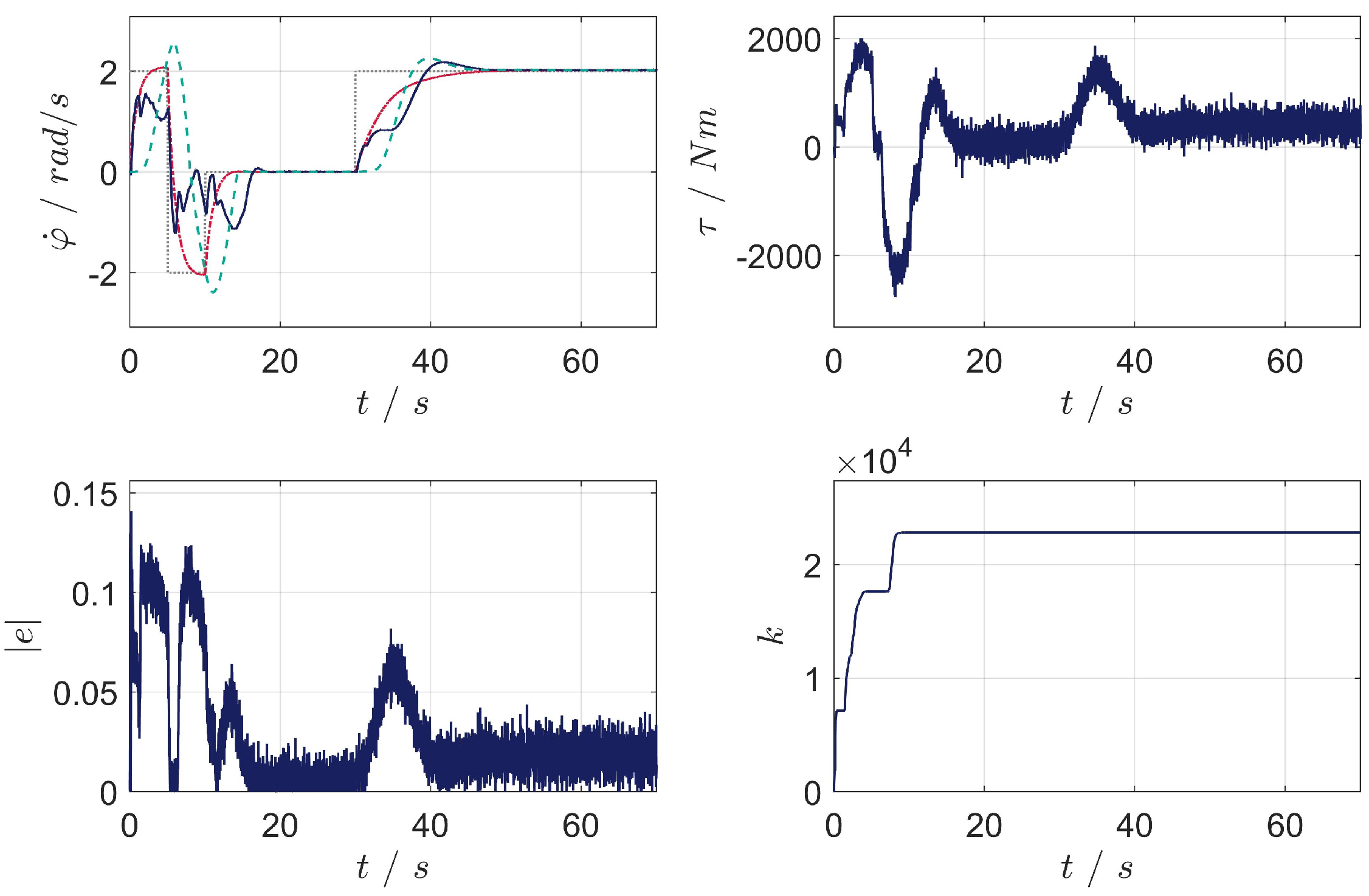
5. Results
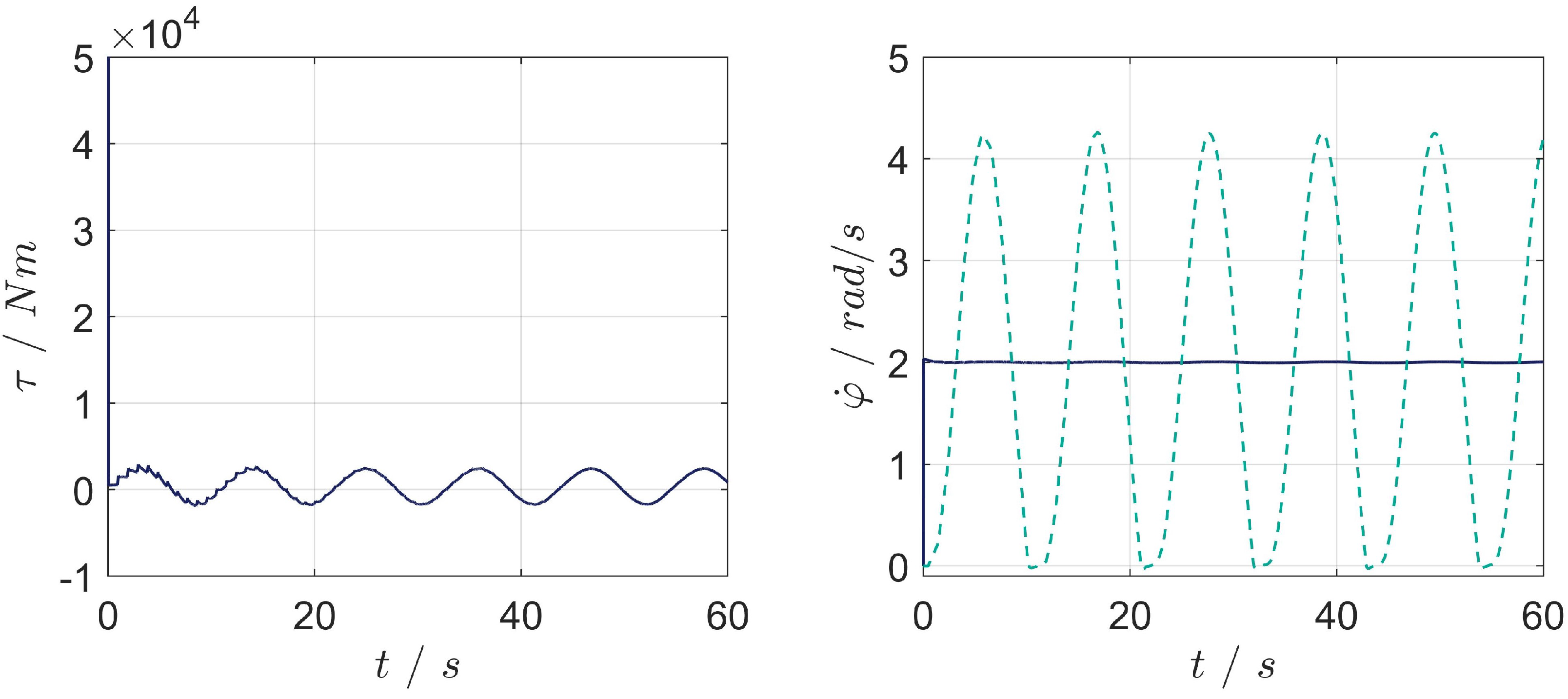
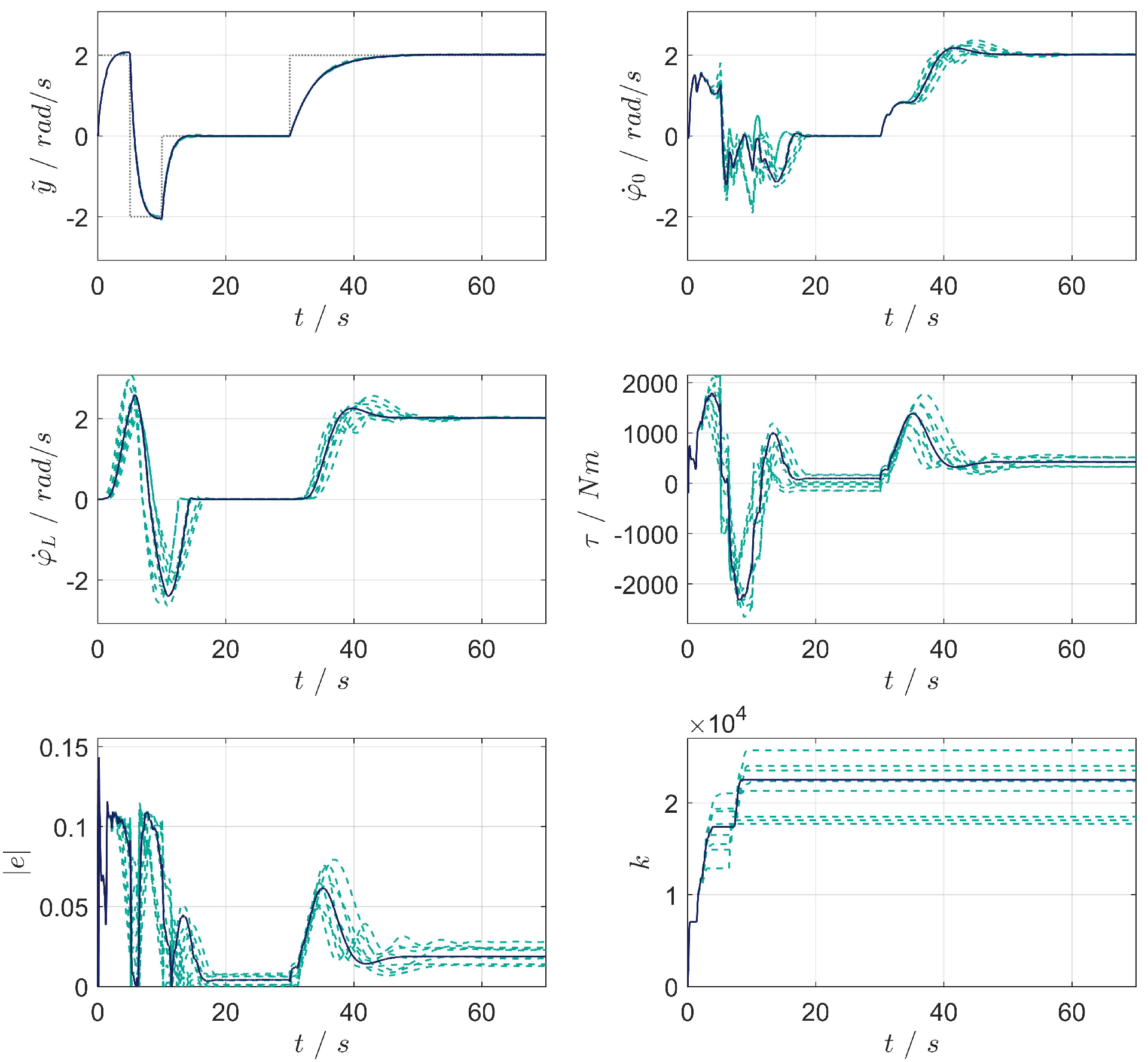
- Scenario 1: adaptation, angular velocity reference tracking and disturbance rejection of the closed-loop system;
- Scenario 2: adaptation and angular velocity reference tracking of the closed-loop system in the presence of measurement noise;
- Scenario 3: adaptation and angular velocity reference tracking of the closed-loop system in the presence of parameters variation.
- is chosen as from the reference value rad/s;
- is chosen to provide a reasonable adaptation rate;
- ;
- s for the reference tracking ( s for the adaptation).
5.1. Scenario 1
5.2. Scenario 2
5.3. Scenario 3
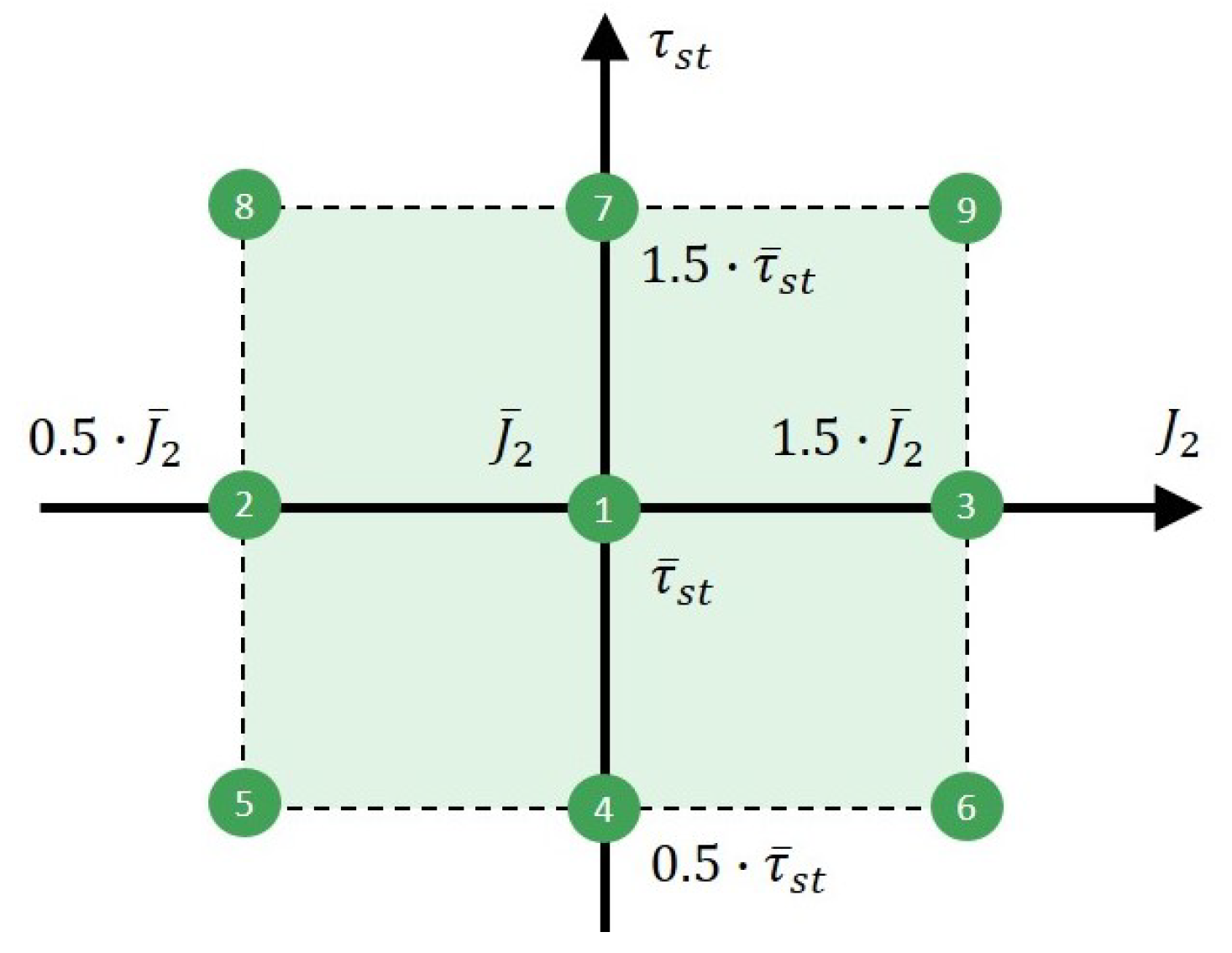
- The static friction torque from (4) is varied in a range of ±50% from its nominal value resulting in a different slope of the friction curve in the operating point of interest;
- The moment of inertia of the second mass is varied in a range of ±50% from its nominal value.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PFC | Parallel feed-forward compensator |
| ASPR | Almost strictly positive real |
| PDE | Partial differential equation |
| RHP | Right-half plane |
| LHP | Left-half plane |
References
- Armstrong-Hélouvry, B.; Dupont, P.; De Wit, C.C. A survey of models, analysis tools and compensation methods for the control of machines with friction. Automatica 1994, 30, 1083–1138. [Google Scholar] [CrossRef]
- Olsson, H.; Åström, K.J.; Gafvert, M.; Lischinsky, P.; Canudas de Wit, C. Friction Models and Friction Compensation. Eur. J. Control 1998, 4, 176–195. [Google Scholar] [CrossRef]
- Keck, A.; Zimmermann, J.; Sawodny, O. Friction parameter identification and compensation using the ElastoPlastic friction model. Mechatronics 2017, 47, 168–182. [Google Scholar] [CrossRef]
- Nechak, L. Nonlinear state observer for estimating and controlling of friction-induced vibrations. Mech. Syst. Signal Process. 2020, 139, 106588. [Google Scholar] [CrossRef]
- Klepikov, V. Dynamics of Electromechanical Systems with Nonlinear Friction (in Russian); NTU “KhPI”: Kharkiv, Ukraine, 2014. [Google Scholar]
- Mihajlović, N. Torsional and Lateral Vibrations in Flexible Rotor Systems with Friction. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2005. [Google Scholar]
- Cui, X.; Huang, B.; Du, Z.; Yang, H.; Jiang, G. Study on the Mechanism of the Abnormal Phenomenon of Rail Corrugation in the Curve Interval of a Mountain City Metro. Tribol. Trans. 2020, 63, 996–1007. [Google Scholar] [CrossRef]
- Wang, C.; Ayalew, B.; Adcox, J.; Dailliez, B.; Rhyne, T.; Cron, S. Self-excited torsional oscillations under locked-wheel braking: Analysis and experiments. Tire Sci. Technol. 2015, 43, 276–296. [Google Scholar] [CrossRef]
- Berthold, C.; Gross, J.; Frey, C.; Krack, M. Development of a fully-coupled harmonic balance method and a refined energy method for the computation of flutter-induced Limit Cycle Oscillations of bladed disks with nonlinear friction contacts. J. Fluids Struct. 2021, 102, 103233. [Google Scholar] [CrossRef]
- Papangelo, A.; Putignano, C.; Hoffmann, N. Self-excited vibrations due to viscoelastic interactions. Mech. Syst. Signal Process. 2020, 144, 106894. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Y.; Pan, G. A combined acoustic and dynamic model of a defective ball bearing. J. Sound Vib. 2021, 501, 116029. [Google Scholar] [CrossRef]
- Marquez, M.B.S.; Boussaada, I.; Mounier, H.; Niculescu, S.I. Analysis and Control of Oilwell Drilling Vibrations: A Time-Delay Systems Approach; Springer: Heidelberg, Germany, 2015. [Google Scholar]
- Lin, W.; Liu, Y. Proportional-Derivative Control of Stick-Slip Oscillations in Drill-Strings. MATEC Web Conf. 2018, 148, 16005. [Google Scholar] [CrossRef][Green Version]
- Ritto, T.; Ghandchi-Tehrani, M. Active control of stick-slip torsional vibrations in drill-strings. J. Vib. Control 2019, 25, 194–202. [Google Scholar] [CrossRef]
- Puebla, H.; Alvarez-Ramirez, J. Suppression of stick-slip in drillstrings: A control approach based on modeling error compensation. J. Sound Vib. 2008, 310, 881–901. [Google Scholar] [CrossRef]
- Wasilewski, M.; Pisarski, D.; Konowrocki, R.; Bajer, C.I. A New Efficient Adaptive Control of Torsional Vibrations Induced by Switched Nonlinear Disturbances. Int. J. Appl. Math. Comput. Sci. 2019, 29, 285–303. [Google Scholar] [CrossRef]
- Chomette, B.; Sinou, J.J. On the Use of Linear and Nonlinear Controls for Mechanical Systems Subjected to Friction-Induced Vibration. Appl. Sci. 2020, 10, 2085. [Google Scholar] [CrossRef]
- Sadeghimehr, R.; Nikoofard, A.; Sedigh, A.K. Predictive-based sliding mode control for mitigating torsional vibration of drill string in the presence of input delay and external disturbance. J. Vib. Control 2020. [Google Scholar] [CrossRef]
- Ullah, F.K.; Duarte, F.; Bohn, C. A novel backstepping approach for the attenuation of torsional oscillations in drill strings. In Solid State Phenomena; Trans Tech Publications Ltd.: Freienbach, Switzerland, 2016; pp. 85–92. [Google Scholar]
- Bar-Kana, I. Parallel feedforward and simplified adaptive control. Int. J. Adapt. Control. Signal Process. 1987, 1, 95–109. [Google Scholar] [CrossRef]
- Palis, S.; Kienle, A. Discrepancy based control of particulate processes. J. Process Control 2014, 24, 33–46. [Google Scholar] [CrossRef]
- Kim, H.; Kim, S.; Back, J.; Shim, H.; Seo, J.H. Design of stable parallel feedforward compensator and its application to synchronization problem. Automatica 2016, 64, 208–216. [Google Scholar] [CrossRef]
- Barkana, I. Positive-realness in discrete-time adaptive control systems. Int. J. Syst. Sci. 1986, 17, 1001–1006. [Google Scholar] [CrossRef]
- Iwai, Z.; Mizumoto, I.; Mingcong, D. A parallel feedforward compensator virtually realizing almost strictly positive real plant. In Proceedings of the 1994 33rd IEEE Conference on Decision and Control, Lake Buena Vista, FL, USA, 14–16 December 1994; Volume 3, pp. 2827–2832. [Google Scholar]
- Hackl, C. Non-Identifier Based Adaptive Control in Mechatronics; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Koser, K.; Pasin, F. Torsional Vibrations of the Drive Shafts of Mechanisms. J. Sound Vib. 1997, 199, 559–565. [Google Scholar] [CrossRef]
- Schiesser, W.E.; Griffiths, G.W. A Compendium of Partial Differential Equation Models: Method of Lines Analysis with Matlab; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Isidori, A. The zero dynamics of a nonlinear system: From the origin to the latest progresses of a long successful story. Eur. J. Control 2013, 19, 369–378. [Google Scholar] [CrossRef]
- Goodwin, G.C.; Graebe, S.F.; Salgado, M.E. Control System Design, 1st ed.; Prentice Hall PTR: Hoboken, NJ, USA, 2000. [Google Scholar]
- Golovin, I.; Palis, S. Robust control for active damping of elastic gantry crane vibrations. Mech. Syst. Signal Process. 2019, 121, 264–278. [Google Scholar] [CrossRef]
- Segovia, V.R.; Hägglund, T.; Åström, K. Measurement noise filtering for PID controllers. J. Process Control 2014, 24, 299–313. [Google Scholar] [CrossRef]


| Name | Symbol | Value | Unit |
|---|---|---|---|
| Density of the motor shaft | 8000 | [kg/m] | |
| Shear modulus of the motor shaft | G | 79.3 | [N/m] |
| Structural damping of the motor shaft | [Nms] | ||
| Length of the motor shaft | L | 1500 | [m] |
| Moment of inertia of the motor shaft | I | [m] | |
| Moments of inertia of the first mass | 150 | [kg m] | |
| Moments of inertia of the second mass | 1500 | [kg m] | |
| Viscous friction on the first mass | 2000 | [Nms] | |
| Coulomb friction torque | 165 | [Nm] | |
| Viscous dissipation torque | 20 | [Nms] | |
| Static friction torque | 515 | [Nm] | |
| Stribeck parameter | [−] | ||
| Slope in the region of zero velocity | [−] |
| Cases | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 9.27 | 8.22 | 10.46 | 9 | 12.25 | 9.92 | 9.80 | 8.68 | 11.15 | |
| 16.62 | 21.15 | 20.64 | 16.11 | 13.94 | 20.15 | 17.12 | 28.07 | 21.25 | |
| 8.97 | 4.32 | 15.08 | 5.53 | 2.04 | 12.01 | 12.96 | 9.48 | 18.52 |
| Cases | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 7.44 | 6.40 | 8.62 | 7.26 | 10.46 | 8.12 | 7.91 | 6.71 | 9.28 | |
| 15 | 19.26 | 23.03 | 14.90 | 14.18 | 18.51 | 15.22 | 26.26 | 34.05 | |
| 12.74 | 5.38 | 22.79 | 7.44 | 1.92 | 18 | 19.03 | 11.57 | 28.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Golovin, I.; Palis, S. PFC-Based Control of Friction-Induced Instabilities in Drive Systems. Machines 2021, 9, 134. https://doi.org/10.3390/machines9070134
Golovin I, Palis S. PFC-Based Control of Friction-Induced Instabilities in Drive Systems. Machines. 2021; 9(7):134. https://doi.org/10.3390/machines9070134
Chicago/Turabian StyleGolovin, Ievgen, and Stefan Palis. 2021. "PFC-Based Control of Friction-Induced Instabilities in Drive Systems" Machines 9, no. 7: 134. https://doi.org/10.3390/machines9070134
APA StyleGolovin, I., & Palis, S. (2021). PFC-Based Control of Friction-Induced Instabilities in Drive Systems. Machines, 9(7), 134. https://doi.org/10.3390/machines9070134






