Development and Application of Fuzzy Proportional-Integral Control Scheme in Pitch Angle Compensation Loop for Wind Turbines
Abstract
:1. Introduction
- The combination of the control of rotor speed and output power using fuzzy tuned PI in power control, allowing the changeable tuning of PI parameters depending on system conditions;
- Regulating the output power while maintaining the desired rotor speed and avoiding equipment overloads;
- For power levels below a nominal value, the power is controlled to reduce the turbine speed according to the power–speed curve (tracking curve) illustrated in [31]. This is approximated by adjusting the reference speed.
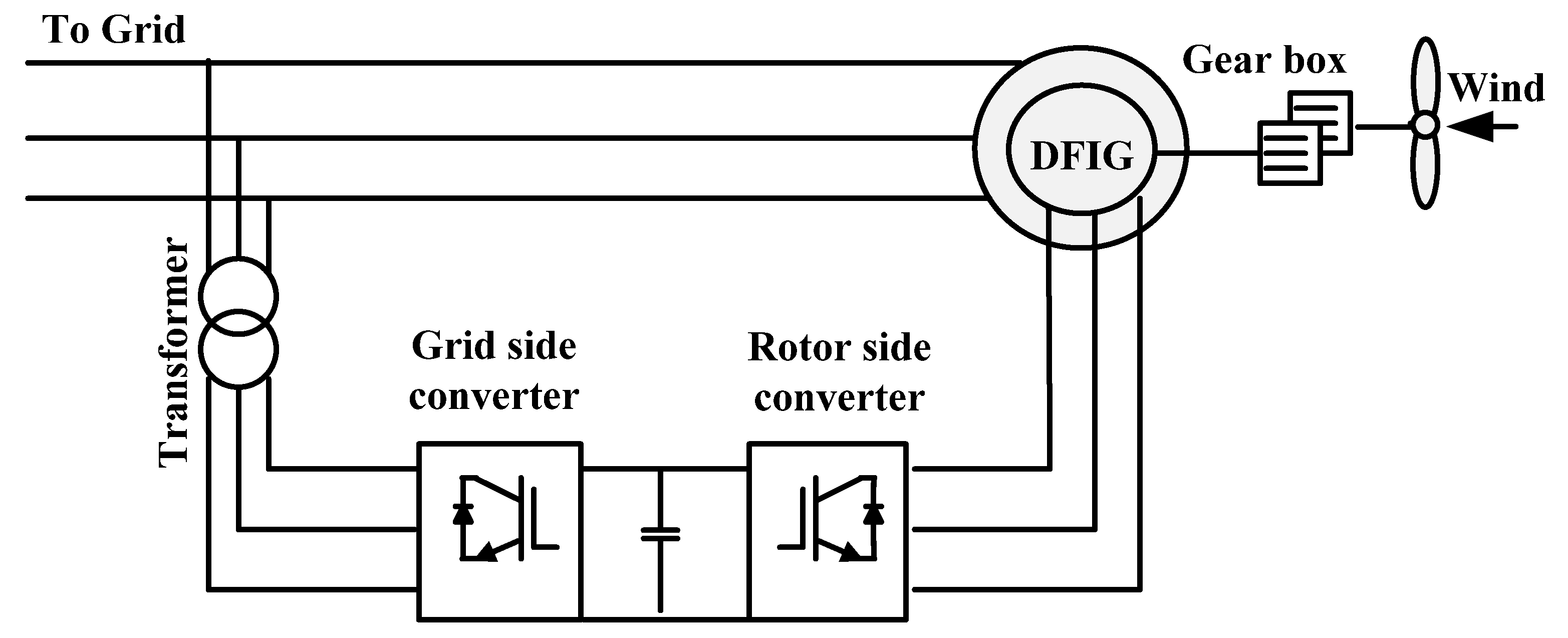
2. Wind Turbine Aerodynamics
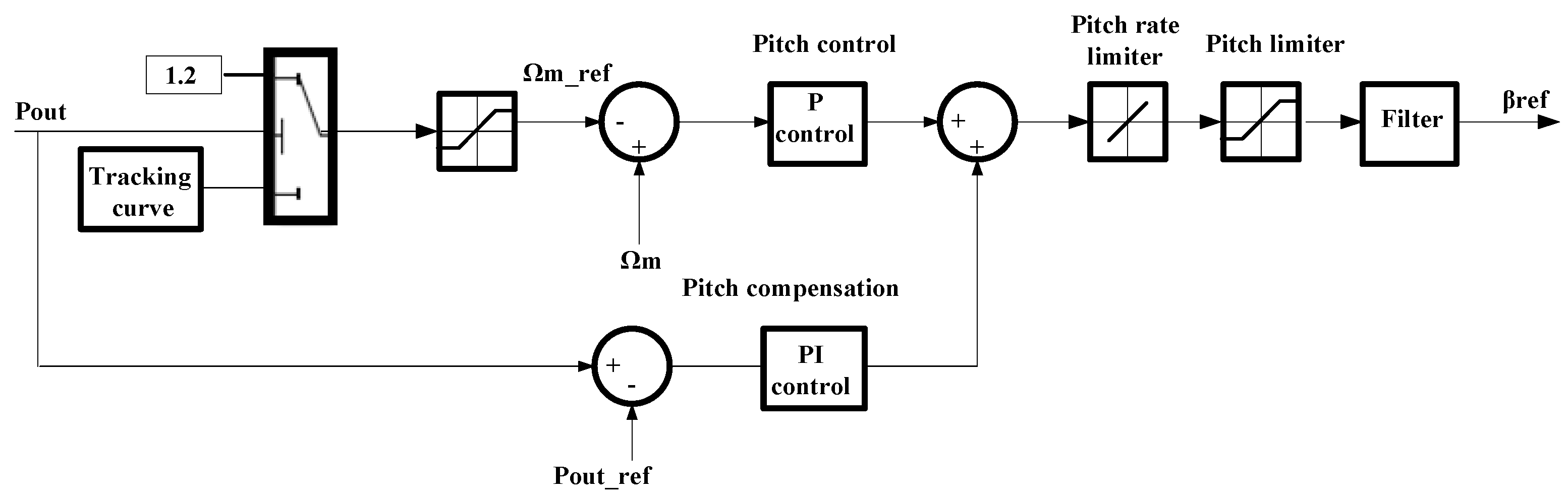
3. Pitch Angle Control
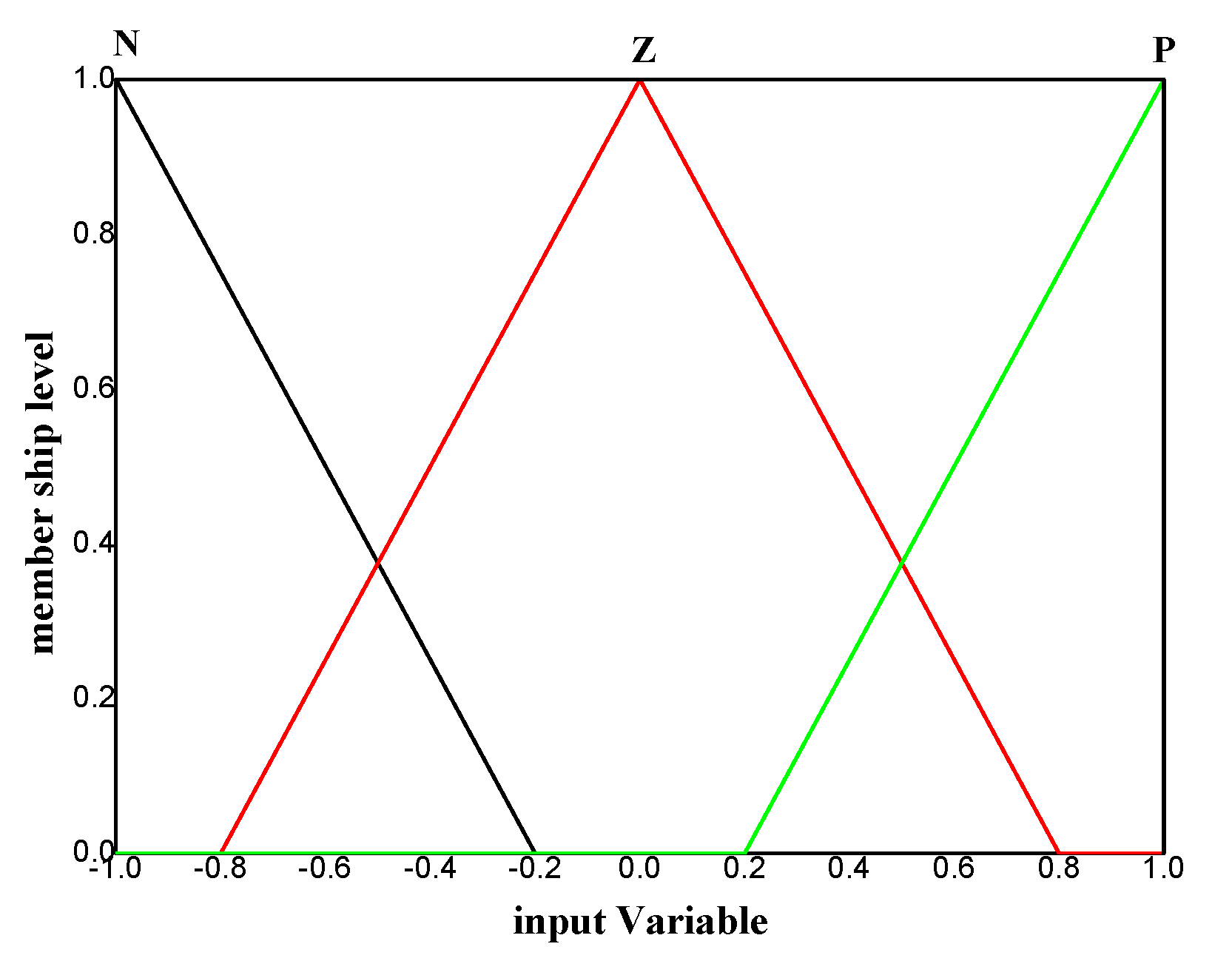
4. Fuzzy Logic Approach
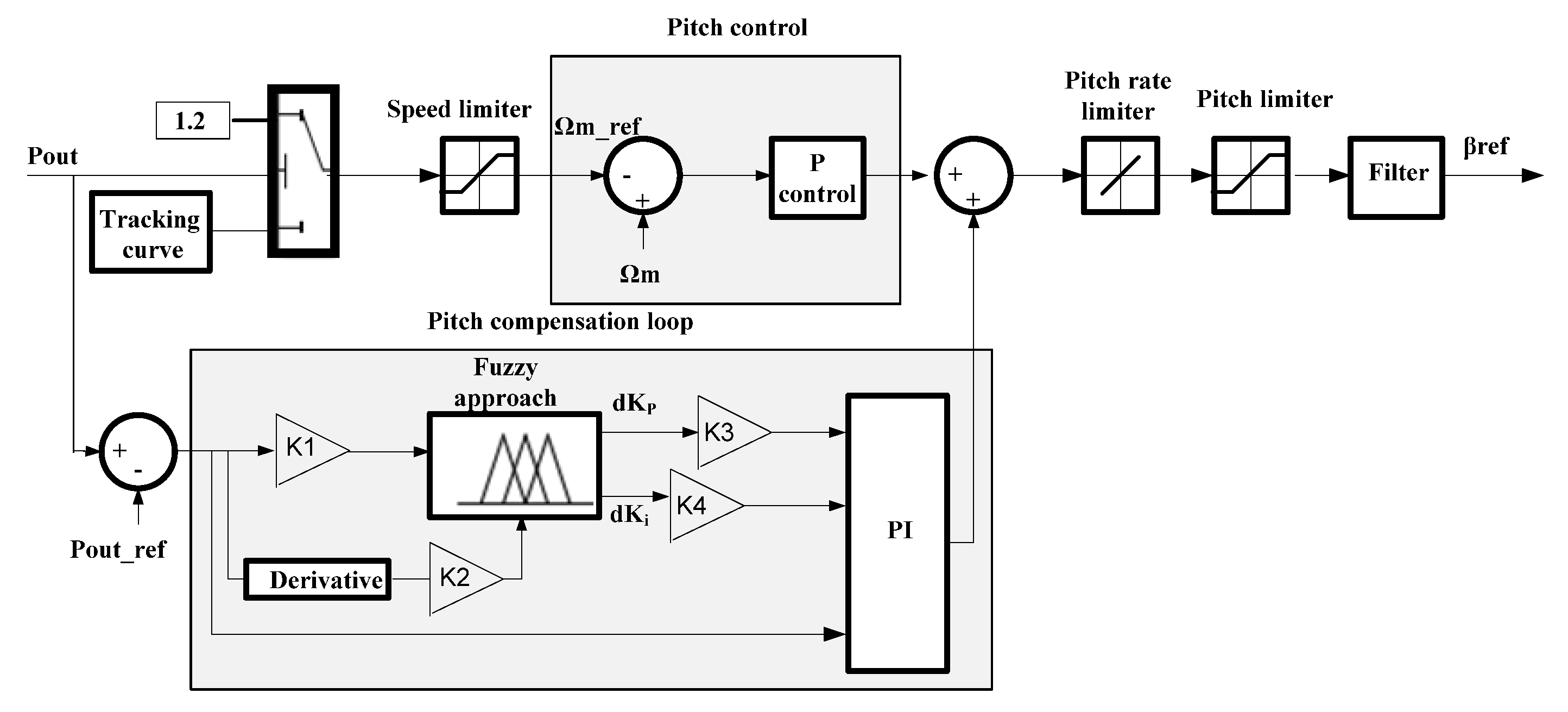
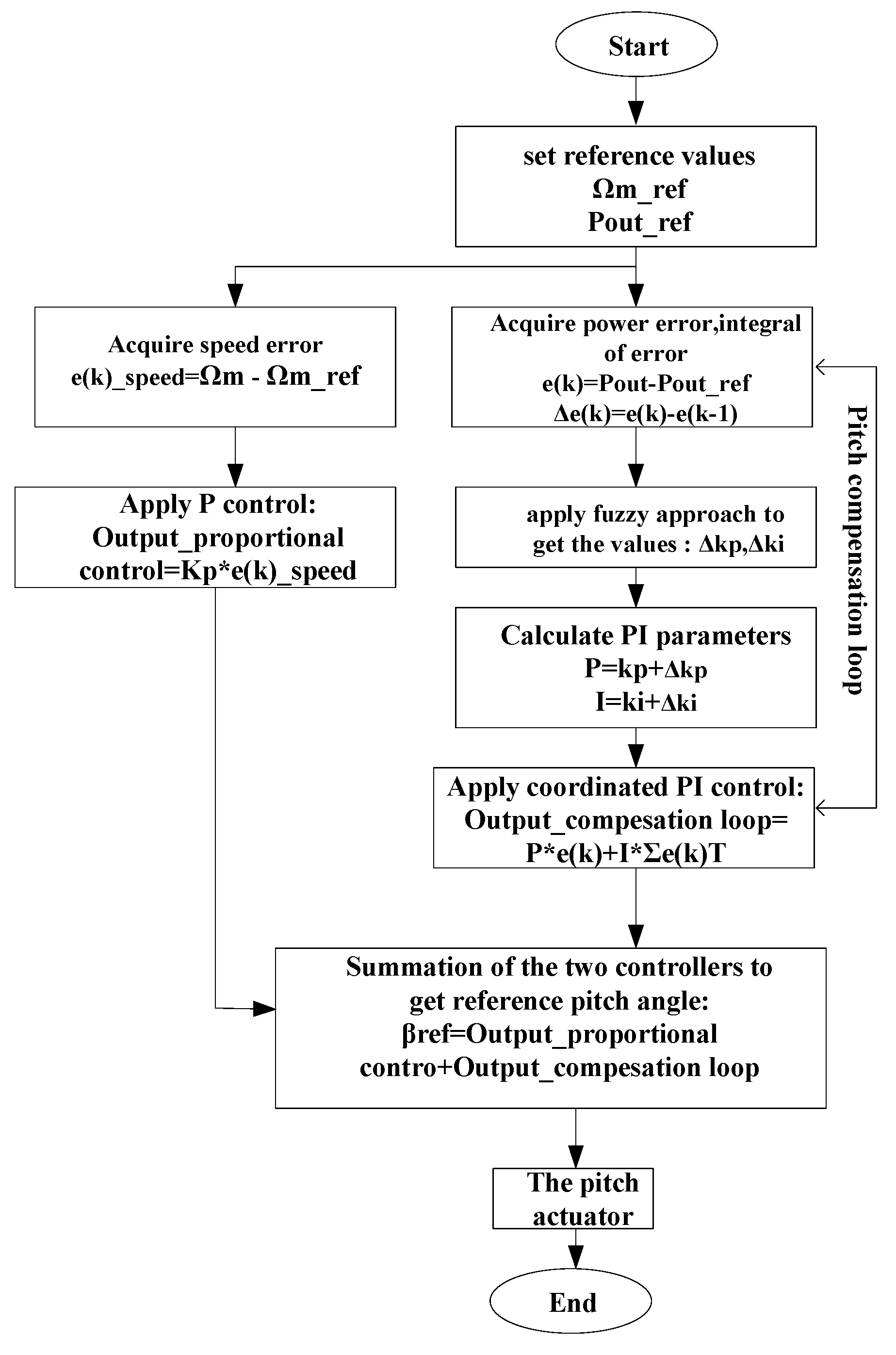
5. Designing and Applying Fuzzy PI in Pitch Angle Control
- IF e is P and Δe is P THEN dkp is NB.
- IF e is Z and Δe is P THEN dkp is Z.
- IF e is N and Δe is N THEN dkp is PB.
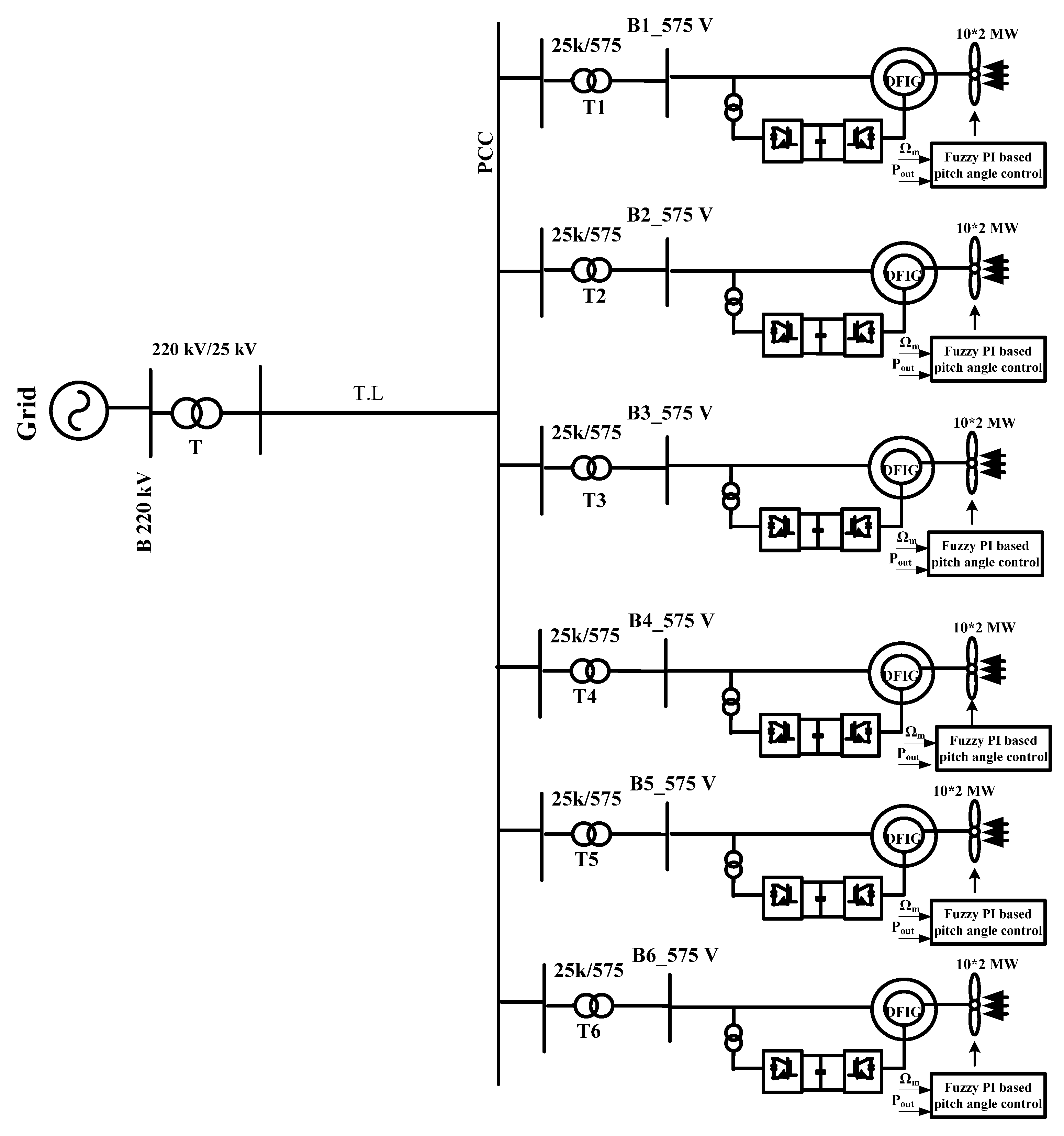
6. Model Configuration and Results Discussion
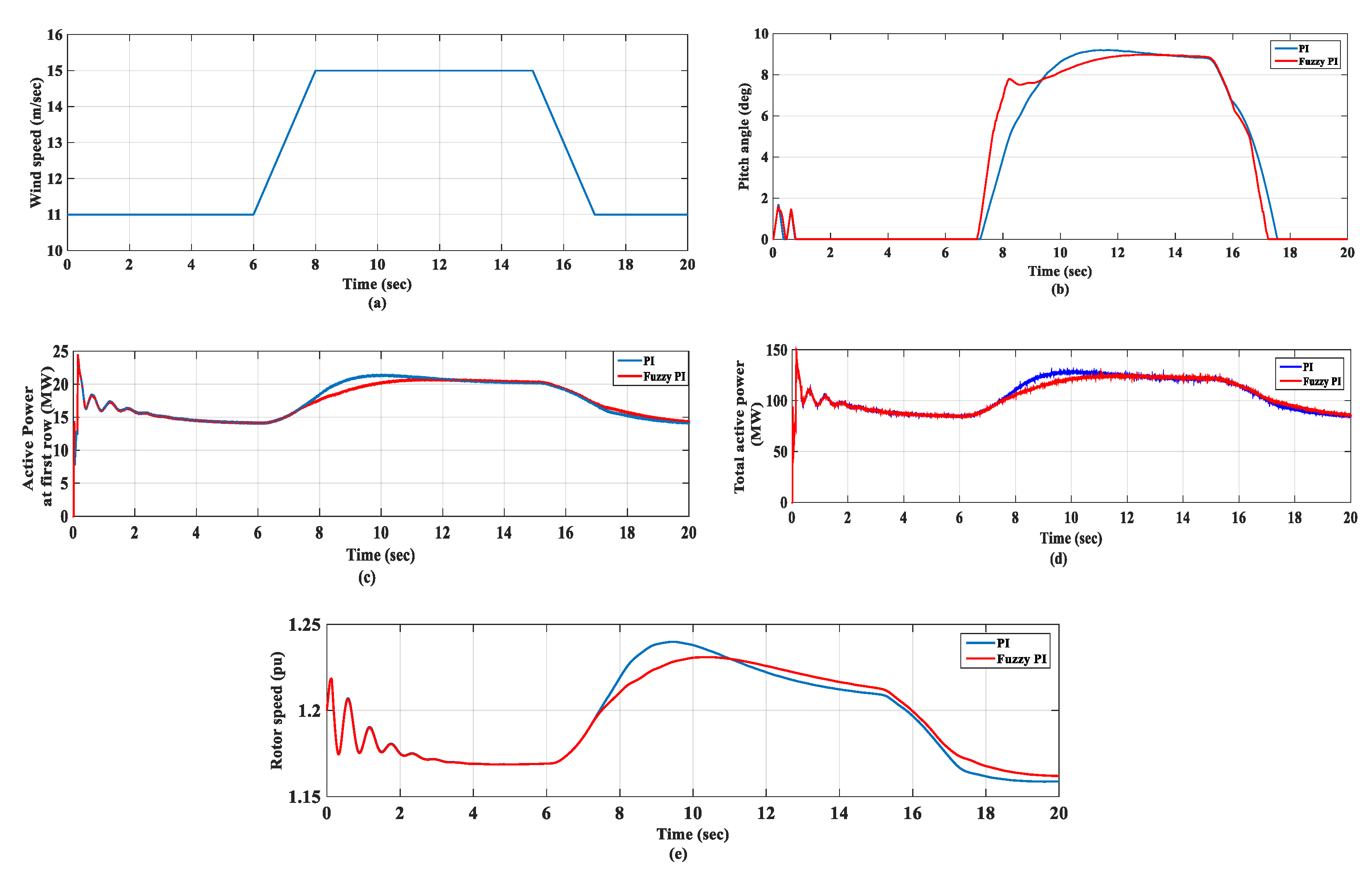
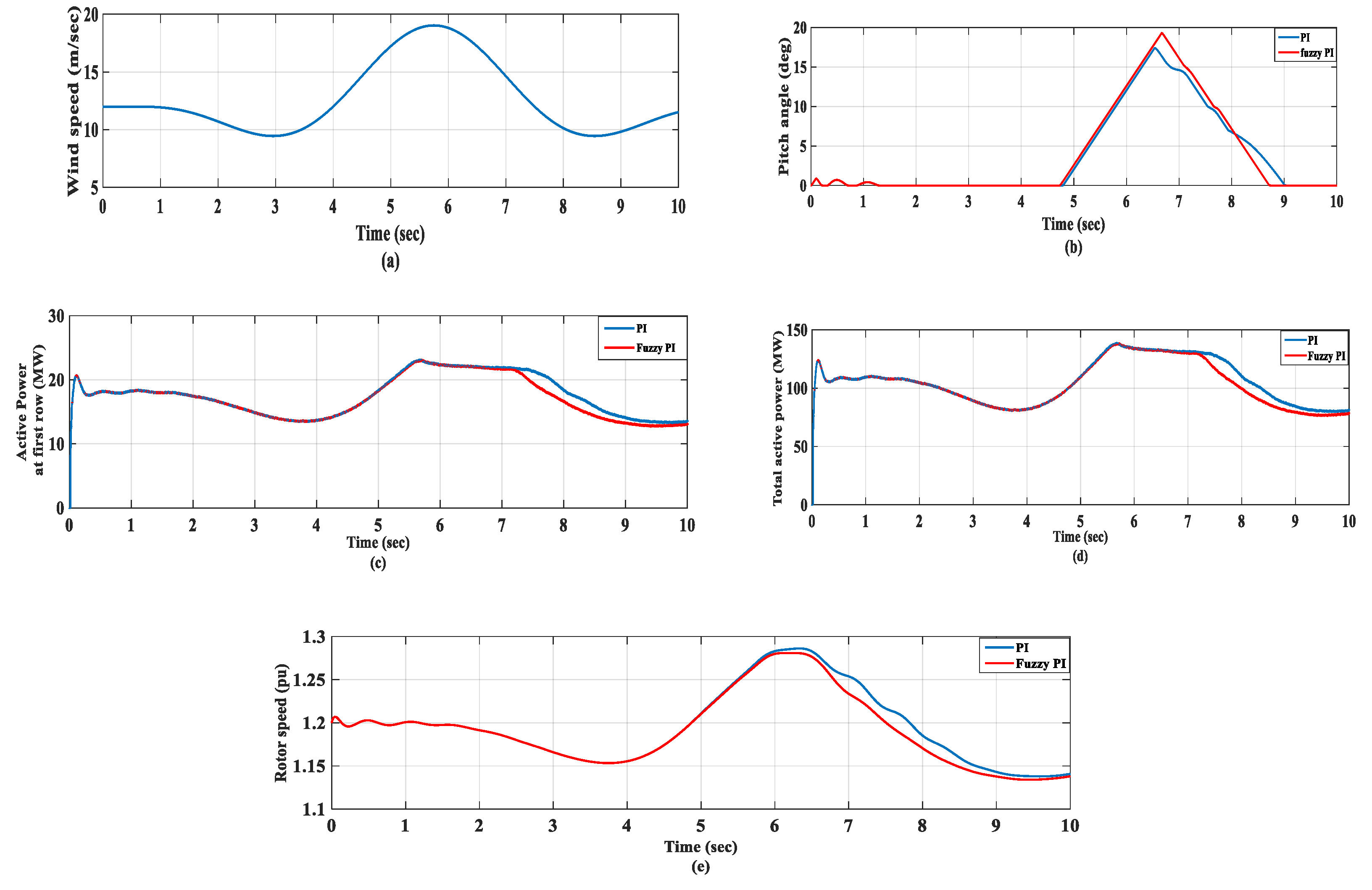
6.1. Ramp Wind Speed
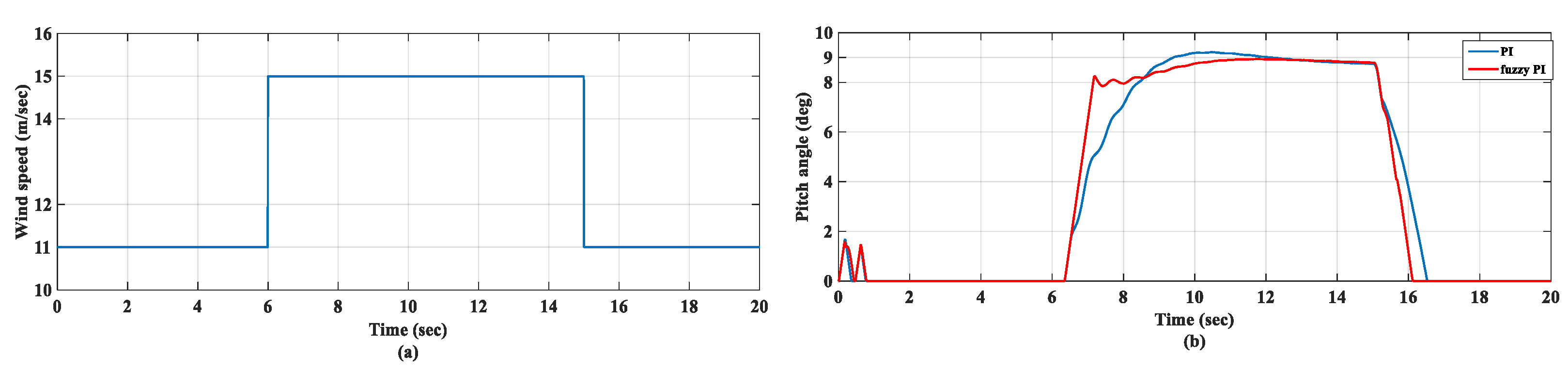
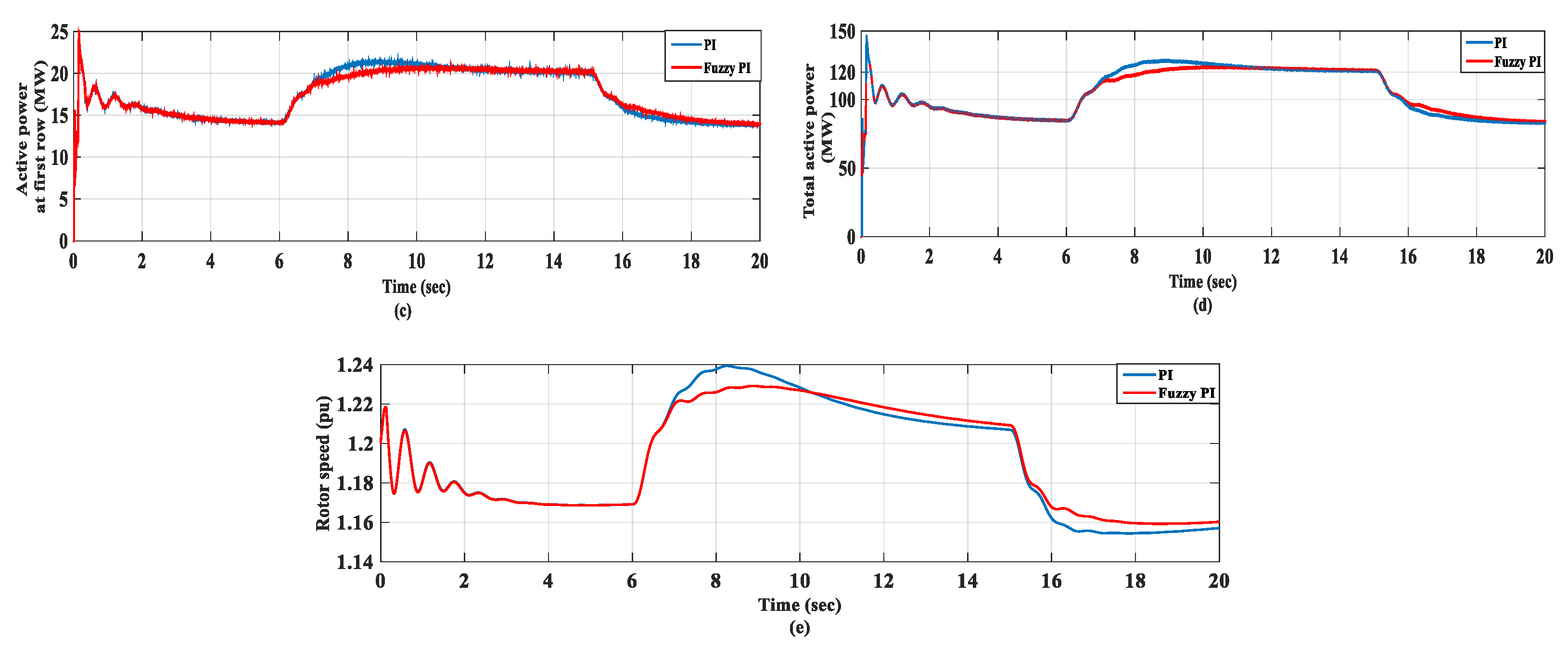
6.2. Step Wind Speed
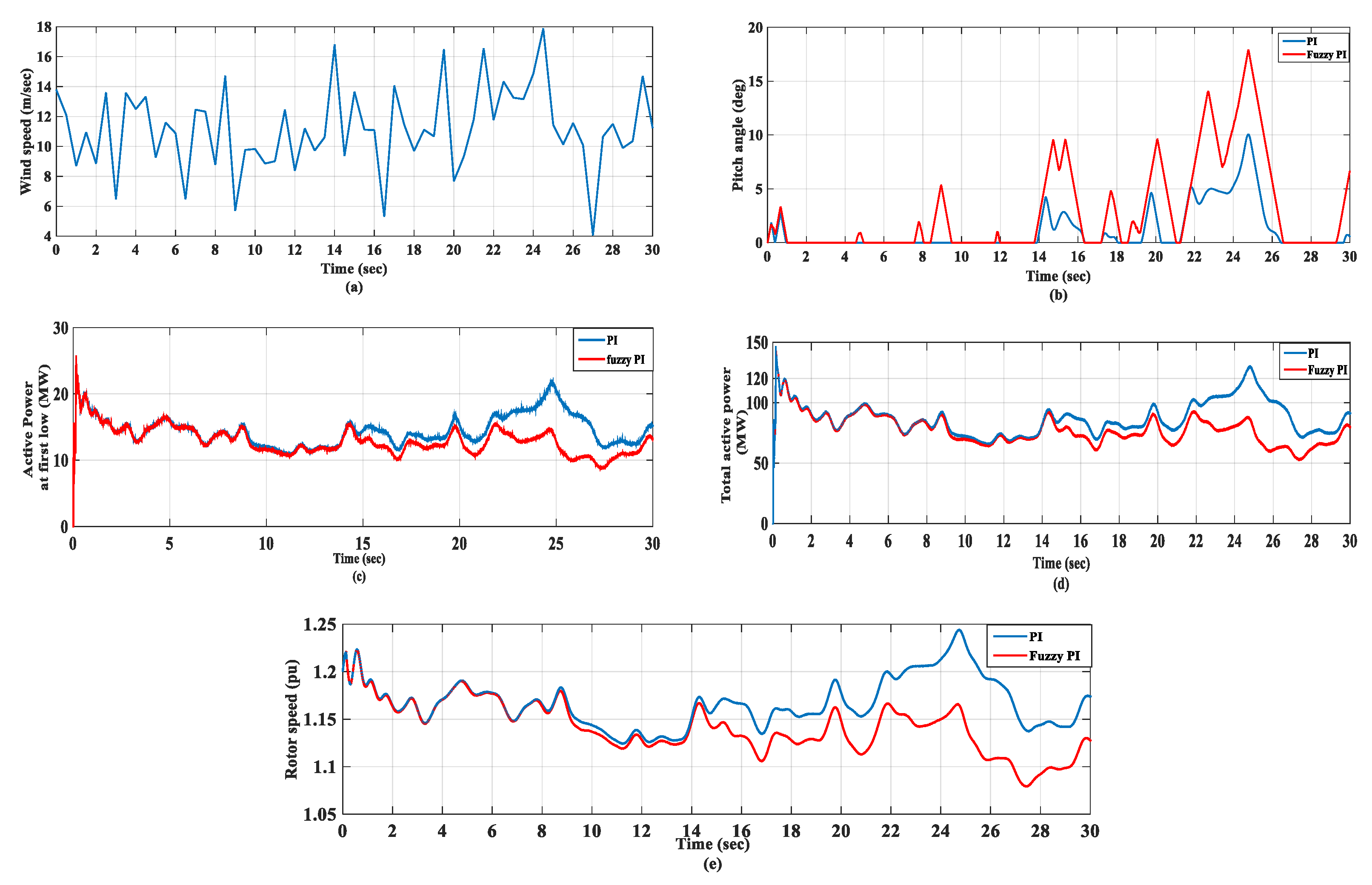
6.3. Random Wind Speed
6.4. Extreme Wind Speed
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Whittlesey, R. Vertical axis wind turbines: Farm and turbine design. In Wind Energy Engineering; Elsevier: Amsterdam, The Netherlands, 2017; pp. 185–202. [Google Scholar]
- Giaourakis, D.G.; Safacas, A.N. Effect of short-circuit faults in the back-to-back power electronic converter and rotor terminals on the operational behavior of the doubly-fed induction generator wind energy conversion system. Machines 2015, 3, 2–26. [Google Scholar] [CrossRef] [Green Version]
- Abdelrahem, M.; Hackl, C.M.; Kennel, R. Limited-Position Set Model-Reference Adaptive Observer for Control of DFIGs without Mechanical Sensors. Machines 2020, 8, 72. [Google Scholar] [CrossRef]
- Habibi, H.; Howard, I.; Simani, S. Reliability improvement of wind turbine power generation using model-based fault detection and fault tolerant control: A review. Renew. Energy 2019, 135, 877–896. [Google Scholar] [CrossRef]
- Lio, W.H.; Jones, B.L.; Rossiter, J.A. Estimation and control of wind turbine tower vibrations based on individual blade-pitch strategies. IEEE Trans. Control Syst. Technol. 2018, 27, 1820–1828. [Google Scholar] [CrossRef] [Green Version]
- Apata, O.; Oyedokun, D. An Overview of Control Techniques for Wind Turbine Systems. Sci. Afr. 2020, 10, e00566. [Google Scholar] [CrossRef]
- Yang, Q.; Jiao, X.; Luo, Q.; Chen, Q.; Sun, Y. L1 adaptive pitch angle controller of wind energy conversion systems. ISA Trans. 2020, 103, 28–36. [Google Scholar] [CrossRef]
- Dida, A.; Merahi, F.; Mekhilef, S. New grid synchronization and power control scheme of doubly-fed induction generator based wind turbine system using fuzzy logic control. Comput. Electr. Eng. 2020, 84, 106647. [Google Scholar] [CrossRef]
- De Carvalho, W.C.; Bataglioli, R.P.; Fernandes, R.A.; Coury, D.V. Fuzzy-based approach for power smoothing of a full-converter wind turbine generator using a supercapacitor energy storage. Electr. Power Syst. Res. 2020, 184, 106287. [Google Scholar] [CrossRef]
- Samet, H.; Ketabipoor, S.; Vafamand, N. EKF-based TS fuzzy prediction for eliminating the extremely fast reactive power variations in Manjil wind farm. Electr. Power Syst. Res. 2021, 199, 107422. [Google Scholar] [CrossRef]
- Fekry, H.M.; Eldesouky, A.A.; Kassem, A.M.; Abdelaziz, A.Y. Power Management Strategy Based on Adaptive Neuro Fuzzy Inference System for AC Microgrid. IEEE Access 2020, 8, 192087–192100. [Google Scholar] [CrossRef]
- Prakash, A.O.; Banu, R.N.; Devaraj, D. Maximum Energy Extraction of a Wind Farm Using Pitch Angle Control. In Proceedings of the 2019 IEEE International Conference on Intelligent Techniques in Control, Optimization and Signal Processing (INCOS), Tamilnadu, India, 11–13 April 2019; pp. 1–7. [Google Scholar]
- Li, P.; Song, Y.D.; Li, D.Y.; Cai, W.C.; Zhang, K. Control and monitoring for grid-friendly wind turbines: Research overview and suggested approach. IEEE Trans. Power Electron. 2014, 30, 1979–1986. [Google Scholar] [CrossRef]
- Iqbal, A.; Ying, D.; Saleem, A.; Hayat, M.A.; Mehmood, K. Efficacious pitch angle control of variable-speed wind turbine using fuzzy based predictive controller. Energy Rep. 2020, 6, 423–427. [Google Scholar] [CrossRef]
- Bououden, S.; Chadli, M.; Filali, S.; El Hajjaji, A. Fuzzy model based multivariable predictive control of a variable speed wind turbine: LMI approach. Renew. Energy 2012, 37, 434–439. [Google Scholar] [CrossRef]
- Poultangari, I.; Shahnazi, R.; Sheikhan, M. RBF neural network based PI pitch controller for a class of 5-MW wind turbines using particle swarm optimization algorithm. ISA Trans. 2012, 51, 641–648. [Google Scholar] [CrossRef] [PubMed]
- Jia, C.; Wang, L.; Meng, E.; Chen, L.; Liu, Y.; Jia, W.; Bao, Y.; Liu, Z. Combining LIDAR and LADRC for intelligent pitch control of wind turbines. Renew. Energy 2021, 169, 1091–1105. [Google Scholar] [CrossRef]
- Frost, S.A.; Balas, M.J.; Wright, A.D. Direct adaptive control of a utility-scale wind turbine for speed regulation. Int. J. Robust Nonlinear Control IFAC-Affil. J. 2009, 19, 59–71. [Google Scholar] [CrossRef]
- Badihi, H.; Zhang, Y.; Pillay, P.; Rakheja, S. Fault-Tolerant Individual Pitch Control for Load Mitigation in Wind Turbines with Actuator Faults. IEEE Trans. Ind. Electron. 2020, 68, 532–543. [Google Scholar] [CrossRef]
- Sarkar, M.R.; Julai, S.; Tong, C.W.; Uddin, M.; Romlie, M.; Shafiullah, G. Hybrid pitch angle controller approaches for stable wind turbine power under variable wind speed. Energies 2020, 13, 3622. [Google Scholar] [CrossRef]
- Bashetty, S.; Guillamon, J.I.; Mutnuri, S.S.; Ozcelik, S. Design of a robust adaptive controller for the pitch and torque control of wind turbines. Energies 2020, 13, 1195. [Google Scholar] [CrossRef] [Green Version]
- Rashid, A.; Ying, D. Fuzzy Inference Based Approach for Pitch Angle Control of Variable Speed Variable Pitch Wind Turbine. In Proceedings of the 2020 Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 28–31 May 2020; pp. 1051–1056. [Google Scholar]
- Ren, H.; Hou, B.; Zhou, G.; Shen, L.; Wei, C.; Li, Q. Variable pitch active disturbance rejection control of wind turbines based on BP neural network PID. IEEE Access 2020, 8, 71782–71797. [Google Scholar] [CrossRef]
- Tang, X.; Yin, M.; Shen, C.; Xu, Y.; Dong, Z.Y.; Zou, Y. Active power control of wind turbine generators via coordinated rotor speed and pitch angle regulation. IEEE Trans. Sustain. Energy 2018, 10, 822–832. [Google Scholar] [CrossRef]
- Yin, X.; Zhao, X. Composite hierarchical pitch angle control for a tidal turbine based on the uncertainty and disturbance estimator. IEEE Trans. Ind. Electron. 2019, 67, 329–339. [Google Scholar] [CrossRef]
- De, T.; Rashid, A.; Ying, D.; Sheng, L.H. Pitch Angle Control of Modern Variable Speed Variable Pitch Wind Turbine Based on Linear Active Disturbance Rejection Control Approach. In Proceedings of the 2020 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Chengdu, China, 13–16 July 2020; pp. 1382–1387. [Google Scholar]
- Datta, U.; Shi, J.; Kalam, A. Primary frequency control of a microgrid with integrated dynamic sectional droop and fuzzy based pitch angle control. Int. J. Electr. Power Energy Syst. 2019, 111, 248–259. [Google Scholar] [CrossRef]
- Prasad, R.; Padhy, N.P. Synergistic frequency regulation control mechanism for DFIG wind turbines with optimal pitch dynamics. IEEE Trans. Power Syst. 2020, 35, 3181–3191. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Kalkman, I.; Blocken, B. Effect of pitch angle on power performance and aerodynamics of a vertical axis wind turbine. Appl. Energy 2017, 197, 132–150. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.C.; Kuo, C.H. Effects of pitch angle and blade camber on flow characteristics and performance of small-size Darrieus VAWT. J. Vis. 2013, 16, 65–74. [Google Scholar] [CrossRef]
- Miller, N.W.; Sanchez-Gasca, J.J.; Price, W.W.; Delmerico, R.W. Dynamic modeling of GE 1.5 and 3.6 MW wind turbine-generators for stability simulations. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting (IEEE Cat. No. 03CH37491), Toronto, ON, Canada, 13–17 July 2003; pp. 1977–1983. [Google Scholar]
- Mahvash, H.; Taher, S.A.; Rahimi, M.; Shahidehpour, M. Enhancement of DFIG performance at high wind speed using fractional order PI controller in pitch compensation loop. Int. J. Electr. Power Energy Syst. 2019, 104, 259–268. [Google Scholar] [CrossRef]
- Noureldeen, O.; Rashad, A. Modeling and investigation of Gulf El-Zayt wind farm for stability studying during extreme gust wind occurrence. Ain Shams Eng. J. 2014, 5, 137–148. [Google Scholar] [CrossRef] [Green Version]
- Pathak, D.; Gaur, P. A fractional order fuzzy-proportional-integral-derivative based pitch angle controller for a direct-drive wind energy system. Comput. Electr. Eng. 2019, 78, 420–436. [Google Scholar] [CrossRef]
- Abad, G.; Lopez, J.; Rodriguez, M.; Marroyo, L.; Iwanski, G. Doubly Fed Induction Machine: Modeling and Control for Wind Energy Generation; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 85. [Google Scholar]
- Smajo, J.; Vukadinovic, D. Electromagnetic torque analysis of a DFIG for wind turbines. WSEAS Trans. Syst. 2008, 7, 479–488. [Google Scholar]
- Tiwari, R.; Babu, N.R. Recent developments of control strategies for wind energy conversion system. Renew. Sustain. Energy Rev. 2016, 66, 268–285. [Google Scholar] [CrossRef]
- Kose, U. Fundamentals of fuzzy logic with an easy-to-use, interactive fuzzy control application. Int. J. Mod. Eng. Res. 2012, 2, 1198–1203. [Google Scholar]
- Kanagaraj, N.; Sivashanmugam, P.; Paramasivam, S. Fuzzy coordinated PI controller: Application to the real-time pressure control process. Adv. Fuzzy Syst. 2008, 2008, 691808. [Google Scholar] [CrossRef] [Green Version]
- Amarendra Reddy, B.; Ram Charan, K.; Kranti Kiran, A.; Ramalingeswara Prasad, K. Control of Non-Linear Systems Using Parallel Structure of Fuzzy PI+PD Controller. Int. J. Eng. Sci. Technol. 2010, 2, 3422–3433. [Google Scholar]
- Civelek, Z.; Lüy, M.; Çam, E.; Barışçı, N. Control of pitch angle of wind turbine by fuzzy PID controller. Intell. Autom. Soft Comput. 2016, 22, 463–471. [Google Scholar] [CrossRef]
- Ngo, Q.V.; Chai, Y.; Nguyen, T.T. The fuzzy-PID based-pitch angle controller for small-scale wind turbine. Int. J. Power Electron. Drive Syst. 2020, 11, 135. [Google Scholar] [CrossRef] [Green Version]
- Badihi, H.; Zhang, Y.; Hong, H. Fuzzy gain-scheduled active fault-tolerant control of a wind turbine. J. Frankl. Inst. 2014, 351, 3677–3706. [Google Scholar] [CrossRef]
- Pan, T.; Ma, Z. Wind turbine individual pitch control for load reduction based on fuzzy controller design. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2013, 227, 320–328. [Google Scholar] [CrossRef]
- Lasheen, A.; Elshafei, A.L. Wind-turbine collective-pitch control via a fuzzy predictive algorithm. Renew. Energy 2016, 87, 298–306. [Google Scholar] [CrossRef]



| dkp | Derivative of Error | |||
|---|---|---|---|---|
| P | Z | N | ||
| Error | P | NB | NM | NS |
| Z | Z | Z | Z | |
| N | PS | PM | PB | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AlGhamdi, S.; Hamdan, I.; Youssef, M.M.M.; Noureldeen, O. Development and Application of Fuzzy Proportional-Integral Control Scheme in Pitch Angle Compensation Loop for Wind Turbines. Machines 2021, 9, 135. https://doi.org/10.3390/machines9070135
AlGhamdi S, Hamdan I, Youssef MMM, Noureldeen O. Development and Application of Fuzzy Proportional-Integral Control Scheme in Pitch Angle Compensation Loop for Wind Turbines. Machines. 2021; 9(7):135. https://doi.org/10.3390/machines9070135
Chicago/Turabian StyleAlGhamdi, S., I. Hamdan, Marwa M. M. Youssef, and Omar Noureldeen. 2021. "Development and Application of Fuzzy Proportional-Integral Control Scheme in Pitch Angle Compensation Loop for Wind Turbines" Machines 9, no. 7: 135. https://doi.org/10.3390/machines9070135
APA StyleAlGhamdi, S., Hamdan, I., Youssef, M. M. M., & Noureldeen, O. (2021). Development and Application of Fuzzy Proportional-Integral Control Scheme in Pitch Angle Compensation Loop for Wind Turbines. Machines, 9(7), 135. https://doi.org/10.3390/machines9070135






