Iron Loss Analysis of a Concentrated Winding Type Interior Permanent Magnet Synchronous Motor with Single and Dual Layer Magnet Shape

Abstract

In this study, the iron losses of high flux density concentrated winding-type interior permanent magnet synchronous motors for three different magnet shapes (single-V, single-flat, and dual-delta) and rotor structures are analyzed and compared. Iron loss is analyzed using the classical Steinmetz equation (CSE) based on the frequency separation approach using the iron loss material table, and each rotor type is compared. In addition, to validate the hysteresis loss for each rotor type, two additional analyses are performed. In the methods considered, the number of minor loops is counted, and the area is calculated based on DC bias. The eddy current loss is compared using two approaches: CSE base frequency separation and the homogenization method considering the skin effect. This study primarily focuses on the comparison of relative iron losses based on different rotor topologies instead of absolute comparisons.

1. Introduction

In the conventional loss separation concept [1,2,3], the total power loss can be expressed as the sum of three independent terms, considering the harmonic and rotational fluxes. However, in many cases, the magnetic flux waveform in the laminated core of an electrical machine is not sinusoidal, and the hysteresis loop contains many minor loops [4,5,6,7]. Therefore, iron loss separation concepts [1,2,3] are insufficient for electric machines with high flux saturation.

In this study, three hysteresis losses were compared. The first hysteresis loss is the frequency separation method [1,2,3], the second method involves counting the number of minor loops, and the third method involves calculating the size of the minor loop based on DC bias. Eddy current losses were compared between the two methods. The first method is based on the loss separation concept [1,2,3], whereas the second analysis method is based on homogenization considering the skin effect. In general, a three-dimensional finite element method (FEM) analysis is required to consider the skin effect. However, using magnetic flux density data obtained from a magnetic field strength test is sufficient for a two-dimensional (2D)-FEM analysis. Therefore, in this study, the JMAG 2D FEM tool was used to perform iron loss analyses of inner permanent magnet synchronous motors (IP-MSMs) comprising high-saturation automotive air conditioner refrigerant compressors.

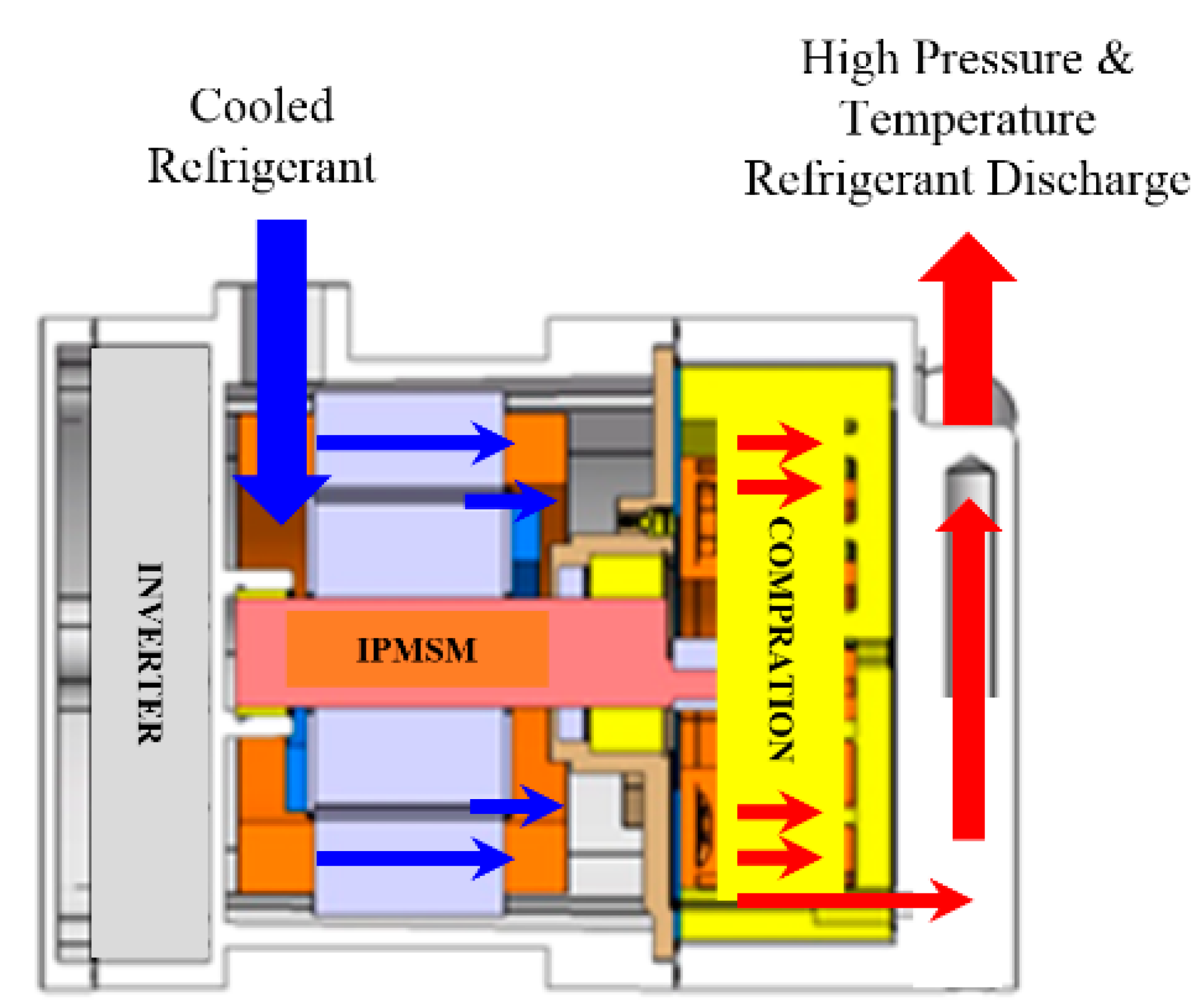
As shown in Figure 1, the IPMSM for driving an electric refrigerant compressor can perform cooling through the cold refrigerant directly through the motor; however, it is a typical high saturation magnetic flux density electric machine. This is because the inner permanent magnet rotor structure is applied to ensure high reliability, and a concentrated winding stator with low flow resistance and low power loss is used to achieve high volumetric efficiency in the compression part. Therefore, the proposed three iron loss analysis methods and three different rotor structures were compared with each other to compare the new iron loss analysis characteristics, and the rotor type with the lowest loss in the same concentrated winding stator structure can be determined.

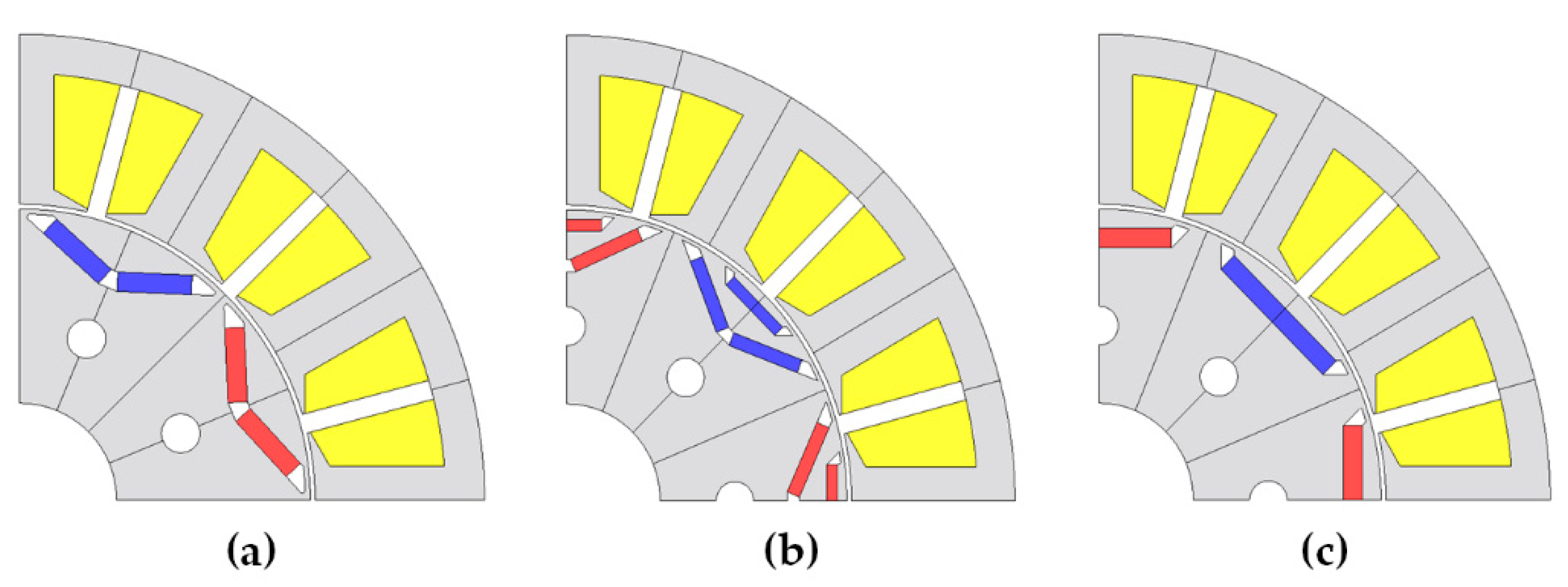
The detailed specifications of the concentrated winding-type IPMSMs for driving the A/C refrigerant compressor are as follows: number of slots in the stator, 12 slots; magnetic wire specification, 28 turns; stator core shape outside diameter, 96 mm; length, 37 mm. The three magnet shapes for comparison were single-V, single-flat (F), and dual-delta (D) magnets. The magnet area for every pole (30.73 mm²) was identical. The main operation points were 6540, 4905, 3270, and 1635 rpm with a 24 A phase current, and the expected torque was approximately 7.0. Figure 2 presents the structure of the concentrated windings of the IPMSMs with three types of rotor structures. Figure 3a illustrates a comparison of the induced voltages of the three different rotor shapes with identical concentrated winding stators without an input current at 1000 rpm. Figure 3b shows a fast Fourier transform (FFT) comparison of the frequency domain. The differential of the back electro-motive forces of the three magnet rotor shapes was lower than 0.25%. This is similar to the FFT results.

2. Iron Loss Calculation

2.1. First Iron Method

The CSE is a traditional method for calculating iron loss (1). However, it is constrained to account for all losses in a real laminated magnetic core. The modified Steinmetz equation (MSE) was modified based on the Bertotti model to reconcile this observed discrepancy. The MSE is still a typical and extensively used method for calculating iron loss; however, it requires additional fitting methods. The MSE is expressed as shown in Equation (2) [2,3]:

$$P_{fe}=P_{hys}+P_{eddy}=a_{hys}f\stackrel{\vee }{B^2}+b_{eddy}{f}^2\stackrel{\vee }{B^2}$$

(1)

$$P_{fe}=P_{hys}+P_{eddy}+P_{exs}=a_{hys}f\stackrel{\vee }{B^2}+b_{eddy}{f}^2\stackrel{\vee }{B^2}+c_{exs}{f}^{1.5}\stackrel{\vee }{B^{1.5}}$$

(2)

The MSE is a function of flux density and frequency. It is configured with static hysteresis losses P_hys, dynamic eddy current losses P_eddy, and excess losses P_exs, with their corresponding coefficients a_hys, b_eddy and c_exs, respectively. Moreover, f is the frequency, and $\stackrel{\vee }{B}$ is the maximum flux density.

In this study, the first iron loss method was based on electromagnetic FEM tools that use the specimen’s iron loss input data. This approach is based on sinusoidal flux conditions using the frequency separation method, and the CSE is fundamental. In other words, iron loss can be classified into two losses: $P_{eddy}$ and $P_{hys}$. This former iron loss method is easy, fast, and simple to calculate based on the FFT. However, it can be used to calculate the overall loss for all flux harmonics. The sum of the total iron losses is calculated as the sum of $P_{eddy}$ and $P_{hys}$, as shown in Equations (3) and (4) [8]:

$$P_{eddy}={\displaystyle \sum _{e=1}^{nelem}\left[{\displaystyle \sum _{k=1}^N{b}_{eddy}\left(\left|B_k\right|,f_k\right)·f_k^2}\right]}\times V_e$$

(3)

$$P_{hys}={\displaystyle \sum _{e=1}^{nelem}\left[{\displaystyle \sum _{k=1}^N{a}_{hys}\left(\left|B_k\right|\right)·f_k}\right]}\times V_e$$

(4)

where $f_k$ and $B_k$ are the frequency and amplitude of the magnetic flux density of k orders, respectively; $nelmen$ is the number of elements; $V_e$ is the element volume; $a_{hys}$ and $b_{eddy}$ are the coefficients of $P_{hys}$ and $P_{eddy}$, respectively.

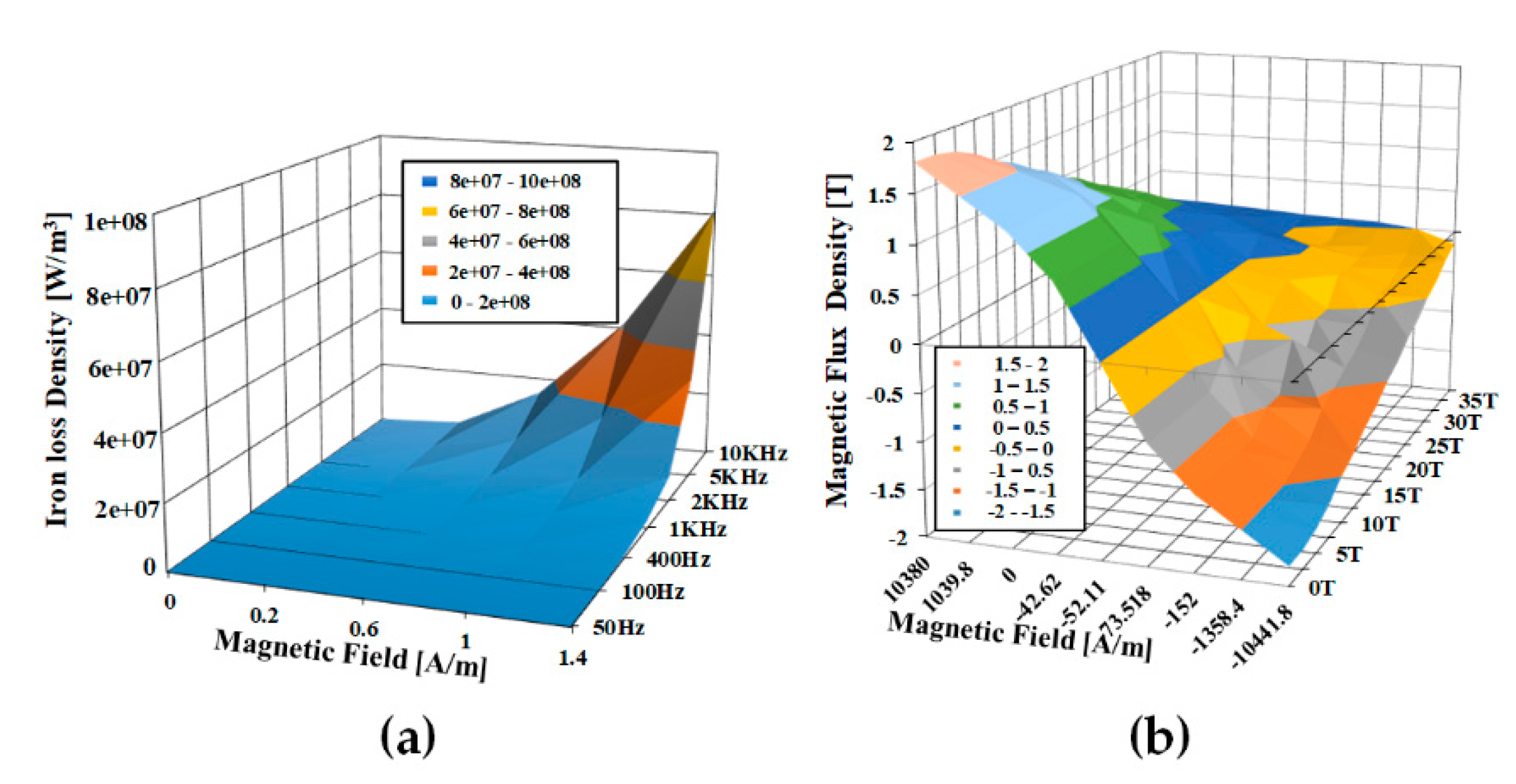
Figure 4a shows the measured iron loss data at two point-frequencies, which were used for other frequency loss estimations. Figure 4b shows the frequency-separation method. In this graph, $P_{fe}/f$ can be simplified and interpolated, as shown in Equation (5):

$$\frac{P_{fe}}{f}=a_{hys}(B)+b_{eddy}(B,f)f$$

(5)

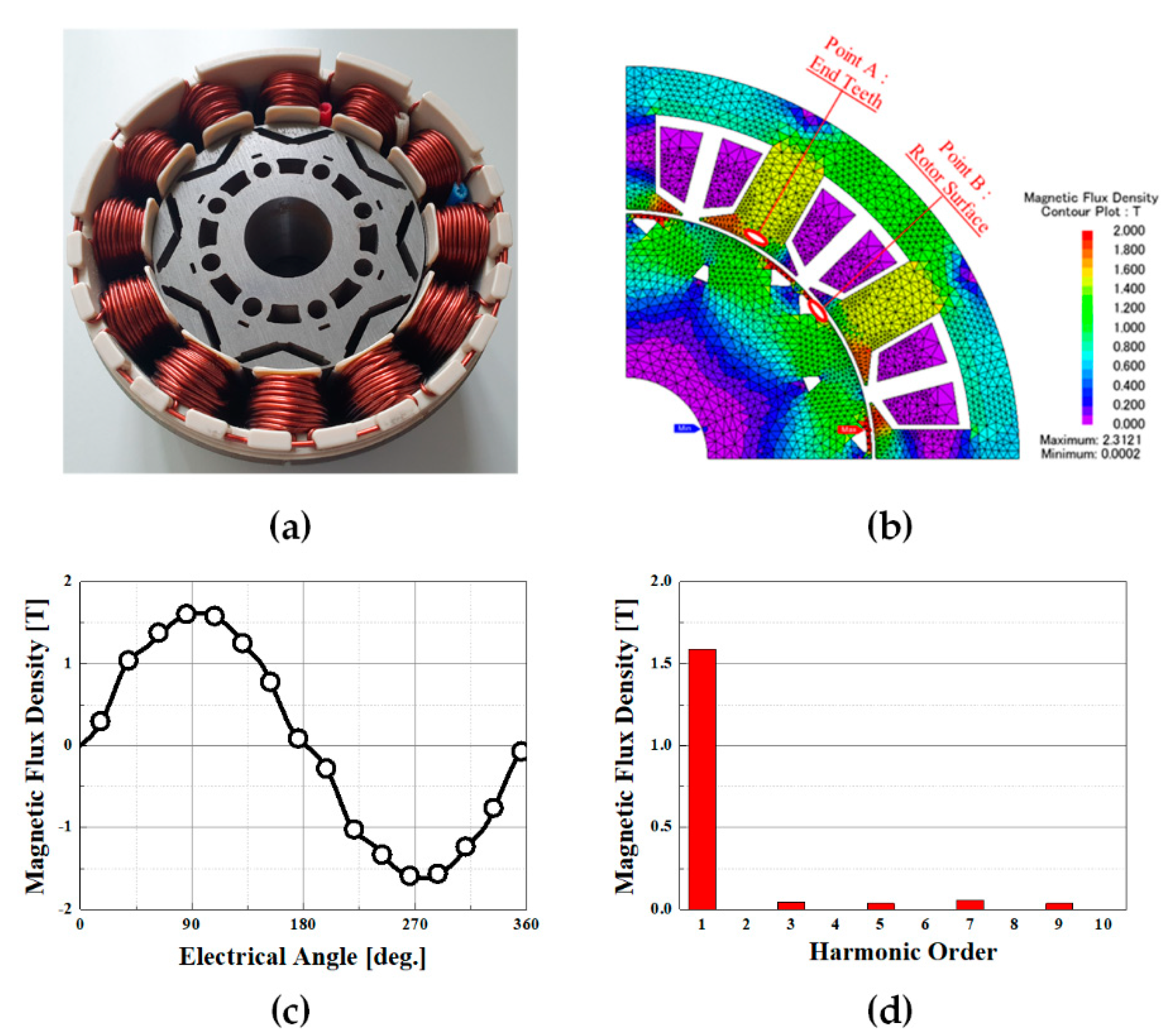
Figure 5a,b show a photograph of a prototype sample and the magnetic flux density distribution in a 2D plane. Figure 5c,d show the magnetic flux density of point A in the time frame and FFT analysis.

2.2. Second Iron Loss Method

The first method, i.e., the FFT frequency separation method, is simple; however, the minor loop effect caused by harmonics is not considered. Hence, by considering the dynamic hysteresis model, the minor loop effect and excess losses can be considered [5,6,7]. Therefore, the second iron loss calculation method is used to calculate the additional $P_{hys}$ separately, as shown in Equation (6) [8]:

$$P_{hys}={\displaystyle \sum _{e=1}^{nelem}\left[f{\displaystyle \sum _{l=1}^{nloop}{a}_{loop}}\left(\left|B_l\right|\right)\right]}$$

(6)

where $nloop$ is the number of loops, $B_l$ the $l$-th loop for each component of the magnetic flux density, and $a_{loop}$ the coefficient of the magnetic flux density.

2.3. Third Iron Loss Method

Calculations for $P_{eddy}$ in the first and second methods were used in the estimation method based on limited high-frequency experimental measurements, even when discrepancy was observed. This is due to the skin effect ($F_{sk}$) of the magnetic steel sheet surfaces. Equation (7) expresses the eddy current loss considering the skin effect [9]:

$$P_{ed\_Fsk}=\frac{1}{6}\sigma {\pi }^2{d}^2{\displaystyle \sum _{k=1}^n{f}_k^2\left[{\left(\stackrel{\vee }{B_{x,k}^a}\right)}^2+{\left(\stackrel{\vee }{B_{y,k}^a}\right)}^2\right]}·F_{sk}({\lambda }_k)$$

(7)

Here, $d$ (z-plane) is the material thickness, $w$ (x-plane) the width, $l$ (y-plane) the length, and $\mu$ a constant; $f_k$ contains $k$ frequencies with amplitudes $\stackrel{\vee }{B_{x,k}^a}$ and $\stackrel{\vee }{B_{y,k}^a}$ of the average induction. The skin effect comprises $F_{sk}$ factors, which are functions of the ratio ${\lambda }_k$ of $d$ and ${\delta }_k$ (skin depths depend on frequency). The skin effect can be summarized as follows and is represented as shown in Equations (8) and (9) [9]:

$$F_{sk}=\frac{3}{{\lambda }_k}\frac{\sinh {\lambda }_k-\sin {\lambda }_k}{\cosh {\lambda }_k-\cos {\lambda }_k}$$

(8)

$${\lambda }_k=\frac{d}{{\delta }_k}$$

(9)

Summary of skin effect:

(1)

The skin effect increases with frequency.

(2)

The decrease in permeability owing to saturation increases the skin depth and increases the eddy current loss.

(3)

The flux saturation induces harmonic eddy currents.

(4)

A greater rotation magnetic flux results in a higher saturation and smaller harmonics for the magnetic field and eddy current.

In the third iron loss calculation, $P_{eddy}$ is calculated using the eddy current distribution via the homogeneous method considering the skin effect. In addition, $P_{hys}$ is calculated using the area of all loops calculated using the play model, which considers the minor loop DC bias. In the hysteresis loss of the second iron loss, a minor loop can be considered, but the loop size based on the DC bias cannot be considered.

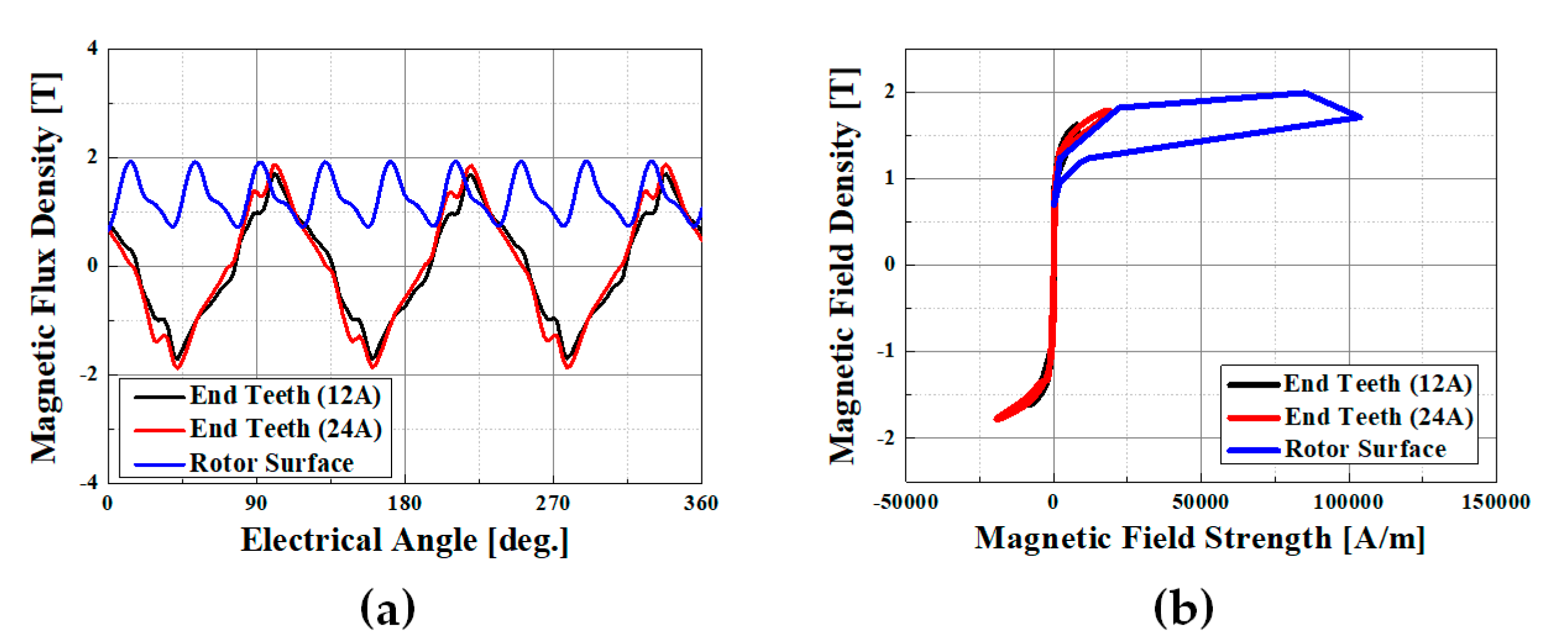
Figure 6a shows the flux density at different (12 A and 24 A) input currents of the stator end-teeth and the rotor surface in the time frame. Figure 6b shows the B–H loop at that time. Although the alternating flux density on the surface of the rotor was smaller than that of the stators, the B–H loop was much larger than the stator. This DC bias and large loops are characteristic of the IPMSM rotor structure; hence, they should be considered [10,11].

Figure 7a shows the conventional estimation of iron losses. In the estimation, the external input value is assumed to be proportional to the input frequency square. This is the most typically used data-estimation method. Figure 7b shows the calculated value of the eddy current loss when an AC magnetic field with an amplitude of 0.04T is applied to a 50A470 single plate. The value obtained is not proportional to the squared frequency.

3. Comparison of Study Result

3.1. Comparison of Iron Losses

Figure 8a and

Table 1. Comparison of iron losses of three different calculation methods at 6540 rpm, 24 A phase current.

Iron Loss	1st Method	2nd Method	3rd Method
Single-V	138.93	132.68	134.38
Dual-D	135.35	128.74	128.67
Single-F	142.86	135.89	141.69

shows a comparison of the three (single-V, single-F, and du-al-D) magnet rotor structures based on different iron loss calculations at 6540 rpm and 24 A phase current. Figure 8b and

Table 2. Comparison of hysteresis losses of three different calculation methods at 6540 rpm, 24 A phase current.

Hysteresis Loss	1st Method (Frequency Sep.)	2nd Method (Loop Count.)	3rd Method (Loop Size Consider)
Single-V	28.62	22.37	24.81
Dual-D	28.05	21.45	22.56
Single-F	28.99	22.02	23.61

shows a comparison of the three magnet rotor structures based on different hysteresis loss calculations under the same conditions. In the same stator structure, the iron losses of single-F increased from 5.3 to 9.2% depending on the calculation method compared with dual-D. The single-V losses increased from 2.6 to 4.3% depending on the calculation method compared with dual-D. This comparison shows that the dual-D iron loss may be improved or similar to the other rotor structures in terms of electromagnetic torque generation. However, owing to the coercive force difference between the rotor structure and the magnet, an absolute comparison is not possible. Therefore, a comparison of the procedures prior to the saturation of the operating voltage and overall range is necessary for a trend comparison.

Table 3. Efficiency comparison of three different rotor structure at 6540 rpm, 24 A phase current based on three different type of iron loss.

Efficiency	1st Method	2nd Method	3rd Method
Single-V	93.52%	93.64%	93.52%
Dual-D	93.44%	93.57%	93.47%
Single-F	93.44%	93.57%	93.37%

shows a comparison of the IPMSM efficiency of three different rotor structure at 6540 rpm and 24 A phase current with three different types of iron losses. When calculating the efficiency, the loss analysis method was used; therefore, the efficiency of the first loss calculation method was lower than that of the second method. This is due to the over consideration of harmonics in the frequency analysis separation method.

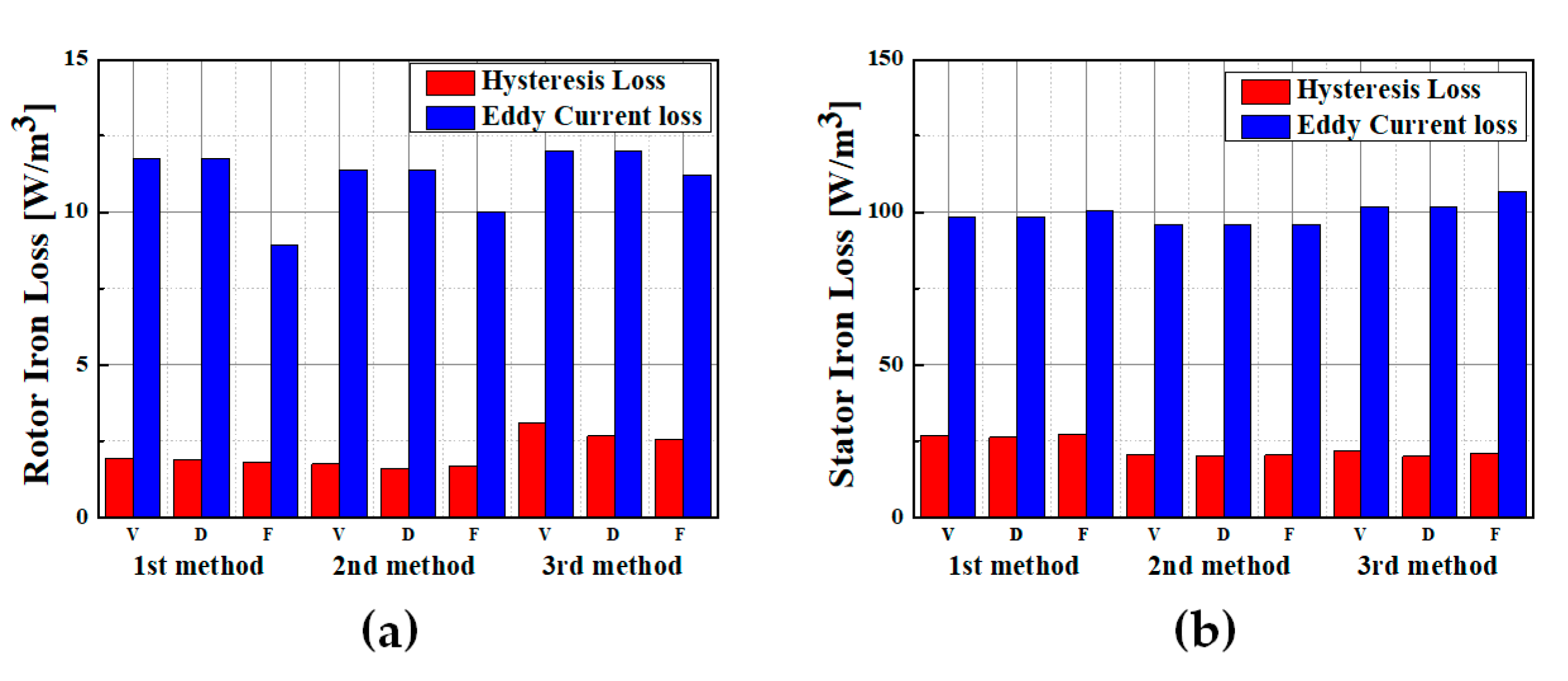
Figure 9a,b show a comparison of the total iron losses for the three hysteresis losses and two different eddy current loss calculation methods at a four-step operating speed. Each point considers the same maximum torque per ampere point at 24 A. The results reveal that the iron loss of single-F in the entire operation range is high, and the total iron loss calculated based on single-F and -V were 2.5–3.4% and 5.2–5.1% higher than that of dual-D, respectively.

3.2. Comparison of Hysteresis Losses

Figure 8b and Table 2 show a comparison of the hysteresis losses of the different calculation methods at the rated operation point: 6540 rpm and 24 A phase input current. Detail regarding the methods used are as follows:

The first method, which is the frequency-separation method, over-calculates $P_{hys}$. This result is over-reflected as a loss, which is not only a sinusoidal $P_{hys}$, but also an FFT with harmonics. The second method, which is the minor loop counting method, can re-duce the excessive analysis based on the hysteresis loop counting method. The third $P_{hys}$ calculation method shows that $P_{hys}$ can be calculated by considering the DC bias and minor loop size.

Figure 9a shows the $P_{hys}$ calculation results for the four operating speeds. The results show a similar pattern to those shown in Figure 8b and Table 2, thereby confirming the suppression of the reflection of excessive $P_{hys}$ in the frequency-separation method.

Figure 10a and

Table 4. Comparison of three rotor structure iron losses in rotor using three different calculation method at 6540 rpm and 24 A phase current.

Response Value	1st Iron Loss			2nd Iron Loss			3rd Iron Loss
	Single-V	Dual-D	Single-F	Single-V	Dual-D	Single-F	Single-V	Dual-D	Single-F
Eddy current loss	11.76	11.38	12.02	11.76	11.38	12.02	8.93	10.02	11.22
Hysteresis loss	1.92	1.89	1.80	1.75	1.58	1.67	3.10	2.65	2.57

show the significant effect of the DC bias on the loss of the third $P_{hys}$ of the rotor. Compared with the second $P_{hys}$, an average increase of 66.3% was observed. This indicates that the effect of DC bias is a prominent feature on the IP-MSM rotor surface, as shown in Figure 6.

Figure 10b and

Table 5. Comparison of three rotor structure iron losses in stator using three different calculation method at 6540 rpm and 24 A phase current.

Response Value	1st Iron Loss			2nd Iron Loss			3rd Iron Loss
	Single-V	Dual-D	Single-F	Single-V	Dual-D	Single-F	Single-V	Dual-D	Single-F
Eddy current loss	98.55	95.91	101.85	98.55	95.91	101.85	100.64	96.09	106.86
Hysteresis loss	26.71	26.16	27.19	20.63	19.87	20.35	21.71	19.91	21.04

show the limited effect of the DC bias on the third $P_{hys}$ of the stator. Compared with the second $P_{hys}$, an average increase of 2.9% was observed.

3.3. Comparison of Eddy Current Losses

Figure 9b shows a comparison of the eddy current losses at 6540 to 1635 rpm in the operating range. The loss obtained using the frequency separation method was higher than that using the homogenized eddy current loss calculation method. This is due to the iron loss data in Figure 7a, this is proportional to the square of the input frequency and, this because data had been used the frequency separation method for eddy current loss calculation. At the same time Figure 9b also shows the calculations result of the homogenization method. In this case, the eddy current loss data from the AC magnetic field in-put conditions in Figure 7b is used.

4. Conclusions

In this study, two types of comparisons were performed. One was a comparison based on the iron loss analysis method, and the other was a comparison of the iron loss based on the structure of the rotor magnet shape (single-V, single-F, and dual-D).

Table 6. Comparison of three different iron losses calculation methods.

Iron Loss		1st Method	2nd Iron Loss	3rd Iron Loss
Hysteresis Loss	Method	Frequency Sep.	Loop Count.	Loop Size Consider
	Data	Iron loss data (FFT)	Iron loss data, DC bias	Loop measurement
Eddy-current Loss	Method	Frequency Sep.		Homogenization
	Data	Iron loss data (FFT)		Electrical resistivity

shows the three methods of iron loss and the data used. The first method was simple and fast; however, in resulted in an over-loss calculation. The second method improved the over-loss problem but did not consider the DC bias of the hysteresis minor loop. Therefore, it may be insufficient for calculating the interior permanent-magnet-type concentrated winding motor loss. Finally, the third method indicated that the DC bias of the hysteresis can be considered, and that the over-loss of the eddy current can be improved by considering the skin effect.

The iron losses based on the rotor magnet shape were compared. The same magnet volume was used in the rotors based on the same concentrated winding-type stator structure, pole-slot combination, number of windings, and wire specifications. Therefore, mechanical and copper losses were excluded from this comparison, and the induced voltages under the no-load condition were almost identical. However, the changed reluctance based on the magnet shapes in the rotor can affect the flux density saturation, not only in the iron losses of the rotor, but also in the stator. This was validated using three iron loss calculation methods, and the contribution of harmonic effects by the calculation method and conditions yielded different results. In addition, the DC bias of the hysteresis of all IPMSM rotors was confirmed. In conclusion, in the relative comparison of rotor structure geometries, the single-F magnet rotor structure indicated the greatest iron loss, whereas the dual-D magnet rotor structure indicated the lowest. This comparison of three iron loss analysis methods is beneficial to not only IPMSMs for automotive electric refrigerant compressors, but also to various electric machine iron loss analyses of high magnetic flux saturation Applications.