Abstract
The study provides a solution to a dimensional synthesis problem for a hexapod-type reconfigurable parallel mechanism, which can change its configuration to realize different trajectories of its output link while having a single drive. The work presents an original procedure to find the dimensions of some mechanism’s links and their initial configuration to reproduce these trajectories. After describing the mechanism, the paper examines kinematic relations representing the basis for the subsequent synthesis algorithm. Next, the obtained expressions are extended and provide a system of equations to be solved. The structure of this equation system allows it to be solved effectively by numerical methods, which is demonstrated with an example. The proposed algorithm of dimensional synthesis does not require solving the optimization problems, in contrast to the familiar methods of dimensional synthesis of parallel mechanisms. Further, the suggested approach to the synthesis problem allows finding solution in a fast and computationally efficient manner.
1. Introduction
Dimensional (parametric) synthesis is one of the basic procedures in mechanisms design. The main geometrical parameters that define a mechanism’s performance and the motion of its output link are determined at this stage. In this study, we focus on parallel mechanisms, where two or more kinematic chains control the output link motion [1,2].
The dimensional synthesis problem of parallel mechanisms is closely associated with workspace construction, rigidity and accuracy criteria, etcetera. Studies [3,4,5,6,7] consider the issues of the dimensional synthesis for the mechanisms with several degrees-of-freedom (DOFs), and the algorithms for determining their geometrical parameters are usually based on solving optimization problems. When synthesizing and evaluating the mechanism performance, kinematic performance indices (e.g., conditioning index, global conditioning index) are considered [8,9].
Several works analyze Jacobian matrix of a mechanism to determine its geometrical parameters. For example, in [10], the authors perform dimensional synthesis of a 5-DOF hybrid mechanism using a homogeneous Jacobian matrix. The optimal design of this mechanism considers key features of parallel mechanical systems, such as workspace dimensions, dexterity, and the geometrical parameters of kinematic chains. Studies [11,12] present the multi-objective optimization problems demonstrated on the 4-DOF mechanisms with Schönflies motion. These problems aim at maximizing the workspace and positioning accuracy. Study [13] proposes a method for the synthesis of 3-DOF mechanisms that allows for the avoidance of singularities at the design stage. Study [14] provides a parametric synthesis algorithm based on a particle swarm optimization method, which was applied to an 8-SPU parallel mechanism. In [15], the authors present an approach that considers positioning accuracy and is based on nonhomogeneous Jacobian matrices.
There are also dimensional synthesis algorithms based on minimizing an objective function. In this case, a cost function is used as an optimization criterion. Study [16] presents the interval analysis method applied to 3-DOF translational parallel mechanisms and aimed to get the largest dexterous workspace. In [17], the authors performed the dimensional synthesis of a Delta-like haptic device, optimizing its workspace. Study [18] provides a mathematical modeling algorithm for the workspace construction of translational parallel mechanisms with different topologies: Delta, 3-UPU, RAF (Romdhane-Affi-Fayet), and Tri-pyramid (TP). Paper [19] shows the comparison of single- and multi-objective optimization problems for the dimensional synthesis of a Delta robot and demonstrates the efficiency of the second one. Another approach to multi-objective optimal design is presented in [20] using the example of a cable-driven parallel robot for upper-limb rehabilitation tasks. The study selects a suitable design by considering minimum cable tensions and the smallest footprint. Paper [21] provides an approach based on interval analysis for the dimensional synthesis of parallel mechanisms, considering accuracy requirements and manufacturing errors. Work [22] demonstrates an approach for the dimensional synthesis of a 3-PRS mechanism based on a dimensionally homogeneous Jacobian matrix. Paper [23] presents another methodological procedure of dimensional synthesis for both parallel and serial mechanisms. This procedure is a multi-objective optimization problem that considers workspace dimensions, Jacobian matrices, and compliant displacements as design criteria. Thus, the parametric synthesis problem for parallel mechanisms is complex, and its solution is important for effective mechanism performance.
The current study focuses on an algorithm for the dimensional synthesis of a reconfigurable parallel mechanism with a single drive. Such mechanisms can change their configurations to vary the motion laws of the output links or the dimensions of their workspaces [24,25,26,27]. Further, these mechanisms can avoid singularities during their motion or find a way out of them [28,29]. Some of these mechanisms can change motion type. For example, a 3-UPU robot presented in [30] can work either as a translational or rotational mechanism by using different platform designs. Such functional properties provide wide application opportunities for these mechanisms. In particular, they are applied in rehabilitation procedures [31], pick-and-place operations [32], additive technology [33], machining [34,35,36], and measuring tasks [37].
This study aims to determine the mechanism’s geometrical parameters based on the prescribed motion laws of the output link. The advantage of the proposed approach is in using simple kinematic relations and, in contrast to the methodologies discussed above, that it does not require solving any optimization problems.
2. Mechanism Design
Let’s consider the structure of the mechanism. Figure 1a shows its virtual prototype with the following elements: 1—circular guide (fixed link), 2—driving wheel (driving link), 3—driven gear, 4—driving pulley, 5—driven pulley, 6—crank, 7—slide block, 8—swinging arm, 9—carriage, 10—leg, 11—platform (output link). Links 3 and 4, as well as 5 and 6, have a common rotation axis; links 8 and 9 form one link; links 4 and 5 are coupled by a belt; joints 9–10 and 10–11 are spherical.
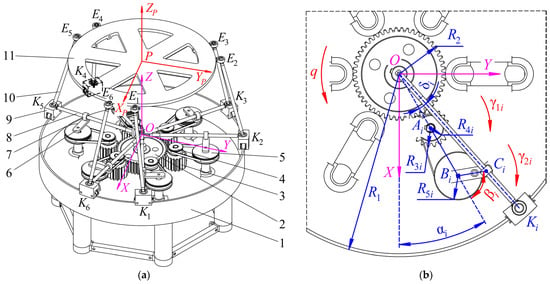
Figure 1.
(a) Hexapod-type parallel mechanism with a reconfigurable design; (b) fragment of the horizontal part of the circular guide with a planar kinematic chain.
Points Ki and Ei with i = 1…6 being the index number of a kinematic chain determine the centers of spherical joints 9–10 and 10–11, respectively. Fixed link 1 has a base reference frame OXYZ, and the movable frame PXPYPZP attaches to platform 11, with point P staying in its center.
This mechanism can vary the platform trajectories using a single drive. To achieve this, one can reorient the cranks in each kinematic chain when the driving wheel is fixed. This becomes possible by disconnecting the belt between pulleys 4 and 5.
One notes the following design features of the proposed mechanism:
- a single drive that stays fixed in the center of the base;
- correctly chosen cranks’ lengths allow for the elimination of the possibility of collision between the adjacent carriages (unlike other types of mechanisms with circular guides);
- reconfigurability, which allows the platform to have diverse trajectories while having a single actuation.
3. Configuration Analysis
This section studies relations that describe the links’ coordinates and present the basis for the subsequent synthesis procedure. Let’s consider how to define the position and configuration of the output link. The former can be specified by Cartesian coordinates of its point P relative to the base frame OXYZ:
where x, y, and z are components of vector .
To describe the orientation of movable frame relative to OXYZ, we can use rotation matrix , which depends on three Euler angles φ, θ, and ψ:
where the elementary rotation matrices are:
We can combine the platform coordinates into vector X:
Next, let’s consider relations that connect vector X with the coordinates of the planar links placed inside circular guide 1. Suppose driving link 2 rotates on angle q. Driven gear 3 and pulley 5 will rotate on angles and , respectively:
where is a radius of driving wheel 2; is a radius of driven gear 3; is a radius of driving pulley 4; is a radius of driven pulley 5.
Consider the triangle (Figure 1b). Since center O of wheel 2, center of pulley 4, and center of pulley 5 are collinear, we can write the distance between the axes of wheel 2 and pulley 5 as follows:
where is a distance between points and (between the centers of pulleys 4 and 5).
A length of can be calculated by the cosine law for the triangle :
where is a length of (length of crank 6); is the crank angle:
where is an initial value of the crank angle.
To find swinging arm rotation angle , we apply the sine theorem for the triangle :
Now, we can write an expression for coordinates of point (coordinates of carriage 9) relative to frame OXYZ:
where is a radius of circular guide 1; is an angle between axis OX of frame OXYZ and line (Figure 1b).
Let’s consider the output link of the mechanism. Coordinates of points (centers of joints 10–11) relative to OXYZ have the following form:
where is the coordinates of point relative to movable frame PXPYPZP.
Finally, we can write a relation that connects coordinates in Equations (10) and (11) with length of leg 10:
Expression (12) written for all the kinematic chains represents a system of six equations that connect coordinates X of the platform with the links’ coordinates in the mechanism’s planar part. In the following section, we will show how to apply these relations for the dimensional synthesis of the mechanism.
4. Dimensional Synthesis Algorithm
We can formulate the dimensional synthesis problem for the considered mechanism in the following general form: finding the lengths of the links required to perform the given output link trajectory. Before proceeding to the synthesis algorithm, we note two important points:
- Since the mechanism has only one degree of freedom, we cannot set all six components of vector X independently. Only one coordinate can be defined explicitly.
- As mentioned earlier in Section 2 and also shown in work [38], the output link can reproduce various trajectories by uncoupling the belt between links 4 and 5 and reorienting crank 6, i.e., by changing values that define the cranks’ initial angles.
Thus, it is reasonable to select these initial angles , i = 1…6, as unknown geometrical parameters. Besides, we can complement our set of unknown parameters with crank and leg lengths and , respectively. These links have an ordinary rod-like design, and we can easily substitute them for analogs with different lengths, if necessary (another possibility is to apply a prismatic structure). We will also study the mechanism with a “symmetrical” design: = l and = L for all i. Other parameters are considered to have constant values.
To solve the dimensional synthesis problem, we will use the relations obtained in the previous section. Given the above, we can rewrite expression (12) in the following way:
Let be the given platform coordinate: it can represent any component of vector X. The five remaining coordinates can be grouped as vector . System of Equation (13) will have the form:
We can solve the system above numerically with respect to variables , l, L, q, and for each value of coordinate . One should note a caveat here. If has a form of some trajectory (t), where t is the time, then variables , l, and L should keep constant values for each value of on a given time interval to realize a specified trajectory. Given this, we can use the following approach to find a solution to system (14).
We can represent trajectory (t) specified on time interval [0, T] as N discrete values:
where [j] corresponds to value () at time , j = 1…N, and [1] = (0), [N] = (T).
For the given trajectory (t), variables and q will also be functions of time (t) and q(t), which we can represent similarly in a discrete form:
With this discretization, system (14) can be written as follows:
The expression above is a system of 6N equations relative to 8 + 8N variables: six unknowns are ; two unknowns are l and L; 5N unknowns are components of vectors [j]; N unknowns are q[j]. We can augment the obtained equations with a relation that constrains crank length l: to exclude the collisions between carriages 9, the crank length should be limited by some value :
To include this condition into our analysis, we can rewrite inequality (19) as an equality using slack variable s:
Work [39] (p. 84) presents a derivation of Equation (20) and its geometrical interpretation. This equation has the following meaning: condition (19) is satisfied if and only if we can solve Equation (20) for some values of s. We can add relation (20) to system (18) as the function :
Let’s consider the structure of the obtained system of Equations (18) and (21). We can group all variables into vector v with dimension 9 + 6N:
where = [ … ]T is a vector of crank initial angles .
We can also group Equations (18) and (21) into vector-function f with dimension 6N + 1:
The Jacobian matrix for vector-function (23) can be written as follows:
For each pair of integers m and n, m = 1…6, n = 1…N, function depends only on variables [j] and q[j] with j = n and only on variable with i = m, and does not depend on other variables. In this regard, the Jacobian matrix (24) will have a sparse structure of the following form:
where
In the expression above, [j] is a k-th component of vector [j], k = 1…5. All elements in the right side of expression (25) are zeros, except for the notated ones and the ones that contain , , , and . One can see that the Jacobian matrix has a highly sparse structure. We can estimate its sparsity sp as a ratio of zero elements to the total number of elements. In the considered case, the latter is equal to (6N + 1) × (9 + 6N), and the former equals 54N + 2, so:
With large values of N, sparsity sp approaches one, i.e., almost all elements of the matrix are zeros. Such a sparse structure significantly facilitates and speeds up the numerical solution of Equations (18) and (21). To find the solution, we should make some initial guess, the choice of which is a key factor. Since the equations are nonlinear and the number of variables is greater than the number of equations, different initial guesses will lead to various solutions. Moreover, the solution may not exist at all for incorrect guesses. The choice of this initial guess remains an open problem. However, there are several methods to facilitate this choice, e.g., using experimental data or the virtual model of the mechanism.
Note that the numerical solution of Equations (18) and (21) provide not only the geometrical values of the mechanism but also the driving wheel angle and five remaining coordinates of the output link. Thus, the dimensional synthesis algorithm implicitly includes the solution to the inverse kinematics problem.
We can also adapt the proposed approach for other mechanisms (not necessarily reconfigurable) in which an output link performs a coupled motion changing several coordinates at a time and for which both the inverse and forward kinematics are challenging to solve in an explicit form. The differences will be in functions f and variables v, but the overall technique will remain the same.
5. Examples of Dimensional Synthesis
Consider an example of the dimensional synthesis for the mechanism with parameters that correspond to the model in Figure 1 and have the following values: = 246 mm, = 64.25 mm, = 69.2 mm; for all i: = 24 mm, = 15 mm, = 30 mm, = 75.5 mm; = 30°, 90°, 150°, 210°, 270°, 330°; , where = 192.7 mm is a platform radius (a distance from point P to centers of spherical joints 10–11), = 10°, 110°, 130°, 230°, 250°, 350° is an angular placement of joints 10–11 that determines their position on the output link.
As a case study, let’s take platform coordinate x as given coordinate with the following time law:
which corresponds to one full oscillation around axis OX with an amplitude of 15 mm.
The numerical solution has been performed in MATLAB using the standard function “fsolve” with the tolerance 1 × 10−8 as a stopping criterion. The value of N was equal to 200, which corresponded to sp = 0.99 according to (27). We applied the following initial guess: 6° for all angles ; 39 mm for crank length l; 220 mm for leg length L; 195 mm for coordinate z; zeros for all other variables, except for s, which had an initial guess calculated using Equation (21). We also used the Jacobian matrix (25), the nonzero elements of which were found in explicit form by the differentiation of expression (13) with respect to the corresponding variables.
The solution was found after 35 iterations, which took about 3.2 s on a laptop with an Intel Core i7-3610QM 2.3 GHz processor and 8 GB RAM. This solution included the following values of lengths l and L and crank initial angles :
We also determined the driving link angle q and five platform coordinates (solid lines in Figure 2). One can see that all five coordinates of the output link vary in time and take the same values for t = 5 s as for t = 0.
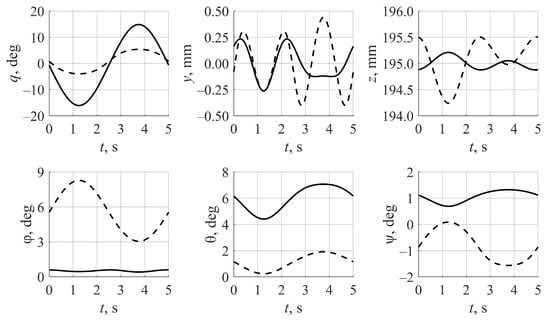
Figure 2.
Driving link angle q and platform coordinates = [y, z, φ, θ, ψ]T calculated for given trajectory (t) according to (29) and different values of the mechanism parameters: solid lines—l, L, and correspond to (29) and (30); dashed lines—l, L, and correspond to (31) and (32).
As mentioned earlier, the numerical solution depends greatly on the initial guess. To demonstrate this, let’s change the initial guess for crank length l from 39 mm to 44 mm and for slack variable s according to (21), keeping other guesses similar to the previous example. The following solution was found after 185 iterations, which took about 16.1 s on the same laptop:
Thus, we can realize given trajectory Xg(t) with different sets of mechanism parameters. Moreover, Figure 2 (dashed lines) shows that driving link angle q and platform coordinates differ from the previous case. For example, in the second case, coordinates z, φ, and ψ vary with greater amplitudes than in the first case. Theoretically, there can exist a set of parameters that provides a minimum variation in unspecified coordinates . If the mechanism follows given trajectory Xg(t) with negligible variations in other coordinates, we can consider the mechanism as able to perform a pure rotational or pure translational motion about a given axis. We can form an optimization problem to find such a set of parameters—this is beyond the scope of the current study but is of interest for future research.
6. Computational Accuracy and Comparison with Other Works
The presented approach allows us to find eight design parameters: six initial crank angles, crank length, and leg length. In addition, the algorithm uses one slack variable and 6N variables corresponding to the mechanism coordinates. To get more accurate results, we can either diminish the tolerance value or increase the value of N. In particular, the bigger the N value, the closer the calculated platform trajectory, which we can find using forward kinematics [38], will be to given trajectory Xg(t). Nevertheless, in both cases, the calculation time will rise. The number of iterations and calculation time also depend on the initial guess as we have seen from the examples in the previous section.
As we mentioned in the introduction, most of the known works devoted to the dimensional synthesis of parallel mechanisms consider solutions to the optimization problems. One of the earliest studies in this field by Bhattacharya et al. [40] considered the optimal design of Stewart platform type manipulators optimizing several rigidity criteria. The authors solved the problem with three design parameters using a sequential quadratic programming technique on an HP 9000/850 computer, which took 12.5 s to find only one local minimum of the objective function. Later, Merlet et al. in works [21,41,42] applied interval analysis to the optimal design of various parallel manipulators. The authors considered single- and multi-criteria optimization problems with a number of design parameters ranging from two to six. The calculation time on different computers varied from 30 min to 48 h. Miller [43] studied the optimal design of a Delta-like robot for manipulability and space utilization criteria. The optimization problem with four design parameters was solved using a MATLAB package in about 3 h on a Pentium II 200 MHz computer. Rao et al. [44] performed the dimensional synthesis of hexaslide machines considering workspace volume and global dexterity indices as optimization objectives for the problem with seven design parameters. It took 211 s on a Pentium IV 1.7 GHz, 256 MB RAM computer to only calculate these indices. Another multi-criteria design optimization problem with four design parameters was studied by Unal et al. [45] using a normal boundary intersection method. The calculation time varied from an hour up to several hours, depending on the tolerance value, on a workstation with an Intel Xeon 3.4 GHz processor and 4 GB RAM. Jiang and Gosselin [46] performed geometric optimization of a Gough-Stewart platform for maximal singularity-free workspace. The authors applied Powell’s search method for the problem with three design parameters, which took about 5 min to find a solution on a Pentium IV 2.4 GHz computer. Parivash and Ghasemi [47] solved an optimal dimensional problem with five design parameters for a parallel manipulator with the desired workspace. The solution was found using the MATLAB optimization toolbox on an Intel Core i7 2.2 GHz, 6 GB RAM computer in about 25 min. Russo et al. [4] also used this toolbox for the optimal design of lower mobility manipulators. The authors solved a multi-loop optimization problem with four design parameters which aimed at minimizing positioning errors. The average calculation time was 273 s on an Intel Core i7-6700HQ 2.6 GHz computer. Muralidharan et al. [48] applied an approach based on a genetic algorithm to the dimensional synthesis of 3-RRR and 3-RRS parallel manipulators. The authors considered two different optimization problems related to the dynamic performance with five design parameters for both mechanisms. The calculation time varied from 13 to 49 h on a computer with an Intel Core i7-4930 3.4 GHz processor.
The abovementioned studies differ in their studied mechanisms, design parameters, objective functions, applied methods, and computers that solve the problems. Though we cannot perform an adequate comparison with the known works, the approach suggested in the current paper seems to be computationally efficient with a proper choice of the initial guess.
7. Conclusions
This study has presented an original dimensional synthesis algorithm for the hexapod-type reconfigurable parallel mechanism with single DOF. The suggested algorithm allows the determination of the links’ dimensions (the crank and the leg lengths) and the crank initial angles required to perform specified platform trajectories. The research has provided the relations that express the coordinates of all links in terms of the drive angle and platform position and orientation. Being written for all the kinematic chains, these relations form a system of six equations that constitute a basis for the subsequent synthesis algorithm. The advantage of the proposed algorithm is in calculation not only of the geometrical values of the mechanism links, but also the driving wheel angle and five remaining coordinates of the platform. From a computational point of view, the highly sparse structure of the equations’ Jacobian matrix allows for the finding of a numerical solution to the synthesis problem quickly and efficiently. The obtained theoretical results have been verified on an example with a given trajectory along one of the platform coordinates. The numerical solution has been found for different initial guesses. In contrast to the known dimensional synthesis methods of parallel mechanisms, the proposed algorithm is straightforward and does not require the solving of any optimization problem. Nevertheless, the techniques suggested by this work can be extended to the optimal design of the mechanism. The proposed approach can be also adapted for other mechanisms.
Author Contributions
Conceptualization, A.F., A.A. and V.G.; methodology, A.F. and A.A.; software, A.F. and A.A.; validation, A.F. and A.A.; formal analysis, A.F. and A.A.; investigation, A.F. and A.A.; resources, A.F. and A.A.; writing—original draft preparation, A.F. and A.A.; writing—review and editing, A.F. and A.A.; visualization, A.F. and A.A.; supervision, A.F. and A.A.; project administration, A.F., A.A., V.G. and G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Merlet, J.-P. Parallel Robots, 2nd ed.; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar] [CrossRef]
- Glazunov, V.A.; Chunichin, A.Y. Development of mechanisms of parallel structure. J. Mach. Manuf. Reliab. 2014, 43, 211–216. [Google Scholar] [CrossRef]
- Rosyid, A.; El-Khasawneh, B.; Alazzam, A. Review article: Performance measures of parallel kinematics manipulators. Mech. Sci. 2020, 11, 49–73. [Google Scholar] [CrossRef]
- Russo, M.; Raimondi, L.; Dong, X.; Axinte, D.; Kell, J. Task-oriented optimal dimensional synthesis of robotic manipulators with limited mobility. Robot. Comput. Manuf. 2021, 69, 102096. [Google Scholar] [CrossRef]
- Huang, T.; Li, Z.; Li, M.; Chetwynd, D.G.; Gosselin, C.M. Conceptual design and dimensional synthesis of a novel 2-DOF translational parallel robot for pick-and-place operations. J. Mech. Des. 2004, 126, 449–455. [Google Scholar] [CrossRef]
- Dastjerdi, A.H.; Sheikhi, M.M.; Masouleh, M.T. A complete analytical solution for the dimensional synthesis of 3-DOF delta parallel robot for a prescribed workspace. Mech. Mach. Theory 2020, 153, 103991. [Google Scholar] [CrossRef]
- Li, J.; Ye, F.; Shen, N.; Wang, Z.; Geng, L. Dimensional synthesis of a 5-DOF hybrid robot. Mech. Mach. Theory 2020, 150, 103865. [Google Scholar] [CrossRef]
- Liu, X.-J.; Jin, Z.-L.; Gao, F. Optimum design of 3-DOF spherical parallel manipulators with respect to the conditioning and stiffness indices. Mech. Mach. Theory 2000, 35, 1257–1267. [Google Scholar] [CrossRef]
- Gosselin, C.; Angeles, J. A global performance index for the kinematic optimization of robotic manipulators. J. Mech. Des. 1991, 113, 220–226. [Google Scholar] [CrossRef]
- Xu, L.; Chen, Q.; He, L.; Li, Q. Kinematic analysis and design of a novel 3T1R 2-(PRR)2RH hybrid manipulator. Mech. Mach. Theory 2017, 112, 105–122. [Google Scholar] [CrossRef]
- Altuzarra, O.; Hernandez, A.; Salgado, O.; Angeles, J. Multiobjective optimum design of a symmetric parallel Schönflies-motion generator. Trans. ASME J. Mech. Des. 2009, 131, 031002. [Google Scholar] [CrossRef]
- Li, Z.; Lou, Y.; Zhang, Y.; Liao, B.; Li, Z. Type synthesis, kinematic analysis, and optimal design of a novel class of Schönflies-motion parallel manipulators. IEEE Trans. Autom. Sci. Eng. 2013, 10, 674–686. [Google Scholar] [CrossRef]
- Urizar, M.; Petuya, V.; Diez, M.; Hernandez, A. Non-singular transitions based design methodology for parallel manipulators. Mech. Mach. Theory 2015, 91, 168–186. [Google Scholar] [CrossRef]
- Wan, X.J.; Li, Q.L. Dimensional synthesis of a robotized cell of support fixture. Robot. Comput. Manuf. 2017, 48, 80–92. [Google Scholar] [CrossRef]
- Cardou, P.; Bouchard, S.; Gosselin, C. Kinematic sensitivity indices for dimensionally nonhomogeneous Jacobian matrices. IEEE Trans. Robot. 2010, 26, 166–173. [Google Scholar] [CrossRef]
- Chablat, D.C.; Wenger, P.; Merlet, J.-P. A Comparative study between two three-DOF parallel kinematic machines using kinetostatic criteria and interval analysis. In Proceedings of the 11th World Congress in Mechanism and Machine Science, Tianjin, China, 1–4 April 2004; pp. 1–6. [Google Scholar]
- Liu, G.; Chen, Y.; Xie, Z.; Geng, X. GA\SQP optimization for the dimensional synthesis of a delta mechanism based haptic device design. Robot. Comput. Manuf. 2018, 51, 73–84. [Google Scholar] [CrossRef]
- Hamida, I.B.; Laribi, M.A.; Mlika, A.; Romdhane, L.; Zeghloul, S. Dimensional synthesis and performance evaluation of four translational parallel manipulators. Robotica 2020, 39. [Google Scholar] [CrossRef]
- Kelaiaia, R.; Zaatri, A.; Company, O.; Chikh, L. Some investigations into the optimal dimensional synthesis of parallel robots. Int. J. Adv. Manuf. Technol. 2016, 83, 1525–1538. [Google Scholar] [CrossRef]
- Hamida, I.B.; Laribi, M.A.; Mlika, A.; Romdhane, L.; Zeghloul, S.; Carbone, G. Multi-objective optimal design of a cable driven parallel robot for rehabilitation tasks. Mech. Mach. Theory 2021, 156, 104141. [Google Scholar] [CrossRef]
- Merlet, J.-P.; Daney, D. Dimensional synthesis of parallel robots with a guaranteed given accuracy over a specific workspace. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 942–947. [Google Scholar] [CrossRef]
- Sun, T.; Song, Y.; Li, Y.; Liu, L. Dimensional synthesis of a 3-DOF parallel manipulator based on dimensionally homogeneous Jacobian matrix. Sci. China Ser. E-Technol. Sci. 2010, 53, 168–174. [Google Scholar] [CrossRef]
- Carbone, G.; Ottaviano, E.; Ceccarelli, M. An optimum design procedure for both serial and parallel manipulators. Proc. Inst. Mech. Eng. Part. C J. Mech. Eng. Sci. 2007, 221, 829–843. [Google Scholar] [CrossRef]
- Affi, Z.; Romdhane, L.; Maalej, A. Dimensional synthesis of a 3-translational-DOF in-parallel manipulator for a desired workspace. Eur. J. Mech. A Solids 2004, 23, 311–324. [Google Scholar] [CrossRef]
- Borras, J.; Thomas, F.; Ottaviano, E.; Ceccarelli, M. A reconfigurable 5-DoF 5-SPU parallel platform. In Proceedings of the ASME/IFToMM International Conference on Reconfigurable Mechanisms and Robots, London, UK, 22–24 June 2009; pp. 617–623. [Google Scholar]
- Kuo, C.-H.; Dai, J.S.; Yan, H.-S. Reconfiguration principles and strategies for reconfigurable mechanisms. In Proceedings of the ASME/IFToMM International Conference on Reconfigurable Mechanisms and Robots, London, UK, 22–24 June 2009; pp. 1–7. [Google Scholar]
- Wu, G.; Dong, H.; Wang, D.; Bai, S. A 3-RRR spherical parallel manipulator reconfigured with four-bar linkages. In Proceedings of the International Conference on Reconfigurable Mechanisms and Robots (ReMAR), Delft, The Netherlands, 20–22 June 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Kong, X.; Gosselin, C.M.; Richard, P. Type synthesis of parallel mechanisms with multiple operation modes. J. Mech. Des. 2007, 129, 595–601. [Google Scholar] [CrossRef]
- Karimi, A.; Masouleh, M.-T.; Cardou, P. Avoiding the singularities of 3-RPR parallel mechanisms via dimensional synthesis and self-reconfigurability. Mech. Mach. Theory 2016, 99, 189–206. [Google Scholar] [CrossRef]
- Sarabandi, S.; Grosch, P.; Porta, J.M.; Thomas, F. A reconfigurable asymmetric 3-UPU parallel robot. In Proceedings of the International Conference on Reconfigurable Mechanisms and Robots (ReMAR), Delft, The Netherlands, 20–22 June 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Zhang, M.; Cao, J.; Zhu, G.; Miao, Q.; Zeng, X.; Xie, S.Q. Reconfigurable workspace and torque capacity of a compliant ankle rehabilitation robot (CARR). Robot. Auton. Syst. 2017, 98, 213–221. [Google Scholar] [CrossRef]
- Herrero, S.; Mannheim, T.; Prause, I.; Pinto, C.; Corves, B.; Altuzarra, O. Enhancing the useful workspace of a reconfigurable parallel manipulator by grasp point optimization. Robot. Comput. Manuf. 2015, 31, 51–60. [Google Scholar] [CrossRef]
- Huang, G.; Guo, S.; Zhang, D.; Qu, H.; Tang, H. Kinematic analysis and multi-objective optimization of a new reconfigurable parallel mechanism with high stiffness. Robotica 2018, 36, 187–203. [Google Scholar] [CrossRef]
- Carbonari, L.; Callegari, M.; Palmieri, G.; Palpacelli, M.-C. A new class of reconfigurable parallel kinematic machines. Mech. Mach. Theory 2014, 79, 173–183. [Google Scholar] [CrossRef]
- Bi, Z.; Wang, L. Optimal design of reconfigurable parallel machining systems. Robot. Comput. Manuf. 2009, 25, 951–961. [Google Scholar] [CrossRef]
- Ye, W.; Chai, X.; Zhang, K. Kinematic modeling and optimization of a new reconfigurable parallel mechanism. Mech. Mach. Theory 2020, 149, 103850. [Google Scholar] [CrossRef]
- Huang, G.; Zhang, D.; Guo, S.; Qu, H. Design and optimization of a novel three-dimensional force sensor with parallel structure. Sensors 2018, 18, 2416. [Google Scholar] [CrossRef]
- Fomin, A.; Antonov, A.; Glazunov, V. Forward kinematic analysis of a rotary hexapod. In ROMANSY 23-Robot Design, Dynamics and Control. ROMANSY 2020; Venture, G., Solis, J., Takeda, Y., Konno, A., Eds.; CISM International Centre for Mechanical Sciences (Courses and Lectures); Springer: Cham, Switzerland, 2021; Volume 601, pp. 486–494. [Google Scholar] [CrossRef]
- Bohigas, O.; Manubens, O.; Ros, L. Singularities of Robot Mechanisms; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Hatwal, H.; Ghosh, A. On the optimum design of Stewart platform type parallel manipulators. Robotica 1995, 13, 133–140. [Google Scholar] [CrossRef]
- Merlet, J.-P. Optimal design for the micro parallel robot MIPS. In Proceedings of the 2001 IEEE International Conference on Robotics and Automation (ICRA), Washington, DC, USA, 11–15 May 2002; pp. 1149–1154. [Google Scholar] [CrossRef]
- Hao, F.; Merlet, J.-P. Multi-criteria optimal design of parallel manipulators based on interval analysis. Mech. Mach. Theory 2005, 40, 157–171. [Google Scholar] [CrossRef]
- Miller, K. Optimal design and modeling of spatial parallel manipulators. Int. J. Robot. Res. 2004, 23, 127–140. [Google Scholar] [CrossRef]
- Rao, A.B.K.; Rao, P.V.M.; Saha, S.K. Dimensional design of hexaslides for optimal workspace and dexterity. IEEE Trans. Robot. 2005, 21, 444–449. [Google Scholar] [CrossRef]
- Unal, R.; Kizitas, G.; Patoglu, V. A multi-criteria design optimization framework for haptic interfaces. In Proceedings of the 2008 Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems, Reno, NV, USA, 13–14 March 2008; pp. 231–238. [Google Scholar] [CrossRef]
- Jiang, Q.; Gosselin, C.M. Geometric optimization of the MSSM Gough–Stewart platform. J. Mech. Robot. 2009, 1, 031006. [Google Scholar] [CrossRef]
- Parivash, F.; Ghasemi, A. Optimum dimensional synthesis of the Gough parallel manipulator for a desired workspace. In Proceedings of the 2017 IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, 22 December 2017; pp. 559–564. [Google Scholar] [CrossRef]
- Muralidharan, V.; Bose, A.; Chatra, K.; Bandyopadhyay, S. Methods for dimensional design of parallel manipulators for optimal dynamic performance over a given safe working zone. Mech. Mach. Theory 2020, 147, 103721. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).