Influence-Coefficient Method for Identifying Maximum-Load Configurations and Variable-Load Issues in Manipulators

Abstract

The dimensioning of general-purpose machines such as manipulators involves the solution of a number of preliminary issues. The determination of reference external loads and the identification of machine configurations that give the maximum internal load for each component are two of these issues. These two problems are commonly addressed through trial-and-error procedures based on dynamic modelling, which are implemented with the support of simulation software, since static analyses are commonly considered inadequate to solve them. Despite this, here, a technique based on influence coefficients and static analyses is presented which solves them. Such technique is also able to foresee and justify dynamic issues (i.e., possible vibrations, etc.) that could heavily affect the machine behavior. The effectiveness of the proposed technique is proved by implementing it on a 3T1R parallel manipulator. The presented design method is general and applicable to any type of non-overconstrained manipulator or mechanism.

1. Introduction

The mechanical design of manipulators has mandatory steps summarizable as follows: type synthesis [1,2,3,4], dimensional synthesis [1,2,4], and machine-element design [5,6,7]. Type synthesis identifies the machine topologies that meet the motion requirements, dimensional synthesis determines the values of the geometric parameters that affect the motion tasks the machine has to perform, and, finally, machine-element design chooses materials and sizes of each component of the machine.

The third step needs, as input data, the reference external loads applied to the machine and the identification of the machine configurations that give the maximum internal loads for each component. In general-purpose machines, such as manipulators, these input data are not straightforwardly obtainable from the design requirements and their deduction becomes even more difficult when dealing with parallel manipulators (PMs) since PMs’ reachable workspace usually includes particular configurations, named “parallel” singularities [8,9,10], where the end effector cannot carry any (even infinitesimal) load without breaking down the PM.

Various performance indices were conceived for identifying PMs’ reachable-workspace regions that are free and far from singularities, where safely locating the useful workspace [11,12,13,14,15,16,17,18]. These indices well identify kinetostatic issues and can be useful to perform the dimensional synthesis and to locate the useful workspace (see, for instance, [19,20]) far from singularities. Nevertheless, they fail in relating the “distance” from singularities to the actual internal loads of the links.

Other indices take into account also robot stiffness and dynamic performances [16,17,18,21,22,23,24,25,26]. These other indices require the knowledge of data (e.g., masses, stiffness, etc.) that are available at the end of the machine design. Therefore, they are certainly suitable for comparing already-built manipulators, but their use during design is not straightforward since it requires trial-and-error procedures.

In general, all these indices can help the design procedure, but do not provide sufficient pieces of information for determining the input data of PMs’ machine-element design. This determination is commonly addressed through trial-and-error procedures based on dynamic modelling, supported by multi-body simulation software, due to the preeminent dynamic nature of the loads applied to a manipulator. This widely adopted procedure is not able to justify unforeseen/unwanted machine behaviors that come out from the simulations thus making difficult to intervene for eliminating them.

Here, an algorithm, based on influence coefficients and static analyses, is presented which provides sufficient pieces of information for determining the input data of PMs’ machine-element design. The proposed algorithm is also able to foresee and justify dynamic issues (i.e., possible vibrations, etc.) that could heavily affect the machine behavior. Its effectiveness is proved by implementing it on a 3T1R parallel manipulator. The presented design method is general and applicable to any type of non-overconstrained manipulator or mechanism.

The proposed algorithm is a novel way of computing and using influence coefficients in the design of general-purpose machines, mainly ideated for PMs, which aims at integrating the design methodologies based on performance indices and/or extended multibody simulations by solving their lacks. Indeed, it can overcome the fact that performance indices are not able to provide sufficient data for the machine-element design, and that extended multibody simulations often do not provide sufficient pieces of information for intervening when an unforeseen phenomenon comes out from the simulations.

The paper is organized as follows. Section 2 provides some background and presents the novel technique. Then, Section 3 applies the proposed method to a 3T1R parallel manipulator. Eventually, Section 4 discusses the results and Section 5 draws the conclusions.

2. Materials and Methods

Most manipulators are based on non-overconstrained architectures [27]. Non-overconstrained manipulators become isostatic structures when the actuated joints are locked. The static analysis of an isostatic structure is sufficient to relate external loads to links’ internal loads and involves the solution of a problem that is linear and homogeneous in the input (i.e., external loads) and the output (i.e., links’ internal loads) variables [28]. This solution does not need to know the materials the links are made of and links’ cross-sections, which is an ideal condition for tools to employ during design when materials and actual sizes of the links are not known since their choice/determination is the design goal. In addition, such static analyses are based only on equilibrium equations and can take into account an esteem of the dynamic loads among the known external loads thus simulating an inverse dynamic problem [27].

Problems that involve the solution of a linear system, as the above-mentioned static analyses do, can be addressed by using the superposition principle [29]. In the case of a static analysis, the linear system to solve can be put into the following canonic form

A x = y

(1)

where x = (x₁,…,x_r)^T is an r-tuple collecting all the scalar components, x_i for i = 1,…,r, of the known external loads applied to the isostatic structure, y = (y₁,…,y_s)^T is an s-tuple collecting all the scalar components, y_j for j = 1,…,s, of links’ internal loads, and A is an s × r rectangular matrix of coefficients whose entries depend on the manipulator configuration.

The linearity of system (1) allows demonstrating that (superposition principle) if x is writable as follows

$$x={\displaystyle \sum _{p=1,n}{\lambda }_p{u}_p}$$

(2)

where λ_p, for p = 1,…,n, are n scalar coefficients and u_p = (δ_1p,…,δ_rp)^T (where δ_ip is the Kronecker delta defined as follows: δ_ip = 0 for i≠p and δ_ip = 1 for i = p), for p = 1,…,n, are n unit r-tuple, then

$$y={\displaystyle \sum _{p=1,n}{\lambda }_p{v}_p}$$

(3)

with $v_p=A{u}_p$ for p = 1,…,n. Hereafter, v_p will be named p-th influence-coefficient vector.

During the design of a manipulator, once the dimensional synthesis has been completed, Equation (3) can be exploited for the determination of the maximum internal loads of the links by implementing the following steps:

(i).

according to the type of motion [30] the end effector can perform, up to three independent unit forces and up to three independent unit moments are identified for characterizing the dynamic loads applied to the end effector during motion and the other dynamic loads reduced to the end effector;

(ii).

the unit forces/moments determined in the previous step are transformed into u_p r-tuples to introduce into Equation (2) for computing the input data of Equation (1);

(iii).

for each u_p determined in the previous step, the corresponding influence-coefficient vector v_p is computed for a discretized set of end-effector poses inside the useful workspace of the manipulator;

(iv).

the so-determined v_p are analyzed for finding the maximum internal loads of each link due to each unit load u_p together with the corresponding manipulator configurations;

(v).

by exploiting Equation (3), the maximum internal loads of each link determined in the previous step are combined to obtain the reference internal loads of each link to use for sizing the link in terms of material choice and cross-section.

This procedure, over providing the input data for the machine-element design, is able to highlight critical conditions due to unbalanced variable loads acting on the links, since it is a static calculus referred to dynamic loads, thus providing pieces of information that orientate the next steps of the manipulator design.

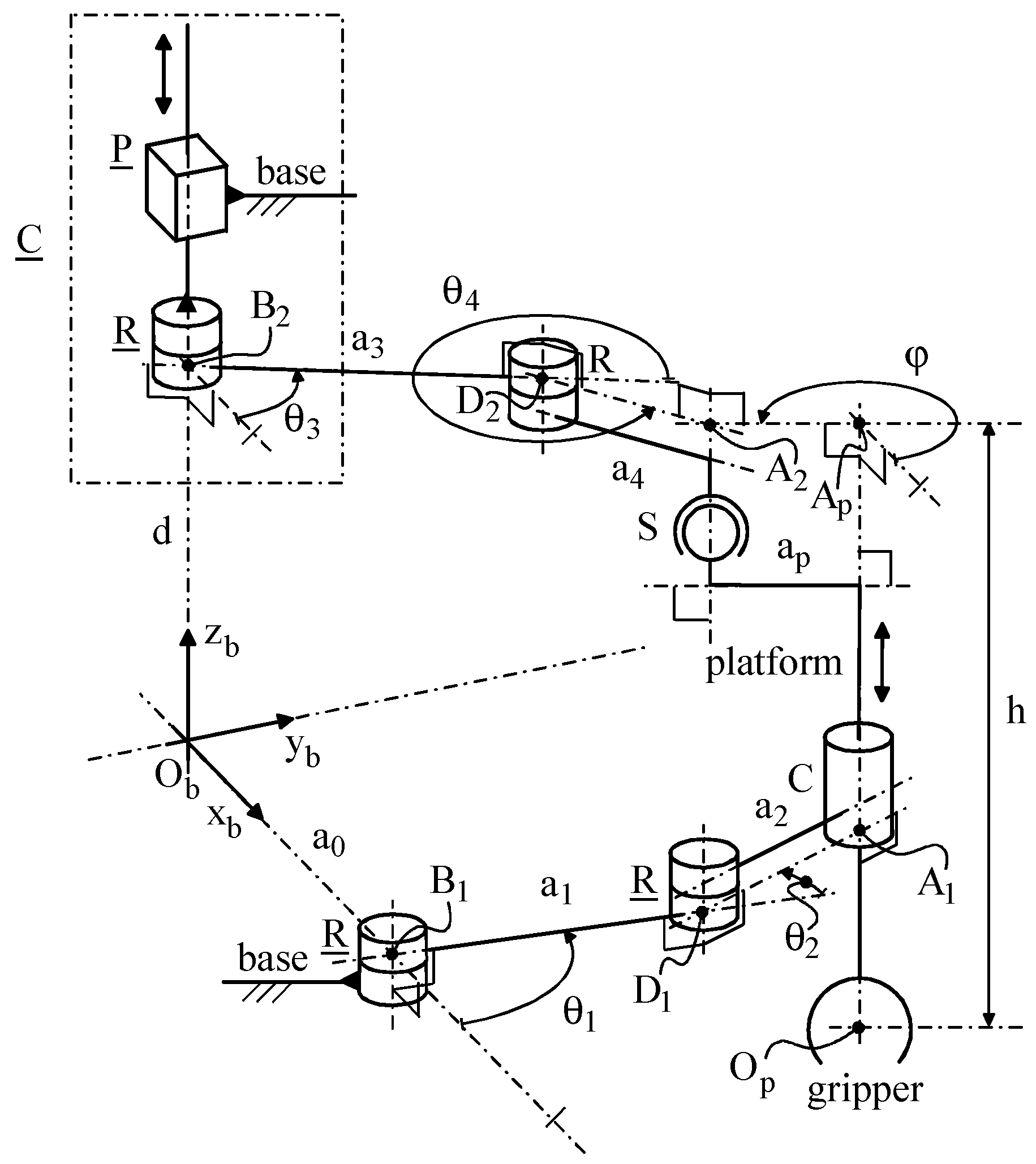
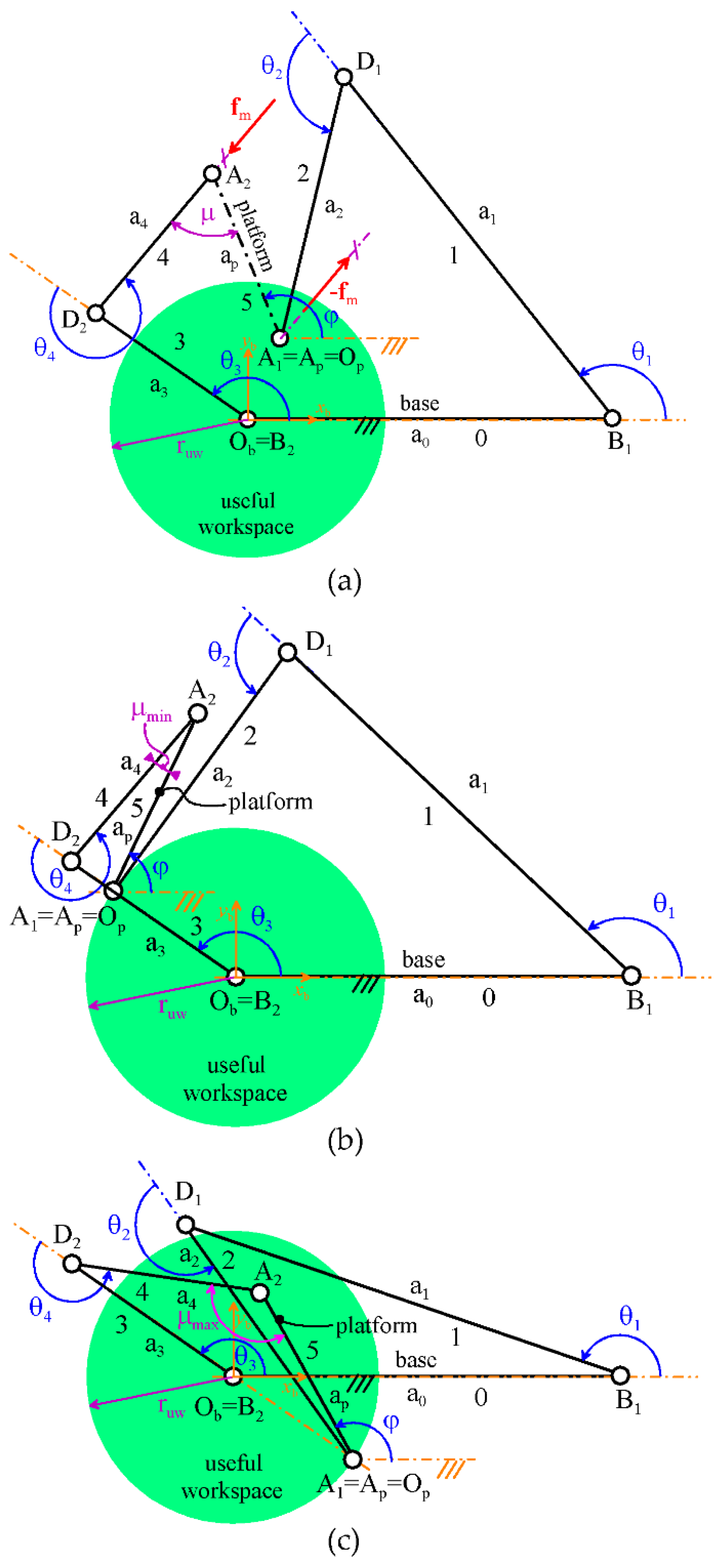
Next section exemplifies the procedure by applying it to the partially decoupled 3T1R PM shown in Figure 1.

3. Results

Figure 1 shows a single-loop PM in which the end effector (platform) is simultaneously connected to the frame (base) through two kinematic chains (limbs), one of type CRS1 and the other of type RRC, that is, it is a PM of type CRS-RRC. The axes of the R and C pairs are all parallel. The actuated C pair of the CRS limb is obtained by means of a PR chain with the sliding direction of the P pair parallel to the axis of the R pair. Such a PM architecture has four degrees of freedom [31] and constrains the platform to perform spatial translations (3T) plus rotations around axes with one fixed direction (1R), that is, the platform can perform only motions of 3T1R type, named Scara or Schoenflies motions [30]. This Scara PM has been ideated [20,31] at the Laboratory of Mechatronics and Virtual Prototyping (LaMaViP) of the University of Ferrara and, hereafter, for the sake of brevity, it will be named “LaMaViP’s CRS-RRC”. In the context of the Scara PMs, LaMaViP’s CRS-RRC is interesting because it can be actuated by keeping all the motors on the base and using commercial components, and it has the platform translation decoupled from the platform rotation [20,31].

The following notations/definitions are introduced (see Figure 1):

-

O_bx_by_bz_b is a Cartesian reference fixed to the base with the direction of the z_b-coordinate axis parallel to the R and C pair axes;

-

O_p is a point fixed to the platform whose coordinates, (x_p, y_p, z_p)^T, measured in O_bx_by_bz_b, locate the position of the platform;

-

B₂ is a point that lies on the axis of the actuated C-pair of the CRS limb and is fixed to the output link of the C-pair;

-

d is the signed distance of B₂ from O_b chosen as linear joint-variable of the actuated C-pair;

-

D₂, A_p, and A₂ are the intersection points between the plane parallel to the x_by_b plane that passes through B₂ and, respectively, the axis of the passive R-pair, the axis of the passive C-pair, and the line parallel to the z_b axis that passes through the center of the S-pair;

-

h is a geometric constant of the platform equal to the length of the segment A_pO_p;

-

a_p is a geometric constant of the platform that is equal to the length of the segment A_pA₂;

-

φ is the angle between the segment A_pA₂ and the line parallel to x_b and passing through A_p (the angle φ uniquely determines the platform orientation);

-

a₃ and a₄ are the lengths of the segments B₂D₂ and D₂A₂, respectively;

-

θ₃ and θ₄ are the angular joint-variables of the actuated C-pair and of the passive R-pair, respectively;

-

θ₁ and θ₂ are the angular joint-variables of the two actuated R-pairs of the RRC limb;

-

B₁, D₁, and A₁ are the intersection points between the x_by_b coordinate plane and, respectively, the axis of the actuated R-pair adjacent to the base, the axis of the intermediate R-pair of the RRC limb and the axis of the passive C-pair;

-

a₀, a₁ and a₂ are the lengths of the segments O_bB₁, B₁D₁ and D₁A₁, respectively.

From a kinematics point of view, the RRC limb constrains the platform to perform Schoenflies motions with rotation axis parallel to the z_b-coordinate axis and controls only the x_p and y_p coordinates of O_p (i.e., the platform translations parallel to the x_by_b coordinate-plane). Moreover, the CRS limb controls the coordinate z_p of point O_p (i.e., the platform translation parallel to the z_b-coordinate axis) through its linear joint-variable, d, and, independently, the platform orientation (i.e., the angle φ) through its angular joint-variable, θ₃.

The dimensional synthesis of LaMaViP’s CRS-RRC was addressed in [19]. In [19], a useful workspace assigned as a right circular cylinder with a radius, r_uw, of 300 mm and a height of 200 mm, whose axis is coincident with the z_b-coordinate axis, brought to choose the following values of the geometric constants (see Figure 1): a₀ = 800 mm, a₁ = 950 mm, a₂ = 600 mm, a₃ = 400 mm, a₄ = 400 mm, and a_p = 400 mm. 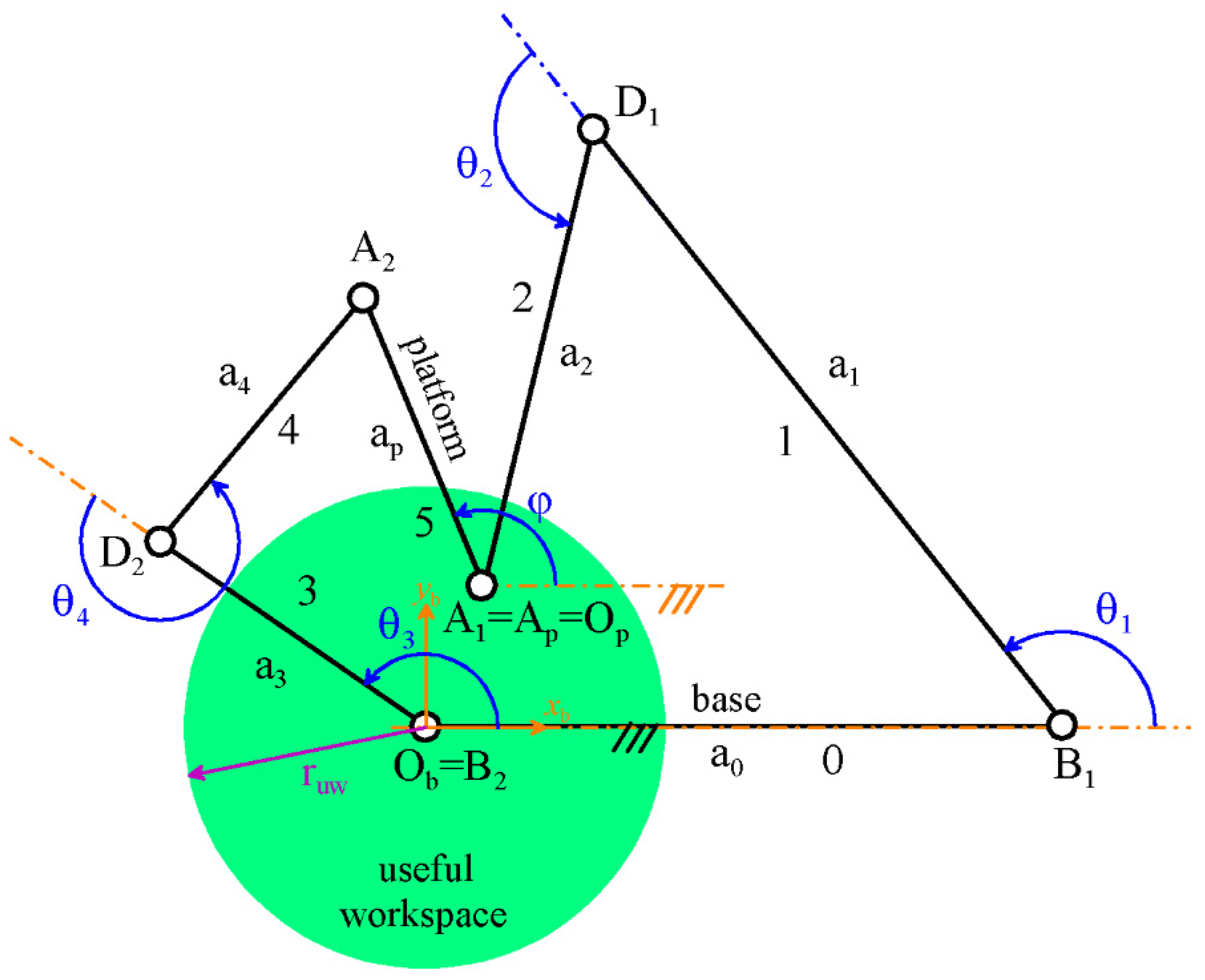Figure 2 shows the scaled top view of a LaMaViP’s CRS-RRC sized according to this geometric data together with the position of the chosen useful workspace (the green circle in Figure 2). The analysis of Figure 2 reveals that the translation of the platform along the direction of the z_b-coordinate axis is fully decoupled from the remaining platform motion. Indeed, the motion due to the prismatic pair does not appear in the top view (Figure 2) where the PM becomes a planar six-bar mechanism controlled by the actuated-joint variables θ₁, θ₂, and θ₃. In addition, in this six-bar, θ₁ and θ₂ just control the position of the platform (i.e., the position of point A₁), whereas θ₃ fully controls the platform orientation (i.e., the angle φ) through a four-bar transmission.

3.1. Implementation of Steps (i) and (ii)

According to the introduced notations, the 4-tuples q = (θ₁,θ₂,θ₃,d)^T and κ = (x_p,y_p,z_p,φ)^T collect the actuated-joint (input) variables and the platform-pose (output) variables, respectively. The inspection of Figure 1 and Figure 2 reveals that the entries of q and κ must satisfy the following constraint equations

x_p = a₀ + a₁cosθ₁ + a₂cos(θ₁ + θ₂),

(4a)

y_p = a₁sinθ₁ + a₂sin(θ₁ + θ₂),

(4b)

z_p = d − h

(4c)

(x_p + a_p cosφ − a₃ cosθ₃)² + (y_p + a_p sinφ − a₃ sinθ₃)² = a₄²,

(4d)

which are holonomic and time-independent.

Equations (4a)–(4d) yield the following relationships between the virtual displacements δq = (δθ₁, δθ₂, δθ₃, δd)^T and δκ = (δx_p, δy_p, δz_p, δφ)^T

$$J_{\mathrm{k}}\mathsf{\delta }\mathsf{\kappa }=J_{\mathrm{q}}\mathsf{\delta }q$$

(5)

with

$$J_{\mathrm{k}}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ {\mathrm{m}}_{\mathrm{x}}& {\mathrm{m}}_{\mathrm{y}}& 0& {\mathrm{a}}_{\mathrm{p}}({\mathrm{m}}_{\mathrm{y}}{\mathrm{c}}_{\mathsf{\phi }}-{\mathrm{m}}_{\mathrm{x}}{\mathrm{s}}_{\mathsf{\phi }})\end{array}\right]$$

(6a)

$$J_{\mathrm{q}}=\left[\begin{array}{cccc}-({\mathrm{a}}_1{\mathrm{s}}_{{\mathsf{\theta }}_1}+{\mathrm{a}}_2{\mathrm{s}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2)})& -{\mathrm{a}}_2{\mathrm{s}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2)}& 0& 0\\ ({\mathrm{a}}_1{\mathrm{c}}_{{\mathsf{\theta }}_1}+{\mathrm{a}}_2{\mathrm{c}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2)})& {\mathrm{a}}_2{\mathrm{c}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2)}& 0& 0\\ 0& 0& 0& 1\\ 0& 0& {\mathrm{a}}_3({\mathrm{m}}_{\mathrm{y}}{\mathrm{c}}_{{\mathsf{\theta }}_3}-{\mathrm{m}}_{\mathrm{x}}{\mathrm{s}}_{{\mathsf{\theta }}_3})& 0\end{array}\right]$$

(6b)

where c_w and s_w stand for cos(w) and sin(w), respectively, whereas, (see Figure 2)

$$\begin{gathered} {\mathrm{m}}_{\mathrm{x}}={\mathrm{x}}_{\mathrm{p}}+{\mathrm{a}}_{\mathrm{p}}{\mathrm{c}}_{\mathsf{\phi }}-{\mathrm{a}}_3{\mathrm{c}}_{{\mathsf{\theta }}_3}={\mathrm{a}}_4{\mathrm{c}}_{{(\mathsf{\theta }}_3+{\mathsf{\theta }}_4)}; \\ {\mathrm{m}}_{\mathrm{y}}={\mathrm{y}}_{\mathrm{p}}+{\mathrm{a}}_{\mathrm{p}}{\mathrm{s}}_{\mathsf{\phi }}-{\mathrm{a}}_3{\mathrm{s}}_{{\mathsf{\theta }}_3}={\mathrm{a}}_4{\mathrm{s}}_{{(\mathsf{\theta }}_3+{\mathsf{\theta }}_4)} \end{gathered}$$

(7)

The active-force2 system applied to LaMaViP’s CRS-RRC consists of the active external forces applied to the end effector and the generalized torques applied inside the actuated joints. The active external forces are collected into the 4-tuple γ = −(F_e,x, F_e,y, F_e,z, M_e,z)^T, where F_e,x, F_e,y, and F_e,z are the components, along x_b, y_b, and z_b, respectively, of their resultant force and M_e,z is the component along z_b of their resultant moment about O_p. In addition, the generalized torques are collected into the 4-tuple $\mathsf{\tau }={({\mathsf{\tau }}_{{\mathsf{\theta }}_1},{\mathsf{\tau }}_{{\mathsf{\theta }}_2},{\mathsf{\tau }}_{{\mathsf{\theta }}_3},{\mathsf{\tau }}_{\mathrm{d}})}^{\mathrm{T}}$ where the right subscripts indicate the actuated joint the generalized torque refers to. The virtual work principle [32] makes it possible to write

$$-{\gamma }^{\mathrm{T}}\mathsf{\delta }\mathsf{\kappa }+{\mathsf{\tau }}^{\mathrm{T}}\mathsf{\delta }q=0\hspace{1em}\forall \mathsf{\delta }q$$

(8)

The elimination of $\mathsf{\delta }\mathsf{\kappa }$ from Equation (8) by means of Equation (5) and the consideration that the resulting expression must hold for any value of $\mathsf{\delta }q$ yield

$$\mathsf{\tau }={(J_{\mathrm{k}}^{-1}{J}_{\mathrm{q}})}^{\mathrm{T}}\gamma$$

(9)

where

$${(J_{\mathrm{k}}^{-1}{J}_{\mathrm{q}})}^{\mathrm{T}}\hspace{0.17em}=\left[\begin{array}{cccc}-({\mathrm{a}}_1{\mathrm{s}}_{{\mathsf{\theta }}_1}+{\mathrm{a}}_2{\mathrm{s}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2)})& ({\mathrm{a}}_1{\mathrm{c}}_{{\mathsf{\theta }}_1}+{\mathrm{a}}_2{\mathrm{c}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2)})& 0& \frac{{\mathrm{m}}_{\mathrm{x}}({\mathrm{a}}_1{\mathrm{s}}_{{\mathsf{\theta }}_1}+{\mathrm{a}}_2{\mathrm{s}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2)})-{\mathrm{m}}_{\mathrm{y}}({\mathrm{a}}_1{\mathrm{c}}_{{\mathsf{\theta }}_1}+{\mathrm{a}}_2{\mathrm{c}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2)})}{{\mathrm{a}}_{\mathrm{p}}({\mathrm{m}}_{\mathrm{y}}{\mathrm{c}}_{\mathsf{\phi }}-{\mathrm{m}}_{\mathrm{x}}{\mathrm{s}}_{\mathsf{\phi }})}\\ -{\mathrm{a}}_2{\mathrm{s}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2)}& {\mathrm{a}}_2{\mathrm{c}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2)}& 0& \frac{{\mathrm{a}}_2{(\mathrm{m}}_{\mathrm{x}}{\mathrm{s}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2)}-{\mathrm{m}}_{\mathrm{y}}{\mathrm{c}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2)})}{{\mathrm{a}}_{\mathrm{p}}({\mathrm{m}}_{\mathrm{y}}{\mathrm{c}}_{\mathsf{\phi }}-{\mathrm{m}}_{\mathrm{x}}{\mathrm{s}}_{\mathsf{\phi }})}\\ 0& 0& 0& \frac{{\mathrm{a}}_3({\mathrm{m}}_{\mathrm{y}}{\mathrm{c}}_{{\mathsf{\theta }}_3}-{\mathrm{m}}_{\mathrm{x}}{\mathrm{s}}_{{\mathsf{\theta }}_3})}{{\mathrm{a}}_{\mathrm{p}}({\mathrm{m}}_{\mathrm{y}}{\mathrm{c}}_{\mathsf{\phi }}-{\mathrm{m}}_{\mathrm{x}}{\mathrm{s}}_{\mathsf{\phi }})}\\ 0& 0& 1& 0\end{array}\right]$$

(10)

The analysis of Equation (9) and of Figure 1 and Figure 2 reveals that, over the platform,

(a)

F_e,x and F_e,y load only the RRC limb, their effects are coupled and do not depend on φ (i.e., on the platform orientation);

(b)

F_e,z loads the CRS limb through the S-pair and its static effect on links 3 and 4 (see Figure 2) depends on the limb configuration. Moreover, the static equilibrium of the platform reveals that, when F_e,z is applied at O_p and the S-pair equilibrates it by applying a force −F_e,z at A₂, a torque, M_p, with magnitude |F_e,z a_p| (see Figure 1) and direction perpendicular to the platform plane (i.e., the plane located by the points O_p, A_p and A₂) arises. M_p must be equilibrated by the reaction in the passive C-pair of the RRC limb. As a consequence, F_e,z makes the RRC limb loaded, too, by the torque M_p, whose static effects on links 1 and 2 depend on the platform pose and the limb configuration;

(c)

M_e,z loads both the limbs and all the links.

During motion, all the components of γ (= −(F_e,x, F_e,y, F_e,z, M_e,z)^T) are generated from the inertia forces arising in the mechanism. Therefore, the static analysis must consider all the above-mentioned cases. Regarding case (a), links’ internal loads, caused by a unit force (F_e,x, F_e,y) = (c_ψ, s_ψ) N for ψ∈[0°, 360°], corresponding to u₁=(c_ψ, s_ψ, 0, 0)^T N for ψ∈[0°, 360°], applied to the RRC limb at A₁ (see Figure 1 and Figure 2), must be determined for a discretized set of A₁ positions inside the useful workspace. Regarding case (b), links’ internal loads, caused by a unit force F_e,z (= 1 N), corresponding to u₂ = (0, 0, 1, 0)^T N, applied at O_p (see Figure 1 and Figure 2), must be determined for a discretized set of O_p positions inside the useful workspace. Regarding case (c), links’ internal loads, caused by an unit moment M_e,z (=1 Nm), corresponding to u₃ = (0, 0, 0, 1)^T Nm, applied to the platform at O_p (see Figure 1 and Figure 2), must be determined for a discretized set of O_p positions inside the useful workspace.

3.2. Implementation of Steps (iii) and (iv)

3.2.1. Case (a): Links’ Internal Loads Due to u₁

In this case, only links 1 and 2 (Figure 2) are loaded and the static problem is planar. Indeed (Figure 2 and Figure 3), it consists in computing the maximum internal loads, for each admissible RRC limb configuration (i.e., for each position of A₁ in the useful workspace), in a RRC limb locked at the analyzed configuration with the planar force f_e = (F_e,x, F_e,y)^T = (c_ψ, s_ψ)^T N for ψ∈[0°, 360°] applied at A₁.

This problem is quite simple. Indeed, due to the planarity of the problem the non-null internal loads of the two links are only three: the bending moment (M_y), the shear force (S_z), and the axial force (A_x)3. Regarding link 2, whatever be the limb configuration, the maximum M_y and S_z always occur at D₁ when f_e is perpendicular to the link axis (i.e., when ψ = θ₁ + θ₂ ± 90°) and their values are M_y,2,max = ±|f_e|a₂ = ±0.6 Nm and S_z,2,max = ±|f_e| = ±1 N, respectively. Further, the maximum A_x occurs when f_e is aligned with the link axis (i.e., when ψ = θ₁ + θ₂ or ψ = θ₁ + θ₂ + 180°) and its value is A_x,2,max = ±|f_e| = ±1 N.

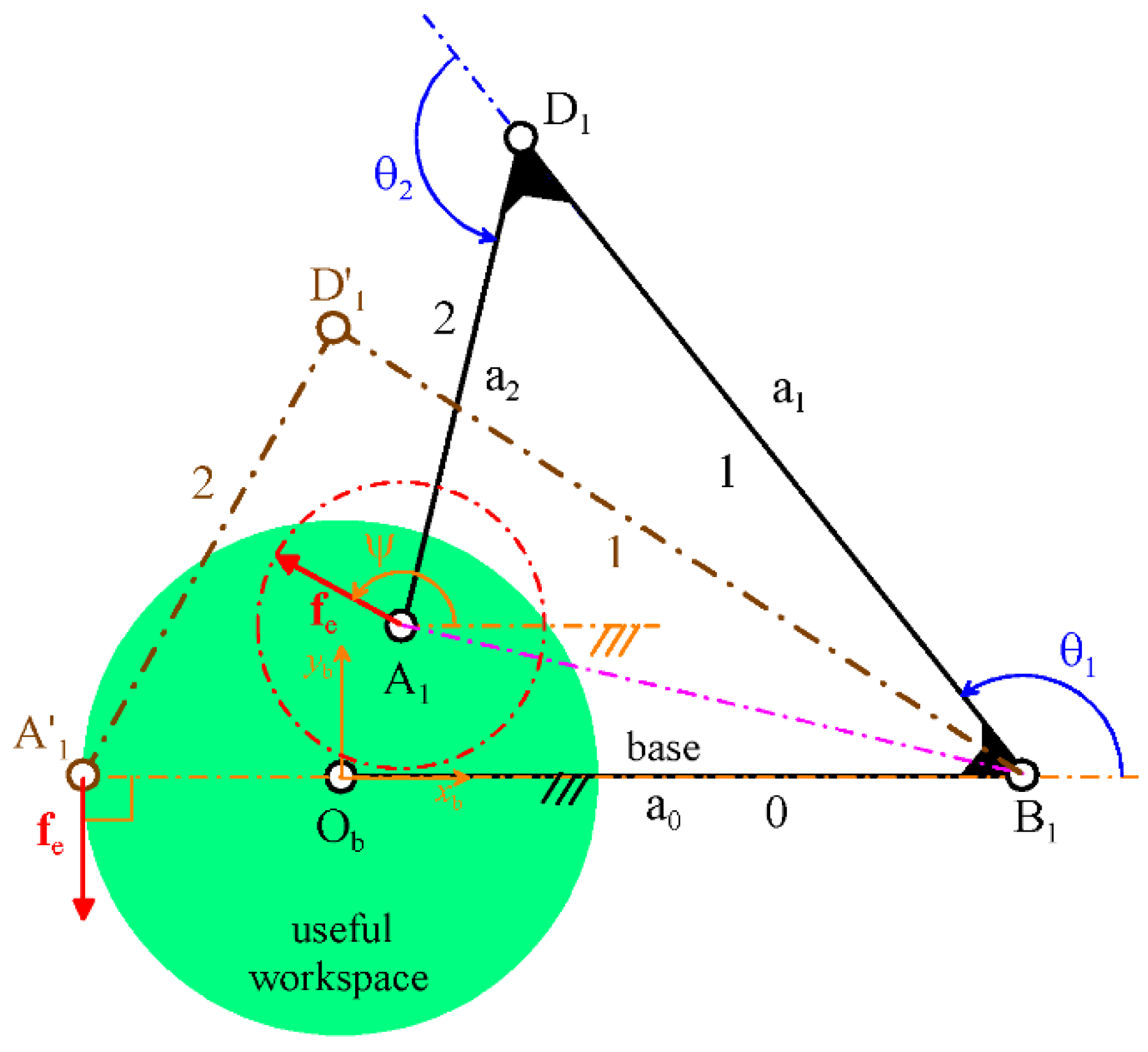
Regarding link 1, at any limb configuration, the maximum M_y occurs either at B₁ when the distance between f_e’ s line of action and B₁ is maximum (i.e., when f_e is perpendicular to the segment A₁B₁ (see Figure 3)), where its value is M_y,1 = ±|f_e||(A₁ − B₁)|, or, for |(A₁ − B₁)| < a₂, at D₁ where M_y,1 = M_y,2,max = ±|f_e|a₂ when ψ = θ₁ + θ₂ ± 90°. Anyway, the limb configuration with the maximum M_y,1 is the one where the point A₁ coincides with the point A’₁ shown in Figure 3. In this configuration, the maximum M_y occurs at B₁ for ψ = ±90° and its value is M_y,1,max = ±|f_e||(A’₁ − B₁)| = ±1.1 Nm. Moreover, whatever be the limb configuration, the maximum S_z (A_x) occurs when f_e is perpendicular (parallel) to the link axis, that is, when ψ = θ₁ ± 90° (when ψ = θ₁ or ψ = θ₁ + 180°), and its value is S_z,1,max = ±|f_e| = ±1 N (A_x,2,max = ±|f_e| = ±1 N).

Table 1. Maximum non-null influence coefficients due to the unit force f_e (Figure 3) of case (a).

i (Link Index)	My,i,max [Nm]	Sz,i,max [N]	Ax,i,max [N]
1	±1.1	±1	±1
2	±0.6	±1	±1

summarizes the results of case (a).

3.2.2. Case (b): Links’ Internal Loads Due to u₂

In this case (a unit force F_e,z (= 1 N) applied at O_p (see Figure 1 and Figure 2)), the equilibrium of the platform shows that the CRS limb is loaded by the same F_e,z (=1 N) applied at the S-pair center. Moreover, it shows that the RRC limb is loaded by a torque, M_b, lying on the motion plane (i.e., the x_by_b coordinate-plane) and applied at A₁ (see Figure 2). In particular, M_b has magnitude |M_b| = |F_e,z a_p| = 0.4 Nm and direction (φ + 90°) in the motion plane, that is, M_b =|F_e,z a_p|(c_(φ+90°), s_(φ+90°))^T = 0.4(s_φ, −c_φ)^T Nm for φ∈[0°, 360°].

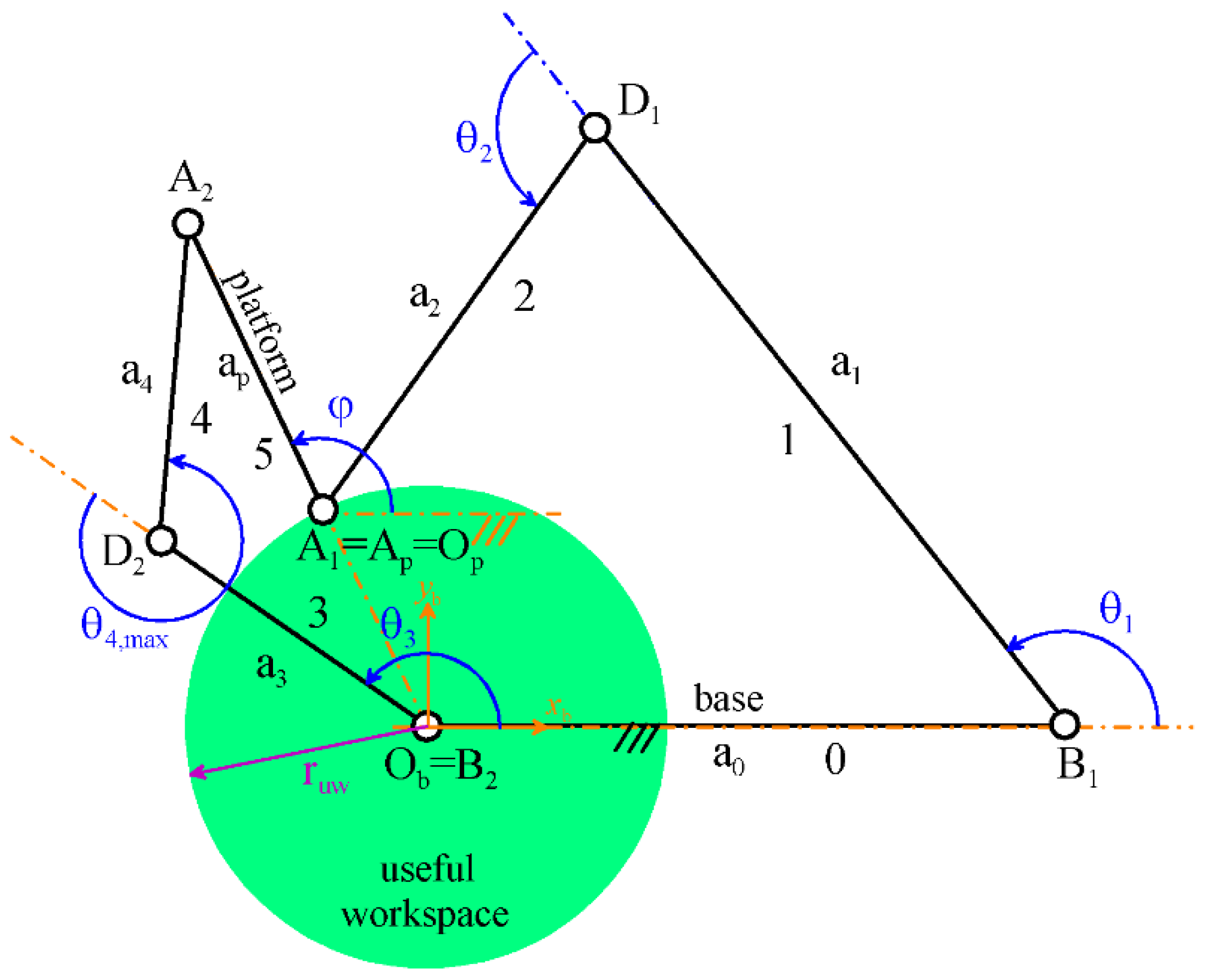
Internal Loads in the CRS Limb

In the horizontal part of link 4 (i.e., the segment A₂D₂ (see Figure 1 and Figure 2)), the unit force F_e,z (= 1 N) applied at the S-pair center generates a constant shear force S_y,4= F_e,z = 1 N, and a bending moment, M_z,4, that linearly grows from 0, at A₂, to M_z,4,max = F_e,za₄ = 0.4 Nm, at D₂. Of course, in the small vertical part of link 4, only a constant axial force equal to A_x,4 = −F_e,z = −1 N is present. These values do not depend on the limb configuration.

The node equilibrium at D₂ shows that link 3, at D₂, is loaded by a shear force S_y,3 = S_y,4 = 1 N, a torsional moment, M_x,3, whose analytic expression is

M_x,3 = M_z,4,max cos(θ₄ − 90°) = F_e,za₄ sinθ₄ = 0.4 sinθ₄ Nm,

and a bending moment, M_z,3, whose analytic expression is

M_z,3 = M_z,4,max cosθ₄ = F_e,za₄ cosθ₄ = 0.4 cosθ₄ Nm.

As a consequence, in link 3, the shear force S_y,3 = 1 N is constant, and the torsional moment M_x,3 (=F_e,za₄ sinθ₄ = 0.4 sinθ₄ Nm) is constant, too, but depends on the limb configurations and its maximum M_x,3,max = ±F_e,za₄ = ±0.4 Nm occurs when θ₄ = ±90°. In addition, the bending moment M_z,3 linearly varies from F_e,za₄cosθ₄, at D₂, to (F_e,za₄cosθ₄ + S_y,3a₃), at B₂, and its maximum values occurs at B₂ when θ₄ reaches its maximum value (see Figure 4). In the studied case (Figure 2 and Figure 4), Carnot’s theorem applied to the triangle B₂A₂D₂ makes it possible to write

$$\cos ({\mathsf{\theta }}_4-{180}^{°})=\frac{{\mathrm{a}}_3^2+{\mathrm{a}}_4^2-{\overline{A_2{B}_2}}^2}{2{\mathrm{a}}_3{\mathrm{a}}_4}\hspace{1em}\mathrm{with}\hspace{1em}{\left(\overline{A_2{B}_2}\right)}_{\min }={\mathrm{a}}_{\mathrm{p}}-{\mathrm{r}}_{\mathrm{uw}}\hspace{1em}\mathrm{and}\hspace{1em}{\left(\overline{A_2{B}_2}\right)}_{\max }={\mathrm{a}}_{\mathrm{p}}+{\mathrm{r}}_{\mathrm{uw}}$$

(11)

which gives θ_4,min = 194.36° and θ_4,max = 302.09°. As a consequence, the maximum bending moment is M_z,3,max = F_e,za₄cosθ_4,max + S_y,3a₃ = 0.6125 Nm.

Internal Loads in the RRC Limb

In link 2, the torque M_b = |F_e,z a_p| (s_φ, −c_φ)^T, for φ∈[0°,360°], applied at A₁, generates a constant torsional moment M_x,2 and a constant bending moment M_z,2 whose analytic expressions are (k_b is the unit vector of the z_b-coordinate axis (Figure 1))

$${\mathrm{M}}_{\mathrm{x},2}=M_b\cdot \frac{(A_1-D_1)}{{\mathrm{a}}_2}=\left|{\mathrm{F}}_{\mathrm{e},\mathrm{z}}{\mathrm{a}}_{\mathrm{p}}\right|({\mathrm{s}}_{\phi }{\mathrm{c}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2)}-{\mathrm{c}}_{\phi }{\mathrm{s}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2)})=-\left|{\mathrm{F}}_{\mathrm{e},\mathrm{z}}{\mathrm{a}}_{\mathrm{p}}\right|{\mathrm{c}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2-\phi )}=-0.4{\mathrm{c}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2-\phi )}\hspace{0.33em}\mathrm{Nm},$$

(12a)

$${\mathrm{M}}_{\mathrm{z},2}=M_b\cdot \left[\frac{(A_1-D_1)}{{\mathrm{a}}_2}\times k_b\right]=\left|{\mathrm{F}}_{\mathrm{e},\mathrm{z}}{\mathrm{a}}_{\mathrm{p}}\right|({\mathrm{s}}_{\phi }{\mathrm{c}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2-{90}^{°})}-{\mathrm{c}}_{\phi }{\mathrm{s}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2-{90}^{°})})=\left|{\mathrm{F}}_{\mathrm{e},\mathrm{z}}{\mathrm{a}}_{\mathrm{p}}\right|{\mathrm{s}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2-\phi )}=0.4{\mathrm{s}}_{({\mathsf{\theta }}_1+{\mathsf{\theta }}_2-\phi )}\hspace{0.33em}\mathrm{Nm}$$

(12b)

and depend on the mechanism configuration. Accordingly, the maximum/minimum values of M_x,2 (M_z,2) are M_x,2,max = ±|F_e,z a_p| = ±0.4 Nm (M_z,2,max = ±|F_e,z a_p| = ±0.4 Nm), occur at φ = θ₁ + θ₂ and at φ = θ₁ + θ₂ + 180° (at φ = θ₁ + θ₂ ± 90°) and do not depend on the mechanism configuration.

In link 1, the same torque M_b = |F_e,z a_p| (s_φ, −c_φ)^T, for φ∈[0°,360°], transmitted through link 2, is applied at D₁ and generates a constant torsional moment M_x,1 and a constant bending moment M_z,1 whose analytic expressions are

$${\mathrm{M}}_{\mathrm{x},1}=M_b\cdot \frac{(D_1-B_1)}{{\mathrm{a}}_1}=\left|{\mathrm{F}}_{\mathrm{e},\mathrm{z}}{\mathrm{a}}_{\mathrm{p}}\right|({\mathrm{s}}_{\phi }{\mathrm{c}}_{{\mathsf{\theta }}_1}-{\mathrm{c}}_{\phi }{\mathrm{s}}_{{\mathsf{\theta }}_1})=-\left|{\mathrm{F}}_{\mathrm{e},\mathrm{z}}{\mathrm{a}}_{\mathrm{p}}\right|{\mathrm{c}}_{({\mathsf{\theta }}_1-\phi )}=-0.4{\mathrm{c}}_{({\mathsf{\theta }}_1-\phi )}\hspace{0.33em}\mathrm{Nm},$$

(13a)

$${\mathrm{M}}_{\mathrm{z},1}=M_b\cdot \left[\frac{(D_1-B_1)}{{\mathrm{a}}_1}\times k_b\right]=\left|{\mathrm{F}}_{\mathrm{e},\mathrm{z}}{\mathrm{a}}_{\mathrm{p}}\right|({\mathrm{s}}_{\phi }{\mathrm{c}}_{({\mathsf{\theta }}_1-{90}^{°})}-{\mathrm{c}}_{\phi }{\mathrm{s}}_{({\mathsf{\theta }}_1-{90}^{°})})=\left|{\mathrm{F}}_{\mathrm{e},\mathrm{z}}{\mathrm{a}}_{\mathrm{p}}\right|{\mathrm{s}}_{({\mathsf{\theta }}_1-\phi )}=0.4{\mathrm{s}}_{({\mathsf{\theta }}_1-\phi )}\hspace{0.33em}\mathrm{Nm},$$

(13b)

and depend on the mechanism configuration. Accordingly, the maximum/minimum values of M_x,1 (M_z,1) are M_x,1,max = ±|F_e,z a_p| = ±0.4 Nm (M_z,1,max = ±|F_e,z a_p| = ±0.4 Nm), occur at φ = θ₁ and at φ = θ₁ + 180° (at φ = θ₁ ± 90°) and do not depend on the mechanism configuration.

Table 2. Maximum non-null influence coefficients due to the unit force F_e,z (= 1 N) of case (b).

i (Link Index)	Mx,i,max [Nm]	My,i,max [Nm]	Mz,i,max [Nm]	Sy,i,max [N]	Sz,i,max [N]	Ax,i,max [N]
1	±0.4	-	±0.4	-	-	-
2	±0.4	-	±0.4	-	-	-
3	±0.4	-	0.6125	1	-	-
4	-	-	0.4	1	-	−1

summarizes the results of case (b).

3.2.3. Case (c): Links’ Internal Loads Due to u₃

In this case (a unit moment M_e,z (=1 Nm) applied at O_p (see Figure 1 and Figure 2)), the equilibrium of the platform shows that the CRS limb is loaded by the force

$$f_m=-\frac{{\mathrm{M}}_{\mathrm{e},\mathrm{z}}}{{\mathrm{a}}_{\mathrm{p}}{\mathrm{s}}_{\mathsf{\mu }}}\left(\begin{array}{c}{\mathrm{c}}_{{(\mathsf{\theta }}_3+{\mathsf{\theta }}_4)}\\ {\mathrm{s}}_{{(\mathsf{\theta }}_3+{\mathsf{\theta }}_4)}\end{array}\right)=-\frac{{\mathrm{M}}_{\mathrm{e},\mathrm{z}}}{{\mathrm{a}}_{\mathrm{p}}{\mathrm{a}}_4{\mathrm{s}}_{\mathsf{\mu }}}\left(\begin{array}{c}{\mathrm{m}}_{\mathrm{x}}\\ {\mathrm{m}}_{\mathrm{y}}\end{array}\right)\hspace{1em}\mathrm{with}\hspace{1em}\mathsf{\mu }=\mathsf{\phi }-{\mathsf{\theta }}_3-{\mathsf{\theta }}_4,$$

(14)

which is applied at the S-pair center and is aligned with link 4 (see Figure 5a), and that the RRC limb is loaded by the force –f_m applied at A₁ through the C-pair (see Figure 5a).

The maximum and minimum magnitudes of f_m occur when the angle μ reaches its minimum, μ_min (see Figure 5b), and maximum, μ_max (see Figure 5c), values, respectively. With reference to Figure 5b,c, in the studied case, the following relationships hold

$${\mathsf{\mu }}_{\min }=2\arcsin \left(\frac{{\mathrm{a}}_3-{\mathrm{r}}_{\mathrm{uw}}}{{2\mathrm{a}}_4}\right)={14.3615}^{°},{\mathsf{\mu }}_{\max }=2\arcsin \left(\frac{{\mathrm{a}}_3+{\mathrm{r}}_{\mathrm{uw}}}{{2\mathrm{a}}_4}\right)={122.09}^{°}$$

(15)

which give

$${\left|f_m\right|}_{\max }=\frac{{\mathrm{M}}_{\mathrm{e},\mathrm{z}}}{{\mathrm{a}}_{\mathrm{p}}{\mathrm{s}}_{{\mathsf{\mu }}_{\min }}}=10.079\hspace{0.33em}\mathrm{N},{\left|f_m\right|}_{\min }=\frac{{\mathrm{M}}_{\mathrm{e},\mathrm{z}}}{{\mathrm{a}}_{\mathrm{p}}{\mathrm{s}}_{{\mathsf{\mu }}_{\max }}}=2.95084\hspace{0.33em}\mathrm{N}.$$

(16)

Internal Loads in the CRS Limb

In link 4, the effect of the small vertical part (i.e., the one parallel to the z_b-coordinate axis (Figure 1)) is minor, depends on its length, which has not been defined during the dimensional synthesis, and will be neglected in this static analysis. This assumption brings to consider the force f_m directly applied at A₂ (see Figure 5a) along the horizontal part of link 4. As a consequence, this load generates only an axial force A_x,4 = –|f_m| whose maximum (negative) value is A_x,4,max = −10.079 N (see Equation (15)).

The node equilibrium at D₂ shows that link 3, at D₂, is loaded by the axial force, A_x,3, and the shear force, S_z,3, given by the relationships

$${\mathrm{A}}_{\mathrm{x},3}=f_m\cdot \frac{(D_2-B_2)}{{\mathrm{a}}_3}=-\frac{{\mathrm{M}}_{\mathrm{e},\mathrm{z}}}{{\mathrm{a}}_{\mathrm{p}}{\mathrm{s}}_{\mathsf{\mu }}}({\mathrm{c}}_{{(\mathsf{\theta }}_3+{\mathsf{\theta }}_4)}{\mathrm{c}}_{{\mathsf{\theta }}_3}+{\mathrm{s}}_{{(\mathsf{\theta }}_3+{\mathsf{\theta }}_4)}{\mathrm{s}}_{{\mathsf{\theta }}_3})=-\frac{{\mathrm{M}}_{\mathrm{e},\mathrm{z}}}{{\mathrm{a}}_{\mathrm{p}}{\mathrm{s}}_{\mathsf{\mu }}}{\mathrm{c}}_{{\mathsf{\theta }}_4}=-2.5\frac{{\mathrm{c}}_{{\mathsf{\theta }}_4}}{{\mathrm{s}}_{\mathsf{\mu }}}\hspace{0.33em}\hspace{0.33em}\mathrm{N}$$

(17a)

$${\mathrm{S}}_{\mathrm{z},3}=f_m\cdot \left[\frac{(D_2-B_2)}{{\mathrm{a}}_3}\times k_b\right]=-\frac{{\mathrm{M}}_{\mathrm{e},\mathrm{z}}}{{\mathrm{a}}_{\mathrm{p}}{\mathrm{s}}_{\mathsf{\mu }}}({\mathrm{c}}_{{(\mathsf{\theta }}_3+{\mathsf{\theta }}_4)}{\mathrm{c}}_{{(\mathsf{\theta }}_3-{90}^{°})}+{\mathrm{s}}_{{(\mathsf{\theta }}_3+{\mathsf{\theta }}_4)}{\mathrm{s}}_{{(\mathsf{\theta }}_3-{90}^{°})})=-\frac{{\mathrm{M}}_{\mathrm{e},\mathrm{z}}}{{\mathrm{a}}_{\mathrm{p}}{\mathrm{s}}_{\mathsf{\mu }}}{\mathrm{c}}_{{(\mathsf{\theta }}_4+{90}^{°})}=2.5\frac{{\mathrm{s}}_{{\mathsf{\theta }}_4}}{{\mathrm{s}}_{\mathsf{\mu }}}\hspace{0.33em}\hspace{0.33em}\mathrm{N}$$

(17b)

These loads, at D₂, generate constant axial, A_x,3, and shear, S_z,3, forces along link 3 that only depend on the mechanism configuration, and a bending moment M_y,3 that linearly varies from 0, at D₂, to −S_z,3a₃, at B₂. 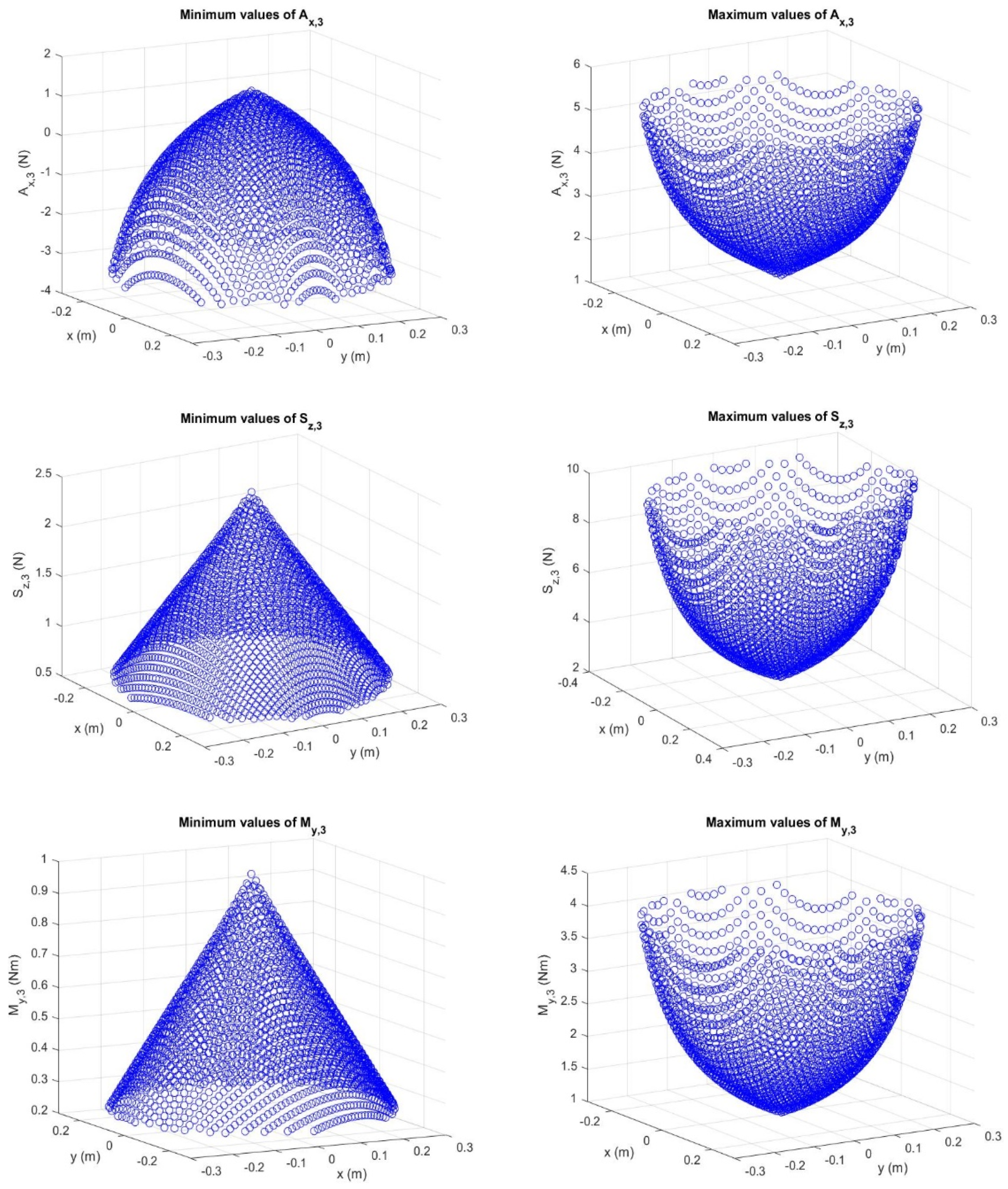Since the angles μ (see Equation (14)) and θ₄ that appear in Equations (17a) and (17b) are not independent (see system (4) and Equation (7)), the determination of the maximum/minimum values of A_x,3, S_z,3, and M_y,3 must be numerically evaluated for a sufficiently high number of mechanism configurations uniformly distributed in the useful workspace and, then, compared. A mash of 3220 positions of A₁(=(x_p, y_p)) uniformly distributed inside the useful-workspace circle have been chosen and, at each A₁ position, Equations (17a) and (17b) have been evaluated for 360 values of the angle φ spaced of 1°. The comparison of the so-computed values yields the diagrams of Figure 6 (The MatLab program that generates Figure 6 can be seen in Supplementary Materials). The analysis of these diagrams and the ranges spanned by the angles θ₄ and μ (see Equations (11) and (15)) bring to the conclusion that, in link 3, the maximum values of the internal loads can be evaluated as follows

$$\begin{gathered} {\mathrm{A}}_{\mathrm{x},3,\max }=\pm 2.5\frac{{\mathrm{c}}_{{\mathsf{\theta }}_{4,\max }}}{{\mathrm{s}}_{{\mathsf{\mu }}_{\min }}}=\pm 5.3545\hspace{0.33em}\mathrm{N},{\mathrm{S}}_{\mathrm{z},3,\max }=2.5\frac{{\mathrm{s}}_{{270}^{°}}}{{\mathrm{s}}_{{\mathsf{\mu }}_{\min }}}=\hspace{0.33em}-10.079\hspace{0.33em}\mathrm{N}, \\ {\mathrm{M}}_{\mathrm{y},3,\max }=-{\mathrm{S}}_{\mathrm{z},3,\max }{\mathrm{a}}_3=4.0316\hspace{0.33em}\mathrm{Nm} \end{gathered}$$

Internal Loads in the RRC Limb

The comparison of Figure 3 and Figure 5a together with Equation (14) reveals that this is a special case of the above-discussed case (a). Consequently, the maximum values of the internal loads of links 1 and 2 are the product of the influence coefficients of Table 1 by |f_m|_max (see Equation (16)).

Table 3. Maximum non-null influence coefficients due to the unit moment M_e,z (= 1 Nm) of case (c).

i (Link Index)	Mx,i,max [Nm]	My,i,max [Nm]	Mz,i,max [Nm]	Sy,i,max [N]	Sz,i,max [N]	Ax,i,max [N]
1	-	±11.087	-	-	±10.079	±10.079
2	-	±6.0474	-	-	±10.079	±10.079
3	-	4.0316	-	-	−10.079	±5.3545
4	-	-	-	-	-	−10.079

summarizes the results of case (c).

3.3. Implementation of Step (v)

The influence coefficients reported in Table 1, Table 2 and Table 3 must be combined by means of Equation (3) to determine the reference internal loads to use for sizing the links. In order to do this, the values of the coefficients λ_p appearing in Equation (3) must be deduced from the task requirements the machine has to satisfy. Assuming that the design requirements are

-

mass of the payload: m_p = 1 kg,

-

gyration radius of the payload: ρ = 0.2 m,

-

maximum linear accelerations: $\ddot{a}=100\hspace{0.33em}{\mathrm{m}/\mathrm{s}}^2$,

-

maximum angular acceleration: $\ddot{\mathsf{\phi }}=1000\hspace{0.33em}{\mathrm{rad}/\mathrm{s}}^2$,

-

global safety coefficient4: γ = 2.5,

the reference values of the external loads become F_e,x = F_e,y = F_e,z = γm_p $\ddot{a}$ = 250 N and M_e,z = γm_pρ² $\ddot{\mathsf{\phi }}$ = 100 Nm. Accordingly, the influence coefficients of Table 1 and Table 2 must be all multiplied by λ_p = 250 and those of Table 3 by λ_p = 100; then, the resulting values must be summed.

Table 4. Reference internal loads to use for sizing the links.

i (Link Index)	Mx,i,max [Nm]	My,i,max [Nm]	Mz,i,max [Nm]	Sy,i,max [N]	Sz,i,max [N]	Ax,i,max [N]
1	±100	±1383.7	±100	-	±1257.9	±1257.9
2	±100	±754.74	±100	-	±1257.9	±1257.9
3	±100	403.16	153.125	250	−1007.9	±535.45
4	-	-	100	250	-	−1257.9

reports the reference internal loads resulting from this computation.

4. Discussion

The implementation reported in the previous section shows that the proposed method is simple and direct to apply and only in a few cases it really requires numerical evaluations. In particular, it only needs the results of the dimensional synthesis and, differently from the techniques based on global performance indices, it is able to relate directly the task requirements to the links’ internal loads.

The analysis of Table 2 reveals that the existence of decoupled motions does not imply a static decoupling between the active forces that cause those motions. Indeed, the unit force F_e,z (see Table 2) has a static effect on links 1 and 2 that belong to a limb, the RRC, that has no effect on the platform translation along the z_b-coordinate axis direction. This happens without considering non-ideal phenomena (e.g., the friction in the joints). Furthermore, the found effects are difficult to compensate since the generated torsional, M_x,(1,2), and bending, M_z,(1,2), moments lie on the RRC-limb motion plane and tend to cause elastic displacements (which, in practice, are vibrations, since all the real external loads are dynamic loads that vary their magnitudes during motion) perpendicular to that plane.

Recognizing static couplings at an early stage of the design procedure with a clear identification of the causes is a peculiarity of the proposed method and is a desirable feature that can orientate the successive design choices. Other design techniques based on the extensive use of multi-body simulation software, together with a trial-and-error sizing procedure, would have found the limb vibration without giving an immediate explanation.

These results prove that the proposed algorithm integrates the design methodologies based on performance indices and/or on extended multibody simulations by solving their lacks.

5. Conclusions

A general technique based on influence coefficients and static analyses has been presented which allows the determination of the input data of the machine-element design (i.e., reference external loads and machine configurations that give the maximum internal load of each component) for non-overconstrained manipulators.

Differently from other techniques, the presented one uses only the results of the dimensional synthesis and does not need any tentative choice, about the materials, the links are made of, and links’ cross-sections, to be adjusted during the design procedure.

The proposed technique directly relates task requirements to links’ internal loads and is able to reveals dynamic phenomena (e.g., vibrations) that have a negative impact on the machine behavior.

The effectiveness of the proposed technique has been proved by implementing it on a 3T1R parallel manipulator.