Operator-Based Nonlinear Control for a Miniature Flexible Actuator Using the Funnel Control Method
Abstract
1. Introduction
2. Modeling
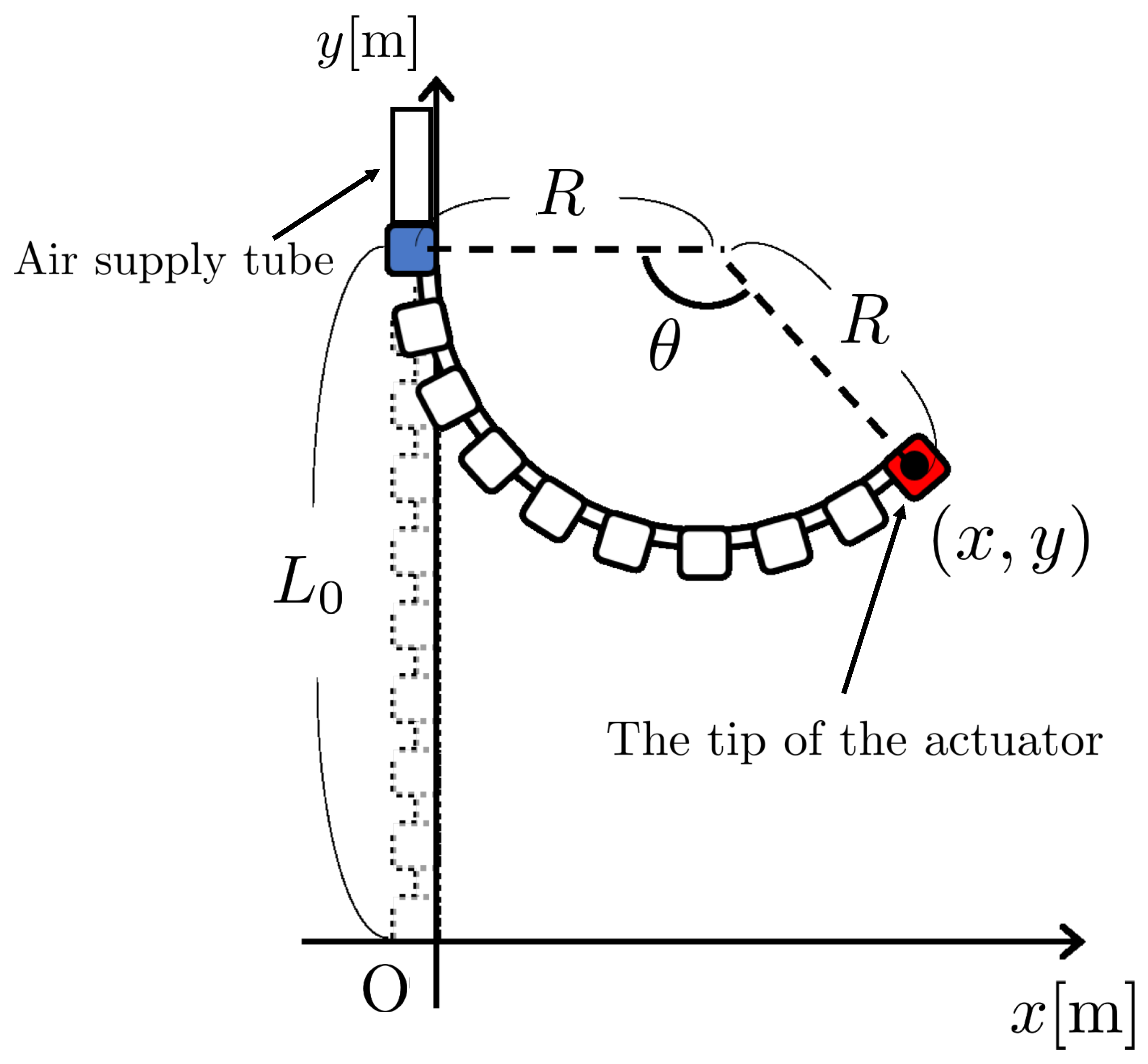
2.1. The Structure of the Miniature Flexible Actuator
2.2. Modeling of the Actuator Characteristics
2.3. Modeling of the Pneumatic Characteristics
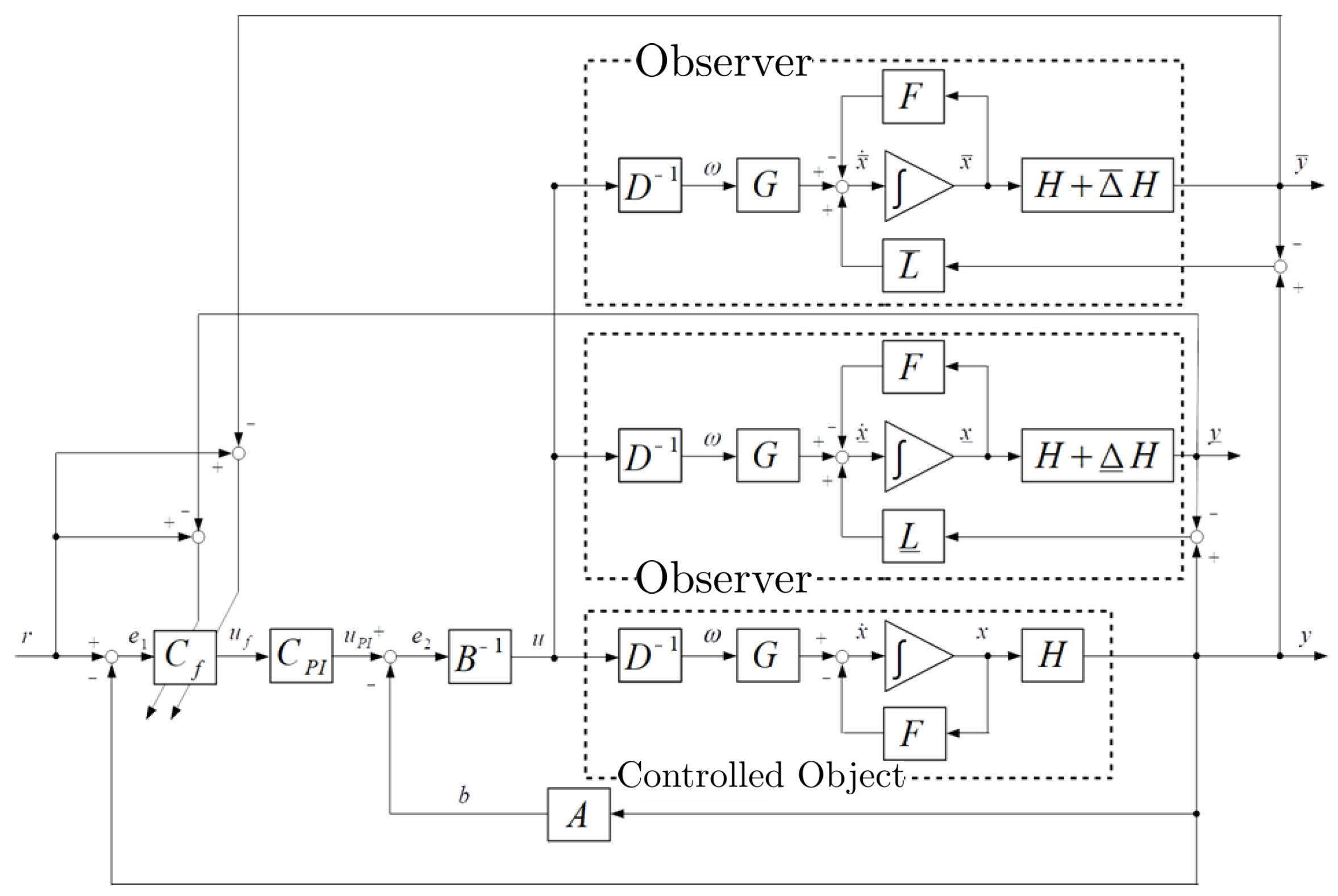
3. Nonlinear Control System Using the Funnel Control Method
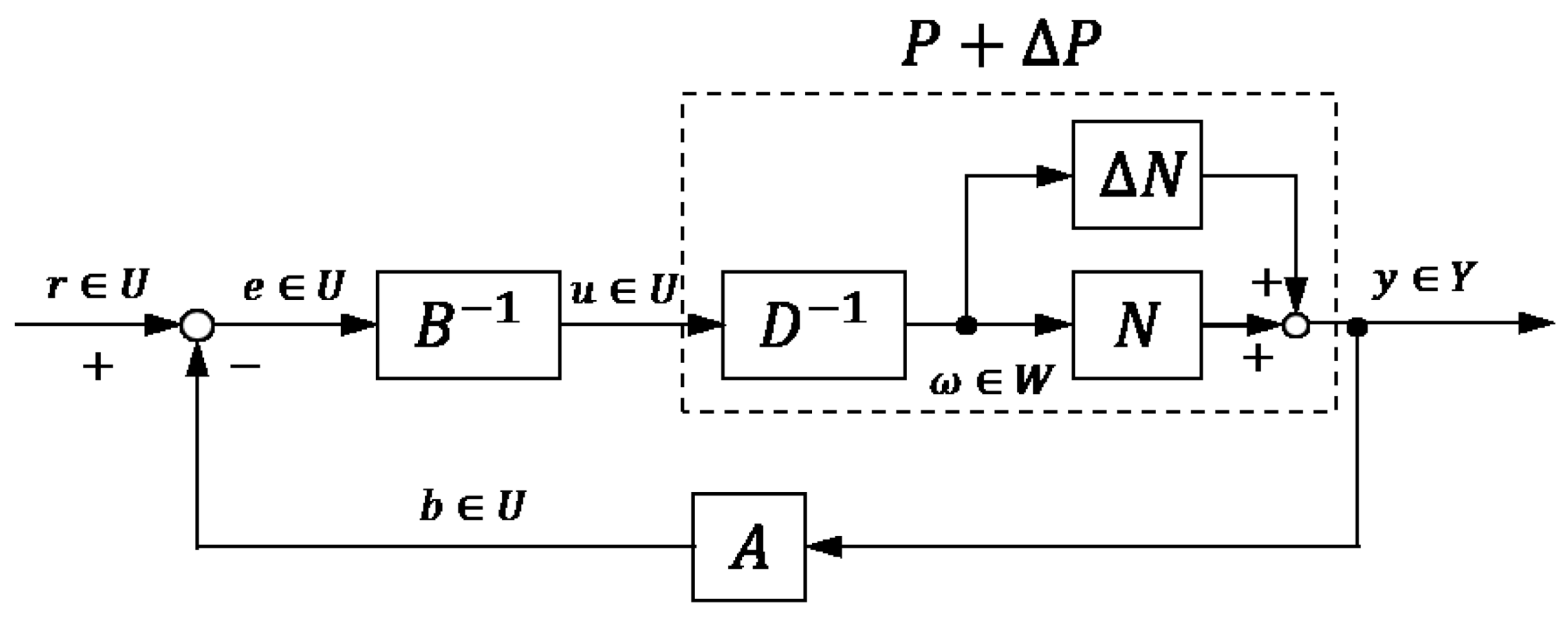
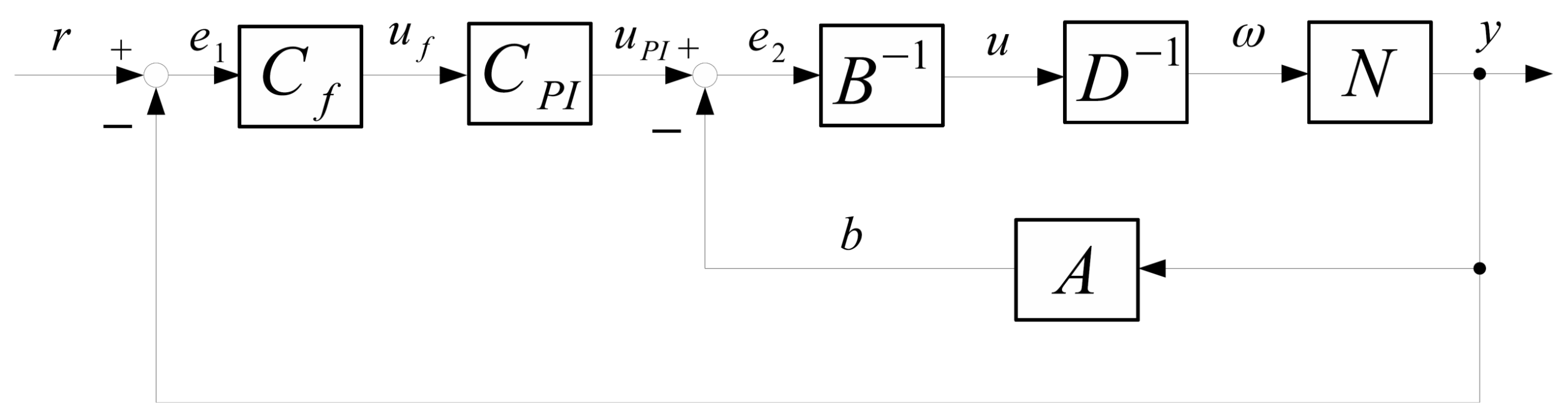
3.1. Operator-Based Nonlinear Control Feedback System Design
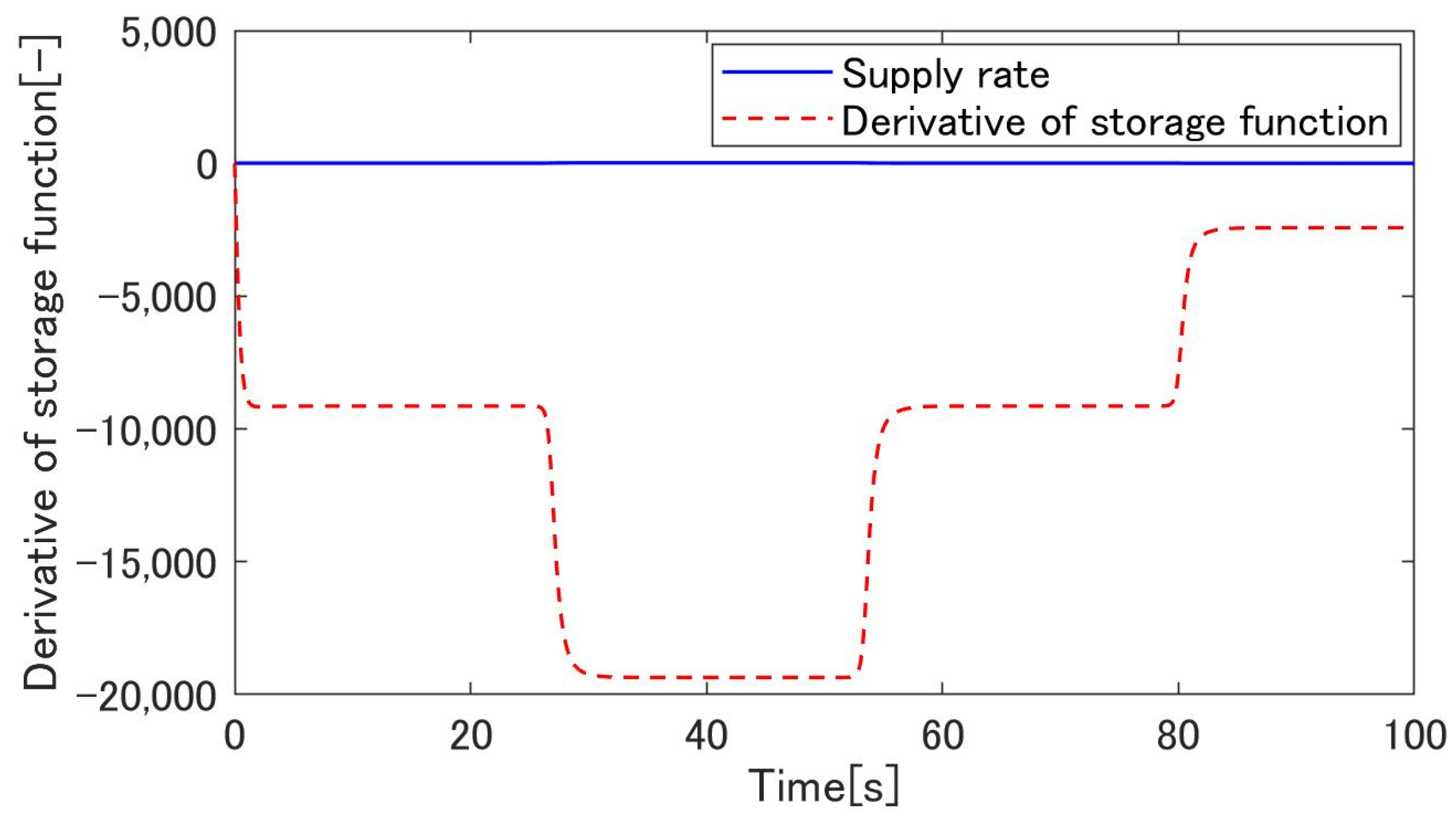
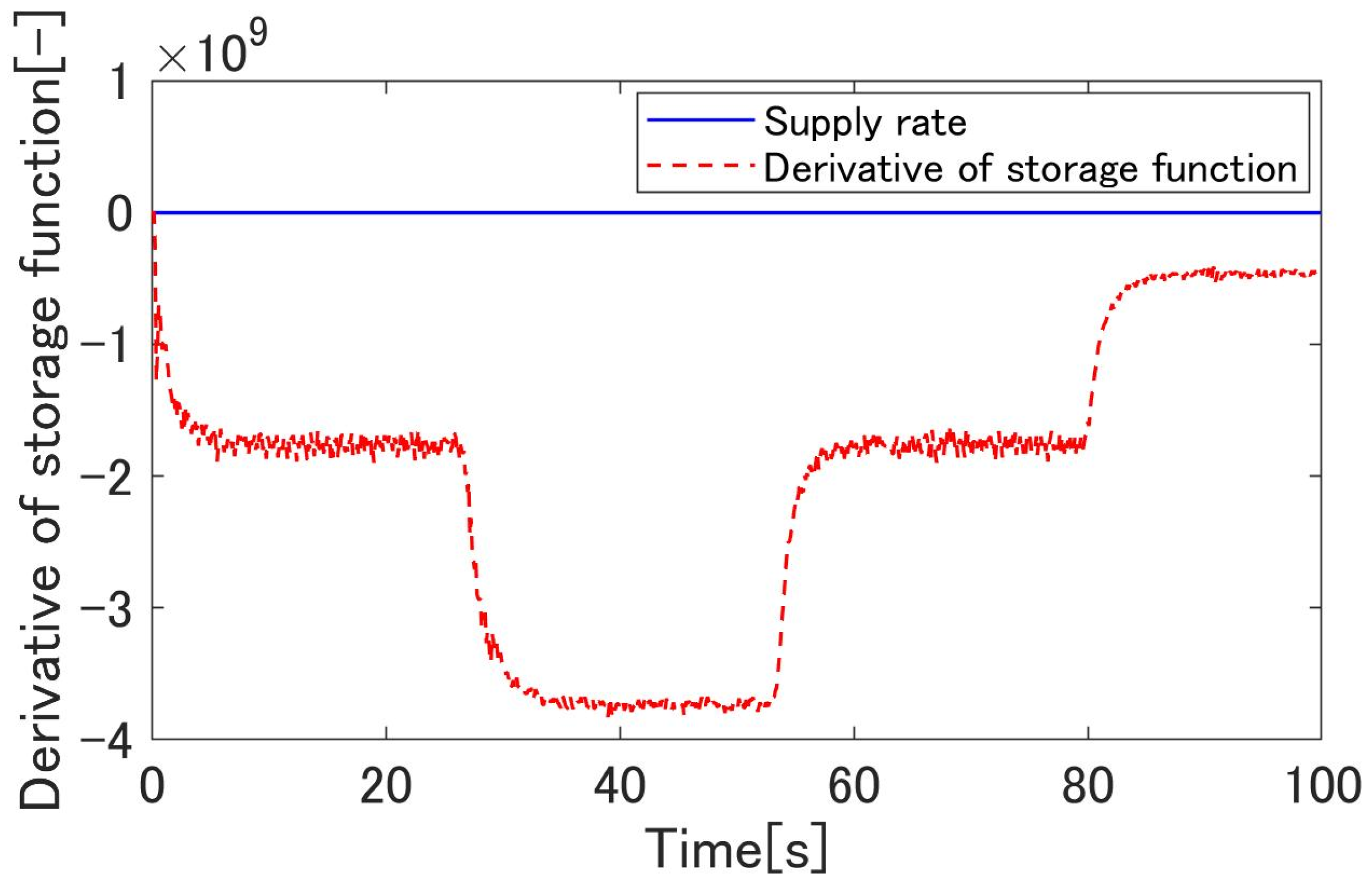
3.2. Passivity of the Proposed System
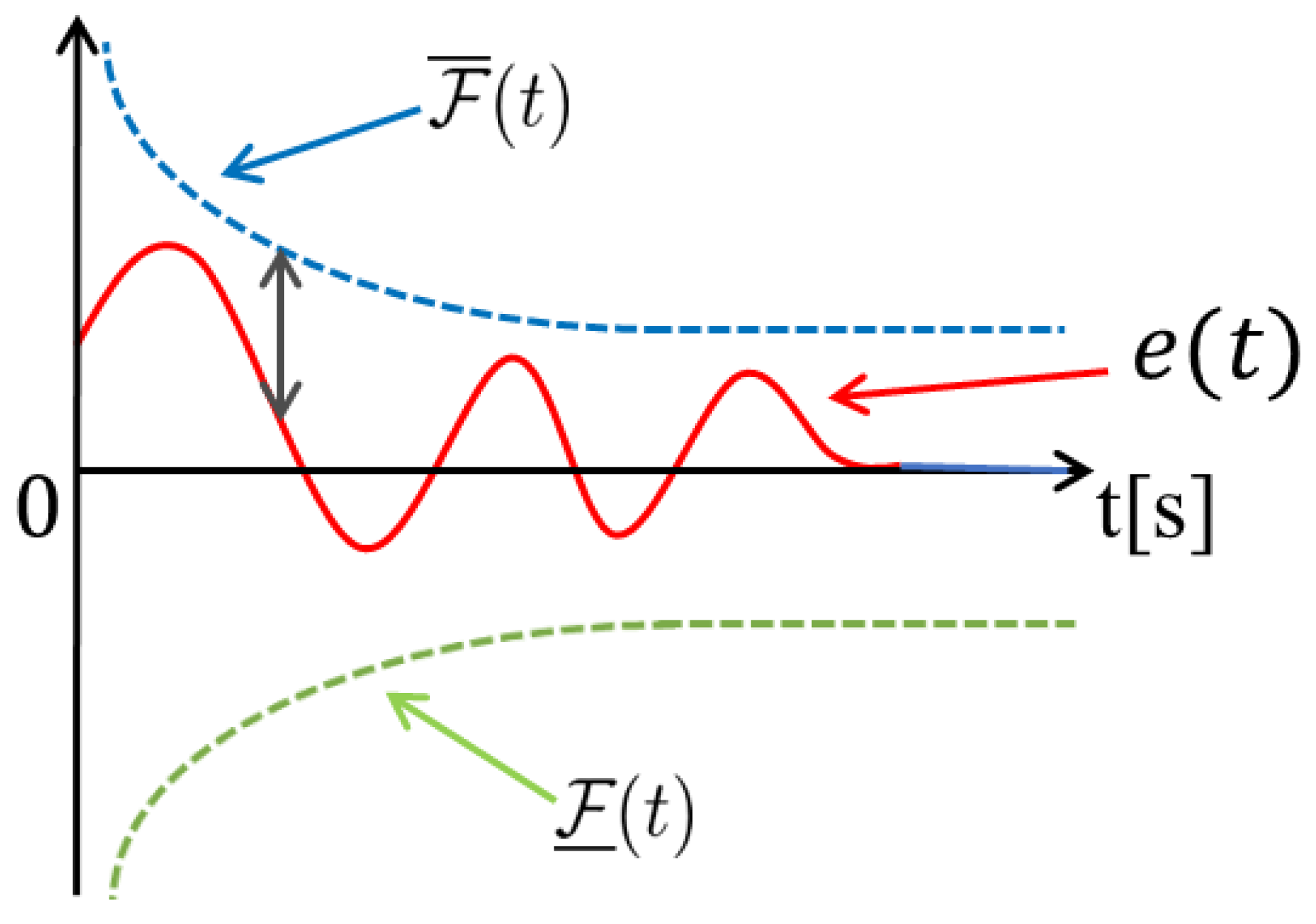
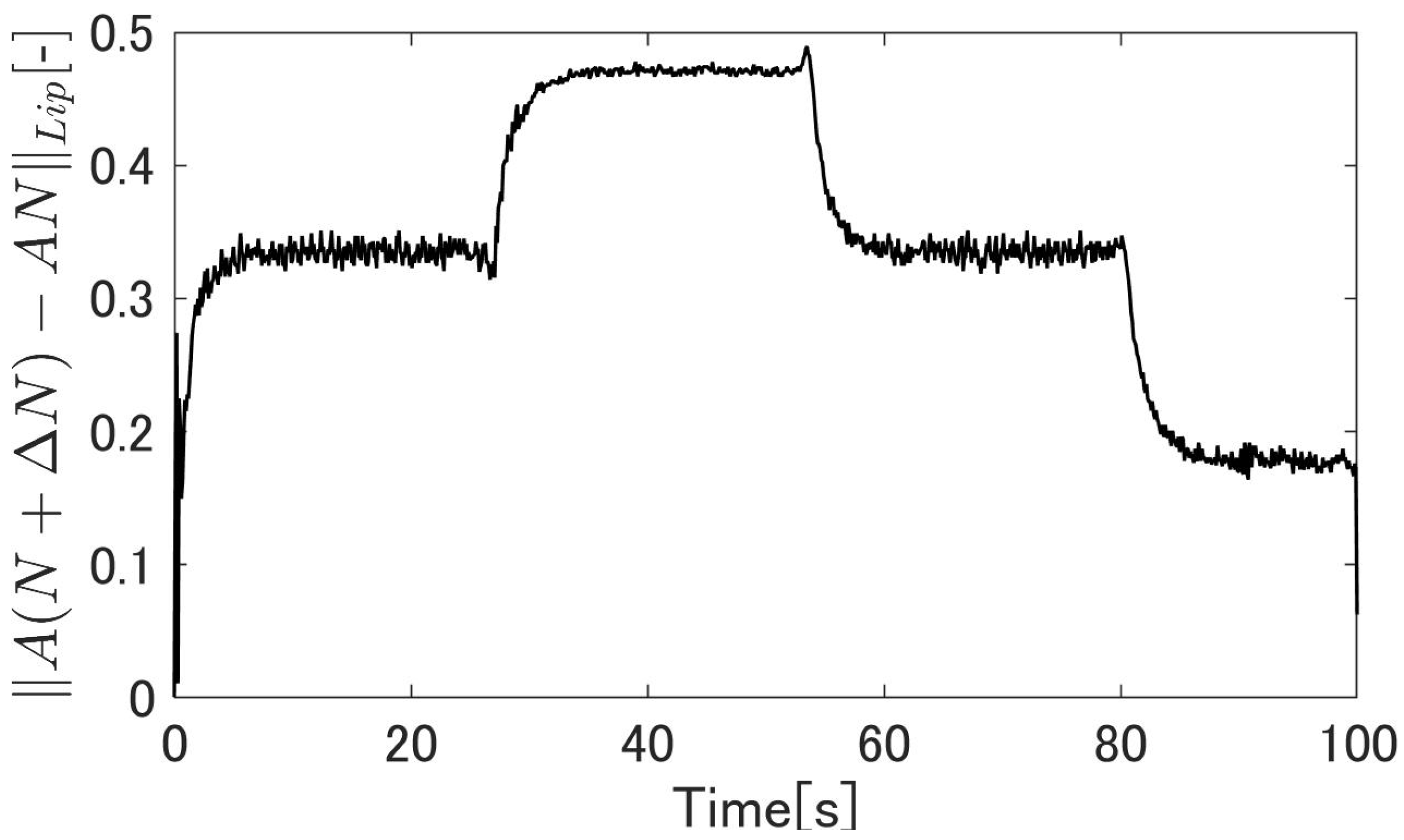
3.3. Funnel Control
3.4. Design Scheme of the Boundary Function
3.4.1. Nonlinear Observer
3.4.2. Boundary Function Using the Nonlinear Observers
4. Results and Discussion
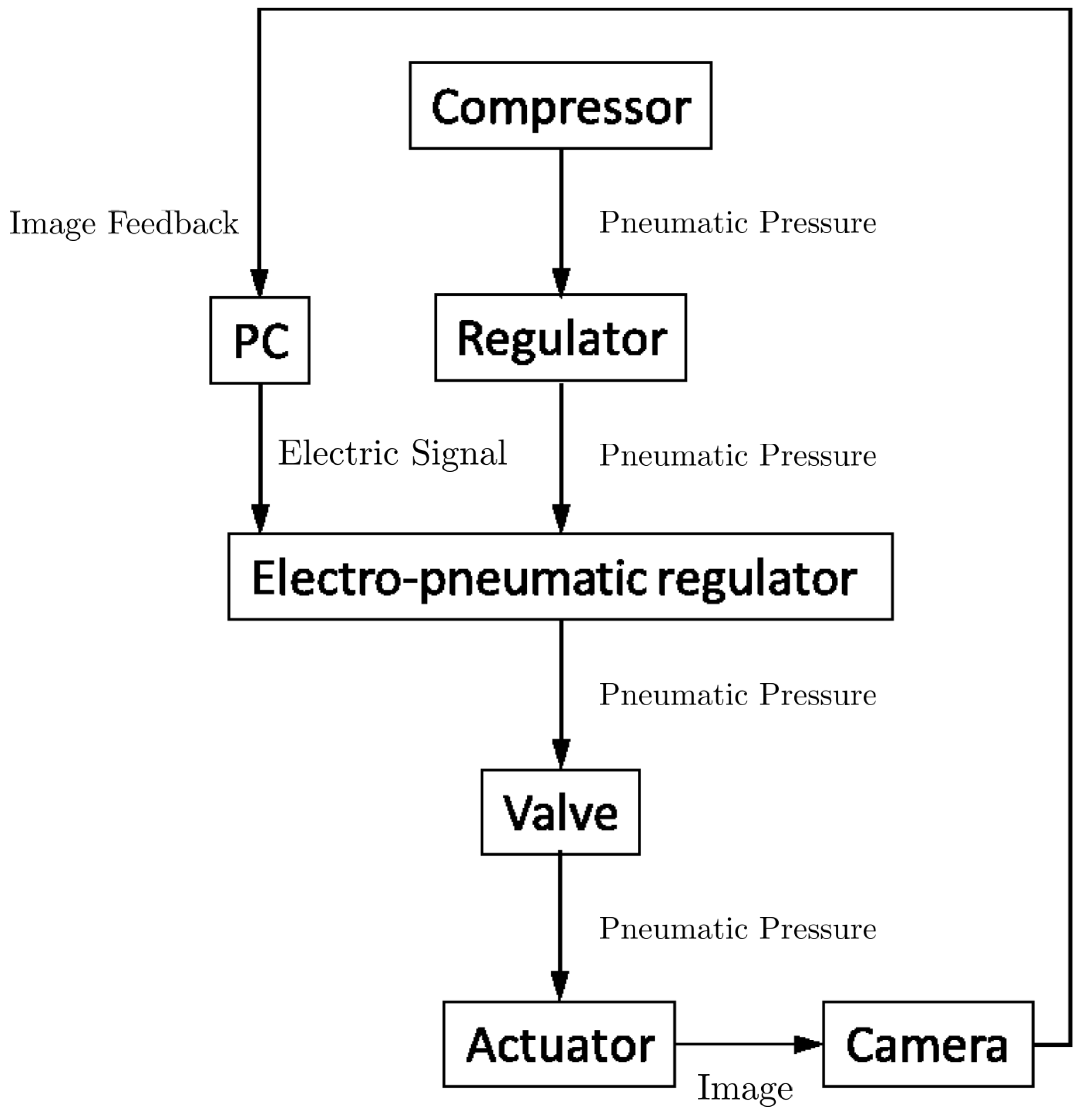
4.1. Experimental System
- The air compressor provides air pressure for the safety regulator.
- The air pressure is regulated by the safety regulator for the sake of not breaking the actuator.
- The computer sends an electrical signal to the electro-pneumatic regulator and decides on the opening of the valve.
- The air pressure is sent into the actuator and it moves.
- The output is captured as an image by a camera and fed back to the computer.
4.2. Parameters Used in the Simulation and Experiment
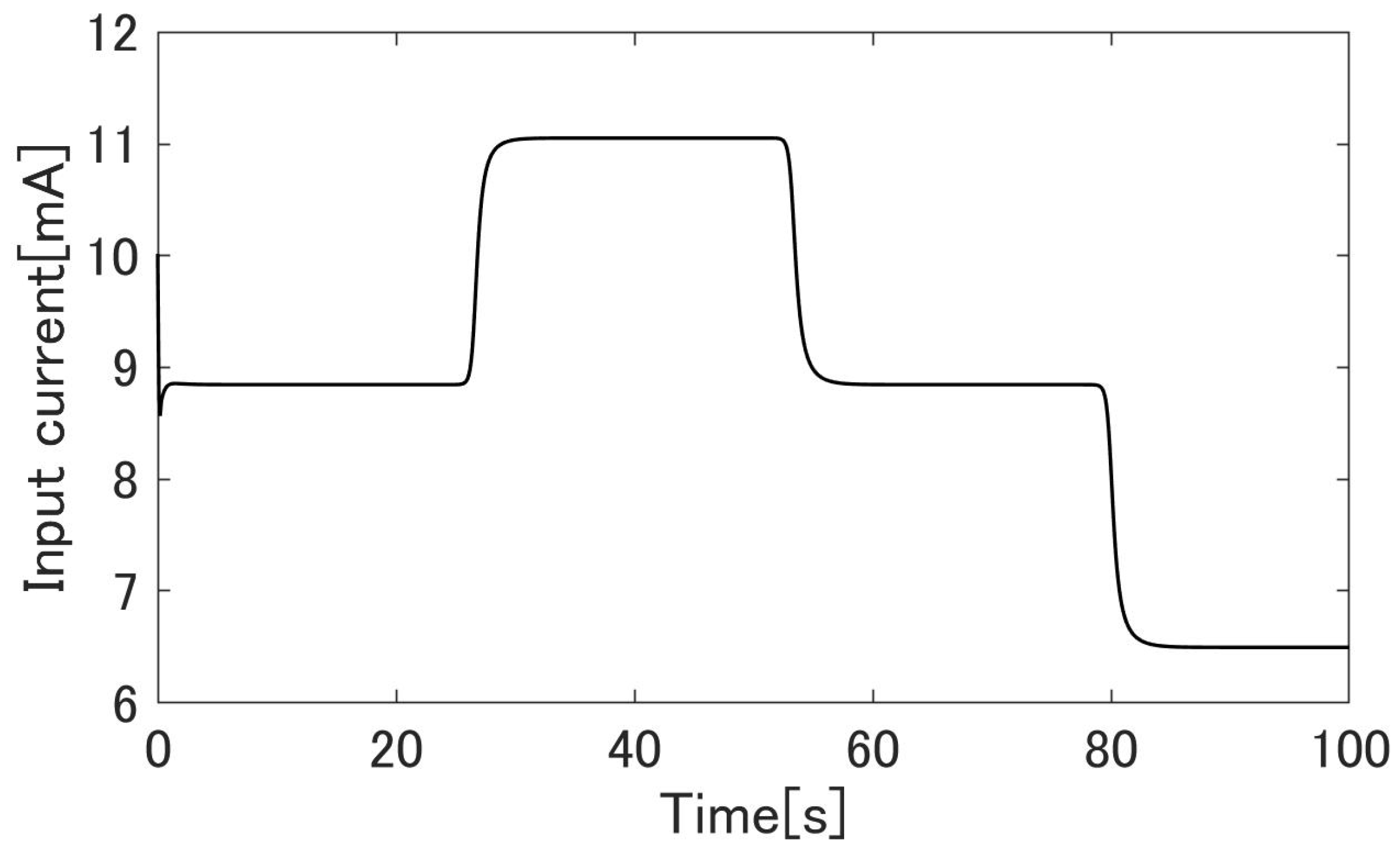
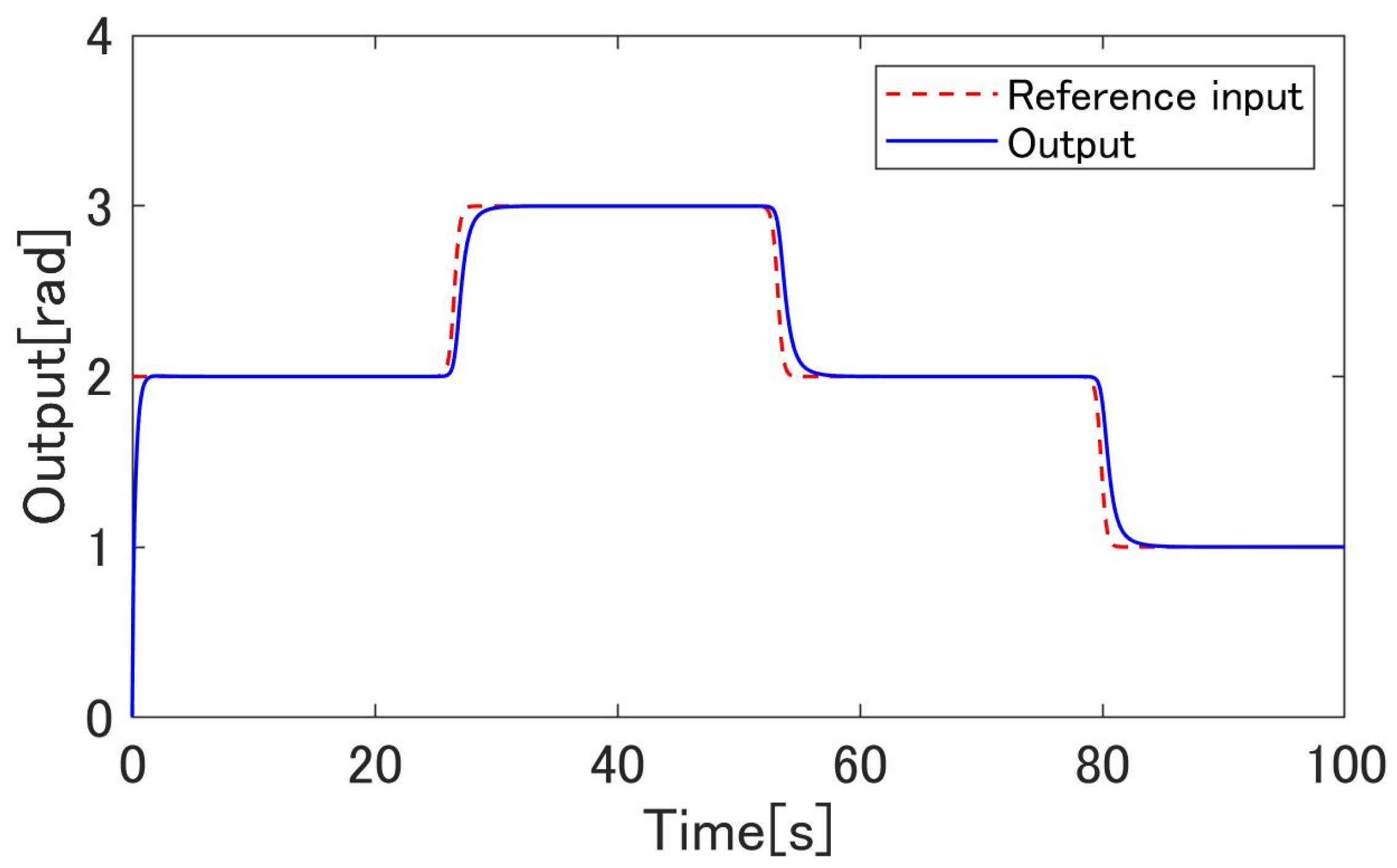
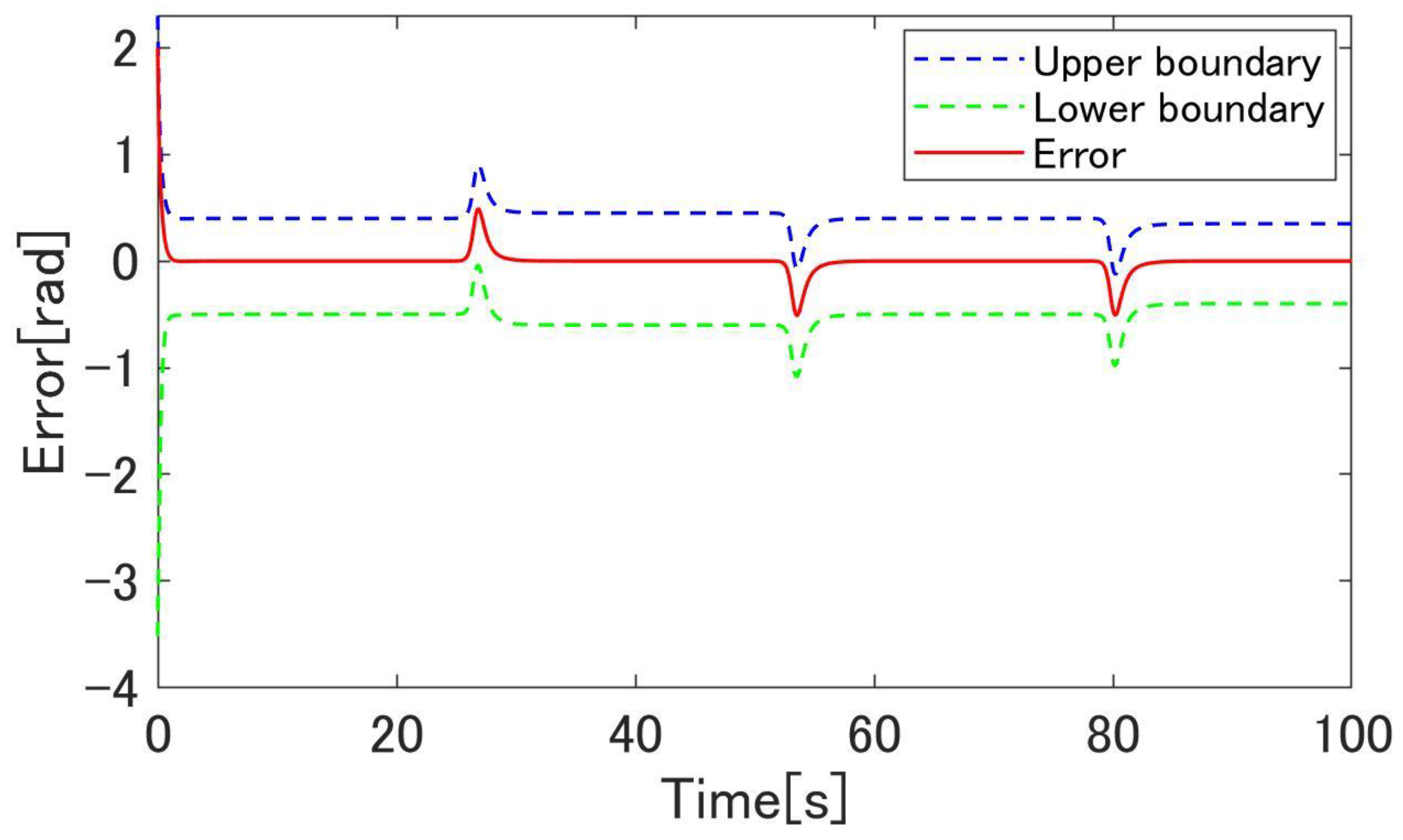
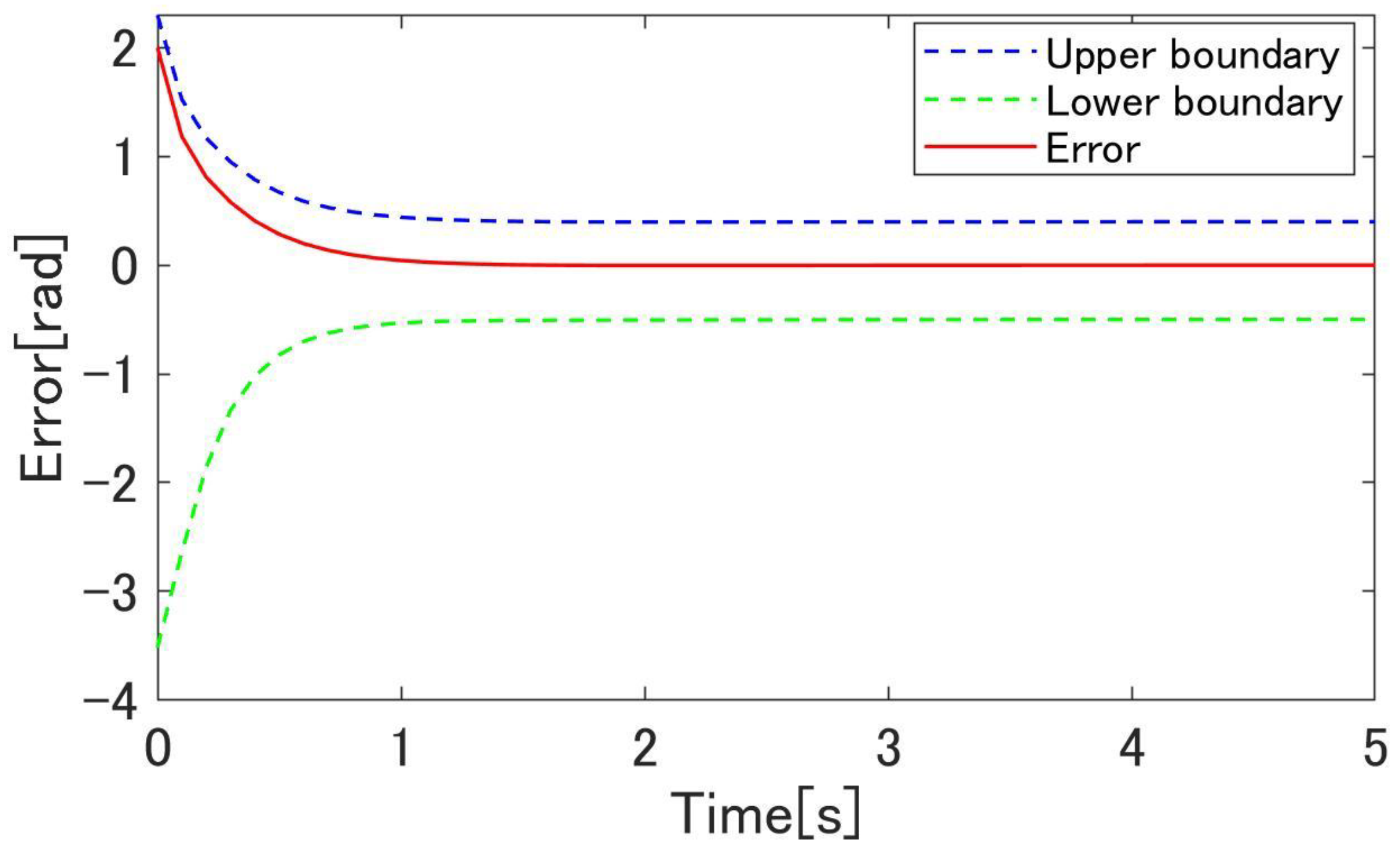
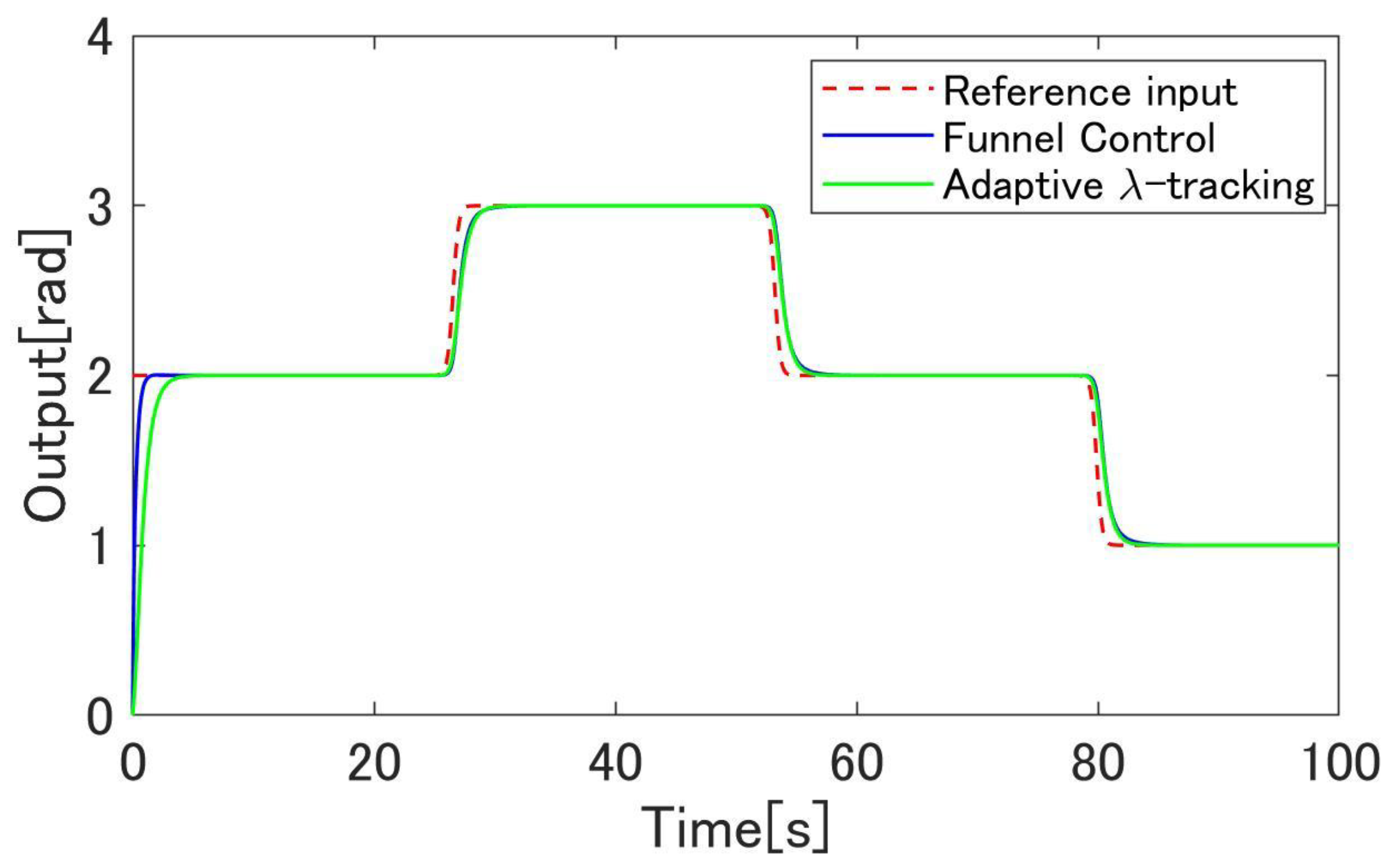
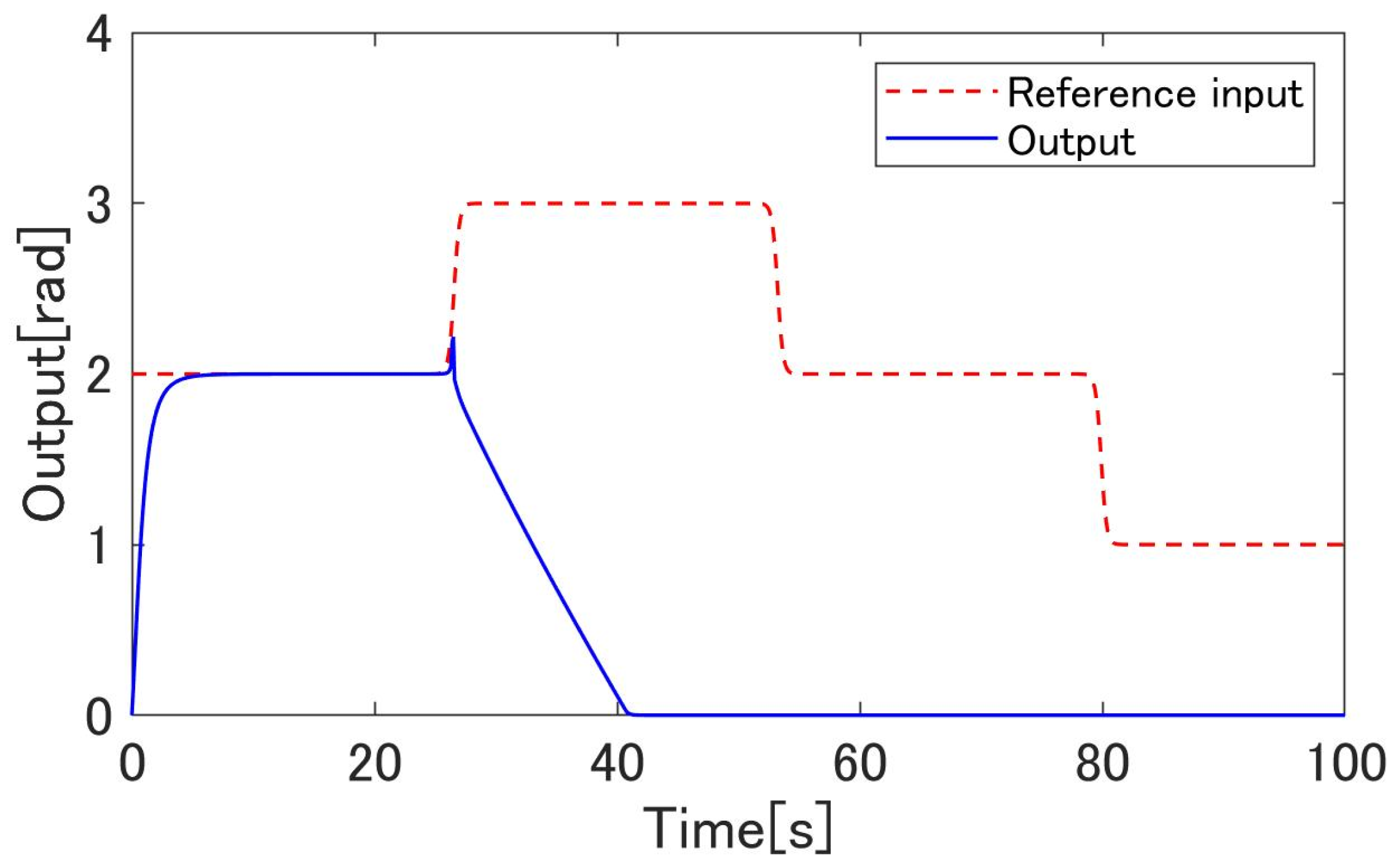
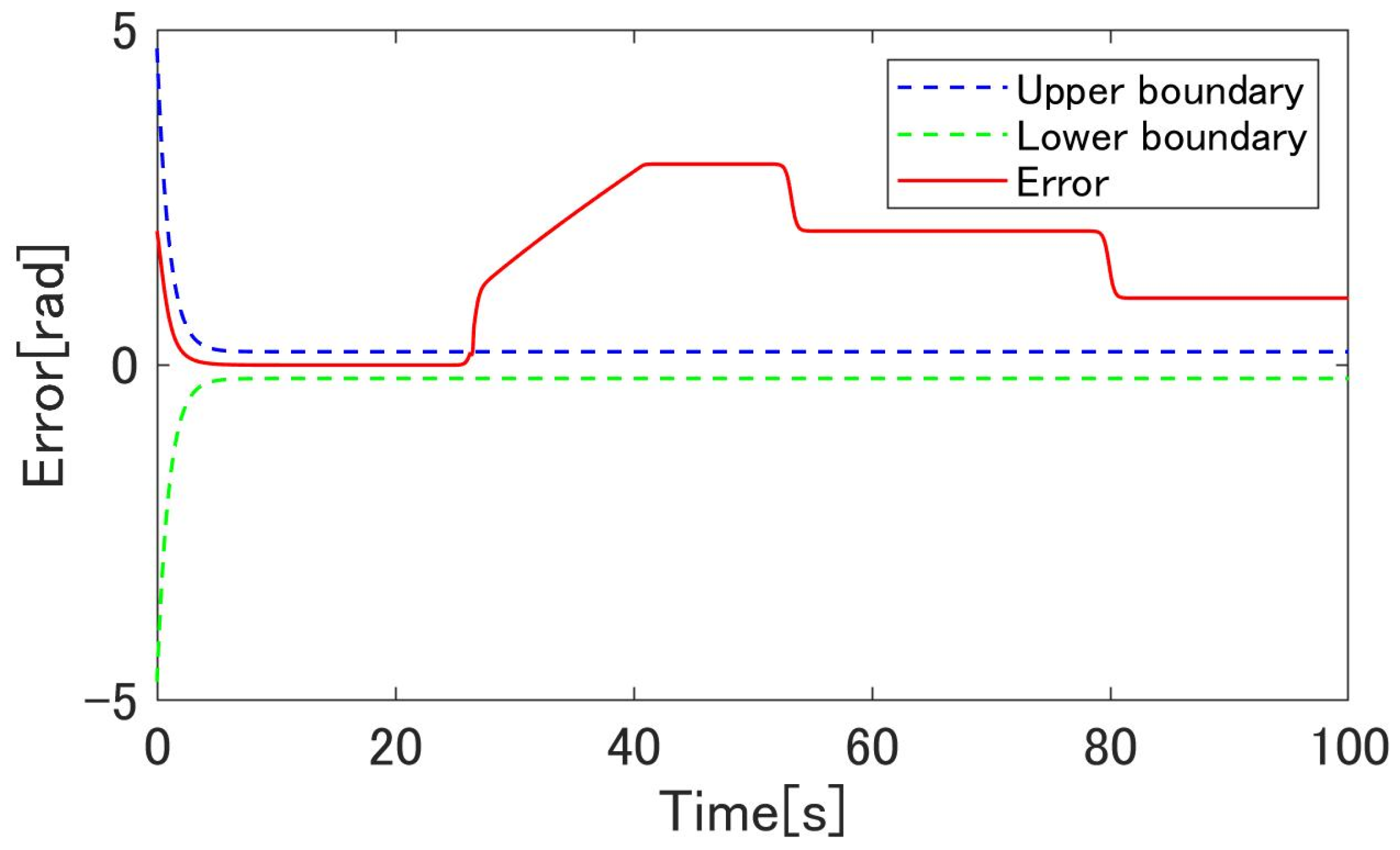
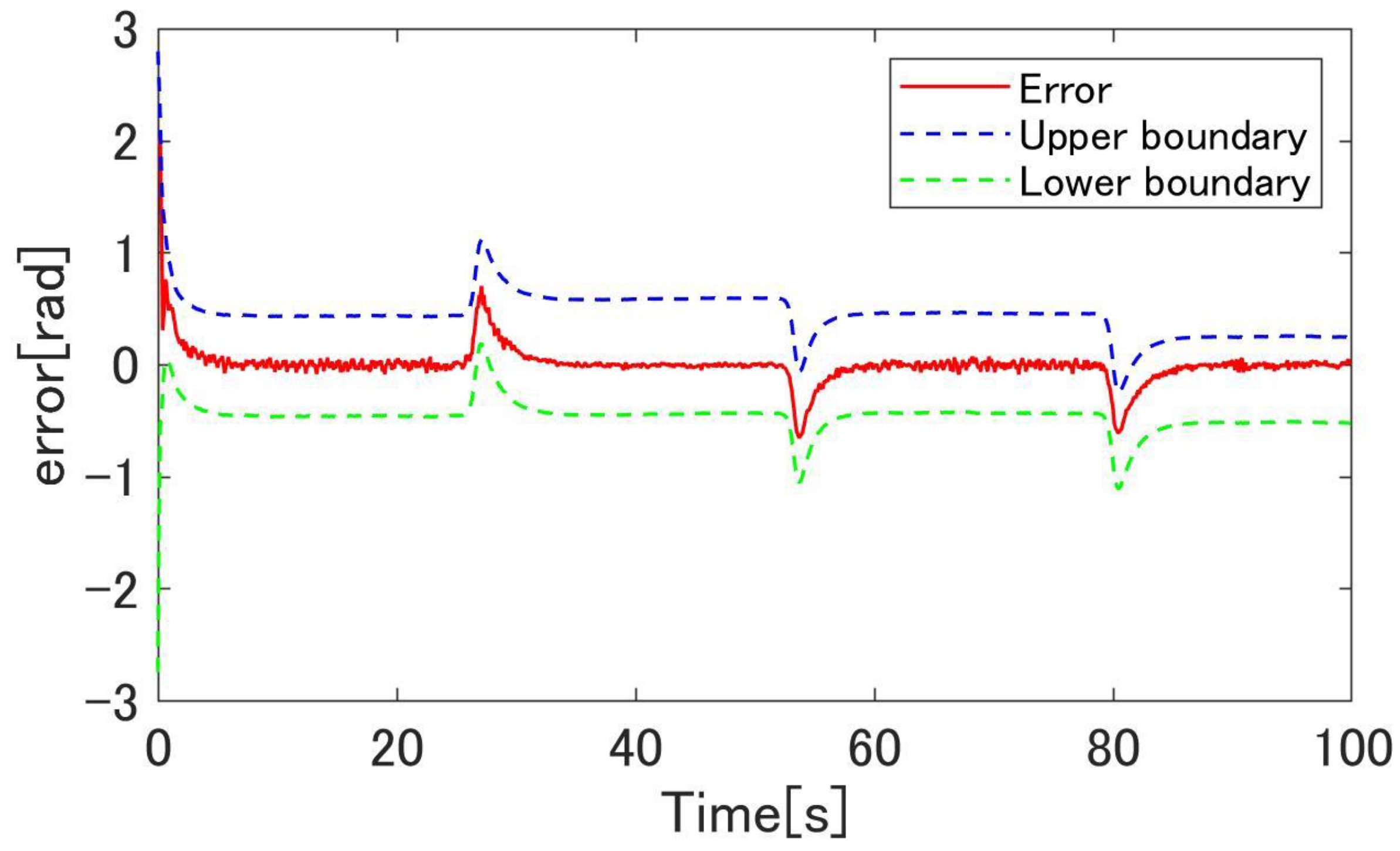
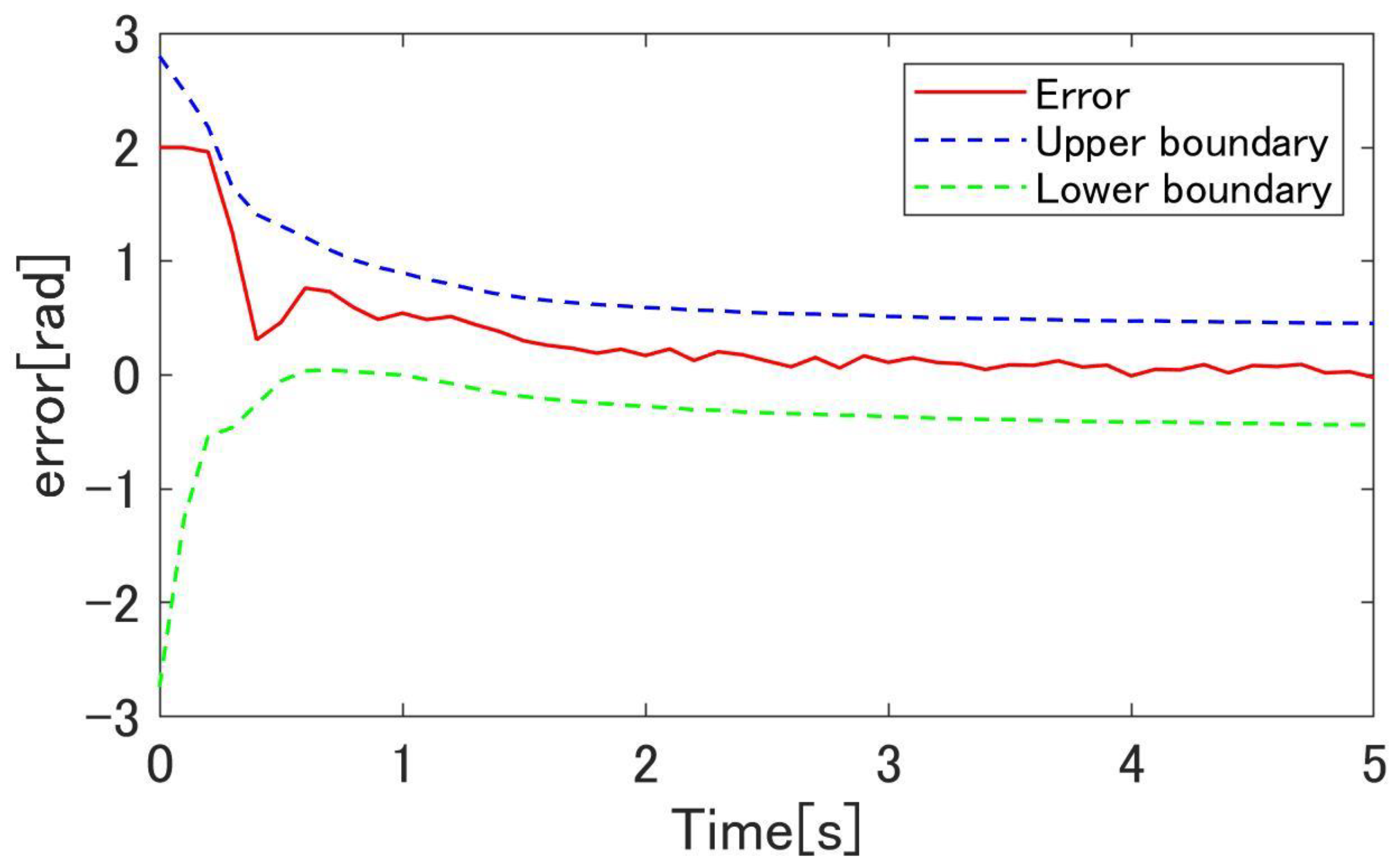
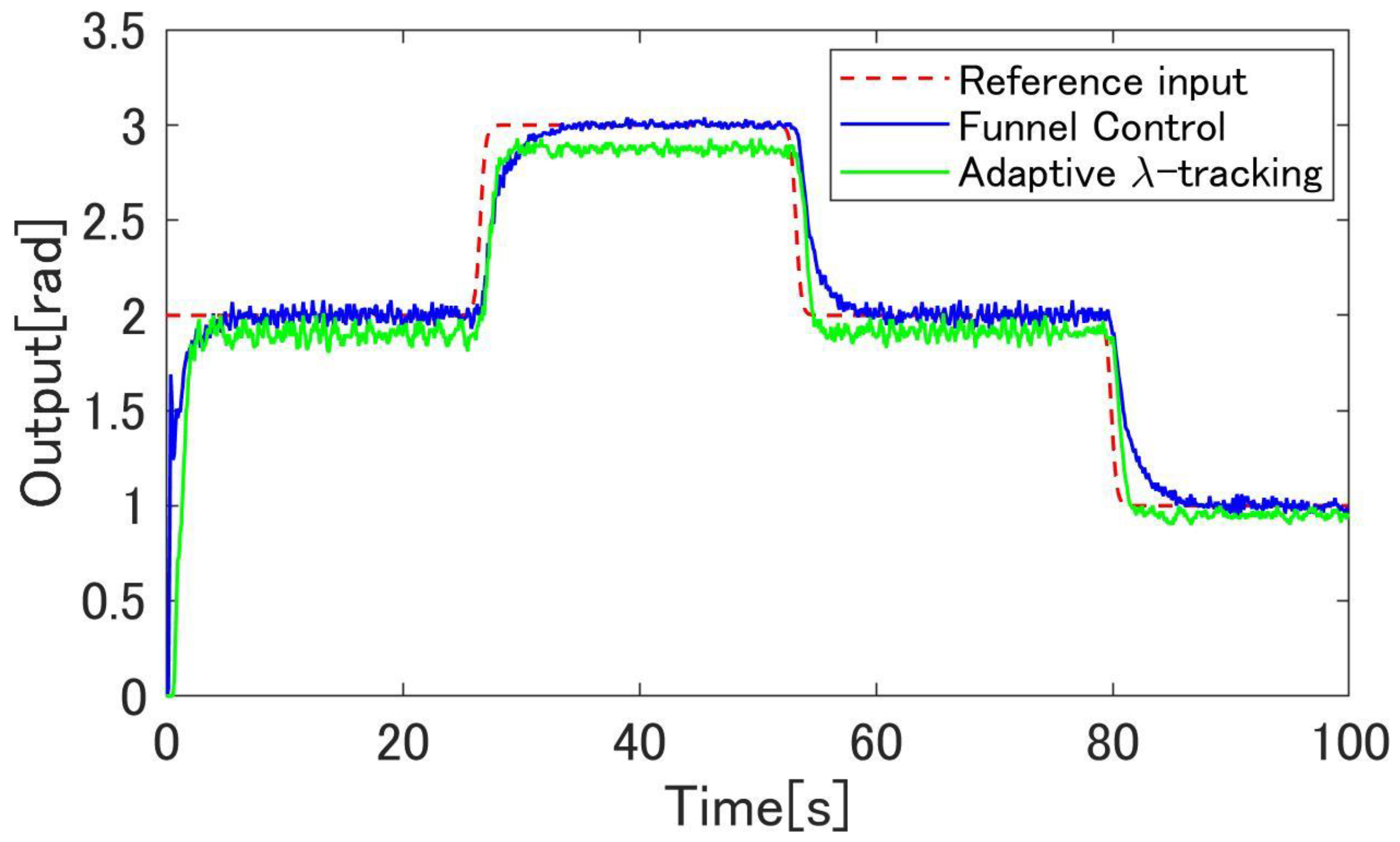
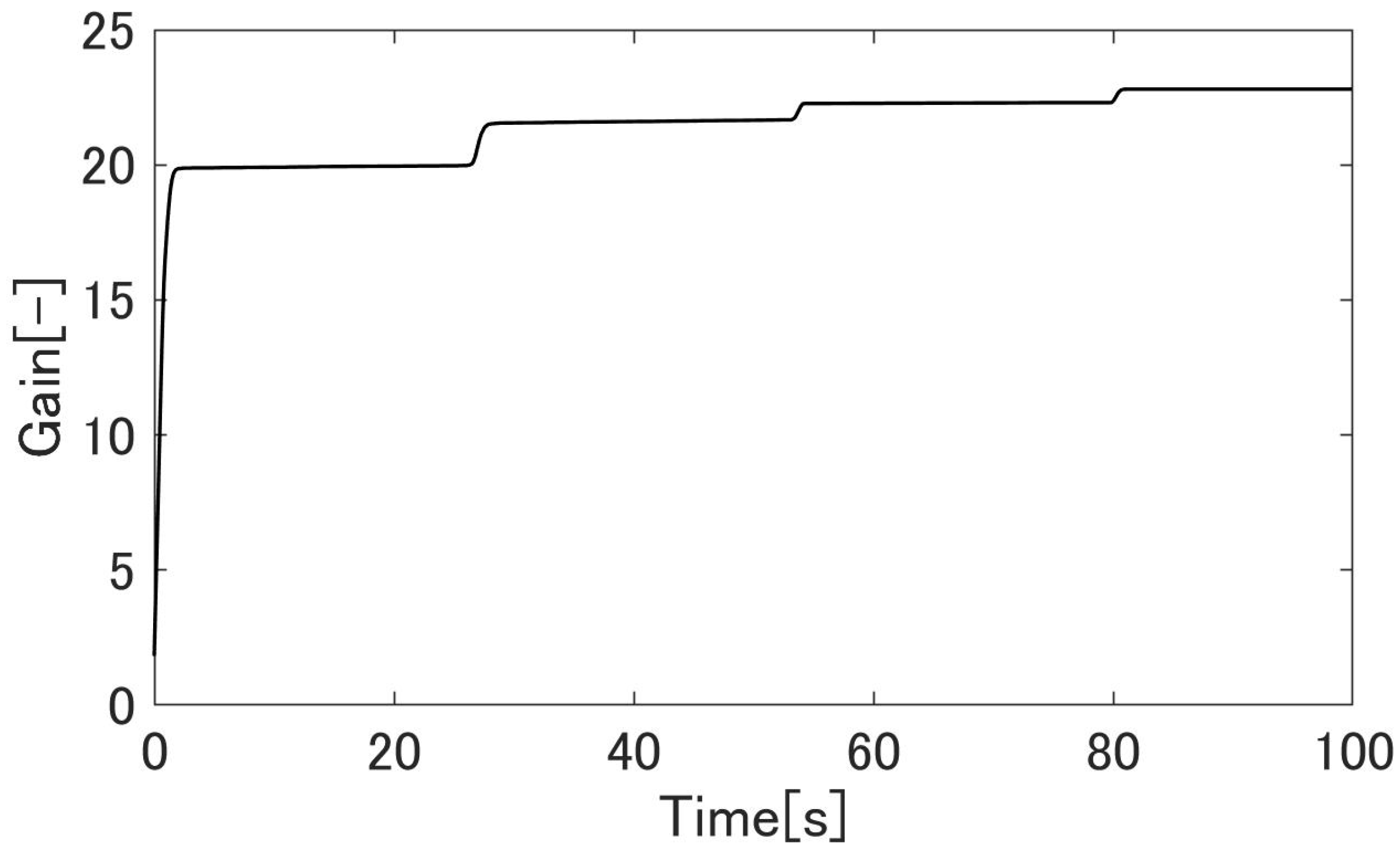
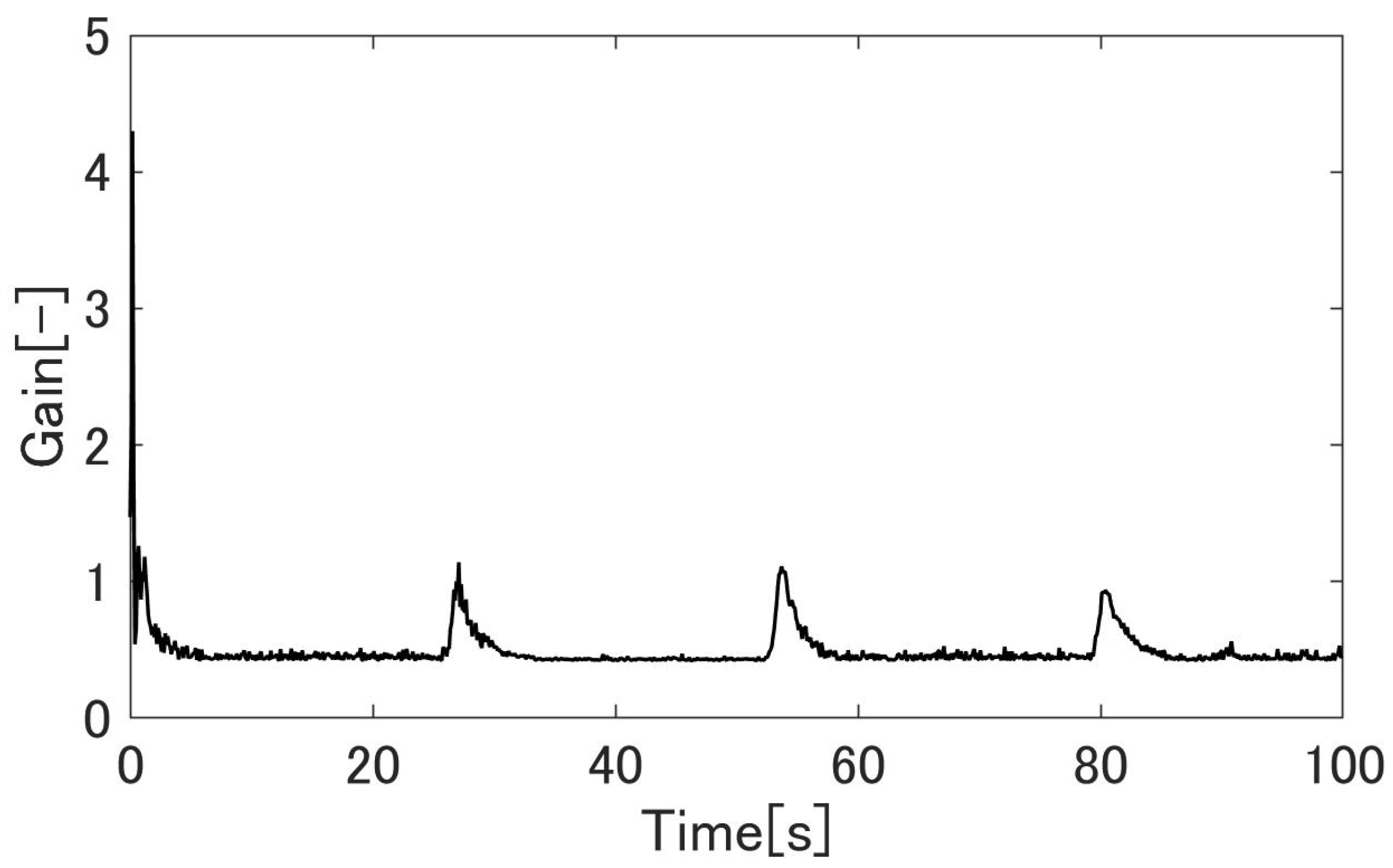
4.3. Simulation Results
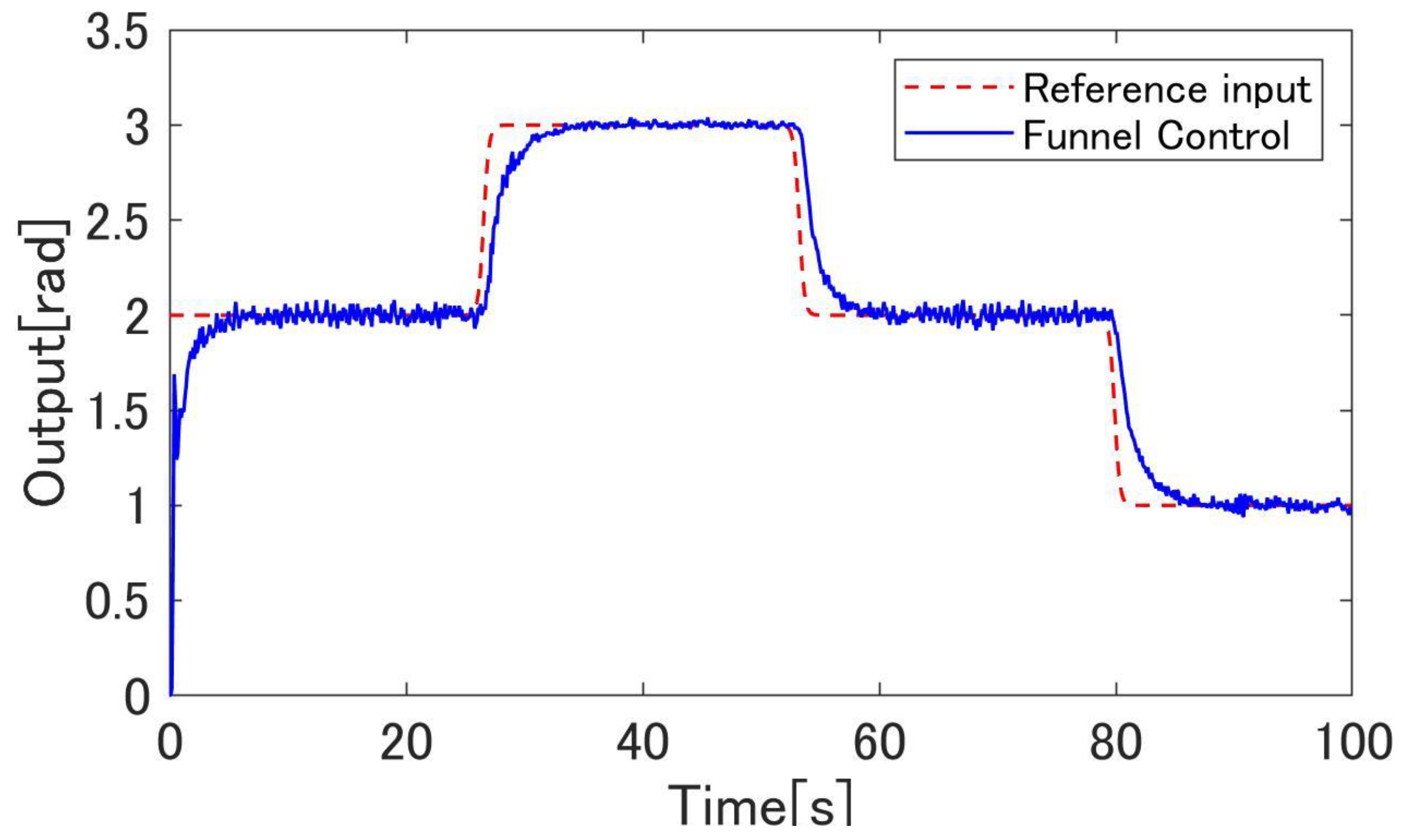
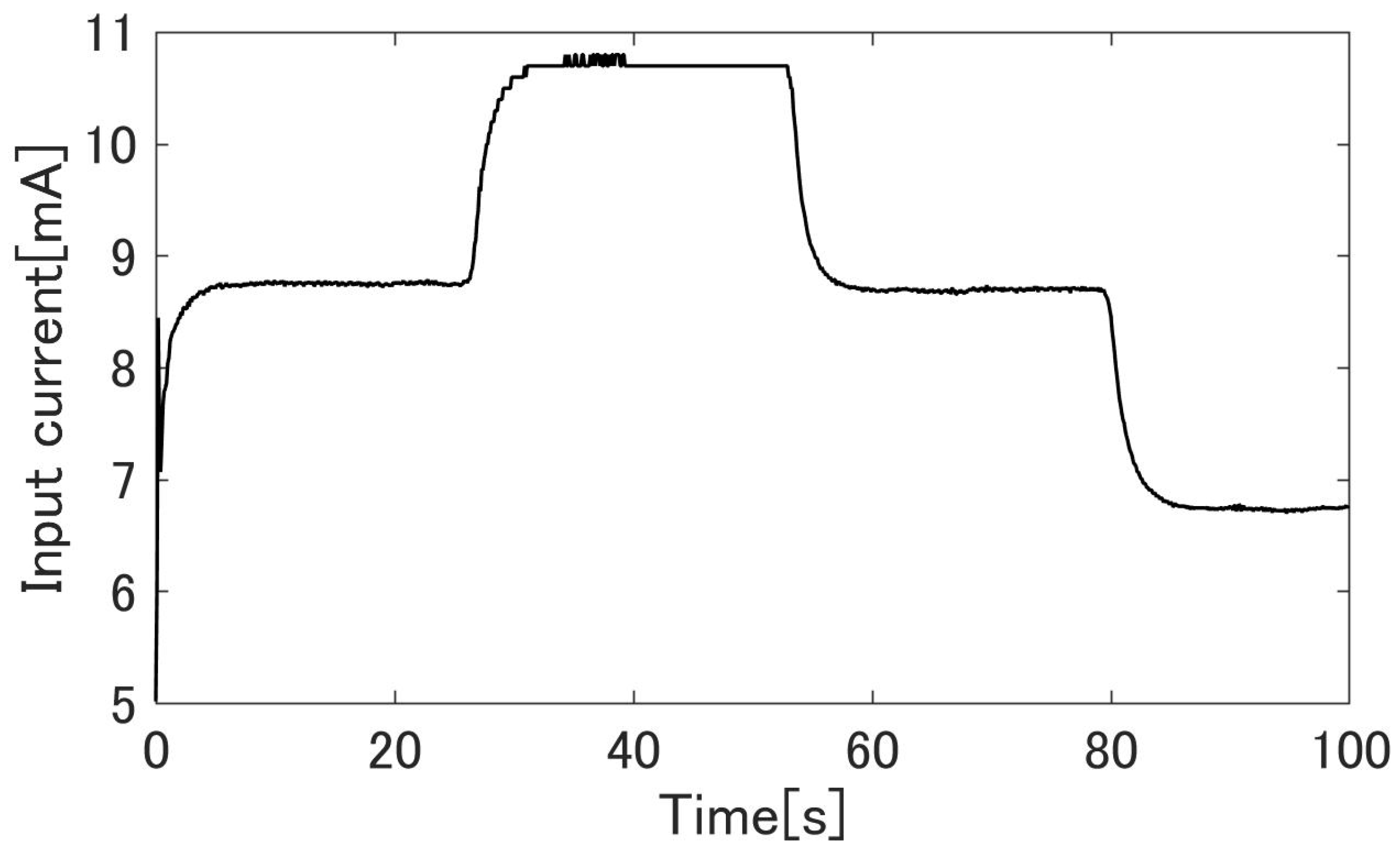
4.4. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FMA | Flexible micro-actuator |
References
- Suzumori, K.; Iikura, S.; Tanaka, H. Development of flexible microactuator and its applications to robotic mechanisms. In Proceedings of the IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; pp. 1622–1627. [Google Scholar] [CrossRef]
- Ichikawa, T.; Shintani, K.; Suzuki, T. Development of mechatronic esophagus using thin straight fibers type artifical muscle. Seisan Kenkyu 2009, 61, 135–138. [Google Scholar]
- Noritsugu, T.; Tanaka, T. Application of rubber artificial muscle manipulator as a rehabilitation robot. IEEE/ASME Trans. Mechatronics 1997, 2, 259–267. [Google Scholar] [CrossRef]
- Kawamura, S.; Sudani, M.; Deng, M.; Noge, Y.; Wakimoto, S. Modeling and system integration for a thin pneumatic rubber 3—DOF actuator. Actuators 2019, 8, 32. [Google Scholar] [CrossRef]
- Tondu, B.; Lopez, P. Modeling and Control of McKibben artificial muscle Robot Actuators. IEEE Control Syst. Mag. 2000, 20, 15–38. [Google Scholar]
- Itto, T.; Kogiso, K. Hybrid modeling of mckibben pneumatic artificial muscle systems. In Proceedings of the Joint IEEE International Conference on Industrial Technology Southeasetern Symposium on System Theory, Auburn, AL, USA, 14–16 March 2011; Volume 3, pp. 65–70. [Google Scholar]
- Nozaki, T.; Noritsugu, T. Motion analysis of McKibben type pneumatic rubber artificial muscle with finite element method. Int. J. Autom. Technol. 2014, 8, 147–158. [Google Scholar] [CrossRef]
- Kawamura, S.; Deng, M. Recent Developments on Modeling for a 3—DOF Micro—Hand Based on AI Methods. Actuators 2020, 11, 792. [Google Scholar] [CrossRef]
- Suzumori, K. Flexible Microactuator: 1st Report, static characteristics of 3 DOF actuator. Trans. Jpn. Soc. Mech. Eng. C 1989, 55, 2547–2552. (In Japanese) [Google Scholar] [CrossRef]
- Wakimoto, S.; Suzumori, K.; Takeda, J. Flexible artificial muscle by bundle of McKibben fiber actuators. IEEE/ASME Int. Conf. Adv. Intell. Mechatronics 2011, 457–462. [Google Scholar] [CrossRef]
- Wakimoto, S.; Suzumori, K.; Ogura, K. Miniature pneumatic curling rubber actuator generating bidirectional motion with one air-supply tube. Adv. Robot. 2011, 25, 1311–1330. [Google Scholar] [CrossRef]
- Wakimoto, S.; Suzumori, K.; Nishioka, Y. Miniaturization of large displacement rubber actuator. JSME Bioeng. Conf. 2011, 22, 104. [Google Scholar] [CrossRef]
- Sudani, M.; Deng, M.; Wakimoto, S. Modeling and operator-based nonlinear control for a miniature pneumatic bending rubber actuator considering bellows. Actuators 2018, 7, 26. [Google Scholar] [CrossRef]
- Deng, M.; Ueno, K. Operator-based nonlinear position control for a micro-hand by using image information. In Proceedings of the 2017 International Conference on Advanced Mechatronic Systems, Xiamen, China, 6–9 December 2017; pp. 46–50. [Google Scholar] [CrossRef]
- Fujita, K.; Deng, M.; Wakimoto, S. A miniature bending rubber controlled by using the PSO-SVR-based motion estimation method with the generalized gaussian kernel. Actuators 2017, 6, 6. [Google Scholar] [CrossRef]
- Deng, M.; Kawashima, T. Adaptive nonlinear sensorless control for an uncertain miniature pneumatic curling rubber actuator using passivity and robust right coprime factorization. IEEE Trans. Control Syst. Technol. 2015, 24, 318–324. [Google Scholar] [CrossRef]
- Deng, M. Operator-Based Nonlinear Control Systems: Design and Applications; Willy-IEEE Press: Piscataway, NJ, USA, 2014. [Google Scholar]
- Deng, M.; Inoue, A.; Ishikawa, K. Operator-based nonlinear feedback control design using robust right coprime factorization. IEEE Trans. Autom. Control 2006, 51, 645–648. [Google Scholar] [CrossRef]
- Chen, G.; Han, Z. Robust right coprime factorization and robust stabilization of nonlinear feedback control system. IEEE Trans. Autom. Control 1998, 43, 1505–1509. [Google Scholar] [CrossRef]
- Deng, M.; Bu, N.; Inoue, A. Output tracking of nonlinear feedback systems with perturbation based on robust right coprime factorization. Int. J. Innov. Comput. Inf. Control 2009, 5, 3359–3366. [Google Scholar]
- Wang, A.; Deng, M. Robust nonlinear multivariable tracking control design to a manipulator with unknown uncertainties using operator-based robust right coprime factorization. Trans. Inst. Meas. Control 2013, 35, 788–797. [Google Scholar] [CrossRef]
- Bu, N.; Deng, M. Passivity—Based Tracking Control for Uncertain Nonlinear Feedback Systems. J. Robot. Mechatronics 2016, 28, 837–841. [Google Scholar] [CrossRef]
- Deng, M.; Ueno, K. Experimental Study on Operator–based Nonlinear Control for a Miniature Pneumatic Bending Rubber Actuator by Using PSO–SVR–GGD Method. In Proceedings of the 2019 IEEE 16th International Conference on Networking, Sensing and Control, Banff, AB, Canada, 9–11 May 2019; pp. 317–322. [Google Scholar] [CrossRef]
- Ilchmann, A.; Ryan, E.P.; Sangwin, C.J. Tracking with prescribed transient behaviour. ESAIM Control Optim. Calc. Var. 2002, 7, 471–493. [Google Scholar] [CrossRef]
- Ilchmann, A.; Ryan, E.P.; Trenn, S. Tracking control: Performance funnels and prescribed transient behaviour. Syst. Control Lett. 2005, 7, 655–670. [Google Scholar] [CrossRef]
- Efimov, D.; Raïssi, T.; Chebotarev, S.; Zolghadri, A. Interval state observer for nonlinear time varying systems. Automatica 2013, 49, 200–205. [Google Scholar] [CrossRef]
- Shimizu, K. Nonlinear state observers by gradient descent method. In Proceedings of the IEEE International Conference on Control Applications, Anchorage, AK, USA, 27 September 2000; pp. 616–622. [Google Scholar] [CrossRef]





| Parameter | Definition | Value |
|---|---|---|
| Initial length of the actuator | [m] | |
| Thickness of the rubber | [m] | |
| Internal radius of small chambers | [m] | |
| Representative radius of small chambers | [m] | |
| Internal radius of large chambers | [m] | |
| Representative radius of large chambers | [m] | |
| n | Number of the bellows | [-] |
| E | Young’s modulus | [Pa] |
| Parameter | Definition | Value |
|---|---|---|
| P | Air pressure of the actuator | [Pa] |
| R | Gas constant | [J/KgK] |
| T | Absolute temperature of air | [K] |
| k | Heat capacity ratio of air | [-] |
| V | Volume of the actuator | [] |
| m | Air flow rate | [Kg] |
| Cross-sectional area of the control valve | [] | |
| Internal pressure of the compressor | [Pa] | |
| u | Input current | [mA] |
| Parameter of the control valve | [Pa/mA] | |
| Parameter of the control valve | [Pa] | |
| Maximum output pressure of the control valve | [Pa] |
| Parameter | Definition | Value |
|---|---|---|
| Initial length of the actuator | m | |
| Thickness of the rubber | m | |
| Internal radius of small chambers | m | |
| Representative radius of small chambers | m | |
| Internal radius of large chambers | m | |
| Representative radius of large chambers | m | |
| n | Number of the bellows | 12 |
| E | Young’s modulus | Pa |
| Parameter of the control valve | ||
| Parameter of the control valve | Pa/mA | |
| Parameter of the control valve | 25 Pa | |
| K | Control parameter | 40 |
| Proportional parameter | ||
| Integral parameter | ||
| Designed parameter | 1 | |
| Designed parameter | 1 | |
| Designed parameter | ||
| Designed parameter | ||
| Designed parameter | ||
| Designed parameter |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ueno, K.; Kawamura, S.; Deng, M. Operator-Based Nonlinear Control for a Miniature Flexible Actuator Using the Funnel Control Method. Machines 2021, 9, 26. https://doi.org/10.3390/machines9020026
Ueno K, Kawamura S, Deng M. Operator-Based Nonlinear Control for a Miniature Flexible Actuator Using the Funnel Control Method. Machines. 2021; 9(2):26. https://doi.org/10.3390/machines9020026
Chicago/Turabian StyleUeno, Keisuke, Shuhei Kawamura, and Mingcong Deng. 2021. "Operator-Based Nonlinear Control for a Miniature Flexible Actuator Using the Funnel Control Method" Machines 9, no. 2: 26. https://doi.org/10.3390/machines9020026
APA StyleUeno, K., Kawamura, S., & Deng, M. (2021). Operator-Based Nonlinear Control for a Miniature Flexible Actuator Using the Funnel Control Method. Machines, 9(2), 26. https://doi.org/10.3390/machines9020026






