Numerical and Experimental Study of Hydraulic Performance and Wear Characteristics of a Slurry Pump
Abstract
:1. Introduction
2. Analysis Model
2.1. 3D Modeling
2.2. Grids
3. Results and Discussion
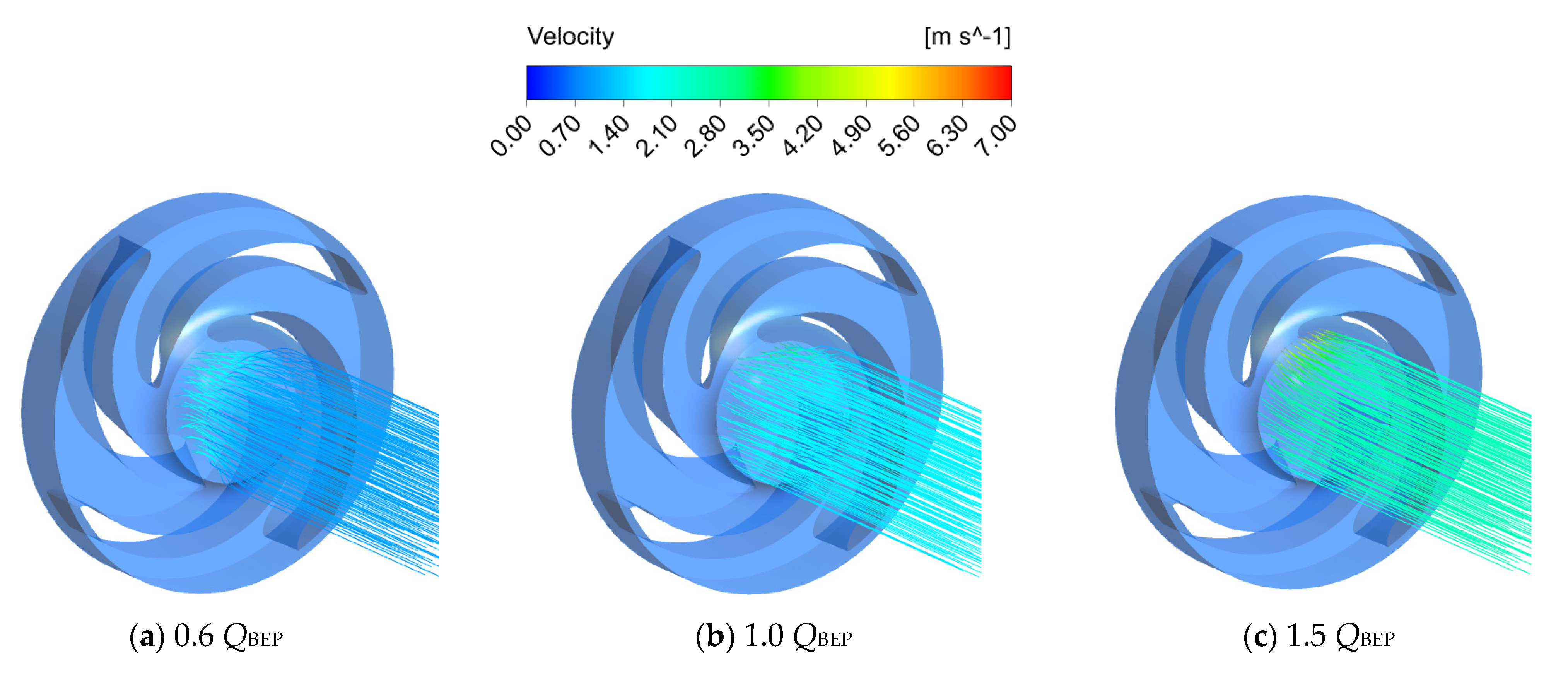
3.1. Flow Field Analysis of Inlet
3.2. Flow Field Analysis of Impeller
3.3. Flow Field Analysis of Volute
3.4. Effect of Particle Parameters on Wear Characteristic
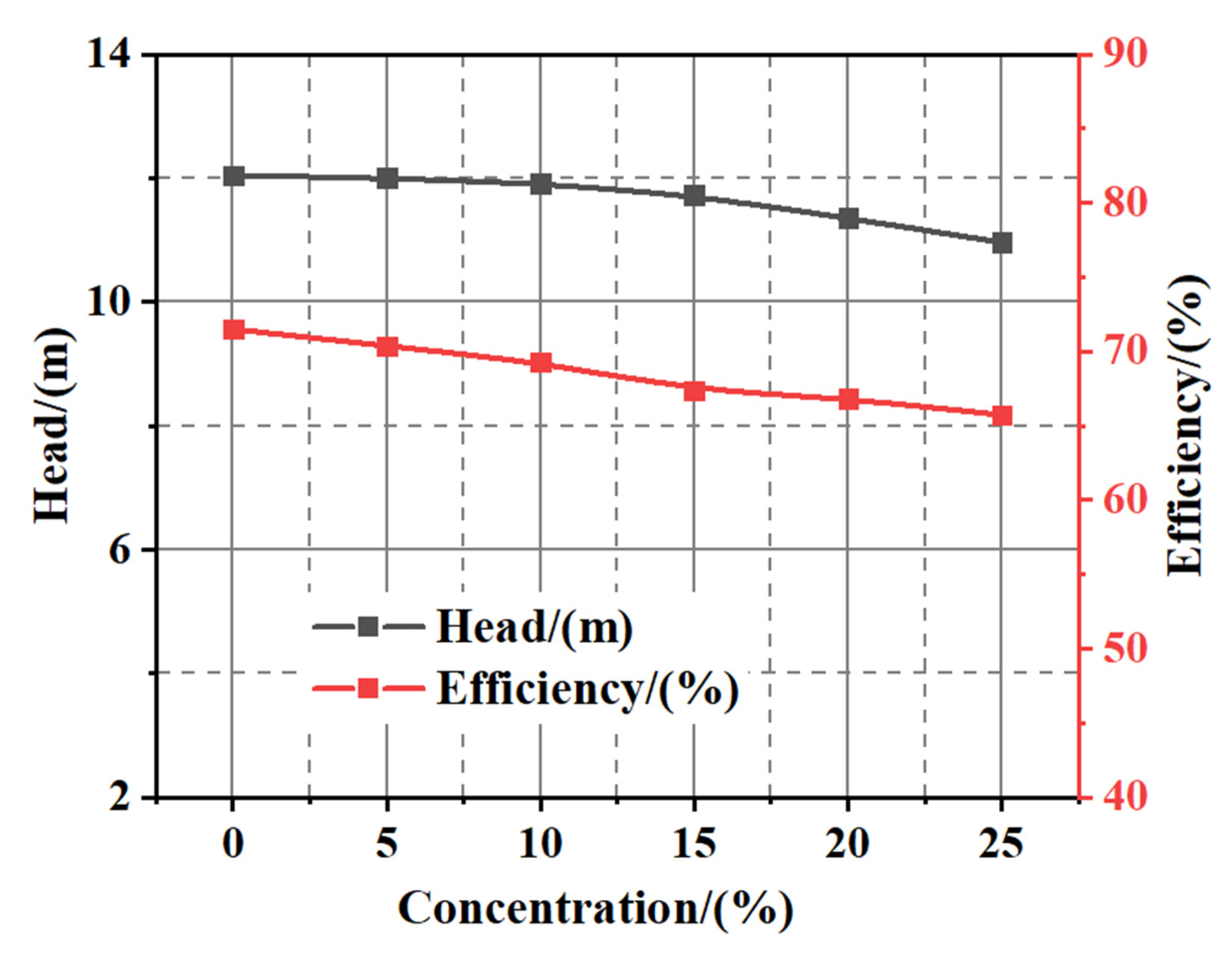
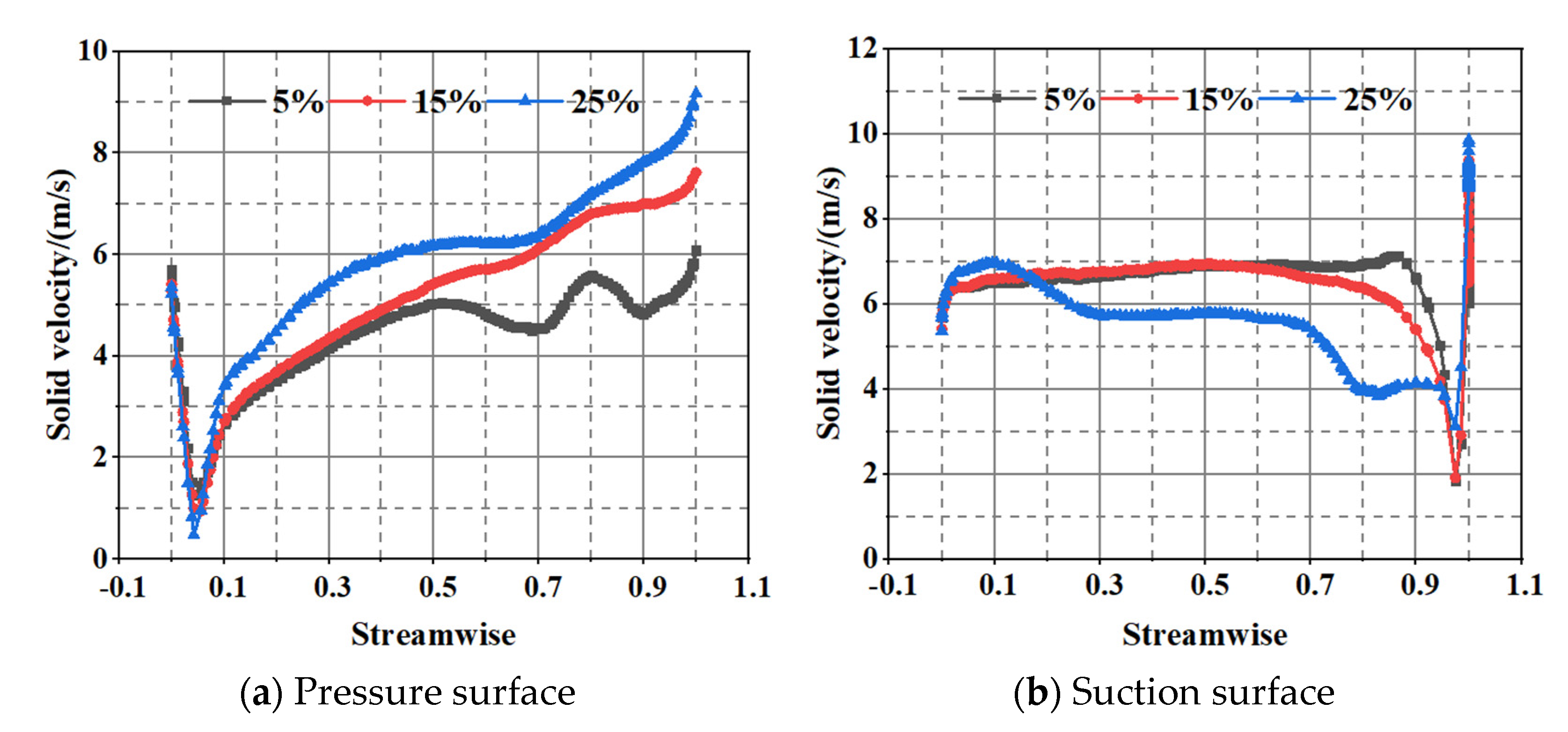
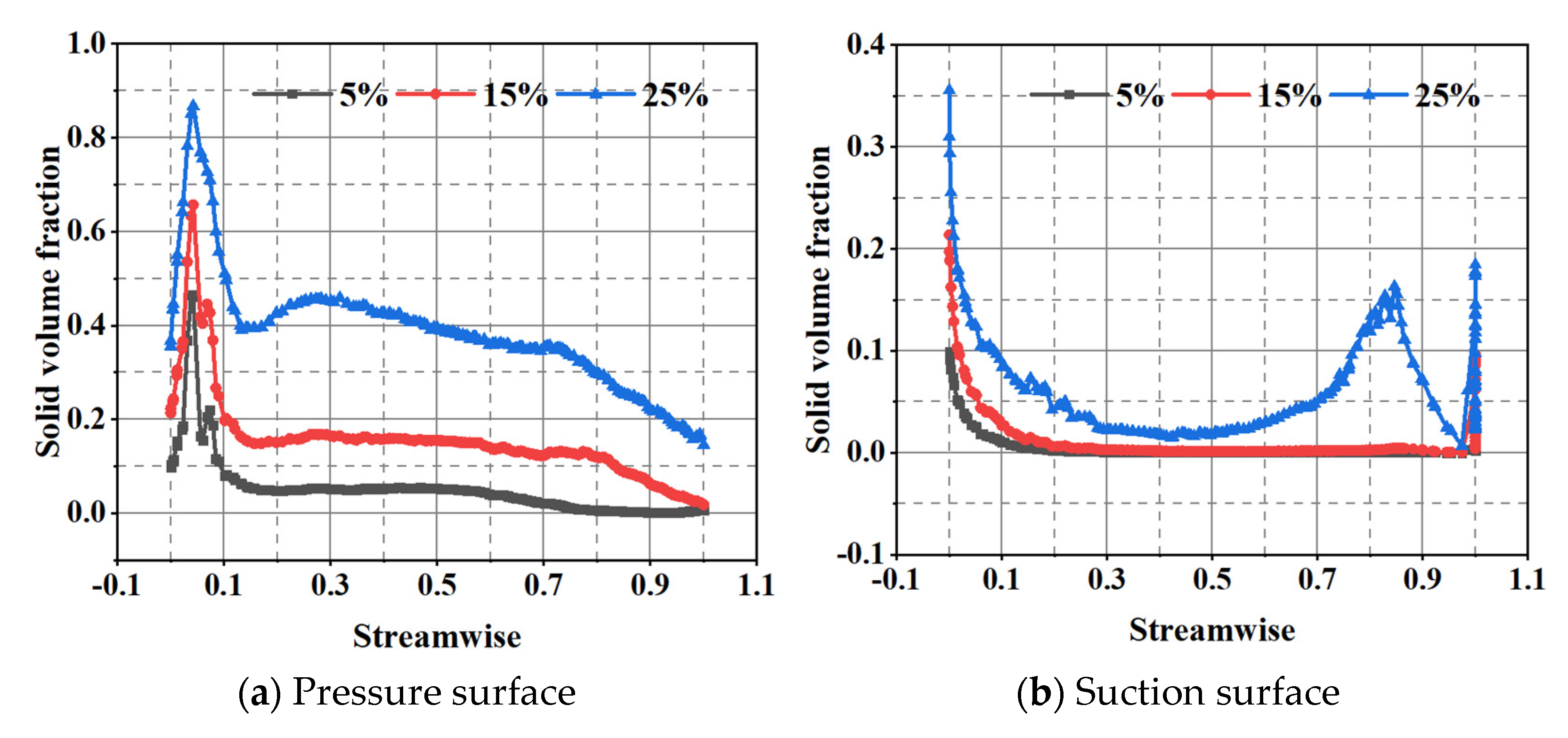
3.4.1. Effect of Particle Volume Concentration on Wear
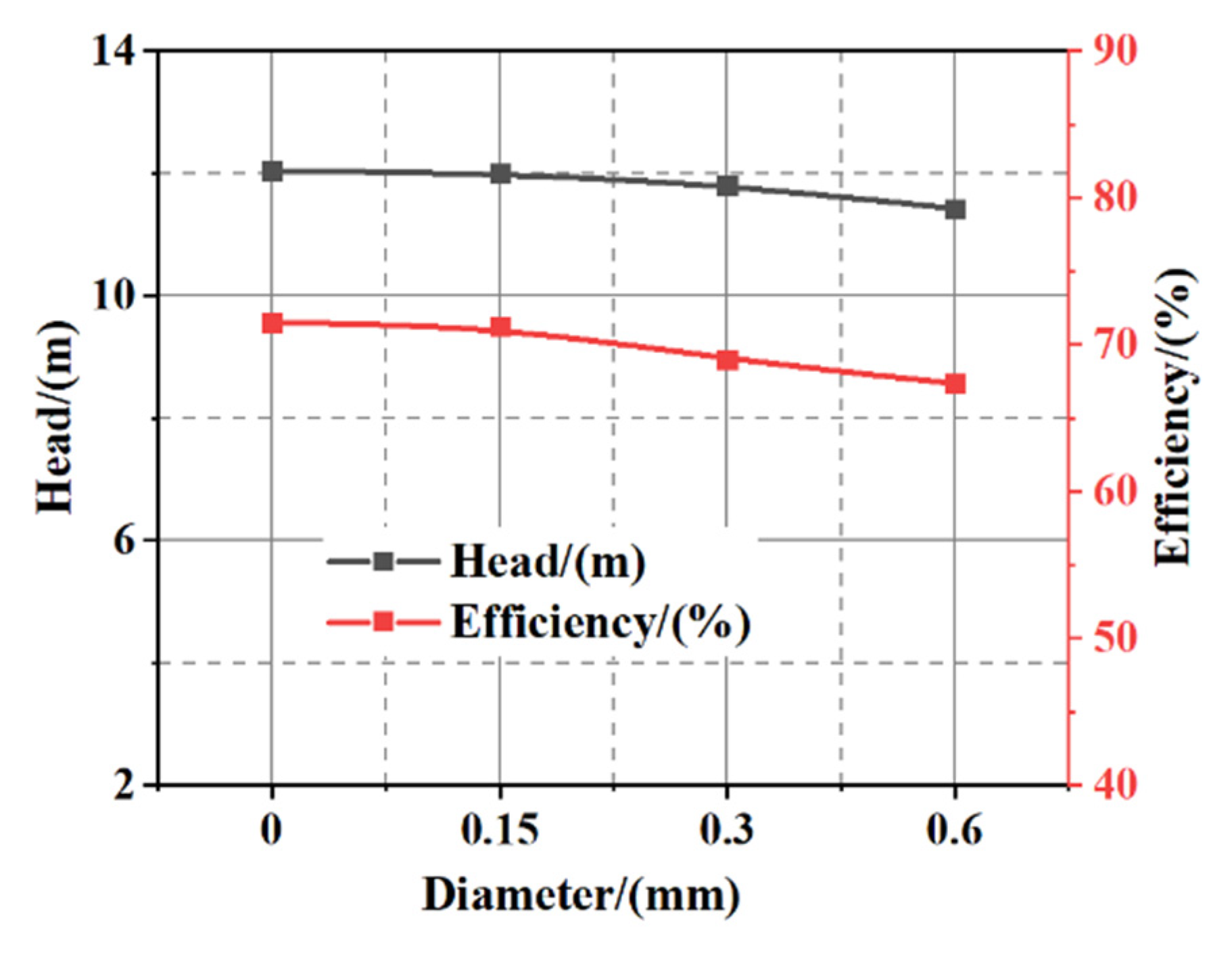
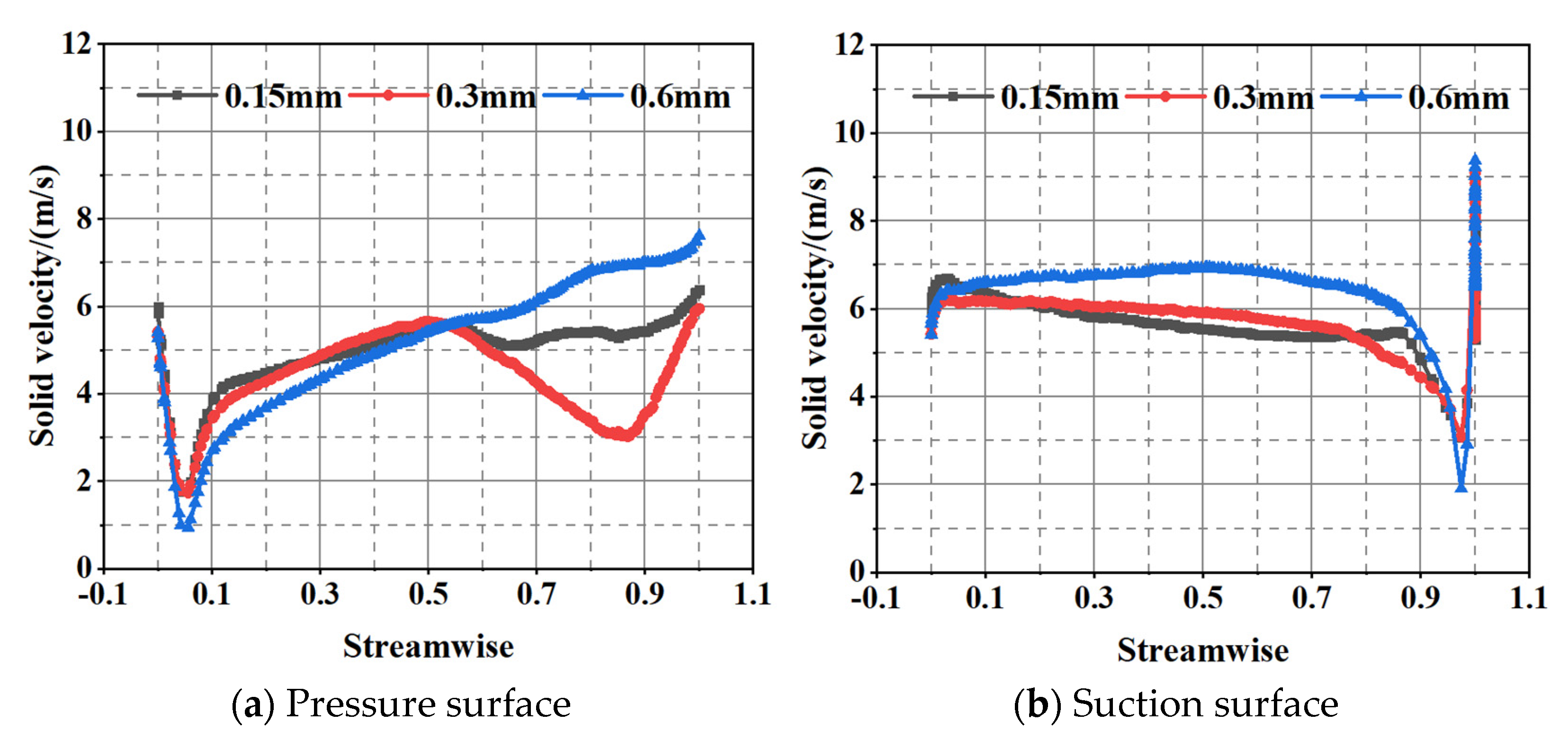
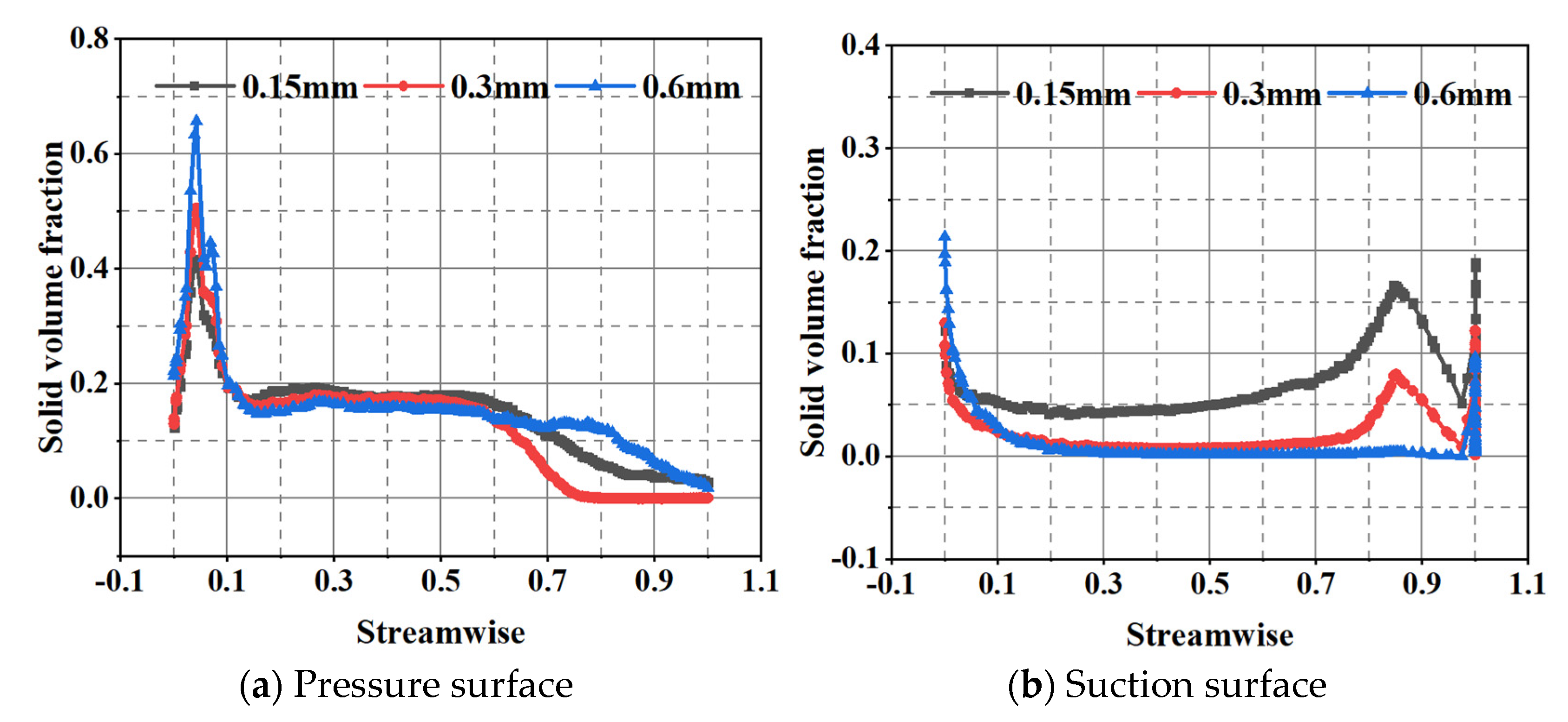
3.4.2. Effect of Particle Size on Wear Characteristic
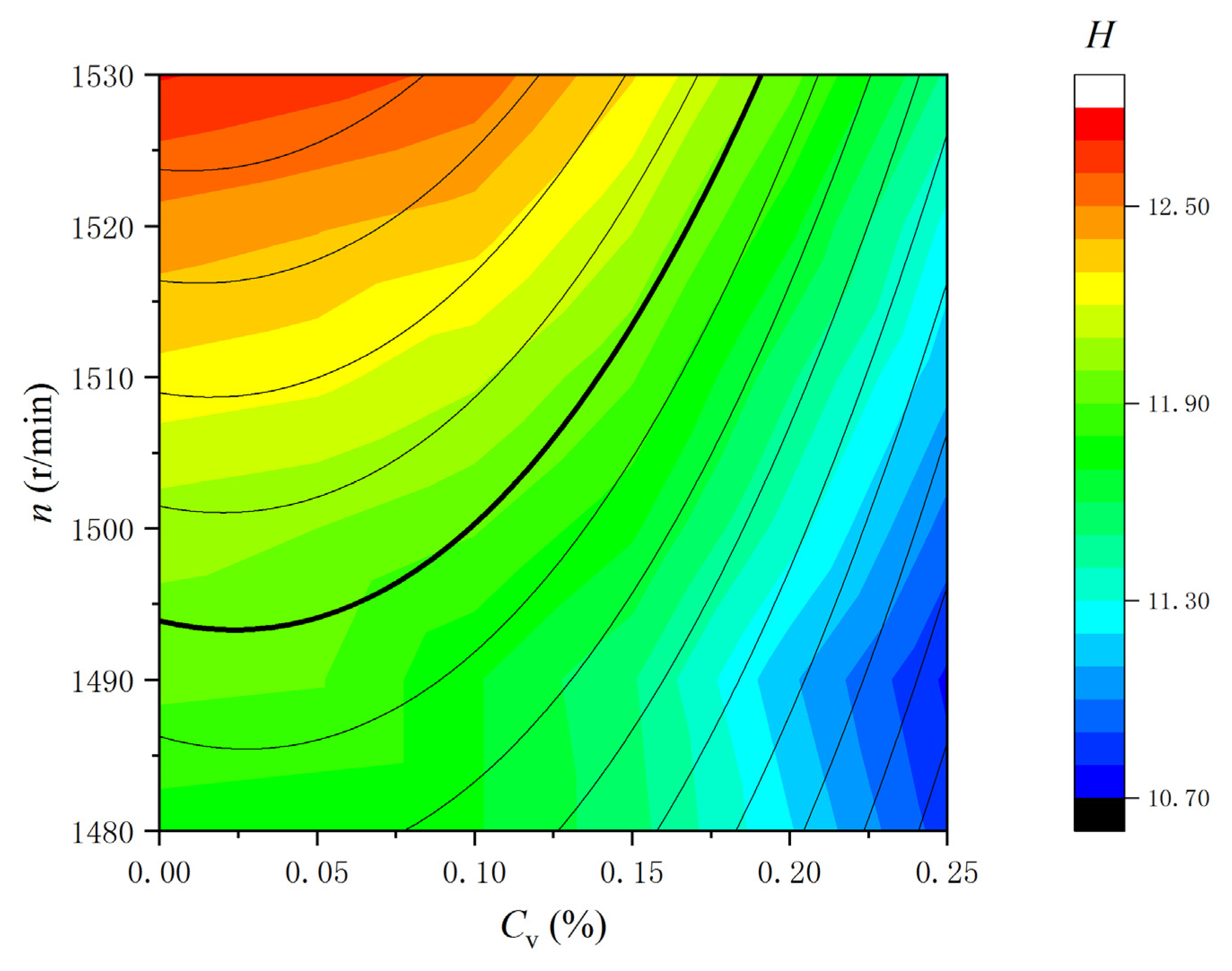
3.5. Effect of Pump Speed on External Performance
4. Experimental Investigation
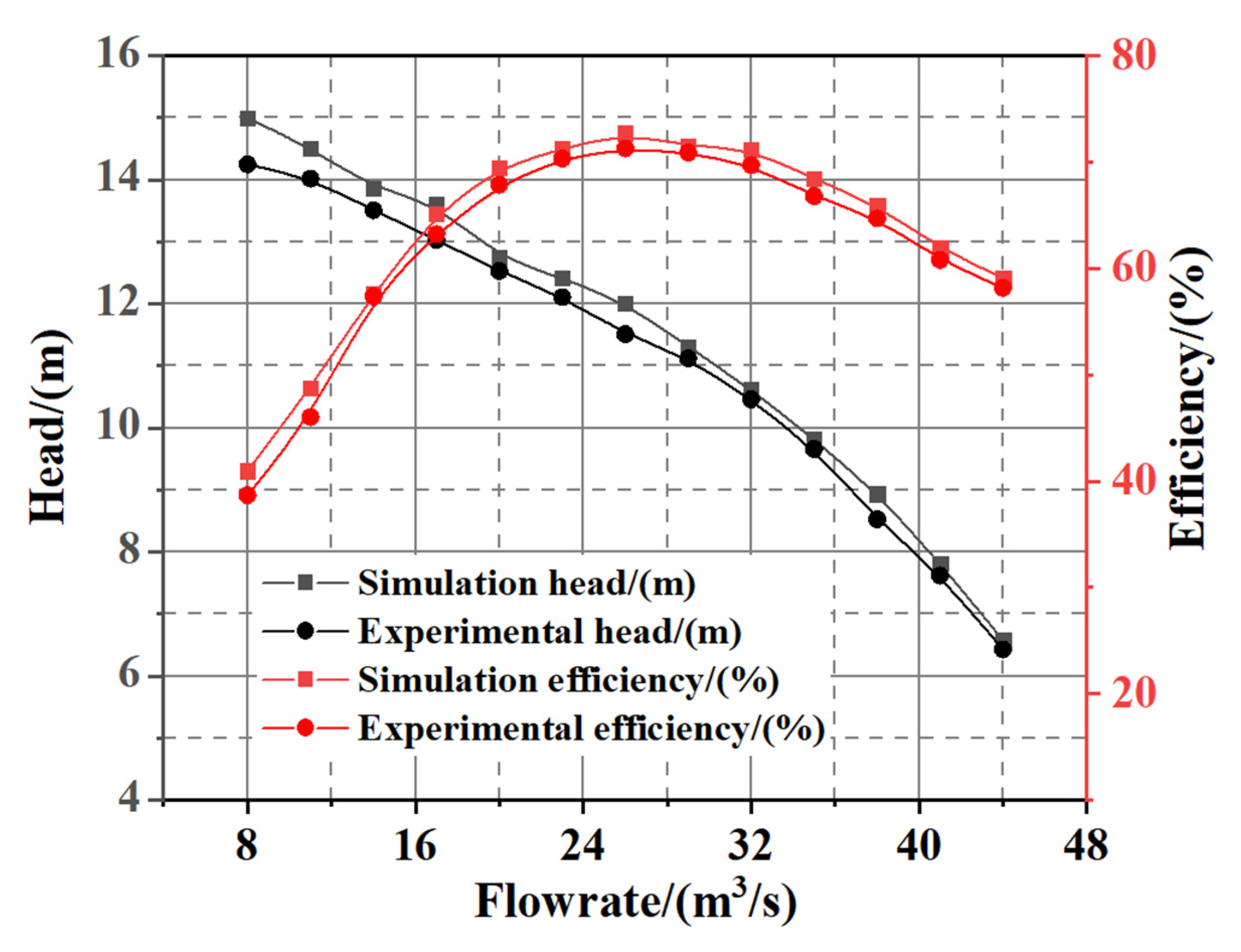
4.1. Hydraulic Performance Test
4.2. Wear Performance Test
- The first stage
- 2.
- The second stage
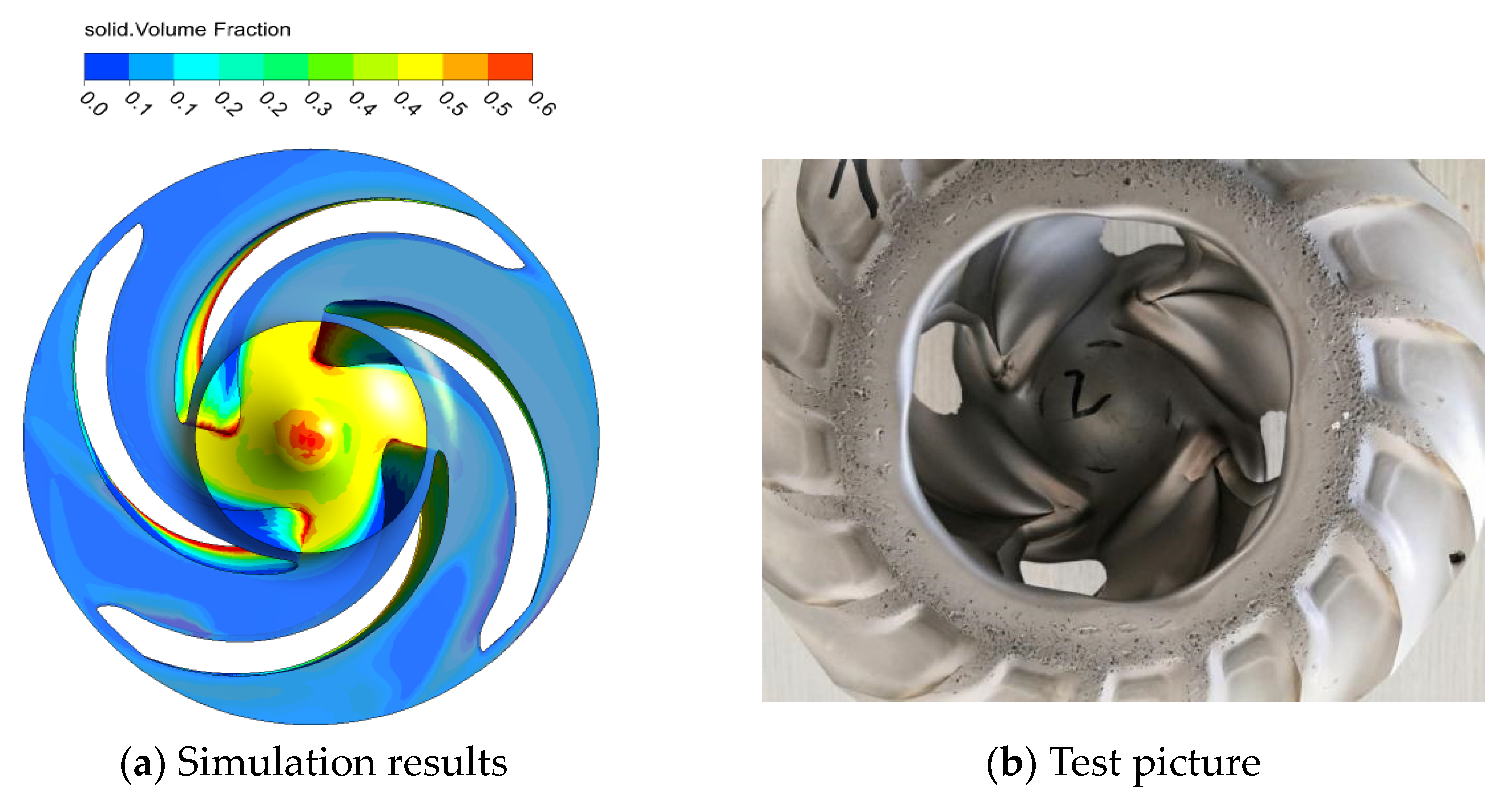
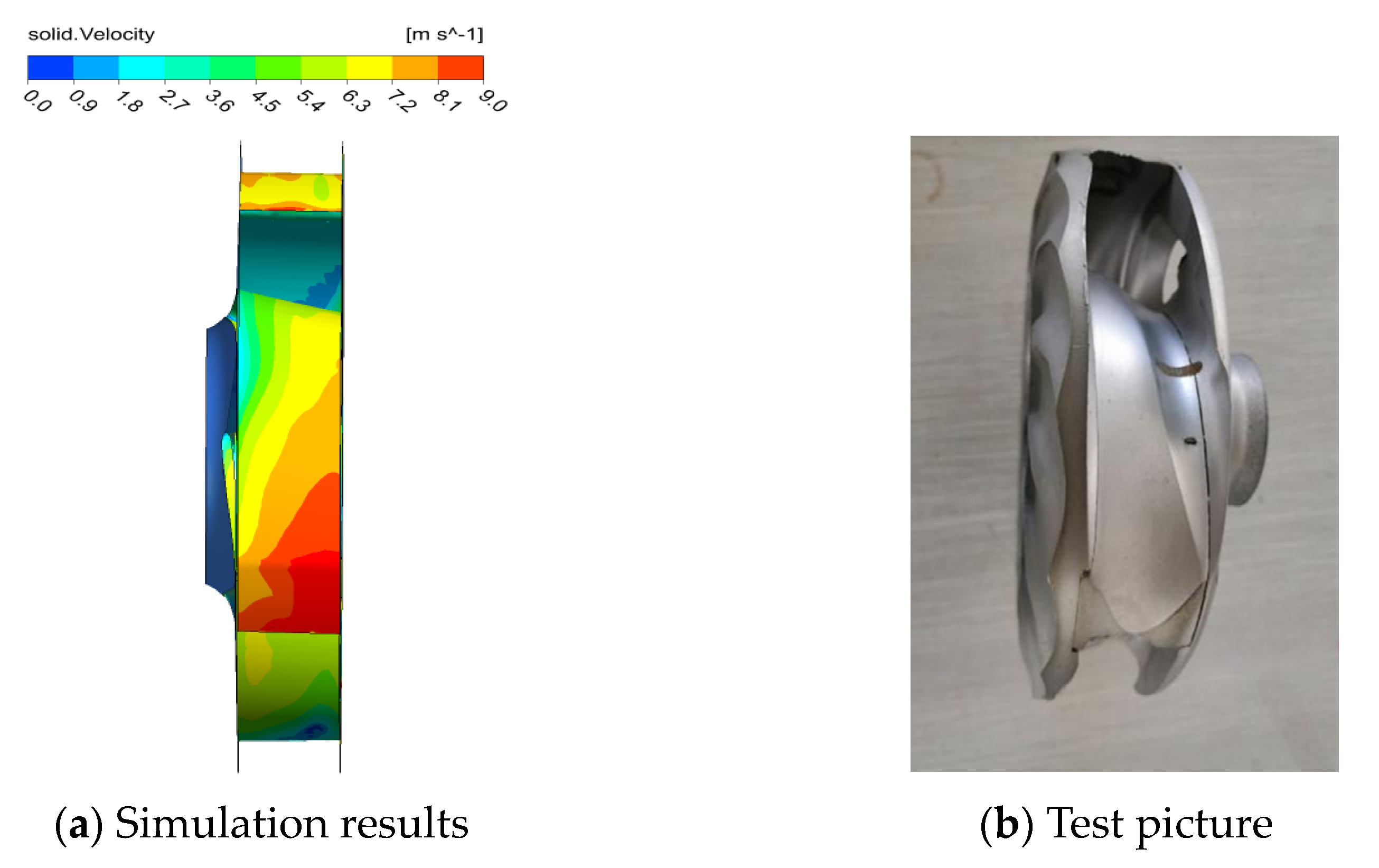
4.3. Analysis of Wear Distribution Characteristic
5. Conclusions
- (1)
- Pre-rotation was generated at the inlet section, and the pre-rotation direction was consistent with the rotation direction of the impeller under part-load conditions. Meanwhile, the ability of the pre-rotation continuously decreased with the increase in flow rate. When the flow rate reached 1.5 QBEP, the flow at the inlet section was relatively stable. Furthermore, the solid volume fraction of the blade pressure surface gradually moved from the leading edge to the trailing edge with the increase in flow rate. When the flow rate increased to 1.5 QBEP, the solid particles moved to the rear cover plate under the effect of inertia force, which resulted in a large solid volume fraction at the interface between the impeller and the rear cover plate.
- (2)
- With the increase in the particle volume concentration, the viscosity of the solid–liquid two-phase flow increased and the friction force and energy loss between the internal fluids gradually increased, which resulted in a decrease in the head. When the concentration was 5%, the head decreased by 0.33% and the efficiency decreased by 1.60%. When the concentration was 25%, the head decreased by 8.9% and the efficiency decreased by 8.09%. Therefore, the head and efficiency of the pump decreased with increases in particle volume concentration.
- (3)
- When the particle diameter gradually increased, the energy driving the solid particles was greater and the head gradually decreased. At the same time, with the increase in solid particle diameter, the friction loss between particles and impeller increased, which led to the increases in impeller torque and motor power consumption. Therefore, when the particle diameter increased from 0.15 to 0.6 mm, the pump head decreased from 12 to 11.42 m and the efficiency decreased from 71.25% to 67.35%.
- (4)
- Finally, clean water and solid–liquid two-phase flow wear tests of the slurry pump were carried out. The calculation deviation in the full flow range was less than 5%, so the calculation model could accurately predict the performance of the pump. By comparing the wear distribution of numerical and experiment, it was found that high solid volume fraction and solid-phase slip velocity were generated at the junction of the blade leading edge and the rear cover plate, which made the latter easier to wear out. Therefore, enhancing the strength of the junction between the blade leading edge and the rear cover plate would be beneficial for improving the service life of a slurry pump.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, R.; Guan, Y.; Jin, X.; Tang, Z.; Zhu, Z.; Su, X. Impact of Particle Sizes on Flow Characteristics of Slurry Pump for Deep-Sea Mining. Shock. Vib. 2021, 2021, 1–13. [Google Scholar] [CrossRef]
- Shi, B.; Pan, J.; Wu, L.; Zhang, X.; Qiu, Y.; Zhang, Y. A Prediction Method of Wear for Volute Casing of a Centrifugal Slurry Pump. Geofluid 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Peng, G.; Huang, X.; Zhou, L.; Zhou, G.; Zhou, H. Solid-liquid two-phase flow and wear analysis in a large-scale centrifugal slurry pump. Eng. Fail. Anal. 2020, 114, 104602. [Google Scholar] [CrossRef]
- Li, Y.; Zeng, X.; Lv, W.; He, Z. Centrifugal pump wear for solid–liquid two-phase flows based on computational fluid dynamics–discrete element method coupling. Adv. Mech. Eng. 2020, 12, 1–17. [Google Scholar] [CrossRef]
- Tan, M.; Lian, Y.; Liu, H.; Wu, X.; Ding, R. Visualizing test on the pass-through and collision characteristics of coarse particles in a double blade pump. Int. J. Nav. Archit. Ocean. Eng. 2018, 10, 1–8. [Google Scholar] [CrossRef]
- Shen, Z.; Chu, W.; Yan, S.; Chen, X.; Guo, Z.; Zhong, Y. Study of the performance and internal flow in centrifugal pump with grooved volute casing. Mod. Phys. Lett. B 2020, 34, 2050268. [Google Scholar] [CrossRef]
- Wang, Y.; Han, C.; Zhou, Y.; Lin, Z.; Ma, J.; Li, X.; Zhang, W. Wear Characteristics of Dense Fine Particles Solid-Liquid Two-Phase Fluid Centrifugal Pump with Open Impellers. Shock. Vib. 2021, 2021, 1–13. [Google Scholar] [CrossRef]
- Zhao, W.; Zhao, G. Numerical investigation on the transient characteristics of sediment-laden two-phase flow in a centrifugal pump. J. Mech. Sci. Technol. 2018, 32, 167–176. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, B.; Zhou, Y.; Ma, J.; Zhang, X.; Zhu, Z.; Li, X. Numerical Simulation of Fine Particle Solid-Liquid Two-Phase Flow in a Centrifugal Pump. Shock. Vib. 2021, 2021, 1–10. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Xie, L.; Liu, H.-L.; Luo, K.-K. Combined experimental and computational investigation of the effect of coating on operation characteristics of solid–liquid two-phase flow centrifugal pump. Mod. Phys. Lett. B 2021, 35, 2150062. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, N.; Mou, J.; Zhou, P.; Qian, H.; Dai, D. Study on solid–liquid two-phase flow characteristics of centrifugal pump impeller with non-smooth surface. Adv. Mech. Eng. 2019, 11, 1–12. [Google Scholar] [CrossRef]
- Yan, C.; Liu, J.; Zheng, S.; Huang, B.; Dai, J. Study on the effects of the wear-rings clearance on the solid-liquid two-phase flow characteristics of centrifugal pumps. Symmetry 2020, 12, 2003. [Google Scholar] [CrossRef]
- Wang, P.; Zhu, X.; Li, Y. Analysis of Flow and Wear Characteristics of Solid–Liquid Two-Phase Flow in Rotating Flow Channel. Processes 2020, 8, 1512. [Google Scholar] [CrossRef]
- Tang, C.; Kim, Y.J. CFD-DEM simulation for the distribution and motion feature of solid particles in single-channel pump. Energies 2020, 13, 4988. [Google Scholar] [CrossRef]
- Wang, H.L.; Hu, Q.X.; Yang, Y.; Wang, C. Performance differences of electrical submersible pump under variable speed schemes. Int. J. Simul. Model. 2021, 20, 76–86. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, M.; Wang, C.; Gao, Z. Optimal design of diversion piers of lateral intake pumping station based on orthogonal test. Shock. Vib. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Shi, L.; Zhu, J.; Tang, F.; Wang, C. Multi-disciplinary optimization design of axial-flow pump impellers based on the approximation model. Energies 2020, 13, 779. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Long, B.; Wang, C.; Han, C.; Li, L. Effects of the impeller blade with a slot structure on the centrifugal pump performance. Energies 2020, 13, 1628. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.; Qiu, N.; Zhu, Y.; Shi, W. Numerical and experimental study on the pressure fluctuation, vibration, and noise of multistage pump with radial diffuser. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 481. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, C.; Zhang, Y.; Xiang, W.; He, Z.; Shi, W. Numerical study of coupled flow in blocking pulsed jet impinging on a rotating wall. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 508. [Google Scholar] [CrossRef]














| Design Flow QBEP (m3/h) | Head H (m) | Speed n (r/min) | Blade Number | Impeller Outer Diameter D2 (mm) | Blade Outlet Width b2 (mm) | Inlet Diameter Dj (mm) |
|---|---|---|---|---|---|---|
| 26 | 11 | 1500 | 4 | 178 | 30 | 75 |
| Cv/% | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 50 |
|---|---|---|---|---|---|---|---|---|
| (kg/m3) | 1000 | 1095 | 1190 | 1285 | 1380 | 1475 | 1575 | 1950 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, G.; Tian, L.; Chang, H.; Hong, S.; Ye, D.; You, B. Numerical and Experimental Study of Hydraulic Performance and Wear Characteristics of a Slurry Pump. Machines 2021, 9, 373. https://doi.org/10.3390/machines9120373
Peng G, Tian L, Chang H, Hong S, Ye D, You B. Numerical and Experimental Study of Hydraulic Performance and Wear Characteristics of a Slurry Pump. Machines. 2021; 9(12):373. https://doi.org/10.3390/machines9120373
Chicago/Turabian StylePeng, Guangjie, Long Tian, Hao Chang, Shiming Hong, Daoxing Ye, and Baojian You. 2021. "Numerical and Experimental Study of Hydraulic Performance and Wear Characteristics of a Slurry Pump" Machines 9, no. 12: 373. https://doi.org/10.3390/machines9120373
APA StylePeng, G., Tian, L., Chang, H., Hong, S., Ye, D., & You, B. (2021). Numerical and Experimental Study of Hydraulic Performance and Wear Characteristics of a Slurry Pump. Machines, 9(12), 373. https://doi.org/10.3390/machines9120373






