Optimization of Sweep and Blade Lean for Diffuser to Suppress Hub Corner Vortex in Multistage Pump
Abstract
1. Introduction
2. Numerical Model and Simulation Setup
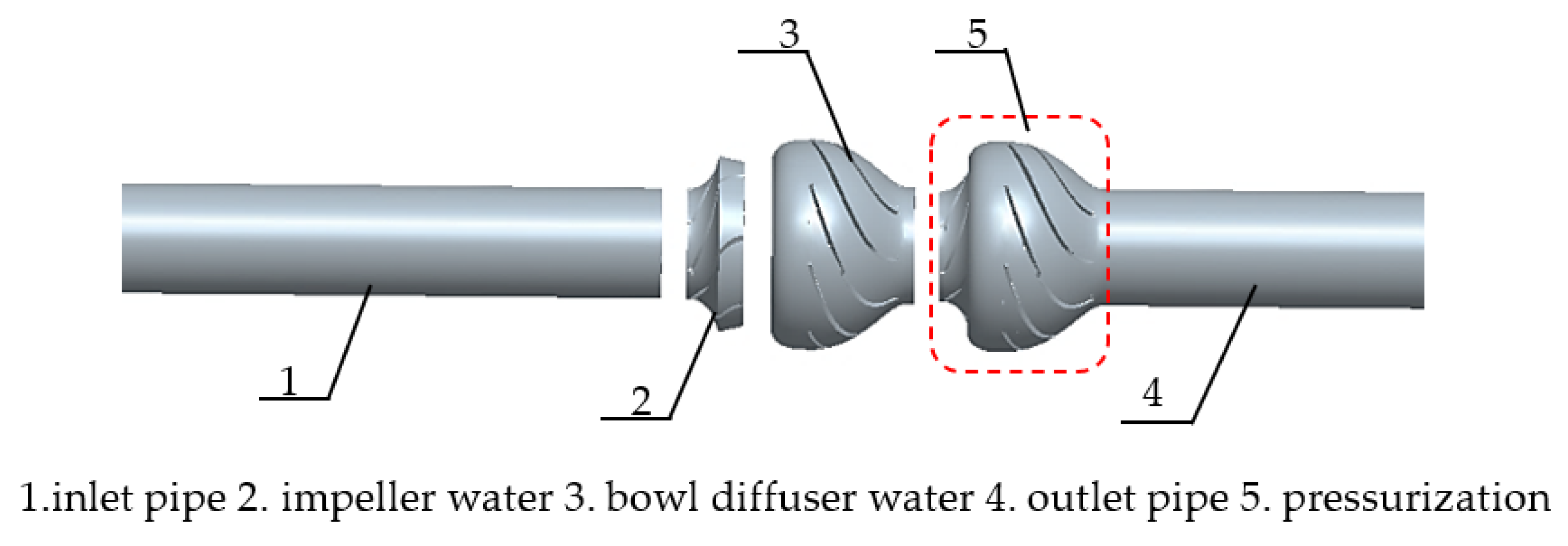
2.1. Computational Domain
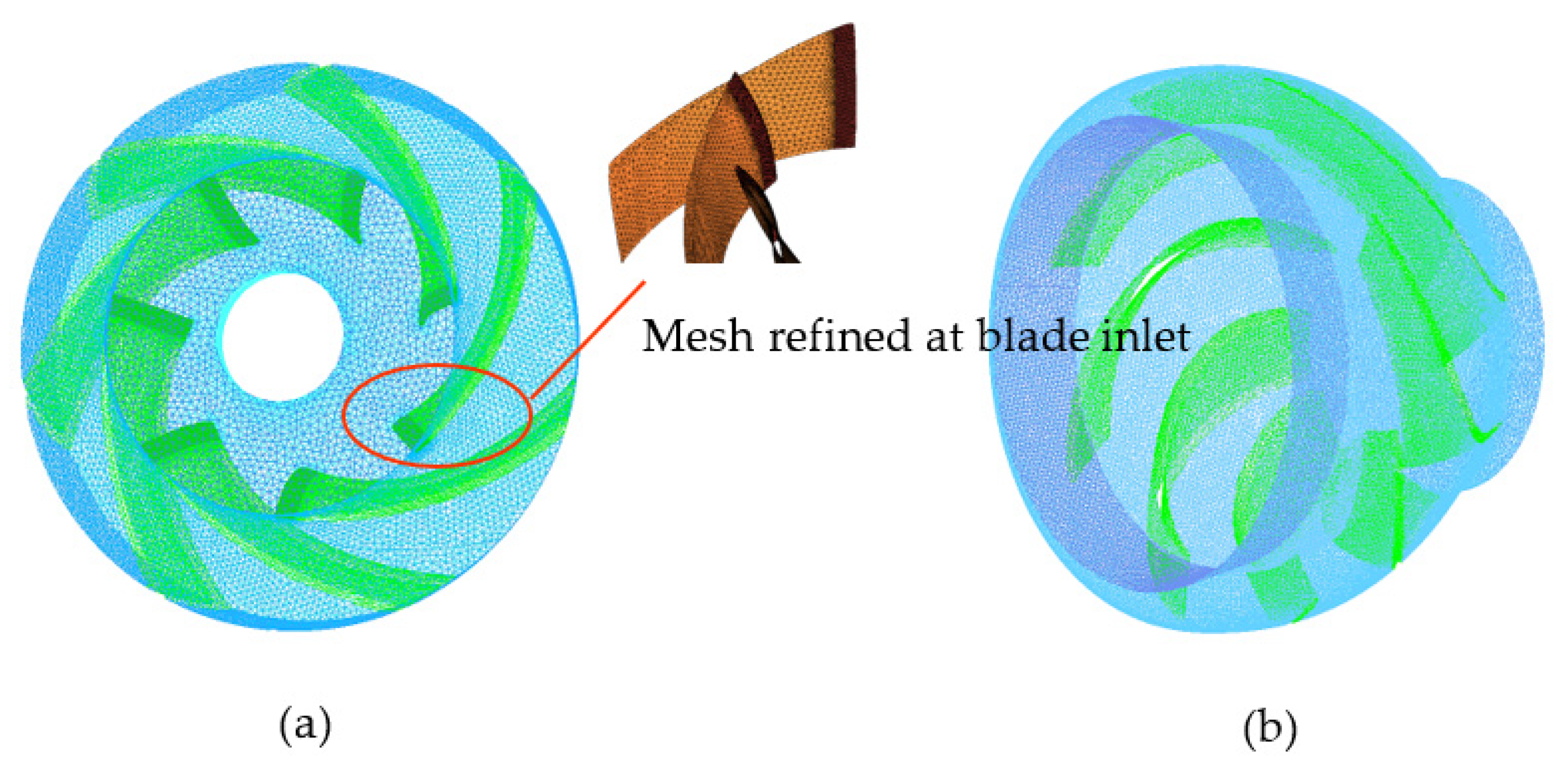
2.2. Mesh Generation
2.3. Turbulent Model
2.4. Simulation Setup
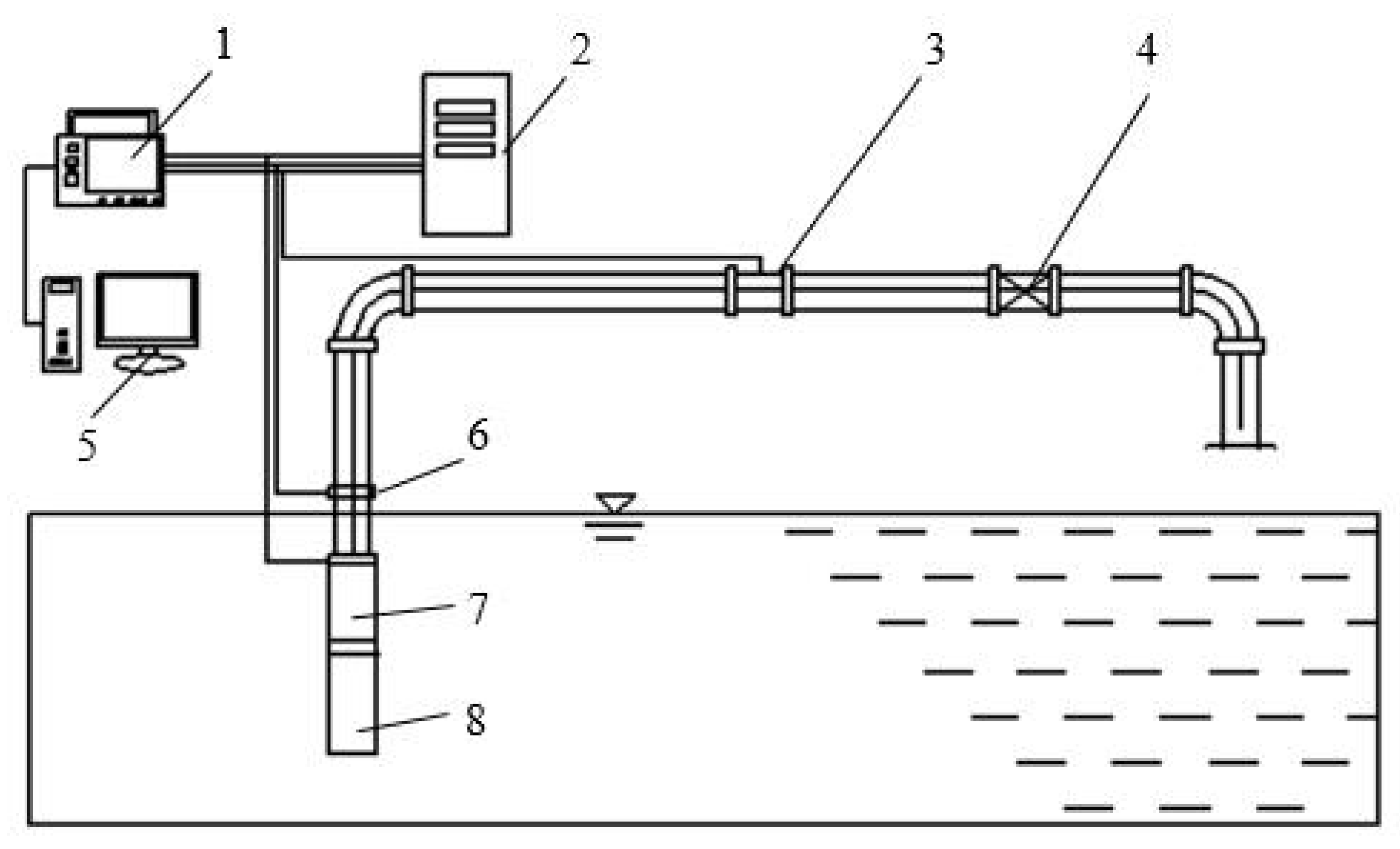
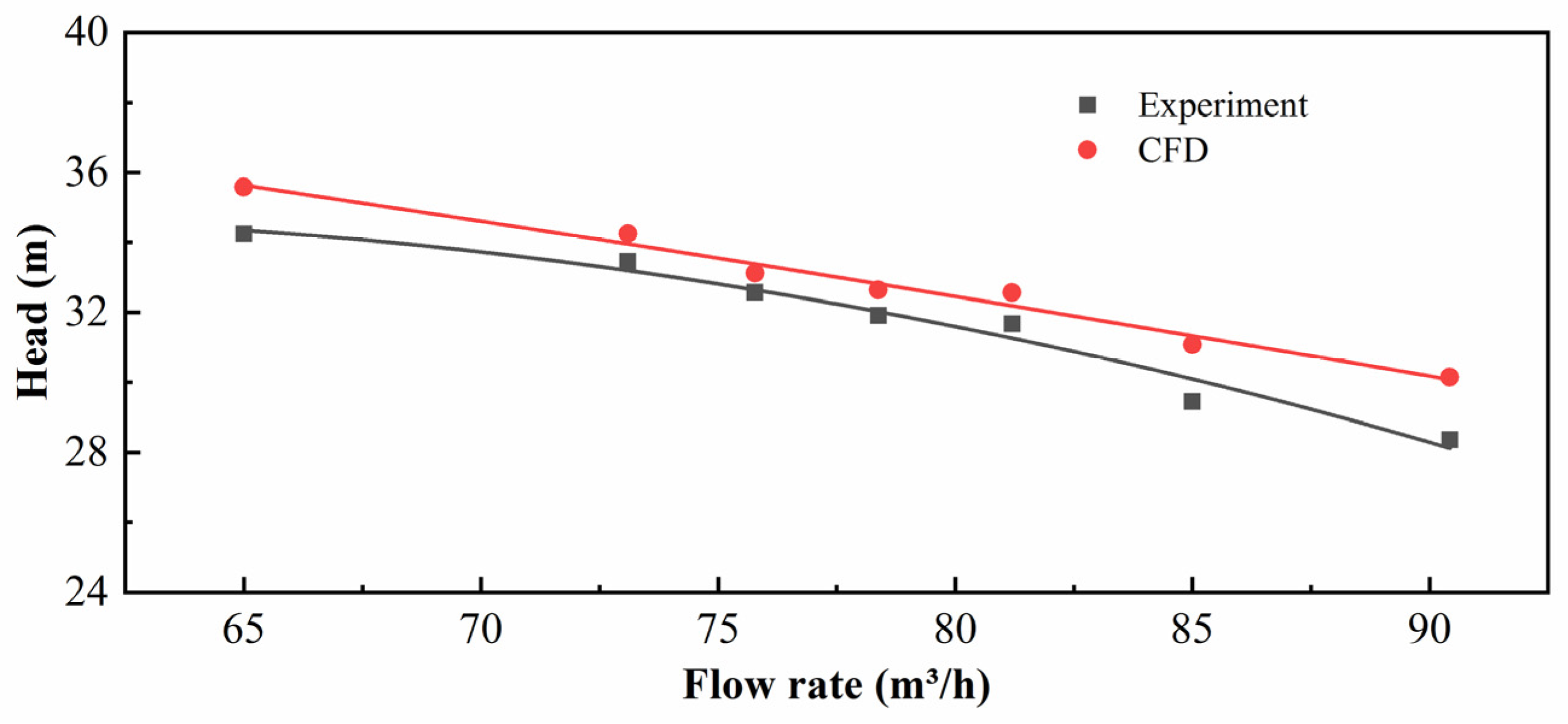
3. Experimental Pump Characteristics
4. Optimization Schemes
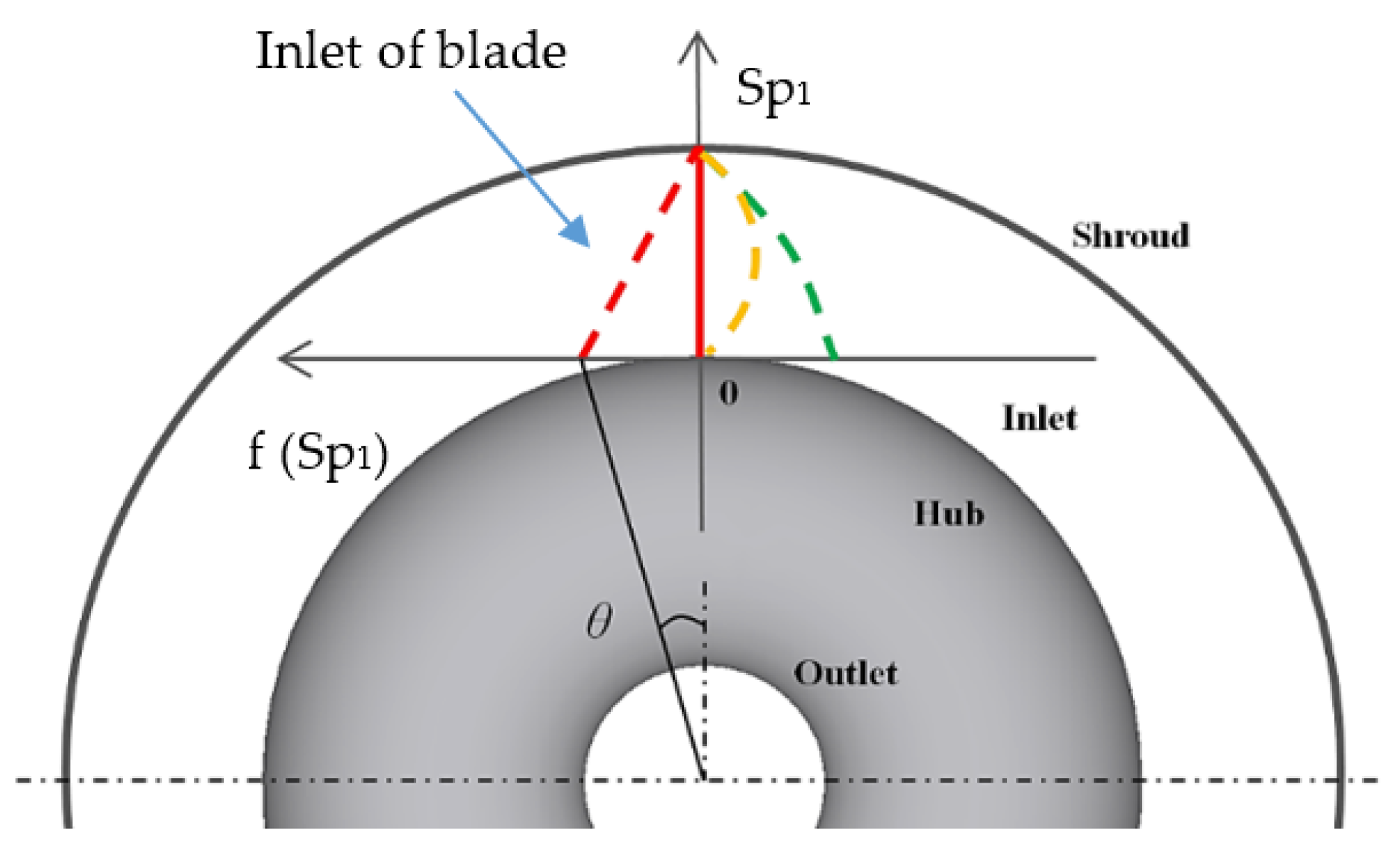
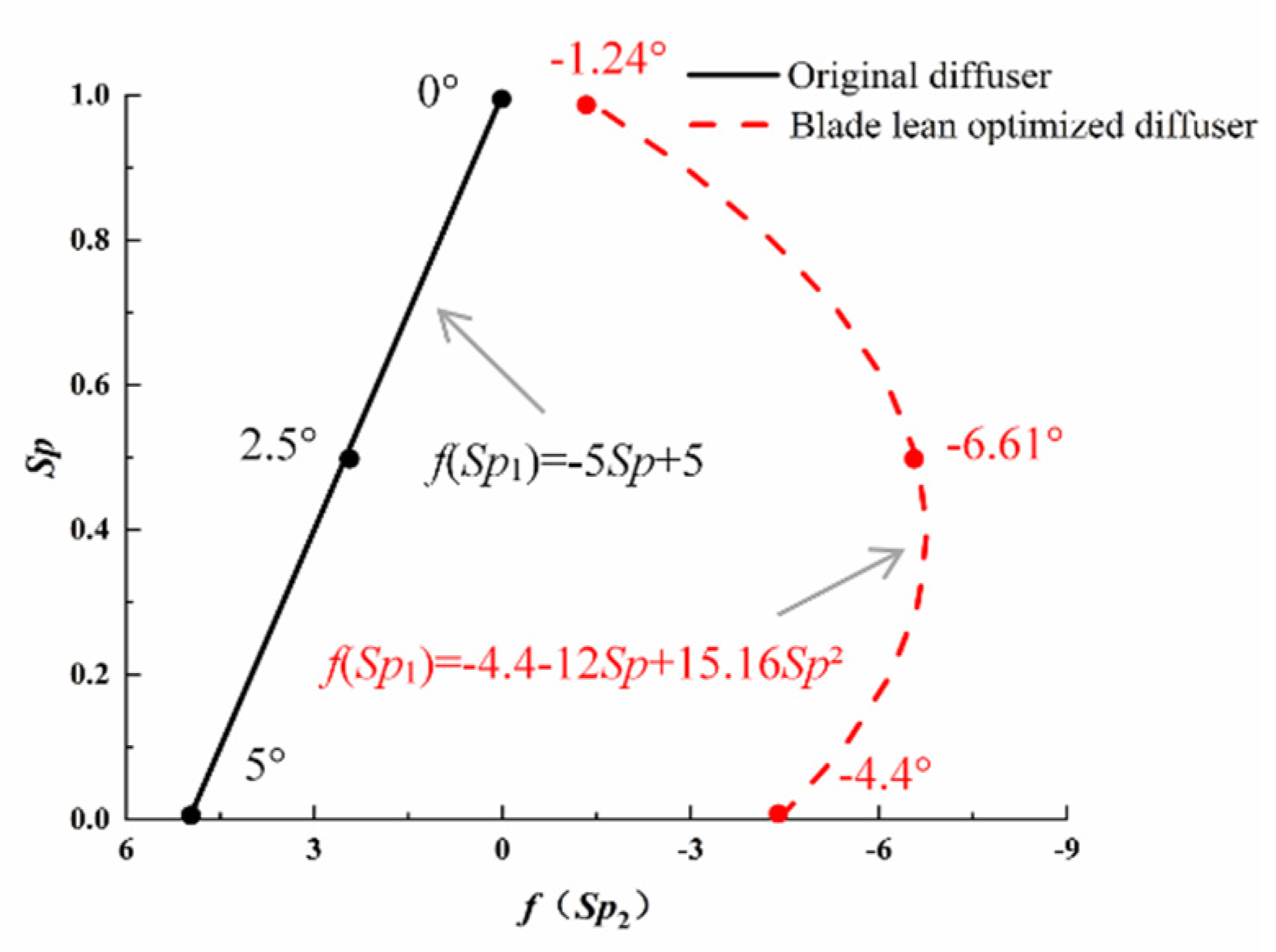
4.1. Design of Blade Lean
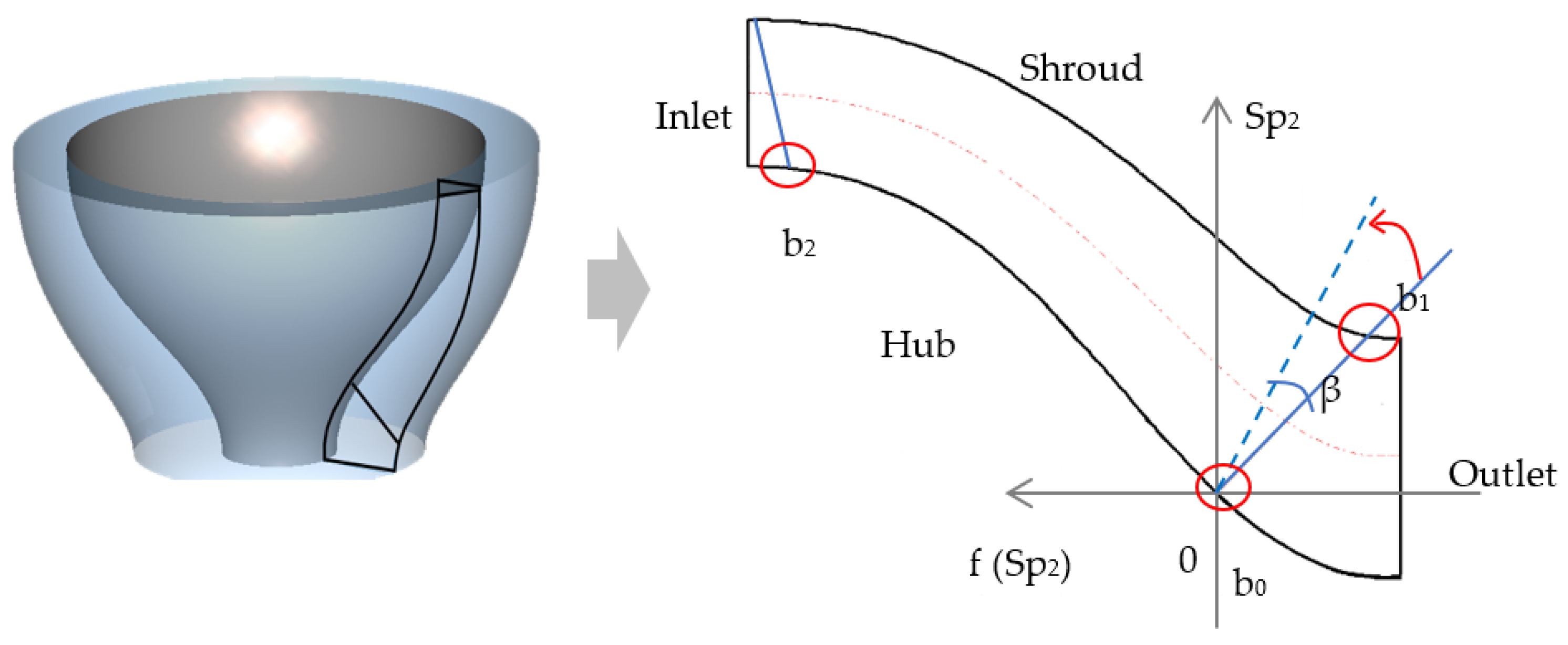
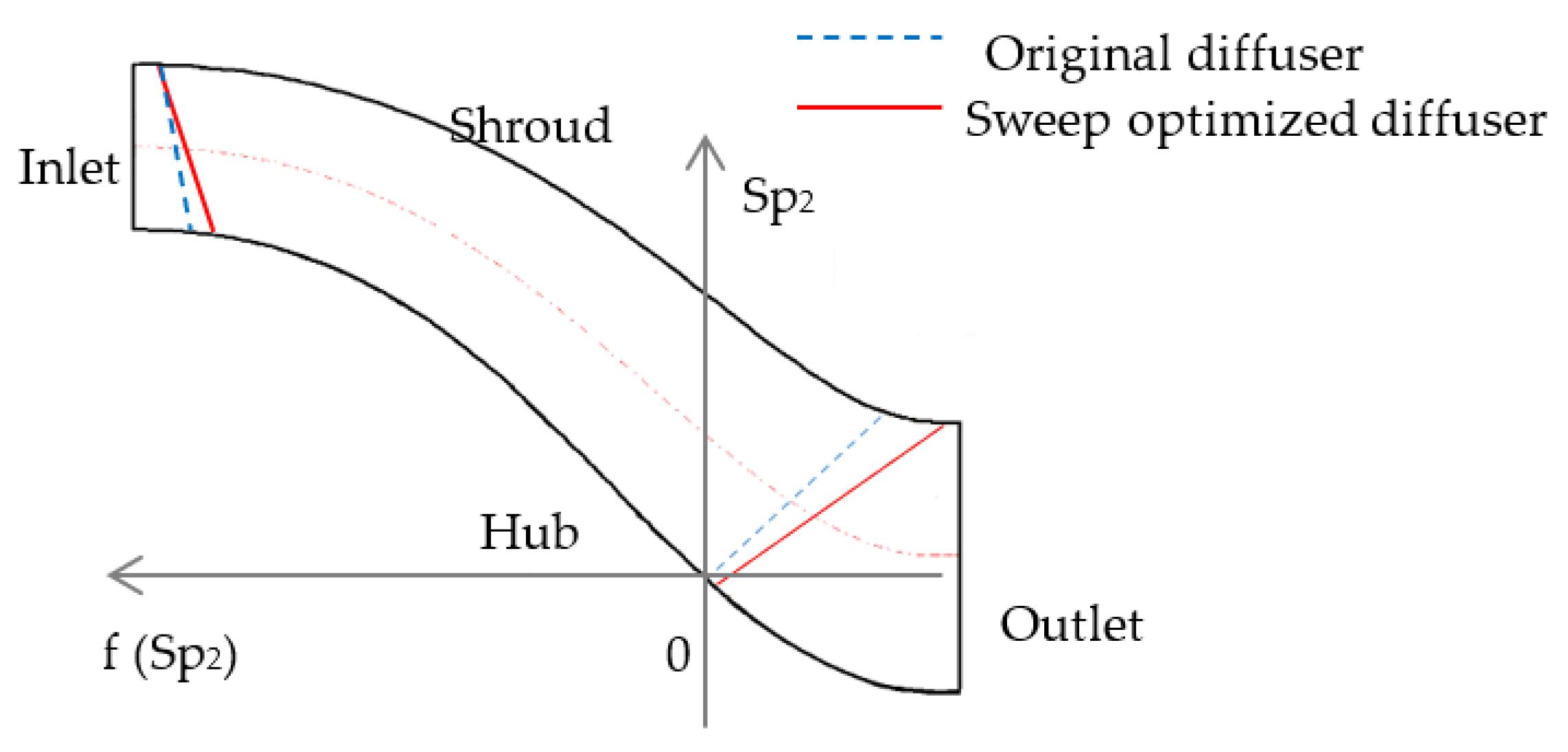
4.2. Design of Sweep
4.3. Analysis Parameters
5. Results
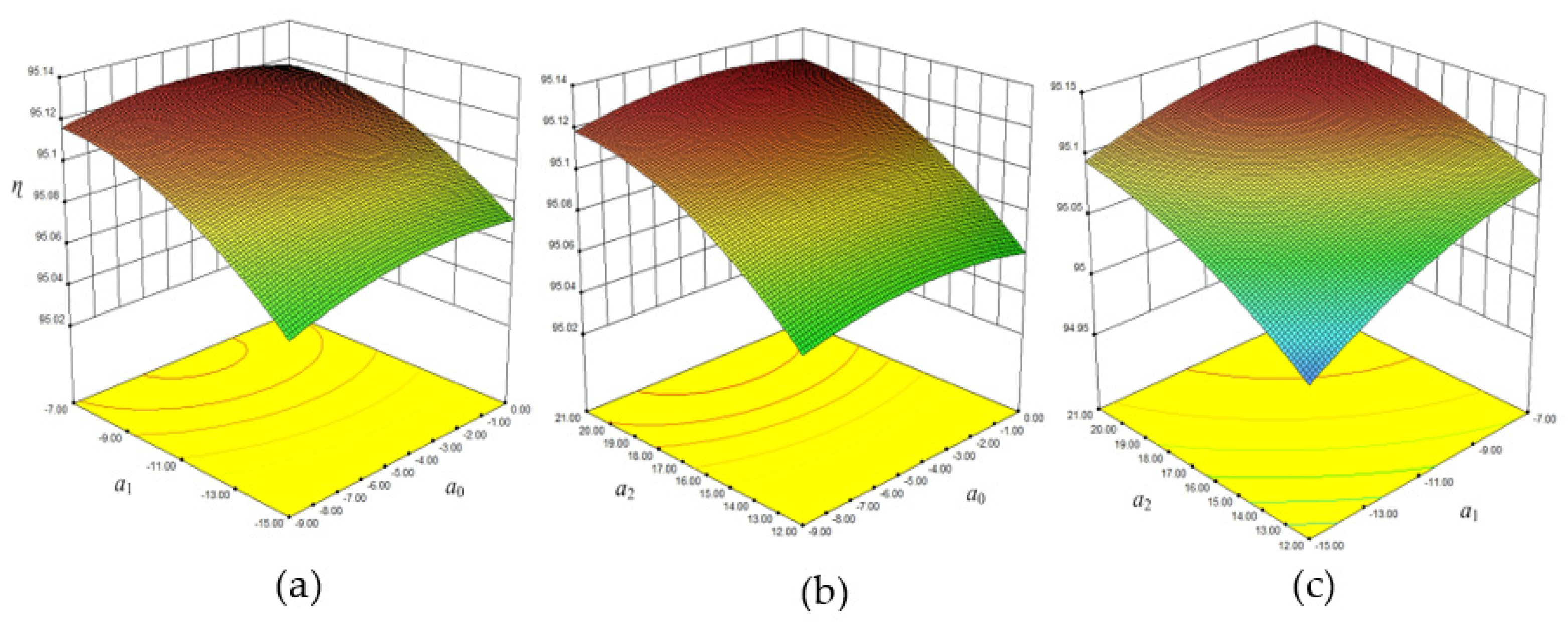
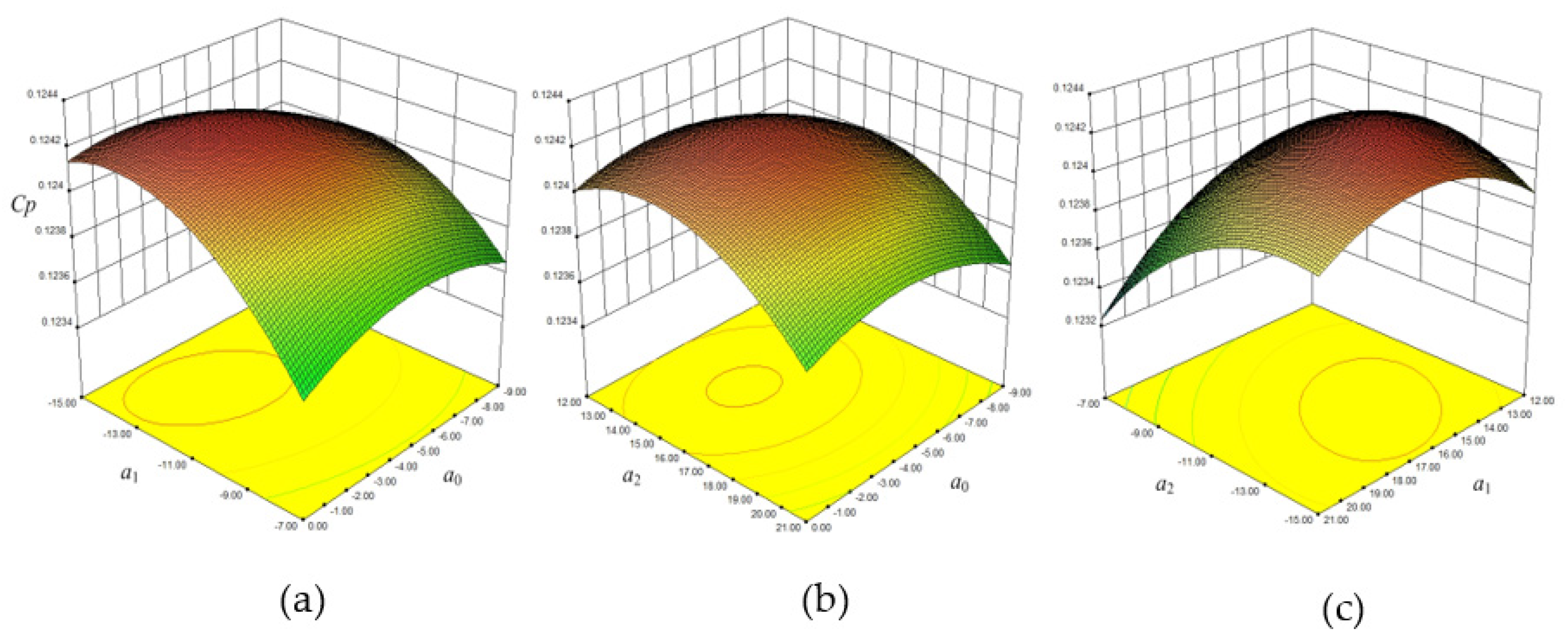
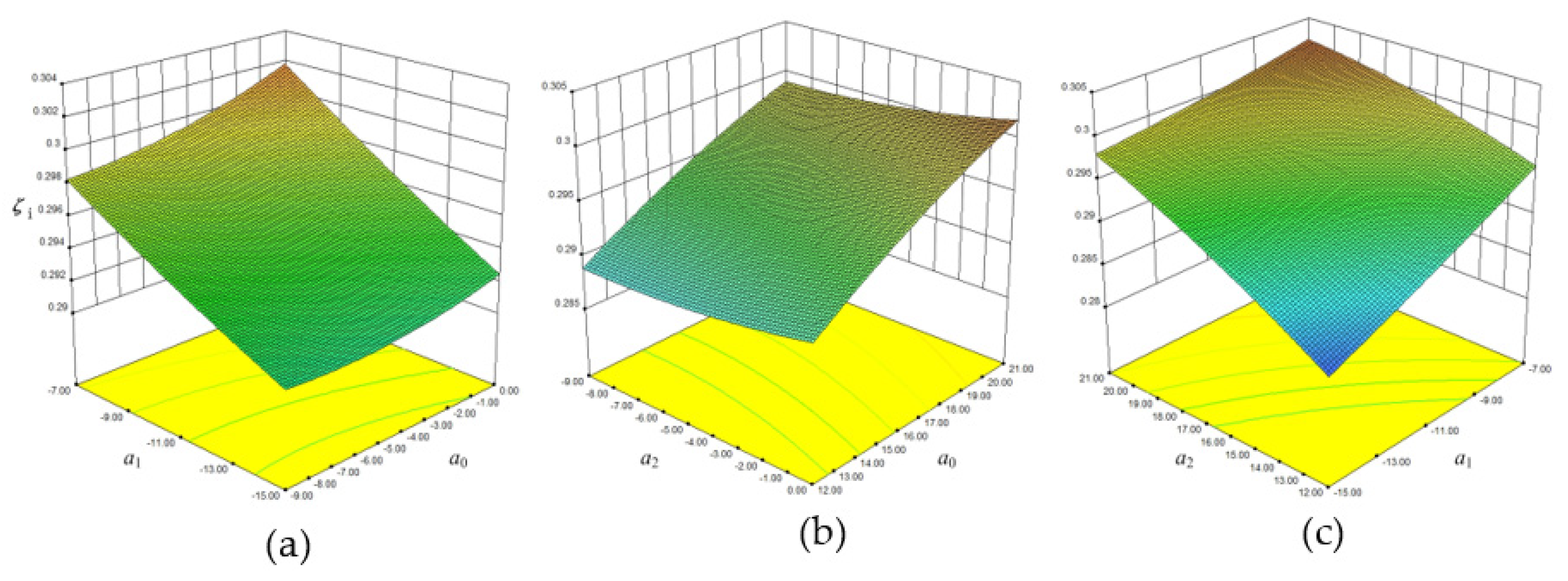
5.1. Response Surface of the Blade Lean Optimized Diffuser
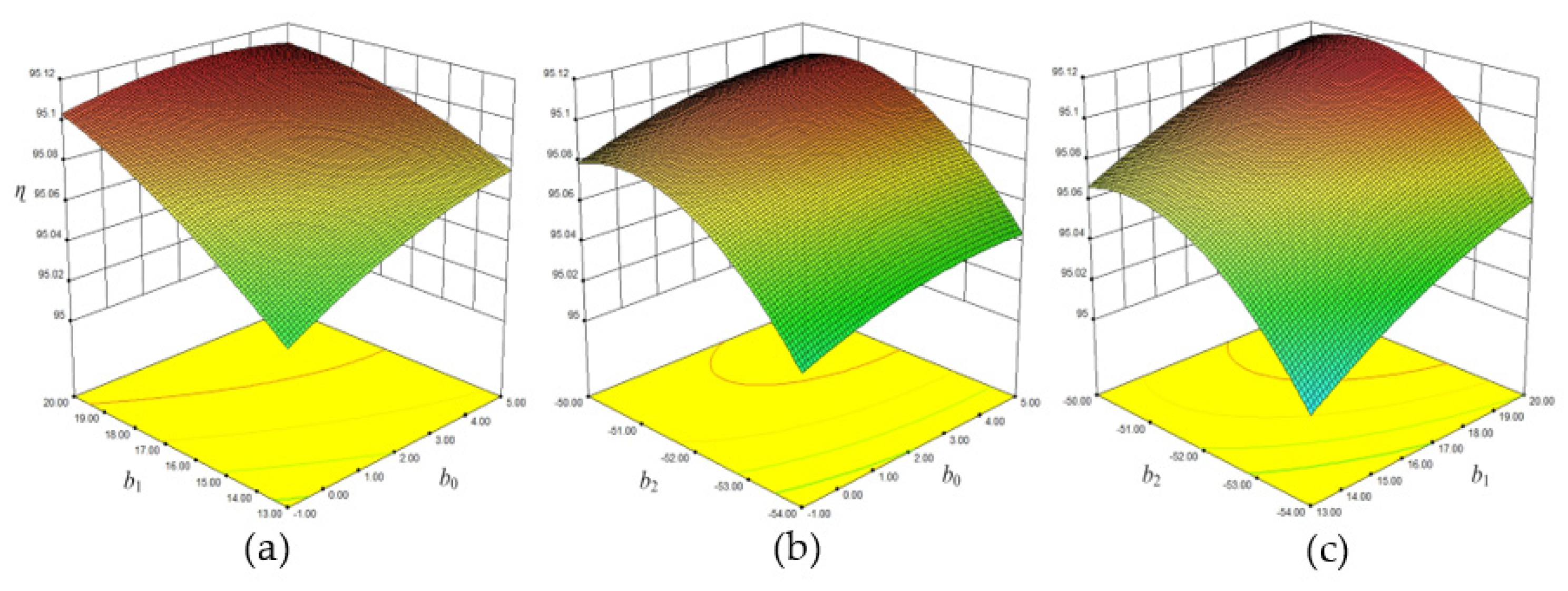
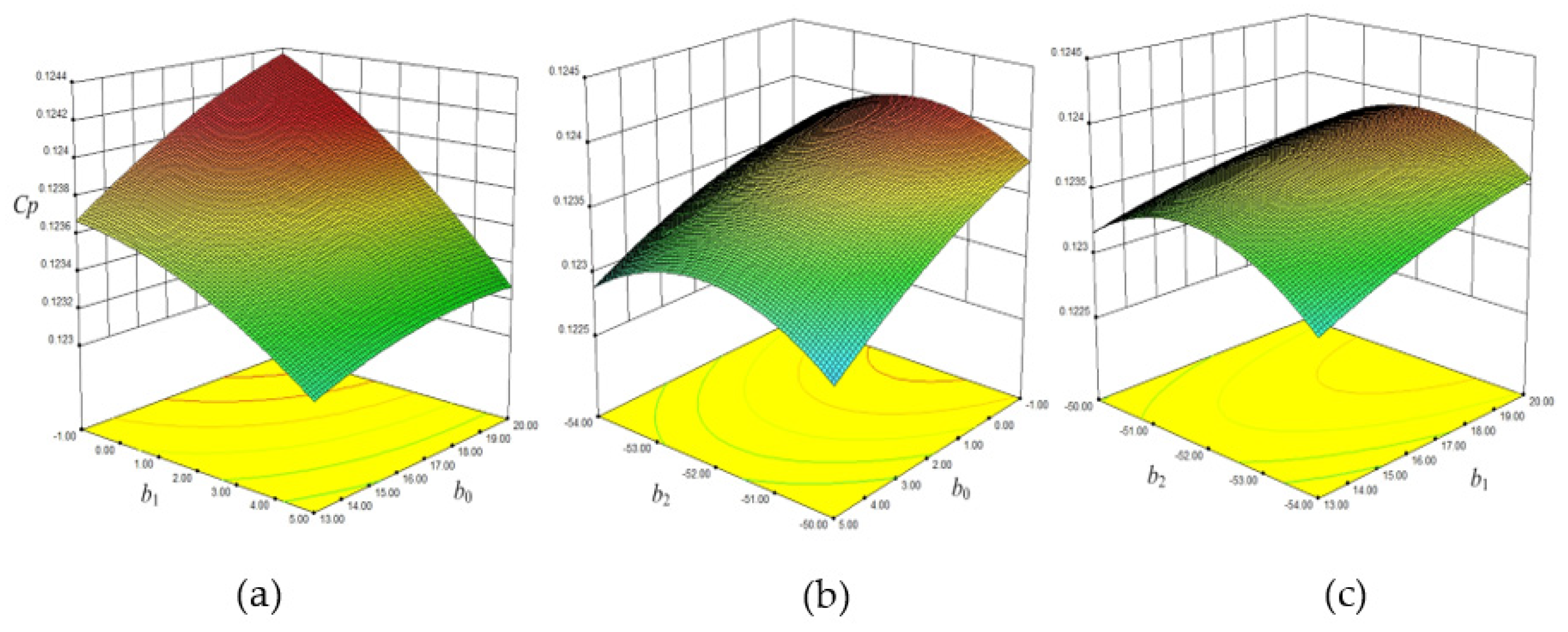
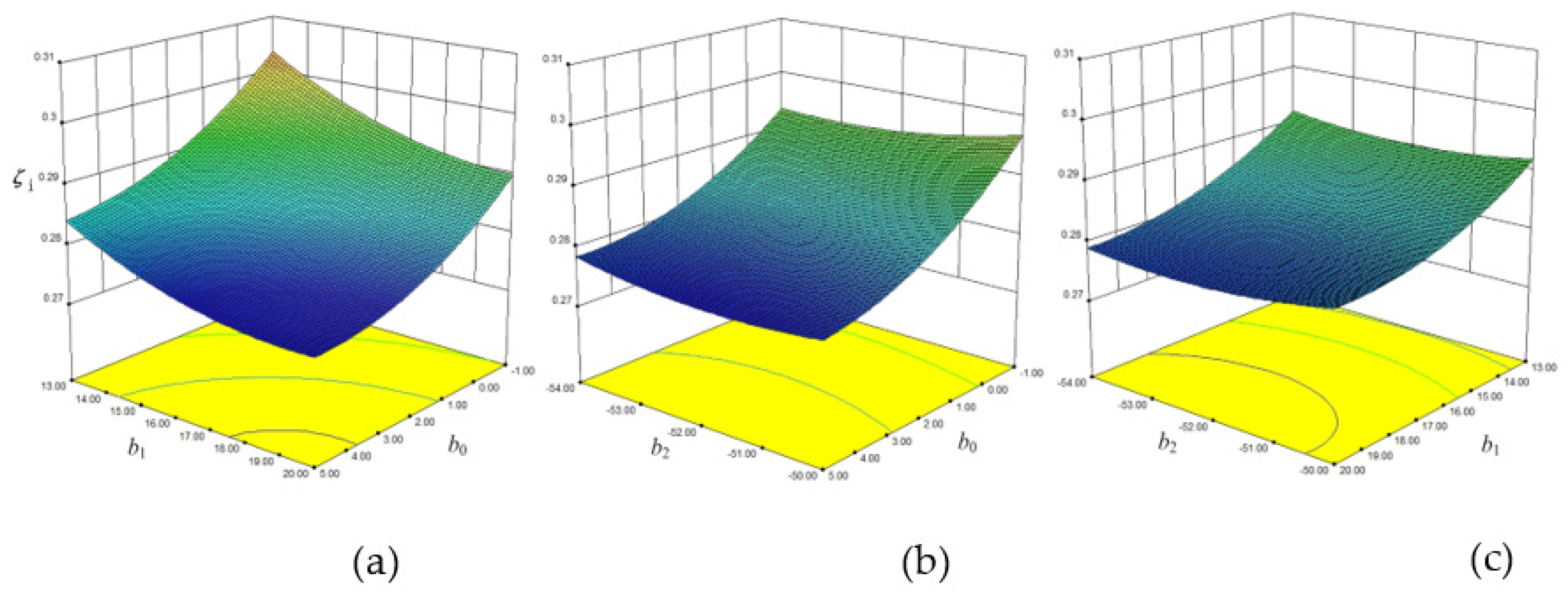
5.2. Response Surface of the Sweep Optimized Diffuser
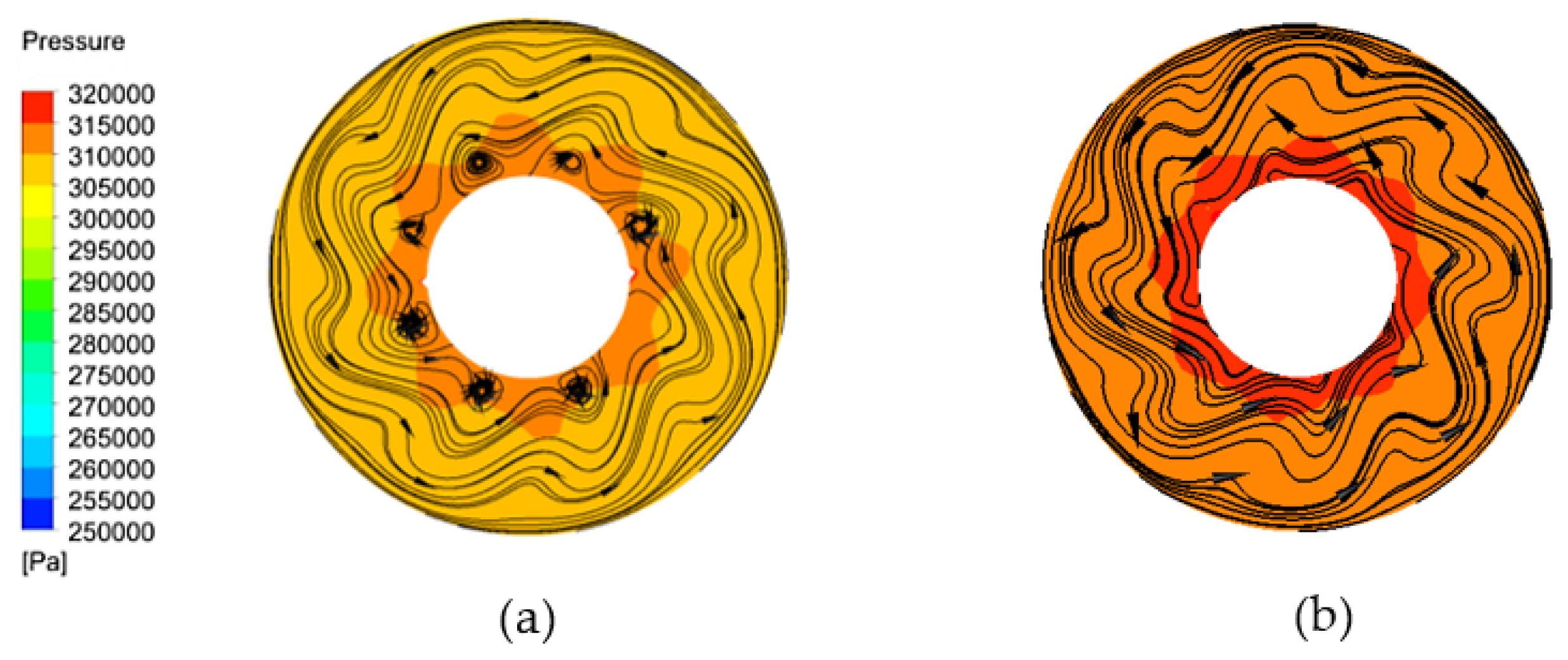
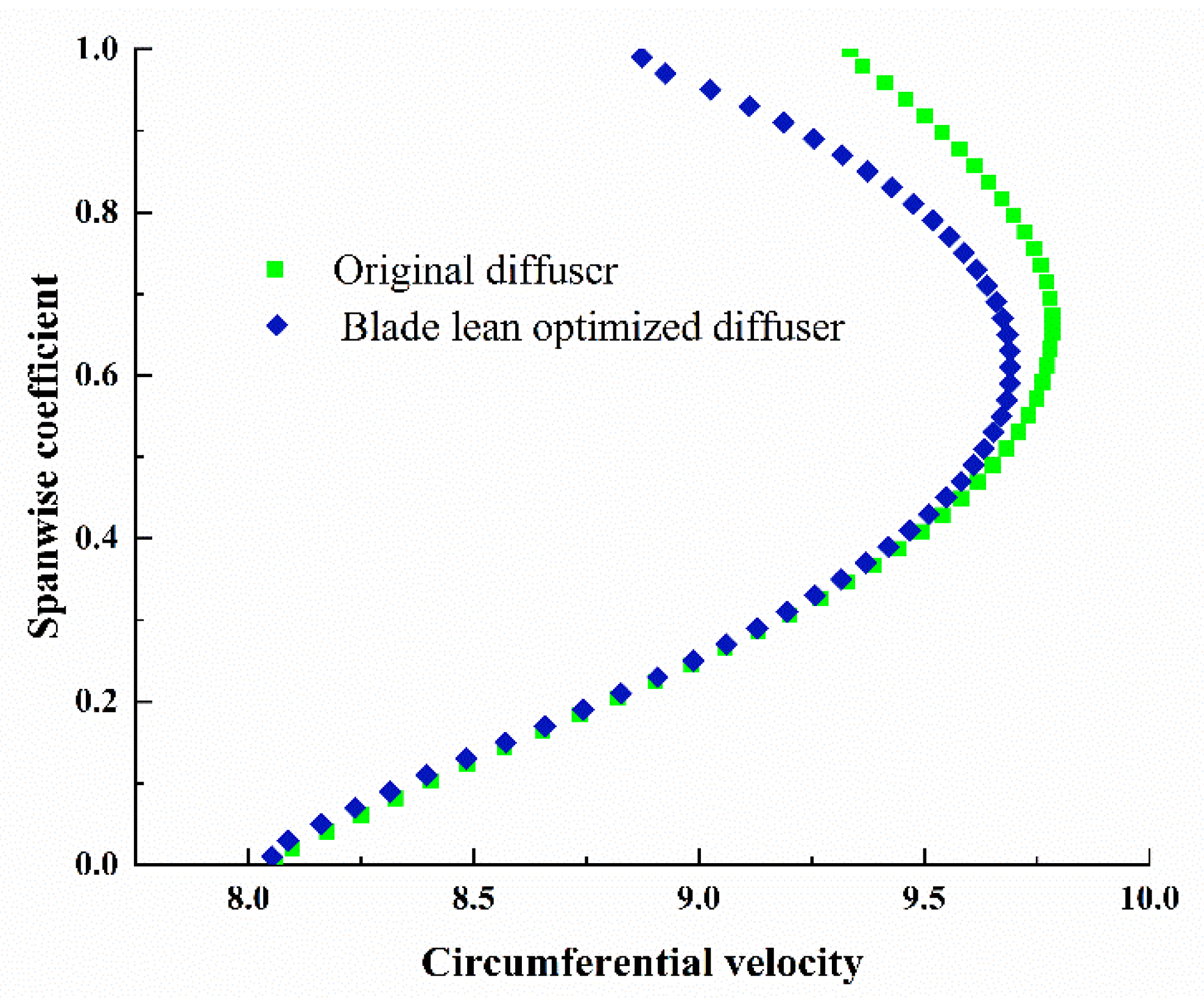
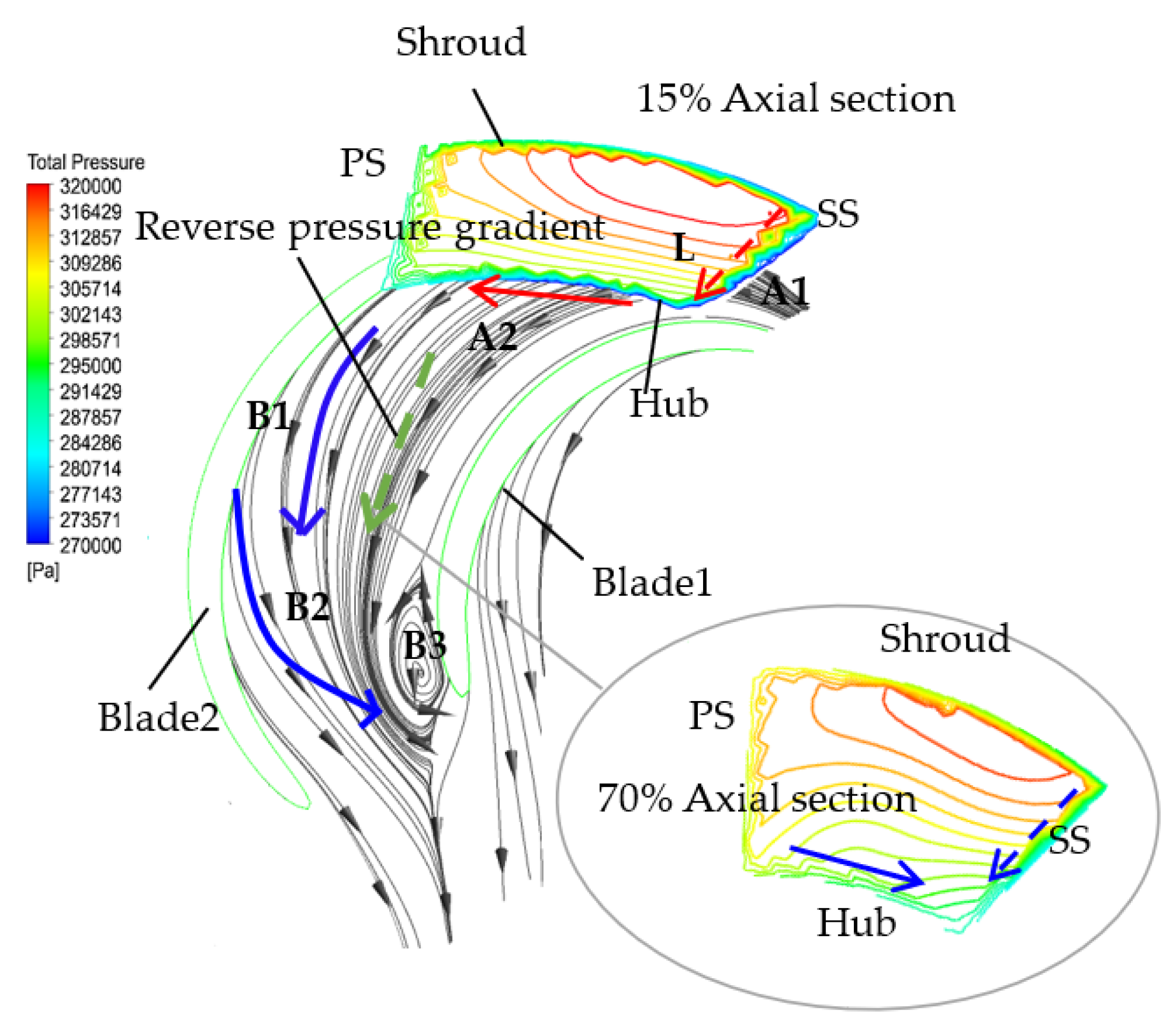
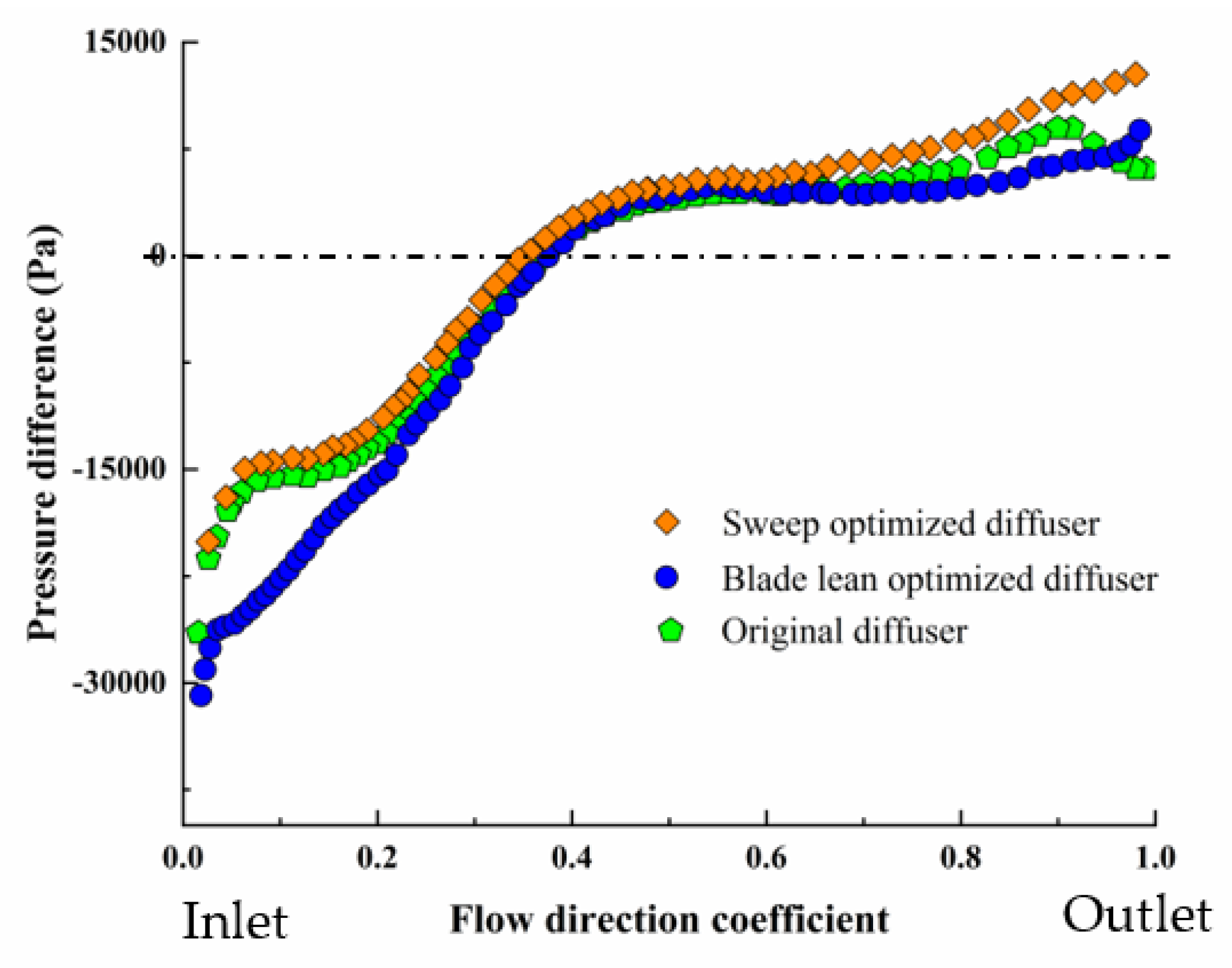
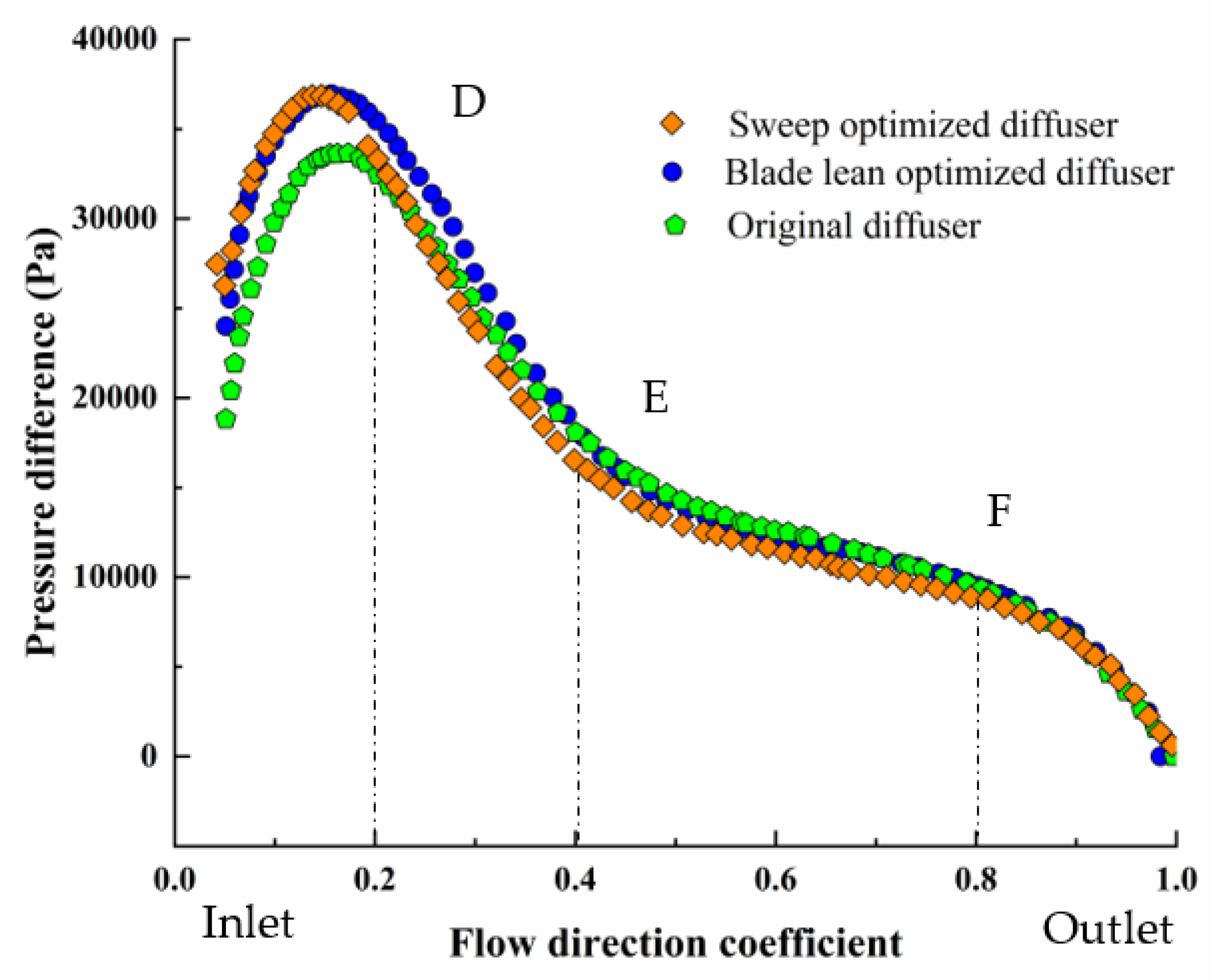
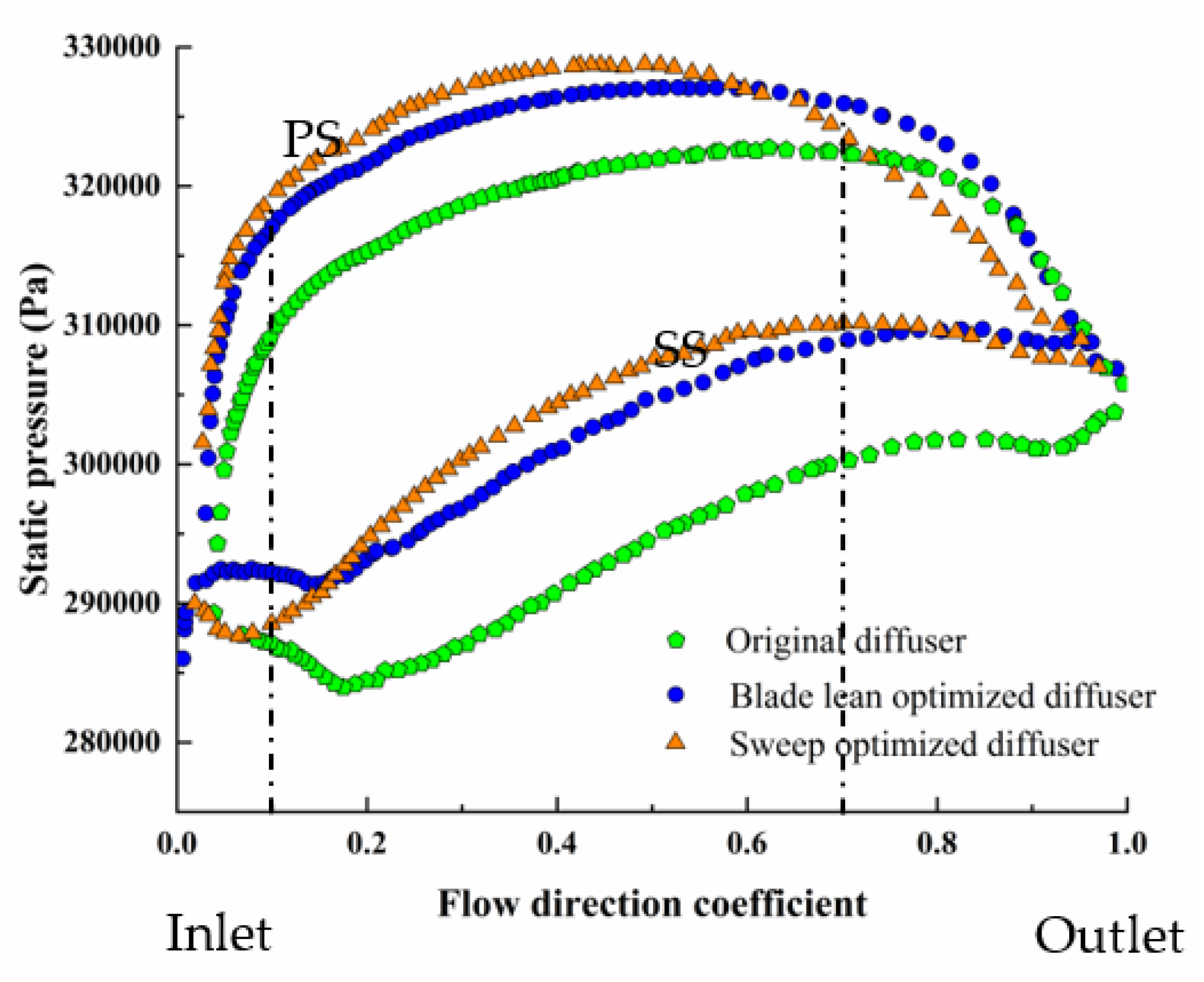
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Cp | Static pressure recovery coefficient |
| CCD | Center composite design |
| H | Head (m) |
| PS | Pressure surface of blade |
| SS | Suction surface of blade |
| k | Turbulent kinetic energy (m²/s²) |
| Pin | Total pressure of pump inlet (Pa) |
| Pout | Total pressure of pump outlet (Pa) |
| Pt3 | Total pressure of diffuser inlet (Pa) |
| Pt4 | Total pressure of diffuser outlet (Pa) |
| Ps3 | Static pressure of diffuser inlet (Pa) |
| Ps4 | Static pressure of diffuser outlet (Pa) |
| ρ | Density of fluid (kg/m³) |
| µt | Turbulent viscosity (kg/m·s) |
| ε | Turbulent energy dissipation (m²/s³) |
| ϕHub | Wrap angle of hub (°) |
| ϕShroud | Wrap angle of shroud (°) |
| θ | Starting angle (°) |
| ∆θ | Starting angle difference (°) |
| θHub | Starting angle of hub flow surface (°) |
| θShroud | Starting angle of shroud flow surface (°) |
| β | Sweep angle of diffuser (°) |
| ɳ | Efficiency of diffuser (%) |
| ζi | Non-uniformity |
References
- Wang, H.L.; Hu, Q.X.; Yang, Y.; Wang, C. Performance Differences of Electrical Submersible Pump under Variable Speed Schemes. Int. J. Simul. Model. 2021, 20, 76–86. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, M.; Wang, C.; Gao, Z. Optimal Design of Diversion Piers of Lateral Intake Pumping Station Based on Orthogonal Test. Shock. Vib. 2021, 2021, 6616456. [Google Scholar] [CrossRef]
- Shi, L.; Zhu, J.; Tang, F.; Wang, C. Multi-Disciplinary Optimization Design of Axial-Flow Pump Impellers Based on the Approximation Model. Energies 2020, 13, 779. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, C.; Zhang, Y.; Xiang, W.; He, Z.; Shi, W. Numerical study of coupled flow in blocking pulsed jet impinging on a rotating wall. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 508. [Google Scholar] [CrossRef]
- Wang, H.; Long, B.; Wang, C.; Han, C.; Li, L. Effects of the Impeller Blade with a Slot Structure on the Centrifugal Pump Performance. Energies 2020, 13, 1628. [Google Scholar] [CrossRef]
- Wang, H.; Qian, Z.; Zhang, D.; Wang, T.; Wang, C. Numerical Study of the Normal Impinging Water Jet at Different Impinging Height, Based on Wray–Agarwal Turbulence Model. Energies 2020, 13, 1744. [Google Scholar] [CrossRef]
- Bellary, S.A.I.; Husain, A.; Samad, A. Effectiveness of meta-models for multi-objective optimization of centrifugal impeller. J. Mech. Sci. Technol. 2014, 28, 4947–4957. [Google Scholar] [CrossRef]
- Bellary, S.A.I.; Samad, A.; Couckuyt, I.; Dhaene, T. A comparative study of kriging variants for the optimization of a turbomachinery system. Eng. Comput. 2016, 32, 49–59. [Google Scholar] [CrossRef]
- Huang, K.L.; Yuan, J.P.; Si, Q.R.; Lin, G. Numerical simulation of pressure pulsation in multistage centrifugal pump under multi-operation condition. J. Drain. Irrig. Mach. Eng. 2019, 37, 387–392. [Google Scholar]
- Tong, S.G.; Zhao, H.; Liu, H.Q.; Tong, Z.M.; Yue, Y.U.; Tang, N. Optimization calculation method for efficiency of multistage split case centrifugal pump. J. Zhejiang Univ. Eng. Sci. 2019, 53, 988–996. [Google Scholar]
- Stel, H.; Sirino, T.; Ponce, F.; Chiva, S.; Morales, R. Numerical investigation of the flow in a multistage electric submersible pump. J. Pet. Sci. Eng. 2015, 136, 41–54. [Google Scholar] [CrossRef]
- Heo, M.W.; Ma, S.-B.; Shim, H.S.; Kim, K.Y. High-efficiency design optimization of a centrifugal pump. J. Mech. Sci. Technol. 2016, 30, 3917–3927. [Google Scholar] [CrossRef]
- Murugesan, C.; Rudramoorthy, R. Numerical And Experimental Study Of Single stage And Multistage Centrifugal Mixed Flow Submersible Borewell Pumps. Int. J. Fluid Mach. Syst. 2016, 9, 107–118. [Google Scholar] [CrossRef][Green Version]
- Kim, J.-H.; Cho, B.-M.; Kim, S.; Lee, Y.-K.; Choi, Y.-S. Steady and Unsteady Flow Characteristics of a Multi-stage Centrifugal Pump under Design and Off-design Conditions. Int. J. Fluid Mach. Syst. 2019, 12, 64–70. [Google Scholar] [CrossRef]
- Rosic, B.; Xu, L. Blade Lean and Shroud Leakage Flows in Low Aspect Ratio Turbines. J. Turbomach. 2011, 134, 031003. [Google Scholar] [CrossRef]
- Razavi, S.R.; Sammak, S.; Boroomand, M. Multidisciplinary Design and Optimizations of Swept and Leaned Transonic Rotor. J. Eng. Gas Turbines Power 2017, 139, 122601. [Google Scholar] [CrossRef]
- He, X.; Zheng, X. Mechanisms of Sweep on the Performance of Transonic Centrifugal Compressor Impellers. Appl. Sci. 2017, 7, 1081. [Google Scholar] [CrossRef]
- He, X.; Zheng, X. Performance improvement of transonic centrifugal compressors by optimization of complex three-dimensional features. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 231, 2723–2738. [Google Scholar] [CrossRef]
- Bagshaw, D.A.; Ingram, G.; Gregory-Smith, D.G.; Stokes, M.R.; Harvey, N.W. The design of three-dimensional turbine blades combined with profiled endwalls. Proc. Inst. Mech. Eng. Part A J. Power Energy 2008, 222, 93–102. [Google Scholar] [CrossRef]
- Goto, A.; Zangeneh, M. Hydrodynamic Design of Pump Diffuser Using Inverse Design Method and CFD. J. Fluids Eng. 2002, 124, 319–328. [Google Scholar] [CrossRef]
- Goto, A.; Nohmi, M.; Sakurai, T.; Sogawa, Y. Hydrodynamic Design System for Pumps Based on 3-D CAD, CFD, and Inverse Design Method. J. Fluids Eng. 2002, 124, 329–335. [Google Scholar] [CrossRef]
- Scillitoe, A.; Tucker, P.G.; Adami, P. Numerical Investigation of Three-Dimensional Separation in an Axial Flow Compressor: The Influence of Freestream Turbulence Intensity and Endwall Boundary Layer State. J. Turbomach. 2016, 139, 021011. [Google Scholar] [CrossRef]
- Şahin, F.C. Experimental investigation on flow improvement in compressor cascades. Int. J. Energy Res. 2016, 41, 526–539. [Google Scholar] [CrossRef]
- Ananthakrishnan, K.; Govardhan, M. Influence of fillet shapes on secondary flow field in a transonic axial flow turbine stage. Aerosp. Sci. Technol. 2018, 82–83, 425–437. [Google Scholar] [CrossRef]
- Shi, W.; Zhou, L.; Lu, W.; Xu, L.; Li, W. Numerical Simulation and Experimental Study of Different Stages Deep-Well Centrifugal Pump. J. Comput. Theor. Nanosci. 2013, 10, 2897–2901. [Google Scholar] [CrossRef]
- Zhou, L.; Shi, W.; Li, W.; Agarwal, R. Numerical and Experimental Study of Axial Force and Hydraulic Performance in a Deep-Well Centrifugal Pump With Different Impeller Rear Shroud Radius. J. Fluids Eng. 2013, 135, 104501. [Google Scholar] [CrossRef]
- Yuan, S.Q.; He, W.T.; Si, Q.R.; Yuan, J.P.; Zhang, H.Y.; Cui, Q.L. Numerical simulation on gas-liquid two-phase flow in centrifugal pump based on MUSIG model. J. Drain. Irrig. Mach. Eng. 2021, 39, 1–7. [Google Scholar]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence. I. Basic theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Lam, S.H. On the RNG theory of turbulence. Phys. Fluids A Fluid Dyn. 1992, 4, 1007–1017. [Google Scholar] [CrossRef]
- Mompean, G. Numerical simulation of a turbulent flow near a right-angled corner using the Speziale non-linear model with RNG K–ε equations. Comput. Fluids 1998, 27, 847–859. [Google Scholar] [CrossRef]
- Cao, P.; Zhu, R.; Yin, G. Spike-type disturbances due to inlet distortion in a centrifugal pump. Renew. Energy 2021, 165, 288–300. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, W.; Hang, J.; Shi, W.; Yan, H.; Zhu, Y. Numerical Investigation of a High-Speed Electrical Submersible Pump with Different End Clearances. Water 2020, 12, 1116. [Google Scholar] [CrossRef]
- Zhou, L.; Bai, L.; Shi, W.; Li, W.; Wang, C.; Ye, D. Numerical analysis and performance experiment of electric submersible pump with different diffuser vanes number. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 89. [Google Scholar] [CrossRef]



| Parameters | Value |
|---|---|
| Blade number of impeller Z Diameter of inlet d1 (mm) Diameter of outlet d2 (mm) Width of blade outlet b2 (mm) Inlet angle of hub β1 (°) Outlet angle of hub β2 (°) | 7 97 134 20 28 34.2 |
| Parameters | Value |
|---|---|
| Blade number of diffuser Zd Diameter of outlet d4 (mm) Axial length e (mm) Inlet angle of hub β3 (°) Outlet angle of hub β4 (°) Wrap angle of hub ϕHub (°) Wrap angle of shroud ϕShroud (°) | 8 95 152 13.7 90 83 60 |
| Parameter | N (×104×104) | H/m | ɳ/% |
|---|---|---|---|
| value | 302 410 553 680 837 988 | 33.20 33.04 32.86 32.74 32.69 32.70 | 95.04 95.00 94.91 94.88 94.88 94.88 |
| Levels | Factors | ||
|---|---|---|---|
| a0 | a1 | a2 | |
| −1.682 | −12.07 | −17.73 | 8.93 |
| −1 | −9 | −15 | 12 |
| 0 | −4.5 | −11 | 16.5 |
| 1 | 0 | −7 | 21 |
| 1.682 | 3.07 | −4.27 | 24.06 |
| Levels | Factors | ||
|---|---|---|---|
| b0 | b1 | b2 | |
| −1.682 | −3.05 | 10.61 | −55.36 |
| −1 | −1 | 13 | −54 |
| 0 | 2 | 16.5 | −52 |
| 1 | 5 | 20 | −50 |
| 1.682 | 7.05 | 22.39 | −48.64 |
| a0 | a1 | a2 | ɳ (%) | Cp | ζi | |
|---|---|---|---|---|---|---|
| Blade lean optimized diffuser | −4.4 | −12 | 15.16 | 95.1 | 0.1242 | 0.292 |
| Original diffuser | 5 | −5 | 0 | 94.8 | 0.1210 | 0.321 |
| b0 | b1 | b2 | ɳ (%) | Cp | ζi | |
|---|---|---|---|---|---|---|
| Sweep optimized diffuser | 1.5 | 20 | −52 | 95.21 | 0.1245 | 0.279 |
| Original diffuser | 0 | 14 | −52.4 | 94.8 | 0.1210 | 0.321 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, C.; Cao, P.; Gong, X.; Zhu, R. Optimization of Sweep and Blade Lean for Diffuser to Suppress Hub Corner Vortex in Multistage Pump. Machines 2021, 9, 316. https://doi.org/10.3390/machines9120316
Ning C, Cao P, Gong X, Zhu R. Optimization of Sweep and Blade Lean for Diffuser to Suppress Hub Corner Vortex in Multistage Pump. Machines. 2021; 9(12):316. https://doi.org/10.3390/machines9120316
Chicago/Turabian StyleNing, Chao, Puyu Cao, Xuran Gong, and Rui Zhu. 2021. "Optimization of Sweep and Blade Lean for Diffuser to Suppress Hub Corner Vortex in Multistage Pump" Machines 9, no. 12: 316. https://doi.org/10.3390/machines9120316
APA StyleNing, C., Cao, P., Gong, X., & Zhu, R. (2021). Optimization of Sweep and Blade Lean for Diffuser to Suppress Hub Corner Vortex in Multistage Pump. Machines, 9(12), 316. https://doi.org/10.3390/machines9120316





