1. Introduction
In recent years, with the rapid development of power electronics technology, as a new type of voltage source converter topology, MMCs have been widely used in various engineering fields [
1,
2,
3], such as high-voltage direct current (HVDC) transmission [
4], high-voltage power drive systems [
5], renewable energy [
6], etc. However, due to exposure to harsh working environments, the safety of power electronic switches is one of the most critical issues in the normal operation of MMCs [
7]. If an internal fault in the converter occurs, it may lead to an increase in voltage harmonics, waveform distortion, power quality decline, or even commutation failure [
8,
9]. MMCs have a large number of submodules (SMs), and because of device aging, overload, and accidental operation, the insulated-gate bipolar transistor (IGBT) in the SMs is most likely to fail [
10]. Therefore, the adoption of efficient fault diagnosis technology helps to improve the operational reliability of MMCs and reduce costs [
11].
The proposed MMC fault diagnosis methods can be divided into three categories according to their working principles, namely, fault diagnosis methods based on mechanism models, signal processing, and data-driven methods [
12].
Mechanism-based fault diagnosis methods mostly use additional sensors. Faults can be detected by comparing the internal characteristics (circulating current, arm current, capacitor voltage, etc. [
13]) and external characteristics. This approach is simple and reliable, but increases costs and hardware complexity. In [
14], an integral sliding mode observer (ISMO)-based fault diagnosis method for MMCs is proposed; the fault is detected by judging whether the observed state deviates from the measured state, and then the average voltage of all SMs and the error between the capacitor voltage and the threshold of an SM is compared to locate the faulty SM; however, the fault detection and location depend on the observer model, so the time of the fault diagnosis process is still long, and the amount of calculation is relatively large. In [
15], a fault diagnosis method based on redundant voltage sensors is proposed; by comparing the output voltage of a group of SMs with two calculated reference voltages, switch and sensor faults can be detected; this method can locate various open-circuit faults, but the computational complexity and cost increase with the increase in the number of SMs.
Fault diagnosis methods based on signal processing use output characteristics rather than internal characteristics to achieve fault diagnosis, by processing voltage or current signals and comparing their characteristics in real time. Data-driven fault diagnosis methods use artificial intelligence algorithms (machine learning, etc.) [
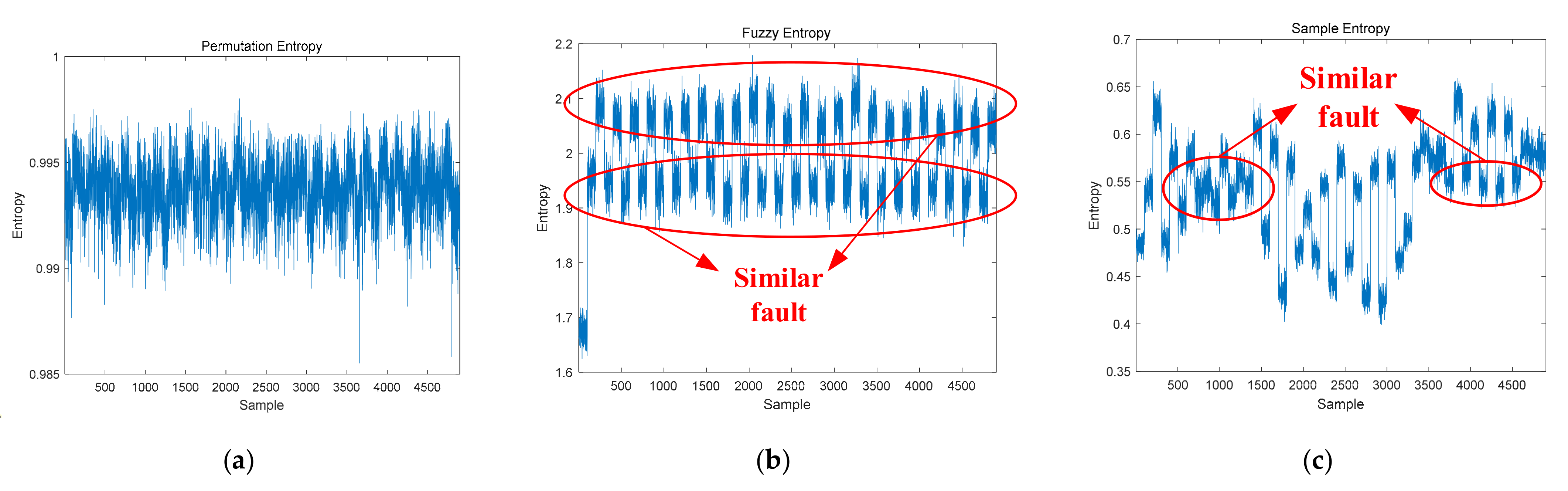
16] to obtain the diagnosis through the analysis of data, reflecting the relationships among system faults and between faults and non-faults. Although the algorithms are complex, they do not require very complex hardware, and their costs are relatively low. Compared with the model-based and signal-based fault diagnosis methods, the data-driven diagnosis methods have better classification ability, and are more suitable for various types of faults and complex systems [
17]. Because of the similarity of faults, it is difficult to locate the faults directly and accurately via signal-based diagnosis methods. Therefore, the data-driven diagnosis methods are more suitable for MMC fault diagnosis, and the key lies in feature extraction and classification methods. Most feature extraction methods for MMC faults use wavelet transform to preprocess the data. Wavelet transform can analyze and process nonstationary signals in both the time and frequency domains. The combination of wavelet transform and information entropy can extract fault features more effectively and accurately. The authors of [
18] proposed a fault diagnosis method based on wavelet analysis and an improved neural network; the wavelet energy spectrum entropy was used to extract the characteristics of the signal after wavelet transform, constituting a statistical analysis of the energy distribution of the signal in each frequency band. The authors of [
19] proposed a method using wavelet time entropy to achieve fast and accurate fault detection. The characteristics of wavelet time entropy enable it to quantify the changes in high-frequency transients by reconstructing the high-frequency component of the current signal, in order to analyze the specific frequency band of the fault current and quickly detect faults. Additionally, improved algorithms for entropy are constantly emerging. The authors of [
20] propose an index based on weighted residual regression to reduce the sensitivity of kurtosis and entropy to impulse noise, which is more effective for the detection of bearing and gear faults.
The common classification methods for MMC fault diagnosis are mainly concentrated in the field of machine learning. In [
21], an optimized support vector machine (SVM) method for fault diagnosis is proposed, and the fault characteristics are extracted by using the average value of three-phase AC current. However, with the development of deep learning technology, classification methods based on deep learning have also achieved good results in MMC fault diagnosis, and have been widely applied. In [
22], the authors used a stacked sparse autoencoder to extract fault features from an MMC, and used classifiers based on deep neural networks to detect faults more accurately. Although these methods use artificial intelligence algorithms and even deep learning algorithms to classify faults, they can only locate one arm of the bridge, rather than a specific SM.
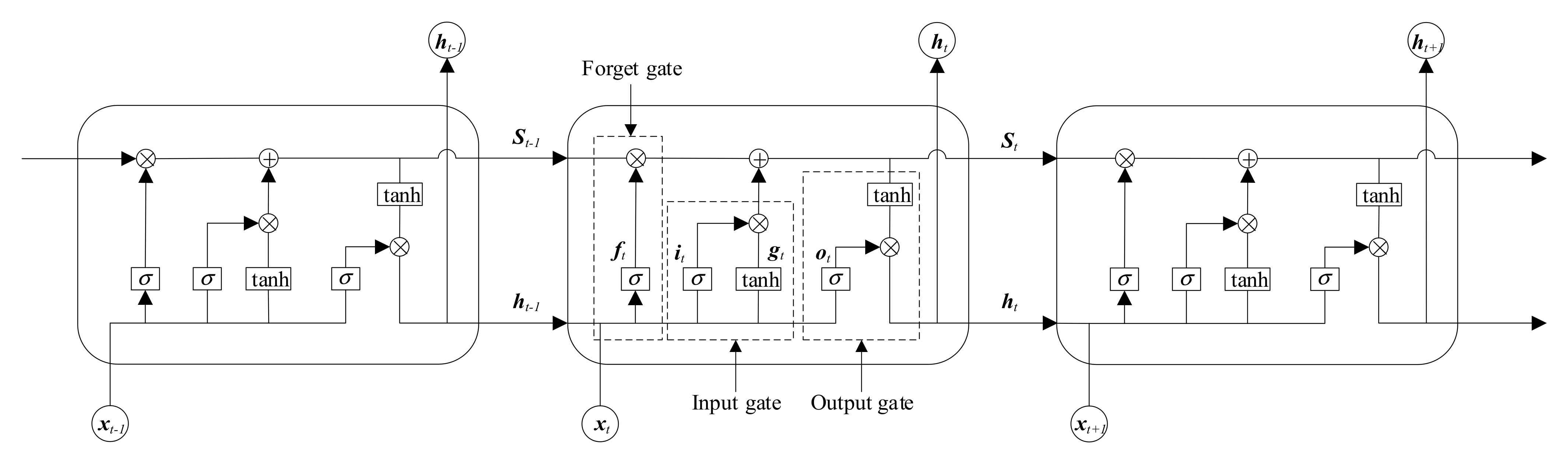
In summary, data-driven methods can accurately locate faults without establishing an accurate mathematical model, making them suitable for complex systems. Therefore, data-driven methods are considered for the fault diagnosis of MMCs. To solve the problem of the similarity of faults in MMCs, this paper proposes a fault diagnosis method based on weighted-amplitude permutation entropy and DS evidence fusion theory. In the first part, the time–frequency information of the three-phase output voltage of the MMC is extracted by wavelet packet transform, and the weighted-amplitude permutation entropy of the reconstructed signal at different scales is calculated. The second part uses LSTM to establish the fault diagnosis model, and outputs the probability matrix of this group of data being classified into a certain fault. The third part uses the advantages of incomplete and uncertain information from DS evidence fusion theory [
23,
24]—the basic probability assignment (BPA) matrix obtained by selecting permutation entropy at different scales as inputs is fused by the DS evidence fusion algorithm to obtain the final classification results. This method is applied to IGBT open-circuit fault diagnosis in a specific SM. The simulation results show that, compared with other algorithms, this method has advantages in both accuracy and diagnosis time.
4. Simulation Validation and Results Discussion
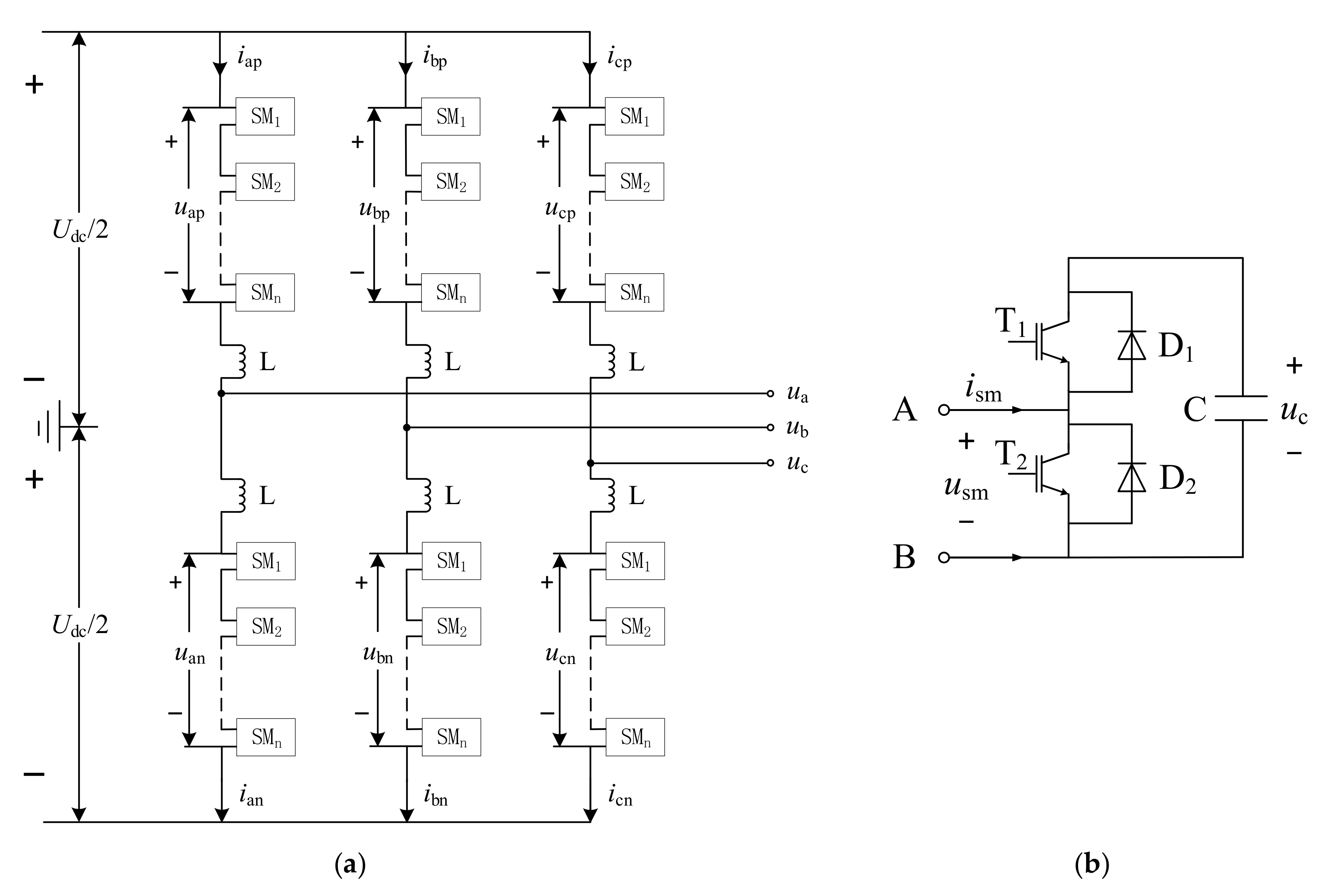
In order to verify the feasibility of the proposed fault diagnosis method, a three-phase five-level MMC simulation model was built on MATLAB/Simulink, the simulation parameters of which are shown in
Table 2. In the simulation, the voltage balancing control strategy based on a carrier phase-shift modulation strategy was adopted. The simulation was mainly aimed at the state of an MMC when it works as an inverter.
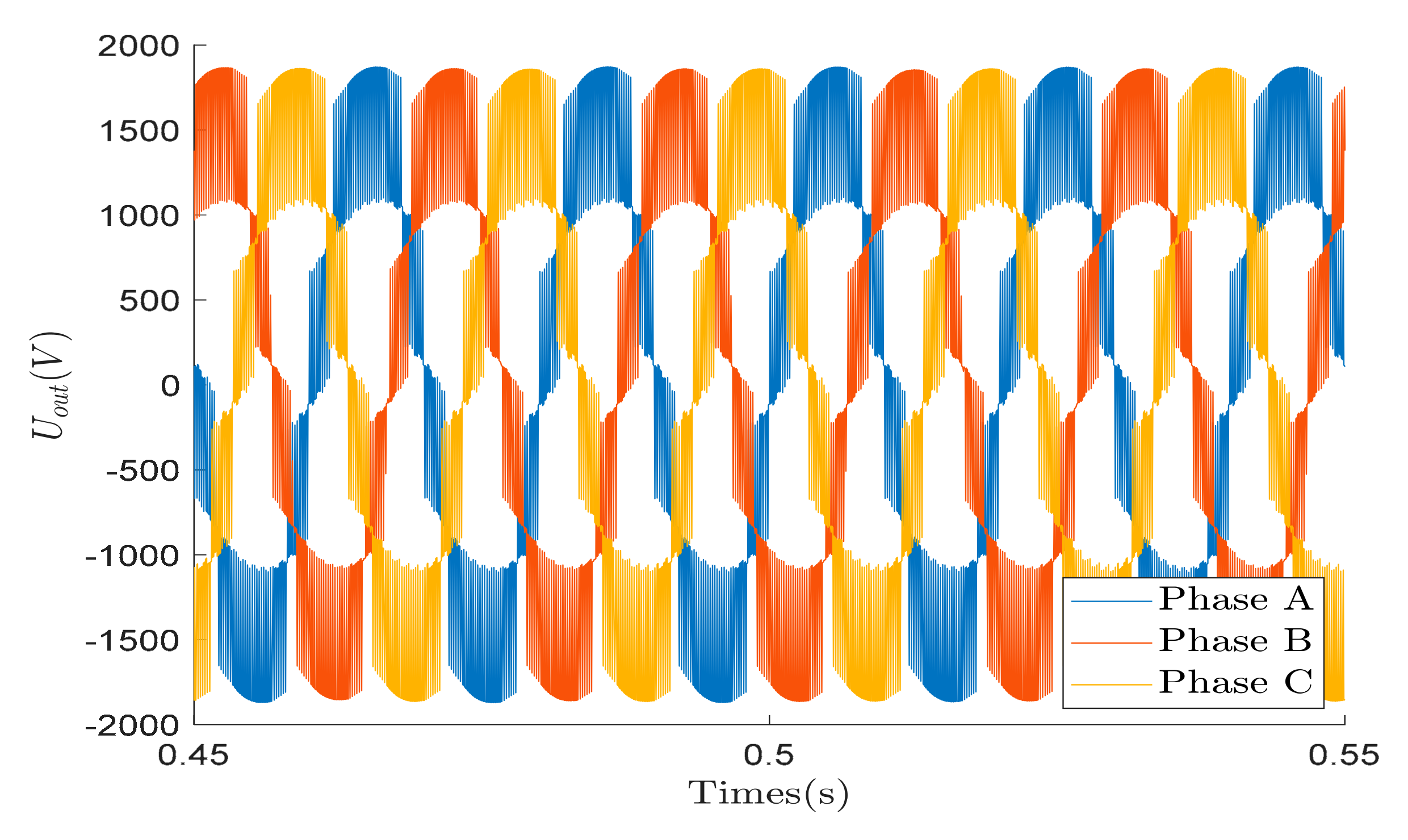
The three-phase output voltage of the simulation under normal operation is shown in
Figure 8.
Under these conditions, the five-level MMC contains a total of 24 SMs and 48 IGBTs. Therefore, the dataset includes the output voltages of the normal state and 48 IGBT open-circuit fault states. Each voltage time series consists of 2 basic periods with 400 sample points in each period after the fault occurs. The normal state is regarded as a special fault state, and each fault type is given an output label with a value of 0–48. Each fault type generates 100 data by adding Gaussian white noise to the signal in order to improve the generalization performance of the network. Finally, the training set and test set are randomly assigned from 100 data to train and test the model.
In the fault diagnosis for the simulation of a five-level MMC, in order to analyze whether WAPE has better ability of feature extraction and fault diagnosis than other entropy algorithms, and to analyze the influence of wavelet packet decomposition with different layers on the diagnosis accuracy, a broken line diagram of the accuracy obtained by using different forms of permutation entropy under wavelet packet decomposition with different layers was drawn, as shown in
Figure 9.
As illustrated in
Figure 9, WAPE shows a great improvement in diagnostic accuracy compared with other forms of entropy. In addition, with the increase in the number of decomposition layers, the diagnostic accuracy also increases. Considering that with the increase in the number of wavelet packet decomposition layers, the computation time and algorithm complexity are multiplied, we only used four-layer wavelet packet decomposition to obtain 16-dimensional decomposed signals.
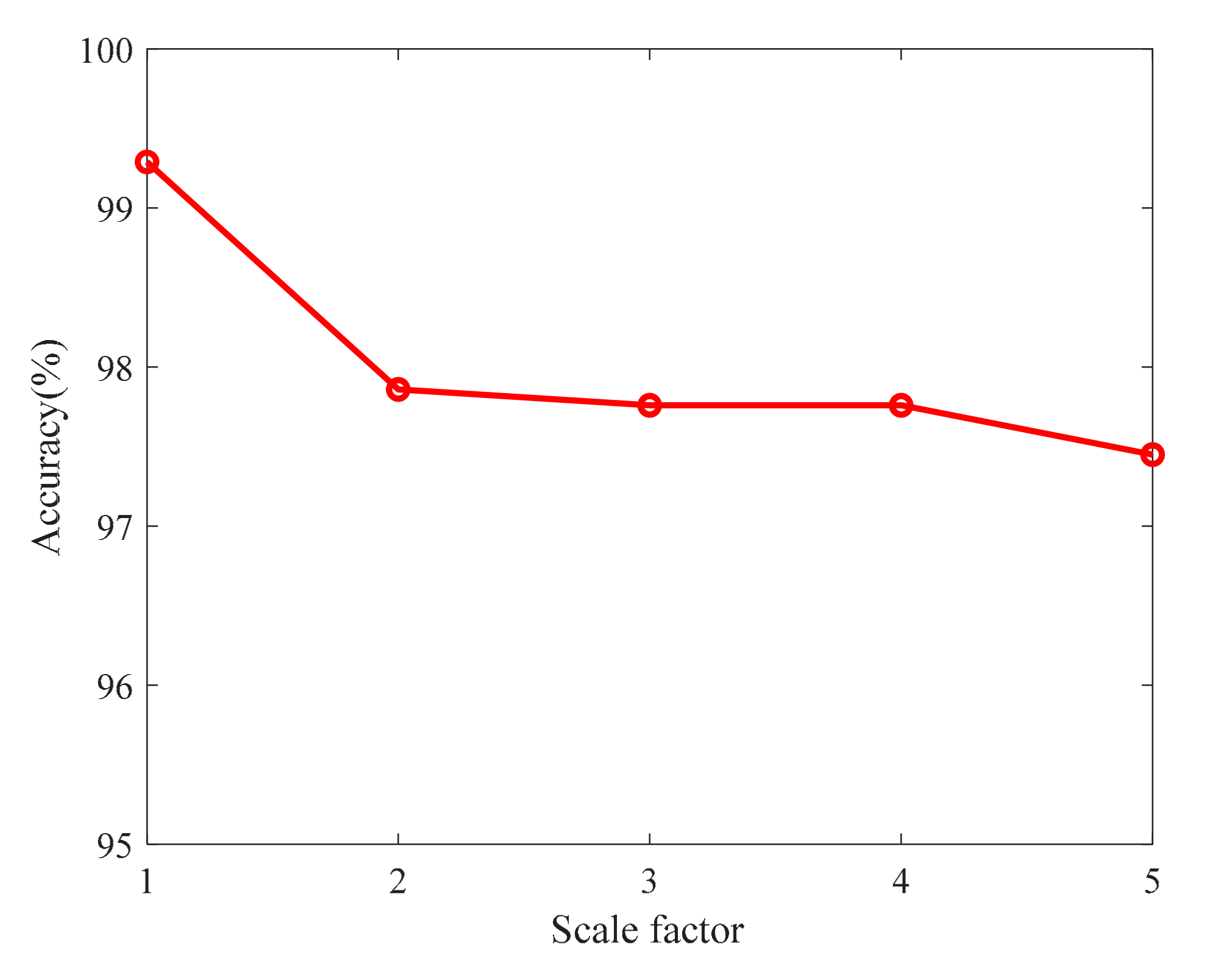
After the data preprocessing of wavelet packet decomposition, the decomposed signals were analyzed by multiscale analysis, and the BPA matrix was obtained by using the LSTM network for fault classification. The diagnostic results of WAPE at different scales are shown in
Figure 10.
It can be seen from
Figure 10 that the diagnostic accuracy of WAPE at different scales is above 97%, and the maximum can reach 99.29%. As the scale increases, the accuracy decreases. The classification BPA of WAPE at different scales is used as the evidence body for DS evidence fusion. Assuming that the fuzzy uncertainty satisfies zero, the evidence is fused according to the formula. From scale 1 to scale 5, the two pairs are fused, and the classification accuracy after fusion is shown in
Table 3.
It can be seen that the classification accuracy of any scale of fusion was improved by more than 99.5%, up to 100%. In order to better display the fusion process of DS evidence fusion theory, two misclassified data in scale 3 and scale 4 are listed below. If the confidence of the actual label is less than that of the predicted label, it means that the data are misclassified, and vice versa. In
Table 4,
Table 5 and
Table 6, the datum NO. 1 is misclassified at s = 3, the datum NO. 2 is misclassified at s = 4, and the datum NO. 3 is misclassified at both scales.
After DS evidence fusion, the misclassified data are classified to the correct label, and the diagnostic accuracy is up to 100%. Therefore, the results show that DS evidence fusion makes use of fault information at different scales, and multiscale WAPE is more effective in feature extraction of fault signals than single-scale WAPE. Finally, the accuracy of fault classification is improved, and the deficiency of random initialization and training randomness in neural network algorithms is also compensated.
Feature extraction and classifiers are two key points of traditional fault diagnosis methods, and have great influence on the final diagnosis results. In order to further verify the performance of the proposed fault diagnosis method, the feature extraction methods used for comparison were fast Fourier transform (FFT), wavelet packet decomposition (WPD), and principal component analysis (PCA). The classifiers used for comparison included a BP neural network, support vector machine (SVM), and extreme learning machine (ELM). The comparison results are shown in
Table 7.
The results show that the proposed method has higher accuracy and faster time than other comparison methods.
In addition, in order to verify the effectiveness of the proposed method under certain double-IGBT open-circuit faults and single-IGBT short-circuit faults in SMs, the fault types studied are shown in
Table 8.
According to the above table, the voltage signals of the MMC under the same SM double-IGBT open-circuit fault and SM single-IGBT short-circuit fault are collected. The expanded dataset includes the output voltages of 24 double-IGBT open-circuit faults and 16 single-IGBT short-circuit faults. The composition of each voltage time series is the same as that of the single-IGBT open-circuit faults, and it is randomly assigned to the training set and test set for model training and testing. According to the results of the above discussion, the proposed method is used to diagnose these cases, and the accuracy of both cases can still reach 100% after decision fusion.
Similarly, for double-IGBT open-circuit faults and single-IGBT short-circuit faults, the proposed method was compared with other methods, and the results are shown in
Table 9 and
Table 10, respectively.
It can be seen from the above two tables that the proposed method outperforms the other two methods in both diagnostic accuracy and time on both double-IGBT open-circuit faults and single-IGBT short-circuit faults, except that the diagnostic time for short-circuit faults in
Table 10 is slightly longer than that of the second method.
Finally, the anti-noise performance of the proposed method was further studied, and noise with different signal-to-noise ratios (SNRs) was added to the signal; the accuracy is shown in
Table 11.
The verification results show that the method still has a certain anti-noise performance for different sizes of noise.