Wind Turbine Bearing Temperature Forecasting Using a New Data-Driven Ensemble Approach
Abstract
:1. Introduction
1.1. Related Works
1.2. The Novelty of This Paper
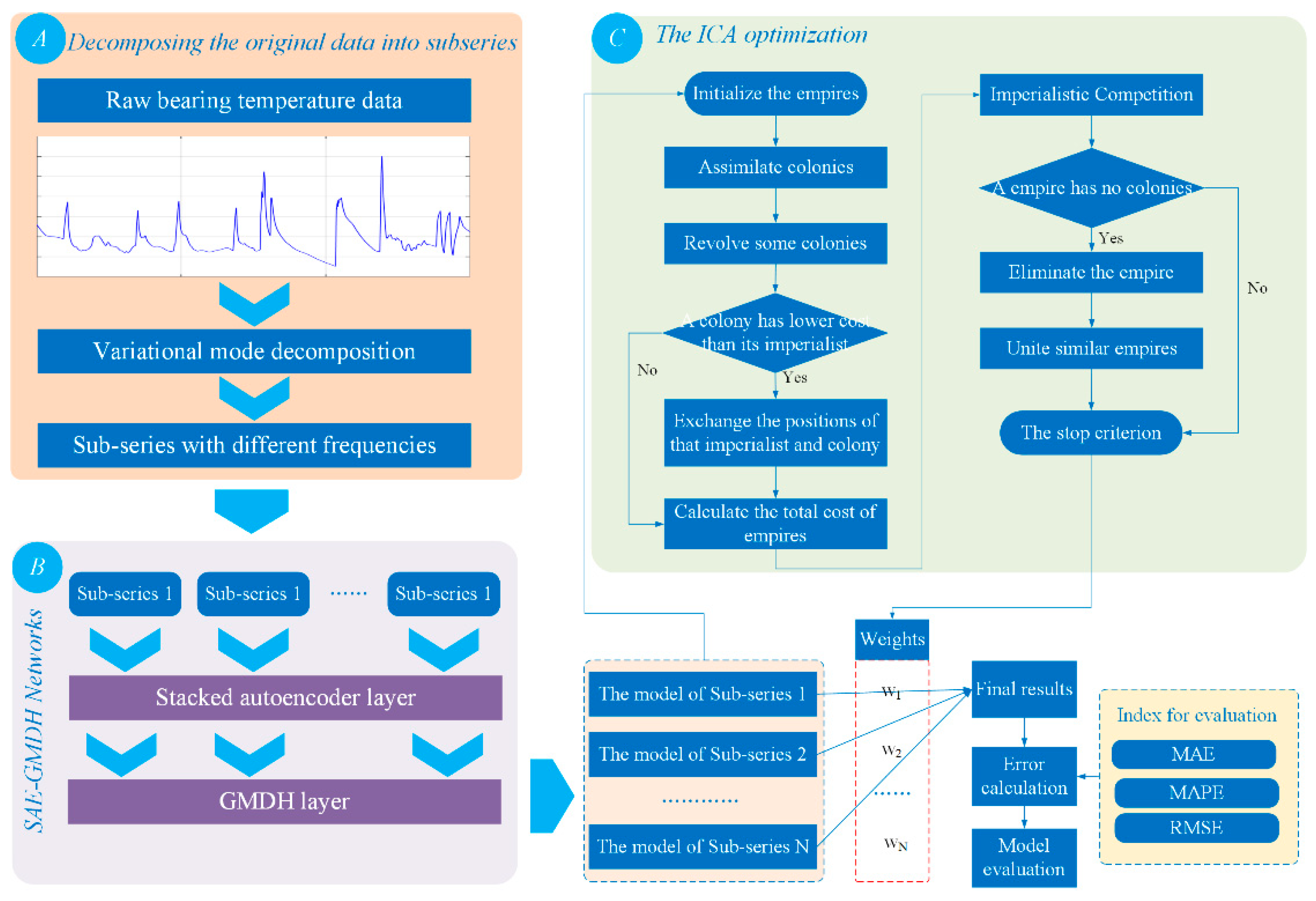
2. The Proposed Methodology
2.1. Topology Framework of the Applied Bearing Temperature Model
2.2. Variational Mode Decomposition
2.3. Stacked Autoencoder
2.4. Group Method of Data Handling
2.5. Imperialist Competitive Algorithm
3. Case Study
3.1. Description of Bearing Temperature Data
3.2. The Evaluation Indexes
3.3. Comparative Analysis with Experiments
3.3.1. Comparison and Analysis of Individual Predictors
3.3.2. Comparison and Analysis of Different Hybrid Models
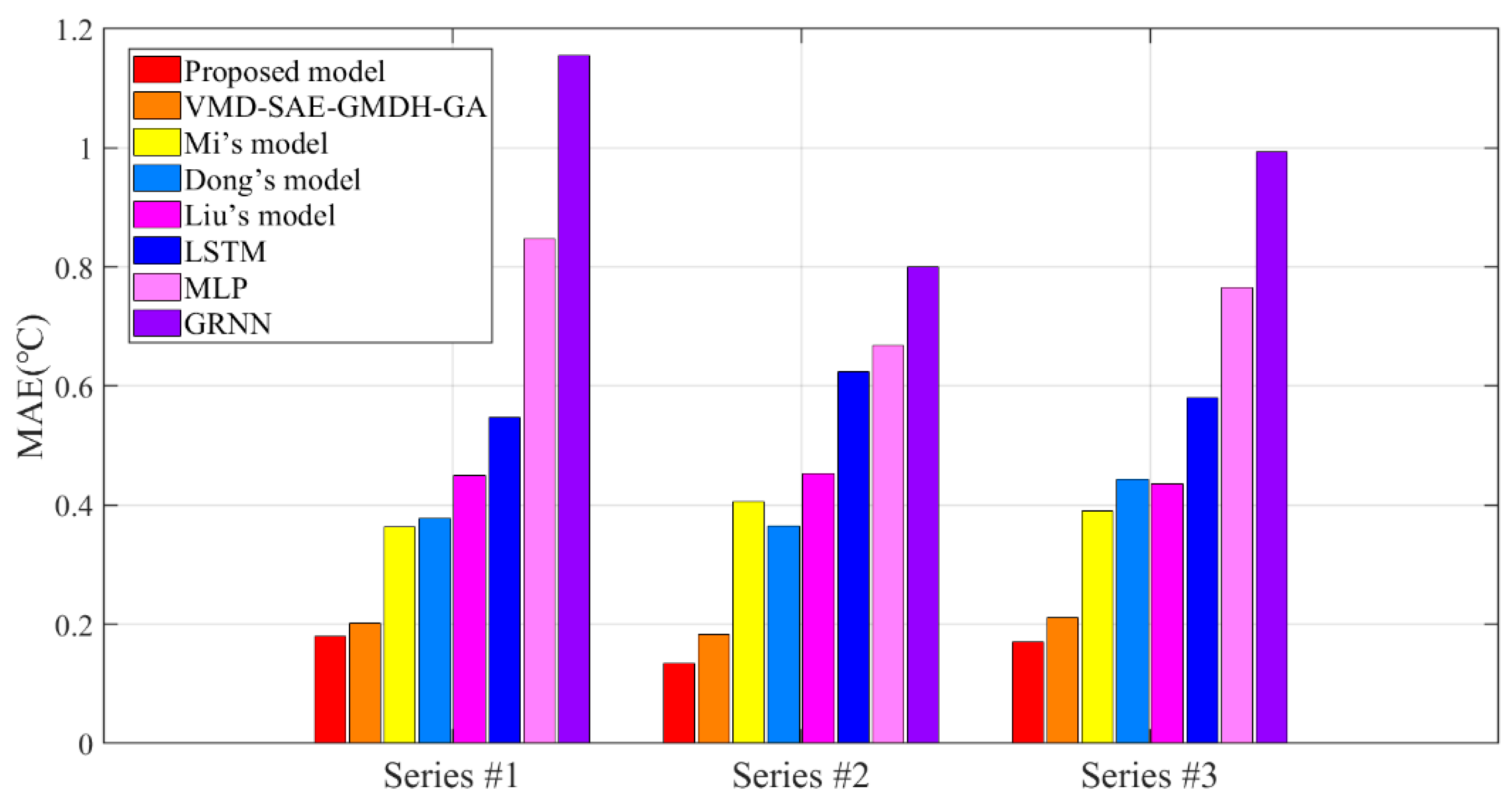
3.3.3. Comparison and Analysis of Existing Models
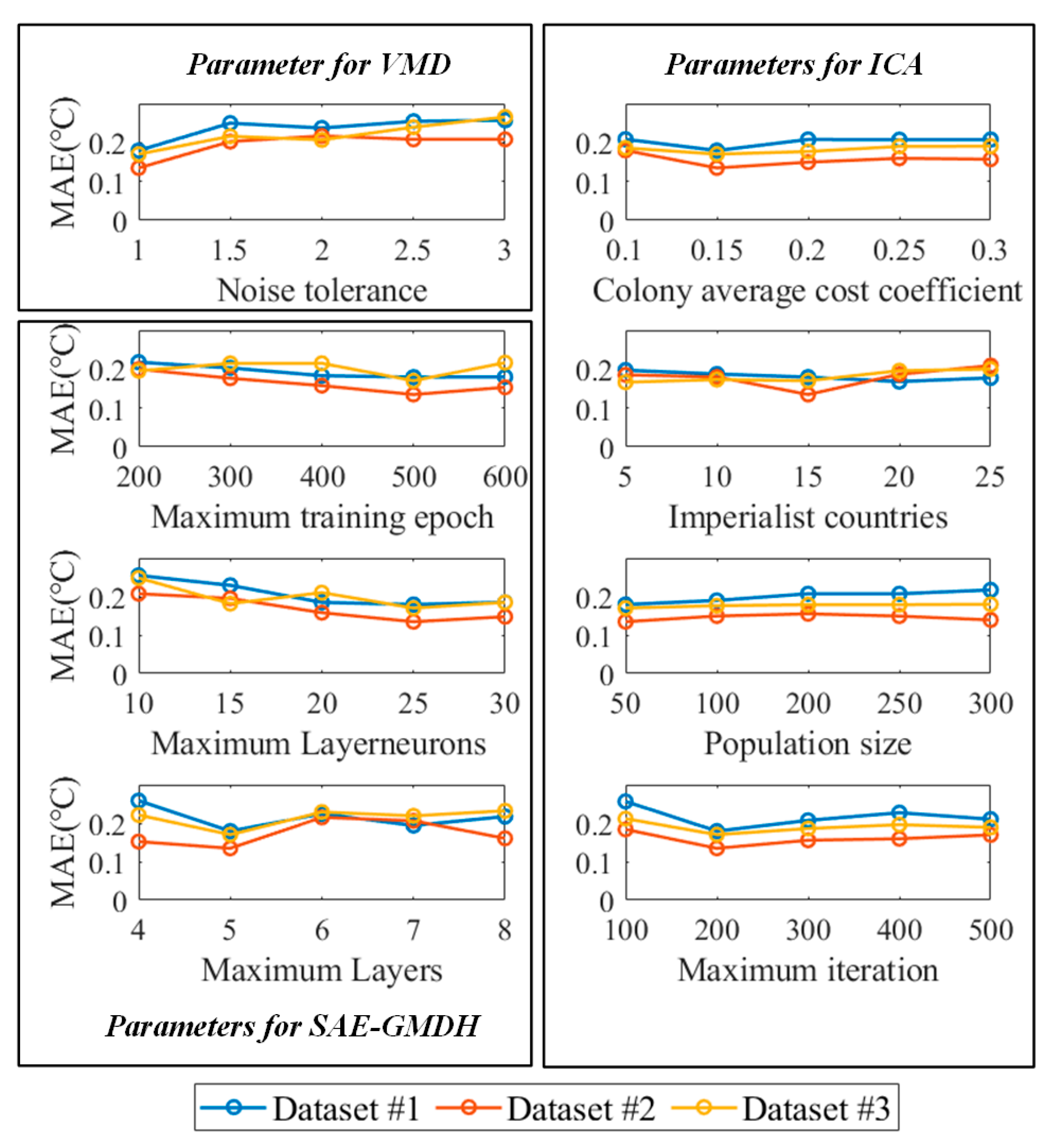
3.4. Sensitive Analysis of the Parameters and the Computational Time
4. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, D.; Wang, J.; Lin, Y.; Si, Y.; Huang, C.; Yang, J.; Huang, B.; Li, W. Present situation and future prospect of renewable energy in China. Renew. Sustain. Energy Rev. 2017, 76, 865–871. [Google Scholar] [CrossRef]
- Zhai, H.; Zhu, C.; Song, C.; Liu, H.; Bai, H. Influences of carrier assembly errors on the dynamic characteristics for wind turbine gearbox. Mech. Mach. Theory 2016, 103, 138–147. [Google Scholar] [CrossRef]
- Escaler, X.; Mebarki, T. Full-scale wind turbine vibration signature analysis. Machines 2018, 6, 63. [Google Scholar] [CrossRef] [Green Version]
- Ding, F.; Tian, Z.; Zhao, F.; Xu, H. An integrated approach for wind turbine gearbox fatigue life prediction considering instantaneously varying load conditions. Renew. Energy 2018, 129, 260–270. [Google Scholar] [CrossRef]
- Schlechtingen, M.; Santos, I.F. Comparative analysis of neural network and regression based condition monitoring approaches for wind turbine fault detection. Mech. Syst. Signal Process. 2011, 25, 1849–1875. [Google Scholar] [CrossRef] [Green Version]
- Ren, Z.; Verma, A.S.; Li, Y.; Teuwen, J.J.; Jiang, Z. Offshore wind turbine operations and maintenance: A state-of-the-art review. Renew. Sustain. Energy Rev. 2021, 144, 110886. [Google Scholar] [CrossRef]
- Yang, W.; Tavner, P.J.; Crabtree, C.J.; Wilkinson, M. Cost-effective condition monitoring for wind turbines. IEEE Trans. Ind. Electron. 2009, 57, 263–271. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Zhang, Z.; Long, H.; Xu, J.; Liu, R. Wind turbine gearbox failure identification with deep neural networks. IEEE Trans. Ind. Inform. 2016, 13, 1360–1368. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, L. A review of failure modes, condition monitoring and fault diagnosis methods for large-scale wind turbine bearings. Measurement 2020, 149, 107002. [Google Scholar] [CrossRef]
- Li, Y.; Liu, S.; Shu, L. Wind turbine fault diagnosis based on Gaussian process classifiers applied to operational data. Renew. Energy 2019, 134, 357–366. [Google Scholar] [CrossRef]
- Stetco, A.; Dinmohammadi, F.; Zhao, X.; Robu, V.; Flynn, D.; Barnes, M.; Keane, J.; Nenadic, G. Machine learning methods for wind turbine condition monitoring: A review. Renew. Energy 2019, 133, 620–635. [Google Scholar] [CrossRef]
- Manobel, B.; Sehnke, F.; Lazzús, J.A.; Salfate, I.; Felder, M.; Montecinos, S. Wind turbine power curve modeling based on Gaussian processes and artificial neural networks. Renew. Energy 2018, 125, 1015–1020. [Google Scholar] [CrossRef]
- Astolfi, D.; Scappaticci, L.; Terzi, L. Fault diagnosis of wind turbine gearboxes through temperature and vibration data. Int. J. Renew. Energy Res. 2017, 7, 965–976. [Google Scholar]
- Zaher, A.S.A.E.; McArthur, S.D.J.; Infield, D.G.; Patel, Y. Online wind turbine fault detection through automated SCADA data analysis. Wind. Energy Int. J. Prog. Appl. Wind. Power Convers. Technol. 2009, 12, 574–593. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, X. Time Series Data-Driven Online Prognosis of Wind Turbine Faults in Presence of SCADA Data Loss. IEEE Trans. Sustain. Energy 2020, 12, 1289–1300. [Google Scholar] [CrossRef]
- Liao, T.W. Clustering of time series data—A survey. Pattern Recognit. 2005, 38, 1857–1874. [Google Scholar] [CrossRef]
- Moayedi, H.; Gör, M.; Foong, L.K.; Bahiraei, M. Imperialist competitive algorithm hybridized with multilayer perceptron to predict the load-settlement of square footing on layered soils. Measurement 2021, 172, 108837. [Google Scholar] [CrossRef]
- Song, L.-K.; Fei, C.-W.; Bai, G.-C.; Yu, L.-C. Dynamic neural network method-based improved PSO and BR algorithms for transient probabilistic analysis of flexible mechanism. Adv. Eng. Inform. 2017, 33, 144–153. [Google Scholar] [CrossRef]
- Xiao, Y.; Dai, R.; Zhang, G.; Chen, W. The use of an improved LSSVM and joint normalization on temperature prediction of gearbox output shaft in DFWT. Energies 2017, 10, 1877. [Google Scholar] [CrossRef] [Green Version]
- Xiao, X.; Liu, J.; Liu, D.; Tang, Y.; Dai, J.; Zhang, F. SSAE-MLP: Stacked sparse autoencoders-based multi-layer perceptron for main bearing temperature prediction of large-scale wind turbines. Concurr. Comput. Pract. Exp. 2021, e6315. [Google Scholar] [CrossRef]
- Abdusamad, K.B.; Gao, D.W.; Muljadi, E. A condition monitoring system for wind turbine generator temperature by applying multiple linear regression model. In Proceedings of the 2013 North American Power Symposium (NAPS 2013), Manhattan, KS, USA, 22–24 September 2013; pp. 1–8. [Google Scholar]
- Chen, S.; Ma, Y.; Ma, L.; Qiao, F.; Yang, H. Early warning of abnormal state of wind turbine based on principal component analysis and RBF neural network. In Proceedings of the 2021 6th Asia Conference on Power and Electrical Engineering (ACPEE), Chongqing, China, 8–11 April 2021; pp. 547–551. [Google Scholar]
- Fu, J.; Chu, J.; Guo, P.; Chen, Z. Condition monitoring of wind turbine gearbox bearing based on deep learning model. IEEE Access 2019, 7, 57078–57087. [Google Scholar] [CrossRef]
- Lu, L.; He, Y.; Ruan, Y.; Yuan, W. Wind turbine planetary gearbox condition monitoring method based on wireless sensor and deep learning approach. IEEE Trans. Instrum. Meas. 2020, 70, 1–16. [Google Scholar] [CrossRef]
- Wang, S.; Chen, J.; Wang, H.; Zhang, D. Degradation evaluation of slewing bearing using HMM and improved GRU. Measurement 2019, 146, 385–395. [Google Scholar] [CrossRef]
- Heydari, A.; Garcia, D.A.; Fekih, A.; Keynia, F.; Tjernberg, L.B.; De Santoli, L. A Hybrid Intelligent Model for the Condition Monitoring and Diagnostics of Wind Turbines Gearbox. IEEE Access 2021, 9, 89878–89890. [Google Scholar] [CrossRef]
- Yu, C.; Li, Y.; Xiang, H.; Zhang, M. Data mining-assisted short-term wind speed forecasting by wavelet packet decomposition and Elman neural network. J. Wind. Eng. Ind. Aerodyn. 2018, 175, 136–143. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, N.; Wu, L.; Wang, Y. Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method. Renew. Energy 2016, 94, 629–636. [Google Scholar] [CrossRef]
- Gendeel, M.; Zhang, Y.; Qian, X.; Xing, Z. Deterministic and probabilistic interval prediction for wind farm based on VMD and weighted LS-SVM. Energy Sources Part A Recovery Util. Environ. Eff. 2021, 43, 800–814. [Google Scholar] [CrossRef]
- Khan, M.; Liu, T.; Ullah, F. A new hybrid approach to forecast wind power for large scale wind turbine data using deep learning with TensorFlow framework and principal component analysis. Energies 2019, 12, 2229. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.; Niu, D.; Hong, W.-C. Short term load forecasting based on feature extraction and improved general regression neural network model. Energy 2019, 166, 653–663. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y. Study on environment-concerned short-term load forecasting model for wind power based on feature extraction and tree regression. J. Clean. Prod. 2020, 264, 121505. [Google Scholar] [CrossRef]
- Jaseena, K.; Kovoor, B.C. A hybrid wind speed forecasting model using stacked autoencoder and LSTM. J. Renew. Sustain. Energy 2020, 12, 023302. [Google Scholar] [CrossRef] [Green Version]
- Nie, Y.; Jiang, P.; Zhang, H. A novel hybrid model based on combined preprocessing method and advanced optimization algorithm for power load forecasting. Appl. Soft Comput. 2020, 97, 106809. [Google Scholar] [CrossRef]
- Zhang, W.; Maleki, A.; Rosen, M.A. A heuristic-based approach for optimizing a small independent solar and wind hybrid power scheme incorporating load forecasting. J. Clean. Prod. 2019, 241, 117920. [Google Scholar] [CrossRef]
- Wen, X. Modeling and performance evaluation of wind turbine based on ant colony optimization-extreme learning machine. Appl. Soft Comput. 2020, 94, 106476. [Google Scholar] [CrossRef]
- Li, Y.; Yang, F.; Zha, W.; Yan, L. Combined Optimization Prediction Model of Regional Wind Power Based on Convolution Neural Network and Similar Days. Machines 2020, 8, 80. [Google Scholar] [CrossRef]
- Yin, Z.; Gao, Q. A novel imperialist competitive algorithm for scheme configuration rules mining of product service system. Arab. J. Sci. Eng. 2020, 45, 3157–3169. [Google Scholar] [CrossRef]
- Afradi, A.; Ebrahimabadi, A. Prediction of TBM penetration rate using the imperialist competitive algorithm (ICA) and quantum fuzzy logic. Innov. Infrastruct. Solut. 2021, 6, 1–17. [Google Scholar] [CrossRef]
- Jaafari, A.; Zenner, E.K.; Panahi, M.; Shahabi, H. Hybrid artificial intelligence models based on a neuro-fuzzy system and metaheuristic optimization algorithms for spatial prediction of wildfire probability. Agric. For. Meteorol. 2019, 266, 198–207. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Jayakumar, C.; Sangeetha, J. Kernellized support vector regressive machine based variational mode decomposition for time frequency analysis of Mirnov coil. Microprocess. Microsyst. 2020, 75, 103036. [Google Scholar] [CrossRef]
- Brzostowski, K.; Światek, J. Dictionary adaptation and variational mode decomposition for gyroscope signal enhancement. Appl. Intell. 2021, 51, 2312–2330. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, P.; Yin, X. A quadratic penalty item optimal variational mode decomposition method based on single-objective salp swarm algorithm. Mech. Syst. Signal Process. 2020, 138, 106567. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, G.; Li, M.; Yin, H. Variational mode decomposition denoising combined the detrended fluctuation analysis. Signal Process. 2016, 125, 349–364. [Google Scholar] [CrossRef]
- Zabalza, J.; Ren, J.; Zheng, J.; Zhao, H.; Qing, C.; Yang, Z.; Du, P.; Marshall, S. Novel segmented stacked autoencoder for effective dimensionality reduction and feature extraction in hyperspectral imaging. Neurocomputing 2016, 185, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Adem, K.; Kiliçarslan, S.; Cömert, O. Classification and diagnosis of cervical cancer with stacked autoencoder and softmax classification. Expert Syst. Appl. 2019, 115, 557–564. [Google Scholar] [CrossRef]
- Mo, L.; Xie, L.; Jiang, X.; Teng, G.; Xu, L.; Xiao, J. GMDH-based hybrid model for container throughput forecasting: Selective combination forecasting in nonlinear subseries. Appl. Soft Comput. 2018, 62, 478–490. [Google Scholar] [CrossRef]
- Kim, D.; Seo, S.-J.; Park, G.-T. Hybrid GMDH-type modeling for nonlinear systems: Synergism to intelligent identification. Adv. Eng. Softw. 2009, 40, 1087–1094. [Google Scholar] [CrossRef]
- Hwang, H.S. Fuzzy GMDH-type neural network model and its application to forecasting of mobile communication. Comput. Ind. Eng. 2006, 50, 450–457. [Google Scholar] [CrossRef]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4661–4667. [Google Scholar]
- Geetha Devasena, M.; Gopu, G.; Valarmathi, M. Automated and optimized software test suite generation technique for structural testing. Int. J. Softw. Eng. Knowl. Eng. 2016, 26, 1–13. [Google Scholar] [CrossRef]
- Khanali, M.; Akram, A.; Behzadi, J.; Mostashari-Rad, F.; Saber, Z.; Chau, K.-W.; Nabavi-Pelesaraei, A. Multi-objective optimization of energy use and environmental emissions for walnut production using imperialist competitive algorithm. Appl. Energy 2021, 284, 116342. [Google Scholar] [CrossRef]
- Gordan, M.; Razak, H.A.; Ismail, Z.; Ghaedi, K. Data mining based damage identification using imperialist competitive algorithm and artificial neural network. Lat. Am. J. Solids Struct. 2018, 15. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Hoang, N.-D.; Pham, B.T.; Bui, Q.-T.; Tran, C.-T.; Panahi, M.; Bin Ahmad, B. A novel integrated approach of relevance vector machine optimized by imperialist competitive algorithm for spatial modeling of shallow landslides. Remote Sens. 2018, 10, 1538. [Google Scholar] [CrossRef] [Green Version]
- Dao, P.B.; Staszewski, W.J.; Barszcz, T.; Uhl, T. Condition monitoring and fault detection in wind turbines based on cointegration analysis of SCADA data. Renew. Energy 2018, 116, 107–122. [Google Scholar] [CrossRef]
- Astolfi, D. Perspectives on SCADA Data Analysis Methods for Multivariate Wind Turbine Power Curve Modeling. Machines 2021, 9, 100. [Google Scholar] [CrossRef]
- Mi, X.; Zhao, S. Wind speed prediction based on singular spectrum analysis and neural network structural learning. Energy Convers. Manag. 2020, 216, 112956. [Google Scholar] [CrossRef]
- Dong, S.; Yu, C.; Yan, G.; Zhu, J.; Hu, H. A Novel Ensemble Reinforcement Learning Gated Recursive Network for Traffic Speed Forecasting. In Proceedings of the 2021 Workshop on Algorithm and Big Data, Fuzhou, China, 12–14 March 2021; pp. 55–60. [Google Scholar]
- Liu, X.; Qin, M.; He, Y.; Mi, X.; Yu, C. A new multi-data-driven spatiotemporal PM2. 5 forecasting model based on an ensemble graph reinforcement learning convolutional network. Atmos. Pollut. Res. 2021, 12, 101197. [Google Scholar] [CrossRef]
- Bangalore, P.; Patriksson, M. Analysis of SCADA data for early fault detection, with application to the maintenance management of wind turbines. Renew. Energy 2018, 115, 521–532. [Google Scholar] [CrossRef]
- Zhang, J.; Kang, J.; Sun, L.; Bai, X. Risk assessment of floating offshore wind turbines based on fuzzy fault tree analysis. Ocean. Eng. 2021, 239, 109859. [Google Scholar] [CrossRef]
- Bilal, B.; Adjallah, K.H.; Sava, A. Data-Driven Fault Detection and Identification in Wind Turbines Through Performance Assessment. In Proceedings of the 2019 10th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Metz, France, 18–21 September 2019; pp. 123–129. [Google Scholar]





| Bearing Temperature Time Series Temperature Time Series | #1 | #2 | #3 |
|---|---|---|---|
| Data resolution (min) | 10 | 10 | 10 |
| Minimum (°C) | 15.3 | 23.6 | 29.6 |
| Mean (°C) | 28.2761 | 32.8573 | 43.1788 |
| Maximum (°C) | 70.1 | 51.8 | 59 |
| Standard derivation | 7.3962 | 5.6234 | 6.3141 |
| Series | Forecasting Models | MAE (°C) | MAPE (%) | RMSE (°C) |
|---|---|---|---|---|
| #1 | GMDH | 0.3629 | 1.1417 | 0.6289 |
| GRU | 0.4678 | 1.2388 | 0.6175 | |
| LSTM | 0.5475 | 1.0563 | 0.7308 | |
| DBN | 0.5794 | 1.5643 | 0.6396 | |
| ENN | 0.6706 | 1.6121 | 0.7831 | |
| ELM | 2.0374 | 3.6405 | 2.9887 | |
| GRNN | 1.1551 | 2.1820 | 1.6379 | |
| MLP | 0.8472 | 1.8956 | 0.9860 | |
| RBFNN | 0.7100 | 1.8539 | 0.9478 | |
| #2 | GMDH | 0.5465 | 0.7063 | 0.4372 |
| GRU | 0.6053 | 0.7378 | 0.5128 | |
| LSTM | 0.6238 | 0.9128 | 0.7628 | |
| DBN | 0.5925 | 0.8290 | 0.5931 | |
| ENN | 0.6286 | 0.8070 | 0.6585 | |
| ELM | 0.8254 | 1.9352 | 0.8224 | |
| GRNN | 0.8002 | 1.2322 | 1.0628 | |
| MLP | 0.6684 | 1.0518 | 0.8478 | |
| RBFNN | 0.5672 | 0.8109 | 0.7466 | |
| #3 | GMDH | 0.5210 | 0.9591 | 0.7920 |
| GRU | 0.6435 | 0.9841 | 0.9429 | |
| LSTM | 0.5798 | 1.2769 | 1.1923 | |
| DBN | 0.5563 | 1.0056 | 0.8681 | |
| ENN | 0.7350 | 1.1608 | 1.0105 | |
| ELM | 0.8348 | 1.4873 | 1.2613 | |
| GRNN | 0.9941 | 2.0563 | 1.4930 | |
| MLP | 0.7663 | 1.4343 | 1.3829 | |
| RBFNN | 0.6198 | 1.2269 | 0.9243 |
| Method | Indexes | Series #1 | Series #2 | Series #3 |
|---|---|---|---|---|
| VMD-SAE-GMDH vs. VMD-GMDH | PMAE (%) | 11.4276 | 17.1861 | 23.1070 |
| PMAPE (%) | 18.5000 | 13.4679 | 17.3433 | |
| PRMSE (%) | 24.7714 | 29.2410 | 19.6399 | |
| SAE-GMDH vs. GMDH | PMAE (%) | 21.6864 | 25.4163 | 20.3223 |
| PMAPE (%) | 39.4149 | 21.9519 | 26.8168 | |
| PRMSE (%) | 31.2768 | 13.1976 | 25.1736 |
| Method | Indexes | Series #1 | Series #2 | Series #3 |
|---|---|---|---|---|
| VMD-SAE-GMDH-ICA vs. VMD-SAE-GMDH-GA | PMAE (%) | 11.1001 | 26.1251 | 19.5364 |
| PMAPE (%) | 6.0493 | 11.7997 | 13.5180 | |
| PRMSE (%) | 21.6826 | 32.4309 | 13.2560 | |
| VMD-SAE-GMDH-ICA vs. VMD-SAE-GMDH | PMAE (%) | 30.4921 | 54.3574 | 38.1904 |
| PMAPE (%) | 13.5825 | 19.3928 | 25.5384 | |
| PRMSE (%) | 28.8642 | 49.8718 | 52.1262 |
| Series | Forecasting Models | MAE (°C) | MAPE (%) | RMSE (°C) |
|---|---|---|---|---|
| #1 | GMDH | 0.3629 | 1.1417 | 0.6289 |
| EMD-GMDH | 0.3004 | 1.0202 | 0.5077 | |
| EEMD-GMDH | 0.2958 | 1.0041 | 0.4179 | |
| VMD-GMDH | 0.2914 | 0.8600 | 0.3827 | |
| SAE-GMDH | 0.2842 | 0.6917 | 0.4322 | |
| VMD-SAE-GMDH | 0.2581 | 0.7009 | 0.2879 | |
| VMD-SAE-GMDH-GA | 0.2018 | 0.6447 | 0.2615 | |
| VMD-SAE-GMDH-ICA | 0.1794 | 0.6057 | 0.2048 | |
| #2 | GMDH | 0.5465 | 0.7070 | 0.4372 |
| EMD-GMDH | 0.4884 | 0.6699 | 0.4088 | |
| EEMD-GMDH | 0.4023 | 0.5655 | 0.3577 | |
| VMD-GMDH | 0.3561 | 0.5101 | 0.3307 | |
| SAE-GMDH | 0.4076 | 0.5518 | 0.3795 | |
| VMD-SAE-GMDH | 0.2949 | 0.4414 | 0.2340 | |
| VMD-SAE-GMDH-GA | 0.1822 | 0.4034 | 0.1736 | |
| VMD-SAE-GMDH-ICA | 0.1346 | 0.3558 | 0.1173 | |
| #3 | GMDH | 0.5211 | 0.9591 | 0.7921 |
| EMD-GMDH | 0.4555 | 0.8899 | 0.7637 | |
| EEMD-GMDH | 0.3831 | 0.8617 | 0.6047 | |
| VMD-GMDH | 0.3579 | 0.6798 | 0.5443 | |
| SAE-GMDH | 0.4152 | 0.7019 | 0.5927 | |
| VMD-SAE-GMDH | 0.2752 | 0.5619 | 0.4374 | |
| VMD-SAE-GMDH-GA | 0.2114 | 0.4838 | 0.2414 | |
| VMD-SAE-GMDH-ICA | 0.1701 | 0.4184 | 0.2094 |
| Method | Indexes | Series #1 | Series #2 | Series #3 |
| EMD-GMDH vs. GMDH | PMAE (%) | 17.2223 | 10.6313 | 12.5887 |
| PMAPE (%) | 10.6420 | 5.2475 | 7.2151 | |
| PRMSE (%) | 19.2717 | 6.4959 | 3.5854 | |
| EEMD-GMDH vs. GMDH | PMAE (%) | 18.4900 | 26.3861 | 26.4824 |
| PMAPE (%) | 12.0259 | 20.0141 | 10.1553 | |
| PRMSE (%) | 33.5506 | 18.1839 | 23.6586 | |
| VMD-GMDH vs. GMDH | PMAE (%) | 19.7023 | 34.8398 | 31.3184 |
| PMAPE (%) | 24.6475 | 27.8501 | 29.1211 | |
| PRMSE (%) | 29.1477 | 24.3596 | 43.9086 |
| Parameters | Value |
|---|---|
| Noise tolerance | 1 |
| Maximum training epoch | 500 |
| Maximum Layerneurons | 25 |
| Maximum Layers | 5 |
| Colony average cost coefficient | 0.2 |
| Imperialist countries | 10 |
| Population size | 50 |
| Maximum iteration | 200 |
| Algorithms | Computational Time |
|---|---|
| VMD | 7.823 s |
| SAE-GMDH | 155.794 s |
| ICA | 118.526 s |
| Total | 282.143 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, G.; Yu, C.; Bai, Y. Wind Turbine Bearing Temperature Forecasting Using a New Data-Driven Ensemble Approach. Machines 2021, 9, 248. https://doi.org/10.3390/machines9110248
Yan G, Yu C, Bai Y. Wind Turbine Bearing Temperature Forecasting Using a New Data-Driven Ensemble Approach. Machines. 2021; 9(11):248. https://doi.org/10.3390/machines9110248
Chicago/Turabian StyleYan, Guangxi, Chengqing Yu, and Yu Bai. 2021. "Wind Turbine Bearing Temperature Forecasting Using a New Data-Driven Ensemble Approach" Machines 9, no. 11: 248. https://doi.org/10.3390/machines9110248
APA StyleYan, G., Yu, C., & Bai, Y. (2021). Wind Turbine Bearing Temperature Forecasting Using a New Data-Driven Ensemble Approach. Machines, 9(11), 248. https://doi.org/10.3390/machines9110248






