Data-Driven Intelligent 3D Surface Measurement in Smart Manufacturing: Review and Outlook
Abstract
1. Introduction
- (1)
- To help industry practitioners choose the most appropriate measurement system and data-driven methods for enhancing the cost-effectiveness of surface measurement;
- (2)
- To identity the key gaps between academic research and industrial practice; and
- (3)
- To determine the critical research gaps and suggest future research directions.
2. 3D Surface Measurement Techniques
2.1. Measurement Instrument
2.1.1. CMM
2.1.2. AFM
2.1.3. CLM
2.1.4. LHI
2.1.5. SLS
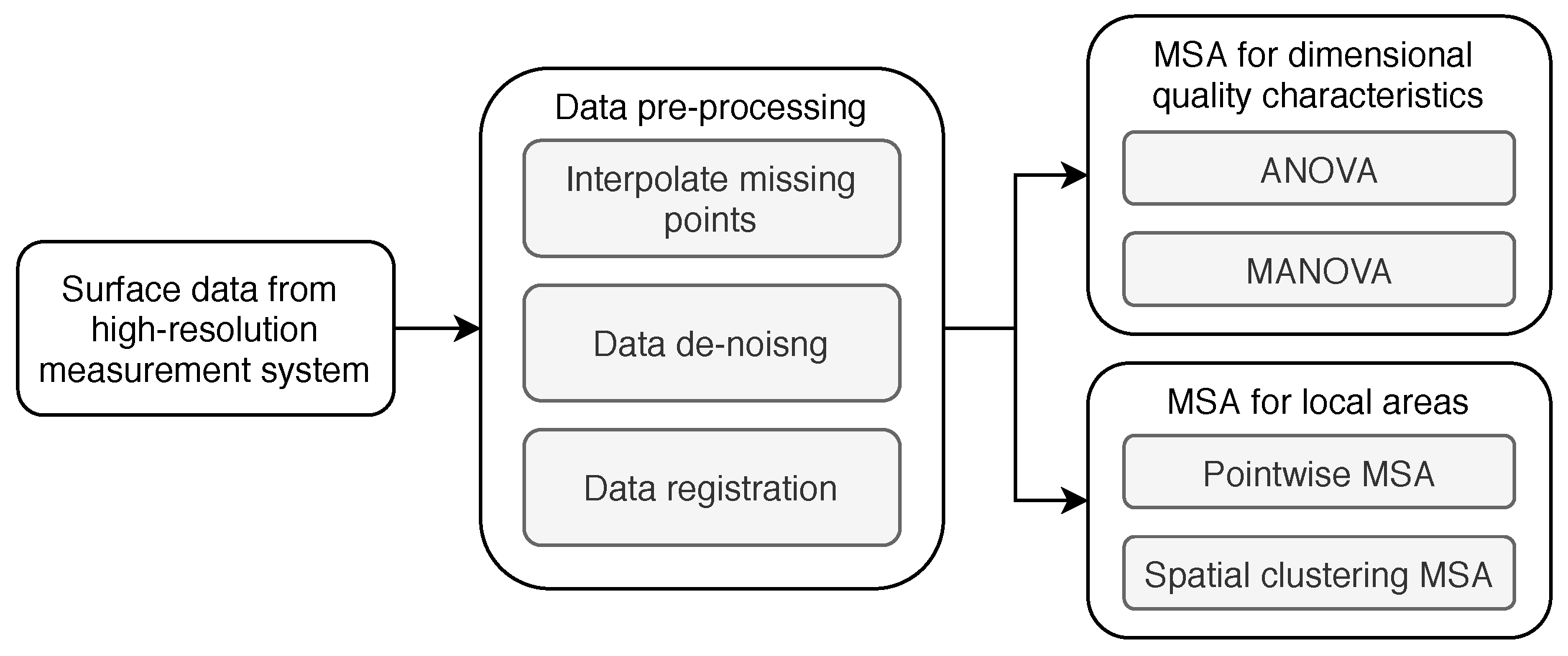
2.2. MSA
3. Interpolation Method
3.1. Classification Framework
3.2. Spatial-Only Methods for Continuous Variation
3.2.1. Sampling or Approximation in Certain Class of Functions
In Shift-Invariant Space: Sampling Theory
In RKHS: Regression with L2 Regularization and RBF Interpolation
Other Methods for Approximation or Curve Fitting
3.2.2. Inference about Spatial Stochastic Fields
3.2.3. Other Methods for Spatial Interpolation
Mesh-Based Methods
- (1)
- Voronoi tessellation: nearest-neighbor interpolation and natural neighbor [77] interpolation.
- (2)
- Triangular tessellation: triangular mesh is usually generated based on Delaunay triangulation. Within each triangular cell, linear (or piecewise cubic) function is selected to meet the interpolant constraint (and smoothness constraints) [76].
- (3)
- Rectangular grid: methods that rely on rectangular grid could actually fit into the previous types, including sampling theories and B-spline related methods, thus not to be repeated here.
Local Regression Methods
3.2.4. Relationships between Aforementioned Spatial-Only Methods
Connection between Kriging, GPR and RKHS Regression Methods
Effect of Aliasing and Low-Pass Filtering for Linear Interpolation Methods
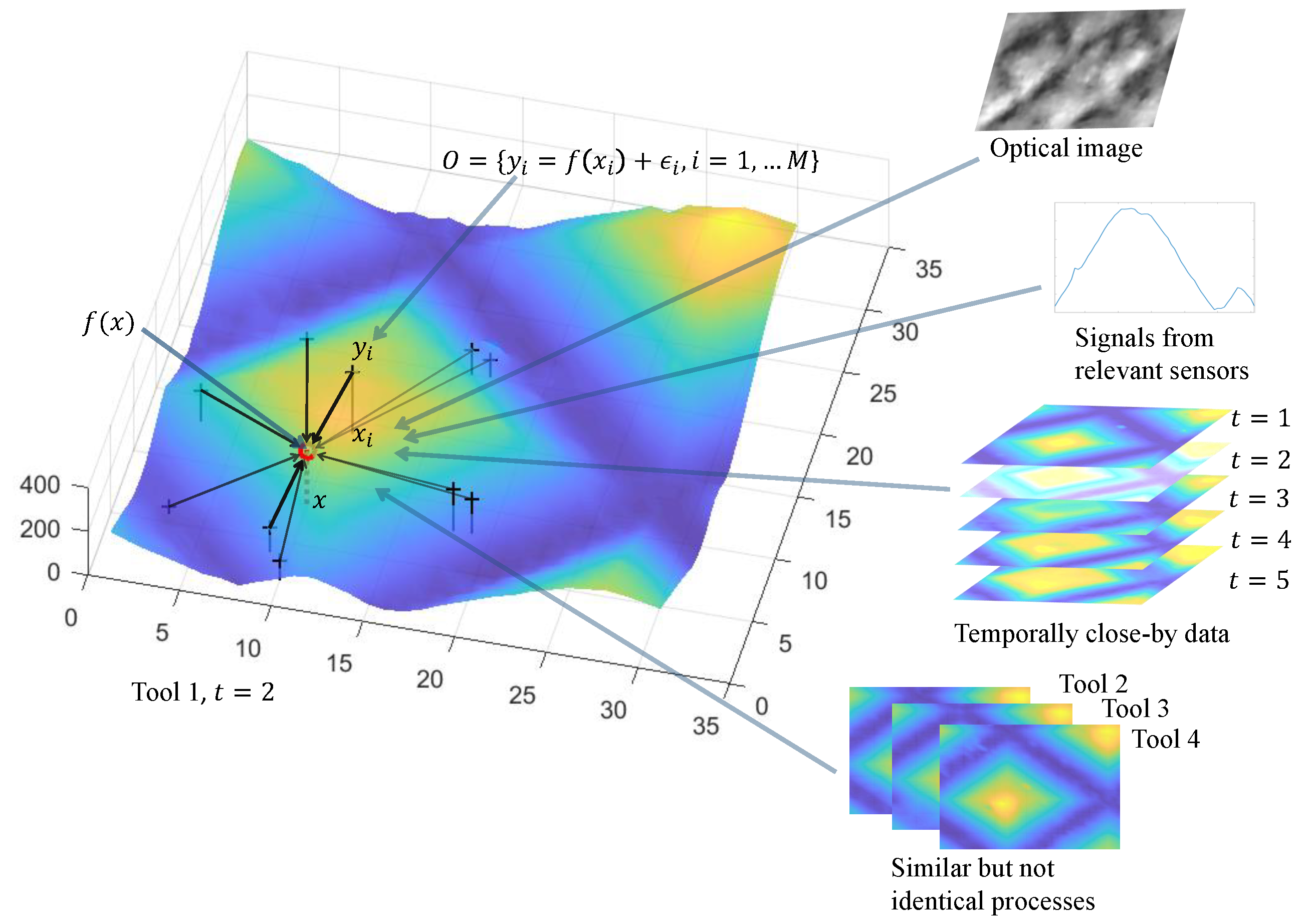
3.3. Data Fusion-Based Interpolation for Continuous Variation
3.3.1. Interpolation with Multiple Explanatory Variables
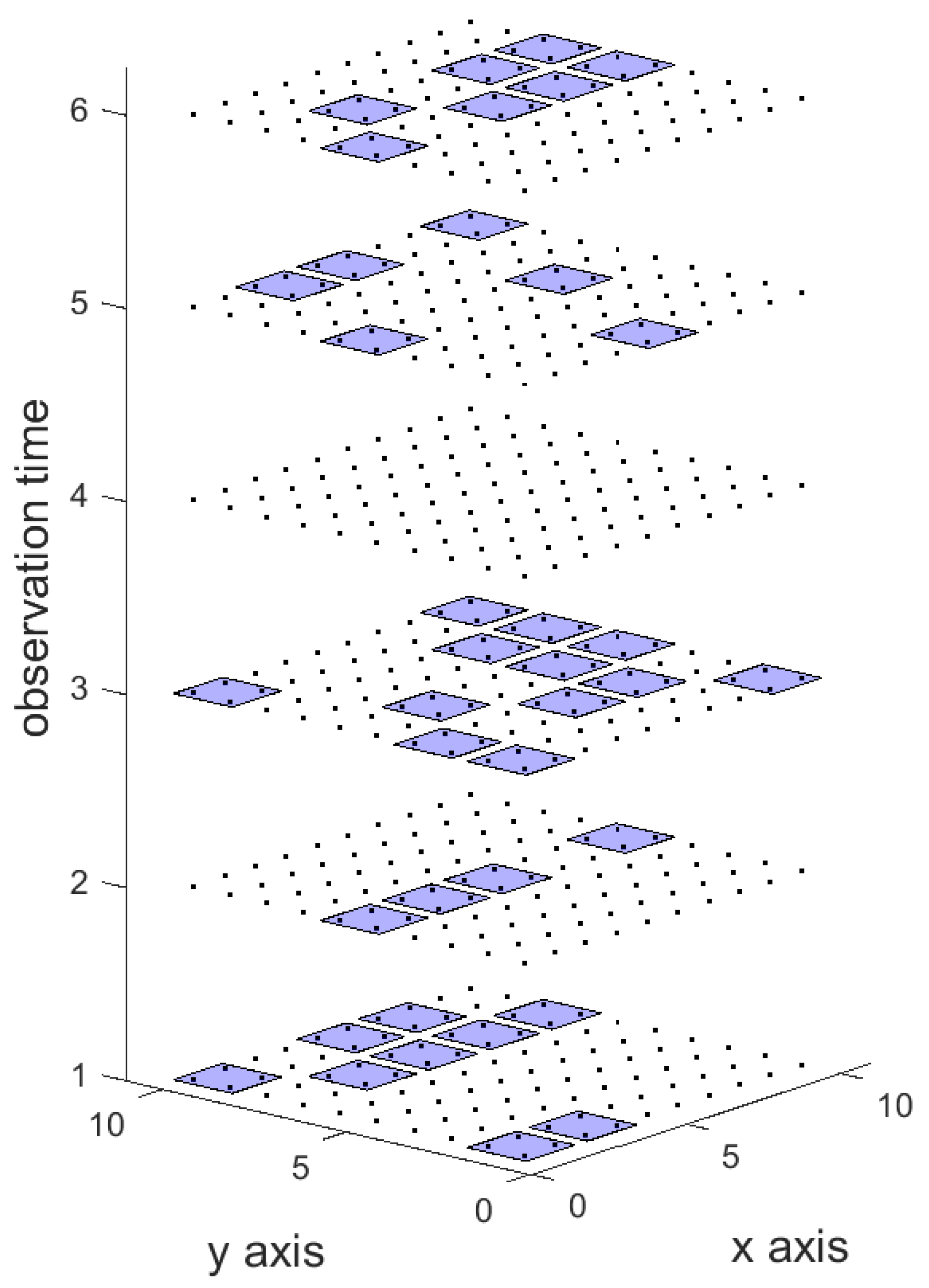
3.3.2. Spatiotemporal Interpolation
3.3.3. Fusing Measurements from Different Instruments
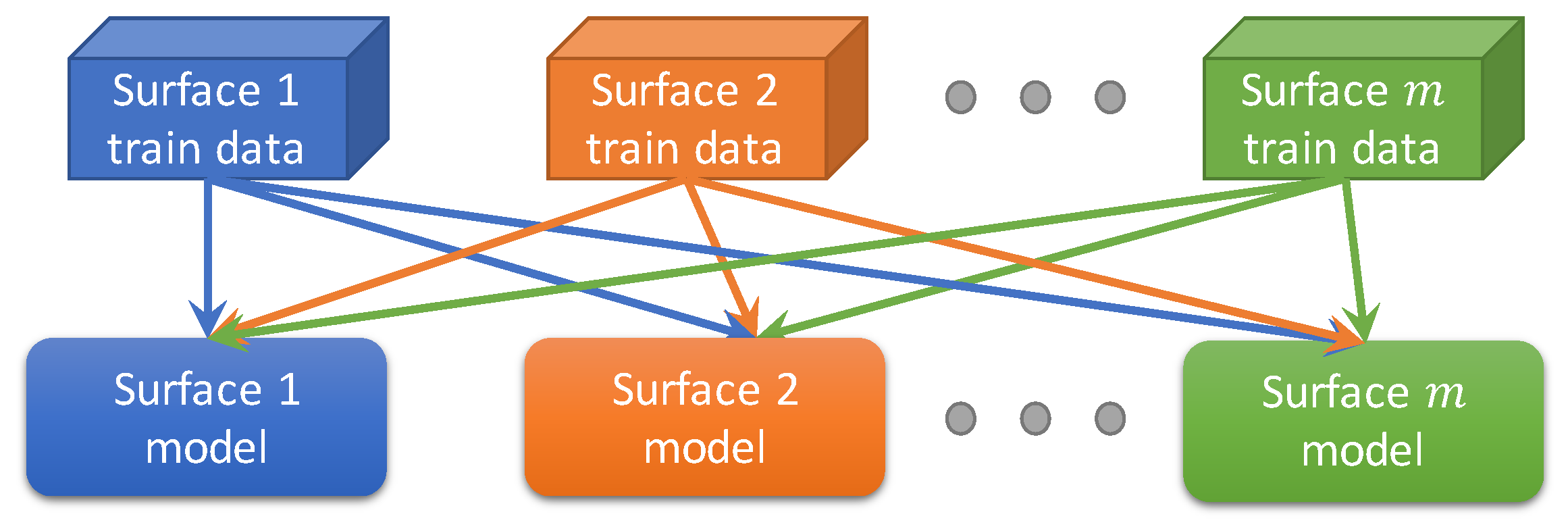
3.3.4. Multi-Task Learning
3.4. Interpolation Methods for Discrete Variation
3.4.1. Inference with Discrete Spatial Processes
3.4.2. Compressed Sensing
3.4.3. Image Super-Resolution
3.4.4. Comments on Discrete Methods
3.5. Surface Interpolation in Manufacturing
4. Sampling Design
4.1. Model-Free Sampling Design
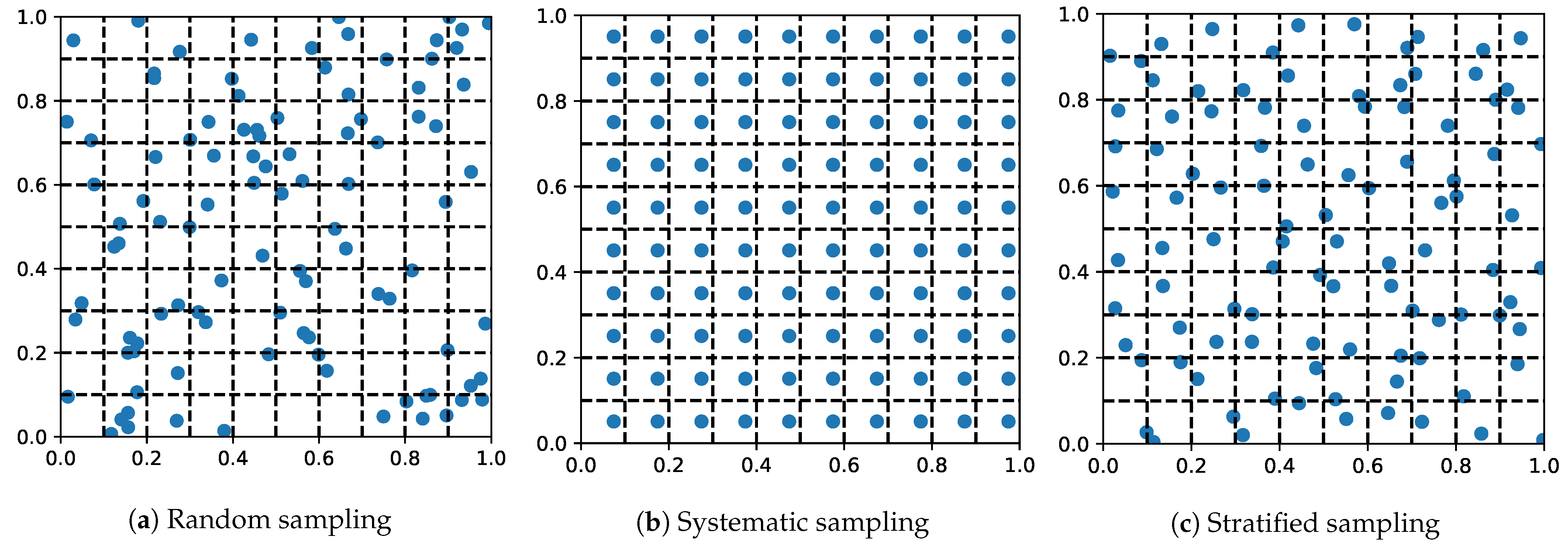
4.1.1. Random Sampling
4.1.2. Systematic Sampling
4.1.3. Stratified Sampling
4.1.4. Two-Stage Sampling
4.2. Model-Based Sampling Design
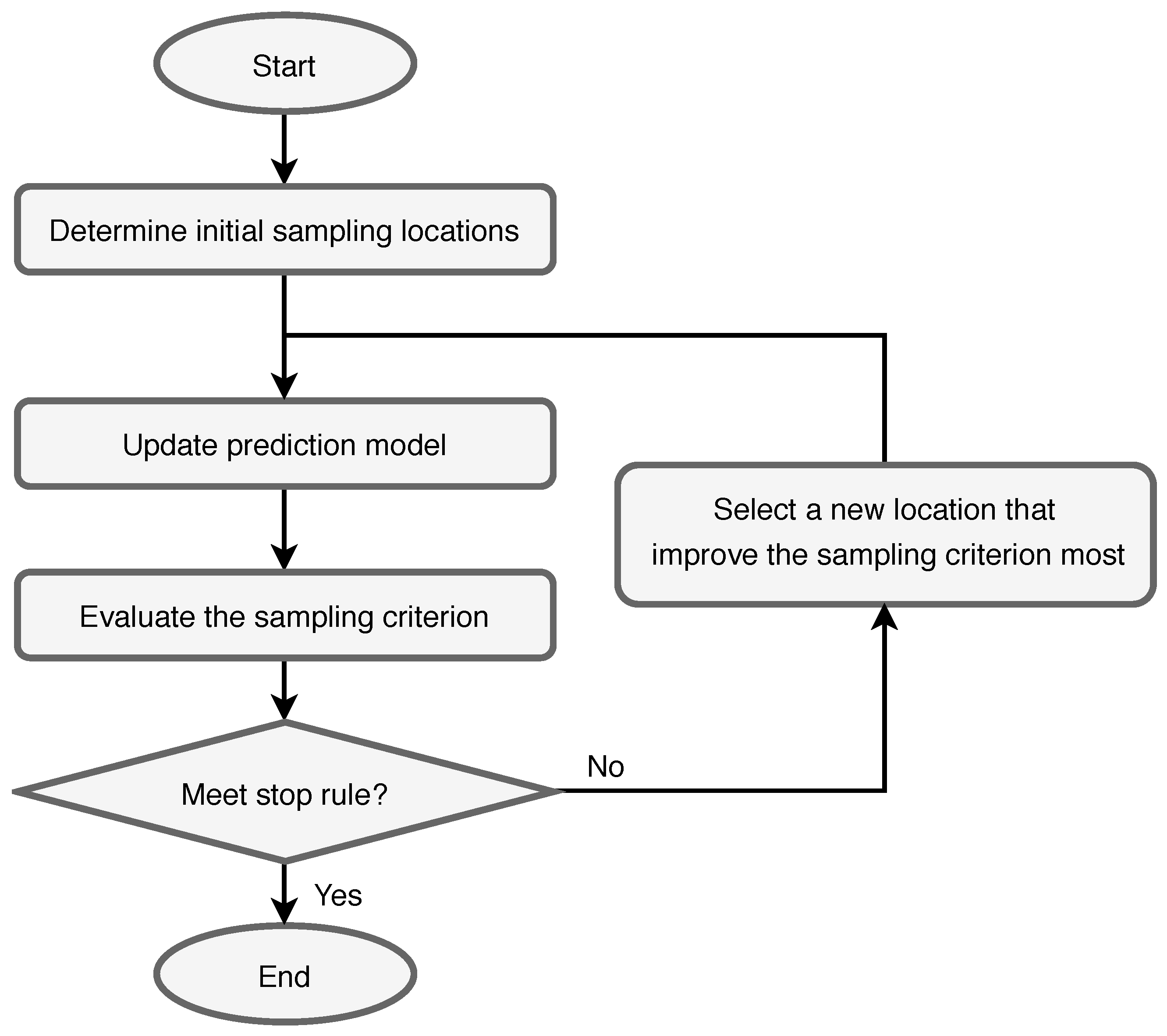
4.2.1. Adaptive Sampling
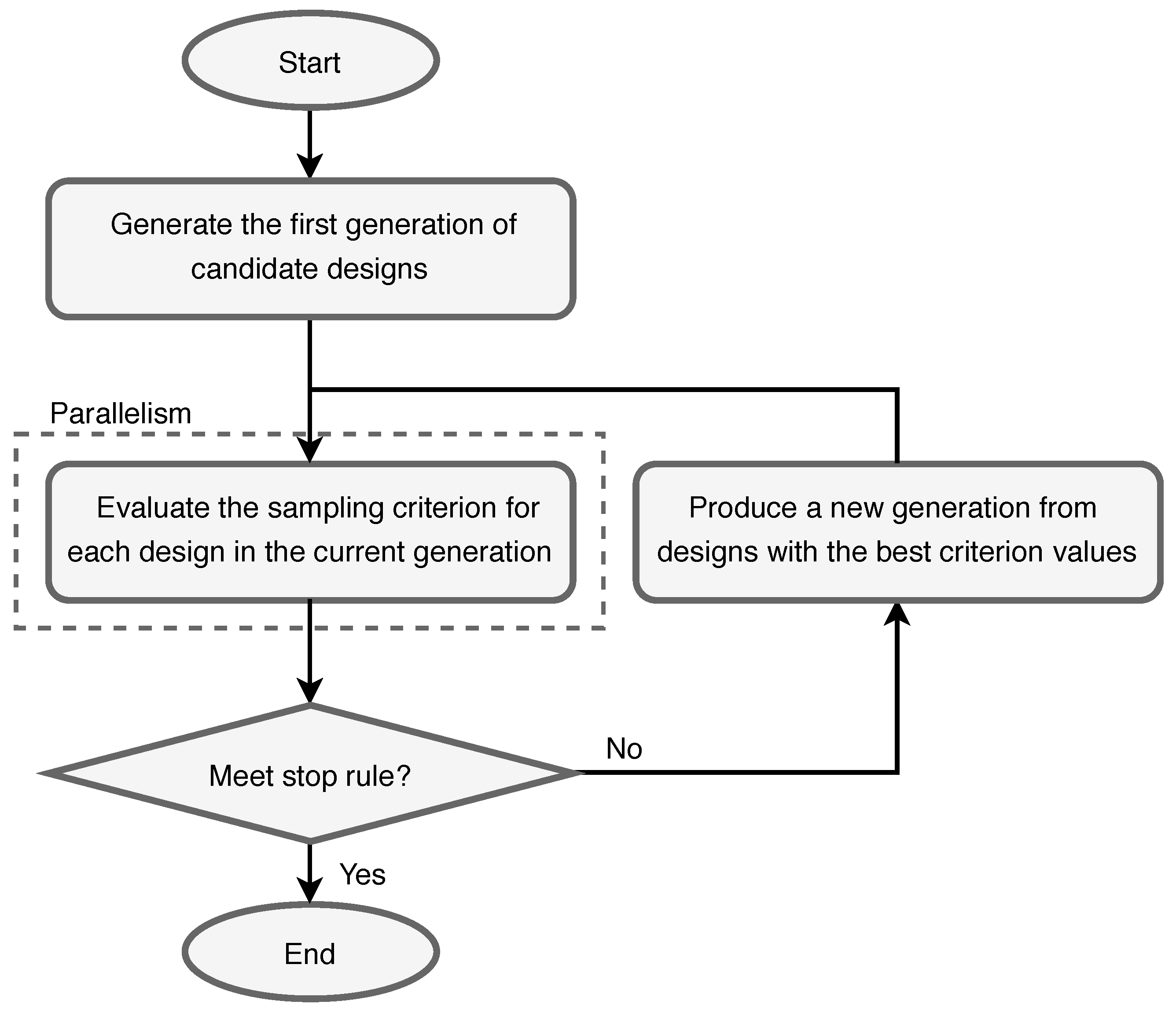
4.2.2. Heuristic Sampling
4.3. Spatiotemporal Sampling
5. Future Work
5.1. Performance Evaluation of Interpolation Methods
5.2. Big Data Fusion for Interpolation
- (1)
- The aforementioned true CS measurements can be implemented with hardware. Prior knowledge about f (e.g., its transform-sparsity) and the mechanism of the instrument need to be integrated, to design proper measurement strategy and reconstruction algorithm. Image SR could also be used to enhance camera-like sensors. Please note that CS reconstruction and image SR are both examples of (mostly linear) inverse problems.
- (2)
- Knowledge of can help reduce the ambiguity of the relevant inverse problem. Also, theory of statistical inverse problem may be adopted [128]. It represents prior knowledge about f in terms of a prior distribution, and the inverse problem naturally converts to Bayesian inference, for which the ambiguity could be quantified as variance of the posterior distribution.
- (3)
- Knowledge of can help build models for in the “operation range” (around ), so that it is more precise, less ambiguous, and computationally simpler to invert.
5.3. Advanced Sampling Design
5.4. Instrument Automation
5.5. MSA of High-Dimensional Surface Data
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFM | Atomic force microscopy |
| ANOVA | Analysis of variance |
| BLUP | Best linear unbiased prediction |
| CLM | Confocal laser microscopy |
| CMM | Coordinate measuring machines |
| CNN | Convolutional neural network |
| CS | Compressed sensing |
| GA | Genetic algorithm |
| GLM | Generalized linear model |
| GMRF | Gaussian Markov random field |
| GP | Gaussian process |
| GPR | Gaussian process regression |
| HPC | High-performance computing |
| HR | High-resolution |
| i.i.d | independent and identically distributed |
| KED | Kriging with external drift |
| LHI | Laser holographic interferometer |
| LR | Low-resolution |
| LS | Least squares |
| MAE | Mean absolute error |
| MANOVA | Multivariate analysis of variance |
| MRF | Markov random field |
| MSA | Measurement system analysis |
| MSE | Mean squared error |
| MTL | Multi-task learning |
| NURBS | Non-uniform rational B-spline |
| PTR | Precision/Tolerance ratio |
| R&R | Repeatability and reproducibility |
| RBF | Radial basis function |
| RKHS | Reproducing kernel Hilbert space |
| RMSE | Root mean square error |
| SISR | Single-image super-resolution |
| SLS | Structured light scanner |
| SR | Super-resolution |
References
- Nguyen, H.T.; Wang, H.; Hu, S.J. Characterization of cutting force induced surface shape variation in face milling using high-definition metrology. J. Manuf. Sci. Eng. 2013, 135, 041014. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Wang, H.; Tai, B.L.; Ren, J.; Jack Hu, S.; Shih, A. High-definition metrology enabled surface variation control by cutting load balancing. J. Manuf. Sci. Eng. 2016, 138. [Google Scholar] [CrossRef]
- Suriano, S.; Wang, H.; Shao, C.; Hu, S.J.; Sekhar, P. Progressive measurement and monitoring for multi-resolution data in surface manufacturing considering spatial and cross correlations. IIE Trans. 2015, 47, 1033–1052. [Google Scholar] [CrossRef]
- Uhlmann, E.; Hoyer, A. Surface Finishing of Zirconium Dioxide with Abrasive Brushing Tools. Machines 2020, 8, 89. [Google Scholar] [CrossRef]
- Grimm, T.; Wiora, G.; Witt, G. Characterization of typical surface effects in additive manufacturing with confocal microscopy. Surf. Topogr. Metrol. Prop. 2015, 3, 014001. [Google Scholar] [CrossRef]
- McGregor, D.J.; Tawfick, S.; King, W.P. Automated metrology and geometric analysis of additively manufactured lattice structures. Addit. Manuf. 2019, 28, 535–545. [Google Scholar] [CrossRef]
- Townsend, A.; Senin, N.; Blunt, L.; Leach, R.; Taylor, J. Surface texture metrology for metal additive manufacturing: A review. Precis. Eng. 2016, 46, 34–47. [Google Scholar] [CrossRef]
- Piotrowski, N. Tool Wear Prediction in Single-Sided Lapping Process. Machines 2020, 8, 59. [Google Scholar] [CrossRef]
- Shao, C.; Jin, J.J.; Jack Hu, S. Dynamic sampling design for characterizing spatiotemporal processes in manufacturing. J. Manuf. Sci. Eng. 2017, 139, 101002. [Google Scholar] [CrossRef]
- Zerehsaz, Y.; Shao, C.; Jin, J. Tool wear monitoring in ultrasonic welding using high-order decomposition. J. Intell. Manuf. 2019, 30, 657–669. [Google Scholar] [CrossRef]
- Yang, Y.; Shao, C. Spatial interpolation for periodic surfaces in manufacturing using a Bessel additive variogram model. J. Manuf. Sci. Eng. 2018, 140, 061001. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Y.; Cai, Y.D.; Lu, Q.; Koric, S.; Shao, C. Hierarchical measurement strategy for cost-effective interpolation of spatiotemporal data in manufacturing. J. Manuf. Syst. 2019, 53, 159–168. [Google Scholar] [CrossRef]
- Suriano, S.; Wang, H.; Hu, S.J. Sequential monitoring of surface spatial variation in automotive machining processes based on high definition metrology. J. Manuf. Syst. 2012, 31, 8–14. [Google Scholar] [CrossRef]
- Shao, C.; Wang, H.; Suriano-Puchala, S.; Hu, S.J. Engineering fusion spatial modeling to enable areal measurement system analysis for optical surface metrology. Measurement 2019, 136, 163–172. [Google Scholar] [CrossRef]
- Shao, C.; Hyung Kim, T.; Jack Hu, S.; Abell, J.A.; Patrick Spicer, J. Tool wear monitoring for ultrasonic metal welding of lithium-ion batteries. J. Manuf. Sci. Eng. 2016, 138, 051005. [Google Scholar] [CrossRef]
- Chen, H.; Yang, Y.; Shao, C. Multi-Task Learning for Data-Efficient Spatiotemporal Modeling of Tool Surface Progression in Ultrasonic Metal Welding. J. Manuf. Syst. 2021, 58, 306–315. [Google Scholar] [CrossRef]
- Fortin, M.J.; Drapeau, P.; Legendre, P. Spatial autocorrelation and sampling design in plant ecology. In Progress in Theoretical Vegetation Science; Springer: Berlin/Heidelberg, Germany, 1990; pp. 209–222. [Google Scholar]
- Andrew, N.; Mapstone, B. Sampling and the description of spatial pattern in marine ecology. Oceanogr. Mar. Biol. 1987, 25, 39–90. [Google Scholar]
- Brown, P.J.; Le, N.D.; Zidek, J.V. Multivariate spatial interpolation and exposure to air pollutants. Can. J. Stat. 1994, 22, 489–509. [Google Scholar] [CrossRef]
- White, D.; Kimerling, J.A.; Overton, S.W. Cartographic and geometric components of a global sampling design for environmental monitoring. Cartogr. Geogr. Inf. Syst. 1992, 19, 5–22. [Google Scholar] [CrossRef]
- Cressie, N. The origins of kriging. Math. Geol. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- David, C.; Sagris, D.; Stergianni, E.; Tsiafis, C.; Tsiafis, I. Experimental Analysis of the Effect of Vibration Phenomena on Workpiece Topomorphy Due to Cutter Runout in End-Milling Process. Machines 2018, 6, 27. [Google Scholar] [CrossRef]
- Dzierwa, A.; Markopoulos, A. Influence of Ball-Burnishing Process on Surface Topography Parameters and Tribological Properties of Hardened Steel. Machines 2019, 7, 11. [Google Scholar] [CrossRef]
- Durakbasa, M.; Osanna, P.; Demircioglu, P. The factors affecting surface roughness measurements of the machined flat and spherical surface structures—The geometry and the precision of the surface. Measurement 2011, 44, 1986–1999. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, S.; Wang, L.; He, J.; Wang, S.M.; Sun, L.; Shao, C. Influence of Coating Spray on Surface Measurement Using 3D Optical Scanning Systems. In Proceedings of the International Manufacturing Science and Engineering Conference, Erie, PA, USA, 10–14 June 2019; Volume 58745, p. V001T02A009. [Google Scholar]
- Küng, A.; Meli, F.; Thalmann, R. Ultraprecision micro-CMM using a low force 3D touch probe. Meas. Sci. Technol. 2007, 18, 319. [Google Scholar] [CrossRef]
- Bernal, C.; de Agustina, B.; Marín, M.M.; Camacho, A.M. Accuracy analysis of fridge projection systems based on blue light technology. Key Eng. Mater. 2014, 615, 9–14. [Google Scholar] [CrossRef]
- Palousek, D.; Omasta, M.; Koutny, D.; Bednar, J.; Koutecky, T.; Dokoupil, F. Effect of matte coating on 3D optical measurement accuracy. Opt. Mater. 2015, 40, 1–9. [Google Scholar] [CrossRef]
- Dury, M.R.; Woodward, S.D.; Brown, B.; McCarthy, M.B. Surface finish and 3D optical scanner measurement performance for precision engineering. In Proceedings of the 30th Annual Meeting of the American Society for Precision Engineering, Austin, TX, USA, 1–6 November 2015; pp. 419–423. [Google Scholar]
- Vora, H.D.; Sanyal, S. A comprehensive review: Metrology in additive manufacturing and 3D printing technology. Prog. Addit. Manuf. 2020, 5, 319–353. [Google Scholar] [CrossRef]
- Echerfaoui, Y.; El Ouafi, A.; Chebak, A. Experimental investigation of dynamic errors in coordinate measuring machines for high speed measurement. Int. J. Precis. Eng. Manuf. 2018, 19, 1115–1124. [Google Scholar] [CrossRef]
- Jin, R.; Chang, C.J.; Shi, J. Sequential measurement strategy for wafer geometric profile estimation. IIE Trans. 2012, 44, 1–12. [Google Scholar] [CrossRef]
- Santos, V.M.R.; Thompson, A.; Sims-Waterhouse, D.; Maskery, I.; Woolliams, P.; Leach, R. Design and characterisation of an additive manufacturing benchmarking artefact following a design-for-metrology approach. Addit. Manuf. 2020, 32, 100964. [Google Scholar] [CrossRef]
- Jiang, R.S.; Wang, W.H.; Wang, Z.Q. Noise filtering and multisample integration for CMM data of free-form surface. Int. J. Adv. Manuf. Technol. 2019, 102, 1239–1247. [Google Scholar] [CrossRef]
- Xie, H.; Zou, Y. Investigation on Finishing Characteristics of Magnetic Abrasive Finishing Process Using an Alternating Magnetic Field. Machines 2020, 8, 75. [Google Scholar] [CrossRef]
- Garcia, R.; Knoll, A.W.; Riedo, E. Advanced scanning probe lithography. Nat. Nanotechnol. 2014, 9, 577. [Google Scholar] [CrossRef] [PubMed]
- Mwema, F.M.; Oladijo, O.P.; Sathiaraj, T.; Akinlabi, E.T. Atomic force microscopy analysis of surface topography of pure thin aluminum films. Mater. Res. Express 2018, 5, 046416. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, J.; Wang, Y.; Liu, R.; Huai, X.; Jiang, J.; Anfuso, C. Atomic force microscopy for two-dimensional materials: A tutorial review. Opt. Commun. 2018, 406, 3–17. [Google Scholar] [CrossRef]
- Paddock, S.W.; Eliceiri, K.W. Laser scanning confocal microscopy: History, applications, and related optical sectioning techniques. In Confocal Microscopy; Springer: Berlin/Heidelberg, Germany, 2014; pp. 9–47. [Google Scholar]
- Jonkman, J.; Brown, C.M. Any way you slice it—A comparison of confocal microscopy techniques. J. Biomol. Tech. JBT 2015, 26, 54. [Google Scholar] [CrossRef] [PubMed]
- Radford, D.R.; Watson, T.F.; Walter, J.D.; Challacombe, S.J. The effects of surface machining on heat cured acrylic resin and two soft denture base materials: A scanning electron microscope and confocal microscope evaluation. J. Prosthet. Dent. 1997, 78, 200–208. [Google Scholar] [CrossRef]
- Al-Shammery, H.A.; Bubb, N.L.; Youngson, C.C.; Fasbinder, D.J.; Wood, D.J. The use of confocal microscopy to assess surface roughness of two milled CAD–CAM ceramics following two polishing techniques. Dent. Mater. 2007, 23, 736–741. [Google Scholar] [CrossRef]
- Park, J.B.; Jeon, Y.; Ko, Y. Effects of titanium brush on machined and sand-blasted/acid-etched titanium disc using confocal microscopy and contact profilometry. Clin. Oral Implant. Res. 2015, 26, 130–136. [Google Scholar] [CrossRef]
- Alqahtani, H.; Ray, A. Neural Network-Based Automated Assessment of Fatigue Damage in Mechanical Structures. Machines 2020, 8, 85. [Google Scholar] [CrossRef]
- Yu, T.Y. Laser-based sensing for assessing and monitoring civil infrastructures. In Sensor Technologies for Civil Infrastructures; Elsevier: Amsterdam, The Netherlands, 2014; pp. 327–356. [Google Scholar]
- Marrugo, A.G.; Gao, F.; Zhang, S. State-of-the-art active optical techniques for three-dimensional surface metrology: A review. JOSA A 2020, 37, B60–B77. [Google Scholar] [CrossRef] [PubMed]
- De Nicola, S.; Ferraro, P.; Finizio, A.; Grilli, S.; Coppola, G.; Iodice, M.; De Natale, P.; Chiarini, M. Surface topography of microstructures in lithium niobate by digital holographic microscopy. Meas. Sci. Technol. 2004, 15, 961. [Google Scholar] [CrossRef]
- Schulze, M.A.; Hunt, M.A.; Voelkl, E.; Hickson, J.D.; Usry, W.R.; Smith, R.G.; Bryant, R.; Thomas, C., Jr. Semiconductor wafer defect detection using digital holography. In Process and Materials Characterization and Diagnostics in IC Manufacturing; International Society for Optics and Photonics: Santa Clara, CA, USA, 2003; Volume 5041, pp. 183–193. [Google Scholar]
- Shao, C.; Ren, J.; Wang, H.; Jin, J.J.; Hu, S.J. Improving Machined Surface Shape Prediction by Integrating Multi-Task Learning With Cutting Force Variation Modeling. J. Manuf. Sci. Eng. 2017, 139. [Google Scholar] [CrossRef]
- Lin, H.; Gao, J.; Zhang, G.; Chen, X.; He, Y.; Liu, Y. Review and comparison of high-dynamic range three-dimensional shape measurement techniques. J. Sens. 2017, 2017, 9576850. [Google Scholar] [CrossRef]
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; et al. Roadmap on structured light. J. Opt. 2016, 19, 013001. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Horton, P.; Bonny, L.; Nicol, A.; Kendrick, K.; Feng, J. Applications of multi-variate analysis of variance (MANOVA) to multi-electrode array electrophysiology data. J. Neurosci. Methods 2005, 146, 22–41. [Google Scholar] [CrossRef][Green Version]
- He, S.G.; Wang, G.A.; Cook, D.F. Multivariate measurement system analysis in multisite testing: An online technique using principal component analysis. Expert Syst. Appl. 2011, 38, 14602–14608. [Google Scholar] [CrossRef]
- Aldroubi, A.; Gröchenig, K. Nonuniform sampling and reconstruction in shift-invariant spaces. SIAM Rev. 2001, 43, 585–620. [Google Scholar] [CrossRef]
- Unser, M. Sampling-50 years after Shannon. Proc. IEEE 2000, 88, 569–587. [Google Scholar] [CrossRef]
- Getreuer, P. Linear Methods for Image Interpolation. Image Process Line 2011, 1, 238–259. [Google Scholar] [CrossRef]
- Wendland, H. Scattered Data Approximation; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Auffray, Y.; Barbillon, P. Conditionally Positive Definite Kernels: Theoretical Contribution, Application to Interpolation and Approximation. Available online: https://hal.inria.fr/inria-00359944 (accessed on 15 November 2020).
- Berlinet, A.; Thomas-Agnan, C. Reproducing Kernel Hilbert Spaces in Probability and Statistics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Mitas, L.; Mitasova, H. Spatial interpolation. Geogr. Inf. Syst. Princ. Tech. Manag. Appl. 1999, 1, 481–492. [Google Scholar]
- Anjyo, K.; Lewis, J.P.; Pighin, F. Scattered data interpolation for computer graphics. In ACM SIGGRAPH 2014 Courses; Association for Computing Machinery: New York, NY, USA, 2014; pp. 1–69. [Google Scholar] [CrossRef]
- Patrikalakis, N.M.; Maekawa, T. Shape Interrogation for Computer Aided Design and Manufacturing; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Ma, W.; Kruth, J.P. NURBS curve and surface fitting for reverse engineering. Int. J. Adv. Manuf. Technol. 1998, 14, 918–927. [Google Scholar] [CrossRef]
- Habermann, C.; Kindermann, F. Multidimensional spline interpolation: Theory and applications. Comput. Econ. 2007, 30, 153–169. [Google Scholar] [CrossRef]
- Gelfand, A.E.; Diggle, P.; Guttorp, P.; Fuentes, M. Handbook of Spatial Statistics; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Cressie, N. Statistics for Spatial Data; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Hengl, T.; Heuvelink, G.B.M.; Rossiter, D.G. About regression-kriging: From equations to case studies. Comput. Geosci. 2007, 33, 1301–1315. [Google Scholar] [CrossRef]
- Sherman, M. Spatial Statistics and Spatio-Temporal Data: Covariance Functions and Directional Properties; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Li, J.; Heap, A.D. Spatial interpolation methods applied in the environmental sciences: A review. Environ. Model. Softw. 2014, 53, 173–189. [Google Scholar] [CrossRef]
- Stein, M.L. Interpolation of Spatial Data: Some Theory for Kriging; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Banerjee, S.; Carlin, B.P.; Gelfand, A.E. Hierarchical Modeling and Analysis for Spatial Data; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Pilz, J.; Spöck, G. Why do we need and how should we implement Bayesian kriging methods. Stoch. Environ. Res. Risk Assess. 2008, 22, 621–632. [Google Scholar] [CrossRef]
- Kleiber, W.; Nychka, D. Nonstationary modeling for multivariate spatial processes. J. Multivar. Anal. 2012, 112, 76–91. [Google Scholar] [CrossRef]
- Fuentes, M. Spectral methods for nonstationary spatial processes. Biometrika 2002, 89, 197–210. [Google Scholar] [CrossRef]
- Amidror, I. Scattered data interpolation methods for electronic imaging systems: A survey. J. Electron. Imaging 2002, 11, 157–176. [Google Scholar] [CrossRef]
- Sibson, R. A vector identity for the Dirichlet tessellation. Math. Proc. Camb. Philos. Soc. 1980, 87, 151–155. [Google Scholar] [CrossRef]
- Loader, C. Local Regression and Likelihood; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Cleveland, W.S.; Loader, C. Smoothing by local regression: Principles and methods. In Statistical Theory and Computational Aspects of Smoothing; Springer: Berlin/Heidelberg, Germany, 1996; pp. 10–49. [Google Scholar]
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 1968 23rd ACM National Conference, Las Vegas, NV, USA, 27–29 August 1968; pp. 517–524. [Google Scholar]
- Wahba, G. Spline Models for Observational Data; CBMS-NSF Regional Conference Series in Applied Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1990. [Google Scholar] [CrossRef]
- Eldredge, N. Analysis and Probability on Infinite-Dimensional Spaces. arXiv 2016, arXiv:1607.03591. [Google Scholar]
- Wang, J.; Su, R.; Leach, R.; Lu, W.; Zhou, L.; Jiang, X. Resolution enhancement for topography measurement of high-dynamic-range surfaces via image fusion. Opt. Express 2018, 26, 34805–34819. [Google Scholar] [CrossRef] [PubMed]
- Babu, M.; Franciosa, P.; Ceglarek, D. Spatio-Temporal Adaptive Sampling for effective coverage measurement planning during quality inspection of free form surfaces using robotic 3D optical scanner. J. Manuf. Syst. 2019, 53, 93–108. [Google Scholar] [CrossRef]
- Colosimo, B.M.; Pacella, M.; Senin, N. Multisensor data fusion via Gaussian process models for dimensional and geometric verification. Precis. Eng. 2015, 40, 199–213. [Google Scholar] [CrossRef]
- Wang, J.; Leach, R.K.; Jiang, X. Review of the mathematical foundations of data fusion techniques in surface metrology. Surf. Topogr. Metrol. Prop. 2015, 3, 023001. [Google Scholar] [CrossRef]
- Yu, K.; Tresp, V.; Schwaighofer, A. Learning Gaussian processes from multiple tasks. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005; pp. 1012–1019. [Google Scholar]
- Bonilla, E.V.; Chai, K.M.; Williams, C. Multi-task Gaussian process prediction. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2008; pp. 153–160. [Google Scholar]
- Shireen, T.; Shao, C.; Wang, H.; Li, J.; Zhang, X.; Li, M. Iterative multi-task learning for time-series modeling of solar panel PV outputs. Appl. Energy 2018, 212, 654–662. [Google Scholar] [CrossRef]
- Rue, H.; Held, L. Gaussian Markov Random Fields: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Zhang, H.; Zhang, Y.; Li, H.; Huang, T.S. Generative Bayesian Image Super Resolution With Natural Image Prior. IEEE Trans. Image Process. 2012, 21, 4054–4067. [Google Scholar] [CrossRef]
- Hinton, G.E. Training Products of Experts by Minimizing Contrastive Divergence. Neural Comput. 2002, 14, 1771–1800. [Google Scholar] [CrossRef] [PubMed]
- Sidén, P.; Lindsten, F. Deep Gaussian Markov Random Fields. arXiv 2020, arXiv:2002.07467. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candes, E.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Boche, H.; Calderbank, R.; Kutyniok, G.; Vybíral, J. Compressed Sensing and Its Applications; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Kutyniok, G. Theory and applications of compressed sensing. Gamm-Mitteilungen 2013, 36, 79–101. [Google Scholar] [CrossRef]
- Foucart, S.; Rauhut, H. A mathematical introduction to compressive sensing. Bull. Am. Math 2017, 54, 151–165. [Google Scholar]
- Candes, E.J.; Wakin, M.B. An Introduction to Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Duarte, M.F.; Eldar, Y.C. Structured Compressed Sensing: From Theory to Applications. IEEE Trans. Signal Process. 2011, 59, 4053–4085. [Google Scholar] [CrossRef]
- Mangia, M.; Pareschi, F.; Rovatti, R.; Setti, G. Adapted Compressed Sensing: A Game Worth Playing. IEEE Circuits Syst. Mag. 2020, 20, 40–60. [Google Scholar] [CrossRef]
- Donoho, D.L.; Javanmard, A.; Montanari, A. Information-Theoretically Optimal Compressed Sensing via Spatial Coupling and Approximate Message Passing. IEEE Trans. Inf. Theory 2013, 59, 7434–7464. [Google Scholar] [CrossRef]
- Adcock, B.; Hansen, A.C.; Poon, C.; Roman, B. Breaking the Coherence Barrier: A new theory for compressed sensing. Forum Math. Sigma 2017, 5. [Google Scholar] [CrossRef]
- Wu, Y.; Rosca, M.; Lillicrap, T. Deep Compressed Sensing. arXiv 2019, arXiv:1905.06723. [Google Scholar]
- Nasrollahi, K.; Moeslund, T.B. Super-resolution: A comprehensive survey. Mach. Vis. Appl. 2014, 25, 1423–1468. [Google Scholar] [CrossRef]
- Leach, R.; Sherlock, B. Applications of super-resolution imaging in the field of surface topography measurement. Surf. Topogr. Metrol. Prop. 2013, 2, 023001. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Hoi, S.C.H. Deep Learning for Image Super-resolution: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020. [Google Scholar] [CrossRef] [PubMed]
- Zhu, K.; Lin, X.; Li, K.; Jiang, L. Compressive sensing and sparse decomposition in precision machining process monitoring: From theory to applications. Mechatronics 2015, 31, 3–15. [Google Scholar] [CrossRef]
- Raid, I.; Kusnezowa, T.; Seewig, J. Application of ordinary kriging for interpolation of micro-structured technical surfaces. Meas. Sci. Technol. 2013, 24, 095201. [Google Scholar] [CrossRef]
- Colosimo, B.M. Modeling and monitoring methods for spatial and image data. Qual. Eng. 2018, 30, 94–111. [Google Scholar] [CrossRef]
- Leach, R. Characterisation of Areal Surface Texture; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Wang, J.; Jiang, X.; Blunt, L.A.; Leach, R.K.; Scott, P.J. Intelligent sampling for the measurement of structured surfaces. Meas. Sci. Technol. 2012, 23, 085006. [Google Scholar] [CrossRef]
- Harris, P.M.; Smith, I.M.; Leach, R.K.; Giusca, C.; Jiang, X.; Scott, P. Software measurement standards for areal surface texture parameters: Part 1—Algorithms. Meas. Sci. Technol. 2012, 23, 105008. [Google Scholar] [CrossRef]
- Huang, S.; Tong, M.; Huang, W.; Zhao, X. An Isotropic Areal Filter Based on High-Order Thin-Plate Spline for Surface Metrology. IEEE Access 2019, 7, 116809–116822. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, H.N.; Wu, R.; Liang, R. Data processing for point-based in situ metrology of freeform optical surface. Opt. Express 2017, 25, 13414–13424. [Google Scholar] [CrossRef]
- El-Hayek, N.; Nouira, H.; Anwer, N.; Damak, M.; Gibaru, O. Reconstruction of freeform surfaces for metrology. J. Phys. Conf. Ser. 2014, 483, 012003. [Google Scholar] [CrossRef]
- Ma, J. Compressed Sensing for Surface Characterization and Metrology. IEEE Trans. Instrum. Meas. 2010, 59, 1600–1615. [Google Scholar] [CrossRef]
- Wang, J.; Leach, R.K.; Jiang, X. Advances in Sampling Techniques for Surface Topography Measurement—A Review. Available online: https://eprintspublications.npl.co.uk/6508/ (accessed on 15 November 2020).
- Braker, R.A.; Luo, Y.; Pao, L.Y.; Andersson, S.B. Improving the Image Acquisition Rate of an Atomic Force Microscope through Spatial Subsampling and Reconstruction. IEEE/ASME Trans. Mechatron. 2020, 25, 570–580. [Google Scholar] [CrossRef]
- Lalehpour, A.; Berry, C.; Barari, A. Adaptive data reduction with neighbourhood search approach in coordinate measurement of planar surfaces. J. Manuf. Syst. 2017, 45, 28–47. [Google Scholar] [CrossRef]
- Wang, J.F.; Stein, A.; Gao, B.B.; Ge, Y. A review of spatial sampling. Spat. Stat. 2012, 2, 1–14. [Google Scholar] [CrossRef]
- King, L.J. Statistical Analysis in Geography; Prentice Hall: Upper Saddle River, NJ, USA, 1969. [Google Scholar]
- Ripley, B.D. Spatial Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 575. [Google Scholar]
- Benedetti, R.; Piersimoni, F.; Postiglione, P. Spatially balanced sampling: A review and a reappraisal. Int. Stat. Rev. 2017, 85, 439–454. [Google Scholar] [CrossRef]
- Heuvelink, G.B.; Griffith, D.A.; Hengl, T.; Melles, S.J. Sampling design optimization for space-time kriging. Spatio-Temporal Des. 2012, 207–230. [Google Scholar] [CrossRef]
- Yang, Y.; Cai, Y.D.; Lu, Q.; Zhang, Y.; Koric, S.; Shao, C. High-Performance Computing Based Big Data Analytics for Smart Manufacturing. In Proceedings of the ASME 2018 13th International Manufacturing Science and Engineering Conference, College Station, TX, USA, 18–22 June 2018; p. V003T02A013. [Google Scholar]
- Senin, N.; Leach, R. Information-rich surface metrology. Procedia CIRP 2018, 75, 19–26. [Google Scholar] [CrossRef]
- Kaipio, J.; Somersalo, E. Statistical and Computational Inverse Problems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
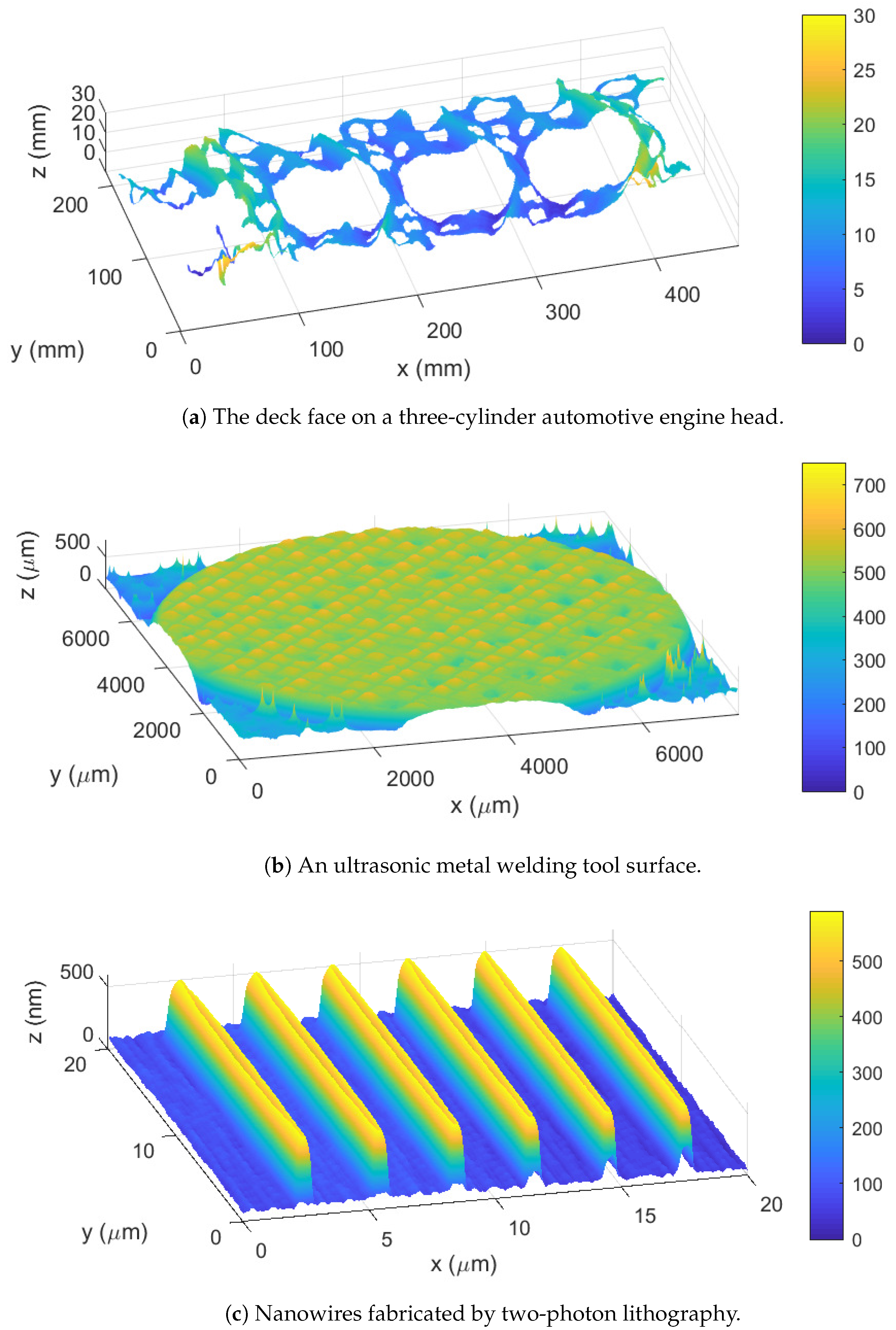
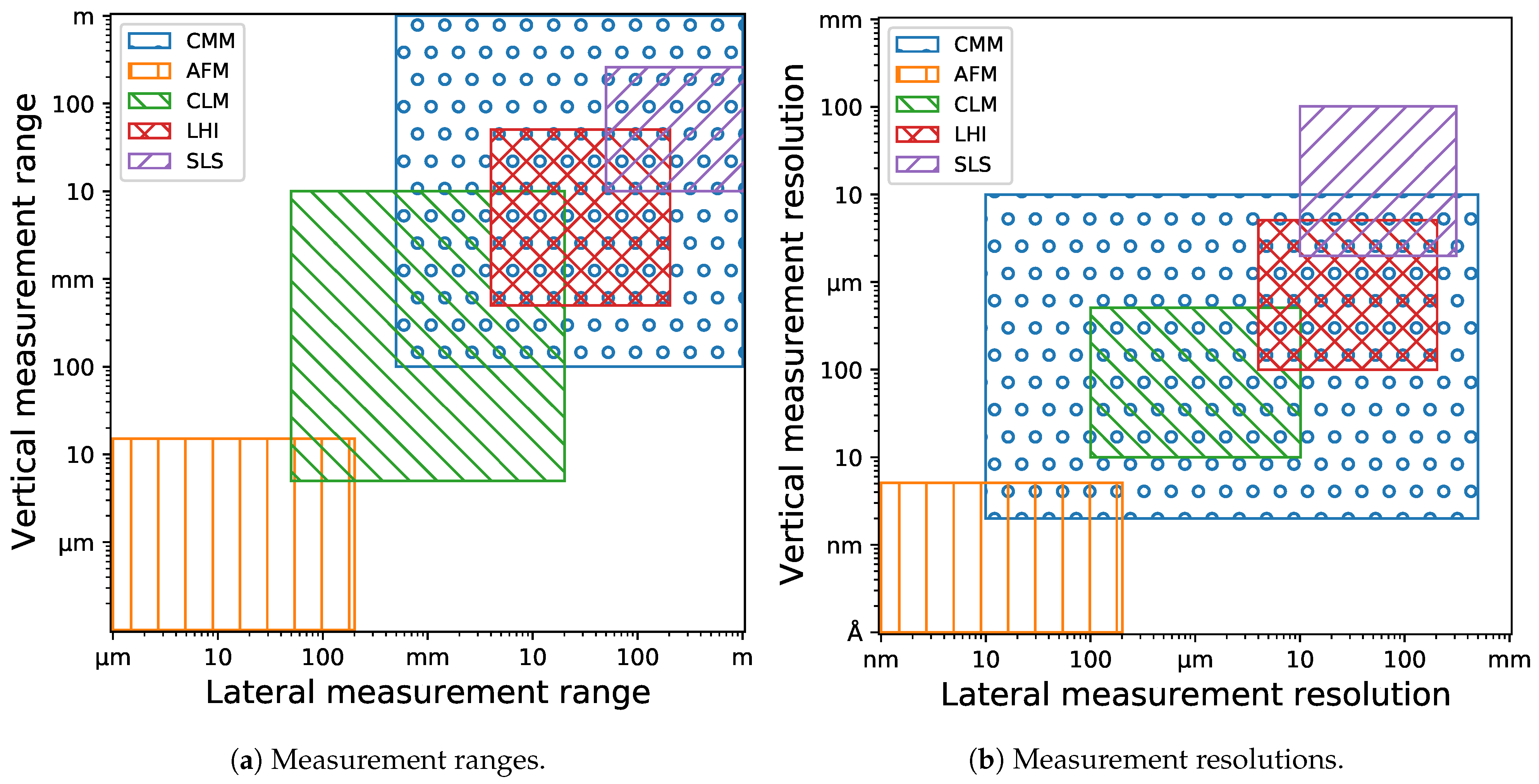
| Measurement System Type | Contact | Non-Contact |
|---|---|---|
| Ultimate resolution | Atomic scale | Diffraction limit |
| Measurement data size | Small | Large |
| Measurement speed | Low | High |
| Measurement noise | Low | Relatively high |
| Maintenance cost | High | Low |
| Damage during measurement | Possible damage | No damage |
| Representative technologies | CMM, AFM | CLM, LHI, SLS |
| Continuous variation | Spatial-only | Sampling or approximation in a certain class of functions |
| Inference about spatial stochastic fields (spatial process) | ||
| Other methods for spatial interpolation | ||
| Data fusion-based | Interpolation with multiple explanatory variables | |
| Spatiotemporal interpolation | ||
| Fusing of measurements from different instruments | ||
| Multi-task learning | ||
| Discrete variation | Inference with discrete spatial process: MRF-based models | |
| “Compressive” methods | Compressed sensing | |
| Image super-resolution | ||
| Sampling or approximation in a certain class of functions | In shift-invariant space: sampling theory |
| In reproducing kernel Hilbert space (RKHS): regression with L2 regularization and radial basis function (RBF) interpolation | |
| Other methods for curve fitting | |
| Inference about spatial stochastic fields (spatial process) | Best linear unbiased estimator kriging and variants |
| Bayesian methods for continuous spatial processes | |
| Other methods for spatial interpolation | Mesh-based methods |
| Local regression |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Dong, Z.; Meng, Y.; Shao, C. Data-Driven Intelligent 3D Surface Measurement in Smart Manufacturing: Review and Outlook. Machines 2021, 9, 13. https://doi.org/10.3390/machines9010013
Yang Y, Dong Z, Meng Y, Shao C. Data-Driven Intelligent 3D Surface Measurement in Smart Manufacturing: Review and Outlook. Machines. 2021; 9(1):13. https://doi.org/10.3390/machines9010013
Chicago/Turabian StyleYang, Yuhang, Zhiqiao Dong, Yuquan Meng, and Chenhui Shao. 2021. "Data-Driven Intelligent 3D Surface Measurement in Smart Manufacturing: Review and Outlook" Machines 9, no. 1: 13. https://doi.org/10.3390/machines9010013
APA StyleYang, Y., Dong, Z., Meng, Y., & Shao, C. (2021). Data-Driven Intelligent 3D Surface Measurement in Smart Manufacturing: Review and Outlook. Machines, 9(1), 13. https://doi.org/10.3390/machines9010013





