Model-Based Manipulation of Linear Flexible Objects: Task Automation in Simulation and Real World †
Abstract
1. Introduction
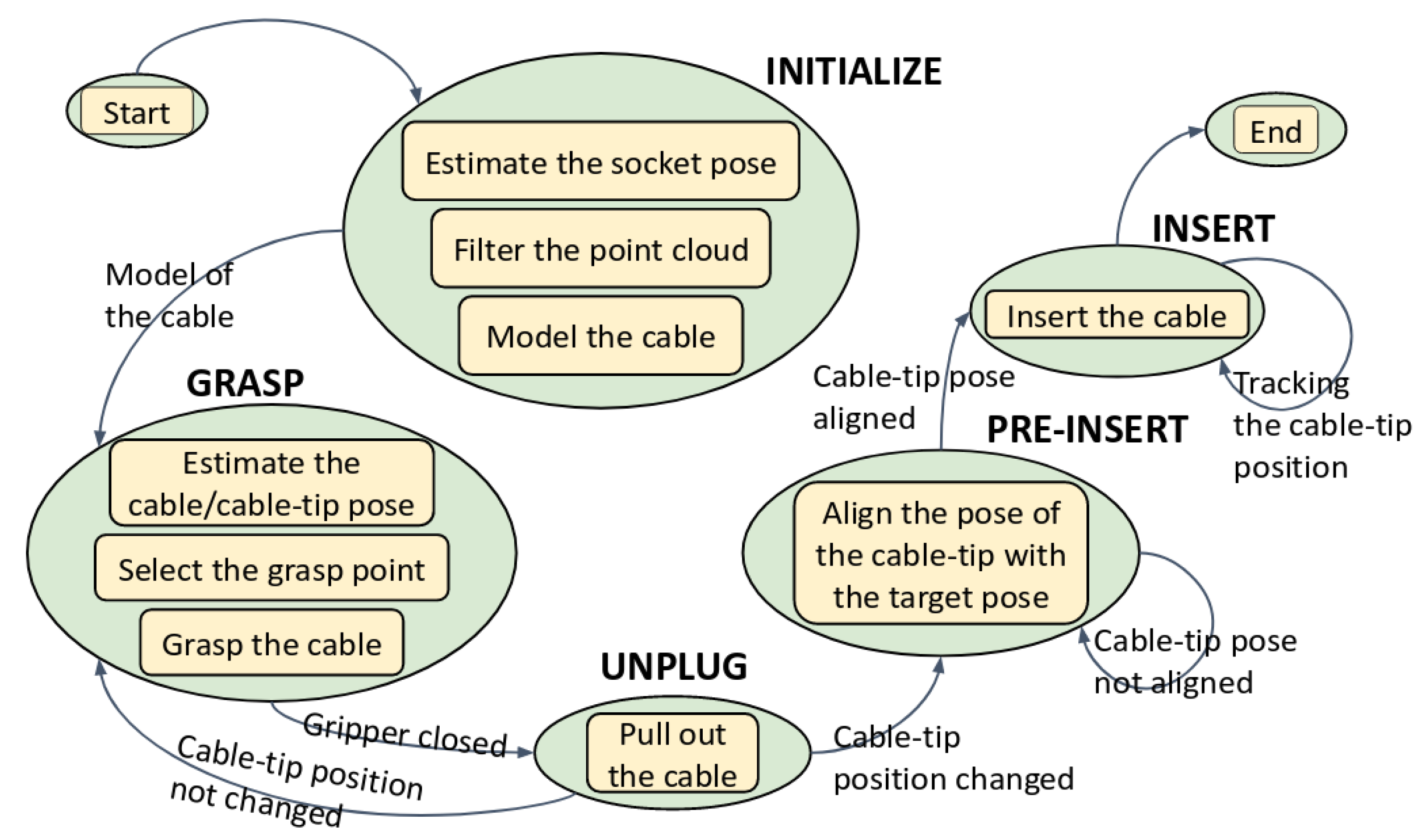
2. Task Automation in Real World Based on Our Geometrical Modeling of the Linear Flexible Objects
2.1. Benchmarking Setup and Flow of Our Designed System
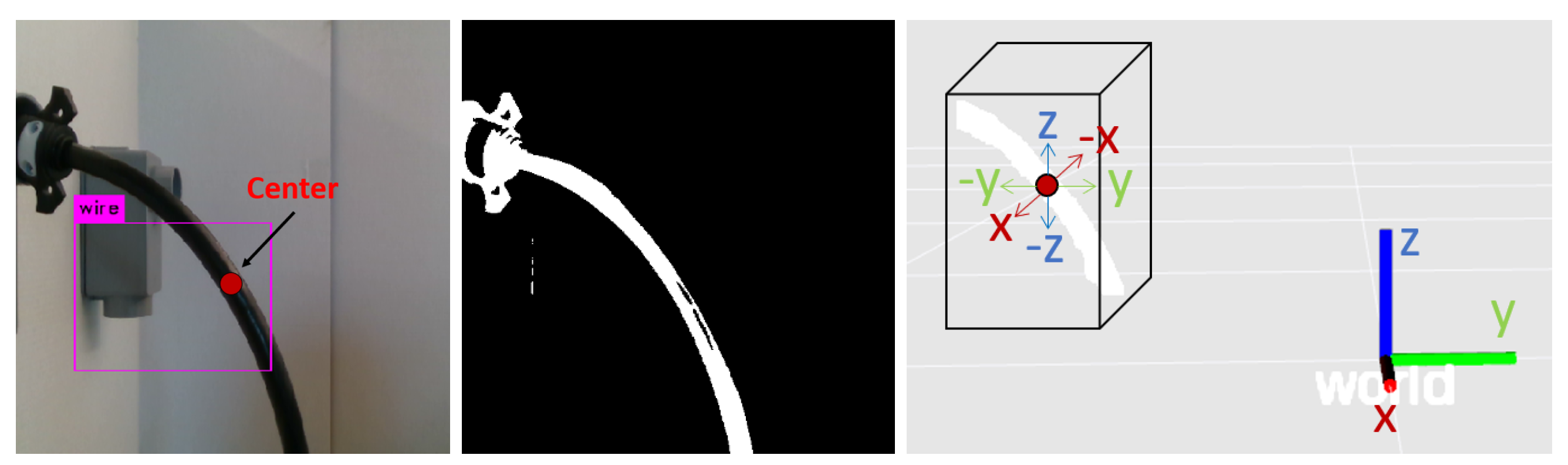
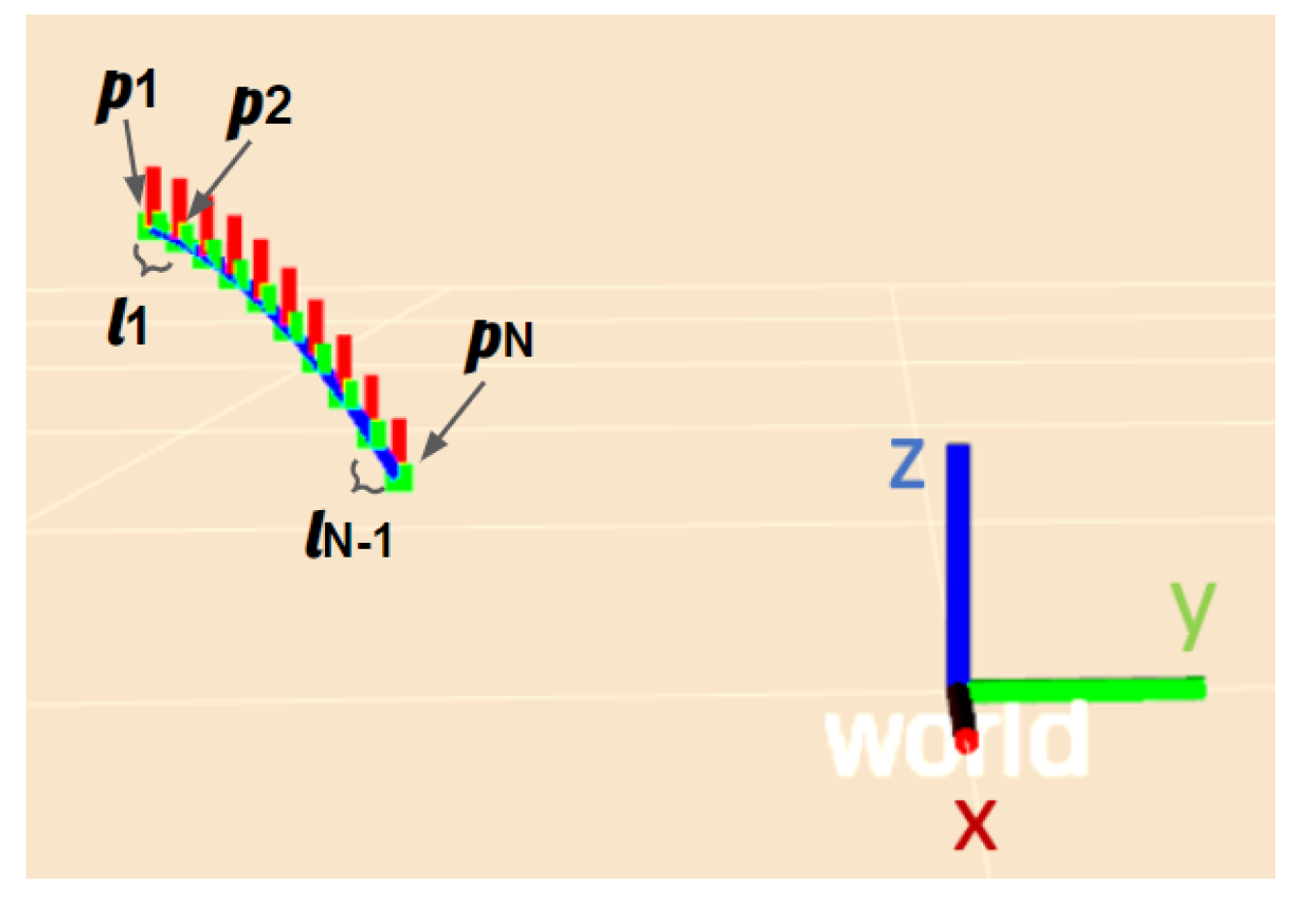
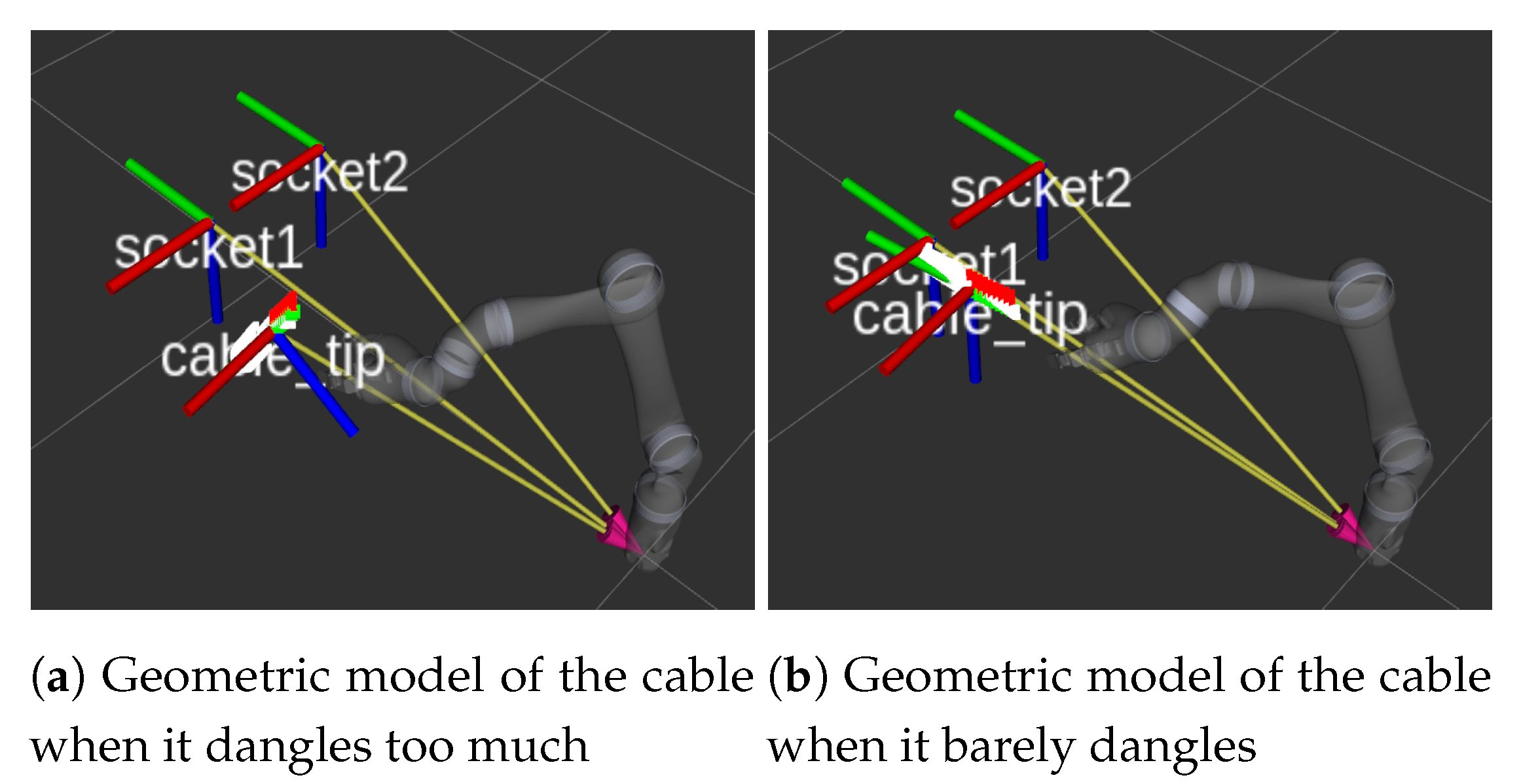
2.2. Geometrical Modeling of the Linear Flexible Objects
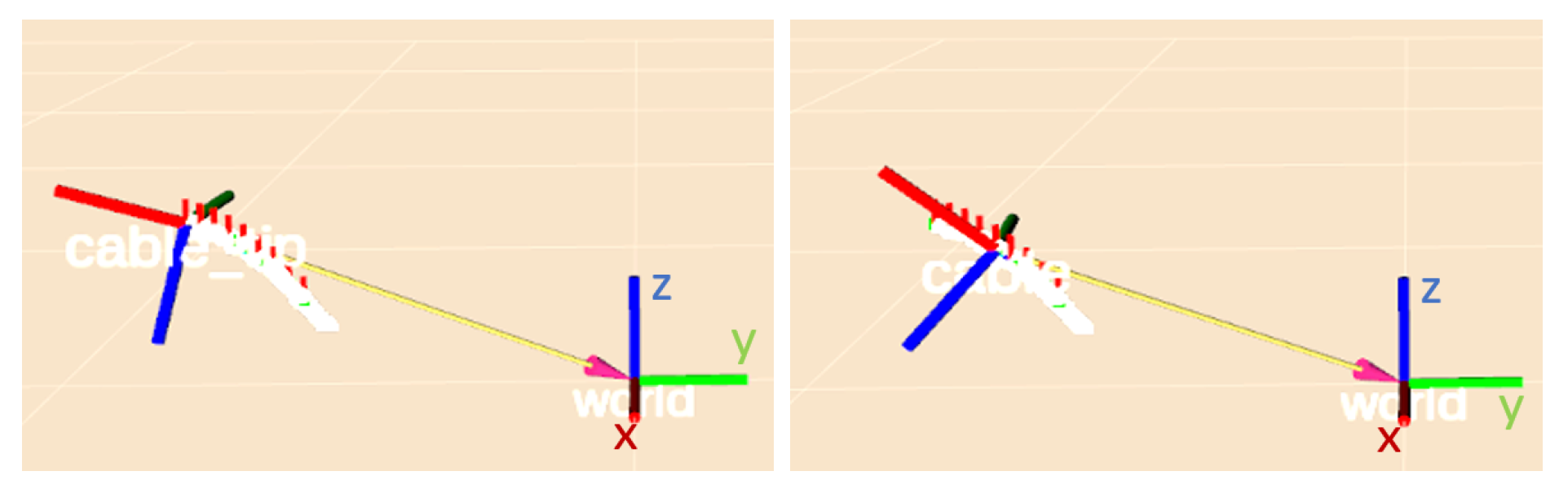
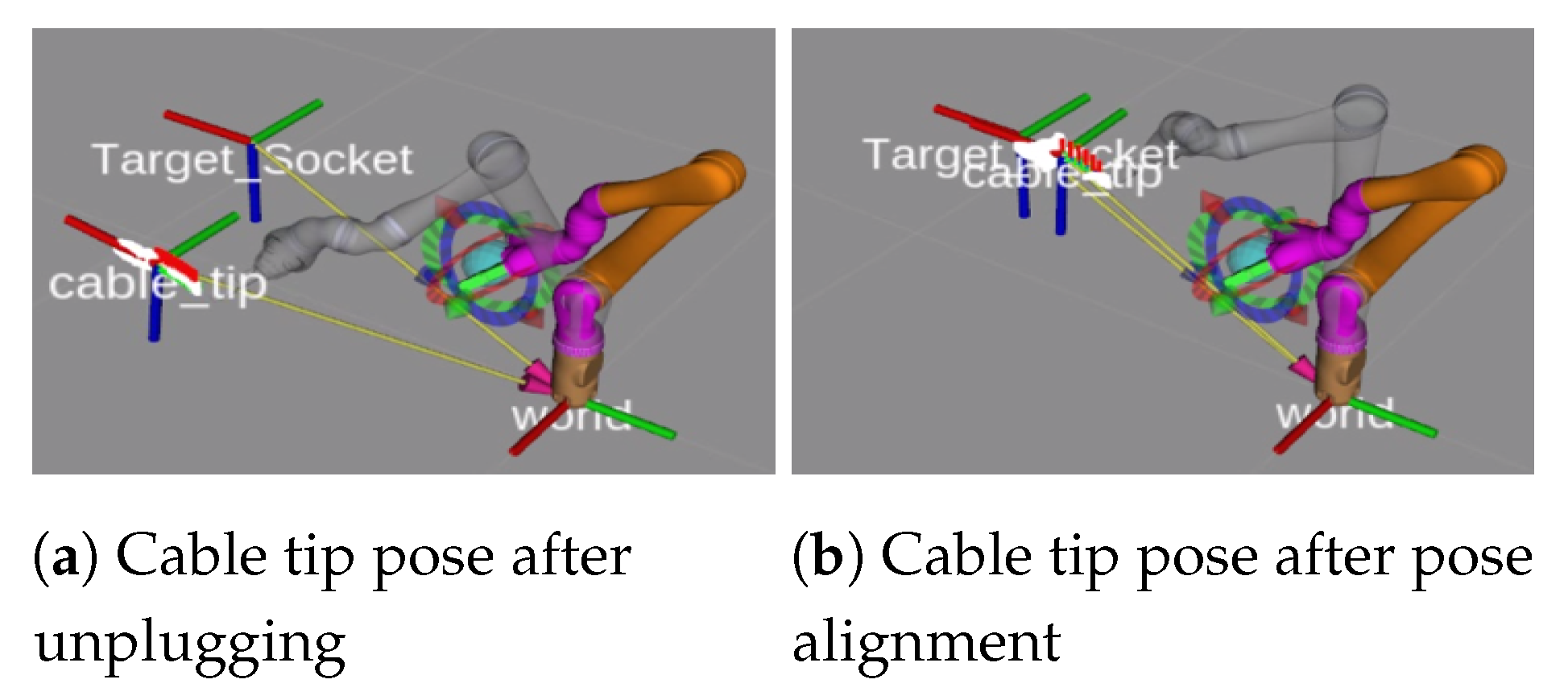
2.3. Pose Alignment Controller
| Algorithm 1: Pose alignment algorithm |
 |
3. Task Automation in Simulation Based on Our Physical Model of the Linear Flexible Objects
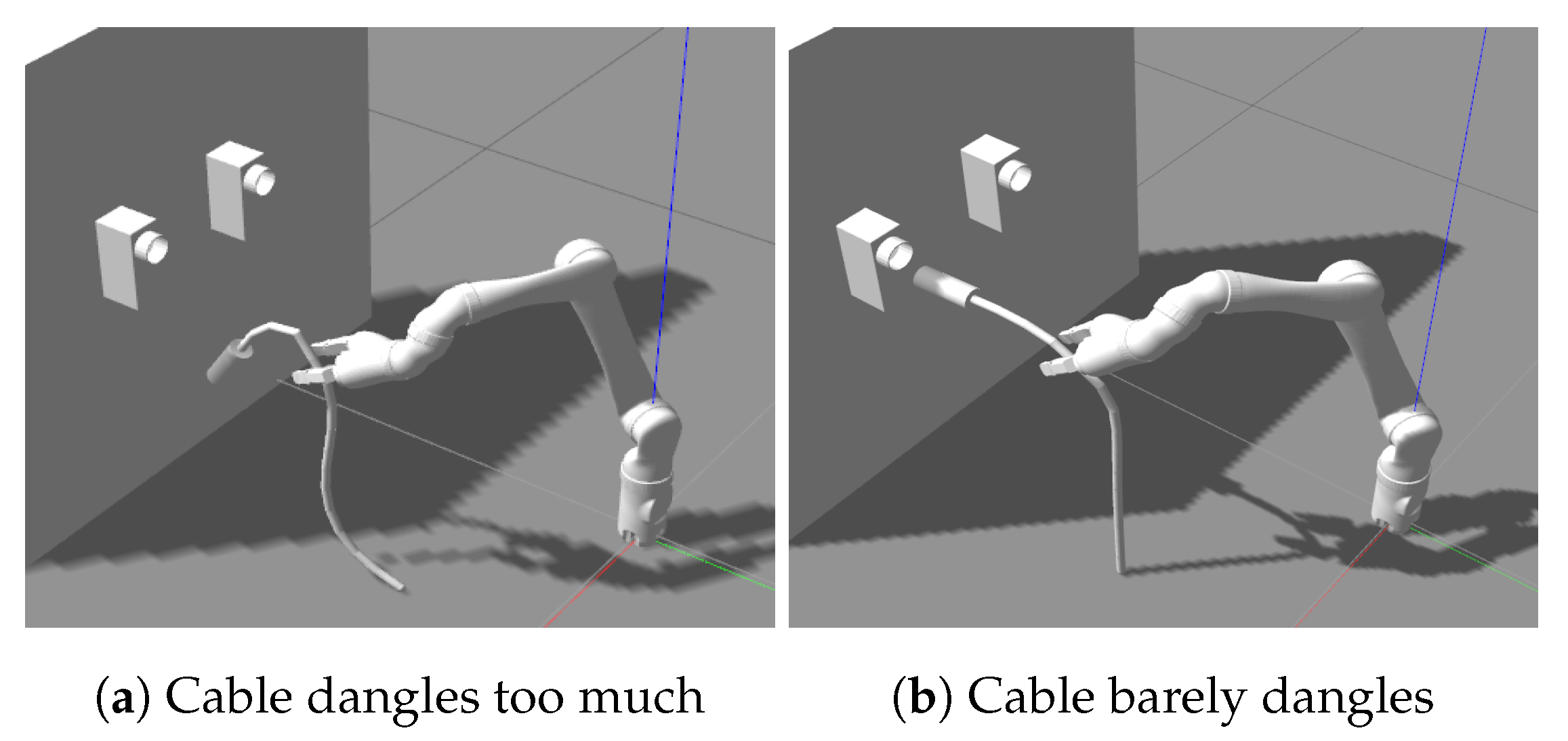
3.1. Simulation Environment Setup
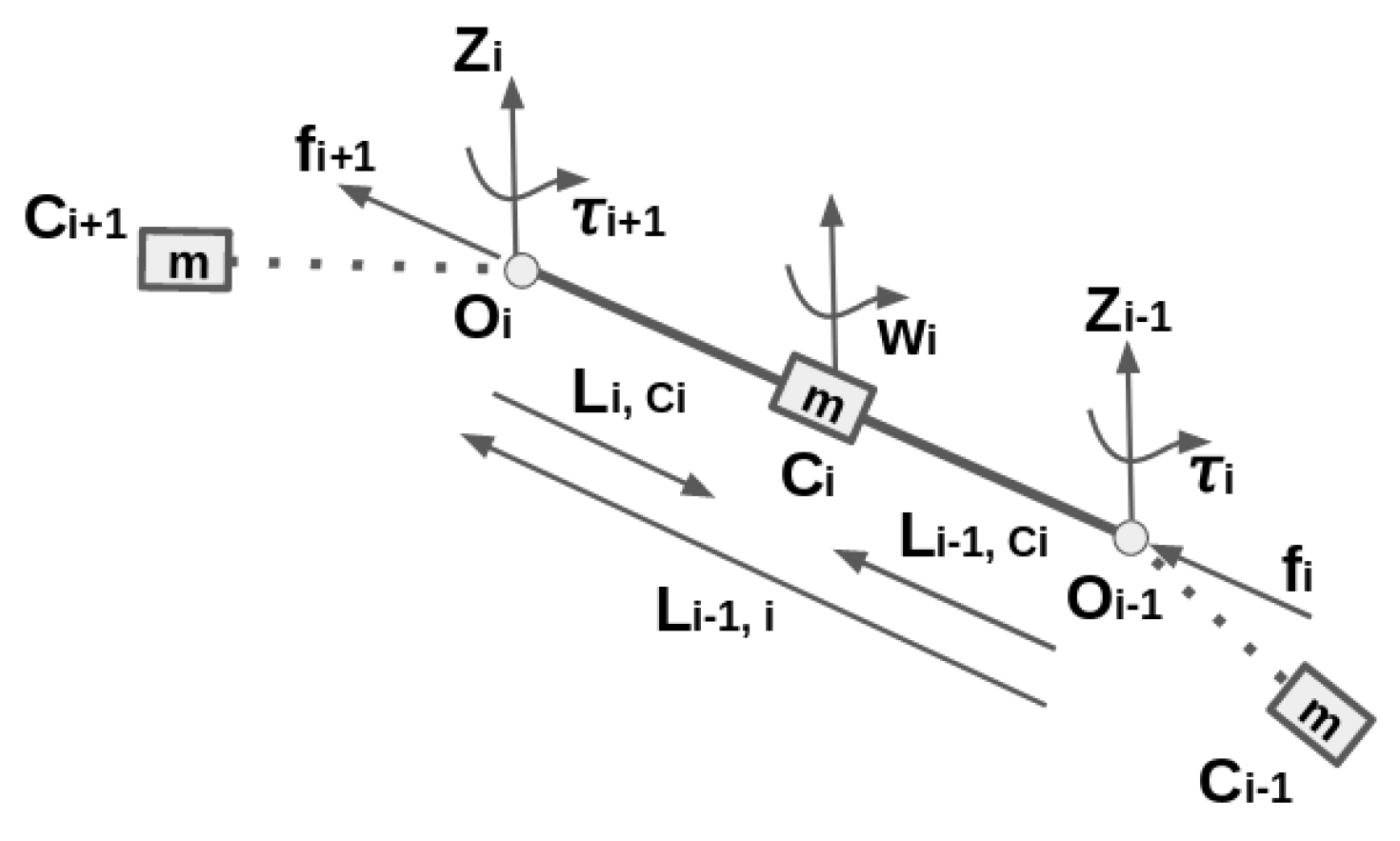
3.2. Physical Model of the Linear Flexible Objects
3.3. Sim2Real2Sim—Achieving Flexible Object Manipulation in Simulation with Identified Physical Model
3.3.1. Simulation to Real World
3.3.2. Real World to Simulation
| Algorithm 2: Recursive Newton Euler algorithm |
| Forward recursion:{ Initial: Velocity and acceleration of the base link both equal to 0 Compute link angular velocity: Compute link angular acceleration: Compute linear acceleration of origin of frame i: Compute linear acceleration of centre of : } Backward recursion:{ Compute force exerted by link on link i: Compute moment exerted by link on link i: Compute torque exerted by link on link i: } |
4. Experiments and Results
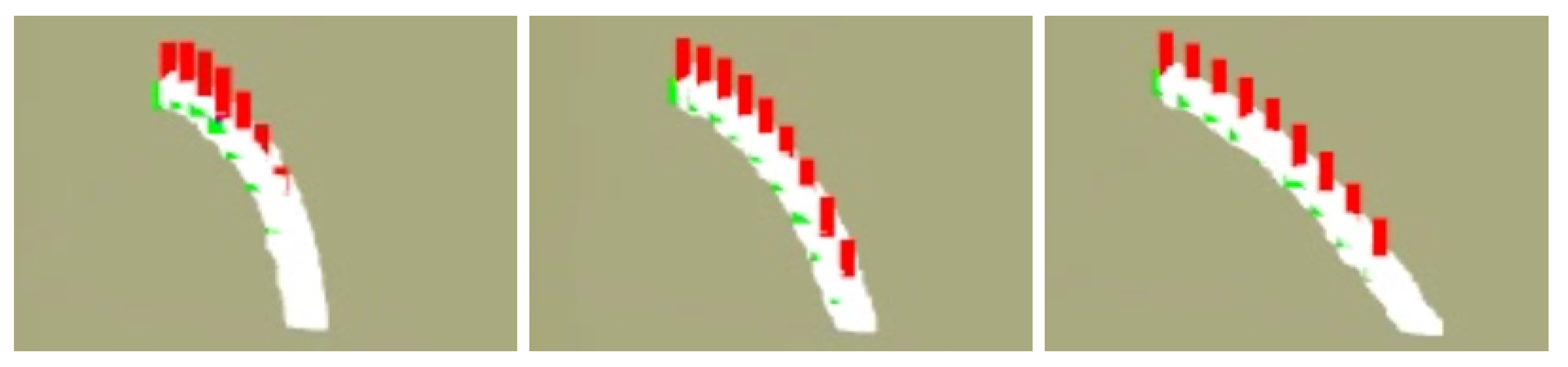
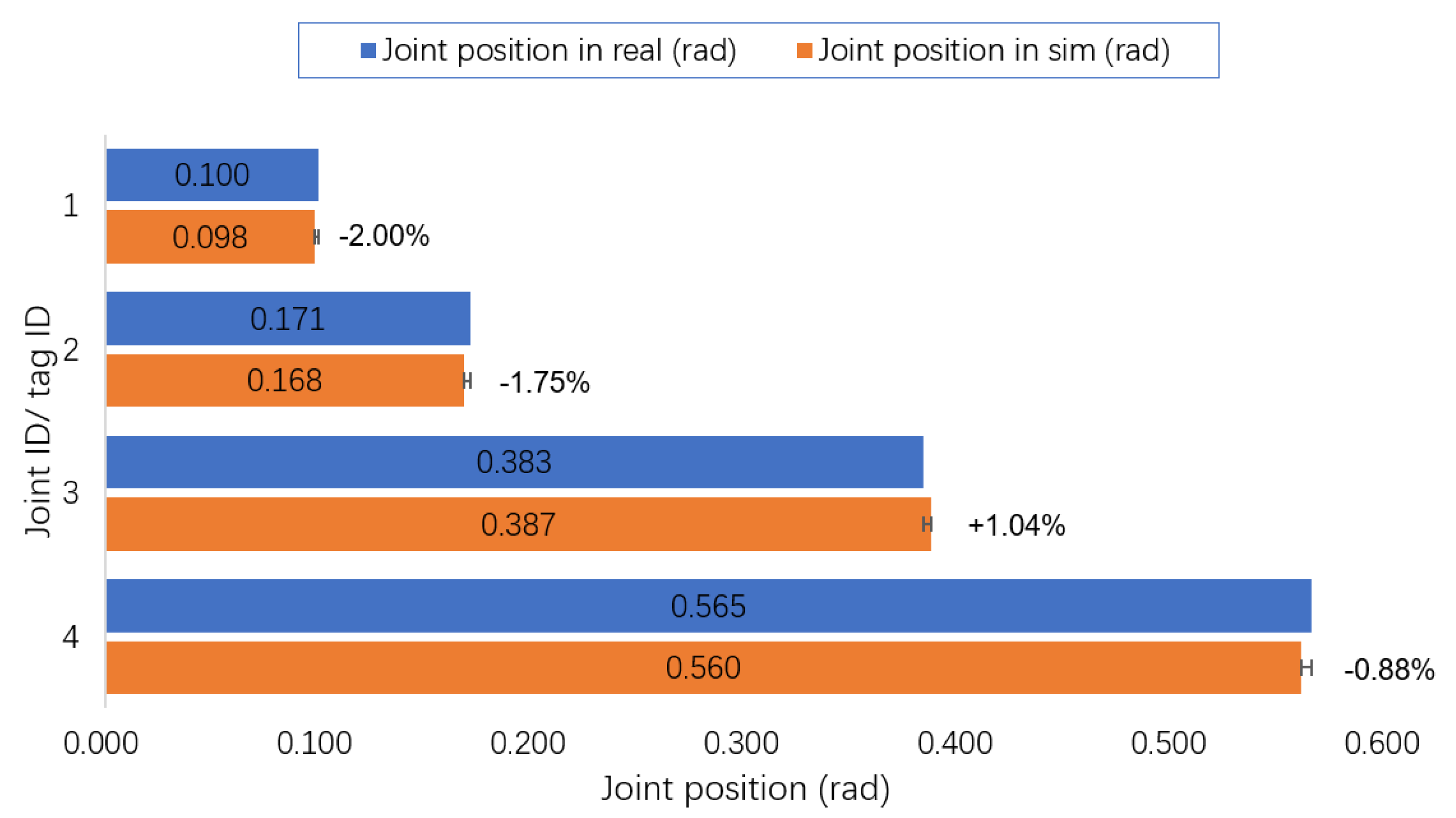
4.1. Validation of the Geometrical Modeling of the Cable and the Pose Alignment Controller
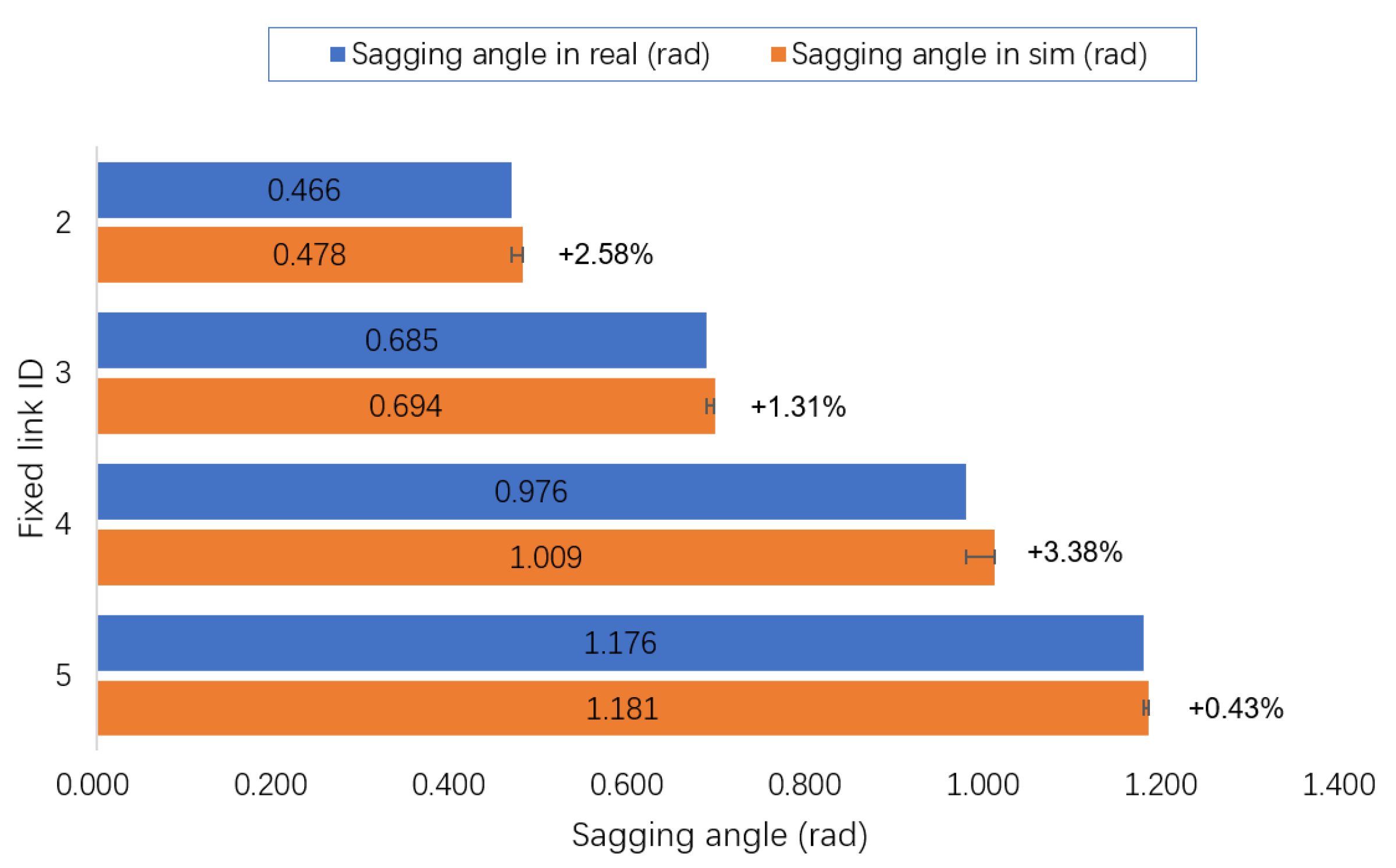
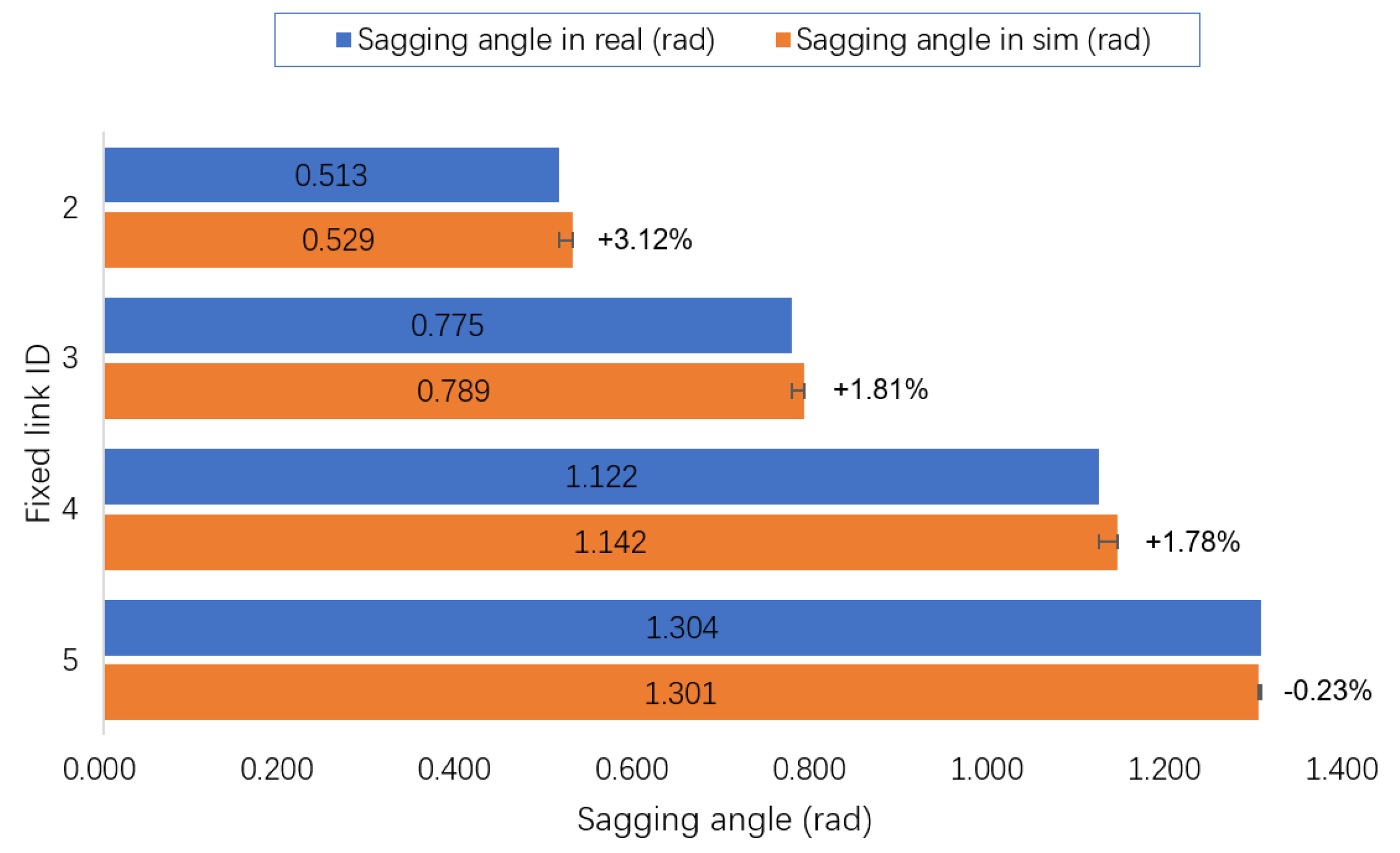
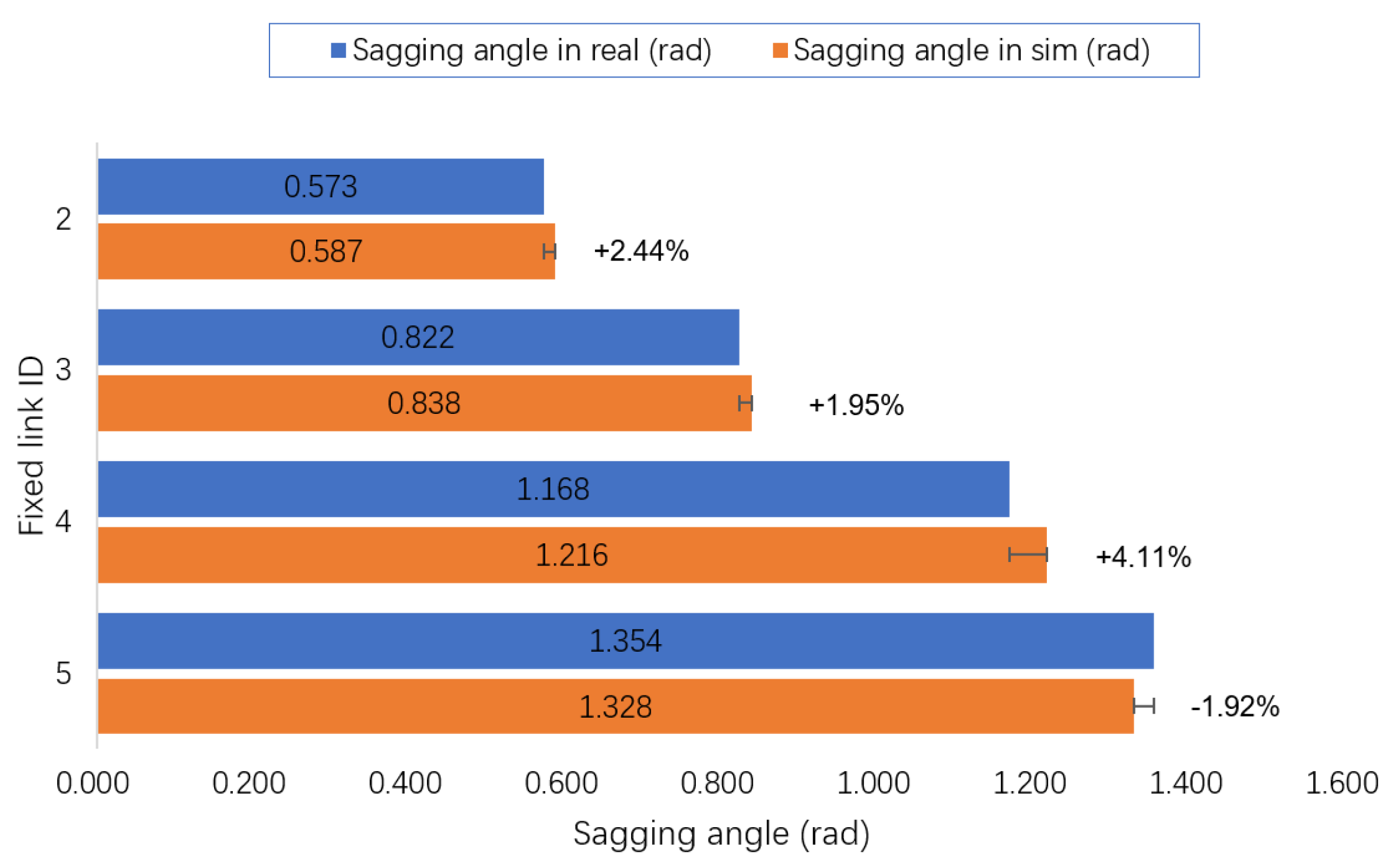
4.2. Validation of the Cable Model in Simulation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sanchez, J.; Corrales, J.A.; Bouzgarrou, B.C.; Mezouar, Y. Robotic manipulation and sensing of deformable objects in domestic and industrial applications: A survey. Int. J. Robot. Res. 2018, 37, 688–716. [Google Scholar] [CrossRef]
- Lee, A.X.; Lu, H.; Gupta, A.; Levine, S.; Abbeel, P. Learning force-based manipulation of deformable objects from multiple demonstrations. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Washington, DC, USA, 26–30 May 2015; pp. 177–184. [Google Scholar]
- Nair, A.; Chen, D.; Agrawal, P.; Isola, P.; Abbeel, P.; Malik, J.; Levine, S. Combining self-supervised learning and imitation for vision-based rope manipulation. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2146–2153. [Google Scholar]
- Miller, S.; Van Den Berg, J.; Fritz, M.; Darrell, T.; Goldberg, K.; Abbeel, P. A geometric approach to robotic laundry folding. Int. J. Robot. Res. 2012, 31, 249–267. [Google Scholar] [CrossRef]
- Mallapragada, V.; Sarkar, N.; Podder, T.K. Toward a robot-assisted breast intervention system. IEEE/ASME Trans. Mechatron. 2011, 16, 1011–1020. [Google Scholar] [CrossRef]
- White, J.R.; Satterlee, P.E., Jr.; Walker, K.L.; Harvey, H.W. Remotely Controlled and/or Powered Mobile Robot with Cable Management Arrangement. U.S. Patent 4,736,826, 12 April 1988. [Google Scholar]
- Tang, T.; Wang, C.; Tomizuka, M. A framework for manipulating deformable linear objects by coherent point drift. IEEE Robot. Autom. Lett. 2018, 3, 3426–3433. [Google Scholar] [CrossRef]
- Wang, W.; Berenson, D.; Balkcom, D. An online method for tight-tolerance insertion tasks for string and rope. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Washington, DC, USA, 26–30 May 2015; pp. 2488–2495. [Google Scholar]
- Lui, W.H.; Saxena, A. Tangled: Learning to untangle ropes with rgb-d perception. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 837–844. [Google Scholar]
- Papacharalampopoulos, A.; Makris, S.; Bitzios, A.; Chryssolouris, G. Prediction of cabling shape during robotic manipulation. Int. J. Adv. Manuf. Technol. 2016, 82, 123–132. [Google Scholar] [CrossRef]
- Zhu, J.; Navarro, B.; Fraisse, P.; Crosnier, A.; Cherubini, A. Dual-arm robotic manipulation of flexible cables. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 479–484. [Google Scholar]
- Spenko, M.; Buerger, S.; Iagnemma, K. The DARPA Robotics Challenge Finals: Humanoid Robots to the Rescue; Springer: Berlin, Germany, 2018; Volume 121. [Google Scholar]
- Cisneros, R.; Nakaoka, S.; Morisawa, M.; Kaneko, K.; Kajita, S.; Sakaguchi, T.; Kanehiro, F. Effective teleoperated manipulation for humanoid robots in partially unknown real environments: Team AIST-NEDO’s approach for performing the Plug Task during the DRC Finals. Adv. Robot. 2016, 30, 1544–1558. [Google Scholar] [CrossRef]
- DeDonato, M.; Polido, F.; Knoedler, K.; Babu, B.P.; Banerjee, N.; Bove, C.P.; Cui, X.; Du, R.; Franklin, P.; Graff, J.P.; et al. Team WPI-CMU: Achieving Reliable Humanoid Behavior in the DARPA Robotics Challenge. J. Field Robot. 2017, 34, 381–399. [Google Scholar] [CrossRef]
- Lv, N.; Liu, J.; Xia, H.; Ma, J.; Yang, X. A review of techniques for modeling flexible cables. Comput. Aided Des. 2020, 122, 102826. [Google Scholar] [CrossRef]
- Chen, C.; Zheng, Y.F. Deformation identification and estimation of one-dimensional objects by vision sensors. J. Robot. Syst. 1992, 9, 595–612. [Google Scholar] [CrossRef]
- Wakamatsu, H.; Hirai, S.; Iwata, K. Modeling of linear objects considering bend, twist, and extensional deformations. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; Volume 1, pp. 433–438. [Google Scholar]
- Nakagaki, H.; Kitagi, K.; Ogasawara, T.; Tsukune, H. Study of insertion task of a flexible wire into a hole by using visual tracking observed by stereo vision. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; Volume 4, pp. 3209–3214. [Google Scholar]
- Linn, J.; Stephan, T.; Carlsson, J.; Bohlin, R. Fast simulation of quasistatic rod deformations for VR applications. In Progress in Industrial Mathematics at ECMI 2006; Springer: Berlin, Germany, 2008; pp. 247–253. [Google Scholar]
- Caldwell, T.M.; Coleman, D.; Correll, N. Optimal parameter identification for discrete mechanical systems with application to flexible object manipulation. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 898–905. [Google Scholar]
- Yoshida, E.; Ayusawa, K.; Ramirez-Alpizar, I.G.; Harada, K.; Duriez, C.; Kheddar, A. Simulation-based optimal motion planning for deformable object. In Proceedings of the 2015 IEEE International Workshop on Advanced Robotics and its Social Impacts (ARSO), Lyon, France, 1–3 July 2015; pp. 1–6. [Google Scholar]
- Lv, N.; Liu, J.; Ding, X.; Liu, J.; Lin, H.; Ma, J. Physically based real-time interactive assembly simulation of cable harness. J. Manuf. Syst. 2017, 43, 385–399. [Google Scholar] [CrossRef]
- Navarro-Alarcón, D.; Liu, Y.H.; Romero, J.G.; Li, P. Model-free visually servoed deformation control of elastic objects by robot manipulators. IEEE Trans. Robot. 2013, 29, 1457–1468. [Google Scholar] [CrossRef]
- Navarro-Alarcon, D.; Liu, Y.h.; Romero, J.G.; Li, P. On the visual deformation servoing of compliant objects: Uncalibrated control methods and experiments. Int. J. Robot. Res. 2014, 33, 1462–1480. [Google Scholar] [CrossRef]
- Navarro-Alarcon, D.; Yip, H.M.; Wang, Z.; Liu, Y.H.; Zhong, F.; Zhang, T.; Li, P. Automatic 3D manipulation of soft objects by robotic arms with an adaptive deformation model. IEEE Trans. Robot. 2016, 32, 429–441. [Google Scholar] [CrossRef]
- Navarro-Alarcon, D.; Liu, Y.H. Fourier-based shape servoing: A new feedback method to actively deform soft objects into desired 2D image contours. IEEE Trans. Robot. 2018, 34, 272–279. [Google Scholar] [CrossRef]
- Jin, S.; Wang, C.; Tomizuka, M. Robust Deformation Model Approximation for Robotic Cable Manipulation. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 6586–6593. [Google Scholar]
- Chang, P.; Padir, T. Sim2Real2Sim: Bridging the Gap Between Simulation and Real World in Flexible Object Manipulation. arXiv 2020, arXiv:2002.02538. [Google Scholar]
- Chang, P.; Padir, T. Model-Based Manipulation of Linear Flexible Objects with Visual Curvature Feedback. arXiv 2020, arXiv:2007.08083. [Google Scholar]
- Yuen, H.; Princen, J.; Illingworth, J.; Kittler, J. Comparative study of Hough transform methods for circle finding. Image Vis. Comput. 1990, 8, 71–77. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 779–788. [Google Scholar]
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Chitta, S.; Sucan, I.; Cousins, S. Moveit! [ROS topics]. IEEE Robot. Autom. Mag. 2012, 19, 18–19. [Google Scholar] [CrossRef]
- Schulman, J.; Duan, Y.; Ho, J.; Lee, A.; Awwal, I.; Bradlow, H.; Pan, J.; Patil, S.; Goldberg, K.; Abbeel, P. Motion planning with sequential convex optimization and convex collision checking. Int. J. Robot. Res. 2014, 33, 1251–1270. [Google Scholar] [CrossRef]
- Khalil, W.; Dombre, E. Modeling, Identification and Control of Robots; Butterworth-Heinemann: Oxford, UK, 2004. [Google Scholar]
- Žlajpah, L. Simulation in robotics. Math. Comput. Simul. 2008, 79, 879–897. [Google Scholar] [CrossRef]
- Koenig, N.; Howard, A. Design and use paradigms for gazebo, an open-source multi-robot simulator. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2149–2154. [Google Scholar]
- Webster, R.J., III; Jones, B.A. Design and kinematic modeling of constant curvature continuum robots: A review. Int. J. Robot. Res. 2010, 29, 1661–1683. [Google Scholar] [CrossRef]
- Della Santina, C.; Katzschmann, R.K.; Biechi, A.; Rus, D. Dynamic control of soft robots interacting with the environment. In Proceedings of the 2018 IEEE International Conference on Soft Robotics (RoboSoft), Livorno, Italy, 24–28 April 2018; pp. 46–53. [Google Scholar]
- Farchy, A.; Barrett, S.; MacAlpine, P.; Stone, P. Humanoid robots learning to walk faster: From the real world to simulation and back. In Proceedings of the 2013 international conference on Autonomous Agents and Multi-Agent Systems, St. Paul, MN, USA, 6–10 May 2013; pp. 39–46. [Google Scholar]
- Lund, H.H.; Miglino, O. From simulated to real robots. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nayoya, Japan, 20–22 May 1996; pp. 362–365. [Google Scholar]
- Koos, S.; Mouret, J.B.; Doncieux, S. Crossing the reality gap in evolutionary robotics by promoting transferable controllers. In Proceedings of the 12th Annual Conference on Genetic and Evolutionary Computation, Portland, OR, USA, 24 July 2010; pp. 119–126. [Google Scholar]
- Carpin, S.; Lewis, M.; Wang, J.; Balakirsky, S.; Scrapper, C. Bridging the Gap between Simulation and Reality in Urban Search and Rescue; Springer: Berlin, Germany, 2006; pp. 1–12. [Google Scholar]
- Hanna, J.P. Bridging the Gap Between Simulation and Reality. In Proceedings of the 16th Conference on Autonomous Agents and MultiAgent Systems, Paulo, Brazil, 8–12 May 2017; pp. 1834–1835. [Google Scholar]
- Wonsick, M.; Dimitrov, V.; Padir, T. Analysis of the Space Robotics Challenge Tasks: From Simulation to Hardware Implementation. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; pp. 1–8. [Google Scholar]
- Peng, X.B.; Andrychowicz, M.; Zaremba, W.; Abbeel, P. Sim-to-real transfer of robotic control with dynamics randomization. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 1–8. [Google Scholar]
- Bousmalis, K.; Irpan, A.; Wohlhart, P.; Bai, Y.; Kelcey, M.; Kalakrishnan, M.; Downs, L.; Ibarz, J.; Pastor, P.; Konolige, K.; et al. Using simulation and domain adaptation to improve efficiency of deep robotic grasping. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 4243–4250. [Google Scholar]
- Olson, E. AprilTag: A robust and flexible visual fiducial system. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3400–3407. [Google Scholar]
- dos Santos Cesar, D.B.; Gaudig, C.; Fritsche, M.; dos Reis, M.A.; Kirchner, F. An evaluation of artificial fiducial markers in underwater environments. In Proceedings of the OCEANS 2015, Genoa, Italy, 18–21 May 2015; pp. 1–6. [Google Scholar]
- Walker, M.W.; Orin, D.E. Efficient Dynamic Computer Simulation of Robotic Mechanisms; Springer: Berlin, Germany, 1982. [Google Scholar]
- Luh, J.Y.; Walker, M.W.; Paul, R.P. On-Line Computational Scheme for Mechanical Manipulators. Dyn. Syst. Meas. Control. 1980, 102, 69–76. [Google Scholar] [CrossRef]
- Siciliano, B.; Sciavicco, L.; Villani, L.; Oriolo, G. Robotics: Modelling, Planning and Control; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Diankov, R.; Kuffner, J. Openrave: A Planning Architecture for Autonomous Robotics; Robotics Institute: Pittsburgh, PA, USA, 2008; Volume 79. [Google Scholar]


















| Poses | ||||||
|---|---|---|---|---|---|---|
| left | −1.882 | −7.295 | −5.773 | −6.041 | −20.004 | −15.528 |
| middle | −0.385 | −2.670 | −2.191 | −1.917 | −6.981 | −5.243 |
| right | 0.006 | −1.377 | −1.125 | −0.979 | −3.955 | −2.806 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, P.; Padır, T. Model-Based Manipulation of Linear Flexible Objects: Task Automation in Simulation and Real World. Machines 2020, 8, 46. https://doi.org/10.3390/machines8030046
Chang P, Padır T. Model-Based Manipulation of Linear Flexible Objects: Task Automation in Simulation and Real World. Machines. 2020; 8(3):46. https://doi.org/10.3390/machines8030046
Chicago/Turabian StyleChang, Peng, and Taşkın Padır. 2020. "Model-Based Manipulation of Linear Flexible Objects: Task Automation in Simulation and Real World" Machines 8, no. 3: 46. https://doi.org/10.3390/machines8030046
APA StyleChang, P., & Padır, T. (2020). Model-Based Manipulation of Linear Flexible Objects: Task Automation in Simulation and Real World. Machines, 8(3), 46. https://doi.org/10.3390/machines8030046





