Dynamic Torque Limitation Principle in the Main Line of a Mill Stand: Explanation and Rationale for Use
Abstract
:1. Introduction
- -
- optimizing the functions to control the electric drive;
- -
- reducing the rigidity of mechanical gears;
- -
- monitoring the elastic torque by special software, etc.
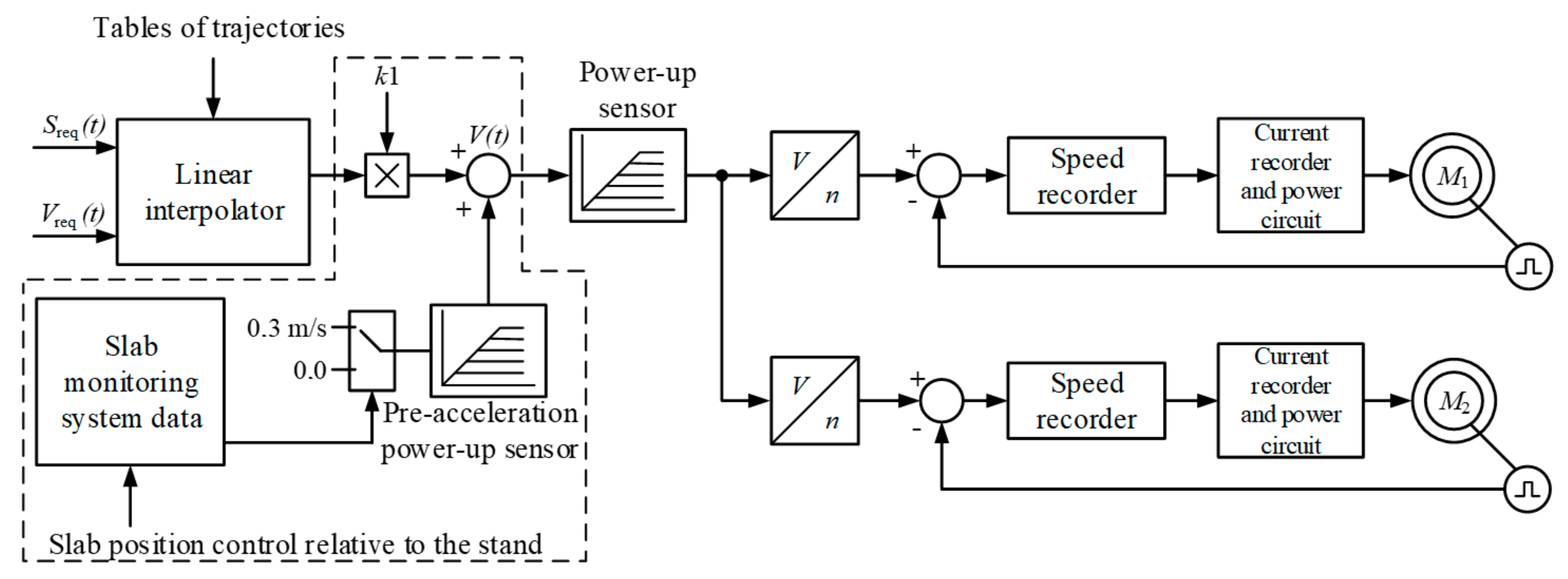
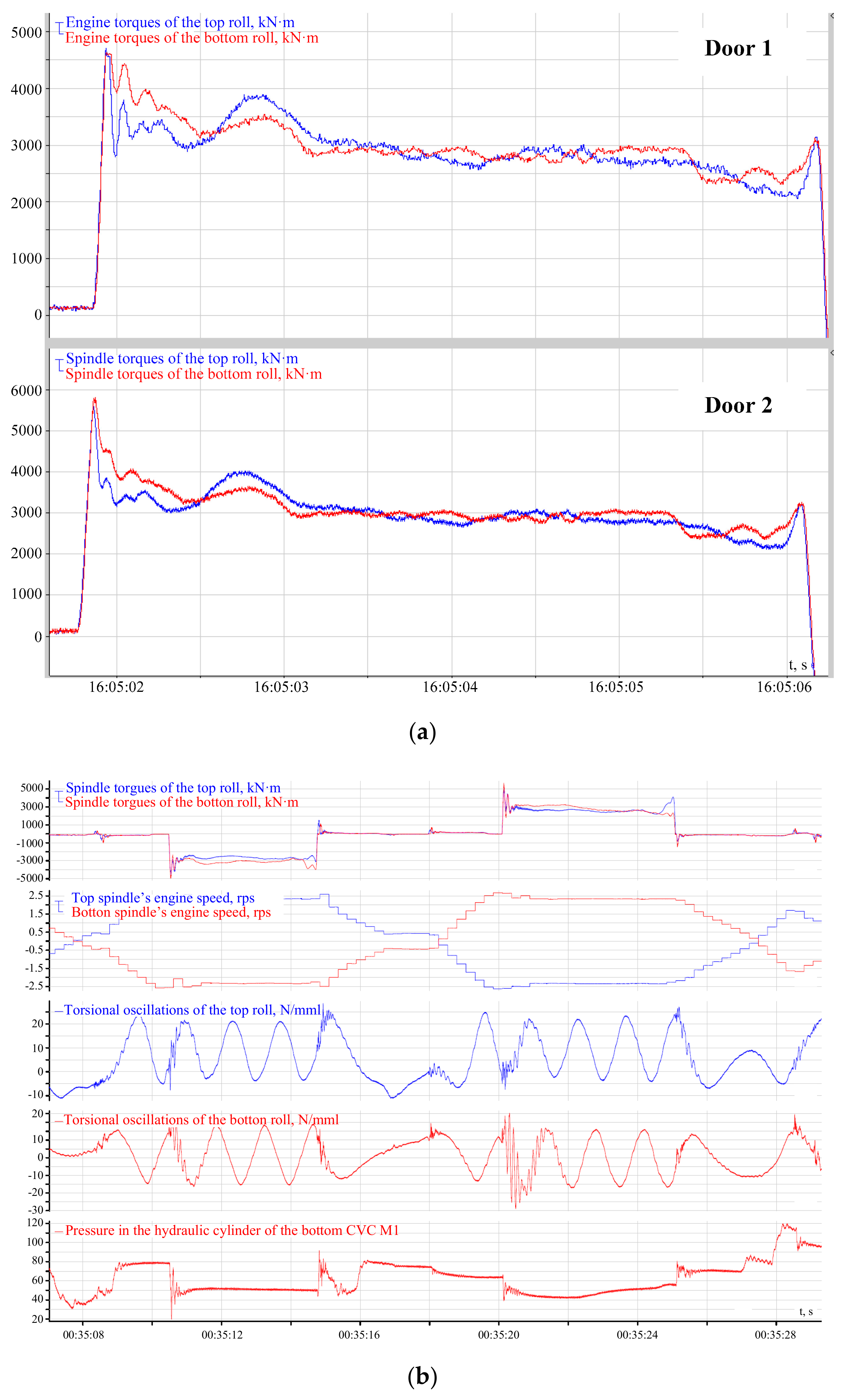
2. Statement of Problem
- (1)
- Impact torque amplitude at the moment of capture (Figure 3a, door 2) is nearly double the configured rolling torque (up to 5.8 MN·m vs. 3 MN·m).
- (2)
- Torsional oscillations overlaying a sine wave caused by shaft rotation feature a high amplitude, especially in case of the bottom spindle (Figure 3b).
- (3)
- Engine and spindle torques change identically with slight differences in the maximum torque and the time attain it. As mechanical and electrical systems are inertial, the maximum shaft torque (Figure 3a, door 2) is attained earlier than that of the engine (door 1). The difference is 0.1–0.15 s.
- (4)
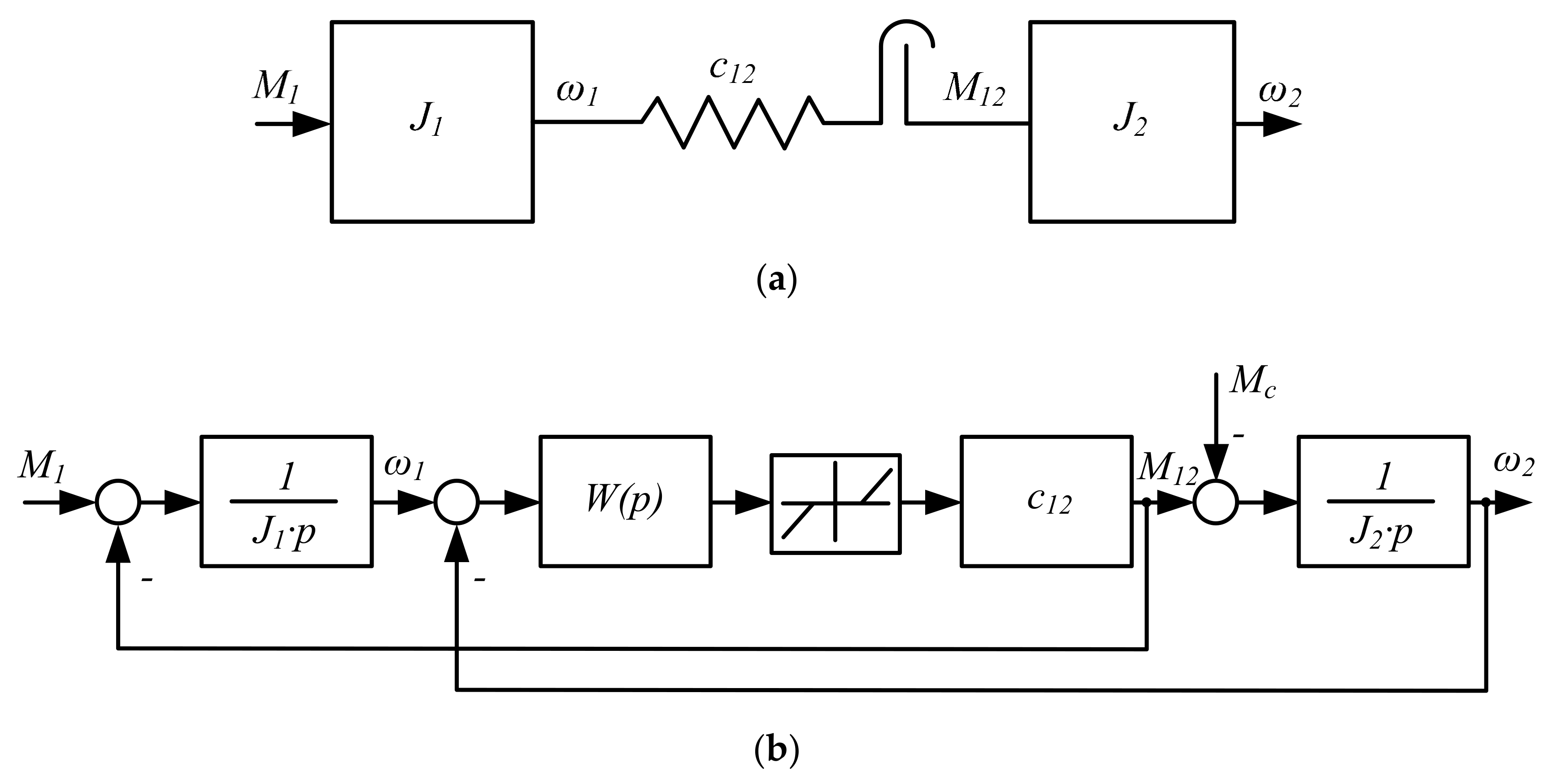
3. Analysis of Elastic Torque Components when Choosing Play
- -
- ensure play closure by means of pre-acceleration to minimize the second component;
- -
- decelerate the electric drive after capture with a set negative acceleration.
4. Dynamic Torque Limitation Principle
- -
- caused by an impact at angular play closure;
- -
- caused by elastic properties of the mechanical gear;
- -
- caused by settings of the automatic electric drive speed control system (ACS).
- (1)
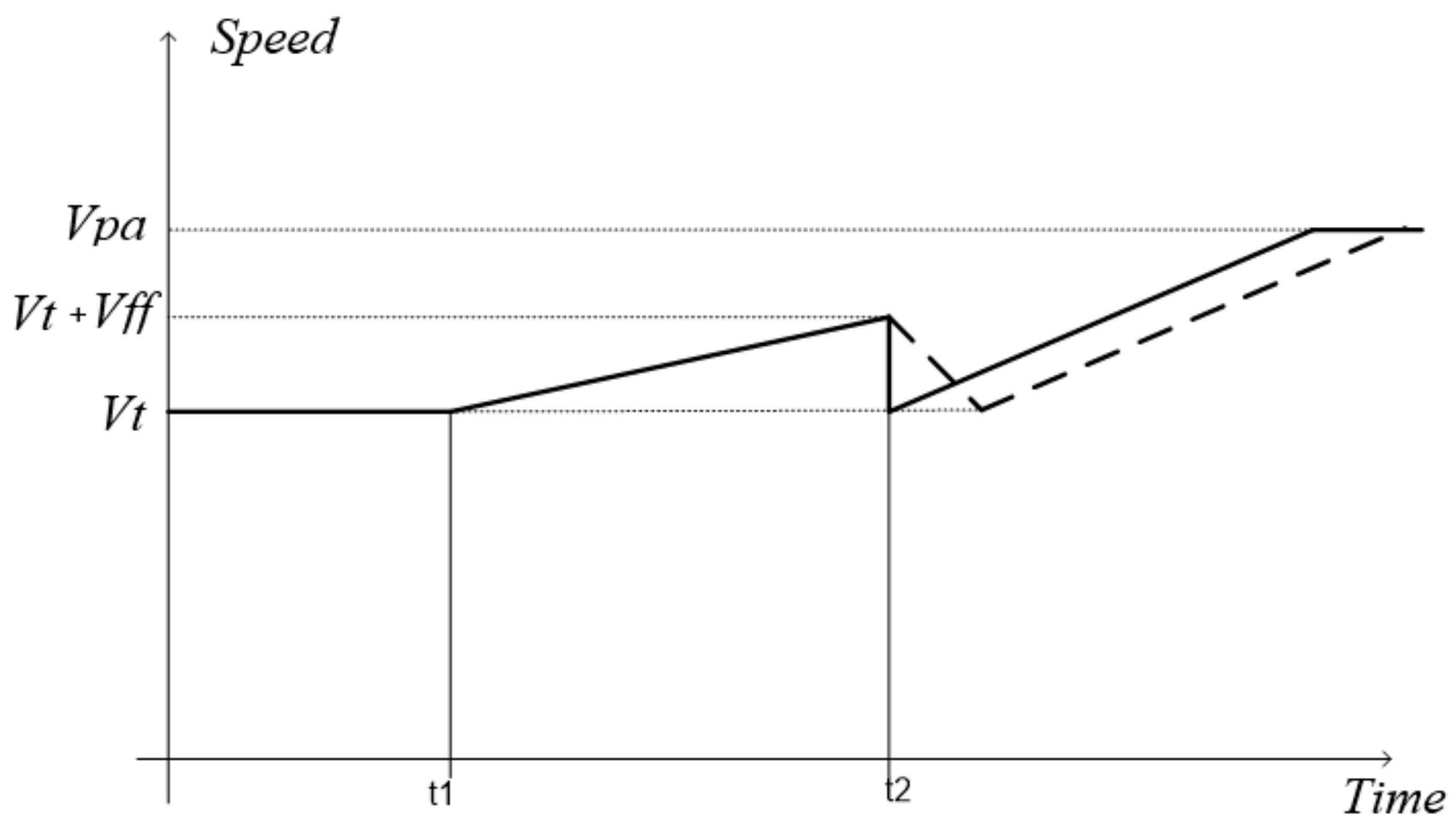
- Before the shock loading, the system is pre-accelerated with the minimum initial acceleration to choose play regardless of its value. This helps to compensate for component M12δ caused by an impact (lower component of the elastic torque).
- (2)
- In order to compensate for component M12y, after the shock loading, the speed is reduced using set negative acceleration (deceleration rate).
- -
- metal is captured when the electric drive is accelerated;
- -
- the speed at the time of capture must be equal to the value required to compensate for the dynamic speed control error;
- -
- when to start accelerating the drive is determined by the distance between the “head” of a slab and the stand calculated as follows:
- -
- the speed is reduced after capture according to the linear law with set negative acceleration (according to simulation results, the optimal acceleration for the electric drive of rolling mill stand 5000 rolls varies from −2.5 to −3.5 rad/s2).
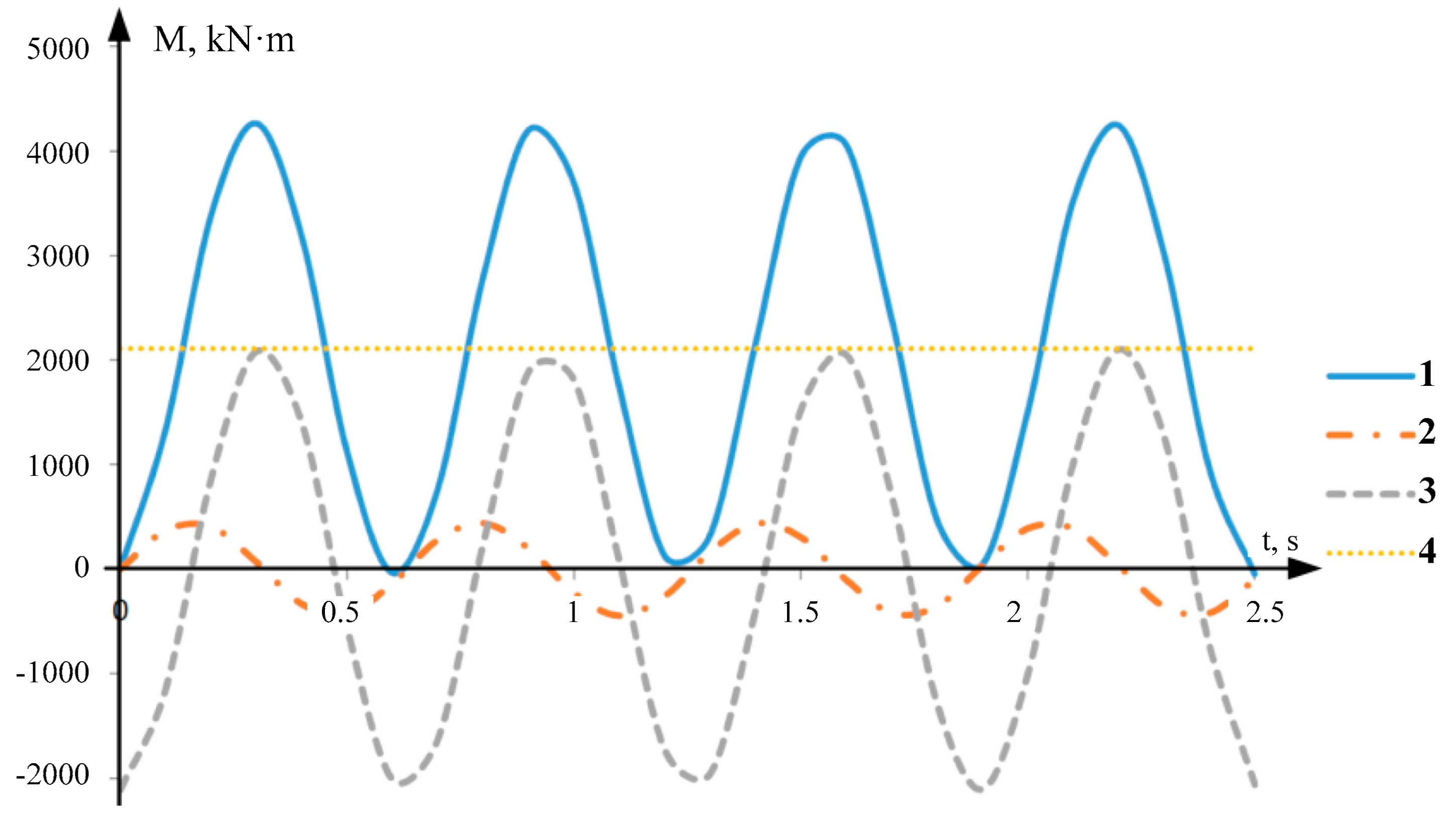
5. Discussion of the Results
6. Conclusions
- (1)
- Caused by an elastic impact at angular play closure.
- (2)
- Caused by elastic properties of the shaft line.
- (3)
- Caused by settings of the automatic electric drive speed control system.
Author Contributions
Funding
Conflicts of Interest
References
- Artyukh, V.G. Fundamentals of protection of metallurgical machines from breakdowns. Mariupol Univ. 2015, 288. Available online: http://eir.pstu.edu/handle/123456789/6946 (accessed on 10 December 2019).
- Artyukh, V.G. Loads and overloads in metallurgical machines. Mariupol PGTU 2008, 246. Available online: http://eir.pstu.edu/handle/123456789/5751 (accessed on 10 December 2019).
- Artyukh, V.G.; Аrtyukh, G.V.; Mazur, V.O. Horizontal rolling forces. Mariupol Bull. Priazov State Tech. Univ. 2009, 19, 128–132. [Google Scholar]
- Mazur, V.O. Horizontal Strength during Rolling as an Indicator of the Manufacturability of the Rolling. Available online: http://nbuv.gov.ua/UJRN/Zmmvp_2013_15_4 (accessed on 9 September 2019).
- Ishchenko, A.A.; Kalinichenko, I.A.; Grishko, V.P. Experimental evaluation of shock loads on beds of working stands of plate mills. Stal 2009, 5, 56–58. [Google Scholar]
- Mazur, V.; Artyukh, V.; Artyukh, G.; Takadzhi, M. Current views on the detailed design of heavily loaded components for rolling mills. Eng. Des. 2012, 37, 26–29. [Google Scholar]
- Artyukh, V.G. Possibility of hot rolling of steel sheets of larger mass. Mariupol 2011, 13, 148–153. [Google Scholar]
- Russian Federation; Ministry of Industry and Trade of the Russian Federation. On approval of the Strategy for the Development of Ferrous Metallurgy in Russia for 2014–2020 and for the Long Term until 2030 and the Strategy for the Development of Non-Ferrous Metallurgy in Russia for 2014–2020 and for the Long Term until 2030. Available online: http://www.garant.ru/products/ipo/prime/doc/70595824/ (accessed on 9 September 2019).
- Denisov, S.V. Innovative achievements of PJSC MMK in the production of modern rolled metal. Magnitogorsk 2017, 2, 21–29. [Google Scholar]
- Khramshin, V.R. Ways to compensate for static deviations in speed in electric drives of broad-strip hot rolling-mill stands. Russ. Electr. Eng. 2013, 84, 221–227. [Google Scholar] [CrossRef]
- Kunitsyn, G.A.; Denisov, S.V.; Gorshkov, S.N.; Galkin, M.G. The commissioning of plate mill 5000 is a new stage in the development of rolled metal production technology at OJSC MMK. Metallurg 2009, 7, 4–5. [Google Scholar]
- Karandaev, A.S.; Loginov, B.M.; Gasiiarov, V.R.; Khramshin, V.R. Force limiting at roll axial shifting of plate mill. Procedia Eng. 2017, 206, 1780–1786. [Google Scholar] [CrossRef]
- Karandaev, A.S.; Loginov, B.M.; Radionov, A.A.; Gasiiarov, V.R. Setting Automated Roll Axial Shifting Control System of Plate Mill. Procedia Eng. 2017, 206, 1753–1760. [Google Scholar] [CrossRef]
- Gasiiarov, V.R.; Radionov, A.A.; Loginov, B.M.; Voronin, S.S.; Khramshin, V.R. Improvement of Work Roll Bending Control System Installed at Plate Mill Stand. In Proceedings of the 9th International Conference on Computer and Automation Engineering (ICCAE 2017), Sydney, Australia, 18–21 February 2017; pp. 269–273. [Google Scholar]
- Krot, P.V. Hot rolling mill drive train dynamics: Torsional vibration control and backlash diagnostics. Millenn. Steel China 2009, 91–95. Available online: https://www.researchgate.net/profile/Pavlo_Krot/publication/202044159_Hot_rolling_mill_drive_train_dynamics_torsional_vibration_control_and_backlashes_diagnostics/links/5c6d17c24585156b570ae2d2/Hot-rolling-mill-drive-train-dynamics-torsional-vibration-control-and-backlashes-diagnostics.pdf (accessed on 10 December 2019).
- Tselikov, A.I.; Polukhin, P.I.; Grebenik, V.M. Machines and assemblies of metallurgical plants. Machines and aggregates for the production of rolled metal. Metallurgiya 1988, 3, 680. [Google Scholar]
- Klyuchev, V.I. Drive dynamic load limitation. Energiya 1971, 320. Available online: https://lib-bkm.ru/load/65-1-0-1272 (accessed on 10 December 2019).
- Meshcheryakov, V.N. Development of a method for reducing dynamic loads of an electric drive of a rolling stand of a cold rolling mill. Electrotech. Syst. Complexes 2015, 3, 14–19. [Google Scholar]
- Verenev, V.V.; Bol'shakov, V.I.; Podobedov, N.I. The influence of the speed of capture of the strip on the dynamic loads in the drive stand. Fundam. Appl. Probl. Steel Ind. (IChM) 2007, 14, 260–266. [Google Scholar]
- Podobedov, N.I. Efficiency conditions for the use of acceleration of the rolling stand drive as a way to close gaps. Fundam. Appl. Probl. Steel Ind. (IChM) 2006, 12, 311–317. [Google Scholar]
- Karandaev, A.S.; Gasiiarov, V.R.; Maklakova, E.A.; Loginov, B.M.; Khramshina, E.A. Method limiting dynamic loads of electromechanical systems of plate mill stand. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Moscow and St. Petersburg, Russia, 29 January–1 February 2018. [Google Scholar]
- Khramshin, V.R.; Gasiiarov, V.R.; Karandaev, A.S.; Baskov, S.N.; Loginov, B.M. Constraining the Dynamic Torque of a Rolling Mill Stand Drive. Bull. South Ural State Univ. Ser. Energy 2018, 18, 101–111. [Google Scholar]
- Shubin, A.G.; Loginov, B.M.; Gasiiarov, V.R.; Maklakova, E.A. Substantiation of methods for limiting dynamic loads of electromechanical systems of a mill stand. Electrotech. Syst. Complexes 2018, 1, 14–25. [Google Scholar] [CrossRef]
- Evdokimov, S.A.; Khal'ko, A.I.; Dorofeev, A.M. A telemetry system for measuring elastic torque in spindles of horizontal rolls of the working stand of mill 5000. Energy Electr. Syst. 2015, 375–382. [Google Scholar]
- Salganik, V.M. Modern technologies for the production of sheet metal. In Proceedings of the Innovative Technologies in Metallurgy and Mechanical Engineering: Materials of the 6th International Youth Scientific-Practical Conference Innovative Technologies in Metallurgy and Mechanical Engineering, Golovin Ural Scientific and Pedagogical School, Yekaterinburg, Russia, 29 October–1 November 2012. [Google Scholar]
- Verenev, V.V.; Podobedov, N.I.; Belodedenko, S.V. Monitoring the dynamic loading of roll lines of a plate mill stand. Metall. Min. Ind. 2015, 7, 110–113. [Google Scholar]

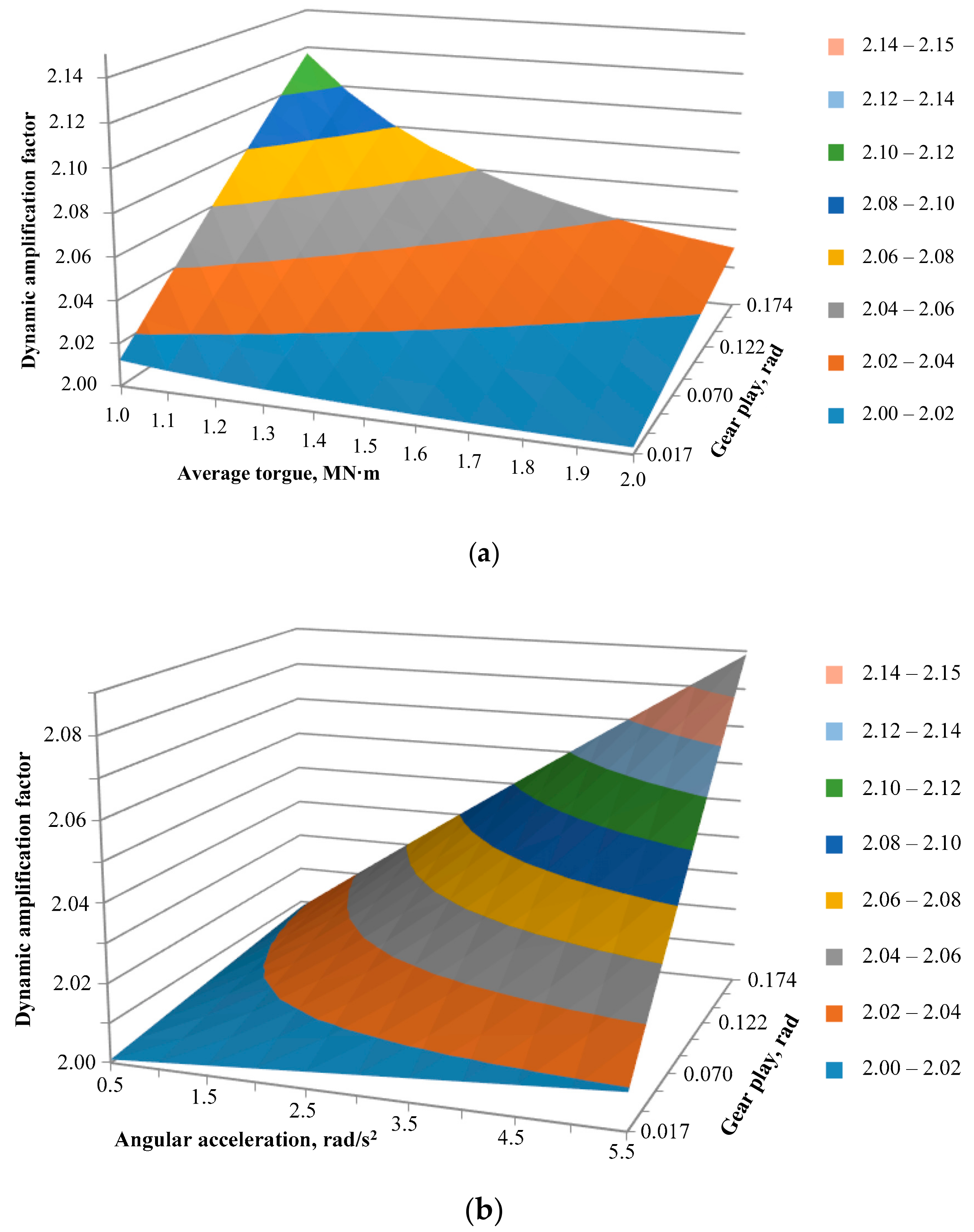
| Parameter | Designation | Value |
|---|---|---|
| Stiffness of the elastic coupling | c12 | 5,934,842 N·m/rad |
| Moment of inertia of the first moving mass (engine) | J1 | 125,000 kg·m2 |
| Moment of inertia of the second moving mass | J2 | 114,571 kg·m2 |
| Natural frequency of elastic oscillations | ω12 | 9.96 rad/s |
| Initial acceleration of the electric drive | ε0 | 1–3 rad/s2 |
| Gear play | δ | 1–10° |
| Average elastic torque | M12c | 1.9 MN·m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gasiyarov, V.R.; Khramshin, V.R.; Voronin, S.S.; Lisovskaya, T.A.; Gasiyarova, O.A. Dynamic Torque Limitation Principle in the Main Line of a Mill Stand: Explanation and Rationale for Use. Machines 2019, 7, 76. https://doi.org/10.3390/machines7040076
Gasiyarov VR, Khramshin VR, Voronin SS, Lisovskaya TA, Gasiyarova OA. Dynamic Torque Limitation Principle in the Main Line of a Mill Stand: Explanation and Rationale for Use. Machines. 2019; 7(4):76. https://doi.org/10.3390/machines7040076
Chicago/Turabian StyleGasiyarov, V.R., V.R. Khramshin, S.S. Voronin, T.A. Lisovskaya, and O.A. Gasiyarova. 2019. "Dynamic Torque Limitation Principle in the Main Line of a Mill Stand: Explanation and Rationale for Use" Machines 7, no. 4: 76. https://doi.org/10.3390/machines7040076
APA StyleGasiyarov, V. R., Khramshin, V. R., Voronin, S. S., Lisovskaya, T. A., & Gasiyarova, O. A. (2019). Dynamic Torque Limitation Principle in the Main Line of a Mill Stand: Explanation and Rationale for Use. Machines, 7(4), 76. https://doi.org/10.3390/machines7040076







