Multivariable Control of Solar Battery Power by Extremum Seeking: Starting from Linear Analysis
Abstract
:1. Some of the Most Important Aspects of the Problem
- The requirements for the quality of transient processes are rarely imposed on closed search engines. The main requirement is the convergence to the minimum/maximum point as fast as possible (studied within the framework of asymptotic stability [28,33]), which is determined by the parameters of the extremal control loops, as well as by the amplitudes and frequencies of the modulating signals.
- The multiparameter system of extremum seeking has the properties of multiply connectedness and requires the use of nonlinear methods of analysis (some of them were mentioned in the annotation, as well as in [28]).
- Introduction to the system of a nonlinear element, which is difficult to reduce to a simple quadratic function with displacement along the axes of the abscissas and ordinates [34], increases the complexity of the exact analytical studies and does not allow them to be made by direct paths.
- with the construction of methods for calculating the parameters of the solar panel using elements of special functions (for example, the Lambert function);
- with accurate dynamic models on their basis that allow us to evaluate the dynamics of the reaction of voltage changes to changes in photocurrent when the angular position changes during modulation.
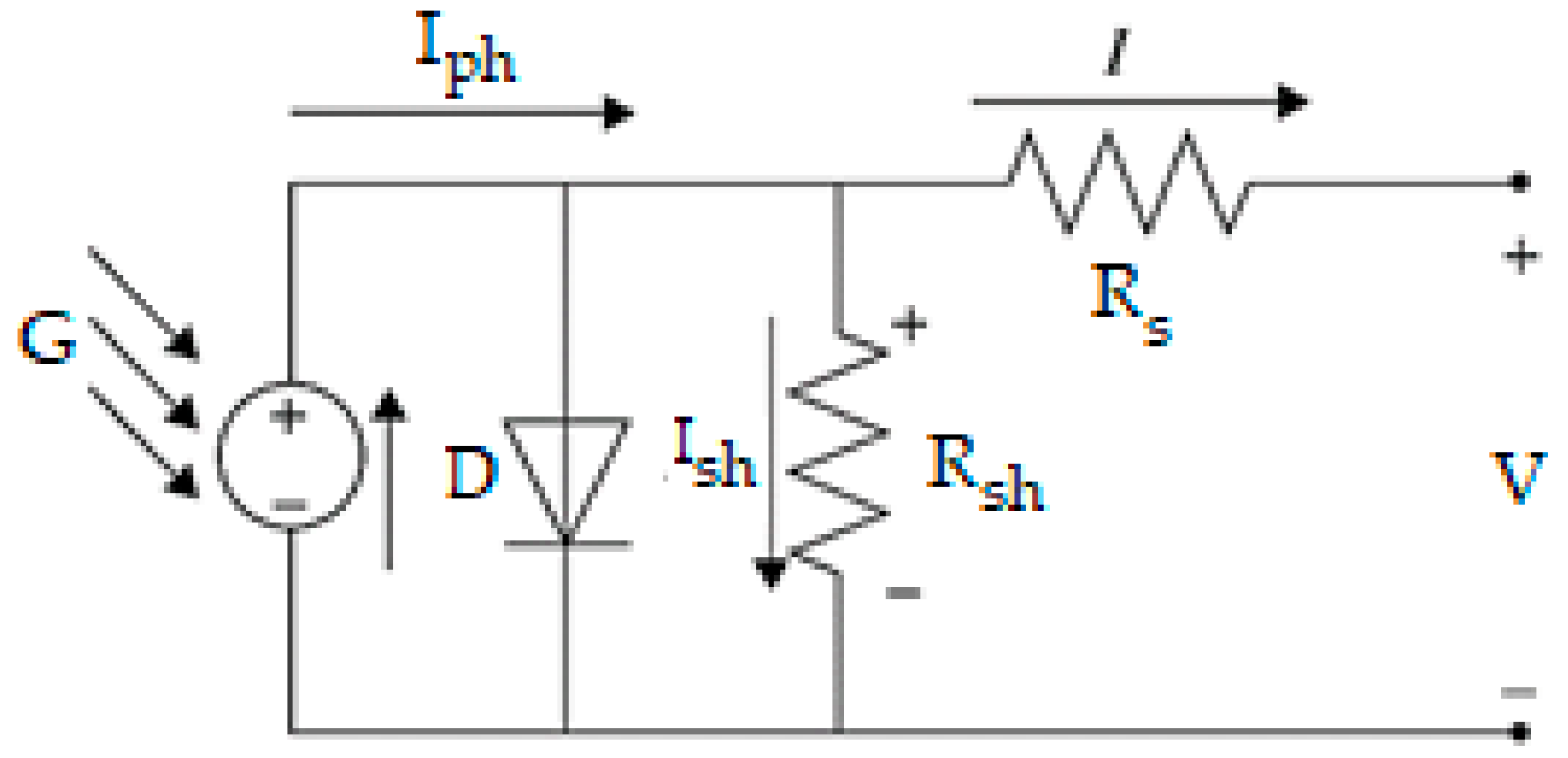
2. Solar Battery—Multiparameter Object of Extremum Seeking Control. Parametric Identification of the Voltage-Current and Volt-Watt Characteristics of the Solar Panel in an Analytical Way
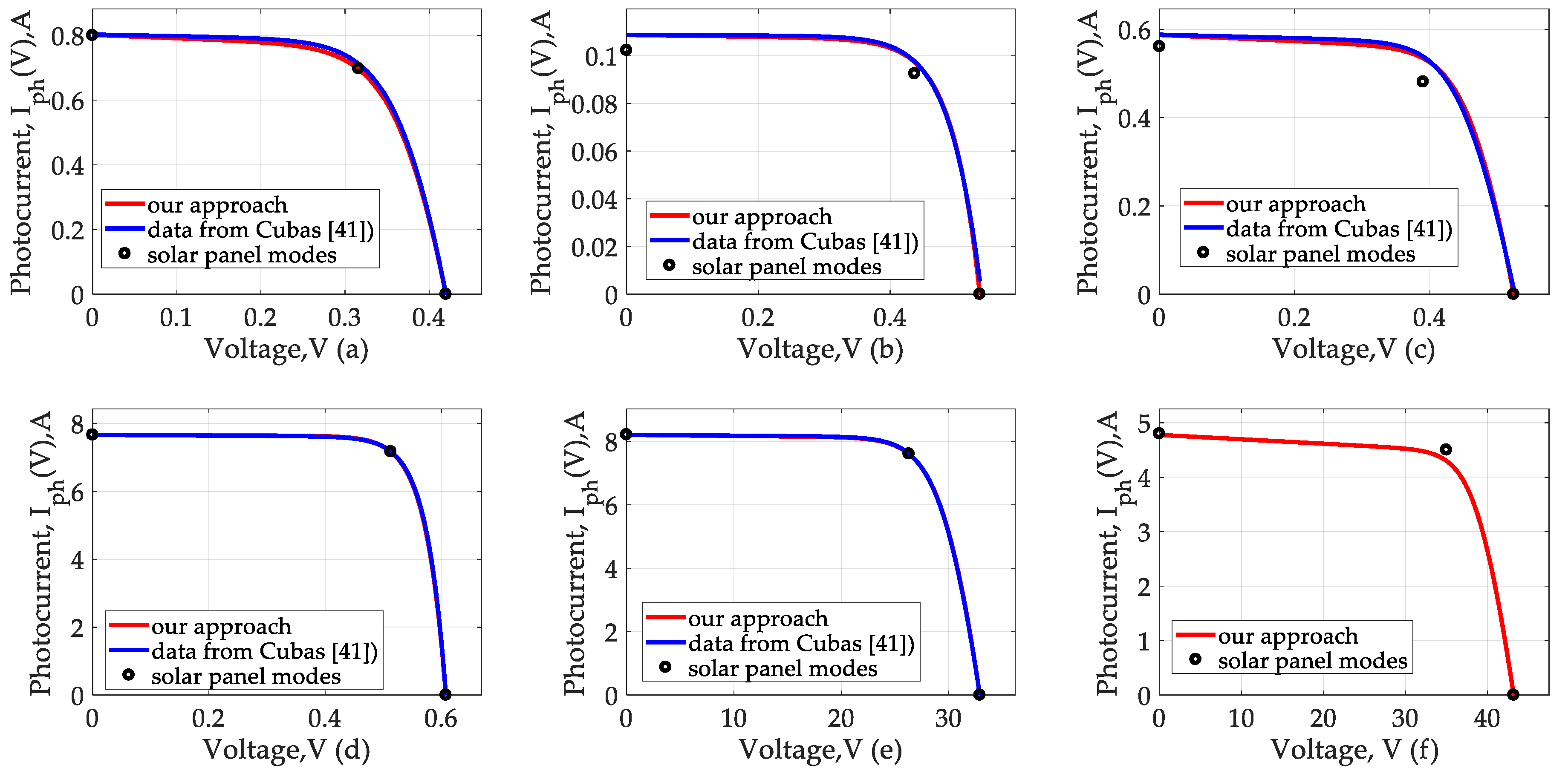
- Short-current mode (V = 0; I = Isc);
- Maximum power point mode (V = Vmp; I = Imp);
- Open-circuit mode (V = Voc; I = 0);
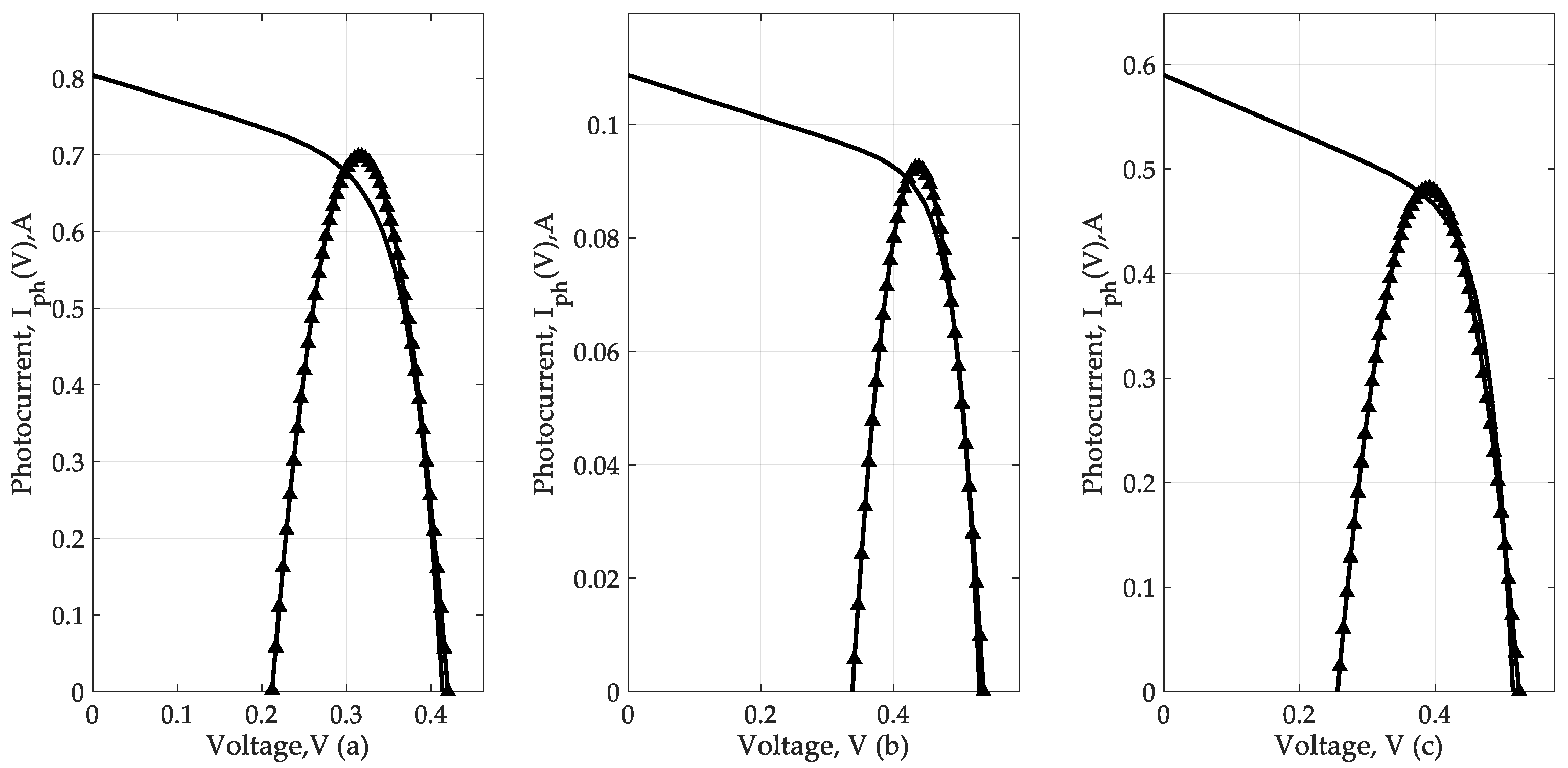
- Difference between the photocurrent Iph and short-circuit current Isc, determined by the ratio through the value (Rs+Rsh)/Rsh [41], is 0.007–0.3%, therefore, it is permissible to take Iph = Isc.
- From this it follows that from the third expression of the system of Equation (3), we can get the formula for calculating the saturation current of the diode:
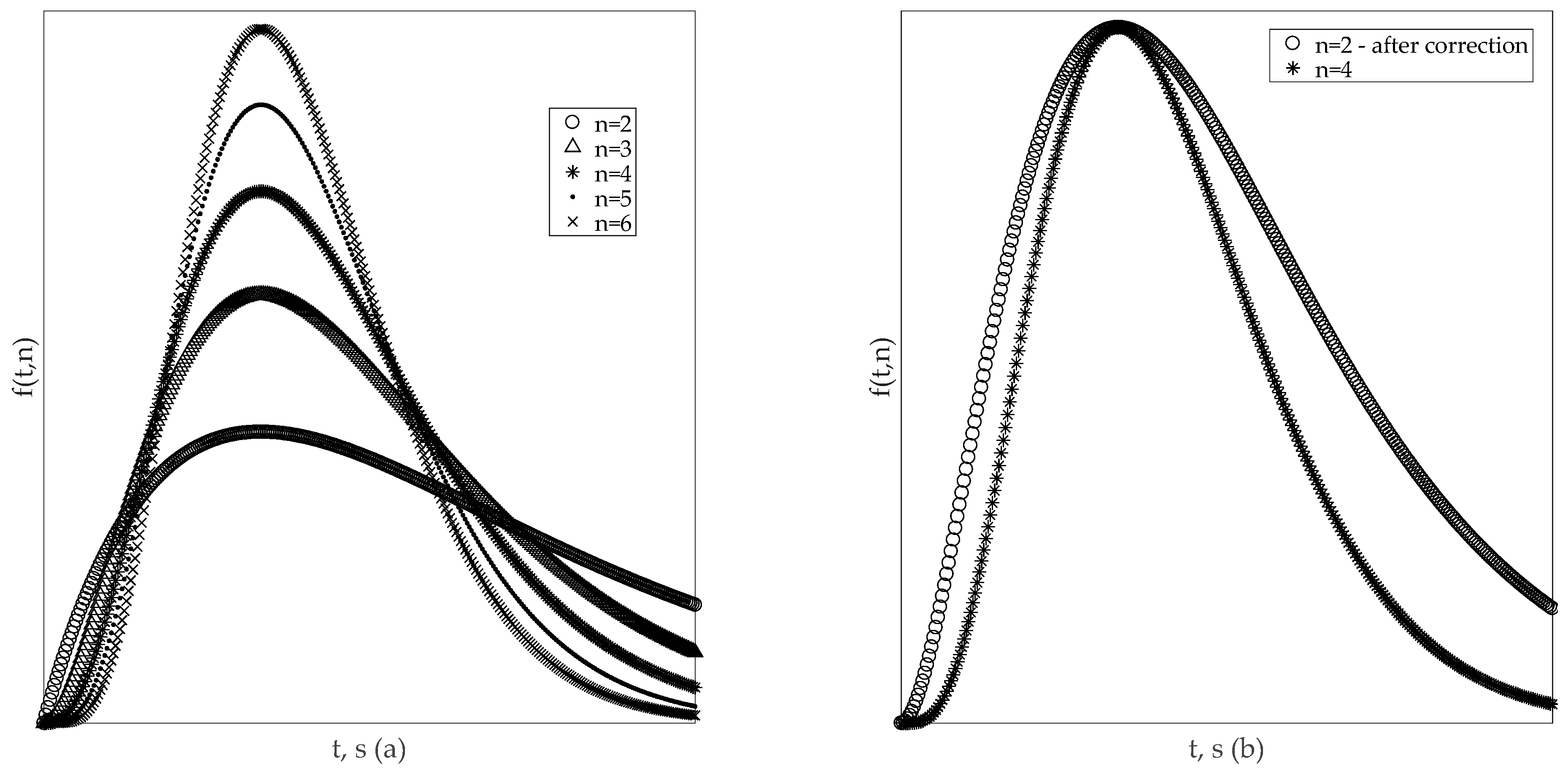
- Term can be decomposed into two components . Due to the fact that , it is permissible not to take into account the variable component . Difference between and = 0.108…8.805%, therefore, at the point of maximum power can be ignored.
- At the maximum power point, according to [50], voltage derivative versus current
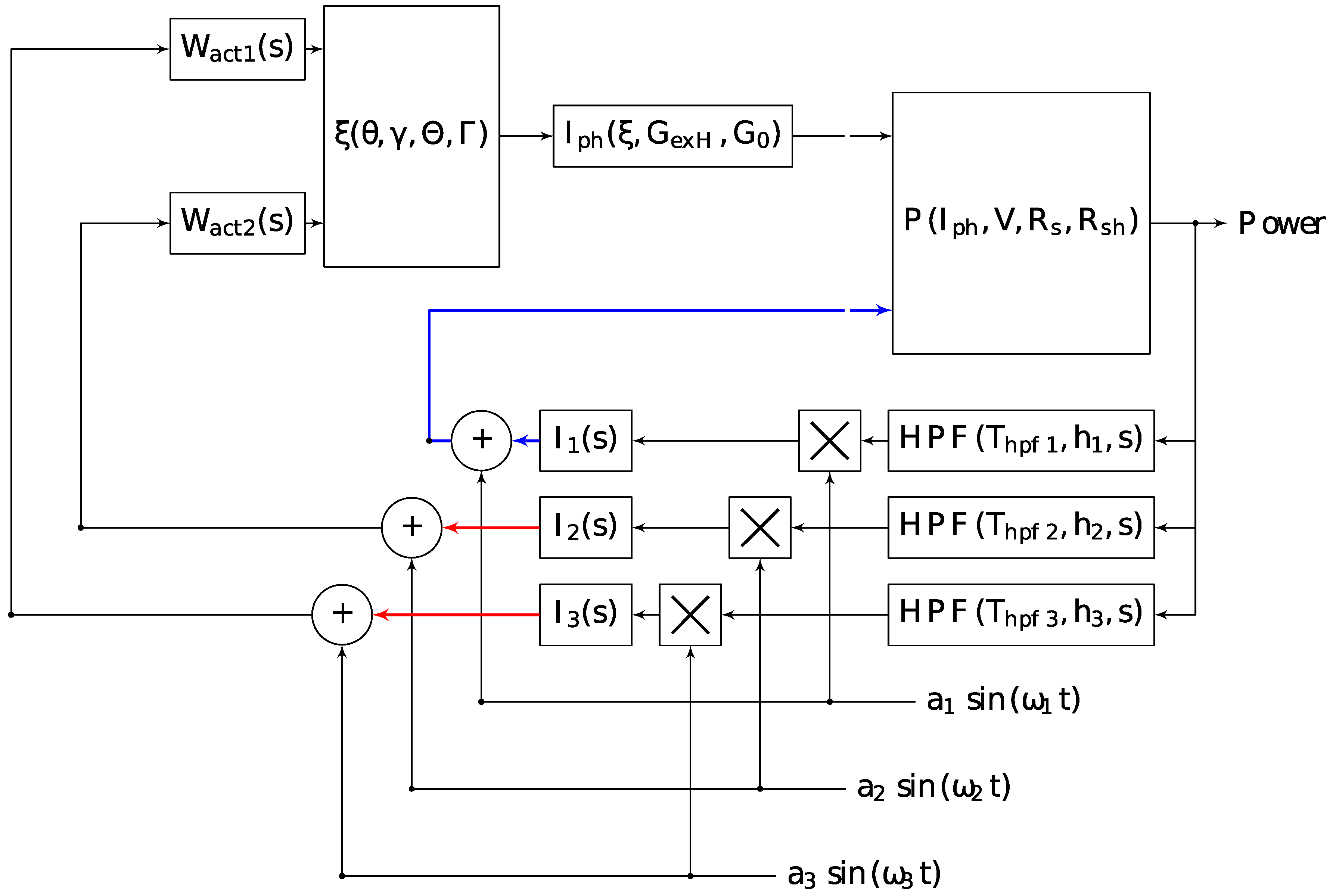
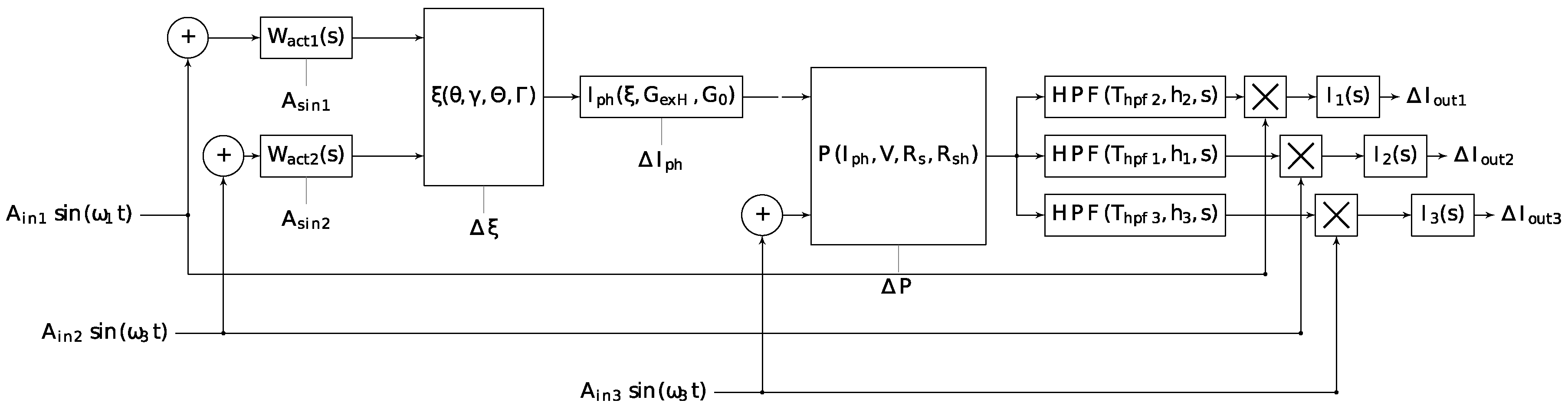
- Solar cell (nonlinear element with extreme characteristic);
- High-pass filter (HPFi);
- Demodulator multiplier;
- Master integrator Ii with gain ki;
- Modulating summator;
- Two high-speed coordinate electric drives Wact_i, tuned to a symmetrical optimum with an additional integral element for converting speed (rad/s) into a rotation angle (rad).
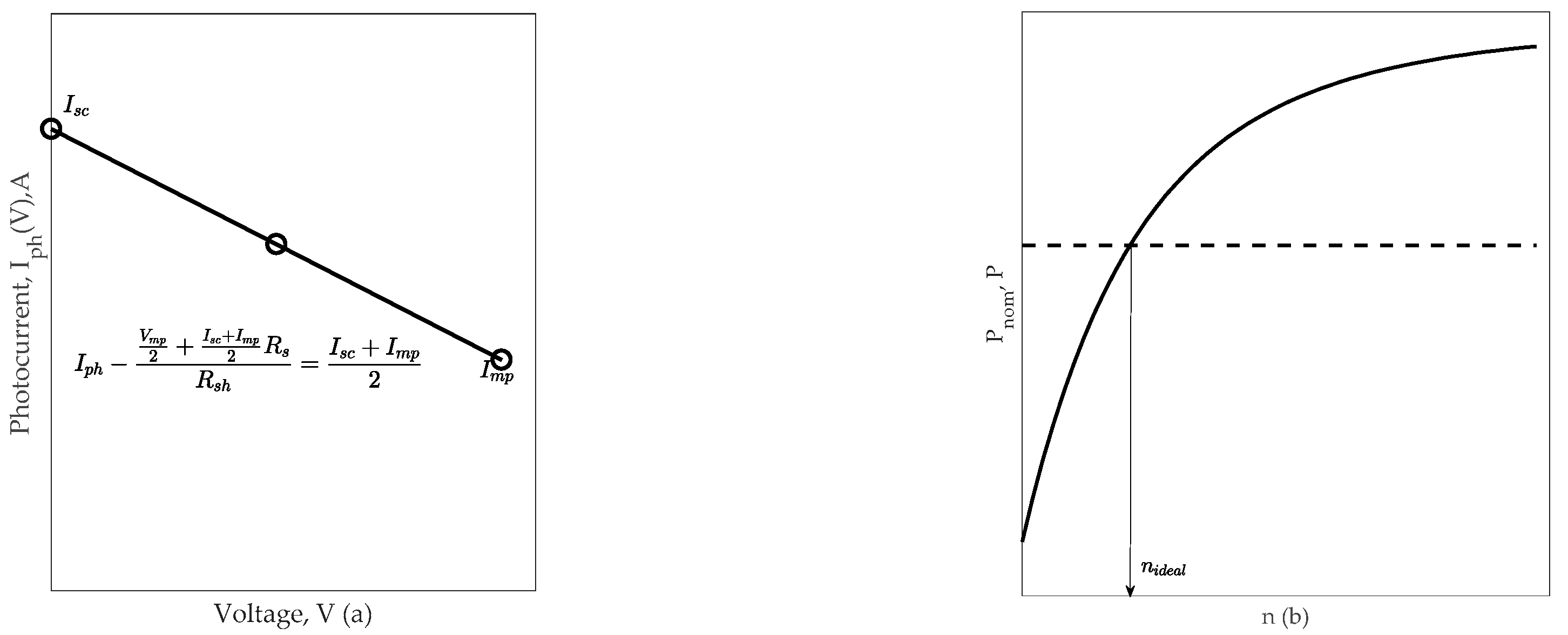
- Having data ;;; calculate and resistances and by the formulas (4), (6) and (7). If necessary, adjust the ideality factor n in accordance with formulas (8).
- Calculate the amplitude incidence coefficient ξ according to formulas (26)–(31).
- Calculate the amplitude of the photocurrent ΔIph by the formula (32).
- Calculate the voltage amplitude ΔV by formulas (38) and (39).
- Calculate the amplitude of the power ΔP by the formulas (40)–(42).
- Given the parameters of the circuits Thpf, h, ki, select the transfer function of the compensators in accordance with formula (19) and taking into account the reduction of a high-order object to a low-order object with formulas (25)
- Selecting the output amplitude of the oscillation signal of the master integrator for each of the extremum seeking loops, calculate the required frequency of the input modulating effects using the formula (47), which will provide the required amplitude of oscillations .
- Knowing the permissible amplitude of oscillations of angular electric drives, by the formula (52) calculate the necessary amplitudes of the main input modulating signals Ain.
- In the absence of satisfactory results on convergence at a given point, change the tuning parameters of Thpf, h, ki contours and repeat steps 7–10. You should strive to make them slightly different from each other in order to ensure that the modulating frequencies differ in accordance with the recommendations [28].
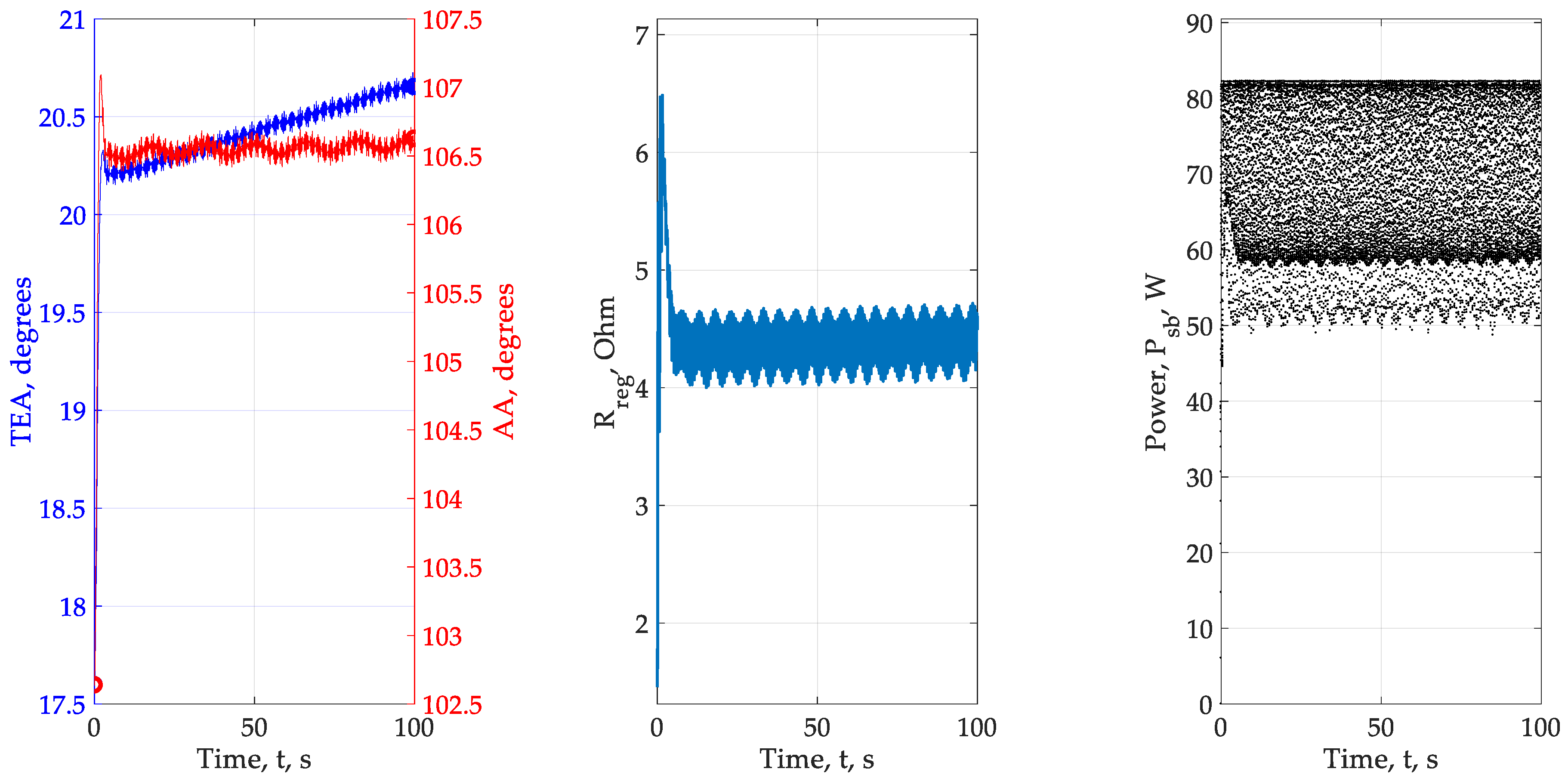
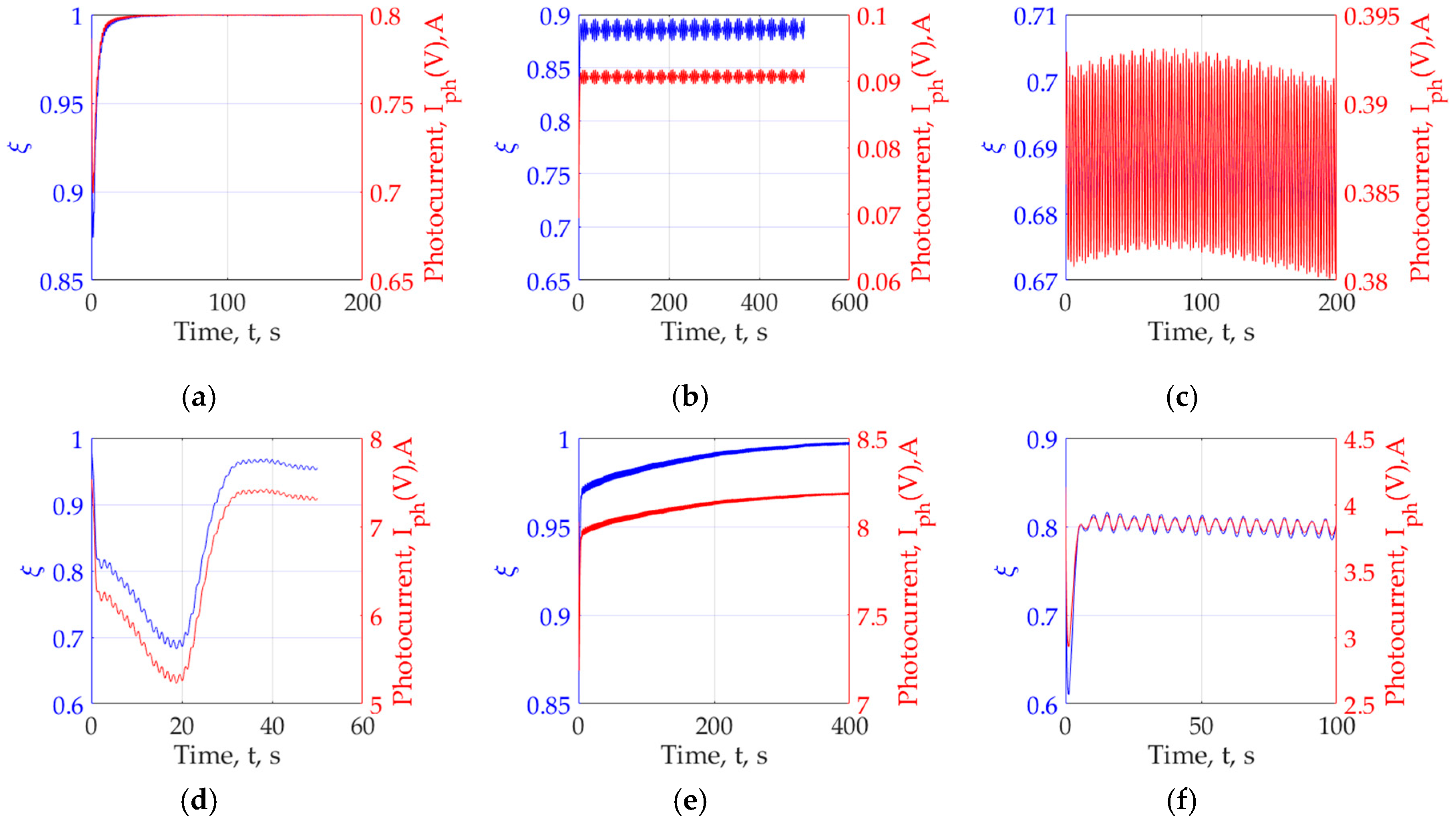
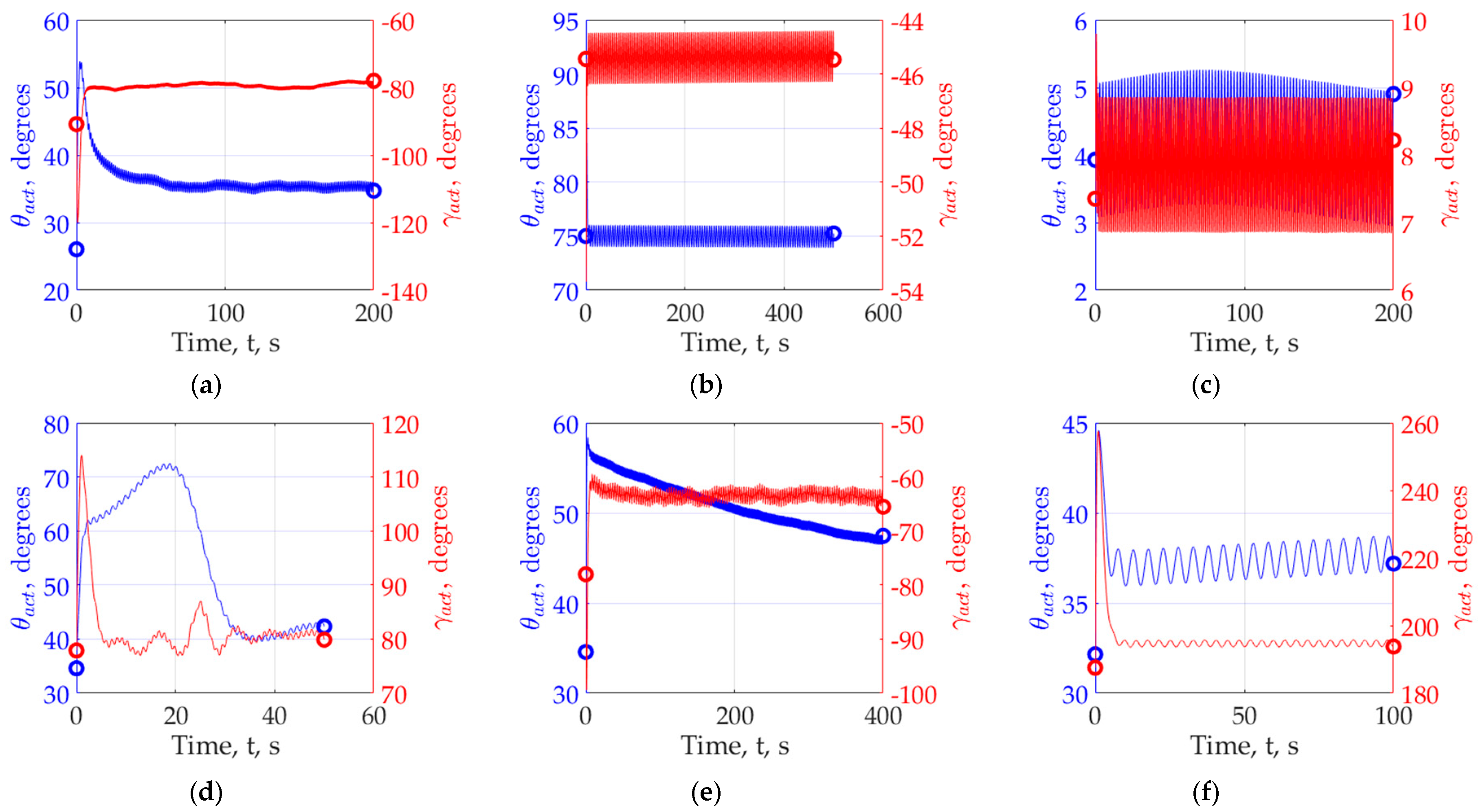
3. Results
- The original position is considered aligned. For this case, the reference signals and the angles of the Sun are the same.
- At the beginning of the motion, the angles of the Sun are changed, but the state of the system has not yet been changed. For this case, the angles of the Sun are equal to the final position, and the angles are set to the previous state.
- At the end of the transition to a new state, the angles of the Sun and the angles of installation again coincide.
4. Discussion. Interpretation of the Results. Limitations of the Study in Question
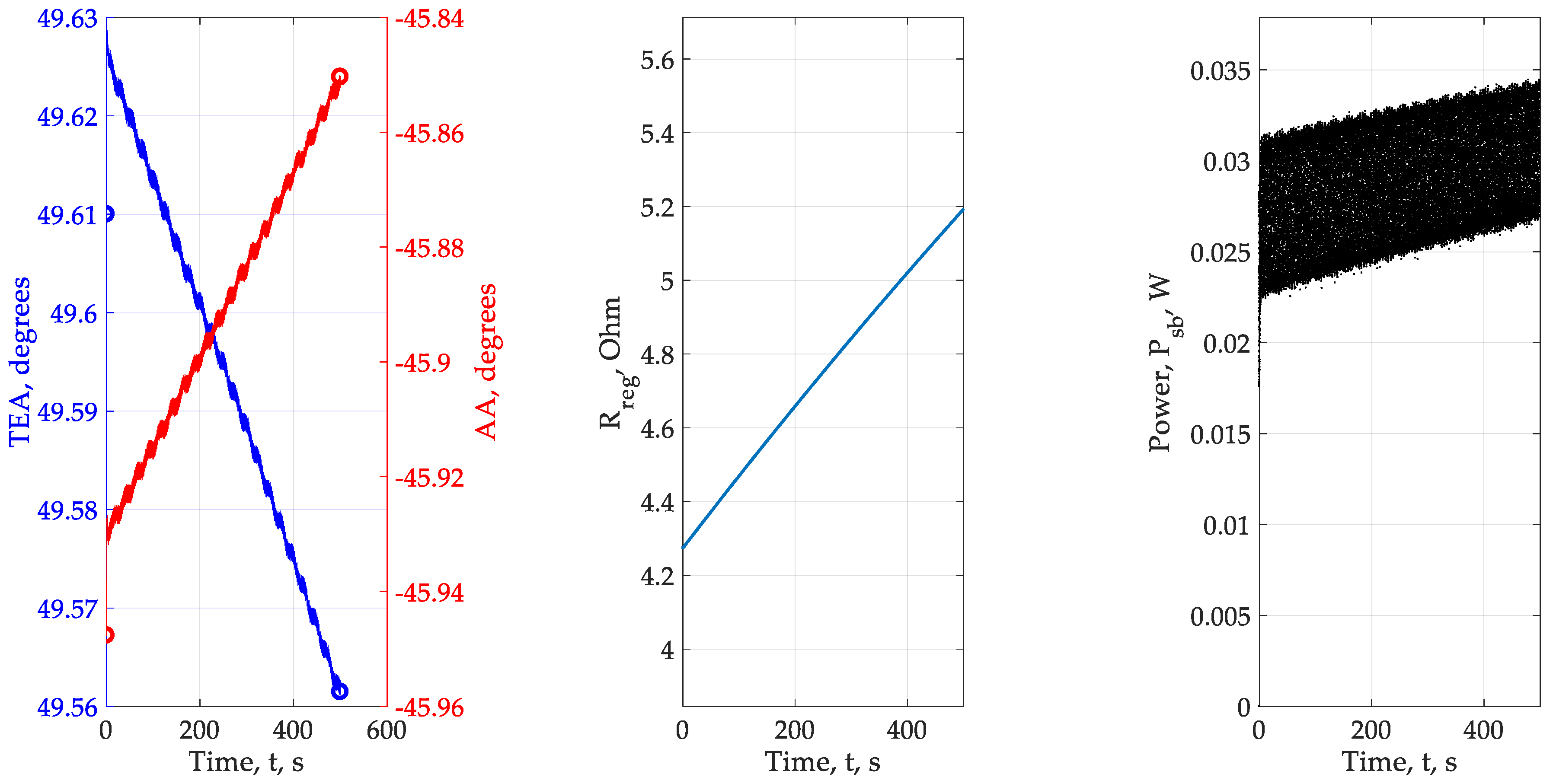
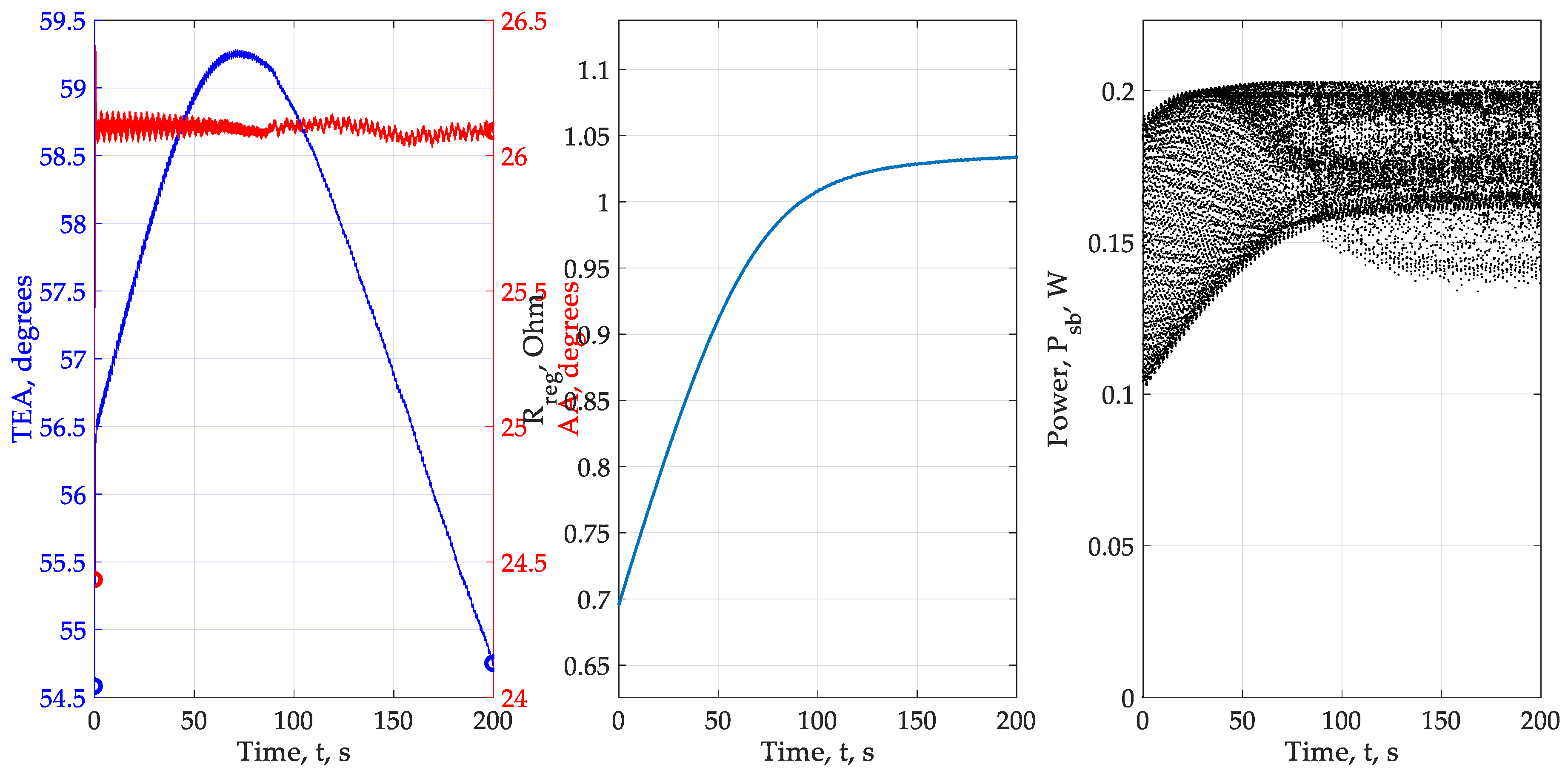
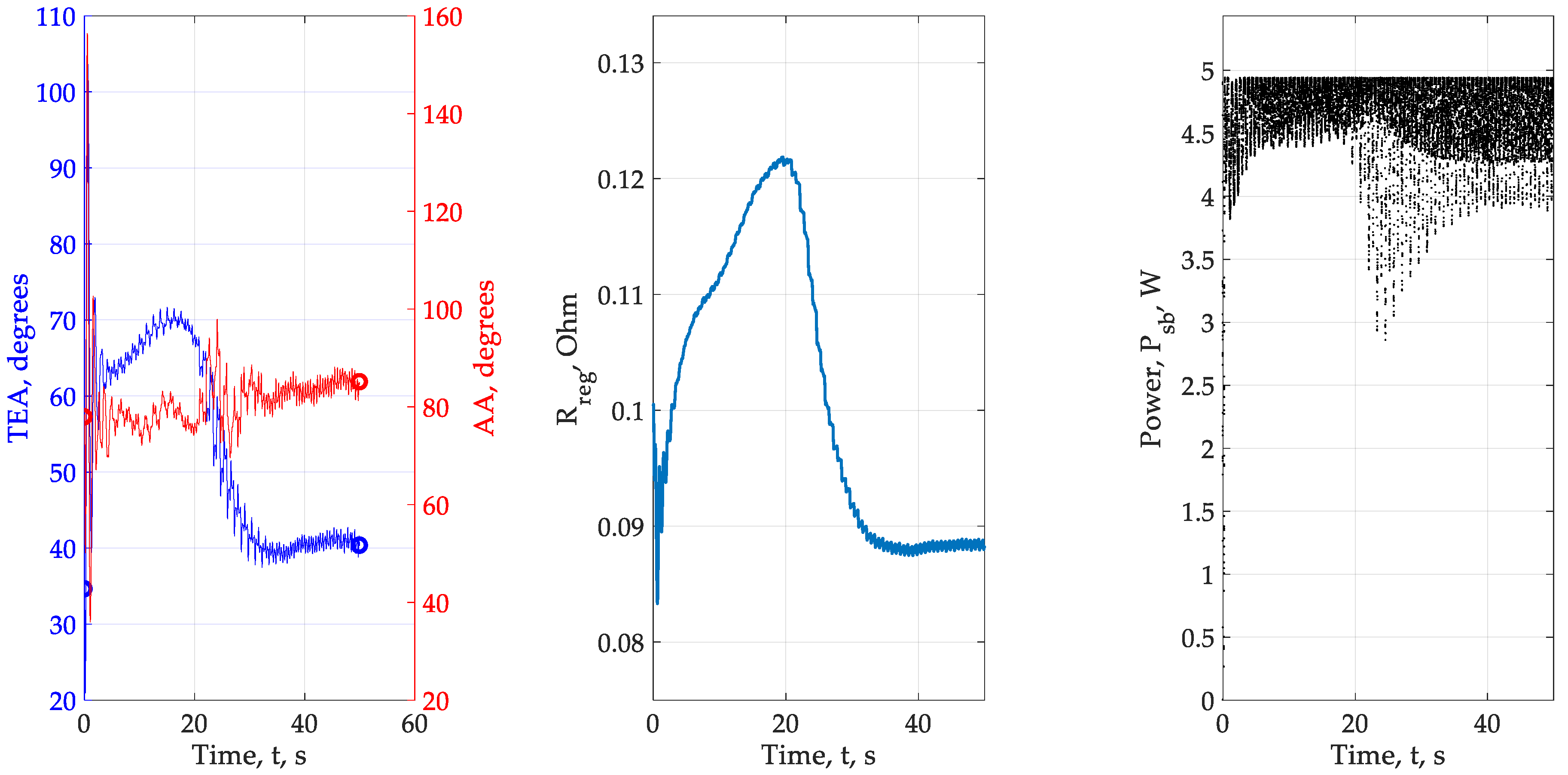
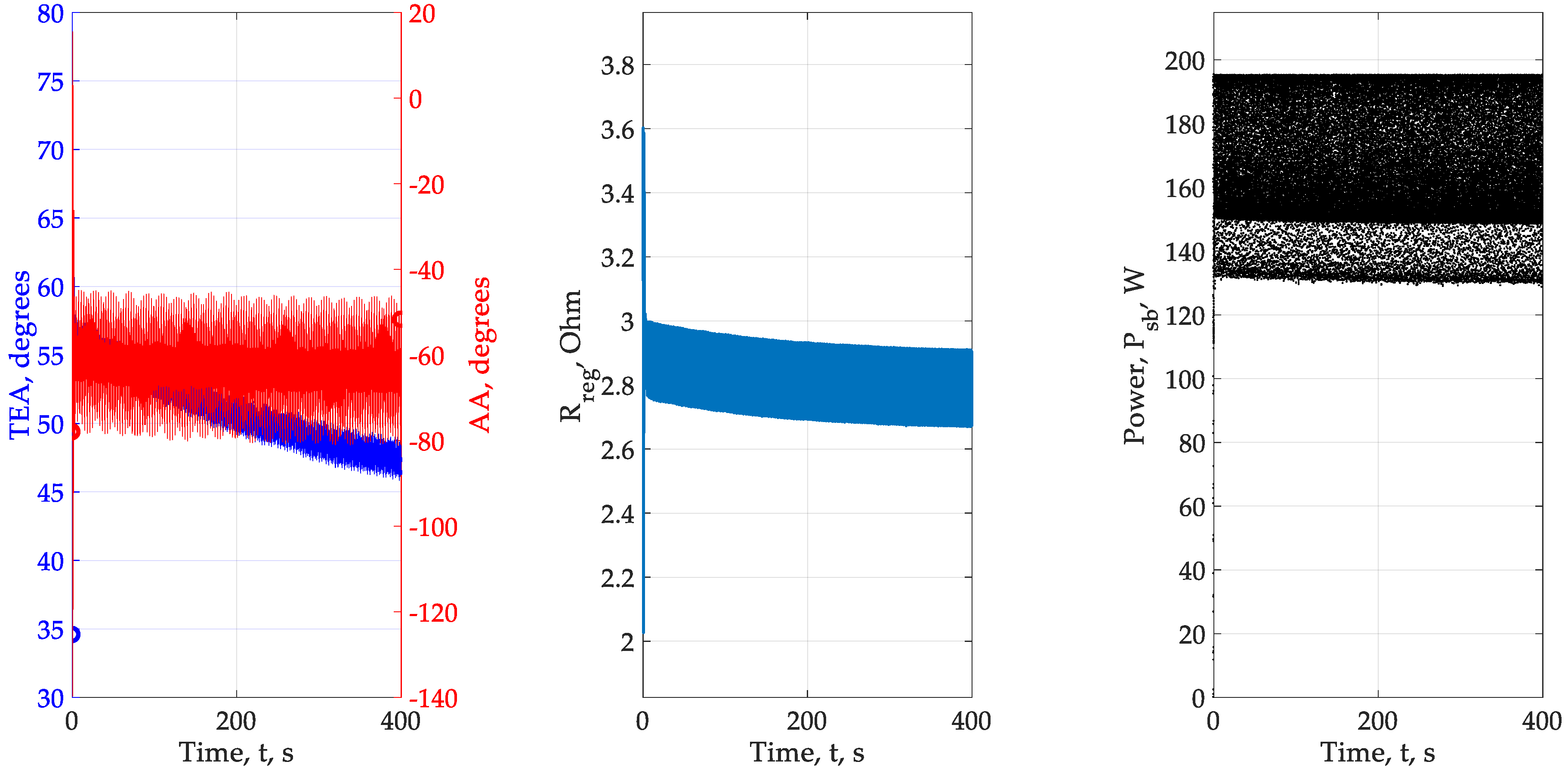
- In almost all experiments, the required parameters of the power fluctuation of the solar panel approximately correspond to the set. We cannot provide an arbitrary amplitude of oscillations of the coordinate electric drive, therefore, we chose a limitation, which, judging by the calculations, is satisfied and corresponds to the given = 1°. The influence of integrators on the input modeling signal is minimized so as to ensure convergence. In experiments 2 and 3, which turned out to be the least successful, we explain the main errors by the unsuccessful choice of the parameters of the optimization loops, amplitudes and frequencies of the modulating signals. The effect of convergence success depending on the power of the solar panel has so far been rejected, but requires additional verification, so the number of experiments needs to be increased from 6 to 20–25 and the power range of the solar panels expanded. It is required to find out how to choose the parameters of the high-pass filter and the integrator. So far, the problem is being solved for the already known or given parameters of the HPF and integrator.
- The effect of inconstancy in the amplitude of the fluctuation of the photocurrent and power, depending on the angular position of the solar panel and the angular position of the Sun in the chosen geographical location, shows that, provided the system is opened, multiplicity can be ignored. In other words, the adjustment of extremum seekeng loops can be done by “removing” nonlinearity from the system, leaving only the change in the effect itself.
- A new problem is highlighted from the previous paragraph. Our calculation shows that the effect varies over time. Consequently, adaptation of amplitudes and frequencies will be required. It is possible that the algorithm can be built on the basis of the presented calculations.
- Particular attention should be paid to restrictions. The number of parameters is limited to 3 (two angular positions and load resistance). Despite the fact that these are the main properties of the control object, additional non-linearities (for example, when expanding the number of adjustable coordinates) can complicate the calculation, because additional nonlinear interconnections appear in an open circuit.
- In general, the presented method can be extended to other nonlinearities, as well as the number of optimized parameters. You only need to learn how to correctly determine the amplitude of the fluctuations in the quantity coming to the extremum seekeng loops and to “remove” nonlinearity from the system (see point 3 of the Discussion section). We assume this is relevant for position-tracking systems of other classes.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
- On the interval 0 ≤ V ≤ Vmp, the term in first equation of the system of Equation (A3) practically does not affect the calculations, so it is assumed to be zero. To calculate the resistances and , it is advisable to enter an additional point in the middle of and , namely (a graphic explanation is given in Figure A1 and Figure A2:This is done in order to correctly characterize the approximately linear nature of the change in the photocurrent with a change in voltage on the specified interval.
- In a sufficiently small-scale neighborhood of the peak power at the voltage of the second term V≈Vmp effect begins to show enough that it cannot be disregarded. This is important, i.e., leads to a specific law of change, on the basis of which the following assumption is made.
- On the section Vmp ≤ V ≤ Voc, the volt-watt curve is close to a quadratic law:where the scaling coefficient Kc is determined from the condition of equality of the 0 curve by Equation (A5) at the idle point :
| Reference | |||||
|---|---|---|---|---|---|
| Kennerud, 1969 | 2.06 × 10−6 | 2.98 | 5.25 × 10−6 | 0.208 | 1.37 |
| Charles, 1981 | 1.37 × 10−8 | 26.98 | 3.4 × 10−9 | 0.0385 | 1.2 |
| Charles, 1981 | 5.12 × 10−8 | 3.58 | 7.74 × 10−8 | 0.186 | 1.25 |
| Lo Brano, 2010 | 2.67 × 10−11 | 1.045 | 3.99 × 10−10 | 3.52 | 1 |
| Cubas | 2.91 × 10−6 | 43.83 | 9.1 × 10−7 | 192.5 | 80 |
| PSM-150 | 1.55 × 10−5 | 116.7 | 2.13 × 10−6 | 147 | 115 |
References
- Krstic, M.; Ghaffari, A.; Seshagiri, S. Extremum seeking for wind and solar energy applications. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; pp. 6184–6193. [Google Scholar] [CrossRef]
- Demenkova, T.A.; Korzhova, O.A.; Phinenko, A.A. Modelling of algorithms for solar panels control systems. Procedia Comput. Sci. 2017, 103, 589–596. [Google Scholar] [CrossRef]
- Pakkiraiah, B.; Sukumar, G.D. Research survey on various MPPT performance issues to improve the solar pv system efficiency. J. Sol. Energy 2016, 2016, 1–20. [Google Scholar] [CrossRef]
- Esram, T.; Chapman, P.L. Comparison of photovoltaic array maximum power point tracking techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar] [CrossRef]
- Sumathi, V.; Jayapragash, R.; Bakshi, A.; Akella, P.K. Solar tracking methods to maximize PV system output—A review of the methods adopted in recent decade. Renew. Sustain. Energy Rev. 2017, 74, 130–138. [Google Scholar] [CrossRef]
- Dogga, R.; Pathak, M.K. Recent trends in solar PV inverter topologies. Sol. Energy 2019, 183, 57–73. [Google Scholar] [CrossRef]
- Ahmad, R.; Murtaza, A.F.; Ahmed, H. Power tracking techniques for efficient operation of photovoltaic array in solar applications—A review. Renew. Sustain. Energy Rev. 2019, 101, 82–102. [Google Scholar] [CrossRef]
- Eltawil, M.A.; Zhaom, Z. MPPT techniques for photovoltaic applications. Renew. Sustain. Energy Rev. 2013, 25, 793–813. [Google Scholar] [CrossRef]
- Salam, Z.; Ahmed, J.; Merugu, B.S. The application of soft computing methods for MPPT of PV system: A technological and status review. Appl. Energy 2013, 107, 135–148. [Google Scholar] [CrossRef]
- Mohanty, P.; Bhuvaneswari, G.; Balasubramanian, R.; Dhaliwal, N.K. MATLAB based modeling to study the performance of different MPPT techniques used for solar PV system under various operating conditions. Renew. Sustain. Energy Rev. 2014, 38, 581–593. [Google Scholar] [CrossRef]
- Bendib, B.; Belmili, H.; Krim, F. A survey of the most used MPPT methods: Conventional and advanced algorithms applied for photovoltaic systems. Renew. Sustain. Energy Rev. 2015, 45, 637–648. [Google Scholar] [CrossRef]
- Rezk, H. A new MATLAB/Simulink model of triple-junction solar cell and MPPT based on artificial neural networks for photovoltaic energy systems. Ain Shams Eng. J. 2015, 6, 873–881. [Google Scholar] [CrossRef] [Green Version]
- Seyedmahmoudian, M.; Horan, B.; Kok Soon, T.; Rahmani, R.; Muang Than Oo, A.; Mekhilef, S.; Stojcevski, A. State of the art arti fi cial intelligence-based MPPT techniques for mitigating partial shading effects on PV systems—A review. Renew. Sustain. Energy Rev. 2016, 64, 435–455. [Google Scholar] [CrossRef]
- Verma, D.; Nema, S.; Shandilya, A.M.; Dash, K.S. Maximum power point tracking (MPPT) techniques: Recapitulation in solar photovoltaic systems. Renew. Sustain. Energy Rev. 2016, 54, 1018–1034. [Google Scholar] [CrossRef]
- Ram, J.P.; Babum, T.S.; Rajasekarm, N. A comprehensive review on solar PV maximum power point tracking techniques. Renew. Sustain. Energy Rev. 2017, 67, 826–847. [Google Scholar] [CrossRef]
- Johnson, M.C.; Brunton, S.L.; Kundtz, N.B.; Kutz, J.N. An extremum-seeking controller for dynamic metamaterial antenna operation. In Proceedings of the 2015 IEEE-APS Topical Conference on Antennas and Propagation in Wireless Communications (APWC), Turin, Italy, 7–11 September 2015; pp. 1220–1223. [Google Scholar] [CrossRef]
- Brunton, S.L.; Rowley, C.W.; Kulkarni, S.R.; Clarkson, C. Maximum Power Point Tracking for Photovoltaic Optimization Using Ripple-Based Extremum Seeking Control. IEEE Trans. Power Electron. 2010, 25, 2531–2540. [Google Scholar] [CrossRef]
- Mousazadeh, H.; Keyhani, A.; Javadi, A.; Mobli, H.; Abriana, K.; Sharifi, A. A review of principle and sun-tracking methods for maximizing solar systems output. Renew. Sustain. Energy Rev. 2009, 13, 1800–1818. [Google Scholar] [CrossRef]
- Hafez, A.Z.; Yousef, A.M.; Harag, N.M. Solar tracking systems: Technologies and trackers drive types—A review. Renew. Sustain. Energy Rev. 2018, 91, 754–782. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Chou, P.-C.; Chiang, C.-M.; Lin, C.-F. Sun tracking systems: A Review. Sensors 2009, 9, 3875–3890. [Google Scholar] [CrossRef]
- Loschi, H.J.; Iano, Y.; Leon, J.; Moretti, A.; Conte, F.D.; Braga, H. A review on photovoltaic systems: Mechanisms and methods for irradiation tracking and prediction. Smart Grid Renew. Energy 2015, 6, 187–208. [Google Scholar] [CrossRef]
- Khalil, F.A.; Asif, M.; Anwar, S. Solar tracking techniques and implementation in photovoltaic power plants: A solar tracking techniques and implementation in photovoltaic power plants: A Review. Phys. Comput. Sci. 2017, 54, 231–241. [Google Scholar]
- Ya’u, M.J. A Review on solar tracking systems and their classifications. J. Energy Environ. Chem. Eng. 2017, 2, 46–50. [Google Scholar]
- Racharla, S.; Rajan, K. Solar tracking system—A review. Int. J. Sustain. Eng. 2017, 7038, 1–10. [Google Scholar]
- Hamid, A.R.; Azim, A.K.; Bakar, M.H. A review on solar tracking system. In Proceedings of the National Innovation and Invention Competition Through Exhibition (iCompEx’17), Jitra, Malaysia, 21–22 March 2017. [Google Scholar]
- Al-Rousan, N.; Isa, N.A.M.; Desa, M.K.M. Advances in solar photovoltaic tracking systems: A review. Renew. Sustain. Energy Rev. 2018, 82, 2548–2569. [Google Scholar] [CrossRef]
- Singh, R.; Kumar, S.; Gehlot, A.; Pachauri, R. An imperative role of sun trackers in photovoltaic technology: A review. Renew. Sustain. Energy Rev. 2018, 82, 3263–3278. [Google Scholar] [CrossRef]
- Ariyur, K.B.; Krstic, M. Real-Time Optimization By Extremum-Seeking Control; John Wiley & Sons: Hoboken, NJ, USA, 2003; p. 230. [Google Scholar]
- Chunlei, Z.; Ordonez, R. Extremum-Seeking Control and Applications; Springer: Cham, Switzerland, 2012; p. 209. [Google Scholar]
- Liu, S.-J.; Krstic, M. Stochastic Averanging and Stochastic Extremum Seeking; Springer: Cham, Switzerland, 2012; p. 226. [Google Scholar]
- Brunton, S.L.; Fu, X.; Kutz, J.N. Extremum-seeking control of a mode-locked laser. IEEE J. Quantum Electron. 2013, 49, 852–861. [Google Scholar] [CrossRef]
- Binetti, P.; Ariyur, K.B.; Krstic, M.; Bernelli, F. Control of formation flight via extremum seeking. In Proceedings of the American Control Conference, Anchorage, AK, USA, 8–10 May 2002; pp. 2848–2853. [Google Scholar]
- Nesic, D. Extremum seeking control: Convergence analysis. Eur. J. Control 2009, 15, 331–347. [Google Scholar] [CrossRef]
- Rastrigin, L.A. Contemporary Principles to Control Complex Objects; Mir Publishers: Moscow, USSR, 1983; p. 248. [Google Scholar]
- Rotea, M.A.; Lafayette, W. Analysis of multivariable extremum seeking algorithms. In Proceedings of the 2000 American Control Conference, Chicago, IL, USA, 28–30 June 2000; pp. 433–437. [Google Scholar]
- Walsh, G.C. On the application of multi-parameter extremum seeking control. In Proceedings of the 2000 American Control Conference, Chicago, IL, USA, 28–30 June 2000. [Google Scholar]
- King, D.L.; Boyson, W.E.; Kratochvil, J.A. Photovoltaic Array Performance Model; United States Department of Energy: Washington, DC, USA, 2004. [Google Scholar]
- Celik, A.N.; Acikgoz, N. Applied modelling and experimental verification of the operating current of mono-crystalline photovoltaic modules using four- and five-parameter models. Appl. Energy 2007, 84, 1–15. [Google Scholar] [CrossRef]
- Bellia, H. A detailed modeling of photovoltaic module using MATLAB. Nriag J. Astronomy Geophys. 2014, 3, 53–61. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, S.; Lazzaroni, M.; Piurim, V. A computational intelligence approach to solar panel modelling. In Proceedings of the 2014 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Montevideo, Uruguay, 12–15 May 2014. [Google Scholar]
- Cubas, J.; Pindado, S.; Victoria, M. On the analytical approach for modeling photovoltaic systems behavior. J. Power Sources 2014, 247, 467–474. [Google Scholar] [CrossRef] [Green Version]
- Ulleberg, O. Stand-alone power systems for the future. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 1998; p. 225. [Google Scholar]
- Alam, M.S.; Alouani, A.T. Dynamic modeling of photovoltaic module for real-time maximum power tracking Dynamic modeling of photovoltaic module for real-time maximum power tracking. J. Renew. Sustain. Energy 2014, 2, 1–17. [Google Scholar]
- Johnson, J.; Schoenwald, D.; Kuszmaul, S.; Strauch, J.; Bower, W. Creating dynamic equivalent PV circuit models with impedance spectroscopy for arc fault modeling. In Proceedings of the 37th IEEE Photovoltaic Specialists Conference, Seattle, WA, USA, 19–24 June 2011; pp. 2328–2333. [Google Scholar]
- Bhatt, P.; Kumar, M.; Kant, P.C.; Pandey, M.K.; Tripathi, B. Optoelectronic modelling of perovskite solar cells under humid conditions and their correlation with power losses to quantify material degradation. Org. Electron. 2016, 39, 258–266. [Google Scholar] [CrossRef]
- Khatib, T.; Elmenreich, W. Modeling of Photovoltaic Systems Using MATLAB; Jon Willey and Sons: Hoboken, NJ, USA, 2016; p. 242. [Google Scholar]
- Moussa, I.; Khedher, A.; Bouallegue, A. Design of a Low-Cost PV Emulator Applied for PVECS electric. Electronics 2019, 8, 232. [Google Scholar] [CrossRef]
- Notton, G.; Cristofari, C.; Mattei, M.; Poggi, P. Modelling of a double-glass photovoltaic module using finite differences. Appl. Therm. Eng. 2005, 25, 2854–2877. [Google Scholar] [CrossRef]
- Wu, H. A maximum power point detection method for photovoltaic module based on lambert w function based on Lambert W function. Math. Problems Eng. 2018, 2018, 8. [Google Scholar] [CrossRef]
- Dunford, W.G.; Capel, A. Novel modeling method for photovoltaic cells. In Proceedings of the 2004 35th Annual IEEE Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; pp. 1950–1956. [Google Scholar]
- Reda, I.; Andreas, A. Solar Position Algorithm for Solar Radiation Applications (Revised). NREL/TP-560-34302. Golden (Colorado). Sol. Energy 2008, 76, 577–589. [Google Scholar] [CrossRef]
- Korn, G.A.; Korn, T.M. Mathematical Handbook for Scientists and Engineers. Definitions, Theorems, and Formulas for Reference and Review; Dover Publications, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Liberzon, L.M.; Rodov, A.B. Extremum Seeking Control Systems; Energy publisher: Moscow, USSR, 1965; p. 162. [Google Scholar]
- Kapre, N.; DeHon, A. Parallelizing sparse Matrix Solve for SPICE circuit simulation using FPGAs. In Proceedings of the 2009 International Conference on Field-Programmable Technology, Sydney, NSW, Australia, 9–11 December 2009; pp. 190–198. [Google Scholar] [CrossRef]
- Sologubov, A.Y.; Kirpichnikova, I.M. Calculation of the parameters of the daily movement of the sun. contour maps of kinematic parameters. In Proceedings of the 2019 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Sochi, Russia, 25–29 March 2019; pp. 1–6. [Google Scholar]
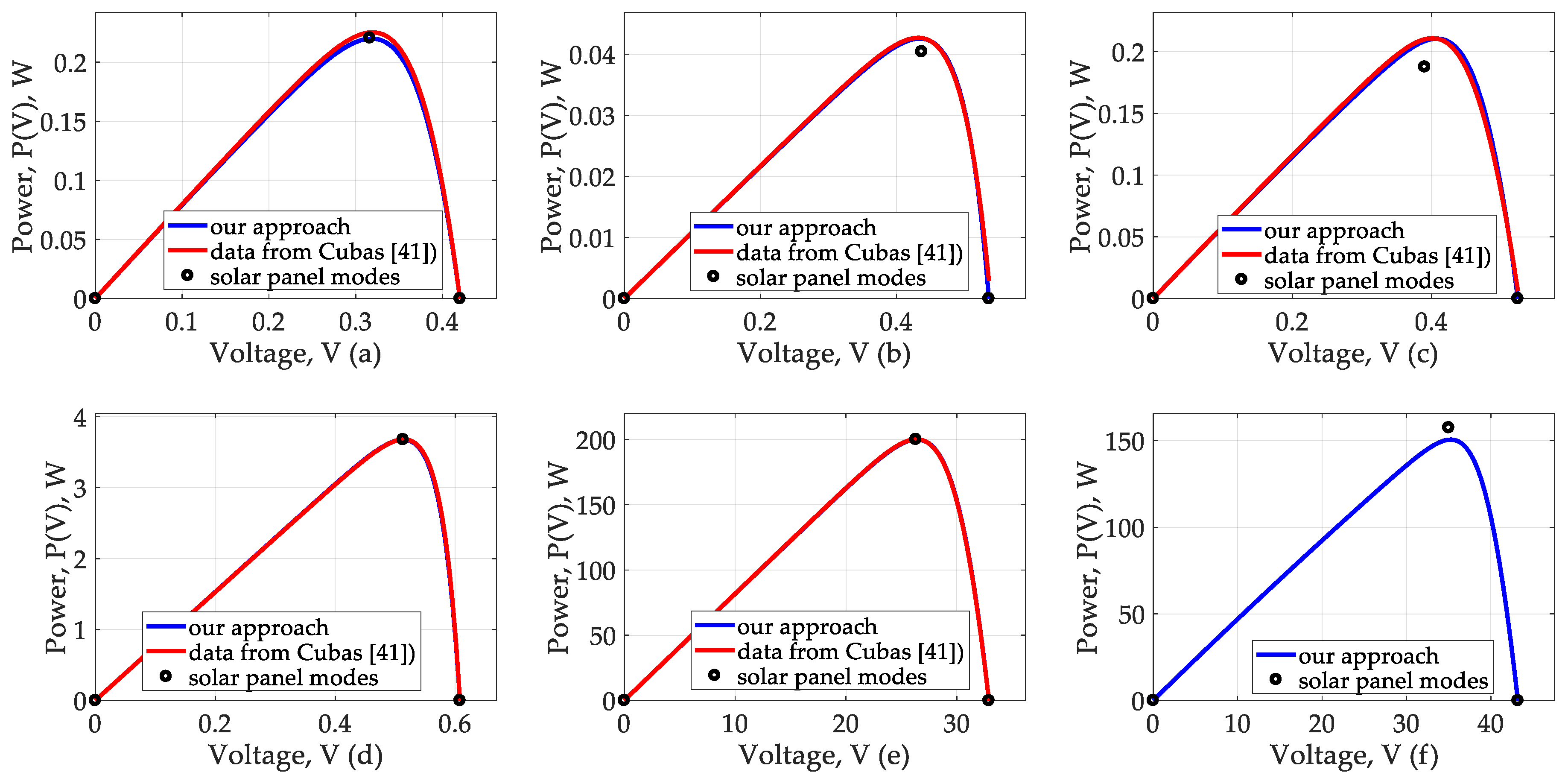
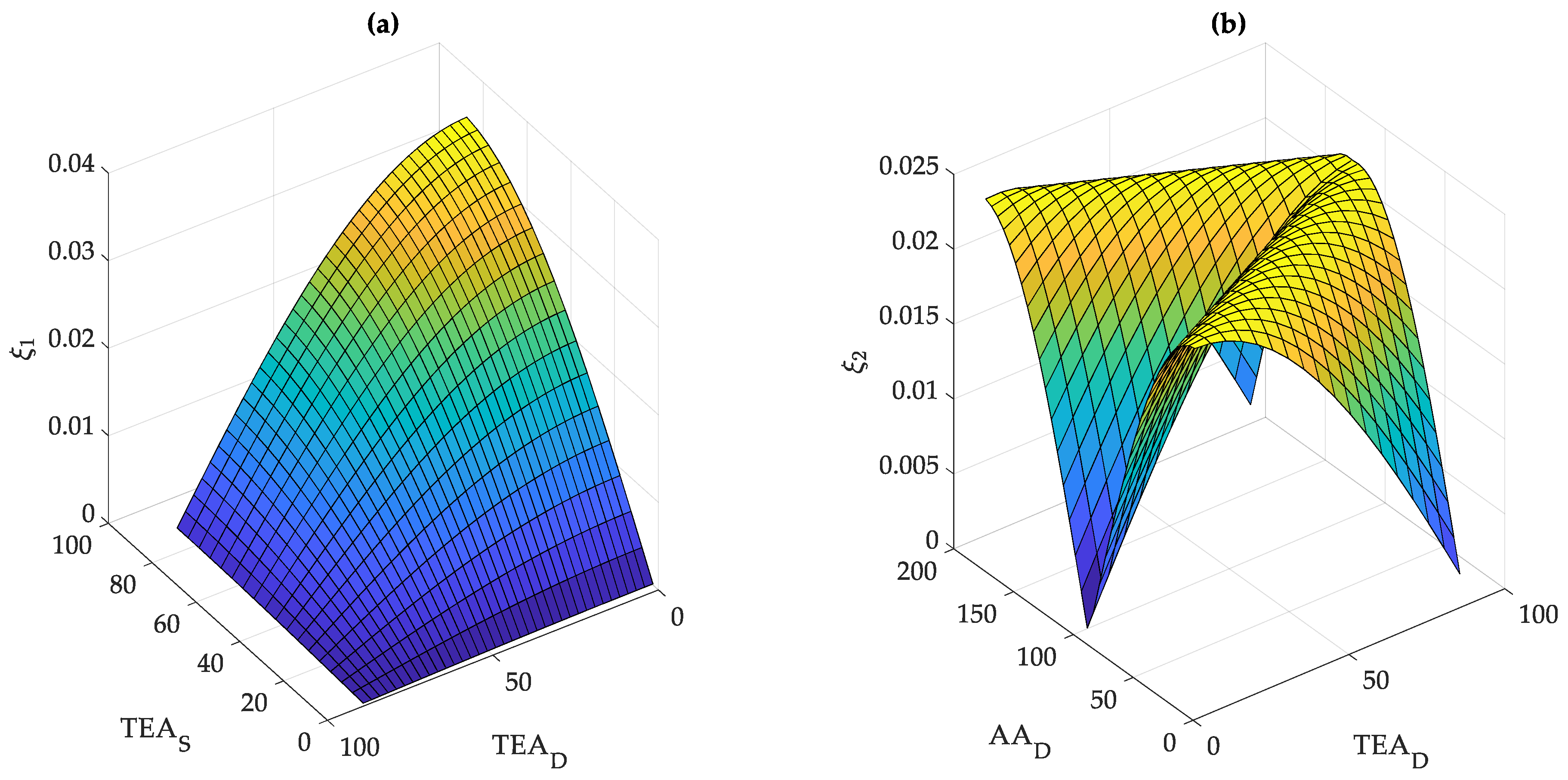
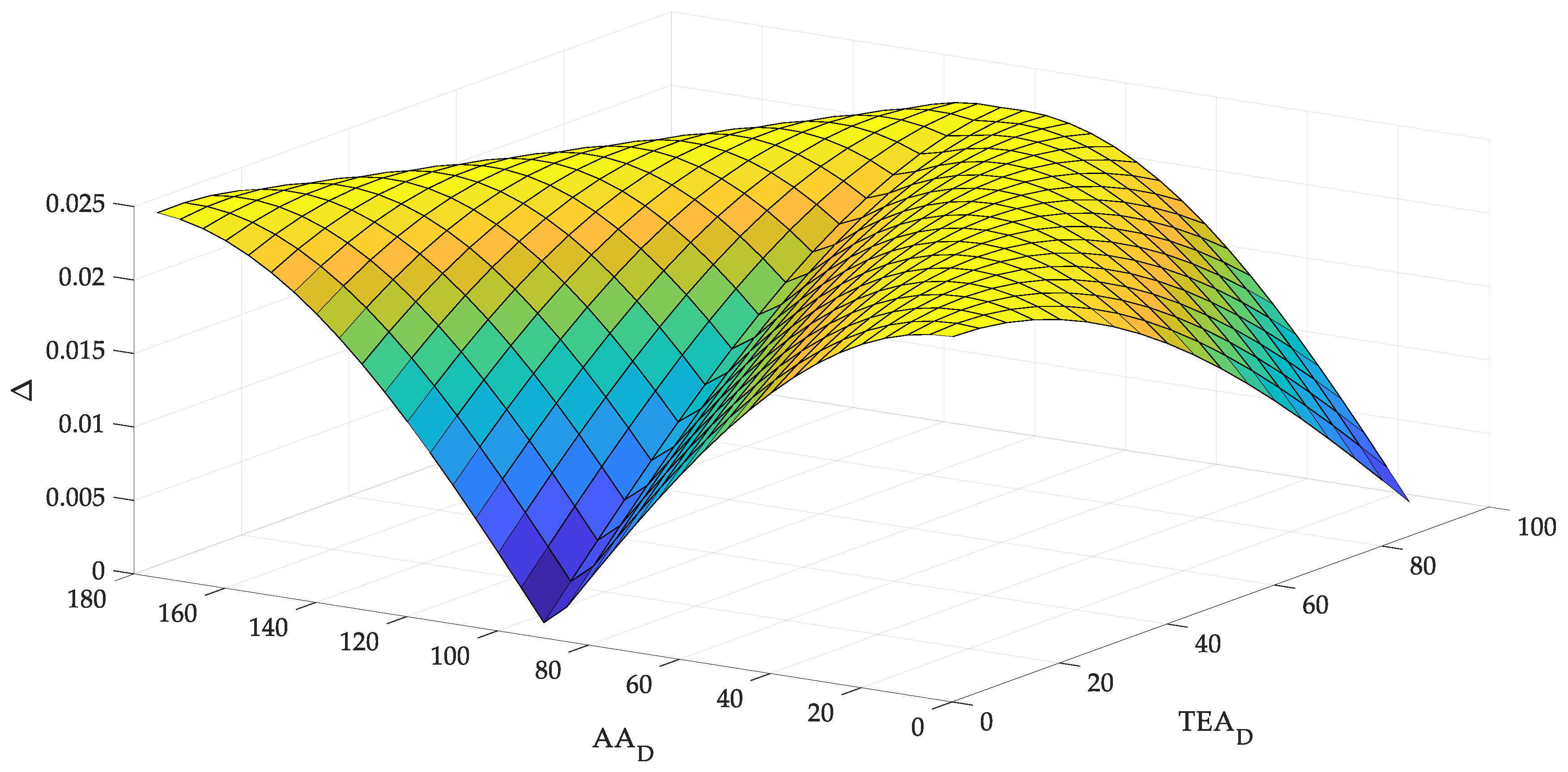
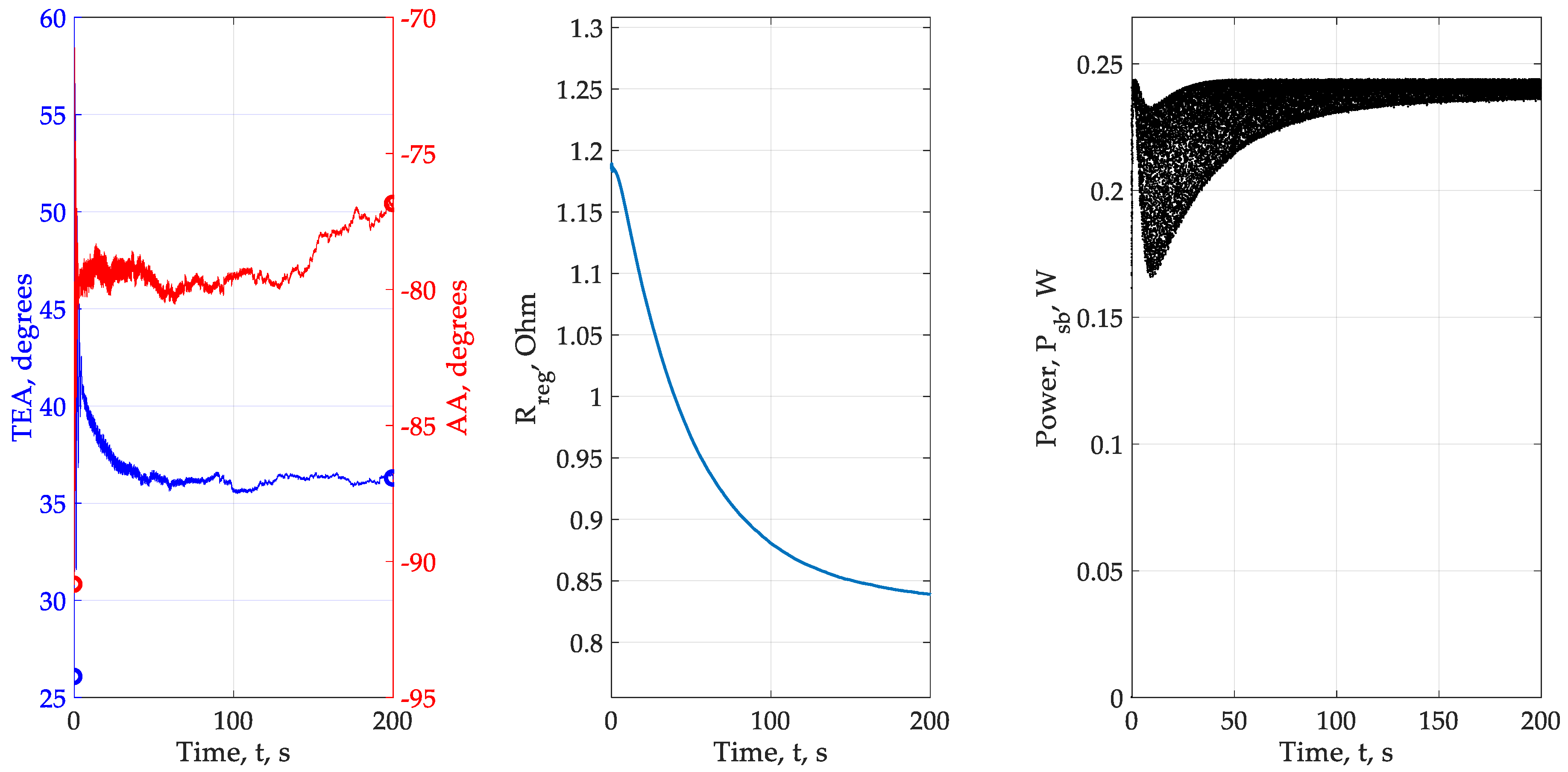
| Condition | ||
|---|---|---|
| 0 < θ < 90° ∧ 0< γ < 90° | ||
| 0 < θ < 90° ∧ γ = 90° | ||
| θ = 90° ∧ 0 < γ < 90° | ||
| θ = 90° ∧ γ = 90° | ||
| 0 < θ < 90° ∧ 90° < γ < 180° | ||
| θ = 90° ∧ 90° < γ < 180° | ||
| 0 < θ < 90° ∧ γ = 180° |
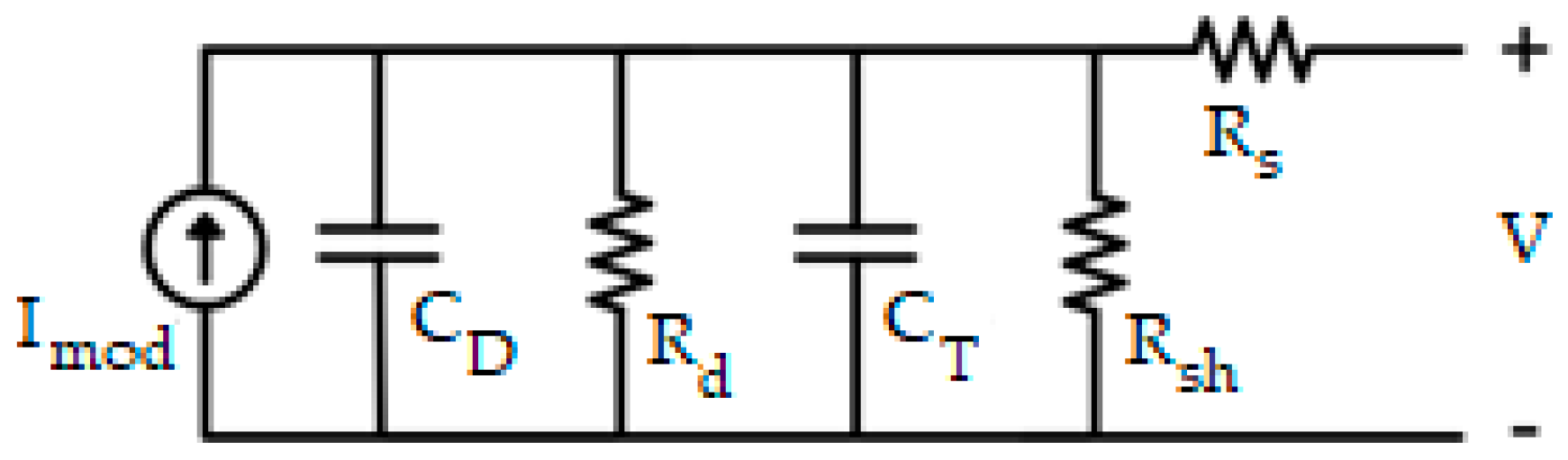
| Element | Exit Node | Entry Node |
|---|---|---|
| Iph | 1 | 2 |
| Rsh | 1 | 2 |
| Rd | 2 | 1 |
| Rs | 2 | 1 |
| CD | 2 | 1 |
| CT | 2 | 1 |
| Reference | T | ||||
|---|---|---|---|---|---|
| Kennerud, 1969 | 0.420 | 0.804 | 0.316 | 0.698 | 330 |
| Charles, 1981 | 0.536 | 0.1023 | 0.437 | 0.0925 | 300 |
| Charles, 1981 | 0.524 | 0.561 | 0.390 | 0.481 | 307 |
| Lo Brano, 2010 | 0.608 | 7.665 | 0.513 | 7.174 | 298 |
| Cubas | 32.9 | 8.21 | 26.3 | 7.61 | 298 |
| PSM-150 | 43.2 | 4.8 | 35 | 4.5 | 298 |
| No. of Experiment | Reference | |||||
|---|---|---|---|---|---|---|
| 1 | Kennerud, 1969 | 0.31606 × 10−1 | 9.9227 | 5.25 × 10−6 | 0.208 | 1.37 |
| 2 | Charles, 1981 | 0.92837 × 10−2 | 258.74 | 3.4 × 10−9 | 0.0385 | 1.51 |
| 3 | Charles, 1981 | 0.61621 × 10−1 | 14.423 | 7.74 × 10−8 | 0.186 | 1.72 |
| 4 | Lo Brano, 2010 | 0.31318 × 10−3 | 16.570 | 3.99 × 10−10 | 3.52 | 1.2867 |
| 5 | Cubas, 2014 | 0.83777 | 44.493 | 9.1 × 10−7 | 192.5 | 70.2 |
| 6 | PSM-150 | 0.59484 | 123.76 | 2.13 × 10−6 | 147 | 70.2 |
| Date | Time | TEA (corrected) [°] | AA (eastward from N) |
|---|---|---|---|
| 7/15/2019 | 8:00:00 | 26.062834 | −90.849174 |
| 7/15/2019 | 9:00:00 | 34.561596 | −78.02713 |
| 7/15/2019 | 10:00:00 | 42.627950 | −63.434196 |
| 7/15/2019 | 11:00:00 | 49.610008 | −45.947623 |
| 7/15/2019 | 12:00:00 | 54.564102 | −24.62469 |
| 7/15/2019 | 13:00:00 | 56.401837 | −0.100691 |
| 7/15/2019 | 14:00:00 | 54.579909 | 24.433072 |
| 7/15/2019 | 15:00:00 | 49.635714 | 45.775489 |
| 7/15/2019 | 16:00:00 | 42.656412 | 63.278413 |
| 7/15/2019 | 17:00:00 | 34.586795 | 77.880929 |
| 7/15/2019 | 18:00:00 | 26.079756 | 90.706762 |
| 7/15/2019 | 19:00:00 | 17.596336 | 102.636741 |
| 7/15/2019 | 20:00:00 | 9.518739 | 114.313934 |
| Experiment | Reference | Time | TEA (corrected) [°] | AA (eastward from N) |
|---|---|---|---|---|
| 1 | Kennerud, 1969 | 8:00:00 | 26.062834 | −90.849174 |
| 9:00:00 | 34.561596 | −78.02713 | ||
| 2 | Charles, 1981 | 11:00:00 | 49.610008 | −45.947623 |
| 12:00:00 | 54.564102 | −24.62469 | ||
| 3 | Charles, 1981 | 14:00:00 | 54.579909 | 24.433072 |
| 15:00:00 | 49.635714 | 45.775489 | ||
| 4 | Lo Brano, 2010 | 17:00:00 | 34.586795 | 77.880929 |
| 18:00:00 | 26.079756 | 90.706762 | ||
| 5 | Cubas | 9:00:00 | 34.561596 | −78.02713 |
| 10:00:00 | 42.627950 | −63.434196 | ||
| 6 | PSM-150 | 19:00:00 | 17.596336 | 102.636741 |
| 20:00:00 | 9.518739 | 114.313934 |
| Experiment | ξmin/ξmax/ Δξ/ | Iph_min/Iph_max/ ΔIph/ | Vmin/Vmax/ ΔV/ | Pmin/Pmax/ ΔP/ |
|---|---|---|---|---|
| 1 | 0.979/ | 0.783/ | 0.175/ | 0.05/ |
| 0.984/ | 0.787/ | 0.272/ | 0.12/ | |
| 0.005 | 0.004/ | 0.097 | 0.07 | |
| 2 | 0.949/ | 0.097/ | 0.239/ | 0.004/ |
| 0.958/ | 0.098/ | 0.333/ | 0.012 | |
| 0.01 | 9.847 × 10−4/ | 0.094/ | 0.008/ | |
| 3 | 0.941/ | 0.528/ | 0.27/ | 0.055/ |
| 0.966/ | 0.542/ | 0.478/ | 0.128/ | |
| 0.025 | 0.014/ | 0.218/ | 0.073/ | |
| 4 | 0.968/ | 7.423/ | 0.418/ | 6.017/ |
| 0.997/ | 7.639/ | 0.588/ | 6.873/ | |
| 0.028 | 0.216 | 0.171/ | 0.9/ | |
| 5 | 0.974/ | 7.994/ | 24.061/ | 204.182/ |
| 0.981/ | 8.057/ | 35.101/ | 742.08/ | |
| 0.008 | 0.063/ | 11.04/ | 40/ | |
| 6 | 0.987/ | 4.736/ | 4.067/ | 278.727/ |
| 0.991/ | 4.758/ | 4.257/ | 288.441/ | |
| 0.005 | 0.022/ | 0.191/ | 32/ |
| Experiment | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| k1 | 50 | 2 | 5 | 5 | 1 | 0.5 |
| k2 | 100 | 2.5 | 6 | 6 | 2 | 0.6 |
| k3 | 3 | 1 | 1 | 1 | 1 | 1 |
| Asin_1, deg. | 1 | 1 | 1 | 1 | 1 | 1 |
| Asin_2, deg. | 1 | 1 | 1 | 1 | 1 | 1 |
| Asin_3 = Areg, Ohm | 0.13 | 0.968 | 0.239 | 0.012 | 0.804 | 1.708 |
| Thpf_1 | 10 | 1 | 1 | 1 | 10 | 10 |
| Thpf_2 | 10 | 1 | 1 | 1 | 10 | 10 |
| Thpf_3 | 1 | 1 | 1 | 1 | 1 | 1 |
| h1 | 5 | 1.5 | 4 | 1 | 10 | 10 |
| h2 | 10 | 2 | 3 | 1 | 10 | 10 |
| h3 | 1 | 1 | 1 | 1 | 1 | 1 |
| Pin = ΔP, W | 0.01 | 0.007 | 0.08 | 2 | 65 | 30 |
| iout | 0.065 | 0.002 | 0.05 | 1.75 | 3 | 0.5 |
| ω1, rad/s | 4.975 | 1.323 | 3 | 4.899 | 3.873 | 1.249 |
| ω2, rad/s | 9.95 | 1.5 | 5.196 | 5.916 | 7.937 | 1.639 |
| ω3, rad/s | 30 | 10 | 80 | 10 | 10 | 10 |
| Ain_1, deg. | 80.542 | 1.176 | 21.564 | 13.683 | 8.757 | 1.401 |
| Ain_2, deg. | 54.734 | 1.58 | 13.282 | 19.704 | 35.03 | 2.018 |
| Ain_3 = Asin_3, Ohm | 0.13 | 0.968 | 0.239 | 0.012 | 0.804 | 1.708 |
| K4→2_1 | 1.242 | 1.512 | 0.072 | 1.827 | 1.827 | 1.827 |
| K4→2_2 | 1.827 | 0.989 | 0.301 | 1.827 | 1.827 | 1.827 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kirpichnikova, I.M.; Sologubov, A.Y. Multivariable Control of Solar Battery Power by Extremum Seeking: Starting from Linear Analysis. Machines 2019, 7, 64. https://doi.org/10.3390/machines7040064
Kirpichnikova IM, Sologubov AY. Multivariable Control of Solar Battery Power by Extremum Seeking: Starting from Linear Analysis. Machines. 2019; 7(4):64. https://doi.org/10.3390/machines7040064
Chicago/Turabian StyleKirpichnikova, I. M., and A. Yu. Sologubov. 2019. "Multivariable Control of Solar Battery Power by Extremum Seeking: Starting from Linear Analysis" Machines 7, no. 4: 64. https://doi.org/10.3390/machines7040064
APA StyleKirpichnikova, I. M., & Sologubov, A. Y. (2019). Multivariable Control of Solar Battery Power by Extremum Seeking: Starting from Linear Analysis. Machines, 7(4), 64. https://doi.org/10.3390/machines7040064





