1. Introduction
Friction is a physical phenomenon that appears when there is relative motion between solid surfaces, fluid layers, and material elements sliding against each other. Essentially friction can be observed and studied using the friction force.
Information concerning friction is important due to the influence exerted by the friction on energy consumption and on the wear of the bodies found in contact.
There are distinct criteria to classify the friction and many factors are able to affect the size specific to the friction phenomenon. Thus, kinetic friction appears when there is a linear relative motion between two solid bodies. Among the factors able to affect the friction processes, we should consider the materials of the bodies found in contact, the surface roughness of the contact surfaces, the normal force exerted between the bodies found in contact, the presence and the nature of the fluid found in the zone between bodies, the temperature of the bodies and of the fluid, etc.
Sliding friction is specific to the operation of distinct machine elements. For example, sliding friction appears in sliding bearings, in gear teeth, in sliding couples. etc. There are certain situations when the friction phenomenon is useful, but more frequently, friction intensifies the machine elements’ wear and consumes additional energy to achieve the relative motion between the machine elements.
As above mentioned, machine manufacturers are interested in diminishing the friction processes’ intensity, to decrease the energy consumption and the wear of the machine elements between which relative motions develop [
1,
2,
3]. Various solutions can be applied to decrease the friction process intensity. We can diminish the height of the asperities corresponding to the bodies’ surfaces found in contact, introduce substances able to facilitate the sliding between the bodies’ surfaces, or use bodies made of or covered with substances able to diminish the friction forces. A good way to diminish the consequences of the friction processes can be offered by the use of the contactless mechanical components [
3], but for now, this solution may be difficult to apply in various situations.
Covering the bodies surfaces involved in intense friction processes with substances that reduce friction forces can be sometimes preferred. For example, the use of the molybdenum disulfide to diminish the friction forces between the punching tools and the workpiece in the process of manufacturing parts by material forming is known. In such a case, the oils containing particles of molybdenum disulfide can be used to cover the surfaces of the punching tools on which intense friction develops. In other situations, the oils including graphite particles can also be used to diminish the intensity of friction.
Currently applied distinct coating alternatives are characterized by various properties, advantages, and disadvantages.
Thus, the
magnetron sputtering technology is based on physical vapor deposition, when the material to be deposited is ejected from a target onto a substrate, as a consequence of ion or atom bombardment [
4,
5]. The magnetron sputtering technology is able to ensure antireflection properties in glass, to facilitate the deposition of very thin layers on transistors or to achieve multilayer deposition with good adhesion to the substrate, to deposit materials with very high melting points, etc. As limitations of the magnetron sputtering technology, we can consider the more difficult control of the deposit layer growth, the risk of contaminating zones where the deposition is not wanted, the high price of the sputtering equipment, etc. Martins et al. used a direct current magnetron sputtering to obtain a low friction composite coating that included molybdenum disulfide and titanium [
5]. A complex technology was designed and applied to ensure the deposition of a MoS
2/Ti layer on the gears’ teeth surfaces. Experimental research was developed to test the gear efficiency and gear anti-scuffing performance when the work surfaces of teeth were covered with MoS
2/Ti. The paper’s authors observed a decrease in the operating temperature, the friction coefficient value, and of the gears’ teeth wear intensity.
The introduction of solid lubricant particles to industrial oil diminishes the friction process by up to 25 to 50 %. The nanoparticles can penetrate into very narrow spaces between parts found in relative motion, and sometimes they can be used inclusively in dry friction conditions [
6,
7,
8,
9,
10]. An essential advantage of using solid lubricant particles is the fact that they do not need specialized equipment to be applied. As for disadvantages, there are situations when the use of the industrial oils is not allowed, when a certain polluting effect is signalized, or when the solid lubricant particles are expensive, etc. Lee et al. investigated the tribological characteristics of the graphite nano lubricants obtained by including graphite nanoparticles in industrial gear oil. They noticed that the nano lubricants ensured a lower friction coefficient and diminished wear of the specimens when using a disk-on-disk tribotester [
9]. In 2011, Hwang et al. published the results of research concerning the influence exerted by the size and morphology of particles included in mineral oil on the friction coefficient value when also using a disk-on-disk tribotest [
10]. They concluded that when spherical nanoparticles additives are found in the mineral oil, diminished value of the friction coefficient could be observed, compared with the situation when carbon black, graphite nanofibers, and nanotubes are dispersed in the mineral oil. Huang et al. appreciated that the explanation could be based on the possible role of ball bearings filled with the spherical nanoparticles.
Arc-sprayed coating uses direct current power to energize two conductive wires that feed into a gun where the electric arc melts the material, and the compressed air sends the molten material to the surface to coat an object [
11,
12]. Such a technology facilitates the deposition of layers with controllable thicknesses and can ensure a protective anodic layer on the steel parts for very long periods. Some essential disadvantages of this coating technology are a certain porosity of the deposited material, the use of only the electroconductive materials, and the fact that these materials must be able to melt without affecting the properties of interest in terms of the use of the coated parts. Pokhmurska et al. used a method of arc-spraying of FeCrB+Al and FeCr+Al+C powder wires to increase wear resistance [
12]. The experimental tests made in a block-on-ring configuration with boundary lubrication and using an abrasive-oil mixture showed a high wear resistance of the coatings.
Laser cladding coating technology facilitates coatings based on the use of nonconductive materials, for example, ceramics. Generally, the laser cladding coating can ensure a high hardness of the deposited layers and, as a consequence, a very high wear resistance. In other situations, the deposited layers obtained by laser cladding can ensure a high bonding strength, better corrosion resistance, good behavior to the adhesive and abrasive wear, the possibility to mix dissimilar materials, achieving of punctual deposit, generation of nonsignificant workpiece distortions, etc. As less convenient aspects of the laser cladding coating, the reduced plasticity of the deposited layer, the necessity of relatively expensive coating equipment, etc., need to be considered [
13,
14,
15,
16]. Wu et al. investigated the wear behavior of laser cladding ceramic coating [
16]. They deposited in situ VC-Cr
7C3 ceramic coating on a steel substrate. A hardness of up to 1050 HV was obtained, far exceeding the hardness of 150 HV of the steel substrate. The wear resistance of the clad coating was higher by about four times than that of the steel substrate.
In the case of
plasma spray coating, the granules, powders, and wires are melted and join the workpiece surface under plasma beam action [
13,
17,
18]. The deposited layers can be characterized by high wear resistance, corrosion and oxidation resistance, low content of impurities, with the possibility of depositing pure or mixture materials, etc. The main disadvantages of this coating technology can be determined by the relatively high cost of the operation and the possible non-homogenization of the layers’ structures. The wear resistance of in-situ TiC reinforced Ni-based composite coating obtained by plasma spray welding was studied by Huang et al. [
18]. The composite coating had a complex microstructure, including γ-Ni, Cr
23C
6, Cr
7C
3, Ni
3Si, Cr
5B
3, CrB, FeNi
3, and TiC phases. The hardness of the composite coating was of 1142 HV and, thus, a higher wear resistance was proved by experimental tests.
The current processes of
electrochemical deposition may ensure hard layers, corrosion resistance layers, decorative surfaces or high reflectance surfaces, etc. [
13,
19,
20]. As some less convenient aspects, the general limitation to the electroconductive materials to be deposited, a certain polluting character of the substances used in the process, and relatively high electrical energy consumption need to be considered. However, we should mention that, at present, a co-deposition of ceramic materials with metals and polymers is possible and hybrid layers can, thus, be generated. The electrochemical deposition of Ni and Ni-Co matrix composites with SiC nano-particles was applied by Srivastava et al. to improve the wear resistance of the parts involved in friction processes [
20]. They appreciated that wear resistance of the composite material is higher than that obtained in the case of pure Ni coatings. Experiments developed a pin-on-disc wear tester which showed an evolution of the composite material’s wear behavior in accordance with Archard’s law.
A comparison of some distinct coating methods by considering the wear behavior of the steel part surface layer was elaborated by Habig [
21]. As coating methods, he used electrochemical deposition, thermomechanical treatment, chemical vapor deposition, and physical vapor deposition. In this way, he succeeded in offering an overview concerning the advantages and disadvantages of the different coating methods.
When selecting a coating technology, one of the criteria used could be the total cost of the operation and of the materials. Generally, parts manufacturing costs are strongly influenced by the production character. For example, in mass production, the cost of a certain operation can be significantly diminished when equipment with a high level of automatization is used. In similar manufacturing costs, a coating operation can be expensive when using complex equipment and high-cost materials, and when there is high energy consumption. In comparison with other coating technologies, including solid lubricant particles in industrial oil is less expensive, essentially due to the simplicity of the operation process, even if the added material (particles of solid lubricant) cost is a little higher.
When it is not possible to use oil between the contact surfaces in relative motion, a decrease in the friction intensity can be obtained by covering the surfaces with layers that incorporate solid lubricants. As above mentioned, metallic layers including molybdenum disulfide can be used. To diminish the coating cost and when the friction processes are not very intense, coating technologies based on the use of plastic layers that include solid lubricants particles can be taken into consideration. One such plastic is polyester, for which electrostatic deposition technologies are largely used in industrial practice. Among the processes of plastic deposition on parts’ friction surfaces, electrostatic deposition can be characterized by low costs, especially when adequate equipment for deposition and for the postdeposition processes is available.
Empirical mathematical models that correspond to the influence exerted by some process input factors on the size of the friction coefficient and lifetime of the layers deposited by electrostatic painting and that included particles of molybdenum disulfide or graphite are presented in [
22]. The problem of finding the set of values of the friction process input factors (normal force, the concentration of solid lubricant particles in the polyester, and the specific sliding) for distinct weightings of the lifetime and friction coefficients as friction process output parameters are addressed in this paper. It was considered that the use of the grey relational analysis to identify the sets of process input factors values able to ensure certain weightings for the process output parameters could be an optimization solution in this case.
4. Experimental Research
To develop an investigation concerning the behavior of the deposited layers of polyester that includes the particles of molybdenum disulfide and graphite in friction conditions using the Amsler type testing machine, the diameters of the disks were calculated by means of the Equation (1), to obtain a specific sliding ε of 0%, 25% and 50%.
As a work/testing principle, it was agreed to use a friction couple that includes a disk covered with the polyester that includes solid lubricant particles and a disk without such a deposited layer. The diameters of the coated disks were of 48 mm. As above mentioned, the thickness of the coating layer was of about 90 µm.
In comparison with other testing equipment and schemes, the Amsler type testing machine and the adopted testing scheme were preferred since they ensure a relatively simple change of the testing conditions (testing normal force, testing speed, replacing of the samples, etc.). Even the testing scheme is simple; it takes into consideration the general operating conditions specific to many industrial machines. Due to the simplicity of the testing scheme, the characteristics of the friction processes can also be clearly highlighted.
The experimental research was developed in accordance with the work conditions shown in Columns 3,4, and 5 from
Table 1. Practically, an
L9 Taguchi triangular arrow (three independent factors and three experimental levels) was taken into consideration for each of the tested coating materials.
As a deposited layer lifetime T, the interval from starting the test up to the complete removal of the polyester layer on the disk cylindrical peripheral surface was considered.
In the Columns 3,4, and 5, the values of the process input factors are written as fractions, considering the codified values (1 for the minimum value, 2 for the intermediate value, and 3 for the maximum value) as numerators and the proper values of the process input factors as denominators. In
Table 1, the values of the process input factors and of the experimental results are written both for the polyester layer that includes particles of molybdenum disulfide and for the polyester layer that contains graphite particles.
The information included in the Columns 8,9,10, and 12 is the result of a partial processing of the experimental results.
The friction moment Mt was determined by means of the pendulum mechanism of the Amsler type testing machine. The normal radial force Q was generated using the screw-spring mechanism of the testing machine.
The values of the layers’ lifetimes,
T, were included in the Column 6 of
Table 1, while the values of the friction coefficient,
µ, were calculated using the Equation (1) and mentioned in the Column 7.
5. Use of the Grey Relational Analysis
To establish the set of the values of the friction process input factors that could ensure convenient values for the process output parameters, the grey relational analysis was considered. The theory of grey systems was proposed by the Chinese professor Julong Deng in the 1980s to characterize situations where there is limited or inadequate information.
Essentially, the grey relational analysis evaluates the quantitative relation between the elements included in two series. One appreciates that one of these series incorporates entities of the best quality. The comparison takes into consideration the grey relational coefficient, whose values depend on the similitude level and variability level, respectively.
To apply the grey relational analysis in the case of the achieved experimental research, a preprocessing of the experimental results (normalization of the experimental results) can be applied using the following Equations [
26,
27,
28].
- For the situation when the higher is the better:
- For the situation when the lower is the better:
where
Yij is the value with the order number
i of the characteristics in the experiment with the order number
j;
max Yij and
min Yij are the minimum and the maximum values of the characteristics in the experiment no.
i for the alternative
j.
In accordance with the above-mentioned equations, the normalized values for
T and
µ are mentioned in the Columns 8 and 9 of
Table 1.
In the case of the presented experimental results, we use Equation (3) in the case of the polyester layer lifetime T (when a higher value of the lifetime is more convenient) and the Equation (4) in the case of the friction coefficient µ (since diminished value of this coefficient is considered more convenient).
After the results normalization,
the grey relational coefficient ξij was determined by means of the relation
where
X0j is the ideal normalized result for the performance characteristics of order
j (this ideal normalized value corresponds to the maximum value of the normalized ratio
S/
N, since a high value of the ratio
S/
N is preferred,
S being the signal, and
N, the noise) and
ξ is the distinguished coefficient, to which distinct values could be attributed.
A shorter expression of the relation that corresponds to the grey relational coefficient
ξ is given by the equation:
where
ξ is the distinguished coefficient and
Δ0i is the difference between the absolute value
X0j of the normalized result for the performance characteristics (the output parameter)
j and
Xij,
Δ0i = |
X0j − Xij|,
Δmin is the lowest value of
Δ0i, and
Δmax is the highest value of
Δ0i.
The
grey relational grade γi is calculated as an average value of the grey relational coefficients
ξij that correspond to each experiment
i, and it is defined by the equation
where
Wk is the normalized weight of the factor, and that could be considered as equal to 1, and
n is the number of the considered performance characteristics. In this case, the lifetime
T and the friction coefficient
µ are the two considered performance characteristics, and this means
n = 2.
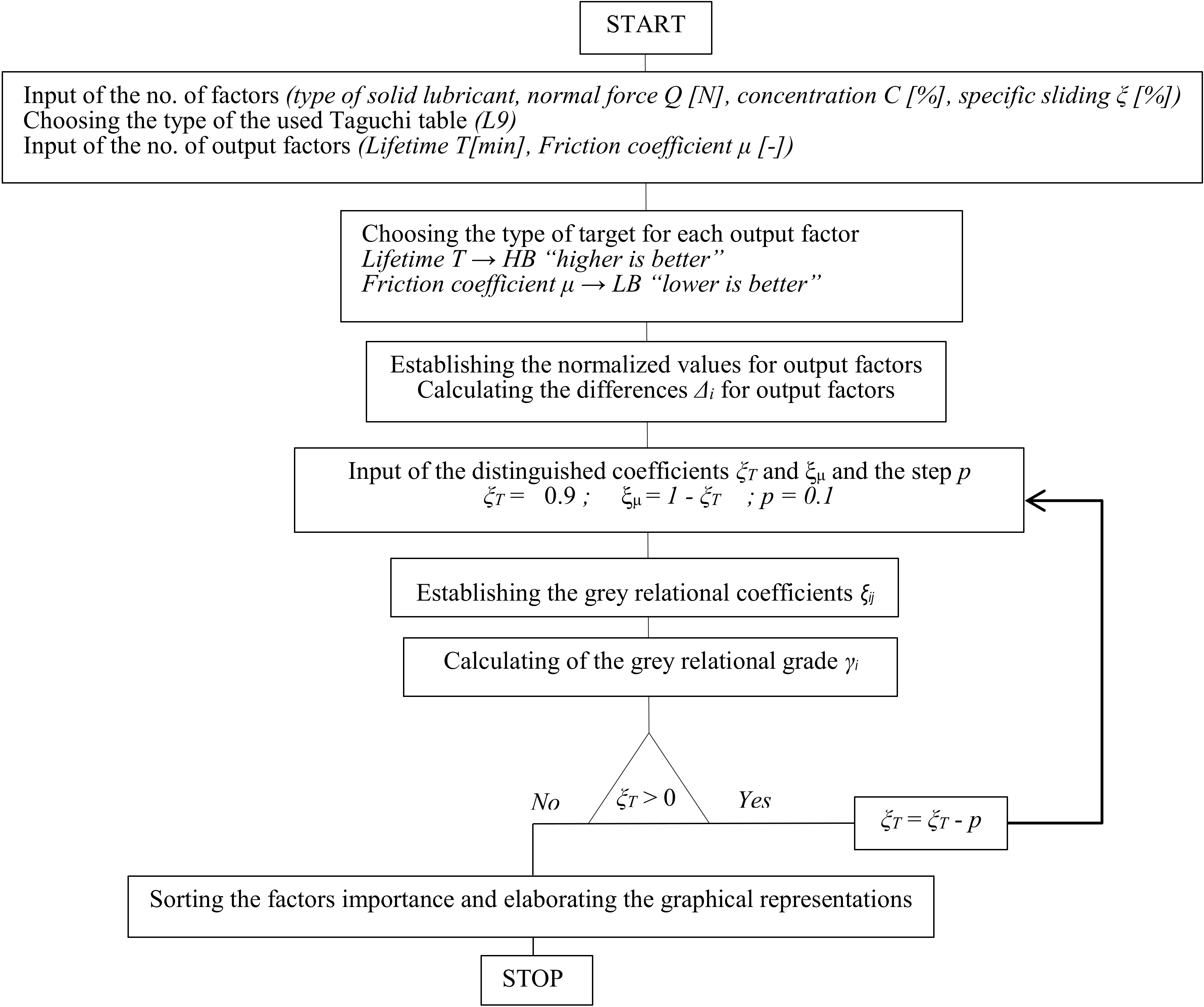
To calculate the values corresponding to the use of the grey relational analysis and to identify the most convenient sets of the values of the friction process input factors faster, specialized software in MATLAB environment was elaborated. The algorithm underlying this software is presented in
Figure 1.
Three distinct situations were initially taken into consideration for distinct values of the distinguished coefficient
ξ, namely a situation when
ξT = ξµ = 0.5 both for the lifetime
T and the friction coefficient
µ; another situation when
ξT = 0.9 for the lifetime
T and
ξµ = 0.1 for the friction coefficient
µ, and the third situation, when
ξT = 0.7 for the lifetime
T and
ξµ = 0.3 for the friction coefficient
µ. The results of the calculus for the first situation in the case of both solid lubricant types are included in
Table 2.
The values of the normalized values of the grey relational grades
γi can be seen in the Column 5 of
Table 2.
In the case when
ξ = 0.5 for both process output factors (
Table 2), the highest value of the grey relational grades
γi corresponds to Experiment 1 for the both types of solid lubricants particles (
γi = 0.846 for the polyester that includes molybdenum disulfide particles and
γi = 0.964 for the polyester that includes graphite particles) and this means that the values of the process input factors that correspond to Experiment 1 both in the case of using molybdenum disulfide and graphite (
Q = 34.2 N,
C = 10%,
ξ = 0 both in the case of molybdenum disulfide and graphite) can be considered as the closest value to those values able to ensure a maximum lifetime
T and a minimum value for the friction coefficient
µ.
We can also consider that the two process output factors are not of equal importance. For example, we can appreciate that the factor lifetime T has higher importance, evaluated by a distinguished coefficient ξT = 0.9, while the friction coefficient importance µ is evaluated by a distinguished coefficient ξ = 0.1. In such a situation, a new order of the experiments can be identified, and the most convenient combination of the process input factors can have values that correspond to the Experiment 8 for the molybdenum disulfide particles (Q = 67.4 N, C = 15%, ξ = 0) and to the Experiment 1 for the graphite particles (Q = 34.2 N, C = 10%, ξ = 0).
Another interpretation of the experimental results can be based on considering, for example, a distinguish coefficient ξT = 0.7, for the lifetime T and ξµ = 0.3, for the friction coefficient µ. For the considered experimental results, this situation shows that the most convenient combination of the process input factors values is the same with that valid in the case when ξT = 0.5, and ξµ = 0.5.
The analysis could be continued by considering some principles specific to the Taguchi method, by using the ratio signal/noise S/N.
Thus, the value of the quality loss function has to be calculated. If an evaluation type “higher the better” is taken into consideration, this function is given by
where
n is the number of experiments for the same values of the input factors,
k—the number of tests and
Yijk—the value of the output parameter obtained for the test
i, the experiment
j and test
k.
If a “lower the better” type evaluation is considered, the function
Lij is given by the equation
The value of the ratio
S/
N can be determined for both above-mentioned situations, using the equation
The ratio
S/
N can be used in the case of the mono-answer problems (mono-criterial optimization), while in the case of the multicriterial optimization, there is the recommendation to use the normalized values
NSN of the ratio’s
S/
N [
26]. Distinct ways can be used to determine the normalized values
NSN [
26,
29]. In this case, the following relation (adapted from [
29]) was preferred to determine the normalized value
NSN of the ratio’s
S/
N:
where
µS/N is the average value of the ratio
S/
N and
σ is the standard deviation of the ratio
S/
N.
The calculated values for the normalized value
NSN are mentioned in the Column 8 of
Table 2, while in the Column 13 the ranks based on the normalized values
NSN of the ratio
S/
N are included. As expected, we can observe that the ranks determined in this case are the same as those resulted by considering the grey relational grades
γi.
We notice that the experiments with the longest lifetime were found in the first position of ranking both for polyester that includes molybdenum disulfide particles and for the polyester that includes graphite particles. This fact can be explained by the developing of the experiments in similar initial conditions (process input factors), and the effects both solid lubricants have on the same action direction.
As above-mentioned, conventionally we took into consideration as the lifetime of the polyester layer that includes particles of solid lubricant, only the interval of time up to the total removal of the polyester layer on the disks surfaces as could be observed by visual examination, but particles of solid lubricant could yet remain (by adhesion) on the surfaces of the disks, thus, improving the disks’ behavior in respect to the friction processes. This aspect could be considered in future research, as comparisons with other types of anti-friction coating can be studied.
An example of the use of layers including solid lubricant particles to improve friction behavior, may be gear transmissions that do not work in oil with the inclusion of solid lubricant particles and when gears can be changed under mild conditions. We considered that in such a case the life of the gears could be higher than the one in which the solid lubricant particles incorporated in a polyester layer are not used. We also considered that the cost of using such a method of coating with a polyester layer including particles of solid lubricants could be lower than that valid in the cases of other coating methods, for example in the cases of arc sprayed coating [
11,
12,
13], laser cladding [
13,
14,
15,
16], plasma spray welding [
17,
18], electrochemical deposition [
19,
20], thermochemical treatment [
21], etc.
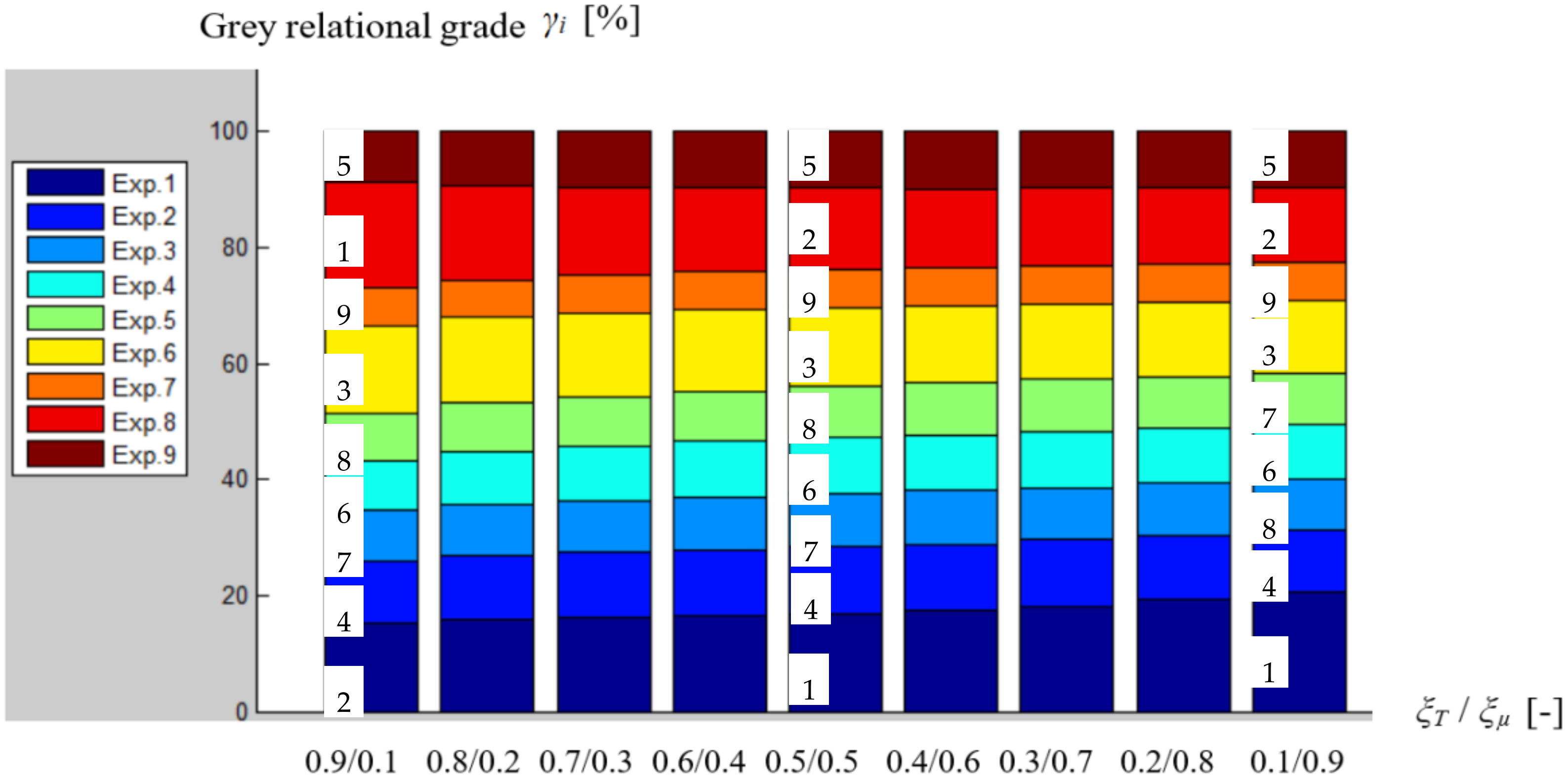
As additional information concerning the influence exerted by the value of the distinguished coefficient
ξ on the size of the ratio
S/
N is offered by the graphical representations in
Figure 2 and
Figure 3, where the values of the grey relational grade
γi are highlighted as functions of the distinct values for the ratio between the distinguished coefficients
ξT/
ξµ, by considering all the nine experimental tests. For ratios,
ξT/
ξµ equals with 0.9/0.1, 0.5/0.5, and 0.1/0.9, the values indicated in
Figure 2 and
Figure 3 corresponds to the rank based on the values of grey relational grade
γi. As a general remark, we can notice that the decrease of the ratio
ξT/
ξµ has, as a result, an increase of the values grey relational grade
γi for the Experiment 1 and a decrease of the value of the same grey relational grade
γi that corresponds to the Experiment 8.
As it is actually formulated, the grey relational analysis only allows the identification of the most convenient set of process input factors among many such experimental sets. To refine the results, another set of experiments could be designed for values of the process input factors found immediately around of the values that correspond to the best results obtained in the first set of experiments; in this way a better prediction of the experimental setting could be made, to obtain a more adequate compromise of the values that correspond to the two output parameters.
If the problem of the cost of applying the electrostatic deposition of polyester layers including particles of solid lubricants is approached, we can notice that the final cost is higher than the cost of simply introducing the particles of solid lubricants in the industrial oil used to diminish the negative effects of the friction processes, but when only dry operation is allowed to the parts involved in friction processes, the coating alternative investigated in this paper could be considered. If the cost of the solid lubricant particles and of applying the electrostatic deposition are analyzed, the final costs are about 1 euros/dm2 when using particles of molybdenum disulfide and of about 1.2 euros/dm2 when using particles of graphite. In this way, even if the deposited layer lifetime is lower than that corresponding to the deposition of hard material layers, the electrostatic deposition of the polyester layer including particles of solid lubricants represents a solution to be considered when the diminishing of the friction processes’ negative effects is investigated, especially if we examine the costs many times higher in the cases of hard material depositions.