Influence of Ball-Burnishing Process on Surface Topography Parameters and Tribological Properties of Hardened Steel
Abstract
1. Introduction
- Surface smoothing (geometrical) mechanism,
- Surface enhancement (mechanical) mechanism,
- The microstructural (metallurgical [11]) mechanism.
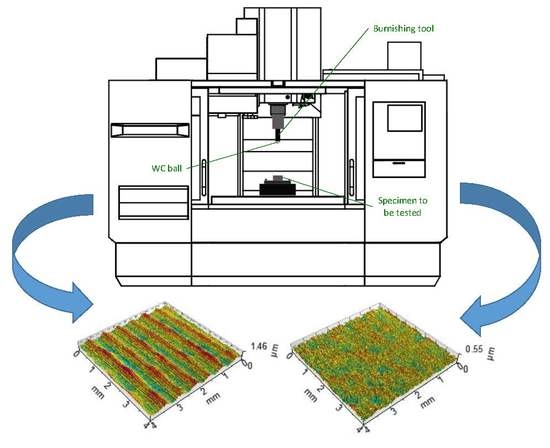
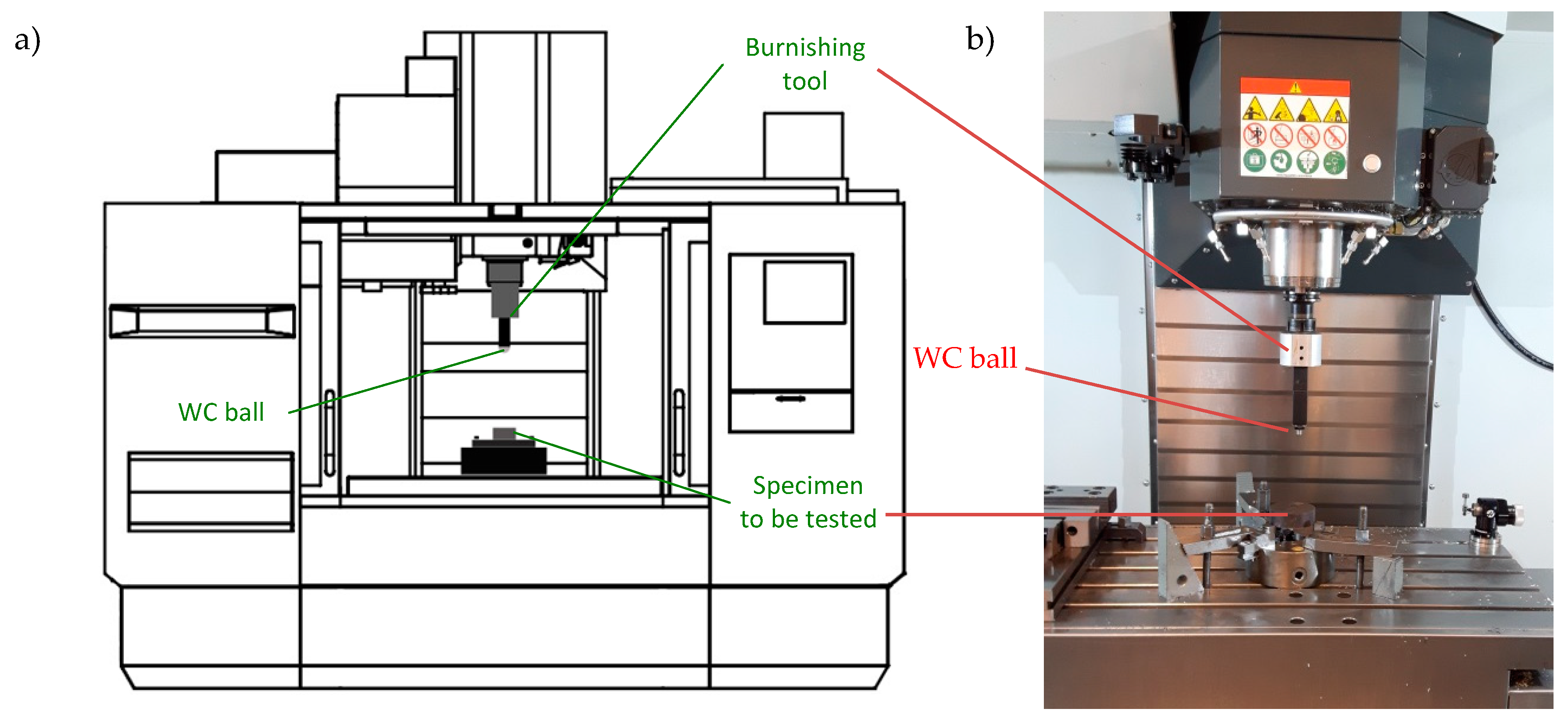
2. Materials and Methods
- x1—burnishing pressure force: 10, 20, and 30 MPa,
- x2—burnishing speed: 400, 700, and 1000 mm/min,
- x3—stepover: 30, 50, and 70 µm:
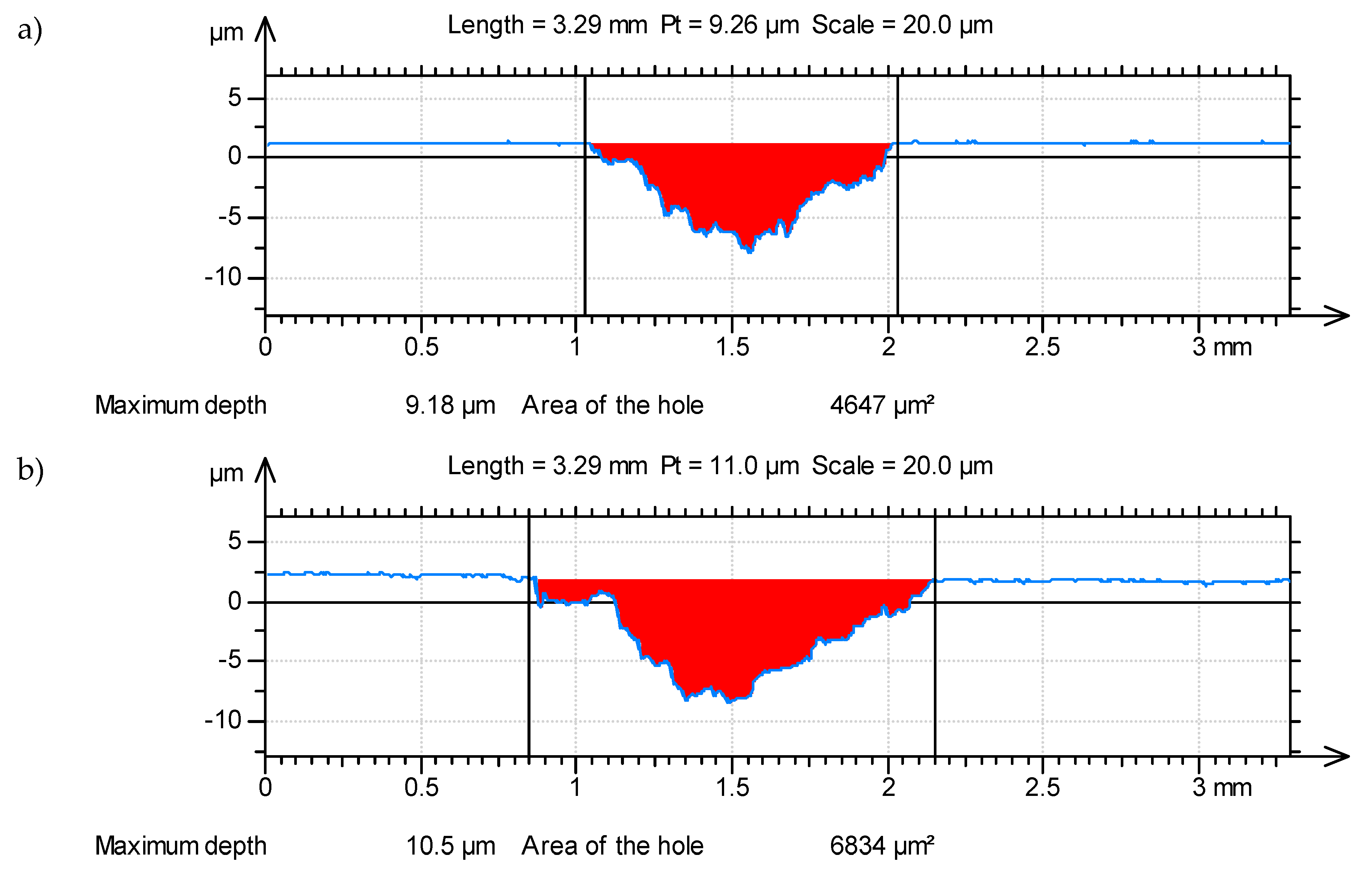
- d—diameter of the wear track (in our tests d = 10 mm),
- S—area of the hole (the cross-sectional area of the wear track).
3. Results and Discussion
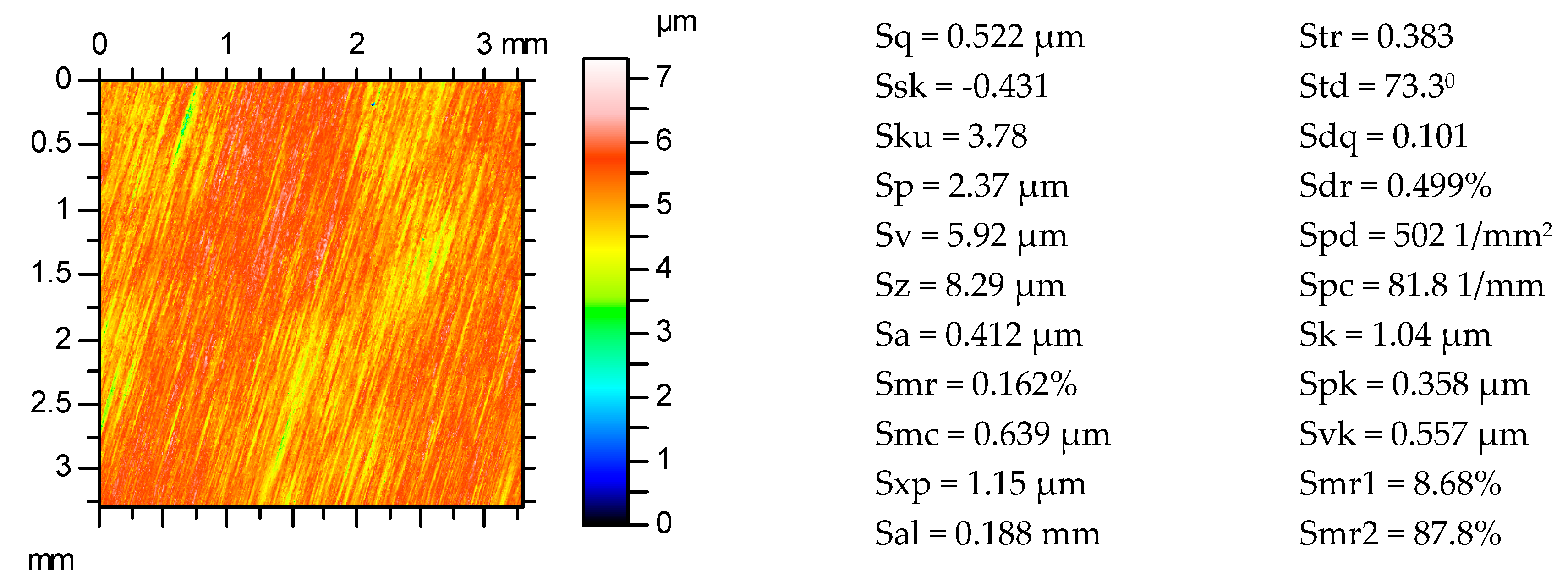
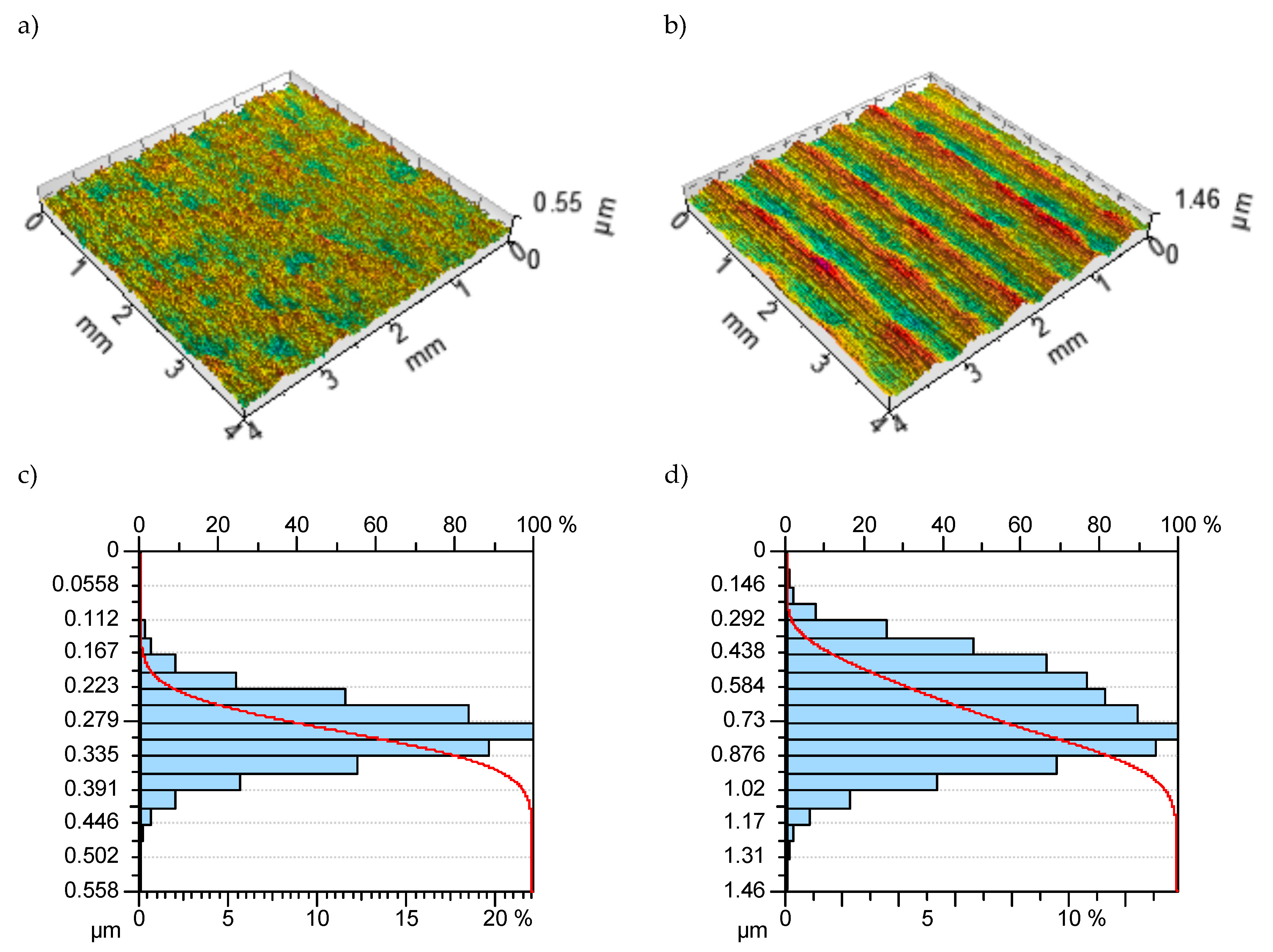
3.1. Effect of the Ball-Burnishing Parameters on the Surface Topography and Residual Stresses
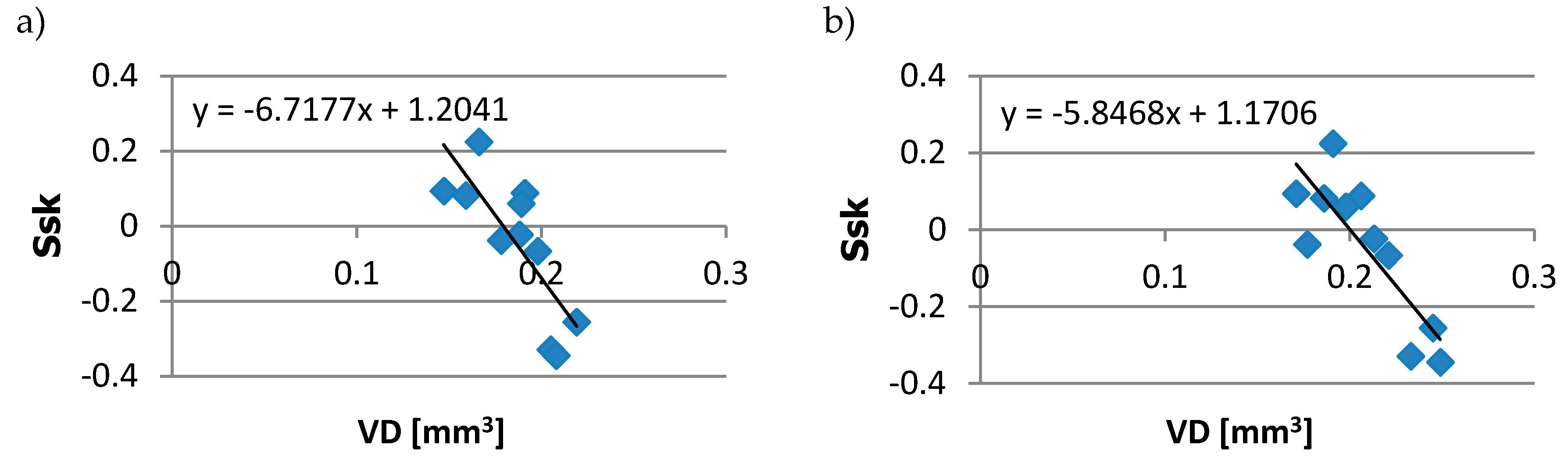
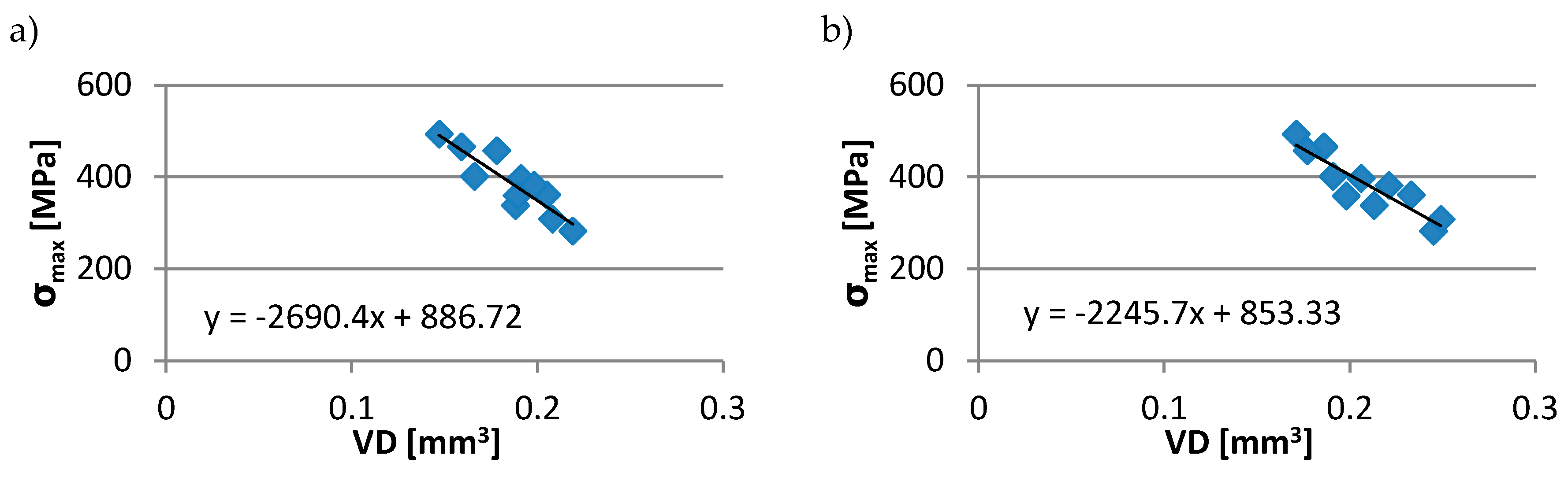
3.2. Effect of the Ball-Burnishing Parameters on the Tribological Properties
- The mean value of the volumetric wear of the disc samples (VD),
- The sliding distance after which the friction force obtains steady-state conditions (DSS),
- The average value of the friction force after obtaining the steady-state condition (Fav).
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- John, M.R.S.; Wilson, A.W.; Bhardwaj, A.P.; Abraham, A.; Vinayagam, B.K. An investigation of ball burnishing process on CNC lathe using finite element analysis. Simul. Model. Pract. Theory 2016, 62, 88–101. [Google Scholar] [CrossRef]
- Sagbas, A. Analysis and optimization of surface roughness in the ball burnishing process using response surface methodology and desirabilty function. Adv. Eng. Softw. 2011, 42, 992–998. [Google Scholar] [CrossRef]
- Revankar, G.D.; Shetty, R.; Rao, S.S.; Gaitonde, V.N. Analysis of surface roughness and hardness in ball burnishing of titanium alloy. Measurement 2014, 58, 256–268. [Google Scholar] [CrossRef]
- Hassan, A.M. The effects of ball and roller burnishing on the surface roughness and hardness of some non-ferrous metals. J. Mater. Process Technol. 1997, 72, 385–391. [Google Scholar] [CrossRef]
- Kovács, Z.F.; Viharos, Z.J.; Kodácsy, J. Determination of the working gap and optimal machining parameters for magnetic assisted ball burnishing. Measurement 2018, 118, 172–180. [Google Scholar] [CrossRef]
- Okada, M.; Shinya, M.; Matsubara, H.; Kozuka, H.; Tachiya, H.; Asakawa, N.; Otsu, M. Development and characterization of diamond tip burnishing with a rotary tool. J. Mater. Process. Technol. 2017, 244, 106–115. [Google Scholar] [CrossRef]
- Korzynski, M.; Dzierwa, A.; Pacana, A.; Cwanek, J. Fatigue strength of chromium coated elements and possibility of its improvement with ball peening. Surf. Coat. Tech. 2009, 204, 615–620. [Google Scholar] [CrossRef]
- Tian, Y.; Shin, Y.C. Laser-assisted burnishing of metals. Int. J. Mach. Tools Manuf. 2007, 47, 14–22. [Google Scholar] [CrossRef]
- Loh, N.H.; Tam, S.C. Effects of ball burnishing parameters on surface finish—A literature survey and discussion. Prec. Eng. 1988, 10, 215–220. [Google Scholar] [CrossRef]
- Li, F.L.; Xia, W.; Zhou, Z.Y.; Zhao, J.; Tang, Z.Q. Analytical prediction and experimental verification of surface roughness during the burnishing process. Int. J. Mach. Tools Manuf. 2012, 62, 67–75. [Google Scholar] [CrossRef]
- Zaborski, A.; Tubielewicz, K.; Major, B. Contribution of burnishing to the microstructure and texture in surface layers of carbon steel. Arch. Metall. 2000, 45, 333–341. [Google Scholar]
- Konefal, K.; Korzynski, M.; Byczkowska, Z.; Korzynska, K. Improved corrosion resistance of stainless steel X6CrNiMoTi17-12-2 by slide diamond burnishing. J. Mater. Process. Technol. 2013, 213, 1997–2004. [Google Scholar] [CrossRef]
- Luca, L.; Neagu-Ventzel, S.; Marinescu, I. Effects of working parameters on surface finish in ball-burnishing of hardened steels. Precis. Eng. 2005, 29, 253–256. [Google Scholar] [CrossRef]
- Shiou, F.J.; Chen, C.H. Freeform surface finish of plastic injection mold by using ball-burnishing proces. J. Mater. Process. Technol. 2003, 140, 248–254. [Google Scholar] [CrossRef]
- El-Axir, M.H. An investigation into roller burnishing. Int. J. Mach. Tools Manuf. 2000, 40, 1603–1617. [Google Scholar] [CrossRef]
- Shiou, F.J.; Hsu, C.C. Surface finishing of hardened and tempered stainless tool steel using sequential ball grinding, ball burnishing and ball polishing processes on a machining centre. J. Mater. Process. Technol. 2008, 205, 249–258. [Google Scholar] [CrossRef]
- Teimouri, R.; Amini, S.; Bami, A.B. Evaluation of optimized surface properties and residual stress in ultrasonic assisted ball burnishing of AA6061-T6. Measurement 2018, 116, 129–139. [Google Scholar] [CrossRef]
- Rodríguez, A.; López de Lacalle, L.N.; Celaya, A.; Lamikiz, A.; Albizuri, J. Surface improvement of shafts by the deep ball-burnishing technique. Surf. Coat. Technol. 2012, 206, 2817–2824. [Google Scholar] [CrossRef]
- Shiou, F.J.; Cheng, C.H. Ultra-precision surface finish of NAK80 mould tool steel using sequential ball burnishing and ball polishing processes. J. Mater. Process. Technol. 2008, 201, 554–559. [Google Scholar] [CrossRef]
- Travieso-Rodríguez, J.A.; Dessein, G.; González-Rojas, H.A. Improving the surface finish of concave and convex surfaces using a ball burnishing process. Mater. Manuf. Process. 2011, 26, 1494–1502. [Google Scholar] [CrossRef]
- Tekkaya, A.E.; Kleiner, M.; Biermann, D.; Hiegemann, L.; Rausch, S.; Franzen, V.; Kwiatkowski, L.; Kersting, P. Friction analysis of thermally sprayed coatings finished by ball burnishing and grinding. Prod. Eng. 2013, 7, 601–610. [Google Scholar] [CrossRef]
- El-Tayeb, N.S.M.; Low, K.O.; Brevern, P.V. Enhancement of surface quality and tribological properties using ball burnishing process. Mach. Sci. Technol. 2008, 12, 234–248. [Google Scholar] [CrossRef]
- Hassan, A.M.; Al-Dhifi, S.Z.S. Improvement in the wear resistance of brass components by the ball burnishing process. J. Mater. Process. Technol. 1999, 96, 73–80. [Google Scholar] [CrossRef]
- Hamadache, H.; Laouar, L.; Zeghib, N.E.; Chaoui, K. Characteristics of Rb40 steel superficial layer under ball and roller burnishing. J. Mater. Process. Technol. 2006, 180, 130–136. [Google Scholar] [CrossRef]
- Revankar, G.D.; Shetty, R.; Rao, S.S.; Gaitonde, V.N. Wear resistance enhancement of titanium alloy (Ti–6Al–4V) by ball burnishing process. J. Mater. Res. Technol. 2017, 6, 13–32. [Google Scholar] [CrossRef]
- Montgomery, D.G. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005; ISBN 978-1-118-14692-7. [Google Scholar]
- Korzynski, M. Methodology of Experiment; Science Publishing Home: Warszawa, Poland, 2006; ISBN 83-204-3203-0. (In Polish) [Google Scholar]
- Fitzpatric, M.E.; Fry, A.T.; Holdway, P.; Kandil, F.A.; Shackleton, J.; Suominen, L.L. Determination of Residual Stresses by X-ray Diffraction—Issue 2. A National Measurement Good Practice Guide No. 52; National Physical Laboratory: Teddington, UK, 2005. [Google Scholar]
- ISO 25178-2:2012. Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms, Definitions and Surface Texture Parameters; ISO: Geneva, Switzerland, 2012. [Google Scholar]
- Dzierwa, A. Influence of surface preparation on surface topography and tribological behaviours. Arch. Civ. Mech. Eng. 2017, 17, 502–510. [Google Scholar] [CrossRef]
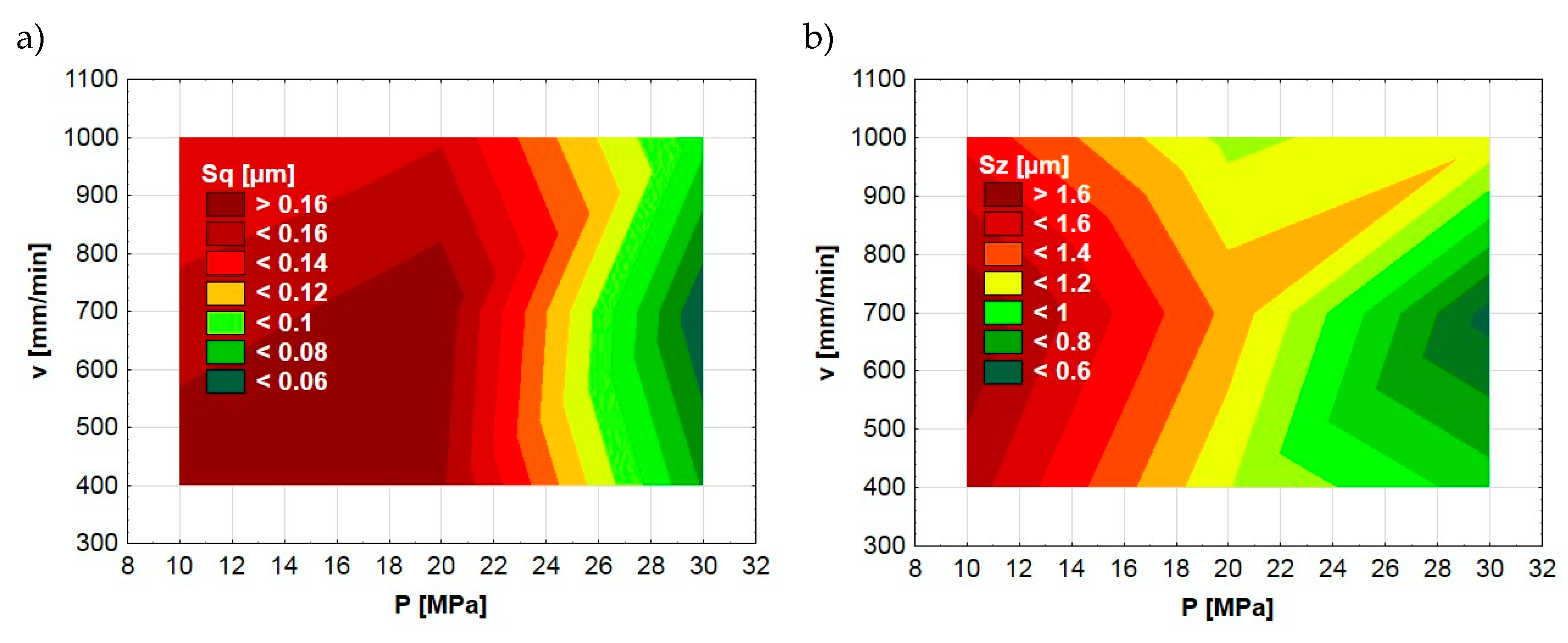
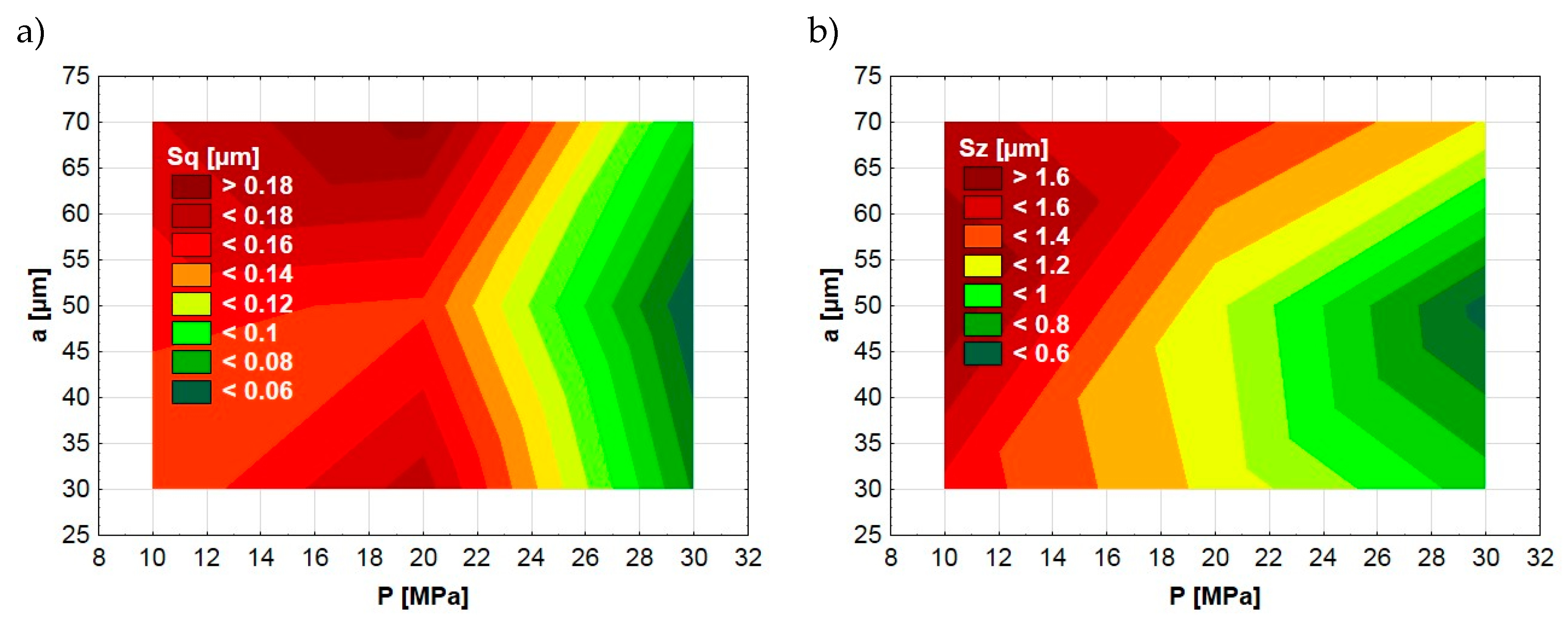
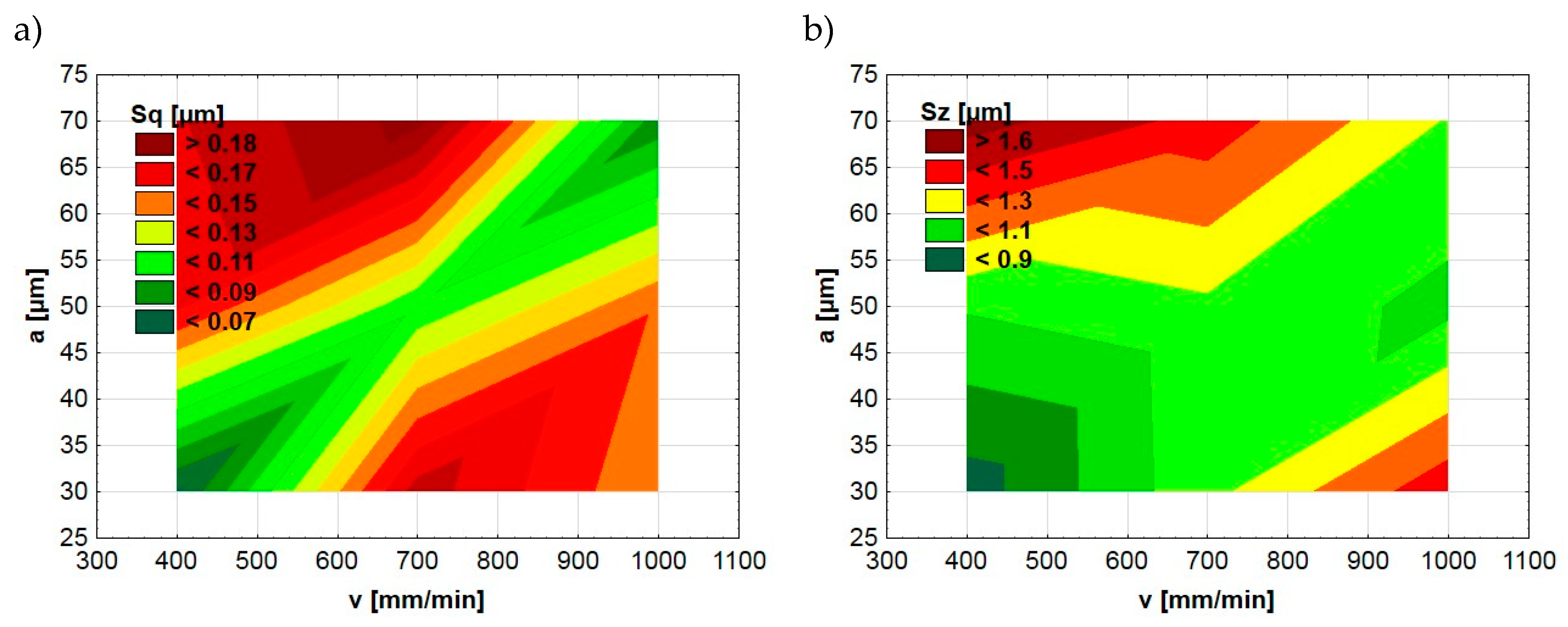
| Central Values of the Entry Factors | Units of Variation | Encoded Input Factors |
|---|---|---|
| No | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | + | + | + | + | + | + | + | − | − | 0.0835 | 1.19 | −401 |
| 2 | + | − | − | + | + | + | − | − | + | 0.0685 | 0.85 | −493 |
| 3 | − | + | − | + | + | + | − | + | − | 0.141 | 1.47 | −282 |
| 4 | − | − | + | + | + | + | + | + | + | 0.169 | 1.65 | −361 |
| 5 | + | 0 | 0 | + | 0 | 0 | 0 | 0 | 0 | 0.051 | 0.558 | −466 |
| 6 | − | 0 | 0 | + | 0 | 0 | 0 | 0 | 0 | 0.153 | 1.79 | −308 |
| 7 | 0 | + | 0 | 0 | + | 0 | 0 | 0 | 0 | 0.149 | 1.07 | −338 |
| 8 | 0 | − | 0 | 0 | + | 0 | 0 | 0 | 0 | 0.162 | 1.11 | −457 |
| 9 | 0 | 0 | + | 0 | 0 | + | 0 | 0 | 0 | 0.194 | 1.46 | −397 |
| 10 | 0 | 0 | − | 0 | 0 | + | 0 | 0 | 0 | 0.175 | 1.17 | −382 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.133 | 1.19 | −359 |
| Surface Topography Parameters [29] | Workpiece | ||||
|---|---|---|---|---|---|
| Ground | Burnished | ||||
| Min. | Max. | ||||
| Height | Root mean square height | Sq [µm] | 0.522 | 0.051 | 0.194 |
| Skewness | Ssk | −0.431 | −0.345 | 0.244 | |
| Kurtosis | Sku | 3.78 | 1.99 | 3.26 | |
| Maximum peak height | Sp [µm] | 2.37 | 0.294 | 0.805 | |
| Maximum pit height | Sv [µm] | 5.92 | 0.264 | 1.03 | |
| Maximum height | Sz [µm] | 8.29 | 0.558 | 1.79 | |
| Arithmetic mean height | Sa [µm] | 0.412 | 0.041 | 0.339 | |
| Functional | Areal material ratio | Smr [%] | 0.162 | 93.5 | 100 |
| Inverse areal material ratio | Smc [µm] | 0.639 | 0.0647 | 0.266 | |
| Extreme peak height | Sxp [µm] | 1.15 | 0.0969 | 0.339 | |
| Spatial | Auto-correlation length | Sal [mm] | 0.188 | 0.0358 | 0.217 |
| Texture-aspect ratio | Str | 0.383 | 0.0237 | 0.245 | |
| Texture direction | Std [o] | 73.3 | 0.623 | 7.1 | |
| Hybrid | Root mean square gradient | Sdq | 0.101 | 0.00613 | 0.0234 |
| Developed interfacial area ratio | Sdr [%] | 0.499 | 0.00188 | 0.0273 | |
| Functional | Material volume | Vm [mm3/mm2] | 2.01 × 10−5 | 2.53 × 10−6 | 6.90 × 10−6 |
| (volume) | Void volume | Vv [mm3/mm2] | 0.000659 | 6.72 × 10−5 | 2.73 × 10−4 |
| Peak material volume | Vmp [mm3/mm2] | 2.01 × 10−5 | 2.53 × 10−6 | 6.90 × 10−6 | |
| Core material volume | Vmc [mm3/mm2] | 0.000466 | 4.47 × 10−5 | 1.88 × 10−4 | |
| Core void volume | Vvc [mm3/mm2] | 0.00059 | 6.16 × 10−5 | 2.55 × 10−4 | |
| Pit void volume | Vvv [mm3/mm2] | 6.93 × 10−5 | 5.61 × 10−6 | 2.08 × 10−5 | |
| Feature | Density of peaks | Spd [1/mm2] | 502 | 243 | 448 |
| Arithmetic mean peak curvature | Spc [1/mm] | 81.8 | 6.05 | 15.5 | |
| Ten-point height | S10z [µm] | 3.77 | 0.325 | 1.08 | |
| Five-point peak height | S5p [µm] | 1.42 | 0.188 | 0.489 | |
| Five-point pit height | S5v [µm] | 2.35 | 0.136 | 0.591 | |
| Mean dale area | Sda [mm2] | 0.0019 | 0.00151 | 0.00447 | |
| Mean hill area | Sha [mm2] | 0.00195 | 0.00181 | 0.00372 | |
| Mean dale volume | Sdv [mm3] | 7.06 × 10−8 | 1.16 × 10−8 | 2.62 × 10−8 | |
| Mean hill volume | Shv [mm3] | 7.85 × 10−8 | 1.19 × 10−8 | 2.14 × 10−8 | |
| Functional | Core roughness depth | Sk [µm] | 1.04 | 0.106 | 0.421 |
| (stratified | Reduced summit height | Spk [µm] | 0.358 | 0.0433 | 0.0853 |
| surfaces) | Reduced valley depth | Svk [µm] | 0.557 | 0.0407 | 0.162 |
| Upper bearing area | Smr1 [%] | 8.68 | 3.66 | 11.4 | |
| Lower bearing area | Smr2 [%] | 87.8 | 90.2 | 95.2 | |
| No | vs = 0.16, m/s | vs = 0.32, m/s | vs = 0.48, m/s | ||||||
|---|---|---|---|---|---|---|---|---|---|
| VD, mm3 | DSS, m | Fav, N | VD, mm3 | DSS, m | Fav, N | VD, mm3 | DSS, m | Fav, N | |
| 1 | 0.166 | 68 | 5.44 | 0.171 | 62 | 4.87 | 0.191 | 54 | 5.42 |
| 2 | 0.147 | 81 | 4.69 | 0.162 | 70 | 4.78 | 0.171 | 62 | 4.92 |
| 3 | 0.219 | 22 | 5.54 | 0.231 | 18 | 5.36 | 0.245 | 19 | 5.48 |
| 4 | 0.205 | 64 | 5.26 | 0.193 | 40 | 4.92 | 0.233 | 28 | 5.37 |
| 5 | 0.159 | 71 | 5.19 | 0.174 | 44 | 4.81 | 0.186 | 37 | 4.98 |
| 6 | 0.208 | 65 | 4.89 | 0.222 | 25 | 5.09 | 0.249 | 15 | 5.49 |
| 7 | 0.188 | 33 | 4.95 | 0.197 | 34 | 5.18 | 0.213 | 46 | 5.14 |
| 8 | 0.178 | 59 | 5.11 | 0.183 | 64 | 5.33 | 0.177 | 37 | 4.98 |
| 9 | 0.191 | 38 | 5.37 | 0.188 | 51 | 4.97 | 0.206 | 55 | 5.23 |
| 10 | 0.198 | 52 | 4.91 | 0.214 | 30 | 5.22 | 0.221 | 49 | 5.31 |
| 11 | 0.189 | 55 | 5.04 | 0.204 | 38 | 5.02 | 0.198 | 61 | 4.92 |
| Ground | 0.278 | 79 | 5.71 | 0.285 | 72 | 5.45 | 0.309 | 68 | 5.77 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dzierwa, A.; Markopoulos, A.P. Influence of Ball-Burnishing Process on Surface Topography Parameters and Tribological Properties of Hardened Steel. Machines 2019, 7, 11. https://doi.org/10.3390/machines7010011
Dzierwa A, Markopoulos AP. Influence of Ball-Burnishing Process on Surface Topography Parameters and Tribological Properties of Hardened Steel. Machines. 2019; 7(1):11. https://doi.org/10.3390/machines7010011
Chicago/Turabian StyleDzierwa, Andrzej, and Angelos P. Markopoulos. 2019. "Influence of Ball-Burnishing Process on Surface Topography Parameters and Tribological Properties of Hardened Steel" Machines 7, no. 1: 11. https://doi.org/10.3390/machines7010011
APA StyleDzierwa, A., & Markopoulos, A. P. (2019). Influence of Ball-Burnishing Process on Surface Topography Parameters and Tribological Properties of Hardened Steel. Machines, 7(1), 11. https://doi.org/10.3390/machines7010011