Bidirectional Haptic Communication: Application to the Teaching and Improvement of Handwriting Capabilities ^†

Abstract

The objective of this work is to study the relevance of haptic feedback in remote communication between people. The application is handwriting. A haptic device designed to help people to improve their writing skills is presented. Two experimental sessions are then proposed to a group of people. In the first test, two subjects communicate through a bilateral system by means of a haptic feedback to accomplish the task. Secondly, a blank test is performed. The results of the two tests are compared and analyzed in order to evaluate the importance of the haptic feedback in the context of collaboration between two people.

1. Introduction

Terms such as haptic devices and tele-operation systems have become more and more significant in the robotics vocabulary over the last years. Haptics is commonly depicted as a perceptual system, mediated by two afferent subsystems, cutaneous and kinesthetic, that involves active manual exploration [1]. In a similar way, haptic technology exploits the sense of touch as a new interesting medium of communication between people [2,3]. Besides, haptic devices can be important tools for teaching people to execute or to recover certain movements. In the literature concerning the field of rehabilitation, this technology plays a more and more significant role [4,5]. In general, several approaches are proposed in the skill motion training domain. A distinction may be done between human-robot and human-human interactions. In the former case, the haptic device is programmed to be capable of interfacing with the human user [6,7]. The other approach to the problem is the use of a human-human interaction, where the haptic device plays the role of intermediate between the expert and the novice. In [8], Yokokohji et al. proposed a “record and replay” strategy. The required movement is to be saved and then replayed by the haptic interface. Hence the problem focuses on which data need to be transferred and how.

In this paper, a system based on a human-human interaction is implemented, but following a different strategy. In order to evaluate the effectiveness of the approach proposed here, human handwriting is selected as the experiment of interest. Over the last decade, many researchers have presented new haptic tools designed to help people to write. Most of them adopted a human-robot interaction, consisting of the offline programming of the haptic interface that is to be used, after, by the student. Kim et al. [9] introduced the use of letter primitives to program the Phantom Omni robot. In [10], the authors presented the Telemaque, a force-feedback programmable pen. An innovative hand-writing font, based on control points, elliptic arcs and straight lines is introduced. Other researchers did actually implement a human-human interaction, following the “record and replay” strategy. In [11], the authors proposed to save both the position and force trajectory of the teacher. The recorded skill is then transferred to the student via haptic display devices. Srimathveeravalli and Thenkurussi [12] presented a virtual writing test-bed, trying different control laws for a test aiming to teach an Indian character. Even if, theoretically, such methodology is a human to human skill transfer, the student is ultimately interfacing with a machine, i.e., the haptic device.

We believe that an effective human-human interaction, via a haptic medium, can provide more interesting results, in terms of performances and satisfaction of the student. The strategy proposed here, therefore, is based on a direct interaction between the teacher and the novice, rather than on the “record and play” paradigm. The figure of the teacher becomes central for a positive outcome of the learning task. The efficiency of a direct human-human collaboration through haptic channels has already been proven for different applications. In [13], the authors show how significantly the error rate for exchanging objects decreases when the force feedback is introduced between two people working together. Reed et al. [14] demonstrate that two people cooperating on a physical task quickly adopt an emergent strategy: participants form a sort of temporary specialization such that each member commands a specific part of the motion. This negotiation does “take place through a haptic channel of communication and it is apparently at a level below the awareness of the participants”. The same result cannot be obtained when the participant interacts with a robot, programmed to perform one of the typical human temporary roles, even if such a person does believe to be interacting with another human [15]. According to the authors, this subtle negotiation that exists in the human-human interaction is not evident to replicate.

Surprisingly, little research has been done on the physical cooperation between two people. In this work, a bilateral teleoperation system is developed to tackle the problem of the training and the assessment of handwriting capabilities by implementing a direct human-human interaction. To the best of our knowledge, this approach is novel, especially in the context of this application.

The paper is organized as follows. In the next section, the bilateral teleoperation system is presented. Section 3 is dedicated to the introduction of two experimental sessions, a haptic test and a blank test, where the results are presented in a qualitative form. A deeper analysis is carried out in Section 4, where statistical results are provided and commented.

Figure 1. One of the two five-bar mechanisms of the proposed bilateral teleoperation system.

Figure 1. One of the two five-bar mechanisms of the proposed bilateral teleoperation system.

2. Bilateral Teleoperation System

The system is composed of two identical five-bar two-degree-of-freedom parallel mechanisms (haptic devices), mechanism A and mechanism B, that can move in a plane (Figure 1). A pencil is attached to the end-effector, via a customized holder, in order to use the mechanisms as writing devices, as shown in Figure 1. The approach is the same as that adopted by Frisoli et al. [16], who presented a haptic interface consisting of a tendon driven closed-loop five-bar linkage. The solution proposed here is simpler. Each mechanism is characterized by 5 joints, two of which, at the base, are actuated. The actuated joints are driven by servomotors.

2.1. Control Law

The objective of the bidirectional haptic system is to make mechanism A follow exactly the same trajectory as mechanism B, and vice versa. To this end, an impedance control law is proposed, which normally guarantees good performances if a proper dynamic compensation term is included [17]. The general control law can be written as:

$${\mathit{\tau }}_i=\mathbf{h}({\mathit{\theta }}_i,{\dot{\mathit{\theta }}}_i)+{\mathbf{W}}^T[C_1({\ddot{\mathbf{p}}}_{0,i}-{\ddot{\mathbf{p}}}_i)+C_2({\dot{\mathbf{p}}}_{0,i}-{\dot{\mathbf{p}}}_i)+C_3({\mathbf{p}}_{0,i}-{\mathbf{p}}_i)]$$

(1)

where ${\mathit{\tau }}_i={\left[{\tau }_{i,1}{\tau }_{i,2}\right]}^T$ is the torque vector applied to the servomotors 1 and 2 of the mechanism on the $i_{th}$ side, with $i=A,B$. Vectors ${\mathbf{p}}_i={\left[x_i{y}_i\right]}^T$, ${\dot{\mathbf{p}}}_i={\left[{\dot{x}}_i{\dot{y}}_i\right]}^T$ and ${\ddot{\mathbf{p}}}_i={\left[{\ddot{x}}_i{\ddot{y}}_i\right]}^T$ are respectively the $i_{th}$ end effector position, velocity and acceleration vectors, whereas ${\mathbf{p}}_{0,i}={\left[x_{0,i}{y}_{0,i}\right]}^T$, ${\dot{\mathbf{p}}}_{0,i}={\left[{\dot{x}}_{0,i}{\dot{y}}_{0,i}\right]}^T$ ${\ddot{\mathbf{p}}}_{0,i}={\left[{\ddot{x}}_{0,i}{\ddot{y}}_{0,i}\right]}^T$ represent the desired end effector position, velocity and acceleration vectors. In this application, their values will be: ${\mathbf{p}}_{0,a}={\mathbf{p}}_b$, ${\mathbf{p}}_{0,b}={\mathbf{p}}_a$, and ${\ddot{\mathbf{p}}}_{0,i}={\dot{\mathbf{p}}}_{0,i}=\mathbf{0}$ for $i\in A,B$. Coefficients $C_1$, $C_2$ and $C_3$ are constant scalars (gains), which are tuned experimentally. $\mathbf{W}$ is the Jacobian matrix of the system.

The term $h({\theta }_i,{\dot{\theta }}_i)$ normally includes the Coriolis and centrifugal forces, gravity as well as friction effects. Since the device developed here is used at low velocities and accelerations, the latter term can be reduced to a simpler term, noted $\mathbf{g}(\theta )$, that is the gravity vector, since the other terms are negligible. Moreover, the acceleration is typically very noisy, which negatively affects the final performance, as it was verified experimentally. Therefore, acceleration is not used in the feedback terms. The control law, in its simplified form, then becomes:

$${\mathit{\tau }}_i=\mathbf{g}({\mathit{\theta }}_i)+{\mathbf{W}}^T[C_2({\dot{\mathbf{p}}}_{0,i}-{\dot{\mathbf{p}}}_i)+C_3({\mathbf{p}}_{0,i}-{\mathbf{p}}_i)]$$

(2)

The servomotor Pittman GM9X36 used in the haptic device has a reduction ratio of 5.9:1. One consequence is the existence of a friction term, which affects the behaviour of the device. Another modification to the control law is therefore introduced, namely:

$${\mathit{\tau }}_i=\mathbf{g}({\mathit{\theta }}_i)+{\mathbf{W}}^T[C_2({\dot{\mathbf{p}}}_{0,i}-{\dot{\mathbf{p}}}_i)+C_3({\mathbf{p}}_{0,i}-{\mathbf{p}}_i)]-\mathbf{F}$$

(3)

where $\mathbf{F}$ is a vector approximating the friction term, which is measured experimentally and defined as

$$\mathbf{F}={\left[f_{1}sign({\dot{\theta }}_{i1})f_{2}sign({\dot{\theta }}_{i2})\right]}^T$$

(4)

where $sign$ stands for the sign function and $f_i$ is the magnitude of the friction associated with motor i.

Finally, in the application proposed here (handwriting), the working plane of the mechanism is parallel to the ground (see Figure 2). Hence, the gravity term becomes superfluous and the control law can be simplified to:

$${\mathbf{ø}}_i={\mathbf{W}}^T[C_2({\dot{\mathbf{p}}}_{0,i}-{\dot{\mathbf{p}}}_i)+C_3({\mathbf{p}}_{0,i}-{\mathbf{p}}_i)]-\mathbf{F}$$

(5)

2.2. Kinematics of the Mechanism

The haptic device consists of a five-bar two-degree-of-freedom parallel mechanism, represented schematically in Figure 2. The two servomotor positions with respect to a fixed frame are described by vectors ${\mathbf{n}}_1$ and ${\mathbf{n}}_2$. ${\theta }_1$ and ${\theta }_2$ are the angles between vectors ${\mathbf{n}}_i$ and ${\mathbf{u}}_i$ (defined along the proximal links) and they describe the orientation of the two proximal bars with respect to the base. Two longer distal bars are passively linked to the respective proximal aluminum bar and to each other. Their intersection represents the end-effector of the mechanism, where a pencil is attached.

Figure 2. Schematic representation of the five-bar mechanism.

Figure 2. Schematic representation of the five-bar mechanism.

The position equations for the mechanism can be written as:

$$\mathbf{p}={\mathbf{n}}_i+{\mathbf{u}}_i+{\mathbf{v}}_i,i=1,2$$

(6)

where $\mathbf{p}={\left[xy\right]}^T$, ${\mathbf{u}}_1={[-L_{1}cos{\theta }_1{L}_{1}sin{\theta }_1]}^T,$ ${\mathbf{u}}_2={[L_{1}cos{\theta }_2{L}_{1}sin{\theta }_2]}^T$, ${\mathbf{n}}_1={[-n0]}^T$, ${\mathbf{n}}_2={\left[n0\right]}^T$, ${\mathbf{v}}_1=L_2{\mathbf{w}}_1$ and ${\mathbf{v}}_2=L_2{\mathbf{w}}_2$. ${\mathbf{w}}_1$ and ${\mathbf{w}}_2$ are unit vectors defined along the distal links. The distance between the motor axis and the centre of mass of $m_1$ and the distance between the elbow joint and the centre of mass of $m_2$ are noted $l_1$ and $l_2$, respectively. From Equation (6), the inverse kinematic problem (IKP) can be solved as follows. Equation (6) is first rearranged as

$$\mathbf{p}-{\mathbf{n}}_i-{\mathbf{u}}_i={\mathbf{v}}_i,i=1,2$$

(7)

Taking the magnitude of both sides of Equation (7) and rearranging them leads to:

$${(\mathbf{p}-{\mathbf{n}}_i)}^T(\mathbf{p}-{\mathbf{n}}_i)+L_1^2-L_2^2=2{(\mathbf{p}-{\mathbf{n}}_i)}^T{\mathbf{u}}_i,i=1,2$$

(8)

There are four global solutions for the IKP, i.e., two solutions for ${\theta }_1$ and two solutions for ${\theta }_2$, since Equation (8) can be written as follows:

$${\Lambda }_{i}cos{\theta }_i+{\Theta }_{i}sin{\theta }_i+{\Gamma }_i=0,i=1,2$$

(9)

with

$$\begin{array}{cc}\hfill {\Lambda }_i& =2{(\mathbf{p}-{\mathbf{n}}_i)}^T{\mathbf{e}}_1{L}_1,\hfill \\ \hfill {\Theta }_i& =2{(\mathbf{p}-{\mathbf{n}}_i)}^T{\mathbf{e}}_2{L}_1,\hfill \\ \hfill {\Gamma }_i& ={(\mathbf{p}-{\mathbf{n}}_i)}^T(\mathbf{p}-{\mathbf{n}}_i)+L_1^2-L_2^2\hfill \end{array}$$

(10)

and ${\mathbf{e}}_1={\left[10\right]}^T$, ${\mathbf{e}}_2={\left[01\right]}^T$.

It can also readily be shown that the solution to the Direct Kinematic Problem (DKP) can be written as:

$$\Delta cos\alpha +\Sigma sin\alpha +\Phi =0$$

(11)

with

$$\begin{array}{cc}\hfill \Delta & =2{\mathbf{s}}^T{\mathbf{e}}_1{L}_2=2{(({\mathbf{n}}_1+{\mathbf{u}}_1-{\mathbf{n}}_2-{\mathbf{u}}_2))}^T{\mathbf{e}}_1{L}_2\hfill \\ \hfill \Sigma & =2{\mathbf{s}}^T{\mathbf{e}}_2{L}_2=2{(({\mathbf{n}}_1+{\mathbf{u}}_1-{\mathbf{n}}_2-{\mathbf{u}}_2))}^T{\mathbf{e}}_2{L}_2\hfill \\ \hfill \Phi & ={\mathbf{s}}^T\mathbf{s}={({\mathbf{n}}_1+{\mathbf{u}}_1-{\mathbf{n}}_2-{\mathbf{u}}_2)}^T({\mathbf{n}}_1+{\mathbf{u}}_1-{\mathbf{n}}_2-{\mathbf{u}}_2)\hfill \end{array}$$

(12)

where α is defined as the angle between the unit vector ${\mathbf{w}}_{\mathbf{1}}$ and the horizontal axis. This solution is also needed for control and the correct branch of solution is determined from the original assembly mode of the mechanism.

The Jacobian matrices of the mechanism can now be defined. For a parallel robot, the following equation applies:

$$\mathbf{K}\dot{\mathit{\theta }}=\mathbf{J}\dot{\mathbf{p}}\to \dot{\mathbf{p}}={\mathbf{J}}^{-1}\mathbf{K}\dot{\mathit{\theta }}\to \mathbf{W}={\mathbf{J}}^{-1}\mathbf{K}$$

(13)

$\mathbf{J}$ and $\mathbf{K}$ are two Jacobian matrices, which can be used to obtain the general Jacobian matrix $\mathbf{W}$. The Jacobian matrices can be obtained by taking the time derivative of Equation (8), which, after a few manipulations, leads to:

$$\mathbf{J}=\left[\begin{array}{c}\hfill {(\mathbf{p}-{\mathbf{n}}_1-{\mathbf{u}}_1)}^T\\ \hfill {(\mathbf{p}-{\mathbf{n}}_2-{\mathbf{u}}_2)}^T\end{array}\right]$$

(14)

$$\mathbf{K}=\left[\begin{array}{cc}\hfill {(\mathbf{p}-{\mathbf{n}}_1-{\mathbf{u}}_1)}^T\mathbf{E}{\mathbf{u}}_1& 0\hfill \\ \hfill 0& {(\mathbf{p}-{\mathbf{n}}_2-{\mathbf{u}}_2)}^T\mathbf{E}{\mathbf{u}}_2\hfill \end{array}\right]$$

(15)

where matrix $\mathbf{E}$ is defined as $\mathbf{E}=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]$ and matrix $\mathbf{W}$ can be computed using Equation (13).

3. Experimental Sessions

From the kinematics and control law point of view, the mechanism is quite simple. It can be programmed to follow a predefined path, e.g., a letter, even if it is designed to be utilized by a teacher as a learning device. In this sense, it is extremely easy and intuitive to use, so that the users do not need any robotics background, even though a little practice is recommended.

In order to test the bilateral teleoperation system, two experimental sessions focusing on the same task are proposed to two groups of eight people. The selected subjects are 25 to 35 years old people with no known abnormalities. In the first session, the haptic rendering of the system is evaluated: the subjects of the first group accomplish the task with the help of a teacher, who guides them by means of the bilateral system (haptic communication). Secondly, a blank test is performed: the subjects of the second group performed the same task, with no external help. As opposed to what has been proposed in the past [12,18,19], the subjects are not asked to learn new characters. On the contrary, the task is to write the word $hello$, using the haptic mechanism with the non-dominant hand, i.e., the left hand for the right-handed subjects and the right one for the left-handed subjects. The purpose is to use the mechanism as a tool for learning/improving the writing technique. For example, the device could be helpful for children with learning difficulties or for adults who need to recover the use of the arm. The use of the non-dominant hand for a well-known task, such as writing the word $hello$, simulates the latter case: the subject does already know, theoretically, how to accomplish such a task, but now he/she has to relearn to perform it practically, with the other hand.

3.1. Haptic Test

First, the haptic test is performed. It consists of six trials. The first time the subjects are asked to write the word $hello$ on their own, using the haptic device A. No suggestion concerning the style is provided. In the trials from the second to the fifth, the subjects work with the teacher, who controls the haptic device B and, thanks to the haptic feedback, is able to help and correct the movements of the students in real time. The haptic feedback goes in both directions, so that the teacher feels the subjects’ movements and vice versa. The sixth trial is again performed by the subjects, with no external intervention. It is important to remember that the teacher and the subjects are separated by a panel, which hides them from one another. The objective is to simulate a remote teaching case. On the other hand, a web camera is mounted on the subject’s work space, as it can be observed in Figure 3. The teacher is then able to see the subject’s progress, if they are working far from each other.

Figure 3. The experimental set-up for the haptic test. In the left figure, the teacher and the student together. Notice that the teacher (left) is left-handed while the student (right) is right-handed. In the right figure, the student’s workspace.

Figure 3. The experimental set-up for the haptic test. In the left figure, the teacher and the student together. Notice that the teacher (left) is left-handed while the student (right) is right-handed. In the right figure, the student’s workspace.

Although the number of guided trials was limited, the final result was quite interesting. A first qualitative comment can be made by comparing the $hellos$ written respectively at the beginning and at the end of the experimental sessions. A few examples are depicted in Figure 4. It can be observed that the writing style undergoes somehow a certain change, which can be connected to the teacher’s influence. Figure 4 compares the first trial of four subjects, on the left, with the last trial of the same people, on the right. Each subject has, of course, its own writing style and that transpires from the left part of Figure 4. On the other hand, some similarities can be noticed between all the words written in the last trial. Consider, for example, the letter L. The first remark is about the shape: in the last trial letters L generally look more rounded than in the first one, especially considering the first two students. Secondly, the intersection point of the letter. In Figure 5, its distance from the ground level is named $l_3$ or $l_6$, depending on what L we take into account. In Figure 4, it can be observed that those distances are generally shorter in the last trial with respect to those measured in the first one. Both features are typical of the teacher’s handwriting style.

Figure 4. Haptic test: Comparison between the first and the last trial for four different students.

Figure 4. Haptic test: Comparison between the first and the last trial for four different students.

Figure 5. The hello model with the considered distances.

Figure 5. The hello model with the considered distances.

These observations seem to apply to all the students, which evidences a considerable influence impressed by the teacher via the haptic device. What is remarkable is that such a change occurred after only four learning trials.

3.2. Blank Test

The blank test is proposed to the second group of eight subjects. As for the haptic test, the blank test consisted of six trials in order to accomplish the same task, i.e., to write with the second hand the word $hello$. Differently from the first experimental session, the subjects were no longer provided with the haptic feedback and they performed the test by means of a simple pen. On the other hand, they were asked to observe and reply at their best the $hello$ model, that is, the word hello written by the teacher (see Figure 5). In brief, the subjects were not guided by the teacher but they did know how to perform the test, that is, they knew the teacher’s writing style. The objective of the blank test is to create an alternative data set that will be compared to the original data set originated by the haptic test. The absence of any haptic interaction will allow to study the complexity of the task and will provide important information about the haptic rendering of the bilateral system.

Similarly to the haptic test, it is possible to make a first qualitative comment about the results of the second test. Figure 6 shows the handwritten $hellos$ of one of the participants to the blank test that can be considered representative. Two observations can be made. First, the subject’s handwriting style appears to be close to the $hello$ model as from the starting trial. Second, the subject’s handwriting style appears to be pretty much the same for all the six trials.

These observations concerning both the haptic test and the blank test are purely qualitative and based on simple visual inspection. A more detailed quantitative analysis of the results is therefore necessary.

Figure 6. Blank test: All six trials of one of the subjects participating to the blank test.

Figure 6. Blank test: All six trials of one of the subjects participating to the blank test.

4. Analysis of the Results

The objective of the following analysis is to study the haptic rendering of the bilateral system. Some qualitative observations have been made on the results of the two experimental sessions and need to be investigated. First, the proposed methodology will be presented. The results of the two experimental sessions will then be examined and compared in order to understand the impact of the haptic learning on the participants.

4.1. Methodology

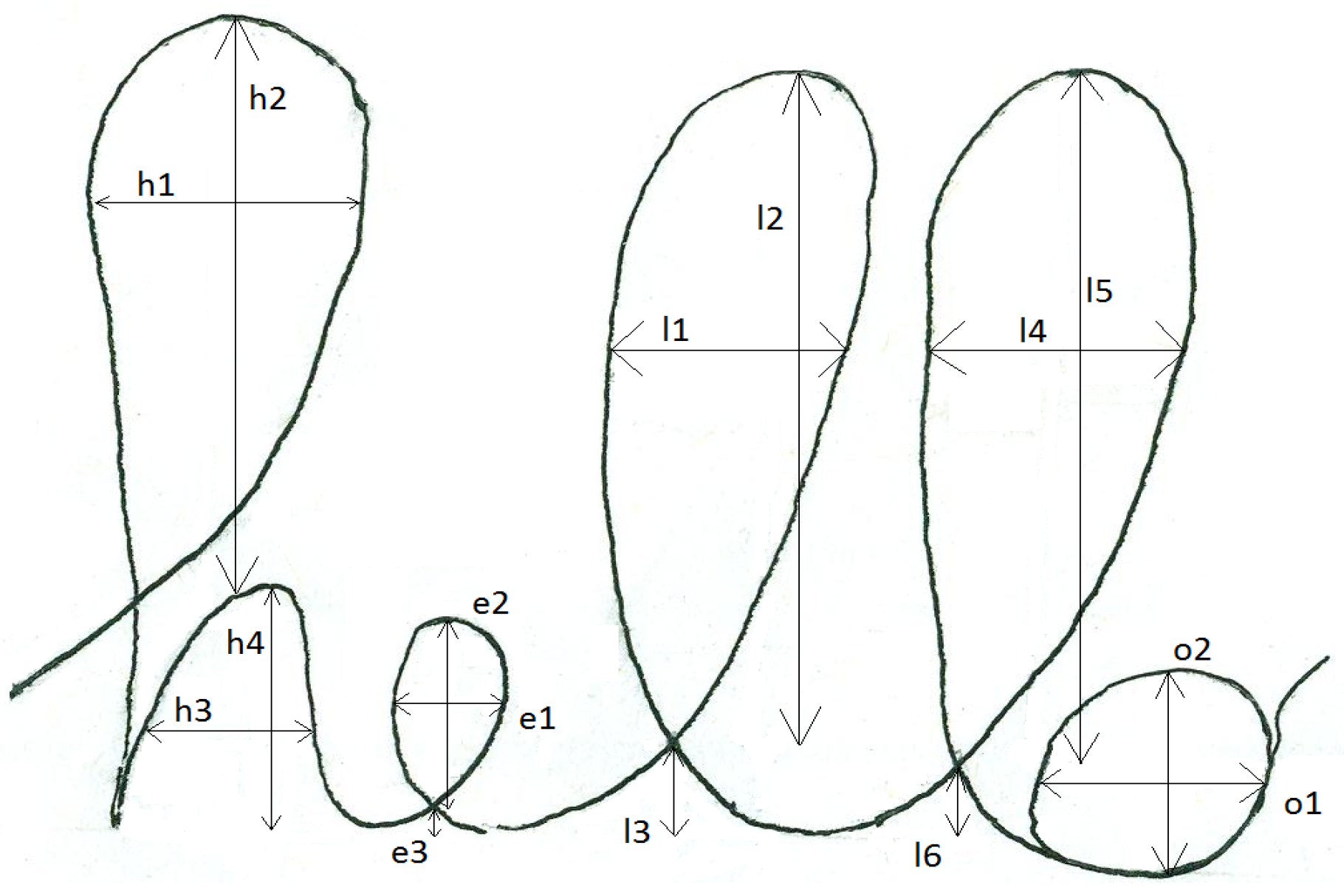
In order to study the subjects’ performances in a quantitative way, we need to define some measurable parameters. The goal is to examine mathematically the writing style of a person, trying not to complicate too much the analysis. It was decided then to consider 15 measures of distance, which have to be taken on the handwritten word hello: four measurements for the letter H, three for the E and for the two L and two for the O, as shown in Figure 5. The fifteen values have been chosen in a well-defined way. The distances $e_3$, $l_3$ and $l_6$ refer to the height of the intersection points with respect to the beginning and the end of the letter respectively for the E and the two L. The other twelve, instead, can be seen as the six couples of major and minor semi-axes of the six ellipses that compose the word hello: two for the letter H, one for each of the other four letters. Even if it is an approximation, they represent a reasonable index of the shape, hence the style, of the handwritten letters. All distances are shown in Figure 5. In this figure, the distances are measured on the model which has been taken to study the students’progress from the first to the last trial. The ideal hello does not represent the perfect handwritten word. In the first session, it is the word written by the teacher, using the mechanism, in the way he wrote during the experiments. Note that the teacher did not change in the course of the experimental session. In other words, it represents the writing style to which, according to our qualitative observation, all the participants get used to write in the course of the test. This is a crucial point: what we want to study is not how well the students perform the test, but how close to the teacher they get while doing it. In the second session, the $hello$ shown in Figure 5 represents the handwriting style that the participants were asked to reply. Similarly to the first experimental session, this model constitutes an approximation. In fact, it is assumed that the teacher wrote in the exact same way during the whole experimental session, which is humanly impossible. On the other hand, it is plausible to assume that the teacher used the same handwriting style. For this reason, we expect to get some relevant indications about the learning process of the students from this analysis.

Once the model to refer to is well defined, the analysis can be performed. At first, we measured the 15 distances in the model, thereby obtaining the reference values. Secondly, the measurements were taken on all the participants’ handwritten words of both the first and the second group. Afterwards, for each analyzed trial, we calculated the fifteen distance gaps noted ${\eta }_i$, as follows:

$${\eta }_x=|x_{model}-D{x}_{student}|$$

(16)

where x represents the considered distance and D a weighting coefficient. The equation is applied for each of the 15 distances, so $x\in h_1,h_2,h_3,h_4,e_1,e_2,e_3,l_1,l_2,l_3,l_4,l_5,l_6,o_1,o_2$. The gap is the absolute value of the difference between the reference distance and the weighted distance value of the student. The total gap, η, is then computed as the sum of all gaps, namely

$$\eta =\sum _{x=h_1}^{o_2}{\eta }_x$$

(17)

The coefficient D is the square root of the ratio between the model’s estimated occupied area, $A_{model}$, and the student’s estimated occupied area, $A_{student}$:

$$D=\sqrt{\frac{A_{Model}}{A_{Student}}}$$

(18)

By occupied area it is meant the portion of space that the student needs to write the prescribed word. Both tests were performed on customized sheets. These sheets were divided into six frames, which were drawn to give to the students some writing limits, but still the word dimension changes from subject to subject. It is worth noting that, in the course of the first test, the teacher did not impose the word size. What the teacher did was to follow the subject’s movement, trying to correct and arrange it according to his/her writing style. If the subject were used to write small letters, the teacher didn’t impose any resizing. On the other hand, the teacher did transmit to the novice other peculiarities. In the considered case, i.e., according to the style of the teacher chosen for the experiment, the letter L did tend to be more rounded and its intersection point lower. Hence, what really matters is the proportion inside each of the letters of the word hello. This is the purpose of the scaling factor: in order to correctly compare these proportions, the words need to be properly scaled.

4.2. Haptic Test

Table 1 shows the distance gaps, calculated by means of Equation (17), between all the participants’ handwritten words and the $hello$ model. These gaps are calculated trial by trial and expressed in millimeters. In general, it can be observed how the distance gaps significantly decrease during the learning session for all participants. The mean distance gap decreased more than 40% at the end of the session. When analysing in more detail, one can notice that the evolution of the distance gaps changes according to the subject and does not decrease in a constant way. Consider for instance the second trial, which is the first one with the haptic learning. As it could be expected, its mean distance gap is 23% less than the mean distance gap of the first trial. This is the largest difference in the sequence and is an evidence of the relevance of the haptic rendering of the bilateral system. Yet, two out of eight subjects’ distance gap increased after the first guided trial. That may depend on a longer period of adaptation of the subjects to the haptic system or to the teacher’s handwriting fashion. Another insteresting consideration can be made about the last two rows of Table 1, which contain the mean distance gaps and the associated standard deviations for all subjects, trial by trial. As it can be noticed, the mean value happens to increase in the fourth trial. This outcome depends very likely on the teacher, who decided to try reducing the haptic guidance on the subjects. On the other hand, that is not the case for all the subjects. For instance, subject 3’s haptic guidance was reduced in the third trial. Hence, the performance of each subject during the learning session, i.e., from the second to the fifth trial, mainly depends on the haptic guidance provided by the teacher, who is free to modulate his/her external assistance according to the student’s needs.

Table 1. The table shows the distance gaps between all participants to the haptic test and the $hello$ model, trial by trial (mm). In bold, the data that are used for the statistical analysis.

Subject	Trial 1	Trial 2	Trial 3	Trial 4	Trial 5	Trial 6
S. 1	8.510	5.283	3.141	6.202	4.612	4.601
S. 2	12.911	6.463	6.651	8.812	6.987	7.373
S. 3	9.812	5.407	7.095	5.070	6.166	5.810
S. 4	5.582	4.084	4.606	3.601	5.105	3.745
S. 5	13.244	17.741	9.473	14.507	9.180	7.682
S. 6	11.397	8.152	7.434	9.837	7.826	5.978
S. 7	14.620	9.156	7.359	8.242	6.849	6.909
S. 8	7.069	7.381	6.144	6.659	7.023	6.562
Mean	10.393	7.958	6.488	7.866	6.719	6.083
SD	2.988	4.007	1.797	3.146	1.361	1.269

Table 1. The table shows the distance gaps between all participants to the haptic test and the $hello$ model, trial by trial (mm). In bold, the data that are used for the statistical analysis.

Subject	Trial 1	Trial 2	Trial 3	Trial 4	Trial 5	Trial 6
S. 1	8.510	5.283	3.141	6.202	4.612	4.601
S. 2	12.911	6.463	6.651	8.812	6.987	7.373
S. 3	9.812	5.407	7.095	5.070	6.166	5.810
S. 4	5.582	4.084	4.606	3.601	5.105	3.745
S. 5	13.244	17.741	9.473	14.507	9.180	7.682
S. 6	11.397	8.152	7.434	9.837	7.826	5.978
S. 7	14.620	9.156	7.359	8.242	6.849	6.909
S. 8	7.069	7.381	6.144	6.659	7.023	6.562
Mean	10.393	7.958	6.488	7.866	6.719	6.083
SD	2.988	4.007	1.797	3.146	1.361	1.269

As it was stated in the introduction of this paper, the figure of the teacher is central in a direct interaction approach. It is the teacher who guides the students (here the subjects of the experimental session) and decides whether to apply a more effective haptic feedback or to let them try on their own. This choice is arbitrary and the teacher’s guidance may be different from student to student and depending on several aspects.

4.3. Blank Test

Table 2 shows the distance gaps, calculated by means of Equation (17), between all the participants’ handwritten words and the $hello$ model. These gaps are calculated trial by trial and expressed in millimeters.

Table 2. The table shows the distance gaps between all participants to the blank test and the $hello$ model, trial by trial (mm). In bold, the data that are used for the statistical analysis.

Subject	Trial 1	Trial 2	Trial 3	Trial 4	Trial 5	Trial 6
S. 1	4.038	4.449	4.402	5.076	5.104	5.918
S. 2	5.565	6.100	4.800	7.099	5.900	6.378
S. 3	8.689	7.605	7.596	7.201	8.268	7.469
S. 4	7.765	6.188	8.127	8.213	7.411	7.709
S. 5	7.588	7.720	7.529	7.057	7.400	7.314
S. 6	7.681	6.079	5.934	6.988	7.745	5.235
S. 7	5.068	4.828	5.446	5.502	5.672	6.221
S. 8	4.936	6.102	8.788	7.064	8.002	6.545
Mean	6.416	6.134	6.578	6.775	6.9378	6.599
SD	1.595	1.074	1.534	0.940	1.120	0.792

Table 2. The table shows the distance gaps between all participants to the blank test and the $hello$ model, trial by trial (mm). In bold, the data that are used for the statistical analysis.

Subject	Trial 1	Trial 2	Trial 3	Trial 4	Trial 5	Trial 6
S. 1	4.038	4.449	4.402	5.076	5.104	5.918
S. 2	5.565	6.100	4.800	7.099	5.900	6.378
S. 3	8.689	7.605	7.596	7.201	8.268	7.469
S. 4	7.765	6.188	8.127	8.213	7.411	7.709
S. 5	7.588	7.720	7.529	7.057	7.400	7.314
S. 6	7.681	6.079	5.934	6.988	7.745	5.235
S. 7	5.068	4.828	5.446	5.502	5.672	6.221
S. 8	4.936	6.102	8.788	7.064	8.002	6.545
Mean	6.416	6.134	6.578	6.775	6.9378	6.599
SD	1.595	1.074	1.534	0.940	1.120	0.792

Two main considerations can be immediately made. First, the distance gaps are much smaller for all participants starting from the very first trial. The most likely explanation is that the proposed task is quite easy for normal people. Second, there is no general improvement in the students’ performances and the mean distance gap is basically constant. In this sense, the most representative case is subject 5’s performance. For subject 7 and subject 1, the final trial is also the worst one. These subjects have probably lost their attention at the end of the experimental session. In general, the blank test participants appear to be capable of reproducing the $hello$ model in an appreciable fashion, but they seem unable to improve their performances in the course of the experiment.

It is now interesting to compare the results of the two experimental sessions in order to better understand the contribution of the proposed bilateral system to the problem of the learning and the assessment of handwriting capabilities. For this reason, a statistical analysis is performed and presented in the next section.

4.4. Statistical Analysis

In order to compare methodologically the results of the two experimental sessions, a statistical analysis is proposed. The objective is to verify whether there is a significant difference in the handwriting style between the two groups of subjects and within these two groups, considering the performances at the beginning and at the end of the tests. Despite the limited number of subjects, some interesting results may be inferred.

The analysis within the two different groups is initially proposed. A suitable statistical test is the within subject one-way ANOVA, also known as repeated measures ANOVA, which allows to study related data sets. In our analysis and considering one experimental session at a time, the data set associated to each trial is related to all other data sets, because the same subjects are tested several times on the same “dependent variable”, here the distance gap.

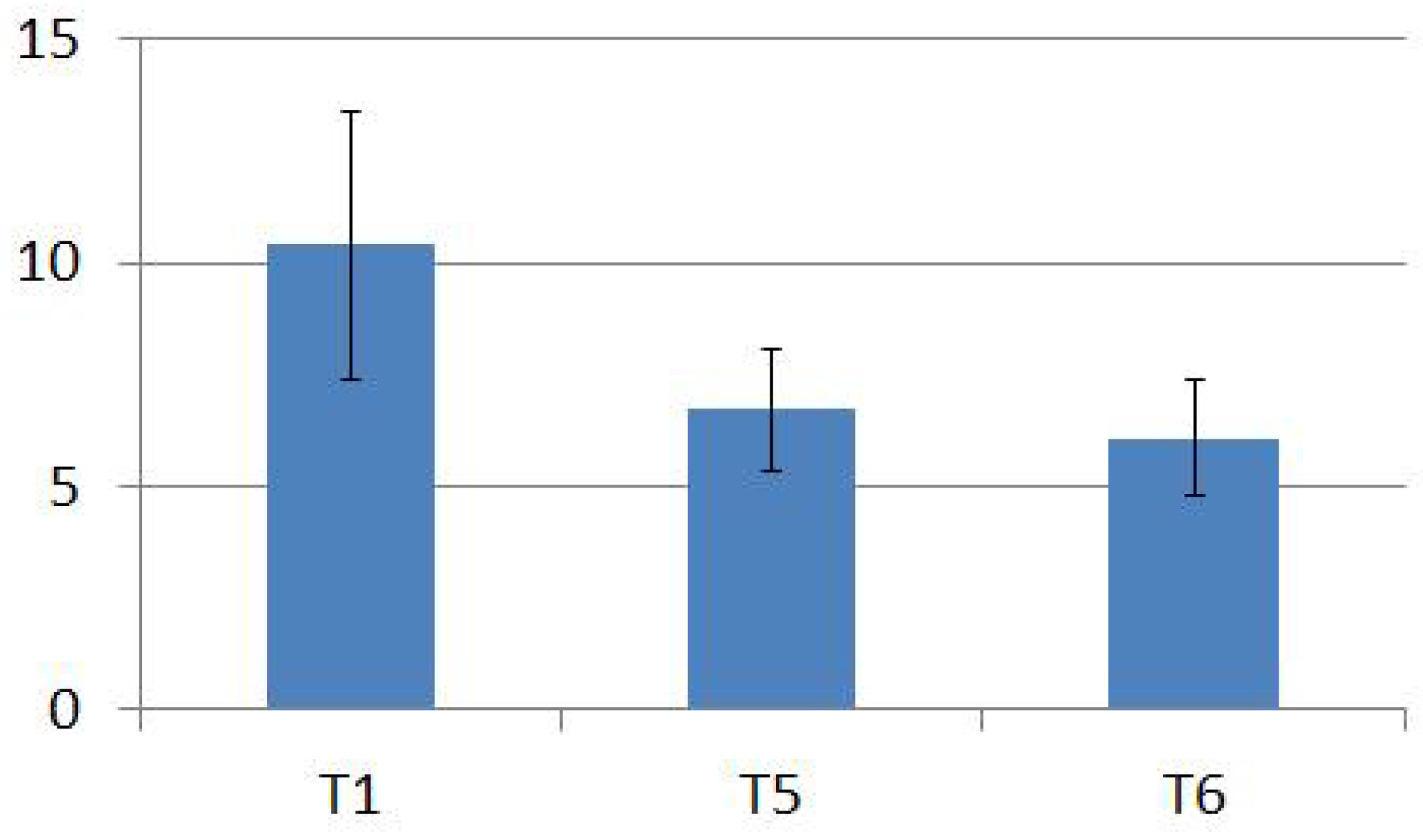
Consider first the haptic experimental session. It is interesting to compare the results of the first trial with those of the last trial of the learning session, that is the fifth trial of the test, and with those of the last trial of the test. Figure 7 represents the mean distance gaps and the standard deviations for the data sets related to these trials. The repeated measures ANOVA performed on these data sets, i.e., the first, the fifth and the sixth columns of Table 1, rejects the null hypothesis, which states that all means are equal. More precisely, one can obtain $\mathbf{F}(\mathbf{2},\mathbf{14})=\mathbf{20}.\mathbf{93261}$, which leads to a p-value $\mathbf{p}=\mathbf{0}.\mathbf{00006207}$. It is easily demonstrable that there is no statistically significant difference between means of the data sets related to the fifth ($6.719\pm 1.361$ mm) and the sixth trials ($6.083\pm 1.269$ mm). Hence, the mean distance gap of the first trial data set ($10.393\pm 2.988$ mm) does differ from the others. In other words, there is a statistically significant effect of the haptic learning on the handwriting style of the subjects of the first group.

Figure 7. Mean distance gaps and standard deviations of all the subjects for the first, the fifth and the sixth trial of the haptic experimental session. The values are expressed in millimeters.

Figure 7. Mean distance gaps and standard deviations of all the subjects for the first, the fifth and the sixth trial of the haptic experimental session. The values are expressed in millimeters.

Note that the variances of the three data sets are quite different, and so are the covariances that can be easily computed. Hence, the assumption of sphericity of the data may not be respected. Violation of sphericity makes a repeated-measures ANOVA test more likely to produce a false positive (a Type 1 error). A Mauchly’s sphericity test might be performed, but it is less efficient on small samples. Besides, an eventual correction to the degrees of freedom of the test, which would increase the p-value, will very unlikely change the final outcome of the test, since the p-value is extremely small.

Consider now the blank test. Since there is no haptic learning, the results measured at each trials of this experimental session are equally relevant. Figure 8 represents the mean distance gaps and the standard deviations for every data set of the blank test. The repeated measures ANOVA performed on the data sets associated to all trials of the blank test, i.e., all columns of Table 2, accepts the null hypothesis, which states that all means are equal. More precisely, one can obtain $\mathbf{F}(\mathbf{5},\mathbf{35})=\mathbf{0}.\mathbf{975747432}$, which leads to a p-value $\mathbf{p}=\mathbf{0}.\mathbf{44614987}$. Hence, the simple repetition of the task with no haptic guidance does not engender any statistically significant effect on the handwriting style of the subjects of the second group.

Figure 8. Mean distance gaps and standard deviations of all the subjects for every trial of the blank test. The values are expressed in millimeters.

Figure 8. Mean distance gaps and standard deviations of all the subjects for every trial of the blank test. The values are expressed in millimeters.

Eventually, one can compare the results of the subjects of the two groups. For instance, it is interesting to study whether there is a statistically significant difference between the two groups at the beginning and at the end of the two experimental sessions. An independent two sample t-test is then performed twice as well as a 95% confidence intervals for the mean difference. First, it is found that the means of the data sets related to the first trial of both experimental sessions (haptic test: $10.393125\pm 2.987934422$ mm; blank test: $6.41625\pm 1.594785546$ mm) are statistically different ($\mathbf{t}=\mathbf{3}.\mathbf{106623}$, $\mathbf{p}=\mathbf{0}.\mathbf{00773}$). Secondly, it is found that the mean of the data set associated to the last trial of the haptic test ($6.0825\pm 1.268894105$ mm) is not significantly different from the mean of the data set associated to the last trial of the blank test ($6.598625\pm 0.792079689$ mm) ($\mathbf{t}=\mathbf{0}.\mathbf{912902}$, $\mathbf{p}=\mathbf{0}.\mathbf{376747}$). In other words, the subjects of the two groups write in different fashions at the beginning of their respective experimental sessions but, eventually, no significant difference is observable in their handwriting styles.

Note that, in both cases, an “equal sample size – equal variance” t-test is performed. Equality of the variances can be assessed by Levene’s test, which tests the null hypothesis that the population variances are equal. The Levene’s test performed on the first trial data sets provides a p-value $\mathbf{p}=\mathbf{0}.\mathbf{0637}$. The Levene’s test performed on the last trial data sets provides a p-value $\mathbf{p}=\mathbf{0}.\mathbf{256559}$. If the significant level is set equal to ${\mathbf{p}}_{\mathbf{0}}=\mathbf{0}.\mathbf{05}$, which is the norm, it results that in both cases the null hypothesis is accepted ($\mathbf{p}>{\mathbf{p}}_{\mathbf{0}}$). Thus, there is no difference between the variances of the data sets and an equal variance t-test can be run.

4.5. Relevance of the Haptic Guidance

The statistical analysis presented in the previous section confirmed the first impressions based on a simple observation of the results. The subjects of the first group started writing using their own handwriting styles, which were more or less different from the teacher’s style, depending on the subject. They were told what to write, not how to do that. Hence, large distance gaps were measured at the very first trial of the session (1st column of Table 1). During the haptic learning session, the teacher guided and corrected the subjects and so taught them to write in his personal fashion. At the end of the session, the subjects’ handwriting style was significantly closer to the teacher’s style, as proven by the statistical test (repeated measures ANOVA). In order to comprehend whether this result was due to the haptic learning, rather than the simple familiarization to the task, the same analysis was performed on the subjects of the second group, who participated to the blank test. These subjects were explicitly told how to write. As a consequence, the first trial distance gaps were much smaller. On the other hand, subjects’ handwriting style did not significantly change in the course of the session, as proven by the statistical test (repeated measures ANOVA). The subjects of the second group were able to perform the task well but, in absence of any haptic feedback, they could not improve their performances in the course of the session.

In conclusion, it was the haptic learning that allowed the subjects of the first group to get closer to the teacher’s handwriting style. The haptic guidance provided by the teacher did affect their handwriting style which became, at the end of the haptic learning, as close to the teacher’s style as the handwriting style of the subjects of the second group, as proven by the last statistical test (independent two-samples t-test). Unconsciously, the subjects of the first group changed their handwriting style after only four guided trials.

These results show how effective the haptic guidance can be in the context of collaboration between two people. Supported by statistical analysis, it can be finally stated that the bilateral teleoperation system composed of two haptic devices allows the transmission of skills in a rapid and effective way. Therefore, it can be very helpful for the learning process of a person. On the other hand, the final outcome of the learning process depends directly on the teacher, on his/her capability and knowledge. The teacher is to be skilled, because he/she has to literally guide the student. That is what was meant by saying that the figure of the teacher was going to get back to a central role in the learning process.

The haptic device is conceived to be small, simple, portable and easily usable. Yet it is capable of producing an important haptic force, not too high but absolutely sufficient for the demanded task. A practical application, for the haptic device, is distance learning. The teacher and the student do not need to be at the same place, not even in the same city. The student could even work at home, with the possibility of practicing on his/her own and being periodically evaluated by the teacher who follows him/her from a distance.

5. Conclusions

In this paper, a bilateral teleoperation system composed of two haptic devices has been presented. This type of five-bar two-degree-of-freedom device, as well as the impedance control law, has already been discussed in the previous literature [16,17]. The novelty here is represented by the approach to the training of handwriting capabilities: a direct teacher-student interaction is proposed. This research explored the potentialities of this on-line interaction between the student and his/her teacher and aimed at evaluating the relevance of the haptic guidance in the context of this collaboration. Two experimental sessions were proposed to two distinct groups of subjects. In the first session, the bilateral system was employed to transmit the haptic feedback from the teacher to the subjects and vice versa. The teacher could perceive the subjects’ movements and correct them properly. The second experimental session consisted of a blank test: no haptic feedback was provided to the subjects. The analysis of the results clearly indicated that the haptic feedback allowed the subjects of the first group to get closer to the teacher’s handwriting style. In absence of any haptic guidance, no significant change is observable. In conclusion, the haptic guidance is proven to be decisive in the learning process. The proposed approach consisting of a direct teacher-student interaction allowed a rapid and effective skill transmission with the use of a relatively simple haptic device.