Effect of Boundary Conditions on Vibration Characteristics of a Sandwich Plate with Viscoelastic Periodic Cores
Abstract
1. Introduction
2. Theory and Formulations
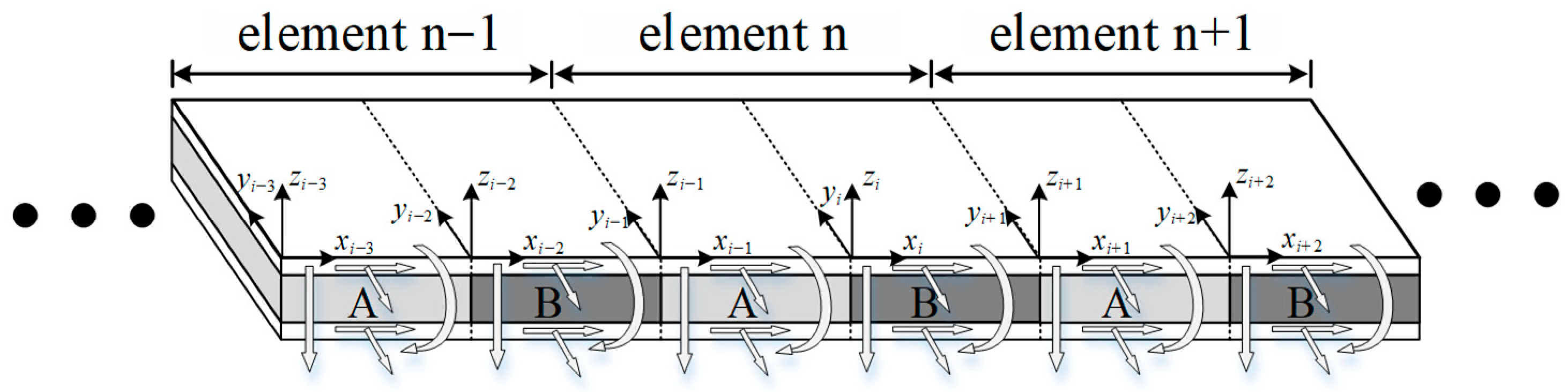
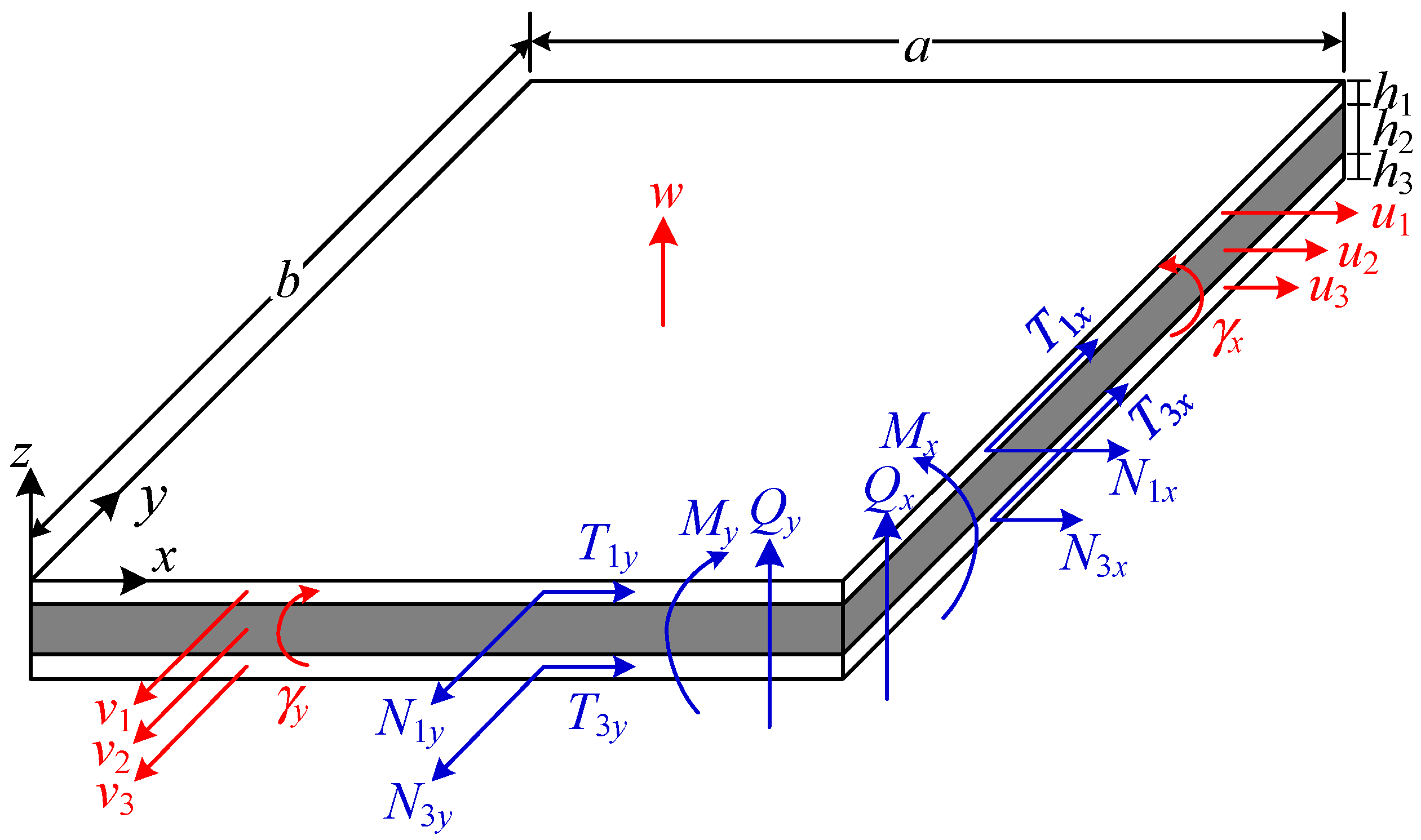
2.1. Structure Configuration and Basic Dynamic Theory
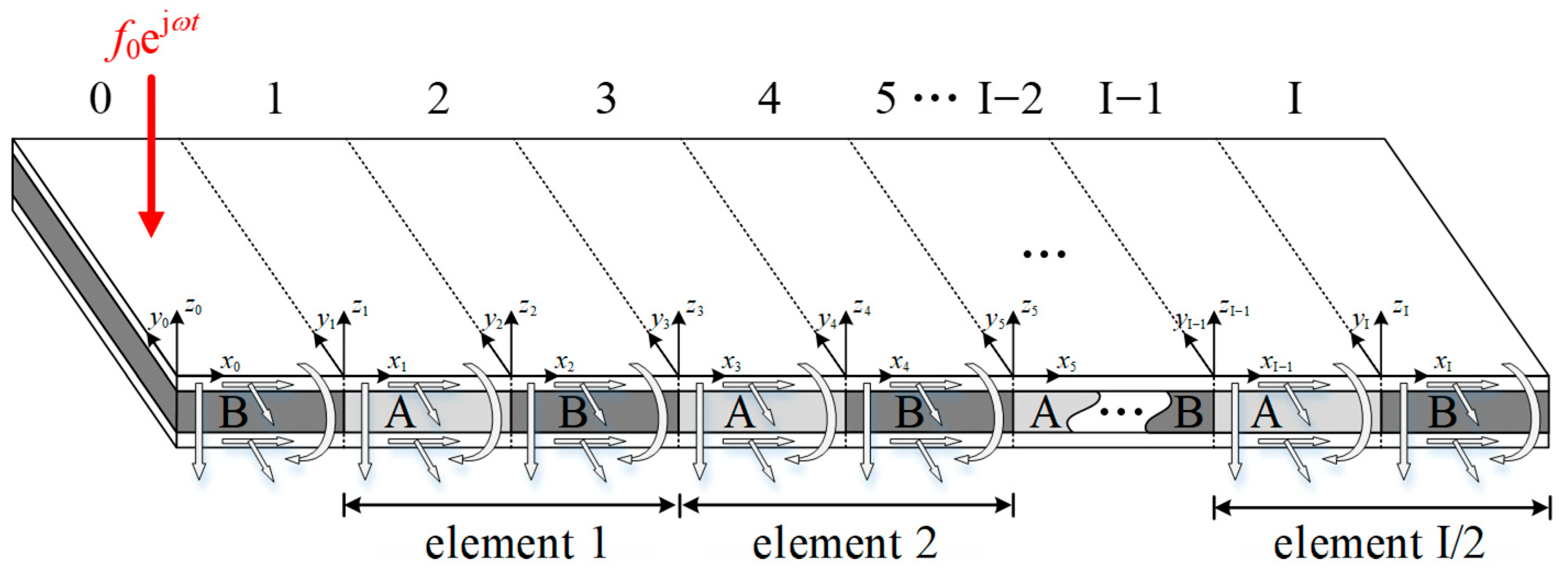
2.2. Forced Response
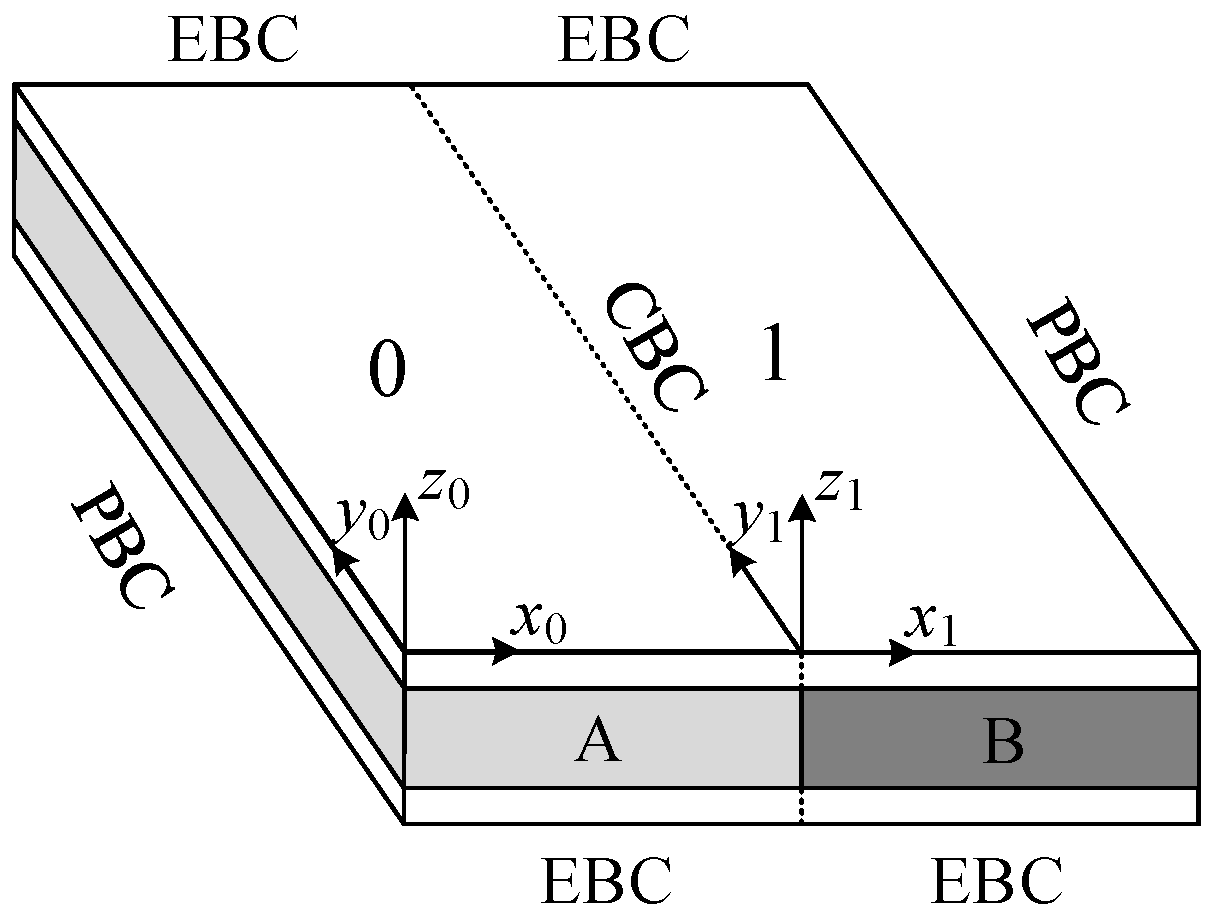
2.2.1. EBC of the Finite Periodic Sandwich Plate
2.2.2. FBC of the Finite Periodic Sandwich Plate
2.2.3. CBC of the Finite Periodic Sandwich Plate
2.3. Band Structure
2.3.1. EBC of the Single Element
2.3.2. PBC of the Single Element
2.3.3. CBC of the Single Element
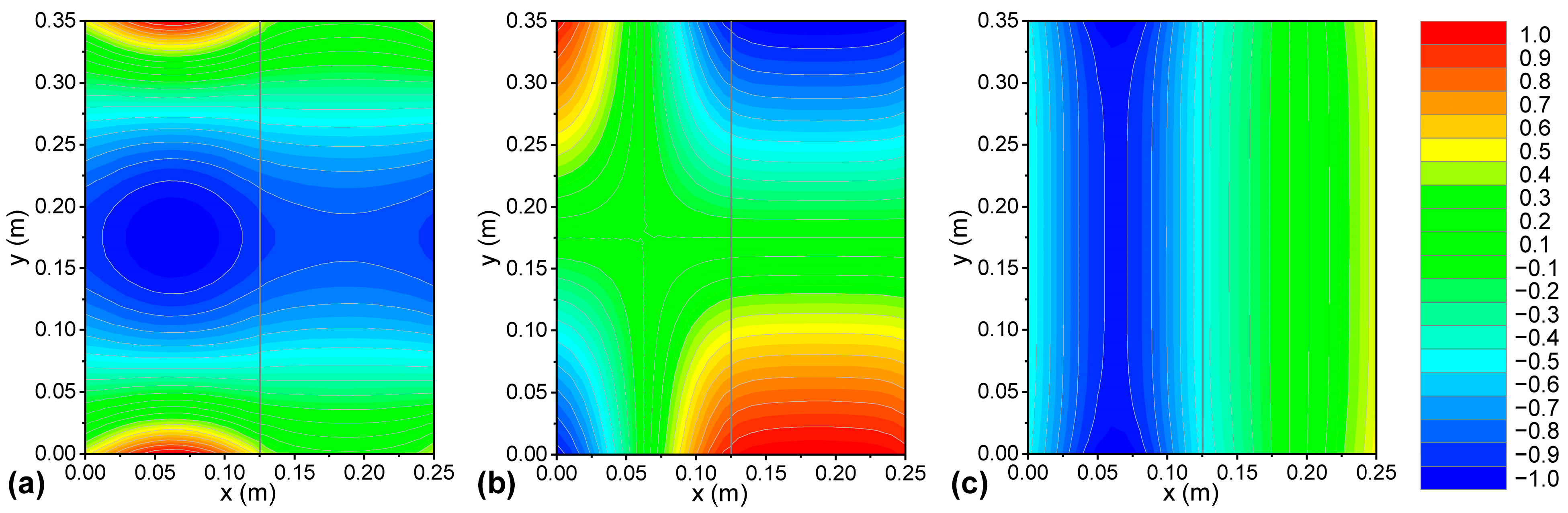
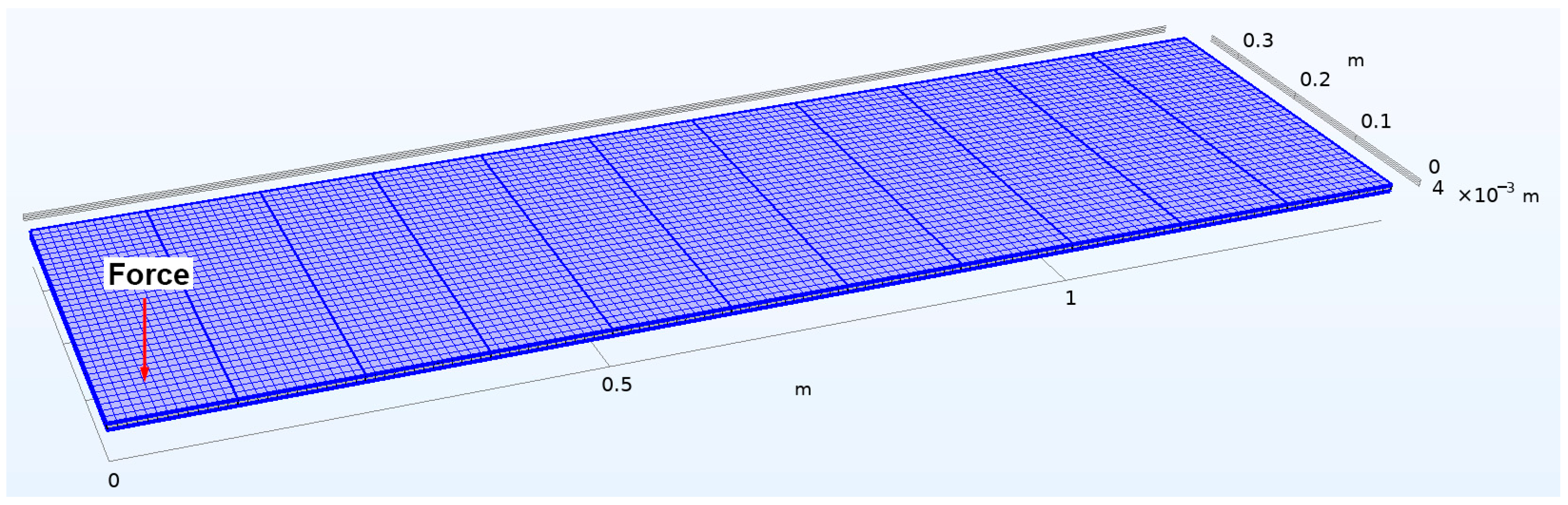
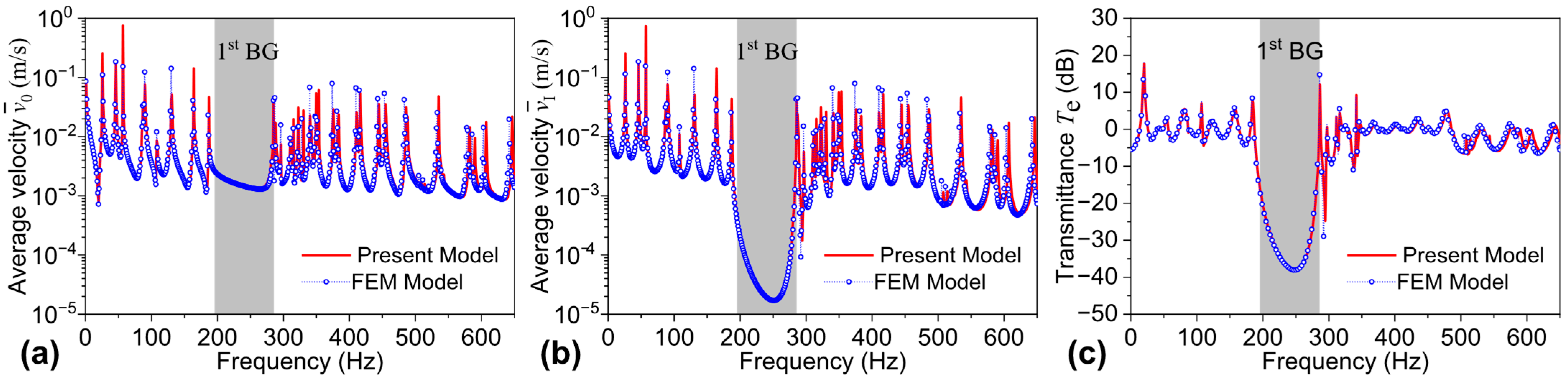
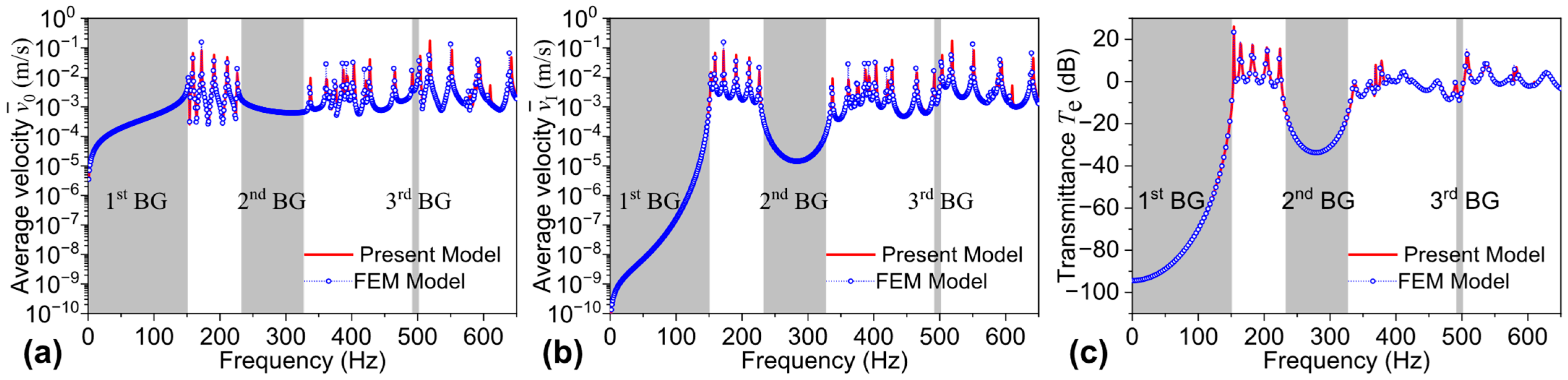
3. Results and Discussion
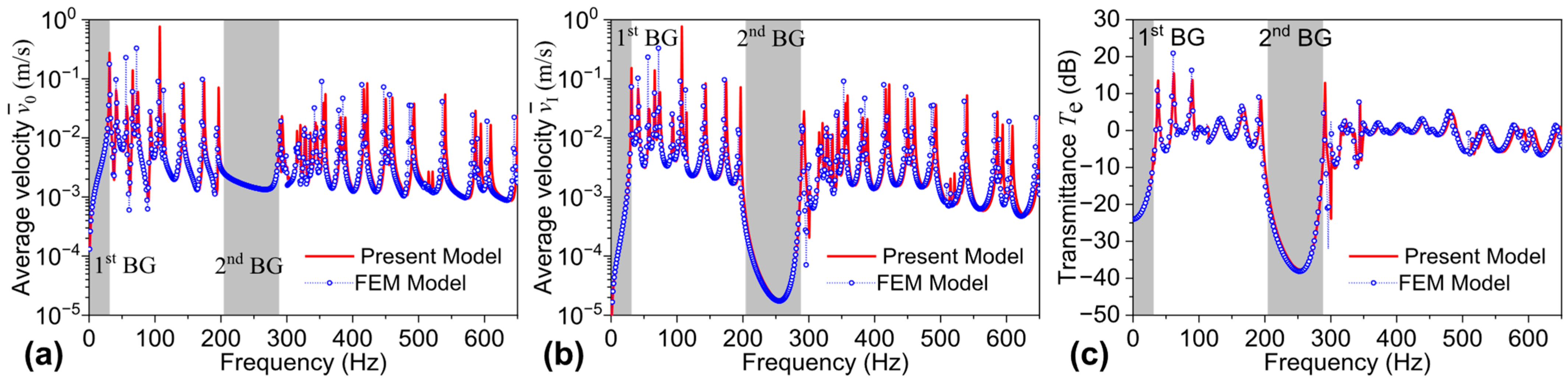
3.1. Illustrative Example and Validation
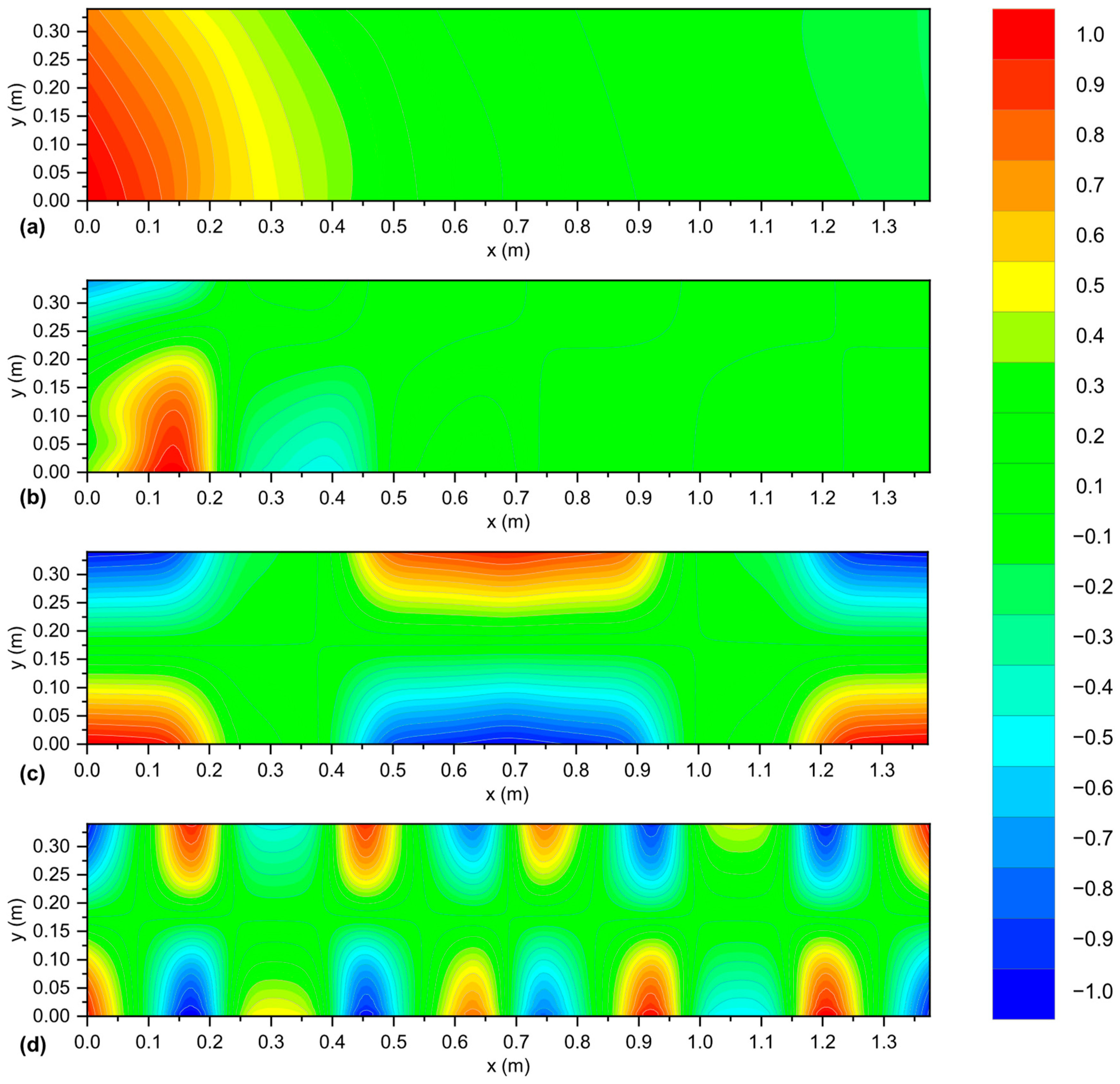
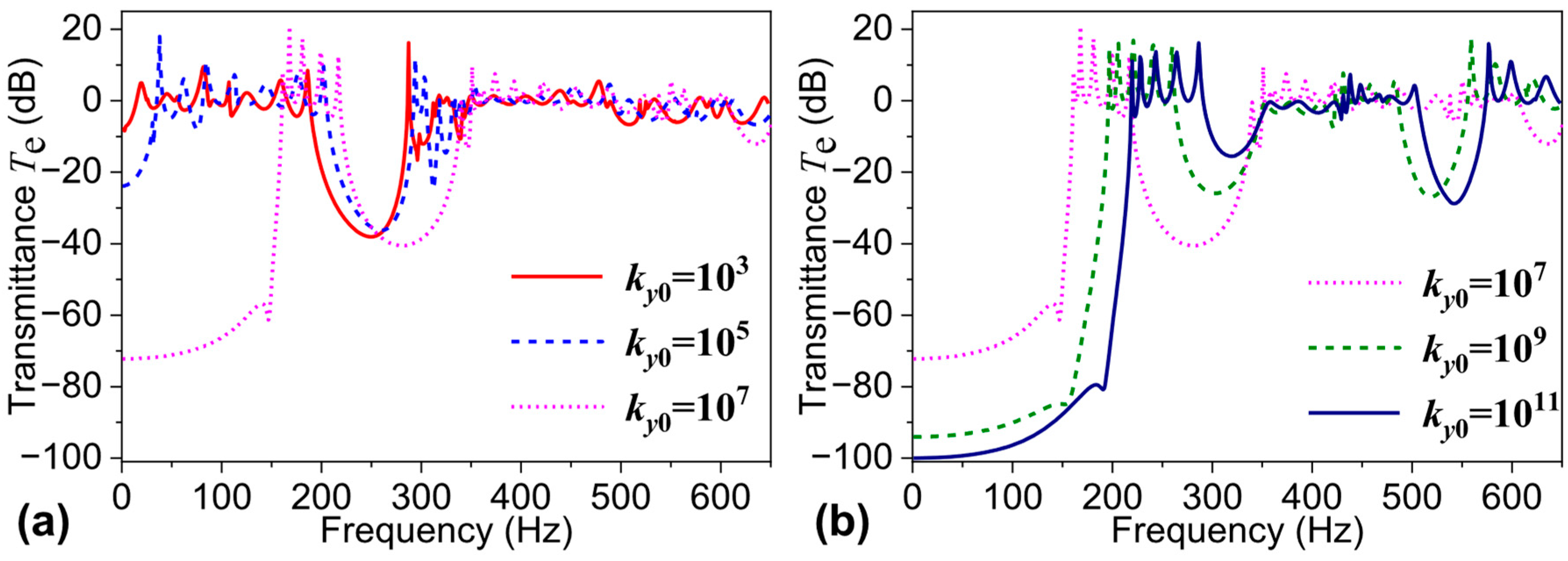
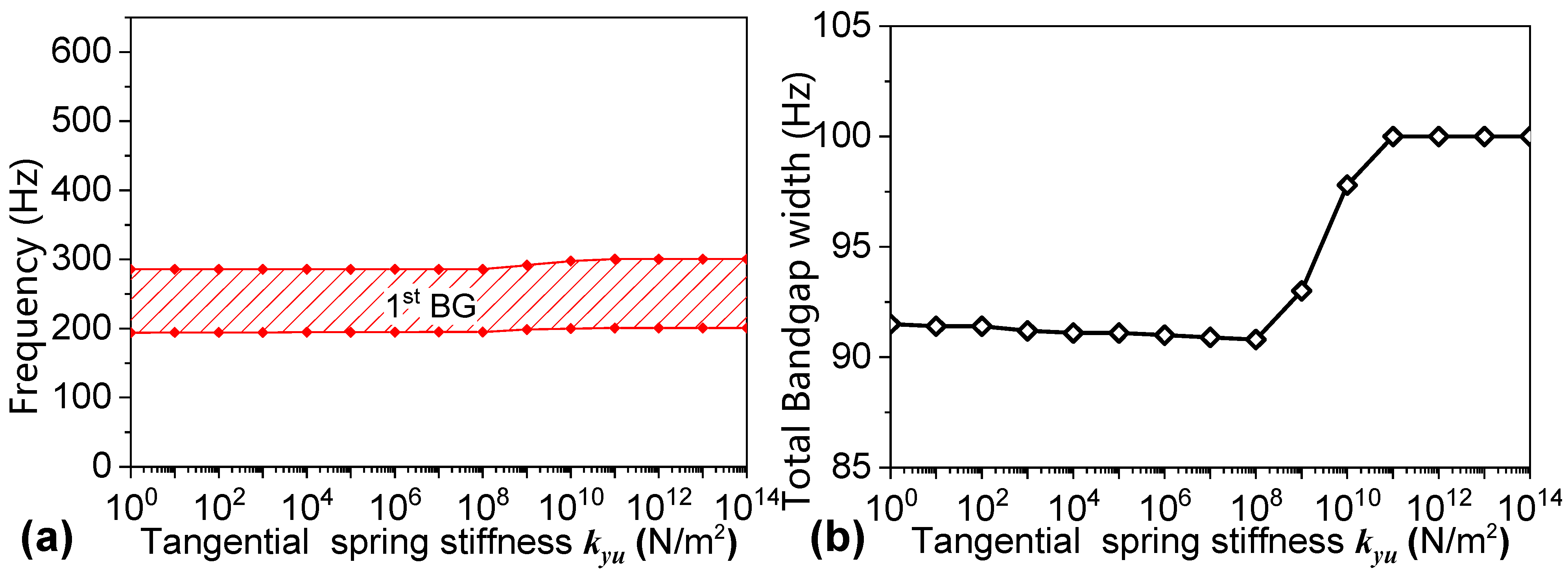
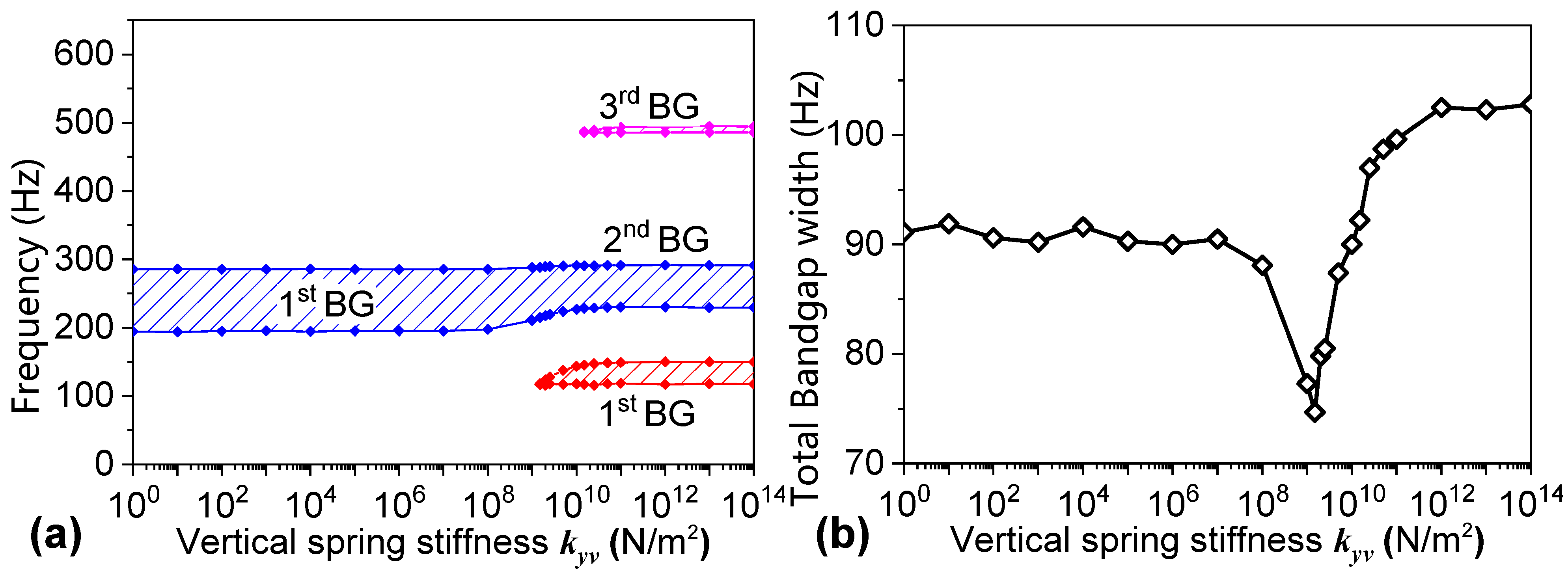
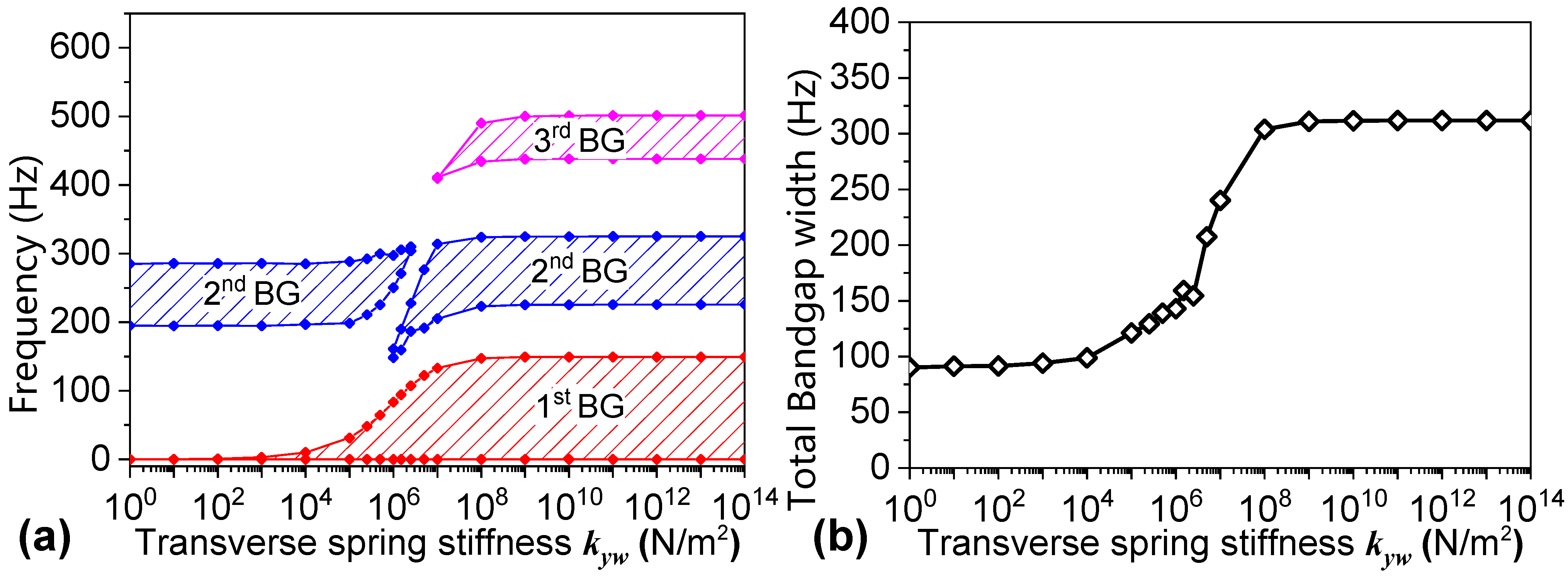
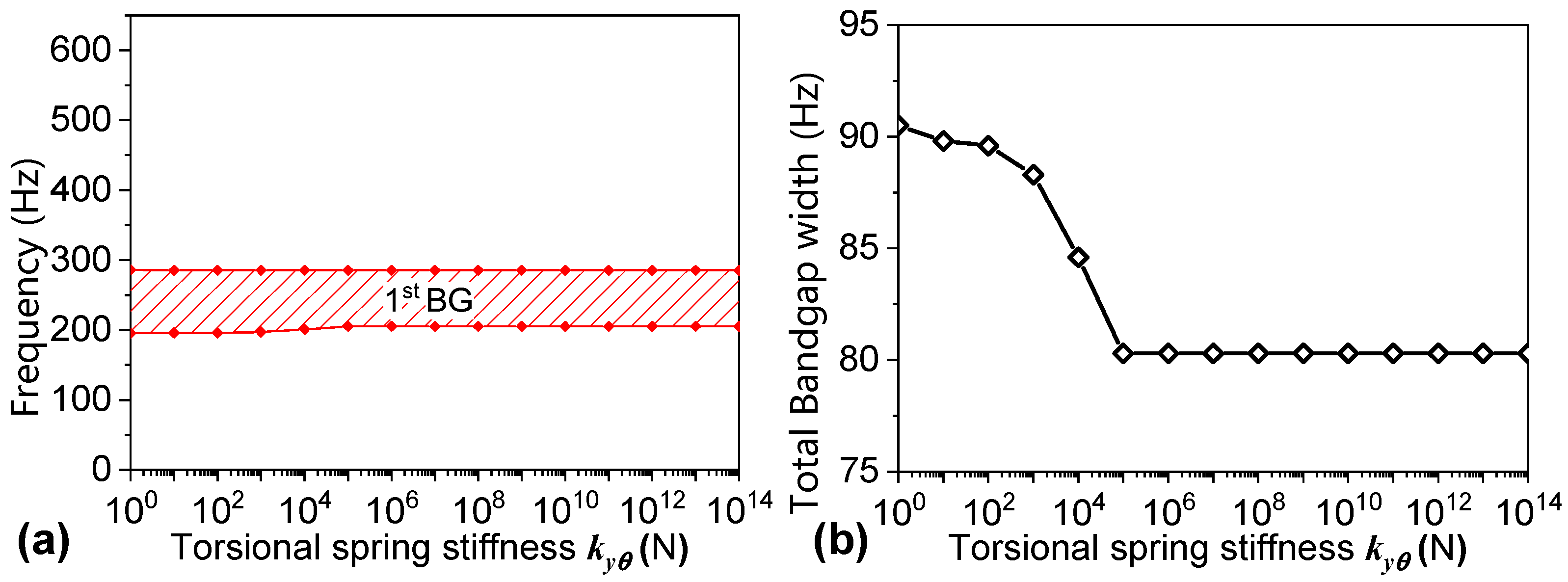
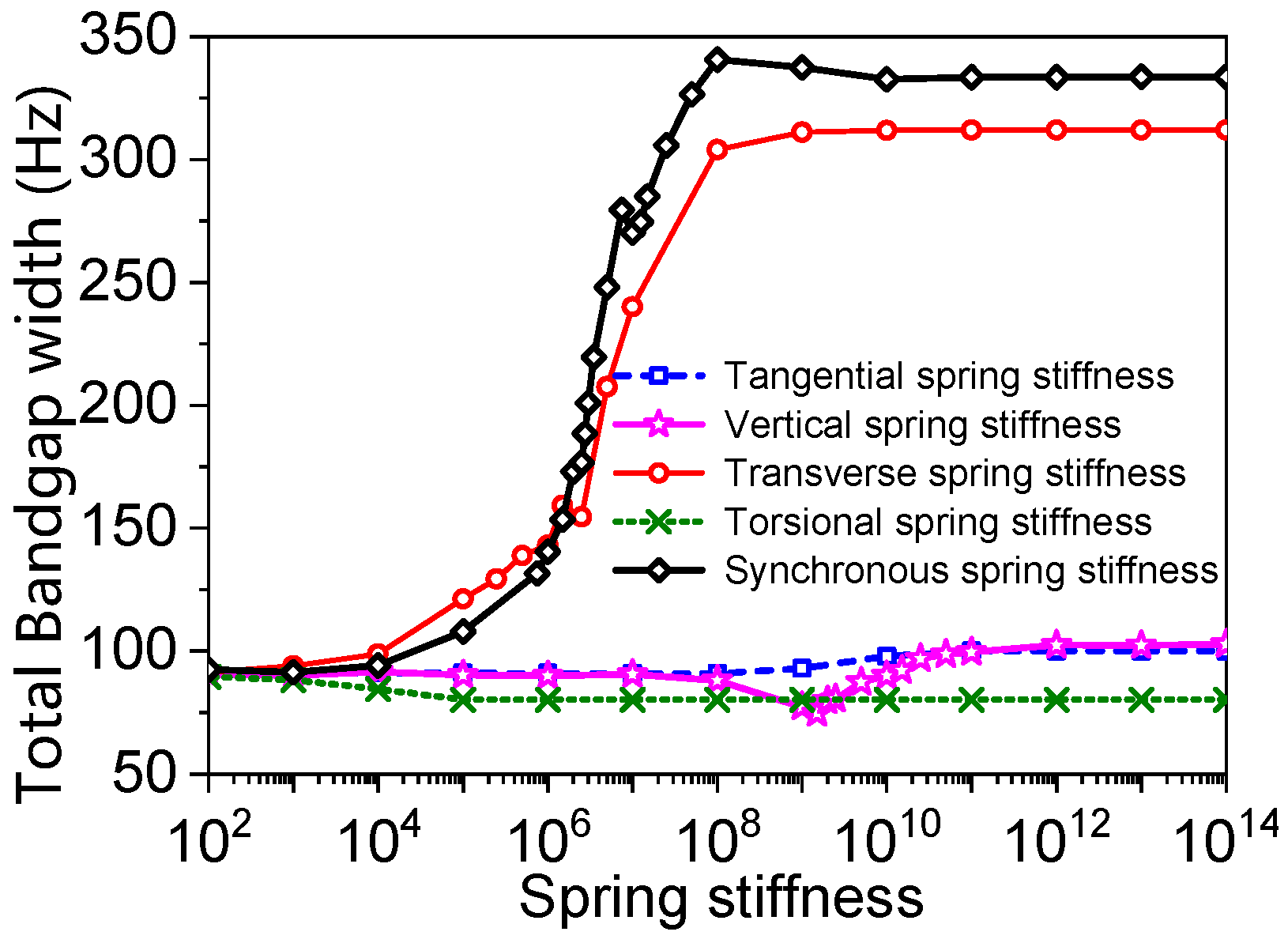
3.2. Parametric Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Mead, D.J. Wave propagation in continuous periodic structures: Research contributions from Southampton, 1964–1995. J. Sound. Vib. 1996, 190, 495–524. [Google Scholar] [CrossRef]
- Gupta, G.S. Vibration of Periodic Structures; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Vasileiadis, T.; Varghese, J.; Babacic, V.; Gomis-Bresco, J.; Urrios, D.N.; Graczykowski, B. Progress and perspectives on phononic crystals. J. Appl. Phys. 2021, 129, 160901. [Google Scholar] [CrossRef]
- Huang, W.; Xu, J.; Yao, Y.; Zhang, Y.; Wang, X.; Han, P. Application of phononic crystals in modern engineering vibration and noise control, a review. Noise Vib. Worldw. 2025, 56, 224–241. [Google Scholar] [CrossRef]
- Aydin, G.; San, S.E. Breaking the limits of acoustic science: A review of acoustic metamaterials. Mat. Sci. Eng. B-Adv. 2024, 305, 117384. [Google Scholar] [CrossRef]
- Brillouin, L. Wave Propagation in Periodic Structures; Dover Publications Inc: New York, NY, USA, 1953. [Google Scholar]
- Narayanamurti, V.; Störmer, H.L.; Chin, M.A.; Gossard, A.C.; Wiegmann, W. Selective transmission of high-frequency phonons by a superlattice: The “dielectric” phonon filter. Phys. Rev. Lett. 1979, 43, 2012. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022. [Google Scholar] [CrossRef]
- Gao, F.C.; Wu, Z.J.; Li, F.M.; Zhang, C.Z. Numerical and experimental analysis of the vibration and band-gap properties of elastic beams with periodically variable cross sections. Wave Random Complex. 2019, 29, 299–316. [Google Scholar] [CrossRef]
- Yu, D.L.; Wen, J.H.; Shen, H.J.; Xiao, Y.; Wen, X.S. Propagation of flexural wave in periodic beam on elastic foundations. Phys. Lett. A 2012, 376, 626–630. [Google Scholar] [CrossRef]
- Ding, L.; Ye, Z.; Wu, Q. Flexural vibration band gaps in periodic Timoshenko beams with oscillators in series resting on flexible supports. Adv. Struct. Eng. 2020, 23, 3117–3127. [Google Scholar] [CrossRef]
- Han, Y.R.; Chen, X.H.; Wei, Y.H.; Jiang, S.; Du, C.; Jiang, G.Q.; Zhang, H. Vibration attenuation of metamaterial dual-beam with simultaneous acoustic black hole and local resonator. Eur. J. Mech. A-Solid. 2025, 111, 105535. [Google Scholar] [CrossRef]
- Chen, J.; Chao, I.; Chen, T. Bandgaps for flexural waves in infinite beams and plates with a periodic array of resonators. J. Mech. 2022, 38, 376–389. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, J.X.; Cai, C.Q.; Xu, D.L.; Ouyang, H.J. Mathematical modeling and analysis of a meta-plate for very low-frequency band gap. Appl. Math. Model. 2019, 73, 581–597. [Google Scholar] [CrossRef]
- Wang, Q.; Li, J.Q.; Zhang, Y.; Xue, Y.; Li, F.M. Bandgap properties in metamaterial sandwich plate with periodically embedded plate-type resonators. Mech. Syst. Signal Process 2021, 151, 107375. [Google Scholar] [CrossRef]
- Miao, Z.; Yin, J.; Yang, Y.; Ke, Y.; Zheng, Z.; Geng, X.; Wang, Q. Design of multi-bandgap metamaterial plate based on composite cylindrical resonators. Mater. Des. 2025, 250, 113570. [Google Scholar] [CrossRef]
- Russillo, A.F.; Failla, G.; Alotta, G. Ultra-wide low-frequency band gap in locally-resonant plates with tunable inerter-based resonators. Appl. Math. Model. 2022, 106, 682–695. [Google Scholar] [CrossRef]
- Heckl, M.A. Coupled waves on a periodically supported Timoshenko beam. J. Sound. Vib. 2002, 252, 849–882. [Google Scholar] [CrossRef]
- Cremer, L.; Leilich, H.O. On theory of flexural periodic systems. Arch. Elektr. Ubertragung 1953, 7, 261–270. [Google Scholar]
- Langley, R.S.; Smith, J.R.D.; Fahy, F.J. Statistical energy analysis of periodically stiffened damped plate structures. J. Sound. Vib. 1997, 208, 407–426. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, H.; Ye, L. A stiffened plate element model for advanced grid stiffened composite plates/shells. J. Compos. Mater. 2011, 45, 187–202. [Google Scholar] [CrossRef]
- Wen, J.H.; Yu, D.L.; Wang, G.; Zhao, H.G.; Liu, Y.Z. Elastic wave band gaps in flexural vibrations of straight beams. J. Mech. Eng. 2015, 41, 1–6. [Google Scholar] [CrossRef]
- Liu, S.; Li, S.; Shu, H.; Wang, W.; Shi, D.; Dong, L.; Lin, H.; Liu, W. Research on the elastic wave band gaps of curved beam of phononic crystals. Phys. B 2015, 457, 82–91. [Google Scholar] [CrossRef]
- Fang, J.; Yu, D.; Han, X.; Cai, L. Coupled flexural-torsional vibration band gap in periodic beam including warping effect. Chin. Phys. B 2009, 18, 1316. [Google Scholar] [CrossRef]
- Cenedese, M.; Belloni, E.; Braghin, F. Interaction of Bragg scattering bandgaps and local resonators in mono-coupled periodic structures. J. Appl. Phys. 2021, 129, 124501. [Google Scholar] [CrossRef]
- Sorokin, S.V.; Ershova, O.A. Plane wave propagation and frequency band gaps in periodic plates and cylindrical shells with and without heavy fluid loading. J. Sound. Vib. 2004, 278, 501–526. [Google Scholar] [CrossRef]
- Zhang, J. Band gap attenuation characteristics of periodic compound plate with wave propagation approach. Acta Phys. Sin-Ch Ed. 2014, 63, 224302. [Google Scholar] [CrossRef]
- Wu, Z.; Li, F.; Wang, Y. Study on vibration characteristics in periodic plate structures using the spectral element method. Acta Mech. 2013, 224, 1089–1101. [Google Scholar] [CrossRef]
- Guo, Z.W.; Sheng, M.P.; Pan, J. Effect of boundary conditions on the band-gap properties of flexural waves in a periodic compound plate. J. Sound. Vib. 2017, 395, 102–126. [Google Scholar] [CrossRef]
- Guo, Z.; Sheng, M.; Zeng, H. Vibration attenuation in a beam structure with a periodic free-layer damping treatment. Machines 2023, 11, 949. [Google Scholar] [CrossRef]
- Ruzzene, M.; Mazzarella, L.; Tsopelas, P.; Scarpa, F. Wave propagation in sandwich plates with periodic auxetic core. J. Intell. Mater. Syst. Struct. 2002, 13, 587–597. [Google Scholar] [CrossRef]
- Ruzzene, M.; Tsopelas, P. Control of wave propagation in sandwich plate rows with periodic honeycomb core. J. Eng. Mech-ASCE 2003, 129, 975–986. [Google Scholar] [CrossRef]
- Sheng, M.P.; Guo, Z.W.; Qin, Q.; He, Y.A. Vibration characteristics of a sandwich plate with viscoelastic periodic cores. Compos. Struct. 2018, 206, 54–69. [Google Scholar] [CrossRef]
- Jiang, C.; Xiang, Y.; He, P.; He, H. Vibration attenuation behaviors of finite sandwich plates with periodic core. Appl. Acoust. 2020, 157, 107009. [Google Scholar] [CrossRef]
- Robin, G.; Huchard, T.; Poncot, M.; Daya, E.M. Experimental investigation of the periodic core sandwich structure: Shape of the vibration modes. Mech. Res. Commun. 2025, 147, 104434. [Google Scholar] [CrossRef]
- Huchard, T.; Robin, G.; Ponçot, M.; Hoppe, S.; Daya, E.M. Elaboration, characterization and modelling of periodic viscoelastic sandwich beams for lightening and vibration damping. Mech. Res. Commun. 2022, 121, 103863. [Google Scholar] [CrossRef]
- Dou, Y.K.; Zhang, J.G.; Wen, X.L.; Cheng, H.; Liu, H.X. Free vibration characteristics of CFRP laminate with one-dimensional periodic structures. Polymers 2023, 15, 1118. [Google Scholar] [CrossRef]
- E, L.Z.Y.; Chen, Z.Y.; Li, F.M.; Zou, G.P. Band-gap properties of elastic sandwich metamaterial plates with composite periodic rod core. Acta Mech. Solida Sin. 2022, 35, 51–62. [Google Scholar] [CrossRef]
- Zi, H.; Li, Y.G. Low-frequency broadband vibration attenuation of sandwich plate-type metastructures with periodic thin-wall tube cores. J. Low. Freq. Noise V. A 2022, 41, 330–339. [Google Scholar] [CrossRef]
- Shen, C.M.; Huang, J.; Zhang, Z.X.; Xue, J.Y.; Qian, D.H. Sandwich plate structure periodically attached by s-shaped oscillators for low frequency ship vibration isolation. Materials 2023, 16, 2467. [Google Scholar] [CrossRef] [PubMed]
- Li, C.F.; Chen, Z.B.; Jiao, Y.H. Vibration and bandgap behavior of sandwich pyramid lattice core plate with resonant rings. Materials 2023, 16, 2730. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Wei, P.J. The band gap of 1D viscoelastic phononic crystal. Comp. Mater. Sci. 2009, 46, 603–606. [Google Scholar] [CrossRef]
- Chen, Y.F.; Guo, D.; Li, Y.F.; Li, G.Y.; Huang, X.D. Maximizing wave attenuation in viscoelastic phononic crystals by topology optimization. Ultrasonics 2019, 94, 419–429. [Google Scholar] [CrossRef]
- Oliveiraa, V.B.S.d.; Schalcherb, L.F.C.; Santosc, J.M.C.D.; de Miranda, E.J.P., Jr. Wave attenuation in 1-D viscoelastic phononic crystal rods using different polymers. Mat. Res. 2023, 26, e20220534. [Google Scholar] [CrossRef]
- Miranda, E.J.P., Jr.; Dal Poggetto, V.F.; Pugno, N.M.; Dos Santos, J.M.C. Extended plane wave expansion formulation for viscoelastic phononic thin plates. Wave Motion 2023, 123, 103222. [Google Scholar] [CrossRef]
- Li, W.; Zhang, X.; Du, J.; Liu, Z. An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports. J. Sound. Vib. 2009, 321, 254–269. [Google Scholar] [CrossRef]
- Thomson, W. On the elasticity and viscosity of metals. Proc. R. Soc. Lond. A Math. Phys. Sci. 1865, 14, 289–297. [Google Scholar] [CrossRef]
- Voigt, W. Ieber innere Reibung fester korper, insbesondere der Metalle. Ann. Phys. 1892, 283, 671–693. [Google Scholar] [CrossRef]
- Maxwell, J.C. On the dynamical theory of gases. Philos. Trans. R. Soc. Lond. A 1867, 157, 49–88. [Google Scholar] [CrossRef]
- Wiechert, E. Gesetze der elastischen Nachwirkung für constante Temperatur. Ann. Phys. 1893, 286, 335–348. [Google Scholar] [CrossRef]
- Cremer, L.; Heckl, M.; Petersson, B.A.T. Structure-Borne Sound: Structural Vibrations and Sound Radiation at Audio Frequencies; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Wikipedia. Available online: https://en.wikipedia.org/wiki/Kelvin%E2%80%93Voigt_material (accessed on 3 September 2025).
- Andreassen, E.; Jensen, J.S. Analysis of phononic bandgap structures with dissipation. J. Vib. Acoust. 2013, 135, 041015. [Google Scholar] [CrossRef]
- Nouh, M.A.; Aldraihem, O.J.; Baz, A. Periodic metamaterial plates with smart tunable local resonators. J. Intell. Mater. Syst. Struct. 2015, 27, 1829–1845. [Google Scholar] [CrossRef]
- MatWeb. Available online: https://www.matweb.com/search/DataSheet.aspx?MatGUID=1ebba7628d0247ebbbd062be91dd3cb4&ckck=1 (accessed on 1 September 2025).






| Notation | Meaning | Unit |
|---|---|---|
| The tangential linear spring stiffness per unit length | N/m2 | |
| The vertical linear spring stiffness per unit length | N/m2 | |
| The transverse linear spring stiffness per unit length | N/m2 | |
| The torsional spring stiffness per unit length | N |
| (N/m2) | (N/m2) | (N/m2) | (N) | |
|---|---|---|---|---|
| FBC | zero | zero | zero | zero |
| CLBC | Infinity | Infinity | Infinity | Infinity |
| SBC | Infinity | zero | Infinity | zero |
| General EBC | Between zero and infinity | Between zero and infinity | Between zero and infinity | Between zero and infinity |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Sheng, M.; Zhang, K. Effect of Boundary Conditions on Vibration Characteristics of a Sandwich Plate with Viscoelastic Periodic Cores. Machines 2025, 13, 863. https://doi.org/10.3390/machines13090863
Guo Z, Sheng M, Zhang K. Effect of Boundary Conditions on Vibration Characteristics of a Sandwich Plate with Viscoelastic Periodic Cores. Machines. 2025; 13(9):863. https://doi.org/10.3390/machines13090863
Chicago/Turabian StyleGuo, Zhiwei, Meiping Sheng, and Kai Zhang. 2025. "Effect of Boundary Conditions on Vibration Characteristics of a Sandwich Plate with Viscoelastic Periodic Cores" Machines 13, no. 9: 863. https://doi.org/10.3390/machines13090863
APA StyleGuo, Z., Sheng, M., & Zhang, K. (2025). Effect of Boundary Conditions on Vibration Characteristics of a Sandwich Plate with Viscoelastic Periodic Cores. Machines, 13(9), 863. https://doi.org/10.3390/machines13090863






