Adaptive PCA-Based Normal Estimation for Automatic Drilling System of Large-Curvature Aerospace Components
Abstract
1. Introduction
Research Gaps, Aims, and Contributions
- (1)
- Develop a vision-integrated robotic drilling system that combines line structured-light sensing with PCA-based normal vector estimation, tailored for single-curvature aerospace components.
- (2)
- Investigate the impact of surface roughness and curvature radius on normal estimation accuracy, which is often neglected in prior works.
- (3)
- Propose a pre-drilling and post-drilling quality verification algorithm that ensures the correct orientation of the drilling tool and checks hole dimensional accuracy after drilling.
- (1)
- A point-cloud-based normal estimation method with adaptive extraction and PCA plane fitting that achieves normal direction accuracy ≤ 0.2° on surfaces with curvature radii up to 50 mm and roughness ≤ Ra4.8.
- (2)
- A robotic drilling platform that achieves sub-millimeter hole position accuracy (0.08–0.25 mm), which meets the positional and angular requirements for aerospace assembly.
- (3)
- A dual-function algorithm for pre-adjusting the drilling normal and post-process inspection, ensuring that deviations in hole position and verticality remain within the target tolerance range.
- (4)
- The study also quantifies the relative influence of surface roughness and curvature radius on normal fitting error, demonstrating that curvature is the dominant factor impacting drilling precision.
2. Robot Automated Hole-Making Technology Driven by Artificial Intelligence in Aerospace Manufacturing
2.1. Design of Robot Automatic Hole-Making System and Camera Calibration
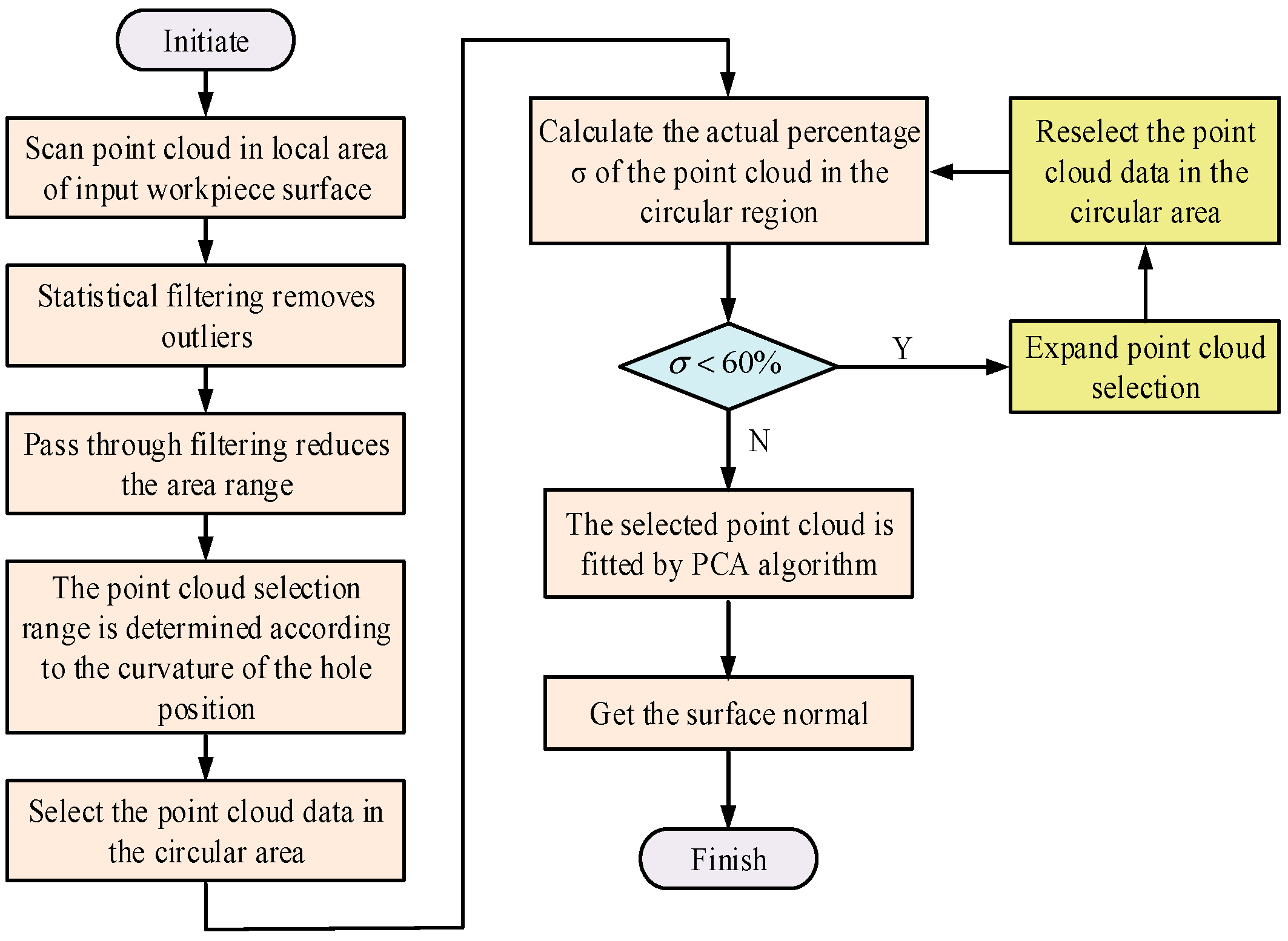
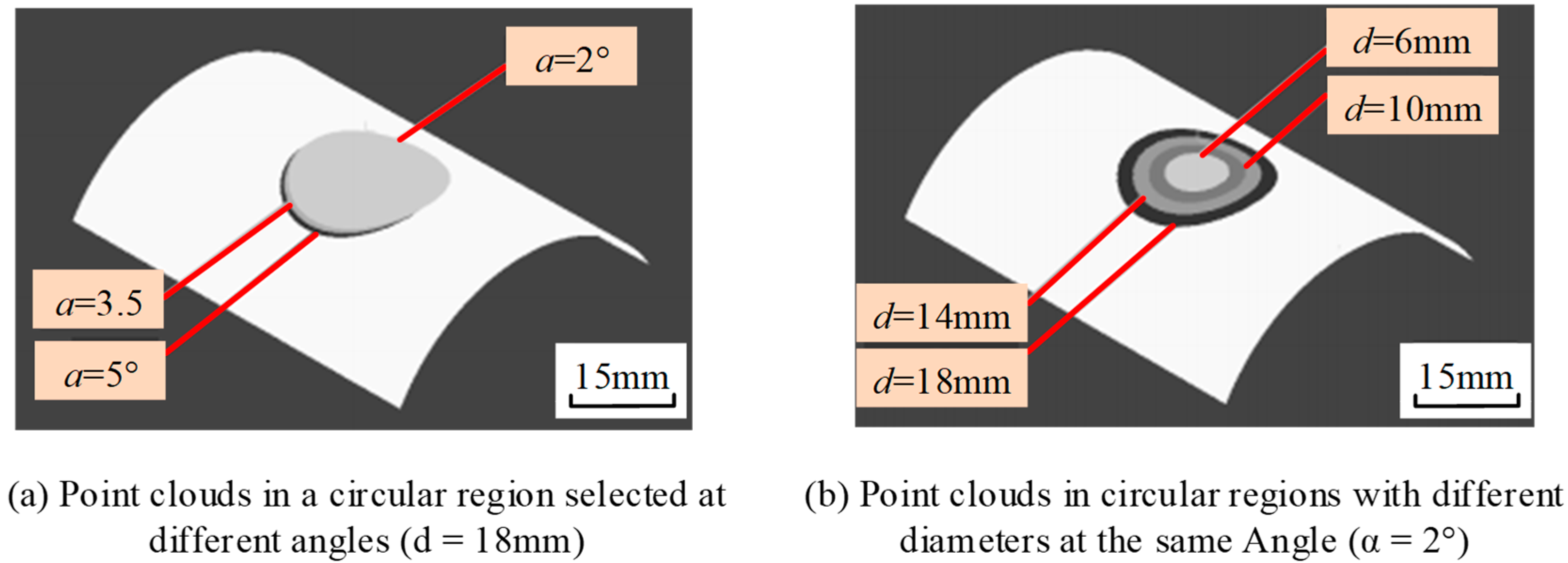
2.2. Point Cloud Data Processing and 3D Reconstruction
- Inputs: Raw point cloud data from the structured-light sensor, surface curvature radius, and predefined point-cloud selection diameter.
- Outputs: The estimated surface normal vector at the selected point, the calculated angular deviation from the theoretical normal, and the filtered point cloud after denoising.
- Decision Criteria: The point cloud neighborhood is adaptively expanded until the true proportion PPP of valid points exceeds the confidence threshold (60%), ensuring that PCA fitting error remains ≤0.2°.
- By verifying the surface point cloud data of aviation components with different curvatures, it was found that when , the local point cloud caused the PCA plane fitting error to exceed the target measurement uncertainty due to the excessively high proportion of voids.
- When , the uniformity of point cloud distribution can meet the requirements of normal fitting accuracy.
3. Performance Verification of Robot Automatic Hole-Making
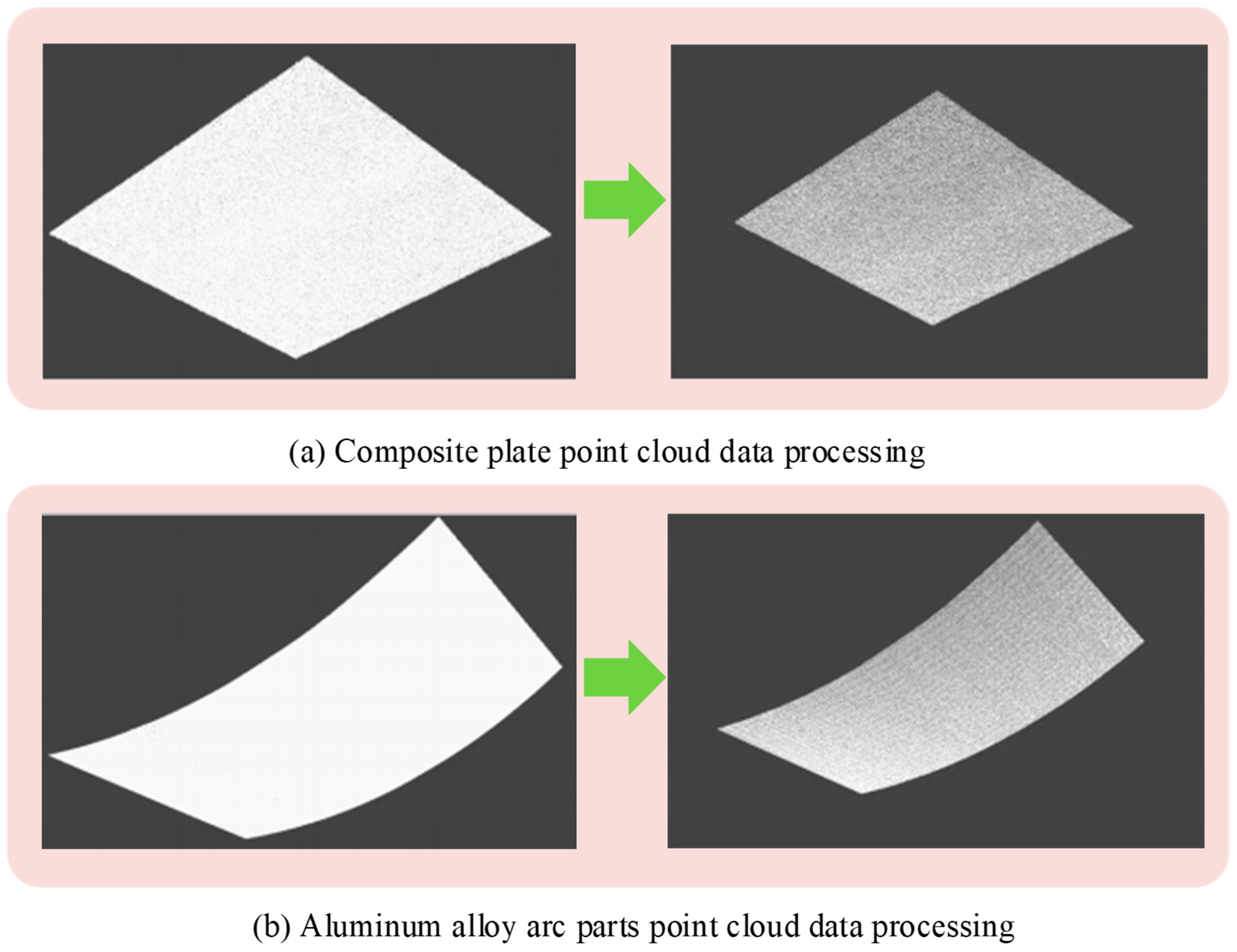
3.1. Preprocessing Effect of Point Cloud Data
3.2. Error Analysis
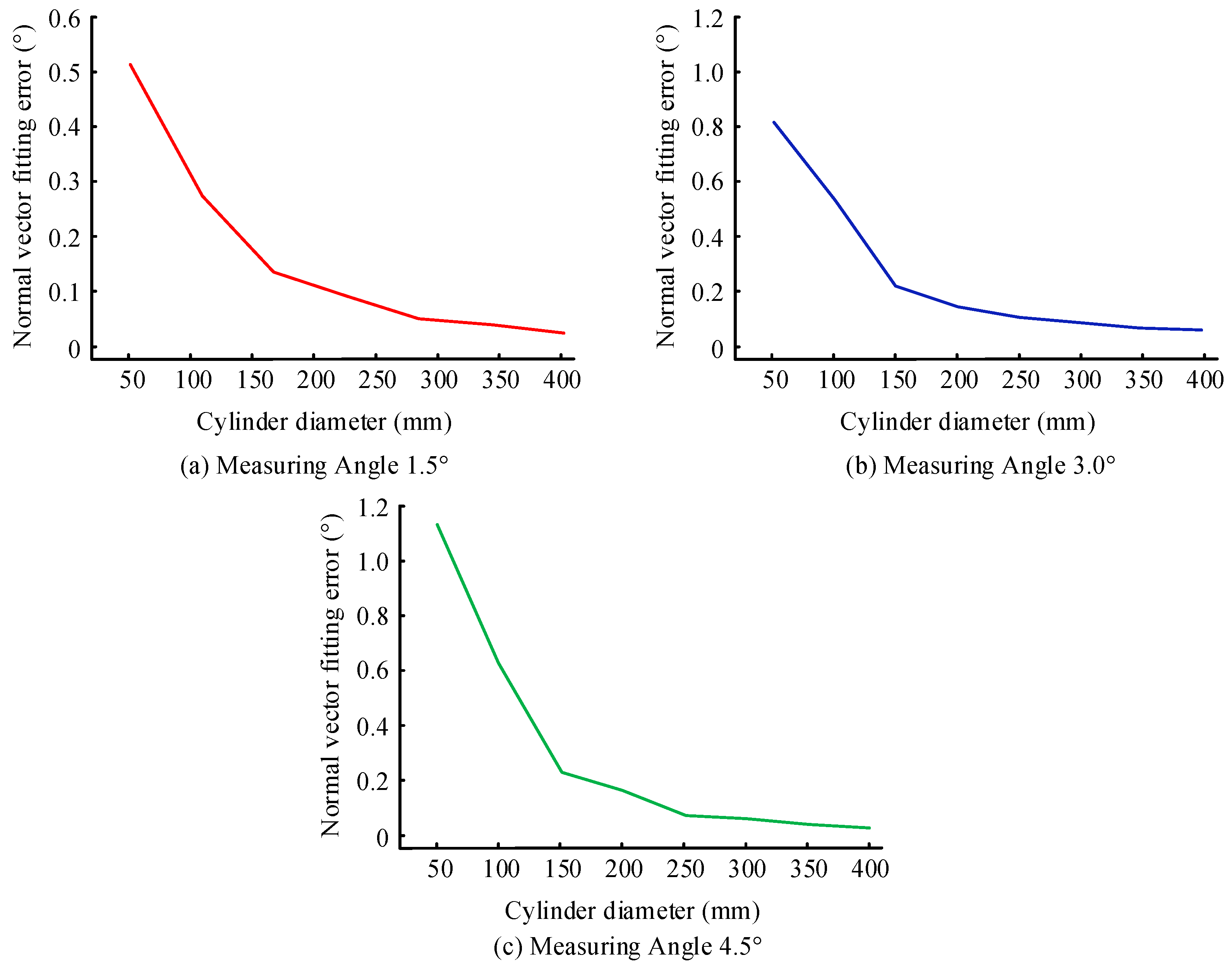
3.3. Influence of Surface Roughness and Curvature on Normal Estimation
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| CAD | Computer-Aided Design |
| CNC | Computer Numerical Control |
| CNN | Convolutional Neural Network |
| FPS | Frames per Second |
| PCA | Principal Component Analysis |
| RMS | Root Mean Square |
| SL | Structured Light |
| 3D | Three-Dimensional |
| 2D | Two-Dimensional |
| Ra | Roughness Average |
| RGB | Red–Green–Blue |
| SLAM | Simultaneous Localization and Mapping |
| CCD | Charge-Coupled Device |
References
- Adel, A. The Convergence of Intelligent Tutoring, Robotics, and IoT in Smart Education for the Transition from Industry 4.0 to 5.0. Smart Cities 2024, 7, 325–369. [Google Scholar] [CrossRef]
- Zhao, D.; Guo, W. Shape and Performance Controlled Advanced Design for Additive Manufacturing: A Review of Slicing and Path Planning. J. Manuf. Sci. Eng. Trans. ASME 2020, 142, 10801. [Google Scholar] [CrossRef]
- Yin, Z.; Liu, Q.; Sun, P.; Ding, J. Kinematic Analysis and Parameter Measurement for Multi-Axis Laser Engraving Machine Tools. Machines 2021, 9, 237. [Google Scholar] [CrossRef]
- Ishfaq, K.; Asad, M.; Mahmood, M.A.; Abdullah, M.; Pruncu, C. Opportunities and Challenges in Additive Manufacturing Used in Space Sector: A Comprehensive Review. Rapid Prototyp. J. 2022, 28, 2027–2042. [Google Scholar] [CrossRef]
- Klocke, F.; Soo, S.L.; Karpuschewski, B.; Webster, J.A.; Novovic, D.; Elfizy, A.; Axinte, D.A.; Tönissen, S. Abrasive Machining of Advanced Aerospace Alloys and Composites. CIRP Ann. Manuf. Technol. 2015, 64, 581–604. [Google Scholar] [CrossRef]
- Rambabu, P.; Prasad, N.E.; Kutumbarao, V.V. Aerospace Materials and Material Technologies; Springer: Berlin/Heidelberg, Germany, 2017; Volume 2, ISBN 978-981-10-2142-8. [Google Scholar]
- Li, J.; Zhou, G.; Zhang, C. A Twin Data and Knowledge-Driven Intelligent Process Planning Framework of Aviation Parts. Int. J. Prod. Res. 2022, 60, 5217–5234. [Google Scholar] [CrossRef]
- Bhundiya, H.G.; Royer, F.; Cordero, Z. Engineering Framework for Assessing Materials and Processes for In-Space Manufacturing. J. Mater. Eng. Perform. 2022, 31, 6045–6059. [Google Scholar] [CrossRef]
- Sarh, B.; Buttrick, J.; Munk, C.; Bossi, R. Aircraft Manufacturing and Assembly. In Springer Handbook of Automation; Springer: Berlin/Heidelberg, Germany, 2009; pp. 893–910. [Google Scholar] [CrossRef]
- Gohardani, A.S.; Doulgeris, G.; Singh, R. Challenges of Future Aircraft Propulsion: A Review of Distributed Propulsion Technology and Its Potential Application for the All-Electric Commercial Aircraft. Prog. Aerosp. Sci. 2011, 47, 369–391. [Google Scholar] [CrossRef]
- Szarski, M.; Chauhan, S. An Unsupervised Defect Detection Model for a Dry Carbon Fiber Textile. J. Intell. Manuf. 2022, 33, 2075–2092. [Google Scholar] [CrossRef]
- Dai, J.; Shen, J.; Tian, W.; Li, P.; Liu, H.; Cui, X. Benchmark Feature Detection Method for Mobile Robot Automatic Drilling System Integrated with Deep Learning. Machines 2025, 13, 154. [Google Scholar] [CrossRef]
- Ding, Z.; Li, R. Point Cloud Reduction Method Based on Curvature Grading and Voxel Filtering. J. Electr. Syst. 2024, 20, 318–326. [Google Scholar] [CrossRef]
- Szarski, M.; Chauhan, S. Instant Flow Distribution Network Optimization in Liquid Composite Molding Using Deep Reinforcement Learning. J. Intell. Manuf. 2023, 34, 197–218. [Google Scholar] [CrossRef]
- Ruiz, L.; Díaz, S.; González, J.M.; Cavas, F. Improving the Competitiveness of Aircraft Manufacturing Automated Processes by a Deep Neural Network. Integr. Comput. Aided. Eng. 2023, 30, 341–352. [Google Scholar] [CrossRef]
- Herzog, T.; Brandt, M.; Trinchi, A.; Sola, A.; Molotnikov, A. Process Monitoring and Machine Learning for Defect Detection in Laser-Based Metal Additive Manufacturing. J. Intell. Manuf. 2024, 35, 1407–1437. [Google Scholar] [CrossRef]
- Zhou, G.; Zhou, K.; Zhang, J.; Yuan, M.; Wang, X.; Feng, P.; Zhang, M.; Feng, F. Digital Modeling-Driven Chatter Suppression for Thin-Walled Part Manufacturing. J. Intell. Manuf. 2024, 35, 289–305. [Google Scholar] [CrossRef]
- Zhu, K.; Fuh, J.Y.H.; Lin, X. Metal-Based Additive Manufacturing Condition Monitoring: A Review on Machine Learning Based Approaches. IEEE/ASME Trans. Mechatron. 2022, 27, 2495–2510. [Google Scholar] [CrossRef]
- Lin, J.; Zheng, B.; Chen, Z. Application of Data Visualization Interaction Technology in Aerospace Data Processing. Scalable Comput. 2023, 24, 641–650. [Google Scholar] [CrossRef]
- Fan, W.; Fu, Q.; Cao, Y.; Zheng, L.; Zhang, X.; Zhang, J. Binocular Vision and Priori Data Based Intelligent Pose Measurement Method of Large Aerospace Cylindrical Components. J. Intell. Manuf. 2024, 35, 2137–2159. [Google Scholar] [CrossRef]
- Simonov, E.N.; Vinogradov, K.M.; Gorozhankin, A.N.; Anikin, A.S.; Khryukin, D.Y. Development and Modeling of a 3D Image Reconstruction Algorithm for Cone-Beam X-Ray Computed Tomography for Non-Destructive Testing in Additive Manufacturing. Russ. Eng. Res. 2024, 44, 563–568. [Google Scholar] [CrossRef]
- Takahashi, H.; Oki, J.; Hirotani, T.; Taguchi, H. Tomographic Reconstruction of Hypersonic Winged Aircraft Model Flowfields in Large-Scale Hypersonic Wind Tunnel Experiment. In Proceedings of the 25th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Bengaluru, India, 28 May–1 June 2023; Volume 62, pp. 869–881. [Google Scholar] [CrossRef]
- Zhao, E.; Zhang, Y.; Gao, J. Monocular Depth Estimation of Noncooperative Spacecraft Based on Deep Learning. J. Aerosp. Inf. Syst. 2023, 20, 334–342. [Google Scholar] [CrossRef]
- Olubodun, P.A.; Fischer, J.D.; Bristow, D.A. Iterative Correction of Robotic Grinding Using Spatial Feedback for Precision Applications. Manuf. Lett. 2024, 41, 264–269. [Google Scholar] [CrossRef]
- Miao, Y.; Wang, Z.; Zhang, X.; Xu, S.; Cai, Z.; Peng, X.; Liu, X. Large Depth-of-Field 3D Measurement with Multi-View Fusion in MEMS-Based Structured Light Field. Opt. Express 2025, 33, 28122–28140. [Google Scholar] [CrossRef]
- Alam, M.A.; Ya, H.H.; Sapuan, S.M.; Mamat, O.; Parveez, B.; Yusuf, M.; Masood, F.; Ilyas, R.A. Recent Advancements in Advanced Composites for Aerospace Applications: A Review. In Advanced Composites in Aerospace Engineering Applications; Springer: Cham, Switzerland, 2022; pp. 319–339. [Google Scholar] [CrossRef]
- HB 7759-2004; Coding for Aircraft Product Structure. China Machinery Industry Federation: Beijing, China, 2004.
- SAE AS 9100D; Quality Management Systems—Requirements for Aviation, Space, and Defense Organizations AS9100D. SAE International: Warwick, PA, USA, 2016.
- GB/T 13914-2021; Tolerance of Dimensions for Stamping Parts. Standardization Administration of China: Beijing, China, 2021.
- Pulipati, D.P.; Kokkada Ravindranath, P.; Jack, D.A. Automated Bondline Thickness Quantification in Adhesively Joined Composites and Metals Using Ultrasound. Polym. Compos. 2024, 45, 2324–2336. [Google Scholar] [CrossRef]
- Spicer, R.; Miranda, F.; Cote, T.; Itchkawich, T.; Black, J. High Vacuum Capable Fused Filament Fabrication 3D Printer, Part I: Low-Temperature Polymers and Early Lessons Learned. J. Spacecr. Rocket. 2024, 61, 543–556. [Google Scholar] [CrossRef]
- Pollefeys, M.; Nistér, D.; Frahm, J.M.; Akbarzadeh, A.; Mordohai, P.; Clipp, B.; Engels, C.; Gallup, D.; Kim, S.J.; Merrell, P.; et al. Detailed Real-Time Urban 3D Reconstruction from Video. Int. J. Comput. Vis. 2008, 78, 143–167. [Google Scholar] [CrossRef]
- Engel, J.; Sturm, J.; Cremers, D. Scale-Aware Navigation of a Low-Cost Quadrocopter with a Monocular Camera. Rob. Auton. Syst. 2014, 62, 1646–1656. [Google Scholar] [CrossRef]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-Scale Direct Monocular SLAM. In Computer Vision—ECCV 2014; Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2014; Volume 8690, pp. 834–849. [Google Scholar]
- Li, H.; Liao, Z.; Cai, W.; Zhong, Y.; Zhang, X. Flexible Calibration of the Telecentric Vision Systems Using Only Planar Calibration Target. IEEE Trans. Instrum. Meas. 2024, 73, 5000610. [Google Scholar] [CrossRef]
- Li, W.; Shan, S.; Liu, H. High-Precision Method of Binocular Camera Calibration with a Distortion Model. Appl. Opt. 2017, 56, 2368. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, Q.; Hu, P.; Zhang, H.; Zhang, Z.; Liu, X.; Zhou, J. Adaptive Exposure Control for Line-Structured Light Sensors Based on Global Grayscale Statistics. Sensors 2025, 25, 1195. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zhang, M.; Zheng, B.; Ma, L. An On-Line Measurement Method of the Medium Thickness Steel Plate Based on Structured Light Vision Sensor. Int. J. Precis. Eng. Manuf. 2023, 24, 1903–1914. [Google Scholar] [CrossRef]
- Antipova, N.V.; Gvozdev, O.G.; Kozub, V.A.; Murynin, A.B.; Richter, A.A. Retrieving Structural Information on Anthropogenic Objects from Single Aerospace Images. J. Comput. Syst. Sci. Int. 2023, 62, 522–537. [Google Scholar] [CrossRef]
- Liu, P.F.; Qian, L.; Lu, H.; Xue, L.; Zhao, X.W.; Tao, B. The Joint Knowledge Reasoning Model Based on Knowledge Representation Learning for Aviation Assembly Domain. Sci. China Technol. Sci. 2024, 67, 143–156. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Y.; Xie, H.; Feng, M.; Wu, H.; Ding, C.; Mian, A. A Systematic Point Cloud Edge Detection Framework for Automatic Aircraft Skin Milling. IEEE Trans. Ind. Inform. 2024, 20, 560–572. [Google Scholar] [CrossRef]
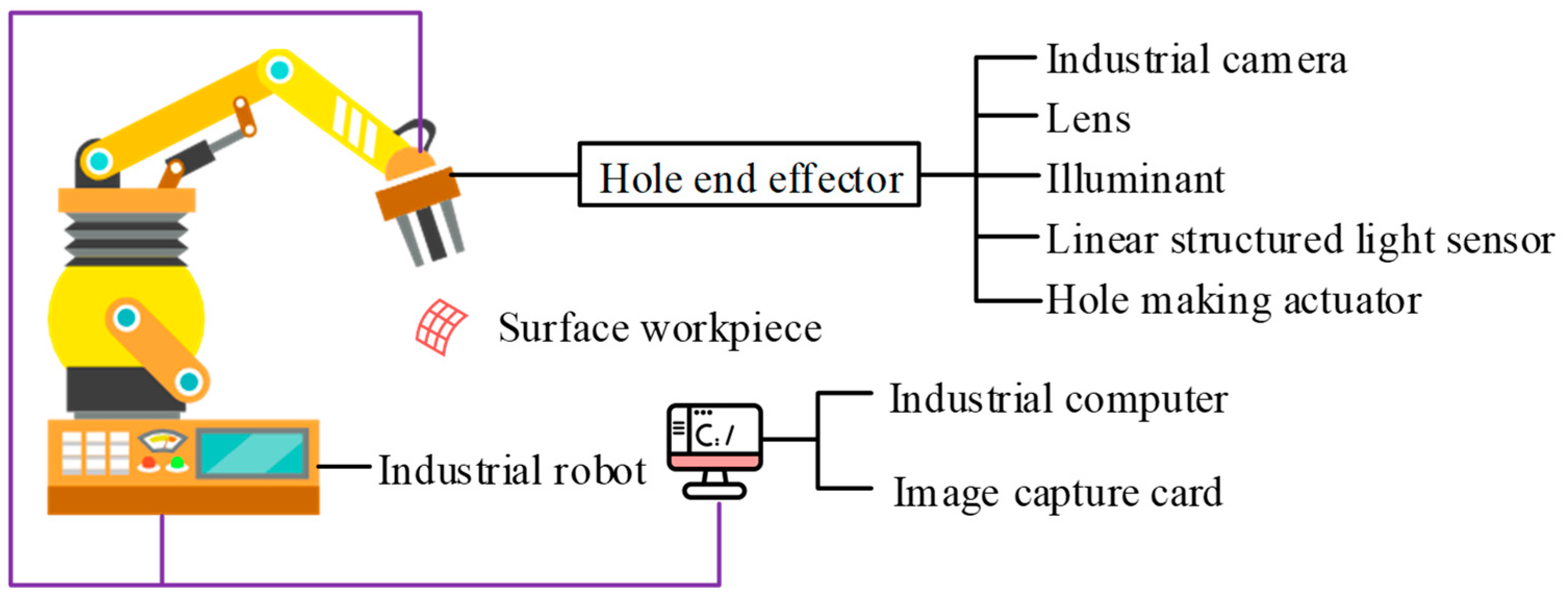

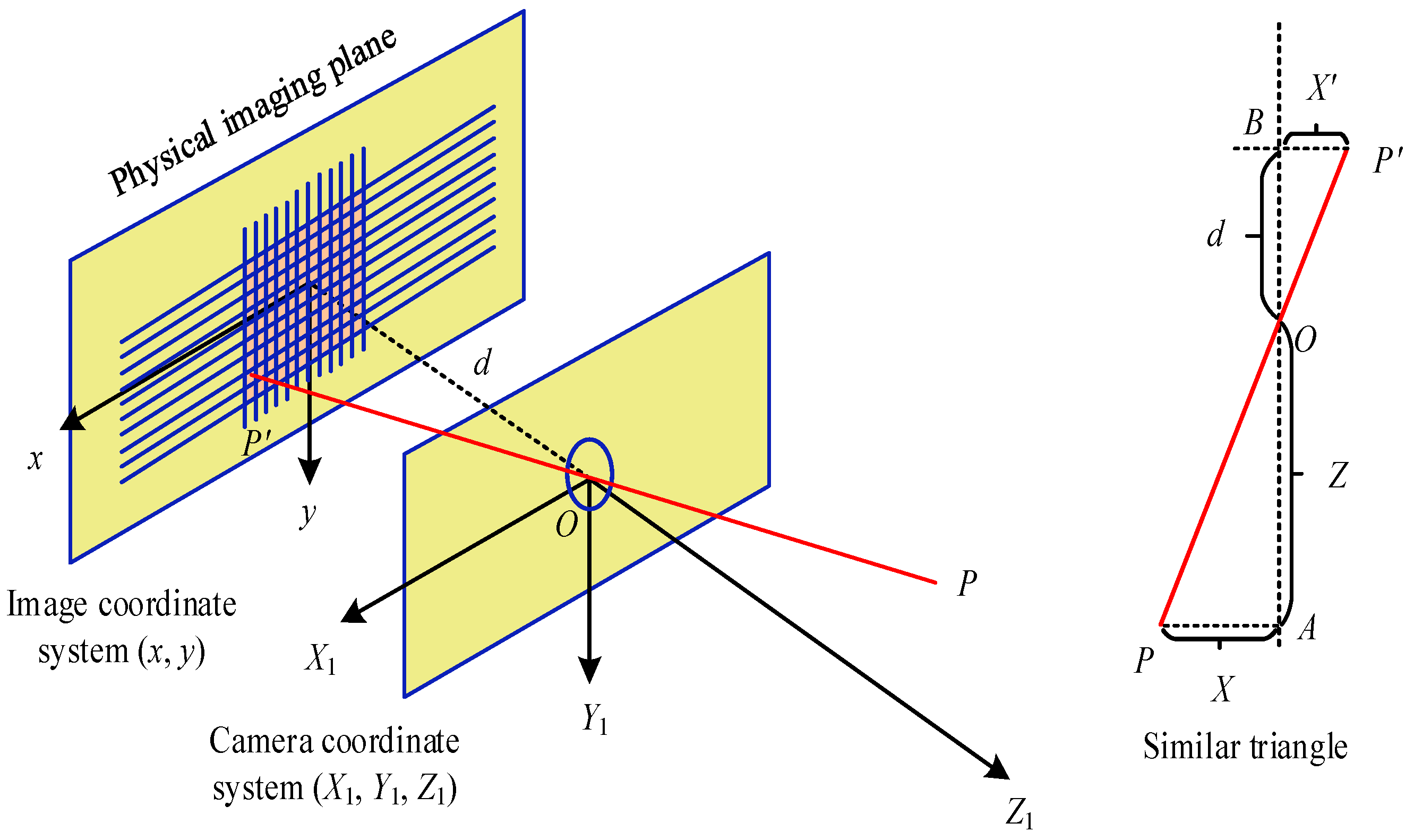





| Industrial Robot Parameters | Industrial Camera Parameters | ||
|---|---|---|---|
| Maximum load (kg) | 150 | Chip type | CMOS |
| Maximum arm span (mm) | 2550 | Chip size | Overall situation |
| Degree of freedom | 6 | Pixel size | 1 inch |
| Repeated positioning accuracy (mm) | ±0.3 | Resolution | 5 µm |
| Hole processing range (mm) | 2–12 | Frame rate | 2560 × 2048 |
| Spindle speed (n/rpm) | 2200 | Lens interface | 138 fps |
| Feed stroke (mm) | 180 | Focal length (mm) | 55 |
| Finished Hole | Measured Value (mm) | Theoretical Position (mm) | Error | Root Mean Square Error (mm) | Mean (mm) | Standard Deviation (mm) | |||
|---|---|---|---|---|---|---|---|---|---|
| x | y | x | y | x | y | ||||
| 1 | 45.08 | 15.12 | 45 | 15 | 0.08 | 0.12 | 0.144 | 0.015 for x −0.012 for y | 0.0163 for x 0.013 for y |
| 2 | 44.75 | 15.03 | 45 | 15 | −0.25 | 0.03 | 0.252 | ||
| 3 | 45.15 | 14.95 | 45 | 15 | 0.15 | −0.05 | 0.158 | ||
| 4 | 44.88 | 14.80 | 45 | 15 | −0.12 | −0.20 | 0.233 | ||
| 5 | 45.09 | 15.13 | 45 | 15 | 0.09 | 0.13 | 0.158 | ||
| 6 | 45.14 | 14.90 | 45 | 15 | 0.14 | −0.10 | 0.172 | ||
| Measuring Angle (°) | Point Cloud Selection Range Diameter (mm) | Simulation Result (°) | Test Result (°) | Mean (°) | Standard Deviation (°) | No. of Trials |
|---|---|---|---|---|---|---|
| 1.5 | 6 | 0.030 | 0.079 | 0.151 | 0.054 | 4 |
| 10 | 0.054 | 0.143 | ||||
| 14 | 0.093 | 0.186 | ||||
| 18 | 0.161 | 0.197 | ||||
| 3.0 | 6 | 0.041 | 0.111 | 0.215 | 0.096 | 4 |
| 10 | 0.089 | 0.184 | ||||
| 14 | 0.171 | 0.225 | ||||
| 18 | 0.282 | 0.341 | ||||
| 4.5 | 6 | 0.066 | 0.147 | 0.269 | 0.118 | 4 |
| 10 | 0.130 | 0.222 | ||||
| 14 | 0.252 | 0.283 | ||||
| 18 | 0.387 | 0.425 |
| Measuring Angle (°) | Baseline Fixed-Range Error (°) | Adaptive PCA Error (°) | Improvement (%) |
|---|---|---|---|
| 1.5 | 0.52 | 0.079 | 84.8% |
| 3.0 | 0.78 | 0.111 | 85.8% |
| 4.5 | 1.12 | 0.147 | 86.9% |
| Radius of Curvature (mm) | Surface Roughness (°) | |||
|---|---|---|---|---|
| Ra1.6 | Ra3.2 | Ra4.8 | Ra6.3 | |
| 50 | 0.18 | 0.22 | 0.27 | 0.32 |
| 100 | 0.12 | 0.15 | 0.19 | 0.23 |
| 200 | 0.08 | 0.1 | 0.13 | 0.16 |
| 400 | 0.05 | 0.07 | 0.09 | 0.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Gao, R.; Du, B.; Bai, Y.; Qi, Y. Adaptive PCA-Based Normal Estimation for Automatic Drilling System of Large-Curvature Aerospace Components. Machines 2025, 13, 809. https://doi.org/10.3390/machines13090809
Yang H, Gao R, Du B, Bai Y, Qi Y. Adaptive PCA-Based Normal Estimation for Automatic Drilling System of Large-Curvature Aerospace Components. Machines. 2025; 13(9):809. https://doi.org/10.3390/machines13090809
Chicago/Turabian StyleYang, Hailong, Renzhi Gao, Baorui Du, Yu Bai, and Yi Qi. 2025. "Adaptive PCA-Based Normal Estimation for Automatic Drilling System of Large-Curvature Aerospace Components" Machines 13, no. 9: 809. https://doi.org/10.3390/machines13090809
APA StyleYang, H., Gao, R., Du, B., Bai, Y., & Qi, Y. (2025). Adaptive PCA-Based Normal Estimation for Automatic Drilling System of Large-Curvature Aerospace Components. Machines, 13(9), 809. https://doi.org/10.3390/machines13090809








