Design and Kinematic Analysis of a Metamorphic Mechanism-Based Robot for Climbing Wind Turbine Blades
Abstract
1. Introduction
- (1)
- Proposing an overall structural design for a wind turbine blade wall-climbing robot based on a metamorphic mechanism, combining wheel-legged composite and cable-climbing mobility methods, and incorporating a 10R-Folding metamorphic trunk to significantly enhance the robot’s mobility flexibility and environmental adaptability;
- (2)
- Conducting systematic kinematic analysis, establishing closed-loop equations for the 10R-Folding trunk, performing higher-order kinematic modeling, and analyzing motion branches and configuration switching paths under singular configurations;
- (3)
- Developing a robot prototype and conducting configuration switching experiments, designing a supporting control system to achieve stable multi-configuration switching and motion verification.
2. Materials and Methods
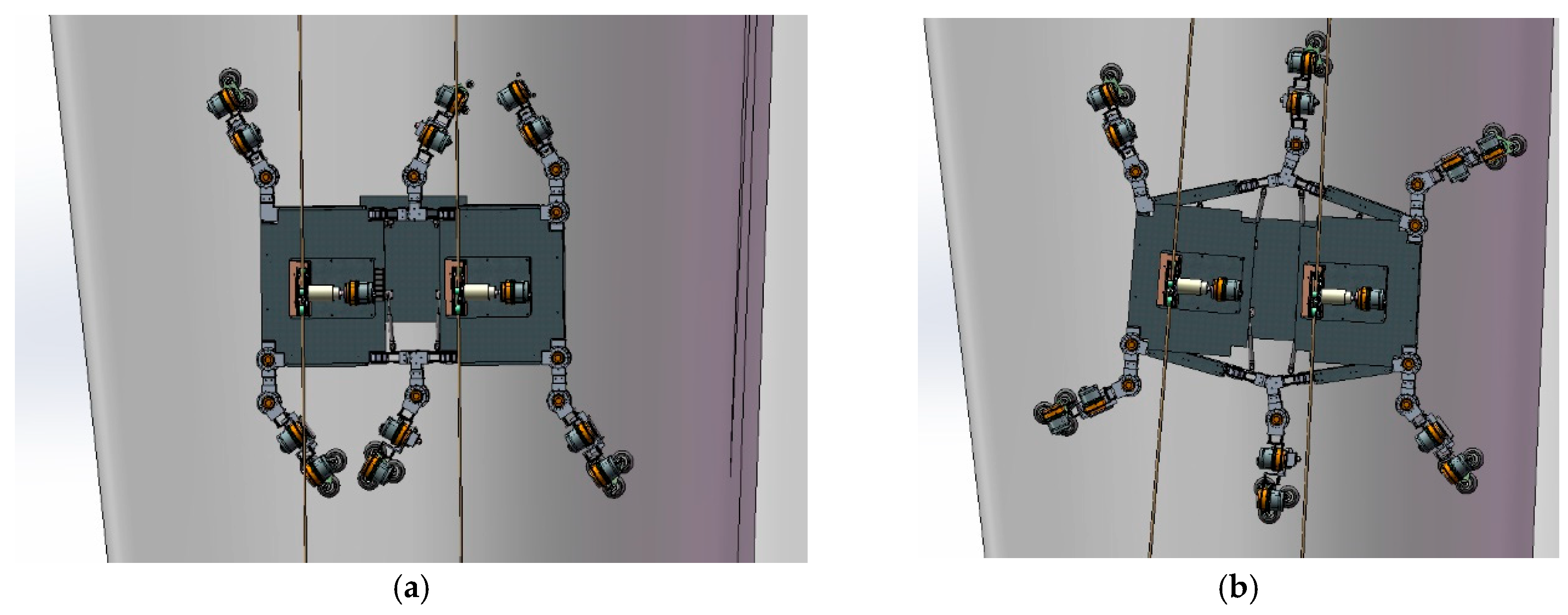
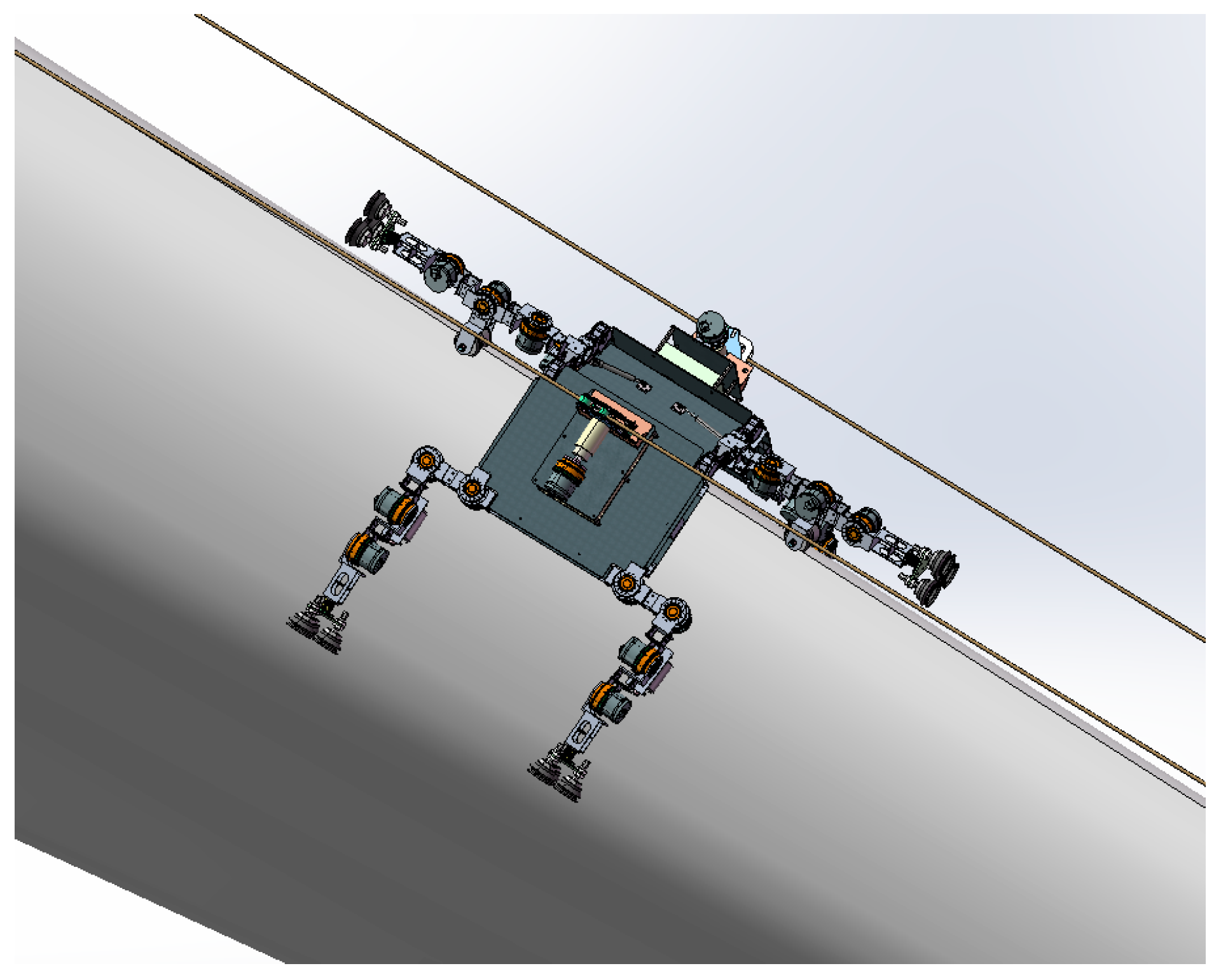
2.1. Structural Design
2.1.1. Design Requirements
2.1.2. Constructive Design
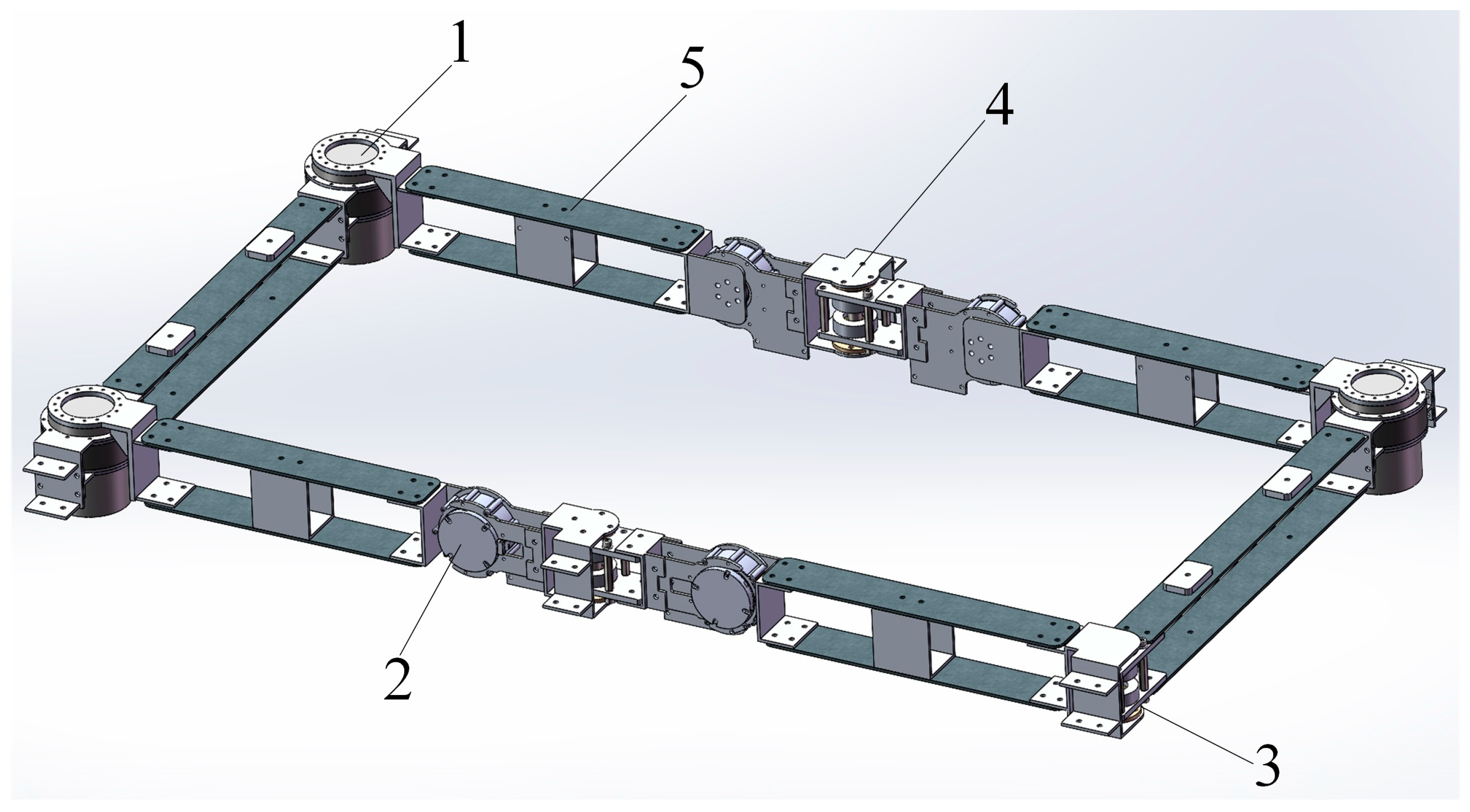
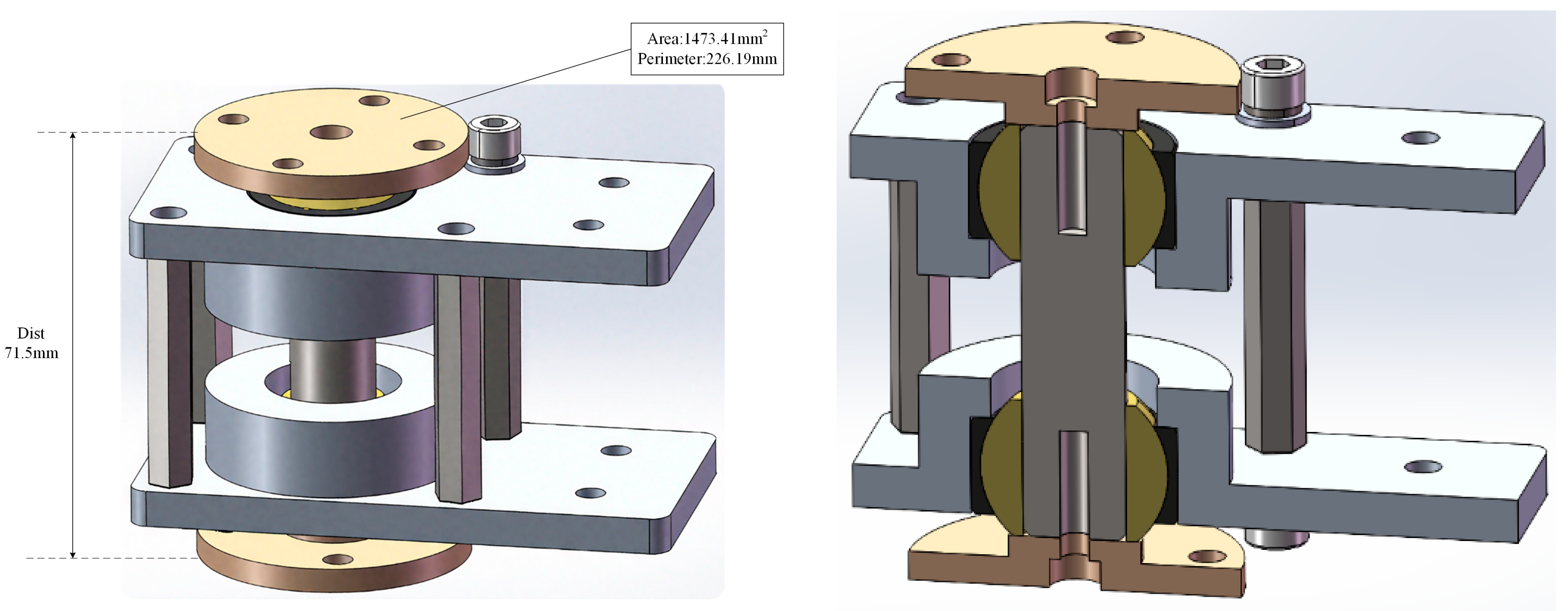
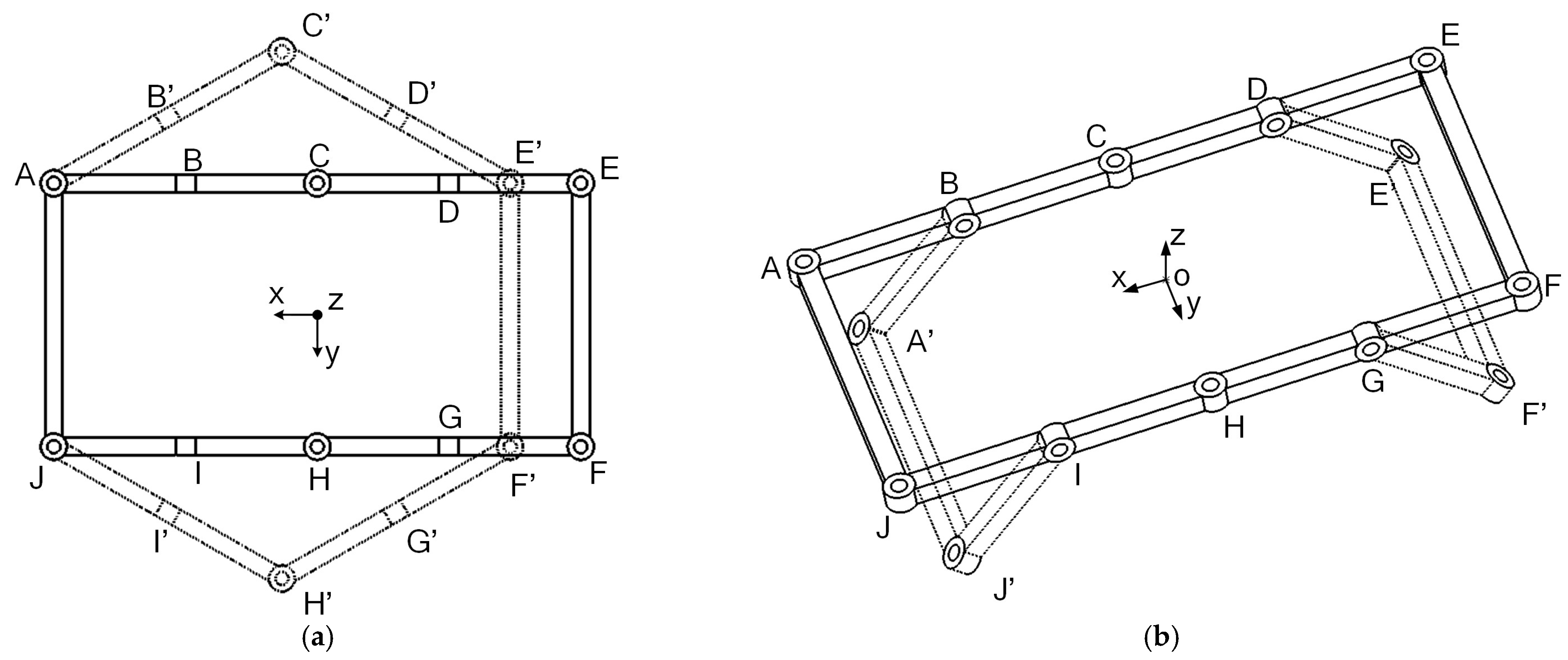
2.1.3. Closed-Loop Folding of the Trunk 10R Folding
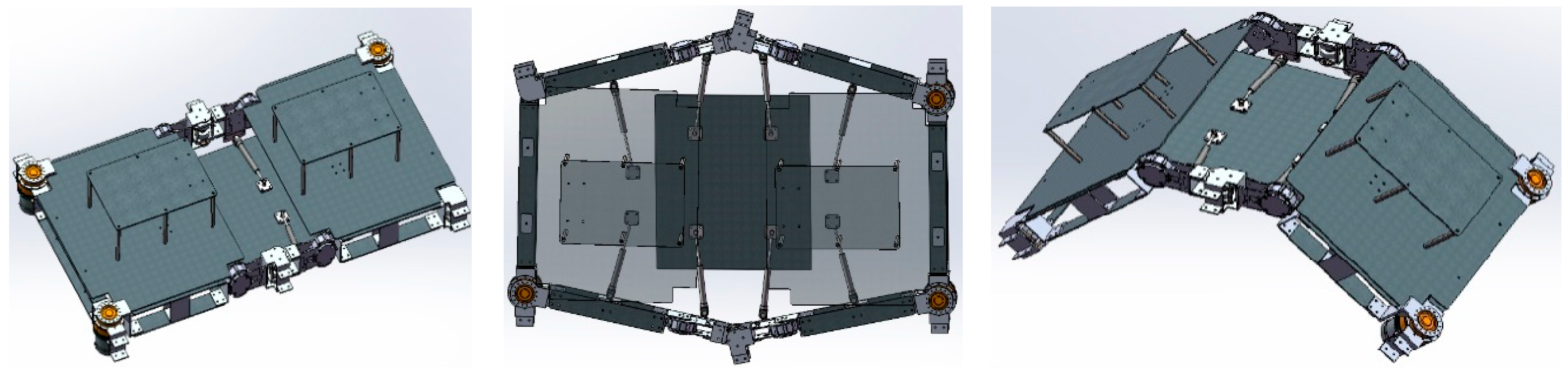
2.1.4. Load Platform Design
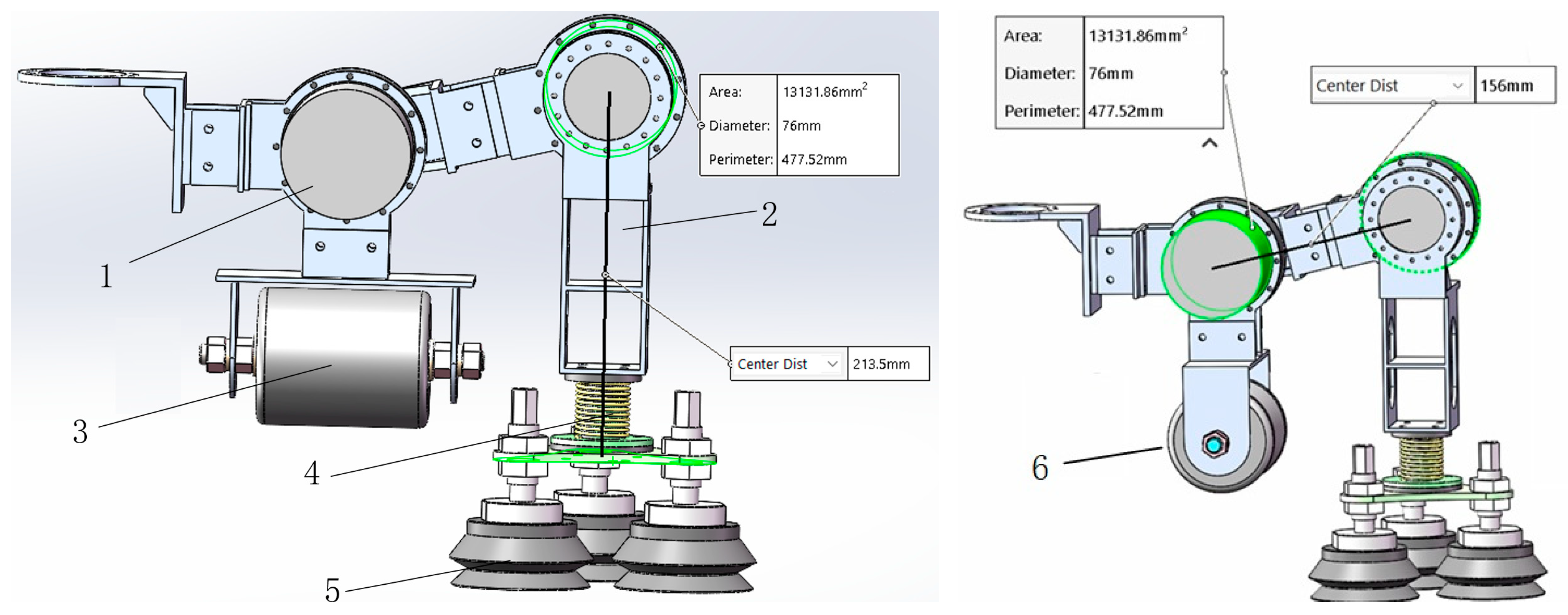
2.1.5. Clamping Leg and Load-Bearing Leg Design
2.1.6. Work Mode Analysis
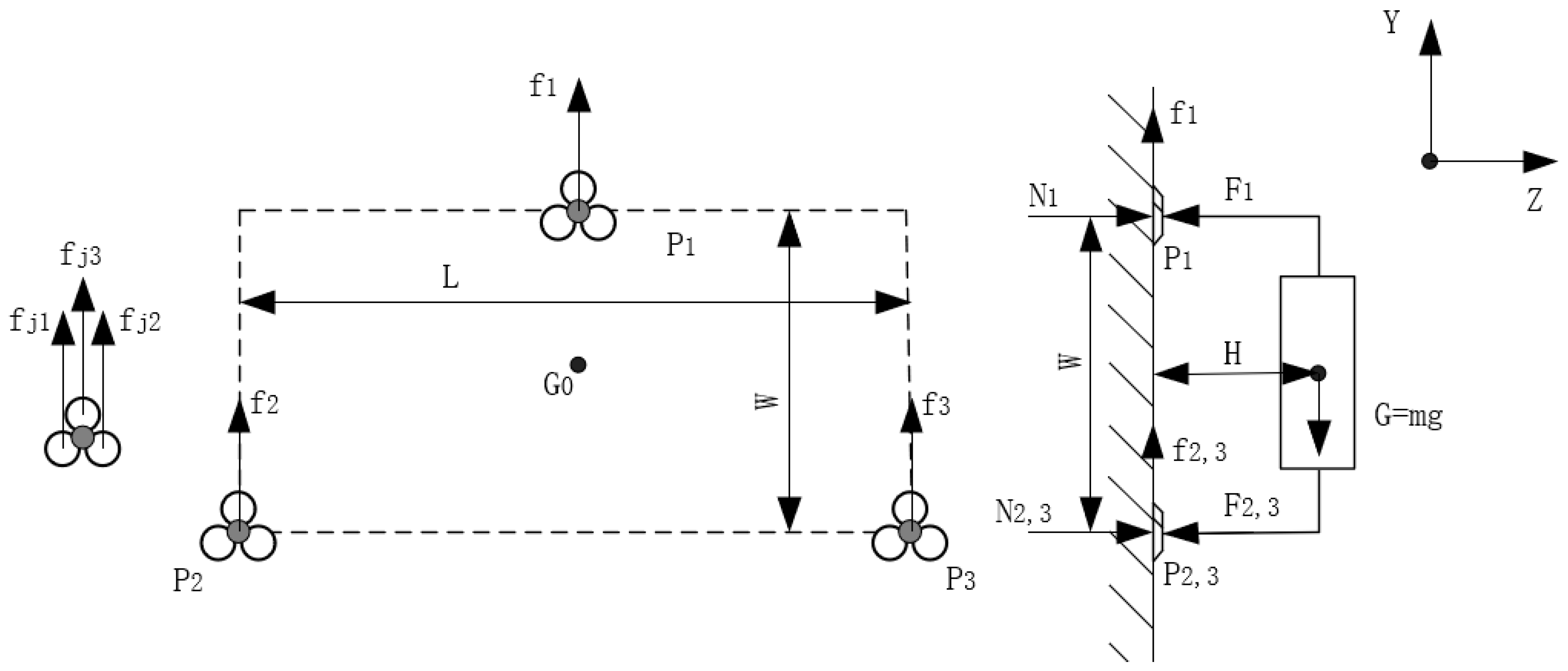
2.1.7. Adsorption Analysis
2.2. Kinematics Modeling
2.2.1. Basic Configuration and D-H Parameter Modeling
2.2.2. Closed-Loop Equations and Degree of Freedom Analysis
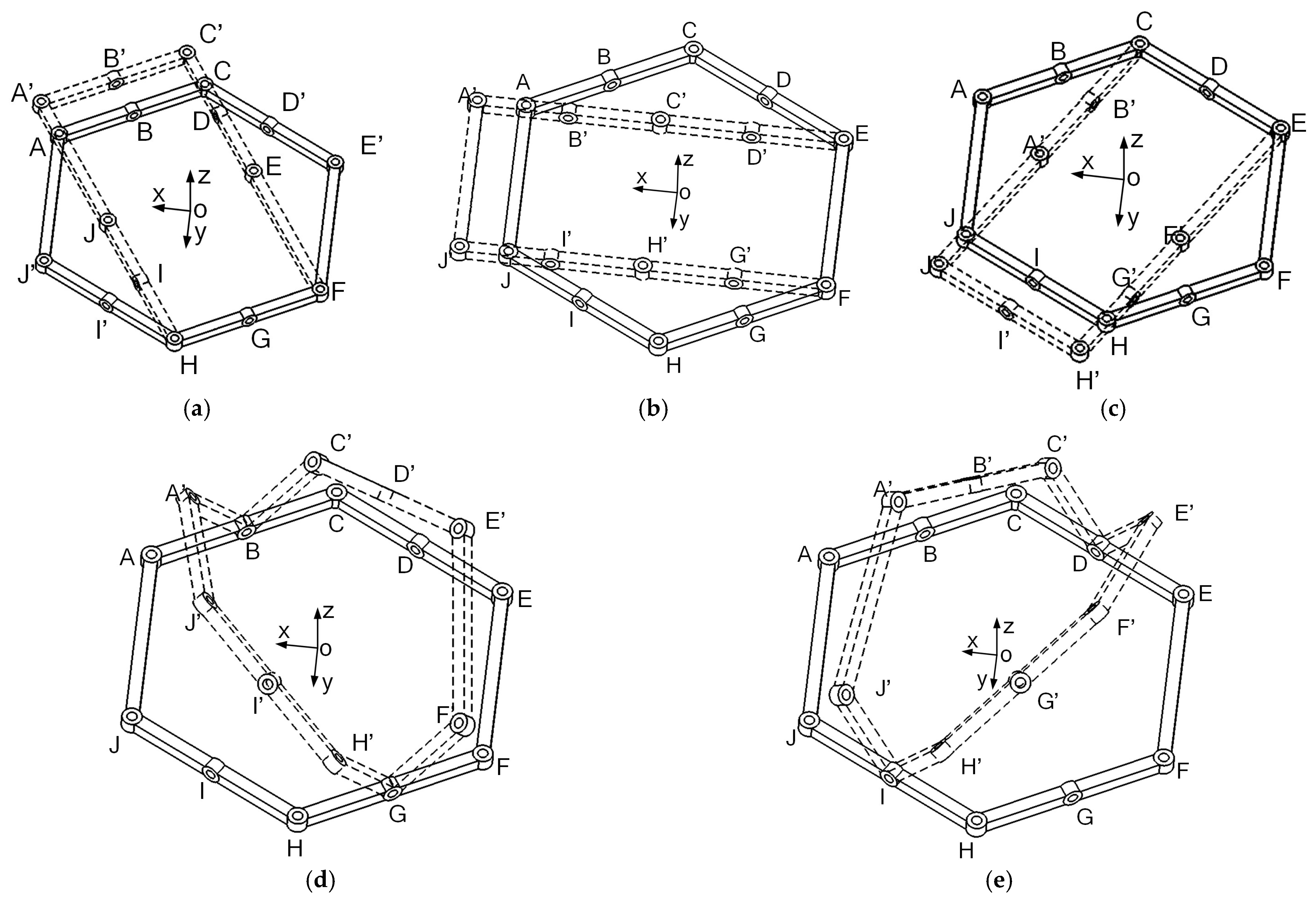
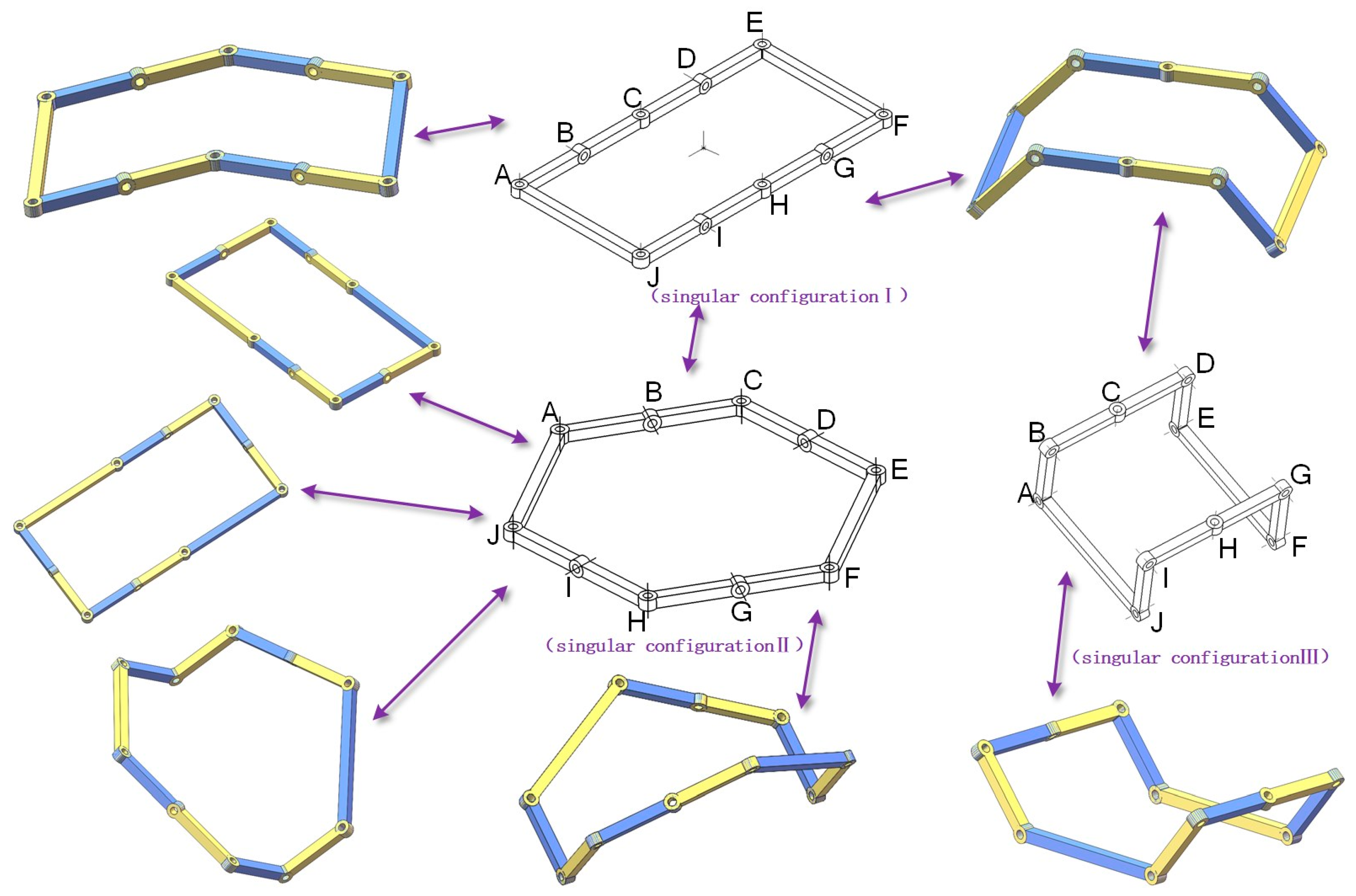
2.3. Higher-Order Kinematic Analysis of Three Types of Singular Configurations
2.3.1. Higher-Order Kinematic Analysis of Singular Configurations I
- (a)
- When , the motion branch 1 of singular configuration I can be obtained, as shown in Figure 14a. This set of solution relationships corresponds to the four rotational pairs B, D, G, and I remaining stationary, while the six rotational pairs A, C, E, F, H, and J rotate. At this point, the mechanism is a planar six-bar mechanism composed of the linkages AC, CE, EF, FH, HJ, and JA, with three DOF.
- (b)
- When , the motion branch 2 of singular configuration I can be obtained, as shown in Figure 14b. In this set of motion states, the six rotating joints A, C, E, F, H, and J remain stationary, the AB, AJ, and IJ links rotate around the BI axis, the DE, EF, and FG links rotate around the DG axis, and the BCD and GHI links remain stationary, with a degree of freedom of 2.
2.3.2. Higher-Order Kinematic Analysis of Singular Configurations II
- (a)
- When , motion branch 1 (Figure 16a) is obtained, as shown in Figure 16a. This set of solution relationships corresponds to the four rotational pairs of joints A, C, E, F, H, and J being fixed in place, the axes of joints B and I coinciding, the axes of joints D and G coinciding, and the links of the mechanism rotating around the BI axis and DG axis, causing the mechanism to unfold in a plane with 2 DOF.
- (b)
- When , motion branch 2 (Figure 16b) is obtained, as shown in Figure 16b. This set of solution relationships corresponds to the rotation pairs B, C, D, G, H, and I remaining stationary, the axes A and E, and the axes D and G coinciding. The links of the mechanism rotate around the axes AE and FJ, causing the mechanism to unfold in the plane, with a degree of freedom of 2.
2.3.3. Higher-Order Kinematic Analysis of Singular Configurations III
- .
- ;
- ;
- (a)
- When , motion branch 1 is obtained, as shown in Figure 18a. This set of solution relationships corresponds to the six rotating pairs B, D, F, G, H, and I being fixed in place, the rotational speeds of pairs A and F being equal, the rotational speeds of pairs C and H being equal, the rotational speeds of E and J being equal, and the sum of the rotational speeds of C and F being equal in magnitude but opposite in direction to the rotational speed of E, and the sum of the rotational speeds of A and H being equal in magnitude but opposite in direction to the rotational speed of J, with 3 DOF.
- (b)
- When , motion branch 2 is obtained, as shown in Figure 18b. This set of solution relationships corresponds to the six rotating pairs B, D, G, I, E, and F being fixed in place, the rotational speeds of rotating pairs A and F being equal, the rotational speeds of rotating pairs C and H being equal, the rotational speeds of E and J being equal, and the sum of the rotational speeds of A and E being equal in magnitude but opposite in direction to the rotational speed of C, and the sum of the rotational speeds of F and J being equal in magnitude but opposite in direction to the rotational speed of H, with 3 DOF.
- (c)
- When , motion branch 3 is obtained, as shown in Figure 18c. This set of solution relationships corresponds to the six rotating pairs B, D, G, I, C, and E being fixed and stationary, the rotational speeds of the rotating pairs A and F being the same, the rotational speeds of the rotating pairs C and H being the same, the rotational speeds of E and J being the same, and the sum of the rotational speeds of E and H being equal in magnitude and opposite in direction to the rotational speed of F, and the sum of the rotational speeds of C and J being equal in magnitude and opposite in direction to the rotational speed of A, with 3 DOF.
- (d)
- When , motion branch 4 is obtained, as shown in Figure 18d. This set of solution relationships corresponds to the eight rotating pairs A, C, D, E, F, H, I, and J being fixed, with the mechanism rotating around the BG joint axis, resulting in 1 degree of freedom.
- (e)
- When , motion branch 5 is obtained, as shown in Figure 18d. This set of solution relationships corresponds to the eight rotating joints A, B, C, E, F, G, H, and J being fixed, with the mechanism rotating around the DI joint axis, resulting in 1 degree of freedom.
2.4. Configuration Switching Analysis
2.4.1. Switch from Singular Configuration I to Singular Configuration II
2.4.2. Switch from Singular Configuration I to Singular Configuration III
3. Prototype Assembly and Experimentation
3.1. Prototype Construction
3.2. Control System Design
3.3. Prototype Configuration Switching Experiment
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, J.; Zhu, Y.; Zhang, P. Review of advancements in wall climbing robot techniques. Frankl. Open 2024, 8, 100148–100156. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Z.; Wu, J.; Wu, H.; Zhang, H. Trajectory Tracking of a Wall-Climbing Cutting Robot Based on Kinematic and PID Joint Optimization. Machines 2025, 13, 229. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, Y.; Liu, H.; Zhong, D. Design and Analysis of a Wheel-Footed Magnetic Adhesion Obstacle-Crossing Wall-Climbing Robot. Trans. Chin. Soc. Mech. Eng. 2024, 60, 248–261. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, H. Design and Analysis of an Adaptive Legged Wall-Climbing Robot. Mech. Des. 2021, 38, 105–112. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Zhang, M.; Sun, L. Design and Analysis of a Modular Flexible Climbing Robot with Adaptive Curvature Facades. J. Mech. Eng. 2021, 57, 10. [Google Scholar] [CrossRef]
- Yang, P.; Zang, J.; Huang, B.; Zhao, J. Electromagnetically Adhering and Self-Inductive Sensing Claw for Continuum Climbing Robots: Design, Control, and Applications. Adv. Intell. Syst. 2025, 7, 2400800. [Google Scholar] [CrossRef]
- Shi, Y.; Gong, Z.; Tao, B.; Yin, Z.; Ding, H. An Active Compliance Adsorption Method for Climbing Machining Robot on Variable Curvature Surface. IEEE/ASME Trans. Mechatron. 2023, 28, 1127–1136. [Google Scholar] [CrossRef]
- Liu, J.-H.; Padrigalan, K.E. The Kinematic Analysis of a Wind Turbine Climbing Robot Mechanism. Appl. Sci. 2022, 12, 1210. [Google Scholar] [CrossRef]
- Padrigalan, K.E.; Liu, J.-H. A Wind-Turbine-Tower-Climbing Robot Prototype Operating at Various Speeds and Payload Capacity: Development and Validation. Appl. Sci. 2023, 13, 1381. [Google Scholar] [CrossRef]
- Liu, J.H.; Padrigalan, K. Design and Development of a Climbing Robot for Wind Turbine Maintenance. Appl. Sci. 2021, 11, 2328. [Google Scholar] [CrossRef]
- Gao, H.; Han, H. Design and Analysis of a Wall-Climbing Robot for Wind Turbines with Wheeled Legs. Mech. Des. 2023, 40, 101–106. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, X.-L.; Wang, K.-M.; Huang, H. Design and Analysis of a Wind Turbine Blade Inspection Robot. J. Eng. Des. 2025, 32, 159–168. [Google Scholar] [CrossRef]
- Chen, D.; Yu, G.; Huang, S. Complete Coverage Path Planning for Wind Turbine Blade Wall-Climbing Robots Based on Bio-Inspired Neural Networks and Energy Consumption Model. Machines 2025, 13, 180. [Google Scholar] [CrossRef]
- Dai, J.S.; Jones, J.R. Mobility in Metamorphic Mechanisms of Foldable/Erectable Kinds. J. Mech. Des. 1999, 121, 375–382. [Google Scholar] [CrossRef]
- Yang, H.; Wei, G.; Ren, L. A Novel Soft Actuator: MISA and Its Application on the Biomimetic Robotic Arm. IEEE Robot. Autom. Lett. 2023, 8, 2373–2380. [Google Scholar] [CrossRef]
- Xu, Y.; Luo, Z.; Shang, J.; Wei, G.; Zhu, Y.; Bai, X. Design and analysis of a concentrated-driven bionic-leg capable of omnidirectional legged locomotion based on 3-Dimensional dual-parallelogram-linkages. Proc. Inst. Mech. Eng. Part C. J. Mech. Eng. Sci. 2024, 238, 459–478. [Google Scholar] [CrossRef]
- Wang, S.; Huang, H.; Jia, G.; Li, B.; Guo, H.; Liu, R. Design of a novel three-limb deployable mechanism with mobility bifurcation. Mech. Mach. Theory 2022, 172, 104789. [Google Scholar] [CrossRef]
- Jia, G.; Huang, H.; Wang, S.; Li, B. Type synthesis of plane-symmetric deployable grasping parallel mechanisms using constraint force parallelogram law. Mech. Mach. Theory 2021, 161, 104330. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, F.; Lv, Y.; Ding, X. Design and analysis of a metamorphic mechanism for automated fibre placement. Mech. Mach. Theory 2018, 130, 463–476. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, W.; Shang, J.; Yi, M.; Wang, S.; Ding, X. A Planar Underactuated Compaction Mechanism with Self-Adaptability for Automated Fiber Placement Heads. Aerospace 2022, 9, 586. [Google Scholar] [CrossRef]
- Suthar, B.; Jung, S. Design and Bending Analysis of a Metamorphic Parallel Twisted-Scissor Mechanism. J. Mech. Robot. 2021, 13, 040901. [Google Scholar] [CrossRef]
- Sun, H.; Sun, W.; Chen, B.; Hou, Y.; Kong, J. Design, Analysis, and Experiment of a Scissor-Shaped Deployable Metamorphic Hand. J. Mech. Robot. 2022, 14, 060909. [Google Scholar] [CrossRef]
- Qin, J.; Yu, C.; Sun, Z.; Cao, L. A Novel Method for Type Synthesis of Parallel Mechanism Without Parasitic Motion Based on 2R1T Parallel Mechanism with Rotational Bifurcation. Chin. J. Mech. Eng. 2022, 35, 191–202. [Google Scholar] [CrossRef]
- An, W.; Wei, J.; Lu, X.; Dai, J.S.; Li, Y. Geometric Design-based Dimensional Synthesis of a Novel Metamorphic Multi-fingered Hand with Maximal Workspace. Chin. J. Mech. Eng. 2021, 34, 41. [Google Scholar] [CrossRef]
- Dong, K.; Li, D.; Xue, X.; Xu, C.; Wang, H.; Gao, X. Workspace and Accuracy Analysis on a Novel 6-UCU Bone-attached Parallel Manipulator. Chin. J. Mech. Eng. 2022, 35, 35. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, K.; Spyrakos-Papastavridis, E.; Dai, J.S. Origaker: A Novel Multi-Mimicry Quadruped Robot Based on a Metamorphic Mechanism. J. Mech. Robot. 2022, 14, 060907. [Google Scholar] [CrossRef]
- Wang, K.; Hou, Y.; Sun, W.; Hou, Y. Multi-posture mechanical analysis of a variable-cell hand-claw climbing robot. Mech. Des. Manuf. 2023, 192–196. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L.; Mei, D.; Tang, G.; Ji, Y.; Tan, K.; Wang, Y. Gait and simulation analysis of quadruped crawling robot based on metamorphic structure. Ind. Robot. Int. J. Robot. Res. Appl. 2023, 51, 91–104. [Google Scholar] [CrossRef]
- Guan, Y.; Zhuang, Z.; Zhang, C.; Tang, Z.; Zhang, Z.; Dai, J.S. Design and Motion Planning of a Metamorphic Flipping Robot. Actuators 2022, 11, 344. [Google Scholar] [CrossRef]
- Han, Y.; Guo, W.; Zhao, D.; Li, Z. Multi-mode unified modeling and operation capability synergistic evaluation for the reconfigurable legged mobile lander. Mech. Mach. Theory 2022, 171, 104714. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, J.; Yang, P.; Cui, T.; Wu, D.; Zhang, L. Modeling and stability control of steering and reconfiguration motion for wheel-legged metamorphic robot. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2025, 239, 4256–4272. [Google Scholar] [CrossRef]




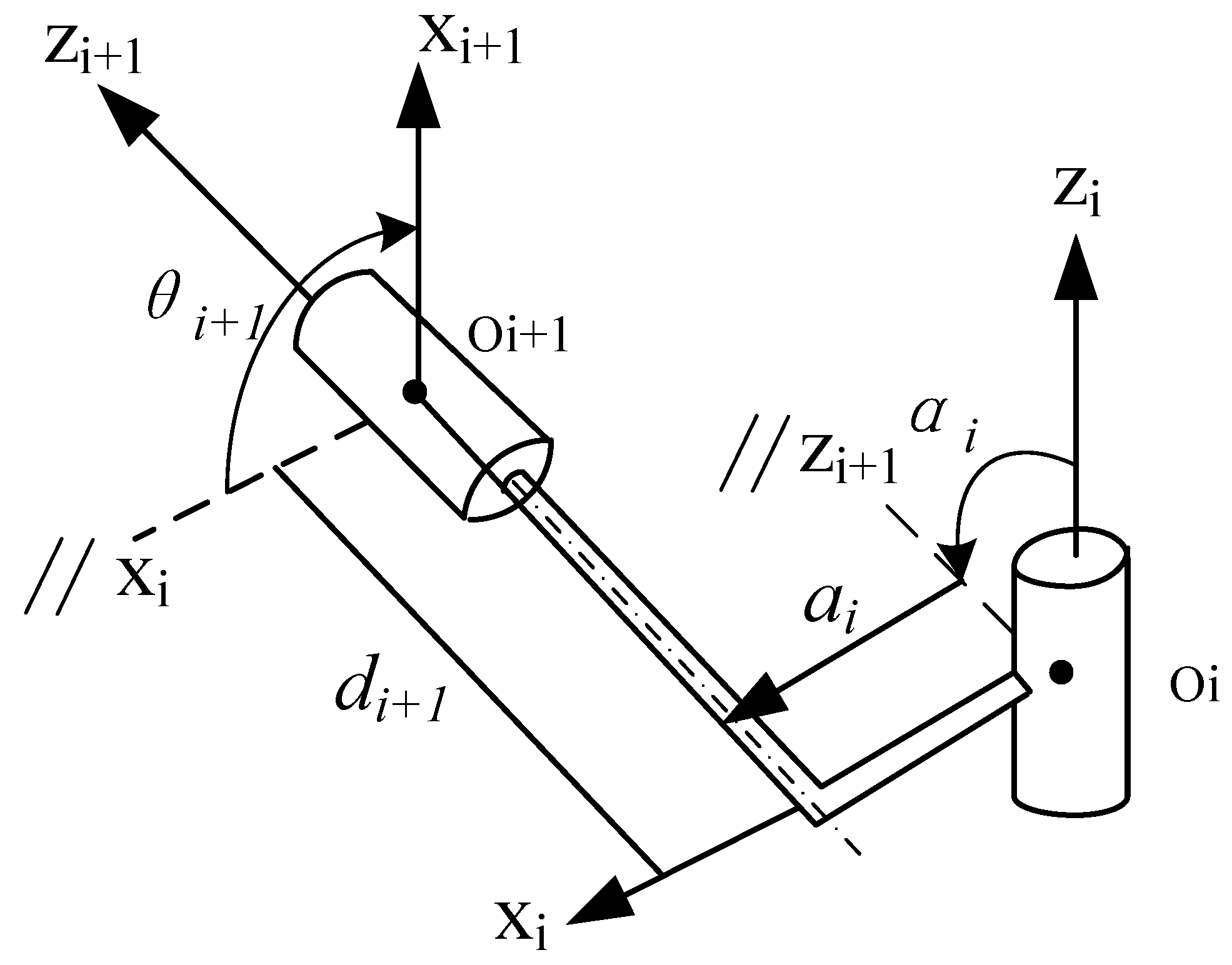



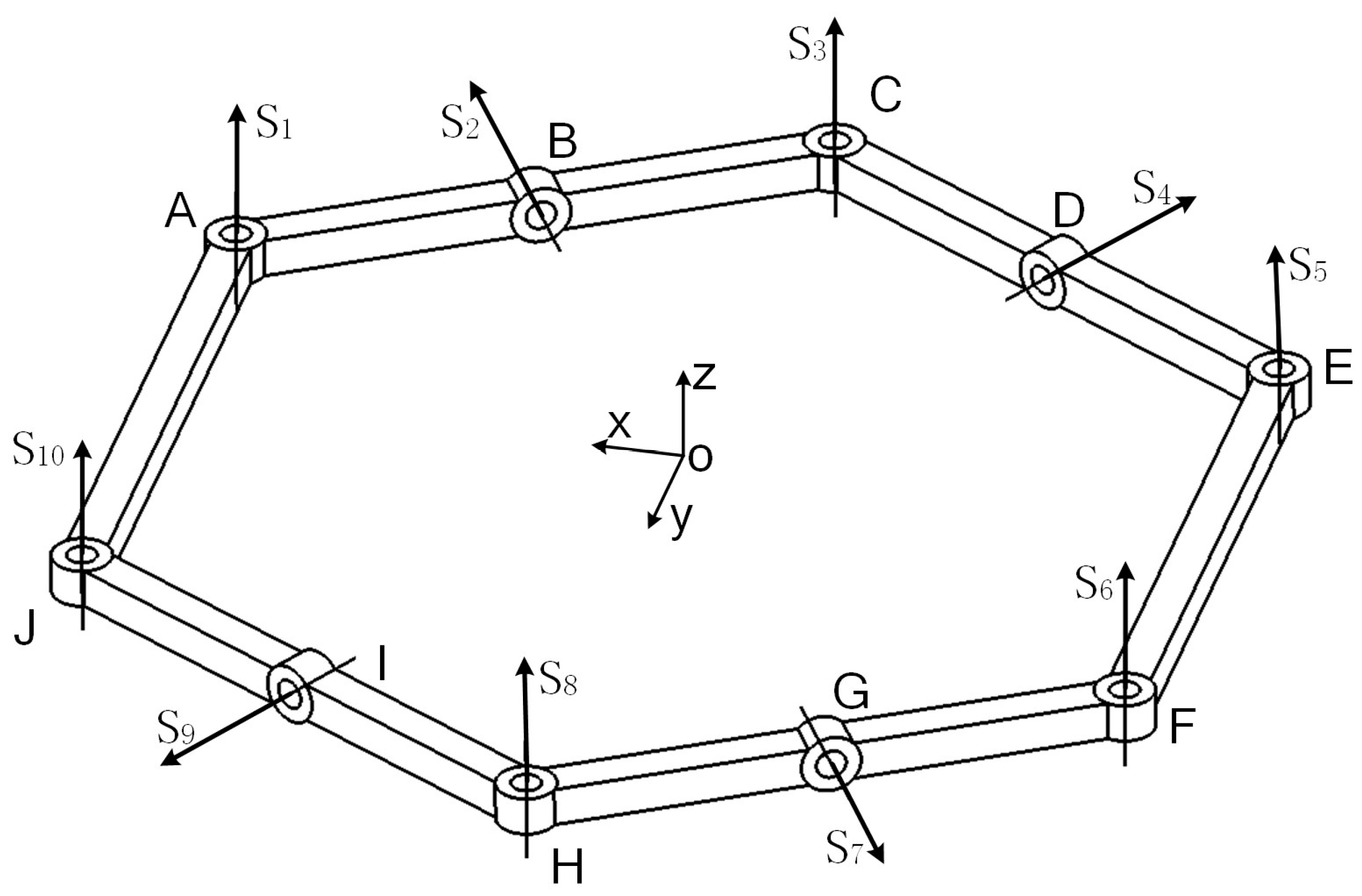

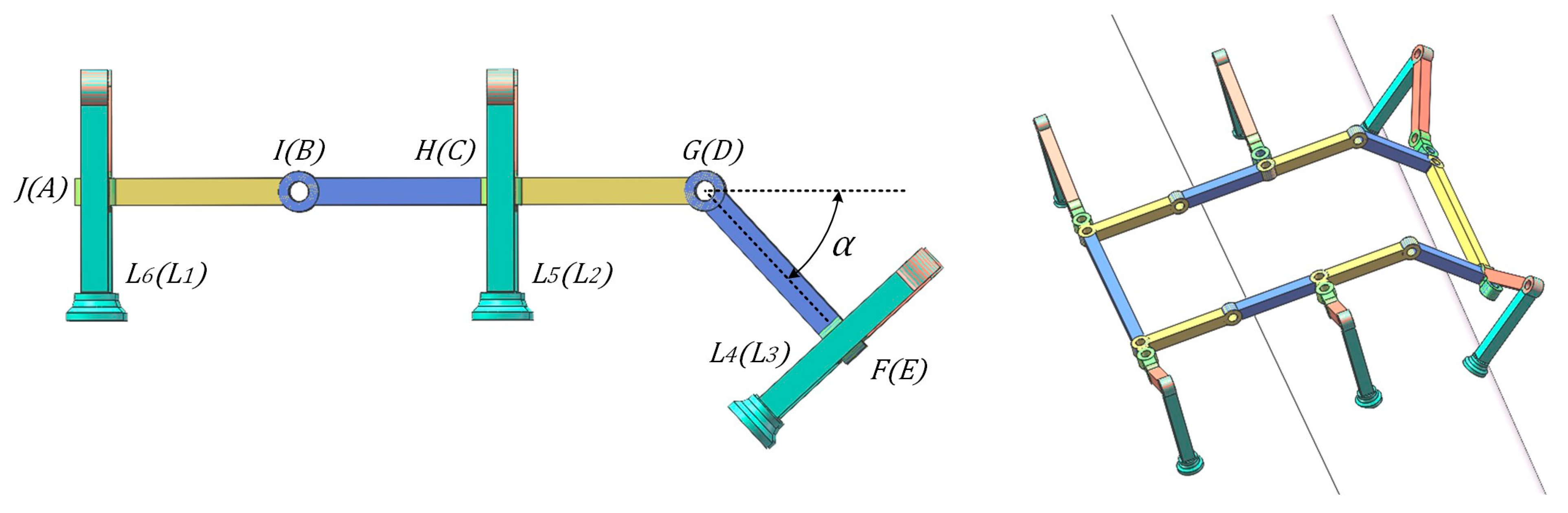
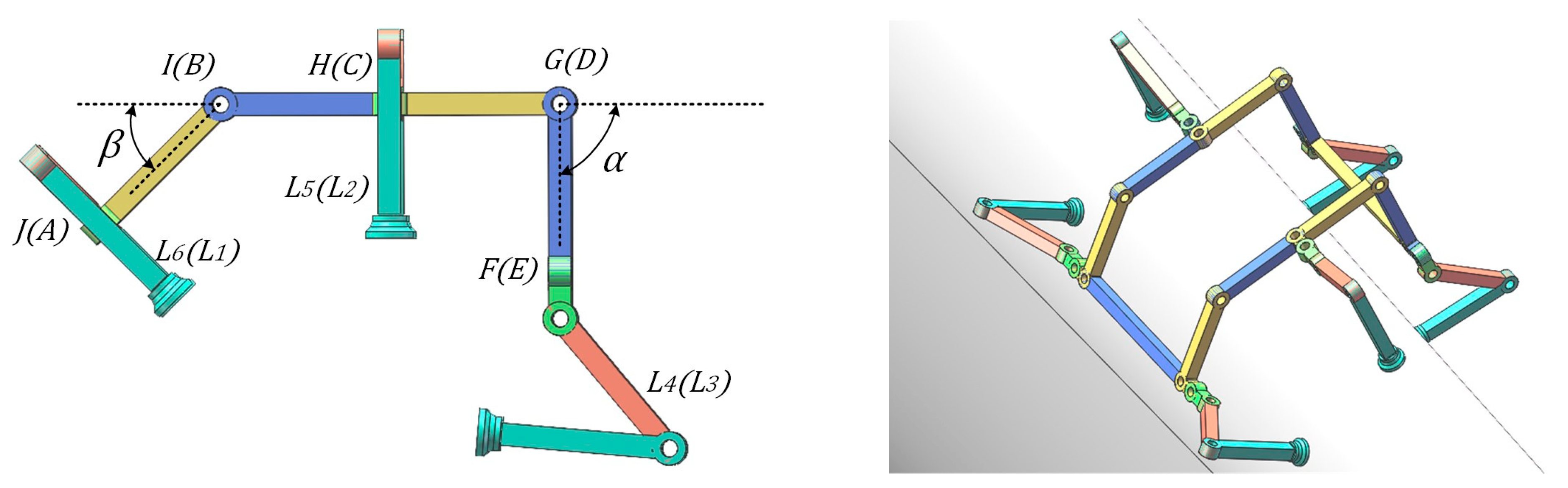
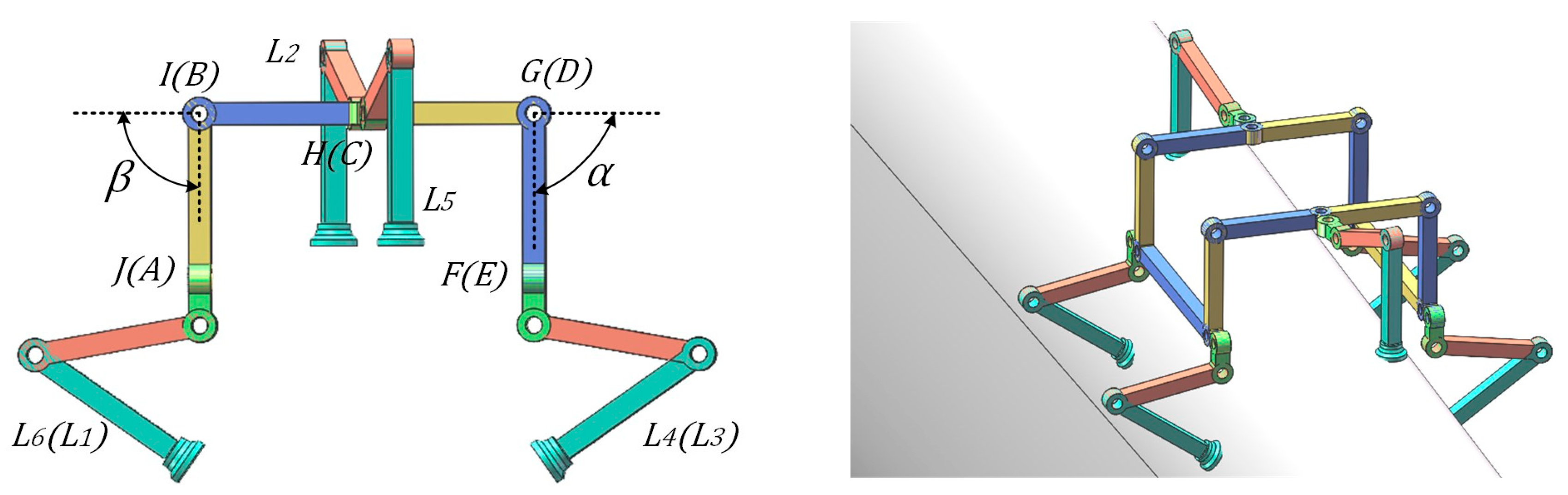







| Joint Pair | a | A | D | Θ |
|---|---|---|---|---|
| 0, 1 | L2 | π/2 | 0 | θ0 |
| 1, 2 | L2 | π/2 | 0 | θ1 |
| 2, 3 | L2 | π/2 | 0 | θ2 |
| 3, 4 | L2 | π/2 | 0 | θ3 |
| 4, 5 | L1 | 0 | 0 | θ4 |
| 5, 6 | L2 | π/2 | 0 | θ5 |
| 6, 7 | L2 | π/2 | 0 | θ6 |
| 7, 8 | L2 | π/2 | 0 | θ7 |
| 8, 9 | L2 | π/2 | 0 | θ8 |
| 9, 0 | L1 | 0 | 0 | θ9 |
| Parameter | Technical Specifications |
|---|---|
| Robot dimensions | 500 mm × 400 mm × 300 mm |
| Weight | 10 kg |
| 30kg servo motor | 11 |
| 60kg servo motor | 12 |
| Servo battery voltage | 11.5 V |
| Load-bearing leg | Leg 2, 5 |
| Clamp legs | Legs 1, 3, 4, 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, X.; Yang, C.; Shao, M.; Lu, H. Design and Kinematic Analysis of a Metamorphic Mechanism-Based Robot for Climbing Wind Turbine Blades. Machines 2025, 13, 808. https://doi.org/10.3390/machines13090808
Shi X, Yang C, Shao M, Lu H. Design and Kinematic Analysis of a Metamorphic Mechanism-Based Robot for Climbing Wind Turbine Blades. Machines. 2025; 13(9):808. https://doi.org/10.3390/machines13090808
Chicago/Turabian StyleShi, Xiaohua, Cuicui Yang, Mingyang Shao, and Hao Lu. 2025. "Design and Kinematic Analysis of a Metamorphic Mechanism-Based Robot for Climbing Wind Turbine Blades" Machines 13, no. 9: 808. https://doi.org/10.3390/machines13090808
APA StyleShi, X., Yang, C., Shao, M., & Lu, H. (2025). Design and Kinematic Analysis of a Metamorphic Mechanism-Based Robot for Climbing Wind Turbine Blades. Machines, 13(9), 808. https://doi.org/10.3390/machines13090808






