Intelligent Fault Diagnosis for Cross-Domain Few-Shot Learning of Rotating Equipment Based on Mixup Data Augmentation

Abstract

Existing fault diagnosis methods assume the identical distribution of training and test data, failing to adapt to source–target domain differences in industrial scenarios and limiting generalization. They also struggle to explore inter-domain correlations with scarce labeled target samples, leading to poor convergence and generalization. To address this, our paper proposes a cross-domain few-shot intelligent fault diagnosis method based on Mixup data augmentation. Firstly, a Mixup data augmentation method is used to linearly combine source domain and target domain data in a specific proportion to generate mixed-domain data, enabling the model to learn correlations and features between data from different domains and improving its generalization ability in cross-domain few-shot learning tasks. Secondly, a feature decoupling module based on the self-attention mechanism is proposed to extract domain-independent features and domain-related features, allowing the model to further reduce the domain distribution gap and effectively generalize source domain knowledge to the target domain. Then, the model parameters are optimized through a multi-task learning mechanism consisting of sample classification tasks and domain classification tasks. Finally, applications in classification tasks on multiple sets of equipment fault datasets show that the proposed method can significantly improve the fault recognition ability of the diagnosis model under the conditions of large distribution differences in the target domain and scarce labeled samples.

1. Introduction

As a core component of the modern industrial system, rotating machinery holds an irreplaceable position in strategic industries such as high-end manufacturing, aerospace, and fine chemicals [1,2,3], with its operational status directly affecting the stability and safety of production systems. Many of the degradation processes of bearings and gears, key components of rotating machinery, stem from friction phenomena at component interfaces, a process that often manifests as a vicious cycle of friction–wear–lubrication failure [4,5]. Intensified friction accelerates the wear rate, while metal debris from wear further contaminates the lubricant, impairs lubrication effectiveness, and in turn, exacerbates friction [6,7]. This cumulative damage gradually weakens the load-carrying capacity and operational precision of the components, ultimately leading to various faults, such as bearing seizure and gear tooth breakage, and posing a serious threat to the safe and stable operation of rotating machinery.

In the context of the intelligent transformation of equipment, equipment reliability has emerged as a pivotal indicator for gauging the level of industrialization [8,9]. In accordance with this trend, the construction of an active maintenance system based on condition monitoring bears particular strategic significance. Through the precise identification of abnormal operational characteristics of machinery and the establishment of a preventive maintenance mechanism, not only can this system effectively prevent major safety accidents, but it also serves as a crucial technical approach to achieve the full life-cycle management of equipment [10,11]. It is noteworthy that intelligent fault diagnosis technology, as the core module of predictive health management, has evolved into a key element in ensuring the safe operation of industry [12,13]. Traditional intelligent fault diagnosis methods, such as artificial neural networks, support vector machines, and random forests, are highly dependent on manual extraction of fault features. These methods exhibit problems such as low efficiency, strong subjectivity, and complex feature engineering, and their generalization ability is limited when dealing with high-dimensional data [14,15]. With the development of deep learning, these methods can leverage the capabilities of automatic learning and feature extraction to overcome experience-based limitations. It mines the relationship between fault features and categories from massive data, providing more efficient and accurate decision-making support for fault identification. Therefore, deep learning has been increasingly widely applied in the field of fault diagnosis [16]. Ding et al. [17] proposed a time–frequency transformer model, which significantly improved the accuracy and robustness of fault diagnosis by capturing global and local features from the time–frequency representations of vibration signals. Li et al. [18] proposed a data-driven method based on a deep convolutional neural network (CNN), which took normalized monitoring data as input and constructed samples through time windows to realize the estimation of the remaining useful life of the system. Xu et al. [19] introduced a multi-scale coarse-graining process with continuous sliding window operations and a feature attention mechanism to process raw vibration signals, which can significantly enhance diagnostic accuracy under complex working conditions. Wang et al. [20] proposed a multi-modal fusion method based on a one-dimensional CNN by fusing vibration and acoustic data, which can achieve high-precision diagnostic results superior to single-modal sensor methods in low signal-to-noise ratio environments. Niu et al. [21] proposed an approach that, by fusing multi-source vibration data with domain knowledge graphs and introducing channel attention modules, as well as non-local attention modules, achieved multi-task bearing fault diagnosis.

In the field of industrial fault diagnosis, deep learning-based methods are widely favored for their strong ability to perform automatic feature extraction. However, these approaches are highly reliant on massive datasets to guarantee model performance and generalization [22,23,24]. In practical industrial scenarios, obtaining sufficient data samples is extremely difficult, which is mainly attributed to factors such as safety restrictions on key equipment and the long cycle of fault evolution. This data scarcity leads to the insufficient robustness of deep learning models when dealing with complex fault states, making few-shot learning a crucial breakthrough. By utilizing technologies like meta-learning and transfer learning, few-shot learning can achieve efficient learning with a small number of samples, significantly reducing the reliance on data scale [25,26,27].

However, in industrial environments, data distributions vary significantly between different devices and operating conditions. Even with the adoption of few-shot learning, traditional methods still fail to handle the problem of mismatched feature distributions in cross-domain data. To address this issue, cross-domain few-shot learning has emerged. It not only inherits the characteristic of few-shot learning, i.e., low dependence on the number of samples, but also effectively bridges the gaps in cross-domain data distribution through techniques such as domain adaptation. As a result, it provides a more universal solution for complex and changing industrial fault diagnosis scenarios [28,29]. Chai et al. [30] proposed a fault prototype adaptive network that learned representative fault prototypes through an identification module based on similarity learning and designed a fault prototype adaptive module to adapt multiple fault prototypes to the target dataset, thereby realizing cross-domain fault diagnosis. Zhang et al. [31] proposed a domain-adaptive meta-learning network with a feature-oriented dropping-supplementing module, which solved problems such as severe domain distribution differences, mismatched label spaces, and scarce labeled samples within a unified framework. Wang et al. [32] proposed a cross-domain few-shot learning method for fault diagnosis, which combined the attention mechanism and 1D CNN, aligning the distribution of the source domain and the target domain through sub-domain adaptation to realize fault state recognition. Tian et al. [33] proposed a deep feature transfer fusion framework based on hybrid domain transfer learning, which transferred data features from the source domain to the target domain to solve the problem that some few-shot working conditions were difficult to diagnose due to the small amount of data in actual industrial processes.

In cross-domain few-shot learning tasks, although both source domain and target domain data are labeled, a huge difference in feature distribution exists between them. This causes the model trained on source domain data to suffer from severe limitations in generalization ability when dealing with target domain data with such large distribution differences [34]. Moreover, when labeled samples in the target domain are scarce, existing methods struggle to fully explore the potential correlations between the source domain and target domain, resulting in the model being unable to achieve effective convergence and good generalization. As a data augmentation method based on linear interpolation, Mixup generates new training samples by linearly combining two training samples. This method can effectively expand the diversity of training samples, thereby reducing the model’s dependence on the original labeled samples. In addition, the feature distribution of samples generated by Mixup through linear interpolation lies between the original samples, which effectively alleviates the problem of feature distribution differences between different domains.

As an effective data augmentation method, Mixup has spawned multiple variant structures in various fields and has been widely applied. For instance, Campbell et al. [35] proposed a Mixup augmentation method based on facial keypoints, which significantly enhanced the ability of deep learning models to recognize facial phenotypes of rare genetic diseases, especially showing outstanding performance regarding diseases not present in the training set. Zhang et al. [36] proposed the Self-Mixup mechanism. This mechanism shifts Mixup from the cross-sample level to the intra-sample level by applying two independent augmentations to the same image to generate heterogeneous perspectives and performing Beta-distribution-based linear interpolation of their feature maps at any intermediate layer of the network, thereby synthesizing pseudo-new samples in the feature space. Compatible with traditional manifold Mixup, this mechanism can improve knowledge utilization with limited samples without external data. Zhang et al. [37] enhanced the support set by linearly interpolating query samples with same-class support samples via Mixup and combined this with bidirectional feature reconstruction, effectively mitigating the support–query bias in few-shot fine-grained classification. Xiao et al. [38] proposed a cross-modal image–text Mixup method, termed MMIT-Mixup, and coupled it with robustness-invariance fine-tuning to form the semantic-guided robustness tuning framework. By leveraging textual features as domain-invariant semantic guidance and performing Mixup at intermediate layers of the Vision Transformer (ViT) [39], this method markedly improved the robustness and generalization of large-scale pre-trained models under extreme domain shifts and few-shot settings. On this basis, relevant studies applying Mixup to cross-domain few-shot tasks have also emerged. For example, Cao et al. [40] innovatively transferred Mixup to the style statistics level for the cross-domain few-shot action recognition task, which involved adversarial mixing of channel-level mean and variance. This significantly bridged the style gap between domains and effectively improved the recognition accuracy of the target domain. Zhuo et al. [41] proposed the target-guided dynamic Mixup framework, including the Mixup-3T classification network and dynamic ratio generation network. They used a bi-level meta-learning strategy for training to adapt to the target domain and current model state, aiming to solve the problems of narrowing the domain gap and knowledge transfer.

However, to date, there has been no research that applies Mixup to the task of mechanical equipment fault diagnosis in cross-domain few-shot scenarios by focusing on the characteristics of mechanical equipment condition monitoring signals. Therefore, this paper applies Mixup to cross-domain few-shot learning and proposes an intelligent fault diagnosis method for cross-domain few-shot learning based on Mixup data augmentation. In this paper, the Mixup data augmentation approach is firstly formulated to mix source domain and target domain data in a specific proportion, constructing mixed-domain data for training. This helps the model better generalize across different domains and improves its performance on the target domain dataset. Secondly, a self-attention-based feature de-coupling module is used to separate domain-independent and domain-related features, further alleviating the problem of domain distribution differences in cross-domain few-shot learning. Then, a multi-task learning mechanism consisting of sample classification tasks and domain classification tasks is employed to further optimize the network model parameters. Finally, in the experimental verification section, the proposed fault diagnosis method based on cross-domain few-shot learning is verified on both laboratory bearing datasets and multiple sets of public data.

2. Theory of Mixup Data Augmentation

Since the proposed method is built on Mixup data augmentation, this section reviews the basic theory of this technique.

Mixup, a computer vision data augmentation method proposed in ICLR 2017 [42], generates new training data by linearly interpolating and fusing the features and labels of multiple samples. The core of Mixup data augmentation technology lies in the weighted combination of input data and labels, prompting the model to learn the smooth transition characteristics between samples, thereby enhancing the generalization performance of the model. Compared with traditional data augmentation techniques, such as rotation, cropping, and flipping, which generate new samples of the same category through geometric transformations, Mixup constructs continuous data manifolds in the feature space. The generated virtual samples not only fill the gaps in the original data distribution but also effectively suppress the phenomenon of overconfidence in prediction at category boundaries through the soft label mechanism.

From the perspective of risk minimization, the optimization of machine learning models often takes Empirical Risk Minimization (ERM) as the core idea—approximating generalization performance by minimizing the average loss of the model on limited training samples. However, ERM only focuses on the local behavior of samples, which easily leads to the model overfitting to the data. This problem becomes more prominent when the scale of model parameters is close to the amount of data.

To alleviate the limitations of ERM, Vicinal Risk Minimization (VRM) attempts to expand training data by constructing a vicinal distribution to generate virtual samples. At its core, it uses the vicinal distribution to measure the probability of finding virtual feature–target pairs within the neighborhood of training feature–target pairs, and then optimizes the model by minimizing the empirical vicinal risk.

The virtual samples generated by the Mixup technique actually construct a vicinal distribution, thereby achieving VRM for the model. Specifically, Mixup can be regarded as a VRM method, and its mathematical expression is as follows [42]:

$$\mu \left(a^{\prime },b^{\prime }\left|a_i,b_i\right.\right)={\displaystyle \frac{1}{n}}\sum _j^n{E}_{\lambda }\left[\delta \left(a^{\prime }=\lambda a_i+\left(1-\lambda \right)a_j,b^{\prime }=\lambda b_i+\left(1-\lambda \right)b_j\right)\right]$$

(1)

$$\mathrm{\lambda }\sim \mathrm{B}\mathrm{e}\mathrm{t}\mathrm{a}\left(\alpha ,\alpha \right)$$

(2)

where the hyperparameter $\alpha \in \left(0,\infty \right)$ determines the shape characteristics of the Beta distribution, thereby influencing the probability distribution features of the mixing coefficient $\mathrm{\lambda }$. $E_{\lambda }$ denotes the expectation operator with respect to the parameter $\mathrm{\lambda }$.$\left(a_i,b_i\right)$ and $\left(a_j,b_j\right)$ represent two feature–target pairs selected from the original dataset, and $\left(a^{\prime },b^{\prime }\right)$ represents a virtual feature–target pair.

When $\alpha \to 0$, Mixup degenerates to ERM as λ approaches 0 or 1. At $\alpha =1$, $\mathrm{\lambda }$ follows a uniform distribution over [0, 1]. When $\alpha >1$, the Beta distribution peaks at 0.5, concentrating $\mathrm{\lambda }$ values around 0.5 and producing equal-weight fusions. In short, Mixup generates virtual feature–target pairs by randomly selecting two labeled samples $\left(a_i,b_i\right)$ and $\left(a_j,b_j\right)$:

$$a^{\prime }=\lambda a_i+\left(1-\lambda \right)a_j$$

(3)

$$b^{\prime }=\lambda b_i+\left(1-\lambda \right)b_j$$

(4)

Its core assumption is that the linear interpolation of feature vectors should lead to the linear interpolation of targets. In general, Mixup constructs a vicinal distribution through linear interpolation, enabling the model to exhibit linear behavior in the interpolation region between training samples. This linear behavior not only reduces the prediction oscillation of the model outside the training samples but also provides the model with a simpler inductive bias, which helps to improve the generalization performance of the model. Additionally, a key characteristic of Mixup is its implicit control over model complexity. As the interpolation intensity increases, the training error on real data may rise, but the generalization error decreases significantly. This indicates that Mixup effectively balances the bias-variance trade-off by introducing virtual samples, thus implicitly regulating model complexity.

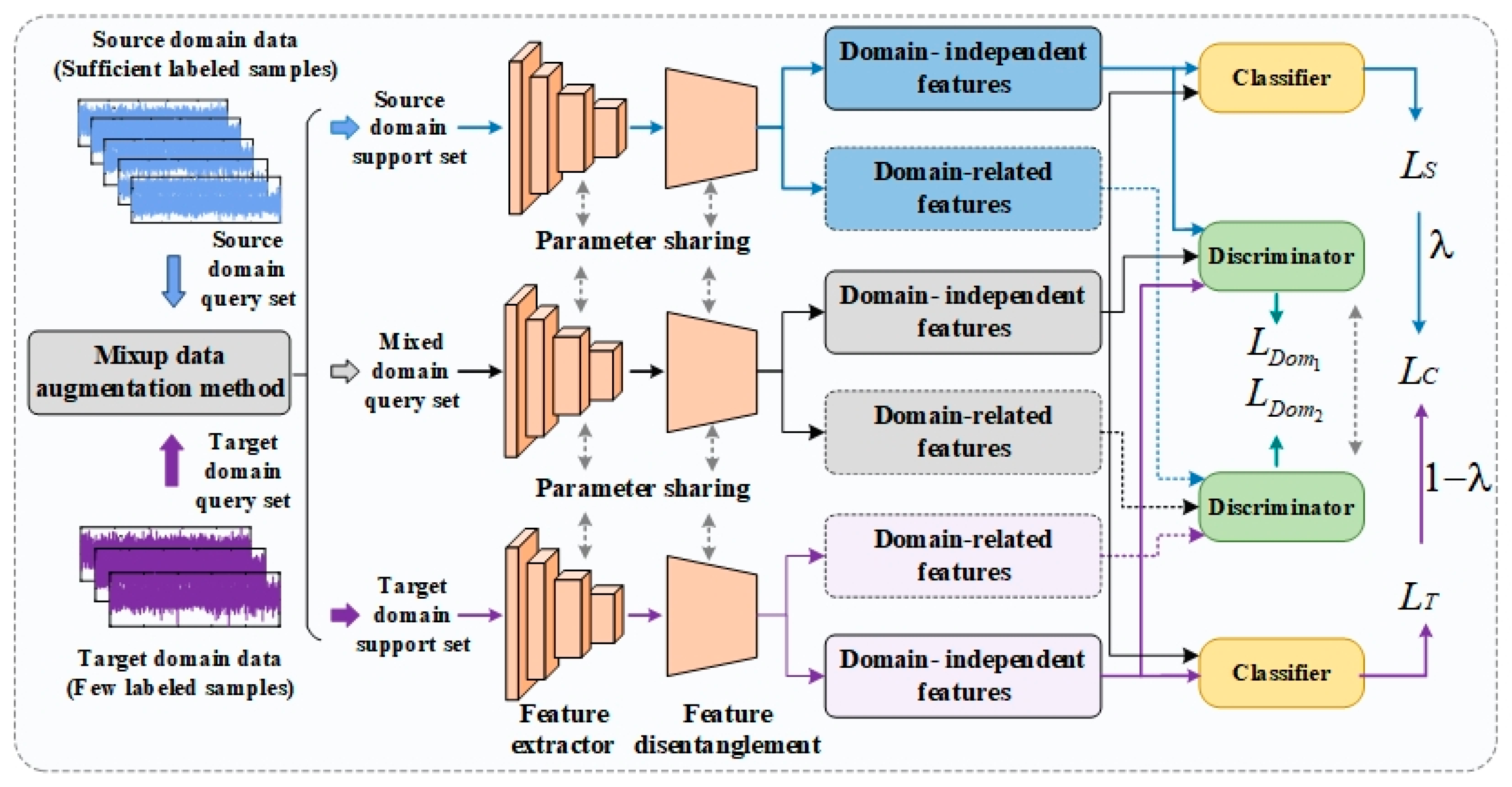
3. Cross-Domain Few-Shot Intelligent Fault Diagnosis Model Based on Mixup Data Augmentation

3.1. Overall Framework of the Proposed Method

In the intelligent fault diagnosis framework based on cross-domain few-shot learning proposed in this paper, the source domain dataset with sufficient labeled samples is defined as $D_S=\left\{\right(x_i^s,p_i^s){\}}_{i=1}^{n_s}$. Among them, $x_i^s\in R^N$ represents the i-th group of labeled samples in the source domain, N denotes the length of each group of labeled samples in the source domain, $p_i^s\in C_S$ stands for the label information of the i-th labeled sample in the source domain, and $n_S$ indicates the number of groups of source domain samples. The target domain dataset with a small number of labeled samples is defined as $D_T=\left\{\right(x_i^t,p_i^t){\}}_{i=1}^{n_t}$. Here, $x_i^t\in R^N$ represents the i-th group of labeled samples in the target domain, $p_i^t\in C_T$ denotes the label information of the i-th labeled sample in the target domain, and the number of groups of labeled samples in the target domain is much smaller than that in the source domain, i.e., $n_T\ll n_S$. Compared with traditional deep learning methods [14,15,17,18,19,20,21,26], where $D_S$ and $D_T$ are sampled from the same domain, the feature distributions of $D_S$ and $D_T$ in this study show significant differences. That is to say, this study attempts to identify the health status of target domain samples by means of the fault knowledge obtained from source domain samples under the conditions of severe domain distribution differences between the source domain and the target domain, as well as the scarcity of labeled samples in the target domain.

The overall framework of the proposed intelligent fault diagnosis method based on cross-domain few-shot learning is illustrated in Figure 1. This framework leverages the Mixup data augmentation technique to generate diverse training samples and enhances the model’s cross-domain generalization capability through dual-domain collaborative training. Specifically, the process is as follows:

First, two task sets (i.e., the query set and the support set) are randomly sampled from the source domain dataset and target domain dataset, respectively. The Mixup data augmentation method is employed to perform linear interpolation on the source domain query set and target domain query set at a certain ratio, thereby generating a new mixed-domain query set, while the original support sets of both domains remain unchanged.

Second, the domain-independent features and domain-related features from the source domain support set, target domain support set, and mixed-domain query set are extracted via a feature extractor and a self-attention mechanism-based feature decoupling module.

Finally, model parameters are optimized through a multi-task loss function mechanism composed of sample classification tasks and domain classification tasks, with the utilization of the domain-independent and domain-related features derived from the source domain support set, target domain support set, and mixed-domain query set.

In the subsequent sections, the main components of the proposed method, namely the Mixup data augmentation method, the feature decoupling module, and the network parameter update method, will be introduced in detail.

3.2. Mixup Data Augmentation Method

Since the source domain data and target domain data are derived from different devices, severe domain distribution differences exist between them. To alleviate this issue, this paper employs the Mixup data augmentation method to linearly combine the sample features of the source domain and target domain at a certain ratio. By making full use of these two datasets, mixed-domain training samples are generated. Specifically, during the model training process, support sets and query sets are randomly sampled and generated from the source domain dataset and target domain dataset, respectively, namely the source domain support set $D_{support}^S=\left\{\right(x_i^s,p_i^s){\}}_{i=1}^K$, query set $D_{query}^S=\left\{\right(x_i^s,p_i^s){\}}_{i=1}^M$, target domain support set $D_{support}^T=\left\{\right(x_i^t,p_i^t){\}}_{i=1}^K$, and query set $D_{query}^T=\left\{\right(x_i^t,p_i^t){\}}_{i=1}^M$. The source domain query set and target domain query set are linearly combined proportionally to form a mixed-domain query set $D_{query}^{mix}=\left\{\right({\stackrel{̑}{x}}_i^{mix}){\}}_{i=1}^M$. Therefore, the samples in the mixed-domain query set contain both source domain features and target domain features. It is worth noting that the Mixup data augmentation method used in this paper only acts on the samples of the source domain query set and target domain query set, and it does not mix the labels. Its specific expression is as follows:

$$D_{query}^{mix}=\lambda D_{query}^S+\left(1-\lambda \right)D_{query}^T$$

(5)

where the ratio $\lambda \in \left[\mathrm{0,1}\right]$ is generated from the $\mathrm{B}\mathrm{e}\mathrm{t}\mathrm{a}\left(\alpha ,\alpha \right)$ distribution.

3.3. Feature Decoupling Module Based on Self-Attention

To further reduce the domain distribution difference between the source domain and the target domain, this paper proposes a self-attention-based feature decoupling module. The module aims to extract domain-independent features for cross-domain sample classification tasks, while retaining domain-related features to incorporate important inductive biases learned from each domain.

The self-attention-based feature decoupling module proposed in this paper mainly consists of a self-attention layer, a batch normalization layer, an activation function layer, and a fully connected layer, as shown in Figure 2. By modeling the long-distance dependencies between features, self-attention enhances the representation of important features and assists the module in dissociating domain-independent features and domain-related features. The normalization layer improves the stability of the model by normalizing the input features. The ReLU layer enhances the model’s ability to express complex features by introducing nonlinear transformations. FC21a and FC22a generate the mean and logarithmic variance of domain-independent features, respectively, and the domain-independent features of the source domain support set $F{1}^s$, mixed-domain query set $F{1}^{mix}$, and target domain support set $F{1}^t$ are obtained using the reparameterization trick shown in Equations (6) and (7). FC21b and FC22b generate the mean and logarithmic variance of domain-related features, respectively, and similarly, the domain-related features of the source domain support set $F{2}^s$, mixed-domain query set $F{2}^{mix}$, and target domain support set $F{2}^t$ are also obtained using the reparameterization trick.

$$\sigma =\exp \left({\displaystyle \frac{\mathit{log}\left({\sigma }^2\right)}{2}}\right)$$

(6)

$$F^{\prime }=\mu +\epsilon \odot \sigma$$

(7)

where $\mathit{log}\left({\sigma }^2\right)$ represents the logarithmic variance, $\mu$ represents the mean, $\sigma$ represents the standard deviation, and $\epsilon \sim N\left(\mathrm{0,1}\right)$ represents the standard Gaussian noise.

The design concept of this module stems from the latent variable separation principle of Variational Autoencoder (VAE), which is a probabilistic generative model that performs two key tasks. It maps input data to a latent space with a probability distribution, and this distribution is used to represent the latent features of the data. It also reconstructs the input data from the latent representations.

In this module, it achieves more accurate feature separation through an explicit supervision mechanism. However, the feature decoupling module is quite different from VAE. VAE only encodes a single latent feature, whereas the feature decoupling module explicitly separates domain-related features and domain-independent features via a dual-branch structure.

3.4. Parameter Updating

The method proposed in this paper optimizes model parameters through a multi-task loss function mechanism composed of a sample classification task and a domain classification task.

3.4.1. Sample Classification Loss

The sample classification loss, composed of the source domain classification loss and the target domain classification loss, aims to facilitate the model to achieve effective knowledge transfer between the source and target domains during cross-domain few-shot learning.

For the source domain classification loss, the source domain feature space $F^s=Concat\left(F{1}^{mix},F{1}^s\right)$ is constructed using the domain-independent features of the mixed-domain query set $F{1}^{mix}$ and the domain-independent features of the source domain support set $F{1}^s$. As indicated in Section 3.2, the samples in the mixed-domain query set contain source domain query set information at a proportion of $\lambda$, but their corresponding source domain query set labels are not processed by Mixup. When the mixed-domain domain-independent features are classified in the source domain classification task, their corresponding labels are those of the source domain query set. Therefore, the labels corresponding to the constructed source domain feature space are the real labels of the source domain. By inputting $F^s$ into the classifier and using the cross-entropy loss function to calculate the difference between the classifier’s prediction results and the real labels of the source domain, the source domain classification loss is obtained, which is defined as follows:

$$L_S=CE\left(G_{cla}\left(F^s\right),p^s\right)$$

(8)

where $G_{cla}$ denotes the classifier, CE denotes the cross-entropy loss function, and $p^s\in C_S$ denotes the source domain label.

For the target domain classification loss, the target domain feature space $F^t=Concat(F{1}^{mix},F{1}^t)$ is constructed using the domain-independent features of the mixed-domain query set $F{1}^{mix}$ and the domain-independent features of the target domain support set $F{1}^t$. As stated in Section 3.2, the mixed-domain query samples contain target domain query set information at a proportion of $1-\lambda$, and similarly, their corresponding target domain query set labels are not processed by Mixup. When the mixed-domain domain-independent features are classified in the target domain classification task, their corresponding labels are those of the target domain query set. Therefore, the labels corresponding to the constructed target domain feature space are the real labels of the target domain. By inputting $F^t$ into the classifier and using the cross-entropy loss function to calculate the difference between the classifier’s prediction results and the real labels of the target domain, the target domain classification loss is obtained, which is defined as follows:

$$L_T=CE\left(G_{cla}\left(F^t\right),p^t\right)$$

(9)

where $p^t\in C_T$ denotes the target domain label.

Since the mixed-domain query set is formed by mixing the source domain query set and the target domain query set in proportion $\lambda$, this proportion $\lambda$ represents the proportion of the source domain query set and the target domain query set in the mixed-domain query set. The model allocates the weights of the source domain classification loss and the target domain classification loss according to this proportion, thereby achieving cross-domain knowledge transfer. The final expression of the sample classification loss is as follows:

$$L_C=\lambda L_S+\left(1-\lambda \right)L_T$$

(10)

3.4.2. Domain Classification Loss

The domain classification loss comprises two components: the loss based on domain-independent features and the loss based on domain-related features. It is designed to effectively tackle the problem of domain distribution discrepancy in cross-domain few-shot learning. Herein, the domain discriminator, composed of fully connected layers, maps the input features to the scores corresponding to the two domains, thereby determining whether the input features originate from the source domain or the target domain.

For the loss related to domain-independent features, the goal is to confuse the domain discriminator, making it unable to correctly distinguish between the source domain and the target domain. The network parameters of the feature decoupling module are optimized by minimizing the following loss function, thereby effectively removing the domain-related interference information in the domain-independent features. The specific loss function is defined as

$$L_{Dom1}={\displaystyle \frac{1}{3}}\sum [KL\left(G_{dom}\left(F{1}^s\right),p{1}^s\right)+KL\left(G_{dom}\left(F{1}^t\right),p{1}^t\right)+KL\left(G_{dom}\left(F{1}^{mix}\right),p{1}^{mix}\right)]$$

(11)

where $G_{dom}$ denotes the discriminator, KL represents the Kullback–Leibler divergence loss function [43], and $p{1}^s$, $p{1}^t$, and $p{1}^{mix}$ represent the corresponding domain classification labels, which are all set to [0.5, 0.5] to confuse the domain discriminator.

For the loss related to domain-related features, the model expects the domain discriminator to correctly determine to which domain the input features belong. The network parameters of the feature decoupling module and the domain classifier are optimized by minimizing the following loss function, thereby effectively separating the domain-related features. Herein, 1 and 0 are used to represent the domain categories of the source domain and the target domain, respectively. The specific loss function is defined as

$$\begin{gathered} L_{Dom2}={\displaystyle \frac{1}{3}}\sum [CE\left(G_{dom}\left(F{2}^s\right),p{2}^s\right)+CE\left(G_{dom}\left(F{2}^t\right),p{2}^t\right) \\ +\lambda \cdot CE\left(G_{dom}\left(F{2}^{mix}\right),p{2}^{mix1}\right)+\left(1-\lambda \right)CE\left(G_{dom}\left(F{2}^{mix}\right),p{2}^{mix2}\right)] \end{gathered}$$

(12)

where $p{2}^s$ and $p{2}^{mix1}$ are set to 1, and $p{2}^t$ and $p{2}^{mix2}$ are set to 0.

3.4.3. Integrated Loss Function

By optimizing both the sample classification loss and the domain classification loss simultaneously, the model can learn domain-independent features and domain-related features, reducing the distribution difference between domains. The expression of the final integrated loss function is as follows:

$$loss=L_C+L_{Dom1}+L_{Dom2}$$

(13)

3.5. Algorithm Implement Process

Algorithm 1 outlines the implementation procedure of the proposed method. In steps 3 and 4, the source domain support set, query set, target domain support set, and query set are obtained by sampling from datasets in both the source and target domains. In step 5, the Mixup data augmentation method is employed to linearly combine samples from the source and target domain query sets at a specific ratio, generating new training samples for the mixed-domain query set. In steps 6 and 7, a self-attention-based feature decoupling module is used to generate domain-independent features and domain-related features. In step 9, the source domain classification loss is computed using the domain-independent features of the source domain support set and those of the mixed-domain query set. In step 10, the target domain classification loss is also calculated using the domain-independent features of the target domain support set and the mixed-domain query set. In step 11, the sample classification loss is calculated according to the Mixup blending ratio $\lambda$ to facilitate effective knowledge transfer between the source and target domains during cross-domain few-shot learning. In step 12, the domain classification loss is computed using domain-independent features to confuse the domain discriminator, preventing it from accurately distinguishing between the source and target domains. Conversely, in step 13, the domain classification loss is calculated using domain-related features, aiming to enable the domain discriminator to correctly identify the domain of input features. Finally, model parameters are updated by minimizing the integrated loss.

It should be further noted that the proposed method leverages the ViT network, which exhibits excellent performance in classification tasks, primarily because it introduces the self-attention mechanism from the Transformer network into the field of image processing [39]. In this study, we modify the ViT network for one-dimensional monitoring data according to the methods of reference [44]. Since the original ViT is designed to process two-dimensional image signals, while this paper applies it to handle one-dimensional vibration signals, we improve the patch embedding of the original ViT network. The specific improvement process is as follows: first, we truncate the one-dimensional vibration signal into several segments with equal intervals; second, we arrange these truncated segments into a matrix form; finally, we use a fully connected network to project the reshaped matrix, thereby constructing a patch embedding tailored to one-dimensional vibration signals. We then employ this modified ViT network as the feature extractor. At the same time, we use fully connected neural networks to construct both the classifier and domain discriminator.

Algorithm 1: Cross-domain few-shot intelligent fault diagnosis algorithm based on Mixup data augmentation
Input:	Source domain dataset $D_S=\left\{\right(x_i^s,p_i^s){\}}_{i=1}^{n_s}$; Target domain dataset $D_T=\left\{\right(x_i^t,p_i^t){\}}_{i=1}^{n_t}$
Output:	Trained feature extractor $V$, Feature decoupling module $F$, Domain discriminator $G_{dom}$, Classifier $G_{cla}$
1:	$\left({\theta }_v,{\theta }_f,{\theta }_{g_{cla}},{\theta }_{g_{dom}}\right)=Ne{t}_{initialize}\left(V,F,G_{cla},G_{dom}\right)$ //Network model parameter initialization
2:	While not done do
3:		$D_{support}^S=\left\{\right(x_i^s,p_i^s){\}}_{i=1}^K,D_{query}^S=\{(x_i^s,p_i^s){\}}_{i=1}^M$ //Sample the support set and query set from the source domain dataset
4:		$D_{support}^T=\left\{\right(x_i^t,p_i^t){\}}_{i=1}^K,D_{query}^T=\{(x_i^t,p_i^t){\}}_{i=1}^M$ //Sample the support set and query set from the target domain dataset
5:		$D_{query}^{mix}=\lambda D_{query}^S+\left(1-\lambda \right)D_{query}^T$ //Obtain the mixed-domain query set $D_{query}^{mix}=\left\{\right({\stackrel{̑}{x}}_i^{mix}){\}}_{i=1}^M$
6:		$\left(\left\{\right(F{1}^s){\}}_{i=1}^K,\{\left(F{1}^t\right){\}}_{i=1}^K,\left\{\right(F{1}^{mix}){\}}_{i=1}^M\right)$ //Extract domain-independent features according to Equation (7)
7:		$\left(\left\{\right(F{2}^s){\}}_{i=1}^K,\{\left(F{2}^t\right){\}}_{i=1}^K,\left\{\right(F{2}^{mix}){\}}_{i=1}^M\right)$ //Extract domain-related features according to Equation (7)
9:		$L_S\leftarrow$ Calculate the source domain classification loss using $\left\{\right(F{1}^s){\}}_{i=1}^K$, $\left\{\right(F{1}^{mix}){\}}_{i=1}^M$ according to Equation (8)
10:		$L_T\leftarrow$ Calculate the target domain classification loss using $\left\{\right(F{1}^t){\}}_{i=1}^K$, $\left\{\right(F{1}^{mix}){\}}_{i=1}^M$ according to Equation (9)
11:		$L_C=\lambda L_S+\left(1-\lambda \right)L_T$//Calculate the sample classification loss
12:		$L_{Dom1}\leftarrow$ Calculate the loss using $\left\{\right(F{1}^s){\}}_{i=1}^K$, $\left\{\right(F{1}^t){\}}_{i=1}^K$, $\left\{\right(F{1}^{mix}){\}}_{i=1}^M$ according to Equation (11)
13:		$L_{Dom2}\leftarrow$ Calculate the loss using $\left\{\right(F{2}^s){\}}_{i=1}^K$, $\left\{\right(F{2}^t){\}}_{i=1}^K$, $\left\{\right(F{2}^{mix}){\}}_{i=1}^M$ according to Equation (12)
14:		$loss=L_C+L_{Dom1}+L_{Dom2}$
15:		$\left({\theta }_v,{\theta }_f,{\theta }_{g_{dom}},{\theta }_{g_{cla}}\right)=Ne{t}_{update}\left(loss,{\theta }_v,{\theta }_f,{\theta }_{g_{dom}},{\theta }_{g_{cla}}\right)$
16:	end while

4. Experimental Verification

4.1. Experimental Setup

The operating environment for the experimental validation includes an Intel Core i9-12900K CPU processor, 32 GB memory with a 3.60 GHz frequency, an NVIDIA GeForce RTX 3060 GPU, the Windows 10 operating system, and the PyTorch 1.7.1 deep learning framework.

The Adam optimization algorithm is used to update the network weights, with the learning rate set to 0.0001 [45]. To reduce the randomness of the experimental results, each group of experiments is repeated five times.

4.2. Comparison Methods

To validate the effectiveness of the proposed method, this test case presents the following three comparative diagnostic methods:

(1)

Comparison Method 1 (Single ViT): This method uses the same feature extractor and classifier as the proposed method but updates network parameters exclusively using labeled samples from the source domain.

(2)

Comparison Method 2 (Prototypical Network): Leveraging a prototypical network for fault diagnosis, this method employs the same base network models for the feature extractor and classifier as the proposed method. It updates network parameters using labeled target domain samples.

(3)

Comparison Method 3 (Without Mixup): This comparative method excludes both the Mixup data augmentation and the subsequent feature processing operations used in the proposed method. It employs the same feature extractor and classifier as the proposed method, and updates network parameters using a large number of labeled samples from the source domain and a small number of labeled samples from the target domain, respectively.

4.3. Test Case 1

4.3.1. Dataset Description of Test Case 1

• Laboratory Bearing Dataset

The laboratory rotating equipment test rig, as shown in Figure 3, primarily consists of a motor, rotor system, load block, and supporting bearings. The experimental bearings were installed in the bearing housing on the right side of the platform. During the experiment, the motor speed was set at 900 r/min and 1500 r/min, and acceleration sensors mounted horizontally on the bearing housing were used to collect bearing fault data. The sampling frequency was set at 10 kHz. The collected bearing fault data covered vibration signals for four fault types: normal state, inner ring fault, ball fault, and outer ring fault. For each bearing fault state, 100 groups of data were collected as source domain training data, with each group of fault data having a length of 10 K.

2.

Jiangnan University (JNU) Bearing Dataset

The Jiangnan University (JNU) bearing dataset [46] was collected from a fault diagnosis experiment conducted on a centrifugal fan system driven by a Mitsubishi induction motor. During the experiment, the test bearings were artificially wire-cut to simulate normal state, outer ring fault, inner ring fault, and ball fault. During the collection of fault data, the sampling frequency was set at 50 kHz. In this test case, fault data at two rotational speeds (600 r/min and 1000 r/min) were selected. For each fault state, 100 groups of data were collected, with each group of fault data having a length of 10 K.

4.3.2. Experimental Results and Analysis of Test Case 1

In this test case, a series of cross-domain diagnostic tasks are constructed from the laboratory bearing dataset to the JNU bearing dataset to evaluate the effectiveness of the proposed method. Detailed information on the experimental working condition settings is presented in

Table 1. Test case 1 working condition settings during the training process.

Domain	Source Domain		Target Domain
Dataset	Laboratory bearing dataset		JNU bearing dataset
Working condition	Speed	Number of samples	Speed	Number of samples
Task 1	1500 r/min	100	1000 r/min	5/10
Task 2	900 r/min	100	1000 r/min	5/10
Task 3	1500 r/min	100	600 r/min	5/10
Task 4	900 r/min	100	600 r/min	5/10

.

As shown in Table 1, during the training process, the source domain data contains 400 sample groups. The purpose of this setup is to enable the model to fully learn the feature distribution of different types of fault data in the source domain. For cross-domain few-shot learning tasks, the target domain data is set to 20 or 40 sample groups to align with the actual scenario of scarce target domain data in such tasks. Additionally, all other target domain data beyond the aforementioned sets are used as testing data. This sample configuration not only covers the basic feature distribution of the four types of faults but also prevents the task from deviating from the core setting of few-shot learning due to excessive data volume.

During the network training process, the training batch size is set to 20. To construct the support set and query set, it is necessary to partition the samples within each batch. The experiment follows the principle that the support set guides feature learning, and the query set verifies generalization ability. Specifically, 5 samples are selected from each batch to form the support set, which means that K equals 5. This selection is intended to balance the diversity of the support set and its adaptability to real-world scenarios. The remaining 15 samples are used to form the query set, which means that M equals 15.

Table 2. The recognition results in test case 1, where five labeled samples are available for each fault condition in the target domain.

Method		Task 1	Task 2	Task 3	Task 4
Comparison method 1	Average accuracy (%)	76.63	75.05	76.32	74.84
	Standard deviation	2.9417	2.7870	2.4792	3.0078
Comparison method 2	Average accuracy (%)	85.24	83.40	82.06	80.53
	Standard deviation	1.6483	1.8227	1.7621	1.8890
Comparison method 3	Average accuracy (%)	85.95	85.79	87.58	87.26
	Standard deviation	1.0729	1.3679	1.0492	1.8878
Proposed method	Average accuracy (%)	87.32	86.21	89.69	91.21
	Standard deviation	0.5824	0.4878	0.5625	1.0325

and

Table 3. The recognition results in test case 1, where 10 labeled samples are available for each fault condition in the target domain.

Method		Task 1	Task 2	Task 3	Task 4
Comparison method 1	Average accuracy (%)	83.06	81.99	82.31	82.16
	Standard deviation	2.4725	1.8354	2.1887	2.0171
Comparison method 2	Average accuracy (%)	88.39	90.34	90.18	89.17
	Standard deviation	1.2595	1.3865	1.3298	1.5010
Comparison method 3	Average accuracy (%)	92.61	94.39	92.28	92.78
	Standard deviation	1.4948	1.2964	1.4402	1.2025
Proposed method	Average accuracy (%)	98.33	98.62	95.44	96.28
	Standard deviation	0.3917	0.3931	0.4153	0.5707

present the recognition results of the proposed method and various comparative methods in test case 1, respectively. Specifically, Table 2 shows the results when 5 labeled samples per fault state are available in the target domain training set, while Table 3 corresponds to the scenario with 10 labeled target domain samples per fault state. The diagnostic results indicate that reducing the number of target domain training samples affects each diagnostic method to varying degrees, yet the proposed method demonstrates relatively stable recognition performance.

Comparison method 1 exhibits the lowest average accuracy, confirming that traditional deep learning methods struggle to converge effectively with limited labeled data. In contrast, comparison method 2, which employs a meta-learning approach, shows an increase in the average accuracy of fault state recognition and a further reduction in the fluctuation of fault state recognition accuracy under data scarcity. However, its performance still lags significantly behind that of the proposed method. When compared with comparison method 3, the Mixup data augmentation employed in the proposed method enhances the model’s generalization ability on the target domain dataset, leading to further improvements in average accuracy. This result indirectly validates the effectiveness of the Mixup technique.

To intuitively observe the feature distribution patterns of training samples and testing samples, Figure 4 presents the t-SNE feature visualization results of source domain samples and target domain samples during the training process, as well as testing samples during the testing process, in the first task when the number of target domain samples is 10. It can be seen from Figure 4a,b that during the training process, both the source domain samples and the target domain samples are correctly classified, and the distinguishability of features of different categories is obvious. It can be seen from Figure 4c that during the testing process, the clustering relationship of features of different fault categories of test samples is clear, with only very few samples being misclassified. For comparison, Figure 5 presents the feature visualization results of testing samples obtained by other comparative methods. It can be observed that the feature classification boundaries obtained by comparison method 3 are relatively clearer than those obtained by comparison methods 1 and 2. However, a small number of misclassification phenomena still occur near the classification boundaries of comparison method 3. The classification boundary corresponding to the testing samples of the proposed diagnostic method is significantly better than that of other comparative diagnostic methods, which proves that the distinguishability of the diagnostic results of the proposed method is significantly better than that of other comparative diagnostic methods.

4.4. Test Case 2

4.4.1. Dataset Description of Test Case 2

• Case Western Reserve University (CWRU) Bearing Dataset

In the CWRU bearing dataset [47,48], bearing faults were created via electrical discharge machining to simulate bearing inner ring faults, outer ring faults, and ball faults. Different fault sizes were introduced for each fault state, specifically 0.007 inches, 0.014 inches, and 0.021 inches. Additionally, data under normal conditions were included, covering a total of 10 types. During the experiment, the sampling frequency was set to 12 kHz, and rotational speeds were adjusted by applying different motor loads of 0–3 HP, corresponding to motor speeds ranging from 1797 r/min to 1720 r/min. Data under four different working conditions were collected for each fault damage diameter. In this test case, data for the normal state under motor loads of 1 HP and 3 HP were selected, along with data for three fault states under motor loads of 1 HP and 3 HP when the fault damage diameter was 0.007 inches. For each fault state, 100 groups of fault data were collected as source domain data, with each group of fault data samples having a length of 10 K.

2.

Huazhong University of Science and Technology (HUST) Bearing Dataset

In the HUST bearing fault dataset [49], the sampling frequency was set to 25.6 kHz. Vibration signals of different fault states under 11 different rotational speeds were obtained by adjusting the motor speed, among which 10 were constant speeds and 1 was a time-varying speed. In this test case, vibration signals of four fault types (normal state, severe inner ring fault, severe outer ring fault, and severe ball fault) under constant speed conditions of 40 Hz and 60 Hz were selected as target domain data. For each faulty bearing, 100 groups of data were collected, with each group of fault data having a length of 10 K. Two sets of experiments were conducted by randomly selecting 5 and 10 groups of data as target domain training data, respectively, and the remaining data were used as testing data.

4.4.2. Experimental Results and Analysis of Test Case 2

In this test case, a series of cross-domain diagnostic tasks from the CWRU bearing dataset to the HUST bearing dataset were constructed to further evaluate the applicability of the proposed method under scenarios involving different faulty equipment. Detailed information regarding the experimental working condition settings is presented in

Table 4. Test case 2 working condition settings during the training process.

Domain	Source Domain		Target Domain
Dataset	CWRU bearing dataset		HUST bearing dataset
Working condition	Load	Number of samples	Speed	Number of samples
Task 1	1 HP	100	40 Hz	5/10
Task 2	3 HP	100	40 Hz	5/10
Task 3	1 HP	100	60 Hz	5/10
Task 4	3 HP	100	60 Hz	5/10

.

Since the amounts of source domain data and target domain data during the training process in this case are the same as those in the previous case, when partitioning the support set and query set within each batch, K is still set to 5, and M is still set to 15.

Table 5. The recognition results in test case 2, where five labeled samples are available for each fault condition in the target domain.

Method		Task 1	Task 2	Task 3	Task 4
Comparison method 1	Average accuracy (%)	81.79	81.26	80.31	82.04
	Standard deviation	2.4932	1.8034	2.4183	1.5228
Comparison method 2	Average accuracy (%)	87.46	87.79	88.16	88.42
	Standard deviation	1.5014	1.7103	1.6727	1.5701
Comparison method 3	Average accuracy (%)	91.11	91.84	93.16	91.05
	Standard deviation	1.0743	1.3005	1.0339	1.3831
Proposed method	Average accuracy (%)	95.05	93.26	95.42	92.21
	Standard deviation	0.6080	0.3964	0.4863	0.5426

and

Table 6. The recognition results in test case 2, where 10 labeled samples are available for each fault condition in the target domain.

Method		Task 1	Task 2	Task 3	Task 4
Comparison method 1	Average accuracy (%)	84.50	84.74	83.91	85.01
	Standard deviation	1.6235	1.5964	1.5833	2.1690
Comparison method 2	Average accuracy (%)	89.94	90.50	92.17	93.28
	Standard deviation	1.1440	1.3615	1.4636	1.5947
Comparison method 3	Average accuracy (%)	96.11	95.61	96.89	96.88
	Standard deviation	1.0688	1.0874	0.9196	1.0940
Proposed method	Average accuracy (%)	98.83	98.95	99.55	99.28
	Standard deviation	0.3265	0.2095	0.2828	0.2812

present the diagnostic results of the proposed diagnostic method and different comparative diagnostic methods in test case 2. Among them, Table 5 shows the recognition results when there are 5 labeled samples available for each fault state in the target domain training process, and Table 6 shows the recognition results when there are 10 labeled samples available for each fault state in the target domain training process. It can be seen that when the number of available labeled samples for each fault state in the target domain is reduced, the proposed diagnostic method still maintains the highest average accuracy of diagnostic results, even under different cross-domain diagnostic tasks. Since the proposed diagnostic method has formulated a variety of strategies for the problem of domain differences and the scarcity of labeled samples in the target domain, by comparing the diagnostic results of the proposed diagnostic method with those of the other three comparative diagnostic methods, it is found that the proposed method exhibits the highest average accuracy of fault diagnosis and the smallest fluctuation of results, which further verifies the applicability of the proposed diagnostic method in scenarios involving different faulty equipment.

To further validate the effectiveness of the proposed method, three quantitative evaluation indicators are introduced, i.e., precision, recall, and F-score.

Table 7. Precision rates of various diagnostic methods on test case 2.

Method	N	IF	RF	OF
Comparative method 1	0.7357	0.8853	1.0000	0.8850
Comparative method 2	0.8293	0.9243	0.9564	0.8972
Comparative method 3	0.9573	0.9819	1.0000	0.9782
Proposed method	0.9890	0.9971	1.0000	0.9890

,

Table 8. Recall rates of various diagnostic methods on test case 2.

Method	N	IF	RF	OF
Comparative method 1	0.9445	0.7556	0.9074	0.8519
Comparative method 2	0.9111	0.8112	0.9667	0.9278
Comparative method 3	0.9815	0.9389	1.0000	0.9889
Proposed method	0.9972	0.9778	1.0000	1.0000

and

Table 9. F-Scores rates of various diagnostic methods on test case 2.

Method	N	IF	RF	OF
Comparative method 1	0.8208	0.7476	0.9203	0.8368
Comparative method 2	0.8079	0.8534	0.9668	0.9122
Comparative method 3	0.9569	0.9548	1.0000	0.9780
Proposed method	0.9917	0.9888	1.0000	0.9890

present the results of these three indicators for different fault states in test case 2, comparing the proposed diagnostic method with other baseline methods under the first task when the number of target domain samples is 10. Higher values of these indicators signify better classifier performance. The results demonstrate that the proposed method outperforms all comparative methods across all three indicators, confirming its superior fault sample classification capability across scenarios involving different faulty equipment.

5. Conclusions

To address the problems of significant domain distribution differences between source domain data and target domain data, as well as the scarcity of labeled samples in the target domain in industrial scenarios, this paper proposes a cross-domain few-shot intelligent fault diagnosis method based on Mixup data augmentation. Firstly, the method introduces the Mixup data augmentation approach, which linearly combines data from the source domain query set and the target domain query set in a specific proportion to generate a mixed query set. This enables the model to learn correlations and features between different domain data, enhancing its ability to handle domain distribution differences and improving generalization across domains, thereby boosting performance on the target domain dataset. Secondly, a self-attention-based feature decoupling module is employed. With the supervision signal from the domain discriminator, it decomposes sample features into domain-independent and domain-related features. This allows the model to acquire cross-domain transferable feature representations while retaining domain-specific knowledge, further alleviating the problem of large domain distribution differences in cross-domain few-shot learning. Then, a multi-task learning mechanism consisting of sample classification and domain classification tasks is utilized to optimize the network model parameters. Finally, experimental verification on multiple sets of bearing datasets, including laboratory and public sets, through comparative analysis with various diagnostic methods, demonstrates that the proposed method significantly enhances the fault recognition ability of the diagnostic model under conditions of large domain distribution differences and scarce labeled samples in the target domain.