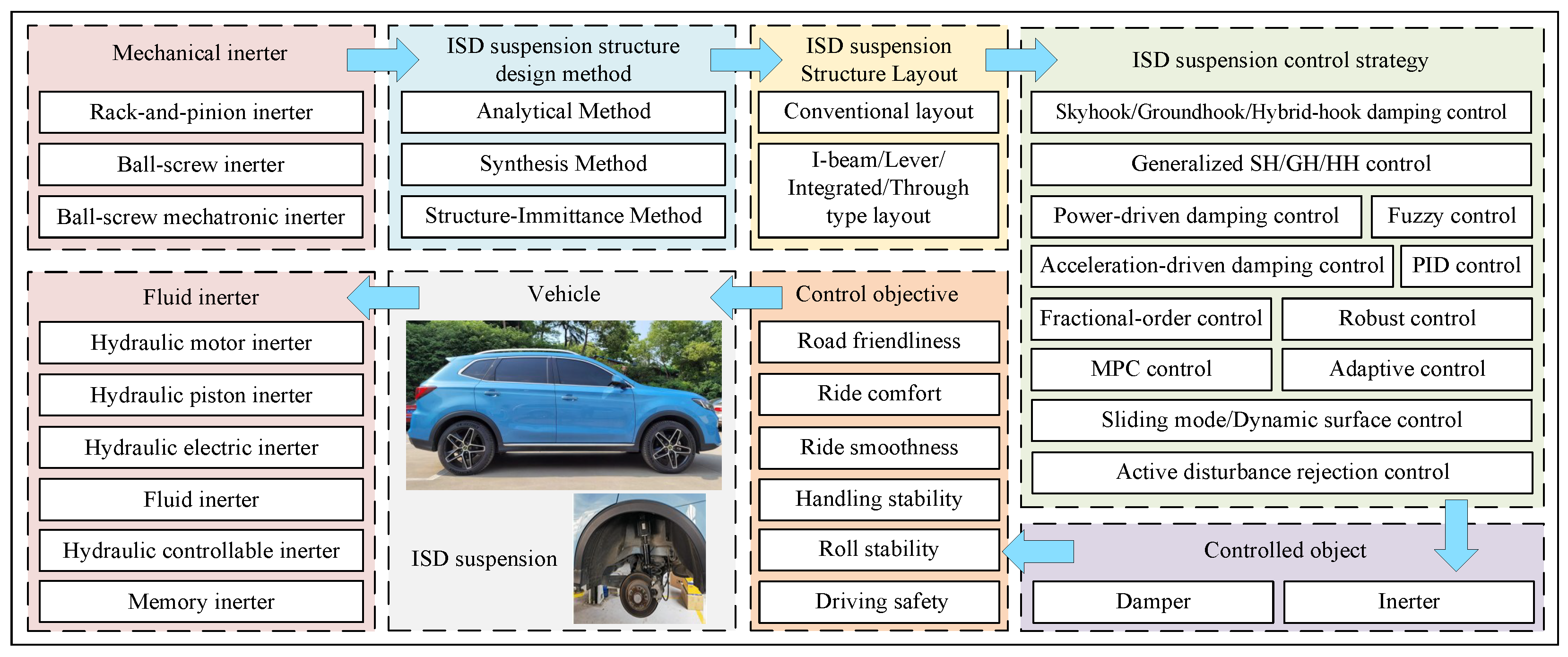
A Review on the Application of Inerters in Vehicle Suspension Systems
Abstract
1. Introduction
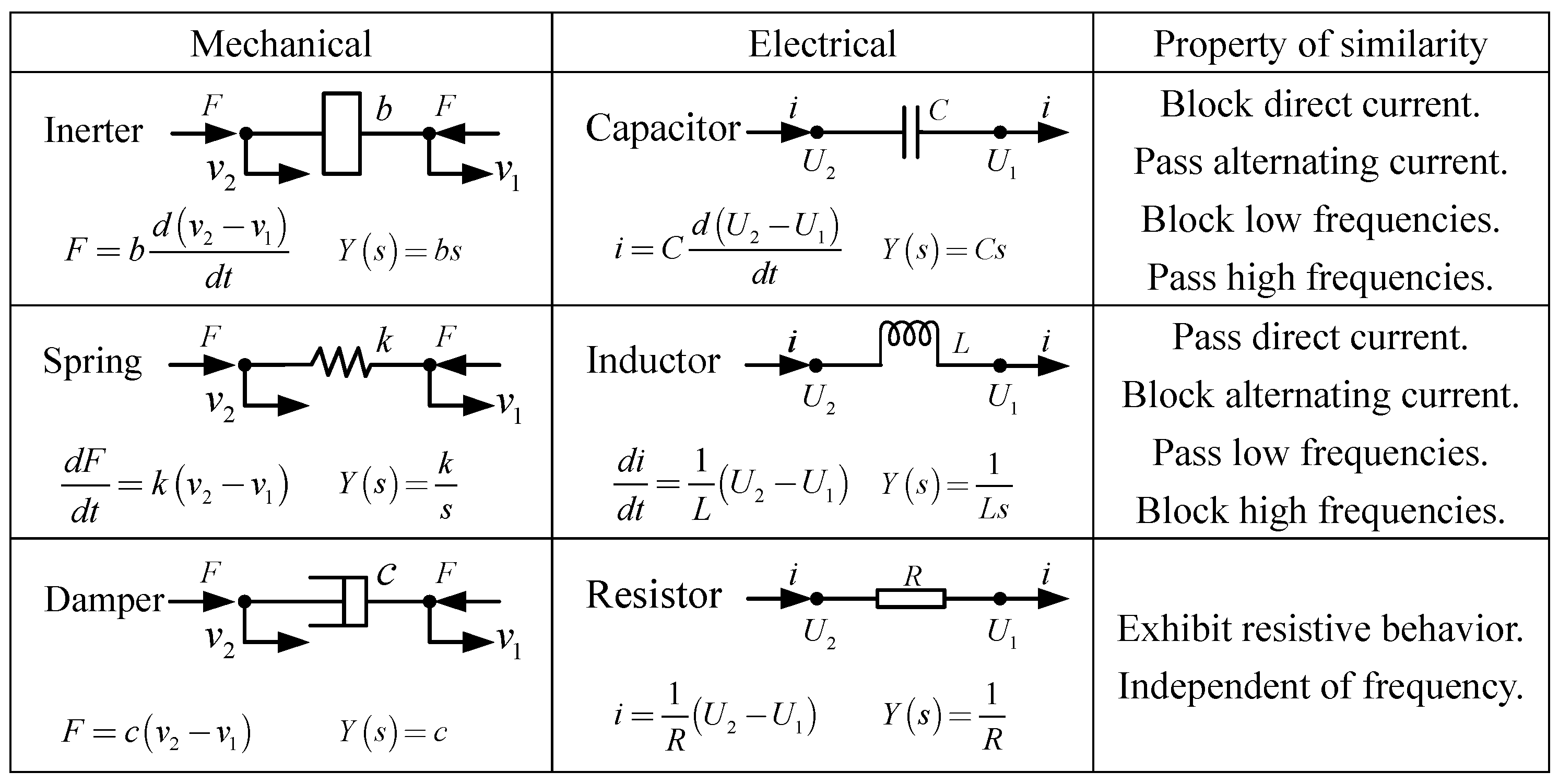
2. Inerter
2.1. The Fundamental Principle of the Inerter
- Two independent, freely moving terminals;
- No additional terminals required on an inertial basis;
- Finite linear stroke with reasonable overall dimension constraints;
- Small mass and independent inertance.
2.2. Structural Types of Inerters
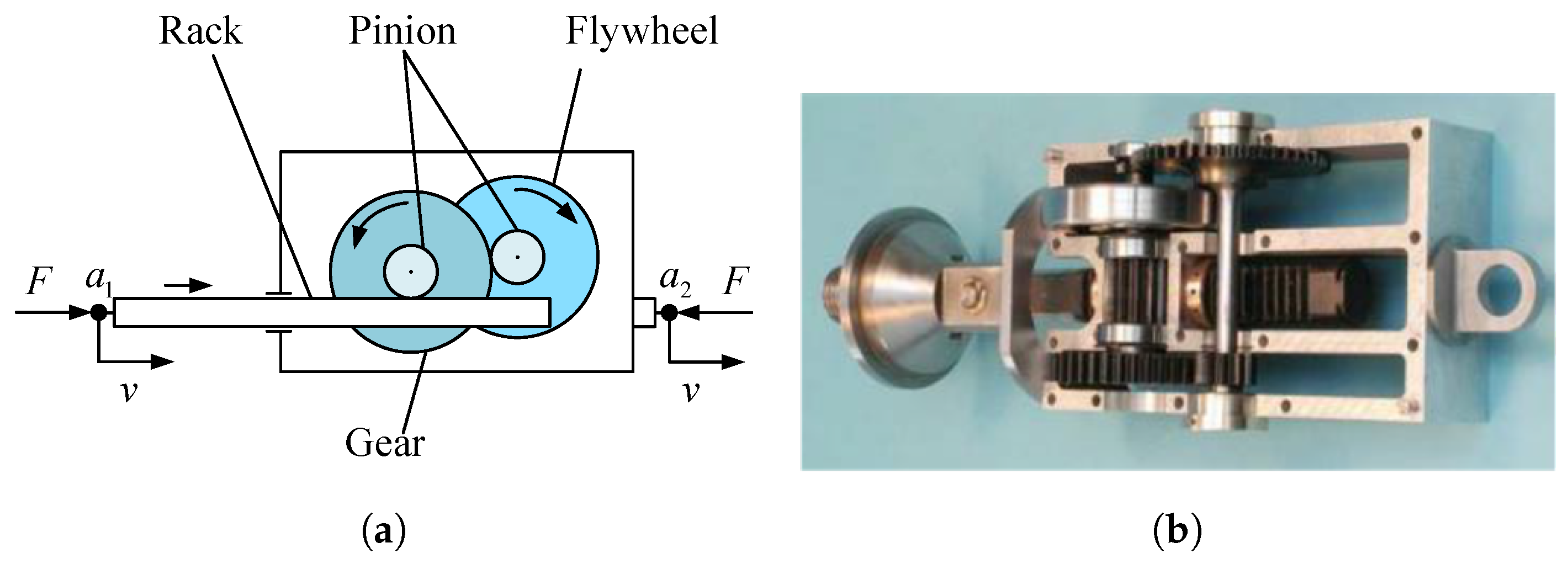
2.2.1. Rack-and-Pinion Inerter
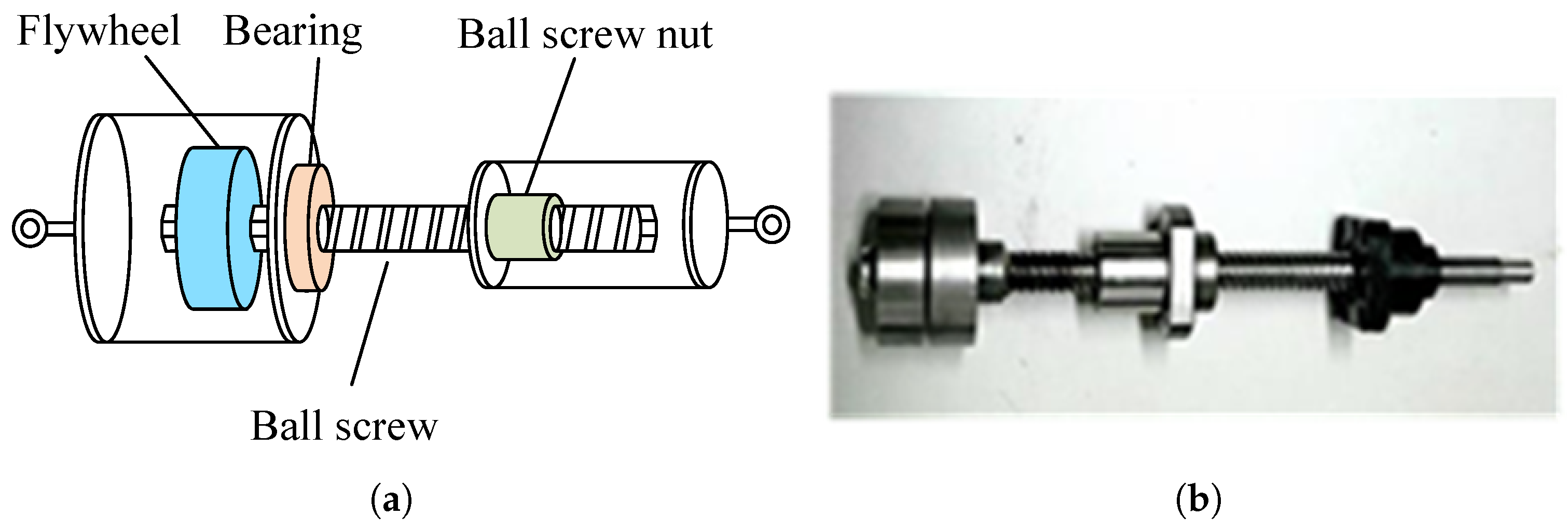
2.2.2. Ball-Screw Inerter
2.2.3. Ball-Screw Mechatronic Inerter
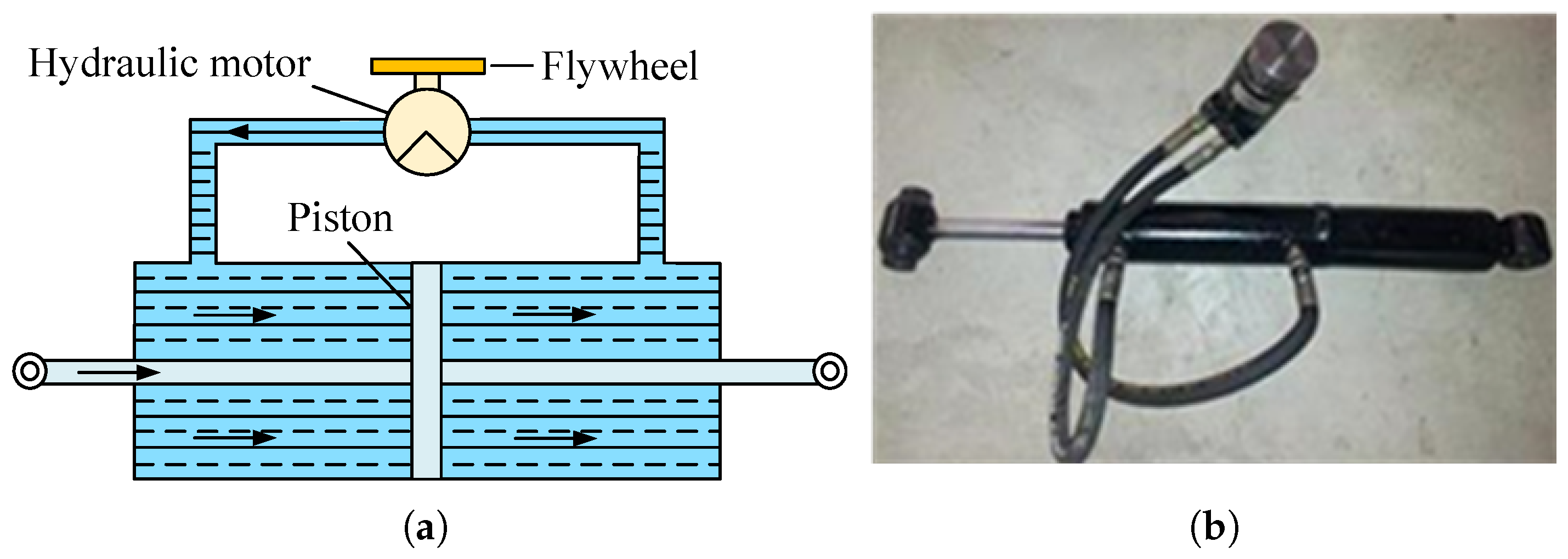
2.2.4. Hydraulic Motor Inerter
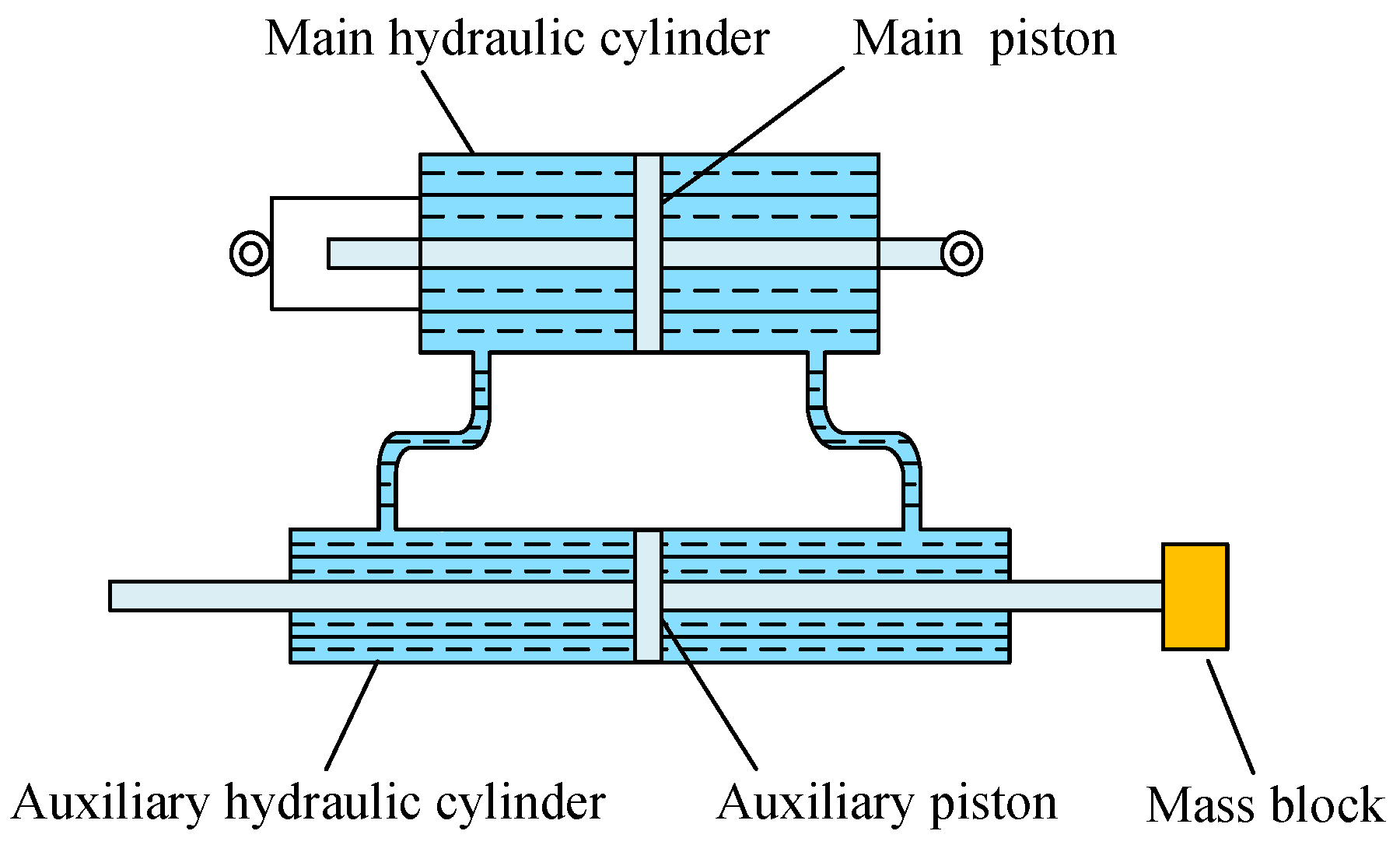
2.2.5. Hydraulic Piston Inerter
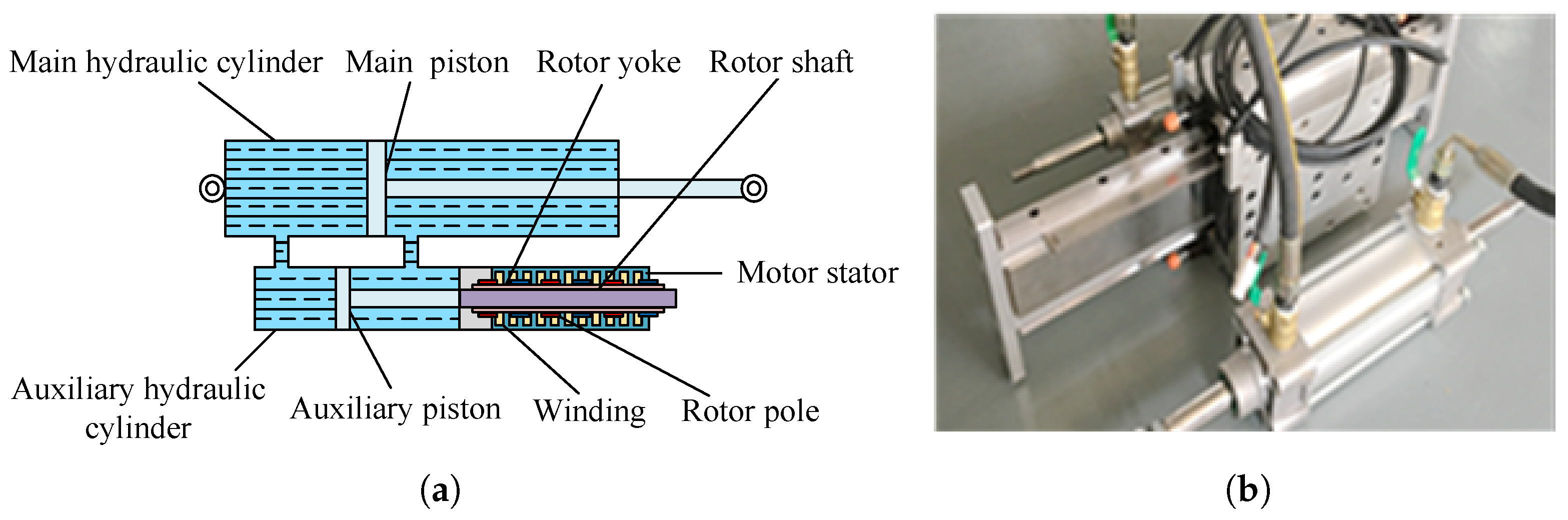
2.2.6. Hydraulic Electric Inerter
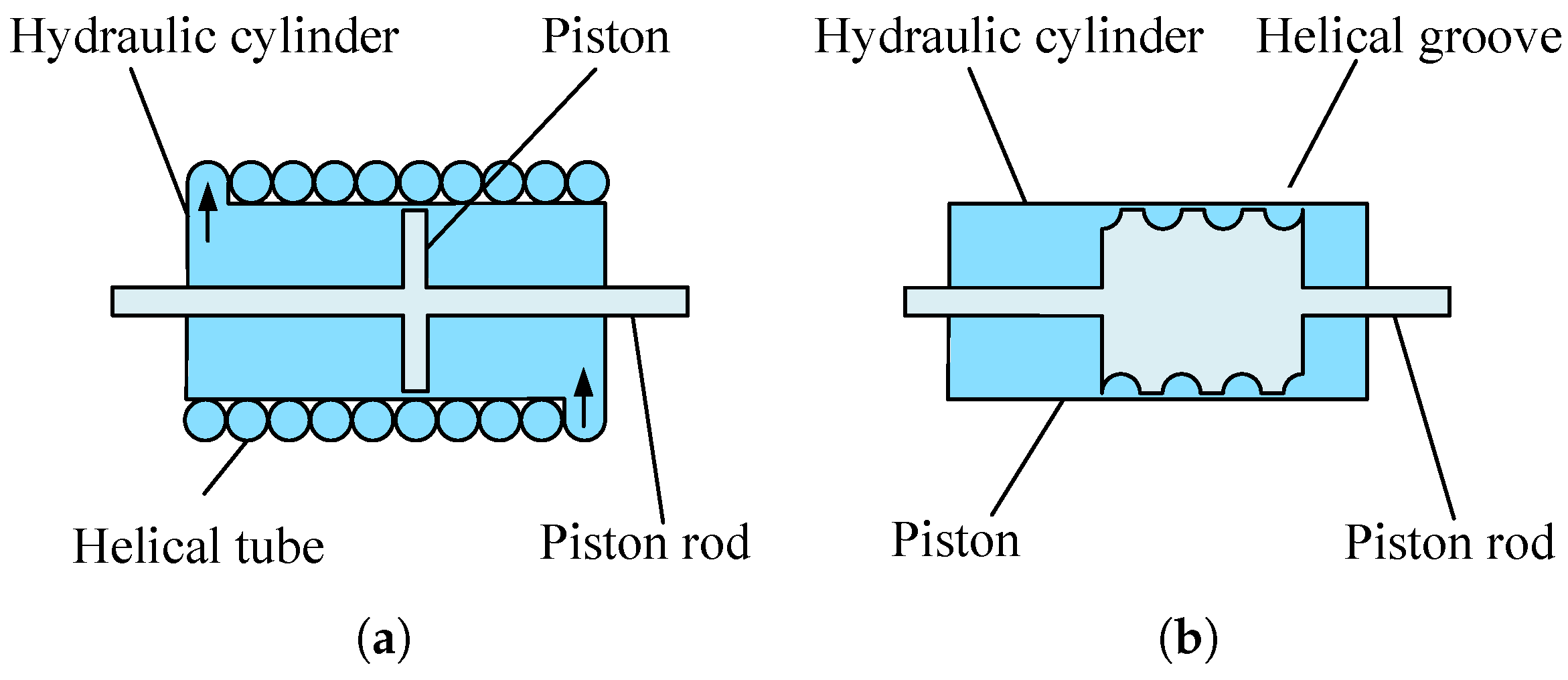
2.2.7. Fluid Inerter
2.2.8. Hydraulic Controllable Inerter
2.2.9. Memory Inerter
2.3. Nonlinear Characteristics of Inerter
2.4. Breakdown Phenomenon
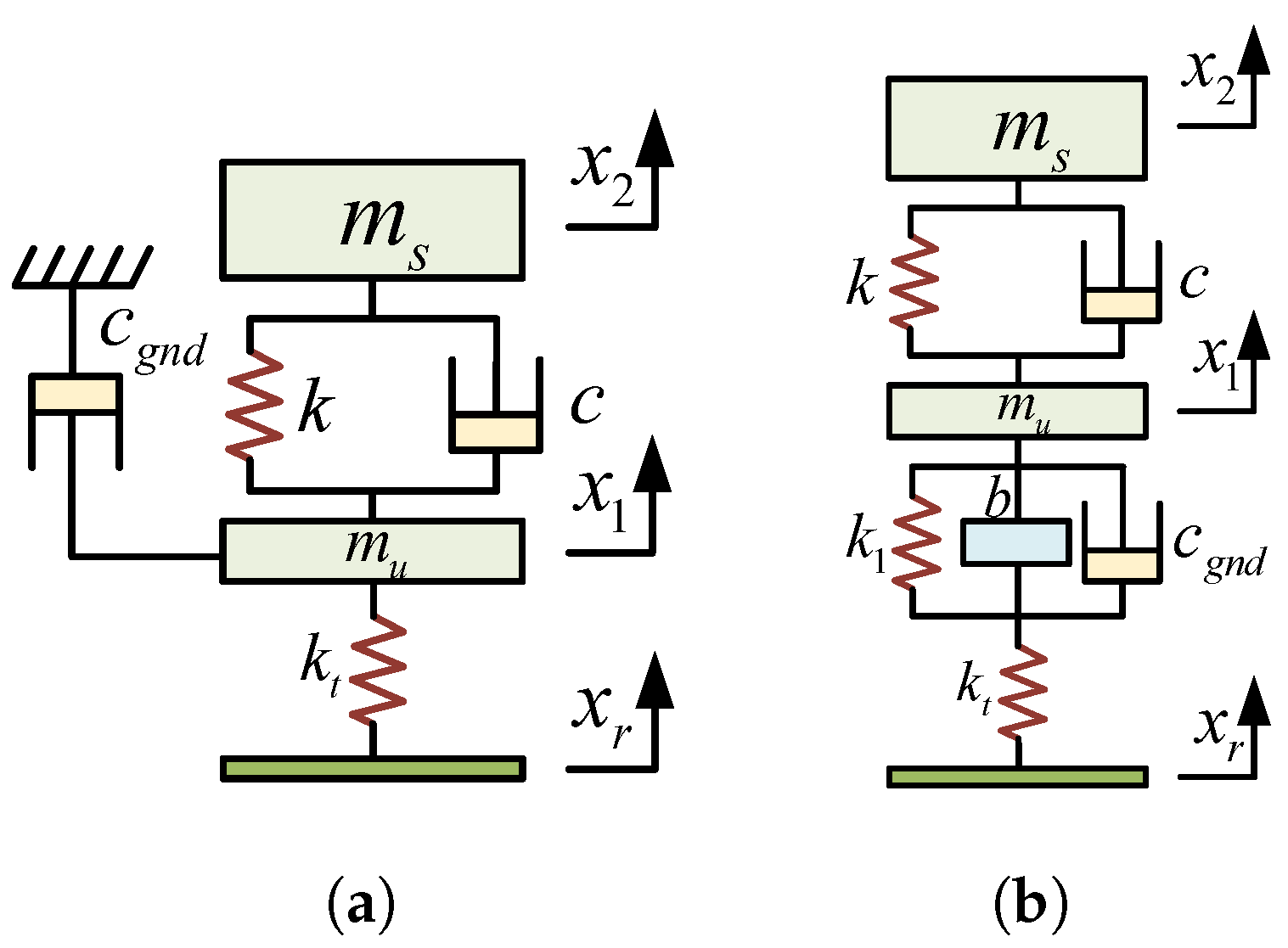
3. ISD Suspension Structural Design
3.1. ISD Suspension Structural Design Based on Analytical Method
- Utilizing the concept of cascaded filtering in electrical networks, while preventing breakdown phenomena, is used to design a two-stage series ISD suspension system;
- Deriving the simplest ISD suspension configuration through combinatorial arrangements of three fundamental elements (spring, damper, and inerter), then proceeding with ISD suspension structural design;
- Determining optimal connection methods between any two of the three elements by analyzing their series/parallel characteristics, then developing ISD suspension structures accordingly;
- Replacing the mass element in the traditional DVA with the two-terminal characteristics of the inerter to create vibration absorption subsystems, then coupling the passive DVA with the vehicle’s primary suspension system to obtain high-performance ISD suspension structures;
- Employing anti-resonance phenomena in inerter-spring-mass systems to address the requirement in ideal skyhook damping/groundhook damping systems where dampers must connect to inertial reference frames, thereby achieving passive implementation of ideal SH systems and resulting in high-performance ISD suspension structures.
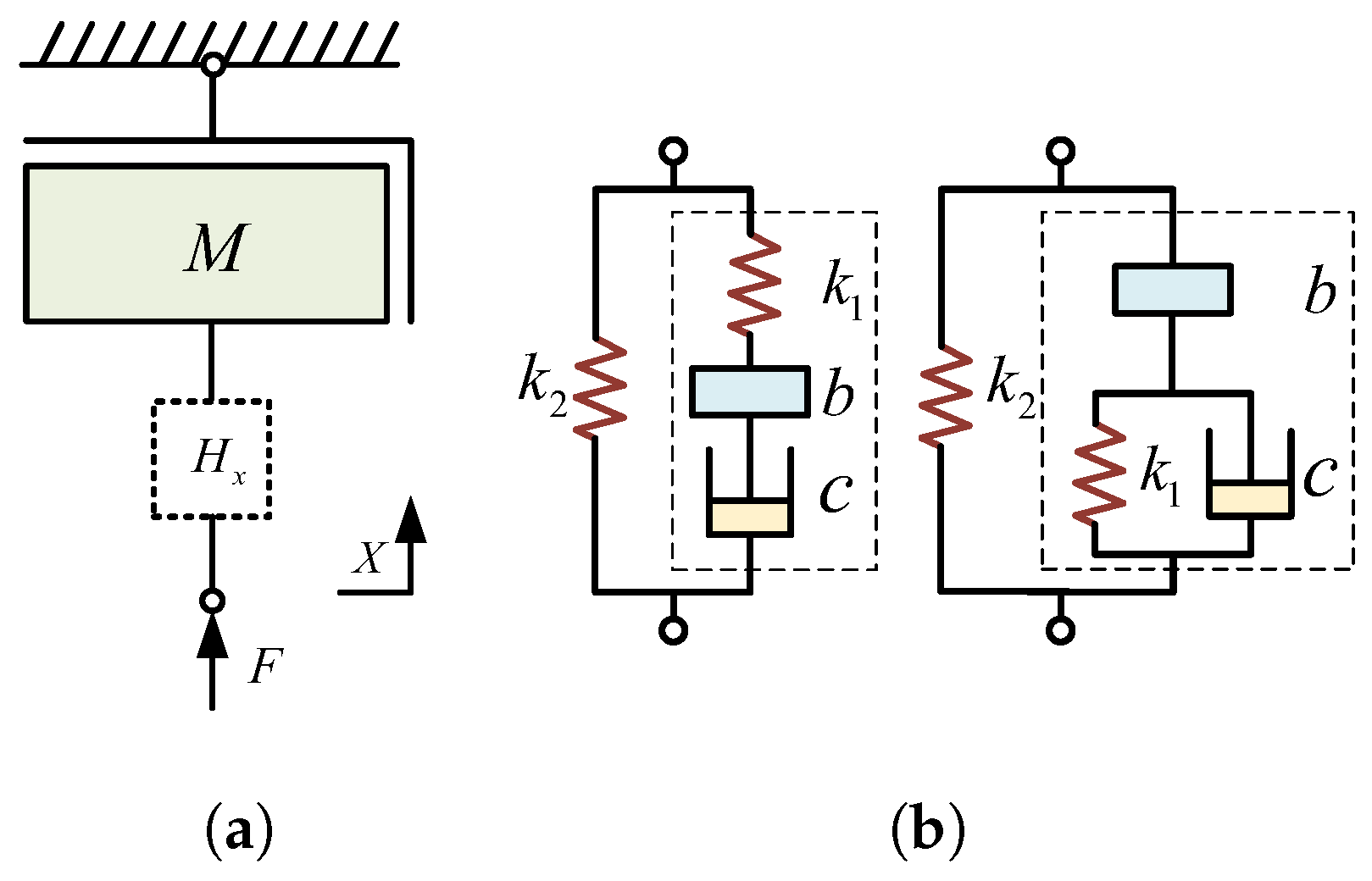
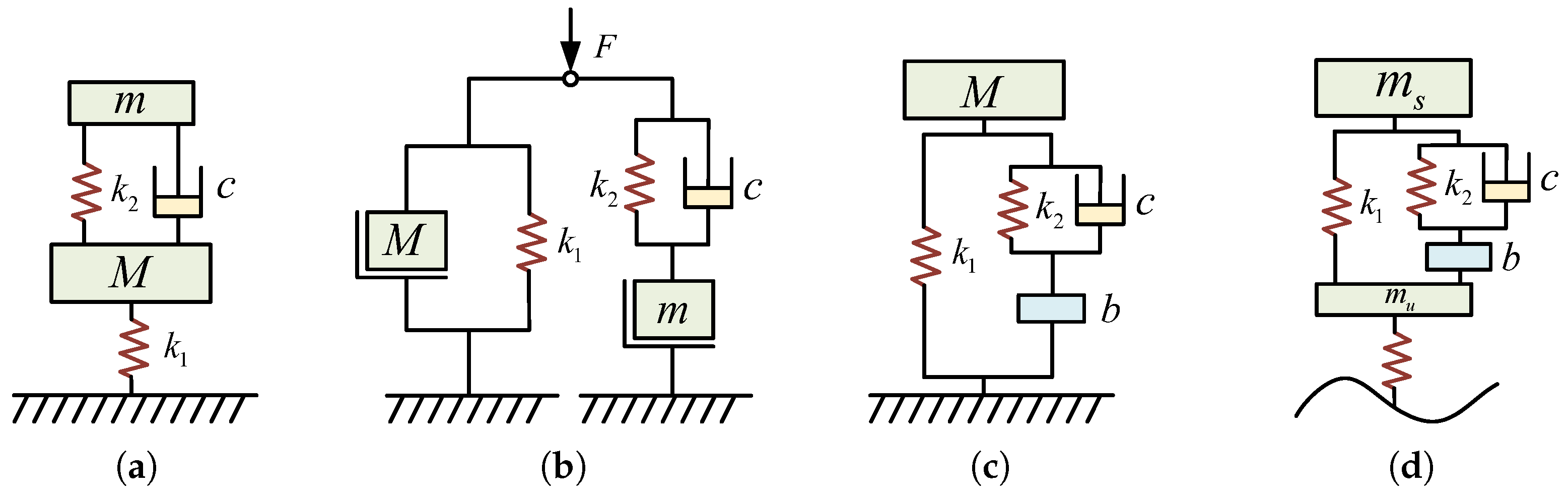
3.1.1. The First Type of Analytical Method
3.1.2. The Second Type of Analytical Method
3.1.3. The Third Type of Analytical Method
3.1.4. The Fourth Type of Analytical Method
3.1.5. The Fifth Type of Analytical Method
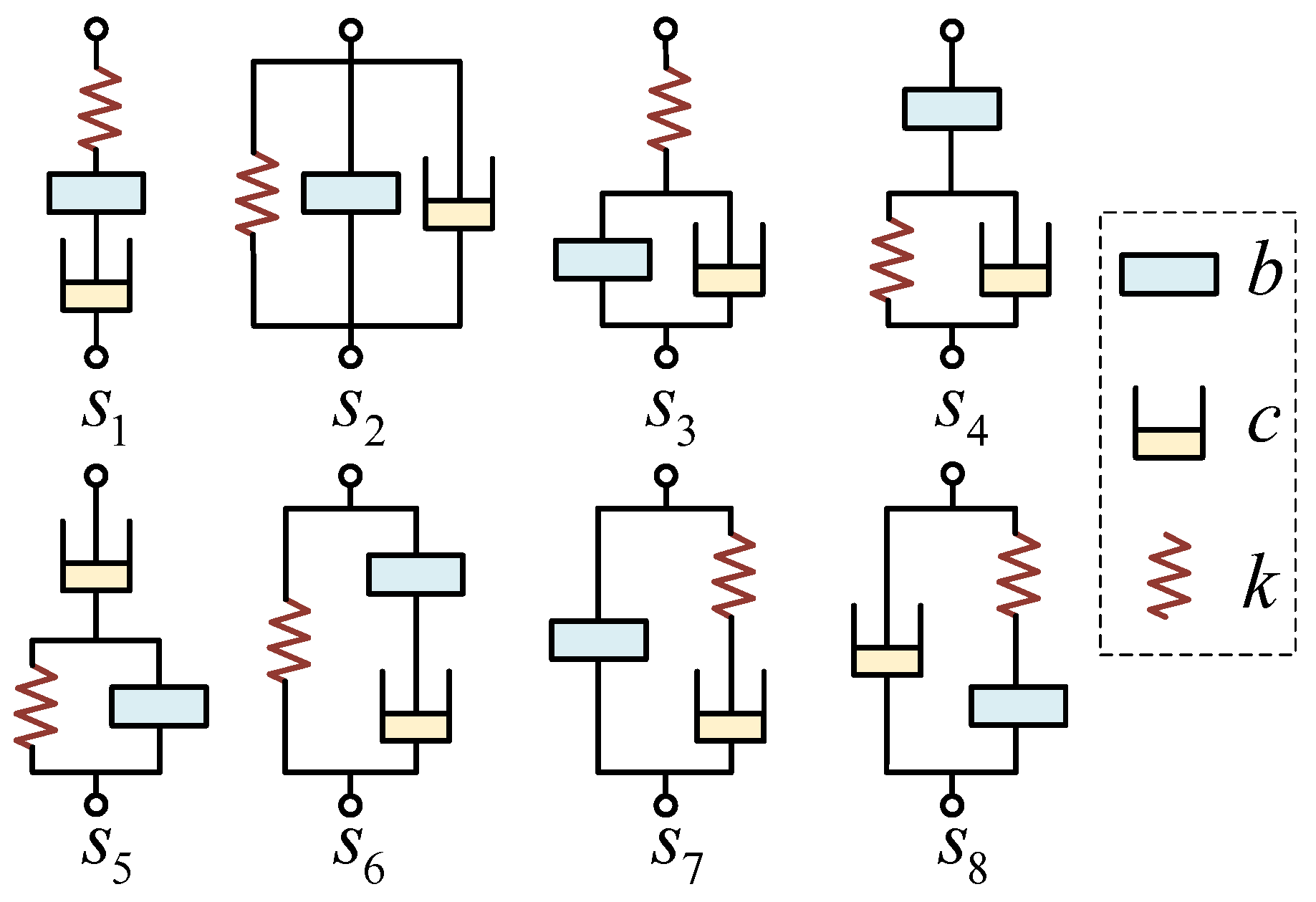
3.2. ISD Suspension Structural Design Based on Synthesis Method
3.2.1. The First Type of Synthesis Method
3.2.2. The Second Type of Synthesis Method
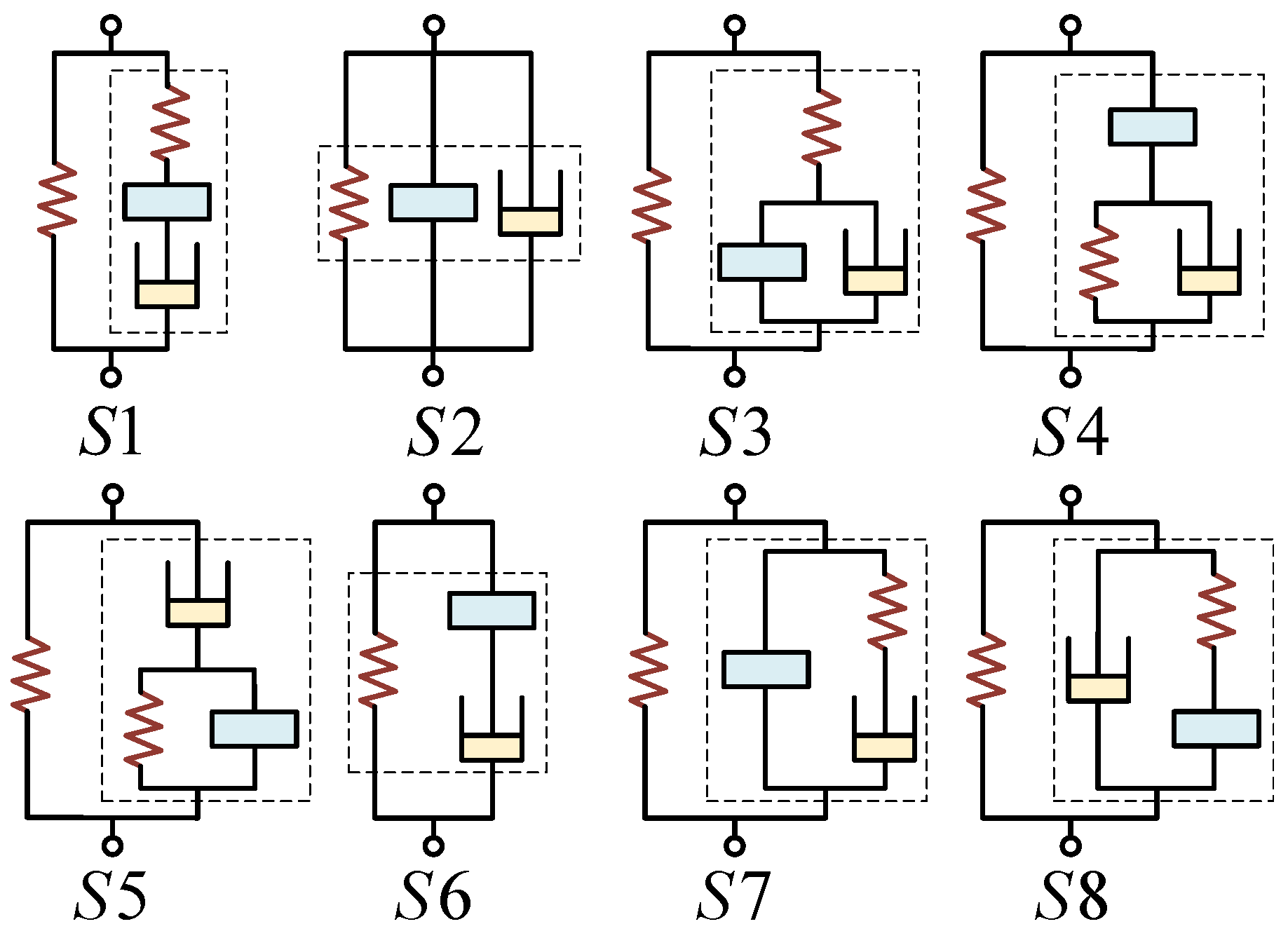
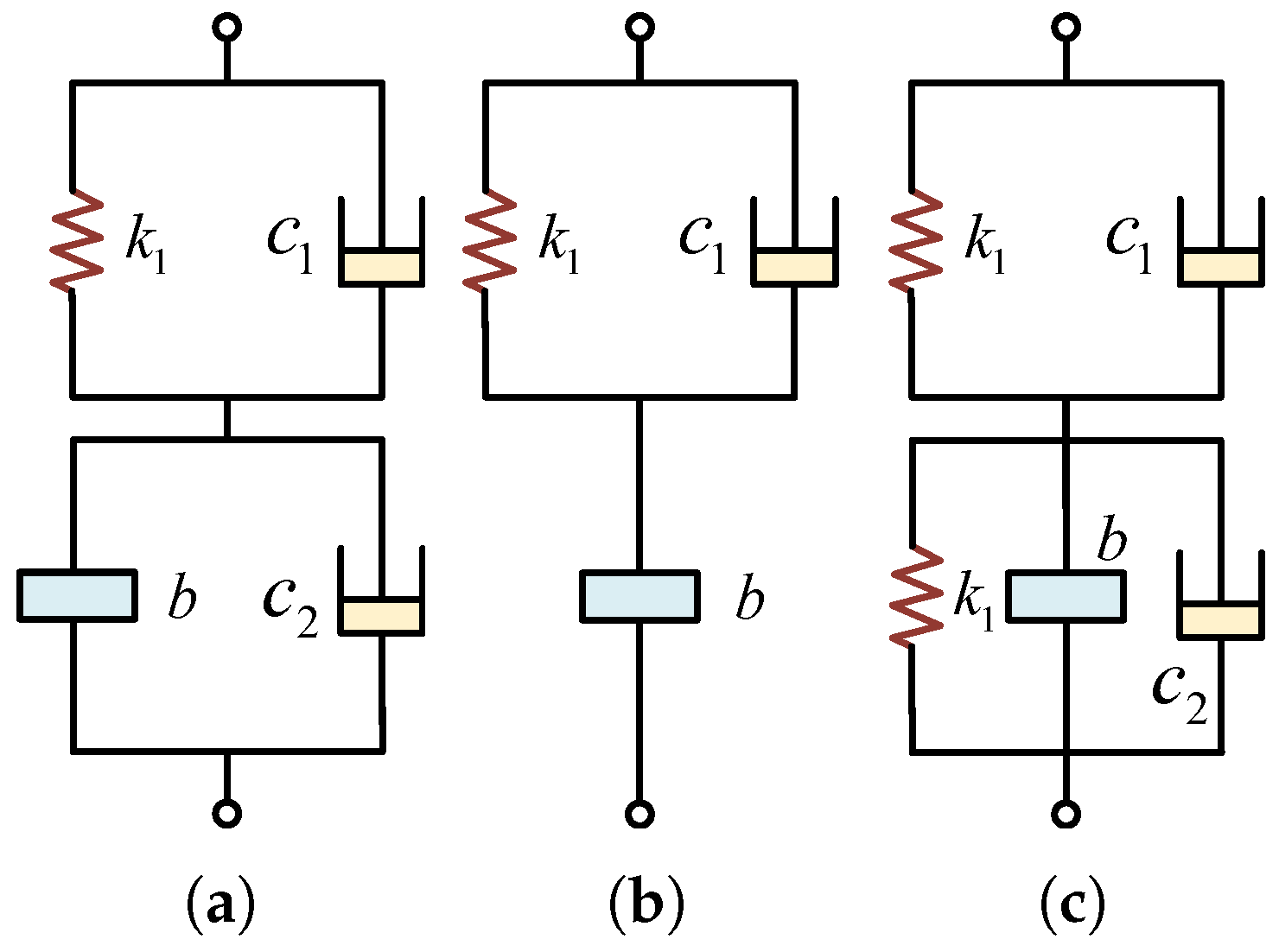
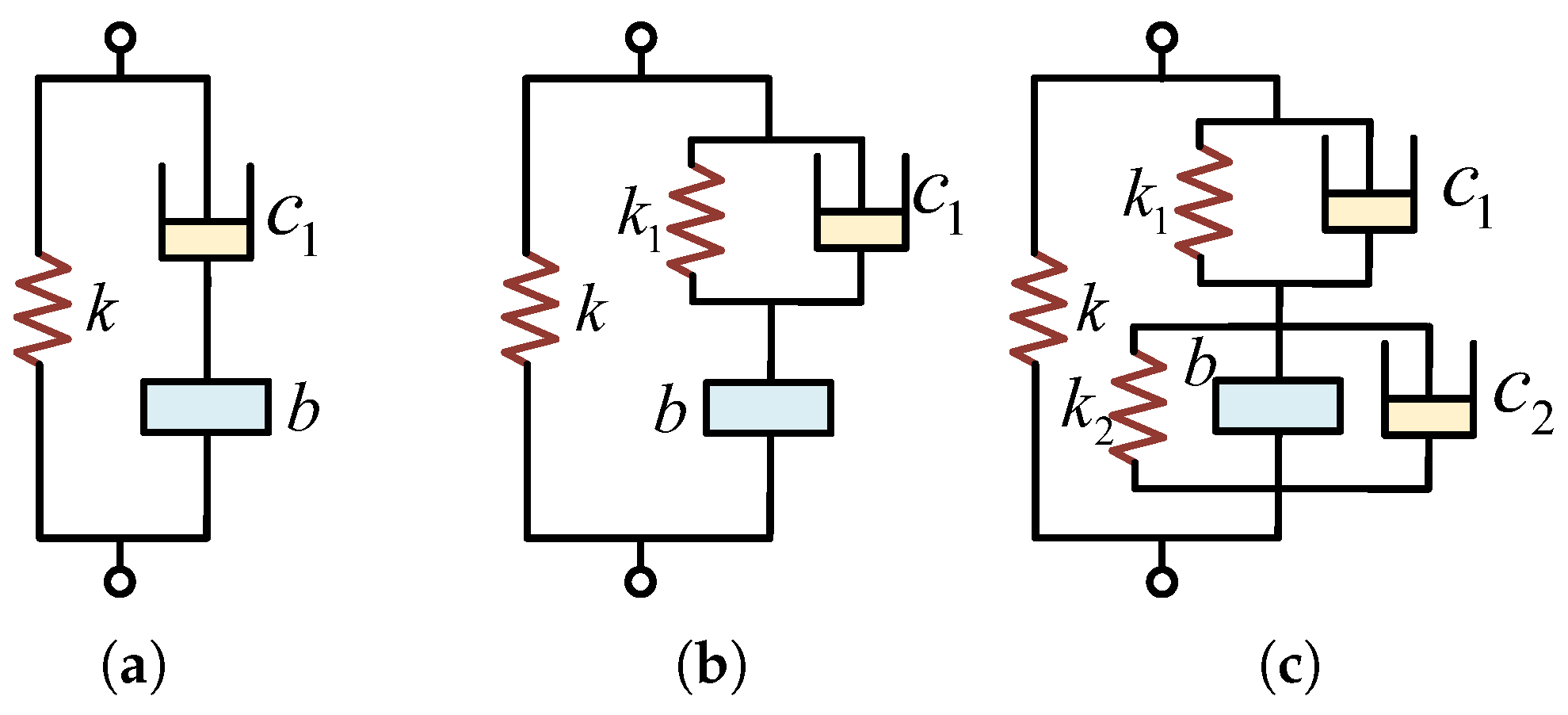
3.3. ISD Suspension Structural Design Based on Structure-Impedance Method
3.4. ISD Suspension Spatial Layout
4. ISD Suspension System Control Strategy
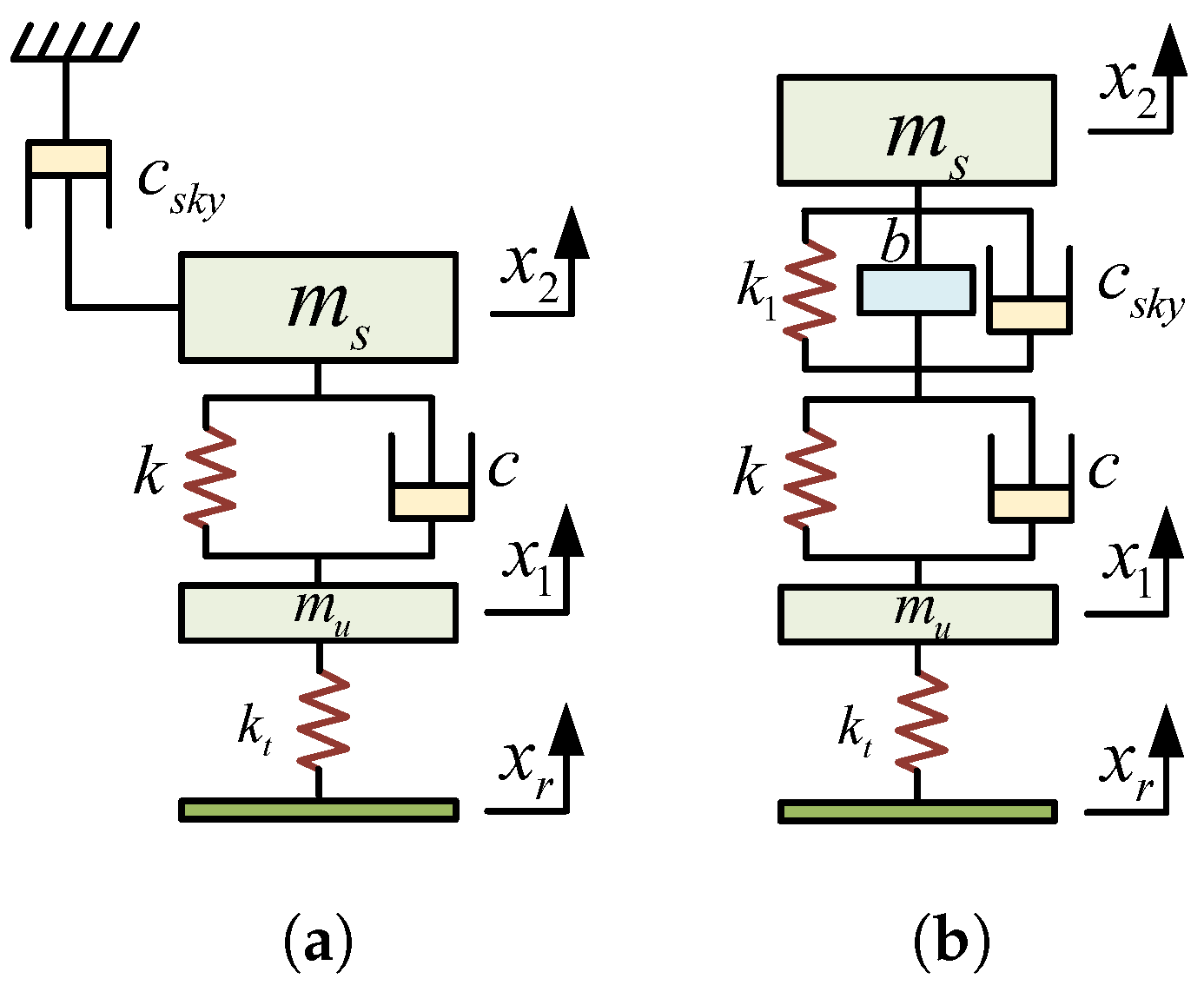
4.1. Skyhook Control
4.2. Groundhook Control
4.3. Hybrid-Hook Control
4.4. Acceleration-Driven Damping Control
4.5. Power-Driven Damping Control
4.6. Other Control
5. Application of ISD Suspension in Vehicles
6. Conclusions and Outlook
- In terms of inerter structural design, further research should be conducted to develop inerters with better performance, lower cost, and adaptability to various operating conditions [194]. Currently, mechanical inerters generally face challenges such as complex structures and high manufacturing costs. Although fluid inerters have a simpler structure, their ability to adjust the inertial mass coefficient is limited. The integration of linear motors with fluid inerters holds the potential to high inertia output capability, and this is expected to be a primary focus for future inerter development.
- Nonlinear factors influence the dynamic behavior of inerters and the vibration suppression performance of ISD suspensions. For example, backlash and friction in ball-screw mechanisms can cause hysteresis and output instability. At the same time, fluid inerters face issues such as viscous damping, parasitic damping, and nonlinear elasticity due to the flow of liquid in the helical pipes. Future research should focus on the nonlinear characteristics of inerters, developing effective modeling and compensation methods to mitigate their adverse impact on system performance.
- Existing ISD suspension structures primarily focus on vibration control within specific frequency bands, making it difficult to achieve collaborative optimization of vibration transmission characteristics across multiple frequency bands. Future research should overcome the limitations of traditional series and parallel topologies, by exploring high-order impedance function structures and complex bridge network configurations. This approach will enable effective regulation of vibration responses across a broader frequency range, significantly enhancing the vibration reduction performance of the suspension system.
- In the practical application of ISD suspension systems, there is a common issue of overall response delay in the control loop. Time delays exist in sensor sampling, controller computation, and the response of actuators, which cannot be ignored. These delays may lead to degraded control performance and even cause system instability. Therefore, future research should focus on developing high-precision system dynamics models that consider delay effects and designing advanced control strategies with strong robustness and quick response in order to effectively compensate for delay impacts and enhance the real-time performance and stability of the suspension system.
- With the development of intelligent vehicles and the concept of energy sustainability, achieving energy recovery while implementing vibration control in suspension systems has become an emerging research hotspot. For example, the design of structures based on the ball-screw mechatronic inerter or hydraulic electric inerter can convert mechanical energy into electrical energy during vibration control, which can then be used for the vehicle’s electrical grid or energy management system. Therefore, designing structural optimization and control strategies that simultaneously consider vibration control and energy harvesting will be a key direction for future research.
- The future development of inerters and ISD suspension systems will not be limited to vertical vibration reduction. It should also consider the overall vehicle system coordination, optimizing the vehicle’s vertical, pitch, and roll dynamic characteristics. The goal is to develop multi-objective control methods that jointly optimize comfort, safety, and road friendliness. Especially for heavy vehicles, off-road vehicles, and other special vehicles in complex operating conditions, further efforts are needed in system modeling, simulation verification, and real vehicle testing. This will help transition ISD suspension from theoretical research to engineering practicality and industrialization.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ISD | Inerter–spring–damper |
| DVA | Dynamic vibration absorber |
| RMS | Root mean square |
| FD | Fractional-order |
| SH | Skyhook damping control |
| GH | Groundhook damping control |
| HH | Hybrid-hook damping control |
| ADD | Acceleration-driven damping control |
| PDD | Power-driven damping control |
| SMC | Sliding mode control |
| MPC | Model predictive control |
| ADRC | Active disturbance rejection control |
References
- Cui, L.; Mao, H.; Xue, X.; Ding, S.; Qiao, B. Optimized design and test for a pendulum suspension of the crop spray boom in dynamic conditions based on a six DOF motion simulator. Int. J. Agric. Biol. Eng. 2018, 11, 76–85. [Google Scholar] [CrossRef]
- Xu, L.; Chai, X.; Gao, Z.; Li, Y.; Wang, Y. Experimental study on driver seat vibration characteristics of crawler-type combine harvester. Int. J. Agric. Biol. Eng. 2019, 12, 90–97. [Google Scholar] [CrossRef]
- Chen, S.; Zhou, Y.; Tang, Z.; Lu, S. Modal vibration response of rice combine harvester frame under multi-source excitation. Biosyst. Eng. 2020, 194, 177–195. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, Y.; Fu, S.; Feng, K.; Han, X.; Hu, Y.; Zhu, Q.; Wei, X. Analysis of vibration characteristics of tractor–rotary cultivator combination based on time domain and frequency domain. Agriculture 2024, 14, 1139. [Google Scholar] [CrossRef]
- Chen, J.; Liu, W.; Ding, R.; Sun, D.; Wang, R. Reference Model-Based Backstepping Control of Semi-Active Suspension for Vehicles Equipped with Non-Pneumatic Wheels. Machines 2025, 13, 476. [Google Scholar] [CrossRef]
- Wang, F.; Wen, H.; Xie, S. Performance Analysis and Hybrid Control Strategy Research of Vehicle Semi-Active Suspension for Ride Comfort and Handling Stability. Machines 2025, 13, 393. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, L.; Wang, R.; Xu, X.; Shen, Y.; Liu, Y. Modeling and test on height adjustment system of electrically-controlled air suspension for agricultural vehicles. Int. J. Agric. Biol. Eng. 2016, 9, 40–47. [Google Scholar] [CrossRef]
- Cui, L.; Xue, X.; Le, F.; Mao, H.; Ding, S. Design and experiment of electro hydraulic active suspension for controlling the rolling motion of spray boom. Int. J. Agric. Biol. Eng. 2019, 12, 72–81. [Google Scholar] [CrossRef]
- Ma, H.; Yan, B.; Zhang, L.; Zheng, W.; Wang, P.; Wu, C. On the design of nonlinear damping with electromagnetic shunt damping. Int. J. Mech. Sci. 2020, 175, 105513. [Google Scholar] [CrossRef]
- Bai, S.; Hou, Z. Impact of dynamic vibration absorbers on vehicle vertical vibration energy and suspension performances. J. Vib. Shock 2020, 39, 169–174. [Google Scholar] [CrossRef]
- Smith, M.C. Synthesis of mechanical networks: The inerter. IEEE Trans. Autom. Control 2002, 47, 1648–1662. [Google Scholar] [CrossRef]
- Smith, M.C. The inerter: A retrospective. Annu. Rev. Control. Robot. Auton. Syst. 2020, 3, 361–391. [Google Scholar] [CrossRef]
- Papageorgiou, C.; Houghton, N.E.; Smith, M.C. Experimental testing and analysis of inerter devices. J. Dyn. Syst. Meas. Control 2009, 131, 011001. [Google Scholar] [CrossRef]
- Papageorgiou, C.; Smith, M.C. Laboratory experimental testing of inerters. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 12–15 December 2005; pp. 3351–3356. [Google Scholar] [CrossRef]
- Jiang, H.; Geng, J.; Zhang, X.; Wang, T. Study on co-simulation of vehicle suspension system employing inerter based on virtual protoype model. J. Vib. Shock 2010, 29, 221–223. [Google Scholar] [CrossRef]
- Fang, Y.; Qin, J.; Di, C. Modeling and Simulation of Light Vehicle Weapon Based on Secondary Tandem ISD Suspension. J. Gun Launch Control 2018, 39, 11–16. [Google Scholar] [CrossRef]
- Li, H. Research on Ride Comfort and Road Friendly of ISD Suspension for Heavy Vehicle Based on Dynamic Inertia Effect. Master’s Thesis, Jiangsu University, Zhenjiang, China, 2019. Available online: https://kns.cnki.net/kcms2/article/abstract?v=liLFU49ICVulCPuNhNuVFMe1Ci1LVC3VQ1AvWLbb3Vsjr3_c7CSmjvIACgzj8wD3cpukGxKGxHDFnAjNpTQ2IDATMsG20W03T6PcKHRJiCnSDuSIHL3D-3Ryz2iChQlyAQ3GxIxQfIUUjBEc2DjnksEVh6pGHeuiHAZCr3r_XD0=&uniplatform=NZKPT (accessed on 20 July 2025).
- Zhao, Z.; Jin, M.; Tian, C.; Yang, S.X. Prediction of seed distribution in rectangular vibrating tray using grey model and artificial neural network. Biosyst. Eng. 2018, 175, 194–205. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, N.; Ma, G.; Taha, M.F.; Mao, H.; Zhang, X.; Shi, Q. Detection of spores using polarization image features and BP neural network. Int. J. Agric. Biol. Eng. 2024, 17, 213–221. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Ma, G.; Du, X.; Shaheen, N.; Mao, H. Recognition of weeds at asparagus fields using multi-feature fusion and backpropagation neural network. Int. J. Agric. Biol. Eng. 2021, 14, 190–198. [Google Scholar] [CrossRef]
- Guo, Y.; Gao, J.; Tunio, M.H.; Wang, L. Study on the identification of mildew disease of cuttings at the base of mulberry cuttings by aeroponics rapid propagation based on a BP neural network. Agronomy 2022, 13, 106. [Google Scholar] [CrossRef]
- Zhu, W.; Feng, Z.; Dai, S.; Zhang, P.; Wei, X. Using UAV multispectral remote sensing with appropriate spatial resolution and machine learning to monitor wheat scab. Agriculture 2022, 12, 1785. [Google Scholar] [CrossRef]
- Sun, X.; Chen, L.; Wang, R.; Zhang, X.; Chen, Y. Experiment and mechanical properties prediction on ball-screw inerter. J. Vib. Shock 2014, 33, 61–65+83. [Google Scholar] [CrossRef]
- Zhang, X.; Nie, J. Influence of the Friction Force on the Frequency Response Characteristics of Ballscrew Inerter. Mech. Sci. Technol. Aerosp. Eng. 2015, 34, 770–774. [Google Scholar] [CrossRef]
- Wen, H.; Zan, H.; Chen, N.; Yang, X. Study of the Impact of Inertia Container on the Dynamic Properties of Vibration Isolation System. J. Exp. Mech. 2015, 30, 483–490. [Google Scholar] [CrossRef]
- Guo, J.; Wen, H.; Liu, Y.; Li, Y. Correction of inertance of ball-screw inerter considering friction. J. Jiangsu Univ. Sci. Technol. (Nat. Sci. Ed.) 2018, 32, 667–671+745. Available online: https://jkdzk.cbpt.cnki.net/WKC/WebPublication/paperDigest.aspx?paperID=5764c532-2b83-4a1f-84d4-04550ab1ef72# (accessed on 18 April 2025).
- Li, Y.; Cheng, Z.; Hu, N.; Yang, Y.; Yin, Z. Study of dynamic breakdown of inerter and the improved design. Mech. Syst. Signal Process. 2022, 167, 108520. [Google Scholar] [CrossRef]
- Li, Y.; Cheng, Z.; Hu, N.; Huang, L.; Xiao, Z. Test and Verification Method of Inertance Based on Virtual-Real Mapping Model. J. Vib. Meas. Diagn. 2023, 43, 1108–1113+1242–1243. [Google Scholar] [CrossRef]
- Ge, Z.; Wang, W. Design and Characteristics Analysis of Ball Screw Type Inerter with Planetary Flywheel. Trans. Chin. Soc. Agric. Mach. 2017, 48, 391–398. [Google Scholar] [CrossRef]
- Yang, S.; Baddour, N.; Li, C. Design and evaluation of a passive inertial mass device for car suspension system. Int. J. Veh. Des. 2019, 80, 41–58. [Google Scholar] [CrossRef]
- Goh, K.; Soong, M.; Ramli, R.; Saifizul, A. Design optimization of variable inerter based on vehicle suspension performance criteria. Microsyst. Technol. 2024, 31, 1597–1609. [Google Scholar] [CrossRef]
- Wang, F.; Chan, H. Vehicle suspensions with a mechatronic network strut. Veh. Syst. Dyn. 2011, 49, 811–830. [Google Scholar] [CrossRef]
- Yang, X.; Yan, L.; Shen, Y.; Liu, Y.; Liu, C. Performance of New Type of Mechatronic Inerter. J. Vib. Meas. Diagn. 2022, 42, 343–349+411. [Google Scholar] [CrossRef]
- Wang, F.; Hong, M.; Lin, T. Designing and testing a hydraulic inerter. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 66–72. [Google Scholar] [CrossRef]
- Chen, L.; Ren, H.; Wang, R.; Sun, Z.; Chen, B. Simulations and tests for mechanical properties of a hydraulic inerter. J. Vib. Shock 2014, 33, 87–92. [Google Scholar] [CrossRef]
- Chen, X. Simulation Analysis of External Characteristics of Hydraulic Inerter Based on AMEsim. J. Yangzhou Polytech. Coll. 2024, 28, 47–51. [Google Scholar] [CrossRef]
- Chen, X. Simulation Analysis of Hydraulic Inerter. Automob. Appl. Technol. 2024, 49, 68–71. [Google Scholar] [CrossRef]
- Soong, M.F.; Ramli, R.; Mahadi, W.N.L.; Saifizul, A. Ride improvement of vehicle suspensions with switchable inerter based on force cancellation strategy. J. Vibroengineering 2017, 19, 1260–1272. [Google Scholar] [CrossRef]
- Bu, X.; Xie, Y. H∞ Control for Inerter Suspension with a Variable-inertance Hydraulic Inerter. J. Highw. Transp. Res. Dev. 2018, 35, 118–123. Available online: https://d.wanfangdata.com.cn/periodical/ChVQZXJpb2RpY2FsQ0hJMjAyNTA2MjISD2dsanRrajIwMTgxMjAxNxoIYmthZXJsMnM%3D (accessed on 25 April 2025).
- Yu, J.; Dong, X.; Su, X.; Tao, X.; Li, X. Design and testing of a semi-active inerter with magneto-rheological fluid valve. Smart Mater. Struct. 2021, 30, 105035. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, W.; Liu, Y.; Shen, Y.; Yan, L. Performance of Vehicle Suspension Based on Hydraulic Piston Inertial Container. J. Vib. Meas. Diagn. 2020, 40, 923–928+1023. [Google Scholar] [CrossRef]
- Shen, Y.; Shi, D.; Chen, L.; Liu, Y.; Yang, X. Modeling and experimental tests of hydraulic electric inerter. Sci. China Technol. Sci. 2019, 62, 2161–2169. [Google Scholar] [CrossRef]
- Zhang, H.; Shen, Y.; Yang, H. Impact of coil factors on a hydraulic electric inerter based vehicle suspension. J. Theor. Appl. Mech. 2020, 58, 711–722. [Google Scholar] [CrossRef]
- Swift, S.; Smith, M.C.; Glover, A.; Papageorgiou, C.; Gartner, B.; Houghton, N.E. Design and modelling of a fluid inerter. Int. J. Control 2013, 86, 2035–2051. [Google Scholar] [CrossRef]
- Wang, L.; Mao, M.; Lei, Q.; Chen, Y.; Zhang, X. Modeling and testing for a hydraulic inerter. J. Vib. Shock 2018, 37, 146–152. [Google Scholar] [CrossRef]
- Shen, T.; Zou, X.; Shi, J.; Li, Z.; Huang, X.; Xu, Y.; Wu, C. Determination geographical origin and flavonoids content of goji berry using near-infrared spectroscopy and chemometrics. Food Anal. Methods 2016, 9, 68–79. [Google Scholar] [CrossRef]
- Sun, J.; Lu, X.; Mao, H.; Wu, X.; Gao, H. Quantitative determination of rice moisture based on hyperspectral imaging technology and BCC-LS-SVR algorithm. J. Food Process Eng. 2017, 40, e12446. [Google Scholar] [CrossRef]
- Tian, Y.; Sun, J.; Zhou, X.; Wu, X.; Lu, B.; Dai, C. Research on apple origin classification based on variable iterative space shrinkage approach with stepwise regression–support vector machine algorithm and visible-near infrared hyperspectral imaging. J. Food Process Eng. 2020, 43, e13432. [Google Scholar] [CrossRef]
- Zareef, M.; Chen, Q.; Hassan, M.M.; Arslan, M.; Hashim, M.M.; Ahmad, W.; Kutsanedzie, F.Y.; Agyekum, A.A. An overview on the applications of typical non-linear algorithms coupled with NIR spectroscopy in food analysis. Food Eng. Rev. 2020, 12, 173–190. Available online: https://link.springer.com/article/10.1007/s12393-020-09210-7 (accessed on 10 July 2025). [CrossRef]
- Tang, N.; Sun, J.; Yao, K.; Zhou, X.; Tian, Y.; Cao, Y.; Nirere, A. Identification of Lycium barbarum varieties based on hyperspectral imaging technique and competitive adaptive reweighted sampling-whale optimization algorithm-support vector machine. J. Food Process Eng. 2021, 44, e13603. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, L.; Liu, Y.; Yang, X.; Zhang, X.; Wang, R. Predicting Model of Fluid Inerter Based on the Quantum Genetic Support Vector Machine. J. Vib. Meas. Diagn. 2018, 38, 897–902+1076. [Google Scholar] [CrossRef]
- Wagg, D.J.; Pei, J.S. Modeling a helical fluid inerter system with time-invariant mem-models. Struct. Control Health Monit. 2020, 27, e2579. [Google Scholar] [CrossRef]
- Wang, S.; Liu, H.; Li, X. Numerical Simulation of Flow Field in Spiral Tube of Hydraulic Inertial Vessel. Chin. Hydraul. Pneum. 2022, 46, 159–166. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Geng, C. Research on load adaptability of dynamic vibration absorption nonlinear inerter-spring-damper suspension. Mach. Des. Manuf. Eng. 2022, 51, 71–76. [Google Scholar] [CrossRef]
- Chillemi, M.; Furtmüller, T.; Adam, C.; Pirrotta, A. Nonlinear mechanical model of a fluid inerter. Mech. Syst. Signal Process. 2023, 188, 109986. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, S.; Wang, S.; Li, X. Numerical simulation of convection heat transfer in a hydraulic inertia vessel spiral tube. Agric. Equip. Veh. Eng. 2024, 62, 112–116. [Google Scholar] [CrossRef]
- Du, F.; Wang, C.; Nie, W. Modeling and Experimental Study of the Dual Cylinder Fluid Inerter. Appl. Sci. 2022, 12, 10849. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Li, H. Tube damping design for fluid-based inerters. J. Vib. Shock 2024, 23, 106–112. [Google Scholar] [CrossRef]
- Liao, Y.; Tang, H.; Guo, T.; Li, R.; Xie, L. An investigation on seismic performance of the separated fluid inerter base on model experiment and shaking table test. Structures 2024, 69, 107379. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, H.; Xie, L.; Long, P.; Xue, S. On the fluid inerter with piecewise nonlinearity for enhanced vibration isolation. Nonlinear Dyn. 2025, 113, 14585–14606. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, L.; Wang, R.; Zhang, X.; Liu, C. Semi-active suspension control based on the general theory of skyhook control. J. Vib. Shock 2021, 40, 66–74. [Google Scholar] [CrossRef]
- Liu, C.; Chen, L.; Zhang, X.; Yang, Y.; Nie, J. Design and tests of a controllable inerter with fluid-air mixture condition. IEEE Access 2020, 8, 125620–125629. [Google Scholar] [CrossRef]
- Liu, C.; Chen, L.; Zhang, X.; Yang, Y. Nonlinear Modelling Analysis and Parameter Identification Test of Controllable Inerter. J. Vib. Meas. Diagn. 2022, 42, 1115–1121. [Google Scholar] [CrossRef]
- Tang, F.; Wang, Y.; Ding, H.; Chen, L. Dynamic characteristics of skyhook semi-active inerter-based vibration isolator. J. Vib. Shock 2021, 40, 65–72. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Ji, M.; Qiao, X.; Wang, Y. Dynamic characteristics of a semi-active fractional-order inerter-based suspension with acceleration-velocity switch control. J. Low Freq. Noise, Vib. Act. Control 2025, 44, 1117–1138. [Google Scholar] [CrossRef]
- Yang, J. Performance Analysis and Test Research of ISD Suspension Based on the Inerter with Variable Inertance. Master’s Thesis, Jiangsu University, Zhenjiang, China, 2016. [Google Scholar] [CrossRef]
- Tran, K.T.; Deng, L.; Jin, S.; Du, H.; Quoc Nguyen, H.; Li, W. Design, modelling and evaluation of a variable inertance bypass fluid inerter. J. Intell. Mater. Syst. Struct. 2024, 1045389X241258417. [Google Scholar] [CrossRef]
- Zhang, X.; Geng, C.; Nie, J.; Gao, Q. Modelling and characteristic test for hydraulic mem-inerter device. J. Zhejiang Univ. Sci. (Eng. Sci.) 2021, 55, 430–440. Available online: https://d.wanfangdata.com.cn/periodical/ChVQZXJpb2RpY2FsQ0hJMjAyNTA2MjISEnpqZHh4Yi1neDIwMjEwMzAwMhoIZDgzeW94dzI%3D (accessed on 5 May 2025).
- Zhang, X.; Gao, Q.; Nie, J. The mem-inerter: A new mechanical element with memory. Adv. Mech. Eng. 2018, 10, 1687814018778428. [Google Scholar] [CrossRef]
- Zhang, X.; He, H.; Nie, J.; Chen, L. Performance analysis of semi-active suspension with skyhook-inertance control. J. Jiangsu Univ. (Nat. Sci. Ed.) 2018, 39, 497–502. [Google Scholar] [CrossRef]
- Zhang, X.; Niu, D.; Nie, J.; Chen, L. Modeling and testing of adjustable device integrated by inerter and damper. J. Guangxi Univ. (Nat. Sci. Ed.) 2020, 45, 1108–1120. [Google Scholar] [CrossRef]
- Li, Y.; Hu, N.; Yang, Y.; Cheng, Z.; Yin, Z.; Zhou, Z.; Hu, J. Physical realizations of inerter and inerter-based vibration control. Heliyon 2024, 10, e35870. [Google Scholar] [CrossRef]
- He, T. Topology Optimization and Performance Research of Vehicle Mechatronic Dynamic Inertial Suspension Based on Bridge Network. Master’s Thesis, Jiangsu University, Zhenjiang, China, 2022. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Jiang, J.Z.; Neild, S.A. Passive vibration control: A structure–immittance approach. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20170011. [Google Scholar] [CrossRef]
- Xu, L.; Mao, M.; Chen, Y.J.; Du, F.; Dai, J. A Systematic Review of Vehicle ISD Suspension Configuration Design. Acta Armamentarii 2020, 41, 822–832. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, X.; Nie, J.; Wang, R. Performance Analysis of Two-stage Series-connected Inerter-spring-damper Suspension Based on Half-car Model. J. Mech. Eng. 2012, 48, 102–108. Available online: https://d.wanfangdata.com.cn/periodical/ChVQZXJpb2RpY2FsQ0hJMjAyNTA2MjISD2p4Z2N4YjIwMTIwNjAxNhoIOTVmc2k2d3M%3D (accessed on 18 May 2025). [CrossRef]
- Zhang, X.; Chen, L.; Nie, J.; Wang, R.; Chen, Y. Analysis and experiment of frequency response characteristics of two-stage series-connected ISD suspension. J. Jiangsu Univ. (Nat. Sci. Ed.) 2012, 33, 255–258. [Google Scholar]
- Sun, X.; Chen, L.; Zhang, X.; Nie, J. Study of Ride Comfort on Ball-screw ISD Suspension Based on ADAMS. Veh. Power Technol. 2012, 126, 1–4. [Google Scholar] [CrossRef]
- Sun, X.; Chen, L.; Wang, S.; Yuan, C.; Zhang, X. Analysis of vibration isolation performance for nolinear inerter-spring-damper suspension. Trans. Chin. Soc. Agric. Eng. 2013, 29, 38–45. [Google Scholar] [CrossRef]
- Sun, X.; Chen, L.; Wang, S.; Yuan, C.; Zhang, X. Nonlinear Modeling and Parameter Optimization of Two-stage Series-connected ISD Suspension. Trans. Chin. Soc. Agric. Mach. 2014, 45, 7–13. [Google Scholar] [CrossRef]
- Li, F.; Li, X.; Shang, D.; Wang, Z. Dynamic modeling and damping performance improvement of two stage ISD suspension system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 2259–2271. [Google Scholar] [CrossRef]
- Chen, L.; Yang, X.; Wang, R.; Huang, C.; Shen, Y. Design and performance study of vehicle passive suspension based on two-element inerter-spring-damper structure vibration isolation mechanism. J. Vib. Shock 2013, 32, 90–95. [Google Scholar] [CrossRef]
- Yang, X.; Chen, L.; Shen, Y.; Wang, R. Analysis on vehicle passive inerter-spring-damper suspension employing simple three-element structure. J. Vib. Shock 2013, 30, 42–47. [Google Scholar] [CrossRef]
- Chen, L.; Yang, X.; Wang, R.; Huang, C.; Shen, Y. A Study on the Performances of Vehicle Passive Suspension with Modified Inerter-spring-damper Three-element Structure. Automot. Eng. 2014, 36, 340–345. [Google Scholar] [CrossRef]
- Zhu, Y.; Zou, X.; Shen, T.; Shi, J.; Zhao, J.; Holmes, M.; Li, G. Determination of total acid content and moisture content during solid-state fermentation processes using hyperspectral imaging. J. Food Eng. 2016, 174, 75–84. [Google Scholar] [CrossRef]
- Kutsanedzie, F.Y.; Chen, Q.; Hassan, M.M.; Yang, M.; Sun, H.; Rahman, M.H. Near infrared system coupled chemometric algorithms for enumeration of total fungi count in cocoa beans neat solution. Food Chem. 2018, 240, 231–238. [Google Scholar] [CrossRef]
- Agyekum, A.A.; Kutsanedzie, F.Y.; Mintah, B.K.; Annavaram, V.; Zareef, M.; Hassan, M.M.; Arslan, M.; Chen, Q. Rapid and nondestructive quantification of trimethylamine by FT-NIR coupled with chemometric techniques. Food Anal. Methods 2019, 12, 2035–2044. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, P.; Wang, M.; Zuo, M.; El-Seedi, H.R.; Chen, Q.; Shi, J.; Zou, X. Rapid enrichment detection of patulin and alternariol in apple using surface enhanced Raman spectroscopy with coffee-ring effect. LWT 2021, 152, 112333. [Google Scholar] [CrossRef]
- Yang, X.; Shen, Y.; Liu, Y.; Yang, J. Research on performance improvement of vehicle ISD suspension in steering condition. J. Chin. Agric. Mech. 2015, 36, 147–151. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, C.; Lai, S.K.; Chen, Z.; Chen, L. Frequency-dependent equivalent impedance analysis for optimizing vehicle inertial suspensions. Nonlinear Dyn. 2025, 113, 9373–9398. [Google Scholar] [CrossRef]
- Jiang, T.; Chen, L.; Zhang, X. Suspension Performance Analysis Based on Combination of Inerter-Spring-Damper. J. Chongqing Univ. Technol. (Nat. Sci.) 2014, 28, 30–35+70. [Google Scholar] [CrossRef]
- Du, F.; Mao, M.; Chen, Y.; Wang, Y.; Zhang, Y. Structure design and performance analysis of inerter-spring-damper suspension structure based on dynamic model and parameter optimization. J. Vib. Shock 2014, 33, 59–65. [Google Scholar] [CrossRef]
- Li, F.; Li, X.; Wo, X.; Wen, B. Analysis and Optimization of Damping Performance of Suspension System of Hybrid Connected Vehicle. J. Northeast. Univ. (Nat. Sci.) 2021, 42, 1098–1104. [Google Scholar] [CrossRef]
- Zhang, X.; Nie, J.; Wang, R.; Chen, L. Passive Skyhook-damping Suspension System Based on Inerter-Spring-Damper Structural System. Trans. Chin. Soc. Agric. Mach. 2013, 44, 10–14+9. [Google Scholar] [CrossRef]
- Zhang, X.; Nie, J.; Yuan, C.; Hou, Y. A Passive Realization Method of Ideal Skyhook Damping. Trans. Beijing Inst. Technol. 2014, 34, 22–26. [Google Scholar] [CrossRef]
- Jiang, T.; Chen, L.; Zhang, X. Passive Skyhook Suspension Reduction and Optimization. Chin. J. Automot. Eng. 2015, 5, 187–192. [Google Scholar] [CrossRef]
- Zhang, X.; Nie, J. Design and Characteristics Analysis of Passive Groundhook-damping Suspension System. Mach. Des. Res. 2014, 30, 170–173. [Google Scholar] [CrossRef]
- Zhang, X.; Nie, J.; Chen, L. Passive realization method for ideal groundhook damping based on Simscape. Mach. Des. Res. 2014, 33, 26–31. [Google Scholar] [CrossRef]
- Nie, J.; Zhang, X. Experiment of vehicle passive skyhook damping suspension system. Trans. Chin. Soc. Agric. Eng. 2015, 31, 66–71. Available online: https://d.wanfangdata.com.cn/periodical/ChVQZXJpb2RpY2FsQ0hJMjAyNTA2MjISD255Z2N4YjIwMTUwNzAxMBoIcXY0ejZvNm8%3D (accessed on 8 June 2025).
- Yang, X.; Shen, Y.; Chen, L.; Wang, R.; Sun, X. Design and Performances Analysis of Vehicle ISD Suspension Based on Dynamic Vibration Absorber Theory. Automot. Eng. 2014, 36, 1262–1266+1277. [Google Scholar] [CrossRef]
- Ge, Z.; Wang, W. Vehicle active ISD-DVA suspension system. J. Vib. Shock 2017, 36, 167–174. [Google Scholar] [CrossRef]
- Yang, X.; Du, Y.; Liu, Y.; Shen, Y. Analysis of the effect of the parameters on vibration response characteristics of the vehicle ISD suspension based on the dynamic vibration absorber. China Sci. 2015, 10, 2592–2595. Available online: https://cstj.cqvip.com/Qikan/Article/Detail?id=667595641 (accessed on 10 June 2025).
- Chen, G.; Chen, L.; Zhang, X.; Wang, R. The PR synthesis research of the ISD suspension system. Mach. Des. Manuf. 2012, 12, 116–118. [Google Scholar] [CrossRef]
- Nie, J.; Huang, X.; Zhang, X.; Wei, H. Network Synthesis Design Method of Nonlinear Mem-inerter Suspension System. J. South China Univ. Technol. (Nat. Sci. Ed.) 2022, 50, 78–89. [Google Scholar] [CrossRef]
- Nie, J.; Zhang, X.; Chen, G. The network synthesis and characteristics analysis of an inerter-spring-damper suspension system. J. Vib. Shock 2016, 35, 115–119. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, K.; Chen, Y.; Chen, M.Z. Inerter-based semi-active suspensions with low-order mechanical admittance via network synthesis. Trans. Inst. Meas. Control 2018, 40, 4233–4245. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, L.; Huang, C.; Lu, Y.; Wang, C. A dynamic tire model based on HPSO-SVM. Int. J. Agric. Biol. Eng. 2019, 12, 36–41. [Google Scholar] [CrossRef]
- Bonah, E.; Huang, X.; Yi, R.; Aheto, J.H.; Osae, R.; Golly, M. Electronic nose classification and differentiation of bacterial foodborne pathogens based on support vector machine optimized with particle swarm optimization algorithm. J. Food Process Eng. 2019, 42, e13236. [Google Scholar] [CrossRef]
- Cao, Y.; Li, H.; Sun, J.; Zhou, X.; Yao, K.; Nirere, A. Nondestructive determination of the total mold colony count in green tea by hyperspectral imaging technology. J. Food Process Eng. 2020, 43, e13570. [Google Scholar] [CrossRef]
- Ding, Y.; Yan, Y.; Li, J.; Chen, X.; Jiang, H. Classification of tea quality levels using near-infrared spectroscopy based on CLPSO-SVM. Foods 2022, 11, 1658. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, Y.; Chen, L.; Yang, X.; Qiu, C. Optimal design and performance analysis of a vehicle ISD suspension based on the high order impedance transfer function. J. Vib. Shock 2019, 38, 95–100. [Google Scholar] [CrossRef]
- Shen, Y.; Li, Z.; Tian, X.; Ji, K.; Yang, X. Vibration suppression of the vehicle mechatronic ISD suspension using the fractional-order biquadratic electrical network. Fractal Fract. 2025, 9, 106. [Google Scholar] [CrossRef]
- Li, Y.; Han, S.; Xiong, J.; Wang, W. Comfort-oriented semi-active suspension configuration with inerter-based network synthesis. Actuators 2023, 12, 290. [Google Scholar] [CrossRef]
- Yang, X.; He, T.; Shen, Y.; Liu, Y.; Zhang, Y. Optimal design and performance research of vehicle mechatronic inertial suspension based on a bridge network. J. Vib. Shock 2023, 42, 96–103. [Google Scholar] [CrossRef]
- Yang, X.; Yan, Y.; Shen, Y.; Liu, X.; Wang, Z. Optimal design and dynamic performance analysis of HMDV suspension based on bridge network. Acta Mech. Sin. 2025, 41, 524208. [Google Scholar] [CrossRef]
- Shen, Y.; Hua, J.; Wu, B.; Chen, Z.; Xiong, X.; Chen, L. Optimal design of the vehicle mechatronic ISD suspension system using the structure-immittance approach. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 512–521. [Google Scholar] [CrossRef]
- Mao, M.; Wang, L.; Chen, Y.; Lei, Q.; Du, F. Research Progress in Inerter and Inerter-spring-damper Suspension. Acta Armamentarii 2016, 37, 525–534. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Z.; Nie, J. Influence of the Parasitic Damping and Additional Stiffness on the Hybrid-Connected ISD Suspension. Trans. Beijing Inst. Technol. 2017, 37, 693–697. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Jiang, T. Vehicle Road Test of ISD Suspension with Inerter and Damper Connected in Series. Automot. Eng. 2016, 38, 1391–1395. [Google Scholar] [CrossRef]
- Nie, J.; Wang, F.; Zhang, X.; Yang, Y. Design and test of hydro-pneumatic ISD suspension in heavy multi-axle vehicles. Adv. Mech. Eng. 2021, 13, 16878140211064737. [Google Scholar] [CrossRef]
- Nie, J.; Wei, H.; Zhang, X.; Yang, Y.; Zhang, H. Simulation analysis and experiment research on hydraulic inerter suspension. Mach. Des. Manuf. Eng. 2023, 52, 20–25. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, J.; Nie, J.; Wei, H.; Chen, L. Simulation Analysis and Experiment Research on Hydro-Pneumatic ISD Suspension. Shock Vib. 2021, 2021, 2095350. [Google Scholar] [CrossRef]
- Yang, L.; Wang, R.; Ding, R.; Liu, W.; Zhu, Z. Investigation on the dynamic performance of a new semi-active hydro-pneumatic inerter-based suspension system with MPC control strategy. Mech. Syst. Signal Process. 2021, 154, 107569. [Google Scholar] [CrossRef]
- Yang, L.; Wang, R.; Meng, X.; Sun, Z.; Liu, W.; Wang, Y. Performance analysis of a new hydropneumatic inerter-based suspension system with semi-active control effect. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 1883–1896. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, L.; Yang, X. Analysis on Structure Design and Performance of Inerter Suspension. Mach. Des. Manuf. 2014, 12, 58–61. [Google Scholar] [CrossRef]
- Lei, L.; Lei, J.; Lin, L.; Chang, C. Integration design and analysis of ISD suspension. J. Guangxi Univ. (Nat. Sci. Ed.) 2018, 43, 869–879. [Google Scholar] [CrossRef]
- Chen, J.; Ning, X.; Li, Y.; Yang, G.; Wu, P.; Chen, S. A fuzzy control strategy for the forward speed of a combine harvester based on KDD. Appl. Eng. Agric. 2017, 33, 15–22. [Google Scholar] [CrossRef]
- Zhu, Z.; Zeng, L.; Chen, L.; Zou, R.; Cai, Y. Fuzzy adaptive energy management strategy for a hybrid agricultural tractor equipped with HMCVT. Agriculture 2022, 12, 1986. [Google Scholar] [CrossRef]
- Yu, Y.; Hao, S.; Guo, S.; Tang, Z.; Chen, S. Motor torque distribution strategy for different tillage modes of agricultural electric tractors. Agriculture 2022, 12, 1373. [Google Scholar] [CrossRef]
- Han, J.; Yan, X.; Tang, H. Method of controlling tillage depth for agricultural tractors considering engine load characteristics. Biosyst. Eng. 2023, 227, 95–106. [Google Scholar] [CrossRef]
- Cui, B.; Cui, X.; Wei, X.; Zhu, Y.; Ma, Z.; Zhao, Y.; Liu, Y. Design and Testing of a Tractor Automatic Navigation System Based on Dynamic Path Search and a Fuzzy Stanley Model. Agriculture 2024, 14, 2136. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, J.; Liu, Y.; Zhang, T.; Meng, Y.; Chen, J.; Zhou, C.; Hu, J.; Chen, X. An Ultrasonic Ridge-Tracking Method Based on Limiter Sliding Window Filter and Fuzzy Pure Pursuit Control for Ridge Transplanter. Agriculture 2024, 14, 1713. [Google Scholar] [CrossRef]
- Song, X.; Li, H.; Chen, C.; Xia, H.; Zhang, Z.; Tang, P. Design and experimental testing of a control system for a solid-fertilizer-dissolving device based on fuzzy PID. Agriculture 2022, 12, 1382. [Google Scholar] [CrossRef]
- Li, J.; Nie, Z.; Chen, Y.; Ge, D.; Li, M. Development of boom posture adjustment and control system for wide spray boom. Agriculture 2023, 13, 2162. [Google Scholar] [CrossRef]
- Li, C.; Wu, J.; Pan, X.; Dou, H.; Zhao, X.; Gao, Y.; Yang, S.; Zhai, C. Design and experiment of a breakpoint continuous spraying system for automatic-guidance boom sprayers. Agriculture 2023, 13, 2203. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhu, Z.; Zhang, H.; Gao, Y.; Chen, L. Design of an electronically controlled fertilization system for an air-assisted side-deep fertilization machine. Agriculture 2023, 13, 2210. [Google Scholar] [CrossRef]
- Zhu, Y.; Cui, B.; Yu, Z.; Gao, Y.; Wei, X. Tillage Depth Detection and Control Based on Attitude Estimation and Online Calibration of Model Parameters. Agriculture 2024, 14, 2130. [Google Scholar] [CrossRef]
- Shi, W.; Xue, X.; Feng, F.; Zheng, W.; Chen, L. Fertigation control system based on the mariotte siphon. Sci. Rep. 2024, 14, 23573. [Google Scholar] [CrossRef]
- Chen, S.; Qi, J.; Gao, J.; Chen, W.; Fei, J.; Meng, H.; Ma, Z. Research on the Control System for the Conveying and Separation Experimental Platform of Tiger Nut Harvester Based on Sensing Technology and Control Algorithms. Agriculture 2025, 15, 115. [Google Scholar] [CrossRef]
- Li, J.; Shang, Z.; Li, R.; Cui, B. Adaptive sliding mode path tracking control of unmanned rice transplanter. Agriculture 2022, 12, 1225. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Z.; Ding, S.; Xia, J.; Xing, G. Adaptive disturbance observer-based fixed time nonsingular terminal sliding mode control for path-tracking of unmanned agricultural tractors. Biosyst. Eng. 2024, 246, 96–109. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, K.; Ding, R.; Jiang, Y.; Jiang, Y. A Novel Hydraulic Interconnection Design and Sliding Mode Synchronization Control of Leveling System for Crawler Work Machine. Agriculture 2025, 15, 137. [Google Scholar] [CrossRef]
- Lu, E.; Ma, Z.; Li, Y.; Xu, L.; Tang, Z. Adaptive backstepping control of tracked robot running trajectory based on real-time slip parameter estimation. Int. J. Agric. Biol. Eng. 2020, 13, 178–187. [Google Scholar] [CrossRef]
- Jin, M.; Zhao, Z.; Chen, S.; Chen, J. Improved piezoelectric grain cleaning loss sensor based on adaptive neuro-fuzzy inference system. Precis. Agric. 2022, 23, 1174–1188. [Google Scholar] [CrossRef]
- Hu, J.; Pan, J.; Dai, B.; Chai, X.; Sun, Y.; Xu, L. Development of an attitude adjustment crawler chassis for combine harvester and experiment of adaptive leveling system. Agronomy 2022, 12, 717. [Google Scholar] [CrossRef]
- Wang, W.; Yang, S.; Zhang, X.; Xia, X. Research on the smart broad bean harvesting system and the self-adaptive control method based on CPS technologies. Agronomy 2024, 14, 1405. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, K.; Yang, S.; Han, X.; Wei, X.; Zhu, Q.; Chen, L. Design and experiment of an unmanned variable-rate fertilization control system with self-calibration of fertilizer discharging shaft speed. Agronomy 2024, 14, 2336. [Google Scholar] [CrossRef]
- Liu, H.; Yan, S.; Shen, Y.; Li, C.; Zhang, Y.; Hussain, F. Model predictive control system based on direct yaw moment control for 4WID self-steering agriculture vehicle. Int. J. Agric. Biol. Eng. 2021, 14, 175–181. [Google Scholar] [CrossRef]
- Lu, E.; Xue, J.; Chen, T.; Jiang, S. Robust trajectory tracking control of an autonomous tractor-trailer considering model parameter uncertainties and disturbances. Agriculture 2023, 13, 869. [Google Scholar] [CrossRef]
- Zhang, S.; Xue, X.; Chen, C.; Sun, Z.; Sun, T. Development of a low-cost quadrotor UAV based on ADRC for agricultural remote sensing. Int. J. Agric. Biol. Eng. 2019, 12, 82–87. [Google Scholar] [CrossRef]
- Ji, X.; Wang, A.; Wei, X. Precision control of spraying quantity based on linear active disturbance rejection control method. Agriculture 2021, 11, 761. [Google Scholar] [CrossRef]
- Tang, L.; Wang, W.; Zhang, C.; Wang, Z.; Ge, Z.; Yuan, S. Linear Active Disturbance Rejection Control System for the Travel Speed of an Electric Reel Sprinkling Irrigation Machine. Agriculture 2024, 14, 1544. [Google Scholar] [CrossRef]
- Karnopp, D.; Crosby, M.J.; Harwood, R.A. Vibration control using semi-active force generators. J. Eng. Ind. 1974, 96, 619–626. [Google Scholar] [CrossRef]
- Liu, C.; Lai, S.K.; Ni, Y.Q.; Chen, L. Dynamic modelling and analysis of a physics-driven strategy for vibration control of railway vehicles. Veh. Syst. Dyn. 2025, 63, 1080–1110. [Google Scholar] [CrossRef]
- Shen, Y.; Ji, K.; Huang, R.; Yang, X.; Liu, Y. Dynamic Performance Analysis of ISD Suspension for Vehicles Based on Fractional-Order Skyhook Control. Automot. Eng. 2025, 47, 332–341. [Google Scholar] [CrossRef]
- Yang, X.; Zeng, S.; Liu, C.; Liu, X.; Wang, Z.; Yang, Y. Optimal design and performance evaluation of HMDV inertial suspension based on generalized skyhook control. Int. J. Struct. Stab. Dyn. 2025, 25, 2550069. [Google Scholar] [CrossRef]
- Valáček, M.; Stejskal, V.; Řika, Z.; Vaculin, O. Control concepts of semi-active damping of truck suspension for road friendliness. Veh. Syst. Dyn. 1998, 29, 766–771. [Google Scholar] [CrossRef]
- Li, Y.; Yang, X.; Shen, Y.; Liu, Y.; Wang, W. Optimal design and dynamic control of the HMDV inertial suspension based on the ground-hook positive real network. Adv. Eng. Softw. 2022, 171, 103171. [Google Scholar] [CrossRef]
- Ping, Y.; Yang, X.; Yang, Y.; Shen, Y.; Zeng, S.; Dai, S.; Hong, J. Phase–Frequency Cooperative Optimization of HMDV Dynamic Inertial Suspension System with Generalized Ground-Hook Control. Machines 2025, 13, 556. [Google Scholar] [CrossRef]
- Ahmadian, M.; Pare, C.A. A quarter-car experimental analysis of alternative semiactive control methods. J. Intell. Mater. Syst. Struct. 2000, 11, 604–612. [Google Scholar] [CrossRef]
- Ahmadian, M.; Vahdati, N. Transient dynamics of semiactive suspensions with hybrid control. J. Intell. Mater. Syst. Struct. 2006, 17, 145–153. [Google Scholar] [CrossRef]
- Liu, D.; Chen, H.; Liu, W.; Jiang, R. Evaluation of road damage based on a full heavy vehicle multi-body dynamic model. J. Vib. Shock 2010, 29, 92–96+233. [Google Scholar] [CrossRef]
- Zhang, X.J.; Ahmadian, M.; Guo, K.H. On the Benefits of Semi-Active Suspensions with Inerters. Shock Vib. 2012, 19, 257–272. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, C.; Chen, L.; Zhang, X. Phase deviation of semi-active suspension control and its compensation with inertial suspension. Acta Mech. Sin. 2024, 40, 523367. [Google Scholar] [CrossRef]
- Liu, C.; Chen, L.; Lee, H.P.; Yang, Y.; Zhang, X. Generalized skyhook-groundhook hybrid strategy and control on vehicle suspension. IEEE Trans. Veh. Technol. 2022, 72, 1689–1700. [Google Scholar] [CrossRef]
- Yang, X.; He, T.; Shen, Y.; Liu, Y.; Yan, L. Research on predictive coordinated control of ride comfort and road friendliness for heavy vehicle ISD suspension based on the hybrid-hook damping strategy. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 443–456. [Google Scholar] [CrossRef]
- Shen, Y.; Li, J.; Huang, R.; Yang, X.; Chen, J.; Chen, L.; Li, M. Vibration control of vehicle ISD suspension based on the fractional-order SH-GH stragety. Mech. Syst. Signal Process. 2025, 234, 112880. [Google Scholar] [CrossRef]
- Savaresi, S.M.; Silani, E.; Bittanti, S. Acceleration-driven-damper (ADD): An optimal control algorithm for comfort-oriented semiactive suspensions. J. Dyn. Syst. Meas. Control 2005, 127, 218–230. [Google Scholar] [CrossRef]
- Zhao, W. Research on Adaptive Control of Vehicle Inertial Suspension Based on Power Driven Damper Strategy. Master’s Thesis, Jiangsu University, Zhenjiang, China, 2020. [Google Scholar] [CrossRef]
- Yang, X.; Yan, L.; Shen, Y.; Liu, Y.; Liu, C. Optimal design and dynamic control of an ISD vehicle suspension based on an ADD positive real network. IEEE Access 2020, 8, 94294–94306. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, D.; Yang, X.; Song, H.; Shen, Y. The adverse effect and control of semi-active inertial suspension of hub motor driven vehicles. Int. J. Automot. Technol. 2024, 25, 777–788. [Google Scholar] [CrossRef]
- Morselli, R.; Zanasi, R. Control of port Hamiltonian systems by dissipative devices and its application to improve the semi-active suspension behaviour. Mechatronics 2008, 18, 364–369. [Google Scholar] [CrossRef]
- Yang, X.; Song, H.; Shen, Y.; Liu, Y.; He, T. Control of the vehicle inertial suspension based on the mixed skyhook and power-driven-damper strategy. IEEE Access 2020, 8, 217473–217482. [Google Scholar] [CrossRef]
- Shen, Y.; Jia, M.; Yang, X.; Liu, Y.; Chen, L. Vibration suppression using a mechatronic PDD-ISD-combined vehicle suspension system. Int. J. Mech. Sci. 2023, 250, 108277. [Google Scholar] [CrossRef]
- Bui, V.; Yang, X.; Shen, Y.; Zhang, T. Control of semi-active inertial suspension system for hub motor driven vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2025, 09544070251315857. Available online: https://journals.sagepub.com/doi/abs/10.1177/09544070251315857 (accessed on 20 June 2025).
- Karim Afshar, K.; Korzeniowski, R.; Konieczny, J. Evaluation of ride performance of active inerter-based vehicle suspension system with parameter uncertainties and input constraint via robust H∞ control. Energies 2023, 16, 4099. [Google Scholar] [CrossRef]
- Afshar, K.K.; Korzeniowski, R.; Konieczny, J. Constrained dynamic output-feedback robust H∞ control of active inerter-based half-car suspension system with parameter uncertainties. IEEE Access 2023, 11, 46051–46072. [Google Scholar] [CrossRef]
- Hua, J.; Shen, Y.; Chen, L.; Liu, Y.; Yang, X. Fractional-order control system for vehicle ISD suspension based on the mechatronic inerter. J. Automot. Saf. Energy 2022, 13, 63–69. [Google Scholar] [CrossRef]
- Yang, X.; Shen, Y.; Liu, C.; Zhang, T. Design and Performance Analysis of HMDV Dynamic Inertial Suspension Based on Active Disturbance Rejection Control. CMES-Comput. Model. Eng. Sci. 2024, 140, 1485–1506. [Google Scholar] [CrossRef]
- Zhao, Y.; Du, F.; Wang, H.; Wang, X.; Yang, X.; Shi, D.; Bui, V.; Zhang, T. Research on Coordinated Control of Vehicle Inertial Suspension Using the Dynamic Surface Control Theory. Actuators 2024, 13, 389. [Google Scholar] [CrossRef]
- Wang, R.; Huang, H.; Meng, X.; Wu, T.; Chen, L. Dynamic Performance Analysis of Hydraulic ISD Suspension Based on Virtual Prototype Model. J. Mech. Eng. 2015, 51, 137–142. [Google Scholar] [CrossRef]
- Wang, R.; Ye, Q.; Sun, Z.; Xie, J.; Chen, L.; Gui, Z. The Analysis and Experimental Study of Hydraulic Container of Inerter-Spring-Damper Suspension Performance. J. Vib. Meas. Diagn. 2016, 36, 366–371+406–407. [Google Scholar] [CrossRef]
- Yan, L.; Yang, X.; Shen, Y.; He, T.; Liu, Y. Ride comfort and road friendliness analysis of ISD suspension for heavy vehicles under variable vehicle mass. J. Jiangsu Univ. (Nat. Sci. Ed.) 2022, 43, 407–415. [Google Scholar] [CrossRef]
- Huang, K.; Zhao, P.; Chen, J. Study on Improvement of Performance of Hydraulically Interconnected Suspensions with the Use of Inerters. Noise Vib. Control 2022, 42, 17–22. [Google Scholar] [CrossRef]
- Seifi, A.; Hassannejad, R. Parameters uncertainty in pareto optimization of nonlinear inerter-based suspension system under nonstationary random road excitation. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 2725–2744. [Google Scholar] [CrossRef]
- Soong, M.F.; Ramli, R.; Saifizul, A.A.; Goh, K.Y.; Long, S.X. Investigation of inerter-based suspension systems for heavy vehicles. PLoS ONE 2023, 18, e0280290. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, L.; Liu, Y.; Zhang, X.; Yang, X. Improvement of the lateral stability of vehicle suspension incorporating inerter. Sci. China Technol. Sci. 2018, 61, 1244–1252. [Google Scholar] [CrossRef]
- Shen, Y.; Qiu, D.; Yang, X.; Chen, J.; Guo, Y.; Zhang, T. Vibration isolation performance analysis of a nonlinear fluid inerter-based hydro-pneumatic suspension. Int. J. Struct. Stab. Dyn. 2024, 2650079. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, X.Y.; Zhang, Y.S.; Ding, H.; Chen, L.Q. Dynamic performance and stability analysis of an active inerter-based suspension with time-delayed acceleration feedback control. Bull. Pol. Acad. Sci. Tech. Sci. 2022, 70, 140687. [Google Scholar] [CrossRef]
- Liu, C.; Chen, L.; Zhang, X.; Yang, X. Stability analysis of semi-active inerter-spring-damper suspensions based on time-delay. J. Theor. Appl. Mech. 2020, 58, 599–610. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Wang, J.; Zhang, W.; Yang, X.; Guo, X.; Liu, T.; Su, X. Synchronization of broadband energy harvesting and vibration mitigation via 1: 2 internal resonance. Int. J. Mech. Sci. 2025, 301, 110503. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, T.; Shen, Y.; Liu, Y.; Bui, V.; Qiu, D. Tradeoff analysis of the energy-harvesting vehicle suspension system employing inerter element. Energy 2024, 308, 132841. [Google Scholar] [CrossRef]
- Wang, H.; Ma, S.; Peng, Y.; Liu, C. Performance Analysis of Seat Inertial Suspension Vibration Suppression and Energy Harvesting for Electric Commercial Vehicles. World Electr. Veh. J. 2025, 16, 216. [Google Scholar] [CrossRef]
- Liu, C.; Chen, L.; Lee, H.P.; Yang, Y.; Zhang, X. A review of the inerter and inerter-based vibration isolation: Theory, devices, and applications. J. Frankl. Inst. 2022, 359, 7677–7707. [Google Scholar] [CrossRef]




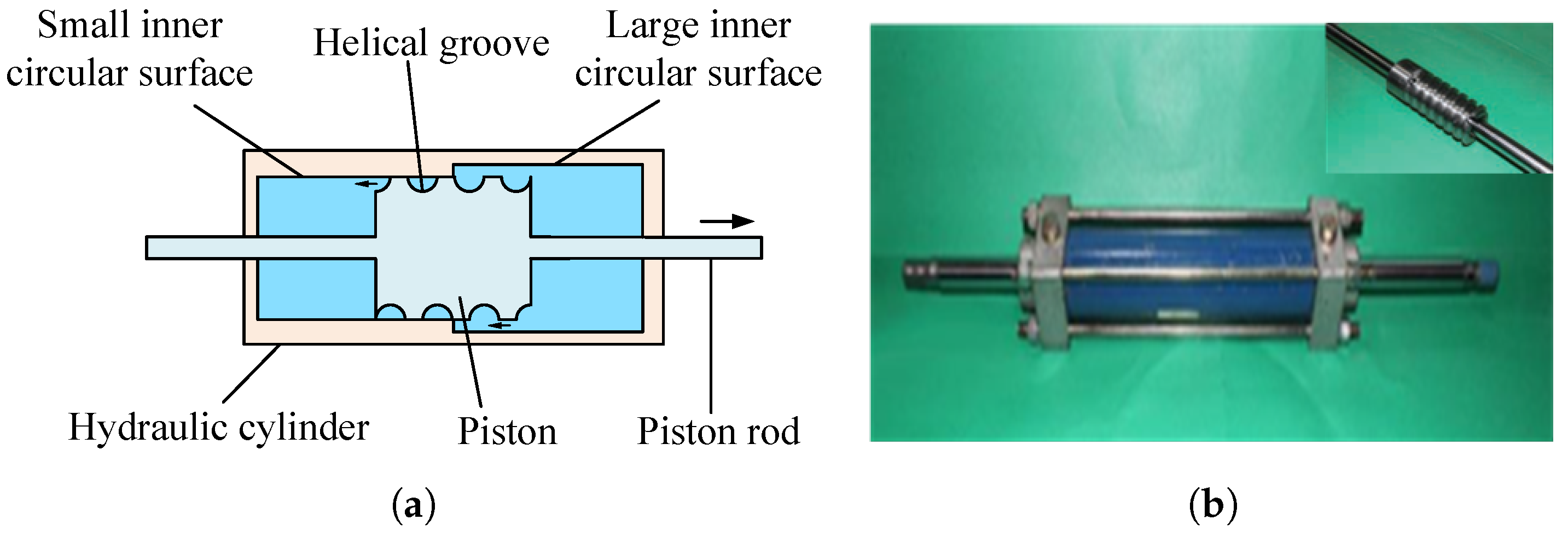
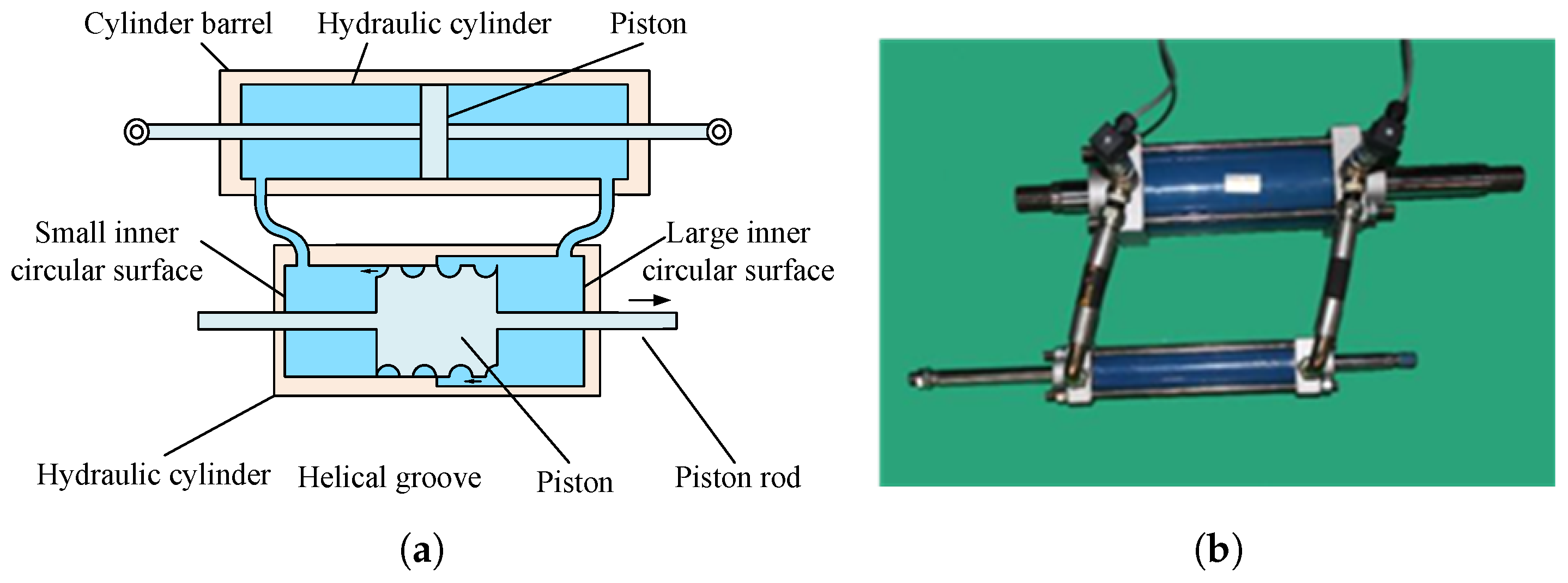
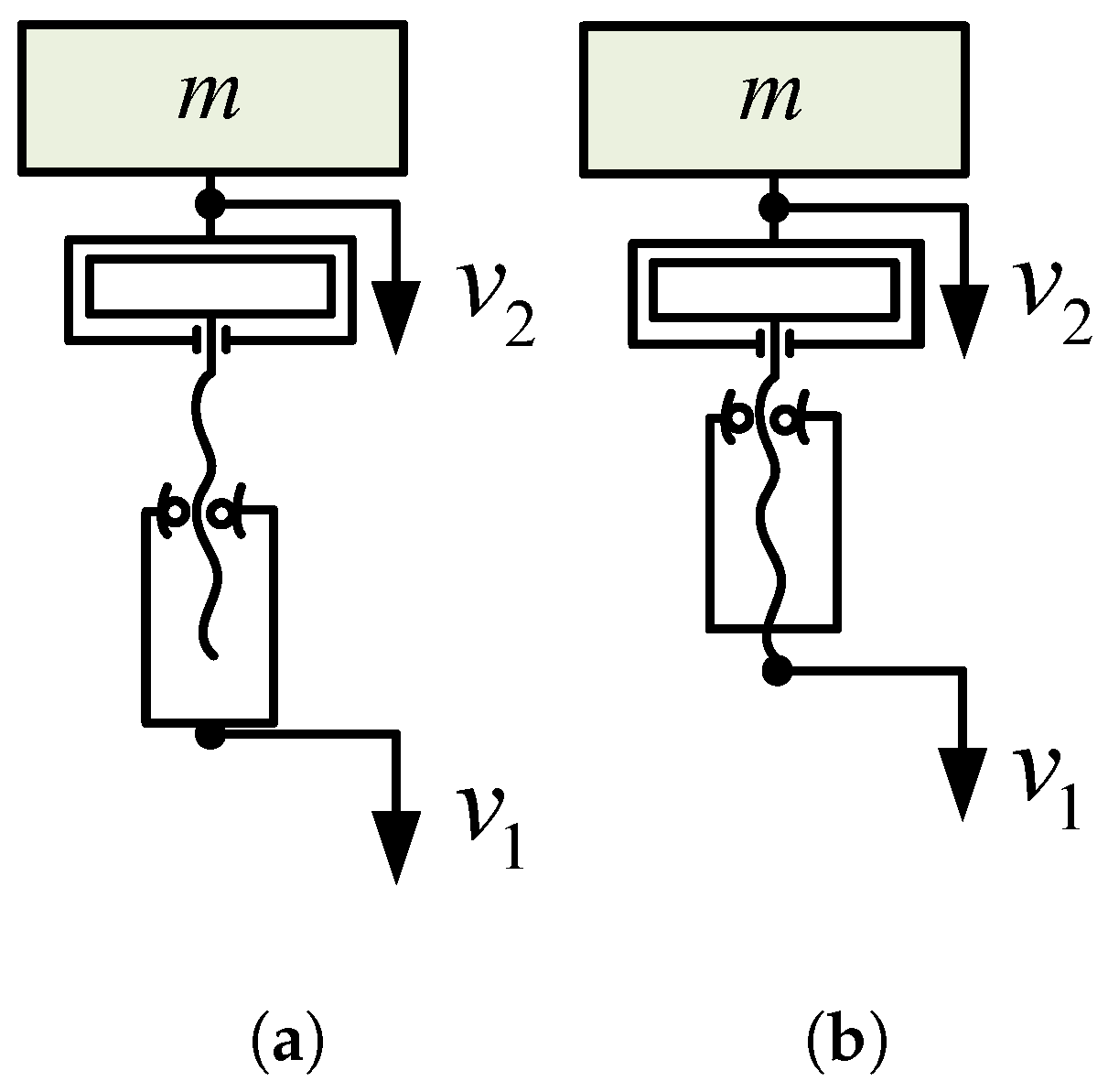
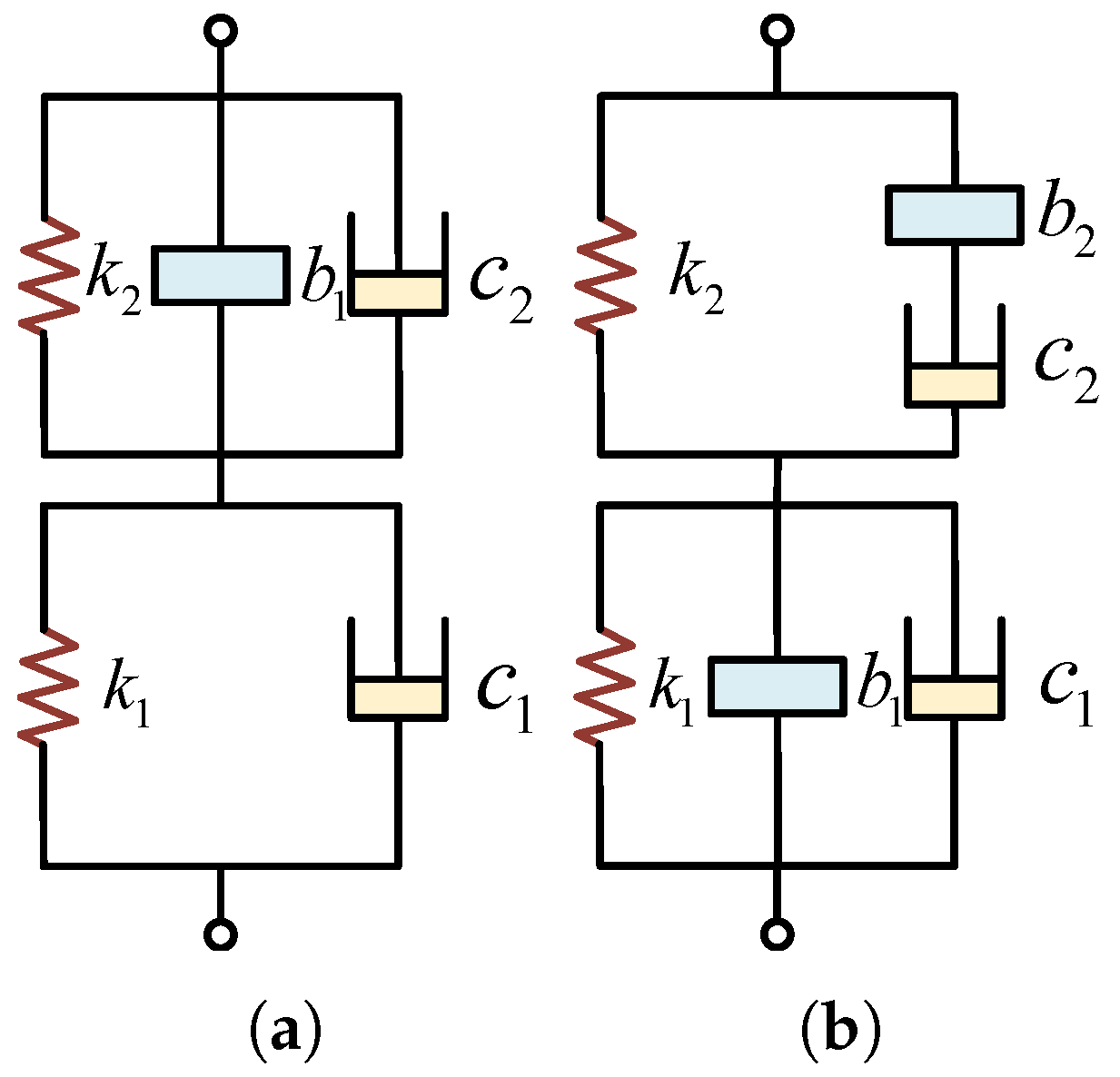





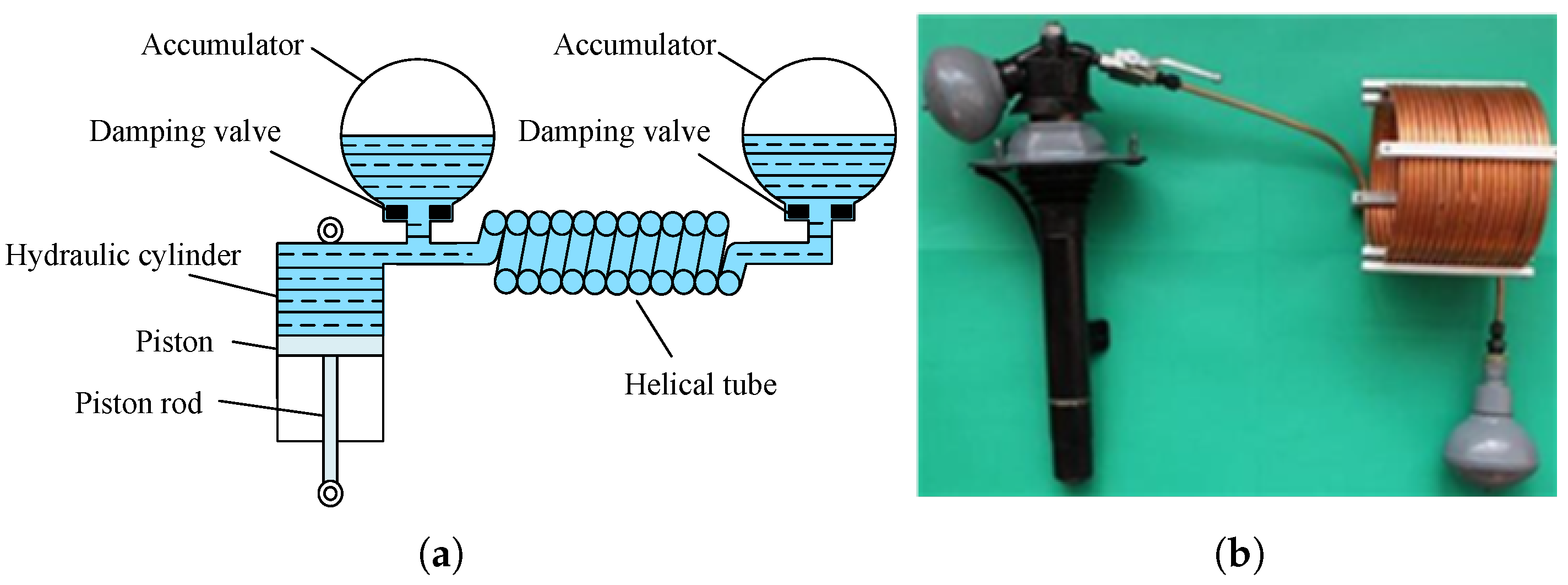
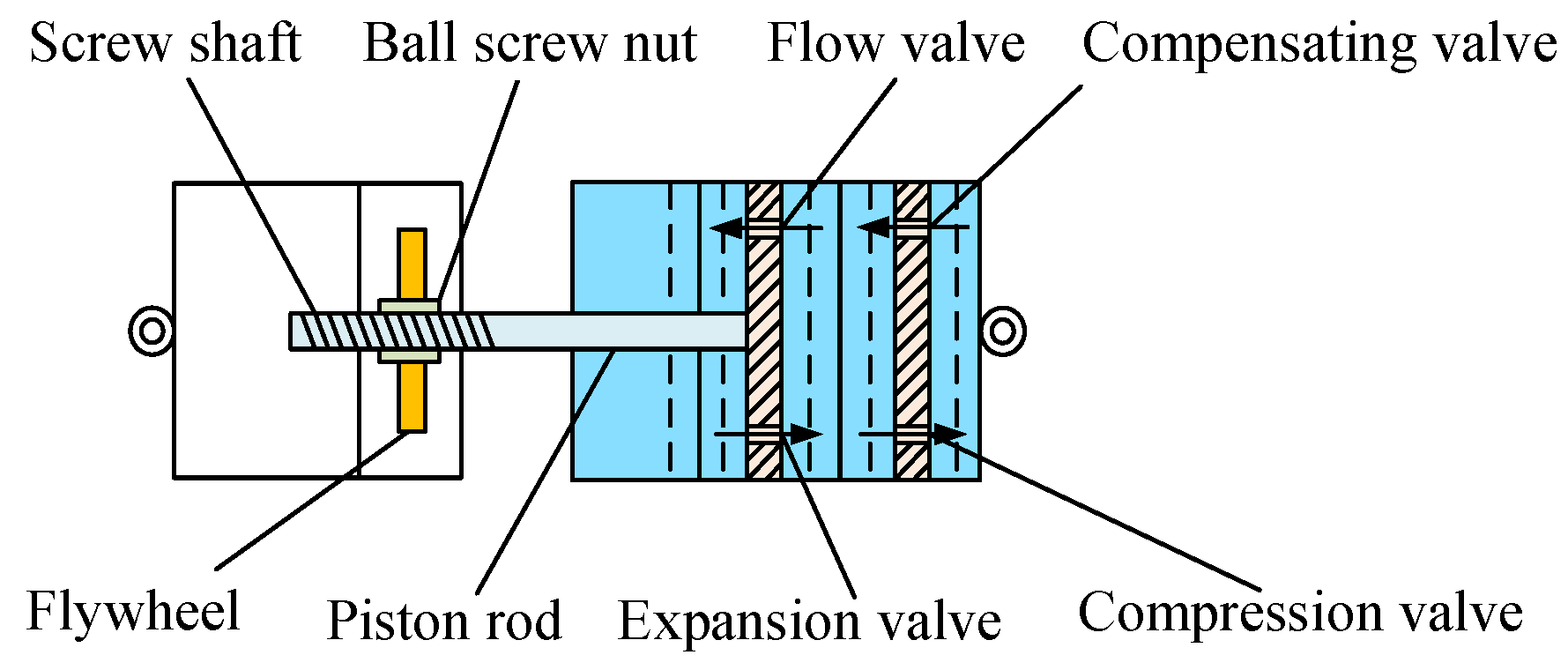
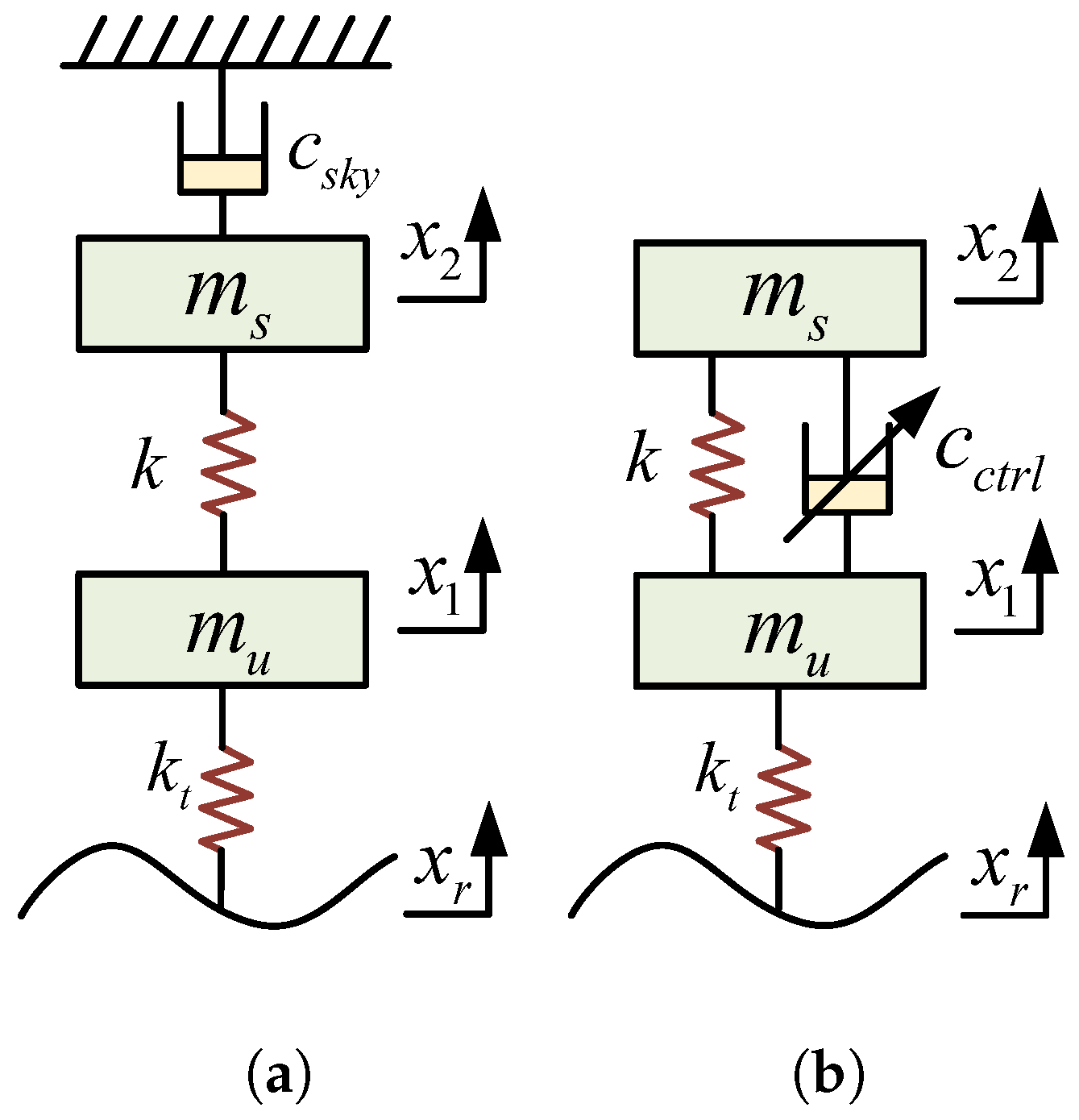


| Inerter Type | Characteristics |
|---|---|
| Rack-and-pinion inerter | • Gear backlash |
| • Moderate durability | |
| • Large inertial amplification effect | |
| Ball-screw inerter | • Moderate friction |
| • Large inertial amplification effect | |
| • Back clearance between ball and screw | |
| Ball-screw mechatronic inerter | • High adaptability |
| • Back clearance between ball and screw | |
| • Capable of realizing network structures | |
| Hydraulic motor inerter | • Simple structure |
| • High loading capacity | |
| • Strong nonlinearity and damping effect | |
| Hydraulic piston inerter | • High loading capacity |
| • Limited in dynamic response speed | |
| • Strong nonlinearity and damping effect | |
| Hydraulic electric inerter | • Complicated structure |
| • High loading capacity | |
| • Capable of realizing network structures | |
| Fluid inerter | • High loading capacity |
| • Low-friction structure | |
| • Strong nonlinearity and damping effect | |
| Memory inerter | • High adaptability |
| • High loading capacity | |
| • Exhibiting memory effect |
| Structure | Impedance Expression | Structures | Impedance Expression |
|---|---|---|---|
| Control Method | Controlled Object | Reference(s) |
|---|---|---|
| FD-SH and adaptive control | Inerter | [155] |
| Generalized SH | Damper and inerter | [156] |
| GH and adaptive control | Inerter | [158] |
| Generalized GH | Damper | [159] |
| HH | Damper | [163] |
| Generalized HH | Damper and inerter | [164,165] |
| HH and MPC | Inerter | [166] |
| FD-HH and adaptive control | Inerter | [167] |
| ADD and SMC | Inerter | [170] |
| HH and SH-PDD | Damper | [171] |
| SH-PDD | Inerter | [173] |
| PDD and FD-SMC | Inerter | [174] |
| Fuzzy control | Damper | [175] |
| Robust control | Actuator | [176,177] |
| FD-PID | Inerter | [178] |
| ADRC | Inerter | [179] |
| Dynamic surface control | Inerter | [180] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Zhang, T.; Li, Y.; Shen, Y.; Liu, Y.; Chen, C. A Review on the Application of Inerters in Vehicle Suspension Systems. Machines 2025, 13, 779. https://doi.org/10.3390/machines13090779
Yang X, Zhang T, Li Y, Shen Y, Liu Y, Chen C. A Review on the Application of Inerters in Vehicle Suspension Systems. Machines. 2025; 13(9):779. https://doi.org/10.3390/machines13090779
Chicago/Turabian StyleYang, Xiaofeng, Tianyi Zhang, Yongchao Li, Yujie Shen, Yanling Liu, and Changzhuang Chen. 2025. "A Review on the Application of Inerters in Vehicle Suspension Systems" Machines 13, no. 9: 779. https://doi.org/10.3390/machines13090779
APA StyleYang, X., Zhang, T., Li, Y., Shen, Y., Liu, Y., & Chen, C. (2025). A Review on the Application of Inerters in Vehicle Suspension Systems. Machines, 13(9), 779. https://doi.org/10.3390/machines13090779







